1. Introduction
Bankruptcy probability—or probability of default (PD)—is of interest to many participants in and observers of corporate financial markets. The purpose of this paper is to explore why bankruptcy models estimated with the use of unbalanced samples generate bankruptcy probabilities that are biased and to recommend techniques for their calibration to unbiased probabilities.
We begin with comments on how bankruptcy as a rare event is studied and predicted from samples of data on insolvencies, defaults, and going concern opinions. We believe that there is rising demand for reliable bankruptcy predictions from users of our models, including company managers, equity owners, lenders (banks), investors, and others. Therefore, there is a constant need to refine the various approaches in this area, including the use of binomial models.
Section 3 on bankruptcy prediction models and unbalanced samples turns to Edward Altman’s legacy of bankruptcy prediction modelling and the influence of his works on the modern finance profession and academia. We also introduce two types of unbalancing in bankruptcy models: (a) when the ratio of bankrupt and non-bankrupt companies in the sample is different than 50:50; and (b) when the percentages of bankrupt and non-bankrupt companies in the sample are different than those in the population. The more general unbalanced sample type (b) is elaborated later in the paper. Unbalanced samples and their treatment in the past, as well as in new research, are discussed in
Section 4.
Prior correction for the unbalanced samples in logit modelling is examined in
Section 5. It is shown that the correction quoted by
King and Zeng (
2001) has been known in microeconometrics since
Anderson (
1972) and
Maddala (
1983). The relevance of prior correction to calibrating the unbiased PD from estimated binomial models is shown in
Section 7, which is preceded by
Section 6 introducing the formula by
Skogsvik and Skogsvik (
2013). This formula represents the relationship between the biased probability of bankruptcy obtained from the model and the population-adjusted unbiased probability of bankruptcy.
Section 7 develops the equivalence of prior correction in the logit model with the Skogsvik formula, which provides additional justification to applying prior correction. Together with solutions for other binomial models, this sets out practical advice for the calibration of unbiased PDs based on biased predictions from binomial bankruptcy models.
Section 7 also discusses the question of sample bias effects on the classification of companies. However, the entire paper puts aside the classification problem and emphasizes questions of PD prediction that are the subject of growing demand from analysts and practitioners in accounting and corporate finance.
2. Bankruptcy: A Rare Event
Bankruptcy or insolvency cases can be qualified as rare among the population of active companies.
Table 1 presents the numbers of insolvencies and filings for bankruptcy in selected European countries for the years 2015–2017. Insolvencies in 2015 and 2016 represent the number of companies that were in such a state that prompted them to file for bankruptcy
1. Failures in 2017 are the numbers of companies that filed for bankruptcy in 2017. From our point of view, the most important is the percentage of failed companies within the number of active companies. It is relatively low and rarely exceeds 1 percent.
Naturally, the percentages of bankrupt and failed companies differ across countries and across industries, as well as fluctuate over time. Countries differ in terms of bankruptcy regulations and their revisions (Entrepreneurship at a Glance, Organisation for Economic Co-operation and Development,
OECD 2017) and in terms of industrial structure. Also, business cycle swings affect companies differently across countries and industries. Therefore, detailed examination of past and present trends in bankruptcies should be performed on a country level. For example, in the Netherlands most bankruptcies in 2017 were recorded in trade, financial services, business services (specialized), and construction.
Table 2 provides detailed figures for all sectors.
All in all, country statistics on bankruptcies that are available in central statistical offices and in specialized companies (e.g., Euler Hermes, Dun and Bradstreet, and Creditreform) indicate the rarity of the “bankruptcy” event. This is evidenced in the data on insolvencies, filings, and court resolutions as compared to the numbers of active companies.
Although instances of insolvency and bankruptcy are rare, the probability of bankruptcy (insolvency, default, etc.) is much talked about in contemporary accounting, corporate finance, and financial markets analysis—for obvious reasons. Bankruptcy is the state many parties would like to be forewarned of. Such parties include company management, equity owners, lenders, potential investors, and insurers. The rarity of actual events of insolvency creates questions of how to model such predictions for the entire population of companies.
3. Bankruptcy Prediction Models and Unbalanced Samples
The infrequent instances of company insolvency in large data sets of companies serve as the benchmark for assessing the probability of bankruptcy for all companies, including those outside the sample. Insolvency, bankruptcy, and default probabilities (PD—probability of default) are expected to be calculated for every firm. The modern methodology for assessing the PD began with the seminal paper by Edward Altman
2 on Z-Score in 1968 (
Altman 1968). Altman’s model uses multivariate discriminant analysis (MDA) to estimate the “score” that apprises stakeholders of a potential state of bankruptcy for the company in question.
Although a Z-Score as the outcome of multivariate discriminant analysis (MDA) is not expressed in terms of probabilities, Z-Scores may be inverted into probabilities with the use of logistic transformation. This conversion is “not strictly correct” (
Hillegeist et al. 2004, p. 16) but may serve as a technique for comparison with other methods. A major complication is that independent variables in MDA must have a normal distribution, otherwise the MDA estimator is not consistent (
Maddala 1983, p. 27). Nonetheless, if the Z-Score is taken as the argument in the logistic function, the result may be interpreted as the “default likelihood” and used as the “equity-implied probability of default” (
Altman et al. 2011).
The Altman models have been challenged by approaches directly producing probabilities of bankruptcy, such as the logit model, as well as by more advanced machine-learning methods. Direct application of the Z-Score or its variants has proved problematic in other countries, under other legal regimes (accounting principles), and in other time frames. However, indirect applications (e.g., models with the same variables estimated for a new data set) are still acceptable. Let us cite here the paper by
Altman et al. (
2017) that shows the validity of the Z-Score approach internationally with large data sets, also compared to logit models that performed similarly or better. It is also worth referencing the paper by
Barboza et al. (
2017), which compares several machine-learning methods to discriminant analysis and logistic regression in predicting bankruptcy. It turns out that the Altman Z-Score variables fare relatively well in other setups and models.
Today a large area of finance is dedicated to forecasting financial distress or bankruptcy, employing appropriate methodology. Nonetheless, it seems that the finance profession in academia still does not recognize this new methodology as staple content in core corporate finance and accounting courses. The notable exceptions are textbooks by Damodaran (
Applied Corporate Finance, 5th ed.,
Damodaran 2015) and Berk and DeMarzo (
Corporate Finance, 4th ed.,
Berk and DeMarzo 2017).
The methodology of bankruptcy modelling may be attributed to financial microeconometrics. and more recently, to advanced data analysis. Financial microeconometrics “emerges as a natural consequence of applying statistical and econometric methods to corporate finance, accounting, and other fields of finance; the applied edge of research in accounting and corporate finance is inevitably linked with the use of notions such as statistical sample, population, and the operation on sets of microdata” (
Gruszczyński 2018).
Technically, bankruptcy prediction models aim at explaining the binomial outcome variable y representing bankruptcy (insolvency) with two possible values: for bankrupt companies; and for non-bankrupt companies. Modelling involves the explanation of the y variable with the set of independent variables X (covariates). Typical goals of modelling the binary y variable are the following:
- (a)
prediction of values for given covariate values (i) within the sample and, possibly, (ii) outside the sample—serving to examine the accuracy of the classification of y by the model;
- (b)
forecast (prediction) of bankruptcy probabilities , which usually precedes (a);
- (c)
finding the best set of covariates X for (a), (b), or both;
- (d)
prediction of the change in probability associated with a unit change of a particular covariate.
A correct bankruptcy prediction model has, possibly, good classification accuracy and supplies reliable predictions of bankruptcy probabilities. As indicated above, the emphasis of this discussion is on the rarity of bankruptcy cases within the population of all companies. This means that the number of cases with is considerably smaller than cases with , and that this population’s proportion is usually not represented in research samples.
There are two types of unbalanced samples (some researchers prefer “imbalanced”) in bankruptcy prediction modelling. Let us consider the n-element sample for bankruptcy modelling that includes bankrupt companies and non-bankrupt companies.
- (a)
If the proportion of and in the sample is different than 50:50, then the sample is considered unbalanced.
- (b)
If the proportions and are different than the fractions of bankrupt and non-bankrupt companies in the population, then the sample is considered unbalanced in terms of and
The sample that is balanced in terms of definition (a) requires undersampling of healthy (survival) firms. This occurs because populations of companies are large—e.g., there are more than 4 million companies in Poland (see
Table 1). It is, therefore, not feasible to sample healthy firms in the same manner as bankrupt ones. The “50:50 samples” appear in the studies that use matching techniques
3—each bankrupt company is matched to a healthy company that is “similar” in terms of size, industry, etc. Such a sample is considered unbalanced from the point of view of definition (b).
Type (b) imbalance, as the more general situation, is the subject of further examination in this paper. In both cases, however, the question is whether the observation enters the sample randomly or not. If not, we have the problem of sampling bias, which is common in bankruptcy prediction models.
4. Sampling Bias, Weighting, Resampling
Since the paper by
Zmijewski (
1984), the question of unbalanced samples has been examined from many angles but is still far from being resolved (see also
Platt and Platt 2002;
Chen et al. 2006). Non-random samples in bankruptcy models are the source of two types of biases:
- -
Choice-based sample bias results when the probability of a company entering a sample depends on the dependent variable attributes (e.g., data on bankrupt companies is collected and then healthy companies are selected using a matching scheme);
- -
Sample selection bias results when only observations with complete data enter the sample.
Zmijewski (
1984) has shown in several simulations with the probit model that choice-based sample bias declines if the ratio of bankrupt and non-bankrupt companies in the sample approaches that in the population. Also, neither bias appears to affect statistical inferences or overall classification rates. However, they were shown to have an impact on the estimates for single observations (e.g., on the estimates of the probability of the bankruptcy of a particular company).
Unbalanced samples are also sometimes handled with appropriate weights for observations in bankruptcy modelling. In their exercise of comparing models internationally,
Altman et al. (
2017) used weights of single units both for unequal numbers of bankrupt and non-bankrupt data and for unequal numbers of observations across countries. In a footnote, the authors state: “Although the score (logit) in principle has a probability interpretation, the ‘probabilities’ estimated using this weighting scheme in this study do not, however, represent empirical PDs (
sic). It would still require calibration procedures for the models to obtain PDs that correspond to associated empirical PDs in the population. But this is not attempted in the study, as our focus is more general (the classification accuracies of the models across countries). It is also worth noting that the original Z-Score does not have a PD interpretation either”.
Weighting is a technique not often utilized in “classical” bankruptcy studies worldwide, despite the known results generated, for example, for the binomial logit (
Manski and Lerman 1977). In the case of logit models, the use of appropriate weights may be as effective as the application of simple correction that is discussed in the next section (see also
Maalouf et al. 2018). On the other hand, as stated by
Long and Freese (
2014), “The use of weights is a complex topic, and it is easy to apply weights incorrectly”. For the logit model, the choice of weights is not straightforward.
The new generation of bankruptcy studies that has emerged with the use of machine learning techniques also propose new solutions for handling unbalanced samples.
Zhou (
2013) describes the use of oversampling and undersampling algorithms applied to 1981–2009 data on US bankruptcies and to 1989–2009 data on Japanese bankruptcies. Oversampling means sampling “the minority class over and over to achieve the balanced distribution of the two classes”. Undersampling means “to select a portion of the majority class to achieve the distribution balance of the two classes” (
Zhou 2013). The sampling techniques are: for oversampling, ROWR (random oversampling with replication) and SMOTE (synthetic minority oversampling technique); and for undersampling, RU (random undersampling), UBOCFNN (undersampling based on clustering from the nearest neighbor), and UBOCFMGD (undersampling based on clustering from a Gaussian mixture distribution). These techniques may generate samples with a 50:50 composition of bankrupt and healthy companies and then may be used to verify various bankruptcy prediction models. What is important is that the major goal in studies using such techniques lies in finding the model that performs best in terms of classification accuracy. Other examples of such an approach are
Choi et al. (
2018) and
Wagenmans (
2017).
How does the unbalanced sampling in bankruptcy models interfere with bankruptcy probabilities? To answer this question, we will concentrate on the binomial logit model.
5. Prior Correction in the Logit Model
Let us consider the binomial logit model of bankruptcy and the consequences of unbalanced samples for prediction of bankruptcy probability. One method for overcoming the effects of unbalancing is weighting, as explained in the previous section. We advocate the use of a simple correction, sometimes called “prior correction” (
King and Zeng 2001) or the “Anderson-Maddala correction” (
Gruszczyński 2017).
King and Zeng (
2001) state that although econometricians attribute the correction to
Manski and Lerman (
1977), in fact, the correction has been well known since 1975 (
Bishop et al. [1975] 2007). We challenge this finding by noting that the paper by
Anderson (
1972) first introduced this result, which was later restated by
Maddala (
1983,
1991).
Prior correction allows the analyst to convert the binomial logit model estimated based on an unbalanced sample to the model for the population. The condition is that the “fraction of ones” (i.e., bankrupt companies) in the population is known. As before,
means a bankrupt company, and
, a non-bankrupt one. The subject of the modelling is the probability
. Let us assume that the fraction of ones in the population is equal to
King and Zeng (
2001) state that knowledge of
“can come from census data, a random sample from the population measuring
y only”. In the case of bankruptcy modelling, the fraction may be established from official data on bankruptcies and companies for a particular country, region, time period, etc. Assume that
, where
is the number of bankrupt companies in the population and
is the population size (with the number of non-bankrupt companies equal to
).
Now, consider the n-size sample for bankruptcy modelling that includes bankrupt companies and non-bankrupt companies. The fraction of ones in the sample is The proportion of bankrupt companies selected for the sample is and the analogous proportion of non-bankrupt companies is
Consider also the following binomial logit model with
k covariates
X and
k + 1 parameters
:
where
Logit model (1) can be written as:
The maximum likelihood estimation of (2) in the n-element sample gives the estimate of intercept that needs to be corrected—if estimated (2) is to represent the population (not only the sample).
The correction, known as “prior correction” or the “Anderson-Maddala correction”, amounts to subtracting the estimate of
by:
or
Corrections (3) and (4) are equal, which can be shown using the definitions of
, and
. For the randomly selected sample, we have
and
and the prior correction is equal to zero. Thus, the non-random samples inherently imply the need to correct the model in order to have it represent the population. However, if the population is not precisely known, the fractions
, and
can only be estimates or calibrations. Then, the correction (3) or (4) should be applied carefully and with a relevant comment. In any case, we apply the correction when we make inferences in the context of the entire population and not the sample itself. Later, we use the correction
from (4). The considerations that follow in this section are a major extension of the paper
Gruszczyński (
2017).
We give a simple explanatory example based on
Gruszczyński (
2012). Let us consider a population of 100,000 companies, of which 60 are bankrupt and 99,940 are non-bankrupt. Typically, all bankrupt companies (i.e., 60) are selected for the sample. Then, from the 99,940 non-bankrupt companies, 60 companies are selected (e.g., at random). As a result, we have a sample of 120 companies with 50 percent of the companies from each group. After running the model based on the sample, we can calculate the estimates (theoretical values) of bankruptcy probabilities for companies in the sample of 120 companies. These are estimates with a sample selection bias. The unbiased estimates are obtained when we consider the entire population from which we did the sampling.
For calculating correction we find that (considering all bankrupt companies) and . The model for all 100,000 companies is obtained from the model estimated for the sample by reducing the intercept in (2) by the value of ; that is, by ln(1)–ln(60/99,940), or 7.417981.
To sum up, a model estimated on a sample not representing the population’s proportion of bankrupt companies gives estimates of bankruptcy probability, which are biased with regard to the entire population. Unbiased probabilities of bankruptcy can be obtained after adjusting the model.
Note that this discussion leaves aside the question of classification and classification accuracy. We concentrate here on estimating the PD, the probability of bankruptcy and insolvency, especially when the model is used for companies outside the sample.
6. Predicting Bankruptcy Probabilities from Non-Random Samples
Prior correction in the form of (3) or (4) coincides with the findings by
Skogsvik and Skogsvik (
2013). They also emphasize that the bankruptcy probabilities obtained from the bankruptcy prediction models depend on the proportion of bankrupt companies in the sample, and they are, therefore, biased (if the proportion of bankrupt companies in the sample is not the same as in the population). According to the authors’ findings, there is an algebraic relationship between the biased bankruptcy probability of a given company (from the sample-based model), and the unbiased probability, which results from the proportion of bankrupts in the population. This proportion of bankrupts in the population (denoted by
π) is treated as the a priori probability of bankruptcy. The probability of bankruptcy of a single company calculated from the model (sample-based) denoted by the Skogsviks as
is, therefore, biased. It is the function of:
- ▪
unbiased probability ;
- ▪
proportion (prop) of bankrupt companies in the sample;
- ▪
proportion π of bankrupt companies in the population.
It follows that if prop > π, then , and vice versa. This means that in the typical situation of bankruptcy modelling (i.e., when prop > π), the PD for a given company calculated from the model is higher than the “population-adjusted” PD for the same company. This leaves the question of how much higher? The authors give the example with , as in matched-pairs modelling and . If the unbiased probabilities are , they correspond to the (biased) predictions from the model , respectively. Thus, the model-predicted probabilities are considerably higher than the unbiased probabilities. It should be noted that Equation (5) has been derived assuming random sampling from the population of bankrupt companies, as well as (separately) from the population of non-bankrupt companies.
Factor
in Equation (5) can also be written in terms of
and
from Equations (3) and (4) as:
and
The factor is equal to 1 when proportions in the sample are the same as in the population (i.e., for a randomly selected sample). In such a case, the probabilities
and
are equal, so the model produces unbiased estimates of bankruptcy probability. Obviously, this result has little practical value, since random samples from the population in the case of bankruptcy studies are not feasible. To simplify, in further formulas we use
and
, where Equation (5) now has the form of:
The Skogsviks’ equation seems to be important for calculating a specific unbiased probability
for a company, needed in financial risk management and in the valuation of a company’s equity or its bonds. From Equation (6) it follows that the adjustment of the unbiased PD is equal to:
This result allows the analyst to translate the model’s predicted PD for a single company into the PD “calibrated for the fraction of failure companies in the population”.
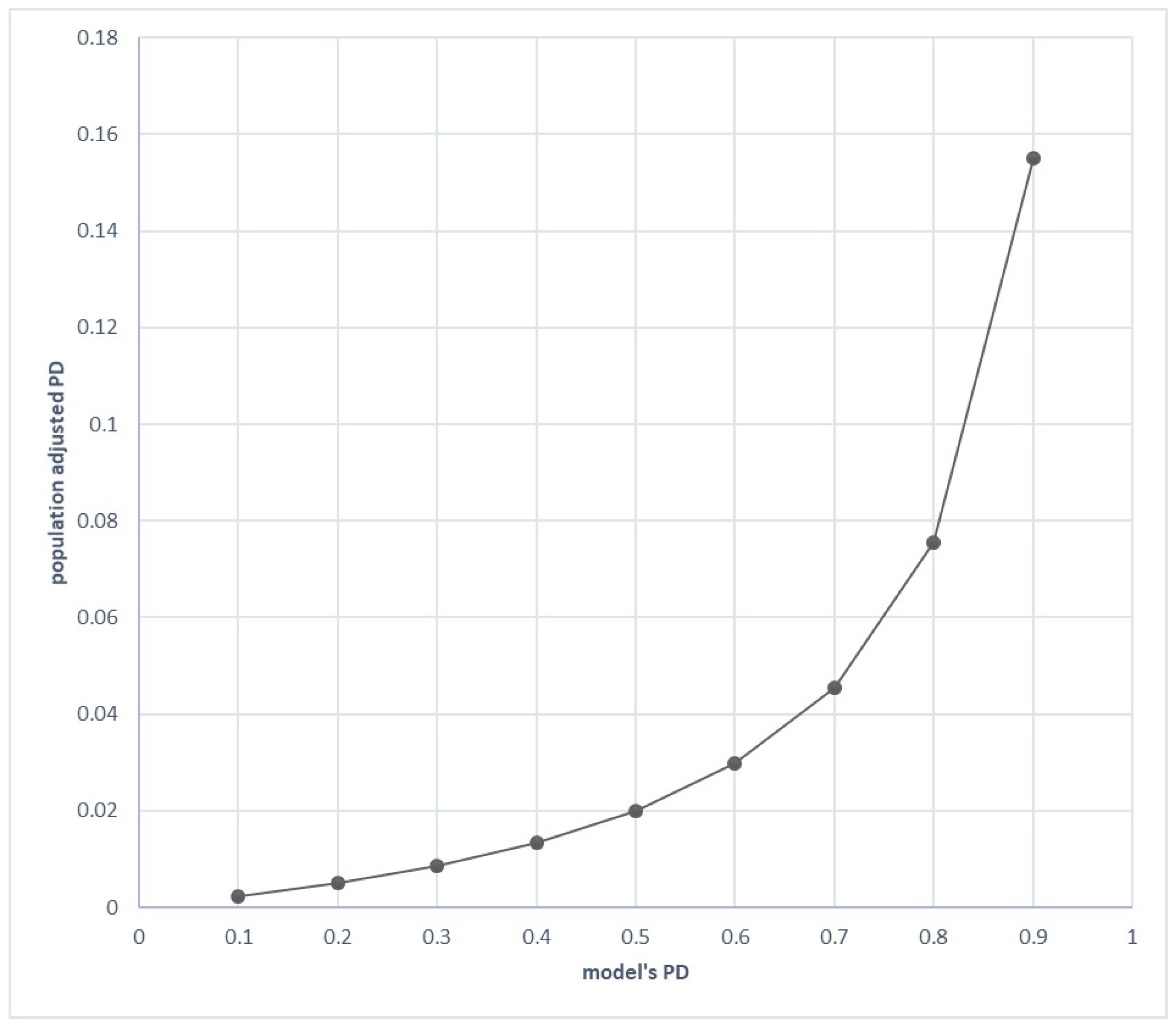
Figure 1 shows how the model PD is related to the population PD for
and
(i.e., for
. This is roughly a “real” case, with 2% solvencies annually and with the “balanced” sample composed of 50% bankrupts and 50% non-bankrupts.
The adjustment of the probability of bankruptcy (default) is only possible when the number representing
(i.e., the fraction of bankruptcies in a recognised population of companies for a given year) is known or may be feasibly approximated. In the case shown in
Figure 1, the bankruptcy probability estimated from the model as 0.7 corresponds to the “population adjusted” probability of 0.045. This exaggeration of unbiased PDs that is inherent in bankruptcy models should be considered in practical uses.
7. Prior Correction: Formulae for Binomial Models and Classification Issues
The transformation of biased into unbiased probabilities can be further specified for various binomial models. We return to prior corrections (3) and (4) for the logit model (2):
The correction
of constant term
estimate defined in (4) can be shown to coincide with the Skogsviks’ equation. From (6) we have:
and
or
and
where
is defined in (4). Therefore, the logit for the biased bankruptcy probability
(i.e., what we receive from the estimated logit model) must be reduced by the value of
in order to obtain the logit of unbiased bankruptcy probability
. The reduction is contained in the constant term.
For example, an estimated logit model with seven explanatory variables is as follows
5:
Equation (10) has been estimated for 40 bankrupt and 40 non-bankrupt companies. It means that the proportion of bankrupt companies in the sample is . For the values of explanatory variables corresponding to one specified case (firm), the probability of bankruptcy resulting from this model is .
Now, let us assume that the proportion of bankrupt companies in the population is
. Therefore, the ratio from Equation (4) is
(as in the
Figure 1 example). In order to calculate the population adjusted (unbiased) probability from Equation (10), the intercept should be reduced by:
The new intercept is now equal to −3.10. The probability of bankruptcy obtained from Equation (10) with the new intercept is exactly equal to the probability calculated from Equation (5) or Equation (6). In this case .
The Skogsviks’ Equation (5) applies to the outcomes of all binomial models. For example, in the linear probability model (LPM) the probability
of bankruptcy is equal to the estimate of the dependent variable for a specific company. From Equation (7), the unbiased
is calculated, provided that the proportions of
p1 and
p2 are known. In the probit model, the estimate of bankruptcy probability can also be calculated and inserted into Equation (7) as
. It should be noted that only in the case of the binomial logit model does there exist a simple correction for the estimated model that coincides with the Skogsviks’ formula.
King and Zeng (
2001) point out that in the case of other binomial models like probit the only possibility is the use of a Skogsviks-like equation.
None of the foregoing considerations refer to the question of classification accuracy (classification of companies by the model). Since the rankings of the companies in terms of probabilities
and
are identical (
Skogsvik and Skogsvik 2013), the classifications of companies within the sample (into two groups, bankrupt and non-bankrupt) based on biased and unbiased predictions are the same, assuming the appropriate choice of the cut-off point.
The cut-off point
is the limit of probability for classification: if the estimated probability is less than
, the company is classified as non-bankrupt; if not, it is classified as bankrupt. The default cut-off point in programs for estimating binomial models such as Stata is
. We advocate the use of Cramer’s rule (
Cramer 1999;
Śmigielski et al. 2010), according to which the cut-off points
are:
- -
for the biased predictions from the bankruptcy model,
- -
for the unbiased predictions from (7), .
Cramer’s rule is based on the notion that the typical cut-off point of 0.5 applied for unbalanced samples does not allow one to reasonably predict less frequent cases.
Cramer (
1999) states: “(The) choice of 0.5 is usually defended by the argument that it is optimal if the predicted
determine a course of action and if moreover the cost of misclassification is the same for either form that this may take. But if the cut-off point is optimal for the use of predictions in actual decisions it need not also be optimal for assessing the within-sample performance of the fitted model”.
Cramer (
1999) proposes using a cut-off point
equal to the proportion of ones in the sample because it yields predictions that are optimal in the sense that they maximize the “index of performance” for each observation
6. In effect, the success rate for the unbalanced samples is better spread over the two alternatives,
and
.
As has been noted in
Section 3, models of multivariate discriminant analysis are not directly used to estimate bankruptcy probabilities. However, the MDA estimation results can be corrected by considering the population’s proportion of bankrupt and non-bankrupt companies (
Zmijewski 1984;
Altman and Eisenbeis 1978).
The classification performance of traditional MDA and binomial models is challenged by new methods of data analysis, sometimes called “classifiers,” applied to bankruptcy data. In
Section 3 above, we mentioned the paper by
Barboza et al. (
2017) that compares several machine-learning methods to discriminant analysis and logistic regression in predicting bankruptcy. The paper by
Jones et al. (
2017) examines “classic classifiers”, such as the logit and MDA, against neural networks, support vector machines, and statistical learning techniques, such as generalized boosting, AdaBoost, and random trees. However, the authors have not commented on the issues of sample selection bias, unlike in the papers cited in
Section 4, in which machine-learning techniques are employed for resampling.
8. Conclusions
Bankruptcy models are typically estimated from non-random samples with the proportion of bankrupt companies differing from that in the population. This causes bias in the estimated bankruptcy probabilities for individual companies. The motivation of this survey-type paper was to explore how this bias may be assessed with the use of the estimation results in typical binomial bankruptcy models. Accurate, or at least calibrated, estimates of the probability of bankruptcy are required in risk assessment, discounted cash flow modelling, and for management and other parties interested in the financial fate of a company. Therefore, it is essential to properly (i.e., unbiasedly) evaluate such probabilities.
The paper introduces two types of unbalancing in the samples for bankruptcy prediction. We concentrate on samples with fractions of bankrupt and non-bankrupt companies differing from those in the population. We show the development of the
Skogsvik and Skogsvik (
2013) formula of the relationship between biased and unbiased estimated probabilities of bankruptcy. Skogsviks’ formula coincides with prior correction (
King and Zeng 2001;
Anderson 1972;
Maddala 1983) for the logit model. Similar solutions for other binomial models are also advocated for use in the calibration of unbiased PDs.
We believe this paper may be of help to researchers and analysts in corporate finance, as well as for company managers, investors, lenders, and auditors. Most issues discussed in this paper are often neglected in the application of bankruptcy models.