Municipal Bond Pricing: A Data Driven Method
Abstract
1. Introduction
1.1. Motivation and Scope
1.2. Method Overview
1.3. Contributions
- A data driven curve fitting procedure that handles a wide variety of yield curve shapes.
- A novel transfer learning method to address insufficient trade information.
- A Bayesian model averaging approach to account for model uncertainty.
- An inference mechanism that can scale well to large datasets.
- Empirical evaluations on real-world municipal bonds data.
2. Related Work
3. Model
3.1. Curve Fitting
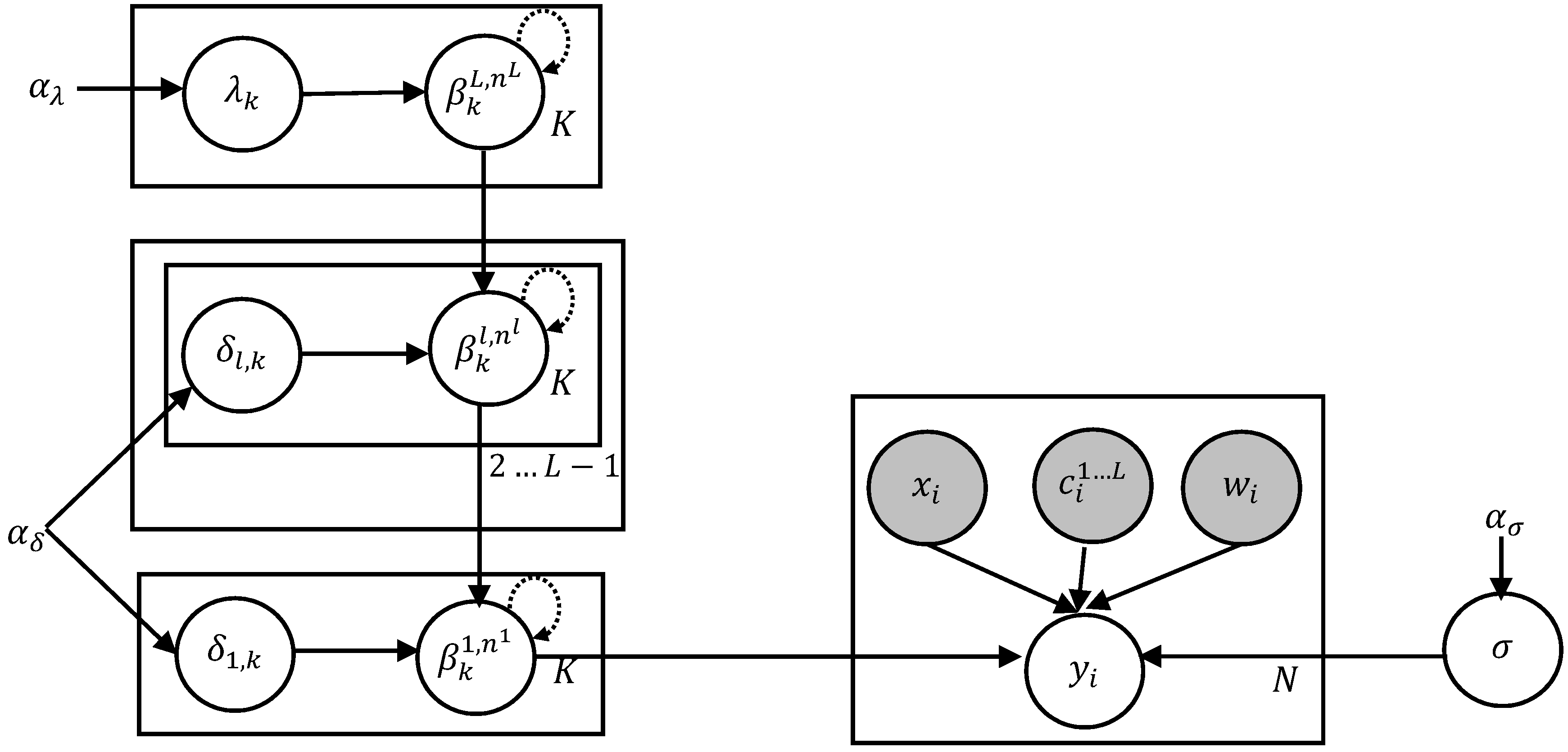
3.2. Hierarchical Model
3.3. Bayesian Extension
4. Inference
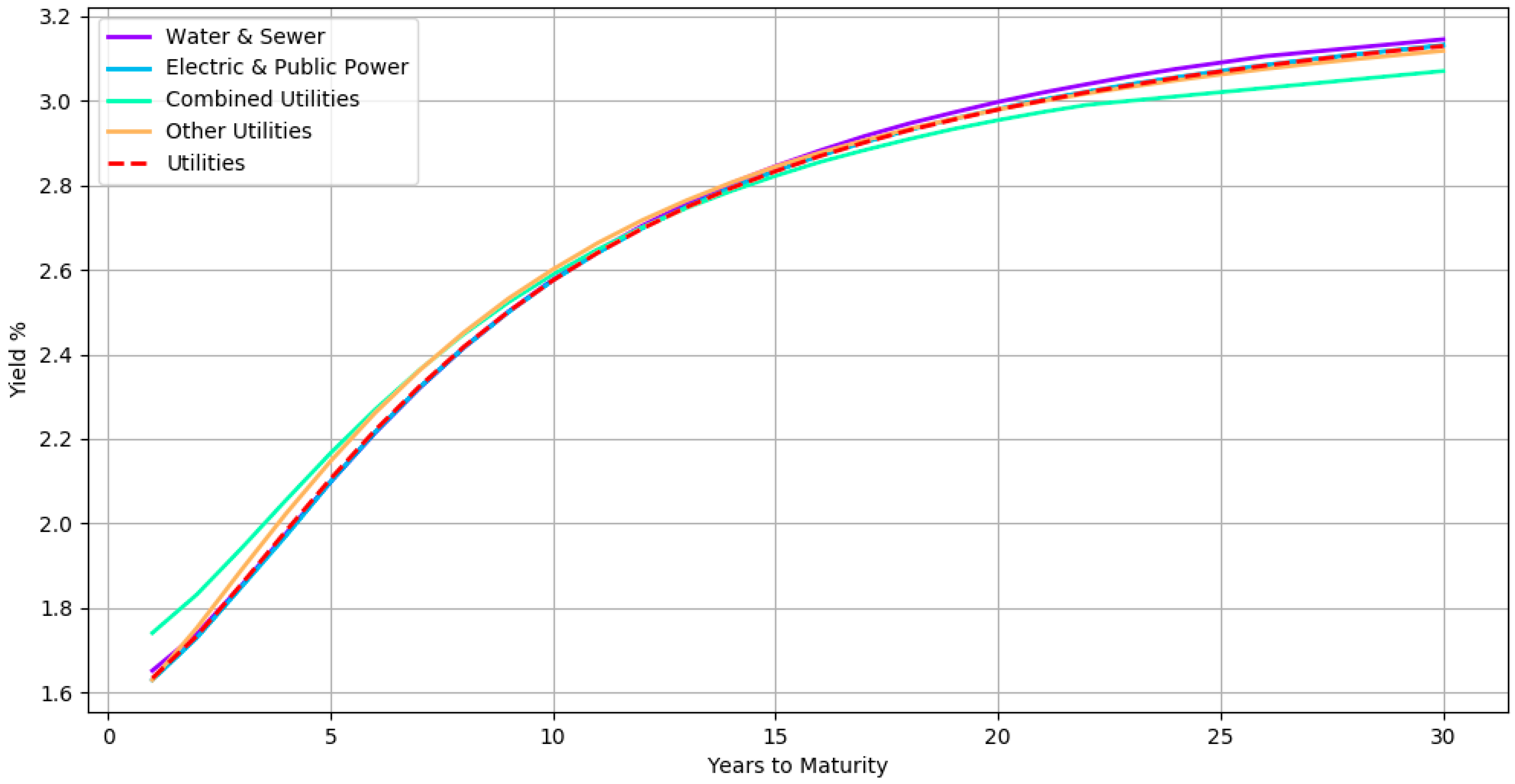
5. Application
5.1. Data Preprocessing and Priors Setting
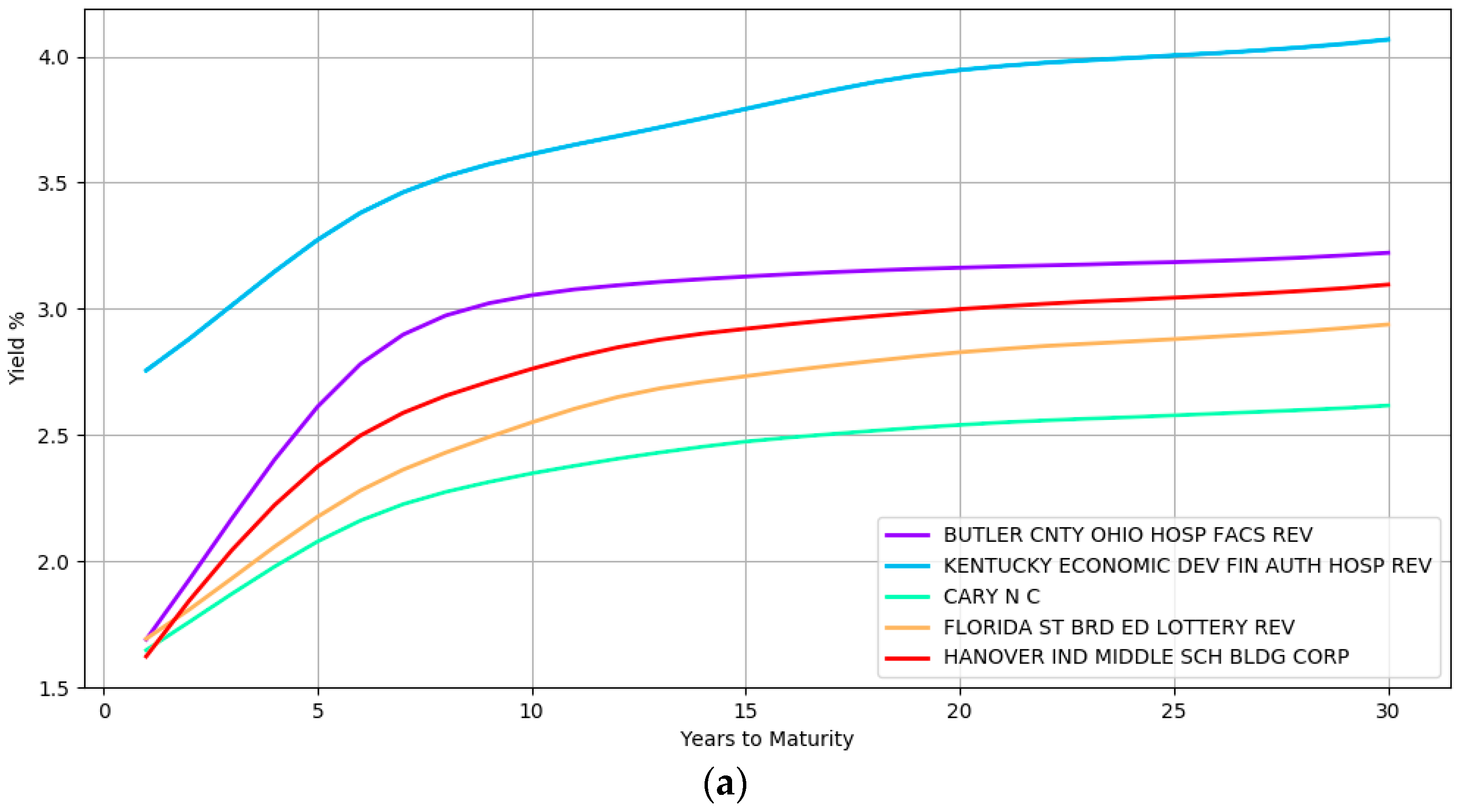
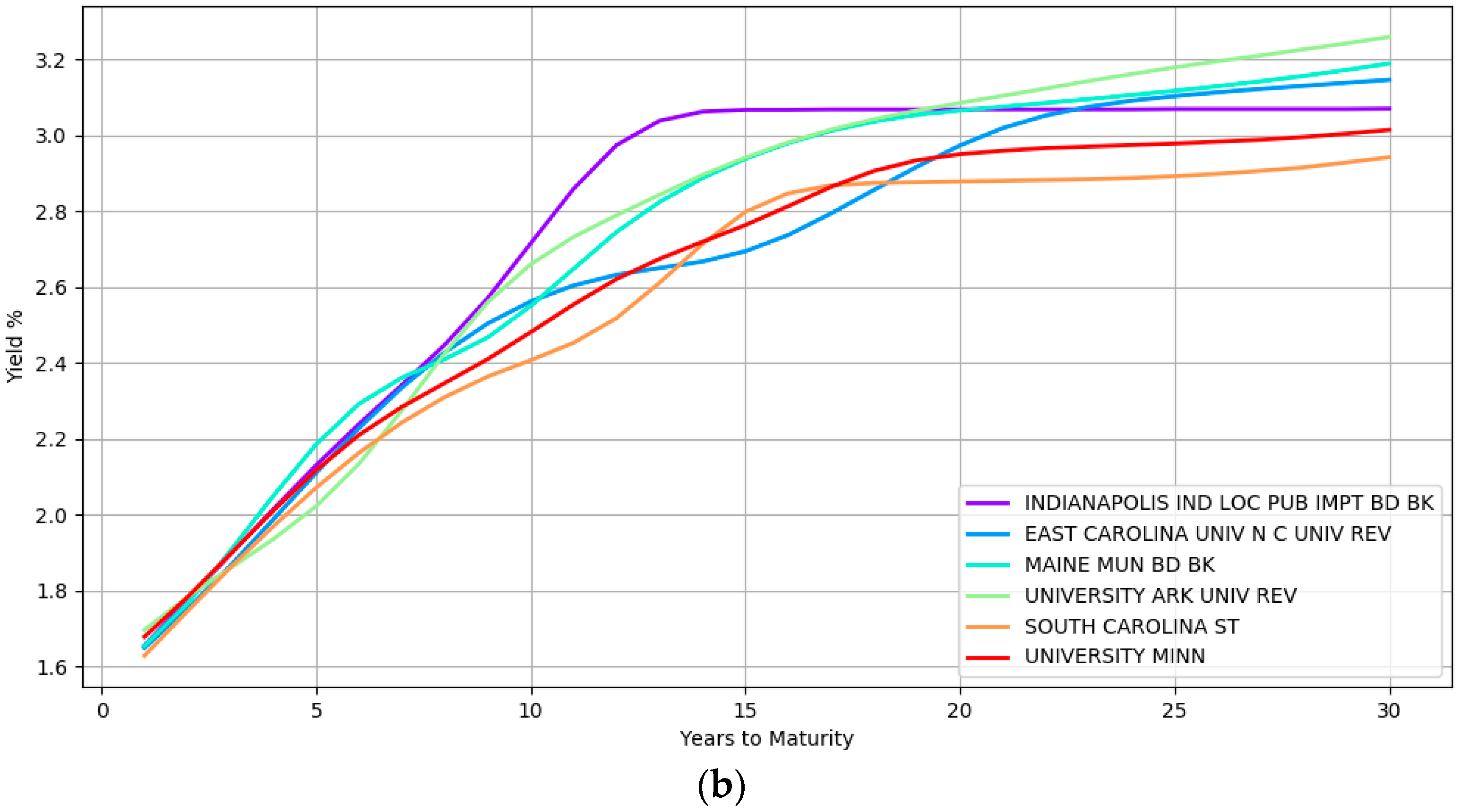
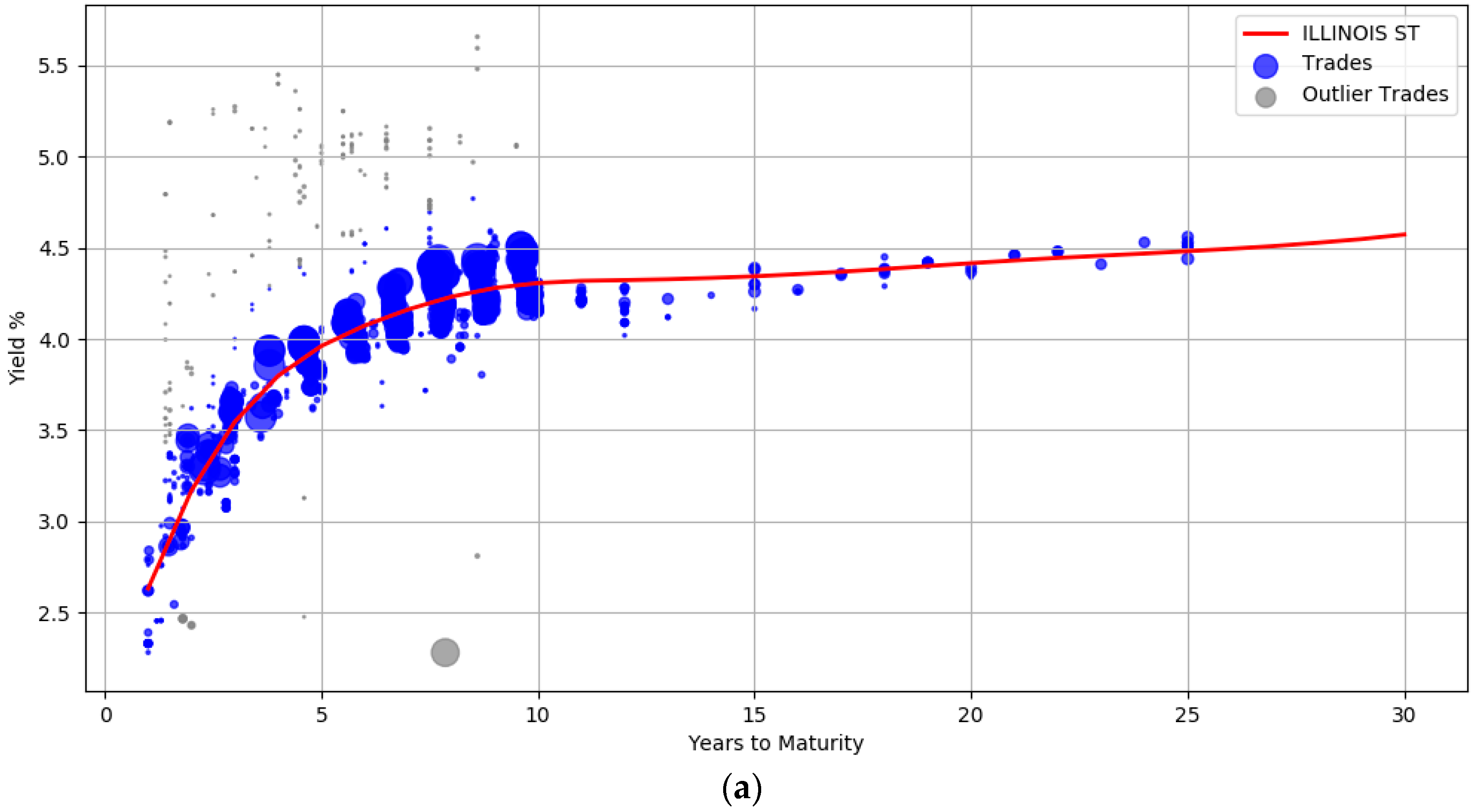
5.2. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andreasen, Martin M., Jens H. E. Christensen, and Glenn D. Rudebusch. 2017. Term Structure Analysis with Big Data. Federal Reserve Bank of San Francisco. [Google Scholar] [CrossRef]
- Baladandayuthapani, Veerabhadran, Bani K. Mallick, and Raymond J. Carroll. 2005. Spatially adaptive Bayesian penalized regression splines (P-splines). Journal of Computational and Graphical Statistics 14: 378–94. [Google Scholar] [CrossRef]
- Betancourt, Michael. 2017. A conceptual introduction to Hamiltonian Monte Carlo. arXiv preprint. arXiv:1701.02434. [Google Scholar]
- Bhojraj, Sanjeev, Charles M. C. Lee, and Derek K. Oler. 2003. What’s my line? A comparison of industry classification schemes for capital market research. Journal of Accounting Research 41: 745–74. [Google Scholar] [CrossRef]
- Boor, Carl D. 2001. A Practical Guide to Splines. New York: Springer. [Google Scholar]
- Brezger, Andreas, and Winfried J. Steiner. 2008. Monotonic Regression Based on Bayesian P–Splines: An Application to Estimating Price Response Functions from Store-Level Scanner Data. Journal of Business & Economic Statistics 26: 90–104. [Google Scholar]
- Chun, Albert L., Ethan Namvar, Xiaoxia Ye, and Fan Yu. 2018. Modeling Municipal Yields with (and without) Bond Insurance. Management Science. [Google Scholar] [CrossRef]
- Cruz-Marcelo, Alejandro, Katherine B. Ensor, and Gary L. Rosner. 2011. Estimating the term structure with a semiparametric Bayesian hierarchical model: An application to corporate bonds. Journal of the American Statistical Association 106: 387–95. [Google Scholar] [CrossRef] [PubMed]
- Dash, Gordon H., Nina Kajiji, and Domenic Vonella. 2017. The role of supervised learning in the decision process to fair trade US municipal debt. EURO Journal on Decision Processes. [Google Scholar] [CrossRef]
- Denison, D. G. T., B. K. Mallick, and A. F. M. Smith. 1998. Automatic Bayesian curve fitting. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 60: 333–50. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Gelman, Andrew, and Jennifer Hill. 2006. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge: Cambridge University Press. [Google Scholar]
- Hattori, Takahiro, and Hiroki Miyake. 2016. The Japan Municipal Bond Yield Curve: 2002 to the Present. International Journal of Economics and Finance 8: 118. [Google Scholar] [CrossRef]
- Hoffman, Matthew D., and Andrew Gelman. 2014. The No-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. Journal of Machine Learning Research 15: 1593–623. [Google Scholar]
- Lorenčič, Eva. 2016. Testing the Performance of Cubic Splines and Nelson–Siegel Model for Estimating the Zero-coupon Yield Curve. Naše Gospodarstvo/Our Economy 62: 42–50. [Google Scholar] [CrossRef]
- Marlowe, Justin. 2015. Municipal Bonds and Infrastructure Development–Past, Present, and Future. International City/County Management Association and Government Finance Officers Association. Available online: https://www.cbd.int/financial/2017docs/usa-municipalbonds2015.pdf (accessed on 1 August 2018).
- Neal, Radford M. 2011. MCMC using Hamiltonian dynamics. In Handbook of Markov Chain Monte Carlo. Boca Raton: CRC Press. [Google Scholar]
- Neelon, Brian, and David B. Dunson. 2004. Bayesian isotonic regression and trend analysis. Biometrics 60: 398–406. [Google Scholar] [CrossRef] [PubMed]
- Nelson, Charles R., and Andrew F. Siegel. 1987. Parsimonious Modeling of Yield Curves. The Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Polson, Nicholas G., and James G. Scott. 2012. On the half-Cauchy prior for a global scale parameter. Bayesian Analysis 7: 887–902. [Google Scholar] [CrossRef]
- Pooter, Michiel D. 2007. Examining the Nelson–Siegel Class of Term Structure Models (No. 07-043/4). Tinbergen Institute Discussion Paper. Available online: https://repub.eur.nl/pub/10219/20070434.pdf (accessed on 1 August 2018).
- Sherrill, D. E., and Rustin T. Yerkes. 2018. Municipal Disclosure Timeliness and the Cost of Debt. Financial Review 53: 51–86. [Google Scholar] [CrossRef]
- Steeley, James M. 1991. Estimating the Gilt-edged Term Structure: Basis Splines and Confidence intervals. Journal of Business Finance & Accounting 18: 513–29. [Google Scholar]
- Svensson, Lars E. 1995. Estimating Forward Interest Rates with the Extended Nelson and Siegel Method. Sveriges Riksbank Quarterly Review 3: 13–26. [Google Scholar]
- Wang, Junbo, Chunchi Wu, and Frank X. Zhang. 2008. Liquidity, default, taxes, and yields on municipal bonds. Journal of Banking & Finance 32: 1133–49. [Google Scholar]
- Woltman, Heather, Andrea Feldstain, J. C. MacKay, and Meredith Rocchi. 2012. An introduction to hierarchical linear modeling. Tutorials in Quantitative Methods for Psychology 8: 52–69. [Google Scholar] [CrossRef]
| 1 |
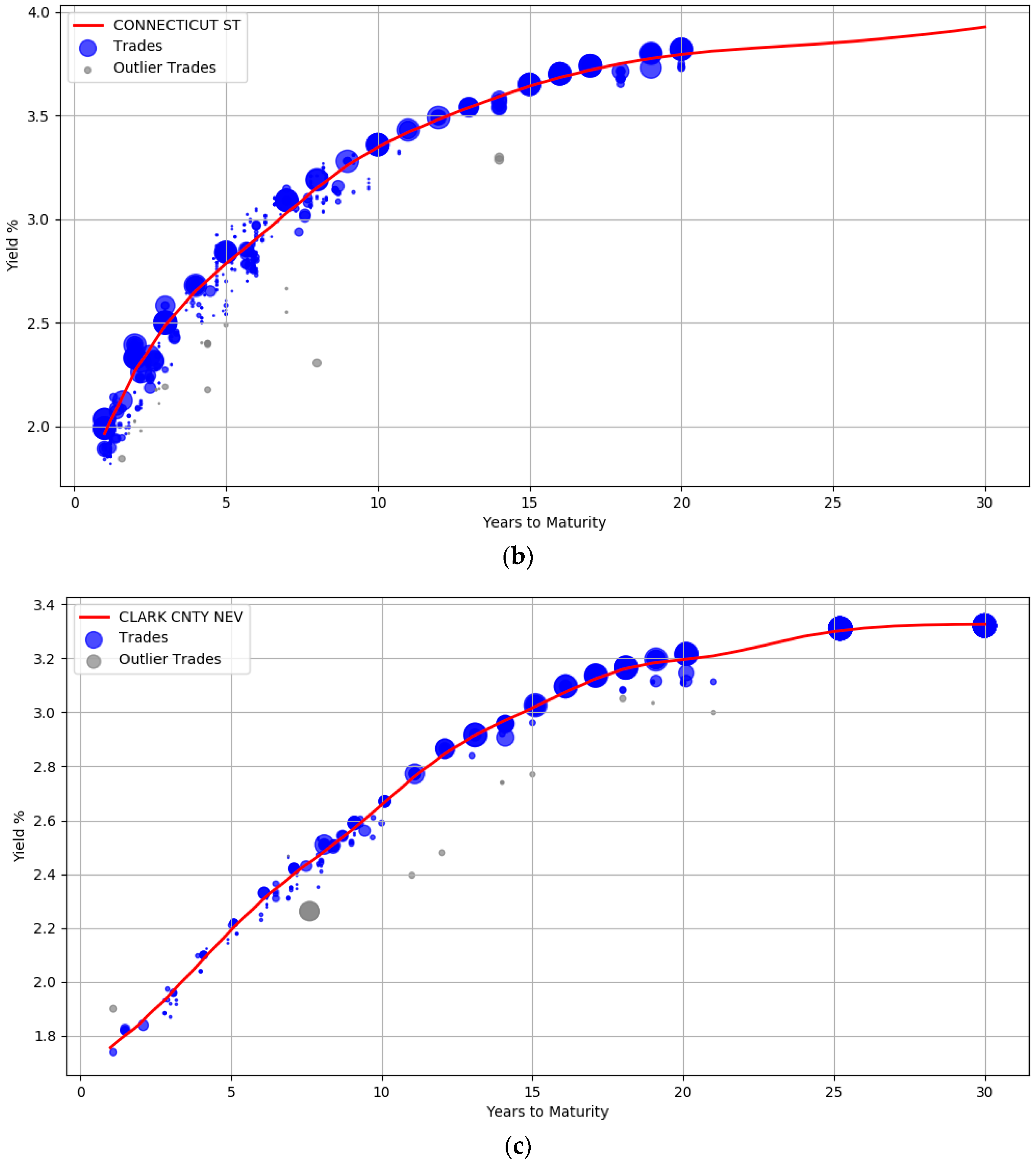
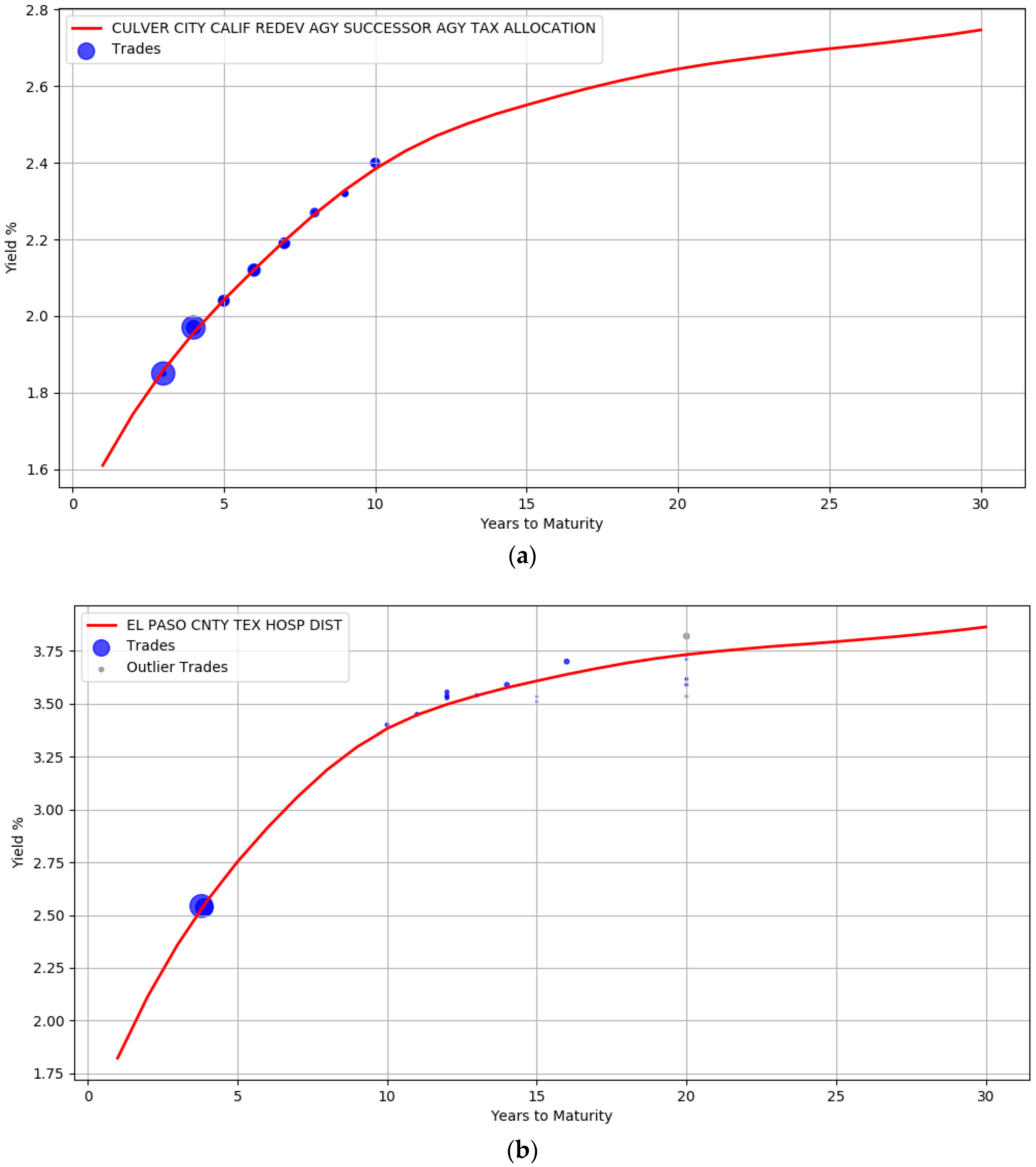
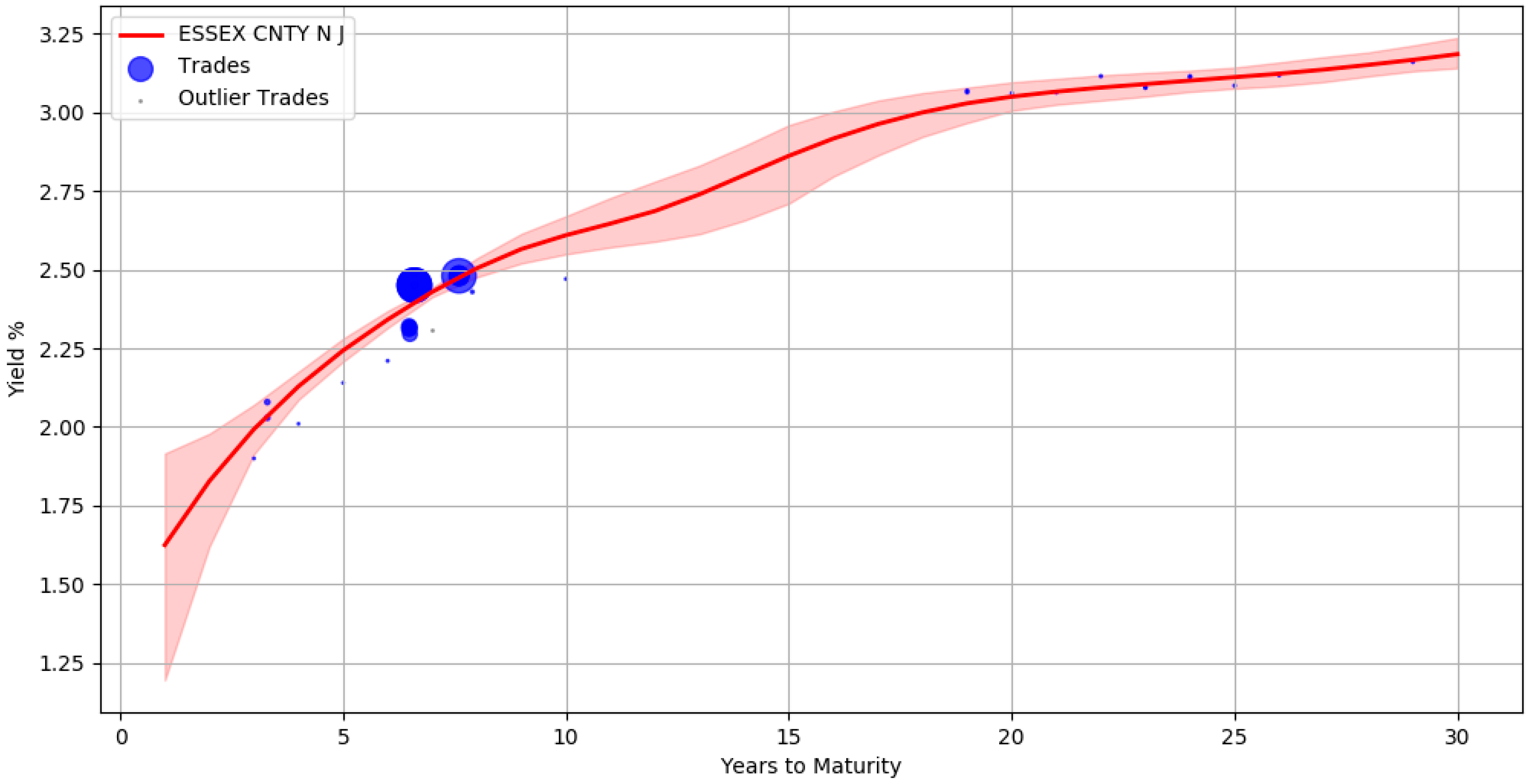
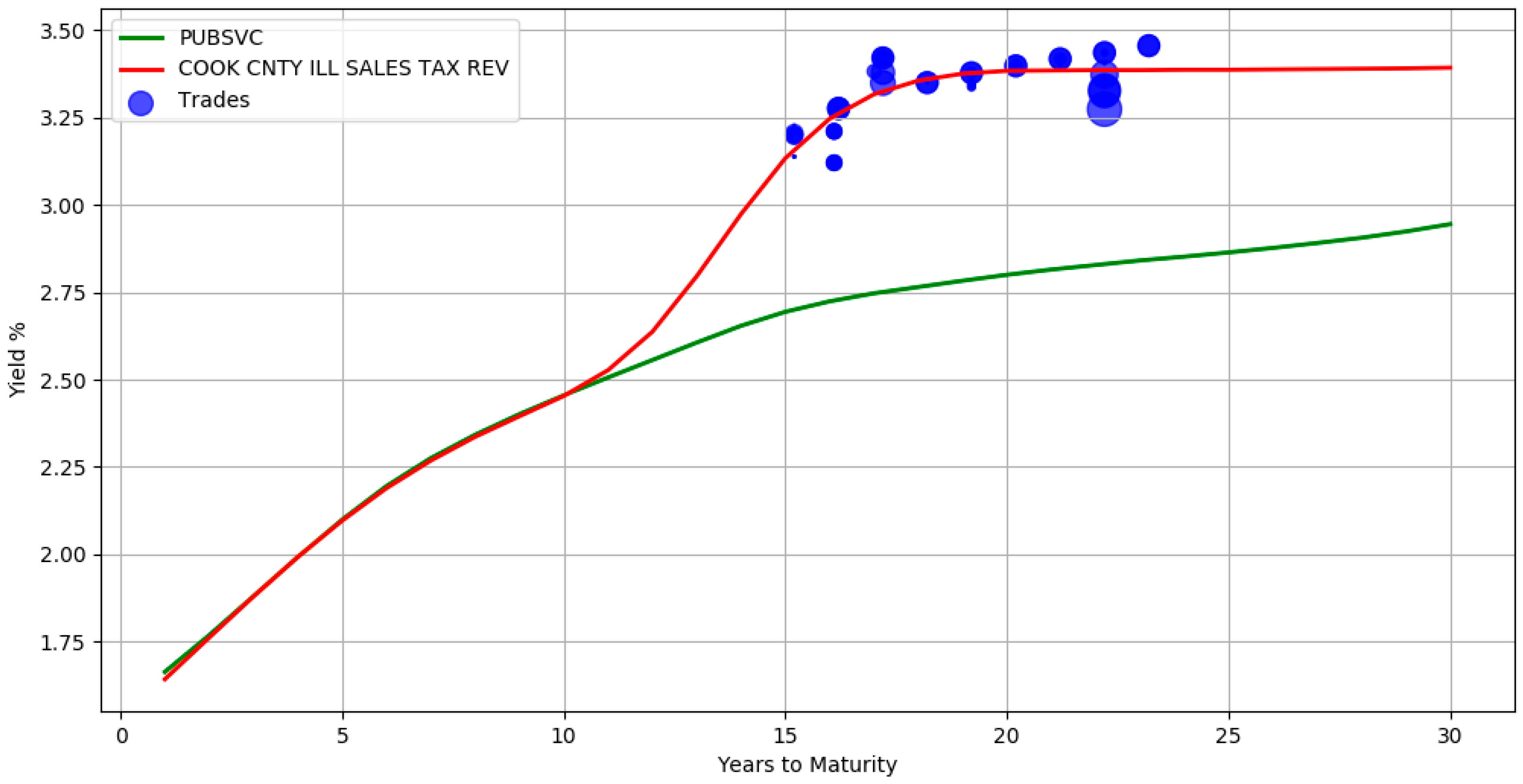
| 1. | Select all bonds with an investment grade credit rating |
| 2. | Exclude bonds that are priced to PUT |
| 3. | Exclude taxable bonds |
| 4. | Exclude bank qualified bonds |
| 5. | Exclude pre-refunded bonds |
| 6. | Exclude escrowed to maturity bonds |
| 7. | Exclude bonds with insurance contract |
| 8. | Exclude short term callable bonds |
| 9. | Exclude bonds obligated to redeem before maturity |
| 10. | Exclude bonds whose maturity date is not between one and thirty years |
| Issuer | CUSIP | Yield Estimate | Certainty Score |
|---|---|---|---|
| ESSEX CNTY N J | 296804KC0 | 1.67% | 0.67 |
| ESSEX CNTY N J | 296804ZN0 | 2.89% | 0.91 |
| ESSEX CNTY N J | 296804C47 | 2.45% | 0.98 |
| Type | Count |
|---|---|
| AAA Rated Bonds | 28,295 |
| AA Rated Bonds | 54,268 |
| A Rated Bonds | 16,290 |
| BBB Rated Bonds | 2501 |
| General Obligation Bonds | 45,296 |
| Revenue Bonds | 56,058 |
| Issuers | 844 |
| Yield Spread between Human Evaluations and Model Estimates | Number of Bonds | Percentage of Bonds |
|---|---|---|
| <5 basis points | 33,906 | 33.45 |
| <10 basis points | 57,441 | 56.67 |
| <15 basis points | 69,974 | 69.03 |
| <20 basis points | 78,281 | 77.23 |
| <25 basis points | 83,990 | 82.86 |
| ≥25 basis points | 101,354 | 100.00 |
| Next Day Yield Spread | Human Evaluation | Model Estimates |
|---|---|---|
| <5 basis points | 39.76% | 37.57% |
| <10 basis points | 57.13% | 54.09% |
| <15 basis points | 66.42% | 62.39% |
| <20 basis points | 75.33% | 67.33% |
| <25 basis points | 80.11% | 72.17% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raman, N.; Leidner, J.L. Municipal Bond Pricing: A Data Driven Method. Int. J. Financial Stud. 2018, 6, 80. https://doi.org/10.3390/ijfs6030080
Raman N, Leidner JL. Municipal Bond Pricing: A Data Driven Method. International Journal of Financial Studies. 2018; 6(3):80. https://doi.org/10.3390/ijfs6030080
Chicago/Turabian StyleRaman, Natraj, and Jochen L. Leidner. 2018. "Municipal Bond Pricing: A Data Driven Method" International Journal of Financial Studies 6, no. 3: 80. https://doi.org/10.3390/ijfs6030080
APA StyleRaman, N., & Leidner, J. L. (2018). Municipal Bond Pricing: A Data Driven Method. International Journal of Financial Studies, 6(3), 80. https://doi.org/10.3390/ijfs6030080





