British-European Trade Relations and Brexit: An Empirical Analysis of the Impact of Economic and Financial Uncertainty on Exports
Abstract
:1. Introduction
“At the core of the European Union must be, as it is now, the single market. Britain is at the heart of that Single Market, and must remain so. […] However, when the Single Market remains in-complete […] it is only half the success it could be. We would need to weigh up very carefully the consequences of no longer being inside the EU and its single market, as a full member.”
2. Path-Dependency and the European Single Market
3. Brief Literature Review
4. Method
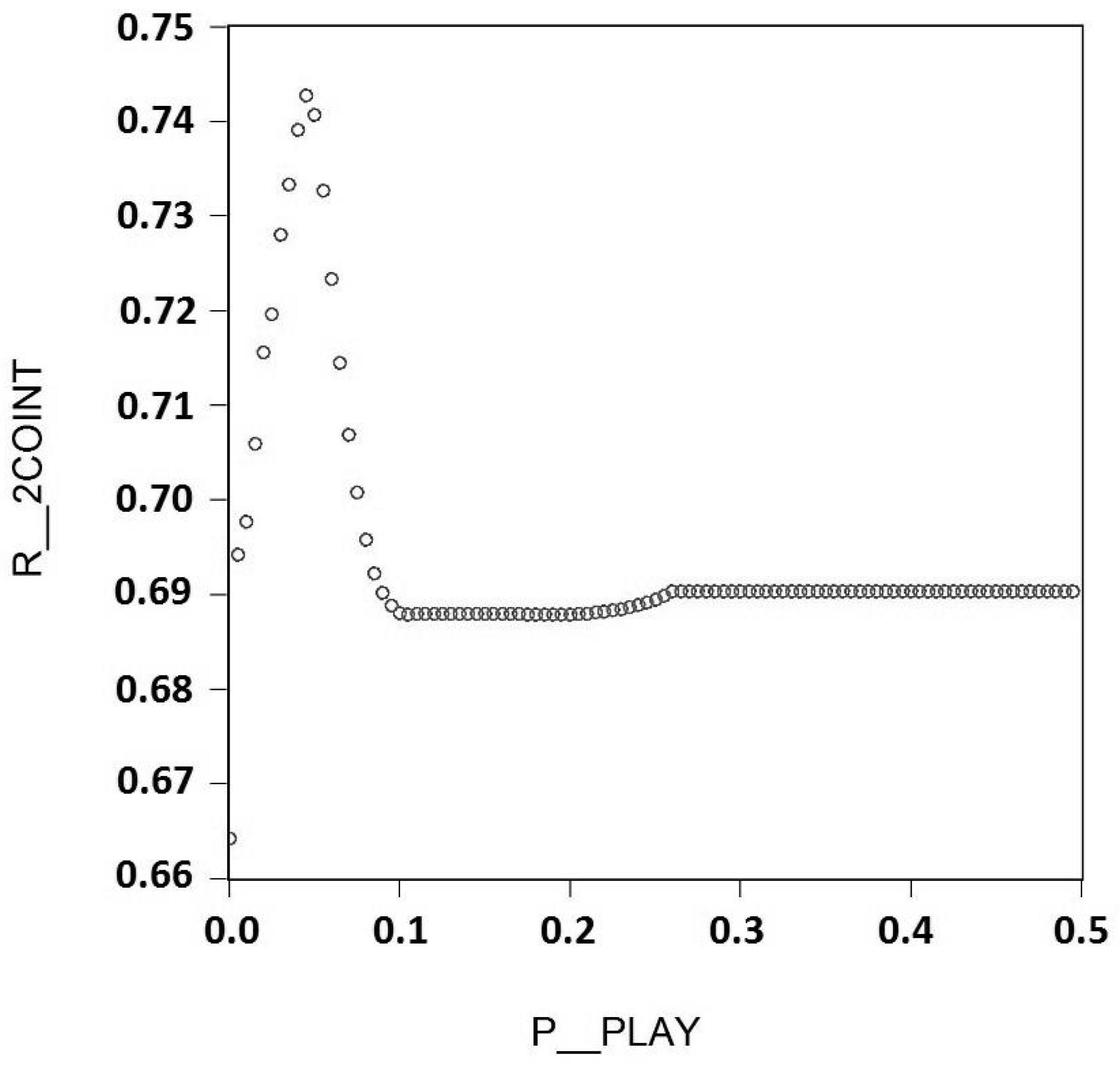
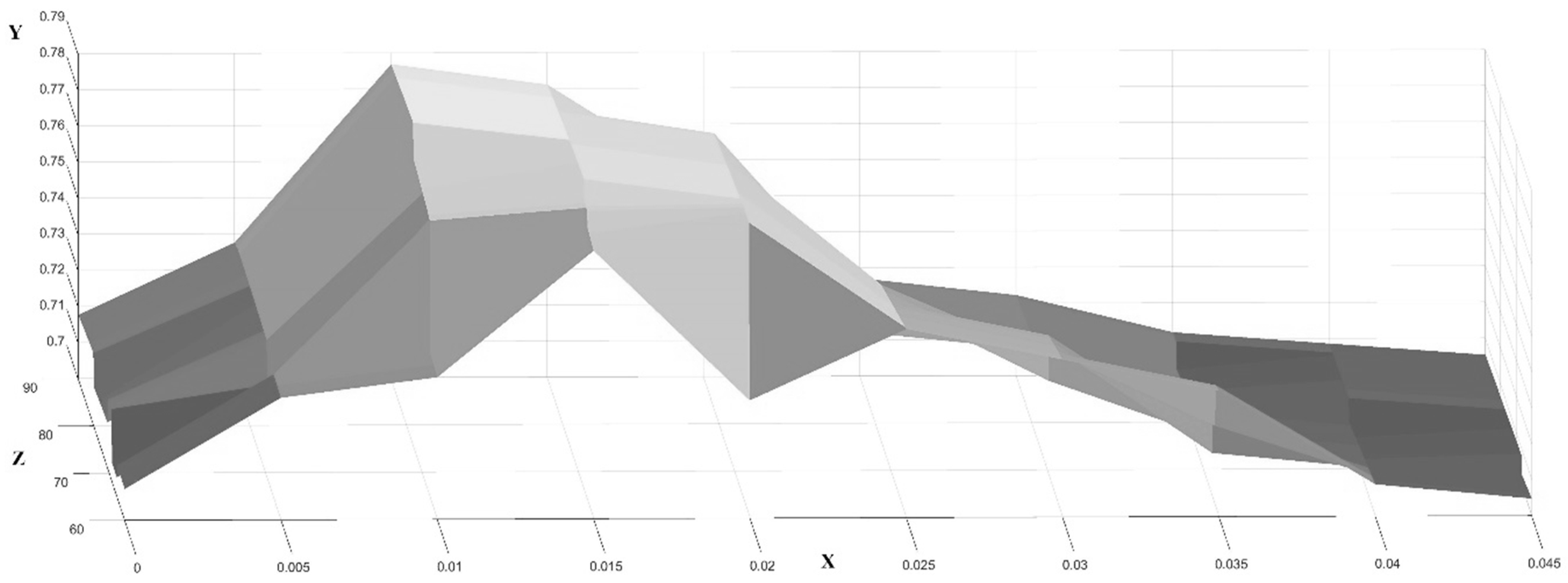
- The coefficient for the spurt variable is significant and negative.
- The coefficient for the real exchange rate is not significant or negative.
- The play area is not so large that it collapses into a structural break.
5. Data
6. Results
- Avoid the reduction of the spurt variable into a dummy variable for a structural break.6
- Avoid cases in which the play area is represented only by a constant despite a variable component.
7. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 2.10 × 108 | α = 1242454 | α = −47165081 | α = 1.35 × 109 | α = 93522388 | α = 5.55 × 108 | α = −4.51 × 108 | α = 2.05 × 108 | α = −26751285 | α = 5.94 × 108 | α = −2.12 × 108 |
| p(α) = 0.0000 | p(α) = 0.9049 | p(α) = 0.0000 | p(α) = 0.0006 | p(α) = 0.0000 | p(α) = 0.0165 | p(α) = 0.0000 | p(α) = 0.2984 | p(α) = 0.6809 | p(α) = 0.0000 | p(α) = 0.5752 | |
| γ(c) = 0.020000 | γ(c) = 0.020000 | γ(c) = 0.085000 | γ(c) = 0.010000 | γ(c) = 0.020000 | γ(c) = 0.005000 | γ(c) = 0.065000 | γ(c) = 0.010000 | γ(c) = 0.015000 | γ(c) = 0.010000 | γ(c) = 0.015000 | |
| γ(v) = 3.600000 | γ(v) = 3.200000 | γ(v) = 18.00000 | γ(v) = 2.400000 | γ(v) = 3.900000 | γ(v) = 3.400000 | γ(v) = 228.4000 | γ(v) = 75.60000 | γ(v) = 35.60000 | γ(v) = 2.300000 | γ(v) = 64.00000 | |
| β = −2.96 × 108 | β = −76659196 | β = 45021690 | β = −1.31 × 108 | β = −77049986 | β = −9.38 × 108 | β = 3.14 × 108 | β = −2.06 × 109 | β = −4.79 × 108 | β = −6.86 × 108 | β = −3.36 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0003 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) =0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 93251455 | α = −50192661 | α = 64293966 | α = −8.46 × 108 | α = 54147458 | α = 6.83 × 108 | α = −28288670 | α = −1.51 × 109 | α = 1.09 × 109 | α = −1.09 × 109 | α = −1.73 × 109 |
| p(α) = 0.0001 | p(α) = 0.0001 | p(α) = 0.0152 | p(α) = 0.0000 | p(α) = 0.0001 | p(α) = 0.0251 | p(α) = 0.7425 | p(α) = 0.0023 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0161 | |
| γ(c) = 0.010000 | γ(c) = 0.015000 | γ(c) = 0.020000 | γ(c) = 0.025000 | γ(c) = 0.005000 | γ(c) = 0.010000 | γ(c) = 0.035000 | γ(c) = 0.070000 | γ(c) = 0.020000 | γ(c) = 0.015000 | γ(c) = 0.050000 | |
| γ(v) = 199.3333 | γ(v) = 10.05000 | γ(v) = 9.000000 | γ(v) = 2.300000 | γ(v) = 6.000000 | γ(v) = 9.200000 | γ(v) = 57.10000 | γ(v) = 6.400000 | γ(v) = 3.600000 | γ(v) = 4.000000 | γ(v) = 10.00000 | |
| β = −2.02× 108 | β = 67425118 | β = −97643977 | β = 9.41 × 108 | β = −64429064 | β = −1.90 × 109 | β = −7.61 × 108 | β = −4.38 × 109 | β = −1.60 × 109 | β = 1.19 × 109 | β = −6.06 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0006 | p(β) = 0.0015 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = −3.86 × 108 | α = 33610219 | α = 1.45 × 108 | α = −4.38 × 108 | α = −23439145 | α = 1.57 × 109 | α = 5.63 × 108 | α = −4.23 × 109 | α = −1.43 × 108 | α = 3.25 × 108 | α = −5.59 × 108 |
| p(α) = 0.0000 | p(α) = 0.0935 | p(α) = 0.0308 | p(α) = 0.0001 | p(α) = 0.0005 | p(α) = 0.0001 | p(α) = 0.0021 | p(α) = 0.0000 | p(α) = 0.0387 | p(α) =0.0000 | p(α) = 0.4245 | |
| γ(c) = 0.000100 | γ(c) = 0.236667 | γ(c) = 0.001150 | γ(c) = 0.000400 | γ(c) = 0.090000 | γ(c) = 0.005000 | γ(c) = 0.005000 | γ(c) = 0.005000 | γ(c) = 0.050000 | γ(c) = 0.000100 | γ(c) = 0.050000 | |
| γ(v) = 2.900000 | γ(v) = 145.0000 | γ(v) = 1.000000 | γ(v) = 2.900000 | γ(v) = 110.0000 | γ(v) = 1.100000 | γ(v) = 1.400000 | γ(v) = 14.25000 | γ(v) = 41.80000 | γ(v) = 2.900000 | γ(v) = 4.900000 | |
| β = 2.76 × 108 | β = −2.69 × 108 | β = −1.90 × 108 | β = 8.93 × 108 | β = 70973392 | β = −2.10 × 109 | β = −7.34 × 108 | β = 2.53 × 109 | β = −4.25 × 108 | β =−3.25 × 108 | β = −3.06 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0124 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0003 | p(β) = 0.0002 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0002 | |
| IT | α = 1.16 × 108 | α = −8434539 | α = 45631207 | α = −1.41 × 108 | α = −11996714 | α = 3.71 × 108 | α = 4.69 × 108 | α = 3.30 × 108 | α = −58098834 | α = 1.19 × 109 | α = −3.18 × 109 |
| p(α) = 0.0000 | p(α) = 0.5484 | p(α) = 0.0027 | p(α) = 0.0390 | p(α) = 0.0585 | p(α) = 0.0000 | p(α) = 0.0035 | p(α) = 0.5107 | p(α) = 0.3462 | p(α) = 0.0127 | p(α) = 0.0000 | |
| γ(c) = 0.015000 | γ(c) = 0.010000 | γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.020000 | γ(c) = 0.001667 | γ(c) = 0.005000 | γ(c) = 0.005000 | γ(c) = 0.065000 | γ(c) = 0.005000 | γ(c) = 0.003500 | |
| γ(v) = 3.800000 | γ(v) = 94.00000 | γ(v) = 2.500000 | γ(v) = 3.200000 | γ(v) = 1.600000 | γ(v) = 2.000000 | γ(v) = 2.400000 | γ(v) = 3.100000 | γ(v) = 7.600000 | γ(v) = 0.600000 | γ(v) = 3.000000 | |
| β = −1.57 × 108 | β = −46459482 | β = −57588745 | β = 1.90 × 108 | β = 18083243 | β = −5.92 × 108 | β = −6.78 × 108 | β = −9.34 × 108 | β = −5.94 × 108 | β = −1.24 × 109 | β = 2.15 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0023 | p(β) = 0.0005 | p(β) = 0.0050 | p(β) = 0.0033 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0569 | p(β) = 0.0000 | p(β) = 0.0141 | p(β) = 0.0002 | |
| NL | α = 2.78 × 108 | α = 49979236 | α = 2.94 × 108 | α = 2.14 × 109 | α = 1.78 × 108 | α = −2.08 × 108 | α = −25875090 | α = 2.23 × 108 | α = 1.52 × 108 | α = 43280160 | α = 1.10 × 108 |
| p(α) = 0.0000 | p(α) = 0.0010 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.2300 | p(α) = 0.5338 | p(α) = 0.4741 | p(α) = 0.1905 | p(α) = 0.0049 | p(α) = 0.8051 | |
| γ(c) = 5 × 10−5 | γ(c) =0.030000 | γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.020000 | γ(c) = 0.055009 | γ(c) = 0.030000 | γ(c) = 0.002000 | γ(c) = 0.025000 | γ(c) = 0.030000 | γ(c) = 0.010000 | |
| γ(v) = 28.00000 | γ(v) = 34.50000 | γ(v) = 67.10000 | γ(v) = 14.60000 | γ(v) = 60.80000 | γ(v) = 45.90000 | γ(v) = 42.20000 | γ(v) = 19.00000 | γ(v) = 1.600000 | γ(v) = 50.10000 | γ(v) = 60.60000 | |
| β = −4.65 × 108 | β = −1.01 × 108 | β = −3.34 × 108 | β = −2.15 × 109 | β = −89039588 | β = −7.93 × 108 | β = −3.01 × 108 | β = −2.32 × 109 | β = −6.92 × 108 | β = −2.08 × 108 | β = −4.14 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| GE | α = 2.52 × 108 | α = −40270674 | α = −44262092 | α = −7.83 × 108 | α = −72624895 | α = −5.37 × 108 | α = −2.35× 108 | α = −2.21 × 109 | α = 7.32 × 108 | α = −5.94 × 108 | α = −2.94 × 109 |
| p(α) = 0.0000 | p(α) = 0.0006 | p(α) = 0.0016 | p(α) = 0.0003 | p(α) = 0.0003 | p(α) = 0.0149 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | |
| γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.030000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.010000 | γ(c) = 0.030000 | γ(c) = 0.015000 | |
| γ(v) = 0.000500 | γ(v) = 0.001600 | γ(v) = 0.001100 | γ(v) = 0.000200 | γ(v) = 0.000200 | γ(v) = 0.000300 | γ(v) = 0.003200 | γ(v) = 0.001500 | γ(v) = 0.000800 | γ(v) = 0.001000 | γ(v) = 0.000900 | |
| β = −3.31 × 108 | β = 41488234 | β = 58539957 | β = 9.73 × 108 | β = 82069923 | β = −7.28 × 108 | β = −6.87× 108 | β = −3.56 × 109 | β = −1.22 × 109 | β = 6.70 × 108 | β = −4.58 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0040 | p(β) = 0.0043 | p(β) = 0.0000 | p(β) = 0.0002 | p(β) = 0.0039 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = 1.87 × 108 | α = 19316317 | α = −25607258 | α = 3.43 × 108 | α = −22902207 | α = −1.45 × 108 | α = −1.06 × 108 | α = −2.68 × 109 | α = −1.43 × 108 | α = −1.71 × 108 | α = −3.32 × 109 |
| p(α) = 0.0040 | p(α) = 0.3105 | p(α) = 0.0010 | p(α) = 0.0000 | p(α) = 0.0003 | p(α) = 0.0101 | p(α) = 0.0004 | p(α) = 0.0000 | p(α) = 0.0270 | p(α) = 0.0006 | p(α) = 0.0000 | |
| γ(c) = 0.000000 | γ(c) = 0.085000 | γ(c) = 0.070000 | γ(c) = 0.075000 | γ(c) = 0.020000 | γ(c) = 0.000000 | γ(c) = 0.075000 | γ(c) = 0.000000 | γ(c) = 0.040000 | γ(c) = 0.000000 | γ(c) = 0.000000 | |
| γ(v) = 0.000300 | γ(v) = 0.001100 | γ(v) = 0.002000 | γ(v) = 0.001900 | γ(v) = 0.000900 | γ(v) = 0.002400 | γ(v) = 0.001900 | γ(v) = 0.004200 | γ(v) = 0.000300 | γ(v) = 0.000400 | γ(v) = 0.004200 | |
| β = −3.78 × 108 | β = −2.35 × 108 | β = −2.08 × 108 | β = −6.31 × 108 | β = 74107731 | β = −7.28 × 108 | β = −2.50 × 108 | β = −4.46 × 109 | β = −4.69 × 108 | β = 2.41 × 108 | β = −6.41 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0307 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = −7.28 × 108 | p(β) = 0.0114 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| IT | α = 70068465 | α = −21210292 | α = −12316790 | α = −1.29 × 108 | α = −6410508 | α = −42185082 | α = −3.37 × 108 | α = −4.54 × 108 | α = −1.18 × 108 | α = 7.42 × 108 | α = −9.43× 108 |
| p(α) = 0.0000 | p(α) = 0.0408 | p(α) = 0.0071 | p(α) = 0.2024 | p(α) = 0.2639 | p(α) = 0.1360 | p(α) = 0.0000 | p(α) = 0.0017 | p(α) = 0.0250 | p(α) = 0.0830 | p(α) = 0.0000 | |
| γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.000000 | |
| γ(v) = 0.001500 | γ(v) = 0.001500 | γ(v) = 0.001200 | γ(v) = 0.000200 | γ(v) = 0.000300 | γ(v) = 0.004700 | γ(v) = 0.001700 | γ(v) = 0.001400 | γ(v) = 0.001200 | γ(v) = 0.000100 | γ(v) = 0.004700 | |
| β = −1.39 × 108 | β = −54519165 | β = 8750755 | β = 1.81 × 108 | β = 12410033 | β = −3.55× 108 | β = 2.04 × 108 | β = −3.08 × 108 | β = −6.27 × 108 | β = −7.61 × 108 | β = −1.60× 109 | |
| p(β) = 0.0000 | p(β) = 0.0015 | p(β) = 0.1601 | p(β) = 0.0797 | p(β) = 0.0233 | p(β) = 0.0000 | p(β) = 0.0071 | p(β) = 0.1276 | p(β) = 0.0000 | p(β) = 0.0914 | p(β) = 0.0001 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 21866974 | α = −25922969 | α = −37254709 | α = 63000971 | α = 38029277 | α = −1.42 × 108 | α = −3.99 × 108 | α = 8.56 × 108 | α = −73505391 | α = −2.52 × 108 | α = 4.82 × 108 |
| p(α) = 0.1893 | p(α) = 0.0561 | p(α) = 0.0000 | p(α) = 0.5419 | p(α) = 0.0000 | p(α) = 0.1146 | p(α) = 0.0000 | p(α) = 0.0136 | p(α) = 0.3431 | p(α) = 0.0000 | p(α) = 0.4013 | |
| γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.015000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.065000 | γ(c) = 0.010000 | γ(c) = 0.000000 | γ(c) = 0.025000 | γ(c) = 0.035000 | |
| γ(v) = 0.001900 | γ(v) = 0.000200 | γ(v) = 0.001200 | γ(v) = 0.001900 | γ(v) = 0.001900 | γ(v) = 0.001000 | γ(v) = 0.000500 | γ(v) = 0.000300 | γ(v) = 0.000600 | γ(v) = 0.000900 | γ(v) = 0.000100 | |
| β = −1.91× 108 | β = −47909297 | β = 45413269 | β = −3.50× 108 | β = −47918652 | β = −3.31 × 108 | β = 3.42 × 108 | β = −2.73 × 109 | β = −3.95 × 108 | β = 2.47 × 108 | β = −3.67 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0007 | p(β) = 0.0000 | p(β) = 0.0787 | p(β) = 0.0000 | p(β) = 0.0066 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.000000 | |
| GE | α = 2.91 × 108 | α = −37922977 | α = −42800804 | α = −4.76 × 108 | α = −1.27 × 108 | α = −5.30 × 108 | α = −2.35 × 108 | α = −2.54 × 109 | α = 4.20 × 108 | α = −4.71 × 108 | α = −2.22 × 109 |
| p(α) = 0.0000 | p(α) = 0.0004 | p(α) = 0.0018 | p(α) = 0.0017 | p(α) = 0.0004 | p(α) = 0.0172 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0008 | |
| γ(c) = 0.010000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.020000 | γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.025000 | γ(c) = 0.005000 | γ(c) = 0.035000 | γ(c) = 0.045000 | |
| γ(v) = 0.000400 | γ(v) = 0.001200 | γ(v) = 0.000900 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000600 | γ(v) = 0.002000 | γ(v) = 0.001100 | γ(v) = 0.001300 | γ(v) = 0.000700 | γ(v) = 0.000300 | |
| β = −3.52 × 108 | β = 49328724 | β = 55070906 | β = 6.06 × 108 | β = 1.35 × 108 | β = −7.57 × 108 | β = −6.87 × 108 | β = −3.94 × 109 | β = −9.50 × 108 | β = 7.99 × 108 | β = −5.49 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0015 | p(β) = 0.0046 | p(β) = 0.0001 | p(β) = 0.0003 | p(β) = 0.0038 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = 1.01 × 108 | α = 33610219 | α = −17031872 | α = −39781479 | α = −23519497 | α = −2.35× 108 | α = −1.80 × 108 | α = −5.56 × 108 | α = −1.49 × 108 | α = −1.15 × 108 | α = −1.14 × 109 |
| p(α) = 0.0669 | p(α) = 0.0935 | p(α) = 0.0394 | p(α) = 0.8102 | p(α) = 0.0001 | p(α) = 0.0002 | p(α) = 0.0000 | p(α) = 0.4288 | p(α) = 0.0249 | p(α) = 0.0026 | p(α) = 0.0648 | |
| γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.050000 | γ(c) = 0.015000 | γ(c) = 0.000000 | γ(c) = 0.005000 | |
| γ(v) = 0.000400 | γ(v) = 0.002000 | γ(v) = 0.002000 | γ(v) = 0.000200 | γ(v) = 0.001200 | γ(v) = 0.002000 | γ(v) = 0.001200 | γ(v) = 0.000000 | γ(v) = 0.000600 | γ(v) = 0.000500 | γ(v) = 0.000600 | |
| β = −2.81 × 108 | β = −2.69× 108 | β = −30269582 | β = 4.39 × 108 | β = 73685802 | β = −4.47× 108 | β = 1.80 × 108 | β = −2.15 × 109 | β = −4.97 × 108 | β = 1.88 × 108 | β = −2.66 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.1170 | p(β) = 0.0135 | p(β) = 0.0000 | p(β) = 0.0023 | p(β) = 0.0016 | p(β) = 0.0042 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0007 | |
| IT | α = 56218788 | α = 258329.9 | α = 13375917 | α = 79727339 | α = 1122092 | α = −42185082 | α = −1.18 × 109 | α = −4.85 × 108 | α = −1.41 × 108 | α = 96695369 | α = −6.29 × 108 |
| p(α) = 0.0009 | p(α) = 0.9876 | p(α) = 0.3389 | p(α) = 0.0010 | p(α) = 0.8132 | p(α) = 0.1360 | p(α) = 0.0001 | p(α) = 0.0001 | p(α) = 0.0047 | p(α) = 0.1064 | p(α) = 0.0073 | |
| γ(c) = 0.010000 | γ(c) = 0.010000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.010000 | γ(c) = 0.000000 | γ(c) = 0.000000 | |
| γ(v) = 0.001400 | γ(v) = 0.000500 | γ(v) = 0.000200 | γ(v) = 0.000900 | γ(v) = 0.000300 | γ(v) = 0.001900 | γ(v) = 0.000100 | γ(v) = 0.001000 | γ(v) = 0.001000 | γ(v) = 0.001200 | γ(v) = 0.000900 | |
| β = −1.06 × 108 | β = −59094035 | β = −22007803 | β = −57628023 | β = 5801011 | β = −3.55× 108 | β = 1.00 × 109 | β = −3.34 × 108 | β = −6.28 × 108 | β = −1.61 × 108 | β = −1.27 × 109 | |
| p(β) = 0.0001 | p(β) = 0.0023 | p(β) = 0.1351 | p(β) = 0.0670 | p(β) = 0.2570 | p(β) = 0.0000 | p(β) = 0.0014 | p(β) = 0.0932 | p(β) = 0.0000 | p(β) = 0.0657 | p(β) = 0.0001 | |
| NL | α = 1.27 × 108 | α = 51345646 | α = 1.38 × 108 | α = 6.65 × 108 | α = 1.73 × 108 | α = −3.26 × 108 | α = −46033106 | α = −1.17 × 109 | α = −54581588 | α = 74903928 | α = 3.59 × 108 |
| p(α) = 0.0034 | p(α) = 0.0027 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0305 | p(α) = 0.3308 | p(α) = 0.0000 | p(α) = 0.5236 | p(α) = 0.0004 | p(α) = 0.5174 | |
| γ(c) = 0.000000 | γ(c) = 0.020000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.020000 | γ(c) = 0.035000 | γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.060000 | γ(c) = 0.020000 | γ(c) = 0.005000 | |
| γ(v) = 0.000900 | γ(v) = 0.000400 | γ(v) = 0.001900 | γ(v) = 0.001900 | γ(v) = 0.000400 | γ(v) = 0.000500 | γ(v) = 0.000700 | γ(v) = 0.001000 | γ(v) = 0.000000 | γ(v) = 0.000400 | γ(v) = 0.000600 | |
| β = −3.74 × 108 | β = −93081641 | β = −3.02 × 108 | β = −1.27 × 109 | β = −77761480 | β = −8.64 × 108 | β = −2.71 × 108 | β = −9.29 × 108 | β = −5.46 × 108 | β = −2.42 × 108 | β = −3.75 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0013 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0004 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 60629813 | α = −43894715 | α = −45591146 | α = −1.34 × 108 | α = 47473572 | α = 5.69 × 108 | α = −9.97 × 108 | α = −4.51 × 108 | α = −1.04 × 108 | α = −1.46 × 109 | α = −1.46 × 109 |
| p(α) = 0.0028 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.1397 | p(α) = 0.0000 | p(α) = 0.0074 | p(α) = 0.0000 | p(α) = 0.0119 | p(α) = 0.0435 | p(α) = 0.0000 | p(α) = 0.0000 | |
| γ(c) = 0.030000 | γ(c) = 0.005000 | γ(c) = 0.015000 | γ(c) = 0.000500 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.007000 | γ(c) = 0.015000 | γ(c) = 0.002500 | γ(c) = 0.002500 | |
| γ(v) = 0.053000 | γ(v) = 0.036000 | γ(v) = 0.014000 | γ(v) = 0.046000 | γ(v) = 0.072000 | γ(v) = 0.001000 | γ(v) = 0.001000 | γ(v) = 0.016000 | γ(v) = 0.012000 | γ(v) = 0.018000 | γ(v) = 0.018000 | |
| β = −1.81 × 108 | β = −44867766 | β = 51065940 | β = 4.93 × 108 | β = −51087138 | β = −9.00 × 108 | β = 7.95 × 108 | β = −1.74 × 109 | β = −3.61 × 108 | β = −2.33 × 109 | β = −2.33 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 1.48 × 108 | α = −29084575 | α = 86401652 | α = −1.68 × 108 | α = −44187476 | α = −5.83 × 108 | α = −52742720 | α = −1.43 × 109 | α = 1.03 × 109 | α = 2195757 | α = −1.15 × 109 |
| p(α) = 0.0000 | p(α) = 0.0024 | p(α) = 0.0019 | p(α) = 0.0014 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.5322 | p(α) = 0.0022 | p(α) = 0.0000 | p(α) = 0.9738 | p(α) = 0.1479 | |
| γ(c) = 0.020000 | γ(c) = 0.225000 | γ(c) = 0.000000 | γ(c) = 0.010000 | γ(c) = 0.015000 | γ(c) = 0.020000 | γ(c) = 0.010000 | γ(c) = 0.020000 | γ(c) = 0.040000 | γ(c) = 0.000000 | γ(c) = 0.055000 | |
| γ(v) = 0.030000 | γ(v) = 0.005000 | γ(v) = 0.006000 | γ(v) = 0.034000 | γ(v) = 0.007000 | γ(v) = 0.032000 | γ(v) = 0.051000 | γ(v) = 0.016000 | γ(v) = 0.001000 | γ(v) = 0.050000 | γ(v) = 0.001000 | |
| β = −7.45 × 108 | β = 56051258 | β = −1.08 × 108 | β = 6.54 × 108 | β = 68303503 | β = −2.65 × 109 | β = −6.62 × 108 | β = −3.52 × 109 | β = −1.47 × 109 | β = 1.22 × 109 | β = −6.54 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0056 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = −29861972 | α = 1.15 × 108 | α = −90780344 | α = −3.30 × 108 | α = −37446555 | α = −5.26 × 108 | α = −5.79 × 108 | α = −1.15 × 109 | α = −2.95 × 108 | α = 2.26 × 108 | α = −1.28 × 109 |
| p(α) = 0.2194 | p(α) = 0.0000 | p(α) = 0.0001 | p(α) = 0.0147 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0074 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0077 | |
| γ(c) = 0.025000 | γ(c) = 0.030000 | γ(c) = 0.000000 | γ(c) = 0.000500 | γ(c) = 0.033000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.040000 | γ(c) = 0.003000 | γ(c) = 0.005000 | γ(c) = 0.035000 | |
| γ(v) = 0.027000 | γ(v) = 0.014000 | γ(v) = 0.003000 | γ(v) = 0.003000 | γ(v) = 0.007000 | γ(v) = 0.034000 | γ(v) = 0.001000 | γ(v) = 0.003000 | γ(v) = 0.022000 | γ(v) = 0.002000 | γ(v) = 0.004000 | |
| β = −2.66 × 108 | β = −2.18 × 108 | β = 72885827 | β = 7.32 × 108 | β = 71359732 | β = 4.65 × 108 | β = 5.11 × 108 | β = −2.20 × 109 | β = −3.83 × 108 | β = −2.72 × 108 | β = −3.18 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0023 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0004 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| IT | α = −7963677 | α = 6337960 | α = 2782612 | α = 1.17 × 108 | α = 13609699 | α = −3.09 × 108 | α = −3.10 × 108 | α = −6.36 × 108 | α = −87288103 | α = 2.37 × 108 | α = −6.36 × 108 |
| p(α) = 0.4452 | p(α) = 0.6236 | p(α) = 0.6932 | p(α) = 0.0031 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0064 | p(α) = 0.1337 | p(α) = 0.1358 | p(α) = 0.0064 | |
| γ(c) = 0.000000 | γ(c) = 0.015000 | γ(c) = 0.005000 | γ(c) = 0.000000 | γ(c) = 0.010000 | γ(c) = 0.005000 | γ(c) = 0.010000 | γ(c) = 0.055000 | γ(c) = 0.055000 | γ(c) = 0.010000 | γ(c) = 0.055000 | |
| γ(v) = 0.039000 | γ(v) = 0.010000 | γ(v) = 0.006000 | γ(v) = 0.010000 | γ(v) = 0.006000 | γ(v) = 0.037000 | γ(v) = 0.039000 | γ(v) = 0.003000 | γ(v) = 0.003000 | γ(v) = 0.002000 | γ(v) = 0.003000 | |
| β = −1.30 × 108 | β = −62273108 | β = −14383708 | β = −89107856 | β = −13607871 | β = 3.27 × 108 | β = 2.81 × 108 | β = −1.30 × 109 | β = −5.79 × 108 | β = −2.62 × 108 | β = −1.30 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.1281 | p(β) = 0.0516 | p(β) = 0.0035 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.1612 | p(β) = 0.0000 | |
| NL | α = −3.78 × 108 | α = 25595615 | α = −58649269 | α = −2.43 × 109 | α = 2.05 × 108 | α = −1.69 × 108 | α = −1.02 × 108 | α = −2.08 × 109 | α = −54581588 | α = −19996907 | α = −1.02 × 109 |
| p(α) = 0.0000 | p(α) = 0.0210 | p(α) = 0.0085 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.2430 | p(α) = 0.0015 | p(α) = 0.0000 | p(α) = 0.5236 | p(α) = 0.1688 | p(α) = 0.0039 | |
| γ(c) = 0.000000 | γ(c) = 0.005000 | γ(c) = 0.010000 | γ(c) = 0.005000 | γ(c) = 0.035000 | γ(c) = 0.055000 | γ(c) = 0.015000 | γ(c) = 0.029500 | γ(c) = 0.060000 | γ(c) = 0.005000 | γ(c) = 0.030000 | |
| γ(v) = 0.003000 | γ(v) = 0.017000 | γ(v) = 0.033000 | γ(v) = 0.001000 | γ(v) = 0.004000 | γ(v) = 0.094000 | γ(v) = 0.029000 | γ(v) = 0.025000 | γ(v) = 0.000000 | γ(v) = 0.017000 | γ(v) = 0.027000 | |
| β = 4.41 × 108 | β = −81868393 | β = 2.23 × 108 | β = 2.59 × 109 | β = −1.64 × 108 | β = −8.63 × 108 | β = −3.23 × 108 | β = 1.46 × 109 | β = −5.46 × 108 | β = −1.65 × 108 | β = −5.15 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 21866974 | α = −49139448 | α = −41460001 | α = 63000971 | α = 38029277 | α = −1.32 × 108 | α = −4.40 × 108 | α = 8.60 × 108 | α = −1.68 × 108 | α = −2.49 × 108 | α = 7.78 × 108 |
| p(α) = 0.1893 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.5419 | p(α) = 0.0000 | p(α) = 0.2083 | p(α) = 0.0000 | p(α) = 0.0197 | p(α) = 0.0007 | p(α) = 0.0000 | p(α) = 0.2130 | |
| γ(c) = 0.000000 | γ(c) = 0.006000 | γ(c) = 0.024000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.024000 | γ(c) = 0.024000 | γ(c) = 0.018000 | γ(c) = 0.006000 | γ(c) = 0.030000 | γ(c) = 0.045000 | |
| γ(v) = 1.100000 | γ(v) = 0.150000 | γ(v) = 0.600000 | γ(v) = 1.100000 | γ(v) = 1.100000 | γ(v) = 0.600000 | γ(v) = 0.600000 | γ(v) = 0.050000 | γ(v) = 0.150000 | γ(v) = 0.750000 | γ(v) = 0.000000 | |
| β = −1.91× 108 | β = −34143157 | β = 46582632 | β = −3.50× 108 | β = −47918652 | β = −2.97 × 108 | β = 3.69 × 108 | β = −2.97 × 109 | β = −3.64 × 108 | β = 2.47 × 108 | β = −3.91 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0787 | p(β) = 0.0000 | p(β) = 0.0288 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 5.61 × 108 | α = −28815160 | α = 25505218 | α = −2.65 × 108 | α = −23883149 | α = −3.54 × 108 | α = −2.35× 108 | α = −2.56 × 109 | α = 3.15 × 108 | α = −4.96 × 108 | α = −2.02 × 109 |
| p(α) = 0.0000 | p(α) = 0.0025 | p(α) = 0.1335 | p(α) = 0.0012 | p(α) = 0.0359 | p(α) = 0.0299 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0067 | |
| γ(c) = 0.000000 | γ(c) = 0.009000 | γ(c) = 0.003000 | γ(c) = 0.003000 | γ(c) = 0.015000 | γ(c) = 0.003000 | γ(c) = 0.000000 | γ(c) = 0.010000 | γ(c) = 0.010000 | γ(c) = 0.010000 | γ(c) = 0.093000 | |
| γ(v) = 0.050000 | γ(v) = 1.000000 | γ(v) = 0.200000 | γ(v) = 0.200000 | γ(v) = 0.150000 | γ(v) = 0.150000 | γ(v) = 1.200000 | γ(v) = 0.810000 | γ(v) = 0.890000 | γ(v) = 0.740000 | γ(v) = 0.000000 | |
| β = −6.38 × 108 | β = 56007847 | β = −54630985 | β = 4.90 × 108 | β = 30875329 | β = −1.04 × 109 | β = −6.87× 108 | β = −3.80 × 109 | β = −8.86 × 108 | β = 8.34 × 108 | β = −5.27 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0057 | p(β) = 0.0050 | p(β) = 0.0000 | p(β) = 0.0164 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = 16510274 | α = 33610219 | α = −17031872 | α = 60782984 | α = −27505920 | α = −6.65 × 108 | α = −2.08 × 108 | α = −5.89 × 108 | α = −1.73 × 108 | α = −1.29 × 108 | α = −6.31 × 108 |
| p(α) = 0.7062 | p(α) = 0.0935 | p(α) = 0.0394 | p(α) = 0.5122 | p(α) = 0.0001 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.3946 | p(α) = 0.0249 | p(α) = 0.0018 | p(α) = 0.4544 | |
| γ(c) = 0.048000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.003000 | γ(c) = 0.051000 | γ(c) = 0.078000 | γ(c) = 0.000000 | γ(c) = 0.051000 | |
| γ(v) = 0.100000 | γ(v) = 1.200000 | γ(v) = 1.200000 | γ(v) = 0.300000 | γ(v) = 0.800000 | γ(v) = 0.200000 | γ(v) = 0.780000 | γ(v) = 0.000000 | γ(v) = 0.000000 | γ(v) = 0.150000 | γ(v) = 0.000000 | |
| β = −1.75 × 108 | β = −2.69× 108 | β = −30269582 | β = 4.46 × 108 | β = 70788585 | β = 5.49 × 108 | β = 2.07 × 108 | β = −2.13 × 109 | β = −3.77 × 108 | β = 1.94 × 108 | β = −2.71 × 109 | |
| p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.1170 | p(β) = 0.0003 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0007 | p(β) = 0.0043 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0029 | |
| IT | α = 1.58 × 108 | α = −2244012 | α = −13417599 | α = −25090006 | α = −19475670 | α = −4.02 × 108 | α = −3.44 × 108 | α = −8.78 × 108 | α = −2.08 × 108 | α = 7.54 × 108 | α = −2.29 × 109 |
| p(α) = 0.0000 | p(α) = 0.8708 | p(α) = 0.0087 | p(α) = 0.4953 | p(α) = 0.2759 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0001 | p(α) = 0.0578 | p(α) = 0.0000 | |
| γ(c) = 0.000000 | γ(c) = 0.007500 | γ(c) = 0.037500 | γ(c) = 0.001500 | γ(c) = 0.000000 | γ(c) = 0.018000 | γ(c) = 0.019500 | γ(c) = 0.003000 | γ(c) = 0.139500 | γ(c) = 0.003000 | γ(c) = 0.018000 | |
| γ(v) = 0.080000 | γ(v) = 0.120000 | γ(v) = 0.500000 | γ(v) = 0.280000 | γ(v) = 0.020000 | γ(v) = 0.120000 | γ(v) = 0.640000 | γ(v) = 0.150000 | γ(v) = 0.420000 | γ(v) = 0.020000 | γ(v) = 0.120000 | |
| β = −2.06 × 108 | β = −60148975 | β = 8743585 | β = 97123967 | β = 26024147 | β = 3.67 × 108 | β = 2.06 × 108 | β = 4.01 × 108 | β = −6.55 × 108 | β = −7.57 × 108 | β = 1.27 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0003 | p(β) = 0.1479 | p(β) = 0.0325 | p(β) = 0.1490 | p(β) = 0.0000 | p(β) = 0.0077 | p(β) = 0.0768 | p(β) = 0.0000 | p(β) = 0.0643 | p(β) = 0.0000 | |
| NL | α = 51104705 | α = 38532165 | α = −1.35 × 108 | α = 6.65× 108 | α = 2.18 × 108 | α = −3.20 × 108 | α = −36455571 | α = −2.30 × 109 | α = −38315865 | α = 27470762 | α = 1.00 × 1010 |
| p(α) = 0.1573 | p(α) = 0.0377 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0284 | p(α) = 0.4489 | p(α) = 0.0000 | p(α) = 0.6623 | p(α) = 0.1329 | p(α) = 0.0000 | |
| γ(c) = 0.000000 | γ(c) = 0.048000 | γ(c) = 0.000000 | γ(c) = 0.000000 | γ(c) = 0.012000 | γ(c) = 0.015000 | γ(c) = 0.006000 | γ(c) = 0.012000 | γ(c) = 0.057000 | γ(c) = 0.042000 | γ(c) = 0.000000 | |
| γ(v) = 1.110000 | γ(v) = 0.030000 | γ(v) = 0.240000 | γ(v) = 1.110000 | γ(v) = 0.012000 | γ(v) = 0.700000 | γ(v) = 0.290000 | γ(v) = 0.012000 | γ(v) = 0.000000 | γ(v) = 0.060000 | γ(v) = 0.020000 | |
| β = −4.29× 108 | β = −77275027 | β = 2.74 × 108 | β = −1.27 × 109 | β = −1.60 × 108 | β = −8.21 × 108 | β = −2.98 × 108 | β = 1.23 × 109 | β = −5.60 × 108 | β = −2.02 × 108 | β = −1.34 × 1010 | |
| p(β) = 0.0000 | p(β) = 0.0003 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| SICT Product groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| GE | α = 1.31 × 108 | α = −40270674 | α = −1.39 × 108 | α = −1.19 × 108 | α = −77335022 | α = −6.79 × 108 | α = 22472405 | α = −2.21 × 109 | α = 7.95 × 108 | α = −1.18 × 109 | α = −3.19 × 109 |
| p(α) = 0.0000 | p(α) = 0.0006 | p(α) = 0.0009 | p(α) = 0.0234 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.7860 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | |
| γ(v) = 0.000700 | γ(v) = 0.001600 | γ(v) = 0.000000 | γ(v) = 0.001100 | γ(v) = 0.000200 | γ(v) = 0.001100 | γ(v) = 0.000400 | γ(v) = 0.001500 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000700 | |
| γ(v2) = 8.800000 | γ(v2) = 0.000000 | γ(v2) = 2.000000 | γ(v2) = 39.50000 | γ(v2) = 1.000000 | γ(v2) = 32.50000 | γ(v2) = 38.00000 | γ(v2) = 0.000000 | γ(v2) = 3.200000 | γ(v2) = 9.400000 | γ(v2) = 17.50000 | |
| β = −3.63 × 108 | β = 41488234 | β = 1.30 × 108 | β = 5.03 × 108 | β = 80755643 | β = −9.94 × 108 | β = −9.71 × 108 | β = −3.56 × 109 | β = −1.13 × 109 | β = 1.35 × 109 | β = −4.88 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0040 | p(β) = 0.0022 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = −1.14 × 108 | α = −28950790 | α = −61679864 | α = −4.25 × 108 | α = −12704366 | α = −1.00 × 108 | α = 2.02 × 108 | α = −2.68 × 109 | α = −3.95 × 108 | α = 3.21 × 108 | α = −3.32 × 109 |
| p(α) = 0.0000 | p(α) = 0.1150 | p(α) = 0.0025 | p(α) = 0.0001 | p(α) = 0.0217 | p(α) = 0.0843 | p(α) = 0.0283 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | |
| γ(v) = 0.001700 | γ(v) = 0.001200 | γ(v) = 0.000000 | γ(v) = 0.000000 | γ(v) = 0.001300 | γ(v) = 0.001500 | γ(v) = 0.000000 | γ(v) = 0.004100 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.004100 | |
| γ(v2) = 86.00000 | γ(v2) = 165.0000 | γ(v2) = 3.000000 | γ(v2) = 2.950000 | γ(v2) = 1.000000 | γ(v2) = 4.000000 | γ(v2) = 5.200000 | γ(v2) = 1.000000 | γ(v2) = 5.000000 | γ(v2) = 2.950000 | γ(v2) = 1.000000 | |
| β = −1.54 × 108 | β = −2.59 × 108 | β = 46293504 | β = 8.79 × 108 | β = 66619369 | β = −7.19 × 108 | β = −4.17 × 108 | β = −4.44 × 109 | β = −2.85 × 108 | β = −3.20 × 108 | β = −6.39 × 109 | |
| p(β) = 0.0007 | p(β) = 0.0000 | p(β) = 0.0358 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0006 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| IT | α = 69906390 | α = −21187139 | α = −18443856 | α = −1.23 × 108 | α = −7706616. | α = 85523775 | α = −4.97 × 108 | α = −3.06 × 108 | α = 42399497 | α = 3.54 × 108 | α = −3.34 × 108 |
| p(α) = 0.0000 | p(α) = 0.0407 | p(α) = 0.0140 | p(α) = 0.0670 | p(α) = 0.1644 | p(α) = 0.0335 | p(α) = 0.0000 | p(α) = 0.0813 | p(α) = 0.5112 | p(α) = 0.0409 | p(α) = 0.2040 | |
| γ(v) = 0.001500 | γ(v) = 0.001500 | γ(v) = 0.000000 | γ(v) = 0.000200 | γ(v) = 0.000200 | γ(v) = 0.000600 | γ(v) = 0.000000 | γ(v) = 0.000600 | γ(v) = 0.000600 | γ(v) = 0.000000 | γ(v) = 0.000600 | |
| γ(v2) = 0.250000 | γ(v2) = 0.250000 | γ(v2) = 41.00000 | γ(v2) = 2.000000 | γ(v2) = 1.000000 | γ(v2) = 18.00000 | γ(v2) = 14.60000 | γ(v2) = 18.00000 | γ(v2) = 18.00000 | γ(v2) = 2.800000 | γ(v2) = 18.00000 | |
| β = −1.39 × 108 | β = −54776223 | β = 12618050 | β = 1.67 × 108 | β = 14131934 | β = −3.48 × 108 | β = 4.41 × 108 | β = −4.82 × 108 | β = −7.15 × 108 | β = −4.18 × 108 | β = −1.63 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0015 | p(β) = 0.1059 | p(β) = 0.0098 | p(β) = 0.0096 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0356 | p(β) = 0.0000 | p(β) = 0.0481 | p(β) = 0.0000 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 1.92 × 108 *** | α = −45136055 *** | α = −33460314 *** | α = 7.96 × 108 *** | α = −45633528 *** | α = 5.07 × 108** | α = −5.06 × 108 *** | α = 2.43 × 108 | α = −43864590 | α = 5.63 × 108 *** | α = −1.67 × 108 |
| p(α) = 0.0000 | p(α) = 0.0000 | p(α) = −33460314 | p(α) = 0.0022 | p(α) = 0.0022 | p(α) = 0.0116 | p(α) = 0.0000 | p(α) = 0.2424 | p(α) = 0.4810 | p(α) = 0.0000 | p(α) = 0.6702 | |
| γ(v) = 0.000200 | γ(v) = 0.000000 | γ(v) = 0.001100 | γ(v) = 0.000000 | γ(v) = 0.000000 | γ(v) = 0.000100 | γ(v) = 0.000500 | γ(v) = 0.000200 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000200 | |
| γ(v2) = 3.000000 | γ(v2) = 184.0000 | γ(v2) = 0.800000 | γ(v2) = 13.80000 | γ(v2) = 3.000000 | γ(v2) = 3.000000 | γ(v2) = 106.0000 | γ(v2) = 62.00000 | γ(v2) = 33.00000 | γ(v2) = 2.000000 | γ(v2) = 56.00000 | |
| β = −2.50 × 108 *** | β = −32277771 *** | β = 38845417 *** | β = −8.97 × 108 *** | β = 72315272 *** | β = −9.53 × 108 *** | β = 3.33 × 108 *** | β = −2.09 × 109 *** | β = −4.86 × 108 *** | β = −6.86 × 108 *** | β = −3.32 × 109 *** | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0008 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 93822114 *** | α = −35351857 *** | α = −1.39 × 108 *** | α = −6.31 × 108 *** | α = −75102201 *** | α = −4.52 × 108** | α = −2.35 × 108 *** | α = −2.83 × 109 *** | α = 9.20 × 108 *** | α = −1.06 × 109 *** | α = −2.20 × 109 *** |
| p(α) = 0.0001 | p(α) = 0.0006 | p(α) = 0.0009 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0118 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0008 | |
| γ(v) = 0.000100 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000400 | γ(v) = 0.001400 | γ(v) = 0.001300 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000600 | |
| γ(v2) = 275.0000 | γ(v2) = 3.000000 | γ(v2) = 2.000000 | γ(v2) = 10.00000 | γ(v2) = 3.000000 | γ(v2) = 62.00000 | γ(v2) = 88.00000 | γ(v2) = 0.000000 | γ(v2) = 3.000000 | γ(v2) = 4.000000 | γ(v2) = 4.000000 | |
| β = −2.44 × 108 *** | β = 48896285 *** | β = 1.30 × 108 *** | β = 6.85 × 108 *** | β = 76972857 *** | β = −8.81 × 108 *** | β = −6.87 × 108 *** | β = −3.77 × 109 *** | β = −1.23 × 109 *** | β = 1.20 × 109 *** | β = −6.32 × 109 *** | |
| p(β) = 0.0000 | p(β) = 0.0018 | p(β) = 0.0022 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = −3.75 × 108 | α = 33610219 | α = 47907338 | α = −3.42 × 108 | α = −20157929 | α = −2.07 × 108 | α = 2.02 × 108 | α = −9.60 × 108 | α = −1.48 × 108 | α = 3.01 × 108 | α = −9.90 × 108 |
| p(α) = 0.0000 | p(α) = 0.0935 | p(α) = 0.0991 | p(α) = 0.0021 | p(α) = 0.0004 | p(α) = 0.0006 | p(α) = 0.0283 | p(α) = 0.0516 | p(α) = 0.0216 | p(α) = 0.0000 | p(α) = 0.1089 | |
| γ(v) = 0.000000 | γ(v) = 0.001700 | γ(v) = 0.000100 | γ(v) = 0.000000 | γ(v) = 0.001200 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000500 | γ(v) = 0.000500 | γ(v) = 0.000000 | γ(v) = 0.000500 | |
| γ(v2) = 3.000000 | γ(v2) = 7.800000 | γ(v2) = 3.100000 | γ(v2) = 3.000000 | γ(v2) = 1.000000 | γ(v2) = 13.00000 | γ(v2) = 5.200000 | γ(v2) = 18.00000 | γ(v2) = 14.00000 | γ(v2) = 3.000000 | γ(v2) = 7.000000 | |
| β = 2.75 × 108 | β = −2.69× 108 | β = −77572526 | β = 8.20 × 108 | β = 72167564 | β = −5.57 × 108 | β = −4.17 × 108 | β = −1.90 × 109 | β = −5.08 × 108 | β = −3.12 × 108 | β = −2.75 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0128 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0006 | p(β) = 0.0007 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0003 | |
| IT | α = 1.11 × 108 | α = −8355379 | α = 45631207 | α = −1.65 × 108 | α = −12536134 | α = −75446519 | α = −4.98 × 108 | α = −4.29 × 108 | α = 62332150 | α = 9.05 × 108 | α = −1.10 × 109 |
| p(α) = 0.0000 | p(α) = 0.5523 | p(α) = 0.0027 | p(α) = 0.0323 | p(α) = 0.0877 | p(α) = 0.0017 | p(α) = 0.0000 | p(α) = 0.0016 | p(α) = 0.3307 | p(α) = 0.0248 | p(α) = 0.0000 | |
| γ(v) = 0.000100 | γ(v) = 0.000100 | γ(v) = 0.000000 | γ(v) = 0.000100 | γ(v) = 0.000100 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000700 | γ(v) = 0.000500 | γ(v) = 5.00 × 10−5 | γ(v) = 0.001300 | |
| γ(v2) = 8.000000 | γ(v2) = 95.00000 | γ(v2) = 2.500000 | γ(v2) = 2.000000 | γ(v2) = 0.000100 | γ(v2) = 9.000000 | γ(v2) = 14.50000 | γ(v2) = 14.00000 | γ(v2) = 16.00000 | γ(v2) = 0.600000 | γ(v2) = 9.000000 | |
| β = −1.46 × 108 | β = −47640379 | β = −57588745 | β = 2.19 × 108 | β = 18373368 | β = −3.39 × 108 | β = 4.42 × 108 | β = −3.48 × 108 | β = −7.34 × 108 | β = −9.12 × 108 | β = −1.52 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0022 | p(β) = 0.0005 | p(β) = 0.0052 | p(β) = 0.0094 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0452 | p(β) = 0.0000 | p(β) = 0.0278 | p(β) = 0.0000 | |
| NL | α = 2.78 × 108 | α = 38605586 | α = 2.94 × 108 | α = −25374134 | α = 1.70 × 108 | α = −3.53 × 108 | α = −26871777 | α = −1.95 × 108 | α = −36321946 | α = 56192718 | α = 7.13 × 108 |
| p(α) = 0.0000 | p(α) = 0.0041 | p(α) = 0.0000 | p(α) = 0.8458 | p(α) = 0.0000 | p(α) = 0.0144 | p(α) = 0.5284 | p(α) = 0.4473 | p(α) = 0.6730 | p(α) = 0.0003 | p(α) = 0.2025 | |
| γ(v) = 0.000000 | γ(v) = 0.000300 | γ(v) = 0.000000 | γ(v) = 0.000800 | γ(v) = 0.000300 | γ(v) = 0.000900 | γ(v) = 0.000300 | γ(v) = 0.000000 | γ(v) = 0.000300 | γ(v) = 0.000200 | γ(v) = 0.000300 | |
| γ(v2) = 28.00000 | γ(v2) = 46.00000 | γ(v2) = 67.00000 | γ(v2) = 35.00000 | γ(v2) = 61.00000 | γ(v2) = 12.00000 | γ(v2) = 46.00000 | γ(v2) = 24.00000 | γ(v2) = 10.00000 | γ(v2) = 56.00000 | γ(v2) = 20.00000 | |
| β = −4.65 × 108 | β = −87889369 | β = −3.34 × 108 | β = 1.05 × 109 | β = −96635944 | β = −7.69 × 108 | β = −2.74 × 108 | β = −1.99 × 109 | β = −5.32 × 108 | β = −2.27 × 108 | β = −4.09 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 21866974 | α = −55309042 | α = −47541453 | α = 63000971 | α = 38029277 | α = −1.80 × 108 | α = −4.49 × 108 | α = 1.09× 109 | α = −28675315 | α = −2.51 × 108 | α = 7.78 × 108 |
| p(α) = 0.1893 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.5419 | p(α) = 0.0000 | p(α) = 0.0775 | p(α) = 0.0000 | p(α) = 0.0073 | p(α) = 0.7820 | p(α) = 0.0000 | p(α) = 0.2130 | |
| γ = 0.260000 | γ = 0.125000 | γ = 0.105000 | γ = 0.260000 | γ = 0.260000 | γ = 0.150007 | γ = 0.125000 | γ = 0.045000 | γ = 0.045000 | γ = 0.185000 | γ = 0.045000 | |
| β = −1.91 × 108 | β = −23718891 | β = 49958982 | β = −3.50 × 108 | β = −47918652 | β = −2.43 × 108 | β = 3.61 × 108 | β = −2.82× 109 | β = −4.08 × 108 | β = 2.46 × 108 | β = −3.91 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0039 | p(β) = 0.0000 | p(β) = 0.0787 | p(β) = 0.0000 | p(β) = 0.0932 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0003 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 92010477 | α = −28695977 | α = 1.56 × 108 | α = 1.44× 108 | α = −29449879 | α = −8.15 × 108 | α = −2.35 × 108 | α = −2.84 × 109 | α = 3.03× 108 | α = −4.84 × 108 | α = −2.11 × 109 |
| p(α) = 0.0101 | p(α) = 0.0026 | p(α) = 0.0569 | p(α) = 0.0037 | p(α) = 0.0312 | p(α) = 0.0000 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0039 | |
| γ = 0.130000 | γ = 0.250000 | γ = 0.015000 | γ = 0.280000 | γ = 0.050000 | γ = 0.120000 | γ = 0.280000 | γ = 0.180000 | γ = 0.185000 | γ = 0.180000 | γ = 0.095000 | |
| β = −1.41 × 108 | β = 55977109 | β = −1.76 × 108 | β = −3.17 × 108 | β = 35053661 | β = −5.01 × 108 | β = −6.87 × 108 | β = −4.01 × 109 | β = −8.95× 108 | β = 8.47 × 108 | β = −5.21 × 109 | |
| p(β) = 0.0029 | p(β) = 0.0057 | p(β) = 0.0362 | p(β) = 0.0032 | p(β) = 0.0175 | p(β) = 0.0104 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = 1.74 × 108 | α = 33610219 | α = −17031872 | α = 4.05 × 108 | α = −17480899 | α = −4.47 × 108 | α = −1.64 × 108 | α = −5.56 × 108 | α = −1.63 × 108 | α = 15029386 | α = −5.82 × 108 |
| p(α) = 0.0524 | p(α) = 0.0935 | p(α) = 0.0394 | p(α) = 0.0000 | p(α) = 0.0074 | p(α) = 0.0023 | p(α) = 0.0001 | p(α) = 0.4288 | p(α) = 0.0398 | p(α) = 0.3310 | p(α) = 0.4967 | |
| γ = 0.030000 | γ = 0.285000 | γ = 0.285000 | γ = 0.285000 | γ = 0.180000 | γ = 0.285000 | γ = 0.165000 | γ = 0.050000 | γ = 0.075000 | γ = 0.280000 | γ = 0.050000 | |
| β = −3.33 × 108 | β = −2.69 × 108 | β = −30269582 | β = −2.80 × 108 | β = 69381445 | β = −2.35 × 108 | β = 1.44 × 108 | β = −2.15 × 109 | β = −3.83 × 108 | β = 1.18 × 108 | β = −2.75 × 109 | |
| p(β) = 0.0004 | p(β) = 0.0000 | p(β) = 0.1170 | p(β) = 0.0148 | p(β) = 0.0000 | p(β) = 0.0002 | p(β) = 0.0353 | p(β) = 0.0042 | p(β) = 0.0000 | p(β) = 0.0013 | p(β) = 0.0028 | |
| IT | α = 56514979 | α = −31002928 | α = −12239438 | α = −1.23 × 108 | α = 1946513 | α = −42185082 | α = −1.56 × 108 | α = −4.80 × 108 | α = −2.07 × 108 | α = 1.35 × 109 | α = −9.43 × 108 |
| p(α) = 0.0008 | p(α) = 0.0114 | p(α) = 0.0129 | p(α) = 0.3962 | p(α) = 0.6772 | p(α) = 0.1360 | p(α) = 0.0002 | p(α) = 0.0097 | p(α) = 0.0001 | p(α) = 0.1786 | p(α) = 0.0000 | |
| γ = 0.165000 | γ = 0.120008 | γ = 0.120000 | γ = 0.015000 | γ = 0.050000 | γ = 0.270000 | γ = 0.270000 | γ = 0.120000 | γ = 0.240000 | γ = 0.005000 | γ = 0.270000 | |
| β = −1.05× 108 | β = −23728318 | β = 7616633 | β = 1.73 × 108 | β = 4855150 | β = −3.55 × 108 | β = −2.42 × 108 | β = −1.95 × 108 | β = −6.55 × 108 | β = −1.33 × 109 | β = −1.60 × 109 | |
| p(β) = 0.0001 | p(β) = 0.1215 | p(β) = 0.2155 | p(β) = 0.2392 | p(β) = 0.3325 | p(β) = 0.0000 | p(β) = 0.0080 | p(β) = 0.3990 | p(β) = 0.0000 | p(β) = 0.1858 | p(β) = 0.0001 | |
| NL | α = 51104705 | α = 46425219 | α = 1.38× 108 | α = 6.65 × 108 | α = 1.50 × 108 | α = −3.56 × 108 | α = 9289179 | α = 7.35 × 109 | α = −54581588 | α = 85513062 | α = −2.21 × 108 |
| p(α) = 0.1573 | p(α) = 0.0311 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0186 | p(α) = 0.8916 | p(α) = 0.1536 | p(α) = 0.5236 | p(α) = 0.0023 | p(α) = 0.7546 | |
| γ = 0.265005 | γ = 0.055009 | γ = 0.265000 | γ = 0.265000 | γ = 0.055000 | γ = 0.150000 | γ = 0.055000 | γ = 1.00 × 10−8 | γ = 0.060000 | γ = 0.055000 | γ = 0.060000 | |
| β = −4.29 × 108 | β = −79055937 | β = −3.02× 108 | β = −1.27 × 109 | β = −44212311 | β = −7.88 × 108 | β = −2.60 × 108 | β = −8.77 × 109 | β = −5.46 × 108 | β = −2.32× 108 | β = −2.64 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0006 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.1203 | p(β) = 0.0003 | p(β) = 0.0004 | p(β) = 0.0897 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0006 | |
References
- Agur, Itai. 2003. Trade-volume Hysteresis: An Investigation Using Aggregate Data. Research Memorandum WO No. 740. Amsterdam, The Netherlands: Research Department, De Nederlandsche Bank NV. [Google Scholar]
- Baker, Scott R., Nick Bloom, and Steven J. Davis. 2016. Economic Political Uncertainty. Available online: http://www.policyuncertainty.com/index.html (accessed on 19 December 2016).
- Baldwin, Richard, and Paul Krugman. 1989. Persistent Trade Effects of Large Exchange Rate Shocks. The Quarterly Journal of Economics 104: 635–54. [Google Scholar] [CrossRef]
- Belke, Ansgar, and Dominik Kronen. 2015. Exchange Rate Bands of Inaction and Play-Hysteresis in Greek Exports to the Euro Area, the US and Turkey: Sectoral Evidence. Empirica 43: 349–90. [Google Scholar] [CrossRef]
- Belke, Ansgar, and Thorsten Polleit. 2009. Monetary Economics in Globalised Financial Markets. Heidelberg: Springer-Verlag. [Google Scholar]
- Belke, Ansgar, and Ulrich Volz. 2015. The Strong Euro Challenges for the European Central Bank and Implications for the Global Economy. AEI Insights 1: 53–68. [Google Scholar]
- Belke, Ansgar, Matthias Göcke, and Martin Günther. 2013. Exchange Rate Bands of Inaction and Play-Hysteresis in German Exports—Sectoral Evidence for Some OECD Destinations. Metroeconomica 64: 152–79. [Google Scholar] [CrossRef]
- Belke, Ansgar, Matthias Göcke, and Laura Werner. 2014. Hysteresis Effects in Economics—Different Methods for Describing Economic Path-dependence. In Hysteresis—Types, Applications and Behavior Patterns in Complex Systems. Edited by José Carlos Dias. New York: Nova Publishers, pp. 19–42. [Google Scholar] [CrossRef]
- Belke, Ansgar, Matthias Göcke, and Laura Werner. 2015a. Exchange Rate Volatility and other Determinants of Hysteresis in Exports—Empirical Evidence for the Euro Area. Review of Economic Analysis 7: 25–53. [Google Scholar]
- Belke, Ansgar, Anne Oeking, and Ralph Setzer. 2015b. Domestic Demand, Capacity Constraints and Exporting Dynamics: Empirical Evidence for Vulnerable Euro Area Countries. Economic Modelling 48: 315–25. [Google Scholar] [CrossRef]
- Bertelsmann-Stiftung. 2016. Fokuspapier. Die Folgen eines Brexit aus der Sicht Deutscher und Britischer Unternehmen. Available online: https://www.bertelsmann-stiftung.de/fileadmin/files/BSt/Publikationen/GrauePublikationen/NW_Brexit-2016_DE.pdf (accessed on 8 August 2018).
- Börse-Online. 2017. Historische Kursdaten für EURO STOXX 50. Available online: http://www.boerse-online.de/index/historisch/Euro_Stoxx_50 (accessed on 12 May 2017).
- Cameron, David. 2013. EU Speech at Bloomberg. Available online: https://www.gov.uk/government/speeches/eu-speech-at-bloomberg (accessed on 9 July 2017).
- Campa, José Manuel. 2004. Exchange Rates and Trade: How Important Is Hysteresis in Trade. European Economic Review 48: 527–48. [Google Scholar] [CrossRef]
- Côté, Agathe. 1994. Exchange Rate Volatility and Trade: A Survey. Working Paper 94-5, International Department, Bank of Canada Ottawa, Ottawa, ON, Canada. Available online: https://www.bankofcanada.ca/wp-content/uploads/2010/04/wp94-5.pdf (accessed on 12 May 2017).
- De Grauwe, Paul. 2016. Economics of Monetary Union. New York: Oxford University Press. [Google Scholar]
- Dixit, Avinash. 1989. Entry and Exit Decisions under Uncertainty. Journal of Political Economy 97: 620–38. [Google Scholar] [CrossRef]
- Eurostat. 2017a. EU Handel nach SITC seit 1988 (DS-018995). Available online: https://data.europa.eu/euodp/de/data/dataset/PNtLrEMxMmcWouzaCbJSg (accessed on 8 August 2017).
- Eurostat. 2017b. Euro/Ecu-Wechselkurse—Monatliche Daten. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=ert_bil_eur_m&lang=de (accessed on 12 May 2017).
- Eurostat. 2017c. Produktion in der Industrie—Monatliche Daten. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=sts_inpr_m&lang=de (accessed on 12 May 2017).
- Federal Reserve Bank of Saint Louis. 2017. TED Spread (TEDRATE). Available online: https://fred.stlouisfed.org/series/TEDRATE (accessed on 12 May 2017).
- Fedoseeva, Svetlana, and Laura Werner. 2014. Asymmetry and Hysteresis: Two Perspectives on Pricing-to-Market Nonlinearity. Working Paper 2014.02, International Network for Economic Research, Cologne, Germany. Available online: www.infer-research.eu/en/publications/download/40 (accessed on 12 May 2017).
- Ilmakunnas, Pekka, and Satu Nurmi. 2010. Dynamics of Export Market Entry and Exit. The Scandinavian Journal of Economics 112: 101–26. [Google Scholar] [CrossRef]
- Impulitti, Giammario, Alfonso A. Irarrazabal, and Luca David Opromolla. 2013. A Theory of Entry into and Exit from Export Markets. Journal of International Economics 90: 75–90. [Google Scholar] [CrossRef]
- Kannebley, Sérgio, Jr. 2008. Tests for the Hysteresis Hypothesis in Brazilian Industrialized Exports. A threshold cointegration analysis. Economic Modelling 252: 171–90. [Google Scholar] [CrossRef]
- Máñez, Juan A., María E. Rochina-Barrachina, and Juan A. Sanchis. 2008. Sunk Costs Hysteresis in Spanish Manufacturing Exports. Review of World Economics 144: 272–94. [Google Scholar] [CrossRef]
- OECD. 2017a. Economic Outlook No. 102. November 2017: GDP Deflators, Forecast Growth. Available online: http://stats.oecd.org/Index.aspx?QueryId=61354# (accessed on 12 May 2017).
- OECD. 2017b. Inflation (CPI). Available online: https://data.oecd.org/price/inflation-cpi.htm (accessed on 12 May 2017).
| 1 | There are also other mechanisms that can widen or narrow the band of inaction. These are described in detail in Belke et al. (2014). |
| 2 | |
| 3 | The following also applies to British exports, but with the reverse (positive) sign: We assume a euro-pound exchange rate expressed as an indirect quotation, that is, in pounds per euro. |
| 4 | Based on the procedure described in Belke et al. (2014). |
| 5 | France: Le Monde and Le Figaro; Italy: Corriere Della Sera and La Repubblica; the United Kingdom: The Times of London and Financial Times; Spain: El Mundo and El País. |
| 6 | The play area may be too large to be passed through completely. |
| 7 | Only in the regression with national EPUI does the exchange rate variable again have a “false”, that is, positive sign. |
| 8 | In this paper, we had all data for the relevant variables up to April 2016. |
| 9 | It makes sense that in general, only an upward movement in the spurt variable is possible, since the pound depreciated sharply in this time period. A downward movement would require a sharp appreciation of the pound. |
| 10 | We counted all cases in which the results were significant and had the theoretically expected sign. |
| 11 | It should be noted, however, that in the framework of the regressions conducted here, a devaluation of the pound appeared to have no positive effect on British exports. |
| SICT Product Groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Total | |
| BE | α = 1.92 × 108 *** | α = −45136055 *** | α = −33460314 *** | α = 7.96 × 108 *** | α = −45633528 *** | α = 5.07 × 108** | α = −5.06 × 108 *** | α = 2.43 × 108 | α = −43864590 | α = 5.63 × 108 *** | α = −1.67 × 108 |
| p(α) = 0.0000 | p(α) = 0.0000 | p(α) = −33460314 | p(α) = 0.0022 | p(α) = 0.0022 | p(α) = 0.0116 | p(α) = 0.0000 | p(α) = 0.2424 | p(α) = 0.4810 | p(α) = 0.0000 | p(α) = 0.6702 | |
| γ(v) = 0.000200 | γ(v) = 0.000000 | γ(v) = 0.001100 | γ(v) = 0.000000 | γ(v) = 0.000000 | γ(v) = 0.000100 | γ(v) = 0.000500 | γ(v) = 0.000200 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000200 | |
| γ(v2) = 3.000000 | γ(v2) = 184.0000 | γ(v2) = 0.800000 | γ(v2) = 13.80000 | γ(v2) = 3.000000 | γ(v2) = 3.000000 | γ(v2) = 106.0000 | γ(v2) = 62.00000 | γ(v2) = 33.00000 | γ(v2) = 2.000000 | γ(v2) = 56.00000 | |
| β = −2.50 × 108 *** | β = −32277771 *** | β = 38845417 *** | β = −8.97 × 108 *** | β = 72315272 *** | β = −9.53 × 108 *** | β = 3.33 × 108 *** | β = −2.09 × 109 *** | β = −4.86 × 108 *** | β = −6.86 × 108 *** | β = −3.32 × 109 *** | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0008 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| GE | α = 93822114 *** | α = −35351857 *** | α = −1.39 × 108 *** | α = −6.31 × 108 *** | α = −75102201 *** | α = −4.52 × 108** | α = −2.35 × 108 *** | α = −2.83 × 109 *** | α = 9.20 × 108 *** | α = −1.06 × 109 *** | α = −2.20 × 109 *** |
| p(α) = 0.0001 | p(α) = 0.0006 | p(α) = 0.0009 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0118 | p(α) = 0.0005 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0000 | p(α) = 0.0008 | |
| γ(v) = 0.000100 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000400 | γ(v) = 0.001400 | γ(v) = 0.001300 | γ(v) = 0.000200 | γ(v) = 0.000100 | γ(v) = 0.000600 | |
| γ(v2) = 275.0000 | γ(v2) = 3.000000 | γ(v2) = 2.000000 | γ(v2) = 10.00000 | γ(v2) = 3.000000 | γ(v2) = 62.00000 | γ(v2) = 88.00000 | γ(v2) = 0.000000 | γ(v2) = 3.000000 | γ(v2) = 4.000000 | γ(v2) = 4.000000 | |
| β = −2.44 × 108 *** | β = 48896285 *** | β = 1.30 × 108 *** | β = 6.85 × 108 *** | β = 76972857 *** | β = −8.81 × 108 *** | β = −6.87 × 108 *** | β = −3.77 × 109 *** | β = −1.23 × 109 *** | β = 1.20 × 109 *** | β = −6.32 × 109 *** | |
| p(β) = 0.0000 | p(β) = 0.0018 | p(β) = 0.0022 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| FR | α = −3.75 × 108 | α = 33610219 | α = 47907338 | α = −3.42 × 108 | α = −20157929 | α = −2.07 × 108 | α = 2.02 × 108 | α = −9.60 × 108 | α = −1.48 × 108 | α = 3.01 × 108 | α = −9.90 × 108 |
| p(α) = 0.0000 | p(α) = 0.0935 | p(α) = 0.0991 | p(α) = 0.0021 | p(α) = 0.0004 | p(α) = 0.0006 | p(α) = 0.0283 | p(α) = 0.0516 | p(α) = 0.0216 | p(α) = 0.0000 | p(α) = 0.1089 | |
| γ(v) = 0.000000 | γ(v) = 0.001700 | γ(v) = 0.000100 | γ(v) = 0.000000 | γ(v) = 0.001200 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000500 | γ(v) = 0.000500 | γ(v) = 0.000000 | γ(v) = 0.000500 | |
| γ(v2) = 3.000000 | γ(v2) = 7.800000 | γ(v2) = 3.100000 | γ(v2) = 3.000000 | γ(v2) = 1.000000 | γ(v2) = 13.00000 | γ(v2) = 5.200000 | γ(v2) = 18.00000 | γ(v2) = 14.00000 | γ(v2) = 3.000000 | γ(v2) = 7.000000 | |
| β = 2.75 × 108 | β = −2.69× 108 | β = −77572526 | β = 8.20 × 108 | β = 72167564 | β = −5.57 × 108 | β = −4.17 × 108 | β = −1.90 × 109 | β = −5.08 × 108 | β = −3.12 × 108 | β = −2.75 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0128 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0006 | p(β) = 0.0007 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0003 | |
| IT | α = 1.11 × 108 | α = −8355379 | α = 45631207 | α = −1.65 × 108 | α = −12536134 | α = −75446519 | α = −4.98 × 108 | α = −4.29 × 108 | α = 62332150 | α = 9.05 × 108 | α = −1.10 × 109 |
| p(α) = 0.0000 | p(α) = 0.5523 | p(α) = 0.0027 | p(α) = 0.0323 | p(α) = 0.0877 | p(α) = 0.0017 | p(α) = 0.0000 | p(α) = 0.0016 | p(α) = 0.3307 | p(α) = 0.0248 | p(α) = 0.0000 | |
| γ(v) = 0.000100 | γ(v) = 0.000100 | γ(v) = 0.000000 | γ(v) = 0.000100 | γ(v) = 0.000100 | γ(v) = 0.001300 | γ(v) = 0.000000 | γ(v) = 0.000700 | γ(v) = 0.000500 | γ(v) = 5.00 × 10−5 | γ(v) = 0.001300 | |
| γ(v2) = 8.000000 | γ(v2) = 95.00000 | γ(v2) = 2.500000 | γ(v2) = 2.000000 | γ(v2) = 0.000100 | γ(v2) = 9.000000 | γ(v2) = 14.50000 | γ(v2) = 14.00000 | γ(v2) = 16.00000 | γ(v2) = 0.600000 | γ(v2) = 9.000000 | |
| β = −1.46 × 108 | β = −47640379 | β = −57588745 | β = 2.19 × 108 | β = 18373368 | β = −3.39 × 108 | β = 4.42 × 108 | β = −3.48 × 108 | β = −7.34 × 108 | β = −9.12 × 108 | β = −1.52 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0022 | p(β) = 0.0005 | p(β) = 0.0052 | p(β) = 0.0094 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0452 | p(β) = 0.0000 | p(β) = 0.0278 | p(β) = 0.0000 | |
| NL | α = 2.78 × 108 | α = 38605586 | α = 2.94 × 108 | α = −25374134 | α = 1.70 × 108 | α = −3.53 × 108 | α = −26871777 | α = −1.95 × 108 | α = −36321946 | α = 56192718 | α = 7.13 × 108 |
| p(α) = 0.0000 | p(α) = 0.0041 | p(α) = 0.0000 | p(α) = 0.8458 | p(α) = 0.0000 | p(α) = 0.0144 | p(α) = 0.5284 | p(α) = 0.4473 | p(α) = 0.6730 | p(α) = 0.0003 | p(α) = 0.2025 | |
| γ(v) = 0.000000 | γ(v) = 0.000300 | γ(v) = 0.000000 | γ(v) = 0.000800 | γ(v) = 0.000300 | γ(v) = 0.000900 | γ(v) = 0.000300 | γ(v) = 0.000000 | γ(v) = 0.000300 | γ(v) = 0.000200 | γ(v) = 0.000300 | |
| γ(v2) = 28.00000 | γ(v2) = 46.00000 | γ(v2) = 67.00000 | γ(v2) = 35.00000 | γ(v2) = 61.00000 | γ(v2) = 12.00000 | γ(v2) = 46.00000 | γ(v2) = 24.00000 | γ(v2) = 10.00000 | γ(v2) = 56.00000 | γ(v2) = 20.00000 | |
| β = −4.65 × 108 | β = −87889369 | β = −3.34 × 108 | β = 1.05 × 109 | β = −96635944 | β = −7.69 × 108 | β = −2.74 × 108 | β = −1.99 × 109 | β = −5.32 × 108 | β = −2.27 × 108 | β = −4.09 × 109 | |
| p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0001 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | p(β) = 0.0000 | |
| Spurt Movements Since January 2016 | Country | SITC Product Groups | ||||
|---|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | TOTAL | ||
| Constant | Belgium | − | − | ↑ | ↑ | ↑ |
| Germany | − | − | − | − | − | |
| France | − | − | ↑ | ↑ | ↑ | |
| Italy | − | − | − | − | ↑ | |
| Netherlands | − | − | ↑ | ↑ | ↑ | |
| Exchange rate volatility | Belgium | ↑ | − | − | − | − |
| Germany | ↑ | − | − | ↑ | − | |
| France | ↑ | ↑ | ↑ | − | ↑ | |
| Italy | − | ↑ | ↑ | − | − | |
| Netherlands | − | − | ↑ | ↑ | ↑ | |
| EPUI | Belgium | − | − | ↑ | − | ↑ |
| Germany | − | − | − | − | − | |
| France | − | − | ↑ | − | − | |
| Italy | − | ↑ | − | − | − | |
| Netherlands | − | − | − | ↑ | − | |
| Euro Stoxx 50 | Belgium | ↑ | ↑ | − | − | − |
| Germany | − | − | − | ↑ | ↑ | |
| France | − | ↑ | ↑ | − | − | |
| Italy | − | − | − | − | − | |
| Netherlands | − | − | − | ↑ | − | |
| TED Spread | Belgium | − | − | ↑ | ↑ | ↑ |
| Germany | ↑ | − | − | − | − | |
| France | ↑ | − | ↑ | ↑ | ↑ | |
| Italy | ↑ | − | ↑ | − | ↑ | |
| Netherlands | − | − | ↑ | ↑ | ↑ | |
| Exchange rate volatility + EPUI | Belgium | ↑ | − | − | − | − |
| Germany | − | − | − | ↑ | − | |
| France | − | ↑ | − | − | − | |
| Italy | − | ↑ | − | − | − | |
| Netherlands | − | − | ↑ | − | − | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belke, A.; Ptok, S. British-European Trade Relations and Brexit: An Empirical Analysis of the Impact of Economic and Financial Uncertainty on Exports. Int. J. Financial Stud. 2018, 6, 73. https://doi.org/10.3390/ijfs6030073
Belke A, Ptok S. British-European Trade Relations and Brexit: An Empirical Analysis of the Impact of Economic and Financial Uncertainty on Exports. International Journal of Financial Studies. 2018; 6(3):73. https://doi.org/10.3390/ijfs6030073
Chicago/Turabian StyleBelke, Ansgar, and Sebastian Ptok. 2018. "British-European Trade Relations and Brexit: An Empirical Analysis of the Impact of Economic and Financial Uncertainty on Exports" International Journal of Financial Studies 6, no. 3: 73. https://doi.org/10.3390/ijfs6030073
APA StyleBelke, A., & Ptok, S. (2018). British-European Trade Relations and Brexit: An Empirical Analysis of the Impact of Economic and Financial Uncertainty on Exports. International Journal of Financial Studies, 6(3), 73. https://doi.org/10.3390/ijfs6030073





