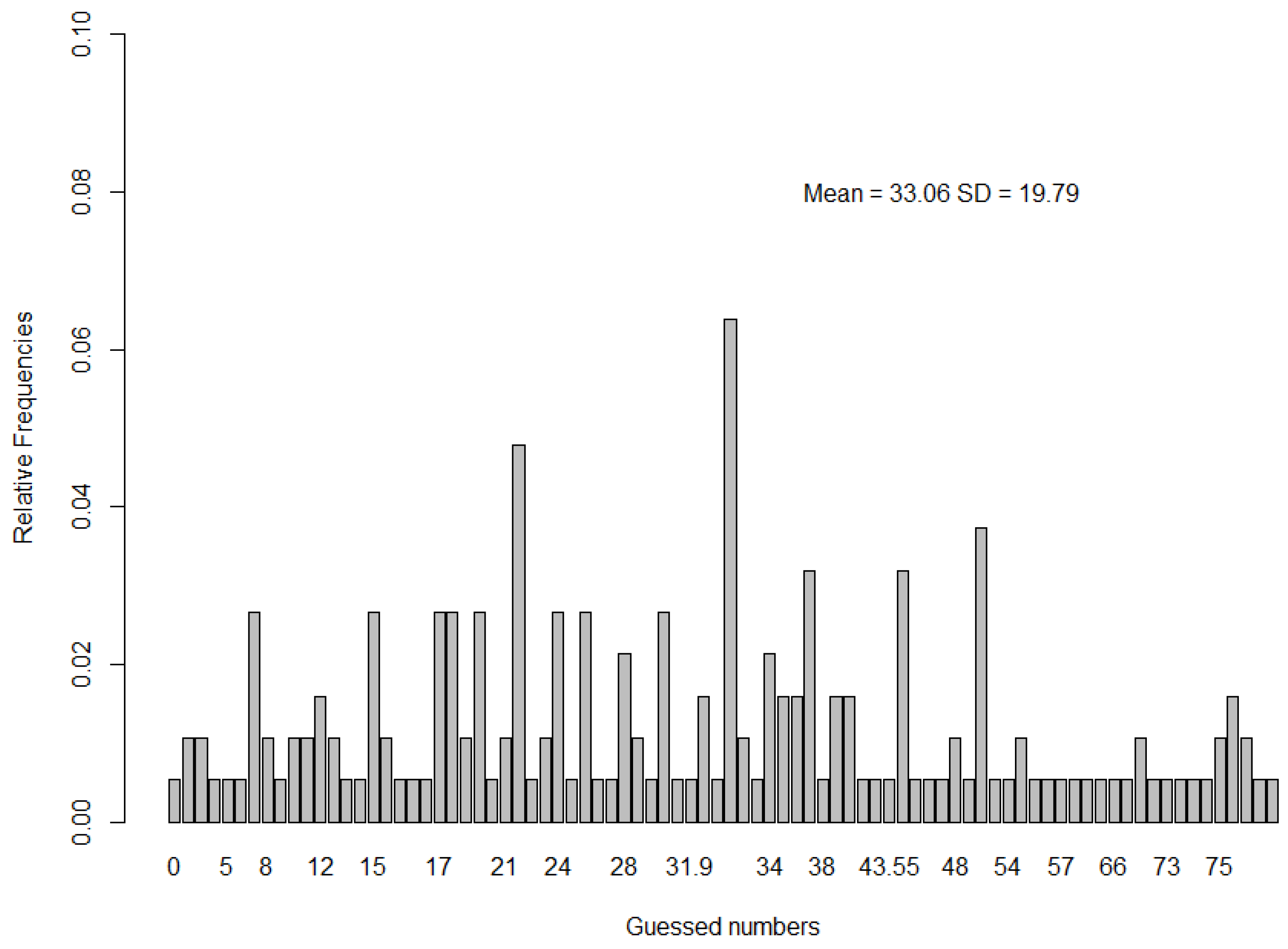
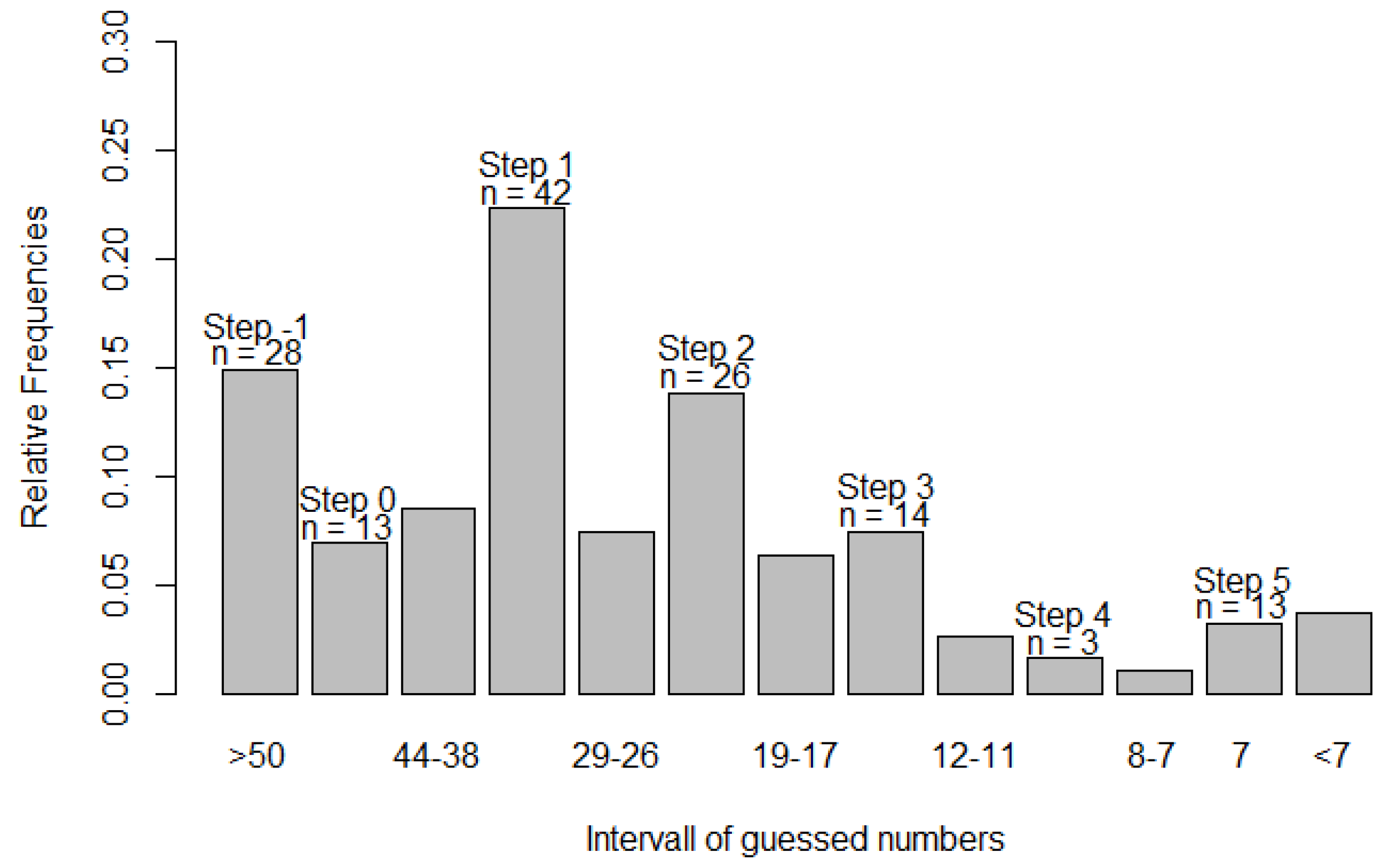
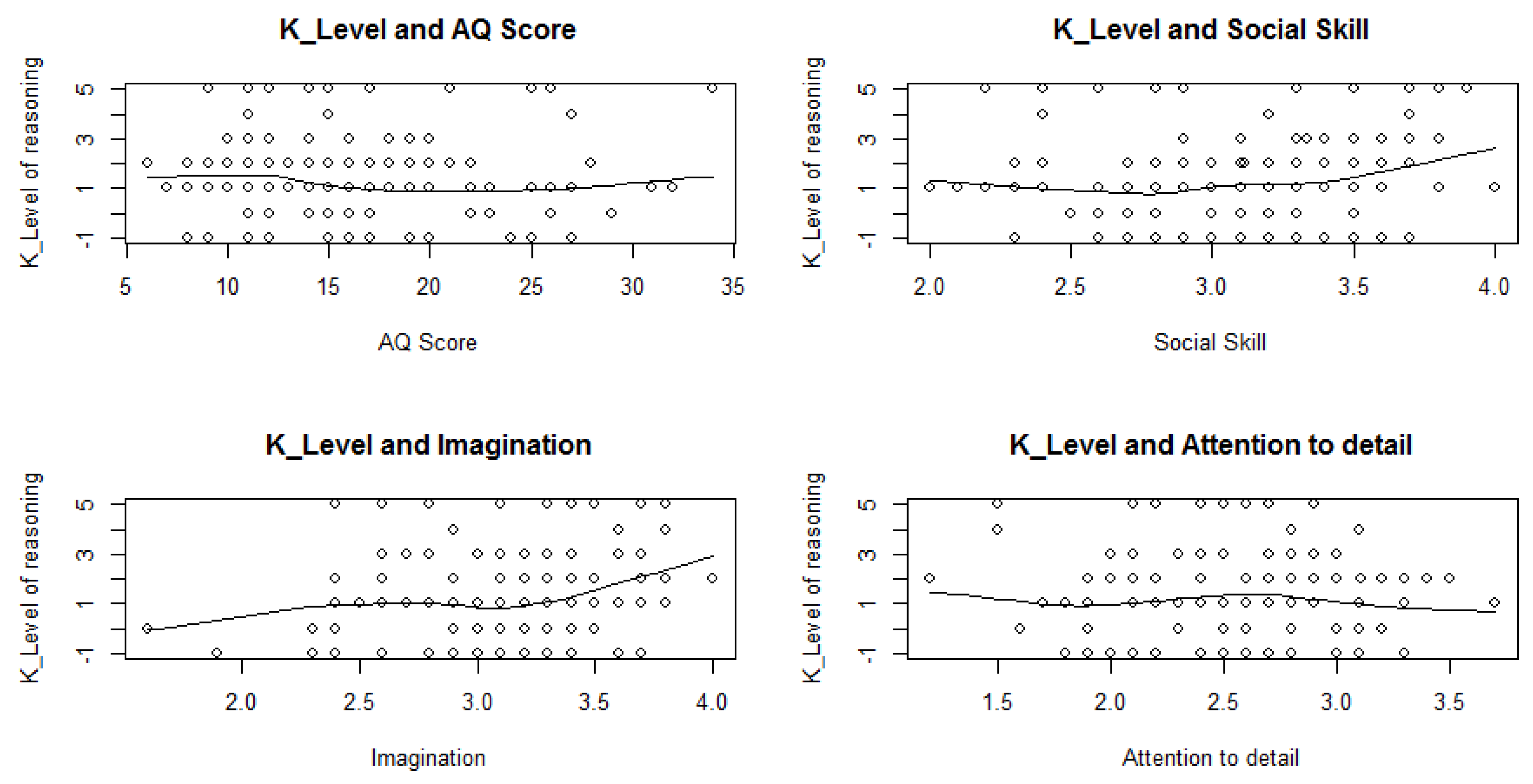
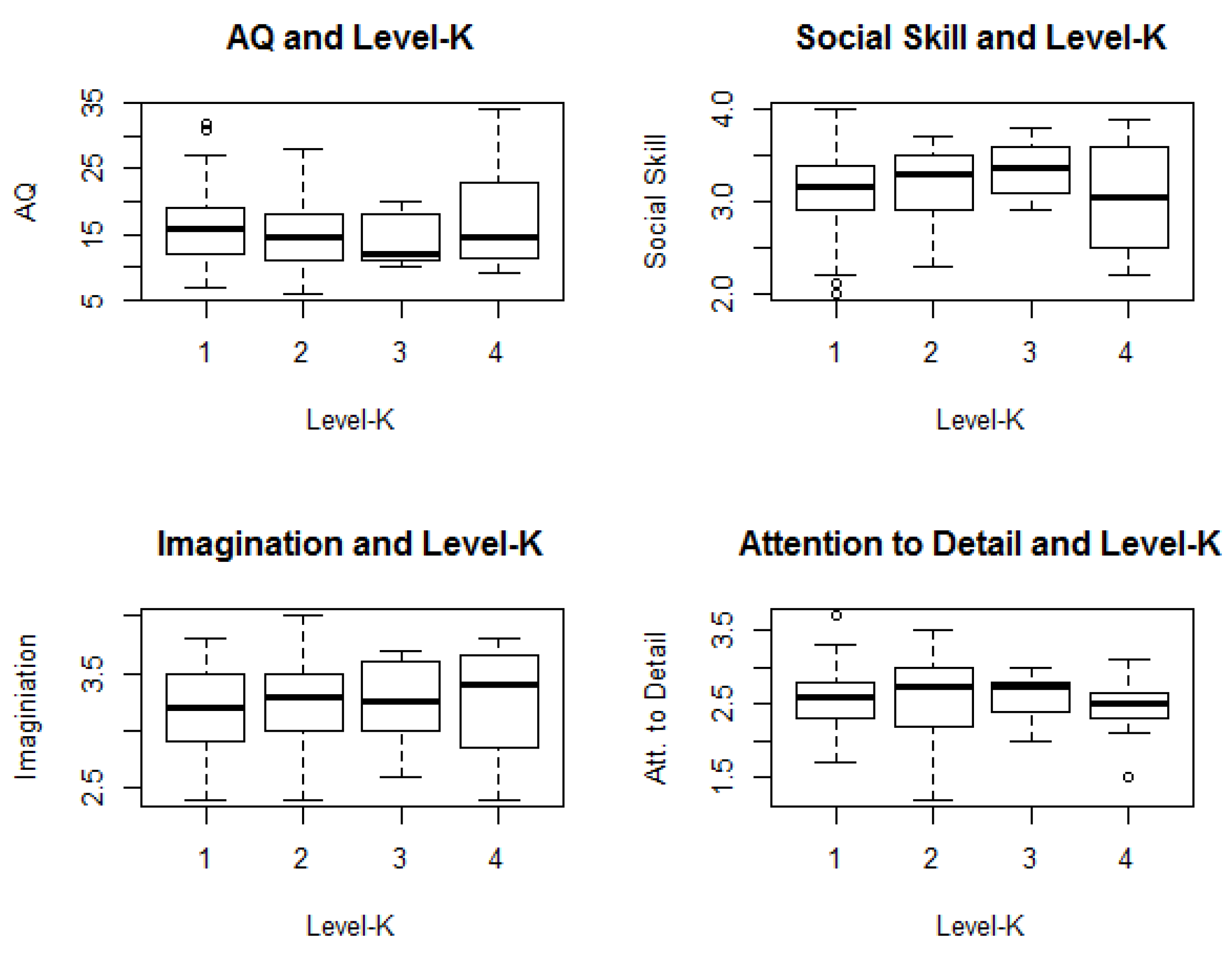
We first report the general distribution of guessed numbers in the beauty contest game and their correlation with all other measures, and then we turn to the analysis of depth of reasoning and its predictors. Finally, we report whether the likelihood of success in strategic decision-making can be predicted using the different subscales of the AQ.
As a second step in the analysis, we calculated correlation coefficients between all measures. In line with previous research (Baron-Cohen [
5], Hoekstra et al. [
27]), we found significant correlations between the AQ score and gender (women = 1, men = 0),
r = −0.16,
p = 0.03 and the AQ score and self-ascribed math skill (
r = −0.24,
p = 0.001), indicating that participants high on AQ rated their own math skills as superior to their fellow students. Furthermore, the correlation between gender and self-ascribed math skill (
r = 0.2,
p = 0.008) indicated that males assumed to hold higher math skills than females, and women scored higher on imagination than males (
r = 0.45,
p < 0.001). Finally, we found significant correlations between some of the subscales of the AQ. The inter-correlations of all measures are depicted in
Table 1.
2.1. Analysis of Level-K Reasoning and AQ Measures
To identify each participant’s depth of reasoning, we computed how many iterated steps of reasoning were carried out. In line with Kocher and Sutter [
28], denoting each player’s
i choice
xi, the depth of reasoning of player
i is defined as
L that solves
xi = qL × m, with
q = 2/3. Since we played a one-shot beauty contest game, we set
m = 50 as has been done in other beauty contest games with an interval [0; 100] (Bosch-Doménech [
2], Ho and Camerer [
7], Kocher and Sutter [
28], Kocher and Sutter [
29]). The resulting continuous values of
L were grouped into discrete categories (
L = 0, 1, 1.5, 2, 2.5, … 5) by defining the neighborhood intervals for chosen numbers with boundaries [
qd + 1/4 × m,
qd − 1/4 × m]. Participants who picked numbers that were greater than 50,
xi >
m, were grouped into a single category with
L < 0 and all values below
xi < 7 were also grouped into the highest level-K. According to this procedure, for example, participants grouped into
L = 1 (referred to as L1 players), picked a number within the interval [30; 37]. The relative frequencies of the depth of reasoning of participants, neighboring intervals, and interim intervals are presented in
Figure 2.
The intermediate intervals were then omitted in the subsequent analyses, since numbers could not be captured by the model (Nagel [
6]). We were able to classify 73.9% of the sample, which reduced the sample size to
N = 139. We then analyzed the results for the AQ score and the three subscales, which yielded internal consistency (Cronbach’s alpha > 6).
We then examined the data using scatterplot with a smoother (Loess, a nonparametric, graphical tool for depicting relationships between variables; Jacoby [
30]) for the AQ score and the three subscales which yielded internal consistency (alpha > 6) (see
Figure 3).
We ran a regression analysis to examine the relationship between the depth of reasoning (as measured by L) with the total AQ score as well as with each of the subscales of the AQ. The data yields a curvilinear relationship for the social skills subscale. We tested this relationship via a linear polynomial regression with a second degree polynomial predictor (quadratic regression). We found that a quadratic regression fit the data significantly better in the case of social skills, F(1,136) = 4.40, p = 0.04, but not in the case of the AQ score, F(1,136) = 2.86, p = 0.09, and the other subscales, that is, imagination, F(1,133) = 1.12, p = 0.29, and attention to detail, F(1,136) = 0.22, p = 0.64. This finding indicates that participants scoring very low as well as very high on social skills are likely to carry out more steps of strategic reasoning than participants with average social skills. Furthermore, while only a trend, this curvilinear pattern can also be observed with regard to the total AQ scores.
Next, we carried out individual stepwise linear regressions since all predictors were highly correlated. We first entered the respective predictor and then added math skill and gender sequentially (see
Table 2). We found that both imagination and social skills were significant predictors of depth of reasoning, even when controlling for math skill and gender. Imagination was linearly related to depth of reasoning,
b = 1.12,
t (126) = 2.9,
p = 0.005. By contrast, we again found a curvilinear relationship between depth of reasoning and social skills. Thus, even when controlling for math skills and gender, both low and high social skills were associated with greater depth of reasoning, while medium social skills were associated with less strategic reasoning as indicated by the significant second polynomial term,
b = 1.48,
t (128) = 2.17,
p = 0.032, and first order polynomial,
b = −8.58,
t (128) = −2.07,
p = 0.04. The resulting estimates for all models are depicted in
Table 2.
Importantly, however, the statistical analyses so far do not shed light on the question of whether social skills actually increased the likelihood of winning the beauty contest game, since very high levels of strategic reasoning (indicated by very low numbers in the beauty contest game) do not necessarily mean that players are likely to be successful in the game. To illustrate, in the present study, the target number was 33.06 × 2/3 = 22.04. Hence, level-3 or level-4 players had picked a number too low to win the game.
2.2. Distance to the Target Number and AQ Scores
To measure success in the beauty contest game, we calculated the absolute difference between the number entered by a participant and the winning number (two-thirds of the mean), thereby following Coricelli and Nagel [
18]. We multiplied the absolute difference with −1, so that less distance between target number and picked number results in values close to zero, while large differences result in higher negative numbers. This measure is referred to as strategic IQ (Coricelli and Nagel [
18]), with high values meaning a high strategic IQ. Next, we used strategic IQ as dependent variable in the same analytical procedure as used above.
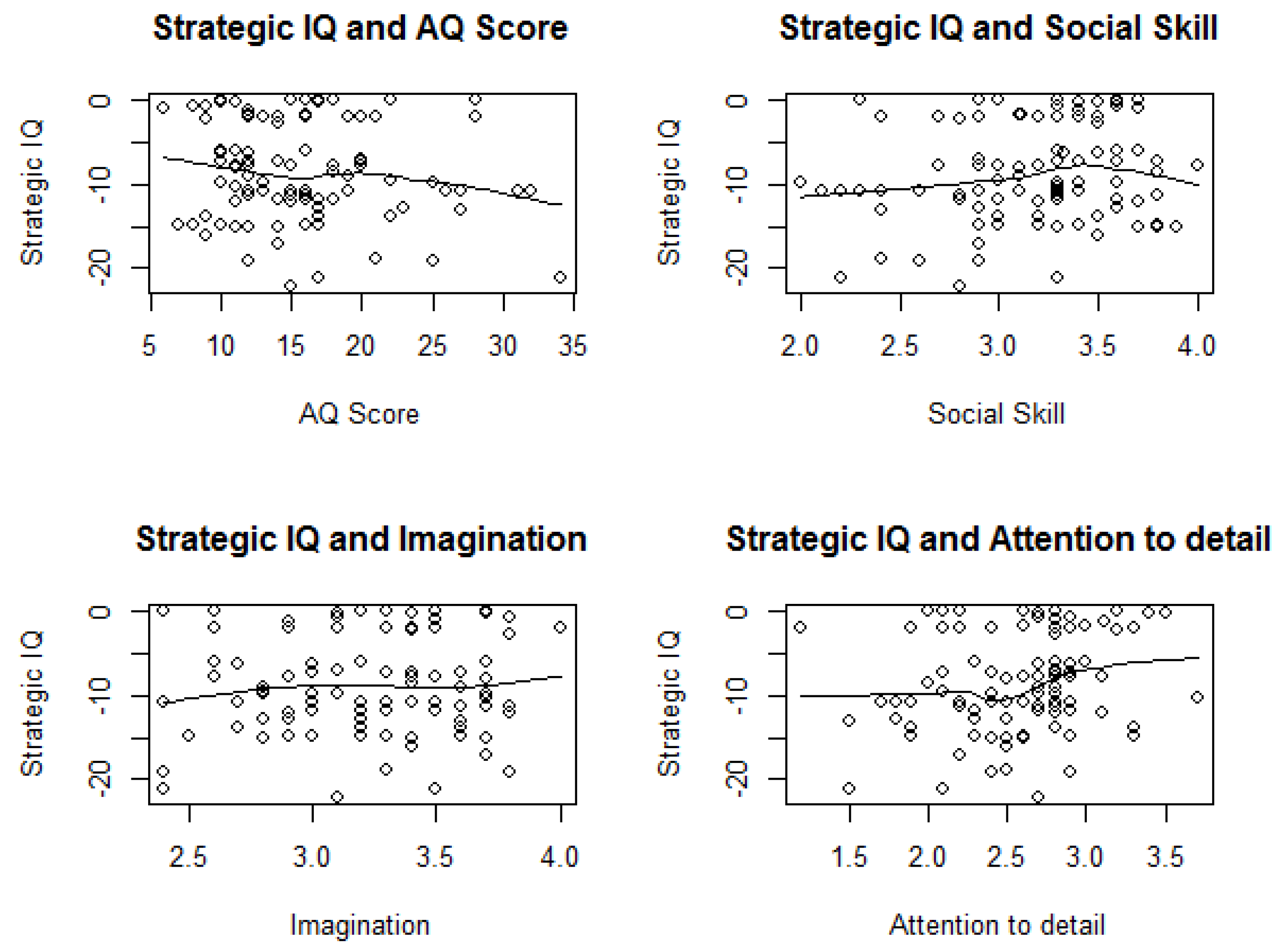
Results showed that strategic IQ was not significantly predicted by the total AQ Score. In line with our hypothesis, however, we found that the social skills subscale of the AQ predicted strategic IQ,
b = 5.23,
t (185) = 1.91,
p = 0.057. Moreover, imagination predicted strategic IQ with
b = 4.42,
t (181) = 1.63,
p = 0.11, although this prediction failed to reach significance. This indicates that higher social skills as well as imagination are associated with higher strategic IQ. All regression models and estimates are depicted in
Table 3.
In sum, the social skills subscale was a marginally significant predictor of successful decision-making in the beauty contest game, indicating that individuals with higher scores in social skills also yielded a higher strategic IQ. In other words, individuals scoring higher in the social skills subscale of the AQ were more successful in the beauty contest game. Furthermore, entering both predictors in one regression and using an ANOVA testing which predictor explains more variance shows a significant effect for social skills, p = 0.05, but not for imagination, p = 0.28. Taken together, our findings show that higher social skills are associated with a higher likelihood of success in strategic decision-making.
2.3. Checking Results for Sophisticated Players with L ≥ 1
Following the suggestion of a reviewer, we checked if our results are only driven by the difference between
L0 players and
L ≥ 1 players. Players with
L0 are qualitatively different from other players in that they are not playing a best response to any belief about their opponent. Therefore, they are not strategically rational in any sense of the word. For this reason we carried out the same analysis as above for players who are considered at least level 1. In addition, we aggregated players with L5 and L4 because of limited cell sizes (L4 with
n = 3 and L5 with
n = 13). We find a trend of the inverted U function only for social skills (see
Figure 4). The plot shows, that participants scoring high on social skills are more frequently in the group of L3, while participants scoring low on social skills are found more frequently in the L4 as well as the L1 group.
To assess if social skills vary significantly between groups of level-K we used ANOVAs. Level-K was entered as the independent variable and AQ, social skill, imagination, and attention to detail were entered as the dependent variable in separate ANOVAs. Although a trend, the difference was not significant for social skill,
F(3,94) = 2.06,
p = 0.11. All other ANOVAs yielded
ps > 0.28. A pairwise comparison for each level-K and social skill with
t-tests show that L1 differs from L3,
p = 0.029 and L3 from L4 with
p = 0.035 (see
Table 4).
We then turned to the second dependent variable strategic IQ. First, we plotted the dependent variable Strategic IQ as a function of AQ, social skill, imagination, and attention to detail (see
Figure 5).
Then we carried out the same analysis as before (see
Table 5). Results were robust for the predictor social skills
1. Furthermore, attention to detail yielded a marginal significant effect, showing that, when having at least L = 1, higher attention to detail is predictive of a higher strategic IQ.