Compliance with the Euro Area Financial Criteria and Economic Convergence in the European Union over the Period 2000–2023

Abstract

The two groups of EU economies, the euro area and the non-euro area, are statistically analyzed taking into account the fulfillment of the euro area financial criteria and economic performance over the period 2000–2023. Compliance with financial criteria, economic performance, and their significant influencing factors are presented comparatively for the two groups of countries. The long-run equilibrium between economic growth and its factors is identified by econometric approaches with the error correction model (ECM) and autoregressive distributed lag (ARDL) models for the two data panels. In the short term, economic shocks are taken into account to compare their different influences on economic growth within the two groups of countries. The GMM system is used to model economic convergence at the EU level over the period under review. Comparisons between GDP growth and its theoretical values from econometric models have led to interesting conclusions regarding the existence and characteristics of economic convergence at the group and EU level. EU countries outside the euro area have higher economic growth rates than euro area economies over the period 2000–2023. In the long run, investment brings a higher increase in economic development in EU countries outside the euro area than in euro area countries. Economic shocks have been felt more deeply on economic growth in the euro area than in the non-euro area. The speed of adjustment towards long-run equilibrium in econometric models is slower for non-euro area economies than in the euro area over a one-year period. At the level of the European Monetary Union, change policies have a faster impact on economic development and a faster speed of adjustment towards equilibrium.

1. Introduction

Currently, 20 EU countries belong to the Eurozone. On 1 January 1999, 11 European Union countries adopted the euro: Austria, Belgium, Finland, France, Germany, Ireland, Italy, Luxembourg, the Netherlands, Portugal, and Spain. The first new member of the Eurozone was Greece on 1 January 2001, and the most recent member of the Eurozone, the 20th, is Croatia on 1 January 2023. Euro area countries have fully implemented the euro-related policies of the Economic and Monetary Union (EMU). On 1 January 1999, the Exchange Rate Mechanism II (ERM II) was established to ensure that volatility in the exchange rates of the euro and other EU currencies does not affect the economic stability of the single market. The Economic and Monetary Union (EMU) provides stability and sustainable growth across the euro area.

The remaining seven EU countries: Bulgaria, the Czech Republic, Denmark, Hungary, Poland, Romania, and Sweden would have to meet the convergence criteria to join the euro area, with the exception of Denmark, which obtained a special opt-out from the Maastricht Treaty in 1992. The other six countries are required to adopt the euro when they meet the convergence criteria, including being part of the European Exchange Rate Mechanism (ERM II) for at least two years.

As part of the regular two-year convergence criteria reporting cycle, the European Central Bank and the European Commission examine and review the economic convergence of EU countries in the process of adopting the euro. Their report covers the last ten years and presents the evolution of prices, fiscal balances, the debt ratio, exchange rates, and long-term interest rates, as well as other socio-economic indicators important for the integration in the euro area of the remaining non-euro EU countries (ECB, 2020).

Denmark meets the conditions for convergence to the euro area, but using the “non-participation clause” in the EU treaties, it is exempted from the obligation to adopt the euro.

The 2022 report assessed the sustainability aspects of convergence for each country, except Denmark (ECB, 2022). A common assessment framework is applied to each EU country under review. The report’s conclusions aim to achieve strong governance with sustainable public finances to ensure production growth in the medium and long term.

Macroeconomic stability is a prerequisite for sustainable convergence to ensure an efficient business environment. Economic integration with the euro zone allows synchronization with economic cycles.

Our work contributes to the analysis of compliance with the convergence criteria by both euro area economies and non-euro area EU Member States. The conclusions underline the importance of respecting the financial convergence criteria to ensure the economic convergence of EU countries. Another contribution is econometric approaches to explain EU economic convergence influenced by national debt management and investment decisions, for the euro area, the EU area outside the euro area, as well as at the EU level.

Our study presents the statistical situation of the Eurozone economies, as well as those outside the EU euro area, for each financial criterion. Compliance with financial criteria ensures economic growth. Testing the existence of a long-term relationship attests to the economic convergence of economic growth, investment, and debt strategies. For both groups, as well as at the EU level, economic growth is mainly influenced by the same factors. Our econometric models explain the different influences on GDP growth in different situations. Testing the significance of differences between the model coefficients provides information about economic convergence and the way and group level at which it operates.

2. Literature Framework and Working Hypotheses

The public debt of Eurozone countries, its dynamic stability, and its nonlinear behavior on economic growth were research subjects for many economists (Baum et al., 2012; Cao et al., 2024; Checherita-Westphal & Rother, 2010; De Soyres et al., 2022; Katsikas et al., 2023; Lagoa et al., 2022).

The economic convergence in euro-based economies was studied by many authors (Haynes & Haynes, 2016; Quiroga, 2007; Vojinović et al., 2010; Yin et al., 2003).

The sustainability of public debt (World Bank & IMF, 2001) was also analyzed in the context of a long-term relationship with economic growth and the financial criteria by Menuet and Villieu (2014), and by Rao Aiyagari and McGrattan (1998).

Our paper analyzes the economic convergence of both the euro area and the non-euro EU area, based on the existence of a long-run relationship between GDP and the debt/GDP ratio, investment, and openness. The convergence in the post-communist economies was studied by Vojinović et al. (2010) and by Vratislav (2009).

Our paper envisages and characterizes the economic convergence as a “dynamic and multivariate concept” (Haynes & Haynes, 2016). The concept of convergence involves multiple cross-sections, analyzed over a period of time; it is also a dynamic and spatial concept. The multivariate aspect takes into account the number of explanatory variables of the countries considered at the level of the studied group.

Economic convergence is described by the long-term relationship between GDP and its significant influencing factors in a given area. The dynamic character is given by the time-varying nature of the long-term relationship under different economic shocks.

The process of economic integration is based on specific objectives and accepted rules to ensure economic convergence (Quiroga, 2007). Compliance with the financial criteria for joining the euro area ensures EU economic convergence.

The financial criteria for joining the euro area were established by the Maastricht Treaty of 1991. Every two years, the financial convergence criteria for joining the euro area are assessed and updated in Convergence Reports by the European Commission and the European Central Bank.

The two last Convergence Reports of 2020 and 2022, with reference periods April 2019 to March 2020 and May 2021 to April 2022, respectively, set the reference value for the price stability criterion of 4.9%, the reference value of the 2022 Convergence Report (1.8% of the 2020 Convergence Report). The inflation rate over one year cannot be higher than 1.5 percentage points above the rate of the three best-performing Member States.

Sound and sustainable public finances presuppose compliance with the following budget deficit and public debt conditions:

-

The criterion of the government’s budgetary position according to which the deficit/GDP ratio is less than 3% of GDP. Candidate countries for the euro area cannot be in the excessive deficit procedure; Romania is the only country in this situation until 2024.

-

Gross public debt (percentage of GDP) should be lower than 60%.

The exchange rate criterion, for the stability of exchange rates of the national currency and the euro, requires that the countries entering the euro area should participate in the Exchange Rate Mechanism II for at least two years.

The long-term interest rate criterion of 2.6% is the reference value of the 2022 Convergence Report (2.9% of the 2020 Convergence Report). The long-term interest rate should not be more than 2 percentage points above the rate of the three best-performing Member States in terms of price stability.

Economic convergence must be followed by legal convergence. Legal convergence assumes the corresponding legal alignment with the EU legislation related to the National Central Banks.

Our study analyzes the state of compliance with the euro area financial criteria by all EU member states’ economies and provides an analysis of economic development through statistical methods in Section 4.1.

The objectives of the study can be summarized in two sets of hypotheses: one to attest to the existence of economic convergence of groups of countries, and the second to explain some general characteristics of the convergence mechanism. The hypotheses regarding the existence of economic convergence are:

H1. 

There is economic convergence between the countries in the euro area.

H2. 

There is economic convergence of EU countries outside the euro area.

H3. 

There is economic convergence between EU countries.

The hypotheses that describe the characteristics of the convergence mechanism are as follows:

H4. 

Economic growth rates are higher in economies outside the euro area than in those within the euro area.

H5. 

Investments are the engine of economic development.

H6. 

The more developed the level of the organizational entity, the faster the speed of adjustment towards equilibrium. The speed of adjustment is slower outside the euro area than inside the euro area.

H7. 

Economic shocks have a smaller negative influence in the non-Euro area than in the euro area.

These hypotheses are verified by the results of statistical analyses and econometric models in Section 4.2 of our paper. The conclusions are formulated in Section 5.

3. Materials and Methods

3.1. Data and Variables

The data for the euro area form a long panel, consisting of twenty countries, and the period analyzed is twenty-three years. The panel data for non-euro area EU countries covers seven countries for the same period, also being a long panel. The following variables were collected from EUROSTAT and were used in the proposed econometric models (Mbaye et al., 2018). Some of these variables were calculated to verify compliance with the convergence criteria through various statistical methods:

CPI—Consumer Price Index (%) with fixed base in 2015;

RINFL—inflation rate (%);

LIM_AVG_RINF—upper limit allowed for accepting price stability (%);

CAB_GDP—current account balance as a percentage of GDP (%);

DEBT_GDP—debt-to-GDP ratio (%);

REXCH—annual changes (%) of exchange rates;

REXCH2015—annual data of real effective exchange rates (REER) (deflator: consumer price index—20 trading partners—euro area from 2023), as dynamic indices with fixed base in 2015;

LONG_INT_R—long-term interest rate (%);

LIM_LONG_INTR—average performance limit of the three best-performing Member States plus 2 percentage points;

GDP—real Gross Domestic Product (mil. euro 2010);

LN_GDP—logarithm of the real Gross Domestic Product;

YRGDP—yearly dynamic rate of GDP (%);

OPN—ratio of commercial flows of Imports plus Exports as a percentage of the GDP (%);

GFCF—investments, as real Gross Fix Capital Formation (mil. euro 2010);

LN_GFCF—logarithm of the investment (GFCF);

GFCF_GDP—ratio between Gross Fix Capital Formation and GDP (%).

The interpretation of the results and the conclusions of the study compare the degree of compliance with the financial criteria by the two groups of EU countries during the period 2000–2023. The study analyses the economic convergence of the euro area, non-euro area, and for the EU countries and shows that this is ensured by compliance with the euro area financial criteria.

3.2. Statistical Analysis and Econometric Models

Considering both groups of euro area and non-euro area EU Member States, it shows the better positions of euro area countries compared to the others and highlights the advantages of membership of the euro area and the European Monetary Union (EMU).

Graphical analyses of the evolution of convergence indicators and comparisons with the upper limits calculated for each criterion each year allow conclusions to be drawn regarding the positions of countries and their efforts to meet the convergence criteria.

The analysis of compliance with the convergence criteria is based on comparing the evolution graphs of the indicators with certain permitted limits. These limits can be fixed, such as 60% for the debt-to-GDP ratio, −3% for the budget deficit, or variable limits calculated as the average level of the three best-performing countries in the euro area, which differ from year to year, in the case of price stability and of the long-term interest rate.

We used the simple correlation coefficient to analyze the compliance of the actual indicators with the price stability and the long-term interest rate criteria in the European Union. This analysis was carried out by sub-periods and for the entire period, both for the euro area and for the EU countries outside the euro area.

We use the SPSS Statistics 23 program for graphs for the variables of the two groups of countries and various tests, such as the t-test for independent samples for equality of means, one-sample t-tests for 95% confidence intervals of the variation in the variables.

The econometric approach to GDP evolution, using its logarithmic expression through LN_GDP (denoted by y_it, where i is the country and t is the year), both in the euro area and outside the euro area, considers as explanatory variables those that are directly influenced by the financial convergence criteria.

Correlation analysis, Granger causality analysis, and panel cointegration tests suggested the following explanatory variables (x_it, with i—country and t—year): investment dynamics through LN_GFCF, the debt-to-GDP ratio, called DEBT_GDP, and the international openness, OPN, as the ratio between the sum of imports and exports and GDP.

The GDP variable is dynamic depending on its own past values, being persistent, and the regressors are not strictly exogenous.

Long-term equilibrium represents the economic convergence of the groups of countries analyzed: the Eurozone, the EU non-euro area, and at the EU level.

Unobserved heterogeneity, heteroscedasticity, and autocorrelation of residuals along cross-sections—that is, within countries but not across them—are addressed by using Generalized Method of Moments (GMM) panel models (Mehrhoff, 2009). When the GMM Difference estimator can produce a biased and inefficient estimate (Blundell & Bond, 1998) of the coefficient of the lagged dependent variable, then the problem is solved by System GMM. But the GMM system proposed by Arellano and Bover (1995) is used for the short panel. We will use GMM panel data models to analyze economic convergence at the EU level during the period 2000–2023, because we have a short panel (n = 27 countries and T = 24 years, n > T).

When handling long panels, ECM (Error Correction Models) and ARDL (Autoregressive Distributed Lag) models can provide a dynamic approach. The existence of a long-run equilibrium supported by the cointegrating relationship of the variables is identified together with the short-run behavior. We use both Error Correction Models and ARDL models.

If the variables y and x in the Fixed Effects (FEs) model (Equation (1)) are integrated of the same order I(1) and the residuals are stationary I(0), then the variables are cointegrated. They tend to a long-run equilibrium, and Equation (1) is the long-run model. The residuals in Equation (1) represent the error correction term (ECT), whose one lagged value is used in the short-run model in Equation (2), called the Error Correction Model (ECM).

$${\mathrm{y}}_{it}=a_i+\tau x_{it}+{\epsilon }_{it}$$

(1)

$$\Delta y_{it}={\beta }_{0i}+{\beta }_1\Delta x_{it}+{\beta }_2\left(y_{it-1}-\tau x_{it-1}-a_i\right)+u_{it},\mathrm{where}$$

(2)

$${{ECT}_{it-1}=y}_{it-1}-\tau x_{it-1}-a_i$$

(3)

If the coefficient ${\beta }_{2i}$ of the ECT Equation (3) in the ECM (Equation (2)) is negative and significant, then there is a long-run equilibrium, and the coefficient ${\beta }_2$ is the speed of adjustment towards equilibrium over a one-year period, for the countries in the group.

The ARDL approach of Mean Group (MG) and Pooled Mean Group (PMG) can also explain long-term and short-term developments. An advantage of the PMG/ARDL method is that in the short-run equation, it allows the coefficients to differ from country to country, Equation (4). The PMG estimator constrains the long-run coefficients to be identical, but allows the short-run coefficients and the variance of the residuals to vary across countries. The coefficient ${\beta }_{2i}$ in Equation (4), is the speed of adjustment towards equilibrium over a one-year period, for each country i.

$$\Delta y_{it}={\beta }_{0i}+{\beta }_{1i}\Delta x_{it}+{\beta }_{2i}\left(y_{it-1}-\tau x_{it-1}-a_i\right)+u_{it}$$

(4)

The long-run model with the same cointegrating coefficient, $\tau$ represents the economic convergence, specific to each analyzed group of countries in the euro area, non-euro area, and EU countries.

To compare the behavior of each group of countries to economic shocks, we also build econometric models with the corresponding dummy variables. For both approaches, based on appropriate dummy variables, we consider the effects of the 2008 economic crisis (c2008), the effects of COVID-19 in 2020 (covid), and the Russian–Ukrainian war (war). For the effects of the 2008 economic crisis on economic growth, the dummy variable c2008 is 1 for the year 2009, and 0 otherwise. The dummy variable covid is 1 for year 2020, and the variable war—for year 2023. The differences between the coefficients of the dummy variables of economic shocks highlight how they affected economic growth, representing the economic responses of each country and the groups analyzed.

4. Results and Discussion

Our study aims to characterize and compare the state of economic convergence of both types of EU countries, belonging to the euro area and those outside the euro area, by analyzing compliance with financial convergence criteria depending on economic conditions. With accession to the Eurozone, the EU’s economic convergence will ensure the well-being of all its member countries.

4.1. Compliance with Financial Convergence Criteria in the Euro Area and Outside the Euro Area over the Period 2000–2023

The convergence criteria are a set of requirements regarding macroeconomic indicators that EU member states must meet in order to join the euro area. The economic criteria refer to price stability, sustainable public finances, exchange rate stability, and stable long-term interest rates.

The analysis of the compliance status of both groups of EU countries for each criterion highlights the differences in financial performance between the euro area and non-euro area. Meanwhile, membership in the Eurozone offers advantages for a more developed and stronger European Union. Economic differences between EU member states give countries that do not comply with the convergence criteria an inferior status, but also a reason to comply with them.

4.1.1. Price Stability Criterion over the Period 2000–2023

The chart in Figure 1 shows for both groups of EU Member States the evolution of the Consumer Price Index (CPI) over the period 2000–2023, with a fixed base in 2015. The upward trend is steeper over a larger range for countries outside the euro area than for the euro area.

The average annual change in the CPI, in Figure 2, highlights two sub-periods for the two areas. The first sub-period, 2000–2008, shows some stability with constant changes in the CPI for the euro area, and a more volatile downward trend for non-euro countries.

The second sub-period, 2009–2023, shows a similar evolution of the average inflation rates for both groups, but with higher values for non-euro economies. The impact of the 2008 economic crisis produced a deeper CPI decrease in 2009 for the euro area than for non-euro area countries. The inflation rate in 2020 was close to 0 for the euro area, while it was around 2% in non-euro EU countries. Russia’s war against Ukraine, which began in 2022, led to a major change in the CPI of around 10% for the Eurozone and over 12% for non-euro countries.

The average of the annual inflation rates of the three best-performing Member States in terms of price stability, plus 1.5 percentage points, represents the upper limit of the convergence criterion on price stability; this is referred to as LIM_AVG_RINFL in Figure 2. In terms of price stability, the three best-performing Member States are those with the smallest variations in the CPI, called RINFL, and these differ from year to year.

In Figure 2, the average inflation rate (RINFL) in the euro area countries exceeds the admissible limit of the convergence criterion on price stability in the years 2007–2010 and 2021–2023; the major causes of the price increase are the economic crisis in 2008 and after the COVID-19 pandemic in 2020, and the Russian–Ukrainian war in 2022. The 1.8% inflation reference value set by the 2020 Convergence Report was met only in that year. The 2022 Convergence Report increased the inflation benchmark to 4.9%, but it was underestimated because the Russian war that began in February 2022 triggered price increases.

For EU countries outside the euro area, the average inflation rate was below the upper permissible limit only in the years 2013–2017; above the reference value of 1.8% in 2020, and much more in 2022 and 2023. The inflation rate (RINFL) was calculated based on fixed-base CPIs in 2015. The summary data on the inflation rate to be taken into account for the price stability criterion are presented in

Table 1. Average annual inflation rate and corresponding average annual limit allowed for the euro area and outside the euro area over the period of 2000–2023.

	Euro Area		Non-Euro
	RINFL (%)	LIM_AVG_INFL (%)	RINFL (%)	LIM_AVG_INFL (%)
Mean	1.128651	2.406957	3.855328	2.406957
Median	0.030261	2.250000	2.468596	2.250000
Maximum	15.25038	7.910000	34.45198	7.910000
Minimum	−1.086025	0.360000	−1.596573	0.360000
Std. Dev.	1.949242	1.622979	4.547391	1.626272
Skewness	2.574073	1.475974	2.976589	1.475974
Observations	460	460	161	161

, for both the euro area and the non-euro area.

In Figure 3, especially in the second sub-period 2009–2023, after the 2008 economic crisis, almost all euro area countries managed to comply with the price stability criterion, but in the last two years 2022–2023, and especially in 2022, some countries violated it, including Estonia, Latvia, Lithuania, Slovakia, Croatia, and the Netherlands.

In Figure 4, starting in 2009, non-euro area EU countries managed the price stability criterion differently until 2021, when the price boom changed the upward trajectory of the inflation rate over the allowed limit. Denmark and Sweden have almost fully fulfilled the price stability criterion, but represent special cases through their formal decision to postpone joining the euro area. Romania, and especially Hungary, had problems during the analysis period in respecting price stability, being above the admissible limit of this criterion in almost all years.

By analyzing the correlation (r—simple correlation coefficient) between the inflation rate and the upper convergence limit for this criterion, in

Table 2. Compliance with the criterion on price stability in the European Union.

EU Groups	Euro Area Countries			Non-Euro Area Countries
Periods	2000–2008	2009–2023	2000–2023	2000–2008	2009–2023	2000–2023
r	0.321	0.857	0.783	0.146	0.800	0.566
conformity	weak	strong	strong	lack	strong	medium

, we can assess the intensity of compliance by the two groups of EU countries with convergence in price stability.

We see in Table 2 that price stability was gradually achieved after the establishment of the euro area in 1999. Before the 2008 economic crisis, weak convergence for euro area countries corresponded to a complete lack of convergence for EU countries outside the euro area.

In the period of 2009–2023, the euro countries were in strong compliance with the price stability criterion, and this was also the case for non-euro EU countries. Considering the entire period analyzed, we observe strong compliance for the euro area and medium compliance in price convergence for the non-euro EU area.

4.1.2. Budget Deficits and Public Debts in the EU in the Period of 2000–2023

The summarized data of the two indicators to be taken into account for the budgetary criteria are presented in

Table 3. Statistical summary of the budget deficit and debt-to-GDP ratio in euro area and non-euro area EU countries over the period of 2000–2023.

	Euro Area		Non-Euro
	CAB_GDP (%)	DEBT_GDP (%)	CAB_GDP (%)	DEBT_GDP (%)
Mean	−0.703958	66.57701	−0.748214	42.34829
Median	−0.200000	63.62830	−0.800000	40.17136
Maximum	13.70000	212.3881	13.50000	79.77408
Minimum	−20.80000	3.764939	−23.90000	11.94916
Std. Dev.	5.467112	38.53018	5.734244	15.09071
Skewness	−0.492769	0.781217	−0.588121	0.562073
Kurtosis	3.564701	3.787907	4.596349	3.046301
Jarque–Bera	25.80344	61.23995	27.52311	8.860938
Probability	0.000002	0.000000	0.000001	0.011909
Observations	480	480	168	168

, both for the euro area and for the non-euro area: the current account balance as a percentage of the GDP (CAB_GDP) and the debt/GDP ratio (DEBT_GDP).

To achieve sustainable public finances, two requirements must be met: a deficit/GDP ratio below 3% and a gross public debt/GDP ratio below 60%. Figure 5, Figure 6, Figure 7 and Figure 8 reflect how both budgetary criteria were met in the period of 2000–2023.

After the 2008 crisis, starting with 2009, both euro area and non-euro area countries respected on average the threshold of below −3% for the current account balance as a percentage of GDP (denoted by CAB_GDP). If Denmark and Sweden are excluded, countries outside the Eurozone still meet this criterion, on average, after 2009, except for 2022, when the war between Russia and Ukraine began, as seen in Figure 5.

We do not consider Sweden and Denmark in the graph in Figure 5 (right) because they had surplus balances in the period of 2000–2023, as seen in Figure 6. They have already met the economic convergence criteria, and joining the Eurozone is their option. The year 2022 was a difficult one for almost all EU non-euro countries, except for Denmark and Sweden.

In Figure 6, we see Denmark and Sweden with budget surpluses, a positive balance in the analyzed period. Only Hungary and Romania had deficits in 2023. Bulgaria, Poland, and the Czech Republic made efforts to maintain the budget balance higher than −3%.

Looking at public debt as a percentage of GDP, in Figure 7, we see that euro area countries have a significantly higher debt-to-GDP ratio compared to non-euro area EU countries.

Euro area countries benefit from the governance framework of EMU policies. Since 2009, the 60% threshold has been exceeded, on average, by all euro area countries. To compare with the euro area group, we kept the same limits of the graph to see the right place in terms of the size of the average debt-to-GDP ratio for the seven non-euro countries. Considering the debt-to-GDP ratio for each non-euro EU country in Figure 8, we note that only Hungary did not meet the criterion; starting with 2005 and for the rest of the period, it was above the 60% limit.

With the exception of Hungary, all other EU countries outside the euro area comply with the debt criterion over the period 2000–2023. Non-euro countries would have to meet both budgetary requirements imposed by the convergence criteria to join the euro area.

4.1.3. Exchange Rate Criterion in the Period of 2000–2023

Using annual data of real effective exchange rates (REER) (deflator: consumer price index—20 trading partners—euro area from 2023), as dynamic indices with a fixed base in 2015 (REXCH2015), we find the annual changes (%) of exchange rates (REXCH). The statistical summary of the annual changes (%) in exchange rates is presented in

Table 4. Statistical summary of the dynamic rhythms of exchange rates in the euro area and in the non-euro area over the period of 2000–2023.

	Euro Area	Non-Euro	Non-Euro Without Denmark and Sweden
	REXCH (%)	REXCH (%)	REXCH (%)
Mean	0.360484	0.807164	1.471498
Median	0.124715	−0.001766	0.626149
Maximum	9.943644	19.45867	19.45867
Minimum	−8.213416	−16.00922	−16.00922
Std. Dev.	1.776734	4.877708	5.260163
Skewness	2.036987	0.461658	0.235303
Kurtosis	13.01488	5.111733	4.649911
Jarque–Bera	2240.488	35.63420	14.10511
Probability	0.000000	0.000000	0.000865
Observations	460	161	115

for the period of 2000–2023 for the euro area and for the non-euro area.

The standard deviation is smaller for the REXCH in the euro area than for the non-euro EU countries. There is a larger variation in exchange rates for the non-euro EU countries, as can also be seen in Figure 9.

We observe a small range of variations in the real effective exchange rate for euro area countries, especially over the period of 2009–2023. For non-euro area EU countries, the 2000–2010 sub-period recorded high volatility, compared to the following sub-period 2011–2022, which is characterized by a certain stability of exchange rates.

To test whether annual exchange rate changes are significantly different for the euro area and the EU outside the euro area, we use the independent samples t-test for equality of means, using SPSS Statistics 23 software, as shown in

Table 5. Independent samples t-test for euro area and non-euro area (REXCH).

	Levene’s Test for Equality of Variances		t-Test for Equality of Means
	F	Sig.	t	df	Sig. (2-Tailed)	Mean Difference	Std. Error Difference	95% Confidence Interval of the Difference
								Lower	Upper
Equal variances assumed	139.921	0.000	−1.674	619	0.095	−0.447	0.267	−0.971	0.077
Equal variances not assumed			−1.136	175.074	0.258	−0.447	0.393	−1.223	0.329

.

Levene’s test for equality of variances accepts the hypothesis of equal variances with a significant p-value (Sig.) < 1%. In this situation, the t-test gives a calculated t-value less than the theoretical t-value for 619 degrees of freedom (dl) with a p-value of Sig. (two-sided) > 5% accepting the null hypothesis of the two-sided test of equality of means.

The 95% confidence interval of the difference in means changes sign from minus to plus, meaning that the interval contains the value 0 and that the two means may be equal. The conclusion is that, in terms of exchange rate stability, the difference between the averages of the two groups of countries is not significant.

We removed Denmark and Sweden from the group of non-Euro countries and repeated the test for equality of means, comparing the euro area with the updated group of non-euro countries without Denmark and Sweden.

In

Table 6. Testing REXCH for the euro area and non-euro area without Denmark and Sweden.

	Levene’s Test for Equality of Variances		t-Test for Equality of Means
	F	Sig.	t	df	Sig. (2-Tailed)	Mean Difference	Std. Error Difference	95% Confidence Interval of the Difference
								Lower	Upper
Equal variances assumed	169.148	0.000	−3.760	573	0.000	−1.111	0.295	−1.691	−0.531
Equal variances not assumed			−2.233	120.57	0.027	−1.111	0.497	−2.096	−0.126

, the F-statistic of the Levene test recognizes equal variances, and the corresponding t-statistic with a significance Sig. < 1% rejects the null hypothesis of equal means. The negative difference between the means belongs to a negative interval with probability 95%, which preserves the sign.

The conclusion is that the very good situations of Denmark and Sweden change the analysis when they are taken into account in determining compliance with this criterion. When we consider them (Table 5), it seems that there is a convergence of exchange rate stability between the two areas, but, in reality (Table 6), there is no convergence between the euro area and the euro area candidate countries in terms of the exchange rate criterion.

Table 7. One-sample t tests and 95% confidence intervals of REXCH in the period of 2000–2023.

Variable REXCH	N	Mean	Std. Deviation	Std. Error Mean	t	df	Sig. (2-Tailed)	95% Confidence Interval
								Lower	Upper
Euro area	460	0.360	1.777	0.083	4.352	459	0.000	0.1977	0.5233
Non-euro area	161	0.807	4.878	0.384	2.100	160	0.037	0.0480	1.5665
Non-euro, no DK, SW	115	1.471	5.260	0.490	3.000	114	0.003	0.4998	2.4432
EU	621	0.476	2.918	0.117	4.067	620	0.000	0.2463	0.7062

contains the one-sample t-tests for the 95% confidence intervals of the REXCH means for the three groups of EU countries and for the entire European Union, all of which are significant at Sig. < 5%.

The conclusion regarding the stability assurance is that the EU countries outside the euro area still have to face this criterion. In Table 7, we see that the REXCH standard deviation and the mean standard error are larger than for the euro area. The confidence interval of the average exchange rate changes has a higher upper limit than that of the euro area range. If we consider the non-euro area, without Denmark and Sweden, as the two developed countries have already met the convergence criteria, the results tilt upwards. The average annual exchange rate variations, as well as the standard deviation and standard error, are much larger than those of the euro area. The 95% confidence interval is larger, with its limits being higher than those corresponding to all other confidence intervals. The wider range of exchange rate fluctuations is determined by its higher volatility.

This criterion is not met by the group of countries outside the euro area, excluding Denmark and Sweden. In addition, countries must have participated in the European Exchange Rate Mechanism (ERM II) for at least two years.

4.1.4. The Long-Term Interest Rate Criterion in the Period of 2000–2023

The statistical summary of the long-term interest rate (LONG_INT_R) of the countries in the three situations for the euro area, the non-euro area, and the non-euro area excluding Denmark and Sweden, as well as the corresponding admitted limit for the long-term interest rate criterion (LIM_LONG_INTR), is presented in

Table 8. Average long-term interest rate and corresponding permitted limit, for both the euro area and non-euro area countries, over the period of 2000–2023.

	Euro Area		Non-Euro		Non-Euro, No Denmark and Sweden
	long_int_r (%)	limit_long_intr (%)	long_int_r (%)	limit_long_intr (%)	long_int_r (%)	limit_long_intr (%)
Mean	3.362	4.246	3.998	3.541	4.654	4.074
Median	3.650	4.697	3.890	3.610	4.540	3.760
Maximum	22.500	7.350	10.680	6.867	10.680	6.867
Minimum	−0.510	1.567	−0.360	−0.433	0.190	1.567
Std. Dev.	2.477	1.758	2.364	1.888	2.283	1.670
Skewness	1.703	−0.032	0.190	−0.160	0.072	−0.018
Kurtosis	12.258	1.669	2.433	2.129	2.401	1.614
Jarque–Bera	1816.664	33.154	3.052	5.627	1.725	8.731
Probability	0.000	0.000	0.217	0.060	0.422	0.013
Observations	448	448	157	157	109	109

.

The upper limit of the criterion for each year is the average of the minimum long-term interest rates of the three best-performing euro area countries, which differ from year to year, plus 2 percentage points.

The long-term interest rate criterion is respected, on average, by euro area countries, as shown in Figure 10 (left). For EU countries outside the euro area, the impact of the 2008 economic crisis and Russia’s war in Ukraine in 2022 led to an increase in the average long-term interest rate since 2008, above the average performance limit of the three best-performing Member States, plus 2 percentage points, as shown in Figure 10 (right).

Denmark and Sweden met the criterion, as seen in Figure 11, and taking them into account could change the conclusion regarding compliance with this criterion by non-euro countries (

Table 9. Summarizing the conformity with the long-term interest rate criterion in the EU.

EU Groups	Correlation Coefficients			Conformity
	2000–2008	2009–2023	2000–2023	2000–2008	2009–2023	2000–2023
Euro area	0.680	0.627	0.661	medium	medium	medium
Non-euro area	0.638	0.826	0.828	medium	strong	strong
Non-euro no DK, SW	0.383	0.739	0.726	weak	medium	medium

).

EU countries that are not part of the euro area must respect this criterion, as seen in Figure 11. Hungary, and especially Romania, did not comply with it, both being placed above the upper limit allowed for the long-term interest rate.

In Table 9, the euro area countries have the same medium intensity of compliance with the long-term interest rate criterion in the sub-periods of the 2000–2023 period.

The non-euro area is in full compliance with this criterion, after the 2008 economic crisis, but thanks to the two developed countries, Denmark and Sweden, which modify the conclusion regarding the efforts of the other countries outside the euro area.

The non-euro area, excluding Denmark and Sweden, is in weak compliance in the first sub-period of 2000–2008 and then in medium compliance for the second sub-period and for the entire period.

4.2. Convergence of Economic Development in the European Union in the Period of 2000–2023

4.2.1. Evolution of GDP per Capita in Euro and Non-Euro Area in the Period of 2000–2023

To characterize economic development, we analyze the evolution of GDP per capita in constant prices of 2010 and the annual changes in this indicator for both the euro area and outside the euro area. We removed Denmark and Sweden from the group of non-euro area EU countries; their very good performance could affect the conclusions regarding the status of EU countries to join the euro area.

In Figure 12, the difference in the size of GDP per capita in Eurozone countries compared to non-euro EU countries is evident. The two shocks of the 2008 economic crisis and the 2020 pandemic had a greater impact on GDP per capita in Eurozone economies than in those outside the zone.

Annual variations in GDP per capita are larger and more volatile in the period of 2000–2008 in EU countries outside the euro area, and the recovery after the crisis is much faster, with higher dynamic rates than in the euro area.

4.2.2. Modeling Economic Convergence in Euro Area Countries in the Period of 2000–2023

Economic convergence in EU countries is seen as a common direction of long-term GDP development, as a macroeconomic indicator characterizing the overall development performance of the EU.

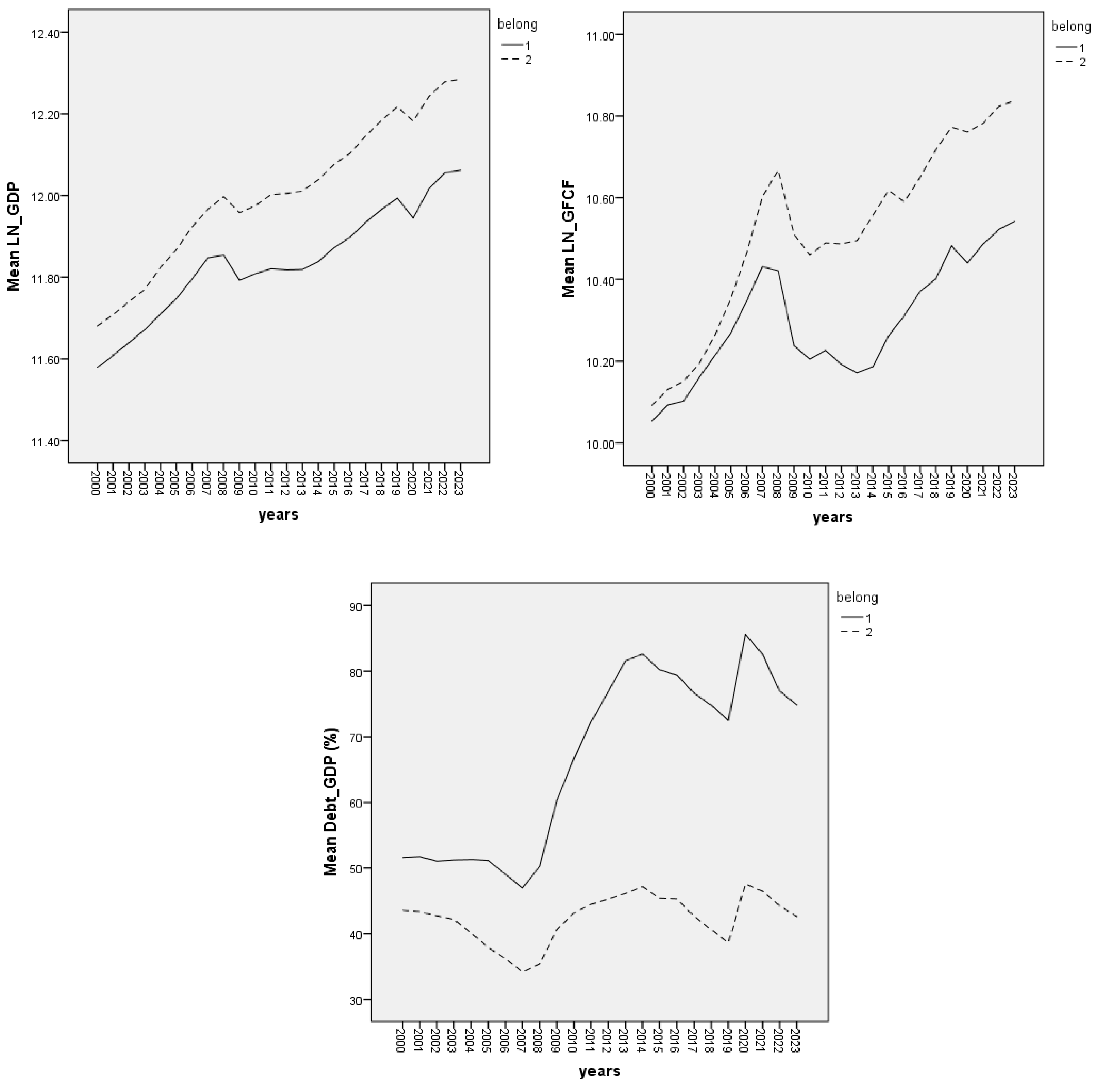
All efforts to meet the convergence criteria are reflected in the size of GDP and its dynamics. All convergence criteria are global indicators that have a national level of determination, and the use of GDP instead of GDP per capita provides a better understanding of economic dynamics at the national and macroeconomic level of the EU. We use the logarithmic expression of GDP, denoted LN_GDP, which allows the interpretation of annual changes as its dynamic rates. Price stability ensures a balanced and predictable business environment. More stable exchange rate variations have positive effects on the efficiency of international trade flows, expressed by the international openness indicator, denoted by OPN. The long-term interest rate determines the basic mechanism of investments, expressed by the Gross Fixed Capital Formation indicator, which is used here as a logarithm and denoted by LN_GFCF. The national capital structure, characterized by budgetary constraints, is represented by the debt-to-GDP ratio, denoted as DEBT_GDP.

Considering the intensity and nature of the correlations between the variables LN_GDP and DEBT_GDP, LN_GFCF and OPN, we conclude that the results are similar for both sub-periods, before and after the 2008 economic crisis, as well as for the entire period presented in

Table 10. Correlations of variables of the euro area in the period of 2000–2023.

	LN_GDP	DEBT_GDP	LN_GFCF	OPN
LN_GDP	1
DEBT_GDP	0.4768	1
LN_GFCF	0.9946	0.4212	1
OPN	−0.5040	−0.3828	−0.5006	1

.

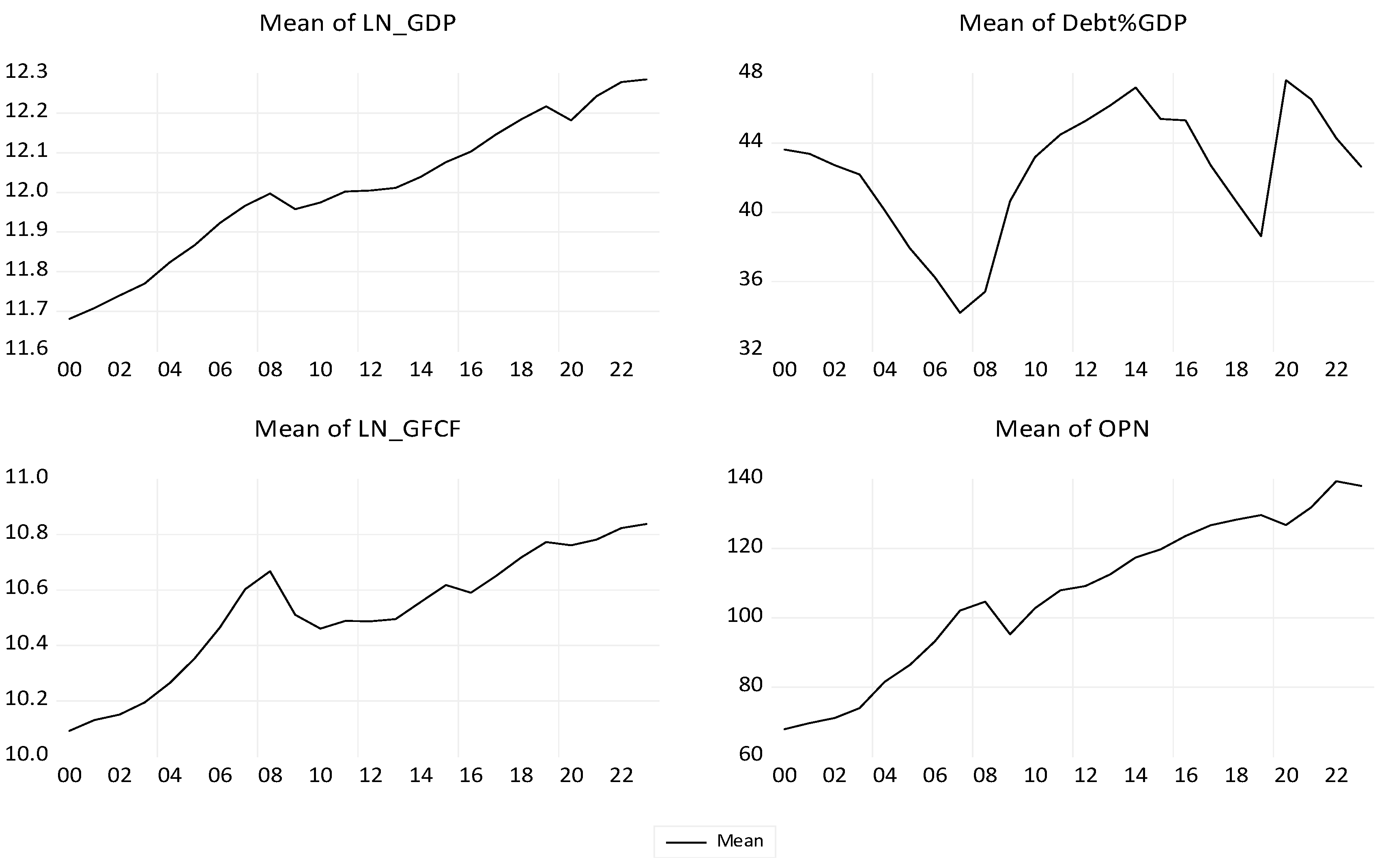
During the analyzed period, the GFCF indicator had a very strong and positive correlation with GDP. The debt-to-GDP ratio had a weak and positive correlation with GDP. International openness (OPN) had a weak and negative correlation with GDP, as well as a weak and negative correlation with investment and the debt-to-GDP ratio. In Figure 13, the evolution of the macroeconomic indicators considered in our econometric approach shows upward trends over the period 2000–2023.

In

Table 11. Granger causality analysis for the euro area by sub-periods and for the period 2000–2023.

Variable Granger Cause	For Variable	2000–2008	2009–2023	2000–2023
No. obs.		180	300	480
LN_GDP	DEBT_GDP	-	-	√
	LN_GFCF	√	√	√
	OPN	-	-	√
DEBT_GDP	LN_GDP	-	-	-
	LN_GFCF	-	√	√
	OPN	-	-	-
LN_GFCF	LN_GDP	-	-	-
	DEBT_GDP	-	-	√
	OPN	-	√	√
OPN	LN_GDP	√	√	-
	DEBT_GDP	-	√	√
	LN_GFCF	-	-	-

, the Granger causality analysis reveals differences according to the sub-periods 2000–2008 and 2009–2023, and compared to the entire period 2000–2023.

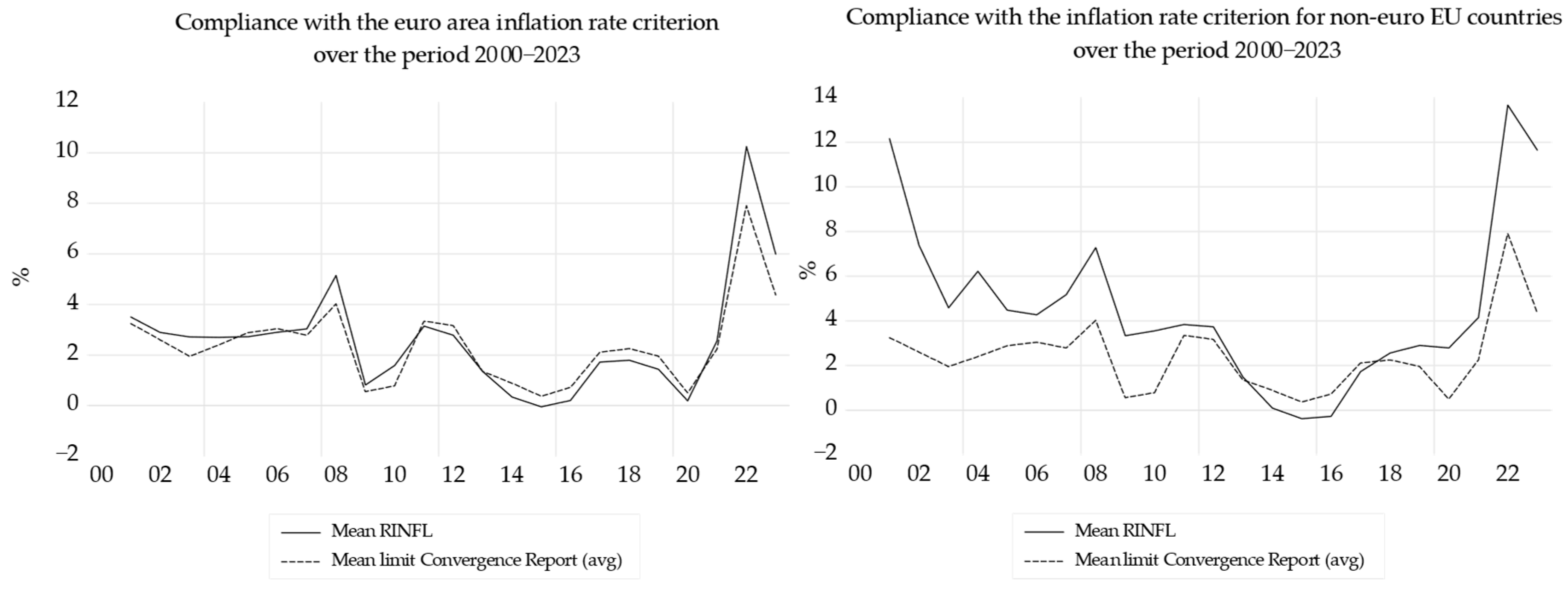
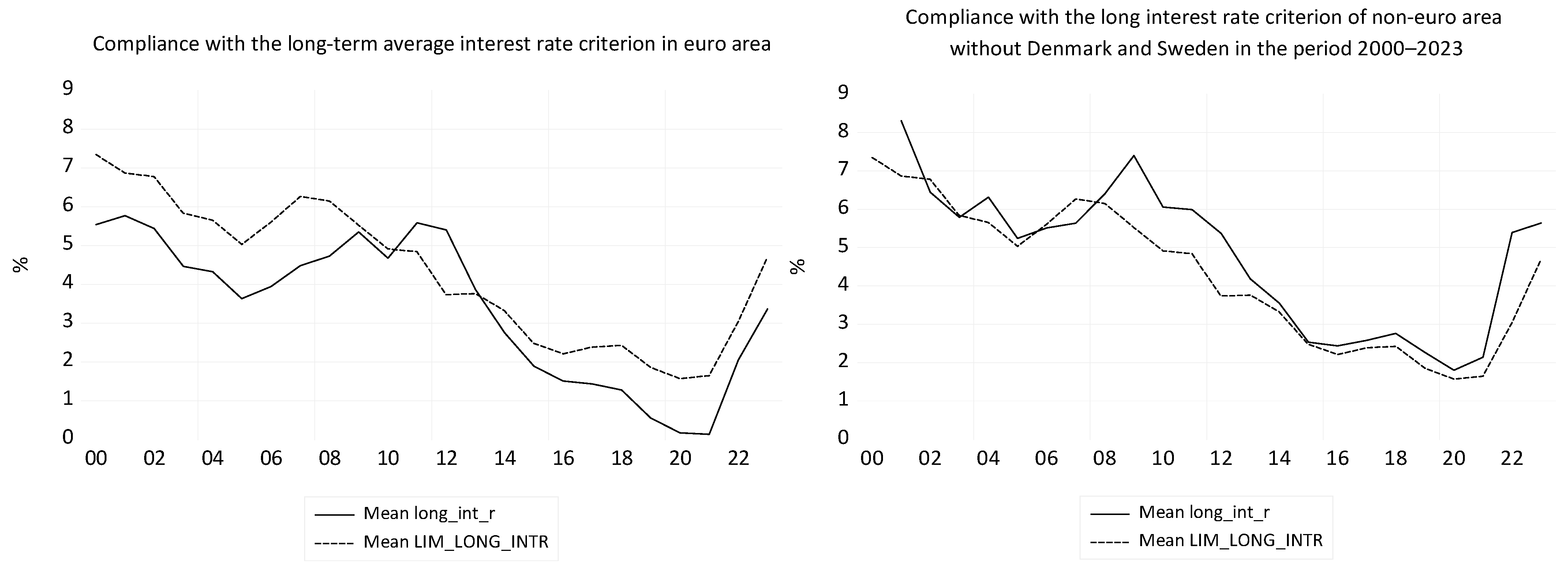
The medium intensity conformity of the long-term interest rate criterion in the three periods, in the euro area (Table 9), determines LN_GDP to be a Granger cause for LN_GFCF in both sub-periods and over the entire period.

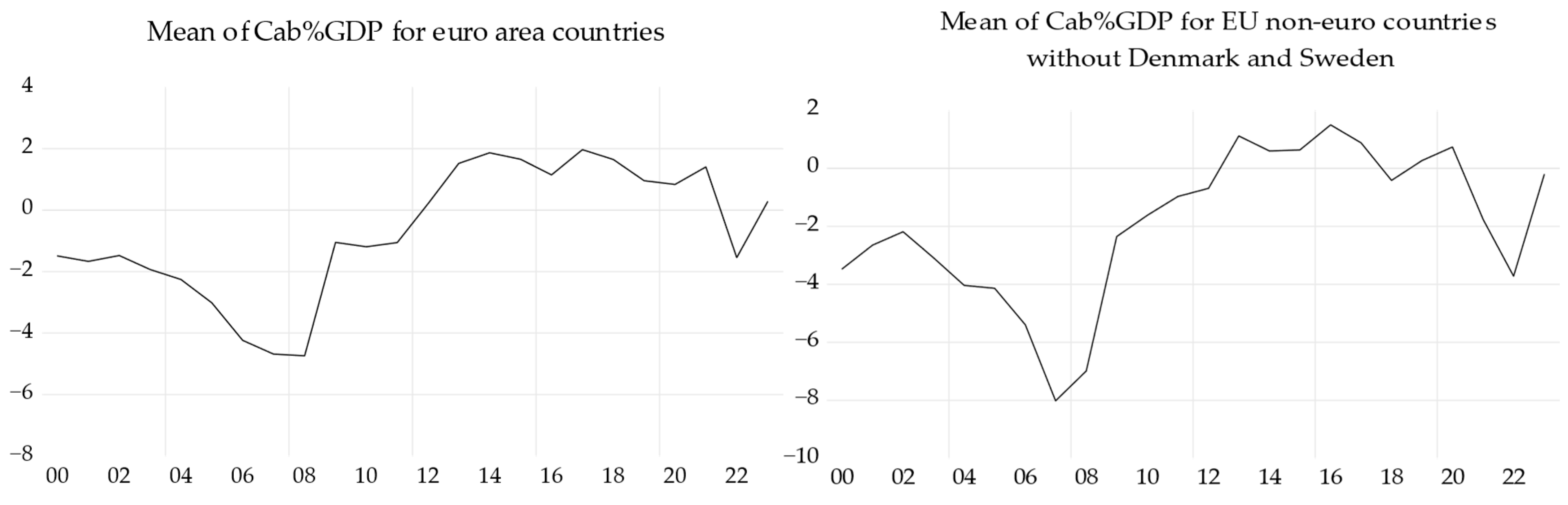
In the first sub-period 2000–2008, the debt-to-GDP ratio was much lower than 60% (Figure 7, left), and the budget deficit was quite moderate (Figure 5, left), and no Granger causality was linked to the DEBT_GDP variable. In the second sub-period 2009–2023, OPN is a Granger cause of DEBT_GDP, and DEBT_GDP in turn Granger causes LN_GFCF. The variable LN_GFCF is a Granger cause of OPN.

Only in the entire period, being a sufficiently long period, LN_GDP was a Granger cause for DEBT_GDP, LN_GFCF, and OPN. LN_GDP Granger causes the DEBT_GDP ratio and also LN_GFCF with a p-value less than 5%, but the converse is not true, meaning that the debt/GDP ratio and LN_GFCF do not Granger cause LN_GDP. Furthermore, a dual Granger causality relationship emerges between LN_GFCF and DEBT_GDP.

The variables LN_GDP, DEBT_GDP, LN_GFCF, and OPN are non-stationary, and for each of them, in the period of 2000–2023, a common unit root with individual effects is present for all cross-sections analyzed, but the cross-sections also have their own unit roots.

The variables LN_GDP, OPN, LN_GFCF, and DEBT_GDP are cointegrated only in the period of 2009–2023, according to the Pedroni test of cointegration, with eight out of eleven test statistics rejecting the null hypothesis of lack of cointegration, in

Table A1. Cointegration of economic convergence indicators in the period of 2009–2023 for euro area countries.

Pedroni Residual Cointegration Test
Series: LN_GDP DEBT_GDP LN_GFCF OPN
Sample: 2009 2023
Included observations: 300
Cross-sections included: 20
Null Hypothesis: No cointegration
Trend assumption: Deterministic intercept and trend
Automatic lag length selection based on SIC with a max lag of 1
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	27.68954	0.0000	6.627176	0.0000
Panel rho-Statistic	3.643286	0.9999	2.746592	0.9970
Panel PP-Statistic	−1.969018	0.0245	−4.068765	0.0000
Panel ADF-Statistic	−4.212502	0.0000	−5.232778	0.0000
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	4.672065	1.0000
Group PP-Statistic	−6.675214	0.0000
Group ADF-Statistic	−5.145170	0.0000

(Appendix A.1); the variables are cointegrated and have a long-run equilibrium.

Since in the two sub-periods the OPN variable acts in the same sense as a Granger cause for LN_GDP, and throughout the period 2000–2023, the cause was reversed, and only LN_GDP is a Granger cause for OPN, we carefully analyze this variable that determines the lack of cointegration in the entire period 2000–2023. After removing it, we find that the remaining variables LN_GDP, DEBT_GDP, and LN_GFCF are cointegrated over the period 2000–2023, based on the Pedroni cointegration test, with eight out of eleven test statistics rejecting the null hypothesis (lack of cointegration) in

Table A2. Cointegration of economic convergence indicators in the period of 2000–2023 for euro area countries.

Pedroni Residual Cointegration Test
Series: LN_GDP DEBT_GDP LN_GFCF
Sample: 2000 2023
Included observations: 480
Cross-sections included: 20
Null Hypothesis: No cointegration
Trend assumption: No deterministic trend
Automatic lag length selection based on SIC with a max lag of 4
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	1.844563	0.0326	1.890360	0.0294
Panel rho-Statistic	−1.538394	0.0620	−1.583068	0.0567
Panel PP-Statistic	−2.385689	0.0085	−3.792736	0.0001
Panel ADF-Statistic	−3.801801	0.0001	−5.089485	0.0000
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	0.380436	0.6482
Group PP-Statistic	−3.426081	0.0003
Group ADF-Statistic	−5.598774	0.0000

(Appendix A.1). The variables LN_GDP, DEBT_GDP, and LN_GFCF are cointegrated for the entire analyzed period 2000–2023, and we will use them in our econometric analysis. Based on Granger causality analysis, in the GDP econometric models, we consider LN_GFCF and the lagged term of DEBT_GDP as explanatory variables.

The economic convergence of the euro area is expressed here by the long-run equilibrium, as resulting from the ARDL models, in

Table A9. ARDL model of economic convergence in the euro area in the period of 2000–2023.

Dependent Variable: D(LN_GDP)
Method: ARDL
Sample: 2002 2023
Included observations: 440
Maximum dependent lags: 2 (Automatic selection)
Model selection method: Akaike info criterion (AIC)
Dynamic regressors (2 lags, automatic): DEBT_GDP(−1) LN_GFCF
Fixed regressors: C
Number of models evalulated: 4
Selected Model: ARDL(1, 1, 1)
Note: final equation sample is larger than selection sample
Variable	Coefficient	Std. Error	t-Statistic	Prob. *
	Long Run Equation
DEBT_GDP(−1)	0.002931	0.000248	11.79974	0.0000
LN_GFCF	0.579513	0.020905	27.72074	0.0000
	Short Run Equation
COINTEQ01	−0.197208	0.030421	−6.482562	0.0000
D(DEBT_GDP(−1))	0.000234	0.000300	0.778735	0.4366
D(LN_GFCF)	0.219598	0.035341	6.213624	0.0000
C	1.117224	0.170248	6.562354	0.0000
Mean dependent var	0.020615	S.D. dependent var		0.041003
S.E. of regression	0.024631	Akaike info criterion		−4.505782
Sum squared resid	0.229333	Schwarz criterion		−3.769346
Log likelihood	1118.330	Hannan-Quinn criter.		−4.215789

* Note: p-values and any subsequent tests do not account for model selection.

and

Table A10. ARDL model of economic convergence in the euro area in the period of 2000–2023 (with variables “c2008”, “COVID” and “war”).

Dependent Variable: D(LN_GDP)
Method: ARDL
Sample: 2002 2023
Included observations: 440
Maximum dependent lags: 1 (Automatic selection)
Model selection method: Akaike info criterion (AIC)
Dynamic regressors (1 lag, automatic): DEBT_GDP(−1) LN_GFCF
Fixed regressors: C2008 COVID WAR1 C
Number of models evalulated: 1
Selected Model: ARDL(1, 1, 1)
Note: final equation sample is larger than selection sample
Variable	Coefficient	Std. Error	t-Statistic	Prob. *
	Long Run Equation
DEBT_GDP(−1)	0.003283	0.000130	25.33702	0.0000
LN_GFCF	0.613360	0.016199	37.86485	0.0000
	Short Run Equation
COINTEQ01	−0.164284	0.036918	−4.449939	0.0000
D(DEBT_GDP(−1))	1.75 × 10−5	0.000215	0.081623	0.9350
D(LN_GFCF)	0.124283	0.028122	4.419364	0.0000
C2008	−0.039435	0.004446	−8.870077	0.0000
COVID	−0.064446	0.008432	−7.642978	0.0000
WAR	−0.016765	0.005599	−2.994416	0.0030
C	0.884424	0.183105	4.830152	0.0000
Mean dependent var	0.020615	S.D. dependent var		0.041003
S.E. of regression	0.019336	Akaike info criterion		−5.186837
Sum squared resid	0.118900	Schwarz criterion		−3.911546
Log likelihood	1334.973	Hannan-Quinn criter.		−4.684654

* Note: p-values and any subsequent tests do not account for model selection.

(Appendix A.2). Another approach is represented by the ECM in

Table A11. Long-term model of economic convergence in the euro area over the period 2000–2023.

Dependent Variable: LN_GDP
Method: Panel Fully Modified Least Squares (FMOLS)
Sample (adjusted): 2002 2023
Periods included: 22
Cross-sections included: 20
Total panel (balanced) observations: 440
Panel method: Pooled estimation
Cointegrating equation deterministics: C
Coefficient covariance computed using default method
Long-run covariance estimates (Bartlett kernel, Newey-West fixed bandwidth)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
DEBT_GDP(−1)	0.003089	0.000242	12.77056	0.0000
LN_GFCF	0.662931	0.019867	33.36762	0.0000
R-squared	0.998250	Mean dependent var		11.85919
Adjusted R-squared	0.998162	S.D. dependent var		1.706018
S.E. of regression	0.073132	Sum squared resid		2.235566
Long-run variance	0.007939

for the long-term model,

Table A12. Short-term model of economic convergence in the euro area over the period 2000–2023.

Dependent Variable: D(LN_GDP)
Method: Panel EGLS (Cross-section SUR)
Sample (adjusted): 2003 2023
Periods included: 21
Cross-sections included: 20
Total panel (balanced) observations: 420
Linear estimation after one-step weighting matrix
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(DEBT_GDP(−1))	0.000926	1.41 × 10−5	65.85361	0.0000
D(LN_GFCF)	0.246289	0.000599	411.0547	0.0000
ECT(−1)	−0.187037	0.001226	−152.5489	0.0000
C	0.012787	6.70 × 10−5	190.9931	0.0000
	Effects Specification
Cross-section fixed (dummy variables)
	Weighted Statistics
R-squared	0.998165	Mean dependent var		−5.644587
Adjusted R-squared	0.998063	S.D. dependent var		34.36002
S.E. of regression	1.024513	Sum squared resid		416.7022
F-statistic	9814.611	Durbin–Watson stat		2.088257
Prob(F-statistic)	0.000000

and

Table A13. Short-term model of economic convergence in the euro area over the period 2000–2023 (with variables “c2008”, “COVID” and “war”).

Dependent Variable: D(LN_GDP)
Method: Panel EGLS (Cross-section SUR)
Sample (adjusted): 2003 2023
Periods included: 21
Cross-sections included: 20
Total panel (balanced) observations: 420
Linear estimation after one-step weighting matrix
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(DEBT_GDP(−1))	0.000392	1.62 × 10−5	24.23351	0.0000
D(LN_GFCF)	0.181271	0.000947	191.4743	0.0000
ECT(−1)	−0.163510	0.001696	−96.41219	0.0000
C2008	−0.052708	0.001736	−30.36998	0.0000
COVID	−0.061874	0.001729	−35.79064	0.0000
WAR	−0.017134	0.001812	−9.458207	0.0000
C	0.021196	0.000397	53.35811	0.0000
	Effects Specification
Cross-section fixed (dummy variables)
	Weighted Statistics
R-squared	0.993125	Mean dependent var		0.706083
Adjusted R-squared	0.992689	S.D. dependent var		11.92490
S.E. of regression	1.021261	Sum squared resid		410.9316
F-statistic	2276.631	Durbin–Watson stat		2.092346
Prob(F-statistic)	0.000000
	Unweighted Statistics
R-squared	0.669339	Mean dependent var		0.020114
Sum squared resid	0.240076	Durbin–Watson stat		1.582105

for the short-term models without and with dummy variables (Appendix A.2). The results are presented in

Table 12. Comparison of ECM and ARDL models for the euro area over the period 2000–2023.

LN_GDP Dependent Variable	Error Correction Model			ARDL(1,1,1)
	Long-Run	Short-Run FE Cross-Sections (GLS-SUR)	Short-Run FE Cross-Sections (GLS-SUR)	Long-Run	Short-Run	Long-Run with Dummies	Short-Run with Dummies
C	-	0.0128 ***	0.0212 ***	-	1.1172 ***	-	0.8844 ***
DEBT_GDP(−1)	0.0031 ***	0.0009 ***	0.0004 ***	0.0029 ***	0.0002	0.0033 ***	−1.75 × 10−5
LN_GFCF	0.6629 ***	0.2463 ***	0.1813 ***	0.5795 ***	0.2196 ***	0.6134 ***	0.1243 ***
C2008			−0.0527 ***				−0.0394 ***
COVID			−0.0619 ***				−0.0644 ***
WAR			−0.0171 ***				−0.0168 ***
ECT(−1)	-	−0.1870 ***	−0.1635 ***	-	−0.1972 ***		−0.1643 ***

*** significance p-value less than 1%.

.

The ARDL approach without economic shocks consists of the long-run and short-run models in Equation (5), and, respectively, the corresponding models ARDL with dummy variables for the economic shocks, are in Equation (6).

$${lngdp}_{it}={\widehat{\propto }}_1{debtgdp}_{it-1}+{\widehat{\propto }}_2{lngfcf}_{it}$$

(5)

$${lngdp}_{it}=0.0029{debtgdp}_{it-1}+0.5795{lngfcf}_{it}+[CX=DETERM]$$

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_2{ECT}_{t-1}$$

$$\begin{gathered} {∆lngdp}_{it}=1.1172+0.0002{∆debtgdp}_{it-1}+0.2196∆{lngfcf}_{it}-0.1972({lngdp}_{it-1}- \\ -0.0029{debtgdp}_{it-2}-0.5795{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

$${lngdp}_{it}=0.0033{debtgdp}_{it-1}+0.6134{lngfcf}_{it}+[CX=DETERM]$$

(6)

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_{13}\mathrm{c}2008+{\widehat{\beta }}_{14}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}+{\widehat{\beta }}_{15}\mathrm{w}\mathrm{a}\mathrm{r}+{\widehat{\beta }}_2{ECT}_{t-1}$$

$$\begin{gathered} {∆lngdp}_{it}=0.8844-1.75·{10}^{-5}{∆debtgdp}_{it-1}+0.1243∆{lngfcf}_{it}-0.0394\mathrm{c}2008-0.0644\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}- \\ -0.0168\mathrm{w}\mathrm{a}\mathrm{r}-0.1643({lngdp}_{it-1}-0.0033{debtgdp}_{it-2}-0.6134{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

In Table 12, the ARDL coefficients in Equations (5) and (6) of the long run equation are significant at Prob. < 1%. The coefficient ${\widehat{\beta }}_2$ of the ECT, in the short-run Equations (5) and (6) is significantly different from 0, negative and less than 1, which attests to the existence of a long-run relationship of the variables; it represents the speed of adjustment towards the long-run equilibrium.

In the long run, a 1 p.p. increase in the lagged debt-to-GDP ratio leads to an average increase of 0.29% in GDP, all other factors remaining constant. A 1% increase in GFCF leads to a 0.5795% increase in GDP, holding all other elements constant. If we take into account economic shocks, a 1 p.p. increase in the lagged debt-to-GDP ratio causes an average increase of 0.33% in GDP, all other factors remaining constant; for every 1% increase in GFCF, GDP increases on average with 0.6134%, keeping all other elements constant. We observe that the coefficients in the long-run ARDL models are significant at a p-value less than 1% and have close values.

In the short run, we observe that in both ARDL models, the coefficient of the DEBT_GDP ratio is not significant; all other variables have significant coefficients at a p-value less than 1%.

The term COINTEQ01 in Table A9 and Table A10 (Appendix A.2) is the Error Correction Term (ECT) in Table 12 and Equations (5) and (6). ECT contributes on average to the correction towards long-term equilibrium—economic convergence—with a proportion of 19.72%, respectively, 16.43%, if economic shocks are considered separately. ECT represents the speed of short-term adjustment over a one-year period of the panel of euro area countries. The difference between the ECT coefficients of the two ARDL models shows a greater effort in terms of the adjustment speed when the separate influences of economic shocks are not taken into account. We note that, following the 2008 economic crisis, euro area GDP fell by an average of 3.94% in 2009, with other factors remaining constant. In 2020, GDP fell by an average of 6.44% in the euro area economies, all other factors remaining constant. The war between Russia and Ukraine caused an average GDP decline of 1.68% in 2023, ceteris paribus.

The Akaike, Schwarz, and Hannan-Quinn information criteria indicate that the better model is the ARDL with economic shocks. The adjustment speeds for each euro area country, resulting from the ARDL approach with dummy variables, based on the short-run coefficients of their models, over the period 2000–2023, are presented in

Table 13. The short-run coefficients for each euro area country over the period of 2000–2023.

Number	Country	COINTEQ01	D(DEBT_GDP(−1))	D(LN_GFCF)	C2008	COVID	WAR	C
1	Croatia	−0.5884 ***	−0.0006 ***	−0.0708 ***	−0.0562 ***	−0.0964 ***	0.0525 ***	2.8983 ***
2	Belgium	−0.3293 ***	0.0011 ***	0.1222 ***	−0.0162 ***	−0.0424 ***	0.0075 ***	1.8292 ***
3	Portugal	−0.3193 ***	−0.0006 ***	0.0565 ***	−0.0195 ***	−0.0942 ***	−0.0042 ***	1.7204 ***
4	Lithuania	−0.3190 ***	0.0005 ***	0.0899 ***	−0.0504 ***	−0.0222 ***	−0.0525 ***	1.5795 ***
5	Spain	−0.3050 ***	−0.0002 ***	−0.0556 ***	−0.0220 ***	−0.1255 ***	−0.0022 ***	1.8574 ***
6	Cyprus	−0.2793 ***	0.0001 ***	0.0048	−0.0319 ***	−0.0558 ***	−0.0059 ***	1.2916 ***
7	Latvia	−0.2015 ***	−0.0014 ***	0.1196 ***	−0.0814 ***	−0.0479 ***	−0.0417 ***	0.9615 ***
8	Austria	−0.1982 ***	0.0004 ***	0.0777 ***	−0.0349 ***	−0.0665 ***	−0.0134 ***	1.1086 **
9	Greece	−0.1943 ***	−0.0004 ***	0.1765 ***	−0.0128 ***	−0.1057 ***	−0.0256 ***	1.0613 ***
10	Estonia	−0.1576 ***	0.0021 ***	0.2141 ***	−0.0367 ***	−0.0571 ***	−0.0425 ***	0.7279 ***
11	Ireland	−0.1066 ***	−0.0020 ***	−0.0783 ***	−0.0727 ***	−0.0410 ***	−0.0650 ***	0.6301
12	Italy	−0.1050 ***	0.0006 ***	0.2303 ***	−0.0283 ***	−0.0736 ***	−0.0178 ***	0.6476 ***
13	Slovenia	−0.0971 ***	0.0005 ***	0.2163 ***	−0.0372 ***	−0.0331 ***	−0.0200 ***	0.4910 ***
14	Slovakia	−0.0892 ***	−0.0010 ***	0.1131 ***	−0.0554 ***	−0.0425 ***	−0.0322 ***	0.4870 ***
15	Netherlands	−0.0688 **	0.0000 ***	0.0548 ***	−0.0491 ***	−0.0528 ***	−0.0130 ***	0.4269
16	France	−0.0598 ***	0.0005 ***	0.3404 ***	−0.0015 ***	−0.0602 ***	−0.0080 ***	0.3809 ***
17	Luxembourg	−0.0336 **	−0.0011 ***	0.0799 ***	−0.0400 ***	−0.0269 ***	−0.0345 ***	0.1995
18	Finland	−0.0288 **	0.0001 ***	0.3340 ***	−0.0488 ***	−0.0325 ***	−0.0045 ***	0.1680
19	Germany	0.0058	0.0012 ***	0.3205 ***	−0.0404 ***	−0.0400 ***	−0.0101 ***	−0.0264
20	Malta	0.1892 ***	0.0006 ***	0.1396 ***	−0.0535 ***	−0.1727 ***	−0.0023 **	−0.7518 ***
	Euro area	−0.1643 ***	0.0000	0.1243 ***	−0.0394 ***	−0.0644 ***	−0.0168 ***	0.8844 ***

*/**/*** significance p-value less than: 10%/5%/1%.

.

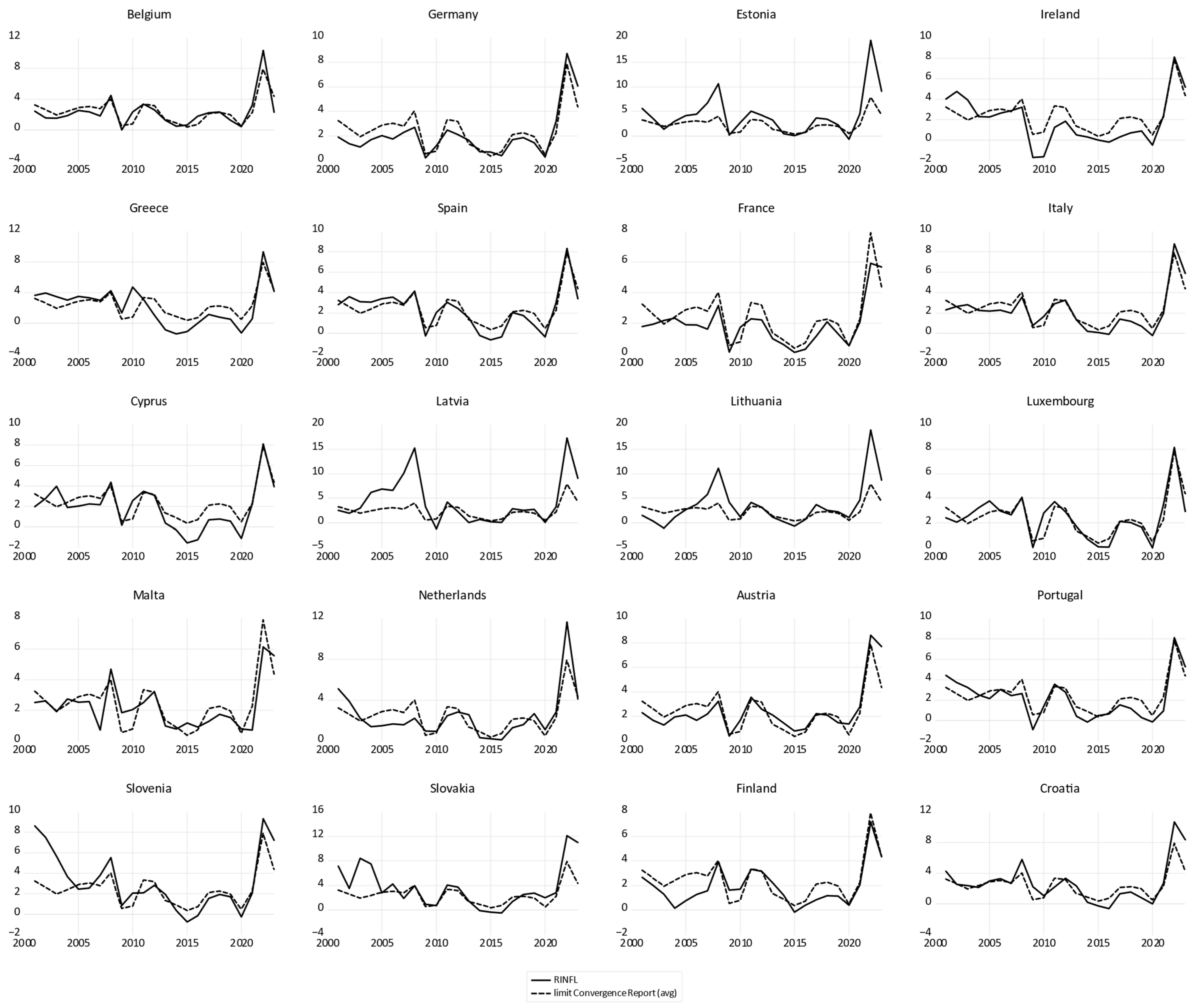
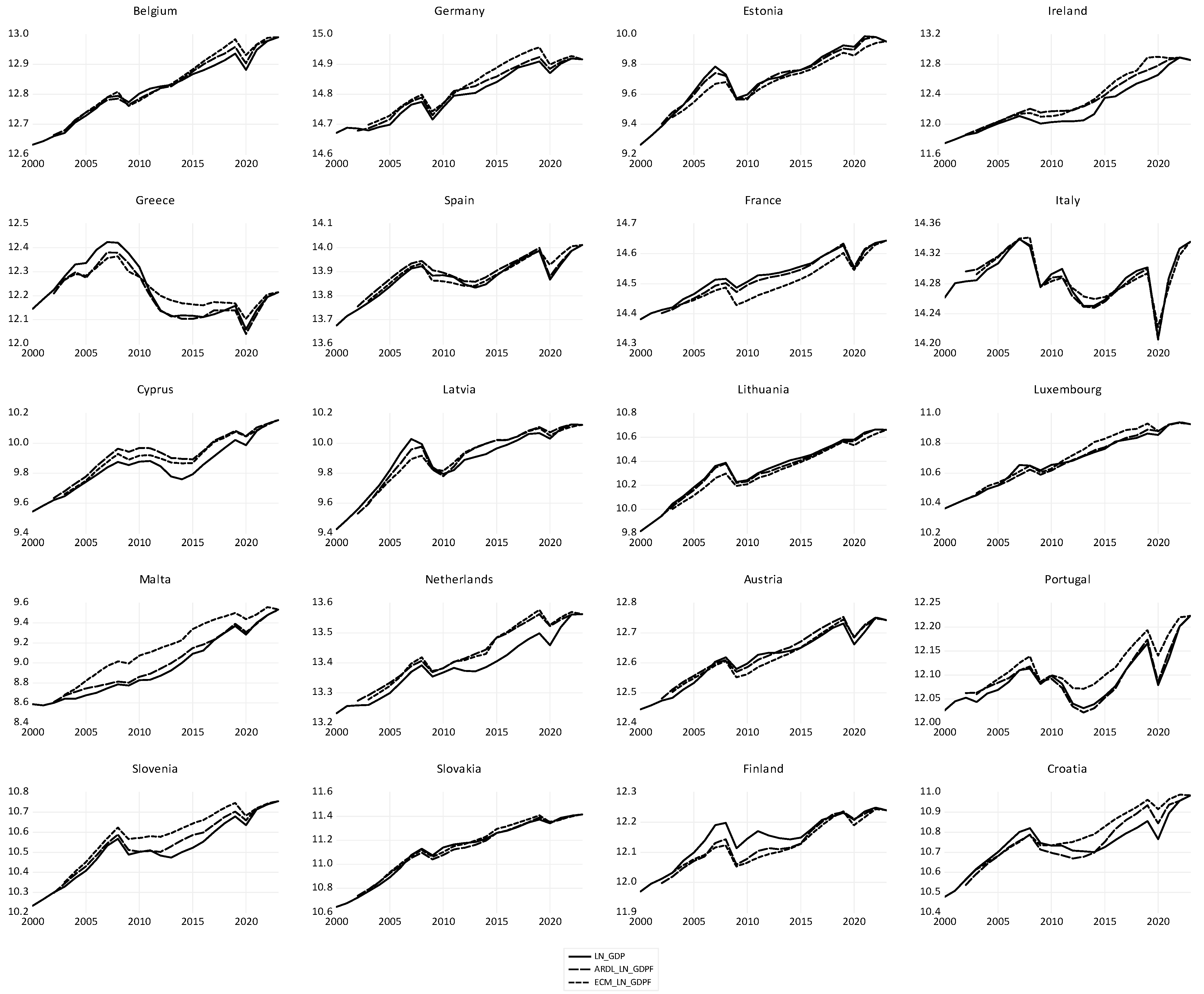
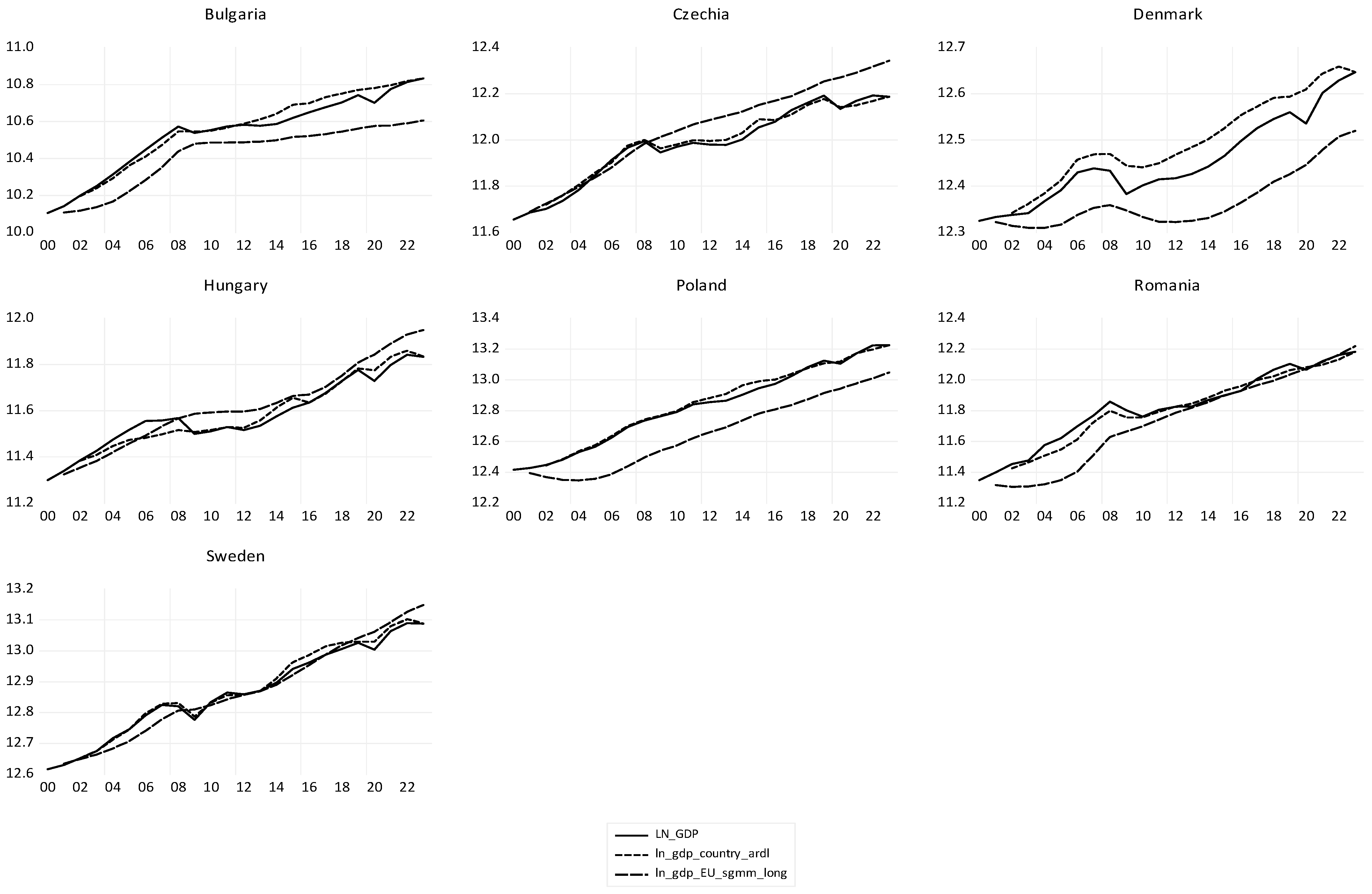
Croatia has the highest adjustment speed, at 58.8% over a one-year period, demonstrating its effort to join the Eurozone in 2023. Luxembourg, the Netherlands, and Finland have significant adjustment speeds at a p-value of 5%; all other countries in the group have a significant ECT coefficient at a p-value of less than 1%. Germany and Malta have positive coefficients of ECT. These two countries do not converge towards the long-term equilibrium of the euro area because they do not have a long-run relationship between GDP and the debt-to-GDP ratio and GFCF.

When we consider ARDL without the influences of economic shocks, we find that in France, Italy, and Malta, there is no long-term relationship between the analyzed variables. However, if economic shocks are taken into account, their crisis adaptation policies bring economic growth towards equilibrium in France and Italy, but not in Malta. Economic shocks affected the existence of a long-term relationship between the variables analyzed in Germany, as seen in Table 13.

The Error Correction Model without dummy variables for economic shocks has the long-term model by the cointegrating regression method and the short-term model in Equation (7) and also in Table A11 and Table A12, in Appendix A.2.

$${lngdp}_{it}={\widehat{\propto }}_1{debtgdp}_{it-1}+{\widehat{\propto }}_2{lngfcf}_{it}$$

(7)

$${lngdp}_{it}=0.0031{debtgdp}_{it-1}+0.6629{lngfcf}_{it}+[CX=DETERM]$$

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_2{ECT}_{t-1}$$

$$\begin{gathered} {∆lngdp}_{it}=0.0128+0.0009{∆debtgdp}_{it-1}+0.2463∆{lngfcf}_{it}-0.1870({lngdp}_{it-1}- \\ -0.0031{debtgdp}_{it-2}-0.6629{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

The ECM with dummy variables has the same long-term Equation (7) (Table A11, Appendix A.2) and the short-run model from Equation (8) (Table A13, Appendix A.2).

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_{13}\mathrm{c}2008+{\widehat{\beta }}_{14}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}+{\widehat{\beta }}_{15}\mathrm{w}\mathrm{a}\mathrm{r}+{\widehat{\beta }}_2{ECT}_{t-1}$$

(8)

$$\begin{gathered} {∆lngdp}_{it}=0.0212-0.0004{∆debtgdp}_{it-1}+0.1813∆{lngfcf}_{it}-0.0527\mathrm{c}2008-0.0619\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}- \\ -0.0171\mathrm{w}\mathrm{a}\mathrm{r}-0.1635({lngdp}_{it-1}-0.0031{debtgdp}_{it-2}-0.6629{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

The ECM residuals have a normal distribution as a result of the Jarque–Bera test and respect the assumption that there are no correlations between the cross-sections. The coefficients of the two ECMs from Equations (7) and (8) are presented in Table 12, comparing them with the coefficients of the two ARDL models.

The coefficients of variables are similar in the two approaches, being smaller in the short term than in the long term, in both. The difference between the short term and the long term is corrected by the ECT with the adjustment speed over a period of one year. In the ECM, the ECT contributes on average to the correction towards the long-term equilibrium of the euro area countries with an adjustment speed of 18.70% over a one-year period, without taking into account economic shocks, and of 16.35% over a one-year period, taking into account the ECM with economic shocks. We observe in Table 12 very close values of the adjustment speed in both ECM and ARDL, with dummy variables for economic shocks. We consider these models in our analysis.

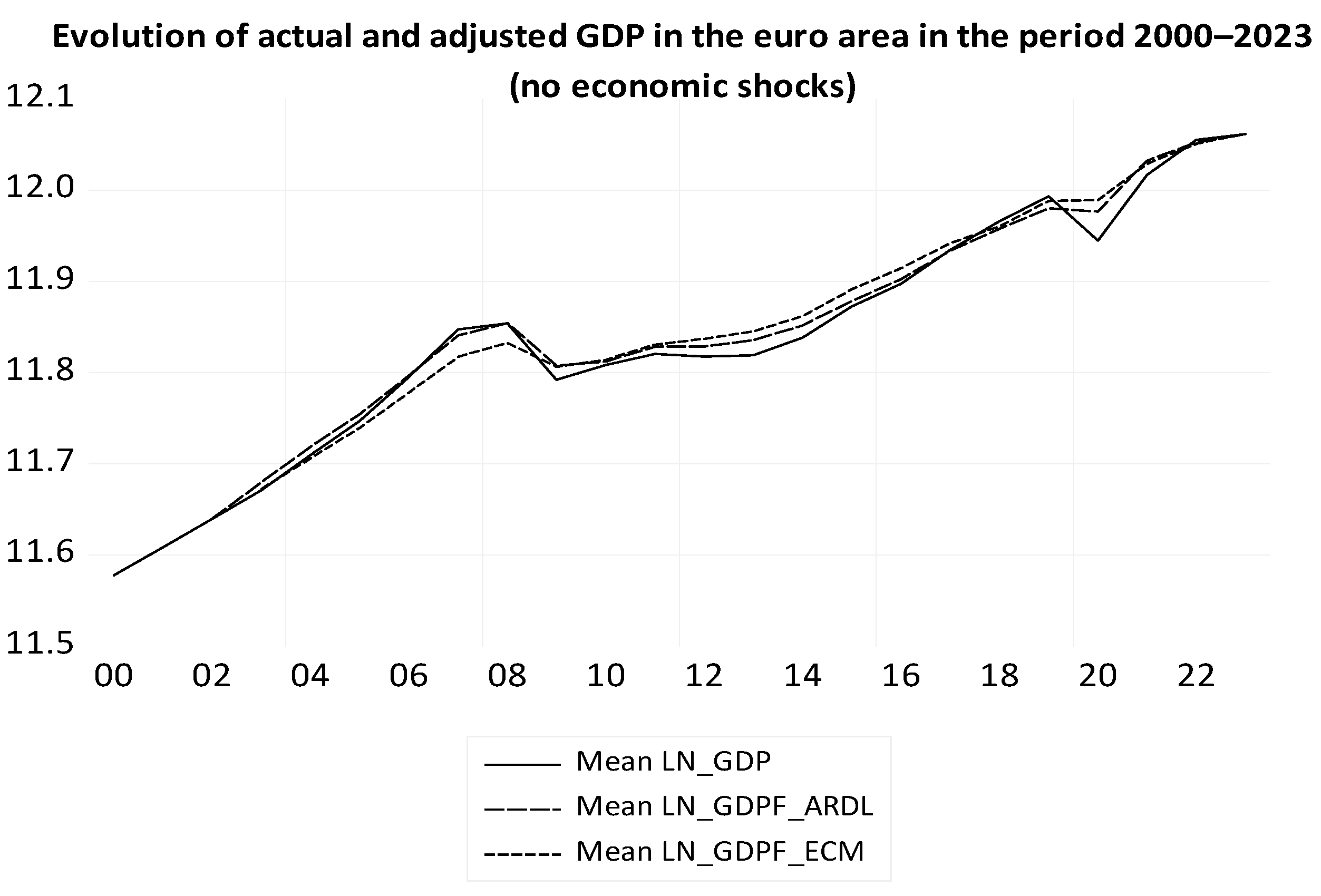
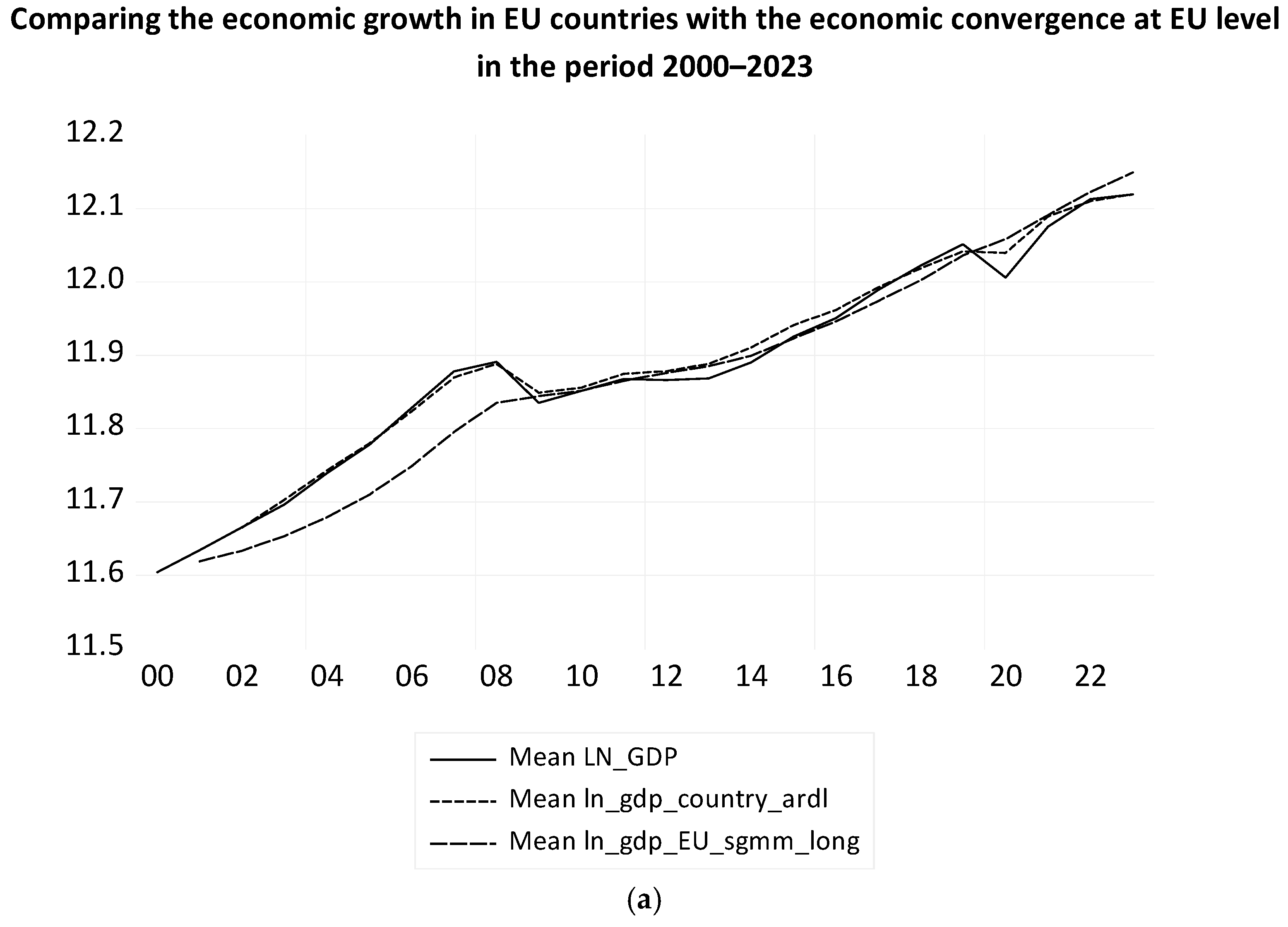
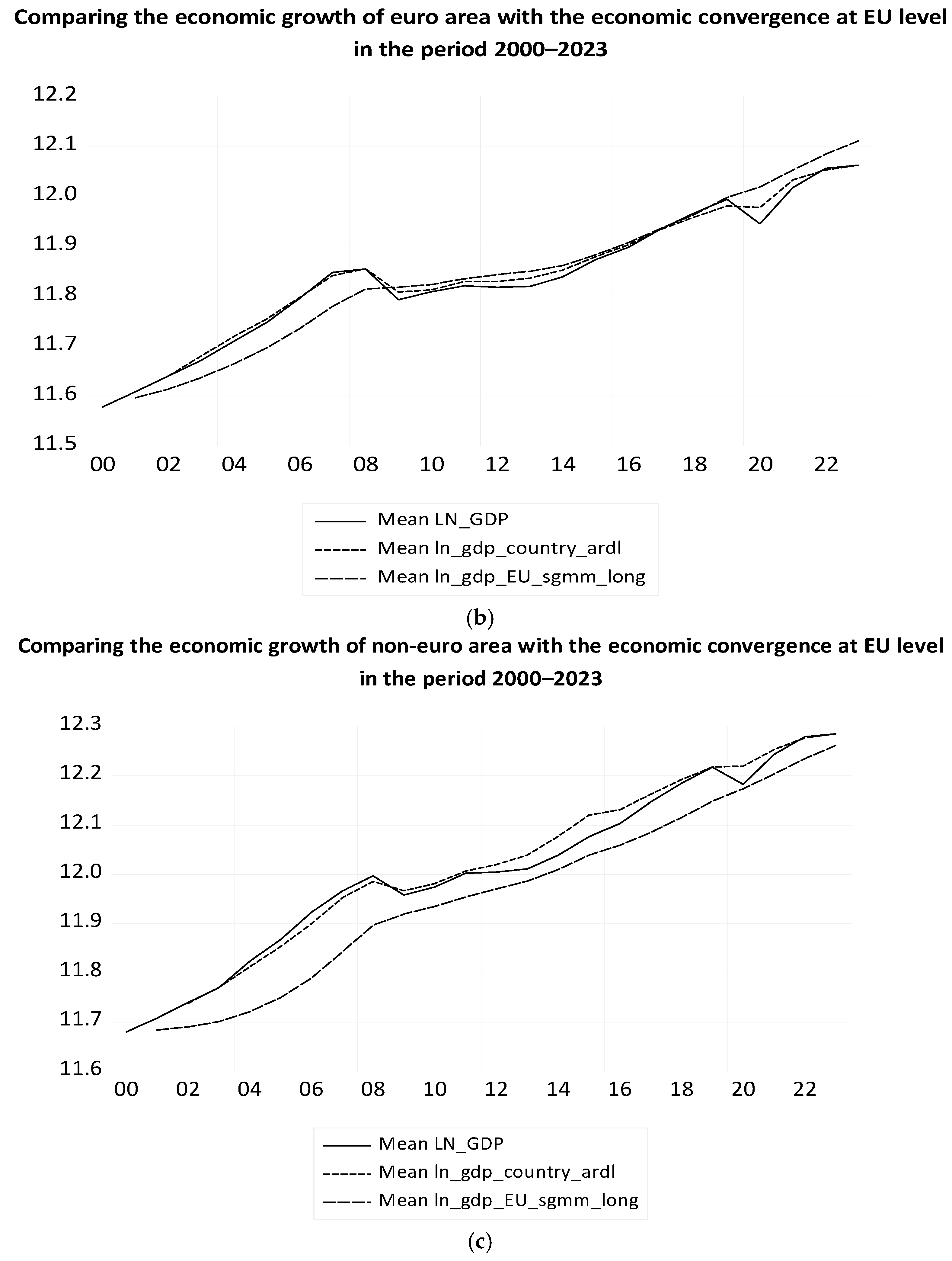
The evolution of the average level of LN_GDP in the euro area countries and its theoretical values, calculated with the ECM and ARDL model without and with dummy variables, are presented in Figure 14. The theoretical average values of LN_GDP without dummies for economic shocks are denoted LN_GDPF_ARDL and LN_GDPF_ECM, respectively. The theoretical average values of LN_GDP of the models that take economic shocks into account are denoted ARDL_LN_GDPF and ECM_LN_GDPF, respectively (Figure 14). The ARDL model is better than the ECM, based on the forecast evaluation indicators in both situations.

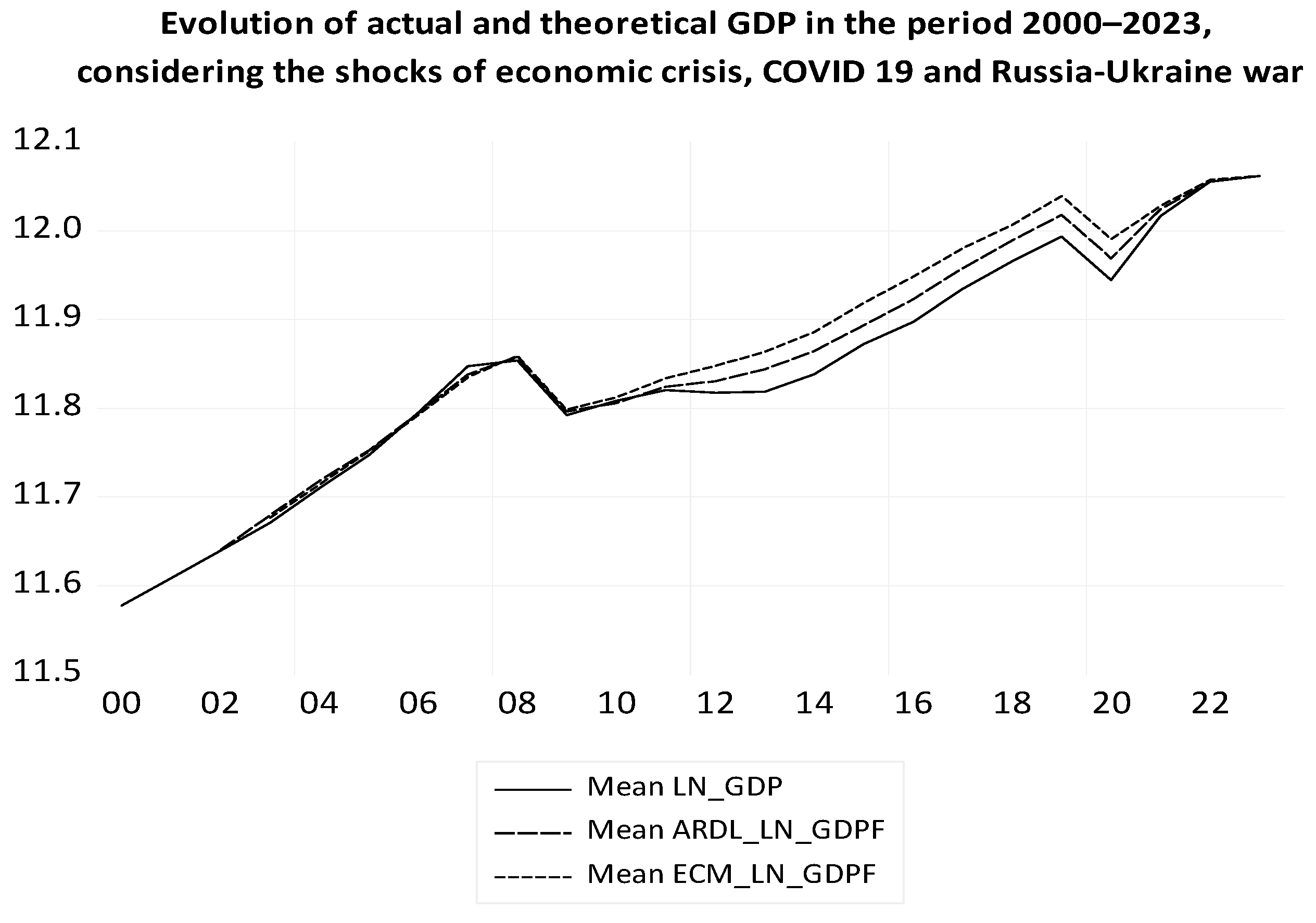
Figure 15 shows the evolution of GDP and its long-term economic convergence in the euro area countries over the period 2000–2023, calculated with ARDL and ECM with dummy variables for economic shocks. There are positive and negative deviations of each euro area country’s real GDP from the euro area’s economic convergence. The theoretical values of LN_GDP with the ECM are very close to those in the ARDL model.

The long-term equilibrium of all euro area countries—economic convergence, is checked with the Pedroni test of residuals, which rejects the null hypothesis of absence of cointegration with ten out of eleven test statistics, regarding the cointegration of LN_GDP and theoretical economic convergence, expressed by ARDL_LN_GDPF, in

Table A3. Cointegration of LN_GDP with the theoretical LN_GDP (ARDL with dummies) in the period of 2000–2023 for euro area countries.

Pedroni Residual Cointegration Test
Series: LN_GDP ARDL_LN_GDPF
Sample: 2000 2023
Included observations: 480
Cross-sections included: 20
Null Hypothesis: No cointegration
Trend assumption: No deterministic intercept or trend
Automatic lag length selection based on SIC with a max lag of 4
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	4.600308	0.0000	4.400345	0.0000
Panel rho-Statistic	−2.337459	0.0097	−2.398636	0.0082
Panel PP-Statistic	−2.429706	0.0076	−2.628664	0.0043
Panel ADF-Statistic	−2.959798	0.0015	−3.416145	0.0003
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	0.312725	0.6228
Group PP-Statistic	−2.332627	0.0098
Group ADF-Statistic	−3.694856	0.0001

(Appendix A.1).

The coefficients of the ECT cointegration terms of the ECM and ARDL models, in Table 12, are negative, less than 1, and significant at a p-value of 1%, proving the existence of a long-run economic equilibrium in the euro area, which attests to hypothesis H1.

4.2.3. Modeling Economic Convergence in the Non-Euro EU Countries in the Period of 2000–2023

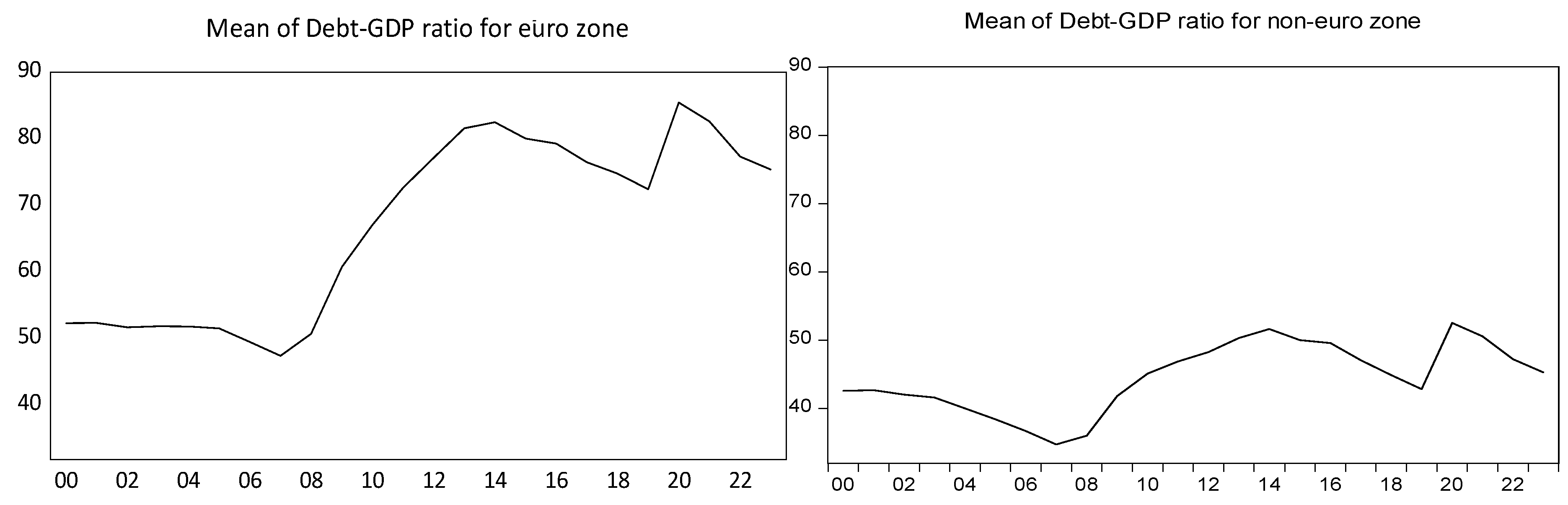
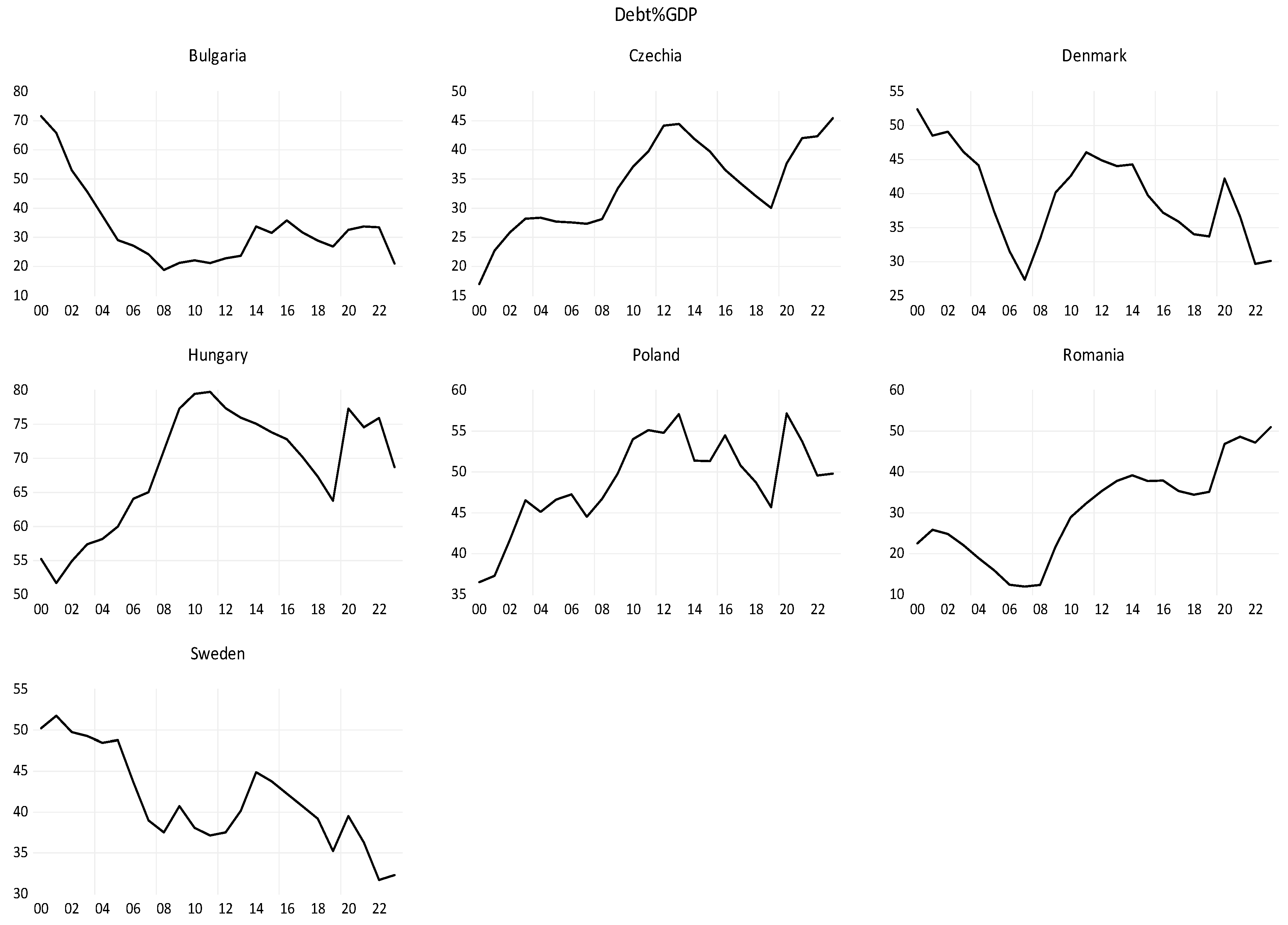
Section 4.1 showed that, thanks to the efforts made, EU countries outside the euro area meet most of the financial convergence criteria, in particular the public debt criterion.

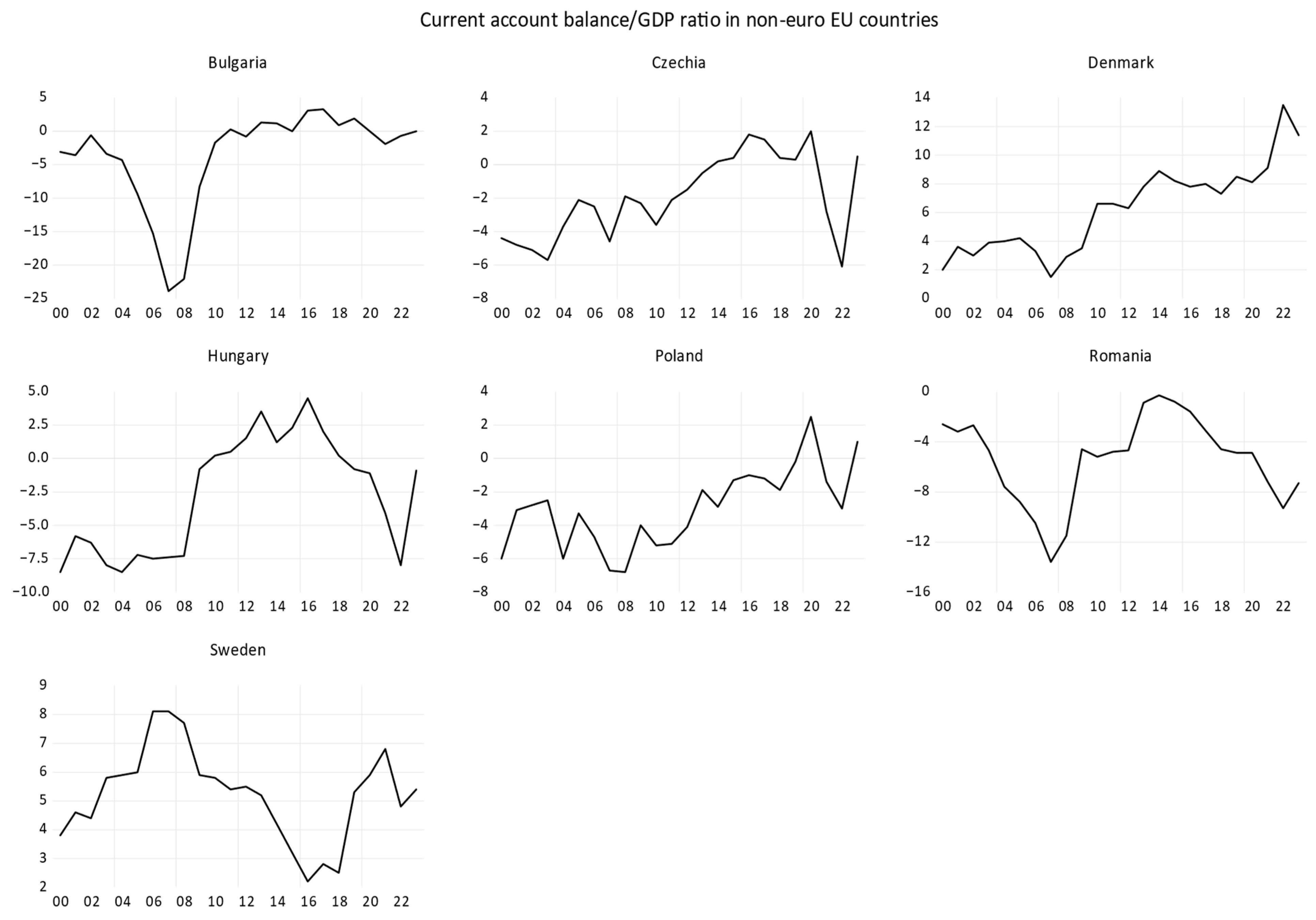
Figure 16 shows the evolution of the variables considered for EU countries outside the euro area over the period 2000–2023. The shocks of the 2008 economic crisis and the 2020 pandemic are evident in the evolution of each variable.

The correlation analysis reveals in

Table 14. Correlations of variables for non-euro area over the period 2000–2023.

	LN_GDP	DEBT_GDP	LN_GFCF	OPN
LN_GDP	1
DEBT_GDP	0.1198	1
LN_GFCF	0.9813	0.0655	1
OPN	−0.2076	0.4388	−0.1576	1

the lack of correlation between DEBT_GDP and LN_GDP, which leads to the elimination of this variable from the econometric model. Investments are very strongly and positively correlated with GDP. International openness, OPN, is very weakly and negatively correlated with GDP.

If we do not consider the two developed countries, Denmark and Sweden, the correlations are similar, and there is even a lack of correlation between LN_GDP and OPN. This means that the two excluded countries contributed to international openness more than all other non-euro countries during the period under review.

The Granger causality analysis, in

Table 15. Granger causality analysis for the non-euro area by sub-periods and for the period of 2000–2023.

Variable Granger Cause	For Variable:	Non-Euro Area			Non-Euro Area Without Denmark and Sweden
		2000–2008	2009–2023	2000–2023	2000–2008	2009–2023	2000–2023
No. obs.		63	105	168	45	75	120
LN_GDP	DEBT_GDP	-	-	-	√	-	√
	LN_GFCF	√	√	√	-	√	√
	OPN	-	-	√	-	√	√
DEBT_GDP	LN_GDP	-	-	-	√	-	-
	LN_GFCF	-	√	-	-	√	-
	OPN	-	-	-		√	-
LN_GFCF	LN_GDP	-	-	√	√	√	√
	DEBT_GDP	-	-	-	√	-	√
	OPN	-	√	√	-	√	√
OPN	LN_GDP	√	-	√	-	-	√
	DEBT_GDP	-	-	-	-	-	-
	LN_GFCF	-	√	√	-	√	√

, shows that, for non-euro EU countries, DEBT_GDP does not Granger influence any other variable in the period of 2000–2023, and the same happens when excluding Denmark and Sweden. DEBT_GDP is a Granger cause for LN_GFCF in the sub-period 2009–2023 in both situations. According to Granger causality, during the analyzed period, the significant factors for economic development are investment and openness.

We prefer DEBT_GDP and LN_GFCF as explanatory variables of GDP growth, in order to make the comparison with the economic convergence of the euro area. We find the cointegration of the variables LN_GDP, LN_GFCF, and DEBT_GDP for the period 2000–2023 affirmed by six of the eleven test statistics, in

Table A4. Cointegration of economic convergence indicators over the period 2000–2023 for non-euro EU countries.

Pedroni Residual Cointegration Test
Series: LN_GDP LN_GFCF OPN
Sample: 2000 2023
Included observations: 168
Cross-sections included: 7
Null Hypothesis: No cointegration
Trend assumption: No deterministic trend
Automatic lag length selection based on SIC with a max lag of 4
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	2.775819	0.0028	2.354102	0.0093
Panel rho-Statistic	−1.404904	0.0800	−1.327019	0.0923
Panel PP-Statistic	−1.946284	0.0258	−1.936193	0.0264
Panel ADF-Statistic	−1.910599	0.0280	−1.941800	0.0261
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	−0.231718	0.4084
Group PP-Statistic	−1.622258	0.0524
Group ADF-Statistic	−1.681344	0.0463

(Appendix A.1).

The Error Correction Model of the LN_GDP, DEBT_GDP, and LN_GFCF variables for the period 2000–2023 has all long-run and short-run equation coefficients significant at Prob. < 1%, as presented in

Table A16. Long-run model of economic convergence in EU non-euro area in the period of 2000–2023.

Dependent Variable: LN_GDP
Method: Panel Fully Modified Least Squares (FMOLS)
Sample (adjusted): 2002 2023
Periods included: 22
Cross-sections included: 7
Total panel (balanced) observations: 154
Panel method: Pooled estimation
Cointegrating equation deterministics: C
Coefficient covariance computed using default method
Long-run covariance estimates (Bartlett kernel, Newey-West fixed bandwidth)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
DEBT_GDP(−1)	0.003002	0.001001	2.998805	0.0032
LN_GFCF	0.704030	0.036318	19.38531	0.0000
R-squared	0.992437	Mean dependent var		12.03604
Adjusted R-squared	0.992019	S.D. dependent var		0.771401
S.E. of regression	0.068913	Sum squared resid		0.688613
Long-run variance	0.009250

and

Table A17. Short-run model of economic convergence in EU non-euro area in the period of 2000–2023.

Dependent Variable: D(LN_GDP)
Method: Panel EGLS (Cross-section SUR)
Sample (adjusted): 2003 2023
Periods included: 21
Cross-sections included: 7
Total panel (balanced) observations: 147
Linear estimation after one-step weighting matrix
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(DEBT_GDP(−1))	0.000702	0.000270	2.602087	0.0103
D(LN_GFCF)	0.224514	0.015928	14.09567	0.0000
ECT_D(−1)	−0.098781	0.020393	−4.843821	0.0000
C	0.017881	0.002002	8.930195	0.0000
	Effects Specification
Cross-section fixed (dummy variables)
	Weighted Statistics
R-squared	0.653125	Mean dependent var		0.681984
Adjusted R-squared	0.630338	S.D. dependent var		1.771561
S.E. of regression	0.988605	Sum squared resid		133.8957
F-statistic	28.66169	Durbin–Watson stat		1.893538
Prob(F-statistic)	0.000000

(Appendix A.2) and summarized in

Table 16. Comparing the ECM and ARDL models for the non-euro EU area in the period of 2000–2023.

LN_GDP Dependent Variable Non-Euro	Error Correction Model			ARDL(1,1,1)
	Long-Run	Short-Run FE Cross-Sections (GLS-SUR)		Long-Run	Short-Run	With Dummies
		No Dummies	With Dummies			Long-Run	Short-Run
C	-	0.0179 ***	0.0245 ***	-	0.8547 ***	-	0.5549 ***
DEBT_GDP(−1)	0.0030 ***	0.0007 **	9.61 × 10−5	0.0049 ***	0.0007	0.0025 ***	0.0002
LN_GFCF	0.7040 ***	0.2245 ***	0.1760 ***	0.6066 ***	0.2088 ***	0.7305 ***	0.1336 ***
C2008			−0.0388 ***				−0.0412 ***
COVID			−0.0457 ***				−0.0565 ***
WAR			−0.0191 **				−0.0149
ECT(−1)	-	−0.0988 ***	−0.0864 ***	-	−0.1583 ***		−0.1268 **

*/**/*** significance p-value less than: 10%/5%/1%.

. The residuals of the ECM with significant fixed effects tested for cross-sectional and SUR GLS weights meet the requirements for model validation, of normal distribution and no correlation between cross-sections. The coefficient of determination, R-squared, is 65%. The ECT contributes on average to the correction towards the long-term equilibrium of non-euro countries with an adjustment speed of 9.88% over a one-year period.

The approach of ECM has the following equations of long-run and short-run (9):

$${lngdp}_{it}={\widehat{\propto }}_1{debtgdp}_{it-1}+{\widehat{\propto }}_2{lngfcf}_{it}$$

(9)

$${lngdp}_{it}=0.0030{debtgdp}_{it-1}+0.7040{lngfcf}_{it}+[CX=DETERM]$$

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_2{ECT}_{t-1}$$

$$\begin{gathered} {∆lngdp}_{it}=0.0179+0.0007{∆debtgdp}_{it-1}+0.2245∆{lngfcf}_{it}-0.0988({lngdp}_{it-1}- \\ -0.0030{debtgdp}_{it-2}-0.7040{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

When considering the economic shocks, the ECM has the same long-run Equation (9) and the short-run Equation (10) (

Table A18. Short-run model of economic convergence in EU non-euro area with economic shocks, in the period of 2000–2023.

Dependent Variable: D(LN_GDP)
Method: Panel EGLS (Cross-section SUR)
Sample (adjusted): 2003 2023
Periods included: 21
Cross-sections included: 7
Total panel (balanced) observations: 147
Linear estimation after one-step weighting matrix
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(DEBT_GDP(−1))	9.61 × 10−5	0.000235	0.409386	0.6829
D(LN_GFCF)	0.176004	0.014220	12.37762	0.0000
C2008	−0.038765	0.009174	−4.225361	0.0000
COVID	−0.045699	0.009026	−5.062895	0.0000
WAR	−0.019144	0.009130	−2.096795	0.0379
ECT(−1)	−0.086449	0.017849	−4.843407	0.0000
C	0.024514	0.002156	11.37097	0.0000
	Effects Specification
Cross-section fixed (dummy variables)
	Weighted Statistics
R-squared	0.689825	Mean dependent var		0.740146
Adjusted R-squared	0.662048	S.D. dependent var		1.789913
S.E. of regression	1.019763	Sum squared resid		139.3489
F-statistic	24.83449	Durbin–Watson stat		1.810348
Prob(F-statistic)	0.000000
	Unweighted Statistics
R-squared	0.682657	Mean dependent var		0.025950
Sum squared resid	0.044173	Durbin–Watson stat		1.707704

in Appendix A.2):

$${∆lngdp}_{it}={\widehat{\beta }}_0+{\widehat{\beta }}_{11}{∆debtgdp}_{it-1}+{\widehat{\beta }}_{12}∆{lngfcf}_{it}+{\widehat{\beta }}_{13}\mathrm{c}2008+{\widehat{\beta }}_{14}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}+{\widehat{\beta }}_{15}\mathrm{w}\mathrm{a}\mathrm{r}+{\widehat{\beta }}_2{ECT}_{t-1}$$

(10)

$$\begin{gathered} {∆lngdp}_{it}=0.0245-9.61·{10}^{-5}{∆debtgdp}_{it-1}+0.1760∆{lngfcf}_{it}-0.0388\mathrm{c}2008-0.0457\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{i}\mathrm{d}- \\ -0.0191\mathrm{w}\mathrm{a}\mathrm{r}-0.0864({lngdp}_{it-1}-0.0030{debtgdp}_{it-2}-0.7040{lngfcf}_{it-1})+[CX=F] \end{gathered}$$

The coefficient of determination, R², is close to 69%, better than that of the ECM without economic shocks. The ECM with dummy variables has an adjustment speed of 8.64% over a one-year period towards the long-run equilibrium of countries outside the euro area. If we exclude Denmark and Sweden, the long-run ECM is very close to that of the non-euro EU countries in Table 16. In this case, the short-run ECM with and without economic shocks does not find significant cross-sectional fixed effects. The ARDL model without economic shocks is not significant in the long run, and the ARDL model with dummy variables for economic shocks has an insignificant ECT coefficient. ARDL models cannot be used due to the small number of cross-sections. We keep all non-euro area EU countries to allow comparisons with the euro area.

The results of ARDL models with and without economic shocks are presented in Table 16,

Table A14. ARDL model of economic convergence in EU non-euro area in the period of 2000–2023.

Dependent Variable: D(LN_GDP)
Method: ARDL
Sample: 2002 2023
Included observations: 154
Maximum dependent lags: 1 (Automatic selection)
Model selection method: Akaike info criterion (AIC)
Dynamic regressors (1 lag, automatic): DEBT_GDP(−1) LN_GFCF
Fixed regressors: C
Number of models evalulated: 1
Selected Model: ARDL(1, 1, 1)
Note: final equation sample is larger than selection sample
Variable	Coefficient	Std. Error	t-Statistic	Prob. *
	Long Run Equation
DEBT_GDP(−1)	0.004912	0.001017	4.831775	0.0000
LN_GFCF	0.606645	0.045147	13.43700	0.0000
	Short Run Equation
COINTEQ01	−0.158315	0.055518	−2.851612	0.0051
D(DEBT_GDP(−1))	0.000693	0.000642	1.080667	0.2818
D(LN_GFCF)	0.208790	0.044771	4.663509	0.0000
C	0.854748	0.279811	3.054733	0.0027
Mean dependent var	0.026205	S.D. dependent var		0.030470
S.E. of regression	0.020538	Akaike info criterion		−4.697029
Sum squared resid	0.055258	Schwarz criterion		−4.122854
Log likelihood	408.1108	Hannan-Quinn criter.		−4.463891

* Note: p-values and any subsequent tests do not account for model selection.

and

Table A15. ARDL model of economic convergence with economic shocks in EU non-euro area in the period of 2000–2023.

Dependent Variable: D(LN_GDP)
Method: ARDL
Sample: 2002 2023
Included observations: 154
Maximum dependent lags: 1 (Automatic selection)
Model selection method: Akaike info criterion (AIC)
Dynamic regressors (1 lag, automatic): DEBT_GDP(−1) LN_GFCF
Fixed regressors: C2008 COVID WAR C
Number of models evalulated: 1
Selected Model: ARDL(1, 1, 1)
Note: final equation sample is larger than selection sample
Variable	Coefficient	Std. Error	t-Statistic	Prob. *
	Long Run Equation
DEBT_GDP(−1)	0.002498	0.000730	3.423317	0.0009
LN_GFCF	0.730505	0.031076	23.50703	0.0000
	Short Run Equation
COINTEQ01	−0.126793	0.049174	−2.578459	0.0112
D(DEBT_GDP(−1))	0.000219	0.000736	0.297764	0.7664
D(LN_GFCF)	0.133586	0.039687	3.365990	0.0011
C2008	−0.041229	0.011913	−3.460888	0.0008
COVID	−0.056494	0.006900	−8.186998	0.0000
WAR	−0.014963	0.010441	−1.433108	0.1547
C	0.554941	0.207153	2.678895	0.0085
Mean dependent var	0.026205	S.D. dependent var		0.030470
S.E. of regression	0.015691	Akaike info criterion		−5.267232
Sum squared resid	0.027082	Schwarz criterion		−4.291135
Log likelihood	475.0122	Hannan-Quinn criter.		−4.870897

* Note: p-values and any subsequent tests do not account for model selection.

(Appendix A.2), and we see that the coefficients of the long-term ARDL models are significant at Prob. < 1%. The speed of adjustment of ECT from short-term towards the long-term equilibrium is 15.83%, respectively, 12.68% over a one-year period, for the group of EU countries of non-euro area. In Table 16 we observe similar corresponding values for economic shocks in both the ECM and ARDL models, and smaller than in the case of the euro area.

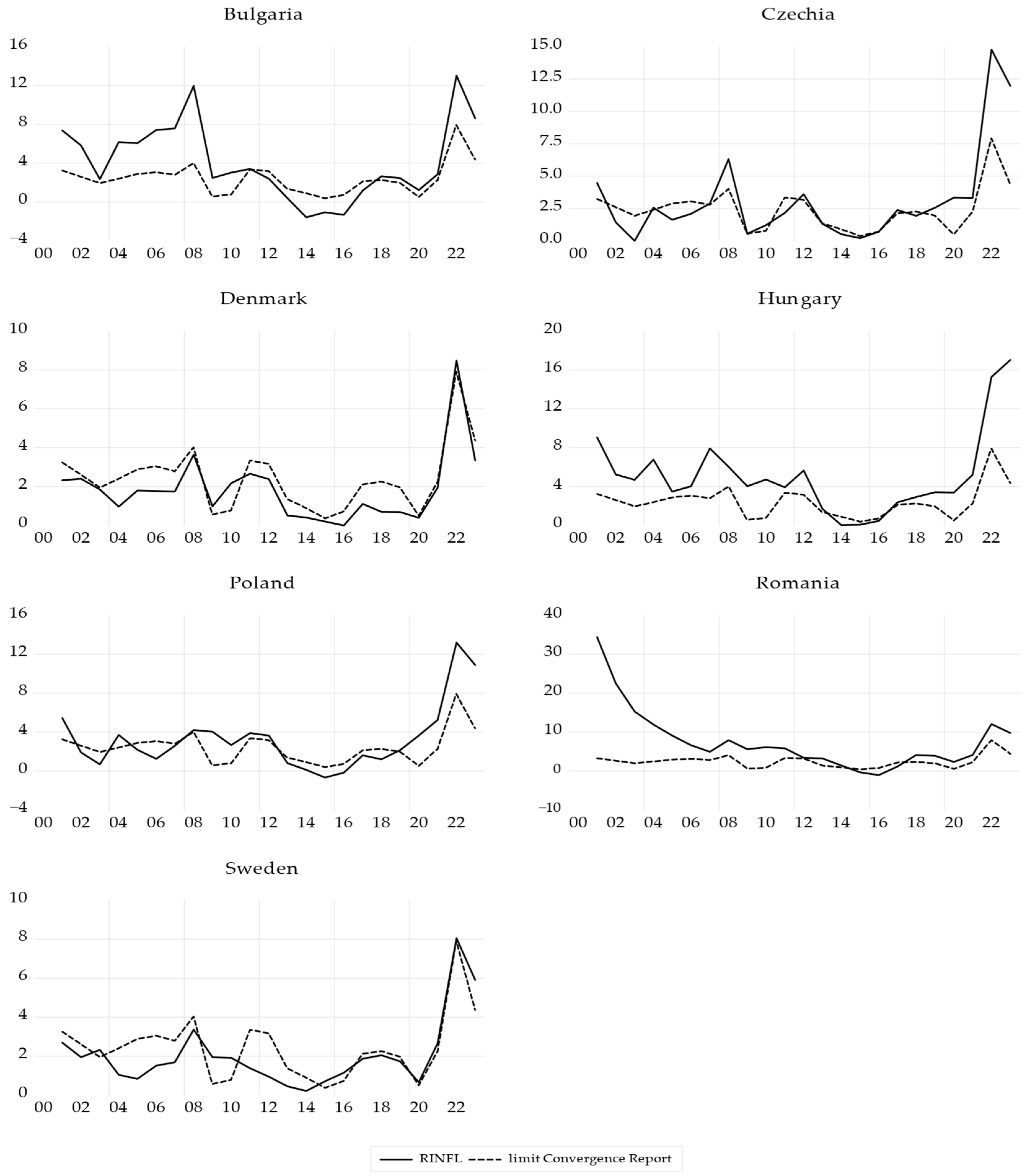
The short-run ARDL coefficients with dummy variables for each non-euro area EU country over the period 2000–2023 are presented in

Table 17. The ARDL coefficients for each non-euro EU country over the period of 2000–2023.

No.	Country	COINTEQ01	D(DEBT_GDP(−1))	D(LN_GFCF)	C2008	COVID	WAR	C
1	Hungary	−0.3061 ***	−0.0002 ***	−0.0234 ***	−0.0815 ***	−0.0765 ***	−0.0199 ***	1.2620 ***
2	Denmark	−0.2410 ***	0.0020 ***	0.1183 ***	−0.0430 ***	−0.0448 ***	0.0333 ***	1.0807 ***
3	Sweden	−0.1699 ***	0.0029 ***	0.2729 ***	−0.0047 ***	−0.0251 ***	0.0033 ***	0.7637 ***
4	Czech Rep.	−0.1423 ***	−0.0016 ***	0.2086 ***	−0.0444 ***	−0.0572 ***	−0.0325 ***	0.6060 ***
5	Bulgaria	−0.0724 ***	−0.0003 ***	0.0449 ***	−0.0685 ***	−0.0674 ***	−0.0057 ***	0.3149 ***
6	Romania	−0.0369 ***	−0.0025 ***	0.0966 ***	−0.0516 ***	−0.0744 ***	−0.0353 ***	0.1911 *
7	Poland	0.0811 ***	0.0013 ***	0.2173 ***	0.0051 ***	−0.0502 ***	−0.0479 ***	−0.3337 ***
Non-euro area		−0.1268 **	0.0002	0.1336 ***	−0.0412 ***	−0.0565 ***	−0.0150	0.5549 ***

*/**/*** significance p-value less than: 10%/5%/1%.

. The countries are in descending order of adjustment speed on short-term to move the system towards the long-term equilibrium. Hungary has the highest speed of adjustment to the long-term equilibrium, at 30.61%. Poland is the only country that has a positive ECT coefficient, indicating the absence of a long-term relationship based on this model. If the ARDL model is used without considering the economic shocks in the period of 2000–2023, all countries in the group have a long-run relationship between the analyzed variables, which means that the ECT coefficients are significant and less than 1. However, considering the separate influence of economic shocks, the speed of adjustment is different for each country and for the entire group.

All the coefficients of the cross-sectional models of the term COINTEQ01, DEBT_GDP(−1), LN_GFCF and the dummy variables are significant at Prob. < 1%. At the level of the group of countries outside the euro area, the coefficient of the lagged term of the variable DEBT_GDP is not significant, but it is significant in the equation of each country; the dummy variable “war” is also significant at Prob. < 1% in the individual model of each country, but not for the group. This difference in significance of the coefficients at the individual and aggregate levels is caused by the unobserved heterogeneity of the countries in the group.

In Figure 17, the theoretical values of LN_GDP with the ECM and ARDL models with dummy variables represent the economic convergence on the graph of each country and for the group of EU countries outside the euro area. The forecast evaluation indicators show the ARDL model with dummy variables to be better than the ECMs. The coefficients of the ECT cointegration terms for ECM and ARDL models, in Table 16, are negative, less than 1 and significant at a p-value < 1%, proving the existence of a long-term economic equilibrium in the EU non-euro area, which attests to hypothesis H2.

4.2.4. Modeling Economic Convergence in EU Countries in the Period of 2000–2023

The variables LN_GDP, DEBT_GDP, and LN_GFCF for all 27 countries of the European Union are cointegrated in the period of 2000–2023. The Pedroni tests reject the null hypothesis of no cointegration with six of eleven statistics, in

Table A6. Cointegration of economic convergence indicators in the period of 2000–2023 for the EU.

Pedroni Residual Cointegration Test
Series: LN_GDP DEBT_GDP LN_GFCF
Sample: 2000 2023
Included observations: 648
Cross-sections included: 27
Null Hypothesis: No cointegration
Trend assumption: No deterministic intercept or trend
Automatic lag length selection based on SIC with a max lag of 4
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	−2.387883	0.9915	−2.582440	0.9951
Panel rho-Statistic	−1.286779	0.0991	−0.794169	0.2135
Panel PP-Statistic	−2.791109	0.0026	−1.972068	0.0243
Panel ADF-Statistic	−4.154787	0.0000	−3.020364	0.0013
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	0.712795	0.7620
Group PP-Statistic	−2.318816	0.0102
Group ADF-Statistic	−4.420519	0.0000

(Appendix A.1), both for “no deterministic trend” and for “no deterministic intercept or trend”.

The correlation matrix at the EU level is presented in

Table 18. Correlation matrix of economic convergence indicators of EU countries in the period of 2000–2023.

	LN_GDP	DEBT_GDP	LN_GFCF	OPN
LN_GDP	1
DEBT_GDP	0.420	1
LN_GFCF	0.993	0.362	1
OPN	−0.484	−0.269	−0.479	1

. The correlations between the variables of EU countries are similar to those of the two groups of EU countries: the euro area and the non-euro area.

We test whether a dynamic model is appropriate, and we choose between Difference GMM and System GMM in

Table 19. Choosing the right GMM model for EU economic convergence in the period of 2000–2023.

2000–2023 LN_GDP(−1) Coefficient	FE Cross-Section, ${\widehat{\mathit{a}}}_1$ Lower Limit	Pool OLS ${\widehat{\mathit{a}}}_1$ Upper Limit	D-GMM (Differences) ${\widehat{\propto }}_1$	Model Choice (D-GMM or S-GMM)?	S-GMM c(2)
EU	0.7487 ***	0.9021 ***	0.7326 ***	S-GMM	0.8496 ***

***—significance at p-value < 1%.

. To identify the appropriate dynamic model for LN_GDP we build the panel data models using the lagged dependent variable as an explanatory variable together with lagged variable DEBT_GDP and LN_GFCF.

In Table 19, the coefficients ${\widehat{a}}_1$ of the lagged dependent variable LN_GDP of the Pool OLS model and the cross-sectional Fixed Effects (FE) model, based on Equation (1), define the upper and lower bounds, respectively, of an interval within which the corresponding coefficient of the lagged dependent variable of the dynamic model is expected to lie.

$${\widehat{ln\_gdp}}_{it}={\widehat{a}}_0+{\widehat{a}}_{1}l{n\_gdp}_{it-1}+{\widehat{a}}_2{debt\_gdp}_{it-1}+{\widehat{a}}_3{ln\_gfcf}_{it}$$

(11)

If the Difference GMM (D-GMM) model has a significant and positive coefficient of the lagged dependent variable ${\widehat{\propto }}_1$ in Equation (12), less than 1, and is comprised within the range bounded by the lower limit by ${\widehat{a}}_1$ of the FE model and the upper limit by ${\widehat{a}}_1$ of the Pool OLS, then the D-GMM is the best choice.

$${\widehat{∆ln\_gdp}}_{it}={\widehat{\propto }}_1∆l{n\_gdp}_{it-1}+{\widehat{\propto }}_2∆{debt\_gdp}_{it-1}+{\widehat{\propto }}_3∆{ln\_gfcf}_{it}$$

(12)

If the coefficient of the lagged dependent variable of the D-GMM, ${\widehat{\propto }}_1$ in Equation (12) is less than the lower bound of the range, then a system GMM model (S-GMM) can correct this by providing a coefficient of the lagged dependent variable within the established range, as is the case in Table 19.

The S-GMM model based on the system of the two equations shown in Equation (13) in Eviews is presented in the regression summary in

Table A19. S-GMM model for the economic convergence of EU countries in the period of 2000–2023.

System: SYS_GMM
Estimation Method: Generalized Method of Moments
Sample: 2002 2023
Included observations: 594
Total system (unbalanced) observations 1161
Kernel: Bartlett, Bandwidth: Fixed (6), No prewhitening
Linear estimation after one-step weighting matrix
	Coefficient	Std. Error	t-Statistic	Prob.
C(1)	0.208342	0.101079	2.061186	0.0395
C(2)	0.849571	0.039957	21.26187	0.0000
C(3)	0.000650	0.000279	2.330926	0.0199
C(4)	0.150431	0.038520	3.905251	0.0001
C(5)	0.628630	0.086917	7.232566	0.0000
C(6)	0.001835	0.000694	2.642509	0.0083
C(7)	0.261656	0.079675	3.284036	0.0011
Determinant residual covariance		1.33 × 10−6
J-statistic		0.001589
Equation: LN_GDP = C(1) + C(2)*LN_GDP(−1) + C(3)*DEBT_GDP(−1) + C(4)*LN_GFCF
Instruments: D(LN_GDP(−2)) D(DEBT_GDP(−2)) D(LN_GFCF(−1)) C
Observations: 567
R-squared	0.999320	Mean dependent var		11.91645
Adjusted R-squared	0.999316	S.D. dependent var		1.516734
S.E. of regression	0.039660	Sum squared resid		0.885548
Durbin–Watson stat	1.082513
Equation: D(LN_GDP) = C(5)*D(LN_GDP(−1)) + C(6)*D(DEBT_GDP(−1)) + C(7)*D(LN_GFCF)
Instruments: LN_GDP(−2) DEBT_GDP(−2) LN_GFCF(−1) C
Observations: 594
R-squared	0.246191	Mean dependent var		0.022064
Adjusted R-squared	0.243640	S.D. dependent var		0.038603
S.E. of regression	0.033573	Sum squared resid		0.666140
Durbin–Watson stat	2.645225

(Appendix A.2) and in

Table 20. S-GMM model for the economic convergence of EU countries in the period of 2000–2023.

	Coefficient	Std. Error	t-Statistic	Prob.
C(1)	0.2083 **	0.101079	2.061186	0.0395
C(2)	0.8496 ***	0.039957	21.26187	0.0000
C(3)	0.0006 **	0.000279	2.330926	0.0199
C(4)	0.1504 ***	0.038520	3.905251	0.0001
C(5)	0.6286 ***	0.086917	7.232566	0.0000
C(6)	0.0018 ***	0.000694	2.642509	0.0083
C(7)	0.2617 ***	0.079675	3.284036	0.0011

*/**/*** significance p-value less than: 10%/5%/1%.

. The two Equation (13) contain the instruments associated with the variables: the first equation of the level variables has as instruments the lagged differenced levels of the variables, and in the second equation of the differences in variables, the instruments are the lagged levels of the variables.

ln_gdp = c(1) + c(2)∙ln_gdp(−1) + c(3) ∙debt_gdp(−1) + c(4) ∙ln_gfcf @ d(ln_gdp(−2)) d(debt_gdp(−2)) d(ln_gfcf(−1))

(13)

d(ln_gdp) = c(5) ∙d(ln_gdp(−1)) + c(6) ∙d(debt_gdp(−1)) + c(7) ∙d(ln_gfcf) @ ln_gdp(−2) debt_gdp(−2) ln_gfcf(−1)

All coefficients of the S-GMM model are on short term; in Table A19 (Appendix A.2) they are significant at Prob. < 5%. The coefficient c(2) of the lagged variable LN_GDP, in Equation (13), is significantly different from 0, positive, less than 1 and represents the speed of adjustment towards the long-run equilibrium. It is within the range bounded by the corresponding coefficient of the FE model and the Pool OLS model, in Table 19.

Even if the S-GMM coefficients are on short-term, we consider the economic convergence of the EU, as being the long part of the S-GMM model expressed here by the first Equation (13), presented in Table 20. The second equation of the system in Equation (13) represents the short-term part of the S-GMM model. Both the theoretical long-run and short-run values of LN_GDP are shown in Figure 18 and Figure 19.

The long-run impact of explanatory variables may be separately calculated by dividing the short-run coefficient of each variable to 1 minus the coefficient of the lagged dependent variable, meaning here (1 − C(2)). The Wald test, in

Table 21. The Wald test for the long-run coefficients based on the S-GMM model for the economic convergence of EU countries in the period of 2000–2023.

Null Hypothesis:	Value	Std. Err.	Probability
C(1)/(1 − C(2)) = 0	1.384981	0.497501	0.0054
C(3)/(1 − C(2)) = 0	0.004320	0.001228	0.0004
C(4)/(1 − C(2)) = 0	1.000013	0.051472	0.0000

, shows the values of the long-run coefficients based on the S-GMM model from Table 20, and affirms that the long-run coefficients are significant at a probability less than 1%.

The cointegration test between LN_GDP and the long part of S-GMM in

Table A7. Cointegration of long-term values of S-GMM and GDP in the EU over the period 2000–2023.

Pedroni Residual Cointegration Test
Series: LN_GDP LN_GDP_LONG
Sample: 2000 2023
Included observations: 648
Cross-sections included: 27
Null Hypothesis: No cointegration
Trend assumption: No deterministic trend
User-specified lag length: 1
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	2.928675	0.0017	1.517113	0.0646
Panel rho-Statistic	−2.722867	0.0032	−4.044708	0.0000
Panel PP-Statistic	−4.311045	0.0000	−5.562821	0.0000
Panel ADF-Statistic	−4.549346	0.0000	−5.986182	0.0000
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	−1.008796	0.1565
Group PP-Statistic	−4.449678	0.0000
Group ADF-Statistic	−5.284258	0.0000

of Appendix A.1 rejects the null hypothesis of no cointegration with nine out of eleven test statistics. Cointegration is confirmed for the short-run S-GMM values in

Table A8. Cointegration of short-term S-GMM and GDP in the EU over the period 2000–2023.

Pedroni Residual Cointegration Test
Series: LN_GDP LN_GDP_SHORT
Sample: 2000 2023
Included observations: 648
Cross-sections included: 27
Null Hypothesis: No cointegration
Trend assumption: No deterministic trend
User-specified lag length: 1
Newey-West automatic bandwidth selection and Bartlett kernel
Alternative hypothesis: common AR coefs. (within-dimension)
			Weighted
	Statistic	Prob.	Statistic	Prob.
Panel v-Statistic	2.242899	0.0125	2.113719	0.0173
Panel rho-Statistic	−0.514967	0.3033	−1.556823	0.0598
Panel PP-Statistic	−0.459301	0.3230	−2.155419	0.0156
Panel ADF-Statistic	−2.073898	0.0190	−3.205335	0.0007
Alternative hypothesis: individual AR coefs. (between-dimension)
	Statistic	Prob.
Group rho-Statistic	0.263183	0.6038
Group PP-Statistic	−1.673105	0.0472
Group ADF-Statistic	−2.923788	0.0017

(Appendix A.1) by rejecting the null hypothesis with seven out of eleven test statistics.

The coefficient c(2) of the lagged variable LN_GDP, in Table 19 and Table 20, is significantly different from 0, positive, and less than 1, and represents the speed of adjustment towards the long-run equilibrium at the EU level, which attests to hypothesis H3.

5. Conclusions

Eurozone countries benefit from the advantages of being part of the European Monetary Union. Higher levels of debt-to-GDP ratios provide greater opportunities for economic development. Non-euro countries must meet the financial convergence criteria to join the euro. Bulgaria, which has already fulfilled the conditions to join the Eurozone, is preparing its entry on 1 January 2026.

5.1. Conclusions on Compliance with Financial Criteria in the Euro Area and Outside the Euro Area, Between 2000 and 2023

Price stability is not achieved by EU countries outside the euro area. As shown in Figure 2, their average inflation rate was below the limit calculated for the three best-performing euro area economies only in the years 2013–2017. After 2018, inflation was on the rise for almost all countries in the non-euro group, except for Denmark and Sweden, as shown in Figure 3. In Table 1, the average inflation rate, median, minimum and maximum values are higher than for the euro area.

The budget deficit criterion of respecting the threshold of below −3% for the current account balance as a percentage of GDP (denoted by CAB_GDP) was met, on average, by both the euro area and non-euro area, since 2009, after the economic crisis, until 2022, when the war between Russia and Ukraine began and most EU countries recorded deficits (Figure 5). The euro area complied with the deficit criterion in the period of 2009–2023, but the non-euro area violated it in 2022 (Figure 5). The non-euro area had positive current account balances in the period of 2013–2017, when the price stability criterion was also met.

Among the non-euro area EU countries, only Hungary and Romania had deficits in 2023, and Romania had the largest deficit. All other countries in the group recorded positive current account balances, as shown in Figure 6.

Regarding the debt criterion, euro area countries have higher debt-to-GDP ratios compared to non-euro area EU countries. Of the non-euro group, only Hungary did not meet the criterion, as its debt-to-GDP ratio exceeded the 60% limit since 2005 (Figure 8).

To assess compliance with the exchange rate stability criterion in the euro area and in EU countries outside the euro area, we use the independent samples t-test for equality of means, in the SPSS program. We conclude that, by removing Denmark and Sweden from the group of non-euro area countries, the test for equality of means shows higher volatility in the non-euro area and significant differences compared to the exchange rate variation in the euro area. We use the one-sample t-tests for the 95% confidence intervals of the variation in the exchange rate means for the countries and the three groups: the euro area group, the non-euro area group and the non-euro area group without Denmark and Sweden. The results lead to the conclusion that the non-euro area group, excluding Denmark and Sweden, had higher volatility and higher confidence interval values of the exchange rate mean.

The long-term interest rate criterion is respected, on average, by euro area countries, but not to the same extent by non-euro area countries. The average long-term interest rate of countries outside the euro area has been above the average limit of this criterion since 2008, as shown in Figure 10 (right). Hungary and Romania did not comply with the limit at all during the entire period. Poland has not complied since 2009. Bulgaria has complied since 2016 and for the rest of the period. The Czech Republic has been in compliance with this criterion for a long time, from 2000 to 2020, but violates it in 2021 and 2022. Denmark follows the criterion limit very closely, as does Sweden, but which is largely above the limit. In Table 8, the descriptive statistics of the long-term interest rate show that the euro area group is the only one that, on average, meets the criterion. The group of countries outside the euro area, without Denmark and Sweden, does not meet the criterion. Even if we take into account the two developed countries in the non-euro group, the criterion is still not met.

We conclude that countries outside the euro area do not meet almost all financial criteria. Compliance with financial criteria provides opportunities for better economic performance and sustainable development.

We conclude that the compliance process is dynamic, as we have observed that the permitted limits for certain criteria change depending on economic dynamics.

5.2. Conclusions on Economic Growth in the Euro Area, Outside the Euro Area, and in the EU, Between 2000 and 2023

We observe very close values of the real GDP and the corresponding theoretical values calculated with the ECM and ARDL models, without and with dummy variables in the euro area (Table 12, Figure 14 and Figure 15) and outside the euro area (Table 16, Figure 17 and Figure 18). To analyze economic convergence that assumes a long-run equilibrium, we will consider econometric models without dummy variables. We can consider ECM and ARDL models with dummy variables only to analyze how economic shocks influenced the Eurozone economies compared to non-euro EU countries.

5.2.1. Conclusions on Economic Growth in Euro Area and Non-Euro Area, Between 2000 and 2023, Based on ECM

The ECM approach has all coefficients significant at Prob. < 1% in the long-run as presented in

Table 22. Comparison of ECM coefficients within EU groups, over the period of 2000–2023.

LN_GDP— Dependent Variable	Error Correction Model
	Euro Area			Non-Euro			Non-Euro Area Without Denmark and Sweden
	Long-Run	Short-Run FE Cross-Sections (GLS-SUR)		Long-Run	Short-Run FE Cross-Sections (GLS-SUR)		Long-Run	Short-Run FE Cross-Section No Dummies
		No Dummies	With Dummies		No Dummies	With Dummies
C	-	0.0128 ***	0.0212 ***	-	0.0179 ***	0.0245 ***	-	0.0216 ***
DEBT_GDP(−1)	0.0031 ***	0.0009 ***	0.0004 ***	0.0030 ***	0.0007 **	9.61 × 10−5	0.0033 ***	0.0005
LN_GFCF	0.6629 ***	0.2463 ***	0.1813 ***	0.7040 ***	0.2245 ***	0.1760 ***	0.6926 ***	0.1873 ***
C2008			−0.0527 ***			−0.0388 ***
COVID			−0.0619 ***			−0.0457 ***
WAR			−0.0171 ***			−0.0191 **
ECT(−1)	-	−0.1870 ***	−0.1635 ***	-	−0.0988 ***	−0.0864 ***	-	−0.1023 ***

*/**/*** significance p-value less than: 10%/5%/1%.

for euro-area and non-euro area. The coefficient of the lagged term DEBT_GDP is the approximately the same in models of the two country groups, showing the very same average influence on economic growth of around 0.30–0.31% for a 1 p.p. increase in the debt-to-GDP ratio of the previous year. It remains for investments to make a difference in terms of economic growth; this fact attests to hypothesis H5. In the long run, a 1% increase in GFCF leads to an average annual increase of 0.663% of GDP for the euro area, 0.704% for the non-euro area.

Economic growth is higher in non-euro area economies than in the euro area because, as we observe, the slower influence of 0.30% GDP growth for every 1 percentage point increase in the debt-to-GDP ratio of the previous year is offset by a higher influence of 0.704% GDP growth for a 1% increase in GFCF, investment. These results support the role of investment as a driver of development, i.e., hypothesis H5.

The short-run ECMs of the euro area and the non-euro area have significant fixed effects of cross-sections. The short-term ECM coefficients of the explanatory variables are smaller than the corresponding long-term ones, consistent with the correction towards the equilibrium relationship, towards their higher values, by the speed of panel adjustment over a one-year period. In the short term, we observe smaller influences on economic growth of the two regressors for the non-euro area group and also a lower adjustment speed, of only 9.88%, compared to 18.7% for the euro area group. We believe that the presence of the two developed countries, Denmark and Sweden in the group of non-euro area, alters the results, as seen in Table 22.

If we exclude Denmark and Sweden from the group of non-Eurozone countries, we observe a long-run equation similar to the previous ones. A 1 percentage point increase in the debt-to-GDP ratio from the previous year leads to a greater influence of an average annual GDP growth of 0.33%, higher than for the euro area (hypothesis H4). A 1% increase in GFCF leads to an average annual GDP growth of 0.69%, slightly slower if we consider the two developed countries in the non-euro group, but still higher than the corresponding coefficient in the euro area. This conclusion further supports hypotheses H5 and H4.

In the short term, for the group of non-euro area, excluding Denmark and Sweden, a 1 percentage point increase in the debt-to-GDP ratio of the previous year has an insignificant influence, of 0.05% on GDP growth, compared to the similar and significant influence of 0.07%, with a p-value of 5%, as for the entire group of non-euro area countries.

Without Denmark and Sweden, the average influence of a 1 percentage point increase in GFCF has an average annual influence of 0.1873% on GDP growth, lower than in the previous non-euro panel and in the euro area. However, the updated non-euro panel has a higher speed of adjustment towards equilibrium of 10.23%, higher than the previous one. These results confirm hypothesis H6, the more homogeneous the group of countries outside the euro area, the higher the speed of adjustment.

The short-term ECM coefficients of the non-euro group show the positive, but insignificant, influence of indebtedness on a convergent economic growth and the positive effects of investment, but still less efficient than in the euro area. Short-term results provide the solution for complying with the euro area’s financial criteria for accession and benefiting from the policies of the Economic and Monetary Union.

However, in the long term, both the effects of indebtedness and investment are greater in the non-euro area than in the euro area, which explains the higher economic growth rates of these countries and their development potential. These conclusions are in line with hypothesis H4.

When economic shocks are taken into account, as shown in Table 22, the long-run ECM is the same as in the case without dummies. Economic shocks act on economic growth in the short run, and this maintains the adjustment towards the equilibrium line for both the euro area and non-euro area, with very similar adjustment speeds as in the case without dummies.

For ECMs with dummy variables, the short-term influences of the two main factors are smaller than in models without dummy variables; the same is true for the speed of adjustment; some of the influences seem to be diffused to economic shocks.

We can conclude that, in the short term, the debt-to-GDP ratio of the previous year and investment have smaller contributions to economic growth in the non-euro area than in the euro area, but in the long term they have higher influences. The crisis that started in 2008 caused a larger decline in the euro area, of around 5.3%, compared to 3.9% in the EU area outside the euro area. The pandemic year 2020 had a larger negative influence, of around 6.2% in the euro area, compared to an average decline of 4.6% in the non-euro area. The Russia–Ukraine war caused a similar decline in 2023, of around 2%, more precisely of −1.7% in the euro area and −1.9% in the non-euro area, respectively. These conclusions attest to hypothesis H7.

5.2.2. Conclusions on Economic Growth in the Euro Area and Outside the Euro Area, Between 2000 and 2023, Based on ARDL

When we compare the ARDL models in

Table 23. Comparison of ARDL coefficients in the EU groups, between 2000 and 2023.

LN_GDP Dependent Variable	ARDL(1,1,1)
	Euro Area				Non-Euro Area
	No Dummies		With Dummies		No Dummies		With Dummies
	Long-Run	Short-Run	Long-Run	Short-Run	Long-Run	Short-Run	Long-Run	Short-Run
C	-	1.1172 ***	-	0.8844 ***	-	0.8547 ***	-	0.5549 ***
DEBT_GDP(−1)	0.0029 ***	0.0002	0.0033 ***	−1.75 × 10−5	0.0049 ***	0.0007	0.0025 ***	0.0002
LN_GFCF	0.5795 ***	0.2196 ***	0.6134 ***	0.1243 ***	0.6066 ***	0.2088 ***	0.7305 ***	0.1336 ***
C2008	-			−0.0394 ***				−0.0412 ***
COVID				−0.0644 ***				−0.0565 ***
WAR				−0.0168 ***				−0.0149
ECT(−1)		−0.1972 ***		−0.1643 ***	-	−0.1583 ***		−0.1268 **

*/**/*** significance p-value less than: 10%/5%/1%.

at the country groups’ level, we observe very similar results to those of the ECMs in Table 22; the same conclusions can be drawn.

We observe in Table 23 that the coefficients of the variables in the short-term models are smaller than the corresponding coefficients in the long-term models, so as to allow the action of the cointegration term in adjusting the system towards the equilibrium coefficients of the long-term models. All the long-run models have significant coefficients at a p-value < 1%. Comparing the results of the two groups of countries, we find that, in the long run, both explanatory variables in the non-euro area EU countries have a greater influence on GDP growth than in euro area countries, over the period analyzed, both in models without and with dummy variables. In the ARDL model without dummy variables, a 1 percentage point increase in DEBT_GDP(−1) leads to a 0.5% increase in GDP, compared to 0.3% for euro area economies. A similar conclusion shows a GDP growth of non-euro area countries of 0.61% for every 1% increase in GFCF, compared to 0.58% in euro area countries; the same conclusion is also valid for the ARDL models with dummies.

In the short run, the four ARDL models with and without economic shocks have all positive and insignificant DEBT_GDP coefficients; they show a larger influence on GDP outside the euro area than inside the euro area. In the short run, without dummy variables, the influence of a 1 percentage point increase in GFCF on GDP growth is on average 0.21–0.22% for the two groups of EU countries; the LN_FBCF coefficients are significant at Prob. < 1%. When economic shocks are taken into account, in ARDL models with dummy variables, the influence of investments becomes smaller, in the non-euro area of 0.1336%, but still higher than in the euro area of 0.1243%. The shocks of the 2008 economic crisis, the pandemic-imposed quarantine, and Russia’s war against Ukraine led to declines in investment; the coefficients of the dummy variables show the negative influences on economic growth, even deeper in the euro area than in non-euro area EU countries. The 2008 crisis caused an average decline of around 4% in GDP in 2009 in both areas. We note that the COVID pandemic caused an average decline of −6.44% in the euro area, compared to −5.65% in the non-euro area. The Russian war caused an average decline of 1.7% in the euro area in 2023, compared to 1.5% in the non-euro area. All these conclusions support hypothesis H7. The speed of adjustment is lower for the non-euro area than in euro area in ARDL models, both with and without dummy variables, confirming hypothesis H6.

In the long run, the influence of investment on GDP growth is larger for non-euro countries than for the euro area; the conclusion is also valid when comparing ARDL with dummy variables (hypothesis H5).

ARDL models perform better than ECMs for both groups of EU countries. The ECM approach supports the validity of the ARDL results.

5.2.3. Conclusions on EU Economic Growth in the Period of 2000–2023 Based on S-GMM

The economic growth of each country and the theoretical values according to the economic convergence of the group to which it belongs, calculated with ARDL without dummy variables, denoted LN-GDP_COUNTRY_ARDL, are compared with the corresponding economic convergence at the EU level, denoted LN_GDP_EU_SGMM_LONG. These analyses are presented at the level of each group: EU, euro area and non-euro area, in

Table 24. S-GMM coefficients at the EU level and group ARDL coefficients, 2000–2023.

LN_GDP Dependent Variable	ARDL(1,1,1)				S-GMM EU Countries
	Euro Area		Non-Euro Area
	Long-Run	Short-Run FE Cross-Section	Long-Run	Short-Run FE Cross-Section	Long-Run	Short-Run
C	-	1.1172 ***	-	0.8547 ***	1.3850 ***	0.2083 **
DEBT_GDP(−1)	0.0029 ***	0.0002	0.0049 ***	0.0007	0.0043 ***	0.0006 **
LN_GFCF	0.5795 ***	0.2196 ***	0.6066 ***	0.2088 ***	1.0000 ***	0.1504 ***
ECT(−1)		−0.1972 ***		−0.1583 ***

*/**/*** significance p-value less than: 10%/5%/1%.

, Figure 20a–c, as well as in the descriptive statistics in

Table A20. Descriptive statistics of real and theoretical economic growth in the EU in the period of 2000–2023.

EU	LN_GDP	LN_GDP_ COUNTRY_ARDL	LN_GDP_EU_ SGMM_LONG
Mean	11.88122	11.91108	11.87820
Median	12.06244	12.06258	12.12210
Maximum	14.91994	14.92519	14.94904
Minimum	8.575519	8.597647	8.541602
Std. Dev.	1.531138	1.512045	1.603301
Skewness	0.061592	0.077048	0.063080
Kurtosis	2.264024	2.246960	2.200130
Jarque–Bera	15.03456	14.62268	16.96645
Probability	0.000544	0.000668	0.000207
Observations	648	594	621

,

Table A21. Descriptive statistics of real and theoretical economic growth in the euro area in the period of 2000–2023.

Euro Area	LN_GDP	LN_GDP_ COUNTRY_ARDL	LN_GDP_EU_ SGMM_LONG
Mean	11.83700	11.86472	11.84823
Median	12.05896	12.05538	12.12835
Maximum	14.91994	14.92519	14.94904
Minimum	8.575519	8.597647	8.541602
Std. Dev.	1.716699	1.694100	1.803951
Skewness	0.140663	0.158904	0.122218
Kurtosis	1.911392	1.904592	1.830346
Jarque–Bera	25.28423	23.85020	27.36693
Probability	0.000003	0.000007	0.000001
Observations	480	440	460

and

Table A22. Descriptive statistics of real and theoretical economic growth in the EU non-euro area in the period of 2000–2023.

Non-Euro Area	LN_GDP	LN_GDP_ COUNTRY_ARDL	LN_GDP_EU_ SGMM_SHORT
Mean	12.00757	12.04356	11.96384
Median	12.07205	12.08704	12.12210
Maximum	13.22491	13.22491	13.14808
Minimum	10.10494	10.19677	10.10741
Std. Dev.	0.779817	0.776272	0.784478
Skewness	−0.621847	−0.598208	−0.765943
Kurtosis	2.638541	2.559750	2.801112
Jarque–Bera	11.74201	10.42857	16.00765
Probability	0.002820	0.005438	0.000334
Observations	168	154	161

in Appendix A.3.

In Table 24, at the EU level, the short-run S-GMM model recognizes a significant and similar influence of the lagged debt-to-GDP ratio of around 0.06% on economic growth, compared to a non-significant coefficient of 0.07% at the non-euro level and 0.02% at the euro area level. The coefficient LN_GFCF in the short-run S-GMM is significant at a p-value of less than 1% and shows that a 1% increase in investment contributes to economic growth, with an average increase of about 0.1504%, holding other factors constant; this value is lower than in the euro area and outside the euro area.

At the EU level, the conformity of the average economic growth and ARDL economic convergence of the belonging groups with that at the EU level calculated by the S-GMM is presented in Figure 20a and Table A20 (Appendix A.3).

We selected euro area countries to compare real economic growth with the euro area economic convergence established with ARDL and with that at the EU level with S-GMM, in Figure 20b and in the descriptive statistics in Table A21 in Appendix A.3.

For the non-euro area, real economic growth and the corresponding economic convergence of the group and with that of the EU level are presented in Figure 20c and Table A22 in Appendix A.3. In both Figure 20c and Table A22, we observe that the average economic growth exceeds the corresponding S-GMM average, which shows that the non-euro area is above the EU level of economic convergence. Non-euro area countries have higher economic growth rates (Table A22) than the euro area (Table A21) and the EU (Table A20), in line with hypothesis H4.

The three tables in Appendix A.3 present very close values of the descriptive statistical indicators, proving the validity of the models at all analyzed levels and confirming hypotheses H1, H2, and H3.

The average levels of economic growth for countries outside the euro area in Table A22 are higher than the euro area, demonstrating hypothesis H4.

Figure 21 presents economic growth for each country, comparing it with economic convergence at the level of each group and at the EU level, established with S-GMM.

Figure 21 shows the evolution of real GDP and economic convergence of its membership group (LN_GDP_COUNTRY_ARDL), as well as the long-term values of S-GMM in EU countries over the period 2000–2023, separately for the non-euro area and the euro area. The long-run model of S-GMM presents theoretical levels of LN_GDP towards long-run equilibrium of EU. The closer the country’s real GDP is to theoretical long-term values, the more consistent it is with EU economic convergence.

The euro area countries that are below the EU economic convergence line identified by the long-term S-GMM model, over the entire period, in Figure 21, are: Portugal, Austria, Italy, France, Spain, Greece and Belgium, as well as Finland after 2009, but almost all are placed above the euro area economic convergence line. We conclude that these Eurozone countries are important economies influencing the economic convergence of the euro group. Nasir (2022), in Chapter 6, “Stagnation in Europe: A Lost Decade”, considered the same euro area countries in some of his analyses.

Some countries are very close to the EU economic convergence, sometimes below it, then above it, especially since 2009, such as: the Netherlands, Cyprus, Croatia, Estonia, Germany, and Ireland, which, with the exception of Estonia, all lie below the euro area economic convergence line. The euro area countries that are above EU economic convergence line, are: Slovakia, Slovenia since 2014, Luxembourg much further ahead, Malta, Lithuania, and Latvia for the entire period; these countries are very close to the euro area convergence line. In Figure 20b, since 2009, the evolution of average economic growth in the euro area has been slightly below the EU convergence line.

Regarding the position of non-euro area countries according to EU economic convergence, we identified in Figure 21, the same three situations are: the countries located above the line throughout the period are Bulgaria, Denmark, and Poland; the countries close to the EU convergence line since 2009 are Sweden and Romania, and the countries placed below the EU economic convergence line after the 2008 economic crisis are Hungary and the Czech Republic. We note that all of these non-euro area countries are very close to the economic convergence line of their group, with the exception of Denmark. In Figure 20c, we observe that the economic growth of countries outside the euro area is above the EU convergence line, demonstrating hypothesis H4.

5.3. General Conclusions on the Economic Growth in the EU in the Period of 2000–2023

The syntheses of the ECM and ARDL models for the euro area and for the non-euro area, both with and without dummy variables for economic shocks, led to similar conclusions regarding the existence and characteristics of economic convergence within the respective groups. Comparisons with economic convergence at the EU level, established using the GMM system, show the consistency of the results. The coefficients of the corresponding variables in the models are very similar, significant, and demonstrate the existence of long-run equilibrium, i.e., economic convergence (hypotheses H1, H2, and H3).

We used econometric models with dummy variables for economic shocks, only to compare their different influences on the economic convergence of the groups they belong to. We found that short-term economic shocks reduced the positive influence of investment on economic growth through even deeper declines in the euro area than in the non-euro area, which supports hypothesis H7.

We conclude that, in the long run, economies outside the euro area have higher economic growth rates compared with euro area countries. We have shown that the same explanatory variables contribute to economic growth to a greater extent for countries outside the euro area compared to those in the euro area (hypothesis H4). These conclusions are supported by the econometric approaches, proving the consistency of our results. The hypothesis H4 supports what the Neoclassical Growth Model establishes: “rich countries tend to grow less than poor countries, once certain conditions are established” (Quiroga, 2007).

Less developed countries need more investment to ensure economic growth. As we have concluded, in the long run, investment brings a greater increase in economic development in countries outside the euro area than in countries within the euro area, being the engine of economic growth (hypothesis H5).

In Figure 22, the SPSS graphs of the evolution of the analyzed variables refer to group 1, consisting of euro area countries, and group 2, consisting of EU countries outside the euro area. To compare GDP and GFCF growth, respectively, both inside and outside the euro area in the EU, we plotted them on the same graph for both groups of countries. We conclude that, for both indicators, the non-euro area group outperforms the euro area. These developments are aligned with the results of econometric models and with hypotheses H4 and H5.

The speed of adjustment towards long-run equilibrium in both models is slower for non-euro economies than in the euro area over a one-year period. The ECM gives an error correction term adjustment speed of 9.88% in non-euro EU countries, compared to 18.7% in the euro area. The ARDL model provides an adjustment speed of 15.83% in the non-euro area compared to 19.72% in the euro area. The results of both short-run econometric approaches, ECM and ARDL, are consistent with hypothesis H6.

The speed of adjustment is lower in the non-euro area than in the euro area, which means that the capacity to adjust towards equilibrium is higher for EMU countries. The European Monetary Union provides the institutional framework for better debt management, investment, and development policies in the euro area, as seen in Figure 22, by a higher average debt-to-GDP ratio than in non-euro area EU countries.

These conclusions are also supported by the following results of the statistical analyses, presented in

Table 25. Summary of group statistics in the period of 2000–2023.

Group Statistics						95% Confidence Interval of the Difference
t-Test	Belong Group	N	Mean	Std. Deviation	Std. Error Mean	Lower	Upper
ln_gdp	1	480	11.8370	1.7167	0.0784	11.6850	11.9820
	2	168	12.0076	0.7798	0.0602	11.8907	12.1239
	EU	648	11.8812	1.5311	0.0601	11.7631	11.9993
ln_gfcf	1	480	10.2973	1.7224	0.0786	10.1422	10.4503
	2	168	10.5199	0.7970	0.0615	10.4000	10.6383
	EU	648	10.3550	1.5394	0.0605	10.2363	10.4738
debt_GDP	1	480	66.5770	38.5302	1.7586	62.9626	70.1128
	2	168	42.3483	15.0907	1.1643	40.1382	44.8474
	EU	648	60.2955	35.6480	1.4004	57.5456	63.0453

1: euro area; 2: EU non-euro area.

and

Table 26. Comparing the equality of means between the two groups.

Independent Samples Test
Equal Variances Assumed	Levene’s Test for Equality of Variances		t-Test for Equality of Means
	F	Sig.	t	df	Sig. (2-Tailed)	Mean Difference	Std. Error Difference	95% Confidence Interval of the Difference
								Lower	Upper
ln_gdp	145.020	0.000	−1.243	646	0.214	−0.1705	0.1372	−0.4400	0.0988
ln_gfcf	149.256	0.000	−1.615	646	0.107	−0.2225	0.1378	−0.4932	0.0481
debt_GDP	86.801	0.000	7.937	646	0.000	24.2287	3.0527	18.2344	30.2230

.

The average values of GDP and GFCF growth of the non-euro group are higher than those of the euro area and the EU. The EU average debt-to-GDP ratio is 60%, which is the debt criterion. The average debt-to-GDP ratio outside the euro area is in line with this criterion, with the 95% confidence limits being below 60%.

From Table 25, we appreciate that group 2 of the EU non-euro area is more homogeneous than group 1 of the euro area, for all three variables.

When analyzing the significance of the differences between the mean values of the indicators for the two groups, in Table 26, we observe that the Levene test considers the hypothesis of equal variances to be significant. The t-test found that the differences in GDP and GFCF growth, respectively, for the two groups are insignificant. With a Sig. value < 1%, the debt-to-GDP ratio is significantly different between the two groups; the t-test rejects the null hypothesis of equal means. The mean of group 1 in the euro area is significantly higher than that of group 2 outside the euro area.

The conclusions of these statistical methods confirm the results of the econometric methods.

The econometric models of our study present the dynamic nature of economic convergence at the group level, but also at the EU level. When EU countries outside the euro area meet the financial criteria, economic convergence is assumed to be at the EU level. The demonstrated hypotheses show that the existence of long-term equilibrium of the two analyzed groups converges towards the long-term economic equilibrium in the EU. Our study has shown that investment dynamics are a key factor in long-term economic development. Membership of the euro area provides the framework for sustainable economic development.

5.4. Contributions and Limitations of Research on Economic Growth Convergence in the EU in the Period of 2000–2023

The pessimistic views of economists who anticipate the failure of the European Union through various scenarios for the euro area (Wright, 2012, 2013) are based on the reality that the economic growth trend changed after the 2008 economic crisis for all EU countries and will not recover in the next two decades. In the graphs in Figure 20, EU economic growth from 2009 to 2023 is clearly below the level that would have been achieved if the dynamic average rate in the 2000–2008 sub-period had been maintained.

The 2009–2019 sub-period that followed the 2008 financial crisis was considered Europe’s Lost Decade, and after the 2020 pandemic comes the Lost Decade 2.0, of economic stagnation, that caused low economic growth, high unemployment, the debt crisis, and vulnerability to external shocks (Nasir, 2022), as the war in Russia proved.

Our study offers a glimmer of hope that a much longer period of analysis might reveal that, in the long run, there will be no lost decades, unless external shocks occur. We are now living through these two lost decades, but looking ahead, and based on our research, we see the economic results of the EU’s diversity in its convergence. The lack of trust in the power of the EU undermines all efforts to achieve this construction, which brings numerous socio-economic benefits to the member states. Some politicians have even led to Brexit from the European Union.

The limitations of our study lie in the technical nature of the analyses, which explain economic growth based on the identified factors: the degree of indebtedness and investment. Historical and political issues (Nasir, 2022) could provide other dimensions of economic convergence.

The upward trend in average GDP per capita, both in the euro area and outside the euro area, shown in Figure 12, shows positive economic growth rates in the decade 2009–2019, in Section 4.2.1. All graphs of the average evolution of real GDP and the corresponding econometric models in Section 4.2.2—for the euro area, Section 4.2.3—for the non-euro area, and Section 4.2.4—for the EU countries, show upward trends over the entire period analyzed, 2000–2023. The significant factors taken into account in the econometric models have positive influences on economic growth. External shocks led to a decrease in economic growth, as demonstrated by the negative sign of their coefficients, differently for the euro area and for the non-euro area, as demonstrated by our research and supported by hypothesis H7.

The working hypotheses support the existence of economic convergence both within and outside the euro area, but also at the EU level. The working hypotheses that identified some characteristics of the economic convergence process refer to how considered factors and external shocks influence economic growth in the two groups of EU countries. These hypotheses are proven by the formulated conclusions and also by Figure 22, which shows the position of the two groups relative to each other in terms of the evolution of GDP, the debt-to-GDP ratio, and investment. The nonlinear evolution of the debt-to-GDP ratio for the euro area (Figure 7 and Figure 22) shows an increase in the period of 2009–2014 to 80%, followed by a decrease to 70% in the period of 2015–2019, but the 2020 pandemic caused a sudden increase to over 80%, and then a decrease between 2021 and 2023 to around 75%. A similar evolution of the debt-to-GDP ratio was also recorded outside the euro area, but the highest average level was below 60% (Figure 7 and Figure 22).

Economic shocks, such as the 2008 economic crisis, the COVID-19 pandemic, the war between Russia and Ukraine, and the fiscal debt crisis, are undermining the Eurozone, diminishing the power of the European Union and its role in world affairs (Nasir, 2022). These challenges to European integration have recovered in the long run, and the economic growth of the European Union is sustainable and proves the existence of economic convergence, as demonstrated in our research.

Our paper contains various econometric approaches and statistical methods to demonstrate and support the validity of our conclusions.

Our research provides a practical way to identify groups of countries (individuals) by positioning them in relation to their convergence in a given domain of interest. Convergence is a dynamic concept and changes depending on the performance of individuals in the respective domain of interest. The characteristics of individuals can define the main features of the positional group of membership.