Predicting the Canadian Yield Curve Using Machine Learning Techniques
Abstract
1. Introduction
- Macro-Finance Models: Ang and Piazzesi (2003), for instance, develop models integrating macroeconomic factors with latent variables under no-arbitrage conditions to explain yield curve dynamics. These models provide economic interpretability but can be complex and rely on specific structural assumptions.
- Factor Models: As an example Cochrane and Piazzesi (2005) explore bond return predictability using single factors derived from forward rates, emphasizing statistical parsimony. While effective, these models may not fully capture the influence of a wide range of macroeconomic drivers.
- Dynamic Latent Factor Models: A prominent example is the dynamic Nelson–Siegel model (Diebold & Li, 2006), an extension of the static Nelson–Siegel model (Nelson & Siegel, 1987). This framework, which allows its parameters to evolve over time, is widely used for its ability to parsimoniously fit and forecast the yield curve using a few latent factors (level, slope, curvature). However, these models inherently rely on specific functional forms and may struggle to capture complex non-linear relationships or leverage a broad spectrum of predictors beyond the latent factors.
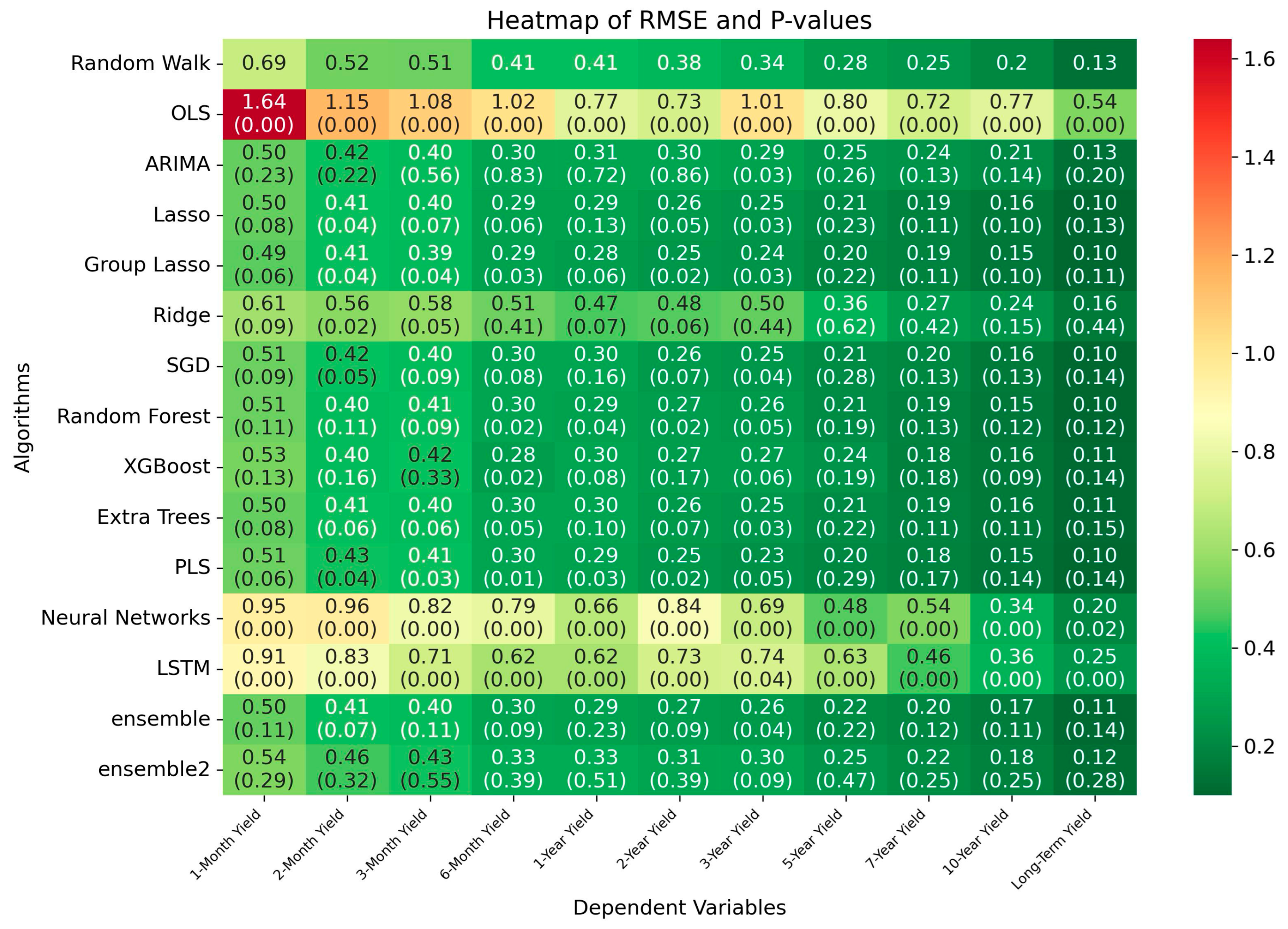
2. Results
2.1. Random Walk
2.2. OLS
2.3. ARIMA
2.4. Lasso
2.5. Group Lasso
2.6. Ridge
2.7. SGD
2.8. Random Forest
2.9. XGBoost
2.10. Extra Trees
2.11. PLS
2.12. Neural Networks
2.13. LSTM
2.14. Ensemble Model 1: ARIMA + Lasso + Random Forest
2.15. Ensemble Model 2: ARIMA + Lasso + Random Forest + SGD + PLS + LSTM
3. Discussion
3.1. Algorithms’ Performance
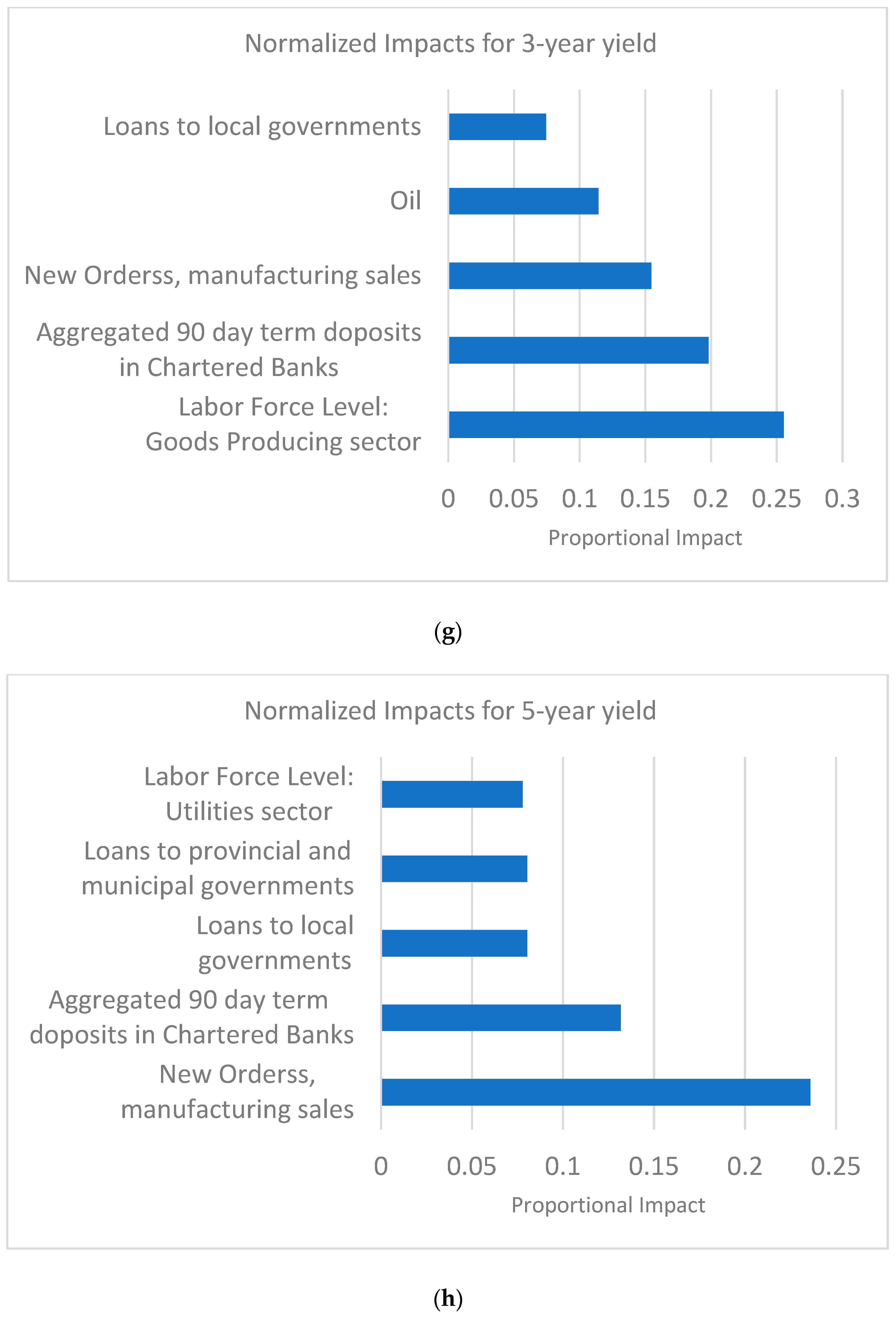
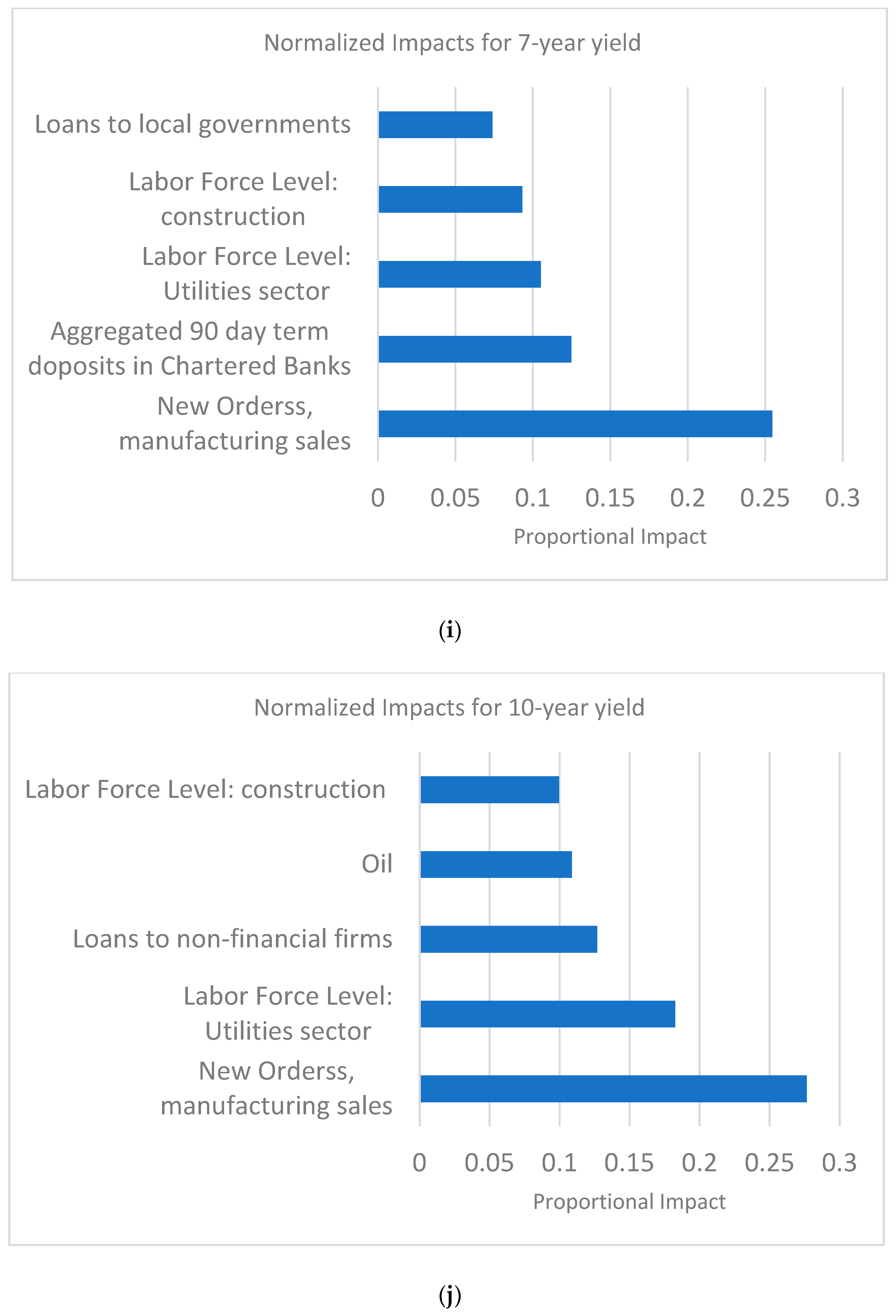
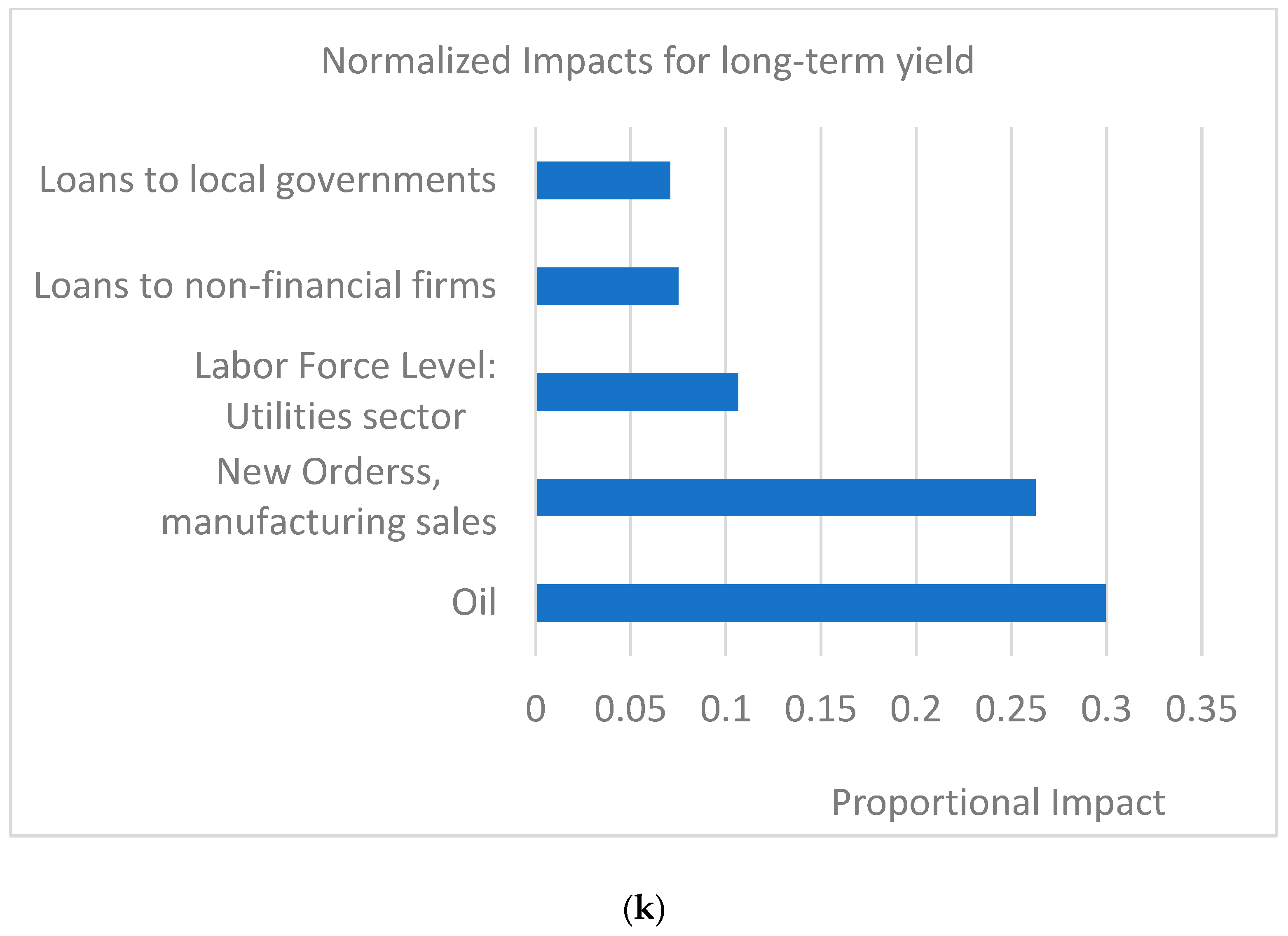
3.2. Feature Importance
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
List of Predictors Used
| Name | Description | |
|---|---|---|
| Bank of Canada | Amount Auctioned: three-month maturity bond | This category includes variables related to Bank of Canada Bond issuance. This category is crucial for monitoring Canadian monetary policy and sovereign bond issuance. Variables such as the amount auctioned, treasury maturities, and Government bonds outstanding directly reflect the supply of government debt, influencing its pricing. Different yield rates (e.g., 2-year, 10-year, long-term periods) and real return bonds provide direct insights into market expectations for future interest rates and inflation, which are core components of the yield curve. Finally, the Bank Rate and target rate, and overnight money market financing, are fundamental short-term interest rate indicators set by the central bank, which anchor the short end of the yield curve and transmit monetary policy signals throughout the economy. |
| Bonds amount auctioned: 6-month maturity | ||
| Bonds amount auctioned: 1-year maturity | ||
| Amount of treasury maturing | ||
| Government bonds outstanding | ||
| Overnight money market financing | ||
| 2-year yield | ||
| 3-year yield | ||
| 5-year yield | ||
| 7-year yield | ||
| 10-year yield | ||
| Long-term yield | ||
| Real return bonds, long-term | ||
| Real return bonds, long-term | ||
| 1-moth yield | ||
| Treasury Bills: 2-month | ||
| 3-month yield | ||
| Treasury Bills: 6-month | ||
| 1-year yield | ||
| Bank rate | ||
| Bank of Canada target rate | ||
| Chartered Banks Balance Sheet | Aggregated 90-day term deposits in Chartered Banks | This category includes major items on Canadian chartered banks’ balance sheets. All items are aggregated. These variables capture the overall health and lending capacity of the Canadian financial system, which is intrinsically linked to broader economic activity and, by extension, the yield curve. Strong bank balance sheets and active lending (e.g., mortgage loans, non-mortgage loans, loans to public/private sectors) indicate financial stability and ample credit supply, influencing risk premia and expectations of future interest rates. Conversely, signs of stress in bank balance sheets can signal tighter credit conditions, impacting economic growth and demand for government bonds. |
| Banks: Conventional mortgage, 1-year | ||
| Banks—conventional mortgage: 3-year | ||
| Banks: Conventional mortgage: 5-year | ||
| Banks: 5-year personal fixed term | ||
| Mortgages in Canada outstanding | ||
| Mortgage loans outside Canada outstanding | ||
| Mortgage loans outstanding | ||
| Non-mortgage loans Total | ||
| Misc. Loans | ||
| Loans to public financial institutions | ||
| Reverse repurchases loans | ||
| Loans to non-residents | ||
| Loans to local governments | ||
| Loans to provincial and municipal governments | ||
| Loans to Canadian individuals to purchase securities | ||
| Labor Force | Total number of unemployed | This category includes variables such as unemployment rate and the number of employees employed at each major industry. Labor market indicators are critical for assessing the overall health and inflationary pressures within an economy. Variables like the total number of unemployed provide insights into overall labor market slack. Importantly, labor force levels across specific industries (e.g., goods producing, manufacturing, retail trade) are included to capture sector-specific economic trends and structural shifts. Strong employment growth in key sectors can signal robust aggregate demand and potential inflationary pressures, which influence long-term bond yields. Conversely, weakness in specific sectors might indicate localized economic challenges or broader deceleration, impacting expectations for future interest rates and, thus, the yield curve. These disaggregated insights allow for a more nuanced understanding of economic health beyond aggregated unemployment figures. |
| Labor Force Level: all industries | ||
| Labor Force Level: Goods Producing sector | ||
| Labor Force Level: Utilities sector | ||
| Labor Force Level: construction sector | ||
| Labor Force Level: manufacturing sector | ||
| Trade employment level: Wholesale sector | ||
| Labor Force Level: retail trade sector | ||
| Labor Force Level: Transportation sector | ||
| Labor Force Level: finance sector | ||
| Manufacturing | Sales of goods manufactured (shipments) | Real manufacturing sales, orders, inventory owned and inventory to sales ratio for major industries. Manufacturing data, including sales, new orders, unfilled orders, and inventories, are key coincident and leading indicators of economic activity. Strong manufacturing performance suggests robust economic growth, which can lead to higher inflation expectations and, consequently, higher bond yields. Conversely, weakening manufacturing activity may signal a slowdown, prompting investors to expect lower future interest rates and thus lower bond yields. |
| New orders | ||
| Unfilled orders | ||
| Inventories | ||
| US Related Data | Euro Dollar Deposits (London) | This category includes US sovereign bond related variables. Given the close economic ties between Canada and the United States, US macroeconomic and financial variables exert significant influence on Canadian bond yields. US government bond yields, Euro Dollar Deposits, commercial paper rates, and the Federal Funds rate reflect US monetary policy, investor sentiment, and economic growth prospects, which often spill over into Canadian markets. Understanding these cross-border influences is crucial for comprehensive yield curve forecasting in Canada. |
| Banks: Commercial paper, 3-month | ||
| US Government bond yield: 5-year | ||
| USD interest rates: 1 month | ||
| Prime rate charged by banks (One of several base rates used by banks to price short-term business loans.) | ||
| Federal funds rate | ||
| US Government bond yield: 10-year | ||
| Misc. | WTI oil | This category includes a diverse set of influential macroeconomic variables. As Canada is a major oil exporter, WTI oil prices directly impact government fiscal capacity and inflation expectations, significantly influencing Canadian bond yields. Surging oil prices can boost national income and the Canadian dollar, potentially reducing imported inflation and affecting interest rate expectations. S&P/TSX Composite Index: This index provides a broad measure of Canadian equity market performance, reflecting overall investor sentiment and the economic outlook. A strong equity market often correlates with optimistic growth expectations, which can translate to higher bond yields as investors anticipate stronger economic activity and potentially higher inflation. Canadian GDP: As the fundamental measure of economic output, GDP is directly linked to expected future growth and inflation, which are primary drivers of bond yields. Higher GDP growth typically implies stronger demand and potential inflationary pressures, leading to an upward revision of future interest rate expectations and thus higher bond yields. |
| S&P/TSX Composite Index | ||
| GDP Canada | ||
| Housing | Housing starts | Housing market indicators such as housing starts and the New Housing Price Index are vital for gauging consumer confidence, construction activity, and inflationary pressures within the real estate sector. A robust housing market can signal strong economic growth and potential inflation, which might lead to higher interest rates and bond yields. Conversely, a weakening housing market could suggest economic deceleration, impacting bond yield expectations. |
| New Housing Price Index |
| 1 | Due to the large number of predictors used in our models, we could not report the summary statistics for each predictor. |
| 2 | For further information regarding Long-Short Term Memory networks, please refer to Hochreiter and Schmidhuber (1997). |
| 3 | RMSE is a widely used criterian across machine learning research. Examples are: Duraj and Giesecke (2023), Babaei et al. (2023). |
| 4 | Normalization is widely used in time series studies. Please refer to Bhanja and Das (2018), Cabello-Solorzano et al. (2023) and H. Zhang et al. (2020) as examples. |
References
- Adrian, T., Crump, R. K., & Moench, E. (2013). Pricing the term structure with linear regressions. Journal of Financial Economics, 110(1), 110–138. [Google Scholar] [CrossRef]
- Adrian, T., & Shin, H. S. (2010). Liquidity and leverage. Journal of Financial Intermediation, 19(3), 418–437. [Google Scholar] [CrossRef]
- Ang, A., & Piazzesi, M. (2003). A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables. Journal of Monetary Economics, 50(4), 745–787. [Google Scholar] [CrossRef]
- Babaei, G., Giudici, P., & Raffinetti, E. (2023). Explainable fintech lending. Journal of Economics and Business, 125, 106126. [Google Scholar] [CrossRef]
- Bank of Canada. (2022). Monetary policy report—July 2022. Bank of Canada. [Google Scholar]
- Bauer, M. D., & Mertens, T. M. (2018). The yield curve and growth forecasts, FRBSF Economic Letter, 2018-07. Federal Reserve Bank of San Francisco. [Google Scholar]
- Bernanke, B. S., & Blinder, A. S. (1992). The federal funds rate and the channels of monetary transmission. American Economic Review, 82(4), 901–921. [Google Scholar]
- Bhanja, S., & Das, A. (2018). Impact of data normalization on deep neural network for time series forecasting. arXiv, arXiv:1812.05519. [Google Scholar]
- Cabello-Solorzano, K., Ortigosa de Araujo, I., Peña, M., Correia, L., & J. Tallón-Ballesteros, A. (2023). The impact of data normalization on the accuracy of machine learning algorithms: A comparative analysis. In International conference on soft computing models in industrial and environmental applications (pp. 344–353). Springer Nature. [Google Scholar]
- Chen, T., & Guestrin, C. (2016, August 13–17). XGBoost: A scalable tree boosting system. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 785–794), San Francisco, CA, USA. [Google Scholar]
- Christensen, K., Siggaard, M., & Veliyev, B. (2023). A machine learning approach to volatility forecasting. Journal of Financial Econometrics, 21(5), 1680–1727. [Google Scholar] [CrossRef]
- Cochrane, J. H., & Piazzesi, M. (2005). Bond risk premia. American Economic Review, 95(1), 138–160. [Google Scholar] [CrossRef]
- Diebold, F. X., & Li, C. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 130(2), 337–364. [Google Scholar] [CrossRef]
- Duraj, J., & Giesecke, O. (2023). Deep learning for corporate bonds. Available online: https://ssrn.com/abstract=4527372 (accessed on 20 February 2024).
- Estrella, A., & Trubin, M. (2006). The yield curve as a leading indicator: Some practical issues. Current Issues in Economics and Finance, 12(5), 1–7. [Google Scholar]
- Geurts, P., Ernst, D., & Wehenkel, L. (2006). Extremely randomized trees. Machine Learning, 63(1), 3–42. [Google Scholar] [CrossRef]
- Gu, S., Kelly, B., & Xiu, D. (2020). Empirical asset pricing via machine learning. The Review of Financial Studies, 33(5), 2223–2273. [Google Scholar] [CrossRef]
- Harvey, C. R. (1988). The real term structure and consumption growth. Journal of Financial Economics, 22(2), 305–333. [Google Scholar] [CrossRef]
- Hillebrand, E., Huang, H., Lee, T. H., & Li, C. (2018). Using the entire yield curve in forecasting output and inflation. Econometrics, 6(3), 40. [Google Scholar] [CrossRef]
- Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8), 1735–1780. [Google Scholar] [CrossRef]
- Hoerl, A. E., & Kennard, R. W. (1970). Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 12(1), 55–67. [Google Scholar] [CrossRef]
- Jeenas, P., & Lagos, R. (2024). Q-monetary transmission. Journal of Political Economy, 132(3), 971–1012. [Google Scholar] [CrossRef]
- Kelly, B. T., Malamud, S., & Zhou, K. (2022). The virtue of complexity everywhere (Swiss Finance Institute research paper 22–57). Swiss Finance Institute. [Google Scholar]
- LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. [Google Scholar] [CrossRef]
- Liaw, A., & Wiener, M. (2002). Classification and regression by randomForest. R News, 2(3), 18–22. [Google Scholar]
- McCracken, M. W., & Ng, S. (2015). FRED-MD: A monthly database for macroeconomic research (Working Paper 2015-012). Federal Reserve Bank of St. Louis. [Google Scholar]
- Naderi, H., & Rayeni, A. (2023). Firm innovation and the transmission of monetary policy. Available online: https://ssrn.com/abstract=4565202 (accessed on 11 March 2024).
- Nelson, C. R., & Siegel, A. F. (1987). Parsimonious modeling of yield curves. The Journal of Business, 60(4), 473–489. [Google Scholar] [CrossRef]
- Rudebusch, G. D., & Williams, J. C. (2009). Forecasting recessions: The puzzle of the enduring power of the yield curve. Journal of Business & Economic Statistics, 27(4), 492–503. [Google Scholar] [CrossRef]
- Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv, arXiv:1609.04747. [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1), 267–288. [Google Scholar]
- Wold, H. (1982). Soft modeling: The basic design and some extensions. Systems Under Indirect Observation, Part II, 2, 36–37. [Google Scholar]
- Yuan, M., & Lin, Y. (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society Series B: Statistical Methodology, 68(1), 49–67. [Google Scholar]
- Zhang, H., He, Q., Jacobsen, B., & Jiang, F. (2020). Forecasting stock returns with model uncertainty and parameter instability. Journal of Applied Econometrics, 35(5), 629–644. [Google Scholar]
- Zhang, M., Zhao, Y., & Nan, J. (2022). Economic policy uncertainty and volatility of treasury futures. Review of Derivatives Research, 25, 93–107. [Google Scholar] [CrossRef]
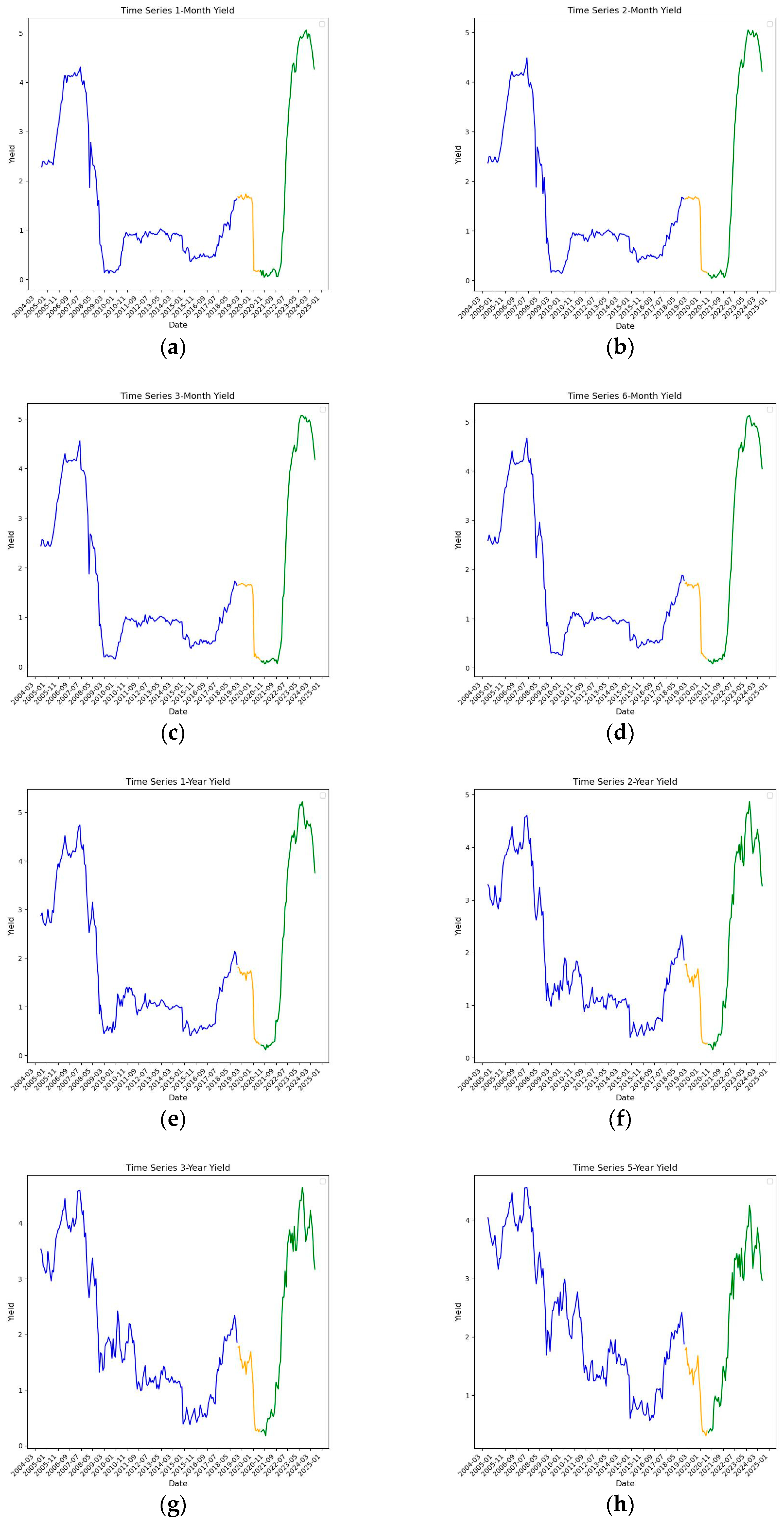

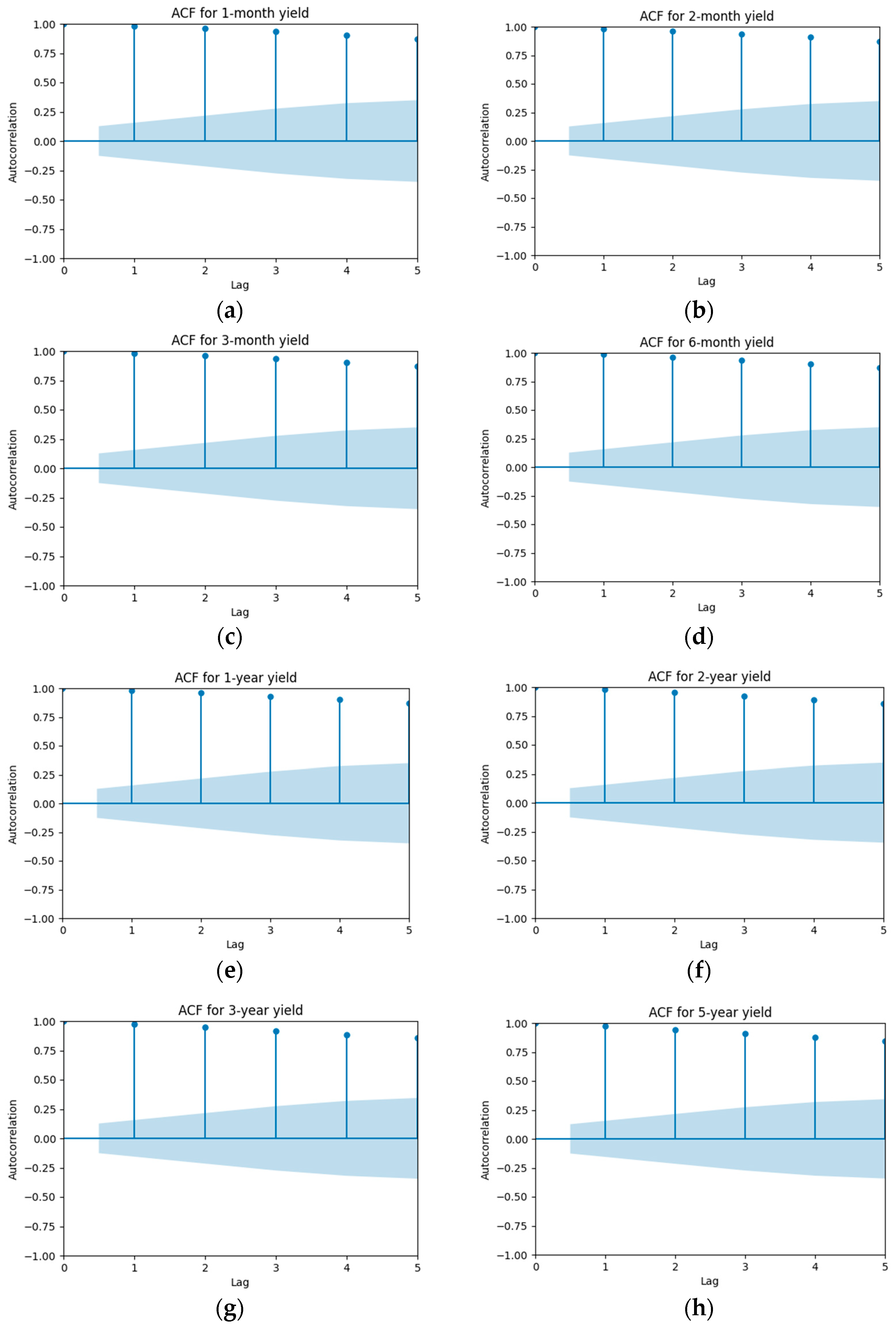

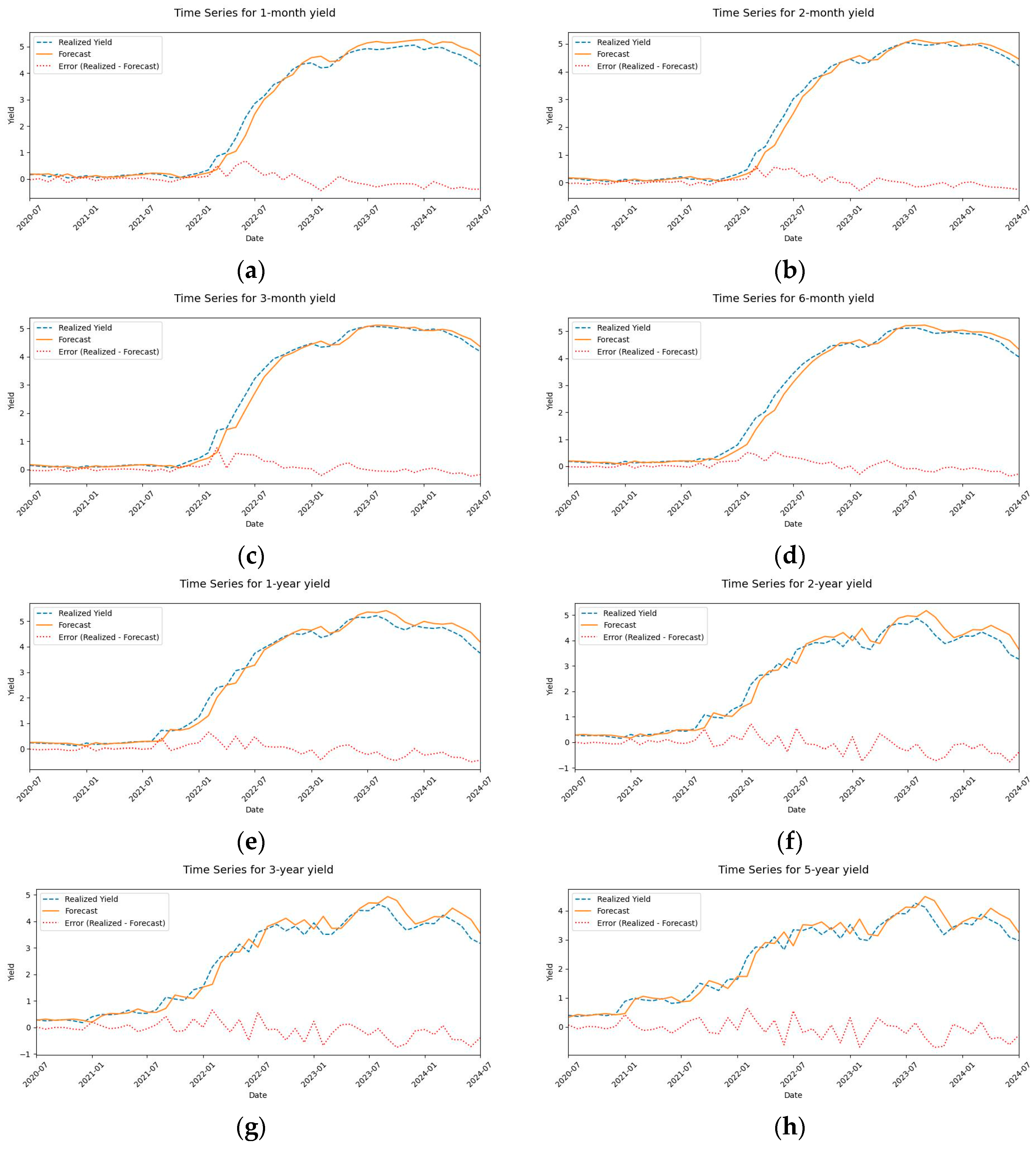
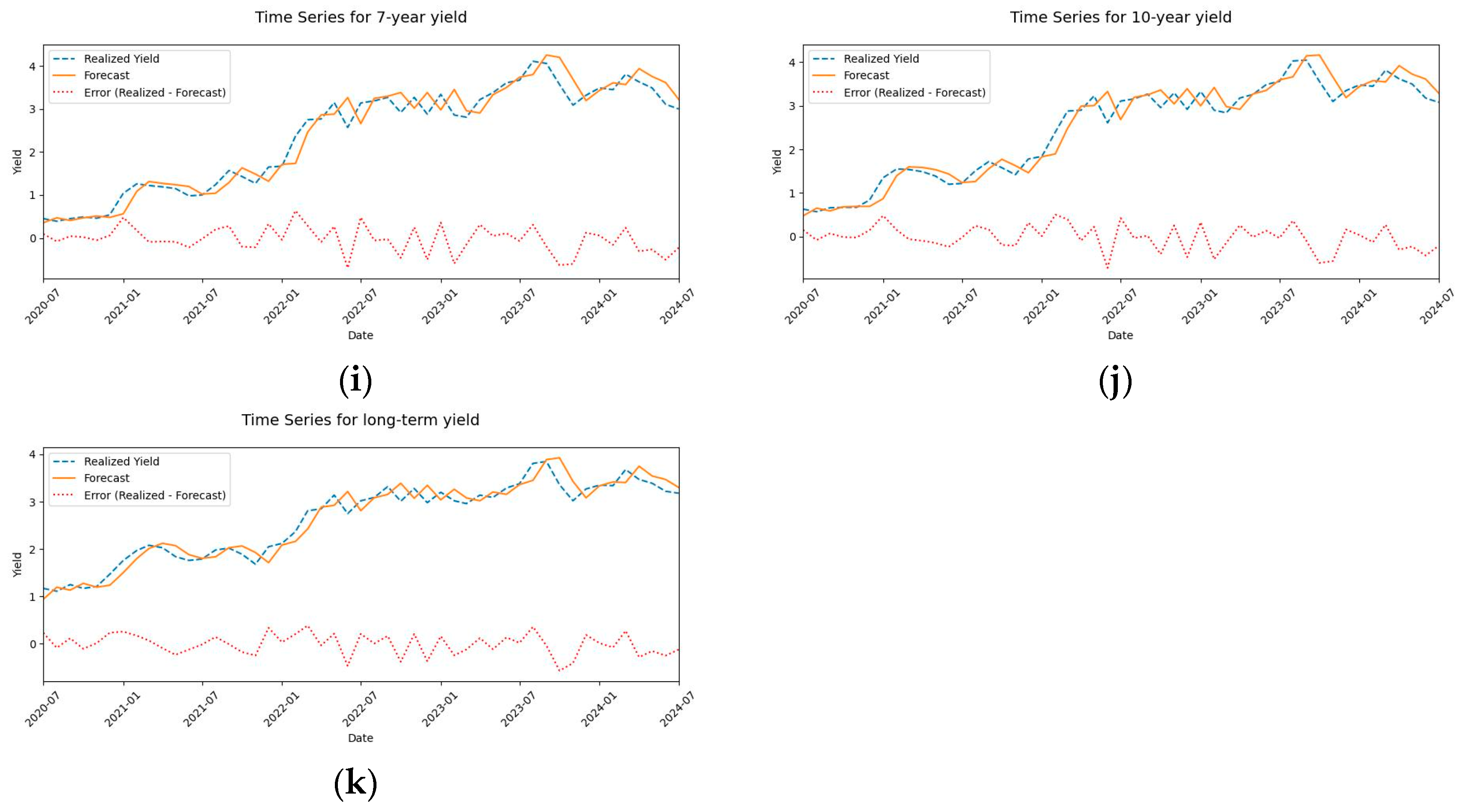
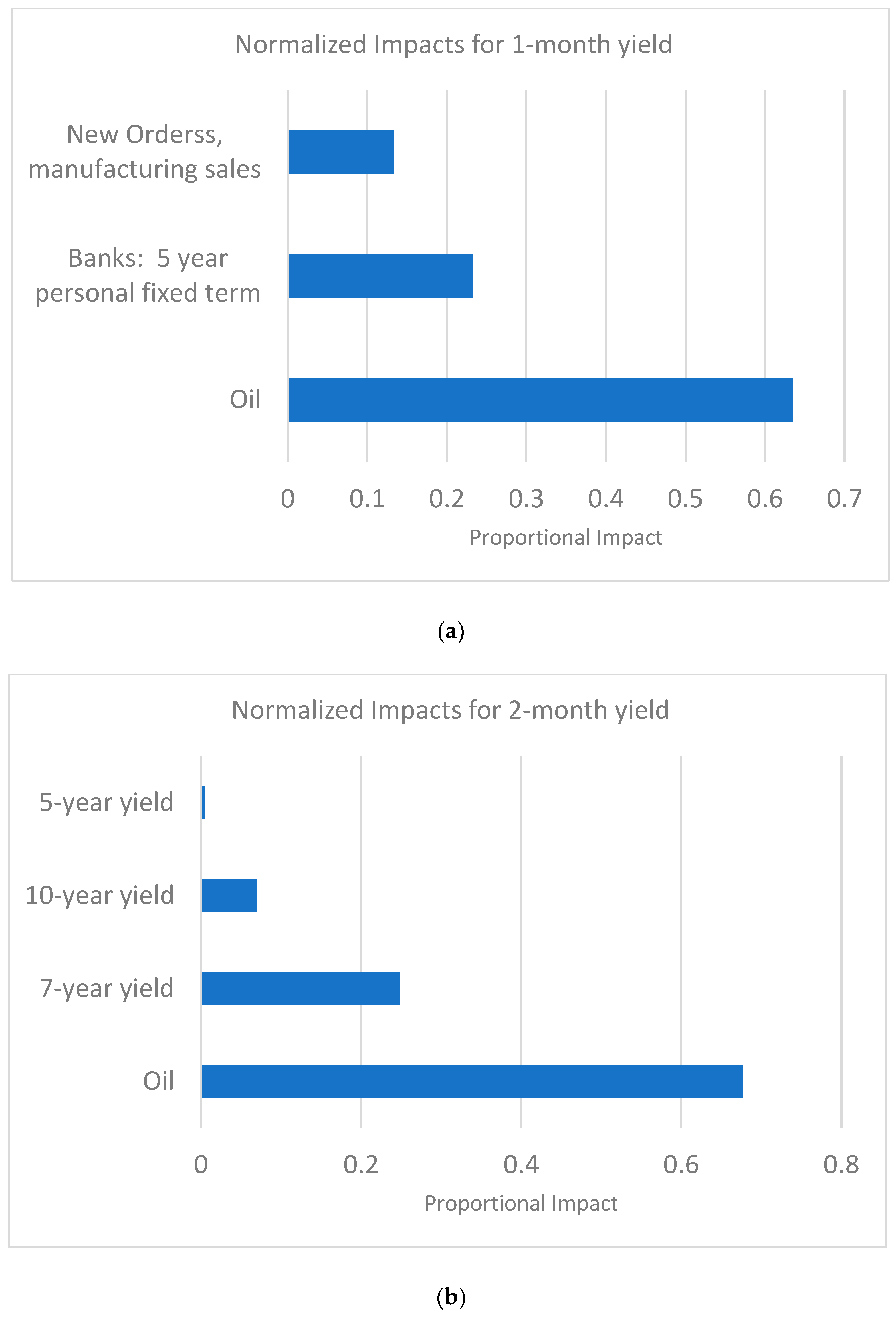

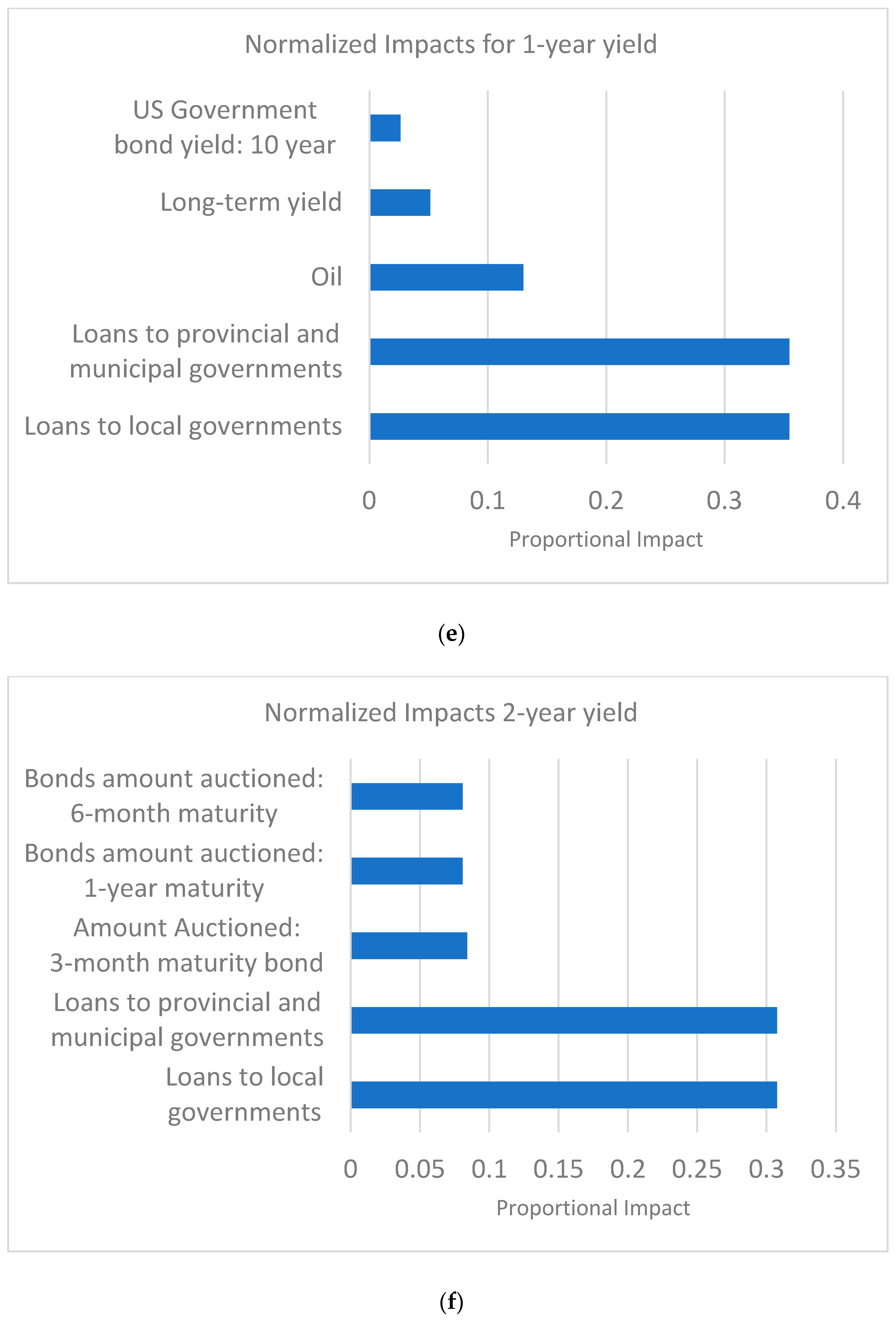
| Whole Sample | Training Sample | Validation Sample | Testing Sample | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 1-month yield | 1.64 | 1.5 | 1.46 | 1.25 | 1.27 | 0.67 | 2.45 | 2.15 |
| 2-month yield | 1.68 | 1.51 | 1.49 | 1.26 | 1.26 | 0.66 | 2.49 | 2.16 |
| 3-month yield | 1.71 | 1.52 | 1.52 | 1.27 | 1.26 | 0.65 | 2.55 | 2.16 |
| 6-month yield | 1.8 | 1.52 | 1.61 | 1.28 | 1.29 | 0.64 | 2.66 | 2.12 |
| 1-year yield | 1.91 | 1.49 | 1.73 | 1.28 | 1.3 | 0.63 | 2.75 | 2.02 |
| 2-year yield | 1.95 | 1.33 | 1.85 | 1.2 | 1.21 | 0.57 | 2.56 | 1.73 |
| 3-year yield | 2.03 | 1.28 | 1.99 | 1.19 | 1.19 | 0.56 | 2.5 | 1.59 |
| 5-year yield | 2.21 | 1.17 | 2.27 | 1.13 | 1.18 | 0.51 | 2.4 | 1.28 |
| 7-year yield | 2.35 | 1.12 | 2.47 | 1.09 | 1.2 | 0.51 | 2.38 | 1.17 |
| 10-year yield | 2.59 | 1.09 | 2.77 | 1.04 | 1.26 | 0.48 | 2.47 | 1.06 |
| Long-term yield | 2.96 | 0.99 | 3.21 | 0.92 | 1.55 | 0.37 | 2.61 | 0.8 |
| Algorithm | Hyperparameters | Tested Values | Final Selected Values |
|---|---|---|---|
| Random Walk | None | None | N/A |
| OLS | None | None | N/A |
| ARIMA | order of autoregression (p), order of differentiation (d), order of moving average (q) | (p, d, q) = (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (0, 1, 1), (2, 0, 0), (0, 2, 0), (0, 0, 2), (2, 1, 0), (0, 2, 1) | (2, 1, 0) |
| Lasso | Alpha | Alpha = 0.0001, 0.01, 0.005 | Alpha = 0.005 |
| Group Lasso | Alpha | Alpha = 0.001, 0.005, 0.1 | Alpha = 0.01 |
| Ridge | Alpha | Alpha = 0.001, 0.005, 0.01, 0.1 | Alpha = 0.1 |
| SGD | Penalty, Alpha | Penalty = L1, L2, Elastic Net Alpha = 0.001, 0.01, 0.1, 1.0 | Elastic Net, Alpha: 1.0 |
| Random Forests | Number of estimators (n_estimators), maximum depth (max_depth) | n_estimators = 50, 100, 150 max_depth = 5, 10, 15 | (n_estimators = 150, max_depth = 15) |
| XGBoost | Number of estimators (n_estimators), maximum depth (max_depth) | n_estimators = 50, 100, 150 max_depth = 5, 10, 15 | (n_estimators = 50, max_depth = 5) |
| Extra Trees | Number of estimators (n_estimators), maximum depth (max_depth) | n_estimators = 50, 100, 150 max_depth = 5, 10, 15 | (n_estimators = 50, max_depth = 5) |
| PLS | Number of components (C) | C = 2, 5, 10, 20 | C = 2 |
| Neural Networks | Number of neurons in layer 1 (l1), Number of neurons in layer 2 (l2) | l1 = 128, 64 l2 = 64, 32 | (64, 64) |
| LSTM | Number of neurons in layer 1 (l1), Number of neurons in layer 2 (l2), Number of LSTM units (l3) | l1 = 128, 64 l2 = 64, 32 l3 = 32, 16 | (128, 64, 16) |
| Algorithm | Performance in Validation Dataset (SRMSE) | Performance in Test Dataset (SRMSE) | Ranking Based on Performance on Test Dataset |
|---|---|---|---|
| Random Walk | - | 4.13 | 11 |
| OLS | 10.23 | 15 | |
| ARIMA | 1.89 | 3.36 | 9 |
| Lasso | 2.04 | 3.05 | 2 |
| Group Lasso | 2.35 | 2.98 | 1 |
| Ridge | 4.37 | 4.75 | 12 |
| SGD | 1.95 | 3.12 | 7 |
| Random Forest | 2.16 | 3.09 | 5 |
| XGBoost | 2.13 | 3.17 | 8 |
| Extra Trees | 2.16 | 3.07 | 4 |
| PLS | 2.19 | 3.05 | 3 |
| Neural Networks | 2.53 | 7.31 | 14 |
| LSTM | 1.93 | 6.87 | 13 |
| Ensemble 1 | 1.96 | 3.12 | 6 |
| Ensemble 2 | 1.9 | 3.47 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rayeni, A.; Naderi, H. Predicting the Canadian Yield Curve Using Machine Learning Techniques. Int. J. Financial Stud. 2025, 13, 170. https://doi.org/10.3390/ijfs13030170
Rayeni A, Naderi H. Predicting the Canadian Yield Curve Using Machine Learning Techniques. International Journal of Financial Studies. 2025; 13(3):170. https://doi.org/10.3390/ijfs13030170
Chicago/Turabian StyleRayeni, Ali, and Hosein Naderi. 2025. "Predicting the Canadian Yield Curve Using Machine Learning Techniques" International Journal of Financial Studies 13, no. 3: 170. https://doi.org/10.3390/ijfs13030170
APA StyleRayeni, A., & Naderi, H. (2025). Predicting the Canadian Yield Curve Using Machine Learning Techniques. International Journal of Financial Studies, 13(3), 170. https://doi.org/10.3390/ijfs13030170





