Markov-Modulated and Shifted Wishart Processes with Applications in Derivatives Pricing

Abstract

The popular Wishart (WI) processes, first introduced by Bru in 1991, exhibit convenient analytical properties for modeling asset prices, particularly a closed-form characteristic function, and the ability to jointly model stochastic volatility and correlation. These features tend to increase substantially during crisis periods, more than predicted by a Wishart dynamic. Moreover, the variance processes implied by the Wishart, similar to CIR models, have no buffer away from zero. In this paper, we introduced the Markov-Modulated Shifted Wishart processes (MMSW) and the embedded Shifted Wishart processes (SW) to address these shortcomings in the modeling of asset prices. We obtain analytical representations for several characteristic functions. We also estimate the parameters and evaluate the price of Spread options via the Fourier transform under the two new models compared to the standard Wishart. Our analyses demonstrate a significant impact of the MMSW process compared to the standard Wishart process of up to $7\%$ in Spread option prices.

1. Introduction

This paper introduces a framework for the phenomenon observed in asset prices’ covariance structure transitioning from normal to turbulent times. This adjustment results in a sharp and temporarily sustained increase, i.e., a shift in variances and correlations during the crisis, receding to their long-term values afterward. Existing stochastic covariance models, even those that allow for jumps, are not explicitly built to replicate this phenomenon. A second motivation for our work is the lack of flexibility on the lower bound of variances in stochastic covariance models. Here, we aim to provide some stochastic machinery to model correlation and volatilities as random processes accounting for shifts during crises while allowing for nonzero lower bounds on variances. In this spirit, the article introduces the Markov-Modulated Shifted Wishart (MMSW) process and, as a byproduct, the Shifted Wishart (SW) process.

Both stochastic covariance processes extend the popular Wishart process, introduced in the literature by researchers, which has innumerable important applications in finance, for instance, in asset price modeling, term structure of interest rates, option pricing, and credit risk. In this paper, we provide analytical and numerical results showing how the enhanced class of Wishart processes can replicate the historical behavior of volatility and correlation, capturing stylized facts about the market behavior of the covariance matrix. Market data clearly shows that the volatility of securities and correlations between financial instruments are not constant and change stochastically over time. Stochastic volatility and correlation modeling provide analytical tools for replicating empirical observations, including volatility smiles and skews, fat-tail return distributions, and volatility clustering. Early developments of stochastic volatility models include Stein and Stein (1991) and Heston (1993) resulted in a wider category of affine stochastic volatility models. In Heston’s model, closed-form formulas for the characteristic function and the probability distribution of the joint log-price and volatility process led to a closed-form solution for the valuation problem of a vast range of popular financial derivatives. The model has been implemented with direct integration, Fast Fourier Transform (FFT), and fractional FFT methods, assuming the asset price is observable.

Modeling stochastic correlation compared to modeling stochastic volatility has difficulties from the analytical and estimation points of view. One of the successful attempts to fix this gap started with a paper on Wishart processes by Bru (1991), which was followed by a series of papers applying, adapting, and enhancing the model to accommodate financial markets, see Gouriéroux and Sufana (2004), Gourieroux (2005), Da Fonseca et al. (2007), Da Fonseca et al. (2008), Da Fonseca et al. (2014). The Wishart process is a positive-definite symmetric random matrix process that satisfies a certain stochastic differential equation and is a natural extension of the Cox-Ingersoll-Ross (CIR) process. The interpretation of the Wishart as the time dynamics of a covariance matrix makes it a good candidate for modeling multi-name assets’ covariance. As risk can be measured using the covariance matrix, the Wishart process can be seen as a tool to model the dynamic behavior of multivariate risk. Bru (1991) proposes the Wishart process as a generalized squared Bessel process for dimensions greater than one and verifies existence and uniqueness, additivity, first hitting time of the smallest eigenvalue, and the distributions of the Wishart process. The developments in Da Fonseca et al. (2008) are an essential enhancement of the Wishart process. The authors use a multi-factor Heston model to show the flexibility of the Wishart process to capture the volatility’s smile and skew. One of the paper’s strengths is introducing a correlation structure between the stock’s and volatility’s noise, capturing multivariate leverage effects. Using the Laplace transform and the distribution of the Wishart process, prices of derivatives with a Wishart stochastic covariance matrix can be easily obtained. For instance, Gouriéroux and Sufana (2004) and Da Fonseca et al. (2007) use the model to price equity options and baskets, Da Fonseca et al. (2011) use it on variance derivatives, Arian (2012) and Escobar et al. (2012) adapt it to applications in credit derivatives. Chiarella et al. (2016) uses the Wishart process to model and price the interest rate term structure.

More recently, extensions of the process have been provided by Abi Jaber (2022), where the author finds a closed form for the Laplacian of the Integrated Volterra Wishart process and applies it to a range of problems from bond pricing to basket option pricing. La Bua and Marazzino (2022) applies the Wishart process to the local volatility pricing paradigm and obtains a hybrid local-stochastic modeling approach. They use this hybrid model to price a vanilla option. Naryongo et al. (2021) uses the model to price equity derivatives. In Da Fonseca (2024), the author develops a linear-rational Wishart model used to model jointly mortality and interest rate. He uses this model to price an annuity option on survival bonds.

One of the complexities of the Wishart process is related to the joint and marginal information sharing the same parameters of the model. This is because the Wishart process models covariance in a way that the marginal and joint parameters are mixed. This invalidates the method of calibrating marginal and joint parameters separately, which is the usual methodology employed by most of the existing estimation techniques in the literature. This makes calibrating the parameters and also interpreting them challenging. Da Fonseca et al. (2014) estimates the Wishart Stochastic Correlation Model on the stock indexes S&P500, FTSE, DAX and CAC40 under the historical measure, while Escobar et al. (2016) uses the Continuum-Generalized Method of Moments (CGMM) and Continuum Method of Moments (CMM) to calibrate and recover parameters of the Wishart Affine Stochastic Correlation (WASC) model and the Principal Components Stochastic Volatility (PCSV) model. More recently, La Bua and Marazzino (2021) proposes a new method for calibration of the process, and they use it for pricing a basket option under the Wishart process.

One of the limitations of the literature on affine stochastic volatility and correlation models is that they cannot capture long-term macroeconomic developments, particularly the abrupt changes in the value of the covariance matrix due to a crisis. This motivates the main proposal in our paper, the Markov-Modulated Shifted Wishart (MMSW) process. We also produce the Shifted Wishart (SW) process as a byproduct. In both cases, the idea is to introduce an additional term modeling a shift in the market environment, increasing both volatility and correlation levels. Employing Markov-modulated processes will enable us to capture long-term macroeconomic developments in the covariance structure. We will also show that our model is consistent with the stylized facts from volatility and correlation market data. Therefore, we effectively combine three popular models in quantitative finance: shifted stochastic processes, Markov-modulated processes, and the aforementioned stochastic covariance processes.

Wishart processes have been combined with jumps in other publications, also in attempts to capture sudden changes in market conditions. For example, jumps were added directly to the Wishart covariance in Mayerhofer et al. (2011) and to the stock returns in the recent work of Deng and Liu (2024). In general, the jump size, either on the stock or the covariance itself, must be pretty pronounced to capture a change in the covariance, and jumps usually die out faster than the length of the crisis. In our case, we use a Markov chain (switching process) to shift the value of the covariance matrix, creating a Markov-modulated covariance dynamic while retaining closed-form solutions for the characteristic functions. Markov-modulated processes are viable alternatives to jump processes due to their simplicity and statistical parsimony.

The branch of Markov-modulated/switching processes has been popular in finance, particularly in capturing market changes between normal and turbulent or crisis times. For long-term horizons, the market regime may vary between two states, normal and crisis, and one way to model this phenomenon is a Markov switching process on the model’s parameters. A series of articles, including Hamilton (1989), Bernhart et al. (2011), Zhou and Mamon (2012), and Elliott and Nishide (2014), motivate the employment of changing regimes in financial models by using Markov chains to model the market environments. The simplest example would be a Markov chain with two regimes corresponding to normal and crisis markets, where, for instance, variances and correlations between assets increase in crisis as if adding a shift to the covariance matrix. As explained by Konikov and Madan (2002), Elliott and Nishide (2014), this would better estimate the realized covariance matrix. Another example is Gribisch (2016), where the author assumed a Markov switching on a discrete-time Wishart process for covariance. The work of Escobar et al. (2015); Neykova et al. (2015) is another example of considering Markov switching on general affine models with multiple stochastic factors.

Lastly, shifted processes have been introduced in quantitative finance for several reasons. Antonov et al. (2007) and Antonov et al. (2008) provide a volatility smile model in Markovian Projection framework. They use a Heston model with shifted volatility and provide estimation results for the case when the affinity is violated. Also, in the short-rate interest rate domain, a constant shifted methodology has been brought to finance by Brigo and Mercurio (2001), where the authors model the short rate by adding a shift integrable deterministic function to a random process. Similarly, Brigo and Alfonsi (2005) introduced a Shifted Square Root Diffusion (SSRD) model to model stochastic intensity in the pricing of credit derivatives. In another application, the shifted CIR process captured the negative implied Japanese shadow rate in Gorovoi and Linetsky (2004). In general, shifted processes have been introduced to gain flexibility in modeling lower bounds of processes, permitting better capture of market behavior (e.g., volatility smile and skew, negative rates).

Although the Wishart process has been extensively studied for multi-variate stochastic correlation modeling, i.e., to capture the effects of crises on shifts in variances and correlations, there are two main gaps in research; one is to capture sudden, sustained shifts in the covariance, and the second is to ensure a nonzero lower bound for volatilities in the covariance matrix. Both can be achieved by combining Wishart and Markov modulation processes. The Jump processes are an alternative to Markov modulation for modeling the shifts in the covariance matrix. But Jump processes do not ensure sustained shifts. On the second gap, Wishart processes consider a stochastic modeling for the covariance matrix that might lead to a zero variance for some assets. As introduced in this paper, the Shifted Wishart process guarantees a minimum positive level for the covariance matrix, which is more realistic.

We can now summarize the main contributions of our paper:

• We introduce two new stochastic covariance models, the MMSW and the SW process, both extensions of the Wishart process. The need for the shifts, both constant (SW) or Markov modulated (MMSW), is motivated empirically by nonzero lower bounds for variances and changes in volatility and correlations during crises, respectively.
• Key properties of these new processes are demonstrated; in particular, several characteristic functions of interest and the long-term dynamics are obtained in closed form.
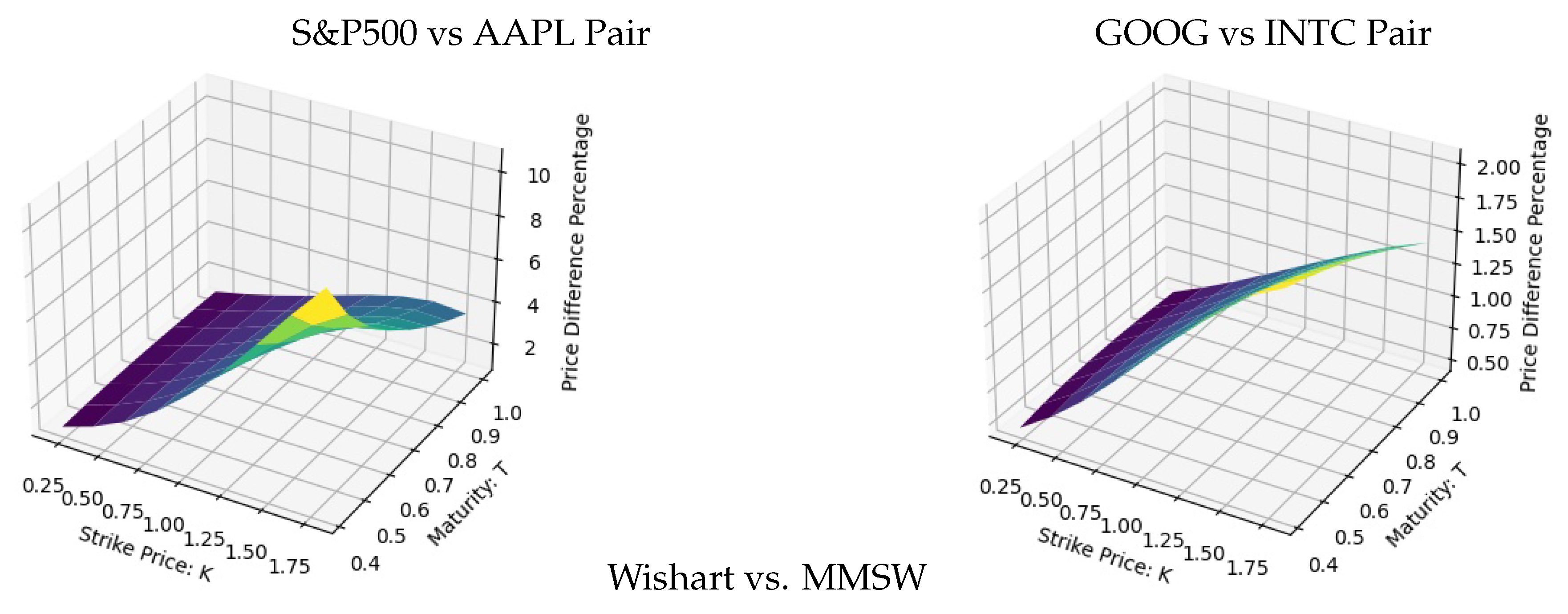
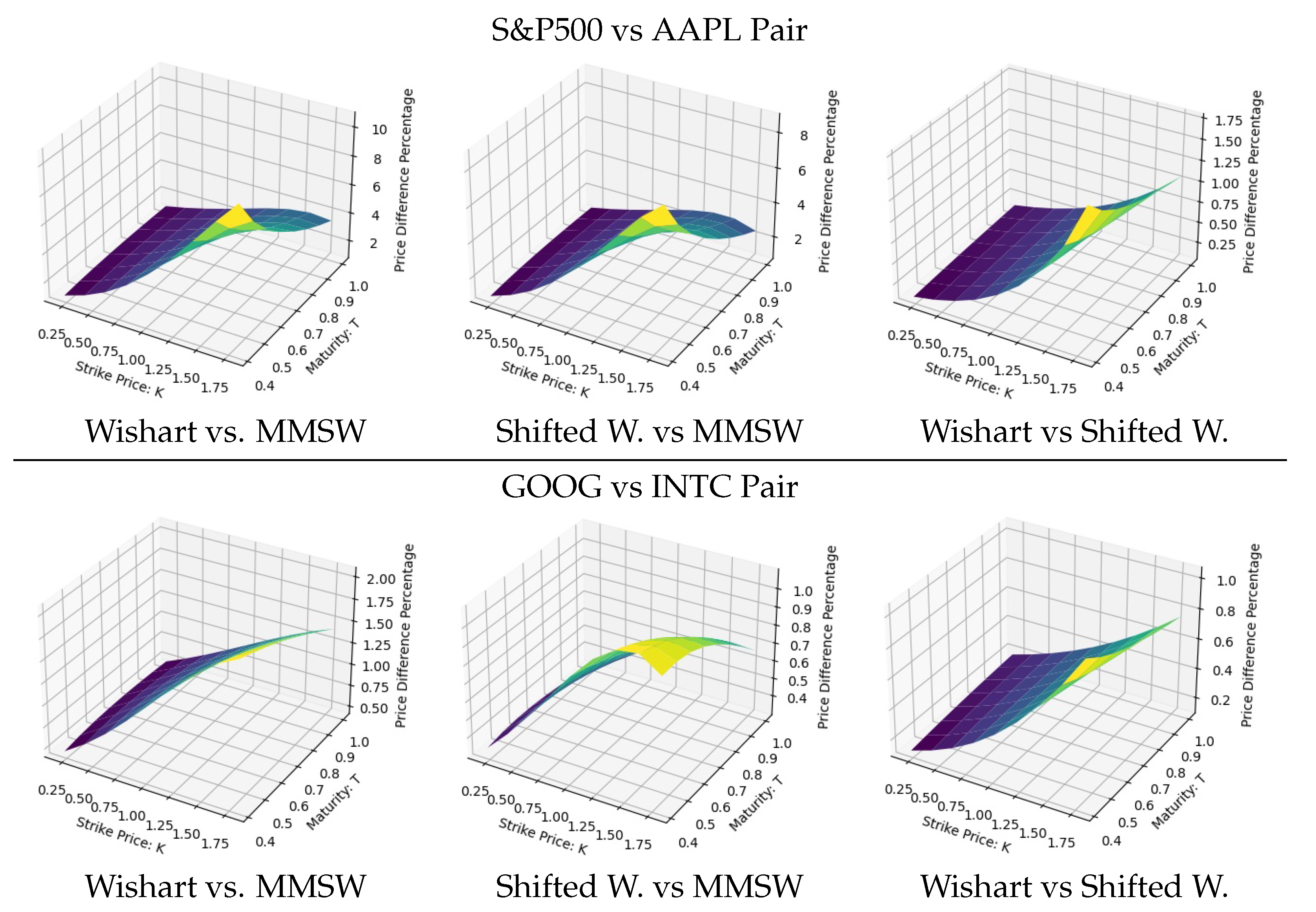
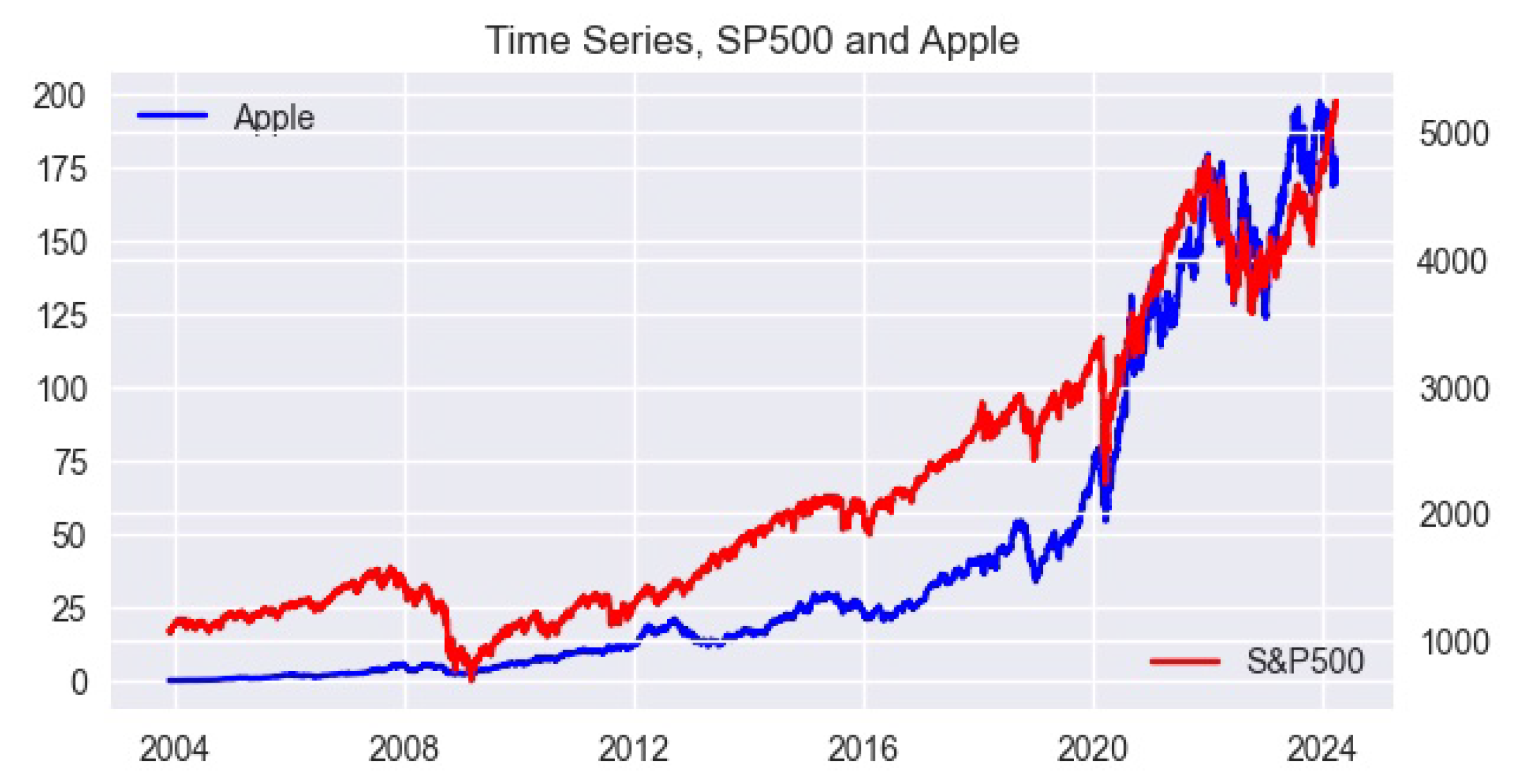
• The CGMM methodology is implemented on two pairs of asset prices, the S&P500 and AAPL symbols, and GOOG and INTC symbols, to produce estimates for the parameters of the Wishart process and the MMSW.
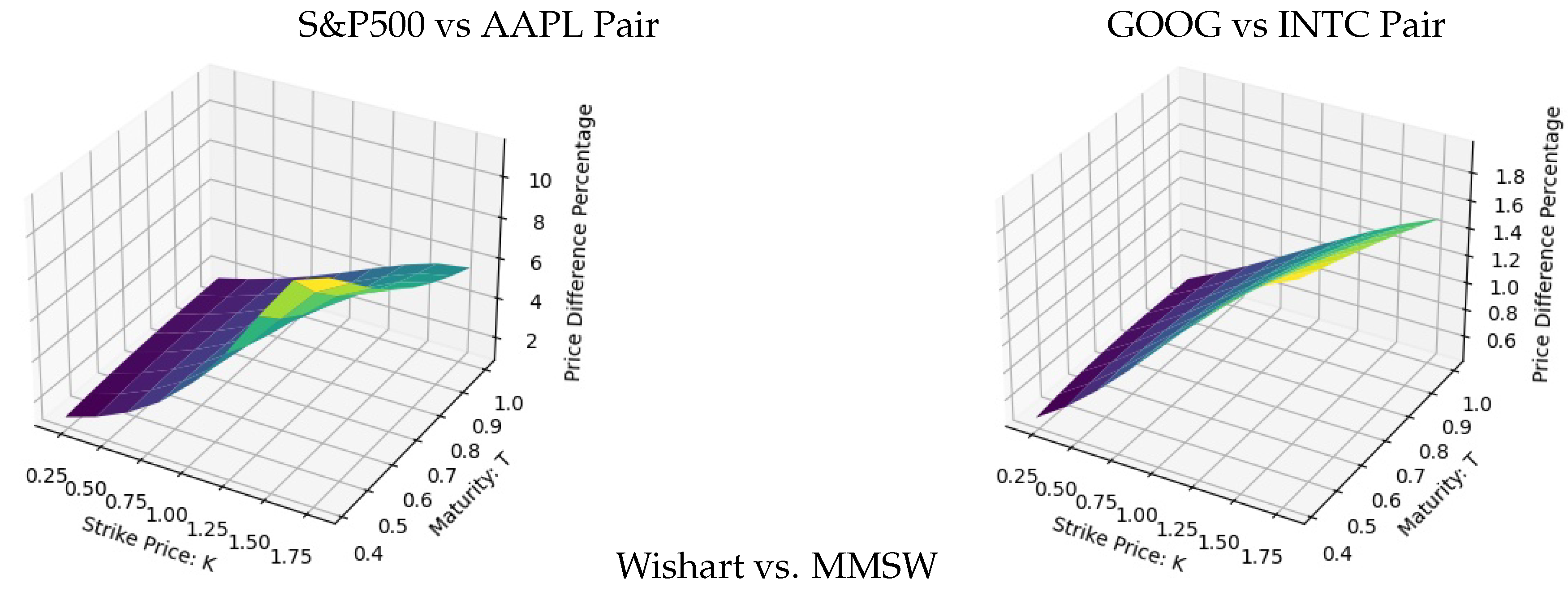
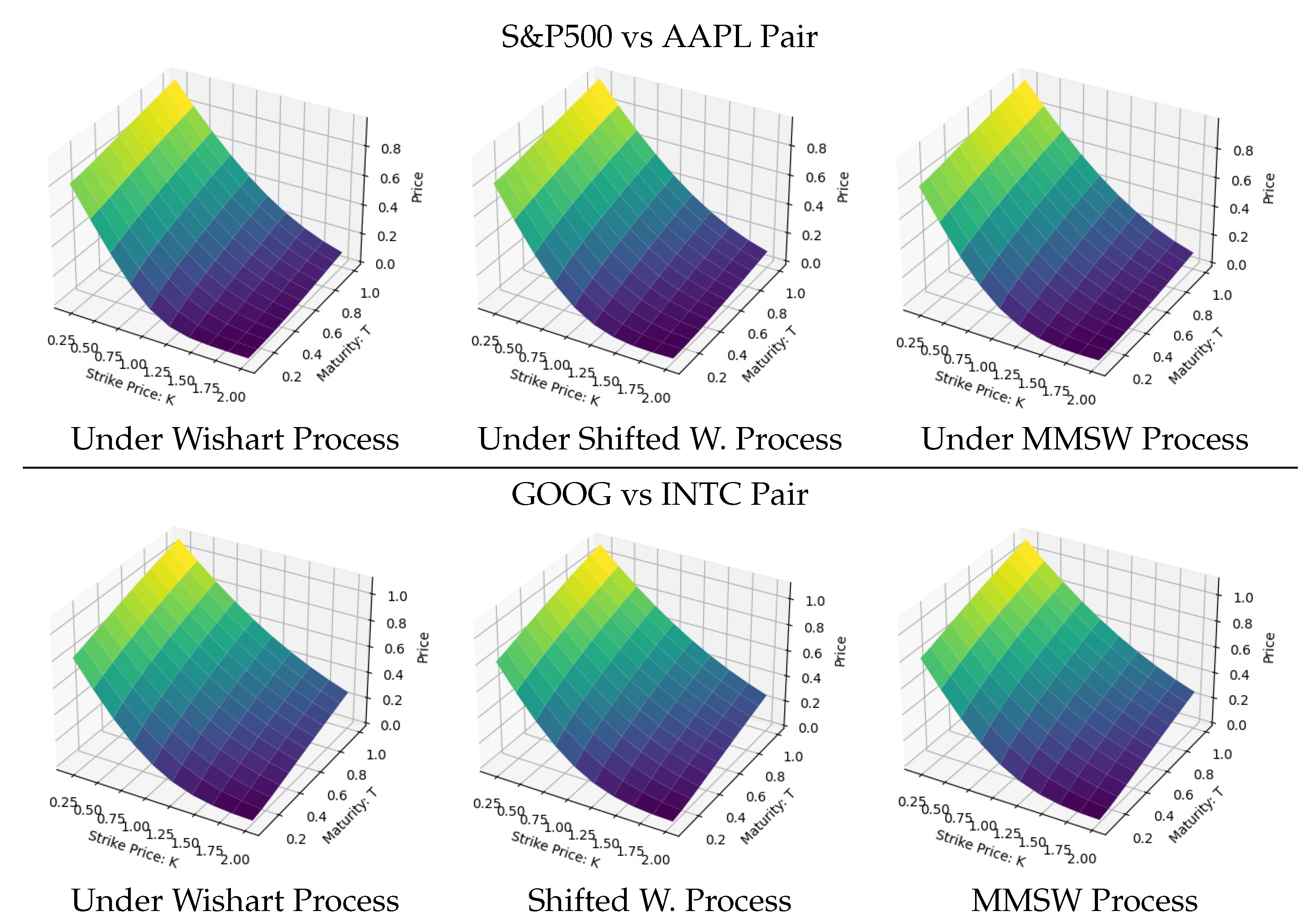
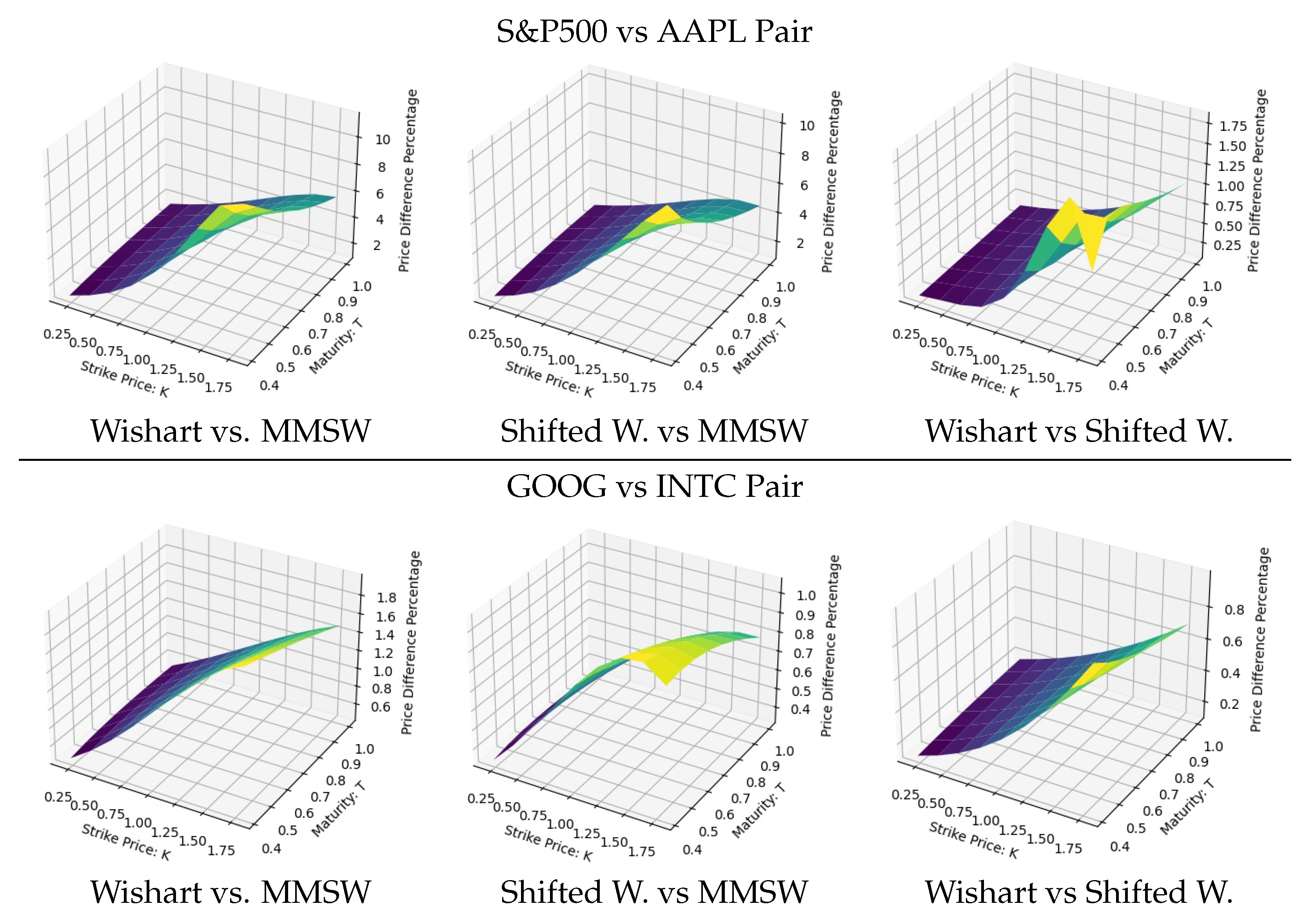
• The Fourier transform method is used, together with the characteristic function (c.f.), to price Spread Options. The accuracy of the c.f. and derivatives prices is confirmed via Monte Carlo simulations. The importance of accounting for crises in the spread options pricing is documented, revealing an impact of up to $7\%$ when the models are calibrated to the same data.

The paper is organized as follows: Section 2 develops the theoretical framework for the Markov-Modulated Shifted (MMSW) and the Shifted (SW) Wishart processes. We derive the characteristic function for the multivariate price and stochastic covariance matrix processes. In Section 3, we provide an estimation procedure for all models and implement it for two financial asset price time series pairs. In Section 4, we use the estimations and the new models to price spread options using the Fourier transform and characteristic functions. We compare it to pricing achieved using the classical Wishart process, with all results validated via simulations. Section 5 concludes and provides some suggestions for further research.

2. Models and Properties

In this section, we first introduce the dynamics of the asset prices and their corresponding stochastic covariance matrix. We extend the Wishart covariance matrix process, creating two new models. In the first step of our modeling, we introduce the Shifted Wishart (SW) process, with constant shifts in the classical dynamics of the Wishart process. In the second step, we will provide a Markov-modulated version of the Shifted Wishart called the MMSW process.

2.1. The SW Process: Wishart Process with Constant Shift

We consider a filtered probability space $(\Omega ,\mathcal{F},{\left({\mathcal{F}}_t\right)}_{t\ge 0},\mathbb{P})$ with probability measure $\mathbb{P}$ and filtration ${\left({\mathcal{F}}_t\right)}_{t\ge 0}$ contained in $\sigma$-algebra $\mathcal{F}$. Investors have access to a bank account with a riskless rate of return $r_t$

$$d{P}_{0,t}=P_{0,t}{r}_{t}dt,$$

(1)

as well as N risky assets with price processes $P_{1,t},P_{2,t},\dots ,P_{N,t}$. Let us assume the N-dimensional log-price process

$$Y_t=ln{P}_t=(ln{P}_{1,t},ln{P}_{2,t},\dots ,ln{P}_{N,t}),$$

(2)

follows the multi-dimensional SDE:1

$$\begin{array}{ccc}\hfill dln{P}_t& =& \left({\mu }_t-{\displaystyle \frac{1}{2}}diag\left(\widehat{\Sigma }\right)-{\displaystyle \frac{1}{2}}diag\left({\Sigma }_t^{WI}\right)\right)dt\hfill \end{array}$$

$$\begin{array}{ccc}& +& \sqrt{\widehat{\Sigma }}d{\widehat{W}}_t^P+\sqrt{{\Sigma }_t^{WI}}d{W}_t^P,\hfill \end{array}$$

(3)

$\begin{array}{ccc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}d{\Sigma }_t^{WI}& =& \left[\beta Q^{T}Q+M{\Sigma }_t^{WI}+{\Sigma }_t^{WI}{M}^T\right]dt\hfill \end{array}$

$$\begin{array}{ccc}& +& \sqrt{{\Sigma }_t^{WI}}d{W}_{t}Q+Q^T{\left(d{W}_t\right)}^T\sqrt{{\Sigma }_t^{WI}}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill d{W}_t^P& =& \sqrt{1-{\rho }^T\rho }d{B}_t+d{W}_t\rho .\hfill \end{array}$$

(5)

where ${\mu }_t$ is a vector, ${\Sigma }_t^{WI}$ is a Wishart process, $\widehat{\Sigma }$ is a positive-definite matrix capturing the shift, $\beta$ is a scalar and $\rho$ is a vector of correlations capturing leverage effect. For a $N\times N$ matrix $\Sigma$, $diag(\Sigma )$ is a N-dimensional vector consisting of the diagonal elements of $\Sigma$, and $\sqrt{\Sigma }$ is the square root of a positive-definite matrix $\Sigma$.2 The matrix $W_t$ is a $N\times N$ matrix Brownian motion, while $W_t^P$ and ${\widehat{W}}_t^P$ are N-dimensional independent Brownian motions. As ${\Sigma }_t^{WI}$ follows the Wishart dynamics, and $\widehat{\Sigma }$ is a positive-definite symmetric covariance matrix, then the process of the covariance follows the equation

$${\Sigma }_t^{SW}=\widehat{\Sigma }+{\Sigma }_t^{WI}.$$

(6)

The model of risky assets with such covariance will be called a Shifted Wishart (SW) process. We refer to ${\Sigma }_t^{WI}$ as the un-shifted, i.e., classical, Wishart. This notion will be helpful for the estimation methodology.3

Hence, if we let ${\Sigma }_t^{SW}$ be the instantaneous covariance of asset prices, then one can show that it follows the stochastic differential equation:

$$\begin{array}{ccc}\hfill d{\Sigma }_t^{SW}& =& \left(\beta Q^{T}Q-\left[M\widehat{\Sigma }+\widehat{\Sigma }{M}^T\right]+M{\Sigma }_t^{SW}+{\Sigma }_t^{SW}{M}^T\right)dt\hfill \\ & +& \sqrt{{\Sigma }_t^{SW}-\widehat{\Sigma }}d{W}_{t}Q+Q^T{\left(d{W}_t\right)}^T\sqrt{{\Sigma }_t^{SW}-\widehat{\Sigma }}.\hfill \end{array}$$

(7)

The parameters of the SW process satisfy the usual conditions similar to the Wishart process: $\beta >N-1$ and the matrix M is negative semi-definite to guarantee the resulting process remains symmetric and positive-definite. The Wishart process is a particular case obtained when $\widehat{\Sigma }$ is zero.

The idea of displaced or shifted processes became popular, in one dimension, as an alternative, more flexible way of capturing implied volatility smiles and skews, as well as a way to place lower bounds in the variance process, see V. V. Piterbarg (2005) and the shifted volatility Heston in Antonov et al. (2007). The shifted Heston volatility can be defined by ${\lambda }_t^S={\lambda }_t+\widehat{\lambda }$ resulting in the following dynamics:

$$d{\lambda }_t^S=\theta \left[\left(\kappa +\widehat{\lambda }\right)-{\lambda }_t^S\right]dt+{\sigma }_{\lambda }\sqrt{{\lambda }_t^S-\widehat{\lambda }}d{W}_t.$$

(8)

In multi-dimensions, developing stochastic volatility and correlation models has been instrumental for quants working in all areas of the financial industry. Stochastic covariance processes would naturally bring extra flexibility in capturing implied volatility behavior and correlation features. Nonetheless, to our knowledge, these types of processes have not been studied in the literature. The closest result in the area is V. Piterbarg (2003), which works in the context of term structures and multi-dimensional LIBOR Market Models with a displacement (shift) coefficient.

An important aspect of our work is based on the observation that asset’ correlations are mean-reverting. From Equation (4), the long-term mean-variance level of the Wishart process, ${\Sigma }_{\infty }^{WI}$, can be written as the solution to the equation:

$$\beta Q^{T}Q+M{\Sigma }_{\infty }^{WI}+{\Sigma }_{\infty }^{WI}{M}^T=0,$$

(9)

whereas the long-term mean reversion level of the shifted Wishart process (7), ${\Sigma }_{\infty }^{SW}$, satisfies the matrix equation

$$\beta Q^{T}Q+M{\Sigma }_{\infty }^{SW}+{\Sigma }_{\infty }^{SW}{M}^T=M\widehat{\Sigma }+\widehat{\Sigma }{M}^T.$$

(10)

Both mean reversion levels for the Wishart and shifted Wishart processes,${\Sigma }_{\infty }^{WI}$ and ${\Sigma }_{\infty }^{SW}$, and the shift parameter $\widehat{\Sigma }$ are related by the following equation:

$$\widehat{\Sigma }={\Sigma }_{\infty }^{SW}-{\Sigma }_{\infty }^W.$$

(11)

In the two-dimensional case, the following lemma provides a closed-form expression for the long-term mean-reverting covariance:

Lemma 1.

For the two dimensional Wishart process (Equation (4) with $N=2$), the long-term standard deviations ${\sigma }_{1,\infty }^2$, ${\sigma }_{2,\infty }^2$, ${\rho }_{\infty }$ in the matrix ${\Sigma }_{\infty }^{WI}$ are given by

$${\rho }_{\infty }={\displaystyle \frac{\frac{a{m}_{21}}{2m_{11}}+\frac{b{m}_{12}}{2m_{22}}-c}{m_{11}+m_{22}-m_{12}{m}_{21}(\frac{1}{m_{11}}+\frac{1}{m_{22}})}},$$

(12)

$${\sigma }_{1,\infty }^2={\displaystyle \frac{-a-2m_{12}{\rho }_{\infty }}{2m_{11}}},{\sigma }_{2,\infty }^2={\displaystyle \frac{-b-2m_{21}{\rho }_{\infty }}{2m_{22}}},$$

(13)

with

$$\begin{array}{cc}\hfill a& =\beta (Q_{11}^2+Q_{12}{Q}_{21}),\hfill \\ \hfill b& =\beta (Q_{22}^2+Q_{21}{Q}_{12}),\hfill \\ \hfill c& =\beta (Q_{21}{Q}_{22}+Q_{11}{Q}_{21}).\hfill \end{array}$$

Proof. 

The results follow directly from Equation (9). □

One could similarly obtain ${\Sigma }_{\infty }^{SW}$ given $\widehat{\Sigma }$ via (11).

Next, we derive characteristic functions related to this model. Let’s rewrite the log-price process as follows:

$$\begin{array}{ccc}\hfill dln{P}_t& =& dln{P}_t^{\left(1\right)}+dln{P}_t^{\left(2\right)},\hfill \\ \hfill dln{P}_t^{\left(1\right)}& =& \left[\left({\mu }_t-{\displaystyle \frac{1}{2}}diag\left({\Sigma }_t^{WI}\right)\right)dt+\sqrt{{\Sigma }_t^{WI}}d{W}_t^P\right],\hfill \\ \hfill dln{P}_t^{\left(2\right)}& =& \left[\left(-{\displaystyle \frac{1}{2}}diag\left(\widehat{\Sigma }\right)\right)dt+\sqrt{\widehat{\Sigma }}d{\widehat{W}}_t^P\right],\hfill \end{array}$$

(14)

Due to the dependence structure of the underlying components, we can write the c.f. of the log price ($ln{P}_t$), denoted ${\Phi }^{SW}(\tau ,u,y,{\sigma }^W)$$:[0,T]\times {\mathbb{R}}^N\times {\mathbb{R}}^N\times {\mathcal{S}}_{N\times N}\to \mathbb{R}$ where ${\mathcal{S}}_{N\times N}$ is the space of $N\times N$ positive-definite matrices as a product of two simpler c.f.’s:

$$\begin{array}{ccc}\hfill {\Phi }^{SW}(\tau ,u,y,{\sigma }^{WI})& & =\mathbb{E}\left[exp\left\{\mathrm{i}〈u,ln{P}_{t+\tau }〉\right\}|ln{P}_t=y,{\Sigma }_t^{WI}={\sigma }^{WI}\right]\hfill \end{array}$$

$$\begin{array}{ccc}& & ={\Phi }^{\left(1\right)}(\tau ,u,y,{\sigma }^{WI}){\Phi }^{\left(2\right)}(\tau ,u),\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\Phi }^{\left(1\right)}(\tau ,u,y,{\sigma }^{WI})& & =\mathbb{E}\left[exp\left\{\mathrm{i}〈u,ln{P}_{t+\tau }^{\left(1\right)}〉\right\}|ln{P}_t^{\left(1\right)}=y,{\Sigma }_t^{WI}={\sigma }^{WI}\right],\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\Phi }^{\left(2\right)}(\tau ,u)& & =\mathbb{E}\left[exp\left\{\mathrm{i}〈u,ln{P}_{t+\tau }^{\left(2\right)}〉\right\}|ln{P}_t^{\left(2\right)}=0\right],\hfill \end{array}$$

(17)

where the symbol $\langle .,.\rangle$ represents the dot product of two vectors.

Proposition 2

(Characteristic Function of log price in SW model). The characteristic function ${\Phi }^{SW}(\tau ,u,y,{\sigma }^{WI})$ can be represented as follows:

$$\begin{array}{ccc}\hfill {\Phi }^{SW}(\tau ,u,y,{\sigma }^{WI})& =& exp(i<u,y>+Tr\left(A\left(\tau \right){\sigma }^{WI}\right)+c\left(\tau \right)\hfill \\ & & -{\displaystyle \frac{1}{2}}i{u}^T·diag\left(\widehat{\Sigma }\right)\tau -{\displaystyle \frac{1}{2}}\tau ·u^T\widehat{\Sigma }u),\hfill \end{array}$$

(18)

where the functions A, and c are given by

$$A\left(\tau \right)={\Lambda }_{22}{\left(\tau ,u\right)}^{-1}{\Lambda }_{21}\left(\tau ,u\right),$$

(19)

with ${\Lambda }_{ij}$’s defined as

$$\begin{array}{ccc}\hfill \Lambda \left(\tau ,u\right)& \equiv & \left(\begin{array}{cc}{\Lambda }_{11}\left(\tau ,u\right)& {\Lambda }_{12}\left(\tau ,u\right)\\ {\Lambda }_{21}\left(\tau ,u\right)& {\Lambda }_{22}\left(\tau ,u\right)\end{array}\right)\hfill \\ & =& exp\left(\tau \left(\begin{array}{cc}M+i{Q}^T\rho u^T& -2Q^{T}Q\\ -{\displaystyle \frac{i}{2}}\left(\sum _{j=1}^n{u}_j{e}_{jj}\right)-{\displaystyle \frac{1}{2}}u{u}^T& -M^T-iu{\rho }^{T}Q\end{array}\right)\right),\hfill \end{array}$$

(20)

and

$$\begin{array}{c}\hfill c\left(\tau \right)=-{\displaystyle \frac{\beta }{2}}Tr\left[ln\left({\Lambda }_{22}\left(\tau \right)\right)+\tau (M^T+iu{\rho }^{T}Q)\right]+\tau i·Tr\left[\mu u^T\right],\end{array}$$

where $e_{jj}$ is the square matrix with one as the element $(j,j)$ and zero elsewhere, and i stands for the square root of $-1$.

Proof. 

This is a direct result of the decomposition in Equation (15), where according to Da Fonseca et al. (2007), ${\Phi }^{\left(1\right)}(\tau ,u,y,{\sigma }^{WI})$ satisfies:

$${\Phi }^{\left(1\right)}(\tau ,u,y,{\sigma }^{WI})=exp\left(\mathrm{i}<u,y>+Tr\left(A\left(\tau \right){\sigma }^{WI}\right)+c\left(\tau \right)\right),$$

(21)

and ${\Phi }^{\left(2\right)}(\tau ,u)$ is just a multivariate Geometric Brownian motion with a simple c.f. Hurd and Zhou (2010):

$${\Phi }^{\left(2\right)}(\tau ,u)=exp\left(\mathrm{i}{u}^T·\left(-{\displaystyle \frac{1}{2}}diag\left(\widehat{\Sigma }\right)\right)\tau -{\displaystyle \frac{1}{2}}\tau ·u^T\widehat{\Sigma }u\right),$$

(22)

□

Let us now define the characteristic function of the shifted Wishart covariance process itself; this is:

$${\Phi }_{\Sigma }^{SW}\left(\tau ,\Delta ,{\sigma }^{WI},\widehat{\Sigma }\right)=\mathbb{E}\left[exp\left\{\mathrm{i}Tr\left(\Delta {\Sigma }_{t+\tau }^{SW}\right)\right\}\mid {\Sigma }_t^{SW}={\sigma }^{WI}+\widehat{\Sigma }\right],$$

(23)

where ${\Phi }_{\Sigma }^{SW}(\tau ,\Delta ,{\sigma }^{WI},\widehat{\Sigma })$$:[0,T]\times M_N\times D_N\times D_N\to \mathbb{R}$, here $M_N$ and $D_N$ are the spaces of $N\times N$ matrices and $N\times N$ positive-definite matrices, respectively. The next proposition provides a closed form for this object.

Proposition 3.

The characteristic function of the shifted Wishart process has the form

$${\Phi }_{\Sigma }^{SW}\left(\tau ,\Delta ,{\sigma }^{WI},\widehat{\Sigma }\right)=e^{Tr\left(i\Delta \widehat{\Sigma }\right)+Tr\left(B\left(\tau \right){\Sigma }_t\right)+C\left(\tau \right)},$$

(24)

where

$$B\left(\tau \right)={\left(i\Delta B_{12}\left(\tau \right)+B_{22}\left(\tau \right)\right)}^{-1}\left(i\Delta B_{11}\left(\tau \right)+B_{21}\left(\tau \right)\right),$$

$$C\left(\tau \right)=\beta Tr\left[Q^{T}Q{\int }_0^{\tau }B\left(s\right)ds\right]$$

with $B_{ij}$’s defined as

$${\left(\begin{array}{cc}{B}_{11}\left(\tau \right)& B_{12}\left(\tau \right)\\ B_{21}\left(\tau \right)& B_{22}\left(\tau \right)\end{array}\right)}_{2N\times 2N}=exp\left(\tau \left(\begin{array}{cc}M& -2Q^{T}Q\\ 0& -M^T\end{array}\right)\right),$$

Proof. 

See Appendix A.1 □

These models fail to capture all stylized facts of market data in one or multiple dimensions. Examples are extreme market conditions or financial crises. The following section presents a solution for capturing this by randomly changing the shifted process for the covariance.

2.2. The MMSW Process: Wishart Process with Markov-Modulated Shift

Similarly to the constant shifted covariance case, we assume the investor has access to the bank account $P_0$ with the same dynamics and N risky assets with price processes following a multi-dimensional SDE provided next termwise, $n=1,2,\dots ,N$

$$d{P}_{n,t}=P_{n,t}\left({\mu }_{n,t}dt+{\left(\sqrt{\widehat{\Sigma }\left({\mathcal{MC}}_t\right)}\right)}_{n}d{\widehat{W}}_t^P+{\left(\sqrt{{\Sigma }_t^{WI}}\right)}_{n}d{W}_t^P\right).$$

(25)

${\mu }_{n,t}$ is the drift coefficient of stock prices assumed constant, ${\left(\sqrt{\widehat{\Sigma }\left({\mathcal{MC}}_t\right)}\right)}_n$ is the nth row of the square root of the shift matrix, and ${\left(\sqrt{{\Sigma }_t^{WI}}\right)}_n$ is the nth row of the square root of a Wishart covariance matrix.4

Let us assume that $\mathcal{MC}\equiv {\left\{{\mathcal{MC}}_t\right\}}_{t>0}$ is an adapted jump process on the filtered probability space $\left(\Omega ,\mathcal{F},{\left({\mathcal{F}}_t\right)}_{t\ge 0},\mathbb{P}\right).$ For $s\le t$

$$\mathbb{P}\left({\mathcal{MC}}_t=e_i\left|\phantom{{\mathcal{MC}}_t=e_i{\mathcal{F}}_s}\right.{\mathcal{F}}_s\right)=\mathbb{P}\left({\mathcal{MC}}_t=e_i\left|\phantom{{\mathcal{MC}}_t=e_i\mathcal{MC}\left(t\right)}\right.{\mathcal{MC}}_s\right).$$

(26)

${\mathcal{MC}}_t$ is a continuous-time Markov chain with two states: the normal state $\{{\mathcal{S}}_{\mathcal{MC}}=e_0\}$ and crisis state $\{{\mathcal{S}}_{\mathcal{MC}}=e_1\}$. The Markov chain $\mathcal{MC}$ is independent of Brownian motions $W_t^p$ and ${\widehat{W}}_t^p$. Then, the process of the covariance can be written as follows

$${\Sigma }_t^{MW}=\widehat{\Sigma }\left({\mathcal{MC}}_t\right)+{\Sigma }_t^{WI}.$$

(27)

The model of risky assets with such covariance will be called a Markov-Modulated Shifted Wishart (MMSW) process. The shift in the normal period, $\widehat{\Sigma }\left(e_0\right)$, will be assumed to be 0 for simplicity in this work; other assumptions are viable. A feasible representation for the covariance matrix of the assets, ${\Sigma }_t^{MW}$, is given next:

$$\begin{array}{cc}\hfill d{\Sigma }_t^{MW}& =(\beta Q^{T}Q-\left[M\widehat{\Sigma }\left({\mathcal{MC}}_t\right)+\widehat{\Sigma }\left({\mathcal{MC}}_t\right)M^T\right]\hfill \\ \hfill & +M{\Sigma }_t^{MW}+{\Sigma }_t^{MW}{M}^T)dt\hfill \\ \hfill & +\sqrt{{\Sigma }_t^{MW}-\widehat{\Sigma }\left({\mathcal{MC}}_t\right)}d{W}_{t}Q+Q^{T}d{W}_t^T\sqrt{{\Sigma }_t^{MW}-\widehat{\Sigma }\left({\mathcal{MC}}_t\right)}.\hfill \end{array}$$

(28)

The MMSW model constitutes an addition of two well-known processes, a Wishart process, and a Markov-modulated process. We can see that, for instance, in Equations (25) and (14). These last two processes have been extensively studied. The mathematical conditions that guarantee the uniqueness and existence of the SDE defining the Wishart process have been extensively studied in the literature starting from Bru (1991). Key findings reveal that the parameter $\beta$ and the dimension N of the process are critical factors. For the existence of a unique, strong solution on the positive-definite matrices, a sufficient condition is $\beta \ge N+1$. For a unique weak solution on the positive semi-definite matrices, the condition $N-1\le \beta <N+1$ is typically required. Furthermore, the rank of the initial value of the process plays a role when $\beta$ is below certain thresholds, particularly for the existence of weak solutions. The condition $\beta \ge N+1$ is not only crucial for the existence of a unique, strong solution but also ensures that the Wishart process remains positive-definite at all times, a vital property for its interpretation as a covariance matrix (Ahdida & Alfonsi, 2013; Bru, 1991; Graczyk et al., 2018; Pfaffel, 2012). In this domain, the coefficients of the Wishart process remain locally Lipschitz, with linear growth globally. A proof for the existence and uniqueness of a strong solution for a Markov-modulated process on finitely many states can be found at Yin and Zhu (2010). In our Markov-modulated process, as the coefficients are only a function of the jump process, they satisfy linear growth and Lipschitz conditions. So, the combined MMSW process satisfies the conditions of the existence and uniqueness of a strong solution.

An advantage of using this model is that the impact of the financial crisis and the stochastic assumption of the correlation are separately constructed under a modular framework. We use the simplest case of a Markov chain when two regimes correspond to normal and crisis markets. We define the set of jump times of $\mathcal{MC}$ as

$${\tau }_J=\left\{t\ge 0\left|\phantom{t\ge 0{\mathcal{MC}}_t\ne {\mathcal{MC}}_t^{-}}\right.{\mathcal{MC}}_t\ne {\mathcal{MC}}_t^{-}\right\},$$

(29)

where ${\mathcal{MC}}_t^{-}$ is the left-side limit of $\mathcal{MC}$ at time t. The initial probabilities for $\mathcal{MC}$ starting from the normal state is $p_0=\mathbb{P}\left({\mathcal{MC}}_0=e_0\right)$ and the probability of starting from the crisis state is $p_1=1-p_0=\mathbb{P}\left({\mathcal{MC}}_0=e_1\right)$. The occupation time of $\mathcal{MC}$ in the state $e_i$ measures how long the jump process has stayed in a particular state and is defined by

$$T_i\left(t\right)={\int }_0^t{\mathbb{I}}_{\left\{{\mathcal{MC}}_s=e_i\right\}}dsfori=0,1.$$

(30)

We let the Markov switching covariance matrix represent the changing market environment and use the Wishart process as a source to simulate the random structure of both volatility and correlation. The time $\mathcal{MC}$ spends in each state before traveling to the other follows an exponential distribution with parameter ${\lambda }_i$ for states $i=0,1$. Assume the transition matrix of the Markov chain governing the covariance structure ${\Sigma }^{MW}$ is given by:

$$\begin{array}{ccc}\hfill M_{\mathcal{MC}}\left(t\right)& =& \left(\begin{array}{cc}{p}_{11}\left(t\right)& p_{12}\left(t\right)\\ p_{21}\left(t\right)& p_{22}\left(t\right)\end{array}\right)=exp\left(t·G\right)\hfill \\ & =& \left(\begin{array}{cc}{\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}+{\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}{e}^{-({\lambda }_0+{\lambda }_1)t}& {\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}-{\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}{e}^{-({\lambda }_0+{\lambda }_1)t}\\ {\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}-{\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}{e}^{-({\lambda }_0+{\lambda }_1)t}& {\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}+{\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}{e}^{-({\lambda }_0+{\lambda }_1)t}\end{array}\right).\hfill \end{array}$$

(31)

where the transition probabilities are defined as:

$$p_{ij}\left(t\right)\equiv \mathbb{P}\left[{\mathcal{MC}}_{t+s}=e_j|{\mathcal{MC}}_s=e_i\right]=\mathbb{P}\left[{\mathcal{MC}}_t=e_j|{\mathcal{MC}}_0=e_i\right],$$

(32)

and G is the generator matrix (transition rate/intensity matrix) given by

$$G=\left(\begin{array}{cc}-{\lambda }_0& {\lambda }_0\\ {\lambda }_1& -{\lambda }_1\end{array}\right).$$

(33)

The initial probabilities are taken to be the stationary ones $p_0=p_{11}={\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}$ and $p_1=p_{22}={\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}$. Also, the transition probabilities are considered to be ${\lambda }_{01}={\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}$ and ${\lambda }_{10}={\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}$.

Since our objective is to model the changing behavior of the covariance matrix during turbulent market conditions, it is clear from Equation (27) that the Markov modulated shifted Wishart processes are an ideal candidate, thanks to the shift matrix $\widehat{\Sigma }$. If ${\Sigma }_{N\infty }^{WI}$ is the long-term covariance of the Wishart process on normal period data, we can see from SDE (28) and Equation (27) that the long-term mean reversion level of the MMSW process is given by:

$${\Sigma }_{\infty }^{MW}={\displaystyle \frac{{\lambda }_1}{{\lambda }_0+{\lambda }_1}}{\Sigma }_{N\infty }^{WI}+{\displaystyle \frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1}}(\widehat{\Sigma }+{\Sigma }_{N\infty }^{WI}).$$

(34)

where ${\lambda }_0$ and ${\lambda }_1$ are the parameters of Markov modulation, leading to

$$\widehat{\Sigma }={\displaystyle \frac{{\lambda }_0+{\lambda }_1}{{\lambda }_0}}({\Sigma }_{\infty }^{MW}-{\Sigma }_{N,\infty }^{WI}).$$

(35)

We now aim to compute the characteristic function of the log prices:

$${\Phi }^{MW}(\tau ,u,y,e_i,{\sigma }^{WI}):=\mathbb{E}\left[exp\left\{\mathrm{i}〈u,ln{P}_{t+\tau }〉\right\}\mid ln{P}_t=y,{\mathcal{MC}}_t=e_i,{\Sigma }_t^{WI}={\sigma }^{WI}\right].$$

(36)

For a two-state Markov process (${\mathcal{MC}}_t\in \{e_0,e_1\}$, where $e_i$ are the states of the Markov process), we first need to find the characteristic function separately in each state, i.e., assuming the Markov process stays in the state for the whole period:

$${\Phi }_i(\tau ,u,y,e_i,{\sigma }^{WI}):=\mathbb{E}\left[exp\left\{\mathrm{i}〈u,ln{P}_{t+\tau }〉\right\}|ln{P}_t=y,{\mathcal{MC}}_s{|}_{s=t}^T=e_i,{\Sigma }_t^{WI}={\sigma }^{WI}\right].$$

(37)

We can find ${\Phi }_1$ using Proposition 2 with shift equal to $\widehat{\Sigma }=\widehat{\Sigma }({\mathcal{MC}}_t=e_1)$. Similarly, ${\Phi }_0$ has a shift of zero, $\widehat{\Sigma }=\widehat{\Sigma }({\mathcal{MC}}_t=e_0)=0$ hence the result follows directly. We can now formulate ${\Phi }^{MW}(\tau ,u,y,e_i,{\sigma }^{WI})$.

Proposition 4 (Characteristic Function of log price in MMSW).

Let ${\mathcal{MC}}_t\in \{e_0,e_1\}$ be the Markov chain defined before, then (37) is given by

$$\begin{array}{ccc}\hfill {\Phi }^{MW}(\tau ,u,y,e_i,{\sigma }^{WI})& =& {\Phi }_0(\tau ,u,y,e_0,{\sigma }^{WI})\vartheta \left(log\left({\displaystyle \frac{{\Phi }_0(\tau ,u,y,e_0,{\sigma }^{WI})}{{\Phi }_1(\tau ,u,y,e_1,{\sigma }^{WI})}}\right)\right),\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill \vartheta \left(x\right)& =& p{\vartheta }_0\left(x\right)+(1-p){\vartheta }_1\left(x\right),\hfill \end{array}$$

(39)

where $p=p_0$ is initial probability of state 0 and ${\vartheta }_0\left(x\right)$ and ${\vartheta }_1\left(x\right)$ are as follows:

$$\begin{array}{ccc}\hfill {\vartheta }_0\left(x\right)& =& exp\left(-\left({\eta }_1\left(x\right)+{\lambda }_{01}\right)\tau \right)\hfill \end{array}$$

$$\begin{array}{ccc}& \times & {\displaystyle \frac{{\eta }_2\left(x\right)+{\lambda }_{01}-\left({\eta }_1\left(x\right)+{\lambda }_{01}\right)e^{-\left({\eta }_2\left(x\right)-{\eta }_1\left(x\right)\right)\tau }}{{\eta }_2\left(x\right)-{\eta }_1\left(x\right)}},\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill {\vartheta }_1\left(x\right)& =& {\displaystyle \frac{1}{{\lambda }_{01}}}exp\left(-\left({\eta }_1\left(x\right)+{\lambda }_{01}\right)\tau \right)\hfill \end{array}$$

$$\begin{array}{ccc}& \times & {\displaystyle \frac{{\eta }_2\left(x\right)\left({\eta }_1\left(x\right)+{\lambda }_{01}\right)e^{-\left({\eta }_2\left(x\right)-{\eta }_1\left(x\right)\right)\tau }-\begin{array}{c}\hfill {\eta }_1\left(x\right)\end{array}\left({\eta }_2\left(x\right)+{\lambda }_{01}\right)}{{\eta }_2\left(x\right)-{\eta }_1\left(x\right)}}\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill {\eta }_1\left(x\right),{\eta }_2\left(x\right)& =& {\displaystyle \frac{x+{\lambda }_{10}-{\lambda }_{01}}{2}}\pm \sqrt{{\displaystyle \frac{{\left(x+{\lambda }_{10}-{\lambda }_{01}\right)}^2}{4}}+{\lambda }_{10}{\lambda }_{01}}.\hfill \end{array}$$

(42)

Proof. 

See Appendix A.2 □

Let us now define the c.f. of the Markov-modulated shifted Wishart covariance process itself:

$$\begin{array}{cc}\hfill {\Phi }_{\Sigma }^{MW}\left(\tau ,\Delta ,e_i,{\sigma }^{WI}\right)=& \mathbb{E}\left[exp\left\{\mathrm{i}Tr\left(\Delta {\Sigma }_{t+\tau }^{MW}\right)\right\}\mid {\Sigma }_t^{WI}={\sigma }^{WI},{\mathcal{MC}}_t=e_i\right]\hfill \\ \hfill =& \mathbb{E}\left[exp\left\{\mathrm{i}Tr\left(\Delta \widehat{\Sigma }\left({\mathcal{MC}}_{t+\tau }\right)\right)\right\}\mid {\mathcal{MC}}_t=e_i\right]\hfill \\ \hfill \times & \mathbb{E}\left[exp\left\{\mathrm{i}Tr\left(\Delta {\Sigma }_{t+\tau }^{WI}\right)\right\}\mid {\Sigma }_t^{WI}={\sigma }^{WI}\right]\hfill \\ \hfill =& {\Phi }_{\widehat{\Sigma }}\left(\tau ,\Delta ,e_i\right){\Phi }_{{\Sigma }^{WI}}\left(\tau ,\Delta ,{\sigma }^{WI}\right).\hfill \end{array}$$

(43)

The next proposition provides a closed-form representation for this object.

Proposition 5.

The characteristic function in (43) has the form

$${\Phi }_{\Sigma }^{MW}\left(\tau ,\Delta ,e_i,{\sigma }^{WI}\right)=(p+(1-p)e^{iTr(\Delta \widehat{\Sigma })})e^{Tr\left(B\left(\tau \right){\Sigma }_t\right)+C\left(\tau \right)},$$

(44)

where $B\left(\tau \right)$ and $C\left(\tau \right)$ are given in Proposition 3.

Proof. 

The characteristic function of Wishart process ${\Phi }_{{\Sigma }^{WI}}$ is given in Proposition 3, and by the definition of the Markov-modulated shifted process ${\Phi }_{\widehat{\Sigma }}$ is given by

$${\Phi }_{\widehat{\Sigma }}\left(\tau ,\Delta ,e_i\right)=p+(1-p)e^{\mathrm{i}Tr\left(\Delta \widehat{\Sigma }\right)}.$$

(45)

□

Let us now define the characteristic function of the integrated Markov-modulated shifted Wishart covariance process:

$$\begin{array}{cc}\hfill {\Phi }_{I\Sigma }^{MW}\left(\tau ,\Delta ,e_i,{\sigma }^{WI}\right)=& \mathbb{E}\left[exp\{\mathrm{i}Tr\left(\Delta \underset{t}{\overset{t+\tau }{\int }}{\Sigma }_s^{MW}ds\right)\}|{\Sigma }^{WI}\left(t\right)={\sigma }^{WI},{\mathcal{MC}}_t=e_i\right]\hfill \\ \hfill =& \mathbb{E}\left[exp\{\mathrm{i}Tr\left(\Delta \underset{t}{\overset{t+\tau }{\int }}\widehat{\Sigma }\left({\mathcal{MC}}_s\right)ds\right)\}|{\mathcal{MC}}_t=e_i\right]\hfill \\ \hfill \times & \mathbb{E}\left[exp\{\mathrm{i}Tr\left(\Delta \underset{t}{\overset{t+\tau }{\int }}{\Sigma }_s^{WI}ds\right)\}|{\Sigma }_t^{WI}={\sigma }^{WI}\right]\hfill \\ \hfill =& {\Phi }_{I\widehat{\Sigma }}\left(\tau ,\Delta ,e_i\right){\Phi }_{I{\Sigma }^{WI}}\left(\tau ,\Delta ,{\sigma }^{WI}\right)\hfill \end{array}$$

(46)

The next proposition provides a closed-form solution for this object.

Proposition 6.

The characteristic function in (46) has the form

$${\Phi }_{I\Sigma }^{MW}\left(\tau ,\Delta ,e_i,{\sigma }^{WI}\right)=e^{i\left(1-p\right)Tr\left(\Delta \widehat{\Sigma }\right)\tau +Tr\left(B\left(\tau \right){\Sigma }_t\right)+C\left(\tau \right)},$$

(47)

where

$$B\left(\tau \right)=B_{22}{\left(\tau \right)}^{-1}{B}_{21}\left(\tau \right),$$

$$\begin{array}{ccc}\hfill C\left(\tau \right)& =& -Tr\left[\left({\displaystyle \frac{{\left(Q^{T}Q\right)}^{-1}\Gamma }{2}}\right)\left(ln\left(B_{22}\left(\tau \right)\right)+\tau M^T)\right)\right],\hfill \end{array}$$

(48)

with $B_{ij}$’s defined as

$${\left(\begin{array}{cc}{B}_{11}\left(\tau \right)& B_{12}\left(\tau \right)\\ B_{21}\left(\tau \right)& B_{22}\left(\tau \right)\end{array}\right)}_{2m\times 2m}=exp\left(\tau \left(\begin{array}{cc}M& -2Q{Q}^T\\ i\Delta & {-M}^T\end{array}\right)\right),$$

such that

$$\Gamma =\beta Q^{T}Q$$

Proof. 

See Appendix A.3 □

Note that the above dynamics of the processes and the c.f.s are considered under the physical measure $\mathbb{P}$. The dynamics and c.f.s under the risk-neutral measure $\mathbb{Q}$ are very similar. To transform them from $\mathbb{P}$ to $\mathbb{Q}$, we need to replace the constant drift terms ${\mu }_n$ by the risk-free rate r and M by $\tilde{M}$ in the equations, as follows:

$$\tilde{M}=M-Q\Lambda ,$$

where

$${\Lambda }_{\tau }=\Lambda \sqrt{\Sigma \left(\tau \right)},$$

is the market price of the risk, and $\Lambda$ is a constant $n\times n$ matrix.5 Here we assume $\Lambda =0$, and in the Appendix A.5 we replicate the numerical results for the case of $\Lambda =I$.

3. Empirical Analysis, Estimation

In this section, we first work with the daily prices of two assets, the index S&P500 and the stock Apple, from 2004 to 2024. We chose the index S&P500 and a large-cap stock, Apple, because they represent the market behavior and especially turbulent and crisis regimes better than small-cap stocks, which might be affected by other minor events. Figure 1 shows their price evolution.

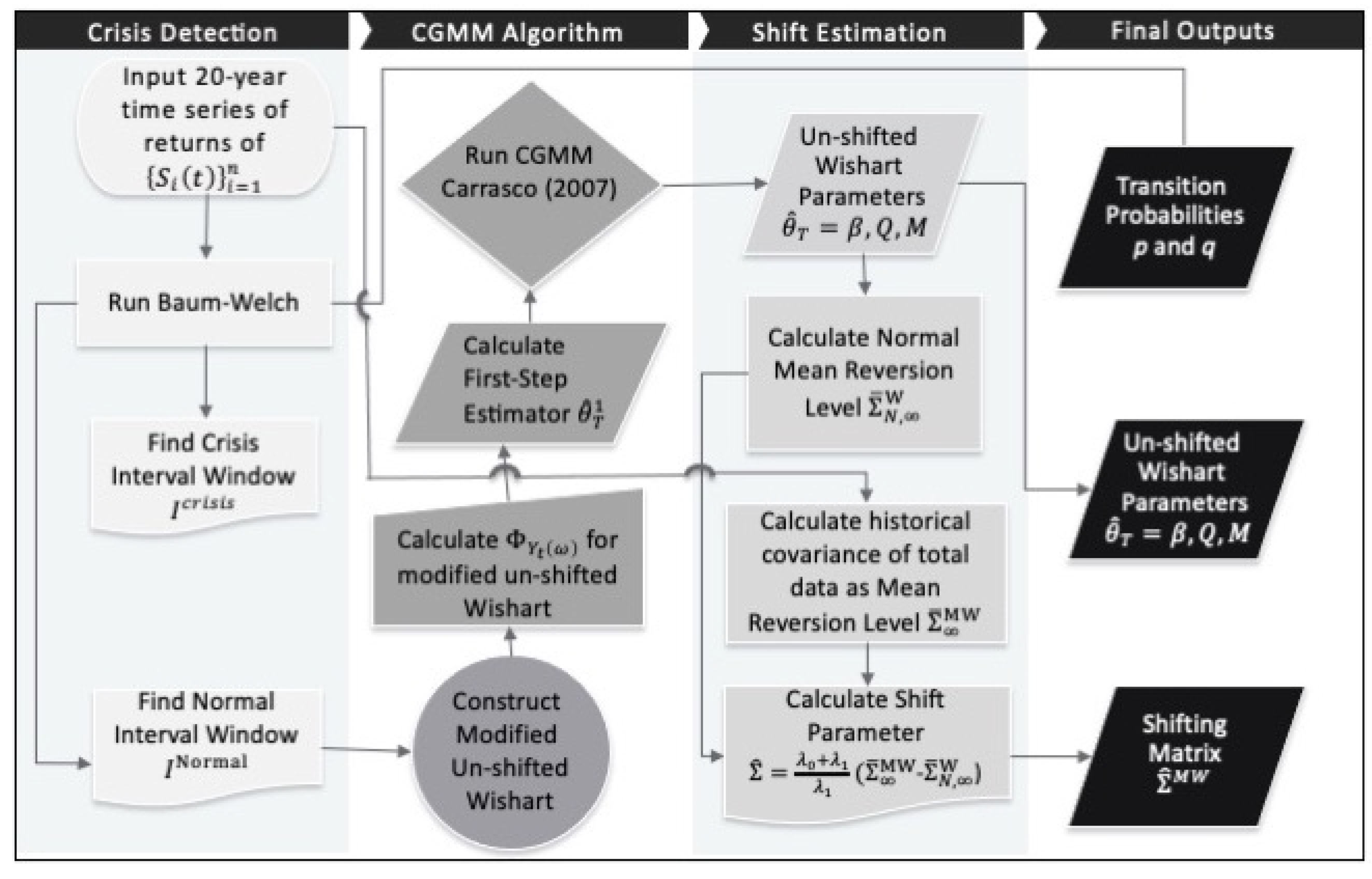
3.1. Estimation Methodology

There have been very few attempts in the literature to estimate a Wishart process. One of the most notable works is Buraschi et al. (2010), the authors work with a stock-bond-cash portfolio problem using: S&P500 Index futures contract (traded at the Chicago Mercantile Exchange) from January 1990 to October 2003, the Treasury bond futures contract (30-year Treasury bond) traded at the Chicago Board of Trade, and a riskless asset. They use the Generalized Method of Moments, assuming covariances are “observable” via Andersen et al. (2003). Alternatively, Da Fonseca et al. (2011) work with S&P500 and DAX quotes from January 2nd 1990 to June 30th 2007, using the CGMM method of Carrasco and Florens (2000, 2007) and therefore treating the covariance as a hidden process. Da Fonseca et al. (2014) uses the same method and stock indexes S&P500, FTSE, DAX and CAC40. Other authors like Branger et al. (2017) collect estimates from those two papers. In other, non-Wishart stochastic covariance settings, Escobar et al. (2016) uses the Continuum Generalized Method of Moments (CGMM) and the Continuum Method of Moments (CMM) to estimate the parameters of the Principal Components Stochastic Volatility (PCSV) model.

In this section, we will follow a three-step approach to estimate the parameters of our main model, the MMSW. We first detect crisis and estimate its parameters $(p,{\lambda }_0,{\lambda }_1)$; second, we estimate a Wishart with the data of normal times, leading to estimates for $Q,M,\beta$ and the long-term covariance of the Wishart, ${\Sigma }_{N,\infty }^{WI}$; next we estimate the long term covariance of the MMSW, ${\Sigma }_{\infty }^{MW}$, as the historical covariance of all available data (normal and crisis periods); in the last step we derive ${\widehat{\Sigma }}^{MW}$ using the Equation (35). We verify that the resulting matrix from the estimation, ${\widehat{\Sigma }}^{MW}$, is positive-definite6. The flowchart of the estimation algorithm is presented in Figure 2.

In the first step, the Baum-Welch algorithm estimates the parameters of a Hidden Markov Model that maximizes the likelihood of the observations. We assume there are M hidden states for the Markov process with transition probability matrix $A=\left\{a_{ij}\right\}$. We assume that the Markov process of regime change, ${\mathcal{MC}}_t$, is time-homogeneous, so the transition matrix is time-independent. Also, we assume the probability of initial hidden states to be given by an M-vector $\pi$, with ${\pi }_i$ being the probability of the initial state being i. We assume the observable quantities $Y_t$ can take one of K values. We assume the probability of observing value j while being at hidden state i is given by the $M\times K$ matrix $B=\left\{b_{ij}\right\}$. Given a sequence of observed data Y, the Baum-Welch algorithm finds the optimal ${\theta }^{\ast }=(A,B,\pi )$ that maximizes $P\left(Y\right|\theta )$.

In Zagst et al. (2014), the authors propose a two-step crisis detection algorithm called Turbulent Time Indicator. In tune with this method, we identify the periods of normal and high volatility regimes for the past T-year window using the Baum-Welch algorithm on rolling standard deviations of the S&P500 index and $T=20$ years. On the minority regime corresponding to the high volatility regime data points, we apply another Baum-Welch on the index’s returns to divide the high volatility regime data points into positive and negative return periods. So we get the crisis periods. In other words, the BW algorithm is applied twice because the crisis detection process involves two levels of refinement. First, it identifies normal and high-volatility regime periods using the rolling standard deviations, broadly classifying data into normal market conditions and high-volatility scenarios. Within the high-volatility regime, the algorithm is applied again to distinguish between positive and negative returns periods, as not all high-volatility phases indicate crises in the same way—some may reflect recovery or sharp upward movements. The methodology also provides the transition probabilities for the Markov switching process from the normal interval $I^{normal}$ to the crisis state $I^{crisis}$ and vice versa. This leads to estimates of the parameters: ${\lambda }_0,{\lambda }_1$ and, therefore, p. In Figure 3, the S&P 500 index is rebalanced to start from 100, and the detected crises by the above algorithm are depicted. We observe that the algorithm has successfully labeled the most important black swans in the period, such as in 2008 and the recession after COVID-19 in 2020.

Next, we present an overview of CGMM in our context. Assume ${\left\{Y_t\right\}}_{t\ge 0}$ is a random vector time series of log prices with p parameters and the parameter set $\theta \in {\mathbb{R}}^p$. GMM provides a solution for the estimation problem by considering a finite set of moments of the log prices. Knowing the characteristic function of the vector process, $Y_t$, allows the CGMM to use all the moments for a robust and computationally efficient estimation algorithm.

In the general case of GMM, one aims to optimize using a moment function $h:R^N\to {\mathbb{C}}^l,$. The moment function depends upon a finite number of moments, and for an optimal parameter set $\widehat{\theta }$

$${\mathbb{E}}^{\widehat{\theta }}\left[h\left(Y_t;\widehat{\theta }\right)\right]=0,$$

Given T observations, the empirical mean of the moments function can be written as:

$$f_{obj}\left({\left(y_t\right)}_{t=1}^T;\theta \right)={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}h\left(y_t;\theta \right).$$

A norm for the routine is defined, allowing for an optimal estimate:

$$\widehat{\theta }=arg\; min{∥f_{obj}\left[{\left(y_t\right)}_{t=1}^T;\theta \right]∥}_{\pi }.$$

(49)

To solve the estimation problem using the CGMM, we define the moment function for any given u as

$$h_t\left(u;\theta \right)=h\left(u,Y_t,Y_{t+\tau };\theta \right)\equiv e^{\mathrm{i}<u,Y_{t+\tau }-Y_t>}-\mathbb{E}\left[e^{\mathrm{i}\langle u,Y_{t+\tau }-Y_t\rangle }\mid {\Sigma }_0\right].$$

The CGMM approach’s main advantage is the closed-form expression for the c.f. $\mathbb{E}\left[e^{\mathrm{i}\langle u,Y_{t+\tau }-Y_t\rangle }\mid {\Sigma }_0\right]$. Another advantage compared to its finite counterpart, GMM, is that the weighting matrix becomes singular for the latter as the number of moments increases. This issue is completely addressed by CGMM, where the characteristic function is used directly.

For the extension of the objective function to a continuum, we assume a probability measure with density function $\pi :{\mathbb{R}}^N\to \mathbb{R}$ is given, and define a norm on the moment function as follows

$${∥f_{obj}\left(u,{\left(y_t\right)}_{t=1}^T;\theta \right)∥}_{\pi }={\int }_{{\mathbb{R}}^N}{f}_{obj}\left(u,{\left(y_t\right)}_{t=1}^T;\theta \right).\overline{f_{obj}\left(u,{\left(y_t\right)}_{t=1}^T;\theta \right)}\pi \left(u\right)du$$

Carrasco and Florens (2000) provides the following solution for the CGMM estimator

Proposition 7.

The solution to the optimization problem (49) is equivalent to

$$\theta =\underset{\theta }{arg\; min}{\overline{\omega }}^T\left(\theta \right){\left({\alpha }_T+C^2\right)}^{-1}\overline{\nu }\left(\theta \right),$$

where

$$\begin{array}{ccc}\hfill {\nu }_t\left(\theta \right)& =& {\int }_{{\mathbb{R}}^n}U{h}_t\left(u;{\widehat{\theta }}_T^1\right){\widehat{h}}_t\left(u;\theta \right)\pi \left(u\right)du,\hfill \\ \hfill {\omega }_t\left(\theta \right)& =& 〈h_t\left(u;{\widehat{\theta }}_T^1\right){\widehat{h}}_T\left(u;\theta \right)〉.\hfill \end{array}$$

The matrix C is given by

$$\begin{array}{ccc}\hfill C& =& {\left({\displaystyle \frac{C_{tl}}{T-p}}\right)}_{T\times T}\hfill \\ \hfill C_{tl}& =& {\int }_{{\mathbb{R}}^n}U{h}_t\left(u;{\widehat{\theta }}_T^1\right)h_l\left(u;{\widehat{\theta }}_T^1\right)\pi \left(u\right)du,\hfill \end{array}$$

with

$$\begin{array}{ccc}\hfill U{h}_t\left(u;{\widehat{\theta }}_T^1\right)& =& \varphi \left(0\right){\overline{h}}_t\left(u;{\widehat{\theta }}_T^1\right)\hfill \\ & +& \sum _{j=1}^T\varphi \left({\displaystyle \frac{\left(\frac{T-1}{2}\right)+j}{B_T^{\ast }}}\right)\left({\overline{h}}_{t-j}\left(u;{\widehat{\theta }}_T^1\right)+{\overline{h}}_{t+j}\left(u;{\widehat{\theta }}_T^1\right)\right).\hfill \end{array}$$

In Proposition 7, we use the evaluation interval $[-3,+3]$, with the bandwidth $B_T^{\ast }=-{\displaystyle \frac{T+1}{6}}$ and the penalized parameter ${\alpha }_T=2\%$.

3.2. Parameter Estimates

We complete the estimation process by calculating the final output parameters: the transition probability between normal and crisis periods, p and q, the shift matrix, $\widehat{\Sigma }$, and the Wishart SDE parameters, $\beta$, Q and M.

The results of estimating the MMSW process on S&P500 vs. AAPL and GOOG vs. INTC are presented in

Table 1. Estimates for the parameters of the MMSW model for the pair of S&P500–AAPL and GOOG–INTC with ${\Sigma }_0^{WI}={\Sigma }_{\infty }^{WI}$.

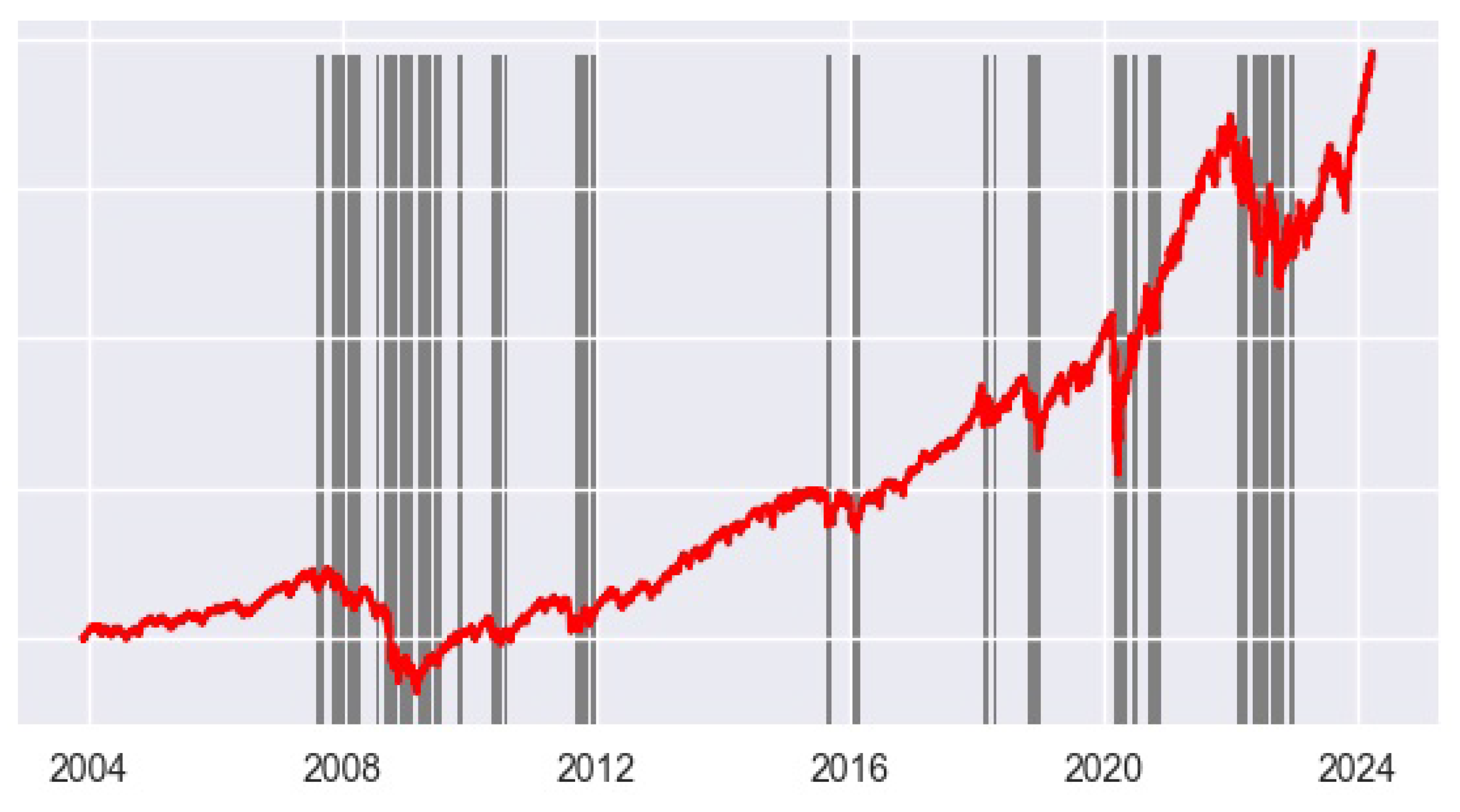
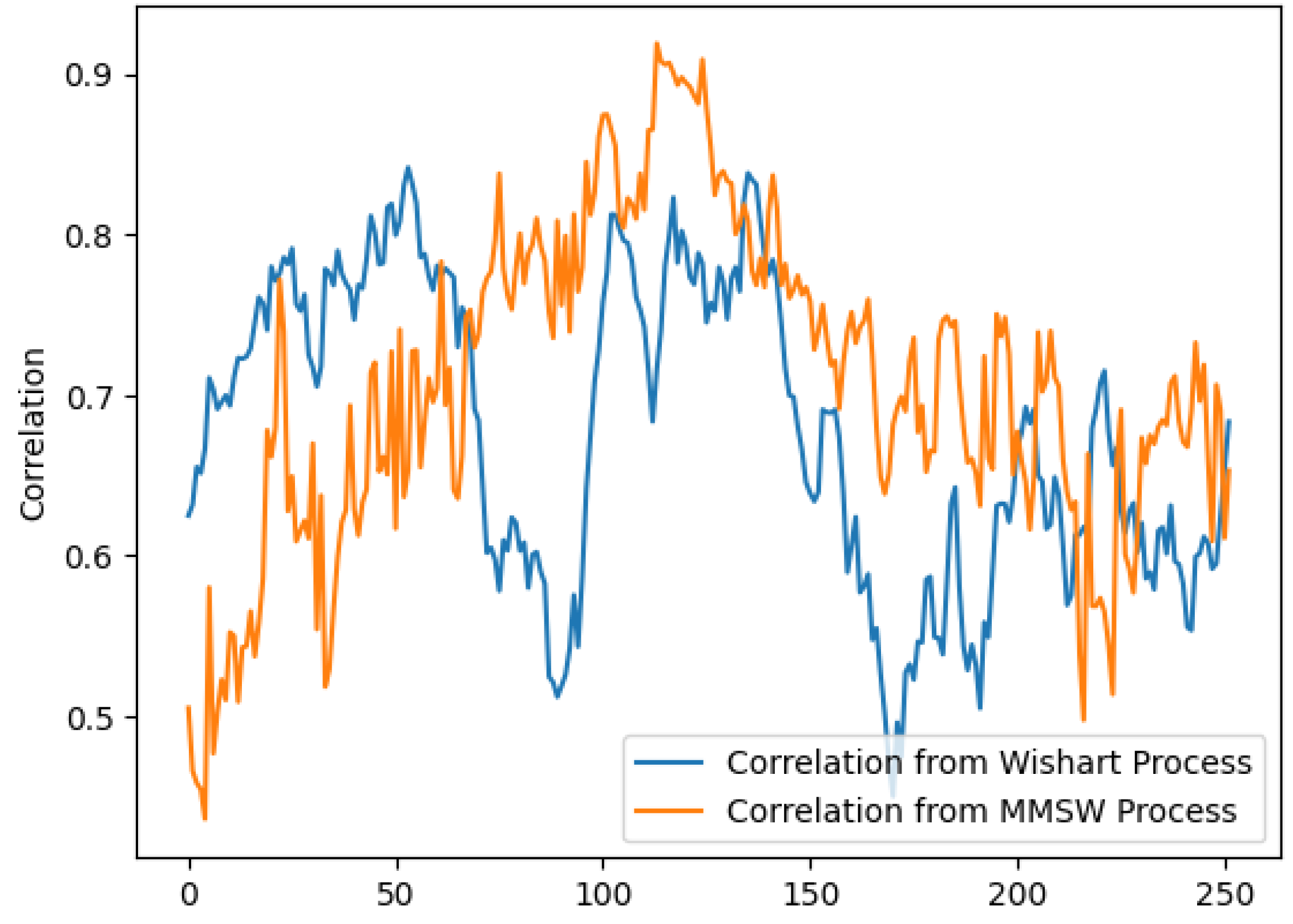
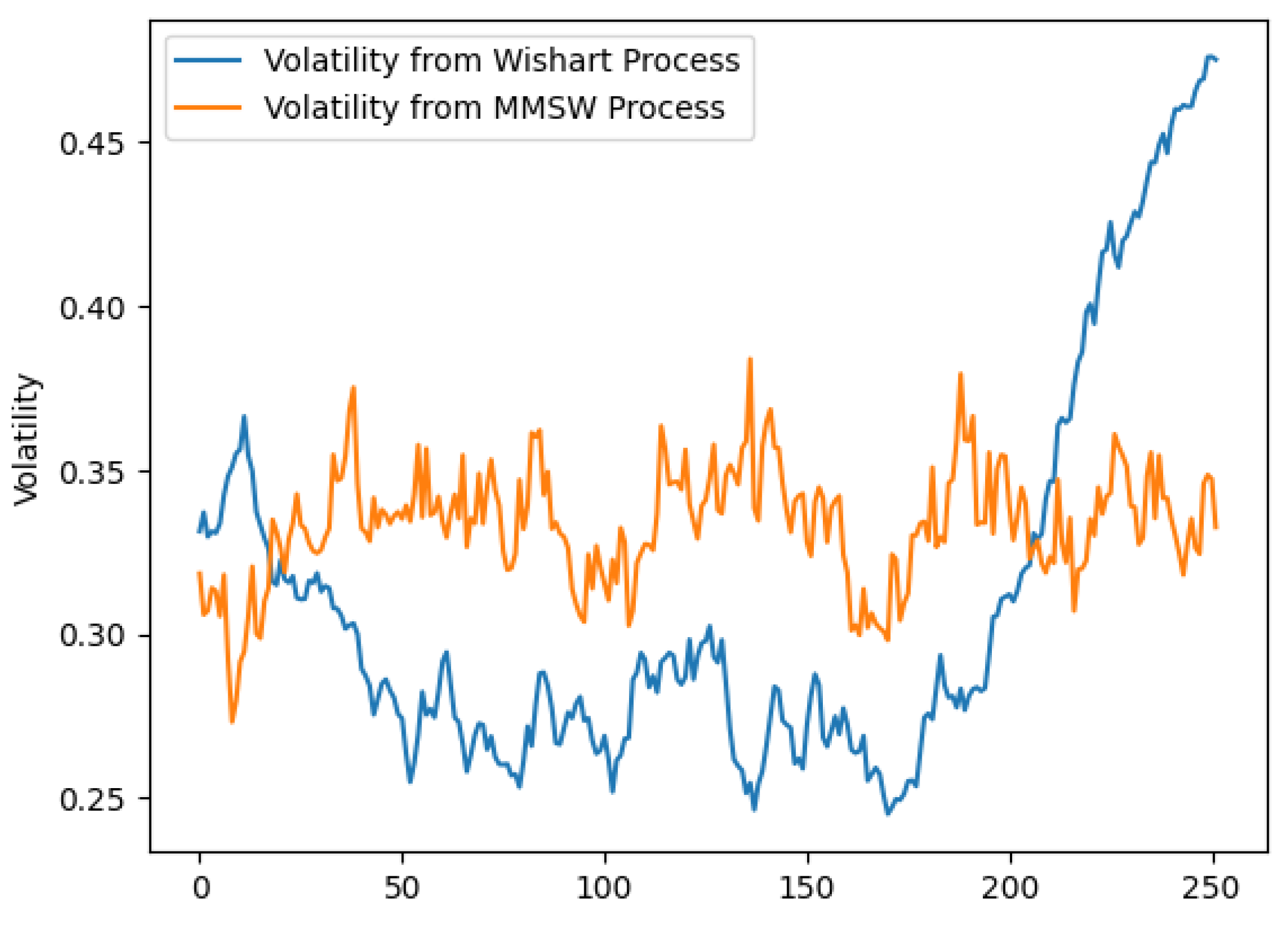
Parameters		Wishart		MMSW		Wishart		MMSW
		S&P500–AAPL		S&P500–AAPL		GOOG–INTC		GOOG–INTC
$M_{11}$	$M_{12}$	−1.003	0.202	−1.020	0.142	−0.999	−0.443	−1	−0.839
$M_{21}$	$M_{22}$	1.559	−1	1.360	−0.822	1.444	−1	1.722	−1
$Q_{11}$	$Q_{12}$	0.077	0	0.069	0	0.149	0	0.152	0
$Q_{21}$	$Q_{22}$	−0.020	0.011	−0.018	0.013	0	0.099	0	0.092
$\beta$		9.732		7.550		9.911		9.935
${\rho }_1$		−0.505		−0.550		−0.386		−0.408
${\rho }_2$		−0.217		−0.193		−0.187		−0.127
${\sigma }_{11,\infty }^{WI}$	${\sigma }_{12,\infty }^{WI}$	0.037	0.040	0.021	0.023	0.092	0.042	0.087	0.033
(${\rho }_{12,\infty }^{WI}$)	${\sigma }_{22,\infty }^{WI}$	(0.627)	0.110	(0.499)	0.101	(0.419)	0.109	(0.355)	0.099
${\widehat{\sigma }}_{11}$	${\widehat{\sigma }}_{12}$			0.021	0.021			0.007	0.012
${\widehat{\sigma }}_{21}$	${\widehat{\sigma }}_{22}$			0.021	0.012			0.012	0.015
${\sigma }_{11,\infty }^{MW}$	${\sigma }_{12,\infty }^{MW}$			0.041	0.045			0.094	0.045
$\left({\rho }_{\infty }^{MW}\right)$	${\sigma }_{22,\infty }^{MW}$			(0.661)	0.113			(0.434)	0.114
p	${\lambda }_0$			0.779	1.066			0.745	44.003
	${\lambda }_1$				3.765				128.68
	${\lambda }_0$ s.e.				0.009				0.008
	${\lambda }_1$ s.e.				0.025				0.122

. In this table, the 2nd and 4th columns represent the parameters of the Wishart, and the 3rd and 5th columns capture the MMSW and the embedded Wishart. Note that the table separately conveys the parameters of the stand-alone Wishart model (columns 2 and 4) and the parameters of the MMSW model (columns 3 and 5). While reporting the parameters of the MMSW, we report the parameters of the underlying Wishart process.

We use this table to compare the Wishart and MMSW models in Section 4. We do not report estimates for the SW model; this will be conducted in future endeavors as it involves extracting minimum values for volatilities and possibly correlations. In the table, we highlight that the parameters of the Markov modulation, ${\lambda }_0,{\lambda }_1$, are non-zero with a confidence level of 99%, which validates the necessity of our Markov-modulated shifted Wishart process model to capture the stylized facts of the historical data.

As mentioned before, we have used 20 years of daily data, from 2004 to 2024, for both pairs, the S&P500 index and Apple’s stock price, as well as the pair Google and Intel stocks. We divided the total data into a normal and a turbulent regime with 3855 and 1116 data points, respectively, using a Hidden Markov Model applied to the returns of the S&P500 index (Figure 3).

Figure 4 and Figure 5 show the behavior of the Wishart and MMSW processes based on a simulation with parameters from Table 1. We used the Euler-Maruyama method to generate samples of covariance matrices from the estimated parameters, and from the covariance matrices, we computed samples of correlations and volatilities. Note that this behavior is similar to that of the Wishart process with the constant shift from Section 2.2; the difference lies in the random time of the shift and the random time for a correction.

As we notice in Figure 4, the correlations of the Markov-modulated Shifted Wishart process shift from normal to turbulent levels and vice versa according to the Markov change process of the market’s regime. We observe the same phenomenon in the simulation of volatility in Figure 5. The volatility of the MMSW process transits between normal and crisis levels with probability p.

In this paper, we used a fixed window of 20 years of daily data to estimate parameters to produce more reliable estimates, i.e., smaller standard errors. However, for applications including backtesting of option pricing or portfolio optimization, one might consider a rolling or increasing window for the estimation of parameters for a more realistic implementation.

4. Results and Discussion on Derivative Pricing

In this section, we compute option pricing using the closed formulas for characteristic functions of the log prices and the covariance processes provided in the previous section. We used the methodology in Carr and Madan (1999) and Hurd and Zhou (2010), which can be used for pricing basket options in two or higher dimensions under any framework where the characteristic function of the joint return processes is analytically tractable.

Our objective is to show the impact of our model on a two-dimensional spread option with two assets, $S_1$ and $S_2$. The price of the spread option with strike K and time to maturity $T-t$ at time t is

$$V\left(t\right)=e^{-r(T-t)}{\mathbb{E}}^{\mathbb{Q}}\left[{\left(S_{1,t}-S_{2,t}-K\right)}^{+}\right].$$

(50)

The section is divided into a description of the Fast Fourier transform approach to pricing, the actual results compared to Monte Carlo, and an analysis of the impact of parameters on price differences from the three models, i.e., Wishart, SW, and MMSW.

4.1. Fast Fourier Approach

Here, we describe the Fourier transform methodology for the product at hand. The price of this basket option can be computed by transforming the problem from the pricing domain to the frequency domain, as the characteristic function of the joint return process has a closed form. The same method of Carr and Madan (1999) and Hurd and Zhou (2010) can be applied to price spread options within the framework of the Markov-modulated stochastic covariance model (25). For the sake of completeness, we present the proof in the Appendix A.

Proposition 8.

The price of a spread option with risk-neutral valuation (50) under stochastic covariance model (25) is given by

$$V\left(t\right)={\displaystyle \frac{e^{-r(T-t)}}{4{\pi }^2}}{\int \int }_{{\mathbb{R}}^2+iϵ}\Phi (\tau ,u,y,e_i,{\sigma }^{WI}){\widehat{P}}_K\left(u\right)du,$$

(51)

where $\Phi (\tau ,u,y,e_i,{\sigma }^{WI})$ is the characteristic function of the log-price process defined by (38) with $\mu ={[r,r]}^T$ and

$${\widehat{P}}_K\left(u\right)=K^{1-i(u_1+u_2)}{\displaystyle \frac{\Gamma (i(u_1+u_2)-1)\Gamma (-i{u}_2)}{\Gamma (i{u}_1+1)}},$$

(52)

where the complex gamma $\Gamma \left(z\right)$ function is defined by

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-t}{t}^{z-1}dt,forRe\left(z\right)>0,$$

(53)

and $ϵ=({ϵ}_1,{ϵ}_2)$ where ${ϵ}_2>0$ and ${ϵ}_1+{ϵ}_2<-1$.

Proof. 

See Appendix A.4. □

The corresponding pricing function for the spread option is defined as $P_K(y_1,y_2)={(e^{y_2}-e^{y_1}-K)}^{+}$ and relates to $\widehat{P}$ by

$$P_K\left(y\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int \int }_{{\mathbb{R}}^2+iϵ}exp\{\mathrm{i}<u,y>\}{\widehat{P}}_K\left(u\right)du.$$

(54)

To implement Proposition 8, separate packages in MATLAB (2024a) and Python (3.10.9), and open-source libraries are available to estimate the gamma and regularized beta functions. We note that Equation (51) is a generalization of Hurd and Zhou (2010), Theorem 1, for any positive strike price K.

4.2. Models vs. Monte Carlo Simulation

Our model is flexible enough to allow for stochastic behavior of the correlation process and a dependent structure on the market environment that differentiates normal periods from turbulent periods. In this section, we report the prices of the MMSW, the embedded Wishart model, and the shifted Wishart model, all comparing our formulas with Monte Carlo simulations.

Table 2. One-year basket option price for three basket options on S&P500 and AAPL.

Option	K	Source of Price	Wishart	Shifted W.	MMSW
		Formula	0.7454	0.7470	0.7617
In The Money	0.5	Monte Carlo	0.7487	0.7368	0.7470
		MC 95% lower bound	0.7288	0.7168	0.7269
		MC 95% upper bound	0.7686	0.7568	0.7671
		Formula	0.4339	0.4357	0.4498
At The Money	1	Monte Carlo	0.4369	0.4309	0.4390
		MC 95% lower bound	0.4212	0.4151	0.4231
		MC 95% upper bound	0.4526	0.4466	0.4549
		Formula	0.2124	0.2140	0.2236
Out of The Money	1.5	Monte Carlo	0.2142	0.2127	0.2184
		MC 95% lower bound	0.2031	0.2016	0.2072
		MC 95% upper bound	0.2253	0.2239	0.2297

shows the price of three Basket options on the pair of S&P500 and AAPL for all three processes. To confirm that the prices proposed by the formula (8) are correct, we have also provided the prices implied by the Monte Carlo simulation at a 95% confidence interval.

We implemented the c.f. of the SW process using Proposition 2, and the parameters of the Wishart process in Table 1 with rather small size of the shift matrix computed according to Equation (6), where we have assumed ${\widehat{\Sigma }}^{SW}$ be equal to the annualized historical covariance.

For the c.f. of MMSW, we implemented Proposition 4 with Table 1 as well, and for the Wishart process, we used the same proposition with $\widehat{\Sigma }=0$. As for the Monte Carlo simulation of the covariance matrices, we used Equation (4). We simulated the SW covariances by adding $\widehat{\Sigma }$ to the Wishart covariances. Then, for the simulation of the MMSW, we considered a two-state Markov process with probability p and added its corresponding $\widehat{\Sigma }$ from Table 1 only for the cases that the Markov process is 1, i.e., turbulent regime. For the simulation of the price process, we used Equation (25). To validate the c.f.s of the three processes, we compared their value from formulas and the expectation definition for different values of u. The same method was used to validate the basket option pricing formula by the Monte Carlo simulation of three price processes and the payoff of the spread option.

We set the initial price $P_0=[5,4]$. To compute the integral (51), as the support of $\widehat{P}$ is mostly in the interval $[-4,4]$, we have chosen the integration interval $[-20,20]$. Also, we have chosen $ϵ=({ϵ}_1,{ϵ}_2)=(-3,1)$ which satisfies the condition in Proposition 8.

To implement the MMSW process, we estimated the parameters of the annual generator matrix ${\lambda }_0$ and ${\lambda }_1$ for $t=1/252$ using the daily transition matrix from the Hidden Markov Model applied to the daily price of S&P500 returns and Equation (31). Then, using ${\lambda }_0$ and ${\lambda }_1$, we computed parameters of the Markov-modulated model: probability of the initial state p, and transition probabilities ${\lambda }_{01}$ and ${\lambda }_{10}$ as explained in the same section. For the Monte Carlo simulation of the MMSW process, we generated 5000 paths of covariance matrices according to the Wishart Process and the same number of paths for Markov-Modulated regime change with the same parameters p, ${\lambda }_{01}$, and ${\lambda }_{10}$. Then, we used the stochastic differential Equation (25) and the Euler-Maruyama method to generate paths of prices with $dt=1/252$ for the MMSW process.

Table 2 confirms the accuracy of our formulas as the computed values lie on the narrow $95\%$ confidence intervals produced by MC.

Table 3. One-year basket option price for three basket options on GOOG and INTC.

Option	K	Source of Price	Wishart	Shifted W.	MMSW
		Formula	0.9030	0.9052	0.9093
In The Money	0.5	Monte Carlo	0.8895	0.9010	0.9263
		MC 95% lower bound	0.8594	0.8701	0.8957
		MC 95% upper bound	0.9195	0.9318	0.9569
		Formula	0.6275	0.6298	0.6339
At The Money	1	Monte Carlo	0.6129	0.6268	0.6472
		MC 95% lower bound	0.5870	0.6001	0.6208
		MC 95% upper bound	0.6388	0.6535	0.6736
		Formula	0.4158	0.4182	0.4214
Out of The Money	1.5	Monte Carlo	0.4022	0.4160	0.4308
		MC 95% lower bound	0.3807	0.3936	0.4088
		MC 95% upper bound	0.4237	0.4384	0.4527

shows the same study for the pair of GOOG-INTC.

4.3. Comparison of Models

In this section, the price of Spread options under the Wishart process and the Markov-modulated shifted Wishart process are reported for various strike prices and maturities for two pairs of asset prices: S&P500-AAPL and GOOG-INTC. For both pairs of data samples, we have used the parameters of the new model, MMSW, from Table 1 and the Wishart process from the same table.

This analysis generates two 3D surfaces of prices for Wishart and Markov-modulated shifted Wishart processes for each pair of assets. In Figure 6, we report the percentage difference between the Spread option price under Wishart and MMSW models for various strike prices and maturities.

We realize from Figure 6 that around $K=1$, which refers to the at-the-money options, the price suggested by the Wishart process is higher than the ones proposed by the MMSW model. Percentage-wise, the difference could be up to 7% in the S&P500-AAPL pair, with 2% in the GOOG-INTC pair.7

To provide more details, the graph in Figure 7 shows the Spread option prices under the three models, Wishart shifted Wishart, and MMSW, all implemented from the parameters of Table 1. For the SW model, we take the parameters of the Wishart process in Table 1.

All six graphs show the expected pattern of spread option price decreasing in the strike price K and increasing maturity time T. Although the two sets of graphs are generated for the same initial price $P_0=(5,4)$, we observe that under each process, the prices of the Spread options of the pair of GOOG-INTC are higher than the prices for the pair of S&P500-AAPL. This is due to the estimated parameters of the models for each pair.

Figure 8 shows the percentage difference between Spread option prices from different models. As we observe in the Wishart versus MMSW graphs, the absolute difference decreases with maturity time, and it could be substantial, up to $7\%$ for the S&P500-AAPL pair when comparing W and MMSW. The difference in the shifted Wishart vs. MMSW graphs decreases with time maturity but increases as K approaches 1, making the option at the money. We realize the same pattern for the absolute difference of Wishart vs. shifted Wishart models.

5. Conclusions and Future Research

We studied two extensions of the Wishart process by shifting the original stochastic process by a constant matrix and a Markov-modulated matrix, respectively. These modifications address two separate limitations of the Wishart Stochastic Covariance process: It is not designed to capture the effect of the crisis on correlation and variance processes, or a non-zero lower bound for variances. So we benefited from stochastic covariance modeling of the Wishart process together with a regime-dependent shift to capture the stylized fact of higher variances and correlations during crises.

For the two new models, we obtained closed-form solutions for the c.f.s of all the underlying interest, e.g., joint log prices, covariance, and integrated covariance. These functions were validated via Monte Carlo. We also estimated the MMSW and the Wishart (not the SW) to two pairs of asset prices by a method based on the Baum-Welch algorithm and CGMM method. We used the Fast Fourier Transform to get a closed-form solution for the price of a basket option via characteristic functions. We used these estimates and formulas to compare the models’ implied Spread option prices.

We found that accounting for the crisis periods. Therefore, a whole shift in the covariance matrix can lead to a difference of up to $7\%$ in spread option prices when the Wishart and MMSW models are calibrated to the same data.

Many areas of future work are viable in the context of our models or their extensions. For instance, we could use the models developed in this paper for portfolio applications such as expected utility or mean-variance optimization. Important extensions of the model must also be considered, such as switching between Wishart covariances or a Wishart and a simpler principal component Heston model; choices of the market price of risk or excess return shall also be explored.