Dynamics of Green and Conventional Bonds: Hedging Effectiveness and Sustainability Implication
Abstract
1. Introduction
2. Literature Review
2.1. The Essence and Principles of Issuing Green Bonds
2.2. The Greenium: Price Difference Between Conventional and Green Bonds
2.3. Identification of Pricing Factors and Market Dynamics of Green Bonds
2.4. Benefits and Risks of Green Bond Issuance for Issuers and Investors
3. Data
4. Research Design
4.1. Modeling Time-Varying Connectedness Using TVP-VAR
Structural Stability of TVP-VAR Residuals: CUSUM Test Analysis
4.2. Dynamic Portfolio Management Strategies
4.2.1. Minimum Variance Approach
4.2.2. Minimum Correlation Approach
4.2.3. Minimum Connectedness Approach
4.2.4. Risk Parity Approach
4.3. Portfolio Back Testing: Hedging Effectiveness
4.3.1. Sharpe Ratio and Hedging Effectiveness
4.3.2. Tail Risk Evaluation Using Expected Shortfall (CVaR)
5. Empirical Results
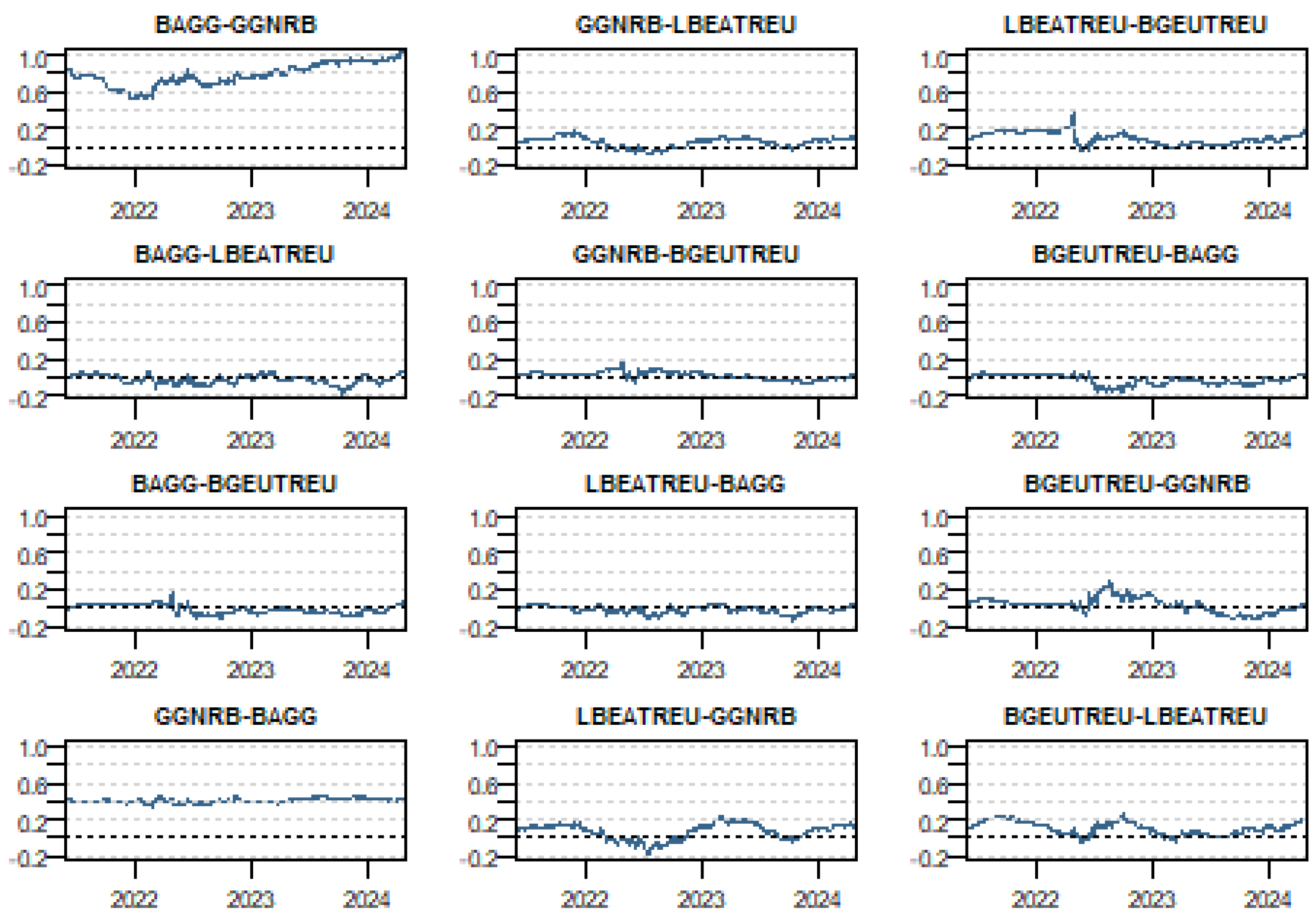
5.1. Dynamic Connectedness
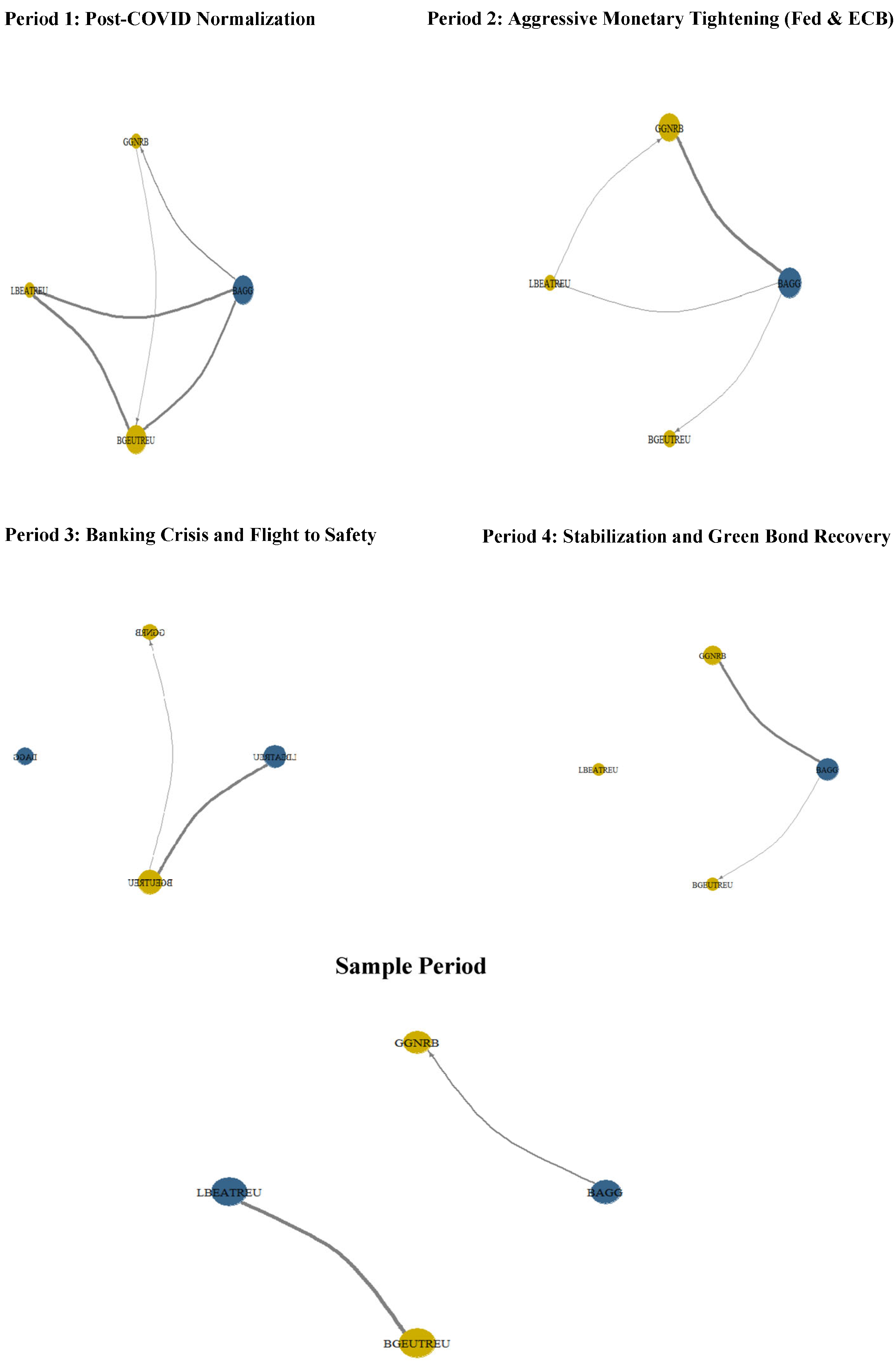
5.2. Network Centrality Analysis
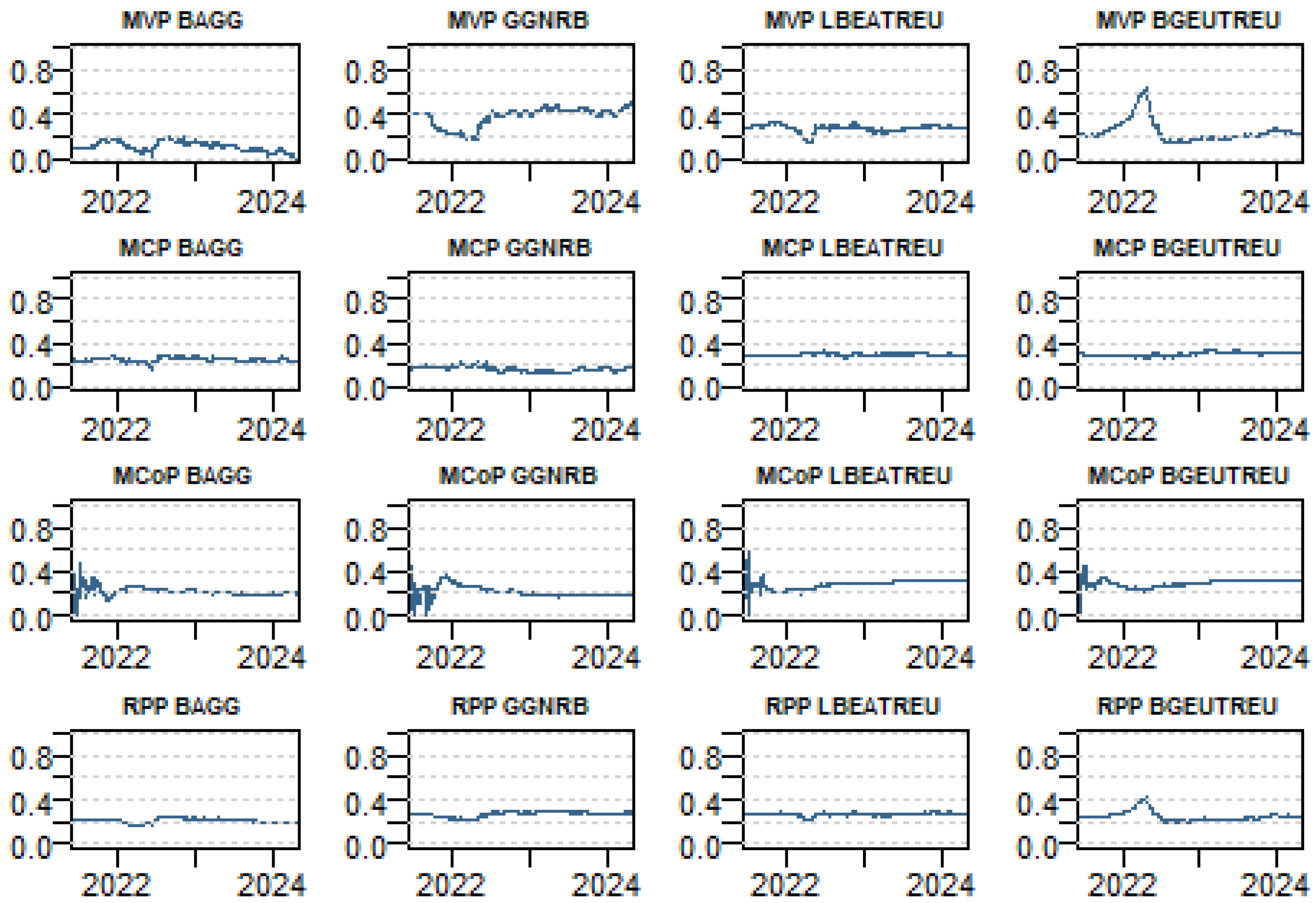
5.3. Dynamic Portfolio
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abuzayed, B., & Al-Fayoumi, N. (2023). Diversification and hedging strategies of green bonds in financial asset portfolios during the COVID-19 pandemic. Applied Economics, 55(36), 4228–4238. [Google Scholar] [CrossRef]
- Antonakakis, N., Chatziantoniou, I., & Gabauer, D. (2020). Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. Journal of Risk and Financial Management, 13(4), 84. [Google Scholar] [CrossRef]
- Antonakakis, N., Chatziantoniou, I., & Gabauer, D. (2021). The impact of Euro through time: Exchange rate dynamics under different regimes. International Journal of Finance & Economics, 26(4), 5176–5194. [Google Scholar]
- Arat, E., Hachenberg, B., Kiesel, F., & Schiereck, D. (2023). Greenium, credit rating, and the COVID-19 pandemic. Journal of Asset Management, 24, 547–557. [Google Scholar] [CrossRef]
- Aynur, A., David, C. B., Xiaoqi, C., & Dong, W. (2019). Time-varying parameter energy demand functions: Benchmarking state-space methods against rolling-regressions. Energy Economics, 82, 26–41. [Google Scholar]
- Bachelet, M. J., Becchetti, L., & Manfredonia, S. (2019). The green bonds premium puzzle: The role of issuer characteristics and third-party verification. Sustainability, 11(4), 1098. [Google Scholar] [CrossRef]
- Bekaert, G., Ehrmann, M., Fratzscher, M., & Mehl, A. (2014). The global crisis and equity market contagion. The Journal of Finance, 69(6), 2597–2649. [Google Scholar] [CrossRef]
- Bouri, E., Jain, A., Roubaud, D., & Kristoufek, L. (2021). Cryptocurrency market contagion during the COVID-19 crisis. Finance Research Letters, 38, 101620. [Google Scholar]
- Broadstock, D. C., Chatziantoniou, I., & Gabauer, D. (2022). Minimum connectedness portfolios and the market for green bonds: Advocating socially responsible investment (SRI) activity. In C. Floros, & I. Chatziantoniou (Eds.), Applications in energy finance (pp. 217–253). Springer. [Google Scholar]
- Brown, R. L., Durbin, J., & Evans, J. M. (1975). Techniques for testing the constancy of regression relationships over time. Journal of the Royal Statistical Society. Series B (Methodological), 37, 149–192. [Google Scholar] [CrossRef]
- Christoffersen, P., Errunza, V., Jacobs, K., & Jin, X. (2014). Correlation dynamics and international diversification benefits. International Journal of Forecasting, 30(3), 807–824. [Google Scholar] [CrossRef]
- Contractor, D., Balli, F., & Hoxha, I. (2023). Market reaction to macroeconomic announcements: Green vs. conventional bonds. Applied Economics, 55(15), 1637–1662. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2009). Measuring financial asset return and volatility spillovers, with application to global equity markets. Economic Journal, 119(534), 158–171. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting, 28(1), 57–66. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yılmaz, K. (2014). On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics, 182(1), 119–134. [Google Scholar] [CrossRef]
- Ederington, L. H. (1979). The hedging performance of the new futures markets. The Journal of Finance, 34(1), 157–170. [Google Scholar] [CrossRef]
- Ejaz, R., Ashraf, S., Hassan, A., & Gupta, A. (2022). An empirical investigation of market risk, dependence structure, and portfolio management between green bonds and international financial markets. Journal of Cleaner Production, 365, 132666. [Google Scholar] [CrossRef]
- Flammer, C. (2021). Corporate green bonds. Journal of Financial Economics, 142(2), 499–516. [Google Scholar] [CrossRef]
- Guo, D., & Zhou, P. (2021). Green bonds as hedging assets before and after COVID: A comparative study between the US and China. Energy Economics, 104, 105696. [Google Scholar] [CrossRef]
- Han, Y., & Li, J. (2022). Should investors include green bonds in their portfolios? Evidence for the USA and Europe. International Review of Financial Analysis, 80, 101998. [Google Scholar] [CrossRef]
- Huynh, T. L. D. (2022). When ‘green’ challenges ‘prime’: Empirical evidence from government bond markets. Journal of Sustainable Finance and Investment, 12(3), 375–388. [Google Scholar] [CrossRef]
- Imran, Z. A., & Ahad, M. (2023). Safe-haven properties of green bonds for industrial sectors (GICS) in the United States: Evidence from the COVID-19 pandemic and Global Financial Crisis. Renewable Energy, 210, 408–423. [Google Scholar] [CrossRef]
- Karpf, A., & Mandel, A. (2018). The changing value of the ‘green’ label on the US municipal bond market. Nature Climate Change, 8(2), 161–165. [Google Scholar] [CrossRef]
- Kenourgios, D., Samitas, A., & Paltalidis, N. (2011). Financial crises and stock market contagion in emerging markets. International Review of Economics & Finance, 20(3), 528–541. [Google Scholar]
- Khamis, M., & Aassouli, D. (2023). The eligibility of green bonds as safe haven assets: A systematic review. Sustainability, 15(8), 6841. [Google Scholar] [CrossRef]
- Khan, S. A. R., Sharif, A., Golpîra, H., & Kumar, A. (2019). A green ideology in Asian emerging economies: From environmental policy and sustainable development. Sustainable Development, 27, 1063–1075. [Google Scholar] [CrossRef]
- Lichtenberger, A., Braga, J. P., & Semmler, W. (2022). Green bonds for the transition to a low-carbon economy. Econometrics, 10(1), 11. [Google Scholar] [CrossRef]
- Maillard, S., Roncalli, T., & Teïletche, J. (2010). The properties of equally weighted risk contributions portfolios. The Journal of Portfolio Management, 36(4), 60–70. [Google Scholar] [CrossRef]
- Man, Y., Zhang, S., & Liu, J. (2023). Dynamic connectedness, asymmetric risk spillovers, and hedging performance of China’s green bonds. Finance Research Letters, 56, 103295. [Google Scholar] [CrossRef]
- Markowitz, H. M. (1959). Portfolio selection: Efficient diversification of investments. Yale University Press. [Google Scholar]
- Mensi, W., Selmi, R., Al-Kharusi, S., Belghouthi, H. E., & Kang, S. H. (2024). Connectedness between green bonds, conventional bonds, oil, heating oil, natural gas, and petrol: New evidence during bear and bull market scenarios. Resources Policy, 91, 104888. [Google Scholar] [CrossRef]
- Mohammed, K. S., Bouri, E., Hunjra, A. I., & Yan, Y. (2024). The heterogeneous reaction of green and conventional bonds to exogenous shocks and the hedging implications. Journal of Environmental Management, 364, 121423. [Google Scholar] [CrossRef]
- Naeem, M. A., Farid, S., Ferrer, R., & Shahzad, S. J. H. (2021). Comparative efficiency of green and conventional bonds pre-and during COVID-19: An asymmetric multifractal detrended fluctuation analysis. Energy Policy, 153, 112285. [Google Scholar] [CrossRef]
- Naeem, M. A., Karim, S., & Tiwari, A. K. (2023). Risk connectedness between green and conventional assets with portfolio implications. Computational Economics, 62(4), 609–637. [Google Scholar] [CrossRef] [PubMed]
- Peng, G., Ding, J., Zhou, Z., & Zhu, L. (2023). Measurement of spillover effect between green bond market and traditional bond market in China. Green Finance, 5(4), 538–561. [Google Scholar] [CrossRef]
- Primiceri, G. E. (2005). Time varying structural vector autoregressions and monetary policy. The Review of Economic Studies, 72(3), 821–852. [Google Scholar] [CrossRef]
- Reboredo, J. C., & Ugolini, A. (2020). Price connectedness between green bond and financial markets. Economic Modelling, 88, 25–38. [Google Scholar] [CrossRef]
- Sharpe, W. F. (1966). Mutual fund performance. The Journal of Business, 39(1), 119–138. [Google Scholar] [CrossRef]
- Tsoukala, A., & Tsiotas, G. (2021). Assessing green bond risk: An empirical investigation. Green Finance, 3(2), 222–252. [Google Scholar] [CrossRef]
- Wang, M.-C., Jiang, P., & Chang, T. (2024). Re-examining China and the U.S.’s respective green bond markets in extreme conditions: Evidence from quantile connectedness. North American Journal of Economics and Finance, 75, 102286. [Google Scholar] [CrossRef]
- Xu, D., Hu, Y., Corbet, S., & Lang, C. (2024). Return connectedness of green bonds and financial investment channels in China: Implications for hedging and regulation. Research in International Business and Finance, 70, 102329. [Google Scholar] [CrossRef]
- Yousfi, M., & Bouzgarrou, H. (2024). Exploring interconnections and risk evaluation of green equities and bonds: Fresh perspectives from TVP-VAR model and wavelet-based VaR analysis. China Finance Review International, 15(1), 117–139. [Google Scholar] [CrossRef]
- Zerbib, O. D. (2019). The effect of pro-environmental preferences on bond prices: Evidence from green bonds. Journal of Banking & Finance, 98, 39–60. [Google Scholar]
- Zhao, M., & Park, H. (2024). Quantile time-frequency spillovers among green bonds, cryptocurrencies, and conventional financial markets. International Review of Financial Analysis, 93, 103198. [Google Scholar] [CrossRef]
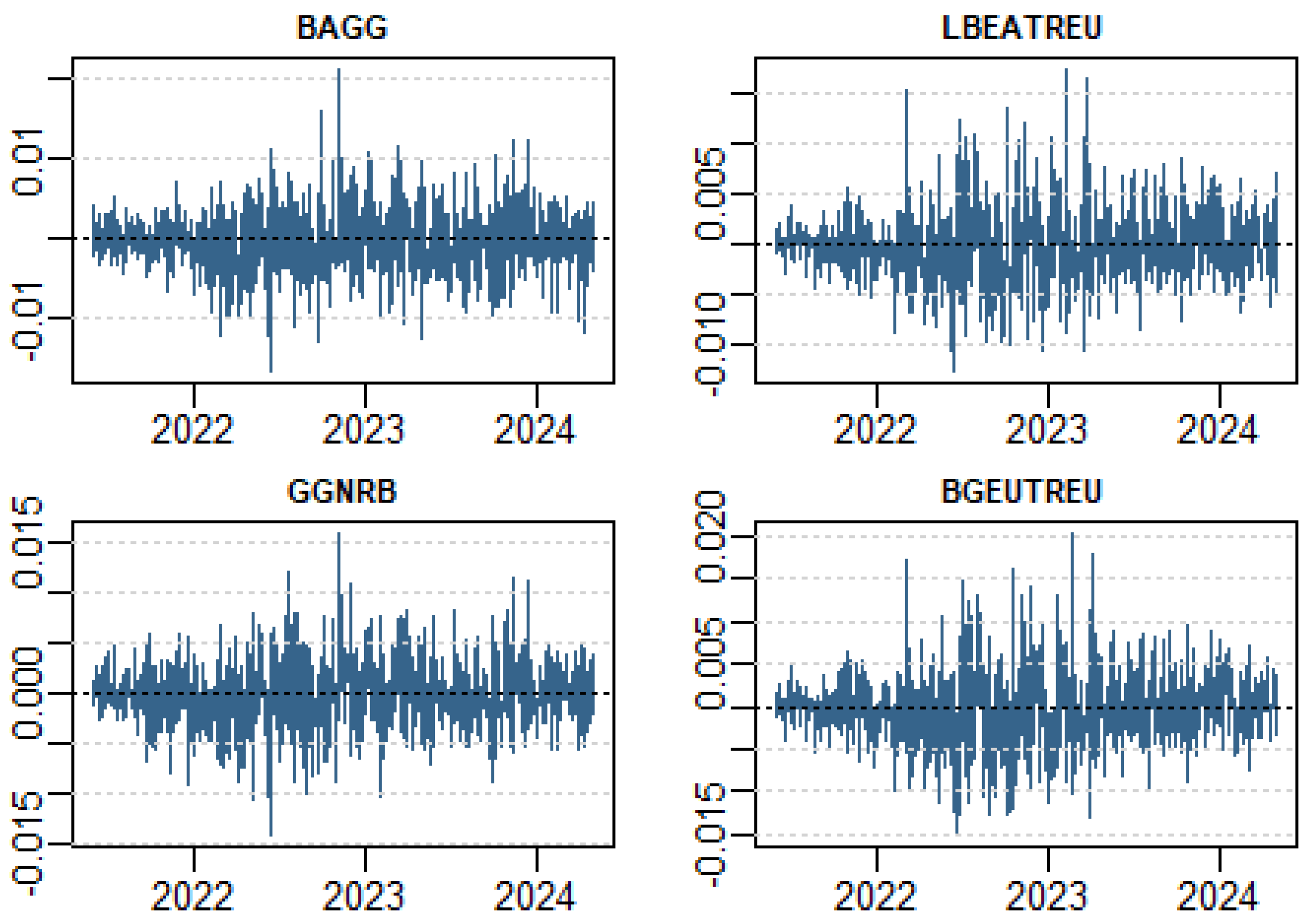
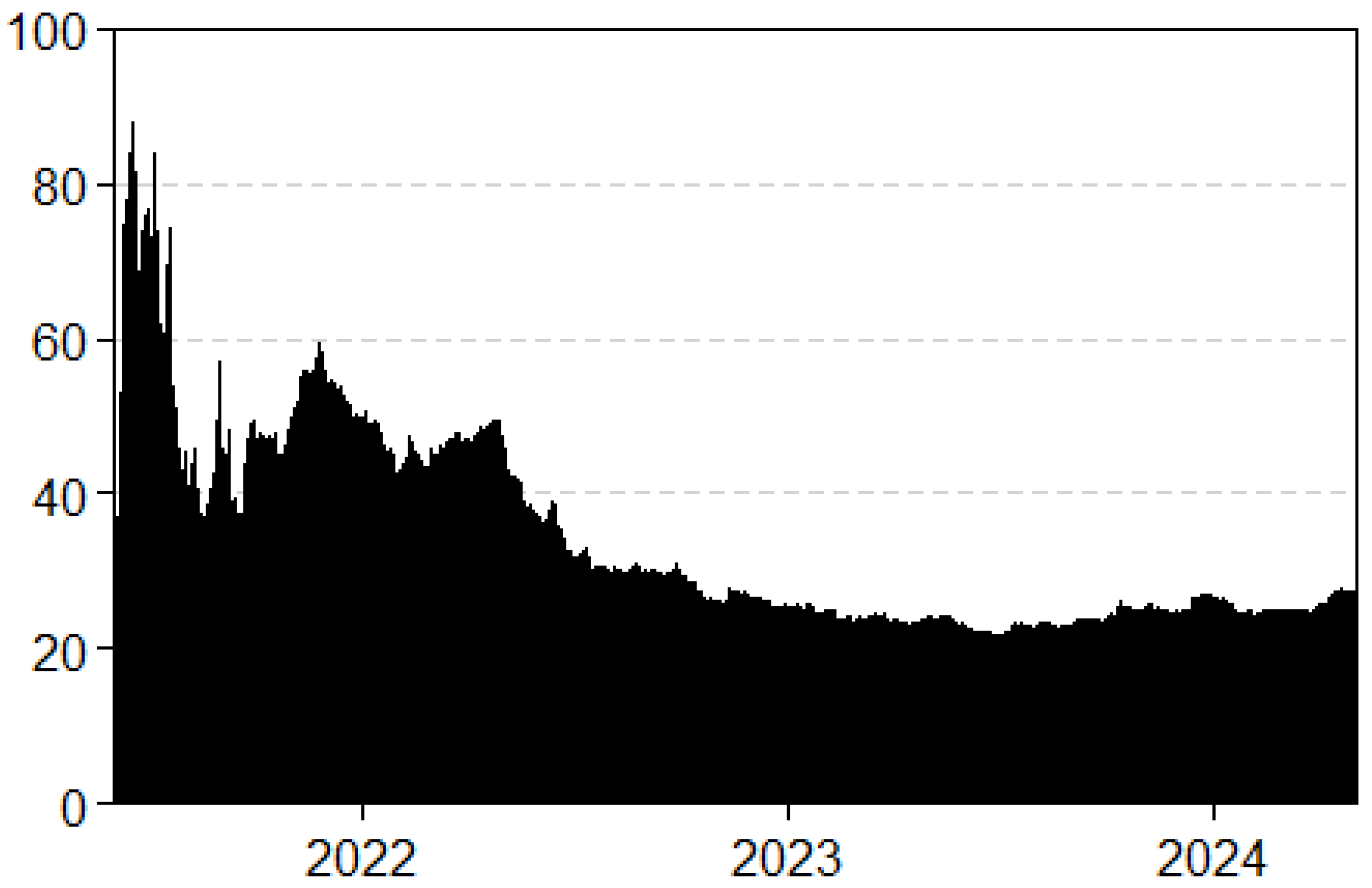
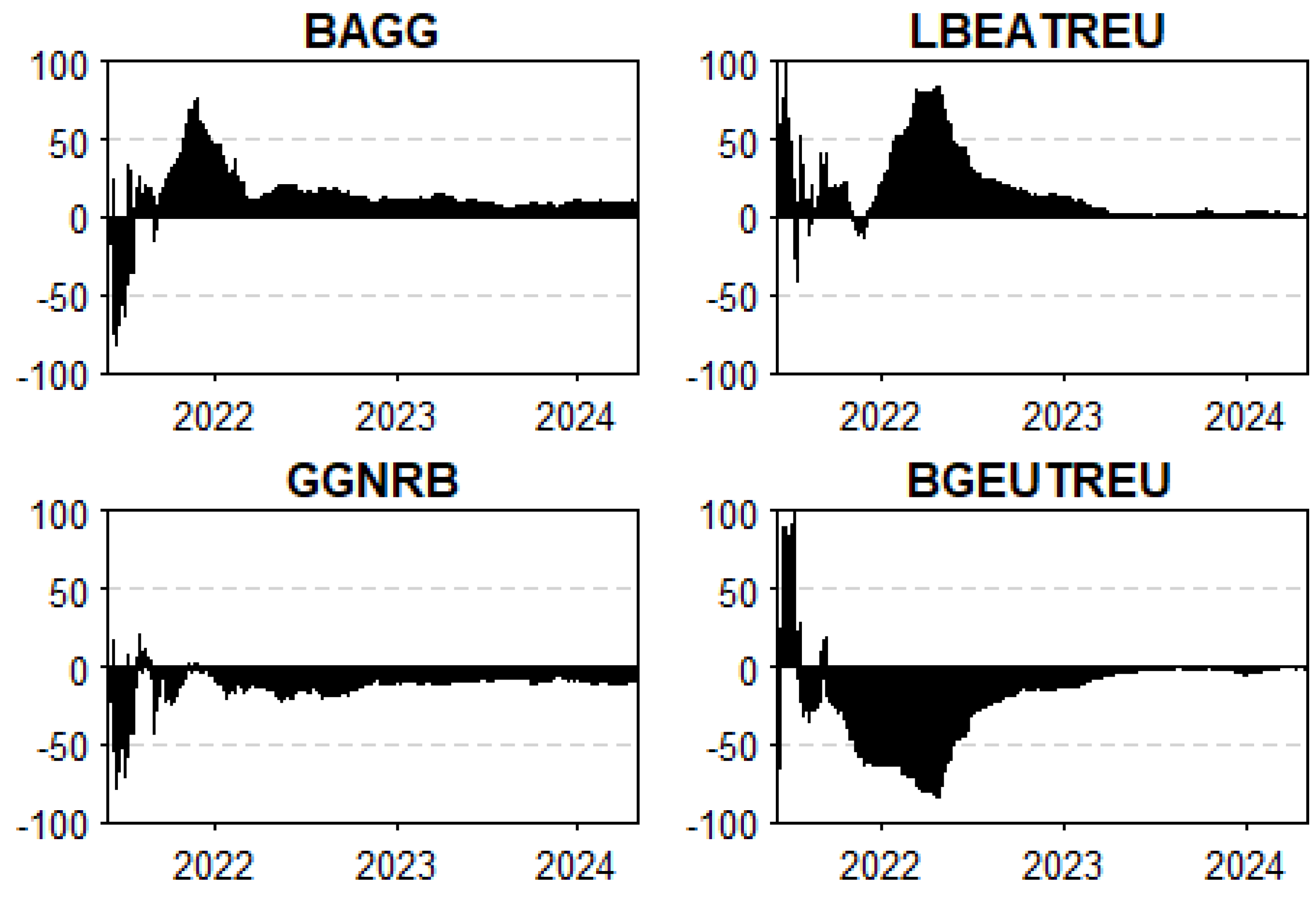
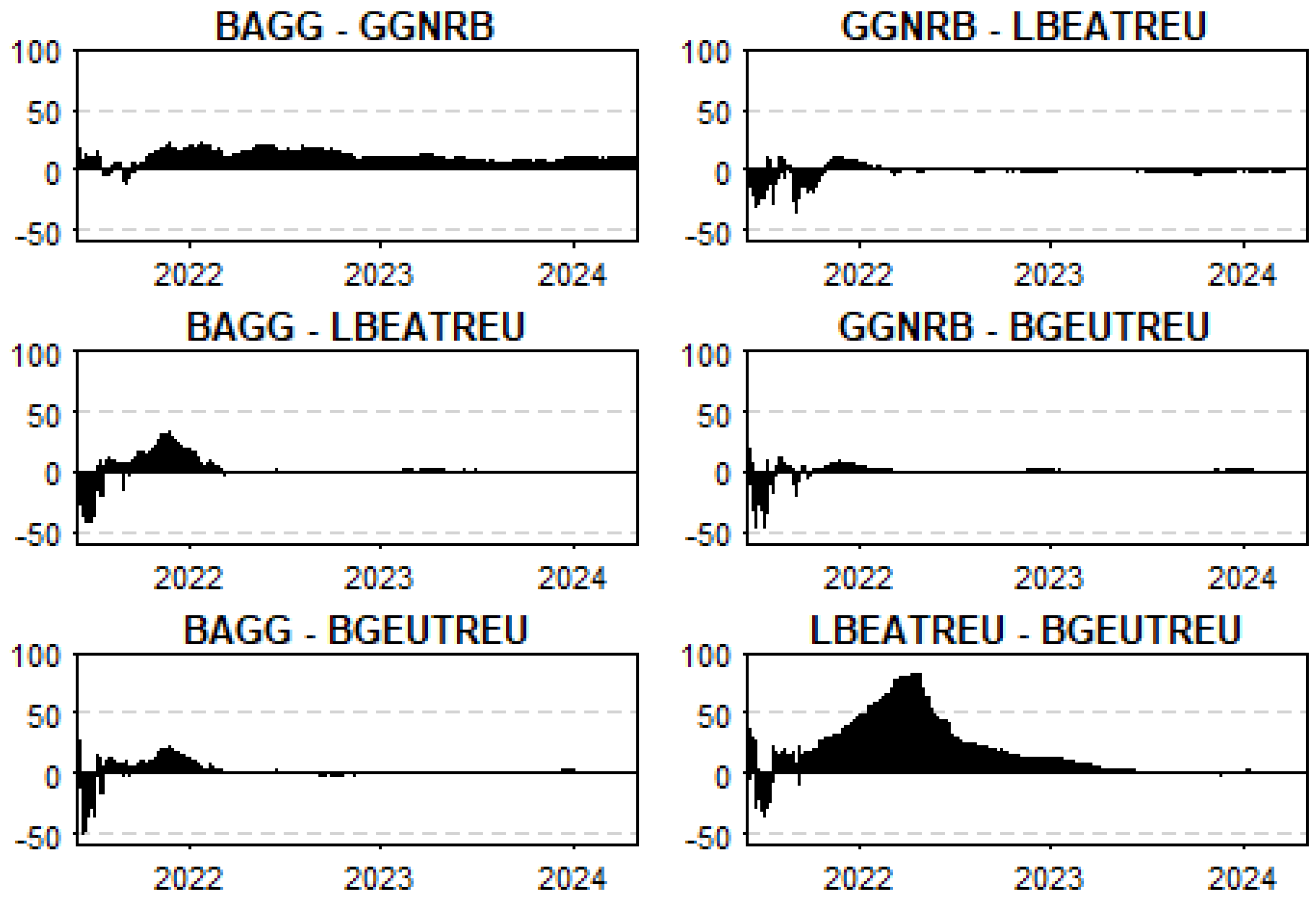
| BAGG | GGNRB | LBEATREU | BGEUTREU | |
|---|---|---|---|---|
| Mean | −0.00024 | −0.00021 | −0.000183 | −0.000221 |
| Std. Dev. | 0.004344 | 0.003529 | 0.0039605 | 0.004605 |
| Skewness | 0.085 | 0.174 * | 0.460 *** | 0.393 *** |
| (0.342) | (0.053) | (0.000) | (0.000) | |
| Ex. Kurtosis | 1.132 *** | 0.939 *** | 1.473 *** | 1.508 *** |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| JB | 40.160 *** | 30.730 *** | 92.328 *** | 88.574 *** |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| ERS | −8.746 | −11.032 | −8.710 | −8.139 |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| Q (20) | 18.824 ** | 9.872 | 9.915 | 11.616 |
| (0.028) | (0.519) | (0.514) | (0.343) | |
| Q2 (20) | 23.738 *** | 23.795 *** | 125.039 *** | 136.198 *** |
| (0.003) | (0.003) | (0.000) | (0.000) | |
| Kendall | BAGG | GGNRB | LBEATREU | BGEUTREU |
| BAGG | 1.000 *** | 0.316 *** | −0.015 | −0.005 |
| GGNRB | 0.316 *** | 1.000 *** | 0.038 | 0.012 |
| LBEATREU | −0.015 | 0.038 | 1.000 *** | 0.088 *** |
| BGEUTREU | −0.005 | 0.012 | 0.088 *** | 1.000 *** |
| BAGG | GGNRB | LBEATREU | BGEUTREU | FROM | |
|---|---|---|---|---|---|
| BAGG | 72.77 | 23.32 | 2.27 | 1.64 | 27.23 |
| GGNRB | 34.11 | 60.34 | 3.47 | 2.08 | 39.66 |
| LBEATREU | 4.03 | 2.43 | 91.09 | 2.45 | 8.91 |
| BGEUTREU | 3.14 | 2.02 | 20.47 | 74.37 | 25.63 |
| TO | 41.28 | 27.77 | 26.21 | 6.17 | 101.43 |
| Inc.Own | 114.05 | 88.11 | 117.30 | 80.54 | cTCI/TCI |
| NET | 14.05 | −11.89 | 17.30 | −19.46 | 33.81/25.36 |
| NPT | 3.00 | 0.00 | 2.00 | 1.00 |
| Minimum Variance approach | ||||||
| Mean | Std. Dev. | 5% | 95% | HE | p-value | |
| U.S. Black «BAGG» | 0.11 | 0.04 | 0.04 | 0.17 | 0.71 | 0.00 |
| U.S. Green «GGNRB» | 0.38 | 0.08 | 0.20 | 0.47 | 0.56 | 0.00 |
| EU Black «LBEATREU» | 0.27 | 0.03 | 0.20 | 0.32 | 0.65 | 0.00 |
| EU Green «BGEUTREU» | 0.24 | 0.10 | 0.15 | 0.50 | 0.74 | 0.00 |
| Minimum Connectedness approach | ||||||
| Mean | Std. Dev. | 5% | 95% | HE | p-value | |
| U.S. Black «BAGG» | 0.21 | 0.04 | 0.17 | 0.27 | 0.71 | 0.00 |
| U.S. Green «GGNRB» | 0.21 | 0.05 | 0.17 | 0.32 | 0.56 | 0.00 |
| EU Black «LBEATREU» | 0.28 | 0.04 | 0.22 | 0.31 | 0.65 | 0.00 |
| EU Green «BGEUTREU» | 0.29 | 0.03 | 0.23 | 0.32 | 0.74 | 0.00 |
| Minimum Correlation approach | ||||||
| Mean | Std. Dev. | 5% | 95% | HE | p-value | |
| U.S. Black «BAGG» | 0.25 | 0.02 | 0.22 | 0.28 | 0.71 | 0.00 |
| U.S. Green «GGNRB » | 0.16 | 0.02 | 0.13 | 0.20 | 0.56 | 0.00 |
| EU Black «LBEATREU» | 0.29 | 0.01 | 0.28 | 0.31 | 0.65 | 0.00 |
| EU Green «BGEUTREU» | 0.30 | 0.02 | 0.27 | 0.32 | 0.74 | 0.00 |
| Risk Parity approach | ||||||
| Mean | Std. Dev. | 5% | 95% | HE | p-value | |
| U.S. Black «BAGG» | 0.21 | 0.02 | 0.18 | 0.24 | 0.72 | 0.00 |
| U.S. Green «GGNRB» | 0.27 | 0.02 | 0.22 | 0.29 | 0.58 | 0.00 |
| EU Black «LBEATREU» | 0.27 | 0.01 | 0.24 | 0.28 | 0.66 | 0.00 |
| EU Green «BGEUTREU» | 0.25 | 0.04 | 0.21 | 0.36 | 0.75 | 0.00 |
| MVP | MCoP | MCP | RPP | |
|---|---|---|---|---|
| Mean | 0.0002114455 | 0.0002118706 | 0.0002148091 | 0.002308136 |
| Sd.Dev. | 0.002318506 | 0.002309053 | 0.002360352 | 0.0002141154 |
| SR | 0.09119904 | 0.09175652 | 0.09100724 | 0.01122623 |
| CVaR (5%) Unhedged | CVaR (5%) Hedged | ΔCVaR 5% | CVaR (1%) Unhedged | CVaR (1%) Hedged | ΔCVaR 1% | |
|---|---|---|---|---|---|---|
| U.S. Bonds | −0.75% | −0.87% | +0.12% | −1.05% | −1.2% | +0.14% |
| E.U. Bonds | −0.98% | −0.82% | +0.16% | −1.26% | −1.05% | +0.21% |
| Mean | Std. Dev. | 5% | 95% | HE | p-Value | |
|---|---|---|---|---|---|---|
| BAGG–GGNRB | 0.16 | 0.09 | 0.03 | 0.32 | 0.41 | 0.00 |
| BAGG–LBEATREU | 0.45 | 0.04 | 0.39 | 0.51 | 0.57 | 0.00 |
| BAGG–BGEUTREU | 0.49 | 0.11 | 0.22 | 0.62 | 0.47 | 0.00 |
| GGNRB–BAGG | 0.84 | 0.09 | 0.68 | 0.97 | 0.11 | 0.12 |
| GGNRB–LBEATREU | 0.61 | 0.06 | 0.50 | 0.70 | 0.42 | 0.00 |
| GGNRB–BGEUTREU | 0.65 | 0.13 | 0.32 | 0.76 | 0.34 | 0.00 |
| LBEATREU–BAGG | 0.55 | 0.04 | 0.49 | 0.61 | 0.48 | 0.00 |
| LBEATREU–GGNRB | 0.39 | 0.06 | 0.30 | 0.50 | 0.54 | 0.00 |
| LBEATREU–BGEUTREU | 0.55 | 0.10 | 0.26 | 0.63 | 0.35 | 0.00 |
| BGEUTREU–BAGG | 0.51 | 0.11 | 0.38 | 0.78 | 0.53 | 0.00 |
| BGEUTREU–GGNRB | 0.35 | 0.13 | 0.24 | 0.68 | 0.61 | 0.00 |
| BGEUTREU–LBEATREU | 0.45 | 0.10 | 0.37 | 0.74 | 0.52 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belguith, R. Dynamics of Green and Conventional Bonds: Hedging Effectiveness and Sustainability Implication. Int. J. Financial Stud. 2025, 13, 106. https://doi.org/10.3390/ijfs13020106
Belguith R. Dynamics of Green and Conventional Bonds: Hedging Effectiveness and Sustainability Implication. International Journal of Financial Studies. 2025; 13(2):106. https://doi.org/10.3390/ijfs13020106
Chicago/Turabian StyleBelguith, Rihab. 2025. "Dynamics of Green and Conventional Bonds: Hedging Effectiveness and Sustainability Implication" International Journal of Financial Studies 13, no. 2: 106. https://doi.org/10.3390/ijfs13020106
APA StyleBelguith, R. (2025). Dynamics of Green and Conventional Bonds: Hedging Effectiveness and Sustainability Implication. International Journal of Financial Studies, 13(2), 106. https://doi.org/10.3390/ijfs13020106








