Abstract
Accurate risk assessment is crucial for predicting potential financial losses. This paper introduces an innovative approach by employing expected risk models that utilize risk samples to capture comprehensive risk characteristics. The innovation lies in the integration of classical credibility theory with expected risk models, enhancing their stability and precision. In this study, two distinct expected risk models were developed, referred to as Model Type I and Model Type II. The Type I model involves independent and identically distributed random samples, while the Type II model incorporates time-varying stochastic processes, including heteroscedastic models like GARCH(p,q). However, these models often exhibit high variability and instability, which can undermine their effectiveness. To mitigate these issues, we applied classical credibility theory, resulting in credible expected risk models. These enhanced models aim to improve the accuracy of Value-at-Risk (VaR) forecasts, a key risk measure defined as the maximum potential loss over a specified period at a given confidence level. The credible expected risk models, referred to as CreVaR, provide more stable and precise VaR forecasts by incorporating credibility adjustments. The effectiveness of these models is evaluated through two complementary approaches: coverage probability, which assesses the accuracy of risk predictions; and scoring functions, which offer a more nuanced evaluation of prediction accuracy by comparing predicted risks with actual observed outcomes. Scoring functions are essential in further assessing the reliability of CreVaR forecasts by quantifying how closely the forecasts align with the actual data, thereby providing a more comprehensive measure of predictive performance. Our findings demonstrate that the CreVaR risk measure delivers more reliable and stable risk forecasts compared to conventional methods. This research contributes to quantitative risk management by offering a robust approach to financial risk prediction, thereby supporting better decision making for companies and financial institutions.
1. Introduction
Financial risk represents the potential for loss that a company or individual may encounter in financial activities, necessitating rigorous risk management and measurement practices. The quantification of such risks, including market risk and credit risk, is essential for informed decision-making, as inaccuracies can lead to substantial financial losses. Quantitative analysis in risk management is typically conducted using risk models designed to predict potential future losses. However, traditional risk models often assume homogeneity in data, which overlooks the inherent heterogeneity and temporal fluctuations of financial data. This assumption can lead to inaccurate predictions and suboptimal decisions, highlighting the need for a more adaptive approach—one that can effectively capture changes in risk dynamics.
The expected risk model proposed in this study seeks to fulfill this need by utilizing a strong representation to comprehensively account for the entire spectrum of risk characteristics, as highlighted by McNeil et al. (2015) in the context of robust quantitative risk management. To achieve this, two distinct expected risk models are developed: Model Type I and Model Type II. Model Type I involves independent and identically distributed random samples, providing a straightforward approach to risk quantification. In contrast, Model Type II accommodates time-varying stochastic processes, such as heteroscedastic models like GARCH(p,q), making it more suitable for capturing the complexity and temporal variability of financial data. These models aim to enhance the understanding of financial risk by integrating the credibility of the data, resulting in more accurate and stable predictions.
Existing risk measures, including the widely used Value-at-Risk (VaR), often fail to fully capture risk dynamics, particularly in the presence of high variability or non-stationary data. VaR is a globally recognized risk measure, defined as the maximum potential loss over a given period at a specified confidence level (Jiang et al. 2022), and is favored for its intuitive interpretation and ease of application (Jorion 2006). VaR is defined as the maximum potential loss over a certain period at a given confidence level (Borer et al. 2023). However, traditional VaR models may fall short in accounting for the severity of losses or the interdependence of risks, as discussed by Josaphat et al. (2021). Estimating VaR is essential for minimizing and preventing adverse financial outcomes (Hull 2018; Syuhada et al. 2021). By introducing credible expected risk models with VaR forecasts, termed CreVaR, this study aims to yield more accurate predictions by comprehensively representing overall risk characteristics.
Duffie and Singleton (2003) shows that expected risk models reduce uncertainty in risk prediction, thereby improving the accuracy and effectiveness of decision-making. However, the calculation of risk measurements based on expected risk models can be unstable when the data shows high variability. The integration of classical credibility theory into the expected risk models, as proposed in this study, is designed to mitigate the instability often observed in high-variation data. Credibility theory, as noted by Klugman et al. (2019), minimizes random error in risk measurement, thereby increasing the stability of risk forecasts. The use of a credibility factor, as suggested by Tse (2009), further refines the model when data is sparse, contributing to more reliable risk predictions. Inspired by the variance premium principle, Yong et al. (2024) proposed a credibility approach that estimates the linear combination of the hypothetical mean and process variance using a quadratic loss function. This approach enhances the model’s ability to capture population information and compares favorably with classical and q-credibility models.
As an alternative to the mean credibility model, Pitselis (2013) introduced the quantile credibility model, which later served as the foundation for Pitselis (2016) to develop Credible VaR (CreVaR) and Credible ES (CreES). These models are designed to assess individual risk based on group risks. In their study, Pitselis (2016); Syuhada and Hakim (2024) employed Bühlmann’s credibility model and successfully demonstrated that risk measurement using credibility theory can provide a more informative and accurate risk assessment compared to conventional methods.
The integration of VaR forecasts with the credible expected risk model, termed CreVaR, is expected to result in improved prediction accuracy. The effectiveness of these predictions are tested through coverage probability analysis (Kabaila and Syuhada 2007), which evaluates the precision of risk forecasts. Scoring functions, as discussed by Song and Li (2023), will also be employed to assess the performance of the predictive models, offering a comprehensive evaluation of the model’s reliability. This research contributes significantly to the field of quantitative risk management by developing both Type I and Type II models, this study captures the complexity of financial data more accurately. The introduction of CreVaR represents a major advancement in risk measurement, enhancing the accuracy of VaR forecasts and providing a robust framework for risk management.
2. Advanced Modeling of Expected Risk: Type I and Type II Approaches
The expected risk model is a random variable constructed by averaging multiple random risks. These risks are treated as random variables, enabling their representation as functions of these variables. This approach provides a more comprehensive understanding of potential outcomes by considering various sources of uncertainty. By integrating multiple random risks into the model, analysts can better assess the overall risk profile associated with a particular decision.
2.1. Expected Risk of Model Type I
The expected risk of Model Type I is constructed from independently and identically distributed random samples. This model is based on the assumption that risk remains constant over time and across different samples. By averaging multiple samples, this approach offers a more accurate estimate of the true risk level, reducing the impact of outliers and random fluctuations in individual samples, resulting in a more stable and reliable risk estimation. However, it is crucial to recognize that the expected risk of Model Type I may not be suitable for all scenarios, particularly when dealing with non-constant risks or time-varying factors.
Suppose , where , , and is a random sample of X with the probability function and the distribution function . In this study, the expected risk model is adjusted such that for each i and j within k. The expected risk of Model Type I can be constructed using the following equation:
resulting in being mutually independent and identically distributed, such that .
There are several methods to determine the distribution of ; the most common is the Moment Generating Function (MGF). However, the MGF distribution may sometimes be complex, making it difficult to approximate with commonly known distributions. Therefore, the theoretical distribution that best fits , denoted as , will be determined through further testing, specifically using Goodness-of-Fit (GoF) tests. In this study, GoF is conducted by applying the Kolmogorov–Smirnov (KS) test and calculating the Akaike Information Criterion (AIC) values for various possible distributions. After obtaining the KS test results and AIC values for each tested distribution, the best-fitting theoretical distribution is identified as the one with the highest p-value from the KS test and the lowest AIC value. The results of testing several distributions of X with different sample sizes m are provided.
Based on the distribution matching test results shown in Table 1, it is generally found that the distribution can be approximated with a normal distribution, resulting in an expected risk of Model Type I distribution, i.e., . Considering the distribution function of , it can be inferred that the expected risk of Model Type I will follow a normal distribution for any underlying distribution, taking into account the mean and variance of the random variable being constructed (see Figure 1). For instance, if and , then .

Table 1.
Goodness-of-Fit test results for the expected risk of Model Type I.
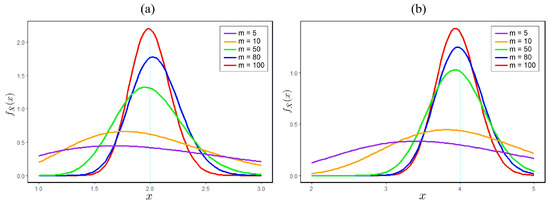
Figure 1.
Illustration of the impact of sample size on variance: (a) shows a random variable following an exponential distribution with a parameter of 0.5, while (b) represents a gamma-distributed random variable with parameters 2 and 0.5. Both (a) and (b) demonstrate that, as the value of m increases, the variance of the sample mean decreases, causing to converge towards .
Table 1 presents the Goodness-of-Fit test results for the expected risk Model Type I across different distributions (Normal, Gamma, Exponential, Uniform, Weibull) and varying sample sizes . The bold values indicate the selected model for each case, with the corresponding AIC values in brackets. These values measure the relative quality of the statistical models for a given dataset.
The accuracy of the constructed expected risk of Model Type I can be determined by comparing the model’s distribution with that of the MGF. A comparison of distribution accuracy is illustrated through simulation results, which clarify the differences between the two approaches. Suppose with and . Suppose the expected risk of Model Type I, based on the distribution of construction results, is denoted as , while the expected risk model using MGF is denoted as . Given a random sample of of size m, an expected risk of Model Type I can be constructed, resulting in a normal distribution . Meanwhile, through MGF, we can obtain , where and m is a real number. Here is an illustration of the simulation of an expected risk of Model Type I with and .
Based on the simulation results illustrated in Figure 2, no significant differences were found between the expected risk model based on the distribution of construction results and the model using MGF. Therefore, the Type I expected risk model that has been constructed can be approximated by a normal distribution according to the central limit theorem.
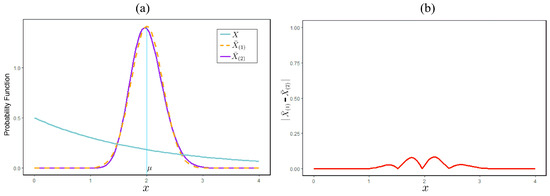
Figure 2.
Comparison of expected risk of Model Type I: (a) shows the probability function of the exponential random variable (0.5) and (b) shows the difference in the probability functions of and .
2.2. Expected Risk of Model Type II
The expected risk of Model Type II involves stochastic processes with time-dependent volatility, which are modeled through heteroscedastic processes. This approach accounts for the reality that risk levels fluctuate over time based on various factors (see Figure 3), leading to a more dynamic and realistic representation of market conditions. By incorporating these time-dependent volatilities into the model, investors can better understand and prepare for potential fluctuations in their investments, ultimately leading to more informed decision-making and improved risk management strategies.
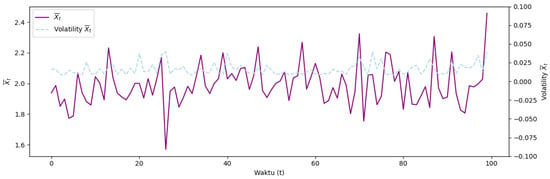
Figure 3.
Detailed representation of the expected risk of Model Type II: This illustration provides an analysis of the model’s volatility, highlighting the fluctuations and uncertainties inherent in its performance over time.
Suppose is a sequence of random variables with representing time, , and . The expected risk of Model Type II can be constructed using the following equation:
which yields , where .
The expected risk model, generally with for i and j within k, results in volatility that changes over time, making it possible to model it through heteroscedastic processes. Since the expected risk model may not be stationary, differentiation is required, as follows:
By applying this transformation, stationarity in the expected risk model can potentially be achieved, allowing for more accurate modeling and forecasting of volatility in financial data (Christoffersen 2023). Additionally, the differentiation process aids in identifying any patterns or trends in the data that may not be apparent in the original series. Theoretically, the expected risk of Model Type II can be modeled as:
where represents dynamic volatility and represents innovation that follows for any time t. Volatility and innovation are assumed to be mutually independent (Syuhada and Hakim 2020).
We apply heteroscedastic processes by considering the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model, as illustrated in Figure 4. The GARCH model states that variance at a given time is influenced by the squares of past observations and the past variance (Kakade et al. 2022). Specifically, a risk model for the heterogeneous process is constructed by GARCH(p,q) with and . This model is commonly used in financial forecasting and risk management to account for volatility clustering, where periods of high volatility are often followed by more periods of high volatility (Bollerslev 2023).
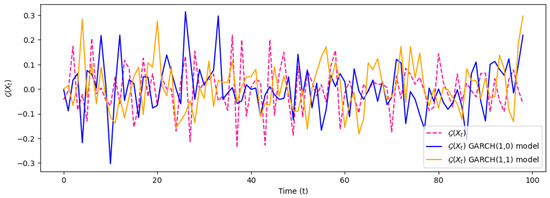
Figure 4.
Application of expected risk of Model Type II to GARCH processes: This illustration demonstrates the expected risk and volatility of Model Type II for GARCH(1,0) and GARCH(1,1) processes.
According to Syuhada (2020), assuming follows the GARCH(1,0) process for , then:
where . Assume follows the GARCH(1,1) model, then
with , , and (Syuhada et al. 2023).
3. Credibility Theory and Its Application to Expected Risk Models
This section utilizes classical credibility theory to determine the standard required to achieve full credibility in an expected risk model. The standard for achieving full credibility is defined as the amount of data necessary for the expected risk model to attain stability. Suppose the expected risk model is generally expressed as . The model is considered stable when is close to , meaning the difference between and is very small with high probability. This ensures that the data used in the model are sufficient to accurately reflect the underlying risk and produce reliable predictions.
where r closes to 0 and p approaches 1. Based on this equation, the minimum amount of data m required for the stability of can be determined as follows:
The stability of directly impacts the accuracy of predictions. If the required amount of m is not met, then can be combined with additional information to enhance the credibility of the prediction. By incorporating other sources of information, the prediction model becomes more robust, reducing the impact of any potential instability in . This approach leads to more reliable forecasts, which in turn supports better decision-making for stakeholders. The expected risk model with classical credibility, hereafter referred to as the credible expected risk model, can be expressed as follows (Cheung et al. 2023):
where is the classical credibility factor, and ℓ represents other information, such as reserve manuals based on guidelines from government or company sources. The expected risk model is an unbiased estimator of , and the determinant of the stability of is its variance. Therefore, the classical credibility factor is given by:
This formula for the classical credibility factor accounts for the risk level r, the mean , the standard deviation , and the scaling factor . The classical credibility factor plays a crucial role in determining the weight assigned to the expected risk model relative to the additional information ℓ in the overall estimation of the variable of interest. By balancing these factors, the credibility factor facilitates a more accurate and stable prediction based on the available data and external information.
4. Credible Value-at-Risk (CreVaR)
Value-at-Risk (VaR) is a widely used risk measure that indicates the maximum potential loss over a specific time period at a given confidence level. VaR is a function of certain parameters, and these parameters must be estimated to obtain the VaR forecast. The forecast of VaR estimates the risk value that may occur in the future. To ensure the accuracy of these forecasts, the reliability of the VaR forecast can be assessed by comparing the coverage probability with the confidence level. This involves evaluating how often actual losses fall within the predicted VaR limits, thereby providing a measure of the forecast’s reliability.
To enhance forecast accuracy, VaR is applied to a credible expected risk model, referred to as Credible Value-at-Risk (CreVaR). This approach is expected to improve the accuracy and stability of VaR forecasts by leveraging both historical data and credibility information. By using a credible expected risk model, CreVaR provides a more reliable estimate of potential losses, thus facilitating more effective and efficient risk management.
Suppose represent a sequence of random variables with a probability function . CreVaR at the confidence level is a forecast for , so the estimated CreVaR is given by:
where is the inverse of the credible expected risk model distribution function. The credible expected risk model aims to improve the VaR forecast by incorporating credibility theory. This model utilizes two types of distribution functions for the credible expected risk Model Type I and Model Type II, which are expressed as follows:
where is the standard normal distribution function. Using these functions, the Credible Value-at-Risk (CreVaR) forecasts for both model types can be derived as follows:
Here, is the classical credibility factor, and ℓ represents additional information, such as reserve manuals based on guidelines from the government or a company.
The accuracy of CreVaR forecasts will be assessed using coverage probability and scoring functions, which measure how well the predictions align with actual outcomes and meet the specified confidence levels. Coverage probability evaluates the effectiveness of a CreVaR forecast by assessing how accurately it reflects actual losses at a specified confidence level. Specifically, it measures the probability that the true loss does not exceed the predicted CreVaR value, aligning with the given confidence level .
where represents the available information up to time n. Generally, the coverage probability for VaR forecasts can be expressed as follows (Syuhada 2020):
with the expectation taken over the distribution of given the available information at time n. Specifically, for credible expected risk of Model Types I and II, the coverage probabilities are
While coverage probability measures how well CreVaR forecasts align with actual losses at a specified confidence level, scoring functions offer a complementary approach to evaluate prediction accuracy. Scoring functions are essential for further evaluating the accuracy and reliability of CreVaR forecasts by quantifying the performance of predictive models through comparison of predicted risks with actual observed outcomes. Effective scoring functions measure how closely the forecasts match the actual data, thereby enhancing the reliability of risk management practices. Specifically, for each forecast of the CreVaR for day t and the realized expected risk model , the scoring function is defined as (Gneiting and Raftery 2007; Saissi Hassani and Dionne 2023)
where is continuously differentiable and is a monotone-increasing function, and is any function.
Let and , then the log scoring function can be expressed as:
Scoring functions also enable the assessment of differences in forecast accuracy between competing models, maintaining homogeneity of degree 0. This property is crucial for the optimal performance of the Diebold-Mariano (DM) test (Diebold and Marino 1995). The DM test compares the predictive accuracy of two forecasting models by examining whether the differences in their forecast errors are statistically significant. The DM test statistic is given by
where is the mean of the difference in forecast errors between the two models, is the estimated variance of these differences, and n is the number of forecasts.
To apply the DM test in comparing the performance of CreVaR models, predictions from different models are evaluated. The DM test is typically used to determine whether there are significant differences in the prediction accuracy between two models or forecasting methods. These models improve the forecast accuracy of CreVaR by applying credibility theory to modify the forecasts based on the stability and reliability of the underlying data. As a result, the predictions of potential losses become more reliable and accurate, which is essential for effective risk management.
5. Empirical Analysis and Results
The focus of the research was on simulating an expected risk of Model Type II with credibility, applied specifically to Bitcoin assets. By incorporating daily average prices and credibility theory, the model aims to deliver reliable and accurate predictions of potential losses. Hourly Bitcoin price data were collected from 28 February 2021 to 28 February 2022, resulting in 8,784 observations. From these data, daily average prices were calculated to obtain the expected risk model, which is expressed as , where represents the average price of the asset at time . Figure 5 illustrates these calculations. The simulation was conducted to demonstrate the effectiveness of the Model Type II expected risk with credibility in enhancing the accuracy of risk predictions for Bitcoin, known for its high volatility. This approach offers a more robust tool for managing risk in the rapidly evolving cryptocurrency market.
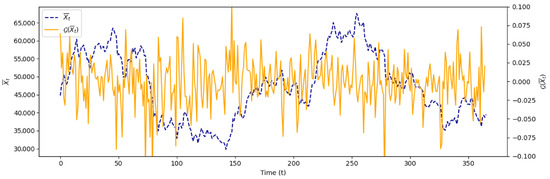
Figure 5.
Illustration of and derived from Bitcoin asset prices.
Subsequently, the GARCH heteroscedastic model (p,q) for and , referring to GARCH(1,0) and GARCH(1,1), was fitted to the data. The most appropriate model for the expected risk model was selected based on the smallest Akaike Information Criterion (AIC) value and the largest log-likelihood value. The model-fitting results and parameter estimates for the GARCH(p,q) models are presented in Table 2.

Table 2.
Model-fitting results and parameter estimation of the expected risk model .
Based on Table 2, the expected risk model for Bitcoin assets is best captured by the GARCH(1,1) process, which can be theoretically modeled as , where . The GARCH(1,1) model has a lower AIC value of −1477.38 compared to −1404.85 for the GARCH(1,0) model and a higher log-likelihood value of 742.688 compared to 705.423. These results suggest that the GARCH(1,1) model provides a better fit for the data, capturing more intricate aspects of Bitcoin’s volatility dynamics. The inclusion of the parameter in the GARCH(1,1) model allows it to account for both short-term and long-term volatility effects, thereby improving the accuracy of risk predictions.
Moreover, the parameter estimates indicate that the GARCH(1,1) model assigns significant weight to the lagged volatility term (), highlighting its role in explaining the persistence of volatility over time. This finding is consistent with the high degree of volatility persistence observed in Bitcoin markets. By effectively incorporating these dynamics, the GARCH(1,1) model enhances the robustness of the risk management strategy, providing a more reliable tool for assessing potential losses in the highly volatile cryptocurrency market. This underscores the importance of selecting appropriate models to capture the complex volatility structure of assets like Bitcoin.
The expected risk model for Bitcoin assets is derived using the GARCH(1,1) process in conjunction with Value-at-Risk (VaR). The GARCH(1,1) model’s ability to capture both short-term and long-term volatility dynamics enables more accurate VaR estimates, which reflect the potential maximum loss at a specified confidence level. This capability is essential for managing risk in volatile markets, such as cryptocurrencies, where price movements can be highly unpredictable. By integrating the detailed volatility structure provided by the GARCH(1,1) model into VaR calculations, investors and risk managers can achieve a more precise measure of potential financial losses, thereby enhancing their decision-making processes and risk management strategies in such a volatile environment (Giot 2005).
Based on the table, the expected risk model for Bitcoin assets is obtained through the GARCH(1,1) process along with VaR, and it is illustrated in Figure 6.
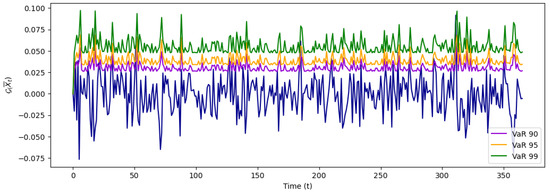
Figure 6.
This illustration demonstrates the Value-at-Risk (VaR) in the expected risk model applied to the GARCH(1,1) process, showcasing how the model estimates risk at different confidence levels. The visual includes VaR metrics for confidence levels of 90%, 95%, and 99%, providing a comprehensive view of how potential risk varies under these different thresholds. By depicting these levels, the illustration highlights the sensitivity of the risk assessment to changes in confidence levels, offering valuable insights into the robustness and precision of the VaR model within the context of the GARCH(1,1) framework.
The expected risk model for Bitcoin assets, derived using the GARCH(1,1) process and Value-at-Risk (VaR), demonstrated the model’s effectiveness in capturing both short-term and long-term volatility dynamics. The practical application involved simulating the VaR and Credible Value-at-Risk (CreVaR) forecasts with 1,000 iterations, resulting in the estimation of GARCH(1,1) parameters: , , and . There may be differences in the estimated parameter values due to iteration and involvement in generating data. It is important to acknowledge these potential discrepancies when interpreting the results of the VaR and CreVaR forecasts. The iterative nature of the process, combined with the generation of data, can introduce variability in the estimated parameter values. Therefore, the forecast of VaR and CreVaR of the expected risk model at the confidence level was captured, as shown in Table 3.

Table 3.
Simulation results of the CreVaR forecast for the expected risk model with .
The simulation results, in Table 3, show that all Diebold–Mariano (DM) statistics were negative across various confidence levels (90%, 95%, and 99%). This indicates that the CreVaR predictions consistently outperform the VaR predictions. A negative DM statistic suggests that the average difference in losses between the two models is negative, meaning CreVaR has a lower average loss score. This implies that CreVaR is more effective in predicting financial risk compared to VaR. The consistency of negative DM statistics across different confidence levels reinforces the robustness of the CreVaR model under various market conditions. This predictive performance advantage is crucial for risk managers as it provides a more reliable estimate of potential losses.
The 1000-iteration simulation introduces variability in parameter estimates, affecting the precision of VaR and CreVaR forecasts. This variability is crucial for accurate result interpretation and emphasizes the need for continuous model evaluation and adjustment in real-world risk management. Despite providing a robust framework for assessing Bitcoin risk, the model requires ongoing refinement to maintain accuracy in dynamic markets. An example of CreVaR predictions for the GARCH(1,1) model at various confidence levels is shown in Figure 7.
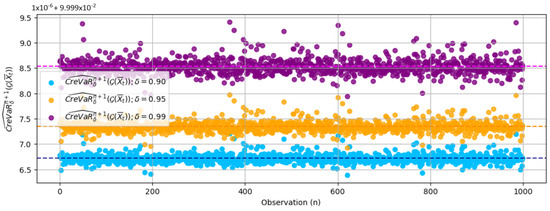
Figure 7.
Illustration of the VaR forecast in the expected risk model with the GARCH(1,1) process.
To better understand the effectiveness of CreVaR forecasts within the credible expected risk model using the GARCH(1,1) process, it is essential to evaluate how accurately these forecasts reflect underlying risk. This involves examining the relationship between coverage probability and the confidence level associated with the CreVaR forecasts, allowing us to assess the model’s ability to predict extreme losses and the alignment of forecasts with confidence levels, as shown in Figure 8.
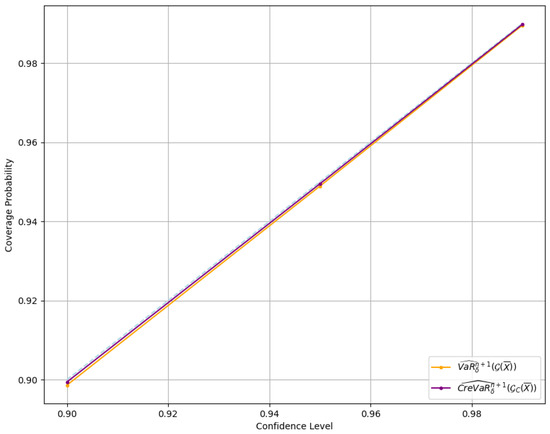
Figure 8.
Illustration of the relationship between coverage probability and confidence level in the CreVaR forecasts of the expected risk model.
Based on the Figure 8, it is evident that CreVaR forecasts are more accurate than VaR, as the coverage probability increasingly aligns with the expected confidence level. This indicates that CreVaR provides a closer match to the desired confidence levels, highlighting its superior performance in predicting extreme losses.
6. Discussion
The findings of this study underscore the crucial role of using daily average asset data instead of traditional daily closing prices when modeling Bitcoin’s price volatility. Daily closing prices can overlook significant intraday fluctuations, but daily average prices provide a more detailed view of Bitcoin’s price movements throughout the trading day. This methodological shift is essential for volatile markets like cryptocurrencies, where precise risk assessment relies on capturing intraday volatility. By utilizing daily average prices, this study presents a refined approach to understanding Bitcoin’s price dynamics across the trading day. The proposed method offers a more comprehensive representation of daily data, incorporating important intraday price variations that are vital for effective risk assessment and management. This approach is better suited to the dynamic nature of Bitcoin’s price movements, addressing the limitations of traditional models that rely solely on daily closing prices. Such models may not fully capture Bitcoin’s true volatility, whereas integrating daily average prices offers a more accurate and nuanced understanding of its price behavior. Additionally, incorporating daily average prices into volatility modeling improves accuracy, especially in estimating risk measures like Value-at-Risk (VaR). VaR forecasts have traditionally been obtained using time series models based on daily return frequencies (Ewald et al. 2023).
Incorporating credibility theory into the expected risk of Model Type II further refines the accuracy of risk forecasts. Credibility theory adjusts the weight of historical data based on its relevance, allowing for a more precise estimation of potential losses. The CreVaR forecasts using expected risk of Model Type II initially overlooked sample size variations due to daily differences in observation data. However, Bitcoin simulations reveal that integrating credibility theory with the GARCH(1,1) process significantly enhances prediction accuracy. By weighting historical data based on its relevance, credibility theory refines risk estimates, capturing Bitcoin’s volatility more effectively and improving risk assessments. This integration also addresses traditional model limitations, such as overfitting or underfitting caused by varying data sizes, providing a more nuanced risk forecasting approach. Overall, this methodological enhancement underscores the importance of advanced techniques in refining risk models for more precise and actionable insights in dynamic financial markets.
The Bitcoin simulation illustrates the practical advantages of the CreVaR model, highlighting its superior capacity for managing risk in volatile financial environments. By combining the detailed volatility structure of the GARCH(1,1) model with credibility theory, CreVaR provides a more precise and actionable measure of potential financial losses. This integration enhances the model’s ability to capture complex volatility dynamics and assess risk more accurately. For investors and risk managers navigating unpredictable markets like cryptocurrencies, the advanced capabilities of the CreVaR model are crucial. The findings emphasize the need for ongoing evaluation and refinement of risk models to ensure their effectiveness in evolving market conditions. Continuously updating and improving these models helps maintain accuracy and reliability in risk assessment, supporting better decision-making in dynamic financial environments.
7. Conclusions
This research makes significant contributions to the field of risk management by introducing and validating novel methods for evaluating the accuracy of risk predictions, particularly through the application of coverage probability and scoring functions. Building on the work of (Syuhada 2020), which emphasized the importance of precise evaluation in risk prediction, this study demonstrates that coverage probability offers a more accurate and reliable assessment of predictive accuracy. Additionally, the work of (Gneiting and Raftery 2007; Saissi Hassani and Dionne 2023) employed scoring functions as a complementary approach, providing an additional layer of evaluation by quantifying the alignment between CreVaR forecasts and actual observed outcomes. This dual-method approach not only reinforces existing theories but also extends them, offering a more comprehensive and nuanced evaluation tool that is highly pertinent to current financial market conditions. The findings of this study contribute to the theoretical understanding of risk management, especially in the context of expected risk models and credibility theory, by enhancing the reliability and precision of predictive models used in practice.
However, this study also presents several limitations that should be considered. Firstly, the expected risk of Model Type I assumes that random samples are independent and identically distributed, a condition that may not hold in more complex market environments. Secondly, the use of the GARCH model within the expected risk of Model Type II has limitations in addressing extreme volatility. Lastly, the focus on Value-at-Risk (VaR) as the primary risk measure may not fully capture extreme risks, indicating that incorporating additional measures such as Conditional Value-at-Risk (CVaR) could provide a more comprehensive evaluation. Future research could explore the development of more sophisticated models by considering additional variables and scenarios, such as incorporating the interactions between various risk factors or employing dynamic models that can adapt over time.
Author Contributions
Conceptualization, K.S., L.M. and M.J.; methodology, K.S., R.P. and E.E.; formal analysis, K.S., R.P., M.J. and A.R.; resources, I.K.D.A.; data curation, I.K.D.A. and L.M.; writing—original draft, R.P. and L.M.; writing—review and editing, K.S., I.K.D.A., M.J. and A.R.; supervision, K.S.; project administration, M.J. and A.R.; funding acquisition, K.S. and A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Institut Teknologi Bandung (ITB), Indonesia, under the grant of Riset Unggulan ITB 2024.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data analyzed are referenced in this article.
Acknowledgments
The authors are grateful to the academic editor and reviewer comments, the careful reading, and numerous suggestions that have greatly improved this paper. The second author (R.P.) and the fourth author (L.M.) express sincere gratitude to the BPPT and LPDP for their generous scholarship support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bollerslev, Tim. 2023. Reprint of: Generalized autoregressive conditional Heteroskedasticity. Journal of Econometrics 234: 25–37. [Google Scholar] [CrossRef]
- Borer, Daniel, Devmali Perera, Fitriya Fauzi, and Trinh Nguyen Chau. 2023. Identifying systemic risk of assets during international financial crises using value at risk elasticities. International Review of Financial Analysis 90: 102832. [Google Scholar] [CrossRef]
- Cheung, Ka Chun, Sheung Chi Phillip Yam, and Yiying Zhang. 2022. Satisficing credibility for heterogeneous risks. European Journal of Operational Research 298: 752–68. [Google Scholar] [CrossRef]
- Christoffersen, Peter. 2003. Elements of Financial Risk Management. Cambridge: Academic Press. [Google Scholar]
- Diebold, Francis X., and Robert S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 253. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 2003. Credit Risk: Pricing, Measurement, and Management. Princeton: Princeton University Press. [Google Scholar]
- Ewald, Christian, Jelena Hadina, Erik Haugom, Gudbrand Lien, Ståle Størdal, and Muhammad Yahya. 2023. Sample frequency robustness and accuracy in forecasting value-at-Risk for Brent crude oil futures. Finance Research Letters 58: 103916. [Google Scholar] [CrossRef]
- Giot, Pierre. 2005. The information content of implied volatility in agricultural commodity markets. European Review of Agricultural Economics 32: 227–45. [Google Scholar] [CrossRef]
- Gneiting, Tilmann, and Adrian E. Raftery. 2007. Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association 102: 359–78. [Google Scholar] [CrossRef]
- Hull, John. 2018. Risk Management and Financial Institutions. Hoboken: John Wiley and Sons. [Google Scholar]
- Jiang, Kunliang, Linhui Zeng, Jiashan Song, and Yimeng Liu. 2022. Forecasting value-at-Risk of cryptocurrencies using the time-varying mixture-accelerating generalized autoregressive score model. Research in International Business and Finance 61: 101634. [Google Scholar] [CrossRef]
- Jorion, Philippe. 2006. Value at Risk, 3rd ed.: The New Benchmark for Managing Financial Risk. New York: McGraw Hill Professional. [Google Scholar]
- Josaphat, Bony Parulian, Moch Fandi Ansori, and Khreshna Syuhada. 2021. On optimization of copula-based extended tail value-at-Risk and its application in energy risk. IEEE Access 9: 122474–85. [Google Scholar] [CrossRef]
- Kabaila, Paul, and Khreshna Syuhada. 2007. The relative efficiency of prediction intervals. Communications in Statistics—Theory and Methods 36: 2673–86. [Google Scholar] [CrossRef]
- Kakade, Kshitij, Ishan Jain, and Aswini Kumar Mishra. 2022. Value-at-Risk forecasting: A hybrid ensemble learning GARCH-LSTM based approach. Resources Policy 78: 102903. [Google Scholar] [CrossRef]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2019. Loss Models: From Data to Decisions. Hoboken: John Wiley and Sons. [Google Scholar]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Pitselis, Georgios. 2013. Quantile credibility models. InsuranAce: Mathematics and Economics 52: 477–89. [Google Scholar] [CrossRef]
- Pitselis, Georgios. 2016. Credible risk measures with applications in actuarial sciences and finance. Insurance: Mathematics and Economics 70: 373–86. [Google Scholar] [CrossRef]
- Saissi Hassani, Samir, and Georges Dionne. 2023. Using skewed exponential power mixture for Var and CVaR forecasts to comply with market risk regulation. SSRN Electronic Journal 2023: 4387680. [Google Scholar] [CrossRef]
- Song, Shijia, and Handong Li. 2023. A method for predicting Var by aggregating generalized distributions driven by the dynamic conditional score. The Quarterly Review of Economics and Finance 88: 203–14. [Google Scholar] [CrossRef]
- Syuhada, Khreshna. 2020. The improved value-at-Risk for Heteroscedastic processes and their coverage probability. Journal of Probability and Statistics 2020: 1–5. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, and Arief Hakim. 2020. Modeling risk dependence and portfolio Var forecast through vine copula for cryptocurrencies. PLoS ONE 15: e0242102. [Google Scholar] [CrossRef] [PubMed]
- Syuhada, Khreshna, and Arief Hakim. 2024. Risk quantification and validation for green energy markets: New insight from a credibility theory approach. Finance Research Letters 62: 105140. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, Arief Hakim, and Risti Nur’aini. 2021. The expected-based value-at-risk and expected shortfall using quantile and expectile with application to electricity market data. Communications in Statistics—Simulation and Computation 52: 3104–21. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, Venansius Tjahjono, and Arief Hakim. 2023. Improving value-at-Risk forecast using GA-ARMA-GARCH and AI-KDE models. Applied Soft Computing 148: 110885. [Google Scholar] [CrossRef]
- Tse, Yiu-Kuen. 2009. Nonlife Actuarial Models: Theory, Methods and Evaluation. Cambridge: Cambridge University Press. [Google Scholar]
- Yong, Yaodi, Pingping Zeng, and Yiying Zhang. 2024. Credibility theory for variance premium principle. North American Actuarial Journal 2024: 1–33. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
