The Relationship between Financial Literacy Misestimation and Misplacement from the Perspective of Inverse Differential Information and Stock Market Participation

Abstract

This study proposes the inverse differential information theory, which predicts a positive relationship between misestimation and misplacement, two types of overconfidence. The inverse differential information theory contrasts with the existing theory of differential information, which argues for a negative relationship between these two types of overconfidence. This study shows that these differences arise from opposing perspectives on the accuracy with which individuals assess their own abilities or performance compared to others’. The inverse differential information theory posits that people tend to evaluate others more objectively than they do themselves. A positive relationship between misestimation and misplacement predicts that overestimation and overplacement, as well as underestimation and underplacement, tend to occur together. Analysis using financial literacy data from South Korean adults supports the prediction of the inverse differential information theory. When these two types of overconfidence form a positive relationship, they are expected to have systematically a significant impact on human decision-making and behavior. This study empirically demonstrates that the positive relationship between misestimation and misplacement in financial literacy significantly influences individuals’ financial behavior, specifically in the context of stock market participation experience. The inverse differential information theory requires further empirical validation across various domains, not just in the field of behavioral finance, to establish whether the positive interaction between misestimation and misplacement consistently influences human decision-making and behavior.

1. Introduction

Overconfidence has been defined in various ways by different researchers. Moore and Healy (2008) classified overconfidence into three main types: misestimation, misplacement, and misprecision. To use the terminology of Moore and Healy (2008), misestimation can be categorized into overestimation, in which individuals erroneously estimate their abilities or performance better than the actual ones, and underestimation, in which individuals erroneously estimate their abilities or performance worse than the actual ones. Misplacement can also be categorized into overplacement, in which individuals believe themselves to be better than others when they are not, and underplacement, in which individuals believe themselves to be worse than others when they are not.

Previous studies on overconfidence have predominantly focused on a single type of overconfidence. There are relatively few studies that simultaneously analyze more than one type of overconfidence, the relationships between them, and the impact of them on human decision-making and behavior (Grežo 2021). In the field of behavioral finance, there are a few studies that have addressed more than one type simultaneously. Glaser and Weber (2007) reported that individual stock investors in Germany exhibited overestimation in their financial literacy and BTA (better-than-average) in their stock investment abilities, with a correlation of 0.17 (p < 0.1) between the two. They found that only BTA had a significant impact on stock trading volume. Deaves et al. (2009), in an experiment with college students, analyzed three types of overconfidence—BTA, overprecision, and the illusion of control—simultaneously, and found that misprecision and BTA had a significant positive impact on trading volume. They also identified a positive correlation of 0.21 (p < 0.1) between BTA and the illusion of control. Yang and Zhu (2016) analyzed the impact of three overconfidence variables—misprecision, BTA, and the illusion of control—on trading volume in an experimental setting. The correlations among these overconfidence variables were not statistically significant. Pikulina et al. (2017) conducted an experiment involving college students and financial professionals, in which they observed general overestimation and better-than-average in financial literacy. They found that actual financial literacy levels, misestimation, and BTA all tended to have a significant positive impact on investment levels. However, they did not provide a correlation analysis between misestimation and BTA. Anderson et al. (2017) showed that misestimation of financial literacy positively affected retirement planning and precautionary saving, while misprecision influenced only precautionary saving, with a correlation coefficient of 0.33 between the two overconfidence variables. Merkle (2017) analyzed the impact of three types of financial overconfidence—misestimation, misplacement, and misprecision—on trading volume, diversification, and the profitability of stock investments. Merkle’s study demonstrated that the correlation between overestimation and overplacement was positive, with values of 0.16 and 0.15, both significant at p < 0.01. Vörös et al. (2021) simultaneously analyzed the impact of the three types of overconfidence in financial literacy—misestimation, misplacement, and misprecision—on the components of financial well-being. Their study found a strong positive correlation of 0.817 (p < 0.01) between misestimation and misplacement.

In all the studies mentioned above, the correlations between overconfidence variables are commonly analyzed as basic statistics rather than the primary focus. In recent review studies on financial overconfidence or overconfidence and financial decision-making, there are no studies that address the relationship between different types of overconfidence and the reasons why such relationships exist (Singh et al. 2024; Karki et al. 2024; Grežo 2021).

Humans living in society always have a basic need to evaluate themselves (Anderson et al. 2012). Especially when there are no objective evaluation criteria or when there is a lack of distributional information on their comparison group, people often engage in social comparison (Festinger 1954; Goethals et al. 1991; Crusius et al. 2022). In such cases, they may evaluate their abilities or performance inaccurately or incorrectly assess them in comparison with others’. Interestingly, both the over-evaluation and under-evaluation of oneself are observed in the same data. This raises the question of the relationship between misestimation and misplacement: Do people who overestimate their abilities or performance tend to overplace them compared to others, or do they tend to underplace them?

Engeler and Häubl (2020) categorized two research streams concerning the relationship between misestimation and misplacement in the field of psychology. One stream suggests a negative association between misestimation and misplacement, while the other suggests a positive association. For example, Krueger and Mueller (2002), Larrick et al. (2007), Moore and Small (2007), and Moore and Healy (2008) report a negative relationship between the two. Larrick et al. (2007) explained the negative correlation between two overconfidence variables by assuming the strong positive correlation between subjective evaluation factors of one’s abilities or performance and the weak correlation between these subjective factors and actual performance. The present study particularly focuses on Moore and Small (2007) and Moore and Healy (2008). They theoretically predicted a negative correlation between misestimation and misplacement in a parsimonious manner using the concept of differential information. They noted that information about others is more limited than information about oneself and referred to this as “differential information”.

On the other hand, studies demonstrating the positive correlation between the two often empirically propose various cognitive biases or distortions to explain it. A variety of cognitive biases have been suggested (e.g., Alicke 1985; Kunda 1990; Goethals et al. 1991; Alicke and Sedikides 2009; Epley and Dunning 2001, 2006; Helzer and Dunning 2012; Balcetis and Dunning 2013). These studies commonly assert that when individuals evaluate their abilities or performance, various cognitive biases and distortions intervene, making these self-assessments inherently subjective and consequently inaccurate. Those studies present findings that when individuals evaluate their own abilities or performance, they tend to overestimate them, believing erroneously they are superior to the average of a comparison group.

Generalizing parsimoniously the findings of the latter studies, “Inaccuracies in self-assessment are greater than in assessing others”. This study conceptualizes this hypothetical claim as “inverse differential information”. The inverse differential information theory presents the following key prediction: there is a positive correlation between misestimation and misplacement, with a tendency for overestimation to pair with overplacement and underestimation to pair with underplacement. This study tests the prediction using financial literacy data. It empirically demonstrates that a positive correlation exists between misestimation and misplacement in financial literacy and then shows that this positive correlation has a significant and combined effect on individuals’ experience with participating in the stock market. The study data come from the survey data of a random sample of South Korean adults aged 20 and older.

The paper is structured as follows: Section 2 introduces the theory of “inverse differential information” as a new way of explaining the positive relationship between misestimation and misplacement. From this, two hypotheses are proposed. Section 3 presents the data, the operational definitions and measurements of variables, and the research methods. Section 4 tests the hypotheses through data analysis. First, the research tests the key prediction of the theory of inverse differential information using financial literacy data. Following this, the paper empirically demonstrates the significant explanatory power of the positive correlation between the two types of financial overconfidence on individual financial behaviors and outcomes, focusing on stock market participation. The final section, Section 5, presents the discussion and conclusions.

2. Literature and Hypotheses

2.1. Overconfidence in Social Comparisons

People have a basic need to understand themselves, and when an objective assessment of themselves is not possible, they tend to engage in social comparison to evaluate their abilities or performance through comparisons with others (Festinger 1954; Goethals et al. 1991; Anderson et al. 2012). Inaccurate assessments of one’s own abilities or performance is likely to occur in social comparison processes, in which individuals attempt to evaluate their abilities or performance relative to others in situations where there are no precise standards of measurement or where basic distributional information is uncertain. For example, traits such as kindness, tolerance, and the good driving skills of the general population are difficult to evaluate because there is no agreed-upon scale, and it is difficult to know the distributional information, such as the mean or variance of the comparison group to which an individual evaluator belongs. This situation provides a favorable environment for social comparison and overconfidence, which is a false evaluation of oneself.

The primary interest and analysis in this study are not the situation where one chooses a specific comparison target.1 This study is concerned with how individuals evaluate their abilities or performance compared to the group they belong to. The focus of the analysis is on how an individual compares his or her own ability or performance to the average ability or performance of the comparison group to which he or she belongs. In the context of social comparison, inaccurate judgments or evaluations of one’s abilities or performance can be divided into two types: misestimation, where one evaluates one’s abilities or performance differently than they actually are, and misplacement, where one incorrectly evaluates one’s abilities or performance in comparison to others.

2.2. Inverse Differential Information Hypothesis

Early studies of overconfidence focused on explaining overestimation and overplacement and attributed the causes of overconfidence to self-enhancing or self-protecting psychological motivations (Festinger 1954; Hakmiller 1966; Alicke 1985). On the other hand, the concept of egocentrism explains overconfidence not as a psychological motivation, but as a result of a cognitive trait. Egocentrism is the tendency for people to evaluate their own abilities or performance based primarily on information about themselves, with little regard for the comparison group. When people perform well on a low-difficulty task, they focus on the fact that they performed well, rather than thinking about whether the comparison group will also perform well, and thus evaluate themselves as better than others (Weinstein and Lachendro 1982; Goethals et al. 1991; Klar and Giladi 1999; Kruger 1999; Chambers and Windschitl 2004; Kruger and Burrus 2004; Windschitl et al. 2008; Logg et al. 2018).

These researchers trace the basis for people’s overestimations and overplacement judgments to a variety of cognitive biases. Goethals et al. (1991) explained that individuals have a uniqueness bias, in which they perceive socially desirable behaviors they take as unique and distinct from others, which leads them to see themselves as better than the average person. Epley and Dunning (2001, 2006) explain that overestimation and overplacement judgments of one’s own performance or abilities result from individuals’ tendency to rely on individual case-based information and ignore distributional information about the comparison group. Helzer and Dunning (2012) argue that overestimation and overplacement are paired because people have an agency bias, which means that when predicting their own future performance, people tend to give more weight to their own subjective aspirations for future performance and less weight to their objective past performance, while giving the opposite weight to others. Balcetis and Dunning (2013) found that when people predict the behavior of others, they consider the impact of changing circumstances and incorporate it into their predictions and estimations, but when they make predictions about themselves, they are less likely to do so. Consequently, their study revealed that greater errors in predictions and estimations of the impact of changing circumstances on behavioral change occur in self-assessments rather than in assessments of others.

These studies use these different kinds of cognitive biases to explain only overestimation and overplacement. However, in the real world, both overestimation and underestimation, and overplacement and underplacement, tend to be observed simultaneously in the same dataset. Therefore, there is a need for explanatory approaches that can address overestimation and underestimation, and overplacement and underplacement, simultaneously (Arkes et al. 1987; Erev et al. 1994; Kruger 1999; Chambers and Windschitl 2004).

First, let us look at the research that explains both overestimation and underestimation. Early on, it was noted that there is a close relationship between task difficulty and misestimation. Lichtenstein et al. (1982) reported a number of examples of the negative correlation between difficulty level and misestimation in probability assessments: people tend to underestimate the outcome when the task is easy and leads to a good outcome, and overestimate the outcome when the task is difficult. For example, people overestimate the probability of unfavorable or unlikely outcomes, such as getting cancer from smoking or dying as a teenager within the next year, while underestimating the probability of favorable or likely outcomes, such as staying healthy (Oskamp 1962; Viscussi 1990; Fishhoff et al. 2010).

Several approaches have been proposed to explain the negative association between difficulty and misestimation. Huttenlocher et al. (1991) found out that individuals, when asked to report an exact value but relying on inexact memory, engage in an estimation process that combines what they remember with the categorical information. They noted that this estimation process involves cognitive regression, wherein individuals focus on the central (prototypic) categorical value while disregarding its periphery. Moreover, individuals demonstrate a strong inclination towards regressive or conservative judgments when processing potentially incorrect information (Edwards 1968; Krueger and Mueller 2002; Fiedler and Unkelbach 2014). This tendency means that upon receiving additional information, people tend to make conservative judgments that only partly reflect the additional information, rather than correctly calculating the posterior probability as per Bayes’ theorem. As a result, it is observed that individuals tend to underestimate their performance on low-difficulty tasks due to insufficiently integrating the additional information, while they tend to overestimate their performance on high-difficulty tasks.

Let us apply the concept of cognitive regression and conservative estimation to financial literacy as follows: Individuals with either high or low actual financial literacy tend to exhibit cognitive regression, accepting some part of their estimation as an error. Those with high actual financial literacy will underestimate their financial literacy, while those with low financial literacy will overestimate theirs. As a result, a negative correlation is observed between actual financial literacy and misestimation.

Next, we will examine research that explains both overplacement and underplacement and the relationship between misestimation and misplacement. Perhaps the most important question for this discussion is “Can a person have a more accurate picture of who they are than others do, or is it the opposite?” Moore and Small (2007) and Moore and Healy (2008) have proposed the differential information theory to answer this question. They noted that information about others is more limited than information about oneself and referred to this as “differential information”. They argued that an individual’s predictions about others’ performance or abilities tend to regress more significantly to the mean compared to predictions about themselves due to this differential information. When a task is easy and the actual outcome is good, cognitive regression in estimation leads to an underestimation of oneself, while cognitive regression is stronger for the relatively less-informed others. Resultantly, an overplacement, where one believes erroneously they are better than others, is observed. Conversely, for difficult tasks, overestimation due to cognitive regression and underplacement due to differential information will be observed together. In other words, based on the differential information perspective, Moore and Healy (2008) explain that misestimation is positively correlated with task difficulty and misplacement is negatively correlated with task difficulty, and consequently, there is a negative correlation between misestimation and misplacement.

We can consider a perspective that is the opposite of differential information. In this paper, this perspective will be called “inverse differential information”. This perspective is well encapsulated in the statement, “We judge others based on what we see, but we judge ourselves based on what we think and feel” (Pronin 2008, p. 1177). The inverse differential information perspective holds that even if an individual has more information about themselves than anyone else, their self-evaluation is inherently subjective and subject to a variety of cognitive biases and distortions. As a result, the inaccuracy of an individual’s self-assessment is likely to be greater than if they were looking at others objectively. More and more specific information about oneself, rather than aiding in accurate evaluation, may be used as a source of cognitive biases and distortion, making objective evaluation more challenging. Furthermore, people are prone to engage in constructive cognitive behaviors to convince themselves that they are more capable than others in order to avoid cognitive dissonance during social comparison (Festinger 1957; Weinstein 1980; Taylor and Brown 1988; Goethals et al. 1991; Kunda 1990; Alicke and Sedikides 2009; Crusius et al. 2022), and it is difficult for people to even recognize that these cognitive processes are taking place (Pronin 2008; Wilson and Dunn 2004; Cohen 1981). As a result, people are hindered from objectively interpreting and storing and recalling information about their abilities or performance, leading to the distortion of information and systematic biases.

A meta-analysis by Mabe and West (1982) of 55 studies on the self-evaluation of people’s abilities or performance in various fields found that the average correlation between the two was 0.29 (standard deviation, 0.25). When Zell and Krizan (2014) synthesized 22 meta-analyses that measured the correlation between the self-evaluation of ability and actual performance, they found a mean correlation of 0.29 (standard deviation, 0.11). Evidently, the recognition of one’s abilities or performance are empirically only weakly related to one’s actual abilities or performance.

The inverse differential information theory is a perspective implicit in the egocentrism account and the work of Dunning and his colleagues. However, these studies merely explain the combination of overestimation and overplacement by invoking various cognitive biases, such as egocentric bias, uniqueness bias, case-based information reliance bias, agency bias, and so on. They do not account for the combination of overestimation and overplacement along with underestimation and underplacement.

The implication of various cognitive biases is that they result in an individual’s self-assessment being less accurate than their assessment of others. The inverse differential information theory is an integrated and parsimonious theory that posits, due to various cognitive biases and distortions, “an individual’s self-assessment is less accurate than their assessment of others”. This theory stands in opposition to Moore and Small (2007) and Moore and Healy’s (2008) differential information theory. The inverse differential information theory offers comprehensive explanatory power, providing a general expectation that encompasses not only the pairing of overestimation and overplacement but also the pairing of underestimation and underplacement, suggesting a positive correlation between misestimation and misplacement.

Let us apply the inverse differential information theory in conjunction with the principle of conservative estimation under uncertainty to changes in task difficulty. When a task is easy and the actual performance appears good, according to cognitive regression or conservative estimation, underestimation will occur. According to the inverse differential information theory, an individual objectively recognizes the low difficulty of a task and, reflecting this, rates the average performance of the comparison group highly. However, they tend not to sufficiently reflect this in their evaluation of their own performance or tend to evaluate their own performance less accurately, leading to a greater regression to the mean. Consequently, with easier tasks, there is a tendency to for individuals not only underestimate but also underplace their performance relative to the group average. Underestimation and under-placement are thus observed simultaneously. In the case of high task difficulty, overestimation along with overplacement will be observed, since misestimation is positively correlated with difficulty and misplacement is also positively correlated with difficulty in the perspective of inverse differential information, leading to the conclusion that there is a positive correlation between misestimation and misplacement. This is in direct opposition to the predictions of Moore and Small (2007) and Moore and Healy’s (2008) differential information theory.

The difference between the two opposing inferences about the relationship between misestimation and misplacement can be illustrated by the calibration curve depicted in Figure 1 and Figure 2. A calibration curve is a line that compares subjective probability judgments to actual probabilities (Lichtenstein et al. 1982). When the subjective probability judgment is the same as the actual one, the measurement is correct (calibrated), and when it is different, the measurement is incorrect (miscalibrated). In the differential information reasoning in Figure 1, the prediction line for one’s own performance is relatively closer to the 45° line than the prediction line for the average performance of unfamiliar others. This is because one believes that the accuracy of predicting one’s own performance is higher than the accuracy of predicting the performance of unfamiliar others. The 45° line is the line that represents actual performance or accurate prediction. In contrast, the inference from the inverse differential information, illustrated in Figure 2, presents the opposite scenario: the relative positions of the two prediction lines are inversed.

For example, for a low-difficulty range with a high actual correct rate of 0.9, the differential information inference suggests that in Figure 1, where the actual correct rate is ‘a’, an individual predicts a lower score of ‘b’ for one own’s score and a much lower score of ‘c’ for others’ average scores. Thus, the underestimation of ‘b-a’ and the overplacement of ‘b-c’ are observed in pairs. On the other hand, the inverse differential information inference suggests that in Figure 2, underestimation by ‘r-p’ and underplacement by ‘r-q’ are observed in pairs. The same can be said for the harder case, where the actual correct rate is 0.2.

What becomes clear from the above discussion is that cognitive conservatism in estimation under uncertainty and differential information are not the same. Cognitive conservatism in estimation is a cognitive tendency to regress observations that deviate from the mean back towards the mean. Differential information posits the separate claim that cognitive conservatism occurs more strongly towards others than towards oneself. In contrast, inverse differential information posits the opposite claim, that cognitive conservatism occurs more strongly towards oneself than towards others. When cognitive conservatism in estimation is combined with differential information, a negative correlation between misestimation and misplacement is predicted. However, when cognitive conservatism in estimation is combined with inverse differential information, a positive correlation between misestimation and misplacement is predicted. Applying the above reasoning to financial literacy yields the following hypothesis:

Hypothesis 1.

If the inverse differential information theory holds, a positive correlation between misestimation and misplacement in financial literacy will be observed.

The inverse differential information theory presupposes that conservative estimation or cognitive regression is valid. That is, Hypothesis 1 predicts that if misestimation in financial literacy shows a negative correlation with the actual score, then the inverse differential information theory will establish a positive correlation between misestimation and misplacement in financial literacy.

2.3. Correlation between Misestimation and Misplacement and Stock Market Participation

The so-called “stock participation puzzle”—the low proportion of households holding stocks despite the equity premium—was noted early on (Haliassos and Bertaut 1995; Campbell 2006), and the lack of financial literacy among households remains one of the leading hypotheses to explain this. Van Rooij et al. (2011) demonstrated that higher financial literacy has a positive effect on stock market participation, while Yoong (2011) and Yeh and Ling (2022) showed that low financial literacy negatively impacts stock market participation. In addition, Lusardi and Mitchell (2007), Van Rooij et al. (2012), Xia et al. (2014), and Allgood and Walstad (2015), Chen and Chen (2023) empirically demonstrated that low financial literacy negatively affects wealth size. They explained that this is because low financial literacy hinders retirement planning or stock market participation, thereby adversely affecting savings and wealth accumulation. In other words, the less financially literate an individual or household is, the less familiar they are with stocks and the more hesitant they are to invest in stocks for fear of making investment mistakes (Campbell 2006; Calvet et al. 2009; Agarwal et al. 2009).

Financial behavior is affected by not only individuals’ financial literacy but also by the way in which they subjectively evaluate their financial literacy. Van Rooij et al. (2012) found that underestimating one’s financial literacy negatively impacts the size of wealth, while Deaves et al. (2009), Xia et al. (2014), Allgood and Walstad (2015), and Ingelbrecht and Tedde (2024) showed overestimating one’s financial literacy has a significant positive relationship with the scale of stock investments, the proportion of stock investments in a portfolio of financial assets, and stock trading. Yeh and Ling (2022) found that overestimation impacts stock market participation experience. However, few studies have analyzed the impact of both types of financial literacy overconfidence—misestimation and misplacement—on stock market participation simultaneously. Merkle (2017) analyzed the impact of three forms of overconfidence in financial literacy—misestimation, misplacement, and overprecision—on the stock trading volume, trading frequency, investment diversification, and risk-taking of individual investors in the UK. When all three types of overconfidence are simultaneously included in the estimation model, he found that misestimation contributes significantly to poor investment diversification, and misplacement has a significantly positive effect on stock trading volume, stock trading frequency, and investment risk acceptance.

This study attempts to simultaneously analyze the impact of two types of financial literacy overconfidence—misestimation and misplacement—on the investment experience in financial securities such as stocks, bonds, and mutual funds. Hereafter, this experience will be referred to as the “stock participation experience”. According to the differential information theory, where overestimation pairs with underplacement and underestimation pairs with overplacement, they would act to cancel each other out. For instance, if individuals with low financial literacy overestimate their abilities or performance but simultaneously underplace them, their tendency toward irrational behavior due to overestimation could be mitigated by their underplacement. In other words, if the differential information theory is correct, it is expected that the interaction of misestimation and misplacement would have difficulty exerting a systematic effect on financial decision-making performance. On the other hand, if a positive correlation between misestimation and misplacement is observed according to the inverse differential information theory, the interaction of overestimation and overplacement would promote the stock participation experience, while the interaction of underestimation and underplacement would inhibit the stock participation experience. Thus, the following hypothesis, Hypothesis 2, can be proposed:

Hypothesis 2.

If misestimation and misplacement show a positive correlation, the interaction of misestimation and misplacement will have a positive impact on securities participation experience.

Although there are differences between countries, people generally have relatively low levels of financial literacy, especially among younger, older, female, and less educated individuals (Lusardi and Mitchell 2007, 2014; Stolper and Walter 2017; Arrondel 2018). For most people, investing in securities is a challenging area. If overestimation and overplacement in financial literacy appear together among those with low financial literacy, those people may participate in securities investment due to overconfidence and suffer financial losses and distress due to irrational investment decisions. On the other hand, the combination of underestimation and underplacement tends to occur in people with high financial literacy. In this case, the individuals are in a situation where they have the necessary knowledge and the ability to apply it, so the damage from irrational decision-making due to overconfidence may not be as severe. However, they might avoid stock participation due to their underestimation and underplacement, and thus experience a loss of opportunities. It is worthwhile to compare the combined impact of misestimation and misplacement on the stock participation experience in low and high financial literacy groups.

3. Materials and Methods

3.1. Materials

The survey, which included a financial literacy questionnaire, was administered to South Korean adults aged 20 and older from June to September 2018 using random digit dialing, with the goal of sampling 1000 observation cases. An observation was obtained when a professional survey company dialed a randomly generated mobile phone number, texted a survey to the phone, and the recipient responded to the survey. A small coffee coupon was offered to respondents online as an incentive to complete the survey.

After this process, we ended up with 1002 observations. There are 533 men and 469 women. By age, the number of respondents in their early 20s, late 20s, 30s, 40s, 50s, and 60s and over is 381, 125, 184, 138, 123, and 51, respectively. The high number of cases in the 20s is due to the fact that we planned to have a sample of 400 college students and 600 non-college adults. As planned, we obtained observations from 402 college students and 600 non-college adults.

As requested in the questionnaire, respondents first provide their demographic personal information. Next, respondents are asked, “How would you rate your financial literacy level compared to the average person?” Next, respondents are asked to indicate their response to each of the 10 questions to measure their financial literacy, and for each question, they rate their level of confidence in the probability that their response is the correct answer. These subjective response tendencies of a respondent are then combined with the respondent’s actual financial literacy score to produce information on misestimation and misplacement.

This research design is a quasi-experimental design in research methodology, because the sample is not randomly assigned (Meyer 1995; Shadish et al. 2002, chap. 4). Respondents categorize their level of comparative belief about their financial literacy by some unknown characteristic, rather than in a way that creates a selection bias, such as voluntariness. A quasi-experimental research design is sufficient, because the focus of this study is not on determining causality between misestimation and misplacement, but rather on the statistical relationship between the two.

3.2. Definitions of Measurement Variables

The survey asks respondents demographic and socioeconomic questions, followed immediately by “Compared to the average person, how do you think your financial literacy level is?” and ask to select one of the following responses: worse than average (WTA), around average (AVRG), or better than average (BTA). The self-assessed financial literacy compared to the group average will be referred to hereafter as the “comparison belief”. The survey is designed to ensure that the comparison belief is not influenced by the financial literacy measurement. Respondents first answer the question about the comparison belief before their financial literacy is assessed.

The assessment tool for measuring actual financial literacy is a test sheet consisting of 10 financial literacy questions in a 4-way multiple-choice format with one correct answer. The 10 questions measuring financial literacy consist of the types and characteristics of financial instruments, such as bank deposits, stocks, and bonds, loan rates and terms, managing personal credit, calculating compound interest, inflation and real interest rates, and the effects of monetary policy. The score a respondent achieved by completing the test paper (hereafter referred to as the “actual score”) is determined by awarding one point for each question answered correctly, for a total of 10 points.

For each individual item measuring financial literacy, respondents record their answer and indicate the degree to which they are confident that their answer is the correct one by selecting one of the following four-point Likert scales: “I don’t know at all”, “half and half”, “almost certain”, or “definitely certain”2 We operationally define the total number of items for which the respondent answered “almost certainly” or “definitely certainly” as the respondent’s self-assessed predicted score (hereafter referred to as “predicted score”). A respondent’s misestimation measure is operationally defined as the difference between his/her predicted score and his/her actual score. A respondent’s misestimation score is an integer that theoretically ranges from a minimum of −10 to a maximum of 10. A positive sign on the misestimation score corresponds to an overestimation and a negative sign to an underestimation.

WTA and BTA, per se, do not imply underplacement and overplacement, respectively. If respondents rate themselves as BTA and their actual performance aligns with this belief, it is not overplacement but a correct placement. Overplacement occurs when individuals rate themselves as BTA despite the fact that they are not. Likewise, underplacement happens when individuals rate themselves as WTA despite the fact that they are not. When the comparison belief matches the actual level, it is not a misplacement but rather a correct or exact placement.

There is a body of research that classifies people as overplacements, underplacements, or exact placements, based on whether their self-rated subjective financial literacy and their actual financial literacy are greater or less than the (standardized) average, respectively (Xia et al. 2014; Kramer 2016; Porto and Xiao 2016; Lewis 2018; Chen and Chen 2023). These categorizations only categorize subjects as “above average” or “below average” without considering the “average level” category. By only categorizing the true scores into below average and above average, it becomes impossible to define an actual score that corresponds to the respondents who rated themselves as AVRG. To avoid this problem, a range for the average score group should be defined for the actual scores. How this range is defined is operational. Once the range for the average score group is operationally determined, respondents with their actual scores will fall into one of the three groups: lower than the middle (LTM), the middle (MDL), or higher than the middle (HTM).

Since the actual score has a mean of 5.55 out of 10 and approximates a normal distribution, one can consider defining the range of average scores narrowly as 5–6, centered around the mean, more broadly as 4–7, or even more broadly as 3–8. The range of 5 to 6 is the smallest possible range that includes the true mean score of 5.55. In this case, the proportion of observations where individuals rate themselves as AVRG and their actual score falls within this average range is 22.7%. If the average range is set to 4–7 points, the proportion is 63.2%, and if set to 3–8 points, the proportion is 83.6%. Setting the range of the actual score group to 4–7 points is closest to the 60.8% of respondents who rate themselves as AVRG. Therefore, the analysis will focus on the case where the MDL group range is set to 4–7 points. Meanwhile, to evaluate the interaction between misestimation and misplacement in financial literacy, an interaction term is generated by multiplying the two overconfidence factors.

3.3. Methods

To test Hypothesis 1, we first verify whether there is a negative correlation between actual financial literacy scores and misestimation through correlation analysis and OLS multiple regression analysis. We set an average range for respondents’ actual financial literacy and categorize the respondent group into LTM, MDL, and HTM. This is combined with the comparison belief about financial literacy to create a variable that operationally measures misplacement. Hypothesis 1 is tested by confirming the correlation between misestimation and misplacement through correlation analysis and OLS multiple regression analysis. Hypothesis 2 is tested by conducting a binary logistic regression analysis, using stock market participation as the dependent variable and financial literacy misestimation, misplacement, and the interaction term of misestimation and misplacement as independent variables.

4. Results

4.1. Basic Statistics

The descriptive statistics of the actual and predicted financial literacy scores and misestimations for the 1002 observations are presented in

Table 1. Basic statistics of financial literacy variables.

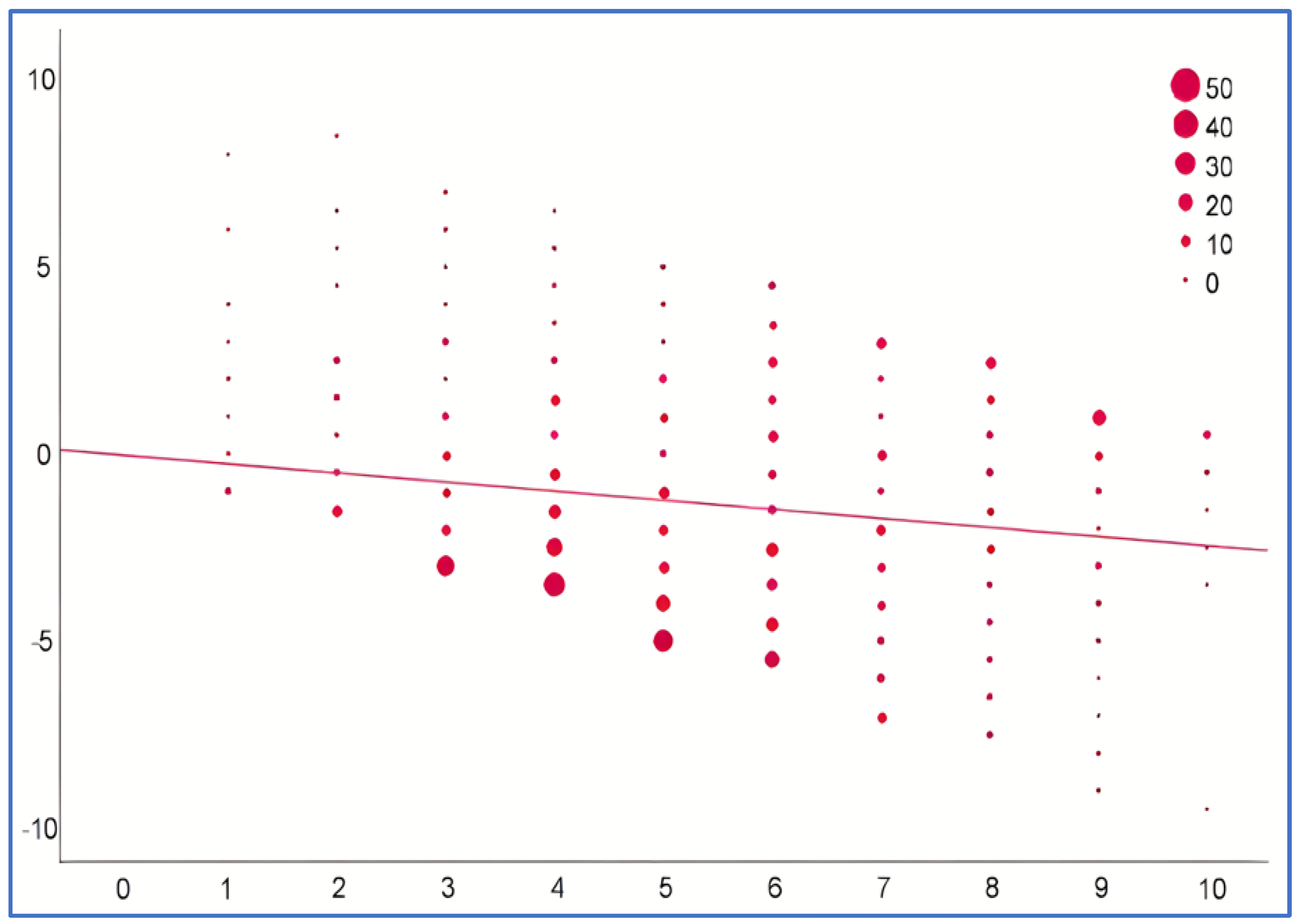
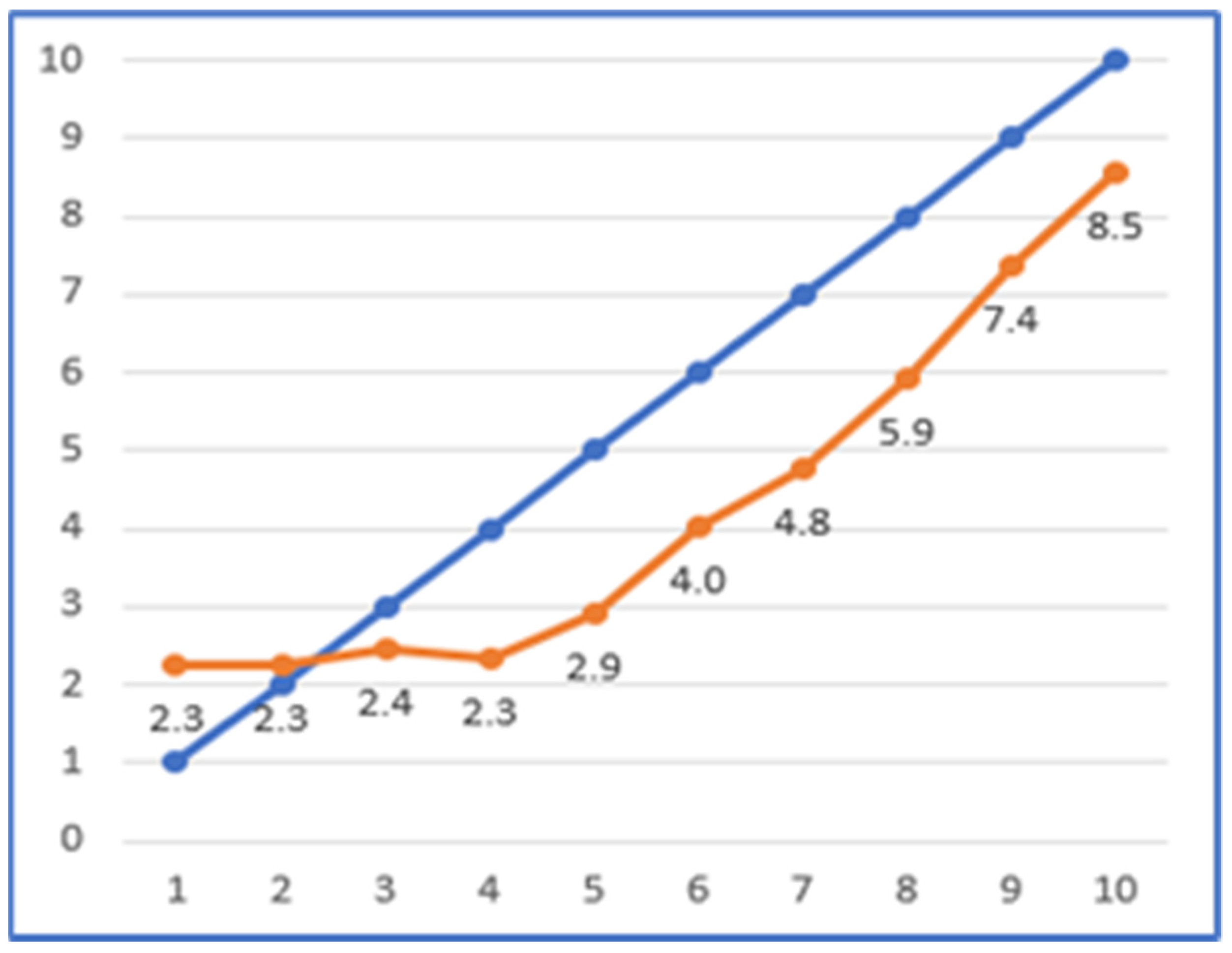
	Min.	Max.	Average	Median	Mode	S. D.
Actual Score	1	10	5.55	6	6	2.09
Predicted score	0	10	3.92	3	0	3.34
Misestimation	−10	8	−1.63	−2	−3	2.98

. Actual scores are near-normally distributed, ranging from 0 to 10, with a median and mode of 6, a mean of 5.55, and a standard deviation of 2.09. The predicted score has a median of 3, a mode of 0, and a mean of 3.92. The observations with a predicted score of 0 and 1 are 20.3% and 12.9% of the total observations.

In the survey, respondents identified themselves as either WTA, AVRG, or BTA. The range for the MDL group was set to 4–7 points. Respondents with an actual score of 8 or above were classified as HTM, and those with an actual score of 3 or below were classified as LTM. By classifying actual scores into the groups of LTM, MDL, and HTM, a 3 × 3 matrix for actual groups and comparison belief levels was created.

Table 2. Cross-tabulation between comparison belief and actual score group.

			Actual Score Group
		LTM	MDL	HTM
Comparison belief	WTA	2.53, 1.87, −0.66 (0.75, 2.74, 2.80)	5.32, 2.66, −2.66 (1.08, 2.80, 2.74)	8.32, 4.43, −3.89 (0.53, 2.82, 2.93)
	AVRG	2.49, 2.30, −0.19 (0.63, 2.56, 2.63)	5.44, 3.49, −1.95 (1.06, 3.02, 2.92)	8.55, 6.44, −2.11 (0.66, 3.16, 3.07)
	BTA	2.29, 4.11, 1.82 (0.85, 2.78, 1.97)	5.61, 4.60, −1.00 (1.15, 3.08, 2.77)	8.81, 8.63, −0.18 (0.74, 2.17, 2.06)
Total		2.48, 2.37, −0.12 (0.69, 2.69, 2.75)	5.44, 3.46, −1.97 (1.08, 3.03, 2.90)	8.58, 6.75, −1.84 (0.68, 3.17, 3.04)

Note: Numbers in parentheses are the standard deviations.

sequentially shows the mean values of the actual score, predicted score, and misestimation in each cell of the 3 × 3 matrix. The cells on the main diagonal of Table 2 are the cases where the comparison belief classification matches the level of actual scores. These include respondents who consider themselves BTA and score above the MDL score range, those who consider themselves AVRG and score within the MDL range, and those who consider themselves WTA and score below the MDL range, which we operationally define as an exact placement. The cells below the main diagonal represent cases where the subjective comparison belief ranking is higher than the actual score ranking, which is defined as overplacement. That is, the individuals in the BTA and LTM cell and the BTA and MDL cell think their financial literacy is better than the average actual score, though their literacy actually belongs to LTM or MDL at most, and the individuals in the AVRG and LTM cell think their financial literacy ranks as average, though their one actually belongs to LTM. The cells above the main diagonal represent cases where the comparison belief ranking is lower than the actual score ranking, which is defined as underplacement. In particular, if the AVRG and LTM cell and the BTA and MDL cell are relatively “weak overplacement”, the BTA and LTM cell can be called “strong overplacement”. Similarly, if the WTA and MDL cell and AVRG and HTM are relatively “weak underplacement”, the WTA and HTM cell can be called “strong underplacement”. The mean overestimation for the LTM group is −0.12, which is not significantly different from zero and is significantly smaller in absolute value at p < 0.001 compared to the means for the MDL and HTM groups. Notably, the strong overplacement group of LTM and BTA has a positive misestimation mean of 1.82.

The placement variables consist of strong underplacement, weak underplacement, exact placement, weak overplacement, and strong overplacement, and since these categories have an ordinal nature, we can assign the numbers 1, 2, 3, 4, and 5 to each of them. Next, we create an interaction variable between misestimation and the ordered placement by multiplying these two variables operationally. You can see the descriptive statistics of the interaction term at

Table 3. Descriptive statistics of the interaction term by financial literacy level.

		Interaction			Misestimation	Misplacement
	N	Mean	Median	S. D.	Mean	Mean
LTM	172	−0.10	−4	10.74	−0.12	3.83
MDL	633	−5.47	−6	8.55	−1.97	2.92
HTM	197	−3.00	−2	5.91	−1.84	2.13
Total	1002	−4.06	−6	8.77	−1.63	2.92

. In the overall sample, the interaction variable ranges from a minimum of −24 to a maximum of 35, with a median of −6, a mean of −4.1, and a standard deviation of 8.76, approximating a normal distribution. When analyzed by financial literacy levels, the mean of the interaction term is smallest for the LTM group at −0.10, followed by −5.47 and −3.00 for the MDL and HTM groups, respectively. The reason for the smallest mean in the LTM group is that the mean of misestimation is close to zero, even though the mean of misplacement is the largest. The magnitude of the standardized deviation is largest for LTM at 10.74 and smallest for HTM at 5.91.

Table 4. Correlations between the interaction term and financial literacy variables.

Target (N)	Actual Score	Misestimation	Misplacement
LTM (172)	−0.22 **	0.99 **	0.18 *
MDL (633)	−0.06	0.97 **	−0.02
HTM (197)	0.05	0.93 **	0.33 **
Total (1002)	−0.11 **	0.95 **	0.07 *

Note: Correlation coefficients with actual score and misestimation are Pearson’s coefficient and Spearman’s rho with misplacement. *, ** indicate statistical significance at p < 0.05, p < 0.01, respectively.

shows the correlation between the interaction term and the actual financial literacy scores, misestimation, and misplacement. The interaction term is significantly negatively correlated with the actual score variable in the LTM group. The interaction term exhibits a strong positive correlation of 0.93 or higher with misestimation across all financial literacy groups. The interaction term shows a significant positive correlation with misplacement in the LTM and HTM groups at p < 0.05, but the relationship is not significant in the MDL group.

4.2. Test of Hypothesis 1

Hypothesis 1 posits that there will be a positive correlation between misestimation and misplacement in financial literacy. First, Figure 3 shows the scatterplot of actual scores and misestimations in financial literacy. The observed calibration curve in Figure 4 plots the average predicted score against each actual score. For each actual score, the difference between the average predicted score and the actual score is the misestimation. This is the typical calibration curve reported by Lichtenstein et al. (1982). The calibration curve in Figure 4 shows that overestimation is observed for the lowest actual scores of 1 and 2, and underestimation is observed for the higher actual scores.

The Pearson correlation between actual score and misestimation is −0.170 at p < 0.01. Furthermore, when misestimation is estimated using OLS regression only with actual scores, the estimated coefficient is −0.243 and significant at p < 0.001. When basic demographic and socioeconomic controls such as gender, age group, and household income are added to the estimation model, the estimated coefficient for the actual score is −0.400, indicating a stronger negative correlation between misestimation and actual score. As a result, there is a significant negative correlation between the misestimation and actual score of financial literacy. This means that the cognitive conservatism in estimating financial literacy is supported by the data.

Table 5. Average financial literacy scores for the five placement groups.

	N	Actual Score (A)	Pred. Score	Misestimation (M)	M/A
Strong overplacement	17	2.29 (0.85)	4.12 (2.78)	1.82 (2.72)	0.79
Weak overplacement	197	3.90 (1.80)	3.34 (3.03)	−0.55 (2.72)	−0.14
Exact placement	512	5.58 (1.77)	3.97 (3.41)	−1.62 (2.89)	−0.29
Weak underplacement	239	6.64 (1.84)	4.21 (3.49)	−2.43 (2.88)	−0.36
Strong underplacement	37	8.32 (0.53)	4.43 (2.82)	−3.89 (2.93)	−0.46

Note: The numbers in parentheses are standard deviations.

shows the average actual scores, predicted scores, and the misestimation of financial literacy for the five placement groups. The average actual scores for each group are significantly different from each other at p < 0.01, while the average predicted scores do not show a significant difference. It implies that the average misestimation for the strong and weak misplacement groups are significantly different from each other at p < 0.1. For the strong and weak underplacement groups, the average misestimation is different from each other at p < 0.05, and for the other groups the differences are significant at p < 0.001.

In Table 5, as we move step-by-step from the strong underplacement to strong overplacement, the values of misestimation and the ratios of misestimation relative to the actual score gradually increase. This indicates an increasing transition from severe underestimation to overestimation. When treating strong and weak underplacement, exact placement, and weak and strong overplacement as ordinal variables (i.e., assigning values 1, 2, 3, 4, 5 in order) or as nominal variables, and calculating the nonparametric correlation coefficients with misestimation, the Spearman rho and Kendall tau-b values are 0.257 and 0.208, respectively, both significant at p < 0.01. This demonstrates a significant tendency for overestimation to pair with overplacement and underestimation to pair with underplacement. The data do not conflict with Hypothesis 1.

Table 6. Results from OLS-regressing misestimation on misplacement dummy variables.

	Model 1		Model 2
	B	t	B	t
Constant	−1.615	−12.800 ***	−1.680	−4.895 ***
Strong overplacement	0.688	4.885 ***	0.604	4.352 ***
Weak overplacement	0.265	4.436 ***	0.223	3.658 ***
Weak underplacement	−0.410	−3.665 ***	−0.365	−3.277 **
Strong underplacement	−2.277	−4.684 ***	−1.939	−3.958 ***
Actual score			−0.195	−3.714 ***
Control variables	Not included		Included
Model Fit, Explanatory Power	F = 23.8 (p = 0.000), adj. R square = 0.083.		F = 15.8 (p = 0.000), adj. R square = 0.172.

Notes: N = 1002. The reference for the placement dummies is the exact calibration group. Control variables include sex, marriage, age, and household income level. Note: **, *** indicate significance at p < 0.01, and p < 0.001, respectively.

shows the results of OLS-regressing misestimation on the placement dummy variables. Model 1 includes only the placement dummies in the model. The reference for the placement dummies is the exact placement group. The results show that the estimated coefficients of all misplacement dummy variables are significant at p < 0.001. Compared to the exact placement group, the misestimations of the strong overplacement group and the weak overplacement group are higher on average by 0.688 and 0.265 points, respectively. On the other hand, the misestimations of the weak underplacement group and the strong underplacement group are, on average, −0.410 and −2.277 higher than that of the reference, respectively. Model 2 includes the actual financial literacy scores and basic demographic and socioeconomic controls in Model 1. The positive correlation between misestimation and misplacement is still significant, and the estimated coefficient of the actual score is −0.195, which is significant at p < 0.001. In conclusion, there is a positive correlation between misestimation and misplacement as well as conservative estimation in financial literacy estimation. In accordance with the inverse differential information theory, there is a statistically significant tendency for overestimation to pair with overplacement and underestimation to pair with underplacement. The data support Hypothesis 1, and the hypothesis cannot be rejected.

4.3. Test of Hypothesis 2

To test Hypothesis 2, we conduct a comparative analysis of the effect of misestimation, misplacement, and their interaction on stock participation experience across the entire sample and within the groups categorized by the levels of financial literacy: LTM, MDL, and HTM. Before performing the regression analysis, we examine the proportion of stock participation experience across the explanatory and control variables in

Table 7. Securities participation experience in the discrete independent variables.

Variable	Item	N	Ratio of Experience	S. D.	F(p)
actual score group	LTM	172	0.25	0.43	26.931(0.000)
	MDL	633	0.34	0.47
	HTM	197	0.58	0.49
placement group	overplacement	276	0.40	0.49	1.251(0.287)
	exact placement	512	0.35	0.48
	underplacement	214	0.40	0.49
Sex	Male	533	0.45	0.50	26.783(0.000)
	Female	469	0.29	0.45
Age group	20s	506	0.21	0.41	31.718(0.000)
	30s	184	0.54	0.50
	40s	138	0.50	0.50
	50s	123	0.55	0.50
	60s or older	51	0.59	0.50
Marriage	Married	382	0.54	0.499	80.958(0.000)
	Unmarried	620	0.27	0.444
Household income level	Below median income	317	0.25	0.435	19.773(0.000)
	Around median income	288	0.39	0.488
	Above median income	349	0.50	0.501
	I do not know income	48	0.15	0.357
Stock participation of family member	Yes	325	0.59	0.492	107.532(0.000)
	No	677	0.27	0.444
	Total	1002	0.37	0.484

Notes: ‘Ratio of experience’ means the average ratio of stock participation experience of the respondents at each corresponding item group. F and p denote F-value and p-value from analysis of variance, respectively.

. A respondent’s stock participation experience is defined as whether the respondent is currently investing or has ever invested in securities such as stocks, bonds, mutual funds, etc.

The percentage of all respondents with stock participation experience is 0.37. As the level of financial literacy increases, the stock participation experience ratio significantly rises. There are no statistically significant differences in the ratios of stock participation experience across the placement groups. The ratio of stock participation experience for men is 0.45 compared to 0.29 for women. Experience in stock investing is significantly lower among those in their 20s than among those in their 30s and older, with no significant difference among those in their 30s and older. Married respondents have a ratio of 0.54 compared to 0.27 for single respondents. When comparing by median household income, the likelihood of stock participation experience increases significantly with household income level. The probability of having stock participation experience is 0.59 for those with a family member who invests in securities, compared to 0.27 for those without such a family member, and the difference is significant.

Table 8. Binary logistic estimation results for stock participation experience.

	Model 1a			Model 1b
	B	Wald	Exp(B)	B	Wald	Exp(B)
Actual score	0.281	34.728	1.324 ***	0.280	34.473	1.323 ***
Misestimation	0.108	15.989	1.114 ***	-	-	-
Overplacement	0.231	10.251	1.260 **	0.234	10.466	1.264 **
Underplacement	−0.234	1.404	0.791	−0.339	2.987	0.712 †
Interaction	-	-	-	0.034	14.581	1.035 ***
Sex (Male)	0.448	7.593	1.565 **	0.459	7.995	1.582 **
Marriage (Married)	0.091	0.153	1.096	0.111	0.226	1.117
Age group (30s)	1.205	23.777	3.335 ***	1.209	24.005	3.349 ***
Age group (40s)	0.989	11.713	2.687 **	0.964	11.133	2.623 **
Age group (50s)	1.292	17.249	3.641 ***	1.273	16.750	3.572 ***
Age group (60s or older)	1.231	9.114	3.425 **	1.250	9.393	3.489 **
Below median income	−0.600	8.537	0.549 **	−0.602	8.581	0.548 **
Above median income	0.081	0.183	1.085	0.088	0.215	1.092
I do not know income	−0.393	0.746	0.675	−0.375	0.681	0.687
Experience of family member	1.231	99.018	3.424 ***	1.237	56.499	3.445 ***
Constant	−3.219	110.857	0.062 ***	−3.019	100.020	0.039 ***
N, Explanatory Power	N = 1002. pseudo R square = 0.355.			N = 1002. pseudo R square = 0.295.

Notes: The pseudo R-squared is Nagelkerke R-squared. Exp(B) is the odds ratio. The reference for placement dummies is the calibration group. The reference variables for sex, marriage, and age brackets are female, unmarried, and 20s, respectively. For income levels, the reference variable is ‘around median household income’. The reference variable for experience of family member is ‘no family member investing in securities. ^†, **, *** denote significance at p < 0.1, p < 0.01, and p < 0.001, respectively.

shows the estimation results of a binary logistic model with stock participation experience as the dependent variable for the entire sample. The dependent variable takes the value of 1 if an individual has ever invested in stocks, bonds or funds or is currently investing in securities, and 0 otherwise. As shown in Table 5, the number of cases of strong overplacement and strong underplacement is not large, at 17 and 37 cases, respectively. This leads to a low degree of freedom issue in a binary logistic regression model when conducted by groups categorized by financial literacy levels. Therefore, strong overplacement and weak overplacement are combined into “overplacement” and strong underplacement and weak underplacement combined into “underplacement” for the analysis model.

In Model 1a of Table 8, the actual financial literacy score, misestimation, misplacement dummies, and basic control variables are included in the model for estimation. To avoid collinearity issues that may arise due to high correlation between misestimation and the interaction term, the interaction term is excluded, and only misestimation is included in the estimation model. In Model 1b, the interaction term is included in the model instead of misestimation for analysis. In addition to the explanatory variables, control variables such as gender dummy, marital status dummy, age group dummies, household income level dummies, and whether family members invest in securities are included. Exp(B) is the odds ratio of an estimated coefficient, indicating the ratio of the probability of having stock participation experience to the probability of not having such experience.

In Model 1a, the odds ratio of the actual financial literacy score is 1.324, indicating that for each 1-point increase in the actual score, the odds of stock participation experience increase by 32.4% at p < 0.001. For each 1-point increase in misestimation, the odds of securities participation experience increase by 11.4% at p < 0.001. Respondents with overplacement have a 26.0% higher odds of stock participation experience than those with exact placement. For underplacement, the odds of having stock participation experience decrease, significant at p < 0.1. In Model 1b, the odds ratio for the interaction term, included instead of misestimation, is 1.035 at p < 0.001, meaning that for 1-point increase in the interaction term, the odds of having securities participation experience increase by 3.5%. In summary, there is a significant tendency for higher financial literacy, a greater overestimation of one’s financial literacy, and larger interaction terms to increase the probability of having stock participation experience. Financial literacy misplacement shows a significant positive relationship with stock participation experience. Overplacement has a positive effect on stock participation experience, while underplacement has a negative effect on the experience. The effect of actual score and financial literacy misestimation on the stock participation experience is consistent with Yeh and Ling (2022), where Japanese survey data in 2015 were used. The effect of misplacement on stock participation is consistent with the findings of Xia et al. (2014).

Looking at the control variables, the probability of having stock participation experience is significantly higher for men compared to women at p < 0.05, and for individuals aged 30 and above compared to those in their twenties at p < 0.01. Respondents with household income below the median are significantly less likely to have the stock participation experience than those with median incomes at p < 0.01. If there is a family member who invests in stocks, the odds of the respondents having their own stock participation experience are more than 3.4 times higher compared to those without such a family member.

Model 2, Model 3, and Model 4 in

Table 9. Results of binary logistic estimation of stock participation experience by financial literacy level.

	Model 2a		Model 2b		Model 3a		Model 3b		Model 4a		Model 4b
	B	Exp(B)	B	Exp(B)	B	Exp(B)	B	Exp(B)	B	Exp(B)	B	Exp(B)
Actual score	0.340	1.404	0.358	1.431	0.304	1.356 **	0.304	1.355 **	0.344	1.410	0.329	1.390
Misestimation	0.228	1.256 **	-	-	0.061	1.063 †	-	-	0.181	1.198 **	-	-
Overplacement	−0.042	0.986	−0.074	0.976	1.037	2.821 ***	1.060	2.888 ***	-	-	-	-
Underplacement	-	-	-	-	0.054	1.056	0.007	1.077	−0.773	0.462 †	−0.921	0.398 *
Interaction	-	-	0.062	1.064 **	-	-	0.021	1.022 †	-	-	0.075	1.078 *
Sex (Male)	0.748	2.114	0.716	2.046	0.445	1.561 *	0.441	1.554 *	0.500	1.649	0.563	1.756
Marriage (Married)	−0.184	0.832	−0.194	0.824	0.013	1.013	0.024	1.025	0.477	1.611	0.515	1.674
Age group (30s)	1.328	3.772 †	1.347	3.846 †	1.283	3.608 ***	1.274	3.576 ***	1.146	3.146 *	1.171	3.225 *
Age group (40s)	0.417	1.518	0.413	1.511	1.006	2.734 **	0.991	2.694 **	1.222	3.395 †	1.145	3.142 †
Age group (50s)	1.378	3.966 †	1.373	3.949 †	1.532	4.627 ***	1.518	4.561 ***	0.736	2.088	0.671	1.956
Age group (60s+)	1.902	6.696	1.980	7.244	1.674	5.332 **	1.674	5.333 **	0.024	1.025	0.024	1.025
Below med. income	−0.932	0.394 †	−0.915	0.400 †	−0.529	0.589 *	−0.533	0.587 *	−0.667	0.513	−0.686	0.503
Above med. income	−0.355	0.701	−0.334	0.716	0.177	1.194	0.181	1.199	−0.114	0.893	−0.094	0.911
I do not know income	−0.811	0.445	−0.831	0.436	−0.201	0.818	−0.187	0.830	−19.863	0.000	−19.680	0.000
Experience of family member	2.182	8.867 ***	2.192	8.597 ***	1.197	3.310 ***	1.200	3.300 ***	0.710	2.034 †	0.708	2.029 †
Constant	−3.000	0.050 **	−3.049	0.047 **	−3.627	0.027 ***	−3.616	0.027 ***	−3.070	0.046	−2.991	0.050
N, Explanatory power	N = 172, pseudo R square = 0.382.		N = 172, pseudo R square = 0.388.		N = 633, pseudo R square = 0.317.		N = 633, pseudo R square = 0.318.		N = 197, pseudo R square = 0.371.		N = 197, pseudo R square = 0.358.

Notes: The pseudo R-squared is Nagelkerke R-squared. Exp(B) is the odds ratio. The reference for placement dummies is the calibration group. The reference variables for sex, marriage, and age brackets are female, unmarried, and 20s, respectively. For income levels, the reference variable is ‘around median household income’. The reference variable for experience of family member is ‘no family member investing in securities. ^†, *, **, *** denote significance at p < 0.1, p < 0.05, p < 0.01, and p < 0.001, respectively.

show the results of binary logistic estimation for the respondents in the LTM, MDL, and HTM groups, respectively. As seen in Table 2, underplacement cases does not exist in the LTM group, so the underplacement variable does not appear in the estimation of Model 2. Likewise, overplacement cases does not exist in the HTM group, so the overplacement variable does not appear in the estimation of Model 4. Since there is a strong positive correlation between misestimation and the interaction term, collinearity issues may arise. Therefore, in Models 2a, 3a, and 4a only misestimation is included for estimation, while in Models 2b, 3b, and 4b, misestimation is dropped, and the interaction term is included instead.

Looking at the estimation result of Model 2a for the LTM group, the estimated coefficients for actual score and overplacement are not significant. A one-point increase in misestimation is associated with a 25.6% increase in the odds of having stock participation experience at p < 0.01. In Model 2b, a one-point increase in the interaction score is associated with a 6.4% increase in the odds of having stock participation experience at p < 0.01. In Models 3a and 3b, which focus on respondents in MDL group, a one-point increase in actual score is associated with a 36% increase in the odds of having stock participation experience at p < 0.01. In Model 3a, a one-point increase in misestimation is associated with a 6.3% increase in the odds of stock participation experience at p < 0.1, and the odds of stock participation experience for overplacement respondents are 2.8 times that of exact placement respondents at p < 0.001. In Model 3b, a one-point increase in the interaction score increases the odds of stock participation experience by 2.2% at p < 0.1. In Model 4 for respondents in HTM group, a one-point increase in misestimation increases the odds of stock participation experience by 19.8% at p < 0.01, while the odds of stock participation experience for underplacement respondents are only 0.4 times that of exact placement respondents at p < 0.001. In Model 4b, a one-point increase in the interaction score is associated with a 7.8% increase in the odds of having invested in securities at p < 0.05.

Summarizing the analysis results in Table 9, both misestimation and overplacement individually tend to significantly increase the probability of stock participation experience. Additionally, misestimation and misplacement interact to significantly increase stock participation experience. Consequently, the data support Hypothesis 2, and we cannot reject Hypothesis 2. On the other hand, underplacement significantly reduces stock participation experience in the high financial literacy group. Highly financially literate individuals with underplacement tend to miss out on valuable opportunities for wealth growth due to their underplacement. This contrasts with individuals with intermediate financial literacy, who tend to have invested in securities due to overplacement.

Meanwhile, in all financial literacy groups, men tend to have a higher probability of stock participation experience than women. Marital status is not associated with the probability of stock participation experience. There is a significant trend in the MDL and HTM groups, indicating that those in their 30s and older are more likely to have stock participation experience than those in their 20s, but in the LTM group, stock participation experience does not significantly increase with age. This suggests that low financial literacy is a barrier to participation in stock investing across the lifespan. People with lower household incomes tend to have difficulty having stock participation experience, while higher household income does not necessarily increase the probability of stock participation experience.

The participation of family members in the stock market has a significant interactive tendency to promote other family members to have participated in the stock market. Additionally, the odds ratios of the interaction are 8.6 (p < 0.001), 3.3 (p < 0.001), and 2.0 (p < 0.1) for the LTM, MDL, and HTM groups, respectively, indicating that the lower the level of financial literacy of an individual, the higher the probability of this interaction occurring. In general, people’s financial decisions and behaviors are influenced by those around them. Hong et al. (2004) show that social households that interact with neighbors or that attend church have higher stock participation rates than non-social ones, possibly due to lower stock participation costs from the social contacts. Kaustia et al. (2023) showed in their analysis, using extensive survey data on individuals aged 50 and above from 20 European countries, that participation in social activities in various areas such as political, religious, charity, education, training, or sports positively influences stock market participation. Van Rooij et al. (2011) and this study show that these peer effects operate within a family. Van Rooij et al. (2011) found that parental financial literacy had a significant positive effect on their children’s stock participation. This study reveals that individuals with lower levels of financial literacy are more likely to have participated in stock investments influenced by their family member’s investments. This suggests that individuals with lower financial literacy are more likely to lower the costs of stock participation and overcome entry barriers by learning from the stock investment of the family members around them. However, it also indicates that they might be at risk of making unwise behaviors in stock investments based on inaccurate knowledge and information for stock investments from their family members.

It is important to note that the estimation results of stock participation experience concerning financial literacy and both types of financial literacy overconfidence in the above analysis do not imply causality. Financial literacy overconfidence is related to subjective beliefs, and subjective assessments of financial literacy generally do not correlate highly with objective financial literacy. Factors influencing subjective judgments, in particular, have a strong psychological nature (Hadar et al. 2013; Allgood and Walstad 2015). While financial literacy and the misestimation and misplacement in it affect the probability of stock participation experience, the possibility of inverse causality cannot be excluded, where stock participation experience influences one’s misestimation and/or misplacement of their financial literacy. The experience of stock participation itself may make individuals more confident and overconfident in their financial literacy. Additionally, due to the limitations of the available data, it was not possible to include the necessary control variables in the estimation models. For example, respondents’ risk aversion tendencies were not controlled for. As a result, the estimated regression coefficients might be overestimated.

5. Discussion and Conclusions

The inverse differential information theory that this study propose is a unifying and parsimonious theory that argues individuals engage in a variety of cognitive biases and distortions when evaluating themselves (their abilities or performance), and that their evaluations of themselves are more inaccurate than their evaluations of others. This is in contrast to Moore and Small (2007) and Moore and Healy’s (2008) differential information theory. The inverse differential information theory predicts a positive relationship between misestimation and misplacement, and the empirical analysis using data on South Korean adult’s financial literacy and overconfidence confirms this positive correlation. Specifically, there is a significant tendency for overestimation to be paired with overplacement in the low financial literacy group and underestimation to be paired with underplacement in the non-low financial literacy group. Other studies that have simultaneously analyzed misestimation and misplacement in financial literacy include Merkle (2017) and Vörös et al. (2021), which also reported significant positive correlations between misestimation and misplacement.

The inverse differential information theory predicts that misestimation and misplacement are positively related, so it is predicted that their combination will positively influence the likelihood of having stock participation experience. The analysis results revealed that both misestimation and misplacement individually and in combination positively influenced an individual’s stock participation experience, both in the full sample and by financial literacy level. When individuals with high financial literacy underplace their financial literacy, they tend to participate much less in the stock market, resulting in significant opportunity losses for wealth accumulation. This contrasts with individuals who have moderate financial literacy but overplace their literacy, leading to a higher tendency to participate in stock market.

At low levels of financial literacy, there is no difference in the probability of stock participation between those in their 20s and older, while at middle and high financial literacy levels, those in their 30s and older are more likely to have experience of participation in the stock market than those in their 20s. This suggests that low financial literacy is one of the barriers to investing in the stock market. People with lower incomes tend to have difficulty gaining experience in stock participation, while high income does not necessarily increase the probability of an individual’s stock participation experience. The probability of an individual’s stock participation experience significantly increases, if his or her family member invests in stocks, in other words, stock participation among family members tends to promote each other’s participation, and this tendency is especially pronounced when his or her financial literacy is low.

There is a significant tendency for the overestimation, overplacement, and their interaction to increase stock participation experience, especially among individuals with low financial literacy. When individuals with inadequate financial literacy participate in stock investment, they are likely to achieve poor returns due to a lack of knowledge about the basic principles of investment, leading to non-diversified investments in a few stocks, leveraged investments, and frequent trading. Therefore, it is necessary to establish and strengthen social efforts and institutional mechanisms to help individuals with low financial literacy and novice investors recognize investment risks and make rational investment decisions.

Financial education is especially important for individuals with low financial literacy to live their life-long sustainable and responsible financial lives in the era of longevity and digitized everyday life (Atkinson et al. 2015; IOSCO and OECD 2018; Suschen et al. 2022). Financial education typically aims to convey objective financial knowledge. However, changes in knowledge and understanding inevitably involve subjective changes, including overconfidence. Subjective financial literacy is generally found to have a stronger influence on financial behavior and decision-making than objective financial literacy. Therefore, it is necessary to pay attention to and control the impact of subjective financial literacy or financial literacy overconfidence during financial education. Financial education for individuals with low financial literacy or novice investors should not only cover the principles of financial investment but also inform them that they may tend to overestimate or overplace their financial knowledge, which could lead to losses in their investments (Cwynar et al. 2020).

The theory of inverse differential information proposed by this study is a general statement. Hypothesis 1, derived from the inverse differential information theory, was supported by data on financial literacy and overconfidence among Korean adults, and was not rejected. However, whether these findings merely report a unique case in South Korea can only be confirmed through subsequent studies. Furthermore, the data used were from a 2018 survey. Since then, the global economy and financial markets have experienced significant impacts due to the COVID-19 pandemic. It is expected that studies using more recent data will empirically demonstrate the relationship between misestimation and misplacement in financial literacy and their effects on financial behavior and markets in the post-pandemic era more accurately.

This study shows that whether misestimation and misplacement are negatively or positively related is crucial in terms of their influence on human decision-making and behavior. It is intuitive that overestimation would pair with overplacement and underestimation with underplacement, with overconfidence exerting a systematic and strong influence. However, this correlation logically follows from the premise that inaccuracies in assessing one’s own abilities and performance are greater than inaccuracies in assessing others’ abilities and performance. This premise—inverse differential information—may not be intuitive and could be seen as controversial. The research analyzed these issues using financial literacy and stock market participation as its subjects. However, overconfidence is a significant factor that can influence human decision-making and behavior in various ways (for a review, see Malmendier and Taylor 2015; Karki et al. 2024). It would be desirable and meaningful to examine the relationship between misestimation and misplacement in different fields and to analyze the impact on decision-making and behavior.