Dynamic Stability of Public Debt: Evidence from the Eurozone Countries

Abstract

This paper investigates the dynamic stability of public debt and its solvency condition in the face of crisis periods (1980–2021) in a sample of 11 euro-area countries. The focus is on the feedback loop between the dynamic stability of public debt and interest rates, discounted by economic growth, in conjunction with budget deficits during tranquil and turbulent periods. Using the GMM panel dynamic model, the results show that dynamic stability was the case before the global financial crisis (GFC), while from GFC to the pandemic, dynamic instability prevailed and persisted in the evolution of public debt. Furthermore, panel threshold estimates show that dynamic instability of debt starts to violate the solvency condition when the borrowing cost is above 3.29%, becomes even stronger when it is above 4.39%, and exerts even more pressure when the level of debt is greater than 91%. However, the debt sustainability condition reverses course when economic growth is higher than 3.4%. The main policy implication drawn from the results is that low interest rates can create a self-reinforcing loop of high debt, which itself is a serious matter for public authorities when designing economic policies.

1. Introduction

From the global financial crisis (GFC) to the COVID-19 pandemic, the debt-to-GDP ratio has risen largely due to higher fiscal deficits in response to emergency budgets undertaken by governments to limit the human and economic impact in both crisis periods (Bianchi et al. 2020). Interestingly, even if fiscal expansion (essential to face economic stress times) fell to pre-crisis levels, public debt soared. Borrowing was a global phenomenon across the crisis periods, and the argument is that interest rates were expected to remain below the economy’s growth rate so as to ease debt rollovers, that is, debt issuance without any fiscal cost (Debrun et al. 2019; Blanchard 2019; Giannini and Oldani 2022). This is what we refer to as the sustainability or solvency condition. However, a complication that might arise is that investors may believe that high(er) debt is risky as governments may not be able to meet future payment obligations. As a result, they will require high risk premiums. Consequently, interest rates will start rising because of higher risk premiums, thus straining and eventually violating the solvency condition. Crucially, the key issue is that a country’s solvency condition ensures the smooth and uninterrupted servicing of sovereign debt contracts, while sovereign insolvency is conceived as a country’s inability to pay its debts as well as its inability to continuously ensure access to borrowing because of high risk premiums. However, there is little evidence in the literature that more debt puts higher pressure on interest rates, leading to violation of the solvency condition and turning a country insolvent. Also, there is no evidence about the growth rate above which debt does not derail.

From the theoretical point of view, the Keynesian school recognizes that the impact of deficits in stress periods is temporary, and timely deficits have favorable effects on the economy. As a result, temporarily elevated debt drops to previous levels. However, the Neoclassical analysis argues that higher debt levels driven by the budget deficits created to face a crisis period (for example, when a crisis hits) are not temporary, and austerity policy needs to be undertaken to restore to previous levels. Interestingly, recent studies claim that higher debt levels might be welfare-enhancing if the growth rate is higher than the borrowing cost, and economic growth is the main factor stabilizing the dynamics of debt, which is essential for debt sustainability in the medium and long term (Debrun et al. 2019; Blanchard 2019; Giannini and Oldani 2022).

In several euro countries, the fiscal deficit fell to pre-crisis levels, and economic growth was higher than interest rates despite a soaring public debt. The main reasons were the sizeable budget deficits and the low cost of borrowing which, over the past few years, became more appealing due to the central bank’s (the Fed) extensive quantitative easing. Although the cost of borrowing may seem sustainable, the indirect cost of not reducing the public debt appears to be very high. The reason may be that higher debt may cause either a higher risk premium or changes in the multiplier effect of the stability of public debt. This second effect can be very important if debt levels are high.

Based on the above discussion, this study aims to investigate how the dynamic stability of solvent affects the sustainability of public debt in view of crisis and regular periods. We use a sample of 11 euro-area countries over the period of about 42 years starting from 1980. We contribute to the literature in four different ways. First, we examine the impact of the dynamic stability/instability of debt on the development of public debt, not only in regular periods but also in times of stress. Second, we examine how the sustainability of public debt fares with increasing interest rates, which, in turn, reflects the fear of default on public debt through high risk premiums. Third, we provide new insights into the threshold effects above which dynamic stability of the debt-to-GDP ratio conditional on interest rates and vice versa, turns into debt instability. Fourth, as economic growth is considered as one of the main factors that can contribute to debt reduction, we examine threshold effects for annual growth to GDP, above which the country’s insolvency condition starts to disappear, thus making the solvency condition recover.

In essence, we pay much more attention to the proper accounting of how the stability of debt (dynamics) affects debt development (growth) in conjunction with continuous budget deficits from before GFC to the COVID-19 pandemic period. We also explore how the debt solvency condition, represented by the interest rate being less than the country’s growth rate, affects the debt’s dynamics and sustainability. Doing so, we provide new insights about the interest rates’ threshold effects above which sustainability of government debt turns to unsustainability (or instability). We also examine the limits of debt dynamics above which the solvency condition is at risk—that is, when the interest rate is growing faster than economic growth because of higher sovereign risk premia. We further investigate the low limits of economic growth above which government debt starts to become sustainable (the solvency condition). We perform a number of estimations of our models during a number of periods during which crises took place. Given that these periods entailed different economic and financial complexities, the insights derived from the findings will be of importance to all market agents. The results provide important implications for governments that may become insolvent and help them avoid being forced to default, given the knowledge of the levels of unsustainable debt dynamics. Also, government authorities can use the borderline (threshold) between a solvent and insolvent public debt and hence avoid any signals of uncertainty being made to the markets.

The remainder of this paper is organized as follows: Section 2 provides a short review of the literature. Section 3 describes the theoretical model, the data sources and variable construction, and the empirical model specification. Section 4 presents and discusses the estimated results, and Section 5 summarizes the main findings.

2. Short Literature Review

Even though many factors go into assessing how much debt an economy can safely carry, a large number of studies in the empirical literature dealing with debt sustainability have focused on fiscal sustainability instead. Early studies on government debt found that debt sustainability can be achieved in the sense of stationary primary deficit, satisfying an intertemporal budget constraint by raising the primary surplus, or equivalently, by reducing the budget deficit in the years that follow (Hamilton and Flavin 1985; Trehan and Walsh 1991; Bohn 1995, 1998). Another strand of literature provided substantial evidence that the non-stationarity of the debt cannot be rejected as government spending is growing faster than revenue (Kremers 1988; Wilcox 1989; Davig 2005). Nevertheless, the authors argued that the consequent rejections of stationarity do not invalidate the propositions of Hamilton and Flavin (1985) and showed that the U.S. government stabilized the ratio of Federal debt to GNP.

Contradictory conclusions are also drawn across studies where different samples of countries are examined, and the sustainability of fiscal deficits has been receiving increasing attention, particularly for advanced economies and in the newly formed euro area. Empirical results by Hamilton and Flavin (1985) and Afonso (2005) suggest that fiscal policy may not have been sustainable1 in a sample of 18 OECD countries over the period 1970–2003 they examined, whereas fiscal sustainability was evidenced for euro-area countries, either by having a high debt-to-GDP ratio or violating the Maastricht treaty by permitting more than three percent of the deficit-to-GDP ratio (Greiner et al. 2007).

In crisis periods, governments attempt to boost household consumption through financial support for the unemployed, thus increasing public spending, which in turn increases government debt, and the main approach for investigating debt sustainability is still fiscal sustainability (Challes et al. 2011). In line with the Keynesian school, empirical evidence suggests that in a depressed economy, any expansionary fiscal policy does not impose a future burden, and the primary mechanism is the extra output because of the government purchases multiplier effects, whereas attempts to reduce the public debt via fiscal consolidation resulted in a high level of debt-to-GDP ratio through their negative impact on output (DeLong et al. 2012; Fatás and Summers 2018).

However, in line with the Neoclassical school, empirical evidence suggests that higher debt levels are driven by budget deficits, mostly created by governments to face a crisis or stress periods. In turn, these fiscal shocks could deteriorate macroeconomic imbalances, and chronic fiscal imbalances might lead to vicious austerity cycles, where only fiscal discipline is a means of achieving credible and shorter adjustments. The stability of public debt depends on a continuing tendency of fiscal policy to reduce the primary deficit (Neaime 2015; Agnello et al. 2015; Dawood et al. 2017; Goedl and Zwick 2018; Gaysset et al. 2019).

Another approach to examining debt sustainability is fiscal solvency, and the basic idea is to verify whether the present value of budget constraint would be pursued over the distant future. The findings suggest that a very high ratio of government debt to GDP affects the spread between government bond yields and increases the risk premium, which subsequently affects the cost of financing for budget deficits. Thus, the solvency condition is at risk (Ardagna et al. 2007; Cournède 2010; Furceri and Mourougane 2012). Furthermore, Ghosh et al. (2013) explored the debt limit above which the solvency condition is rejected, thus measuring the fiscal space, and showed that, as the debt is around 90–100 percent of GDP, the risk premium increases due to the higher probability of default, making higher interest rate expenses and, in turn, increasing the possibility of a permanently increasing debt-to-GDP ratio.

From a different perspective, a factor that can contribute to debt sustainability is economic growth. Many studies have reported that public spending volatility results in interest rate and output volatility, which, in turn, undermine economic growth (Fatás and Mihov 2003; Furceri 2007; Afonso and Furceri 2010; Afonso and Jalles 2012). Gómez-Puig and Sosvilla-Rivero (2018) argue that public debt always has a negative impact on the long-run performance of a country’s economy if public debt goes beyond 77% of GDP in a study with a sample of 101 countries (Grennes et al. 2010), and above 90% in a sample of 12 euro-area countries (Checherita-Westphal and Rother 2012). Interestingly, empirical studies predict that the possibility of reducing debt through inflation is applicable in the medium and long term (Kwon et al. 2006; Aizenman and Marion 2011; Akitoby et al. 2017; Giannini and Oldani 2022).

Nevertheless, after the GFC, a prolonged period of low interest rates in the European Union has favored the stockpiling of debt because of the countries’ increased capacity to borrow, but this does not necessarily translate to an ability to service higher debt levels. One question is whether debt-carrying capacities can sufficiently handle the elevated debt levels as additional burdens of debt need to be more carefully managed. Also, controlling the sustainability of fiscal deficits is insufficient if the countries are unable to roll over their debt, and the intertemporal solvency condition imposes mild restrictions on the paths of fiscal balances and debt levels that are consistent with a country being solvent. From our perspective, the intertemporal solvency condition seems to be a weak criterion since only adjustments through taxes and spending have to be made to achieve debt sustainability. The solvency condition through fiscal adjustments is not supported; a change in policy or in relevant macroeconomic variables (growth, inflation, interest rate) must occur to stabilize the debt ratio and satisfy the solvency condition. If the debt-to-GDP ratio increases over time, dynamic stability may become unstable, which, in turn, violates the solvency condition reflected by higher risk premiums. This implies that dynamic instability is a stronger condition.

3. Methodology and Data

In this section, we lay out the theoretical motivation of the study and then the econometric specification. We also include a section on the data sources and variable construction. We begin with the theoretical model.

3.1. Theoretical Model

Before proceeding to the empirical analysis, we first introduce the theoretical Keynesian model for government debt, which is proposed by Schmitt-Grohé and Uribe (2003), Philippopoulos et al. (2017), and Blanchard and Johnson (2017). The main macroeconomic policy instruments (fiscal and monetary) are linked through the government budget constraint as below:

$$T_t+{(B}_t-B_{t-1})+{(M}_t-M_{t-1})=G_t+i_{t-1}{B}_{t-1}$$

where, on the left-hand side, we have government revenue (comprising taxes, T_t, change in debt, B_t − B_t−1, and seigniorage, M_t − M_t−1) equaling the government expenditure on the right-hand side (government spending, G_t, and interest payments on previous debt, i_t−1 × B_t−1).

Dividing all terms by nominal output, Y_t = P_ty_t, the public debt-to-output ratio and the dynamics of public debt are given below:

$$\frac{B_t}{Y_t}=\left(1+i_{t-1}\right)\frac{Y_{t-1}}{Y_t}\frac{B_{t-1}}{Y_{t-1}}+\frac{G_t}{Y_t}-\frac{T_t}{Y_t}-\left[\frac{M_t}{Y_t}-\frac{Y_{t-1}}{Y_t}\frac{M_{t-1}}{Y_{t-1}}\right]$$

or

$$b_t=\left[\frac{{1+i}_{t-1}}{{(1+\gamma }_t\left){(1+\pi }_t\right)}\right]b_{t-1}+g_t-t_t-\left[m_t-\frac{m_{t-1}}{{(1+\gamma }_t\left){(1+\pi }_t\right)}\right]$$

(1)

where

$b_t=\frac{B_t}{Y_t}$ represents the public debt to GDP at period t;

${\gamma }_t=\frac{Y_t-Y_{t-1}}{Y_{t-1}}$ denotes the growth rate of real output at period t;

${\pi }_t=\frac{P_t-P_{t-1}}{P_{t-1-1}}$ denotes the inflation rate at period t;

$m_t-\frac{m_{t-1}}{{(1+\gamma }_t\left){(1+\pi }_t\right)}$ is the real change in the monetary base or seigniorage at period t.

Other things equal, dynamic stability of the debt-to-GDP ratio depends on the magnitude $\frac{{1+i}_{t-1}}{{(1+\gamma }_t\left){(1+\pi }_t\right)}$ on the inherited debt in Equation (1) above. Dynamic instability means that the debt-to-GDP ratio increases over time. Also, fiscal solvency holds when it is believed that $g_t+\frac{g_{t+1}}{1+i_t}=t_t+\frac{t_{t+1}}{1+i_t} or t_t-g_t=\frac{t_{t+1}}{1+i_t}-\frac{g_{t+1}}{1+i_t}$, which suggests that the current level of budget deficit should be equal to the expected discounted present value of future primary surpluses. If it is believed that $g_t+\frac{g_{t+1}}{1+i_t}>t_t+\frac{t_{t+1}}{1+i_t} or t_t-g_t>\frac{t_{t+1}}{1+i_t}-\frac{g_{t+1}}{1+i_t} ,$ which implies that future deficits become worse, then the fiscal solvency condition is violated, and we have fiscal insolvency.

3.2. Data Sources and Variable Construction

This study employs annual data for a panel of 11-euro area countries over the period 1980–2021 with a total of 462 observations. The sample countries are Austria, Belgium, Finland, France, Germany, Greece, Ireland, Italy, Netherlands, Portugal and Spain.

Table 1. List of variables.

Variables	Description of Variables	Sources
ggd	General government debt as a fraction of GDP (%)	IMF, Global Debt Database
ggdp	Annual percentage growth rate of GDP (%)	World Bank
cpi	Inflation rate (%)	World Bank
int	Long-term interest rates (%)	International Monetary Fund
pb	Primary balance as a fraction of GDP (%)	International Monetary Fund
ms	Growth rate of money supply (%)	European Data Warehouse
fdi	Net foreign direct investment as a fraction of GDP (%)	World Bank
open	Trade openness (exports + imports as a fraction of GDP (%))	European Data Warehouse

presents the data and their sources.

Following Equation (1) of the theoretical model, we construct the variable describing (measuring) dynamic stability as follows:

$$dyn=\left[\frac{{1+int}_{t-1}}{{(1+ggdp}_t\left){(1+cpi}_t\right)}\right]{ggd}_{t-1}$$

where ${int}_{t-1}$ is the long-term interest rates for government bonds at time t − 1; ${ggdp}_t$ and ${cpi}_t$ stand for economic growth and inflation rate at time t, respectively; and ${ggd}_{t-1}$ is the level of public debt in the previous year.

Table 2. Summary statistics.

	ggd	ggdp	cpi	int	pb	ms	fdi	Open
Mean	74.86	2.01	3.89	2.90	−3.81	80.14	4.08	81.217
Median	66.06	2.00	2.74	2.75	−3.15	77.91	1.49	66.10
Maximum	212.4	24.40	13.88	6.18	6.86	151.9	86.47	252.2
Minimum	10.89	−10.80	0.100	−2.216	−31.31	6.204	−36.14035	31.56
Std. Dev.	35.05	3.090	3.506	2.014	4.064	24.20	9.733269	41.36
Skewness	0.851	0.162	1.467	−0.191	−0.931	0.103	3.753070	1.350
Kurtosis	3.89	11.23	4.352	2.547	7.197	3.188	26.21	4.637
Obs.	462	461	462	462	462	462	462	462

Note: The variables are used as defined in Table 1.

displays some summary statistics on the main magnitudes for the entire period. First, we can observe that the general government debt (ggd) ranged from a low value of 10.89% to a high of 212.4% for the sample of countries examined. This high range shows up in the high standard deviation value as well. Hence, we have countries with tractable levels of debt to GDP and others that far exceed their GDP value. Second, the GDP growth rate (ggdp) or economic growth magnitude ranged from negative to positive among these countries, which suggests that they have gone through contraction or recession periods. Third, the negative interest rates, int, followed by very high inflation rates (the cpi magnitude), suggest desperate efforts by these countries’ central banks to boost investments and thus economic growth. Fourth, this is also corroborated by the very high rate of growth of the money supply (ms), which is seen to have exceeded 150%. Fifth, the values of the two indicators of foreign exposure/influences (fdi and open) suggest additional attempts to spur economic growth. Finally, the negative skewness values of the interest rate and the primary balance (pb) imply frequent, unexpected, asymmetric, and negative changes in these magnitudes, both of which adversely affect economic growth and, consequently, budget deficits and debt.

3.3. Econometric Model

Equation (2) below presents our panel model used to investigate how dynamic instability affects public debt:

$$y_1={\alpha }_1+{\beta }_1{X}_1+{\gamma }_1\mathrm{Z}+u_1$$

(2)

where the dependent variable $y_1$ is the general government debt (ggd) expressed as a percentage of GDP. Next, matrix X₁ includes the dynamic stability of public debt (dyn) and the primary balance (pb). Matrix $Z$ includes some macroeconomic variables—to be used as control variables—that are considered significant for the debt evolution, namely, foreign direct investment (fdi) and trade openness (open). Foreign direct investment and trade openness are both expected to be negatively associated with public debt because of the endogenous relationship with economic growth (Li and Liu 2005; Asteriou et al. 2023). Trade openness is the sum of exports and imports to GDP and constitutes an index for the degree of international trade.

Next, in Equation (3), we investigate the mechanisms linking dynamic stability with public debt:

$$y_2={\alpha }_2+{\beta }_2{X}_2+{\gamma }_2\mathrm{Z}+u_2$$

(3)

where the dependent variable $y_2$ is dynamic stability (dyn), and matrix X₂ contains the lag of dependent variable (L_dyn) and the primary balance (pb).

In Equations (4) and (5) below, we examine the feedback of debt’s dynamic stability (dyn) with regard to two main components of its coefficient (the fraction constructed following Equation (1) above): interest rates and economic growth. In this sense, we investigate how the solvency condition is affected by dynamic stability.

$$y_3={\alpha }_3+{\beta }_3{X}_3+{\gamma }_{3}Z+u_3$$

(4)

$$y_4={\alpha }_4+{\beta }_4{X}_4+{\gamma }_{4}Z+u_4$$

(5)

where the dependent variables $y_3$ and $y_4$ are interest rates (int) and economic growth (ggdp), respectively, while matrices X₃ in Equation (4) and X₄ in Equation (5) contain the lag of dependent variables, dynamic stability (L_dyn), and economic growth (L_ggdp). In essence, we examine the nature and extent of the mutual interdependence between the two magnitudes. $y_{s, }$ and $u_s$, are $\sum _{i=1}^N{ T}_i{X}_1$ matrices representing the dependent variables and error terms, respectively, while ${\alpha }_{s }$ are $\sum _{i=1}^j T_i{X}_1$ associated with unobservable variables. ${\beta }_s$ are ${ T}_i{X}_1$ matrices for coefficients.

Panel methodologies such as OLS and fixed effects estimators are consistent when N (No. of variables) is large but also when T (No. of periods) is large (Baltagi et al. 2016). However, a number of econometric problems plague such panel models, such as the existence of bi-directional causality between variables, omitted variable bias, time-invariant (time-fixed effects), and country characteristics (country-fixed effects), which may be correlated with the explanatory variables that can lead to endogeneity and misspecification-as well as the presence of autocorrelation (Bond and Windmeijer 2002). Hence, the generalized method of moments (GMM) estimator was developed to overcome the above shortcomings as it controls for possible specification bias (Blundell and Bond 1998), and it is suited well for datasets with small T and larger N. Following Holtz-Eakin et al. (1988), Arellano and Bond (1991) developed a GMM estimator that instruments the differenced variables with all their available lags in levels. A problem with this estimator is that lagged levels are poor instruments for first differences if the variables are close to behaving like a random walk. A system GMM is an augmented version developed by Blundell and Bond (1998) that overcomes this issue by employing both levels and differences as instruments, while the assumption is that these differences are uncorrelated with the country-specific effects.

Difference- and System-GMM are applied in one- and two-step variants. The two-step variants use a weighting matrix that makes two-step GMM asymptotically efficient. In this paper, we employ the system GMM estimator proposed by Roodman (2009) using a two-step approach and obtain robust standard errors with Windmeijer’s (2005) finite sample correction. We provide results for the robustness and sensitivity of the instruments and coefficients and report Hansen’s test of instrument validity and overidentifying restrictions, as well as the Arellano and Bond test for serial correlation.

3.4. Model Specification for Threshold Effects

Further, we attempt to investigate possible threshold effects of dynamic stability and solvency conditions on public debt. For this reason, we examine the panel threshold effects of the interest rates above which dynamic stability is converted to instability or debt derailment. We also examine the solvency to insolvency transition mechanism. If the debt-to-GDP ratio increases, the impact of interest rates will increase because of the risk premium, thus violating the solvency condition. We apply the fixed-effect panel threshold model proposed by Hansen (1999). All panel threshold models are examined for a triple threshold, which divides the equations into three distinct regimes with β_s and δ_s coefficients. Each regime has different coefficients for the regime-dependent variable while maintaining common coefficients for the control variables. The empirical models are provided below.

$$\begin{gathered} y=\mu +{\beta }_{11}X+{\beta }_{12}int\left(I\right)\left(dyn\le {\gamma }_1\right)+{\beta }_{13}int\left(I\right)\left({\gamma }_1\le dyn\le {\gamma }_2\right) \\ +{\beta }_{14}int\left(I\right)(dyn\ge {\gamma }_2)+{\epsilon }_1 \end{gathered}$$

(6)

and

$$\begin{gathered} y=\eta +{\beta }_{21}X+{\beta }_{22}dyn\left(I\right)\left(int\le {\zeta }_1\right)+{\beta }_{23}dyn\left(I\right)\left({\zeta }_1\le int\le {\zeta }_2\right) \\ +{\beta }_{24}dyn\left(I\right)(int\ge {\zeta }_2)+{\epsilon }_2 \end{gathered}$$

(7)

where y is a $\sum _{i=1}^N{ T}_{i}X1$ matrix representing the dependent variable general government debt (ggd), µ and η are $\sum _{i=1}^j T_{i}X1$ matrices associated with unobservable variables, X is a matrix that includes the primary balance (budget deficit/surplus) variable and the control variables (that is, net foreign direct investment and trade openness), and ϵ_1it, ϵ_2it are the error terms. In Equation (6), int is the variable used as the regime-dependent variable to split the sample into regimes, and dyn is the threshold variable, while in Equation (7), dyn is the variable used as the regime-dependent variable to split the sample into regimes, and int is the threshold variable. Finally, γ_s, ζ_s are the unknown threshold parameters for the threshold variables of debt dynamics and interest rates, respectively. I is the indicator (dummy) variable, which takes the value 1 if the argument in parenthesis is valid and 0 otherwise.

We also apply the fixed-effects panel threshold model (Equation (8)) to examine possible threshold effects above which economic growth can recover the solvency condition.

$$\begin{gathered} y=\nu +{\delta }_{1}X+{\delta }_{2}dyn\left(I\right)\left(ggdp\le {\theta }_1\right)+{\delta }_{3}dyn\left(I\right)\left({\theta }_1\le ggdp\le {\theta }_2\right) \\ +{\delta }_{4}dyn\left(I\right)(ggdp\ge {\theta }_2)+{\epsilon }_3 \end{gathered}$$

(8)

where dyn is the variable used as the regime-dependent variable, and economic growth, ggdp, is the threshold variable. θ_s are the unknown threshold parameters for the threshold variable economic growth.

4. Estimation Results

4.1. System GMM Panel Estimation Results

To investigate the impact of dynamic stability during several crisis periods, we conducted estimates with different samples along the time dimension. The results of the empirical model (2) are presented in

Table 3. Panel estimation results. (Dependent variable: public debt to GDP).

	(I)	(II)	(III)	(IV)	(V)	(VI)
	1980–1990	1990–2000	2000–2007	2007–2012	2012–2018	2018–2021
Δdyn	0.0233 ***	0.493 ***	0.787 ***	0.360 ***	0.498 ***	0.962 ***
	(5.56)	(8.83)	(13.31)	(8.36)	(4.85)	(7.98)
Δpb	−0.589 ***	−0.893 ***	−0.514 ***	−0.880 ***	−0.483 **	−0.903 ***
	(−8.79)	(−4.88)	(−4.87)	(−8.44)	(−2.79)	(−8.09)
fdi	−0.372 ***	−0.0598 ***	−0.0366 **	0.0149	−0.0871 *	−0.0698
	(−11.49)	(−5.35)	(−2.47)	(0.34)	(−1.99)	(−0.55)
Δopen	−0.0253	−0.148 **	−0.0228	0.222 **	−0.208 **	−0.150 *
	(−1.32)	(−3.26)	(−0.77)	(2.70)	(−2.78)	(−1.93)
cons	3.231 ***	1.146 ***	0.266	2.000 ***	0.208	0.0333
	(18.79)	(8.51)	(1.59)	(5.23)	(0.53)	(0.07)
N	109	110	88	55	66	33
AR(1)	0.080	0.118	0.132	0.107	0.133	0.133
AR(2)	0.383	0.119	0.253	0.314	0.822	0.157
Hansen	0.751	0.724	0.725	0.243	0.307	0.182
No. of instruments	10	11	10	10	8	8

Notes: * p < 0.10, ** p < 0.05, *** p < 0.01. Numbers in parentheses denote t-statistics. The letter Δ denotes the first difference operator used for the variables that were transformed to become stationary. The AR(1) and AR(2) entries represent the autoregressive coefficients. Hansen refers to Hansen’s J-statistic used to determine validity of the over-identifying restrictions in the model.

. We employed six different ranges of time periods, including normal and stress times, in the examined period 1981–2021. In version I of the model, we examine the period 1980–1990, when the savings and loan (1980) and Latin America sovereign debt (1982) crises occurred, as well as a stock market crash (1987) and crash of junk bonds (1989). In version II of the model, the period 1990–2000 is examined, where a massive interest rate crisis occurred in Mexico (1994), while in 1997–1998 and 1999–2000, the Asia crisis and dotcom bubble occurred, respectively. In versions III and IV of the models, two subperiods are examined: the tranquil period in Europe (2000–2007), where the new euro currency was created, and the global financial crisis (GFC) (2007–2013), which is a period that includes the EU debt crisis (2012) as well. Finally, in version V of the model, a normal (tranquil) period is examined covering the post-GFC period up to the COVID-19 health crisis (2012–2018), while version VI examines the stress time during the pandemic.

The findings of Table 3 reveal that across all examined periods, debt dynamics have a significantly positive effect on public debt, while the impact of budget deficit2 is significantly negative. Both signs were expected since debt dynamics include the past accumulated debt, thus having higher levels of debt to service, whereas lower levels of budget deficit lead to lower levels of public debt. Interestingly, the results indicate that the impact of dynamic stability is stronger compared to the effect of budget deficit on public debt over the periods 2000–2007 (pre-GFC), 2012–2018 (post-GFC), and during the pandemic (2018–2021).

A general conclusion is that debt dynamics seem to prevail in regular, normal economic periods rather than in stressful economic times, while this is not the case for budget deficit, which has a stronger impact when the aforementioned stress events occur. However, during the 2020 health crisis, the effects of both variables tended to be equivalent.

Regarding foreign direct investment (fdi), a significantly negative impact on debt was found before the GFC period, while in the post-GFC period, the impact seems to be very weak. Additionally, international trade (open) seems to be the driver in the reduction in public debt after the crisis. However, this is not the case during the GFC, as openness is significantly positive.

We further investigated the mechanisms for higher levels of debt dynamics (dyn), and the results are presented in

Table 4. Panel estimation results. (Dependent variable: dynamic stability).

	(I)	(II)	(III)	(IV)	(V)	(VI)
	1980–1990	1990–2000	2000–2007	2007–2012	2012–2018	2018–2021
L_Δdyn	0.00629	0.434 ***	0.399 ***	1.879 ***	0.464 ***	0.266 ***
	(0.85)	(4.97)	(7.49)	(8.07)	(7.18)	(5.18)
Δpb	0.146	0.0549	0.380 ***	0.257	−0.892 **	−1.506 ***
	(1.32)	(0.24)	(3.46)	(0.77)	(−2.39)	(−9.57)
fdi	−0.274 ***	−0.128 ***	−0.0809 ***	0.306 **	0.474 ***	0.130 **
	(−4.45)	(−3.88)	(−7.88)	(2.65)	(4.38)	(3.08)
Δopen	−0.123	−0.297 **	−0.203 ***	−1.846 ***	−0.631 **	0.137 ***
	(−1.81)	(−2.69)	(−4.90)	(−4.22)	(−2.41)	(3.22)
cons	2.929 ***	1.551 ***	0.697 ***	−1.711	−1.272 **	−0.628
	(7.61)	(4.87)	(5.62)	(−1.61)	(−2.30)	(−1.76)
N	98	110	88	55	77	44
AR(1)	0.087	0.071	0.095	0.04	0.033	0.017
AR(2)	0.910	0.124	0.333	0.250	0.296	0.853
Hansen	0.283	0.535	0.317	0.110	0.131	0.515
No. of instruments	10	10	10	10	8	10

Notes: see Table 2. **, *** refer to statistical significance at the 1% and 5% levels, respectively.

. The results indicate that lower budget deficits increase the debt dynamics in the pre-GFC period, but this is not the case in the after-GFC period and until the pandemic period. This suggests that austerity through lower budget deficits contributes to dynamic stability. In contrast, the findings imply that before the GFC, foreign direct investment contributed to the dynamic stability of debt, but again, this was not the case during and after the GFC until the pandemic period. Moreover, trade openness corroborates the above result not only in the pre-GFC period but also in financial stress times by indicating that international trade contributes to debt sustainability.

Next, we investigated the feedback of debt dynamics to borrowing costs, thus examining the relationship between dynamic instability and solvency conditions expressed by the relationship between the interest and economic growth rates. The results are reported in

Table 5. Panel estimation results (Dependent variable: interest rates).

	(I)	(II)	(III)	(IV)	(V)	(VI)
	1980–1990	1990–2000	2000–2007	2007–2012	2012–2018	2018–2021
L_int	0.911 ***	1.030 ***	0.610 ***	1.159 ***	0.586 ***	0.919 ***
	(8.87)	(33.41)	(6.78)	(8.81)	(47.34)	(4.50)
Δdyn	−0.00218	0.00319	−0.0819 ***	0.0862 **	0.102 ***	−0.112 **
	(−0.27)	(0.20)	(−4.74)	(2.35)	(7.53)	(−2.44)
Δpb	−0.133 *	−0.0898	0.0561	0.153 ***	0.115 ***	−0.379 ***
	(−1.98)	(−1.27)	(1.05)	(3.23)	(3.50)	(−6.95)
fdi	−0.0368	0.0253 **	−0.00302	−0.148 **	0.0655 ***	−0.0205
	(−0.27)	(2.23)	(−0.27)	(−2.43)	(3.80)	(−0.28)
Δopen	−0.0562 **	−0.138 ***	0.0230	−0.163 ***	−0.0768 ***	−0.00129
	(−2.58)	(−4.57)	(0.96)	(−4.54)	(−3.96)	(−0.06)
cons	0.854	−0.180	0.510 **	0.206	−0.245 **	−1.078 ***
	(1.51)	(−1.11)	(2.38)	(0.59)	(−2.60)	(−7.28)
N	109	110	88	55	66	33
AR(1)	0.029	0.036	0.056	0.043	0.014	0.047
AR(2)	0.977	0.587	0.390	0.125	0.343	0.753
Hansen	0.753	0.456	0.156	0.358	0.617	0.616
No. of instruments	10	10	10	10	10	10

Notes: see Table 3.

. The findings show that dynamic instability was not a problem before the GFC, but during and after the GFC periods, debt instability emerged and contributed to higher borrowing costs (interest rates), thus endangering (and violating) the debt solvency condition. However, this was not the case during the pandemic period.

Finally, in

Table 6. Panel estimation results. (Dependent variable: growth).

	(I)	(II)	(III)	(IV)	(V)	(VI)
	1980–1990	1990–2000	2000–2007	2007–2012	2012–2018	2018–2021
L_ggdp	0.730 ***	1.129 ***	0.407 ***	−0.231 **	0.0613	−0.1000
	(9.22)	(4.05)	(5.55)	(−2.42)	(1.30)	(−1.39)
Δdyn	0.0278 ***	0.190	−0.239 ***	−0.265 ***	−0.206 *	−0.283 ***
	(4.02)	(1.77)	(−14.71)	(−9.39)	(−1.89)	(−3.57)
Δpb	0.103	−0.133	0.226 ***	0.255 ***	0.116	0.722 ***
	(0.88)	(−0.47)	(7.58)	(7.80)	(0.63)	(12.33)
fdi	−0.0105	0.0776	−0.0635 ***	−0.0681	−0.00896	0.207 ***
	(−0.31)	(1.65)	(−6.10)	(−1.48)	(−0.12)	(3.79)
Δopen	0.0101	0.322 ***	0.146 ***	0.152	0.0672 **	0.0365
	(0.63)	(6.40)	(10.24)	(1.72)	(2.36)	(1.32)
cons	0.834 ***	−1.411	1.472 ***	1.827 ***	1.322 ***	1.608 ***
	(4.47)	(−1.42)	(4.27)	(8.41)	(4.30)	(3.40)
N	109	110	88	55	66	33
AR(1)	0.021	0.017	0.042	0.104	0.023	0.033
AR(2)	0.130	0.167	0.160	0.165	0.255	0.962
Hansen	0.505	0.891	0.164	0.463	0.963	0.457
No. of instruments	10	10	10	10	10	10

Notes: see Table 3.

, we present the results from the feedback of debt dynamics to economic growth. The overall findings suggest that debt dynamics contributed to higher economic activity only in the early period between 1980 and 1990, while after 2000, this effect was converted to negative, indicating that higher levels of debt hinder economic performance. Additional results imply that trade openness (open) positively (and statistically) contributes to economic growth, whereas foreign direct investment (fdi) is not always significant and with the correct sign (it is possible to assume that its impact is embedded or absorbed by the open magnitude). These findings are in line with the findings by Alsamara et al. (2024) for their oil- and non-oil-producing countries sample.

4.2. Panel Threshold Results

Table 7. Panel threshold estimation. Dependent variable: public debt to GDP.

		Threshold var.: dyn			Threshold var.: Interest Rate			Threshold var.: Growth
	dyn ≤ 69.3	69.3 ≤ dyn ≤91.9	91.9 ≤ dyn	int ≤ 3.3	3.3 ≤ int ≤ 4.4	4.4 ≤ int	gdp ≤ −0.7	0.75 ≤ ggdp ≤ 3.4	3.4 ≤ ggdp
Δint	−0.109 (−0.67)	0.250 ** (2.08)	6.275 *** (8.68)
Δdyn				0.004	0.030 *	0.152 ***	0.054 ***	−0.0026	−0.025 ***
				(0.42)	(1.92)	(5.04)	(5.99)	(−0.24)	(−5.94)
					Common controls
Δpb		1.362 *** (12.70)			0.964 *** (5.83)			0.586 *** (5.83)
ms		−0.126 ***			−0.138 ***			−0.097 ***
		(−3.63)			(−2.96)			(−2.96)
fdi		−0.046 *			−0.049 **			−0.069 **
		(−1.74)			(−2.74)			(−2.74)
Δopen		−0.081 * (−1.72)			−0.152 *** (−3.37)			0.030 (0.67)
constant		0.933 ***			1.144			3.518 ***
		(2.39)			(1.460)			(4.89)

Note: Double threshold model is estimated, where two different thresholds are found with significant levels splitting the regime-dependent variables into three different segments. *, **, *** refer to statistical significance at the 10%, 5% and 1% levels, respectively.

reports the results of estimating Equations (6), (7), and (8), respectively. In Table 6, we first examine the effect of interest rates, which is the regime-dependent variable for public debt conditional on debt dynamics (dynamic stability), and which, in turn, acts as the threshold variable. The results suggest that debt sustainability (or the solvency condition) is not a problem when the debt level is under 69.28% (as a fraction of GDP): that is, when the impact of interest rates is negative and statistically insignificant. This negative effect converts to significantly positive when the level of debt lies between 69.28% and 91.86%, when the estimated coefficient turns from negative (−0.109) to positive (0.250) and statistically significant. When debt dynamics (dyn) exceed the 91.86% threshold value, we observe that the magnitude of the estimated coefficient on interest rates rises significantly, from 0.250 to 6.275, with a significantly positive effect at the 1% level of significance. This indicates that when the debt level is around 92%, interest rates start to push debt to higher levels, and this will trigger a violation of the debt solvency condition, turning it to insolvency. This obviously implies that investors doubt that countries will be able to meet their financial obligations to repay their debt via the means of higher risk premia (which causes higher interest rates).

Next, we provide new insights within the estimated results, where dynamic stability is used as a regime-dependent variable and interest rates act as the threshold variable. The findings suggest that dynamic stability (dyn) starts to push to higher levels of debt when the interest rate is above 3.3% and becomes even stronger when it goes beyond 4.4%, thus leading to unsustainability of debt dynamics. However, when economic growth is examined as the threshold variable, the results show that dynamic instability reverses to stability when economic growth exceeds 3.4%.

The findings of threshold effects of public debt are in line with the existing literature (Checherita-Westphal and Rother 2012; Alsamara et al. 2024), but threshold effects of interest rates and economic growth above which debt raises or drops are not demonstrated. Our results provide new insights regarding the mechanisms—the solvency condition and dynamic instability—through which public debt rises and creates threshold effects of interest rates and economic growth on public debt.

4.3. Discussion of Results

The overall results indicate that in regular periods, the debt dynamics of euro countries present a stronger effect on debt development rather than fiscal deficits, while during stress times, the latter’s impact is more pronounced. The dominance of budget deficits in the debt’s evolution in periods of crisis is in line with the Keynesian theoretical perspective as well as many empirical findings (Bianchi et al. 2020; Fatás and Summers 2018; DeLong et al. 2012). However, one of the most important findings in the current study is that the main mechanism of the stronger effect of debt dynamics on debt development appears to be the multiplier effect of the coefficient $\frac{{1+i}_{t-1}}{{(1+\gamma }_t{\left)\right(1+\pi }_t)}$. 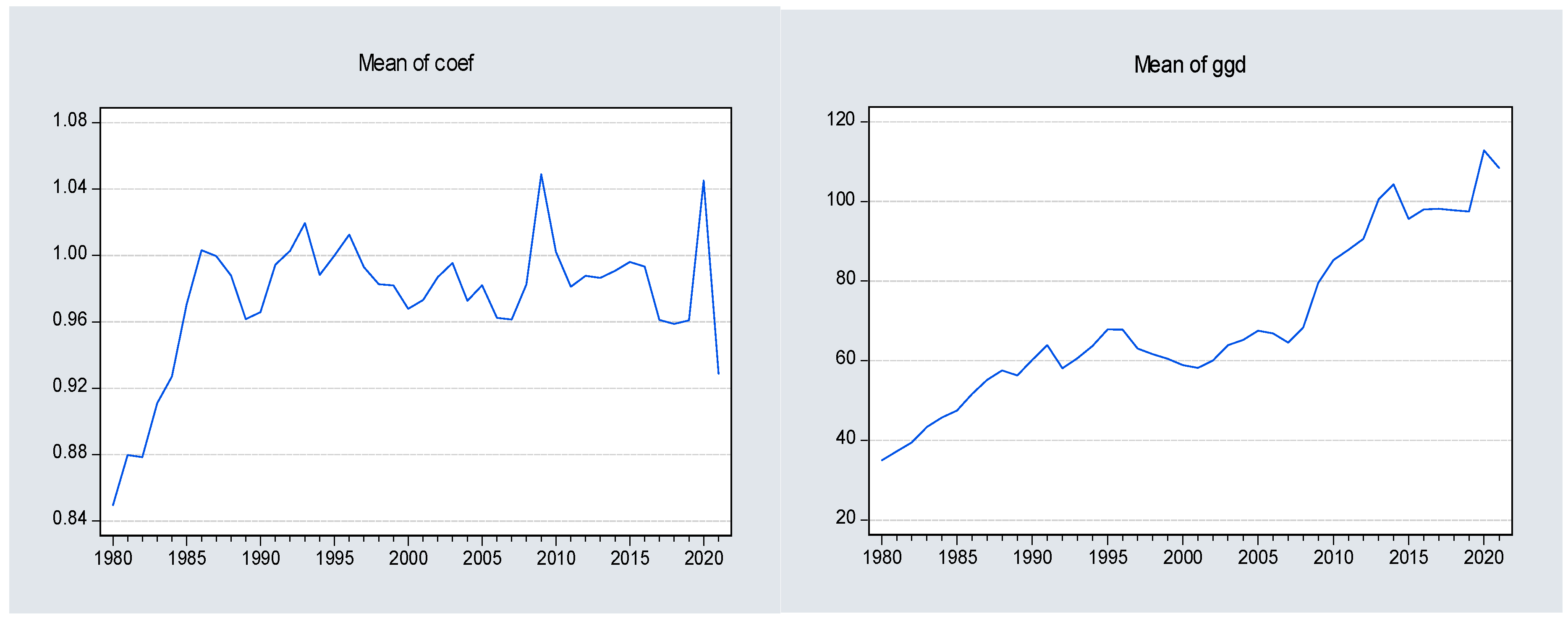That is, when this coefficient tends to be greater than 1 (Figure 1-left graph), dynamic stability is converted to instability, and the results in Table 5, Table 6 and Table 7 indicate that this is attributable to higher interest rates (nominator of the coefficient), lower economic growth, and the inflation rate (the denominator of the coefficient). 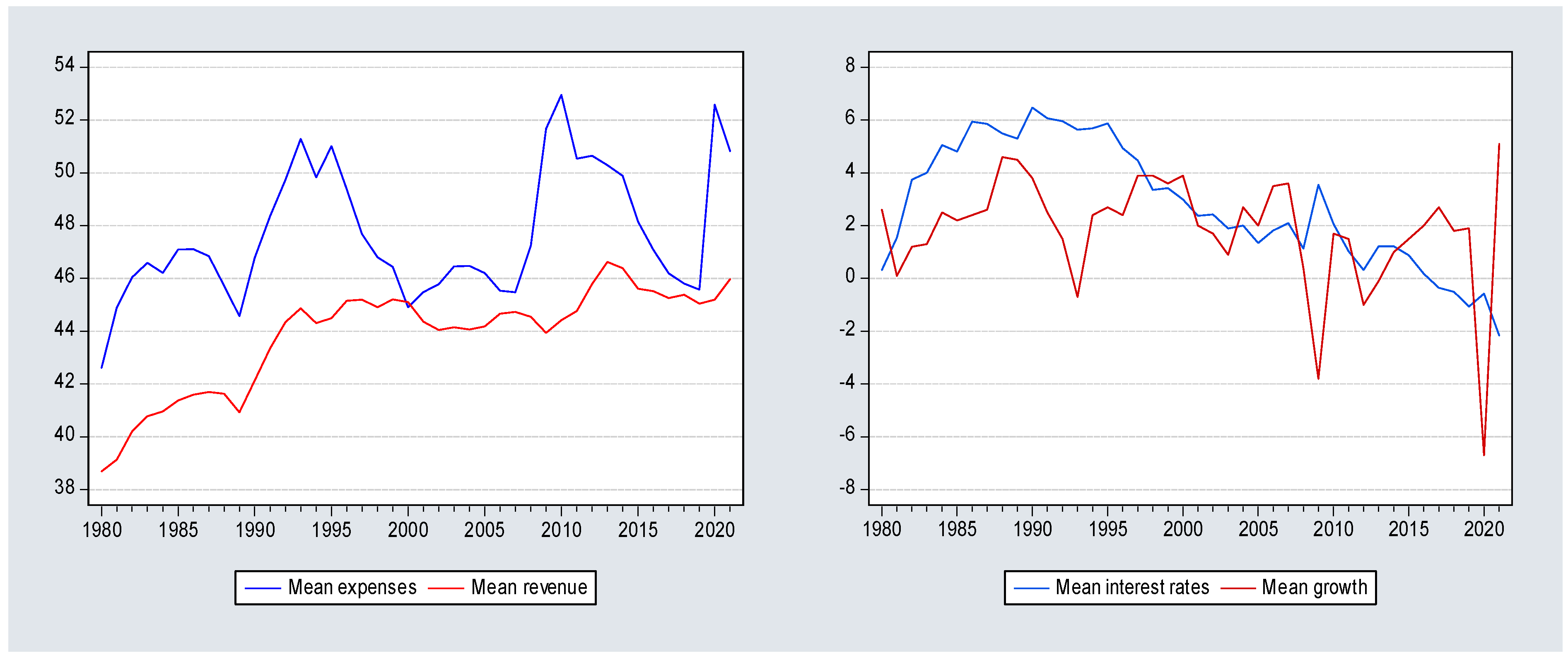Moreover, the detrimental multiplier effect on debt dynamics started with the onset of GFC (Figure 1-right graph). In this sense, the left graphs in Figure 1 and Figure 2 illustrate that a possible mechanism of the multiplier effect is government expenses in crisis periods.

Finally, the panel threshold results show that interest rates above 3% might be a problem for debt stability and seem to be true during the GFC period (Figure 2-right graph), but after the crisis, they remained low for a long time until the pandemic. On the other hand, the findings reveal that economic growth above 3.4% helps to stabilize public debt, but it appears that is hovering around 2% and never exceeds the 3.4% (see Figure 2-right graph). Regarding the debt dynamics threshold being above 92%, we can infer that, on the one hand, it exerts pressure on interest rates to rise, but on the other hand, it hinders economic performance and keeps growth at levels lower than 3.4%. Regarding the threshold of public debt, our results are in line with a more recent study from Alsamara et al. (2024), who found that low public debt ratios promote economic growth, whereas relatively high public debt beyond the 90%–91% threshold impedes economic growth in MENA countries. However, in our study, we provide new evidence of mechanisms and threshold of interest rates and growth above which debt becomes unsustainable or sustainable.

The overall conclusion that can be drawn from the discussion of results is that low interest rates might tempt governments to borrow more, thus leading to higher debt accumulation, and instead of leading to higher risk premia as was expected, they hinder economic growth and lead to a dynamic, self-reinforcing high-debt loop, which can drive it to an explosive path.

5. Conclusions

In this study, we used a Keynesian theoretical model proposed by Philippopoulos et al. (2017) to investigate how the dynamic instability of public debt affects its inter-temporal sustainability (or the solvency condition) in view of the global financial crisis and the health crisis pandemic. We used a sample of 11 euro area countries over the period from 1980 to 2021. Employing the GMM panel dynamic model, the overall results show that dynamic stability was the case before the global financial crisis, thus not violating the debt sustainability condition and that only budget deficits significantly affected the public debt’s evolution. However, after the global financial crisis and until the pandemic period, the public debt’s dynamic stability was converted to instability, and this further impacted the evolution of public debt negatively.

Furthermore, the findings suggest that after the global financial crisis, dynamic instability showed a highly persistent effect on the evolution of debt. The results (estimates) from the panel threshold models revealed that the dynamic instability of debt started to reverse (violate) the debt’s sustainability condition, especially when the borrowing cost was above 3.29% and becoming even stronger when it was above 4.39%. A final finding was that dynamic instability exerted even more pressure when debt to GDP was greater than a threshold level of 91% of GDP. However, the solvency condition recovered when economic growth was higher than 3.4%.

The policy implications of these results are clear. First, low interest rates can create a self-reinforcing loop of high debt, which itself is a serious matter for public authorities when designing economic policies. Hence, the findings of this study can serve as a valuable lesson for other countries which depend heavily on public debt. Second, high debt levels cause stock and other financial instruments’ prices to soar, thus additionally burdening an economy and derailing it. Also, it is interesting to determine the crucial level of general government debt above which the debt becomes unsustainable and poses serious threats to the economy’s agents. Finally, one of the main policy implications of our results for countries without fiscal space is that economic growth is the main discount factor for maintaining debt stability or even drastically reducing it. However, the main limitation of the current study is that the GMM econometric technique is appropriate for short-term periods but not for the long run. Further, it may be necessary to test for cointegration or, more generally, for the existence of a long-run relationship among the variables of interest, but this is an issue for future investigation.