Abstract
The Moroccan banking system suffered a significant impact due to the extreme market conditions caused by the COVID-19 outbreak, which led to an increase in non-performance loans. This, in turn, reduced the value of banks’ assets and their ability to meet their obligations, implicitly raising systemic risk. In such circumstances, the collapse of one financial institution could cause a series of bankruptcies and endanger the overall state of the economy. Given the limited attention devoted to the analysis of systemic risk in the Moroccan banking system, this paper aimed to fill this gap by analyzing the Moroccan banks’ systemic risk exposure and assessing their stability during the COVID-19 crisis, using Quantile Regression Neural Network (QRNN) optimized by Adam algorithm to calibrate the Conditional Value at Risk (CoVaR). This study revealed a significant increase in systemic risk during the pandemic crisis and highlights the suitability of more complex QRNN in assessing systemic risk. The findings emphasize the need for regulators to pay close attention to banks’ risk exposures when implementing measures to mitigate systemic risk, such as increasing banks’ capital requirements or increasing the amount of high-quality liquid assets.
1. Introduction
Systemic risk within the banking system has received considerable attention from academics and regulators in the aftermath of the pandemic. Systemic risk occurs when the distress of one financial institution spreads to others, potentially causing a domino effect that could lead to broader economic impacts (Bisias et al. 2012). The banking sector forms an interconnected system that enables banks to redistribute their funds, providing liquidity between institutions and implicitly spreading systemic risk, which refers to a macro-level risk that propagates through complex linkages between banks and leads to severe instabilities. First, one institution fails and becomes unable to repay its loans. Second, the interconnected institutions face counterparty risk, which rapidly changes to take a systemic amplitude and impair the functioning of the entire system. Recognition of the systemic risk of banks’ exposure is crucial for regulators and supervising agencies to mitigate systemic crises.
The Moroccan economy faced its worst recession in 25 years during the COVID-19 crisis. The World Bank (2020) reported a significant drop in the Gross Domestic Product (GDP) of −6.3% during the crisis. The Moroccan Capital Market Authority (AMMC) reported that the Moroccan All Share Index (MASI) exhibited negative performance across most sectoral indices, ranging from −1.51% to −44.11%. Furthermore, eight of these indices recorded double-digit underperformance (AMMC 2020). The Moroccan banking system faced numerous impairment factors, such as a 14.73% increase in non-performing loans from 69.9 billion MAD in 2019 to 80.2 billion MAD in 2020 (BKAM 2020). The inability of borrowers to service their debts carried a risk of a vicious circle that put further pressure on the capital position of the Moroccan banks, which could threaten the whole economy (Locurcio et al. 2021). Moreover, the Moroccan banking sector’s net income, average liquidity, and return on equity decreased by −1.9%, −7.1%, and −0.8%, respectively (BKAM 2020). These factors, in turn, led to a −2.97% decrease in the global net profit of the banking sector (BKAM 2020). Under such extreme circumstances, banks highly exposed to systemic risk within a weak regulatory environment create the ideal conditions for the propagation of a systemic crisis. Given the significant economic costs associated with financial institutions’ failure, an increase in systemic risk can impede global sustainable development support, particularly in emerging economies (Popkova and Sergi 2021).
The empirical findings of this paper support the hypothesis that Moroccan banks experienced a significant increase in systemic risk during the pandemic crisis. Unlike previous articles that try to model systemic risk using linear measures, this paper estimated the systemic risk directly using a complex non-linear approach that captures non-linear relationships in the provided data. This paper aimed to analyze Moroccan banks’ risk exposure and evaluate their stability in the face of the COVID-19 crisis, thereby addressing the existing gap in the literature.
We outline the methodology as follows: first, we estimated the VaR of every Moroccan bank in isolation conditioned on state-variables by the QRNN to simulate extreme economic conditions. Second, the computed VaR vector results were used to fit the CoVaR for every bank, conditioned on other banks being in distress scenarios. Following this methodology, we were able to draw significant conclusions about the effects of the COVID-19 crisis on the Moroccan banks’ systemic risk exposure.
The remainder of this paper is presented as follows: Section 2 presents the literature review; Section 3 introduces the materials and methods; Section 4 presents the data used; Section 5 presents the model selection process; Section 6 analyzes and discusses the results; Section 7 concludes the paper.
2. Literature Review
The literature suggests several measurements of systemic risk. Brownlees et al. (2015) back-tested and evaluated various systemic risk measures and determined that the CoVaR approach effectively alerts regulators of the riskiest financial institutions. Tobias and Brunnermeier (2016) developed a novel approach, which is the Value at Risk (VaR) variation of a company conditional on other companies being in distress compared to its median level. The authors demonstrated that features such as leverage and size might significantly predict systemic risk. Siebenbrunner and Sigmund (2019) used various quantile panel estimators to evaluate the performance of some bank-specific drivers; regulators used these during extreme events. The authors concluded that quantile estimators are more appropriate for describing the distribution of systemic contagion losses. Lan et al. (2020) employed dynamic CoVaR through quantile regression (QR) on the Chinese A-shares. They demonstrated that the pandemic crisis substantially increased systemic risk within the Chinese financial industry. Xu et al. (2021) proposed the wavelet-based quantile regression approach to investigate systemic risk within the Chinese banking industry. They concluded that small-size banks with the highest leverage are catalysts of systemic risk. Keilbar and Wang (2021) applied the QRNN on log-returns of the USA’s global systemically important banks to measure the CoVaR throughout financial crises. The authors identified the banks that pose the greatest risk to the banking system. Rivera-Escobar et al. (2022) employed various methodologies to measure systemic risk in the Colombian banking system, such as the well-known CoVaR approach, to conclude that the banking sector was not experiencing an increase in systemic risk between 2008 and 2017. Naeem et al. (2022) used the QRNN approach on the log-returns of the top 10 US industries to quantify systemic risk spillover. They found that the manufacturing industry highly contributes to systemic risk.
One must recognize the extreme events in the financial time-series to identify the systemic risk and measure the tail effect within financial systems. Since the first introduction of the QR (Koenker and Bassett 1978), this method has taken a significant place in estimating high conditional quantiles. Subsequently, the literature has constantly improved the QR approach. White (1992) demonstrated that non-parametric conditional quantile estimators built on artificial neural networks (ANN) could learn conditional quantiles for any predetermined precision. Taylor (2000) aimed to enhance the measurement of the conditional probability distribution using ANN. By conducting a comparative analysis, the author suggested that the QRNN provides an alternative to estimating conditional density. Takeuchi et al. (2006) presented a non-parametric quantile estimator with constraints and demonstrated the feasibility and competitiveness of the method compared to the existing ones. Bondell et al. (2010) proposed a novel QR that avoids the problem of crossing quantiles. The authors achieved this by incorporating stability and smoothing across the various quantile levels, which improved considerably over existing methods. Cannon (2011) implemented the QRNN in the R programming language, including features such as bootstrap aggregation and left censoring. The author demonstrated that QRNN outperforms the baseline QR. Xu et al. (2017) proposed the Composite-QRNN approach to investigate the non-linear relations linking variables and demonstrated an improvement in the processing capability of standard QRNN. Zhang et al. (2018) integrated techniques used in deep learning areas, such as the Adam optimizer and batch training, to enhance the approximation and stability of the QRNN. The authors proved that the proposed QRNN is more robust than the standard QRNN and the Composite-QRNN.
This paper contributes to the current body of knowledge by proposing a new methodology for estimating the CoVaR, achieved through a two-step QRNN fitting approach.
3. Materials and Methods
3.1. QRNN
Linear QR is an adequate method for measuring systemic risk. However, ANN approaches have demonstrated their pertinence in fitting non-linear functions and detecting tail risk events through non-normal distributions (Keilbar and Wang 2021). This paper used the QRNN architecture to model the VaR and CoVaR (Scheme 1). The QRNN combines the Multi-layer Perceptron Neural Network (MLPNN) (Zhang and Zhang 1999; Lang 2005; Minin et al. 2010) and the resulting papers of (White 1992; Taylor 2000; Cannon 2011; Hagan et al. 1997; Kingma and Ba 2014; Demuth et al. 2014; Zhang et al. 2018).
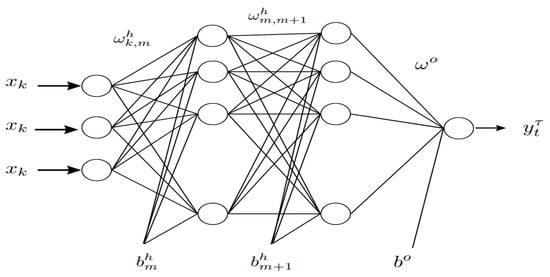
Scheme 1.
The QRNN architecture.
Equation (1) defines the QRNN by considering K dimensional vectors of predictors and a predictand for . The error term is denoted by ; the ELU activation function is represented by . The weights linking the input-layer and the hidden-layer are indicated by , where . The hidden-layer bias is represented by . The weights of the output-layer and the output-layer bias are represented by and , respectively. represents the node’s number within hidden-layers and represents the quantile level.
In summary, the used QRNN is a neural network architecture that takes into account the predictors and a predictand, as well as various weights and biases, and uses the ELU activation function to estimate quantiles at a given level . The QRNN method is more robust and stable due to incorporating into the fitting process complex techniques used in deep learning areas, such as the widely adopted Adam optimizer (Keskar and Socher 2017; Zhang et al. 2018) and the batch training technique, to enhance the approximation by feeding the neural networks with numerous batches instead of adding the whole data set at once (Hagan et al. 1997). The optimal estimate is obtained by defining the QRNN parameters through the minimization of the quantile error function .
The regularization term with the tilted absolute value function penalizes the amplitude of the weight parameters, while the contribution of the weight decay term is controlled by a constant .
The titled absolute value function is presented as follows:
refers to the Huber norm (Huber 1964); it ensures a smooth and stable transition between absolute and squared errors. α refers to the threshold magnitude.
VaR and CoVaR measures have become widely used among regulators worldwide for monitoring and supervising financial institutions. This paper used a double QRNN fitting to provide more accurate systemic risk assessments.
3.2. VaR
VaR estimates the maximum potential losses an institution could incur during extreme events at a specific confidence level. VaR was first publicized in 1994 by J.P. Morgan and obtained an increasingly important role in managing market risk, forming the core of international regulation. According to (Chao et al. 2015; Härdle et al. 2016), the linear QR on state-variables is used to estimate the VaR. Following the same reasoning, this paper used the QRNN architecture for estimating VaR.
Let denote the daily stock prices of bank at time used to calculate the log-returns of the bank at time by , and let represent the state-variables. We estimated the VaR by regressing the conditional quantile of j’s returns on the state-variables.
where is the optimal estimate of the neural network. The fitted model must be evaluated at distress as follows:
VaR is a standard measurement to understand the critical risk level for a given bank. For instance, VaR captures the risk level in isolation and does not capture the potential tail losses and interdependence among banks.
3.3. CoVaR
To capture the risk of the system as a whole, one must use the CoVaR approach to measure the loss of institution conditioned on ’s institutions being at their VaR level (Rockafellar and Uryasev 2000). Literature on the CoVaR estimation approaches has emerged (Mainik and Schaanning 2014; Oh and Patton 2013; Girardi and Ergün 2013; Bernardi et al. 2013; Cao 2013; Hautsch et al. 2015; Härdle et al. 2016). For instance, the CoVaR of bank given the other banks being at level at time is given by:
where correspond to the log-return vectors of all banks excluding at time , knowing that represents the corresponding VaR vectors. To measure the CoVaR of firm , first, the conditional quantiles of bank j’s returns are regressed on all other banks’ log-returns using the QRNN by the equation below:
Second, we obtained CoVaR by replacing by , where is the optimal estimate of the QRNN:
4. Data
The empirical analysis focused on the Moroccan banks listed in Table 1: Attijariwafa Bank, Banque Centrale Populaire, Bank of Africa, Banque Marocaine du Commerce et Industrie, Crédit Immobilier et Hotelier, and Credit du Maroc. One must recognize the systematically important banks based on their risk exposure. To achieve this, we considered the daily stock log-returns of the Moroccan banks over the studied period from 4 January 2016 to 28 June 2022. This study utilized a dataset of the historical closing prices of the Moroccan banks publicly listed on the Casablanca stock exchange market (CSE), which were then transformed into daily historical log-returns.

Table 1.
List of the Moroccan banks.
It is important to note significant dates during the studied period, particularly in March 2020. According to the Moroccan Ministry of Health in 2020, the first case of COVID-19 in Morocco was officially confirmed on 2 March 2020. The World Health Organization (2020) declared the COVID-19 outbreak a pandemic on 12 March 2020. Local transmission of COVID-19 was first reported in Morocco on 13 March 2020 (The Moroccan Ministry of Health 2020); on the same date, the CDM bank recorded the lowest log-return level (−9.53%) over the studied period. Moreover, the opening of the next trading day (16 March 2020) was characterized by the collapse of almost all of the Moroccan banks. The log-returns of AWB, BOA, CIH, BCP, and BMCI were, respectively, −10.52%, −10.43%, −10.49%, −10.51%, and −10.52%, spreading the chaos over the banking system.
To measure the banks’ VaR in the first step of the methodology, we considered the daily state-variables listed in Table 2: Morocco’s interbank market weighted average minus policy rate, changes in Morocco’s interbank daily transactions volume, 10-Year minus 3-Month Moroccan treasury yield spread, MASI’s daily log-returns, and Morocco’s banking index daily log-returns. State-variables can be defined as macroeconomic or market-specific drivers representing different aspects, such as the stock market’s performance, the liquidity and credit conditions in the interbank market, and the economy’s overall health. By combining these state-variables, it is possible to obtain a more comprehensive and accurate assessment of systemic risk.

Table 2.
List of the state-variables.
First, Morocco’s interbank market weighted average minus policy rate is the difference between the interest rate that banks charge each other for short-term loans in the interbank market and the central bank’s policy rate, which is an essential indicator of the overall liquidity and credit conditions in the financial system. If the interbank market rate is significantly higher than the policy rate, it may indicate that banks are facing liquidity shortages and are willing to pay a premium to borrow funds, which can be a sign of stress in the financial system. Conversely, if the interbank market rate is significantly lower than the policy rate, it may indicate that banks have excess liquidity and are looking for investment opportunities, which can be a sign of economic growth and stability. Hence, this variable is critical for assessing systemic risk. Second, interbank transactions are crucial for banks to manage liquidity, lend and borrow money, and settle payments. Changes in Morocco’s interbank daily transactions volume can signal changes in trust and confidence among banks. A significant decrease in interbank transactions can indicate that banks are becoming more risk-averse and less willing to lend to each other. This can lead to financial stress and potentially cause a liquidity crisis if banks are unable to access funds to meet their obligations. Therefore, monitoring the changes in Morocco’s interbank daily transactions volume can provide insights into the health of the financial system and the level of systemic risk. Third, monitoring the 10-Year minus 3-Month Moroccan Treasury yield spread is essential for assessing systemic risk, as it provides insights into the market’s expectations of future economic conditions. Fourth, MASI’s daily log-returns provide a comprehensive view of the market’s reaction to extreme events. In the end, the Moroccan banking index daily log-returns provide accurate information about the overall health of the Moroccan banking sector.
Table 3 and Table 4 display the data statistics reports. One can observe that all kurtosis values are superior to three. Furthermore, the Jarque–Bera (J–B) test demonstrates that the data are not normally distributed and contains fat tails. In addition, the augmented Dickey–Fuller (ADF) test shows that the data used are stationary.

Table 3.
The Moroccan banks log-returns statistics.

Table 4.
The state-variables statistics.
5. Model Selection
To choose adequate VaR estimates, we compared different models with various levels of complexity. For instance, one must choose the model with the minimal average quantile loss value (González-Rivera et al. 2004), which is an asymmetric loss function that penalizes the observations for which we observe returns VaR exceedance. QRNN with one hidden-layer of 100 nodes optimized using Newton–Raphson algorithms (QRNN-100), QRNN with double hidden layers of 100 nodes at each optimized using Adam algorithms (QRNN-100-100-A), and the linear baseline QR constitute the benchmark models. Table 5 clearly shows that the QRNN-100-100-A outperforms the benchmark models for every bank except BMCI, where the QRNN-100-100-A fails against the QRNN-100 model.

Table 5.
The benchmark model’s average quantile loss for the Moroccan banks.
Furthermore, the Diebold and Mariano (2002) test was used to evaluate the benchmark models forecasting performance for the second step fitting (CoVaR). Table 6 shows that the QRNN-100-100-A outperforms all the Moroccan banks with high statistical significance. The test fails to reject the alternative hypothesis that QRNN-100-100 and baseline QR forecasts are more accurate than the QRNN-100-100-A model under a significance level of 5%. This paper used the QRNN-100-100-A model to calibrate both risk measures. Finally, we concluded that more complex models with integrated deep-learning techniques are suitable for risk measurement under distress scenarios.

Table 6.
Comparison of the QRNN-100-100-A with the candidate models using the Diebold–Mariano test.
6. Results and Discussion
This work was carried out in two steps. First, we used QRNN fitting, starting by estimating VaR on a set of state-variables. Then, we used the computed VaR results to measure the CoVaR of the Moroccan banks at a quantile level of .
Figure 1 displays the log-returns, VaR, and CoVaR results for the Bank of Africa. One can notice that the VaR and CoVaR estimations have a similar pattern. The red line for CoVaR is mostly below the grey line for VaR, following a stable evolution in the period anterior to the emergence of the pandemic crisis in Morocco. After the record of the first COVID-19 case in Morocco, as illustrated by the vertically dashed blue line, several spikes are observed in both VaR and CoVaR, demonstrating evidence of an increase in systemic risk. Similar patterns are found for the other banks (see Appendix A). These findings match the results of (Lan et al. 2020); these authors demonstrated, using the dynamic CoVaR, a rise in systemic risk within the Chinese financial sector throughout the outbreak of the pandemic crisis. Moreover, Duan et al. (2021) demonstrated that the pandemic crisis had a role in the rise of systemic risk within the banking industry across numerous countries, namely Morocco, with an estimated ∆CoVaR of 0.820. In addition, Rizwan et al. (2020) found evidence of a rise in systemic risk during the pandemic crisis among countries such as the USA, China, and France.
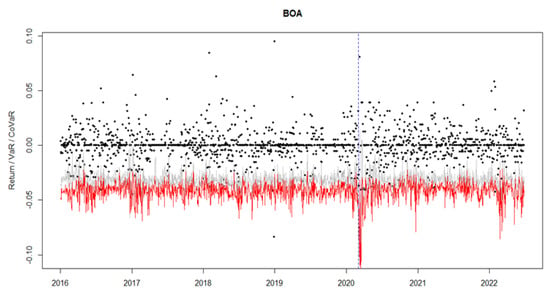
Figure 1.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for BOA, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
Furthermore, Table 7 draws the means of VaR and CoVaR measures for every quarter starting from 2019Q4 (before the crisis) and going by 2020Q1 (the crisis occurrence) until 2020Q4 (after the crisis). The analysis aimed to identify any significant changes in the VaR and CoVaR of the banks due to the pandemic’s impact on the financial market. The following sections present the detailed results of our analysis.

Table 7.
The quarter mean of VaR and CoVaR measures from 2019Q4 to 2020Q4 of every bank.
From Table 7, one can notice that AWB’s VaR rose between 2019Q4 and 2020Q1 from −0.0190 to −0.0285, by 50.20%, which is the highest variation recorded among the Moroccan banks and went afterward in a decreasing trend during 2020Q2, 2020Q3, and 2020Q4 by, respectively, −27.30%, −6.09% and −7.74% to reach −0.0179, which is less than the level recorded before the crisis. BOA’s VaR went from −0.0308 to −0.0371, with a 20.42% variation between 2019Q4 and 2020Q1. Then, it fluctuated for the next 2020 quarters by −15.25%, −3.28%, and −4.62% to reach the level of −0.0309 in 2020Q4, slightly near to the VaR before the pandemic crisis. As for CIH, VaR increased from 2019Q4 to 2020Q1 by 0.27% and dropped continuously for the next 2020 quarters by −18.83%, −3.45%, and −1.57% to reach a level (−0.0348) less than the level recorded before the crisis (−0.0450). The VaR for BCP increased from −0.0135 to −0.0175 by 29.64% between 2019Q4 and 2020Q1 and fluctuated during the next 2020 quarters to reach its highest level (−0.0176) during 2020Q3. Regarding BMCI, the VaR increased between 2019Q4 and 2020Q1 by 15.38%, from −0.0557 to −0.0643, the highest observation recorded among the Moroccan banks. Next, it fluctuated continuously during the next 2020 quarters to reach −0.0527, which is less than levels recorded before the pandemic crisis. Contrary to the other banks, the VaR of CDM dropped between 2019Q4 and 2020Q1 by −5.63% and fluctuated during 2020Q2 and 2020Q3 to stand at −0.0506 during 2020Q4.
Concerning CoVaR, AWB passed from −0.0613 to −0.0662 by 7.97% between 2019Q4 and 2020Q1 and fluctuated subsequently to reach −0.0588 in 2020Q4. BOA’s CoVaR increased from −0.0409 to −0.0499, by 22.04%, between 2019Q4 and 2020Q1. It declined continuously during the next 2020 quarters to reach −0.0392 in 2020Q4, less than levels recorded before the pandemic crisis. CIH, BCP, and BMCI CoVaR increased between 2019Q4 and 2020Q1, by 12.79%, 17.68%, and 4.17%, to reach, respectively, −0.0669, −0.0469, and −0.1034 and decreased until reaching levels smaller than those recorded before the pandemic crisis of, respectively, −0.0573, −0.0385, and −0.0908. Conversely, CDM’s CoVaR dropped between 2019Q4 and 2020Q1 by −1.14% to continue decreasing throughout 2020Q2, 2020Q3, and 2020Q4 by −4.66%, −3.74%, and −0.58%, respectively.
Graphically (see Appendix B), the figures display the evolution of the Moroccan banking system structure over the quarters according to the VaR and CoVaR means. These figures show a wide dispersion of risk levels for all quarters, except for 2020Q1, when four banks gathered in the middle of the graph, indicating a high resemblance in terms of risk level during the pandemic crisis occurrence. Furthermore, BCP maintained its position at the top right of the scatter-plot, reflecting a low level of VaR and CoVaR and, thus, considered the least vulnerable bank in Morocco. On the other hand, BMCI was positioned at the bottom left, demonstrating a high level of risk and considered the most vulnerable Moroccan bank.
In response, the Moroccan central bank implemented various measures to support the banking system, demonstrating its commitment to stabilizing the economy during the crisis. These measures included the largest policy rate cut in the past decade, reducing the rate by 75 basis points from 2.25% to 1.5%, to address the situation’s urgency. Additionally, the monetary reserve ratio was lowered by 200 basis points from 2% to 0% to increase liquidity in the banking system (BKAM 2020). These measures were instrumental in sustaining the banking system’s resilience during the pandemic, as evidenced by the decline in both risk measures in subsequent quarters. Subsequently, Figure 1 shows that the risk measures returned to a stable pattern with few non-persistent spikes to reach levels less than those recorded before the pandemic crisis for almost all of the Moroccan banks. This recovery might depend on the supportive measures undertaken by the Moroccan central bank. Queyranne et al. (2021) argued that measures undertaken by the central bank have significantly mitigated the negative impact of the COVID-19 crisis.
This paper’s results carry significant implications for policymakers, investors, and academics. From the policymakers’ perspective, these findings emphasize the importance of closely monitoring the systemic risk exposure of Moroccan banks individually and implementing appropriate prudential measures to mitigate systemic risk in the future. Moreover, policymakers can adjust macroprudential policy tools, such as increasing capital requirements or liquidity buffers according to the banks’ systemic risk, thus reducing the likelihood of future crises (Drehmann et al. 2010). Policymakers can consider imposing higher taxes on Moroccan banks with high systemic risk exposure. This can incentivize banks to avoid taking excessive risks that could harm the financial stability and the broader economy in the event of their failure. Acharya et al. (2017) argued that banks that pose a higher systemic risk to the financial system should be subject to higher taxes. The reasoning behind this is that such banks can cause significant damage to the financial system in the event of their failure. Measuring Moroccan banks’ systemic risk can facilitate international coordination and cooperation among policymakers. This is particularly important because the Moroccan banks have a significant presence in the banking markets of West Africa and North Africa, as the failure of a single Moroccan bank can have considerable and significant implications. The banks are mutually interconnected, sharing the same depositors and investing in the same sectors (Allen and Babus 2009); these interconnections draw bridges of risk transmission that can amplify the amplitude of possible crises. Systemic risk is characterized by its inherent potential for contagion, which arises when the risk materializes (Martínez-Jaramillo et al. 2010). In such conditions, the collapse of a single bank can trigger a series of bankruptcies throughout the banking system, leading to a widespread crisis that can reach the macroeconomic dimension and result in a catastrophic drop in all economic activities. Policymakers could encourage highly exposed Moroccan banks to diversify their loan portfolios and expand into new markets to reduce these indirect interconnections.
From the investor’s perspective, Moroccan banks’ systemic risk measurement can help them make informed investment decisions. Investors can potentially reduce the risk of losses resulting from failures of financial institutions. This, in turn, can contribute to the efficient allocation of capital and the mitigation of systemic risk, ultimately benefiting investors and the broader economy. One of the critical academic implications of this study is that it fills a gap in the literature on systemic risk measurement in the Moroccan banking system, contributing to the overall understanding of systemic risk in emerging countries.
7. Conclusions
This paper investigated the systemic risk inherent to the Moroccan banking system. First, we used the QRNN model to regress the banks’ log-returns on state-variables. Then, the computed banks’ VaR vectors were used to model the CoVaR of the Moroccan banks at . We presented the major findings as follows:
First, this study’s results indicate that most Moroccan banks’ VaR and CoVaR maintained a stable pattern before the emergence of the COVID-19 crisis. However, after the announcement of the first COVID-19 case in Morocco, there was a sharp increase in both measures for all banks, indicating an increase in systemic risk. Second, the recovery of the Moroccan banks was rapid and might, in part, be the result of the supportive measures undertaken by the Moroccan central bank in mitigating the effects of the pandemic crisis on the banking system, which could help regulators in other countries when facing similar crises in the future. Third, the analysis of CoVaR means across the studied quarters shows that BMCI poses the highest systemic risk level to the Moroccan banking system. Conversely, BCP poses the lowest systemic risk level to the Moroccan banking system.
This study’s innovative contribution lies in using the QRNN model and incorporating some widely used deep learning techniques into the fitting processes, which provides a more accurate and efficient method for computing VaR and CoVaR compared to traditional QRNN. This study also contributed to understanding the systemic risk exposure of individual Moroccan banks that could be used to inform the decisions of regulators or investors.
Future research could explore systemic risk using more complex ANN architectures or combine different methods to yield more relevant results. However, using different methodologies may lead to different results, and assumptions may influence the choice of methodology. Additionally, the study analysis was limited to the Moroccan banking system during the pandemic crisis and may need to be more generalizable across other contexts.
Overall, this study provides important insights into the systemic risk inherent in the Moroccan banking system and could serve as a benchmark for future research on financial stability in emerging countries.
Author Contributions
Conceptualization, A.K., C.E.M. and J.M.; methodology, A.K., C.E.M. and J.M.; software, A.K., C.E.M. and J.M.; validation, C.E.M. and J.M.; formal analysis, A.K., C.E.M. and J.M.; investigation, A.K., C.E.M. and J.M.; resources, A.K., C.E.M. and J.M.; data curation, A.K., C.E.M. and J.M.; writing—original draft preparation, A.K., C.E.M. and J.M.; writing—review and editing, A.K., C.E.M. and J.M.; visualization, A.K., C.E.M. and J.M.; supervision, C.E.M. and J.M.; project administration, C.E.M. and J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available from the first author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
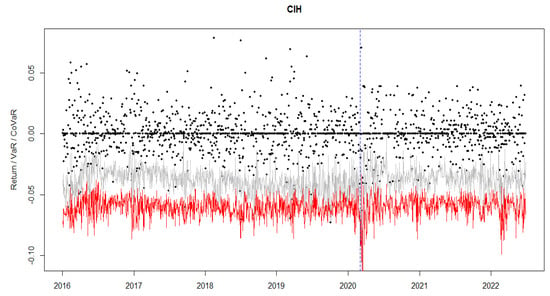
Figure A1.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for CIH, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
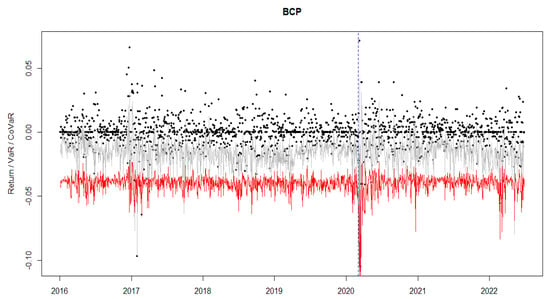
Figure A2.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for BCP, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
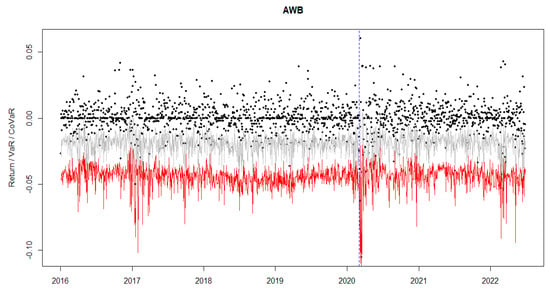
Figure A3.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for AWB, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
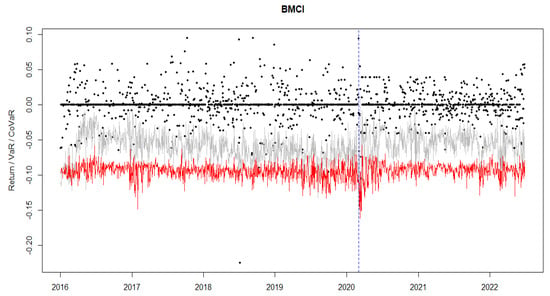
Figure A4.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for BMCI, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
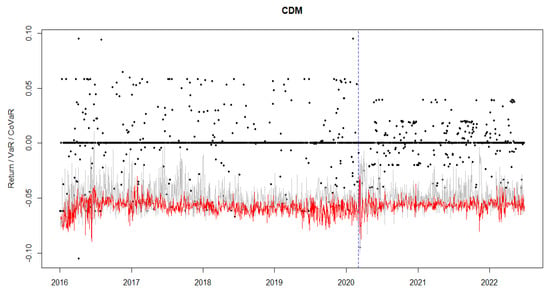
Figure A5.
The plot of VaR (grey line), CoVaR (red line), log-returns (black dots) for CDM, the recorded date of the first COVID-19 case in Morocco (vertical dashed blue line), τ = 1%.
Appendix B
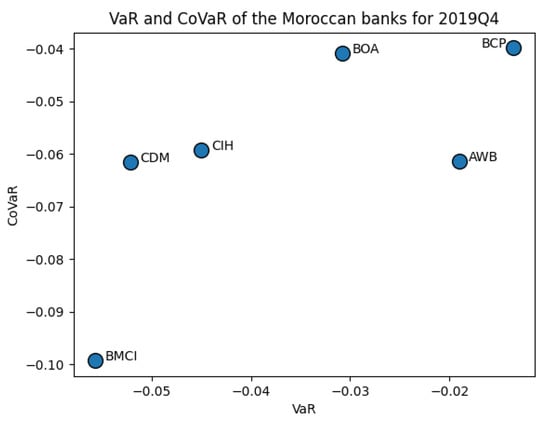
Figure A6.
Scatter-plots of the Moroccan banks according to VaR and CoVaR means for 2019Q4.
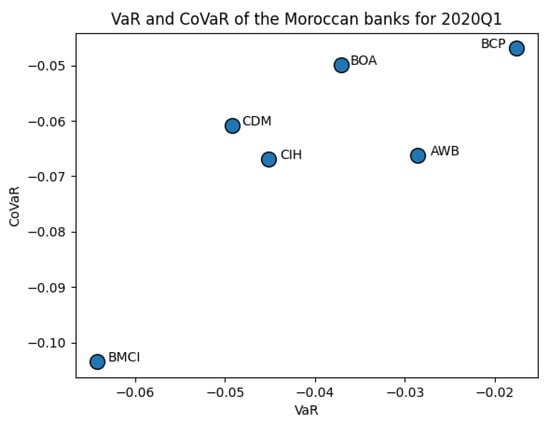
Figure A7.
Scatter-plots of the Moroccan banks according to VaR and CoVaR means for 2020Q1.
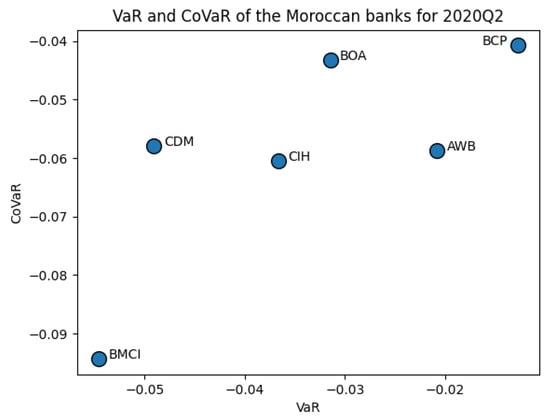
Figure A8.
Scatter-plots of the Moroccan banks according to VaR and CoVaR means for 2020Q2.
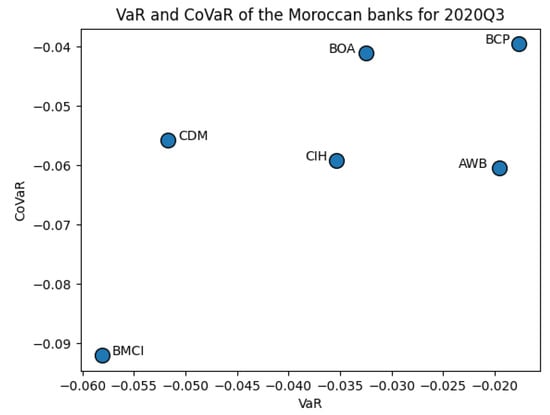
Figure A9.
Scatter-plots of the Moroccan banks according to VaR and CoVaR means for 2020Q3.
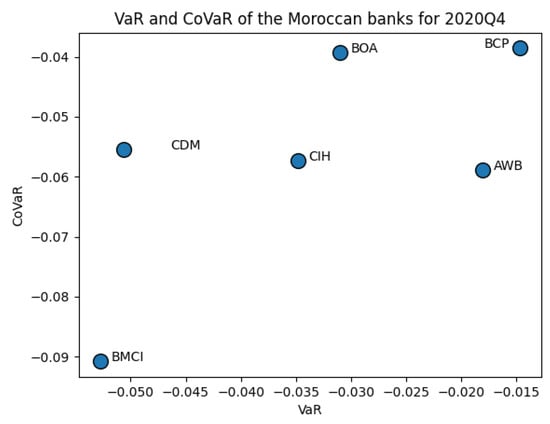
Figure A10.
Scatter-plots of the Moroccan banks according to VaR and CoVaR means for 2020Q4.
References
- Acharya, Viral V., Lasse H. Pedersen, Thomas Philippon, and Matthew Richardson. 2017. Measuring systemic risk. The Review of Financial Studies 30: 2–47. [Google Scholar] [CrossRef]
- Allen, Franklin, and Ana Babus. 2009. Networks in finance. In The Network Challenge: Strategy, Profit, and Risk in an Interlinked World. Westford: Prentice Hall Professional. [Google Scholar]
- AMMC. 2020. Autorité Marocaine du Marché des Capitaux Annual Report. Available online: https://www.ammc.ma/fr/rapports-annuel (accessed on 1 January 2023).
- Bernardi, Mauro, Ghislaine Gayraud, and Lea Petrella. 2013. Bayesian inference for CoVaR. arXiv arXiv:1306.2834. [Google Scholar] [CrossRef]
- Bisias, Dimitrios, Mark Flood, Andrew W. Lo, and Stavros Valavanis. 2012. A survey of systemic risk analytics. Annual Review of Financial Economics 4: 255–96. [Google Scholar] [CrossRef]
- BKAM. 2020. BANK AL-MAGHRIB (BKAM) Annual Report. Available online: https://www.bkam.ma/en/Publications-and-research/Institutional-publications/Annual-report-presented-to-his-majesty-the-king (accessed on 1 January 2023).
- Bondell, Howard D., Brian J. Reich, and Huixia Wang. 2010. Noncrossing quantile regression curve estimation. Biometrika 97: 825–38. [Google Scholar] [CrossRef]
- Brownlees, Christian T., Benjamin Remy Chabot, Eric Ghysels, and Christopher Kurz. 2015. Backtesting Systemic Risk Measures during Historical Bank Runs. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2702258 (accessed on 21 November 2022).
- Cannon, Alex J. 2011. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Computers & Geosciences 37: 1277–84. [Google Scholar] [CrossRef]
- Cao, Zhili. 2013. Multi-Covar and Shapley Value: A Systemic Risk Measure. Banque de France Working Paper. Paris: French National Bank. [Google Scholar]
- Chao, Shih-Kang, Wolfgang Karl Hardle, and Weining Wang. 2015. Quantile regression in risk calibration. In Handbook of Financial Econometrics and Statistics. New York: Springer. [Google Scholar] [CrossRef]
- Demuth, Howard B., Mark H. Beale, Orlando De Jess, and Martin T. Hagan. 2014. Neural Network Design, 2nd ed. Stillwater: Martin Hagan. [Google Scholar]
- Diebold, Francis X., and Robert S. Mariano. 2002. Comparing predictive accuracy. Journal of Business & Economic Statistics 20: 134–44. [Google Scholar] [CrossRef]
- Drehmann, Mathias, Claudio E. V. Borio, Leonardo Gambacorta, Gabriel Jimenez, and Carlos Trucharte. 2010. Countercyclical Capital Buffers: Exploring Options. Basel: Bank for International Settlements Communications. [Google Scholar] [CrossRef]
- Duan, Yuejiao, Sadok El Ghoul, Omrane Guedhami, Haoran Li, and Xinming Li. 2021. Bank systemic risk around COVID-19: A cross-country analysis. Journal of Banking & Finance 133: 106299. [Google Scholar] [CrossRef]
- Girardi, Giulio, and A. Tolga Ergün. 2013. Systemic risk measurement: Multivariate GARCH estimation of CoVaR. Journal of Banking & Finance 37: 3169–80. [Google Scholar] [CrossRef]
- González-Rivera, Gloria, Tae-Hwy Lee, and Santosh Mishra. 2004. Forecasting volatility: A reality check based on option pricing, utility function, value-at-risk, and predictive likelihood. International Journal of Forecasting 20: 629–45. [Google Scholar] [CrossRef]
- Hagan, Martin T., Howard B. Demuth, and Mark Beale. 1997. Neural Network Design. Boston: PWS Publishing Co. [Google Scholar]
- Hautsch, Nikolaus, Julia Schaumburg, and Melanie Schienle. 2015. Financial Network Systemic Risk Contributions. Review of Finance 19: 685–738. [Google Scholar] [CrossRef]
- Härdle, Wolfgang Karl, Weining Wang, and Lining Yu. 2016. Tenet: Tail-event driven network risk. Journal of Econometrics 192: 499–513. [Google Scholar] [CrossRef]
- Huber, Peter J. 1964. Robust estimation of a location parameter: Annals Mathematics Statistics. IEEE Transactions on Signal Processing 56: 2346–56. [Google Scholar] [CrossRef]
- Keilbar, Georg, and Weining Wang. 2021. Modelling systemic risk using neural network quantile regression. Empirical Economics 62: 93–118. [Google Scholar] [CrossRef]
- Keskar, Nitish Shirish, and Richard Socher. 2017. Improving generalization performance by switching from adam to sgd. arXiv arXiv:1712.07628. [Google Scholar] [CrossRef]
- Kingma, Diederik P., and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv arXiv:1412.6980. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett, Jr. 1978. Regression quantiles. Econometrica: Journal of the Econometric Society 46: 33–50. [Google Scholar] [CrossRef]
- Lan, Cheng, Ziyi Huang, and Wenli Huang. 2020. Systemic risk in China’s financial industry due to the COVID-19 pandemic. Asian Economics Letters 1: 18070. [Google Scholar] [CrossRef]
- Lang, Bernhard. 2005. Monotonic multi-layer perceptron networks as universal approximators. Paper presented at 15th International Conference on Artificial Neural Networks, Warsaw, Poland, September 11–15; pp. 31–37. [Google Scholar] [CrossRef]
- Locurcio, Marco, Francesco Tajani, Pierluigi Morano, Debora Anelli, and Benedetto Manganelli. 2021. Credit risk management of property investments through multi-criteria indicators. Risks 9: 106. [Google Scholar] [CrossRef]
- Mainik, Georg, and Eric Schaanning. 2014. On dependence consistency of CoVaR and some other systemic risk measures. Statistics & Risk Modeling 31: 49–77. [Google Scholar] [CrossRef]
- Martínez-Jaramillo, Serafín, Omar Pérez Pérez, Fernando Avila Embriz, and Fabrizio López Gallo Dey. 2010. Systemic risk, financial contagion and financial fragility. Journal of Economic Dynamics and Control 34: 2358–74. [Google Scholar] [CrossRef]
- Minin, Alexey, Marina Velikova, Bernhard Lang, and Hennie Daniels. 2010. Comparison of universal approximators incorporating partial monotonicity by structure. Neural Networks 23: 471–75. [Google Scholar] [CrossRef] [PubMed]
- Naeem, Muhammad Abubakr, Sitara Karim, and Aviral Kumar Tiwari. 2022. Quantifying systemic risk in US industries using neural network quantile regression. Research in International Business and Finance 61: 101648. [Google Scholar] [CrossRef]
- Oh, Dong Hwan, and Andrew J. Patton. 2013. Simulated method of moments estimation for copula-based multivariate models. Journal of the American Statistical Association 108: 689–700. [Google Scholar] [CrossRef]
- Popkova, Elena G., and Bruno S. Sergi. 2021. Dataset modelling of the financial risk management of social entrepreneurship in emerging economies. Risks 9: 211. [Google Scholar] [CrossRef]
- Queyranne, Maximilien, Daniel Baksa, Azhin Abdulkarim, and Vassili Bazinas. 2021. Morocco’s Monetary Policy Transmission in the Wake of the COVID-19 Pandemic. Washington, DC: IMF. [Google Scholar]
- Rivera-Escobar, Orlando, John Willmer Escobar, and Diego Fernando Manotas. 2022. Measurement of Systemic Risk in the Colombian Banking Sector. Risks 10: 22. [Google Scholar] [CrossRef]
- Rizwan, Muhammad Suhail, Ghufran Ahmad, and Dawood Ashraf. 2020. Systemic risk: The impact of COVID-19. Finance Research Letters 36: 101682. [Google Scholar] [CrossRef] [PubMed]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–42. [Google Scholar] [CrossRef]
- Siebenbrunner, Christoph, and Michael Sigmund. 2019. Quantile panel estimation of financial contagion effects. In Panel Data Econometrics. New York: Elsevier, pp. 639–64. [Google Scholar] [CrossRef]
- Takeuchi, Ichiro, Quoc Le, Timothy Sears, and Alexander Smola. 2006. Nonparametric quantile estimation. The Journal of Machine Learning Research 7: 1231–64. [Google Scholar]
- Taylor, James W. 2000. A quantile regression neural network approach to estimating the conditional density of multiperiod returns. Journal of Forecasting 19: 299–311. [Google Scholar] [CrossRef]
- The Moroccan Ministry of Health. 2020. Morocco Announces the Registration of the First Case of the New Coronavirus. Rabat: Moroccan Ministry of Health. [Google Scholar]
- The World Bank. 2020. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD.ZG?locations=MA (accessed on 1 January 2023).
- The World Health Organization. 2020. WHO Director-General’s Opening Remarks at the Mission Briefing on COVID-19—12 March 2020. Geneva: World Health Organization. [Google Scholar]
- Tobias, Adrian, and Markus K. Brunnermeier. 2016. CoVaR. The American Economic Review 106: 1705. [Google Scholar] [CrossRef]
- White, Halbert. 1992. Nonparametric estimation of conditional quantiles using neural networks. In Computing Science and Statistics: Statistics of Many Parameters: Curves, Images, Spatial Models. New York: Springer, pp. 190–99. [Google Scholar] [CrossRef]
- Xu, Qifa, Bei Jin, and Cuixia Jiang. 2021. Measuring systemic risk of the Chinese banking industry: A wavelet-based quantile regression approach. The North American Journal of Economics and Finance 55: 101354. [Google Scholar] [CrossRef]
- Xu, Qifa, Kai Deng, Cuixia Jiang, Fang Sun, and Xue Huang. 2017. Composite quantile regression neural network with applications. Expert Systems with Applications 76: 129–39. [Google Scholar] [CrossRef]
- Zhang, Hong, and Zhen Zhang. 1999. Feedforward networks with monotone constraints. Paper presented at IJCNN’99. International Joint Conference on Neural Networks. Proceedings (Cat. No.99CH36339), Washington, DC, USA, July 10–16, vol. 3, pp. 1820–23. [Google Scholar] [CrossRef]
- Zhang, Wenjie, Hao Quan, and Dipti Srinivasan. 2018. An improved quantile regression neural network for probabilistic load forecasting. IEEE Transactions on Smart Grid 10: 4425–34. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).