GALSTM-FDP: A Time-Series Modeling Approach Using Hybrid GA and LSTM for Financial Distress Prediction
Abstract
1. Introduction
2. Related Research
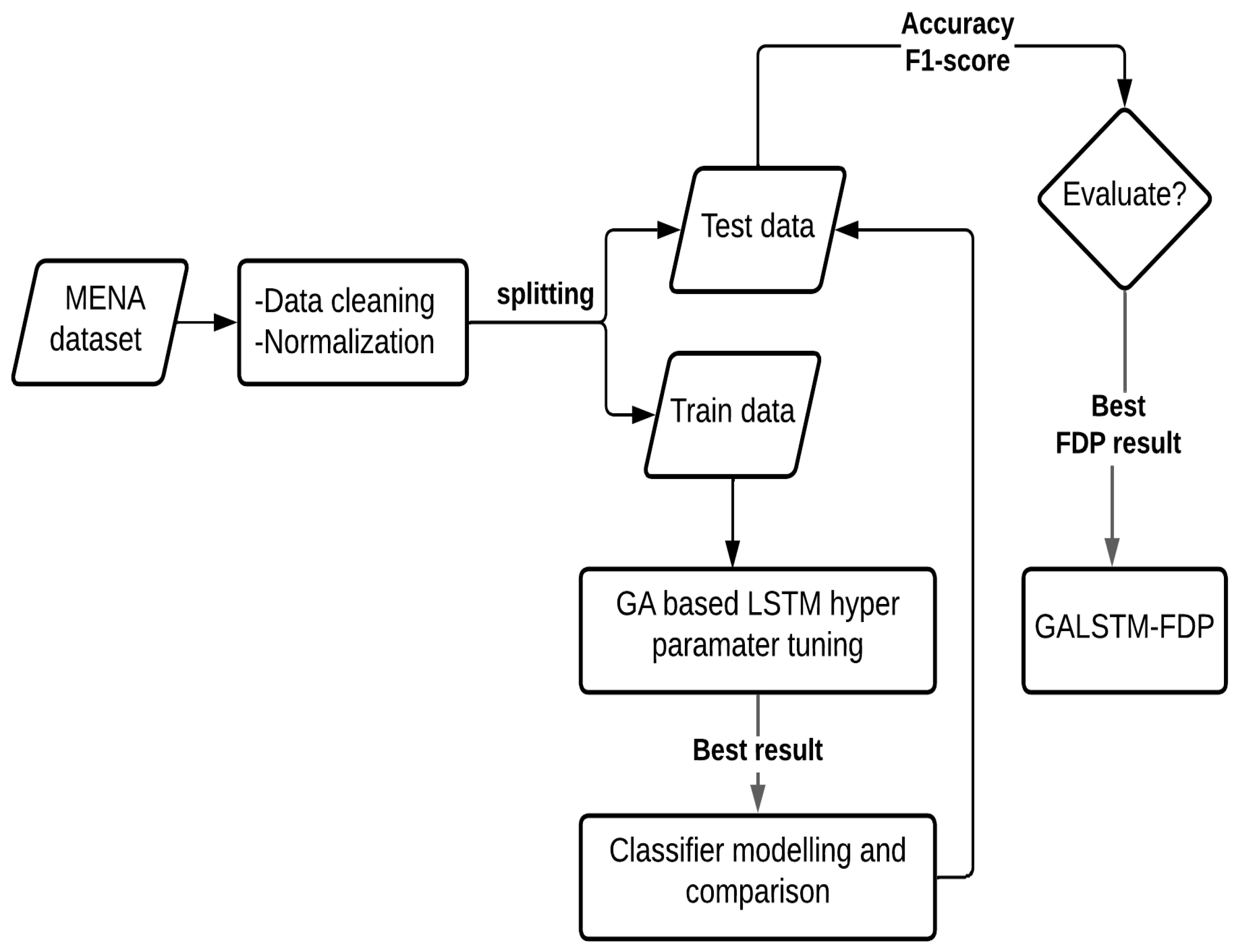
3. Proposed GALSTM-FDP Model Formation
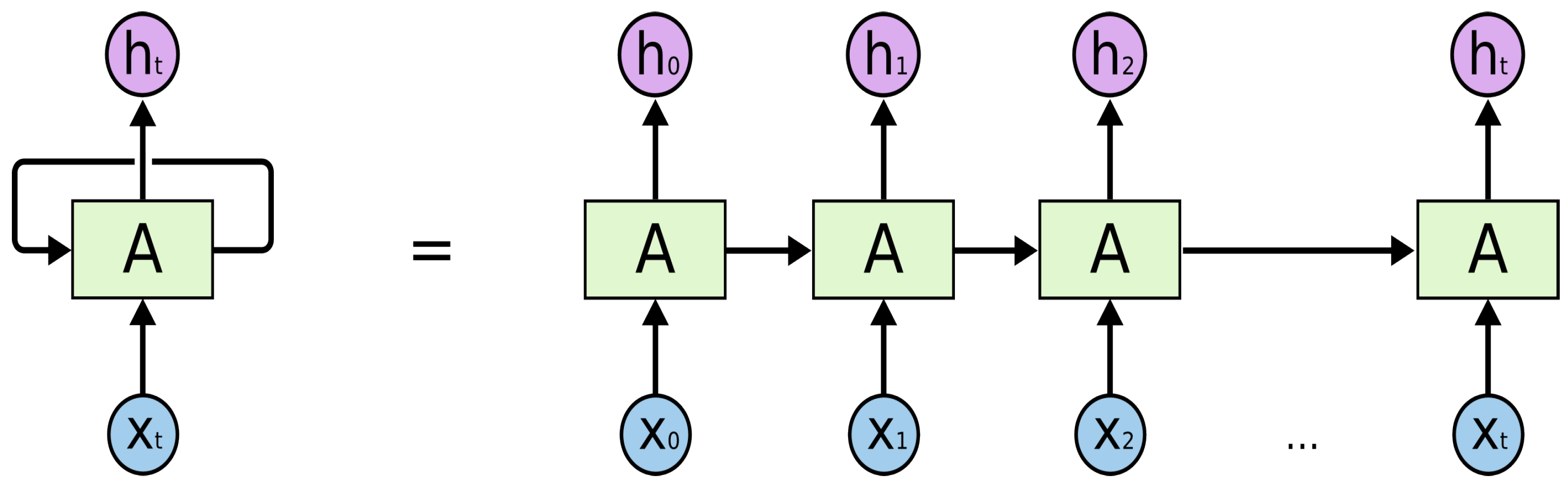
3.1. Long Short-Term Memory (LSTM)
3.2. Genetic Algorithm (GA)
3.3. Hybrid GALSTM-FDP Model for FDP
Optimizing the LSTM Model Using GA
- Generate the initial population: The creation of the initial population, which forms the basis of GA is the first step. By randomly mixing various hyperparameter values, 20 distinct LSTM networks are produced, constituting the starting population of the GA. Antonio has offered a solid rule of thumb for avoiding over-fitting: start with [Number of Training Samples/2 × (Number of Input Neurons + Number of Output Neurons). In most cases, it works, but if the problem is too simple or complex, we can experiment increasing or decreasing the number of neurons. We have picked two values that are less than 64 and two values that are larger than 64. The popular Adam optimizer was chosen as the activation function for this model. The initial population in this study is made up of a collection of 20 random networks. The other two parameters that can be varied are the number of epochs and batch size.
- Compute fitness: Each individual network in the population is trained and tested using the MENA dataset and scored according to the predictive accuracy. We did not run cross-validation on this dataset because it is a time-specific dataset. The highest-scoring networks are retained in order to increase the population of the next generation. The remaining networks of the existing population are discarded.
- Selection: An LSTM network with high accuracy has a greater probability of being chosen for the following generation. During the selection phase, we identify networks from the present population that will be passed down unchanged to the future generation. The top-ranked quarter (five numbers) networks based on accuracy scores are transferred directly to the next population. In order to prevent being trapped at the local maximum, three low-performing networks are also preserved and transferred to the next generation.
- Breeding: For the next generation, we currently have eight networks in the population. The remaining 12 are the product of crossover or breeding. To produce one or more children for the following generation, two networks from the current population, known as parents, are required. The parents are chosen based on their scores, and the network parameters are combined to generate a new offspring that is a hybrid of its parents. Each child in this study is a network with a random set of parameters from its parents.
- Mutation: We randomly adjust some of the properties of random networks in the population to have a population for the next generation. This technique aims to create better networks for the population.
| Algorithm 1 GALSTM-FDP |
|
4. Data and Modeling
- Data cleaning: This phase is used to validate the data contained within the dataset. As seen in Table 2, the value ranges between variables have a wide variation. Our samples, like most real datasets, contain null values and missing properties. These issues were resolved during the pre-processing stage, where we scaled the dataset after filling in the missing values with forward and backward fill within each company as the units of several variables were also different.
- Normalization: The model rescales the variables to a range of −1 to 1 to produce a fair result. This process is needed to convert all of the column values in the dataset to a common scale without distorting the value ranges or causing data loss.
- Dataset samples splitting: The dataset was then turned into the time-series data that the LSTM network required. For a realistic evaluation of performance, datasets must be divided into testing and training sets. We cannot partition our data like other non-time specific datasets because they are time series. At any given time, our network receives 5 years’ worth of data (first 3 years of data from 5 years as input and fifth year as output). Considering this, we have divided our training set into a multiple of 5: 7810 samples in the training set and the remaining 1955 years in the testing set. This is approximately 80% of data in the training samples and the remaining 20% in the testing samples.
5. Empirical Analysis
5.1. FDP Performance Evaluation Metrics
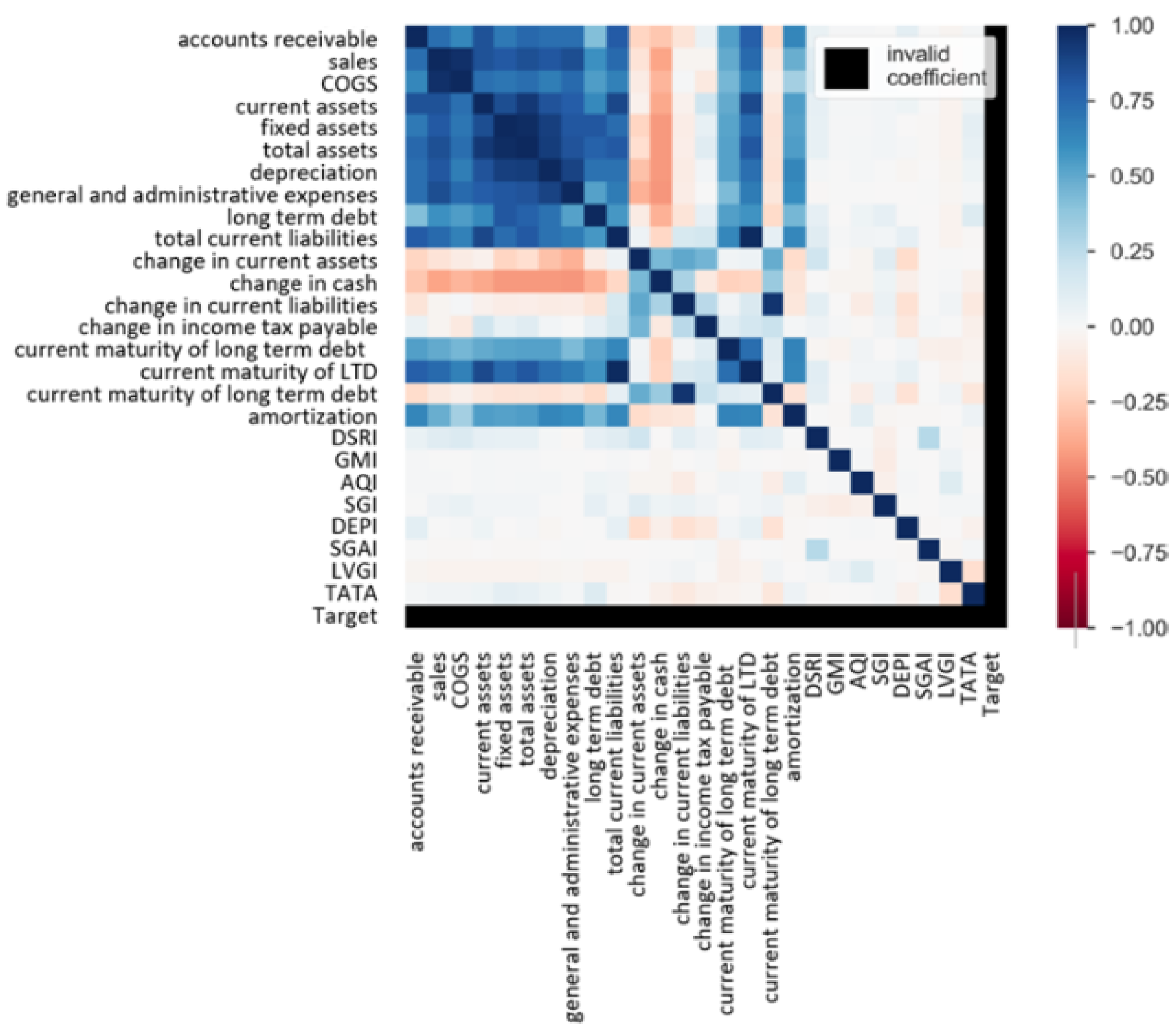
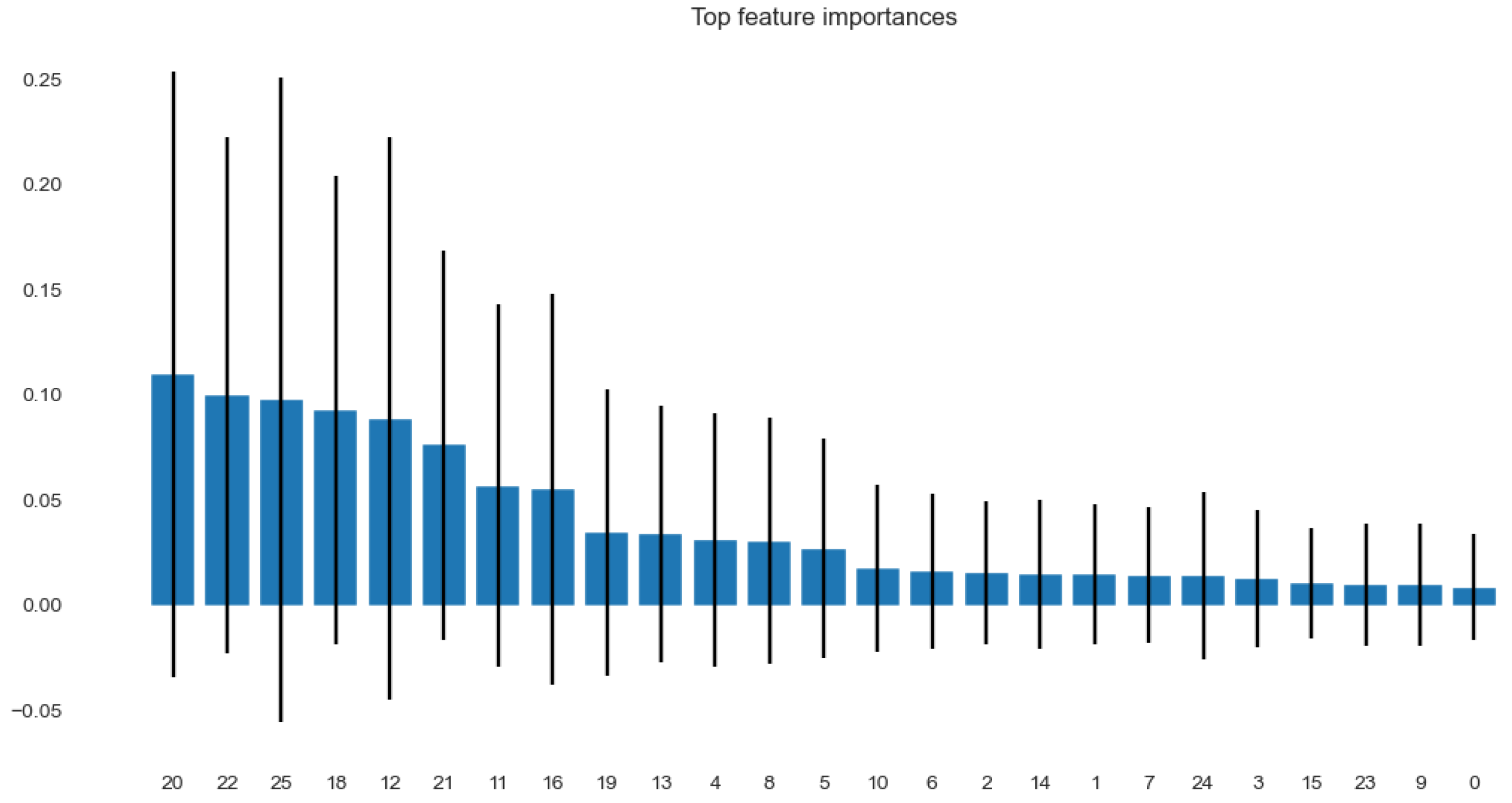
5.2. Correlation and Feature Importance
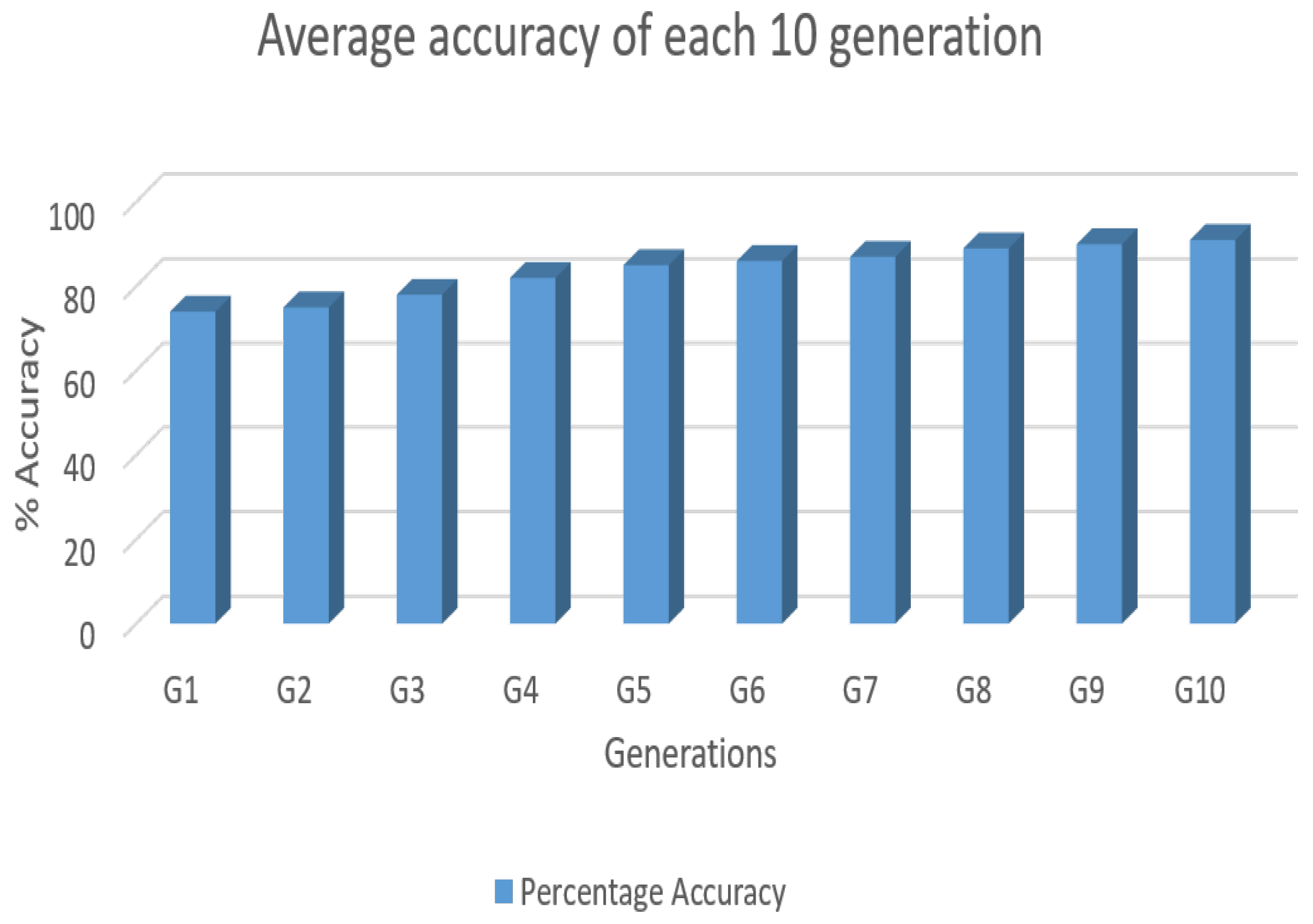
5.3. Analysis of the Proposed Hybrid GALSTM-FDP Model for FDP
5.4. GALSTM-FDP: Overall Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Altman, Edward I. Altman. 1968. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Bae, Jae Kwon Bae. 2012. Predicting financial distress of the South Korean manufacturing industries. Expert Systems with Applications 39: 9159–65. [Google Scholar] [CrossRef]
- Başoğlu Kabran, F., and Kamil Demirberk Ünlü. 2021. A two-step machine learning approach to predict S&P 500 bubbles. Journal of Applied Statistics 48: 2776–94. [Google Scholar]
- Bukhari, Ayaz H., Muhammad Asif Zahoor Raja, Muhammad Sulaiman, Saeed Islam, Muhammad Shoaib, and Poom Kumam. 2020. Fractional neuro-sequential ARFIMA-LSTM for financial market forecasting. IEEE Access 8: 71326–38. [Google Scholar] [CrossRef]
- Chou, Chih-Hsun, Su-Chen Hsieh, and Chui-Jie Qiu. 2017. Hybrid genetic algorithm and fuzzy clustering for bankruptcy prediction. Applied Soft Computing 56: 298–316. [Google Scholar] [CrossRef]
- Cleofas-Sánchez, Laura, Vicente. García Jiménez, Ana Isabel Marqués, and J. S. Sánchez. 2016. Financial distress prediction using the hybrid associative memory with translation. Applied Soft Computing 44: 144–52. [Google Scholar] [CrossRef]
- El-Bannany, Magdi, Ahlam H. Dehghan, and Ahmed M. Khedr. 2021. Prediction of Financial Statement Fraud using Machine Learning Techniques in UAE. Paper presented at the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, March 22–25; pp. 649–54. [Google Scholar]
- El-Bannany, Magdi, Meenu Sreedharan, and Ahmed M. Khedr. 2020. A robust deep learning model for financial distress prediction. International Journal of Advanced Computer Science and Applications (IJACSA) 11: 170–75. [Google Scholar] [CrossRef]
- El Bannany, Magdi, Ahmed M. Khedr, Meenu Sreedharan, and Sakeena Kanakkayil. 2021. Financial Distress Prediction based on Multi-Layer Perceptron with Parameter Optimization. IAENG International Journal of Computer Science 48: 1–12. [Google Scholar]
- Falbo, Paolo. 1991. Credit-scoring by enlarged discriminant models. Omega 19: 275–89. [Google Scholar] [CrossRef]
- Geng, Ruibin, Indranil Bose, and Xi Chen. 2015. Prediction of financial distress: An empirical study of listed Chinese companies using data mining. European Journal of Operational Research 241: 236–47. [Google Scholar] [CrossRef]
- Gepp, Adrian, and Kuldeep Kumar. 2015. Predicting Financial Distress: A Comparison of Survival Analysis and Decision Tree Techniques. Procedia Computer Science 54: 396–404. [Google Scholar] [CrossRef]
- Glorot, Xavier, Antoine Bordes, and Yoshua Bengio. 2011. Domain adaptation for large-scale sentiment classification: A deep learning approach. Paper presented at the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July. [Google Scholar]
- Halim, Zulkifli, Shuhaida Mohamed Shuhidan, and Zuraidah Mohd Sanusi. 2021. Corporation financial distress prediction with deep learning: Analysis of public listed companies in Malaysia. Business Process Management Journal 27: 1163–78. [Google Scholar] [CrossRef]
- Hu, Hui, and Milind Sathye. 2015. Predicting Financial Distress in the Hong Kong Growth Enterprises Market from the Perspective of Financial Sustainability. Sustainability 7: 1186–1200. [Google Scholar] [CrossRef]
- Huang, Yu-Pei, and Meng-Feng Yen. 2019. A new perspective of performance comparison among machine learning algorithms for financial distress prediction. Applied Soft Computing 83: 105663. [Google Scholar] [CrossRef]
- Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. Long short-term memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef] [PubMed]
- Hou, Baozhen. 2016. Financial distress prediction of k-means clustering based on genetic algorithm and rough set theory. Chemical Engineering Transactions 51: 505–10. [Google Scholar]
- Jang, Youjin, Inbae Jeong, Yong K. Cho, and Yong Han Ahn. 2019. Predicting business failure of construction contractors using long short-term memory recurrent neural network. Journal of Construction Engineering and Management 145: 04019067. [Google Scholar] [CrossRef]
- Khan, Naushad, Shah Fahad, Mahnoor Naushad, and Shah Faisal. 2020. COVID-2019 Locked Down Effects on Oil Prices and Its Effects on the World Economy. Available at SSRN 3588810. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3588810 (accessed on 10 January 2023).
- Khedr, Ahmed M., Ifra Arif, Magdi El-Bannany, Saadat M. Alhashmi, and Meenu Sreedharan. 2021. Cryptocurrency price prediction using traditional statistical and machine-learning techniques: A survey. Intelligent Systems in Accounting, Finance and Management 28: 3–34. [Google Scholar] [CrossRef]
- Khedr, Ahmed M., Magdi El Bannany, and Sakeena Kanakkayil. 2021. An ensemble model for financial statement fraud detection. ARPHA Preprints 2: e69590. [Google Scholar]
- Kim, Kyoung-jae, Kichun Lee, and Hyunchul Ahn. 2019. Predicting Corporate Financial Sustainability Using Novel Business Analytics. Sustainability 11: 64. [Google Scholar] [CrossRef]
- Matin, Rastin, Casper Hansen, Christian Hansen, and Pia Mølgaard. 2019. Predicting distresses using deep learning of text segments in annual reports. Expert Systems with Applications 132: 199–208. [Google Scholar] [CrossRef]
- Mehreen, Mehreen, Maran Marimuthu, Samsul Ariffin Abdul Karim, and Amin Jan. 2020. Proposing a multidimensional bankruptcy prediction model: An approach for sustainable Islamic banking. Sustainability 12: 3226. [Google Scholar] [CrossRef]
- Min, Jae H., and Young-Chan Lee. 2005. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Systems with Applications 28: 603–14. [Google Scholar] [CrossRef]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Ravisankar, P., and V. Ravi. 2010. Financial distress prediction in banks using Group Method of Data Handling neural network, counter propagation neural network and fuzzy ARTMAP. Knowledge-Based Systems 23: 823–31. [Google Scholar] [CrossRef]
- Ribeiro, Bernardete, and Noel Lopes. 2011. Deep belief networks for financial prediction. Paper presented at the International Conference on Neural Information Processing, Shanghai, China, November 13–17; Berlin and Heidelberg: Springer, pp. 766–73. [Google Scholar]
- Sun, Jie, Hamido Fujita, Peng Chen, and Hui Li. 2017. Dynamic financial distress prediction with concept drift based on time weighting combined with Adaboost support vector machine ensemble. Knowledge-Based Systems 120: 4–14. [Google Scholar] [CrossRef]
- Sun, Jie, and Xiaofeng Hui. 2006. An application of decision tree and genetic algorithms for financial ratios’ dynamic selection and financial distress prediction. Paper presented at the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, August 13–16; pp. 2413–18. [Google Scholar]
- Shen, Furao, Jing Chao, and Jinxi Zhao. 2015. Forecasting exchange rate using deep belief networks and conjugate gradient method. Neurocomputing 167: 243–253. [Google Scholar] [CrossRef]
- Shin, Kyung-Shik, and Yong-Joo Lee. 2002. A genetic algorithm application in bankruptcy prediction modeling. Expert Systems with Applications 23: 321–28. [Google Scholar] [CrossRef]
- Sreedharan, Meenu, Ahmed M. Khedr, and Magdi El Bannany. 2020a. A multi-layer perceptron approach to financial distress prediction with genetic algorithm. Automatic Control and Computer Sciences 54: 475–482. [Google Scholar] [CrossRef]
- Sreedharan, Meenu, Ahmed M. Khedr, and Magdi El Bannany. 2020b. A comparative analysis of machine learning classifiers and ensemble techniques in financial distress prediction. Paper presented at the 2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, July 20–23; pp. 653–57. [Google Scholar]
- Wanke, Peter, Carlos Barros, and João Faria. 2015. Financial distress drivers in Brazilian banks: A dynamic slacks approach. European Journal of Operational Research 240: 258–68. [Google Scholar] [CrossRef]
- Wu, Desheng, Liang Liang, and Zijiang Yang. 2008. Analyzing the financial distress of Chinese public companies using probabilistic neural networks and multivariate discriminate analysis. Socio-Economic Planning Sciences 42: 206–20. [Google Scholar] [CrossRef]
- Zhu, Lin, Dawen Yan, Zhihua Zhang, and Guotai Chi. 2022. Financial Distress Prediction of Chinese Listed Companies Using the Combination of Optimization Model and Convolutional Neural Network. Mathematical Problems in Engineering 2022: 9038992. [Google Scholar] [CrossRef]

| Indicators | Formula |
|---|---|
| Total liabilities/Total assets | |
| Current assets/Current liabilities | |
| Current assets-inventory/Current liabilities | |
| Total liabilities/total shareholders’ equity | |
| Current liabilities/total assets | |
| Net operating cash flow/current liabilities | |
| Earnings before interest and tax/interest expense | |
| Net profit/number of ordinary shares at the end of year | |
| Net assets/number of ordinary shares at the end of year | |
| Net increase in cash and cash equivalents/number of ordinary shares at the end of year | |
| Capital reserves/number of ordinary shares at the end of year | |
| (Sales revenue–sales cost)/sales revenue | |
| Net profit/sales revenue | |
| Earnings before income tax/average total assets | |
| Net profit/average total assets | |
| Net profit/average current assets | |
| Net profit/average fixed assets | |
| Net profit/average shareholders’ equity | |
| Business income of this year/Business income of last year | |
| Total assets of this year/total assets of last year | |
| Net profit of this year/net profit of last year | |
| Main business income/average total assets | |
| Sales revenue/average current assets | |
| Sales revenue/average fixed assets | |
| Main business cost/average inventory | |
| Main business income/average balance of accounts receivable | |
| Cost of sales/average payable accounts | |
| Current assets total assets | |
| Fixed assets/total assets | |
| Shareholders’ equity/fixed assets | |
| Current liabilities/total liabilities |
| Variables | Mean | Min | Max |
|---|---|---|---|
| Total Liabilities | 88,751.36508 | 13 | 1,669,220 |
| Total Assets | 183,280.635 | 5763 | 3,091,702 |
| Current Assets | 43,249.87 | 138 | 676,520 |
| Current Liabilities | 46,492.642 | 10 | 790,074 |
| Accounts Receivable | 11,041.079 | 5.63 | 200,071 |
| Accounts Payable | 11,966.0634 | 205 | 374,494 |
| Total Shareholders Equity | 93,131.111 | 5565 | 1,422,482 |
| Net Cash Flow | 17,297.667 | −4600 | 481,539 |
| EBIT | 8274 | 16 | 267,461 |
| Net Profit | 4253.9524 | −31,571 | 156,702 |
| Cash and Cash Equivalent | 12,907.0158 | 19 | 209,716 |
| Cost of Goods Sold | 22,169.1746 | 345 | 266,764 |
| Sales | 1,730,068.53 | 93 | 10,301,478 |
| Shares | 402,708 | 30,318.8 | 3,901,347 |
| Capital Reserves | 5774.65 | −615 | 182,827 |
| Fixed Assets | 140,030.76 | 599 | 2,415,182 |
| Average Total Assets | 274,315.7778 | 8815 | 4,608,537.5 |
| Average Current Assets | 66,022.484 | 210 | 1,048,037 |
| Average Fixed Assets | 208,293.2937 | 825 | 3,560,500 |
| Average Equity | 140,519.53 | 8476 | 2,227,284 |
| Average Accounts Receivable | 13,773.69 | 4069 | 327,807 |
| Average Accounts Payable | 16,861.05 | 794 | 555,164.5 |
| Net Increase in Cash | −3622.984 | −151,247 | 16,129 |
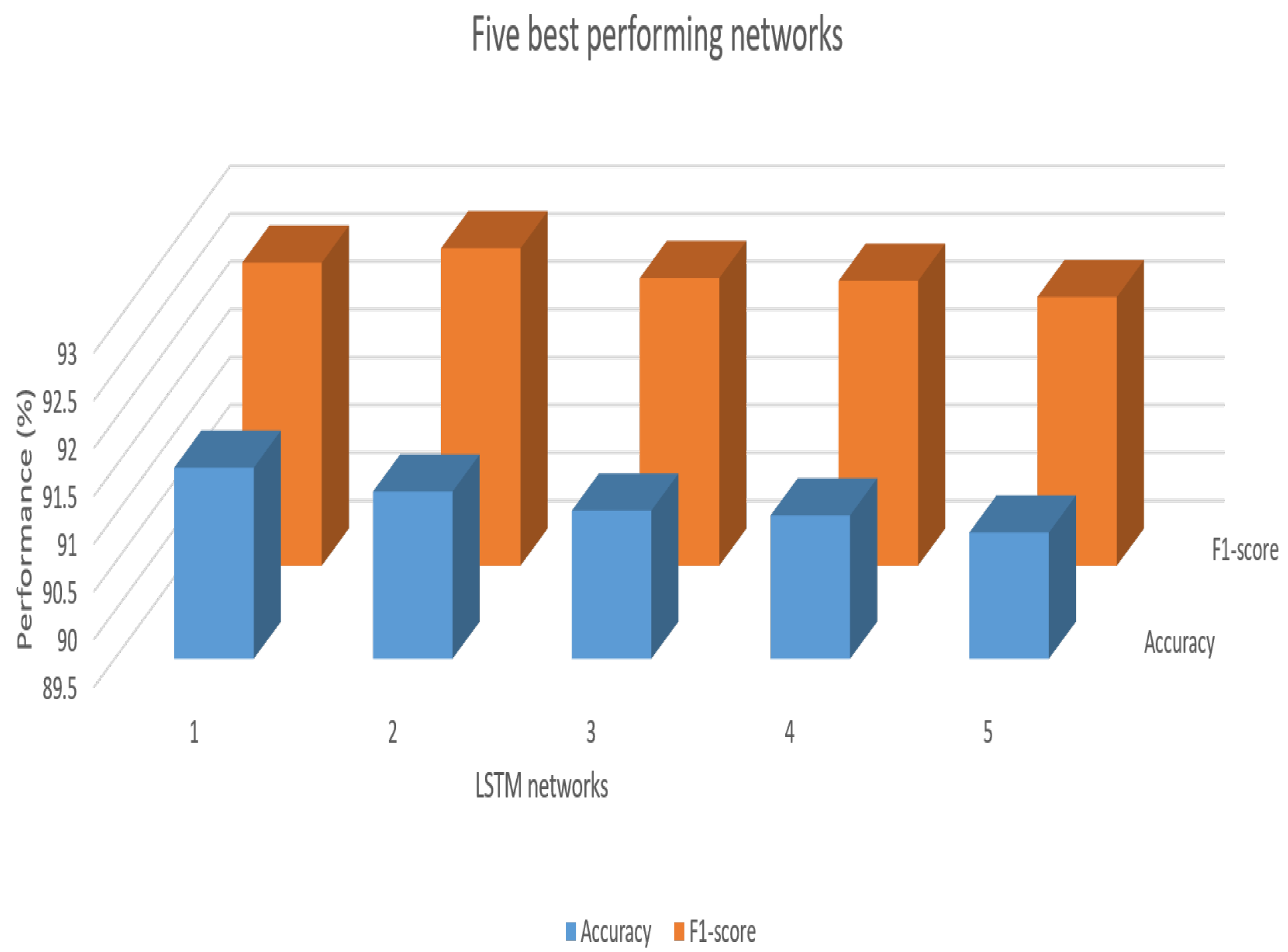
| Network | Hidden Layers | Neurons per Layer | Batch Size | Epoch | Testing Accuracy (%) | Testing F1-Score (%) |
|---|---|---|---|---|---|---|
| 1 | 2 | 64 | 35 | 500 | 91.50 | 92.67 |
| 2 | 2 | 64 | 70 | 400 | 91.25 | 92.82 |
| 3 | 1 | 64 | 35 | 500 | 91.05 | 92.51 |
| 4 | 2 | 128 | 35 | 400 | 91.00 | 92.48 |
| 5 | 1 | 128 | 70 | 500 | 90.82 | 92.31 |
| Financial Distress Prediction Performance | ||
|---|---|---|
| Classifiers | Accuracy | F1-Score |
| - | 91.50 | 92.67 |
| 88.75 | 90.46 | |
| 86.50 | 89.67 | |
| 81.75 | 85.46 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Ali, A.; Khedr, A.M.; El Bannany, M.; Kanakkayil, S. GALSTM-FDP: A Time-Series Modeling Approach Using Hybrid GA and LSTM for Financial Distress Prediction. Int. J. Financial Stud. 2023, 11, 38. https://doi.org/10.3390/ijfs11010038
Al Ali A, Khedr AM, El Bannany M, Kanakkayil S. GALSTM-FDP: A Time-Series Modeling Approach Using Hybrid GA and LSTM for Financial Distress Prediction. International Journal of Financial Studies. 2023; 11(1):38. https://doi.org/10.3390/ijfs11010038
Chicago/Turabian StyleAl Ali, Amal, Ahmed M. Khedr, Magdi El Bannany, and Sakeena Kanakkayil. 2023. "GALSTM-FDP: A Time-Series Modeling Approach Using Hybrid GA and LSTM for Financial Distress Prediction" International Journal of Financial Studies 11, no. 1: 38. https://doi.org/10.3390/ijfs11010038
APA StyleAl Ali, A., Khedr, A. M., El Bannany, M., & Kanakkayil, S. (2023). GALSTM-FDP: A Time-Series Modeling Approach Using Hybrid GA and LSTM for Financial Distress Prediction. International Journal of Financial Studies, 11(1), 38. https://doi.org/10.3390/ijfs11010038







