Fama–French–Carhart Factor-Based Premiums in the US REIT Market: A Risk Based Explanation, and the Impact of Financial Distress and Liquidity Crisis from 2001 to 2020
Abstract
1. Introduction
2. Literature Review
2.1. SMB and HML Premiums; Empirical Evidence from Stock/REIT Market and Extrapolation Theory
2.2. RMW and CMA Premiums: Empirical Evidence from Stock/REIT Market and Sound Mind Effect
2.3. WML Premium: Empirical Evidence from Stock/REIT Market and Their Interpretation
2.4. Impact of Financial Distress and Liquidity Crisis on Factor Premiums
2.5. The Effect of Stock Market Returns
3. Data and Methodology
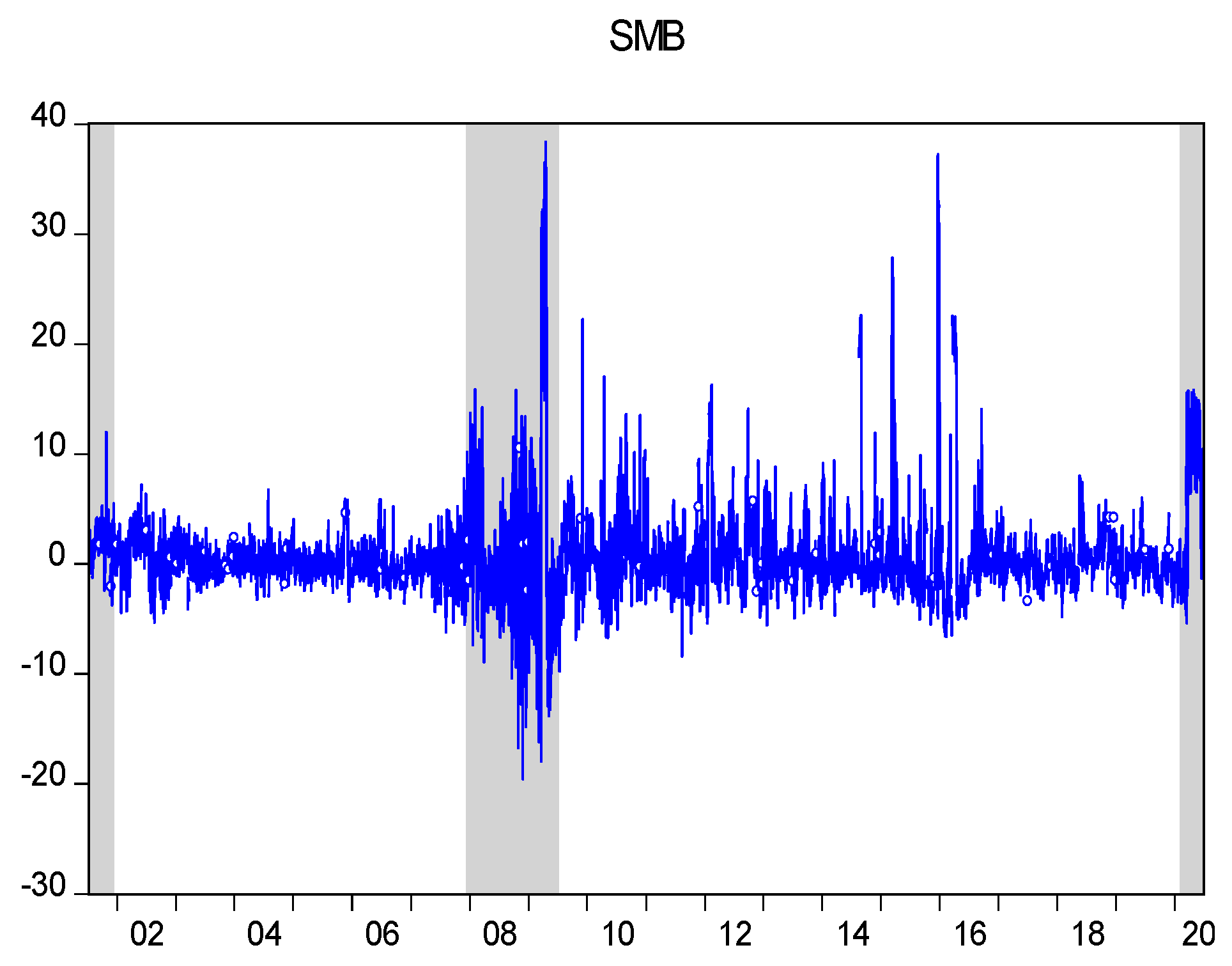
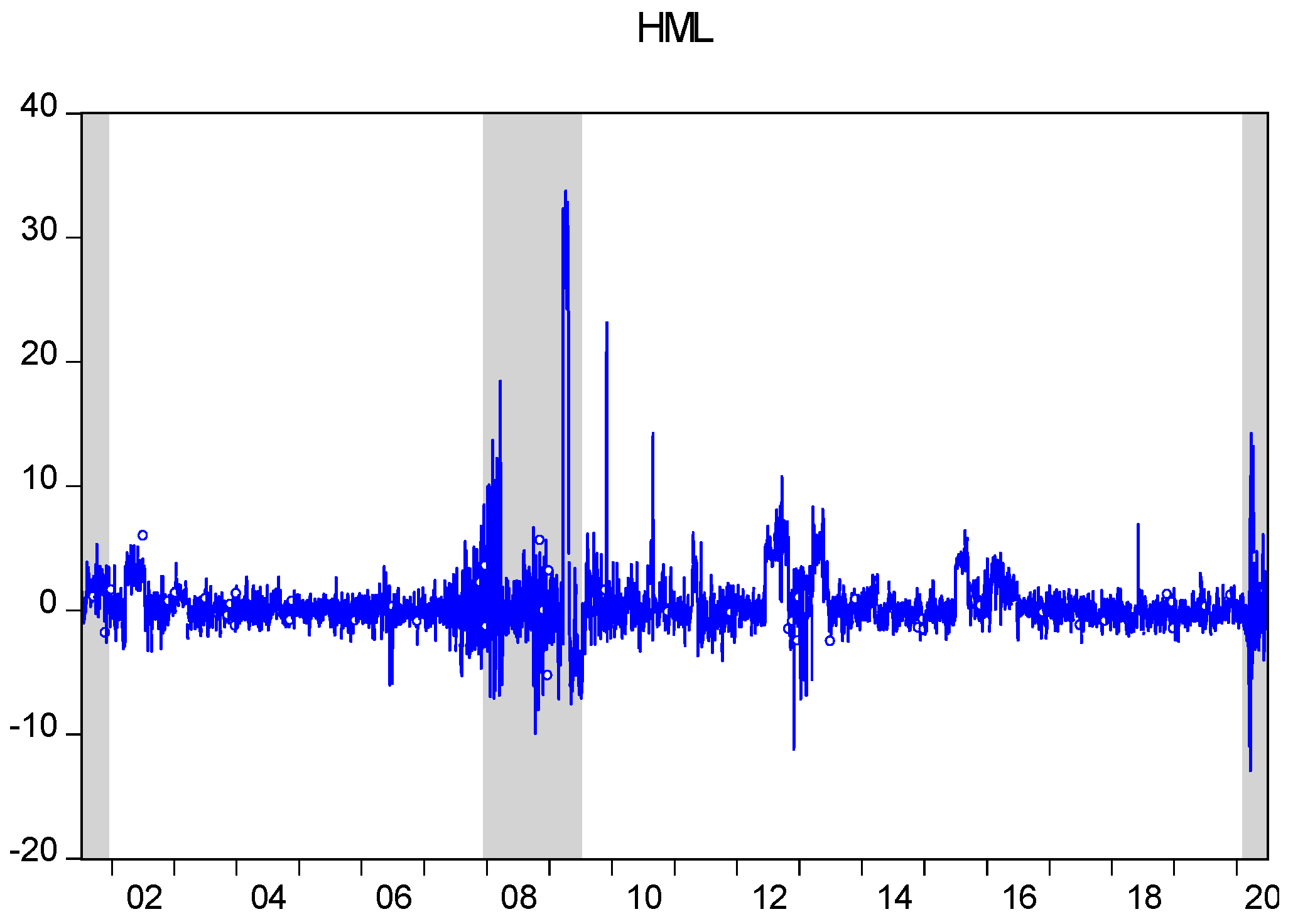
3.1. Measuring Factor Premiums and Construction of Factor-Based Portfolios
3.2. Gauging Risk and Risk Adjusted Performance of Factor-Based Strategies
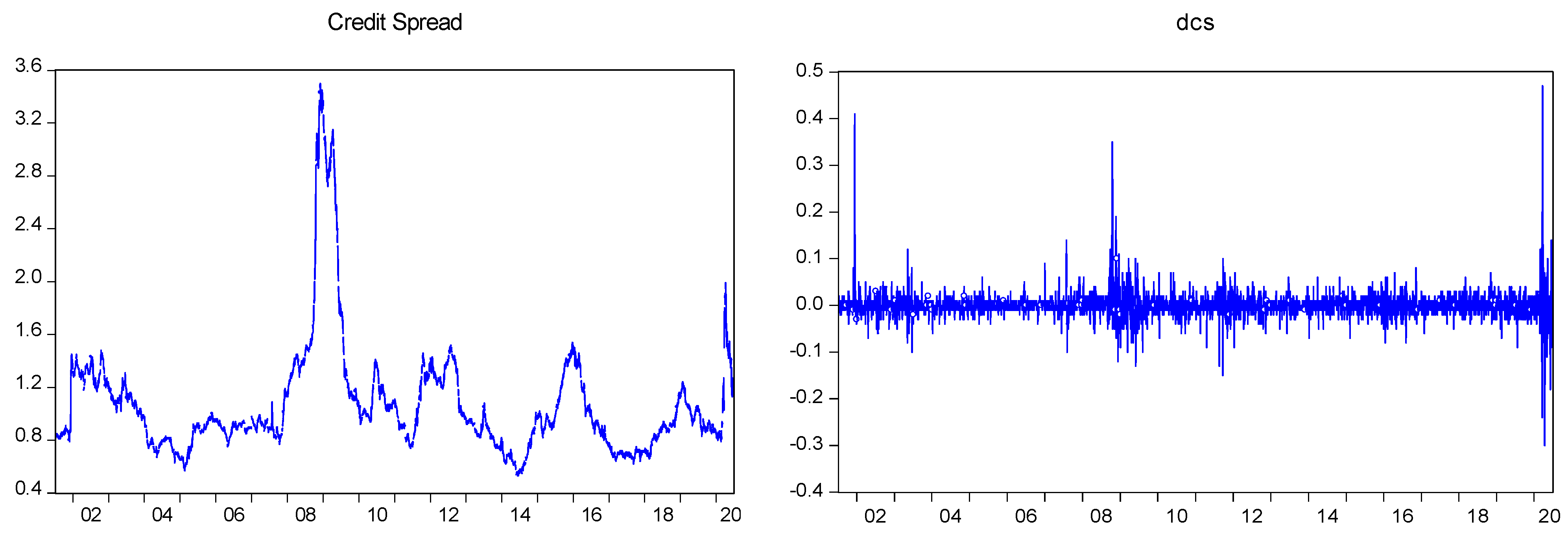
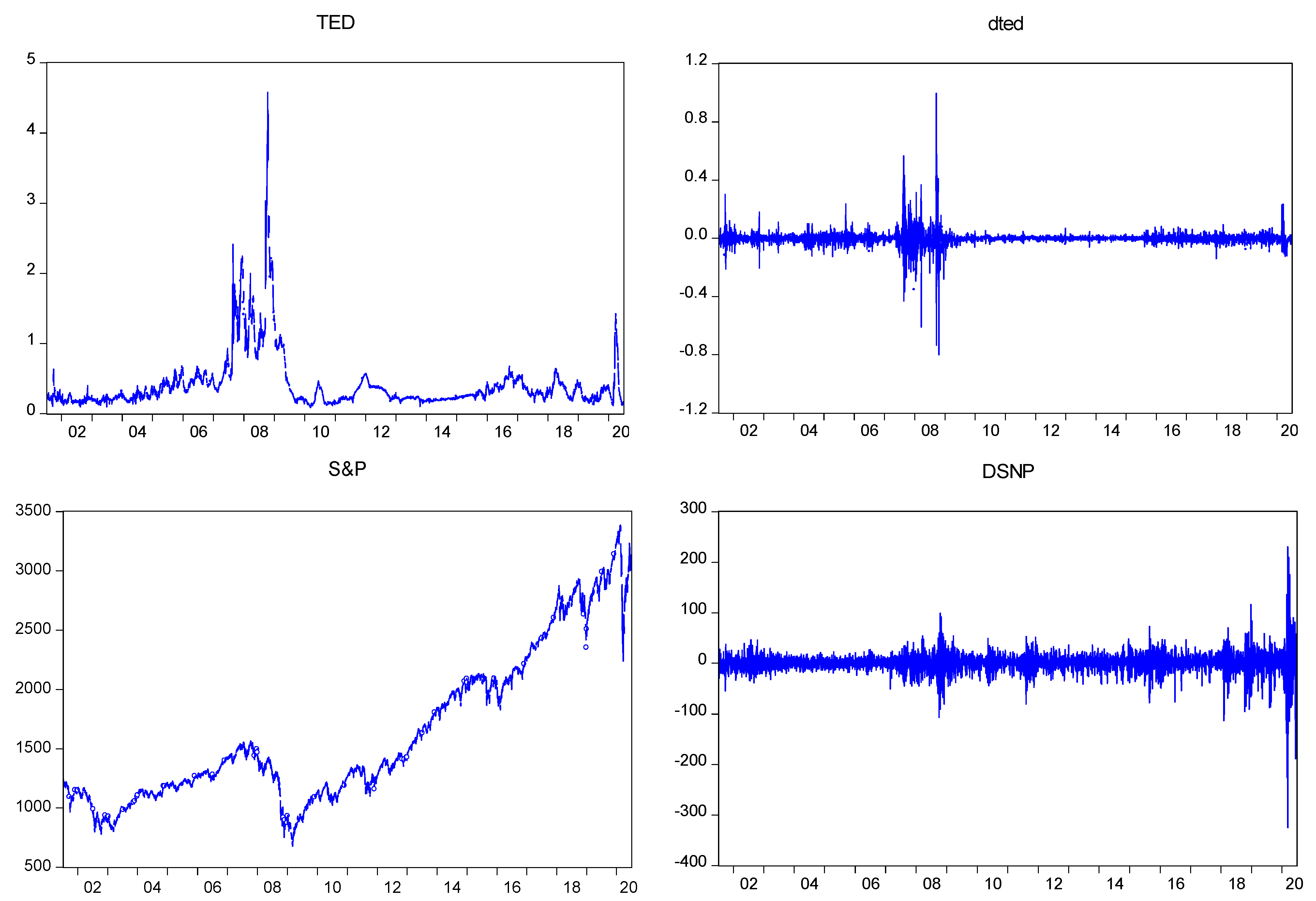
3.3. Explanatory Variables
3.4. Bounds Test for Cointegration/Long-Run and Short-Run Elasticity: The Long-Run ARDL Model and the Short-Run Error Correction Model
3.5. Subperiods
4. Empirical Results
4.1. Significance, Direction and Magnitude of Factor Premiums
4.2. Risk Associated with Factor-Based Strategies
4.2.1. SMB
4.2.2. HML
4.2.3. RMW
4.2.4. CMA
4.2.5. WML
4.3. Robustness Check for Excess Returns and Risk
4.4. Statistical Analysis for Explanatory Variables
4.5. Bounds Test for Cointegration
4.6. The Long-Run ARDL Model and the Short-Run Error Correction Model
4.6.1. SMB, HML and CMA
Recession
Non-Recession
4.6.2. RMW and WML
Recession
Non-Recession
5. Practical Implication for REIT Investors
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Portfolio Formation
| Computed F-Statistic | 10% Critical I(0) | 10% Critical I(1) | 5% Critical I(0) | 5% Critical I(1) | ARDL Specs | H0: No Cointegration |
|---|---|---|---|---|---|---|
| 4.50259 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,1) | Reject |
| 127.15276 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 22.34528 | 2.12 | 3.23 | 2.45 | 3.61 | (1,1,1,1) | Reject |
| 78.040046 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,1,0) | Reject |
| 13.34180 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,1) | Reject |
| Computed F-Statistic | 10% Critical I(0) | 10% Critical I(1) | 5% Critical I(0) | 5% Critical I(1) | ARDL Specs | H0: No Cointegration |
|---|---|---|---|---|---|---|
| 7.97392 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 107.38706 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 7.74321 | 2.12 | 3.23 | 2.45 | 3.61 | (1,1,1,1) | Reject |
| 79.15930 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 13.55075 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,1,1) | Reject |
| Computed F-Statistic | 10% Critical I(0) | 10% Critical I(1) | 5% Critical I(0) | 5% Critical I(1) | ARDL Specs | H0: No Cointegration |
|---|---|---|---|---|---|---|
| 6.68511 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 41.47505 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 123.26916 | 2.12 | 3.23 | 2.45 | 3.61 | (1,1,1,0) | Reject |
| 80.04605 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,1) | Reject |
| 7.224149 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| Computed F-Statistic | 10% Critical I(0) | 10% Critical I(1) | 5% Critical I(0) | 5% Critical I(1) | ARDL Specs | H0: No Cointegration |
|---|---|---|---|---|---|---|
| 11.78537 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,1,0) | Reject |
| 258.17366 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 51.30978 | 2.12 | 3.23 | 2.45 | 3.61 | (1,1,2,1) | Reject |
| 83.47141 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,2) | Reject |
| 13.05765 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| Computed F-Statistic | 10% Critical I(0) | 10% Critical I(1) | 5% Critical I(0) | 5% Critical I(1) | ARDL Specs | H0: No Cointegration |
|---|---|---|---|---|---|---|
| 3.67679 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 123.17816 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 64.07647 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 221.19466 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 9.049073 | 2.12 | 3.23 | 2.45 | 3.61 | (1,0,0,0) | Reject |
| 1 | According to the National Association of Real Estate Trusts (NAREIT), the 2021 REIT market cap was $1.74 trillion, which translates to 3.3% of the $53 trillion US stock market cap (NAREIT 2022b). The market cap of listed REITs globally has risen from $10 billion in 1990 to approximately $2.5 trillion today, operating within 41 countries and regions (NAREIT 2022a). This allows global investors to incorporate the real estate sector within multi-asset portfolios, as an investment vehicle and diversification tool. Based on market cap, the US accounts for approximately 70% of the global REIT market. |
| 2 | For this reason, we collect daily data for REIT returns inclusive of dividends. |
| 3 | These excess returns have given rise to style based investment strategies, where the size premium strategy involves buying small stocks and selling big stocks, while the value premium strategy involves buying value stocks and selling growth stocks. |
| 4 | Excess return earned by the portfolio (over the risk free rate) relative to its total risk. |
| 5 | Excess return earned by the portfolio (over the risk free rate) relative to its systematic risk. |
| 6 | We use an Augmented Dickey–Fuller unit root test to confirm that both credit spread and TED spread are stationary in levels while the S&P 500 index is stationary in first difference. |
| 7 | We use an Augmented Dickey–Fuller unit root test to confirm that all variables are stationary in returns (factor premiums associated with size, value, profitability, investment and momentum). |
| 8 | Most values are clustered on the left tail of the distribution, right tail is longer. The outliers of the distribution are further out towards the right. |
| 9 | Excess kurtosis means fat tails. This means that there are lots of outliers on both sides. This indicates instances of extremely small and extremely large values. |
| 10 | The x-axis shows years while the y-axis shows the premiums in percentage terms. Note that the scaling on the y-axis in these graphs varies based on the dispersion of these individual premiums. |
| 11 | The square root of the residual variance derived from the univariate CAPM model is used to represent idiosyncratic return volatility, and this is an indicator for arbitrage risk. |
| 12 | For reasons of brevity, these results are presented in the Appendix A section. |
| 13 | Investors tend to be overly optimistic about future prospects of growth stocks, while they tend to be overly pessimistic about prospects of value stocks, and when these expectations are not realized, it results in a higher return on value stocks and a lower return on growth stocks (Ooi et al. 2007). |
| 14 | We find a significant and negative correlation between the S&P 500 Index and WML premiums (−2.3%) for our full sample. For reasons of brevity, a table of these results has not been included in the main body of this paper. |
| 15 | We find significant and negative correlation between the S&P 500 Index and HML premiums during the non-recessionary phase that follows the dot-com crash (−13.5%) and the non-recessionary phase that follows the 2007/08 recession (−16%). For reasons of brevity, a table of these results has not been included in the main body of this paper. |
| 16 | Stock price multiplied by shares outstanding. |
References
- Acharya, Viral, and Lasse Pendersen. 2005. Asset pricing with liquidity risk. Journal of Financial Economics 77: 375–410. [Google Scholar] [CrossRef]
- Akdi, Yilmaz, Serdar Varlik, and M. Hakan Berument. 2020. Duration of Global Financial Cycles. Physica A: Statistical Mechanics and Its Applications 549: 124331. [Google Scholar] [CrossRef]
- Ali, Fahad, and Numan Ülkü. 2019. Monday effect in the RMW and the short-term reversal factors. International Review of Finance 19: 681–91. [Google Scholar] [CrossRef]
- Ali, Ashiq, Lee-Seok Hwang, and Mark A. Trombley. 2003. Arbitrage Risk and the Book-to-Market Anomaly. Journal of Financial Economics 69: 355–73. [Google Scholar] [CrossRef]
- Allen, Marcus T., Jeff Madura, and Thomas M. Springer. 2000. REIT characteristics and the sensitivity of REIT returns. The Journal of Real Estate Finance and Economics 21: 141–52. [Google Scholar] [CrossRef]
- Amihud, Yakov, Allaudeen Hameed, Wenjin Kang, and Huiping Zhang. 2015. The illiquidity premium: International evidence. Journal of Financial Economics 117: 350–68. [Google Scholar] [CrossRef]
- Barkham, Richard, and Charles Ward. 1999. Investor sentiment and noise traders: Discount to net asset value in listed property companies in the UK. Journal of Real Estate Research 18: 291–312. [Google Scholar] [CrossRef]
- Bernanke, Ben S. 1983. Irreversibility, uncertainty, and cyclical investment. The Quarterly Journal of Economics 98: 85–106. [Google Scholar] [CrossRef]
- Bond, Shaun, and Chen Xue. 2016. The Cross Section of Expected Real Estate Returns: Insights from Investment-Based Asset Pricing. The Journal of Real Estate Finance and Economics 54: 403–28. [Google Scholar] [CrossRef]
- Boudry, Walter I. 2011. An Examination of REIT Dividend Payout Policy. Real Estate Economics 39: 601–34. [Google Scholar] [CrossRef]
- Bouri, Elie, Rangan Gupta, and Shixuan Wang. 2020. Nonlinear contagion between stock and real estate markets: International evidence from a local Gaussian correlation approach. International Journal of Finance & Economics 27: 2089–109. [Google Scholar] [CrossRef]
- Breen, William, Lawrence R. Glosten, and Ravi Jagannathan. 1989. Economic significance of predictable variations in stock index returns. The Journal of Finance 44: 1177–89. [Google Scholar] [CrossRef]
- Brown, Keith C., W. V. Harlow, and Seha M. Tinic. 1988. Risk aversion, uncertain information, and market efficiency. Journal of Financial Economics 22: 355–85. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K. 2009. Deciphering the Liquidity and Credit Crunch 2007–2008. Journal of Economic Perspectives 23: 77–100. [Google Scholar] [CrossRef]
- Caballero, Ricardo J., and Arvind Krishnamurthy. 2009. Global Imbalances and Financial Fragility. American Economic Review 99: 584–88. [Google Scholar] [CrossRef]
- Campbell, John Y., Jens Hilscher, and Jan Szilagyi. 2008. In Search of Distress Risk. The Journal of Finance 63: 2899–939. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Cesa-Bianchi, Ambrogio, Luis Felipe Cespedes, and Alessandro Rebucci. 2015. Global Liquidity, House Prices, and the Macroeconomy: Evidence from Advanced and Emerging Economies. Journal of Money, Credit and Banking 47: 301–35. [Google Scholar] [CrossRef]
- Chan, K. C., and Nai-Fu Chen. 1991. Structural and return characteristics of small and large firms. The Journal of Finance 46: 1467–84. [Google Scholar] [CrossRef]
- Chaudhry, Mukesh K., F. C. Neil Myer, and James R. Webb. 1999. Stationarity and cointegration in systems with real estate and financial assets. The Journal of Real Estate Finance and Economics 18: 339–49. [Google Scholar] [CrossRef]
- Chen, Nai-Fu, and Feng Zhang. 1998. Risk and Return of Value Stocks. Journal of Business 71: 501–35. [Google Scholar] [CrossRef]
- Chui, Andy C. W., Sheridan Titman, and K. C. John Wei. 2003. The Cross-Section of Expected REIT Returns. Real Estate Economics 31: 451–79. [Google Scholar] [CrossRef]
- Chung, Richard, Scott Fung, James D. Shilling, and Tammie X. Simmons-Mosley. 2016. REIT stock market volatility and expected returns. Real Estate Economics 44: 968–95. [Google Scholar] [CrossRef]
- Clayton, Jim, and Greg MacKinnon. 2003. The relative importance of stock, bond and real estate factors in explaining REIT returns. The Journal of Real Estate Finance and Economics 27: 39–60. [Google Scholar] [CrossRef]
- Crotty, James. 2009. Structural causes of the global financial crisis: A critical assessment of the ‘new financial architecture’. Cambridge Journal of Economics 33: 563–80. [Google Scholar] [CrossRef]
- Edelen, Roger M., Ozgur S. Ince, and Gregory B. Kadlec. 2016. Institutional investors and stock return anomalies. Journal of Financial Economics 119: 472–88. [Google Scholar] [CrossRef]
- Elgammal, Mohammed M., and David Gordon McMillan. 2014. Value premium and default risk. Journal of Asset Management 15: 48–61. [Google Scholar] [CrossRef]
- Elgammal, Mohammed M., Tugba Bas, Orla Gough, Neeta Shah, and Stefan van Dellen. 2016. Do financial distress and liquidity crises affect value and size premiums? Applied Economics 48: 3734–51. [Google Scholar] [CrossRef]
- Essa, Mohammad Sharik, and Evangelos Giouvris. 2020. Oil price, oil price implied volatility (OVX) and illiquidity premiums in the US: A symmetry and the impact of macroeconomic factors. Journal of Risk and Financial Management 13: 70. [Google Scholar] [CrossRef]
- Eun, Cheol S., Sandy Lai, Frans A. De Roon, and Zhe Zhang. 2010. International diversification with factor funds. Management Science 56: 1500–18. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-Section of Expected Stock Returns. The Journal of Finance 47: 427–65. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1996. Multifactor Explanations of Asset Pricing Anomalies. The Journal of Finance 51: 55–84. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2006. The value premium and the CAPM. The Journal of Finance 61: 2163–85. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. International Tests of a Five-Factor Asset Pricing Model. SSRN Electronic Journal 123: 441–63. [Google Scholar] [CrossRef]
- Foster, F. Douglas, and S. Viswanathan. 1990. A Theory of the Interday Variations in Volume, Variance, and Trading Costs in Securities Markets. Review of Financial Studies 3: 593–624. [Google Scholar] [CrossRef]
- Galariotis, Emilios C., and Evangelos Giouvris. 2007. Liquidity Commonality in the London Stock Exchange. Journal of Business Finance and Accounting 34: 374–88. [Google Scholar] [CrossRef]
- Galariotis, Emilios C., and Evangelos Giouvris. 2009. Systematic liquidity and excess returns: Evidence from the London Stock Exchange. Review of Accounting and Finance 8: 279–307. [Google Scholar] [CrossRef]
- Garlappi, Lorenzo, and Hong Yan. 2011. Financial Distress and the Cross-section of Equity Returns. The Journal of Finance 66: 789–822. [Google Scholar] [CrossRef]
- Giesecke, Kay, Francis A. Longstaff, Stephen Schaefer, and Ilya A. Strebulaev. 2014. Macroeconomic effects of corporate default crisis: A long-term perspective. Journal of Financial Economics 111: 297–310. [Google Scholar] [CrossRef]
- Glascock, John L., and Ran Lu-Andrews. 2014. The Profitability Premium in Real Estate Investment Trusts. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Glascock, John L., Chiuling Lu, and Raymond W. So. 2000. Further Evidence on the Integration of REIT, Bond, and Stock Returns. Journal of Real Estate Finance and Economics 20: 177–94. [Google Scholar] [CrossRef]
- Goebel, Paul, David Harrison, Jeffrey Mercer, and Ryan Whitby. 2012. REIT Momentum and Characteristic-Related REIT Returns. The Journal of Real Estate Finance and Economics 47: 564–81. [Google Scholar] [CrossRef]
- Griffin, John M., and Michael L. Lemmon. 2002. Book-to-Market Equity, Distress Risk, and Stock Returns. The Journal of Finance 57: 2317–36. [Google Scholar] [CrossRef]
- Gyourko, Joseph, and Donald B. Keim. 1992. What Does the Stock Market Tell Us About Real Estate Returns? Real Estate Economics 20: 457–85. [Google Scholar] [CrossRef]
- Hahn, Jaehoon, and Hangyong Lee. 2006. Yield Spreads as Alternative Risk Factors for Size and Book-to-Market. Journal of Financial and Quantitative Analysis 41: 245–69. [Google Scholar] [CrossRef]
- Harrison, David M., Christine A. Panasian, and Michael J. Seiler. 2011. Further Evidence on the Capital Structure of REITs. Real Estate Economics 39: 133–66. [Google Scholar] [CrossRef]
- Hoesli, Martin, Jon Lekander, and Witold Witkiewicz. 2004. International Evidence on Real Estate as a Portfolio Diversifier. Journal of Real Estate Research 26: 161–206. [Google Scholar] [CrossRef]
- Huang, Jing-Zhi, and Ming Huang. 2012. How much of the corporate-treasury yield spread is due to credit risk? The Review of Asset Pricing Studies 2: 153–202. [Google Scholar] [CrossRef]
- Huang, Yujia, Jiawen Yang, and Yongji Zhang. 2013. Value premium in the Chinese stock market: Free lunch or paid lunch? Applied Financial Economics 23: 315–24. [Google Scholar] [CrossRef]
- Hull, John, Mirela Predescu, and Alan White. 2004. The relationship between credit default swap spreads, bond yields, and credit rating announcements. Journal of Banking & Finance 28: 2789–811. [Google Scholar] [CrossRef]
- Hung, Szu-Yin Kathy, and John L. Glascock. 2008. Momentum Profitability and Market Trend: Evidence from REITs. The Journal of Real Estate Finance and Economics 37: 51–69. [Google Scholar] [CrossRef]
- Ibbotson, Roger G., Zhiwu Chen, Daniel Y.-J. Kim, and Wendy Y. Hu. 2013. Liquidity as an Investment Style. Financial Analysts Journal 69: 30–44. [Google Scholar] [CrossRef]
- Idzorek, Thomas M., and Maciej Kowara. 2013. Factor-based asset allocation vs. asset-class-based asset allocation. Financial Analysts Journal 69: 19–29. [Google Scholar] [CrossRef]
- Ince, Ozgur, and R. Bert Porter. 2006. Individual Equity Return Data from Thomson Datastream: Handle with Care! Journal of Financial Research 29: 463–79. [Google Scholar] [CrossRef]
- Ivaschenko, Iryna V. 2003. How Much Leverage is Too Much, or Does Corporate Risk Determine the Severity of a Recession? SSRN Electronic Journal. Available online: https://ssrn.com/abstract=879078 (accessed on 10 March 2021). [CrossRef]
- Jegadeesh, Narasimhan, and Sheridan Titman. 1993. Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. The Journal of Finance 48: 65–91. [Google Scholar] [CrossRef]
- Johnson, Timothy C. 2002. Rational Momentum Effects. The Journal of Finance 57: 585–608. [Google Scholar] [CrossRef]
- Kaplan, Steven, and Antoinette Schoar. 2005. Private Equity Performance: Returns, Persistence, and Capital Flows. The Journal of Finance 60: 1791–823. [Google Scholar] [CrossRef]
- Karolyi, G. A., and Anthony Sanders. 1998. The variation of economic risk premiums in real estate returns. Journal of Real Estate Finance and Economics 17: 245–62. [Google Scholar] [CrossRef]
- Lakonishok, Josef, Andrei Shleifer, and Robert W. Vishny. 1994. Contrarian investment, extrapolation, and risk. The Journal of Finance 49: 1541–78. [Google Scholar] [CrossRef]
- Lee, Kuan-Hui. 2011. The world price of liquidity risk. Journal of Financial Economics 99: 136–61. [Google Scholar] [CrossRef]
- Lim, S., and E. Giouvris. 2017. On the Pricing of Commonality Across Various Liquidity Proxies in the London Stock Exchange and the Crisis. In Handbook of Investors’ Behavior During Financial Crises. Edited by Fotini Economou. Cambridge: Academic Press, pp. 447–70. [Google Scholar]
- Liu, Laura Xiaolei, and Lu Zhang. 2008. Momentum Profits, Factor Pricing, and Macroeconomic Risk. Review of Financial Studies 21: 2417–48. [Google Scholar] [CrossRef]
- Liu, Crocker H., David J. Hartzell, and Martin E. Hoesli. 1997. International Evidence on Real Estate Securities as an Inflation Hedge. Real Estate Economics 25: 193–221. [Google Scholar] [CrossRef]
- Longstaff, Francis A., and Eduardo S. Schwartz. 1995. A Simple Approach to Valuing Risky Fixed and Floating Rate Debt. The Journal of Finance 50: 789–819. [Google Scholar] [CrossRef]
- Miranda-Agrippino, Silvia, and Helene Rey. 2015. World Asset Markets and the Global Financial Cycle. NBER Working Paper 21722. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Mohanram, Partha S. 2005. Separating Winners from Losers among Low Book-to-Market Stocks Using Financial Statement Analysis. Review of Accounting Studies 10: 133–70. [Google Scholar] [CrossRef]
- Molina, Carlos A. 2005. Are firms underleveraged? An examination of the effect of leverage on default probabilities. The Journal of Finance 60: 1427–59. [Google Scholar] [CrossRef]
- NAREIT. 2022a. REITs Widen Their Global Reach. Available online: https://www.reit.com/news/reit-magazine/march-april-2022/reits-widen-their-global-reach (accessed on 15 November 2022).
- NAREIT. 2022b. REITWatch. Available online: https://www.reit.com/sites/default/files/reitwatch/RW2207.pdf (accessed on 15 November 2022).
- Nazlioglu, Saban, N. Aper Gormus, and Ugur Soytas. 2016. Oil prices and real estate investment trusts (REITs): Gradual-shift causality and volatility transmission analysis. Energy Economics 60: 168–75. [Google Scholar] [CrossRef]
- Novy-Marx, Robert. 2013. The other side of value: The gross profitability premium. Journal of Financial Economics 108: 1–28. [Google Scholar] [CrossRef]
- Ooi, Joseph T. L., James Webb, and Dingding Zhou. 2007. Extrapolation Theory and the Pricing of REIT Stocks. Journal of Real Estate Research 29: 27–56. [Google Scholar] [CrossRef]
- Penman, Stephen H., Scott A. Richardson, and Irem Tuna. 2007. The Book-To-Price Effect in Stock Returns: Accounting for Leverage. Journal of Accounting Research 45: 427–67. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Piotroski, Joseph D. 2000. Value Investing: The Use of Historical Financial Statement Information to Separate Winners from Losers. Journal of Accounting Research 38: 1. [Google Scholar] [CrossRef]
- Said, Husaini, and Evangelos Giouvris. 2017. Illiquidity as an investment style during the financial crisis in the United Kingdom. In Handbook of Investors’ Behavior during Financial Crises. Edited by Fotini Economou. Cambridge: Academic Press, pp. 419–45. [Google Scholar]
- Shahe Emran, M., Forhad Shilpi, and M. Imam Alam. 2007. Economic liberalization and price response of aggregate private investment: Time series evidence from India. Canadian Journal of Economics/Revue Canadienne D’économique 40: 914–34. [Google Scholar] [CrossRef]
- Sharpe, William F. 1992. Asset allocation. The Journal of Portfolio Management 18: 7–19. [Google Scholar] [CrossRef]
- Shen, Jianfu, Eddie C. M. Hui, and Kwokyuen Fan. 2020. The Beta Anomaly in the REIT Market. The Journal of Real Estate Finance and Economics 63: 414–36. [Google Scholar] [CrossRef]
- Shleifer, Andrei, and Robert W. Vishny. 1997. The Limits of Arbitrage. Journal of Finance 52: 35–55. [Google Scholar] [CrossRef]
- Skinner, Douglas J., and Richard G. Sloan. 2002. Earnings Surprises, Growth Expectations, and Stock Returns: Don’t Let an Earnings Torpedo Sink Your Portfolio. Review of Accounting Studies 7: 289–312. [Google Scholar] [CrossRef]
- Stephen, Lee, and Stevenson Simon. 2005. The case for REITs in the mixed-asset portfolio in the short and long run. Journal of Real Estate Portfolio Management 11: 55–80. [Google Scholar] [CrossRef]
- Tang, Dragon Yongjun, and Hong Yan. 2010. Market conditions, default risk and credit spreads. Journal of Banking & Finance 34: 743–53. [Google Scholar] [CrossRef]
- Titman, Sheridan, and Arthur Warga. 1986. Risk and the Performance of Real Estate Investment Trusts: A Multiple Index Approach. Real Estate Economics 14: 414–31. [Google Scholar] [CrossRef]
- Titman, Sheridan, K. C. John Wei, and Feixue Xie. 2004. Capital Investments and Stock Returns. Journal of Financial and Quantitative Analysis 39: 677–700. [Google Scholar] [CrossRef]
- Tse, Yiuman, and G. Geoffrey Booth. 1996. Common volatility and volatility spillovers between US and Eurodollar interest rates: Evidence from the futures market. Journal of Economics and Business 48: 299–312. [Google Scholar] [CrossRef]
- Ülkü, Numan. 2017. Monday effect in Fama–French’s RMW factor. Economics Letters 150: 44–47. [Google Scholar] [CrossRef]
- Vassalou, Maria, and Yuhang Xing. 2004. Default risk in equity returns. The Journal of Finance 59: 831–68. [Google Scholar] [CrossRef]
- Zhang, Ying, and J. Andrew Hansz. 2019. Industry Concentration and U.S. REIT Returns. Real Estate Economics 50: 247–67. [Google Scholar] [CrossRef]



| Variables | Mean | SD | Min | Max | Skewness | Kurtosis | Jarque–Bera (p-Value) |
|---|---|---|---|---|---|---|---|
| SMB | 0.0082 *** | 0.0429 | −0.1957 | 0.3837 | 3.0162 | 20.2315 | 0.0000 *** |
| HML | 0.0048 *** | 0.0285 | −0.1292 | 0.3377 | 5.1486 | 51.5316 | 0.0000 *** |
| RMW | 0.0005 * | 0.0193 | −0.0908 | 0.1033 | −0.1349 | 6.2990 | 0.0000 *** |
| CMA | 0.0008 *** | 0.0142 | −0.0844 | 0.0918 | 0.9882 | 8.5094 | 0.0000 *** |
| WML | 0.0010 *** | 0.0150 | −0.1346 | 0.1008 | −0.1195 | 9.9946 | 0.0000 *** |
| Panel A: Summary Statistics | Q1 (Small) | Q2 | Q3 | Q4 | Q5 (Big) |
| Excess Means | 0.8320 | 0.0251 | 0.0028 | 0.0137 | 0.0099 |
| Standard Deviation | 4.1054 | 1.7094 | 1.8459 | 1.9179 | 1.8732 |
| CAPM Beta (Univariate) | 0.1702 *** | 0.1211 *** | 0.1491 *** | 0.1587 *** | 0.1605 *** |
| Sharpe Ratio | 0.2027 | 0.0147 | 0.0015 | 0.0071 | 0.0053 |
| Treynor Ratio | 0.0489 | 0.0021 | 0.00002 | 0.0009 | 0.0006 |
| √Var(e) (Involatility)11 | 4.0877 | 1.6826 | 1.8067 | 1.8752 | 1.8283 |
| Panel B: Fama and French Five Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + riRMW + ciCMA + ei | Q1 (Small) | Q2 | Q3 | Q4 | Q5 (Big) |
| ai | 0.7752 *** | −0.0163 | −0.0476 * | −0.0400 | 0.0440 * |
| Beta | 0.1698 *** | 0.1209 *** | 0.1486 *** | 0.1582 *** | 0.1599 *** |
| SMB | 0.0321 | 0.1051 ** | 0.0966 *** | 0.0954 ** | 0.0783 * |
| HML | 0.0878 | 0.1233 *** | 0.1369 *** | 0.1381 *** | 0.1189 *** |
| RMW | −0.0702 | 0.0262 | 0.0048 | 0.0036 | −0.0211 |
| CMA | −0.0477 | −0.1412 *** | −0.1799 *** | −0.1636 *** | −0.1724 *** |
| Panel A: Summary Statistics | Q1 (Value) | Q2 | Q3 | Q4 | Q5 (Growth) |
| Excess Means | 0.4379 | 0.0301 | 0.0052 | 0.0870 | −0.0432 |
| Standard Deviation | 3.0111 | 1.7988 | 1.7861 | 1.8996 | 1.7315 |
| CAPM Beta (Univariate) | 0.0888 *** | 0.1326 *** | 0.1287 *** | 0.1442 *** | 0.1370 *** |
| Sharpe Ratio | 0.1454 | 0.0167 | 0.0029 | 0.0458 | −0.0250 |
| Treynor Ratio | 0.0493 | 0.0023 | 0.0004 | 0.0060 | −0.0032 |
| √Var(e) (Involatility) | 3.0064 | 1.7680 | 1.7554 | 1.8653 | 1.6939 |
| Panel B: Fama and French Five Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + riRMW + ciCMA + ei | Q1 (Value) | Q2 | Q3 | Q4 | Q5 (Growth) |
| ai | 0.4088 *** | −0.0153 *** | −0.0382 | 0.0388 | −0.0894 *** |
| Beta | 0.0885 *** | 0.1324 *** | 0.1283 *** | 0.1436 *** | 0.1366 *** |
| SMB | 0.0346 *** | 0.0869 ** | 0.0891 *** | 0.0932 ** | 0.0744 * |
| HML | 0.2412 *** | 0.1543 *** | 0.1273 *** | 0.1128 *** | 0.0886 *** |
| RMW | 0.0032 | 0.0357 | −0.0038 | −0.0321 | −0.0160 |
| CMA | −0.1340 | −0.1537 *** | −0.1433 *** | −0.1576 *** | −0.1380 *** |
| Panel A: Summary Statistics | Q1 (Robust) | Q2 | Q3 | Q4 | Q5 (Weak) |
| Excess Means | 0.1513 | 0.0083 | 0.2534 | 0.0863 | 0.1049 |
| Standard Deviation | 1.9689 | 1.8534 | 1.9755 | 1.7389 | 1.8390 |
| CAPM Beta (Univariate) | 0.1712 *** | 0.1451 *** | 0.1158 *** | 0.1206 *** | 0.0902 *** |
| Sharpe Ratio | 0.0768 | 0.0045 | 0.1283 | 0.0496 | 0.0570 |
| Treynor Ratio | 0.0088 | 0.0006 | 0.0219 | 0.0072 | 0.0116 |
| √Var(e) (Involatility) | 1.9207 | 1.8158 | 1.9387 | 1.7119 | 1.8218 |
| Panel B: Fama and French Five Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + riRMW + ciCMA + ei | Q1 (Robust) | Q2 | Q3 | Q4 | Q5 (Weak) |
| ai | 0.0925 *** | −0.0404 | 0.2142 *** | 0.0445 * | 0.0740 *** |
| Beta | 0.1710 *** | 0.1445 *** | 0.1155 *** | 0.1207 *** | 0.0901 *** |
| SMB | 0.0742 * | 0.1060 *** | 0.0779 * | 0.1082 *** | 0.0326 |
| HML | 0.1170 *** | 0.1431 *** | 0.1190 *** | 0.1378 *** | 0.1050 *** |
| RMW | 0.0278 | −0.0113 | 0.0081 | 0.0462 | 0.0210 |
| CMA | −0.1275 ** | −0.1915 *** | −0.1462 *** | −0.1075 ** | −0.0758 |
| Panel A: Summary Statistics | Q1 (Conservative) | Q2 | Q3 | Q4 | Q5 (Aggressive) |
| Excess Means | 0.0369 | 0.0104 | 0.0436 | 0.1854 | −0.0450 |
| Standard Deviation | 1.8521 | 1.7424 | 1.7496 | 1.8793 | 1.6339 |
| CAPM Beta (Univariate) | 0.1014 *** | 0.1398 *** | 0.1308 *** | 0.1235 *** | 0.1264 *** |
| Sharpe Ratio | 0.0199 | 0.0059 | 0.0249 | 0.0987 | −0.0275 |
| Treynor Ratio | 0.0036 | 0.0007 | 0.0033 | 0.0150 | −0.0036 |
| √Var(e) (Involatility) | 1.8346 | 1.7062 | 1.7202 | 1.8473 | 1.6010 |
| Panel B: Fama and French Five Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + riRMW + ciCMA + ei | Q1 (Conservative) | Q2 | Q3 | Q4 | Q5 (Aggressive) |
| ai | 0.0023 | −0.0370 | −0.0010 | 0.1427 *** | −0.0875 *** |
| Beta | 0.1014 *** | 0.1393 *** | 0.1305 *** | 0.1235 *** | 0.1259 *** |
| SMB | 0.0887 ** | 0.0952 ** | 0.0989 ** | 0.1066 ** | 0.0622 * |
| HML | 0.1429 *** | 0.1319 *** | 0.1186 *** | 0.1352 *** | 0.1100 *** |
| RMW | 0.0189 | 0.0076 | 0.0215 | 0.0451 | −0.0020 |
| CMA | −0.0949 * | −0.1667 *** | −0.1582 *** | −0.1132 ** | −0.1614 *** |
| Panel A: Summary Statistics | Q1 (Winner) | Q2 | Q3 | Q4 | Q5 (Loser) |
| Excess Means | 0.1599 | 0.0068 | 0.0147 | 0.0073 | 0.0560 |
| Standard Deviation | 1.6832 | 1.6312 | 1.6552 | 1.6301 | 1.8184 |
| CAPM Beta (Univariate) | 0.1132 *** | 0.1285 *** | 0.1309 *** | 0.1315 *** | 0.1217 *** |
| Sharpe Ratio | 0.0950 | 0.0041 | 0.0089 | 0.0045 | 0.0308 |
| Treynor Ratio | 0.0141 | 0.0005 | 0.0011 | 0.0006 | 0.0046 |
| √Var(e) (Involatility) | 1.6581 | 1.5984 | 1.6218 | 1.5959 | 1.7935 |
| Panel B: Fama and French Five Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + riRMW + ciCMA + ei | Q1 (Winner) | Q2 | Q3 | Q4 | Q5 (Loser) |
| ai | 0.1215 *** | −0.0369 | −0.0297 | −0.0376 | 0.0153 |
| Beta | 0.1129 *** | 0.1281 *** | 0.1305 *** | 0.1312 *** | 0.1211 *** |
| SMB | 0.0665 * | 0.0894 ** | 0.0831 ** | 0.0879 ** | 0.0905 ** |
| HML | 0.0976 *** | 0.0973 *** | 0.1332 *** | 0.1181 *** | 0.1247 *** |
| RMW | 0.0015 | 0.0076 | 0.0158 | 0.0211 | −0.0099 |
| CMA | −0.1113 ** | −0.1458 *** | −0.1582 *** | −0.1379 *** | −0.1701 *** |
| Carhart Four Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + wiWML + ei | Q1 (Small) | Q2 | Q3 | Q4 | Q5 (Big) |
|---|---|---|---|---|---|
| ai | 0.7775 *** | −0.0143 | −0.0460 * | −0.0383 | −0.0431 |
| Beta | 0.1659 *** | 0.1188 *** | 0.1464 *** | 0.1560 *** | 0.1582 *** |
| SMB | 0.0897 | 0.1194 *** | 0.1193 *** | 0.1187 *** | 0.1049 *** |
| HML | −0.0174 | 0.0222 | 0.0284 | 0.0322 | 0.0311 |
| WML | −0.2376 | −0.1370 *** | −0.1544 *** | −0.1549 *** | −0.1338 *** |
| Carhart Four Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + wiWML + ei | Q1 (Value) | Q2 | Q3 | Q4 | Q5 (Growth) |
|---|---|---|---|---|---|
| ai | 0.4118 *** | −0.0131 | −0.0366 | 0.0398 | −0.0887 *** |
| Beta | 0.0847 *** | 0.1303 *** | 0.1261 *** | 0.1416 *** | 0.1352 *** |
| SMB | 0.0698 | 0.0988 *** | 0.1133 *** | 0.1257 *** | 0.0955 *** |
| HML | 0.1027 * | 0.0469 | 0.0306 | 0.0224 | 0.0179 |
| WML | −0.2272 *** | −0.1392 *** | −0.1480 *** | −0.1508 *** | −0.1075 *** |
| Carhart Four Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + wiWML + ei | Q1 (Robust) | Q2 | Q3 | Q4 | Q5 (Weak) |
|---|---|---|---|---|---|
| ai | 0.0938 *** | −0.0392 | 0.2155 *** | 0.0467 * | 0.0761 *** |
| Beta | 0.1697 *** | 0.1426 *** | 0.1139 *** | 0.1187 *** | 0.0880 *** |
| SMB | 0.0801 * | 0.1320 *** | 0.0937 ** | 0.1140 *** | 0.0456 |
| HML | 0.0428 | 0.0422 | 0.0342 | 0.0448 | 0.0223 |
| WML | −0.0877 *** | −0.1470 *** | −0.1161 *** | −0.1177 *** | −0.1241 *** |
| Carhart Four Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + wiWML + ei | Q1 (Conservative) | Q2 | Q3 | Q4 | Q5 (Aggressive) |
|---|---|---|---|---|---|
| ai | 0.0039 | −0.0351 | 0.0007 | 0.1446 *** | −0.0864 *** |
| Beta | 0.0997 *** | 0.1370 *** | 0.1286 *** | 0.1218 *** | 0.1242 *** |
| SMB | 0.1003 ** | 0.1181 *** | 0.1132 *** | 0.1101 *** | 0.0825 ** |
| HML | 0.0670 * | 0.0220 | 0.0204 | 0.0500 | 0.0205 |
| WML | −0.1067 *** | −0.1593 *** | −0.1295 *** | −0.1018 *** | −0.1276 *** |
| Carhart Four Factor Model: Ri − Rf = ai + bi(Rm − Rf) + siSMB + hiHML + wiWML + ei | Q1 (Winner) | Q2 | Q3 | Q4 | Q5 (Loser) |
|---|---|---|---|---|---|
| ai | 0.1223 *** | −0.0358 | −0.0281 | −0.0359 | 0.0173 * |
| Beta | 0.1119 *** | 0.1267 *** | 0.1287 *** | 0.1294 *** | 0.1184 *** |
| SMB | 0.0785 ** | 0.1042 *** | 0.0993 *** | 0.1013 *** | 0.1227 *** |
| HML | 0.0388 | 0.0165 | 0.0358 | 0.0268 | 0.0057 |
| WML | −0.0804 *** | −0.1088 *** | −0.1318 *** | −0.1226 *** | −0.1877 *** |
| Variables | Mean | SD | Min | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| DCS | 0.0000905 | 0.024616 | −0.300000 | 0.470000 | 3.096665 | 70.96143 |
| DTED | 0.0000261 | 0.049873. | −0.800000 | 0.996250 | 0.758200 | 88.69920 |
| DSNP | 0.394754 | 20.42972 | −324.8900 | 230.3800 | −1.331192 | 39.33516 |
| Correlation | |||
|---|---|---|---|
| Probability | CS | TED | DSNP |
| CS | 1.000000 | ||
| ----- | |||
| TED | −8.71 × 10−16 | 1.000000 | |
| 1.0000 | ----- | ||
| DSNP | −2.10 × 10−15 | 8.32 × 10−16 | 1.000000 |
| 1.0000 | 1.0000 | ----- | |
| Null Hypothesis: | F-Statistic | Prob. |
|---|---|---|
| DTED does not Granger Cause DCS | 7.2165 | 0.0007 *** |
| DCS does not Granger Cause DTED | 2.9158 | 0.0543 * |
| DSNP does not Granger Cause DCS | 25.0571 | 0.0000 *** |
| DCS does not Granger Cause DSNP | 1.5750 | 0.2071 |
| DSNP does not Granger Cause DTED | 5.3350 | 0.0048 *** |
| DTED does not Granger Cause DSNP | 3.0718 | 0.0464 ** |
| Long Run | Short-Run | |||||
|---|---|---|---|---|---|---|
| Variable | Dot-Com | 2007/08 | COVID-19 | Dot-Com | 2007/08 | COVID-19 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Con | 72.06 (0.01) | −23.45 (0.29) | 29.44 (0.65) | −0.14 (0.75) | −0.02 (0.94) | 0.39 (0.57) |
| SMB (−1) | 0.21 (0.03) | 0.35 (0.00) | 0.39 (0.00) | 1.07 (0.00) | 1.31 (0.01) | 0.95 (0.00) |
| CR | 23.72 (0.11) | 2.13 (0.75) | 8.24 (0.11) | 16.61 (0.24) | 4.99 (0.44) | 2.69 (0.57) |
| CR (−1) | 20.79 (0.02) | 24.32 (0.00) | ||||
| TED | 6.10 (0.44) | −1.43 (0.71) | 1.60 (0.86) | 4.94 (0.50) | −0.61 (0.87) | −1.92 (0.80) |
| TED (−1) | 17.27 (0.00) | 19.42 (0.00) | ||||
| S&P | −57.93 (0.00) | −152.86 (0.00) | −42.25 (0.00) | −56.36 (0.00) | −156.95 (0.00) | −24.67 (0.08) |
| S&P (−1) | 48.17 (0.00) | 237.68 (0.00) | 38.38 (0.01) | 39.22 (0.03) | 235.16 (0.00) | 45.06 (0.00) |
| ECM (−1) | −0.87 (0.00) | −0.99 (0.05) | −0.55 (0.00) | |||
| Long-Run | Short-Run | |||||
|---|---|---|---|---|---|---|
| Variable | Dot-Com | 2007/08 | COVID-19 | Dot-Com | 2007/08 | COVID-19 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 29.47 (0.09) | −33.14 (0.10) | −161.02 (0.12) | 0.51 (0.09) | 0.01 (0.97) | −0.06 (0.84) |
| HML (−1) | 0.43 (0.00) | 0.76 (0.00) | 0.18 (0.09) | 0.66 (0.00) | 0.99 (0.00) | 0.59 (0.03) |
| CR | 17.19 (0.08) | 6.16 (0.32) | 19.37 (0.00) | 13.09 (0.16) | 5.26 (0.28) | 16.82 (0.01) |
| CR (−1) | 10.93 (0.03) | |||||
| TED | 4.35 (0.40) | 1.04 (0.77) | −3.42 (0.68) | 4.04 (0.41) | 0.76 (0.79) | −10.73 (0.18) |
| TED (−1) | 23.21 (0.02) | 11.92 (0.00) | 15.47 (0.07) | |||
| S&P | −10.66 (0.29) | −42.36 (0.00) | 0.35 (0.98) | −5.99 (0.52) | −40.01 (0.00) | 8.68 (0.53) |
| S&P (−1) | 46.98 (0.00) | 51.16 (0.00) | 70.93 (0.00) | 47.76 (0.00) | ||
| ECM (−1) | −0.20 (0.09) | −0.51 (0.00) | −0.49 (0.09) | |||
| Long-Run | Short-Run | |||||
|---|---|---|---|---|---|---|
| Variable | Dot-Com | 2007/08 | COVID-19 | DOT-COM | 2007/08 | COVID-19 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 14.85 (0.58) | −20.56 (0.10) | −8.48 (0.76) | 0.03 (0.85) | 0.01 (0.90) | −0.09 (0.60) |
| CMA (−1) | 0.15 (0.15) | 0.15 (0.00) | 0.19 (0.06) | 0.45 (0.38) | 0.91 (0.00) | 0.52 (0.09) |
| CR | 12.90 (0.23) | −13.42 (0.03) | 1.68 (0.07) | 11.43 (0.26) | −10.34 (0.08) | 6.28 (0.02) |
| CR (−1) | 18.20 (0.03) | 18.57 (0.00) | ||||
| TED | −0.86 (0.31) | −0.95 (0.53) | 0.02 (0.96) | −0.36 (0.66) | −1.26 (0.40) | 0.44 (0.70) |
| TED (−1) | −0.87 (0.71) | 1.36 (0.09) | −0.50 (0.75) | |||
| TED (−2) | 4.58 (0.05) | 3.95 (0.01) | ||||
| S&P | 7.49 (0.55) | −37.16 (0.00) | 0.99 (0.78) | 10.60 (0.39) | −38.85 (0.00) | 14.71 (0.01) |
| S&P (−1) | 47.51 (0.00) | 38.17 (0.00) | ||||
| ECM (−1) | −0.31 (0.08) | −0.77 (0.00) | −0.25 (0.00) | |||
| Long-Run | Short-Run | |||
|---|---|---|---|---|
| Variable | Post Dot-Com | Post 2007/08 | Post Dot-Com | Post 2007/08 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 2.13 (0.38) | 2.47 (0.14) | 0.02 (0.71) | 0.13 (0.03) |
| SMB (−1) | 0.27 (0.00) | 0.67 (0.00) | 1.01 (0.00) | 0.81 (0.00) |
| CR | −0.48 (0.81) | 2.31 (0.48) | −0.65 (0.75) | 2.68 (0.40) |
| TED | 0.51 (0.69) | 7.14 (0.06) | 0.43 (0.74) | 5.91 (0.11) |
| S&P | −58.87 (0.00) | −62.70 (0.00) | −58.45 (0.00) | −60.07 (0.00) |
| ECM (−1) | −0.75 (0.00) | −0.22 (0.00) | ||
| Long-Run | Short-Run | |||
|---|---|---|---|---|
| Variable | Post Dot-Com | Post 2007/08 | Post Dot-Com | Post 2007/08 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 1.08 (0.59) | 1.62 (0.05) | −0.01 (0.65) | 0.07 (0.02) |
| HML (−1) | 0.37 (0.00) | 0.67 (0.00) | 1.09 (0.00) | 0.85 (0.00) |
| CR | 1.26 (0.45) | 0.69 (0.66) | 0.43 (0.78) | 0.40 (0.80) |
| TED | 0.83 (0.43) | −0.61 (0.74) | 0.29 (0.76) | −0.50 (0.77) |
| S&P | −24.29 (0.00) | −12.58 (0.00) | −23.71 (0.00) | −10.67 (0.00) |
| ECM (−1) | −0.84 (0.00) | −0.32 (0.00) | ||
| Long-Run | Short-Run | |||
|---|---|---|---|---|
| Variable | Post Dot-Com | Post 2007/08 | Post Dot-Com | Post 2007/08 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 1.75 (0.28) | 0.68 (0.24) | 0.03 (0.31) | −0.00 (0.99) |
| CMA (−1) | −0.09 (0.00) | 0.46 (0.00) | 0.30 (0.06) | 1.27 (0.00) |
| CR | 0.77 (0.56) | 1.04 (0.35) | 0.62 (0.64) | 1.20 (0.28) |
| TED | −0.03 (0.97) | 0.12 (0.93) | −0.30 (0.72) | 0.11 (0.93) |
| S&P | −4.96 (0.05) | 3.56 (0.10) | −5.04 (0.05) | 3.69 (0.09) |
| S&P (−2) | −4.57 (0.04) | |||
| ECM (−1) | −0.39 (0.01) | −0.88 (0.00) | ||
| Long-Run | Short-Run | |||||
|---|---|---|---|---|---|---|
| Variable | Dot-Com | 2007/08 | COVID-19 | Dot-Com | 2007/08 | COVID-19 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | −9.83 (0.53) | 7.10 (0.44) | 102.38 (0.00) | −0.02 (0.86) | −0.01 (0.91) | 0.28 (0.36) |
| RMW (−1) | 0.34 (0.00) | −0.08 (0.14) | 0.39 (0.00) | 0.70 (0.01) | 0.93 (0.01) | 0.87 (0.00) |
| CR | −17.78 (0.06) | 5.13 (0.07) | −2.59 (0.39) | −20.26 (0.02) | 4.36 (0.11) | −3.10 (0.22) |
| CR (−1) | −14.51 (0.00) | −15.54 (0.00) | ||||
| TED | −4.42 (0.36) | 4.57 (0.01) | −0.54 (0.91) | −5.43 (0.23) | 4.36 (0.01) | 0.09 (0.98) |
| TED (−1) | −10.72 (0.00) | −11.16 (0.00) | ||||
| S&P | 1.35 (0.89) | 59.57 (0.00) | −2.77 (0.68) | 2.26 (0.80) | 59.29 (0.00) | 3.58 (0.61) |
| ECM (−1) | −0.33 (0.08) | −1.09 (0.01) | −0.52 (0.00) | |||
| Long-Run | Short-Run | |||||
|---|---|---|---|---|---|---|
| Variable | Dot-Com | 2007/08 | COVID-19 | Dot-Com | 2007/08 | COVID-19 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 13.77 (0.50) | 21.22 (0.02) | 91.65 (0.09) | 0.02 (0.92) | −0.01 (0.92) | 0.18 (0.63) |
| WML (−1) | 0.56 (0.00) | −0.07 (0.16) | 0.19 (0.06) | 0.79 (0.00) | 0.41 (0.13) | 0.53 (0.07) |
| CR | 2.68 (0.74) | −1.13 (0.00) | −3.59 (0.02) | 5.20 (0.65) | −0.97 (0.71) | −10.31 (0.03) |
| TED | 4.48 (0.34) | −0.05 (0.80) | −2.64 (0.10) | 1.31 (0.83) | 1.36 (0.39) | 1.52 (0.84) |
| S&P | −1.74 (0.55) | −2.96 (0.01) | −11.20 (0.09) | −28.33 (0.02) | −9.04 (0.05) | −28.04 (0.02) |
| ECM (−1) | −0.28 (0.07) | −0.47 (0.09) | −0.27 (0.02) | |||
| Long-Run | Short-Run | |||
|---|---|---|---|---|
| Variable | Post Dot-Com | Post 2007/08 | Post Dot-Com | Post 2007/08 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 1.05 (0.48) | −2.10 (0.01) | −0.01 (0.70) | 0.02 (0.58) |
| RMW (−1) | 0.33 (0.00) | 0.54 (0.00) | 0.88 (0.01) | 1.02 (0.00) |
| CR | 2.46 (0.04) | 3.31 (0.04) | 2.41 (0.05) | 3.39 (0.03) |
| TED | 1.80 (0.02) | 1.65 (0.38) | 1.68 (0.03) | 2.09 (0.27) |
| S&P | −10.21 (0.00) | −5.27 (0.09) | −9.92 (0.00) | −5.42 (0.09) |
| S&P (−1) | −8.50 (0.01) | |||
| ECM (−1) | −0.56 (0.08) | −0.48 (0.05) | ||
| Long-Run | Short-Run | |||
|---|---|---|---|---|
| Variable | Post Dot-Com | Post 2007/08 | Post Dot-Com | Post 2007/08 |
| Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | Coefficient (p-Value) | |
| Constant | 0.42 (0.82) | −1.76 (0.01) | 0.04 (0.33) | 0.00 (0.84) |
| WML (−1) | 0.19 (0.00) | 0.26 (0.00) | 0.80 (0.00) | 0.44 (0.00) |
| CR | 3.56 (0.02) | −2.43 (0.06) | 3.07 (0.05) | −2.58 (0.05) |
| TED | 1.83 (0.06) | 0.40 (0.79) | 1.57 (0.11) | 0.29 (0.85) |
| S&P | −10.54 (0.00) | −2.18 (0.39) | −9.90 (0.00) | −2.41 (0.35) |
| ECM (−1) | −0.62 (0.00) | −0.19 (0.01) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Essa, M.S.; Giouvris, E. Fama–French–Carhart Factor-Based Premiums in the US REIT Market: A Risk Based Explanation, and the Impact of Financial Distress and Liquidity Crisis from 2001 to 2020. Int. J. Financial Stud. 2023, 11, 12. https://doi.org/10.3390/ijfs11010012
Essa MS, Giouvris E. Fama–French–Carhart Factor-Based Premiums in the US REIT Market: A Risk Based Explanation, and the Impact of Financial Distress and Liquidity Crisis from 2001 to 2020. International Journal of Financial Studies. 2023; 11(1):12. https://doi.org/10.3390/ijfs11010012
Chicago/Turabian StyleEssa, Mohammad Sharik, and Evangelos Giouvris. 2023. "Fama–French–Carhart Factor-Based Premiums in the US REIT Market: A Risk Based Explanation, and the Impact of Financial Distress and Liquidity Crisis from 2001 to 2020" International Journal of Financial Studies 11, no. 1: 12. https://doi.org/10.3390/ijfs11010012
APA StyleEssa, M. S., & Giouvris, E. (2023). Fama–French–Carhart Factor-Based Premiums in the US REIT Market: A Risk Based Explanation, and the Impact of Financial Distress and Liquidity Crisis from 2001 to 2020. International Journal of Financial Studies, 11(1), 12. https://doi.org/10.3390/ijfs11010012





