Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning
Abstract
:1. Introduction
2. Literature Review
3. Background Knowledge
3.1. Mean-Variance Optimization
3.2. CNN
3.3. LSTM
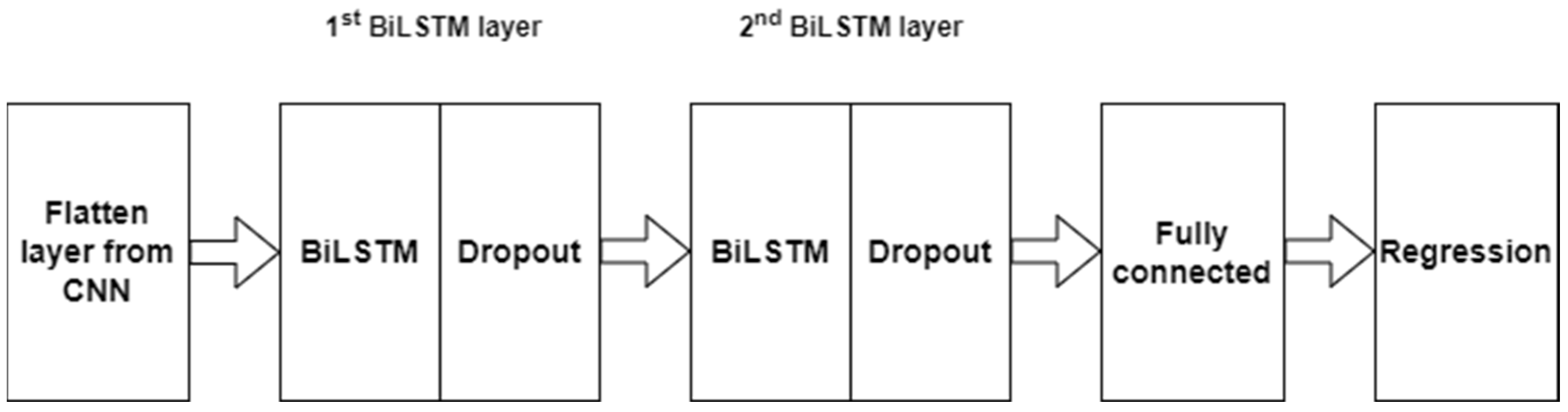
3.4. BiLSTM
3.5. Robust Statistics
3.5.1. The Classical Robust Location Estimator
3.5.2. Huber’s Location Estimator
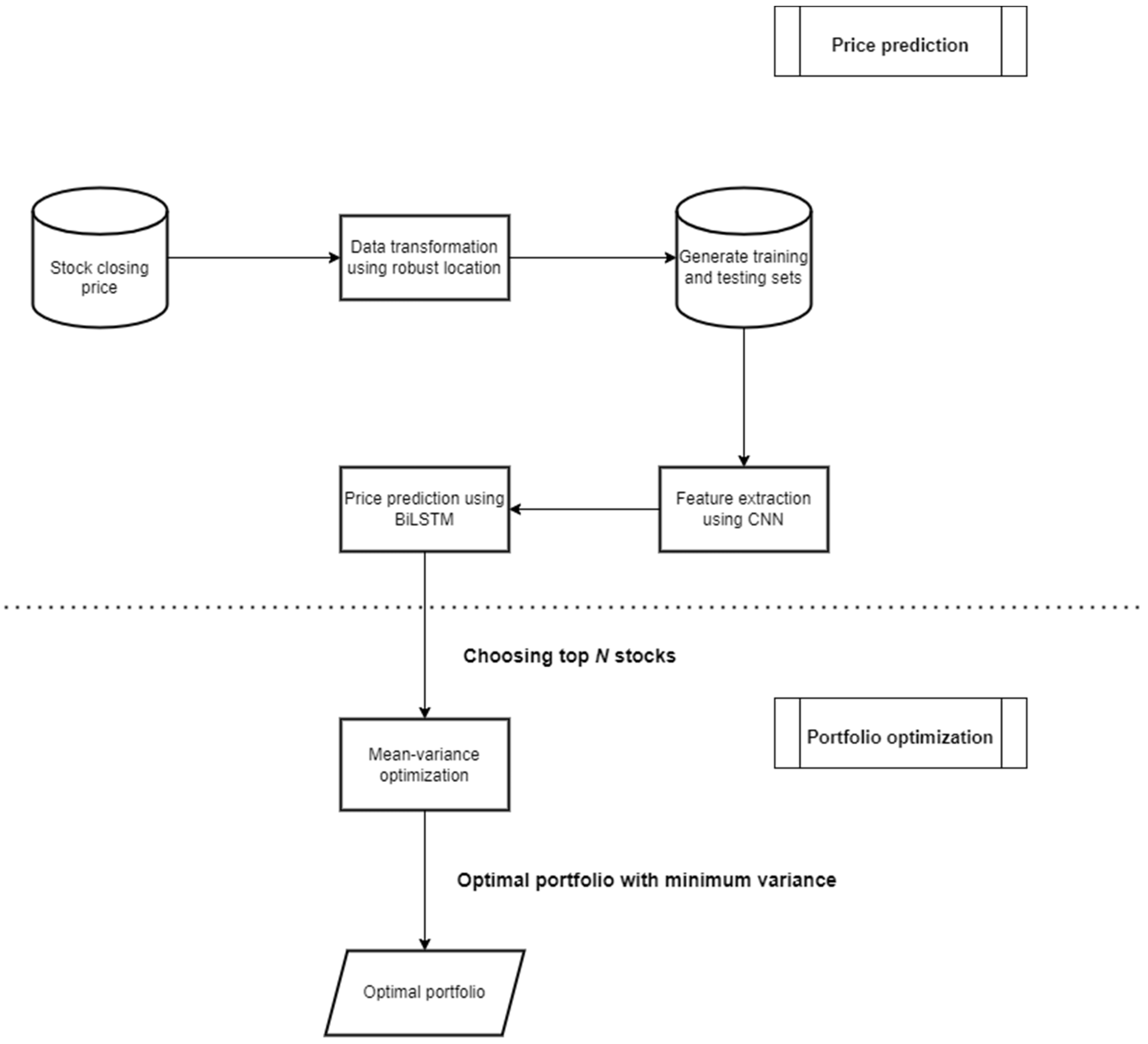
4. Experimental Process
4.1. Data Preparation
4.1.1. Architecture of R-CNN-BiLSTM
4.1.2. Process of Training and Testing
4.1.3. Hyperparameter Setting
- The number of epochs: An epoch is one round of full training. In our experiments, we set the number of epochs to 100 and performed our training. After training, we found that all training stops at a maximum of 100 to 120 epochs. Therefore, 100 is selected as the value for this hyperparameter.
- The number of hidden layers: This is the number of layers between input and output layers. For the CNN network, we set the hidden convolutional layer counts to 100, 100, and 50. In the BiLSTM network, we set these numbers to 128 and 16.
- Learning rate: This value is set for the accurate model convergence of the model in prediction. In our experiment, we set a learning rate to 0.0001. Many researchers recommend using a learning value lower than 0.01 (Hastie et al. 2017).
- Optimizer: This is the optimization function used to obtain the best results. In our work, we use the Adam optimizer, as it works well for LSTM based networks.
- Loss function: Mean Squared Error (MSE) was used as the loss function. Our implementation was written using MATLAB with GPU computing.
4.1.4. Stock Selection
4.2. Benchmark with Comparison Models
4.2.1. Comparison Model 1: R-CNN-BiLSTM+1/N
4.2.2. Comparison Model 2: Machine Learning+MV and Machine Learning+1/N
4.2.3. Comparison Model 3: Random+MV and Random+1/N
5. Experimental Results
5.1. Prediction Performance Results
5.1.1. Machine Learning Metrics
5.1.2. Performance of the Prediction
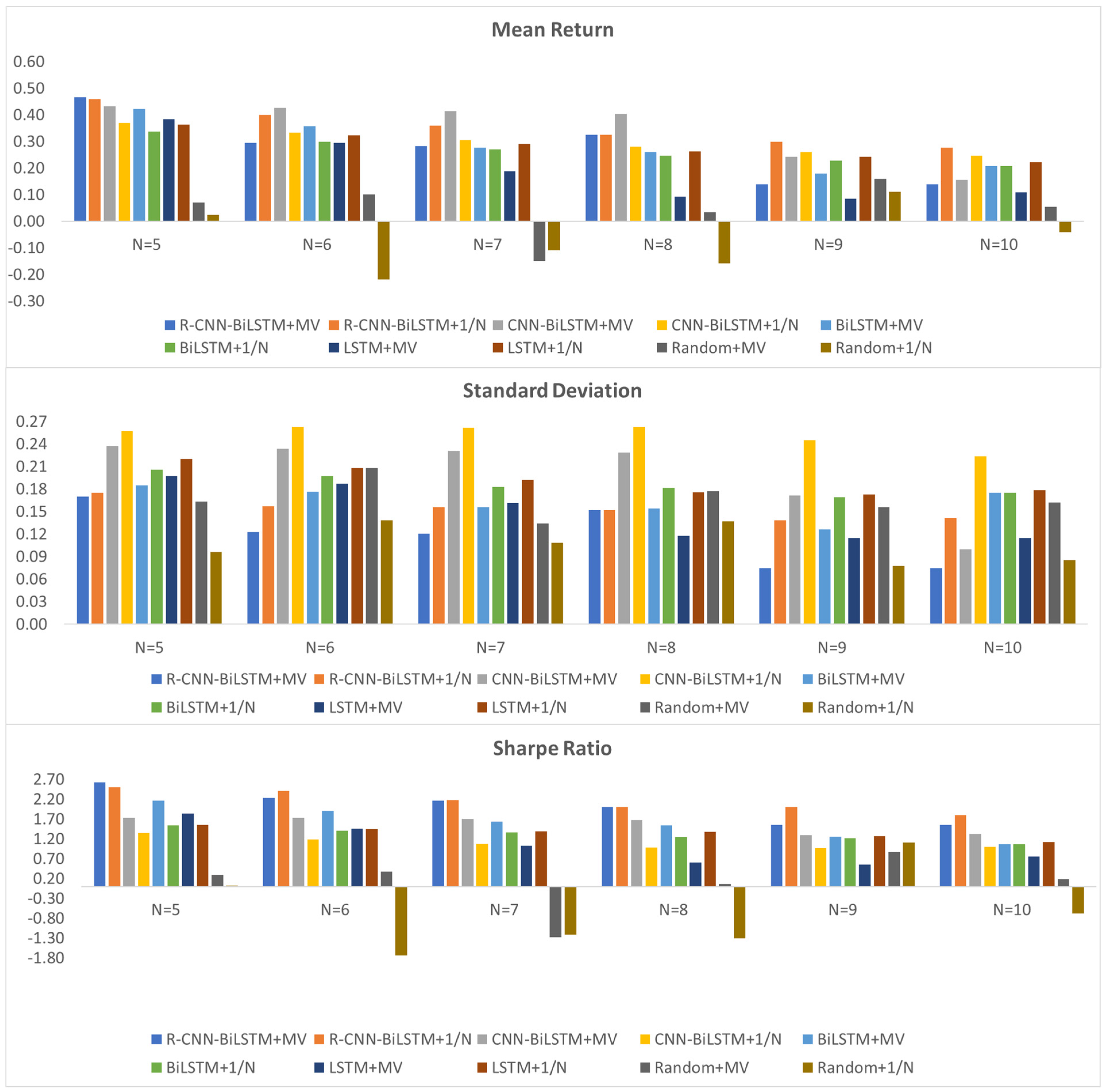
5.2. Portfolio Optimization Results
5.2.1. Portfolio Metrics
5.2.2. Performance of Different-Sized Portfolios
6. Discussion and Conclusions
6.1. Discussion and Key Findings
6.2. Theoretical Implications
6.3. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | R-CNN-BiLSTM is used for stock prediction before optimizing the portfolio using the 1/N model. |
References
- Abrami, Rizkar, and Santoso Marsoem. 2021. Optimal portfolio Formation with Single Index Model Approach on Lq-45 Stocks on Indonesia Stock Exchange. International Journal of Innovative Science and Research Technology 6: 1301–1309. [Google Scholar]
- Albawi, Saad, Tareq A. Mohammed, and Saad Al-Zawi. 2017. Understanding of a convolutional neural network. Paper presented at 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, August 21–23. [Google Scholar]
- Alizadeh, Meysam, Roy Rada, Fariboz Jolai, and Elnaz Fotoohi. 2010. An adaptive neuro-fuzzy system for stock portfolio analysis. International Journal of Intelligent Systems 26: 99–114. [Google Scholar] [CrossRef]
- Almahdi, Saud, and Steve Y. Yang. 2017. An adaptive portfolio trading system: A risk-return portfolio optimization using recurrent reinforcement learning with expected maximum drawdown. Expert Systems with Applications 87: 267–79. [Google Scholar] [CrossRef]
- Beheshti, Bijan. 2018. Effective stock selection and portfolio construction within US, International, and emerging markets. Frontiers in Applied Mathematics and Statistics 4: 17. [Google Scholar] [CrossRef]
- Ben Salah, Hanen, Jan G. De Gooijer, Ali Gannoun, and Mathieu Ribatet. 2018. Mean–variance and mean–semivariance portfolio selection: A multivariate nonparametric approach. Financial Markets and Portfolio Management 32: 419–36. [Google Scholar] [CrossRef]
- Bodnar, Taras, Stepan Mazur, and Yarema Okhrin. 2017. Bayesian estimation of the global minimum variance portfolio. European Journal of Operational Research 256: 292–307. [Google Scholar] [CrossRef] [Green Version]
- Brown, David B., and Jame E. Smith. 2011. Dynamic portfolio optimization with transaction costs: Heuristics and dual bounds. Management Science 57: 1752–70. [Google Scholar] [CrossRef] [Green Version]
- Chen, Wei, Haoyu Zhang, Mukesh Kumar Mehlawat, and Lifen Jia. 2021. Mean–variance portfolio optimization using machine learning-based stock price prediction. Applied Soft Computing 100: 106943. [Google Scholar] [CrossRef]
- Dixon, Matthew F., Igor Halperin, and Paul Bilokon. 2020. Machine Learning in Finance. Berlin and Heidelberg: Springer International Publishing. [Google Scholar]
- Dong, Li, Furu Wei, Chuanqi Tan, Duyu Tang, Ming Zhou, and Ke Xu. 2014. Adaptive Recursive Neural Network for Target-dependent Twitter Sentiment Classification. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers). Baltimore: Association for Computational Linguistics, pp. 49–54. [Google Scholar] [CrossRef] [Green Version]
- Fischer, Thomas, and Christopher Krauss. 2018. Deep learning with long short-term memory networks for financial market predictions. European Journal of Operational Research 270: 654–69. [Google Scholar] [CrossRef] [Green Version]
- Fox, John, and Sanford Weisberg. 2019. An R Companion to Applied Regression. New York: SAGE Publication, Inc. [Google Scholar]
- Gao, Yo, Rong Wang, and Enmin Zhou. 2021. Stock prediction based on optimized LSTM and GRU models. Scientific Programming 2021: 4055281. [Google Scholar] [CrossRef]
- Hampel, Frank, Christian Hennig, and Elvezio Ronchetti. 2011. A smoothing principle for the Huber and other location M-estimators. Computational Statistics & Data Analysis 55: 324–37. [Google Scholar] [CrossRef]
- Hastie, Trevor, Jerome Friedman, and Robert Tisbshirani. 2017. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Berlin and Heidelberg: Springer. [Google Scholar]
- Henrique, Bruno M., Vinicius A. Sobreiro, and Herbert Kimura. 2019. Literature review: Machine learning techniques applied to financial market prediction. Expert Systems with Applications 124: 226–51. [Google Scholar] [CrossRef]
- Hochreiter, Sepp, and Jurgen Schmidhuber. 1997. Long short-term memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef] [PubMed]
- Huang, Chien-Feng. 2012. A hybrid stock selection model using genetic algorithms and support vector regression. Applied Soft Computing 12: 807–18. [Google Scholar] [CrossRef]
- Huang, Ripeng, Shaojian Qu, Xiaoguang Yang, Fengmin Xu, Zeshui Xu, and Wei Zhou. 2021. Sparse portfolio selection with uncertain probability distribution. Applied Intelligence 51: 6665–84. [Google Scholar] [CrossRef]
- Huber, Peter J. 1964. Robust estimation of a location parameter. The Annals of Mathematical Statistics 35: 73–101. [Google Scholar] [CrossRef]
- Jierula, Alipujiang, Shuhong Wang, Tae-Min OH, and Pengyu Wang. 2021. Study on accuracy metrics for evaluating the predictions of damage locations in deep piles using artificial neural networks with acoustic emission data. Applied Sciences 11: 2314. [Google Scholar] [CrossRef]
- Katsikis, Vasilios N., Spyridon D. Mourtas, Predrag S. Stanimirović, Shuai Li, and Xinwei Cao. 2021. Time-varying mean-variance portfolio selection under transaction costs and cardinality constraint problem via beetle antennae search algorithm (BAS). Operations Research Forum 2: 18. [Google Scholar] [CrossRef]
- Khan, Ameer Hamza, Xinwei Cao, Vasilio N. Katsikis, Predrag Stanimirovic, Ivona Brajevic, Shuai Li, Seifedine Kadry, and Y. Nam. 2020. Optimal portfolio management for engineering problems using nonconvex cardinality constraint: A computing perspective. IEEE Access 8: 57437–50. [Google Scholar] [CrossRef]
- Khan, Ameer Tamoor, Xinwei Cao, Inova Brajevic, Predrag S. Stanimirovic, Vasilio N. Katsikis, and Shuai Li. 2022. Non-linear activated beetle antennae search: A novel technique for non-convex tax-aware portfolio optimization problem. Expert Systems with Applications 197: 116631. [Google Scholar] [CrossRef]
- Khan, Ameer Tamoor, Xinwei Cao, Shuai Li, Bin Hu, and Vasilio N. Katsikis. 2021. Quantum beetle antennae search: A novel technique for the constrained portfolio optimization problem. Science China Information Sciences 64: 152204. [Google Scholar] [CrossRef]
- Kolm, Petter N., Reha Tütüncü, and Frank J. Fabozzi. 2014. 60 years of portfolio optimization: Practical challenges and current trends. European Journal of Operational Research 234: 356–71. [Google Scholar] [CrossRef]
- Le Caillec, Jean-Marc, Alya Itani, Didier Guriot, and Yves Rakotondratsimba. 2017. Stock picking by probability–possibility approaches. IEEE Transactions on Fuzzy Systems 25: 333–49. [Google Scholar] [CrossRef]
- Lefebvre, William, Gregoire Loeper, and Huyen Pham. 2020. Mean-variance portfolio selection with Tracking Error Penalization. Mathematics 8: 1915. [Google Scholar] [CrossRef]
- Li, Ting, Weiguo Zhang, and Weijun Xu. 2015. A fuzzy portfolio selection model with background risk. Applied Mathematics and Computation 256: 505–13. [Google Scholar] [CrossRef]
- Lozza, Sergio Ortobelli, Enrico Angelelli, and Daniele Toninelli. 2011. Set-portfolio selection with the use of market stochastic bounds. Emerging Markets Finance and Trade 47: 5–24. [Google Scholar] [CrossRef] [Green Version]
- Ma, Yilin, Ruizhu Han, and Weizhing Wang. 2021. Portfolio optimization with return prediction using Deep Learning and machine learning. Expert Systems with Applications 165: 113973. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection*. The Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Maronna, Ricardo A., Douglas Martin, and Víctor J. Yohai. 2006. Robust Statistics: Theory and Methods. Hoboken: John Wiley & Sons. [Google Scholar]
- Maronna, Ricardo A., Douglas Martin, Victor J. Yohai, and Matías Salibián-Barrera. 2019. Robust Statistics Theory and Methods (with R). Hoboken: John Wiley & Sons. [Google Scholar]
- Mba, Jules Clement, Kofi Agyarko Ababio, and Samuel Kwaku Agyei. 2022. Markowitz mean-variance portfolio selection and optimization under a behavioral spectacle: New empirical evidence. International Journal of Financial Studies 10: 28. [Google Scholar] [CrossRef]
- Milošević, Nemanja, and Milos Racković. 2019. Classification based on missing features in deep convolutional neural networks. Neural Network World 29: 221–34. [Google Scholar] [CrossRef]
- Mitra Thakur, Gour Sundar, Rupak Bhattacharyya, and Seema Sarkar (Mondal). 2018. Stock portfolio selection using Dempster–Shafer Evidence theory. Journal of King Saud University-Computer and Information Sciences 30: 223–35. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Than Thi. 2014. Selection of the right risk measures for portfolio allocation. International Journal of Monetary Economics and Finance 7: 135. [Google Scholar] [CrossRef]
- Ortiz, Roberto, Mauricio Contreras, and Cristhian Mellado. 2021. Improving the volatility of the optimal weights of the Markowitz model. Economic Research-Ekonomska Istraživanja, September 29. [Google Scholar] [CrossRef]
- Paiva, Felipe D., Rodrigo T. Cardoso, Gustova P. Hanaoka, and Wendel M. Duarte. 2019. Decision-making for financial trading: A fusion approach of machine learning and portfolio selection. Expert Systems with Applications 115: 635–55. [Google Scholar] [CrossRef]
- Rahiminezhad Galankashi, Masoud, Farimah Mokhatab Rafiei, and Maryam Ghezelbash. 2020. Portfolio selection: A fuzzy-ANP approach. Financial Innovation 6: 17. [Google Scholar] [CrossRef]
- Rather, Akhter M., Arun Agarwal, and V. N. Sastry. 2015. Recurrent neural network and a hybrid model for prediction of Stock returns. Expert Systems with Applications 42: 3234–41. [Google Scholar] [CrossRef]
- Sadouk, Lamyaa. 2019. CNN approaches for Time Series Classification. Time Series Analysis-Data, Methods, and Applications, November 5. [Google Scholar] [CrossRef] [Green Version]
- Sharpe, William F., and Harry M. Markowitz. 1989. Mean-variance analysis in portfolio choice and capital markets. The Journal of Finance 44: 531. [Google Scholar] [CrossRef]
- Siami-Namini, Sima, Neda Tavakoli, and Akbar S. Namin. 2019. The performance of LSTM and BiLSTM in forecasting time series. Paper presented at 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, December 9–12. [Google Scholar]
- Sikalo, Mirza, Almira Arnaut-Berilo, and Azra Zaimovic. 2022. Efficient Asset Allocation: Application of game theory-based model for superior performance. International Journal of Financial Studies 10: 20. [Google Scholar] [CrossRef]
- Singh, Upma, Mohammad Rizwan, Muhannad Alaraj, and I. Alsaidan. 2021. A machine learning-based gradient boosting regression approach for wind power production forecasting: A step towards Smart Grid Environments. Energies 14: 5196. [Google Scholar] [CrossRef]
- Soeryana, E., N. Fadhlina, Sukono, E. Rusyaman, and S. Supian. 2017. Mean-variance portfolio optimization by using time series approaches based on logarithmic utility function. IOP Conference Series: Materials Science and Engineering 166: 012003. [Google Scholar] [CrossRef] [Green Version]
- Ta, Van-Dai, Chuan-Ming Liu, and Direselign A. Tadesse. 2020. Portfolio optimization-based stock prediction using long-short term memory network in quantitative trading. Applied Sciences 10: 437. [Google Scholar] [CrossRef] [Green Version]
- Tu, Juntu, and Guofu Zhou. 2010. Incorporating economic objectives into bayesian priors: Portfolio choice under parameter uncertainty. Journal of Financial and Quantitative Analysis 45: 959–86. [Google Scholar] [CrossRef]
- Wan, Yuqing, Raymond Y. Lau, and Yain-Whar Si. 2020. Mining subsequent trend patterns from financial time series. International Journal of Wavelets, Multiresolution and Information Processing 18: 2050010. [Google Scholar] [CrossRef]
- Wang, Wuyu, Weizi Li, Ning Zhang, and Kecheng Liu. 2020. Portfolio formation with preselection using deep learning from long-term financial data. Expert Systems with Applications 143: 113042. [Google Scholar] [CrossRef]
- Yang, Mo, and Jing Wang. 2022. Adaptability of Financial Time Series prediction based on bilstm. Procedia Computer Science 199: 18–25. [Google Scholar] [CrossRef]
- Zaimovic, Azra, Adna Omanovic, and Almira Arnaut-Berilo. 2021. How many stocks are sufficient for equity portfolio diversification? A review of the literature. Journal of Risk and Financial Management 14: 551. [Google Scholar] [CrossRef]

| Stock | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|
| AOT | 81 | 25.4 | 52.74 | 15.72 |
| BDMS | 27.25 | 17.5 | 22.26 | 2.27 |
| BEM | 12 | 4.07 | 7.8 | 2.06 |
| BJC | 66 | 27.22 | 44.42 | 9.12 |
| BTS | 14.2 | 7.85 | 9.79 | 1.53 |
| CPALL | 90 | 37.5 | 63.81 | 13.46 |
| CPN | 86.25 | 33.25 | 60.99 | 13.53 |
| DELTA | 684 | 30 | 81.12 | 44.62 |
| DTAC | 96.25 | 27.75 | 48.93 | 15.18 |
| EA | 69.5 | 19.1 | 36.46 | 11.48 |
| GLOBAL | 19.61 | 6.33 | 13.24 | 3.58 |
| INTUCH | 83.5 | 43 | 59.31 | 8.8 |
| IRPC | 8.15 | 1.88 | 4.77 | 1.38 |
| IVL | 62.5 | 16.9 | 36.27 | 12.24 |
| KCE | 64.5 | 12 | 34.45 | 12.31 |
| KTC | 60 | 6.22 | 23.28 | 13.15 |
| LH | 12.2 | 6 | 9.53 | 1.26 |
| MINT | 45.25 | 13.49 | 34.28 | 6.63 |
| MTC | 68.25 | 12 | 36.75 | 15.01 |
| PTT | 58.8 | 19.8 | 39.54 | 8.32 |
| PTTEP | 160 | 42.5 | 101.83 | 23.64 |
| PTTGC | 103 | 24 | 63.98 | 14.4 |
| RATCH | 81.5 | 46 | 56.01 | 6.73 |
| SAWAD | 78.75 | 19.49 | 43.52 | 11.55 |
| SCC | 550 | 267 | 454.1 | 59.68 |
| Stock | LSTM | BiLSTM | ||||
|---|---|---|---|---|---|---|
| MAE | MSE | SMAPE | MAE | MSE | SMAPE | |
| AOT | 1.8492 | 6.0365 | 1.4947 | 1.3972 | 3.8694 | 1.1617 |
| BDMS | 0.3848 | 0.2955 | 0.9173 | 0.3652 | 0.2743 | 0.8640 |
| BEM | 0.2085 | 0.0845 | 1.1439 | 0.2095 | 0.0897 | 1.1524 |
| BJC | 0.9812 | 1.7666 | 1.2952 | 1.1242 | 2.1052 | 1.4813 |
| BTS | 0.2837 | 0.1599 | 1.2865 | 0.2313 | 0.1095 | 1.0495 |
| CPALL | 0.9605 | 1.6107 | 0.7317 | 0.9228 | 1.5193 | 0.7042 |
| CPN | 1.8462 | 7.1009 | 1.9229 | 1.7676 | 6.5828 | 1.8486 |
| DELTA | 4.0368 | 8.0218 | 13.123 | 3.8862 | 7.7699 | 12.226 |
| DTAC | 0.9254 | 1.5075 | 1.1961 | 0.9695 | 1.5263 | 1.2567 |
| EA | 1.0341 | 2.0658 | 1.2442 | 1.0010 | 1.9209 | 1.2035 |
| GLOBAL | 0.4385 | 0.3665 | 1.5382 | 0.4237 | 0.3466 | 1.4796 |
| IRPC | 0.7735 | 0.6996 | 1.3212 | 0.6152 | 0.4566 | 1.0894 |
| INTUCH | 0.7602 | 1.3049 | 0.7142 | 0.7457 | 1.2532 | 0.7002 |
| IVL | 1.1677 | 2.4750 | 2.2526 | 1.1137 | 2.1696 | 2.1337 |
| KCE | 1.3583 | 2.9136 | 3.0482 | 1.2504 | 2.6176 | 2.9376 |
| KTC | 1.6230 | 7.4166 | 2.0531 | 1.5991 | 7.5624 | 2.0145 |
| LH | 0.4567 | 0.3537 | 3.0500 | 0.3830 | 0.2645 | 2.5767 |
| MINT | 4.2719 | 2.5754 | 9.3568 | 3.5595 | 1.8810 | 7.9947 |
| MTC | 2.9454 | 1.3472 | 2.7505 | 2.2480 | 8.7324 | 2.1013 |
| PTT | 0.9246 | 2.2412 | 1.2935 | 0.9153 | 2.0173 | 1.2794 |
| PTTEP | 2.6926 | 2.1457 | 1.5534 | 2.5247 | 2.0952 | 1.4822 |
| PTTGC | 4.7754 | 4.1757 | 5.5750 | 3.2552 | 2.5053 | 3.9878 |
| RATCH | 1.0472 | 2.4033 | 0.8817 | 1.3077 | 3.1643 | 1.0816 |
| SAWAD | 3.8613 | 3.1299 | 3.2622 | 3.5476 | 2.5694 | 2.9785 |
| SCC | 3.6151 | 1.7271 | 4.9859 | 2.6922 | 1.0819 | 3.7868 |
| Stock | CNN-BiLSTM | R-CNN-BiLSTM | ||||
|---|---|---|---|---|---|---|
| MAE | MSE | SMAPE | MAE | MSE | SMAPE | |
| AOT | 1.3178 | 3.3801 | 1.0902 | 1.3700 | 3.1541 | 1.1104 |
| BDMS | 0.4277 | 0.3319 | 1.0172 | 0.3292 | 0.1934 | 0.7758 |
| BEM | 0.1651 | 0.0585 | 0.9034 | 0.1747 | 0.0523 | 0.9577 |
| BJC | 1.0290 | 1.8592 | 1.3327 | 0.8566 | 1.1691 | 1.1343 |
| BTS | 0.3006 | 0.2078 | 1.3639 | 0.2627 | 0.1243 | 1.1716 |
| CPALL | 1.0490 | 2.0394 | 0.7842 | 0.7528 | 1.0157 | 0.5713 |
| CPN | 1.8837 | 6.6585 | 1.9341 | 1.2533 | 2.8825 | 1.3019 |
| DELTA | 4.1104 | 8.1768 | 13.487 | 3.4162 | 5.0508 | 12.143 |
| DTAC | 1.1074 | 1.9661 | 1.4468 | 0.8781 | 1.2819 | 1.1335 |
| EA | 0.9578 | 1.6883 | 1.1501 | 0.8770 | 1.3480 | 1.0603 |
| GLOBAL | 0.3636 | 0.2451 | 1.2451 | 0.3325 | 0.2011 | 1.1091 |
| IRPC | 0.7817 | 1.2752 | 0.7347 | 0.7434 | 1.1314 | 0.6960 |
| INTUCH | 0.7479 | 0.7327 | 1.2883 | 0.9645 | 1.0976 | 1.5837 |
| IVL | 0.9090 | 1.5083 | 1.7234 | 0.8079 | 1.0826 | 1.5329 |
| KCE | 1.2586 | 2.5306 | 2.8828 | 0.7679 | 0.9975 | 1.7225 |
| KTC | 1.8072 | 8.4518 | 2.3359 | 0.9608 | 2.2998 | 1.2831 |
| LH | 0.4215 | 0.3194 | 2.8259 | 0.4915 | 0.3743 | 3.2514 |
| MINT | 3.1798 | 1.5235 | 7.2280 | 3.1251 | 1.3556 | 7.0846 |
| MTC | 2.2111 | 9.3412 | 2.0425 | 1.8174 | 6.4816 | 1.6748 |
| PTT | 0.7665 | 1.2902 | 1.0616 | 0.6891 | 0.9916 | 0.9468 |
| PTTEP | 2.0733 | 1.1074 | 1.1690 | 2.0274 | 1.0305 | 1.1313 |
| PTTGC | 4.7207 | 4.3939 | 5.5390 | 5.1528 | 4.9323 | 5.9606 |
| RATCH | 1.1446 | 2.8712 | 0.9626 | 1.0720 | 2.0291 | 0.8916 |
| SAWAD | 3.5888 | 2.8325 | 2.9873 | 3.6310 | 3.0988 | 3.0133 |
| SCC | 2.0515 | 7.7104 | 2.9372 | 3.7010 | 1.8256 | 5.0882 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaweewanchon, A.; Chaysiri, R. Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning. Int. J. Financial Stud. 2022, 10, 64. https://doi.org/10.3390/ijfs10030064
Chaweewanchon A, Chaysiri R. Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning. International Journal of Financial Studies. 2022; 10(3):64. https://doi.org/10.3390/ijfs10030064
Chicago/Turabian StyleChaweewanchon, Apichat, and Rujira Chaysiri. 2022. "Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning" International Journal of Financial Studies 10, no. 3: 64. https://doi.org/10.3390/ijfs10030064
APA StyleChaweewanchon, A., & Chaysiri, R. (2022). Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning. International Journal of Financial Studies, 10(3), 64. https://doi.org/10.3390/ijfs10030064






