Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models
Abstract
:1. Introduction
2. Research Background
2.1. Model Specifications
2.1.1. GARCH Model
2.1.2. Standard GARCH (sGARCH) Models
2.1.3. EGARCH Model
2.1.4. GJR-GARCH Model
2.1.5. Threshold GARCH Model
2.1.6. DCC-GARCH Model
2.2. Methodological Development
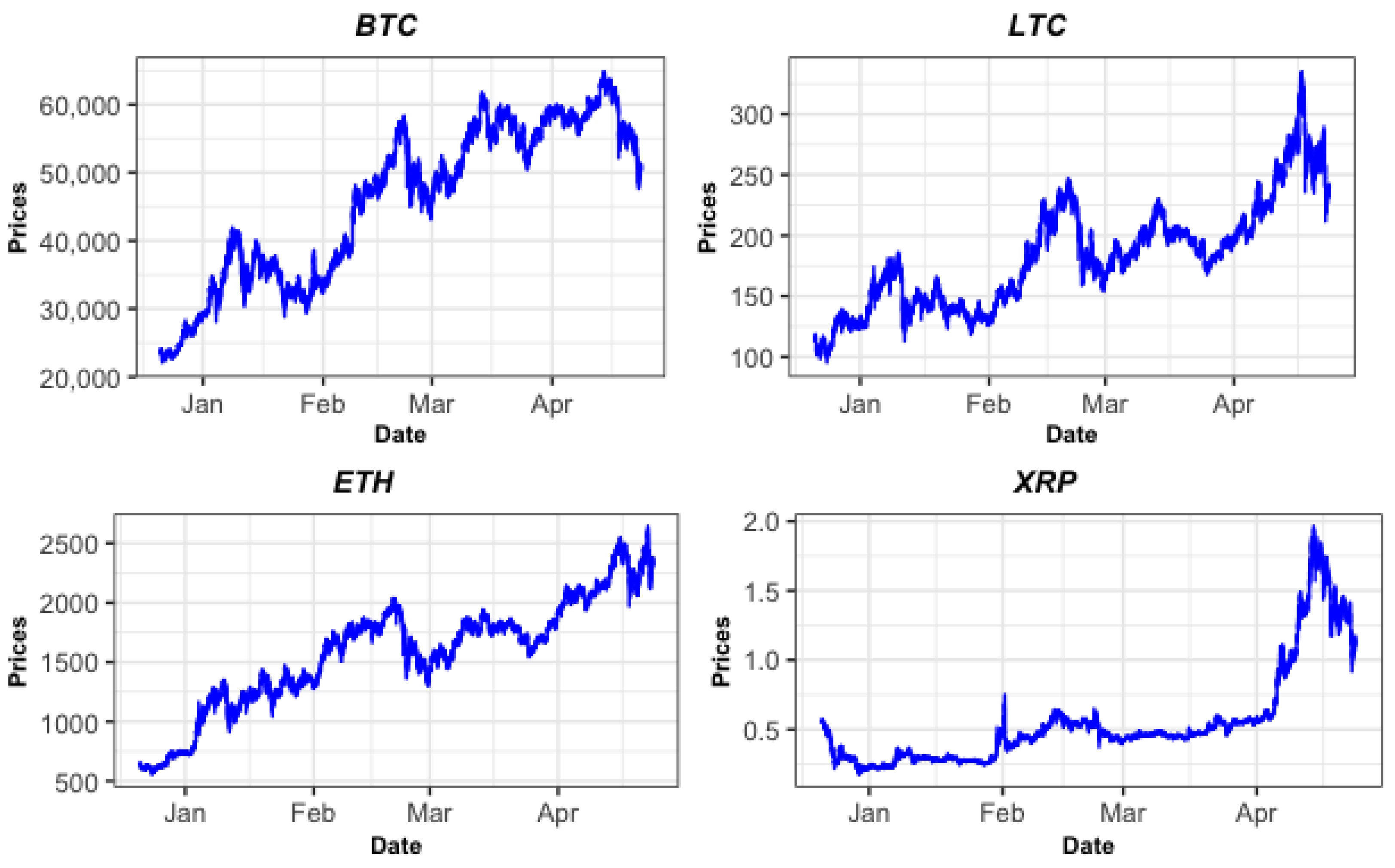
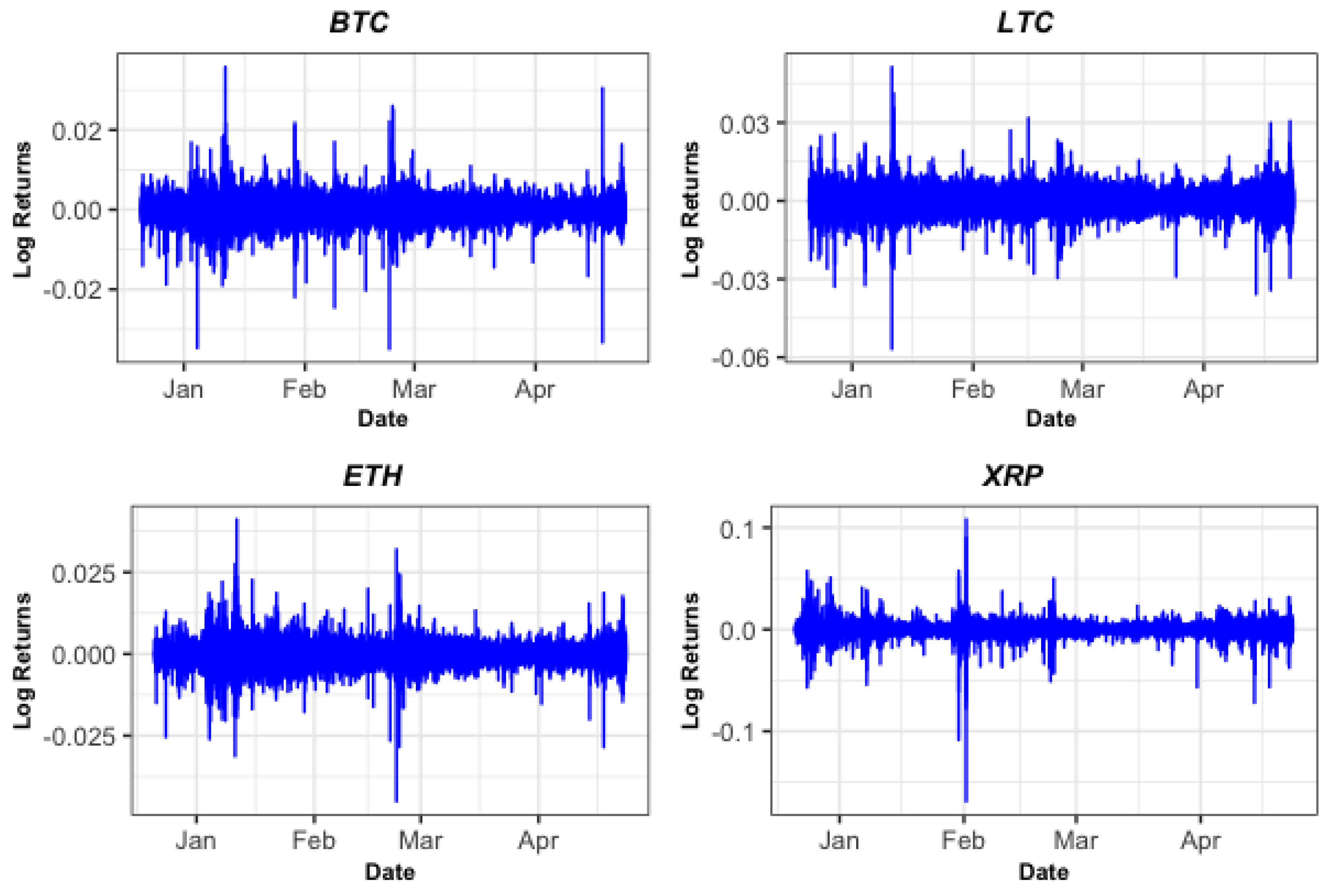
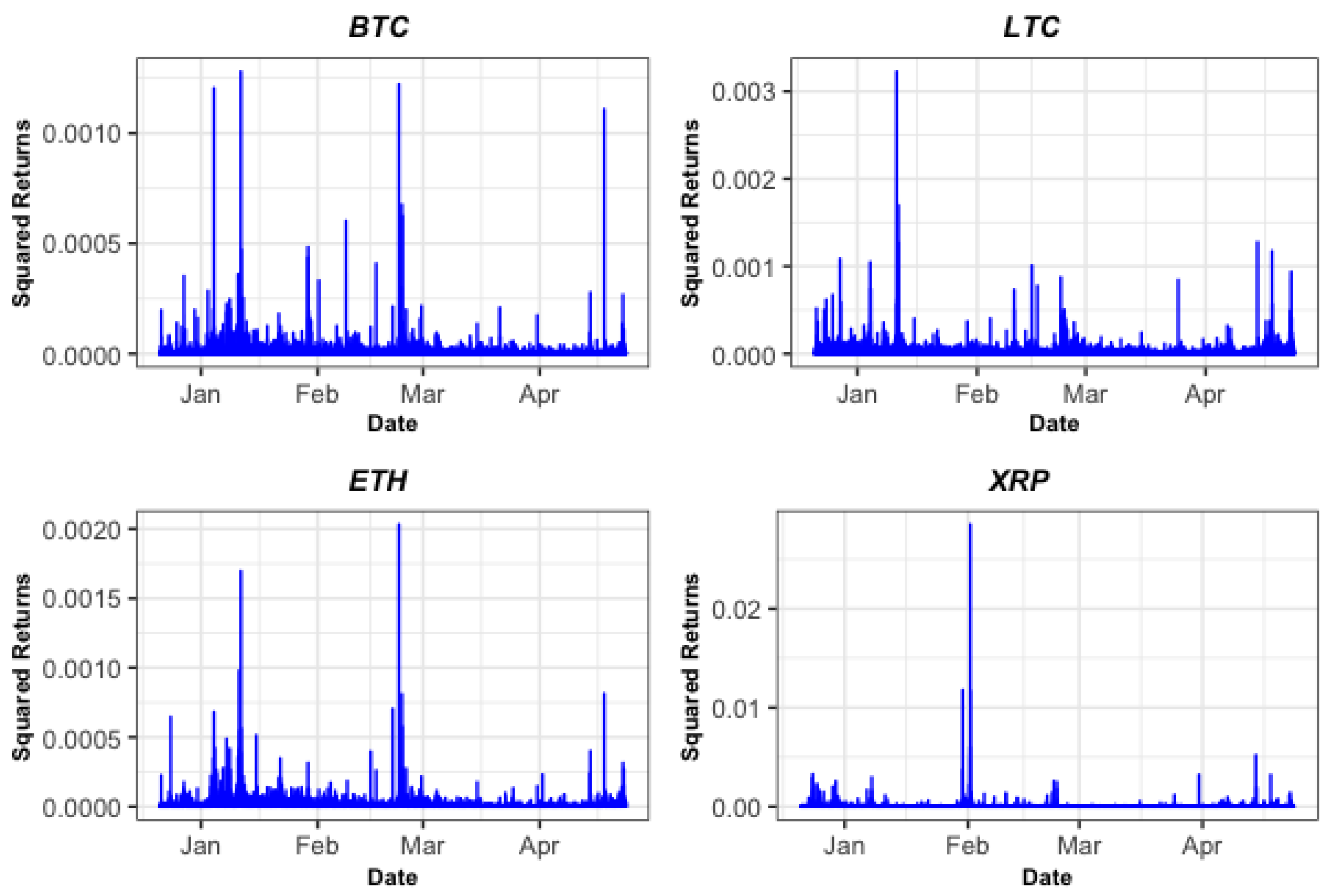
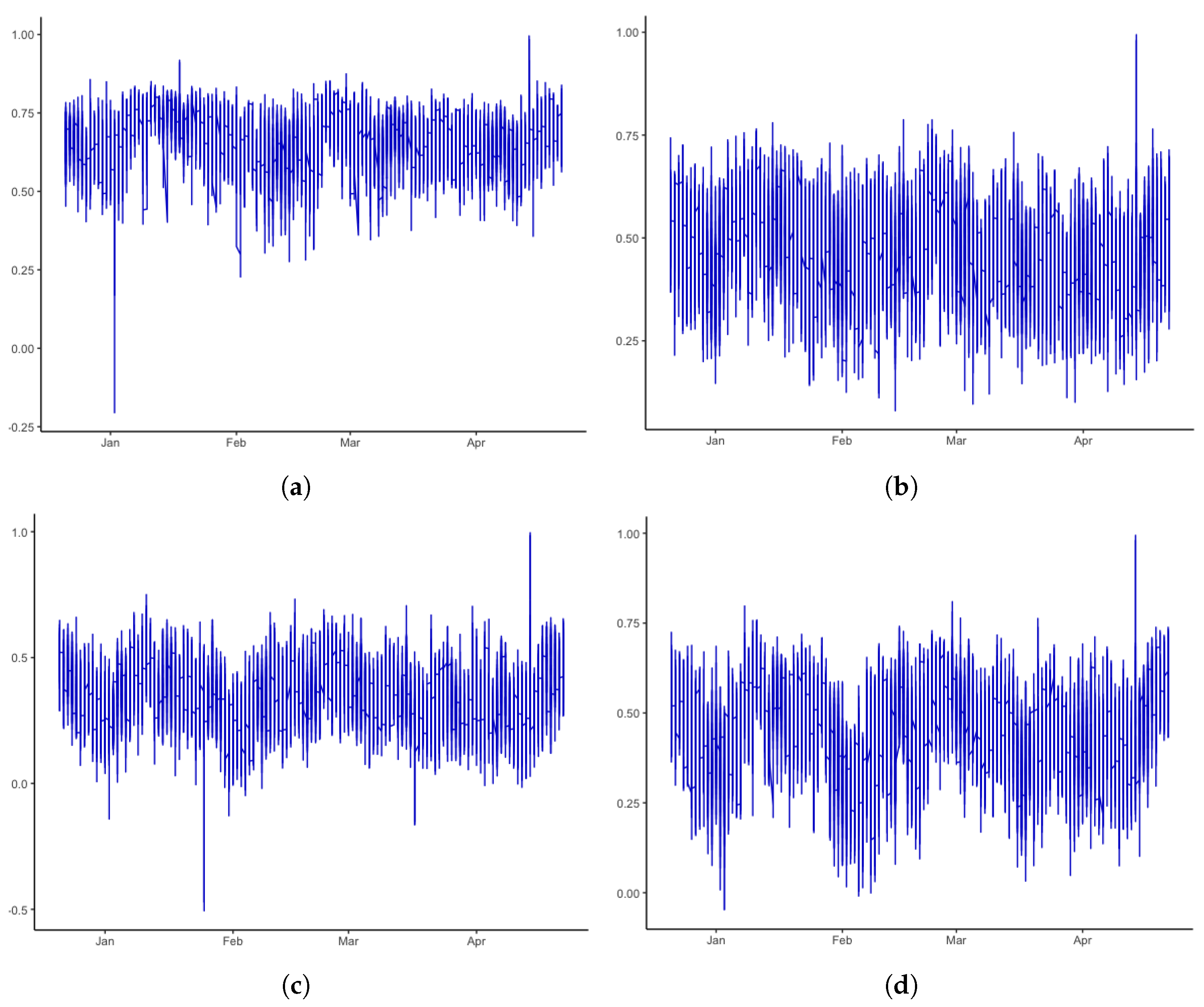
3. Data and Results
3.1. Estimation Results
3.2. Model Selection
3.3. Forecasting Volatility Accuracy
4. Conclusions
Funding
Conflicts of Interest
| 1 | Data are publicly available at https://www.cryptodatadownload.com/data/ (accessed on 4 May 2021). |
References
- Akaike, Hirotugu. 1981. Likelihood of a model and information criteria. Journal of Econometrics 16: 3–14. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, Duc Khuong Nguyen, and Molla Ramizur Rahman. 2022. Systemic risk-sharing framework of cryptocurrencies in the COVID-19 crisis. Finance Research Letters 47: 102787. [Google Scholar] [CrossRef] [PubMed]
- Ampountolas, Apostolos. 2021. Modeling and Forecasting Daily Hotel Demand: A Comparison Based on SARIMAX, Neural Networks, and GARCH Models. Forecasting 3: 580–95. [Google Scholar] [CrossRef]
- Bauwens, Luc, Arie Preminger, and Jeroen V. K. Rombouts. 2010. Theory and inference for a markov switching garch model. The Econometrics Journal 13: 218–44. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef] [Green Version]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model. The Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Bouoiyour, Jamal, and Refk Selmi. 2016. Bitcoin: A beginning of a new phase. Economics Bulletin 36: 1430–40. [Google Scholar]
- Briere, Marie, Kim Oosterlinck, and Ariane Szafarz. 2015. Virtual currency, tangible return: Portfolio diversification with bitcoin. Journal of Asset Management 16: 365–73. [Google Scholar] [CrossRef]
- Brockwell, Peter J., and Richard A Davis. 1991. Stationary time series. In Time Series: Theory and Methods. New York: Springer, pp. 1–41. [Google Scholar]
- Carbone, Anna, Giuliano Castelli, and H Eugene Stanley. 2004. Time-dependent hurst exponent in financial time series. Physica A: Statistical Mechanics and Its Applications 344: 267–71. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2019. Volatility estimation for bitcoin: Replication and robustness. International Economics 157: 23–32. [Google Scholar] [CrossRef]
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative bubbles in bitcoin markets? an empirical investigation into the fundamental value of bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef] [Green Version]
- Choi, In. 2002. Econometrics: By fumio hayashi, princeton university press, 2000. Econometric Theory 18: 1000–6. [Google Scholar] [CrossRef]
- Chou, Ray Yeutien, Chun-Chou Wu, and Nathan Liu. 2009. Forecasting time-varying covariance with a range-based dynamic conditional correlation model. Review of Quantitative Finance and Accounting 33: 327–45. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Stephen Chan, Saralees Nadarajah, and Joerg Osterrieder. 2017. Garch modelling of cryptocurrencies. Journal of Risk and Financial Management 10: 17. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, Andrew Urquhart, and Larisa Yarovaya. 2019. Cryptocurrencies as a financial asset: A systematic analysis. International Review of Financial Analysis 62: 182–99. [Google Scholar] [CrossRef] [Green Version]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Dyhrberg, Anne Haubo. 2016. Bitcoin, gold and the dollar—A garch volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef] [Green Version]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Fiszeder, Piotr, Marcin Fałdziński, and Peter Molnár. 2019. Range-based dcc models for covariance and value-at-risk forecasting. Journal of Empirical Finance 54: 58–76. [Google Scholar] [CrossRef]
- Fry, John, and Eng-Tuck Cheah. 2016. Negative bubbles and shocks in cryptocurrency markets. International Review of Financial Analysis 47: 343–52. [Google Scholar] [CrossRef] [Green Version]
- Ghalanos, Alexios. 2015. The Rmgarch Models: Background and Properties, Version 1.3-0; Available online: https://cran.r-project.org/web/packages/rmgarch/vignettes/The_rmgarch_models.pdf (accessed on 20 September 2021).
- Ghalanos, Alexios. 2018. Introduction to the Rugarch Package. R Vignette. pp. 1–3. Available online: https://cran.r-project.org/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf (accessed on 20 September 2021).
- Gilli, Manfred, Dietmar Maringer, and Enrico Schumann. 2019. Numerical Methods and Optimization in Finance. Cambridge: Academic Press. [Google Scholar]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Roselyne Joyeux. 1980. An introduction to long-memory time series models and fractional differencing. Journal of time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Hannan, Edward J., and Barry G. Quinn. 1979. The determination of the order of an autoregression. Journal of the Royal Statistical Society: Series B (Methodological) 41: 190–95. [Google Scholar] [CrossRef]
- Hansen, Peter R., and Asger Lunde. 2005. A forecast comparison of volatility models: Does anything beat a garch (1, 1)? Journal of Applied Econometrics 20: 873–89. [Google Scholar] [CrossRef] [Green Version]
- Harvey, David, Stephen Leybourne, and Paul Newbold. 1997. Testing the equality of prediction mean squared errors. International Journal of Forecasting 13: 281–91. [Google Scholar] [CrossRef]
- Hyun, Steve, Jimin Lee, Jong-Min Kim, and Chulhee Jun. 2019. What coins lead in the cryptocurrency market: Using copula and neural networks models. Journal of Risk and Financial Management 12: 132. [Google Scholar] [CrossRef] [Green Version]
- Jarque, Carlos M., and Anil K. Bera. 1987. A test for normality of observations and regression residuals. International Statistical Review/Revue Internationale de Statistique 55: 163–72. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for bitcoin: A comparison of garch models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef] [Green Version]
- Katsiampa, Paraskevi, Shaen Corbet, and Brian Lucey. 2019. High frequency volatility co-movements in cryptocurrency markets. Journal of International Financial Markets, Institutions and Money 62: 35–52. [Google Scholar] [CrossRef]
- Kim, Jong-Min, Chulhee Jun, and Junyoup Lee. 2021. Forecasting the volatility of the cryptocurrency market by garch and stochastic volatility. Mathematics 9: 1614. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2013. Bitcoin meets google trends and wikipedia: Quantifying the relationship between phenomena of the internet era. Scientific Reports 3: 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lahmiri, Salim, Stelios Bekiros, and Antonio Salvi. 2018. Long-range memory, distributional variation and randomness of bitcoin volatility. Chaos, Solitons & Fractals 107: 43–48. [Google Scholar]
- Liu, Jinan, and Apostolos Serletis. 2019. Volatility in the cryptocurrency market. Open Economies Review 30: 779–811. [Google Scholar] [CrossRef] [Green Version]
- Liu, Ruiping, Zhichao Shao, Guodong Wei, and Wei Wang. 2017. Garch model with fat-tailed distributions and bitcoin exchange rate returns. Journal of Accounting, Business and Finance Research 1: 71–75. [Google Scholar] [CrossRef] [Green Version]
- McDonald, Oonagh. 2021. The Bank of England Should Beware the Lure of Digital Currency. Available online: https://www.ft.com/content/96b14a1d-c9ad-4c55-8494-741c9adf8220 (accessed on 12 September 2021).
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society 59: 347–70. [Google Scholar] [CrossRef]
- Parker, Richard I., Kimberly J. Vannest, and Leanne Brown. 2009. The improvement rate difference for single-case research. Exceptional Children 75: 135–50. [Google Scholar] [CrossRef] [Green Version]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Pindyck, Robert S., and Daniel L. Rubinfeld. 1998. Econometric Models and Economic Forecasts. Boston: Irwin/McGraw-Hill, Volume 4. [Google Scholar]
- Rabemananjara, Roger, and Jean-Michel Zakoian. 1993. Threshold arch models and asymmetries in volatility. Journal of Applied Econometrics 8: 31–49. [Google Scholar] [CrossRef]
- Revill, John, and Tom Wilson. 2022. Switzerland Tests Digital Currency Payments with Top Investment Banks. Available online: https://www.reuters.com/technology/switzerland-tests-digital-currency-payments-with-top-investment-banks-2022-01-13/ (accessed on 14 January 2022).
- Tiwari, Aviral Kumar, Ibrahim Dolapo Raheem, and Sang Hoon Kang. 2019. Time-varying dynamic conditional correlation between stock and cryptocurrency markets using the copula-adcc-egarch model. Physica A: Statistical Mechanics and Its Applications 535: 122295. [Google Scholar] [CrossRef]
- Triacca, Umberto. 2016. Lesson19: Comparing Predictive Accuracy of Two Forecasts: The Diebold-Mariano Test. Available online: https://www.phdeconomics.sssup.it/documents/Lesson19.pdf (accessed on 10 January 2022).
- Trucíos, Carlos. 2019. Forecasting bitcoin risk measures: A robust approach. International Journal of Forecasting 35: 836–47. [Google Scholar] [CrossRef]
- Urquhart, Andrew, and Hanxiong Zhang. 2019. Is bitcoin a hedge or safe haven for currencies? an intraday analysis. International Review of Financial Analysis 63: 49–57. [Google Scholar] [CrossRef]
- Wang, Jinghua, and Geoffrey M. Ngene. 2020. Does bitcoin still own the dominant power? an intraday analysis. International Review of Financial Analysis 71: 101551. [Google Scholar] [CrossRef]
- Zakoian, Jean-Michel. 1994. Threshold heteroskedastic models. Journal of Economic Dynamics and Control 18: 931–55. [Google Scholar] [CrossRef]
| Symbol | Name | Market Cap (USD) | Price (USD) | Circulating Supply |
|---|---|---|---|---|
| BTC | Bitcoin | $704,141,870,936 | $37,019.80 | 18,939,768 BTC |
| ETH | Ethereum | $295,477,305,134 | $2461.43 | 119,308,579 ETH |
| LTC | Litecoin | $7,535,211,234 | $107.95 | 69,492,969 LTC |
| XRP | Ripple | $29,254,109,616 | $0.6101 | 47,736,918,345 XRP |
| Bitcoin—BTC | Ethereum—ETH | Litecoin—LTC | Ripple—XRP | |
|---|---|---|---|---|
| A. Descriptive statistics | ||||
| Obs | 178,560 | 178,560 | 178,560 | 178,560 |
| Minimum | −0.034947 | −0.045088 | −0.056805 | −0.168867 |
| 1-Quartile | −0.000711 | −0.000800 | −0.000779 | −0.001183 |
| Mean | 0.000004 | 0.000007 | 0.000004 | 0.000004 |
| Median | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 3-Quartile | 0.000713 | 0.000822 | 0.000789 | 0.001156 |
| Maximum | 0.035773 | 0.041179 | 0.051331 | 0.108117 |
| Stdev | 0.001541 | 0.001865 | 0.002275 | 0.003355 |
| Skewness | −0.022956 | −0.075367 | −0.099042 | −1.384401 |
| Kurtosis | 19.791322 | 15.802376 | 19.215616 | 86.717473 |
| Hurst exponent | 0.492180 | 0.492006 | 0.463128 | 0.523267 |
| VaR 5% | −0.002235 | −0.002763 | −0.003451 | −0.004500 |
| VaR 1% | −0.010735 | −0.011320 | −0.015664 | −0.076805 |
| JB p-value | <0.001 | <0.001 | <0.001 | <0.001 |
| B. Test Statistics | ||||
| ADF | −58.998 ** | −59.065 ** | −60.263 ** | −57467 ** |
| PP | −169567 ** | −169173 ** | −170385 ** | −172599 ** |
| KPSS | 0.18957 | 0.12696 | 0.024004 | 0.21985 |
| Bitcoin—BTC | Ethereum—ETH | Litecoin—LTC | |
|---|---|---|---|
| Bitcoin | |||
| Ethereum | 0.72296 *** | ||
| Litecoin | 0.54538 *** | 0.56353 *** | |
| Ripple | 0.41015 *** | 0.40855 *** | 0.37183 *** |
| BTC | sGARCH | EGARCH | GJRGARCH | TGARCH | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sged | sstd | std | sged | sstd | std | sged | sstd | std | sged | sstd | std | |
| 0.000004 *** (0.000000) | 0.000001 (0.000002) | 0.000005 ** (0.000002) | −0.000036 *** (0.000002) | 0.000027 *** (0.000001) | 0.000026*** (0.000001) | 0.000004 *** (0.000000) | 0.000009 *** (0.000002) | 0.000008 *** (0.000002) | 0.000004 *** (0.000000) | 0.000000 (0.000002) | 0.000001 (0.000002) | |
| 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | −0.199788 *** (0.000296) | −0.127159 *** (0.000086) | −0.128498 *** (0.000099) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000008 *** (0.000001) | 0.000008 *** (0.000001) | |
| 0.050000 *** (0.000000) | 0.070629 *** (0.002009) | 0.056567 *** (0.001466) | −0.027195 *** (0.001304) | −0.022736 *** (0.001235) | −0.022642 *** (0.001235) | 0.050000 *** (0.000000) | 0.054460 *** (0.001369) | 0.053428 *** (0.001243) | 0.050000 *** (0.000000) | 0.071472 *** (0.001217) | 0.071333 *** (0.001209) | |
| 0.900000 *** (0.000005) | 0.916645 *** (0.002002) | 0.934692 *** (0.001450) | 0.985003 *** (0.000002) | 0.990558 *** (0.000022) | 0.990458 *** (0.000022) | 0.900000 *** (0.000006) | 0.920309 *** (0.001706) | 0.921220 *** (0.001626) | 0.900000 *** (0.000005) | 0.940540 *** (0.000941) | 0.940661 *** (0.000948) | |
| 0.143372 *** (0.000400) | 0.127978 *** (0.000515) | 0.128087 *** (0.000526) | 0.050000 *** (0.000000) | 0.028111 *** (0.001627) | 0.028138 *** (0.001588) | |||||||
| 0.050000 *** (0.000000) | 0.213108 *** (0.010034) | 0.214260 *** (0.010001) | ||||||||||
| 773619.2 | 946853.5 | 946946.3 | 945566.8 | 947018.3 | 947014.9 | 746828.2 | 947081.6 | 947056.3 | 702209 | 947359.8 | 947358 | |
| AIC | −8.665 | −10.605 | −10.606 | −10.591 | −10.607 | −10.607 | −8.3649 | −10.608 | −10.608 | −7.8651 | −10.611 | −10.611 |
| HQ | −8.6648 | −10.605 | −10.606 | −10.591 | −10.607 | −10.607 | −8.3647 | −10.608 | −10.607 | −7.8649 | −10.611 | −10.611 |
| ETH | ||||||||||||
| 0.000007 *** (0.000000) | 0.000000 (0.000003) | 0.000014 *** (0.000002) | 0.000008 *** (0.000002) | −0.000045 *** (0.000002) | −0.000037 *** (0.000002) | 0.000007 *** (0.000000) | −0.000003 (0.000003) | 0.000021 *** (0.000002) | 0.000007 *** (0.000000) | 0.000000 (0.000001) | 0.000000 (0.000001) | |
| 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | −0.252306 *** (0.000314) | −0.189859 *** (0.000054) | −0.195798 *** (0.000227) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | |
| 0.050000 *** (0.000000) | 0.066440 *** (0.001338) | 0.069004 *** (0.001272) | −0.034462 *** (0.001480) | −0.031997 *** (0.001399) | −0.031576 *** (0.001391) | 0.050000 *** (0.000000) | 0.053718 *** (0.001034) | 0.051967 *** (0.000715) | 0.050000 *** (0.000000) | 0.089606 *** (0.001234) | 0.087648 *** (0.001176) | |
| 0.900000 *** (0.000005) | 0.928220 *** (0.001199) | 0.924150 *** (0.001249) | 0.980649 *** (0.000007) | 0.985219 *** (0.000032) | 0.984798 *** (0.000036) | 0.900000 *** (0.000006) | 0.917992 *** (0.001482) | 0.926868 *** (0.001130) | 0.900000 *** (0.000005) | 0.933196 *** (0.000876) | 0.934648 *** (0.000827) | |
| 0.143349 *** (0.000423) | 0.155793 *** (0.000996) | 0.152671 *** (0.001001) | 0.050000 *** (0.000000) | 0.039489 *** (0.001635) | 0.033988 *** (0.001618) | |||||||
| 0.050000 *** (0.000000) | 0.167657 *** (0.008134) | 0.172251 *** (0.008216) | ||||||||||
| 745916 | 917369.2 | 917288.2 | 917453 | 917216.6 | 917137.9 | 719008.2 | 917515.1 | 917591.5 | 678231.9 | 917187.1 | 917188.2 | |
| AIC | −8.3547 | −10.275 | −10.274 | −10.276 | −10.273 | −10.273 | −8.0533 | −10.277 | −10.278 | −7.5966 | −10.273 | −10.273 |
| HQ | −8.3545 | −10.275 | −10.274 | −10.276 | −10.273 | −10.272 | −8.0531 | −10.277 | −10.277 | −7.5964 | −10.273 | −10.273 |
| sGARCH | EGARCH | GJRGARCH | TGARCH | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sged | sstd | std | sged | sstd | std | sged | sstd | std | sged | sstd | std | |
| LTC | ||||||||||||
| 0.000004 *** (0.000000) | 0.000002 (0.000002) | 0.000003 * (0.000002) | 0.000000 * (0.000000) | −0.000016 *** (0.000004) | 0.000000 (0.000001) | 0.000004 *** (0.000000) | −0.000001 (0.000002) | 0.000004 ** (0.000002) | 0.000004 *** (0.000000) | 0.000000 (0.000001) | 0.000000 (0.000001) | |
| 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | −0.042510 *** (0.000038) | 0.003790 *** (0.000139) | −0.124647 *** (0.000590) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000101 *** (0.000011) | 0.000020 *** (0.000004) | |
| 0.050000 *** (0.000000) | 0.059881 *** (0.000658) | 0.060617 *** (0.000663) | 0.069596 *** (0.002222) | 0.042853 *** (0.009338) | −0.047306 *** (0.004832) | 0.050000 *** (0.000000) | 0.052327 *** (0.000366) | 0.053982*** (0.000360) | 0.050000*** (0.000000) | 1.000000 *** (0.006372) | 0.258998 *** (0.002287) | |
| 0.900000 *** (0.000005) | 0.938900 *** (0.000670) | 0.937879 *** (0.000681) | 0.992120 *** (0.000003) | 1.000000 *** (0.000001) | 0.987396 *** (0.000014) | 0.900000 *** (0.000006) | 0.939018*** (0.000671) | 0.937384 *** (0.000690) | 0.900000 *** (0.000005) | 0.899687 *** (0.001938) | 0.922289 *** (0.001787) | |
| 0.339121 *** (0.001074) | 0.459831 *** (0.010359) | 0.602413 *** (0.008646) | 0.050000 *** (0.000000) | 0.014514 *** (0.001480) | 0.013659 *** (0.001496) | |||||||
| 0.050000 *** (0.000000) | 0.083975 *** (0.009137) | 0.067701 *** (0.009897) | ||||||||||
| 709188.6 | 888892.2 | 888860.8 | 1050125 | 891656.5 | 891469.1 | 682631.5 | 888907.3 | 888866.9 | 660488 | 893258.3 | 893294.8 | |
| AIC | −7.9433 | −9.9561 | −9.9558 | −11.762 | −9.9871 | −9.985 | −7.6458 | −9.9563 | −9.9558 | −7.3978 | −10.005 | −10.005 |
| HQ | −7.9431 | −9.9559 | −9.9556 | −11.762 | −9.9869 | −9.9848 | −7.6456 | −9.9561 | −9.9556 | −7.3976 | −10.005 | −10.005 |
| XRP | ||||||||||||
| 0.000004 (0.000004) | 0.000006 * (0.000004) | 0.000001 (0.000003) | −0.000023 *** (0.000001) | 0.000000 (0.000001) | 0.000000 (0.000001) | 0.000004 (0.000019) | 0.000002 (0.000004) | −0.000005 * (0.000003) | 0.000004 *** (0.000000) | 0.000000 (0.000003) | −0.000002 (0.000003) | |
| 0.000000 ** (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | −0.274114 *** (0.000527) | −0.205692 *** (0.000087) | −0.198845 *** (0.000284) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000013 *** (0.000001) | 0.000013 *** (0.000001) | |
| 0.050000 *** (0.000000) | 0.068878 *** (0.001179) | 0.074544 *** (0.001150) | −0.014142 *** (0.002111) | −0.010385 *** (0.001973) | −0.011185 *** (0.001910) | 0.050000 *** (0.000001) | 0.061845 *** (0.000548) | 0.062147 *** (0.000622) | 0.050000 *** (0.000000) | 0.096955 *** (0.001677) | 0.097085 *** (0.001668) | |
| 0.900000 *** (0.000003) | 0.927172 *** (0.001102) | 0.923875 *** (0.001034) | 0.977363 *** (0.000004) | 0.982719 *** (0.000054) | 0.983362 *** (0.000026) | 0.900000 *** (0.000008) | 0.932527 *** (0.000954) | 0.930476 *** (0.001035) | 0.900000 *** (0.000001) | 0.927709 *** (0.000952) | 0.927631 *** (0.000953) | |
| 0.241130 *** (0.001435) | 0.255071 *** (0.001119) | 0.241243 *** (0.002419) | 0.050000 *** (0.000001) | 0.008515 *** (0.001582) | 0.009471 *** (0.001604) | |||||||
| 0.050000 *** (0.000000) | 0.057707 *** (0.009731) | 0.059406 *** (0.009682) | ||||||||||
| 673665.1 | 845577.4 | 845630.5 | 845364.3 | 844559.4 | 844557.4 | 647702.6 | 845649 | 845613.5 | 612925.9 | 846029.6 | 846018.7 | |
| AIC | −7.5455 | −9.471 | −9.4716 | −9.4686 | −9.4596 | −9.4596 | −7.2547 | −9.4718 | −9.4714 | −6.8651 | −9.4761 | −9.4759 |
| HQ | −7.5454 | −9.4709 | −9.4715 | −9.4685 | −9.4595 | −9.4595 | −7.2545 | −9.4717 | −9.4713 | −6.865 | −9.4759 | −9.4758 |
| BTC | ETH | LTC | XRP | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GJRGARCH | ||||||||||||||||
| Minutes | MSE | Rank | MAE | Rank | MSE | Rank | MAE | Rank | MSE | Rank | MAE | Rank | MSE | Rank | MAE | Rank |
| 1 min | 0.00000743 | 17 | 0.00272521 | 18 | 0.00000485 | 7 | 0.00220320 | 10 | 0.00004644 | 14 | 0.00681453 | 15 | 0.00000742 | 8 | 0.00272411 | 11 |
| 5 min | 0.00000173 | 4 | 0.00076404 | 4 | 0.00001100 | 14 | 0.00185668 | 7 | 0.00001082 | 9 | 0.00191696 | 6 | 0.00002454 | 12 | 0.00269211 | 9 |
| 15 min | 0.00000120 | 3 | 0.00045877 | 3 | 0.00000490 | 8 | 0.00090568 | 3 | 0.00000393 | 5 | 0.00078603 | 3 | 0.00000892 | 10 | 0.00111919 | 3 |
| 30 min | 0.00000060 | 2 | 0.00023282 | 2 | 0.00000245 | 2 | 0.00045977 | 2 | 0.00000211 | 2 | 0.00046304 | 2 | 0.00000447 | 6 | 0.00057457 | 2 |
| 60 min | 0.00000033 | 1 | 0.00013856 | 1 | 0.00000126 | 1 | 0.00025217 | 1 | 0.00000107 | 1 | 0.00024752 | 1 | 0.00000228 | 1 | 0.00031409 | 1 |
| sGARCH | ||||||||||||||||
| Minutes | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | ||||||||
| 1 min | 0.00000578 | 13 | 0.00240351 | 16 | 0.00000296 | 4 | 0.00172090 | 6 | 0.00003905 | 13 | 0.00624863 | 13 | 0.00000337 | 3 | 0.00183641 | 6 |
| 5 min | 0.00000832 | 19 | 0.00257684 | 17 | 0.00002617 | 19 | 0.00465479 | 19 | 0.00005256 | 15 | 0.00660735 | 14 | 0.00005055 | 17 | 0.00649120 | 18 |
| 15 min | 0.00000593 | 14 | 0.00202695 | 13 | 0.00001548 | 17 | 0.00304218 | 17 | 0.00002747 | 12 | 0.00454032 | 12 | 0.00006212 | 19 | 0.00638460 | 17 |
| 30 min | 0.00000349 | 9 | 0.00144101 | 8 | 0.00001001 | 13 | 0.00236939 | 11 | 0.00001548 | 11 | 0.00310212 | 11 | 0.00003988 | 15 | 0.00491923 | 14 |
| 60 min | 0.00000294 | 6 | 0.00138984 | 7 | 0.00000969 | 12 | 0.00246646 | 13 | 0.00001218 | 10 | 0.00275465 | 10 | 0.00003060 | 13 | 0.00441387 | 13 |
| EGARCH | ||||||||||||||||
| Minutes | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | ||||||||
| 1 min | 0.00000780 | 18 | 0.00279231 | 19 | 0.00000677 | 10 | 0.00260150 | 14 | 0.00013980 | 20 | 0.01182353 | 20 | 0.00000404 | 5 | 0.00200991 | 7 |
| 5 min | 0.00001015 | 20 | 0.00284840 | 20 | 0.00003212 | 20 | 0.00521955 | 20 | 0.00012304 | 19 | 0.01001655 | 19 | 0.00005326 | 18 | 0.00669586 | 20 |
| 15 min | 0.00000688 | 16 | 0.00211564 | 14 | 0.00001818 | 18 | 0.00322996 | 18 | 0.00007135 | 18 | 0.00706960 | 16 | 0.00006373 | 20 | 0.00654225 | 19 |
| 30 min | 0.00000478 | 10 | 0.00179136 | 10 | 0.00001267 | 15 | 0.00271726 | 15 | 0.00006382 | 16 | 0.00721222 | 17 | 0.00004247 | 16 | 0.00510121 | 16 |
| 60 min | 0.00000490 | 11 | 0.00191453 | 11 | 0.00001428 | 16 | 0.00301768 | 16 | 0.00006664 | 17 | 0.00756150 | 18 | 0.00003789 | 14 | 0.00506421 | 15 |
| TGARCH | ||||||||||||||||
| Minutes | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | ||||||||
| 1 min | 0.00000321 | 8 | 0.00179101 | 9 | 0.00000454 | 6 | 0.00213031 | 9 | 0.00000494 | 6 | 0.00222331 | 8 | 0.00000761 | 9 | 0.00275831 | 12 |
| 5 min | 0.00000640 | 15 | 0.00219810 | 15 | 0.00000721 | 11 | 0.00237138 | 12 | 0.00000746 | 8 | 0.00241906 | 9 | 0.00000919 | 11 | 0.00269240 | 10 |
| 15 min | 0.00000542 | 12 | 0.00193153 | 12 | 0.00000562 | 9 | 0.00196485 | 8 | 0.00000569 | 7 | 0.00198221 | 7 | 0.00000628 | 7 | 0.00208186 | 8 |
| 30 min | 0.00000304 | 7 | 0.00127807 | 6 | 0.00000314 | 5 | 0.00129822 | 5 | 0.00000319 | 4 | 0.00131020 | 5 | 0.00000352 | 4 | 0.00138427 | 5 |
| 60 min | 0.00000244 | 5 | 0.00118351 | 5 | 0.00000251 | 3 | 0.00120136 | 4 | 0.00000253 | 3 | 0.00120950 | 4 | 0.00000272 | 2 | 0.00125883 | 4 |
| 60 Min | BTC | ETH | LTC | XRP |
|---|---|---|---|---|
| GJR-GARCH | −0.887914 | −0.870400 | −0.911985 | −0.925626 |
| EGARCH | 0.664820 | 0.474607 | 4.472185 | 0.238292 |
| TGARCH | −0.169938 | −0.741103 | −0.792089 | −0.911139 |
| BTC to ETH | ETH to LTC | LTC to XRP | BTC to XRP | |
|---|---|---|---|---|
| 0.000009 *** (0.000002) | 0.000014 *** (0.000002) | 0.000003 * (0.000002) | 0.000008 * (0.000002) | |
| 0.000011 *** (0.000002) | 0.000003 * (0.000002) | −0.000004 (0.000003) | −0.000004 (0.000003) | |
| 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | |
| 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | 0.000000 (0.000000) | |
| 0.077681 *** (0.000957) | 0.069304 *** (0.00218) | 0.066071 *** (0.001038) | 0.072285 *** (0.002915) | |
| 0.069877 *** (0.002227) | 0.066071 *** (0.001039) | 0.070768 *** (0.001636) | 0.070768 *** (0.001533) | |
| 0.911222 *** (0.000939) | 0.923727 *** (0.002094) | 0.932672 *** (0.000908) | 0.917494 *** (0.002862) | |
| 0.922965 *** (0.002138) | 0.932672 *** (0.000907) | 0.92767 *** (0.001515) | 0.92767 *** (0.001392) | |
| 6.761541 *** (0.10571) | 6.077415 *** (0.091198) | 3.155579 *** (0.020067) | 6.833 *** (0.09398) | |
| 6.222508 *** (0.099647) | 3.155579 *** (0.020122) | 4.871043 *** (0.056171) | 4.871043 *** (0.061898) | |
| 1907809 | 1783877 | 1688118 | 1774470 | |
| AIC | −21.369 | −20.143 | −19.062 | −20.037 |
| HQ | −21.368 | −20.143 | −19.061 | −20.036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ampountolas, A. Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models. Int. J. Financial Stud. 2022, 10, 51. https://doi.org/10.3390/ijfs10030051
Ampountolas A. Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models. International Journal of Financial Studies. 2022; 10(3):51. https://doi.org/10.3390/ijfs10030051
Chicago/Turabian StyleAmpountolas, Apostolos. 2022. "Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models" International Journal of Financial Studies 10, no. 3: 51. https://doi.org/10.3390/ijfs10030051
APA StyleAmpountolas, A. (2022). Cryptocurrencies Intraday High-Frequency Volatility Spillover Effects Using Univariate and Multivariate GARCH Models. International Journal of Financial Studies, 10(3), 51. https://doi.org/10.3390/ijfs10030051






