How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets?
Abstract
:1. Introduction
2. Data and Preliminary Analysis
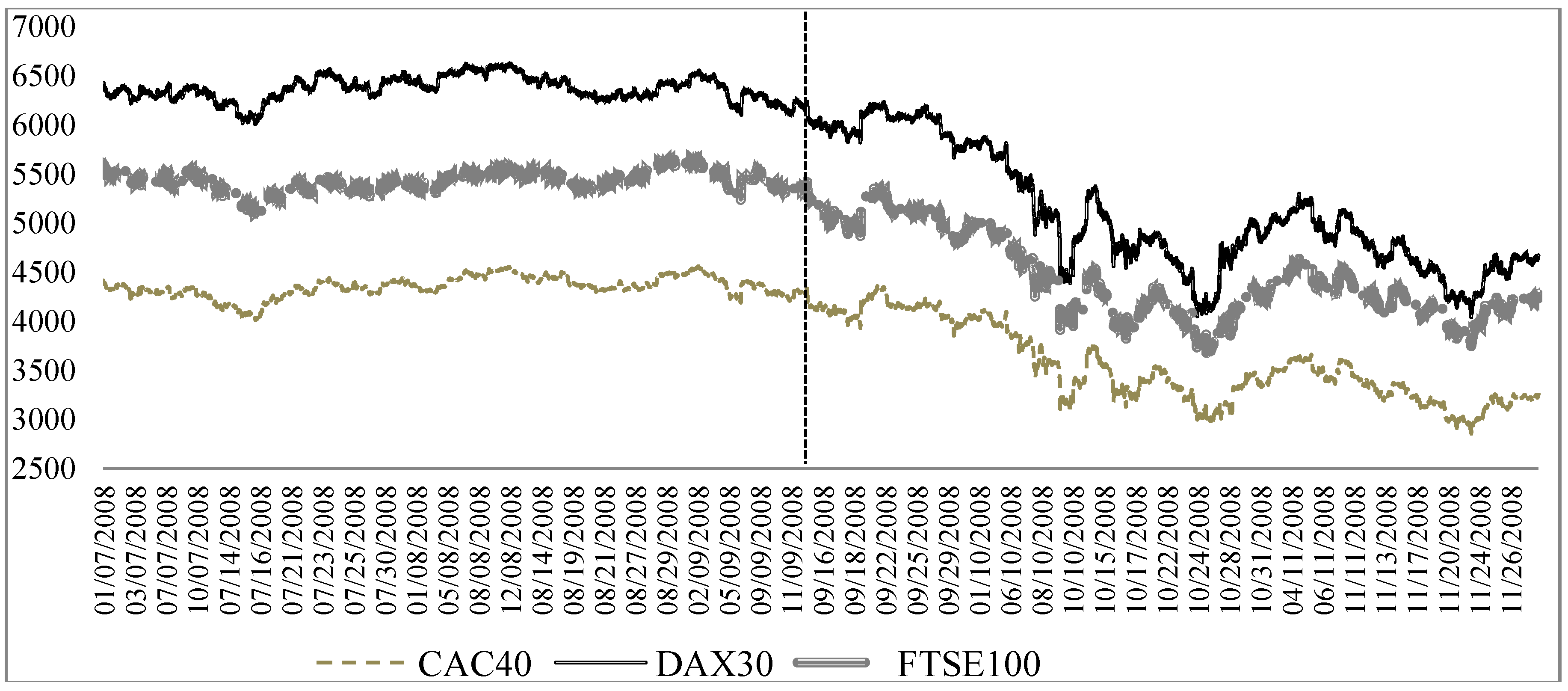
2.1. Turmoil Period Specification

2.2. Data Analysis
3. Methodology Framework
| Whole Period 1 July 2008 to 28 November 2008 | Calm Period 1 July 2008 to 12 September 2008 | Turmoil Period 13 September 2008 to 28 November 2008 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RSCAC | RSDAX | RSFTS | RSCAC | RSDAX | RSFTS | RSCAC | RSDAX | RSFTS | |
| Mean | −0.002332 | −0.001905 | −0.001426 | 0.000530 | 0.001422 | 0.000463 | −0.005036 | −0.005047 | −0.003211 |
| Median | −0.003149 | −0.003858 | −0.004682 | −0.002501 | 0.000450 | −0.002814 | −0.004013 | −0.009451 | −0.008791 |
| Maximum | 2.768749 | 2.838545 | 2.900669 | 1.132326 | 1.395331 | 1.060863 | 2.768749 | 2.838545 | 2.900669 |
| Minimum | −1.673299 | −1.791665 | −3.044328 | −1.090163 | −1.079340 | −0.842513 | −1.673299 | −1.791665 | −3.044328 |
| Std. Dev. | 0.232476 | 0.243903 | 0.226617 | 0.182200 | 0.185796 | 0.178694 | 0.271532 | 0.288201 | 0.264012 |
| Skewness | 0.103355 | 0.107824 | 0.093690 | 0.071269 | 0.050567 | −0.034998 | 0.122225 | 0.133416 | 0.136466 |
| Kurtosis | 6.938096 | 7.023621 | 12.08220 | 4.948796 | 5.879413 | 4.397209 | 6.305681 | 6.051845 | 11.88740 |
| Jarque-Bera | 6939.780 | 7245.328 | 36825.20 | 827.5778 | 1799.296 | 424.2000 | 2521.581 | 2153.848 | 18144.36 |
| Probability | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Observations | 10,710 | 10,710 | 10,710 | 5,202 | 5,202 | 5,202 | 5,508 | 5,508 | 5,508 |
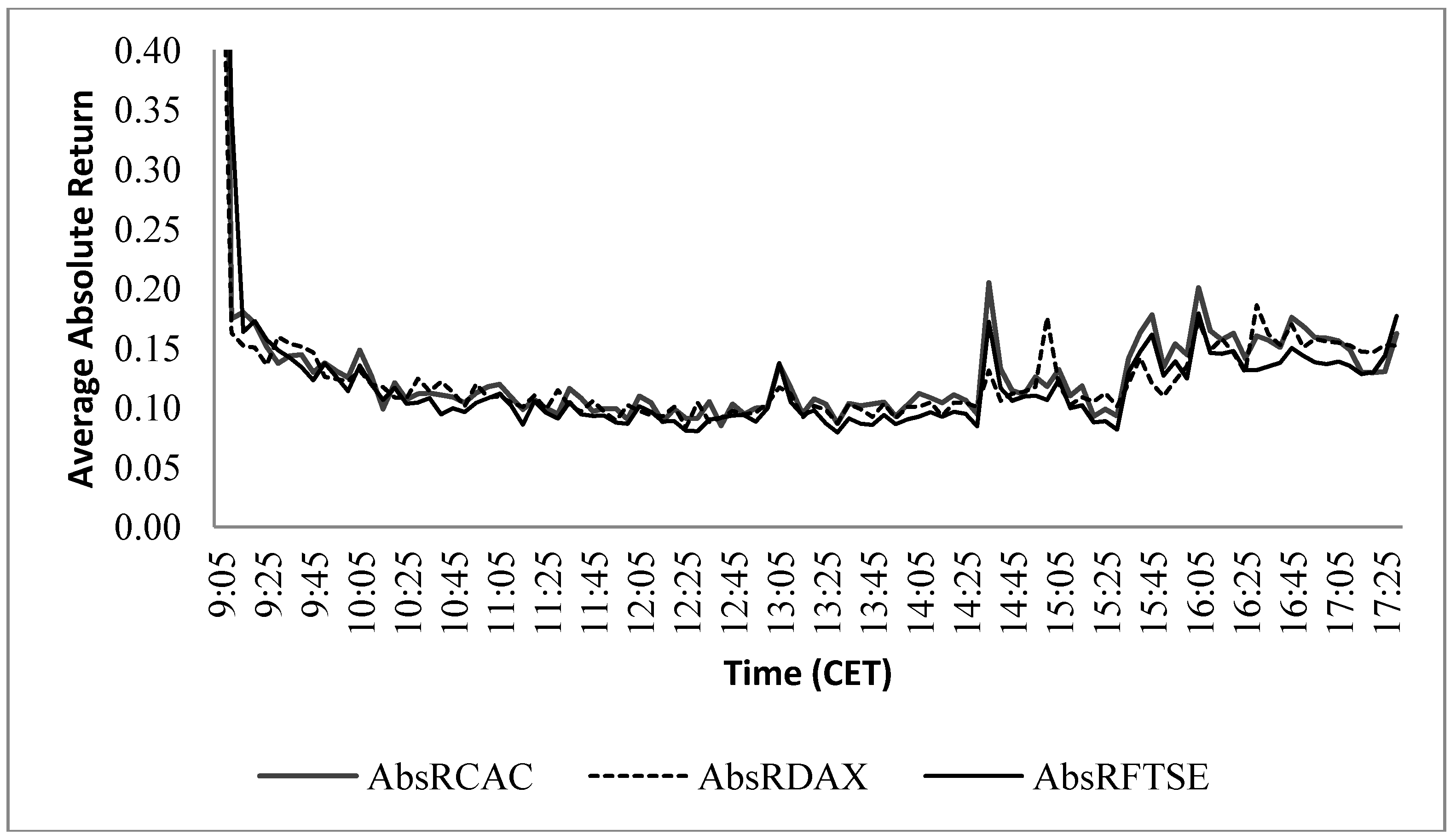
3.1. Deseasonalization of Data via the Flexible Fourier Form (FFF)


 was obtained. The seasonal pattern was estimated by using ordinary least square estimation (OLS).
was obtained. The seasonal pattern was estimated by using ordinary least square estimation (OLS).



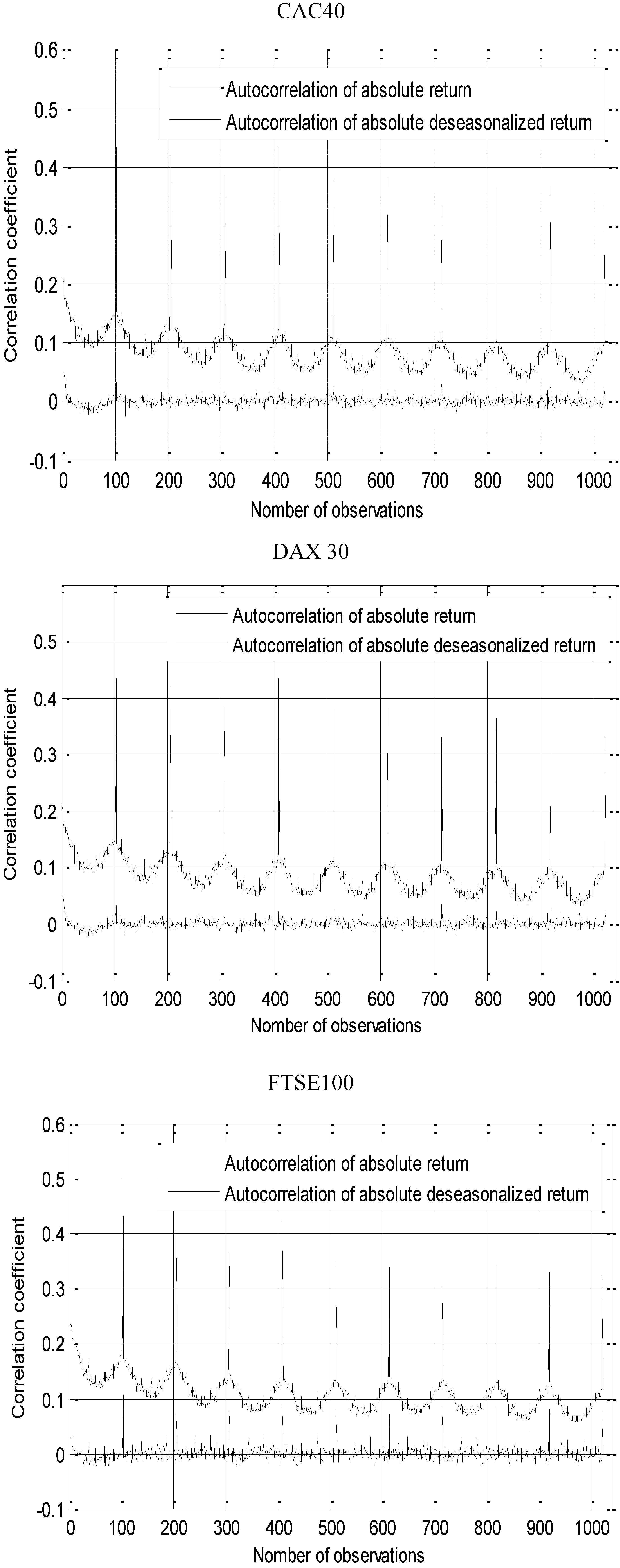
3.2. Bi-Variate VAR EGARCH Process



 .
.4. Results and Discussion
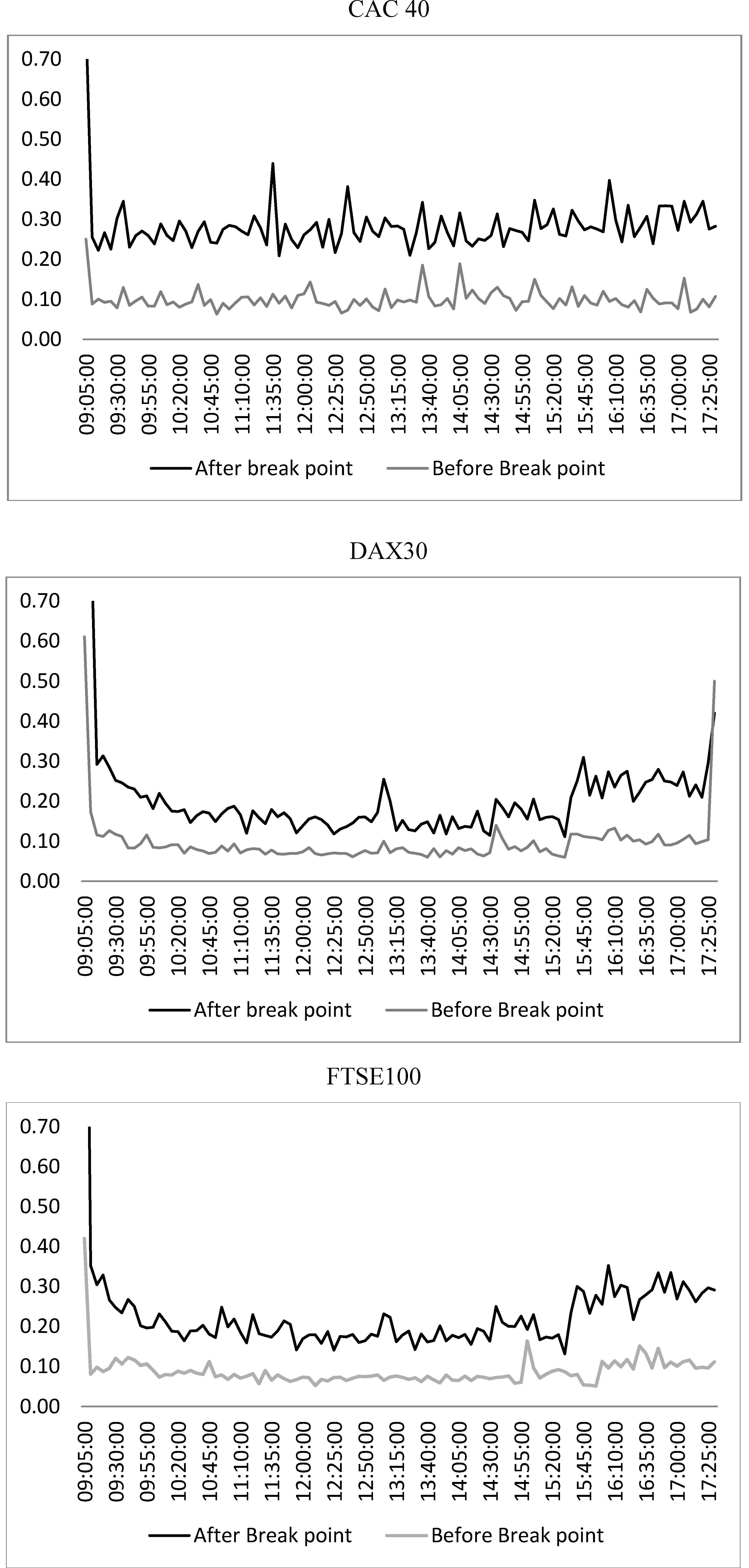
4.1. FFF Estimates
4.2. Modeling Intraday Volatility Specifications and Analysis—Bivariate VAR-EGARCH Estimates
4.2.1. Market Behaviour during the Calm Period
| Variable | Before 12 September 2008 | After 12 September 2008 | ||||
|---|---|---|---|---|---|---|
| Coeff | Std Error | T-Stat | Coeff | Std Error | T-Stat | |
| β1,0 | 0.0001 | 0.0013 | 0.0594 | −0.0068 ** | 0.0031 | −2.2115 |
| β1,1 | −0.0980 *** | 0.0203 | −4.8173 | −0.1269 *** | 0.019 | −6.6757 |
| β1,2 | 0.1253 *** | 0.023 | 5.4433 | 0.1255 *** | 0.0184 | 6.8089 |
| β2,0 | 0.0003 | 0.0018 | 0.1959 | −0.0053 * | 0.0029 | −1.8372 |
| β2,1 | 0.0409 ** | 0.02 | 2.0482 | 0.0340 * | 0.0187 | 1.8172 |
| β2,2 | −0.0081 | 0.0223 | −0.3648 | 0.0118 | 0.017 | 0.6939 |
| α1,0 | −0.6520 *** | 0.0788 | −8.2732 | −0.1839 *** | 0.0306 | −6.017 |
| α1,1 | 0.0732 *** | 0.0207 | 3.5432 | 0.1598 *** | 0.0191 | 8.3607 |
| α1,2 | 0.1141 *** | 0.0213 | 5.3674 | 0.0845 *** | 0.0149 | 5.6717 |
| α2,0 | −0.5698 *** | 0.0062 | −91.7875 | −0.1912 *** | 0.0299 | −6.4019 |
| α2,1 | 0.0558 *** | 0.0171 | 3.2598 | 0.2253 *** | 0.0196 | 11.4981 |
| α2,2 | 0.1050 *** | 0.0203 | 5.1841 | 0.0460 *** | 0.0146 | 3.1477 |
| γ12 | 0.5602 * | 0.3016 | 1.8571 | −0.0938 *** | 0.033 | −2.8477 |
| γ21 | −0.4119 ** | 0.1643 | −2.5075 | −0.2250 *** | 0.0828 | −2.7162 |
| δ1 | 0.8087 *** | 0.0229 | 35.2466 | 0.9287 *** | 0.0115 | 80.783 |
| δ2 | 0.8344 *** | 0.0024 | 353.2126 | 0.9278 *** | 0.011 | 84.6729 |
| ρ | 0.8060 *** | 0.0046 | 174.3189 | 0.8329 *** | 0.0036 | 232.3012 |
| QCAC(20) | 27.60 | p-value 0.119 | 24.612 | p-value 0.326 | ||
| QFTSE(20) | 29.155 | p-value 0.098 | 26.054 | p-value 0.128 | ||
| Q²CAC(20) | 25.661 | p-value 0.130 | 21.739 | p-value 0.344 | ||
| Q²FTSE(20) | 21.525 | p-value 0.202 | 21.441 | p-value 0.550 | ||
| Variable | Before 12 September 2008 | After 12 September 2008 | ||||
|---|---|---|---|---|---|---|
| Coeff | Std Error | T-Stat | Coeff | Std Error | T-Stat | |
| β1,0 | 0.0009 | 0.0025 | 0.3609 | −0.0051 * | 0.0031 | −1.667 |
| β1,1 | 0.0166 | 0.0209 | 0.7939 | −0.0639 *** | 0.0163 | −3.9165 |
| β1,2 | 0.0011 | 0.0212 | 0.0508 | 0.0318 ** | 0.0161 | 1.9744 |
| β2,0 | 0.0006 | 0.0024 | 0.2618 | −0.0035 | 0.003 | −1.1677 |
| β2,1 | 0.1516 *** | 0.0197 | 7.6869 | 0.0941 *** | 0.0164 | 5.734 |
| β2,2 | −0.0915 *** | 0.0206 | −4.4342 | −0.0411 ** | 0.0174 | −2.3638 |
| α1,0 | −0.5183 *** | 0.0963 | −5.3824 | −0.0869 *** | 0.0141 | −6.1684 |
| α1,1 | 0.1373 *** | 0.0208 | 6.5894 | 0.1705 *** | 0.0147 | 11.6273 |
| α1,2 | 0.0323 | 0.0205 | 1.5715 | 0.0165 | 0.0117 | 1.4082 |
| α2,0 | −0.4229 *** | 0.0792 | −5.3407 | −0.1270 *** | 0.0209 | −6.0909 |
| α2,1 | 0.0758 *** | 0.0182 | 4.152 | 0.1795 *** | 0.0161 | 11.1249 |
| α2,2 | 0.0859 *** | 0.0209 | 4.109 | 0.0681 *** | 0.0123 | 5.53 |
| γ12 | −0.049 | 0.0754 | −0.6501 | −0.1301 *** | 0.0393 | −3.3083 |
| γ21 | −0.1007 | 0.0931 | −1.0824 | −0.0314 * | 0.1092 | −1.9881 |
| δ1 | 0.8452 *** | 0.0285 | 29.6699 | 0.9639 *** | 0.0055 | 174.1163 |
| δ2 | 0.8770 *** | 0.0228 | 38.4051 | 0.9508 *** | 0.0077 | 122.8481 |
| Ρ | 0.7521 *** | 0.0059 | 127.4695 | 0.7783 *** | 0.0051 | 151.5845 |
| QDAX(20) | 29.602 | p-value 0.091 | 23.048 | p-value 0.112 | ||
| QFTSE(20) | 27.648 | p-value 0.150 | 20.226 | p-value 0.323 | ||
| Q²DAX(20) | 18.812 | p-value 0.564 | 12.377 | p-value 0.749 | ||
| Q²FTSE(20) | 17.303 | p-value 0.627 | 19.255 | p-value 0.315 | ||
| Variable | Before 12 September 2008 | After 12 September 2008 | ||||
|---|---|---|---|---|---|---|
| Coeff | Std Error | T-Stat | Coeff | Std Error | T-Stat | |
| β1,0 | −0.0003 | 0.0022 | −0.1555 | −0.0045 * | 0.0025 | −1.8015 |
| β1,1 | −0.2742 *** | 0.0248 | −11.0468 | −0.1438 *** | 0.0189 | −7.5974 |
| β1,2 | −0.0810 *** | 0.0245 | −3.3041 | 0.1649 *** | 0.0171 | 9.655 |
| β1,3 | 0.3156 *** | 0.0231 | 13.6933 | |||
| β1,4 | 0.0475 * | 0.025 | 1.904 | |||
| β2,0 | 0.0003 | 0.0023 | 0.1407 | −0.0050 * | 0.0026 | −1.8952 |
| β2,1 | −0.0375 | 0.0251 | −1.4949 | 0.0442 ** | 0.0184 | 2.4 |
| β2,2 | −0.0217 | 0.025 | −0.868 | −0.0767 *** | 0.0167 | −4.5822 |
| β2,3 | 0.0441 * | 0.0228 | 1.93 | |||
| α1,0 | −0.5982 *** | 0.0898 | −6.6635 | −0.0251 *** | 0.0097 | −2.5853 |
| α1,1 | 0.0373 * | 0.0224 | 1.661 | 0.0047 *** | 0.0007 | 7.1456 |
| α1,2 | 0.1748 *** | 0.0249 | 7.014 | 0.1107 *** | 0.0094 | 11.7436 |
| α2,0 | −0.6357 *** | 0.1367 | −4.6502 | −0.0204 ** | 0.009 | −2.2539 |
| α2,1 | 0.0044 | 0.023 | 0.1928 | 0.0046 *** | 0.0007 | 6.954 |
| α2,2 | 0.1951 *** | 0.0272 | 7.1742 | 0.1141 *** | 0.0082 | 13.9236 |
| γ12 | 0.1976 | 0.2764 | 0.715 | −11.135 *** | 0.0785 | −141.822 |
| γ21 | −0.0893 * | 0.0504 | −1.7731 | 0.2671 *** | 0.0486 | 5.5001 |
| δ1 | 0.8249 *** | 0.026 | 31.7162 | 0.9894 *** | 0.0036 | 276.041 |
| δ2 | 0.8099 *** | 0.0404 | 20.0285 | 0.9908 *** | 0.0034 | 287.5268 |
| ρ | 0.8341 *** | 0.0038 | 221.2988 | 0.8283 *** | 0.0044 | 188.0018 |
| QCAC(20) | 27.665 | p-value 0.073 | 25.433 | p-value 0.209 | ||
| QDAX(20) | 29.377 | p-value 0.059 | 23.058 | p-value 0.310 | ||
| Q²CAC(20) | 32.485 | p-value 0.052 | 21.739 | p-value 0.363 | ||
| Q²DAX(20) | 25.211 | p-value 0.197 | 26.162 | p-value 0.215 | ||
4.2.2. Markets Behaviour during the Turmoil Period
5. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- S. Bartram, and G. Bodnar. “No place to hide: The global crisis in equity markets in 2008/2009.” J. Int. Money Financ. 28 (2009): 1246–1292. [Google Scholar] [CrossRef]
- K. Forbes, and R. Rigobon. “No contagion, only interdependence: measuring stock market co-movements.” J. Financ. 57 (2002): 2223–2261. [Google Scholar]
- M. King, and S. Wadhwani. “Transmission of volatility between stock markets.” Rev. Financ. Stud. 3 (1990): 5–33. [Google Scholar]
- S. Lee, and K. Kim. “Does the October 1987 crash strengthen the co-movements among national stock markets? ” Rev. Financ. Econ. 3 (1993): 89–102. [Google Scholar]
- S. Calvo, and C. Reinhart. Private Capital Flows to Emerging Markets after the Mexican Crisis. Edited by G. Calvo, M. Goldstein and E. Hochreiter. Washington, DC, USA: Institute for International Economics, 1996, pp. 151–171. [Google Scholar]
- T. Baig, and I. Goldfajn. “Financial market contagion in the Asian crisis.” IMF Staff Pap. 46 (1999): 167–195. [Google Scholar]
- G. Bekaert, M. Ehrmann, M. Fratzcher, and J. Mehl. Global Crises and Equity Market Contagion. NBER Working Paper Series #17121; Cambridge, MA, USA: National Bureau of Economic Research, Inc., 2011. [Google Scholar]
- D. Kenourgios, A. Samitas, and N. Paltalidis. “Financial crises and stock market contagion in a multivariate time-vaying asymmetric framework.” J. Int. Financ. Mark. Inst. Money 21 (2011): 92–106. [Google Scholar]
- M. Syllignakis, and G. Kouretas. “Dynamic correlation analysis of financial contagion: Evidence from the central and eastern European markets.” Int. Rev. Econ. Financ. 20 (2011): 717–732. [Google Scholar] [CrossRef]
- F. Longin, and B. Solnik. “Is the international correlation of equity returns constant: 1960–1990? ” J. Int. Money Financ. 14 (1995): 3–26. [Google Scholar]
- B. Eichengreen, A. Rose, and C. Wyplosz. “Contagious currency crises: First test.” Scand. J. Econ. 98 (1996): 463–484. [Google Scholar] [CrossRef]
- K. Forbes. “Are Trade Effects Significant in the International Transmission of Crises? ” In Proceedings of NBER Conference on Currency Crises Prevention 2000, Cheeca Lodge, Islamorada, FL, USA, 11–13 January 2001; Chicago, IL, USA: University of Chicago Press, 2002. [Google Scholar]
- M. Dungey, and V. Martin. “Unravelling financial market linkages during crises.” J. Appl. Econ. 22 (2007): 89–119. [Google Scholar]
- D. Kenourgios, and P. Padhi. “Emerging markets and financial crises: Regional, global or isolated shocks? ” J. of Multinatl. Financ. Manag. 22 (2012): 24–38. [Google Scholar]
- R. Aloui, M. Ben Aïssa, and D. Nguyen. “Global financial crisis, extreme interdependences, and contagion effects: The role of economic structure? ” J. Bank. Financ. 35 (2011): 130–141. [Google Scholar]
- D. Dimitriou, D. Kenourgios, and T. Simos. “Global financial crisis and emerging stock market contagion: A multivariate FIAPARCH-DCC approach.” Int. Rev. Financ. Anal. 30 (2013): 46–56. [Google Scholar] [CrossRef]
- L. Baele. “Volatility spillover effects in European equity markets.” J. Financ. Quant. Anal. 40 (2005): 373–401. [Google Scholar]
- C. Savva, D. Osborn, and L. Gill. “Spillovers and correlations between US and major European stock markets: The role of the euro.” Appl. Financ. Econ. 19 (2009): 1595–1604. [Google Scholar] [CrossRef]
- S. Bartram, S. Taylor, and Y. Wang. “The Euro and European financial market.” J. Bank. Financ. 51 (2007): 1461–1481. [Google Scholar]
- A. Ghosh, R. Saidi, and K. Johnson. “Who moves the Asia-Pacific stock markets–US or Japan? Empirical evidence based on the theory of cointegration.” Financ. Rev. 34 (1999): 159–170. [Google Scholar]
- J. Yang, J. Kolari, and J. Min. “Stock market integration and financial crises: The case of Asia.” Appl. Financ. Econ. 13 (2003): 477–486. [Google Scholar]
- C. Chen, T. Chiang, and M. So. “Asymmetrical reaction to US stock-return news: Evidence from major stock markets based on a double-threshold model.” J. Econ. Bus. 55 (2003): 487–502. [Google Scholar]
- J. Nikkinen, V. Piljak, and J. Äijö. “Baltic stock markets and the financial crisis of 2008–2009.” Res. Int. Bus. Financ. 26 (2012): 398–409. [Google Scholar]
- L.T. Orlowski. “Financial crisis and extreme market risks/Evidence from Europe.” Rev. Financ. Econ. 21 (2012): 120–130. [Google Scholar]
- D. Kenourgios, and A. Samitas. “Equity market integration in emerging Balkan markets.” Res. Int. Bus. Financ. 25 (2011): 296–307. [Google Scholar]
- P. Singh, B. Kumar, and A. Pandey. “Price and volatility spillover across North American, European and Asian stock markets.” Int. Rev. Financ. Anal. 19 (2010): 55–64. [Google Scholar] [CrossRef]
- T.G. Andersen, and T. Bollerslev. “Deutsche mark-dollar volatility: Intraday activity patterns, macroeconomic announcements, and longer run dependencies.” J. Financ. 53 (1998): 219–265. [Google Scholar]
- J. Bai, and P. Perron. “Estimating and testing linear models with multiple structural changes.” Econometrica 66 (1998): 47–78. [Google Scholar]
- J. Bai, and P. Perron. “Computation and analysis of multiple structural change models.” J. Appl. Econ. 18 (2003): 1–22. [Google Scholar]
- T. Bollerslev. “Generalized autoregressive conditional heteroskedasticity.” J. Econ. 31 (1986): 307–327. [Google Scholar]
- J. Taylor, and X. Xu. “The incremental volatility information in one million foreign exchange quotations.” J. Empir. Financ. 4 (1997): 317–340. [Google Scholar]
- J. Taylor. Modelling Financial Time Series. Chichester, UK: John Willey & Sons, 1986. [Google Scholar]
- A. Admati, and D. Pfleiderer. “A theory of intraday patterns: Volume and price variability.” Rev. Financ. Stud. 1 (1988): 3–40. [Google Scholar]
- T.G. Andersen, and T. Bollerslev. “Intraday periodicity and volatility persistence in financial markets.” J. Empir. Financ. 4 (1997): 115–158. [Google Scholar]
- We calculate returns using the equation Ri,t = 100 × (lnPi,t – lnPi,t-1) where Ri,t is the return for stock market index i at time t, ln(Pi,t) is the log of stock price at time t, and ln(Pi,t-1) is the log of the laged value of the stock price at time t. Following Andersen et al. (2000), we delete the return inverval 9.00ߝ9.05 CET to avoid statistical inference.
- A.R. Gallant. “On the bias in flexible functional forms and an essentially unbiased form: The fourier flexible form.” J. Econ. 15 (1981): 211–245. [Google Scholar]
- We assume that: E(Rt,n) = 0, E(Rt,n , Rs,m) = 0 and that the variance and covariance of squared returns exist and are finite. The continuously compounded daily squared returns may be decomposed as: Rt ² = (∑Rt,n²).
- D.B. Nelson. “Conditional heteroskedasticity in asset pricing: A new approach.” Econometrica 59 (1991): 347–370. [Google Scholar]
- L. Hentschel. “All in the family: Nesting symmetric and asymmetric GARCH models.” J. Financ. Econ. 39 (1995): 71–104. [Google Scholar]
- Following Andersen et al. (2000), we delete 9.00-9.05 CET return interval to avoid statistical inference.
- We use VAR(1)-EGARCH (1,1) for the three bivariate relations during calm and turbulent periods except for the CAC40/DAX30 pair during the calm phase where a VAR(2)-EGARCH(1,1) is more appropriate.
- N. Ahlgren, and J. Antell. “Stock market linkages and financial contagion: A cobreaking analysis.” Q. Rev. Econ. Financ. 50 (2010): 157–166. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD), Economic Survey of Germany 2010. Paris, France: OECD Publishing, 2010.
- R. Anderson. “German Economic Strength: The Secrets of Success.” BBC News. 15 August 2012. Available online: http://www.bbc.co.uk/news/business-18868704 (accessed on 15 August 2012).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ben Slimane, F.; Mehanaoui, M.; Kazi, I.A. How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets? Int. J. Financial Stud. 2013, 1, 81-101. https://doi.org/10.3390/ijfs1030081
Ben Slimane F, Mehanaoui M, Kazi IA. How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets? International Journal of Financial Studies. 2013; 1(3):81-101. https://doi.org/10.3390/ijfs1030081
Chicago/Turabian StyleBen Slimane, Faten, Mohamed Mehanaoui, and Irfan Akbar Kazi. 2013. "How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets?" International Journal of Financial Studies 1, no. 3: 81-101. https://doi.org/10.3390/ijfs1030081
APA StyleBen Slimane, F., Mehanaoui, M., & Kazi, I. A. (2013). How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets? International Journal of Financial Studies, 1(3), 81-101. https://doi.org/10.3390/ijfs1030081




