Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment
Abstract
:1. Introduction
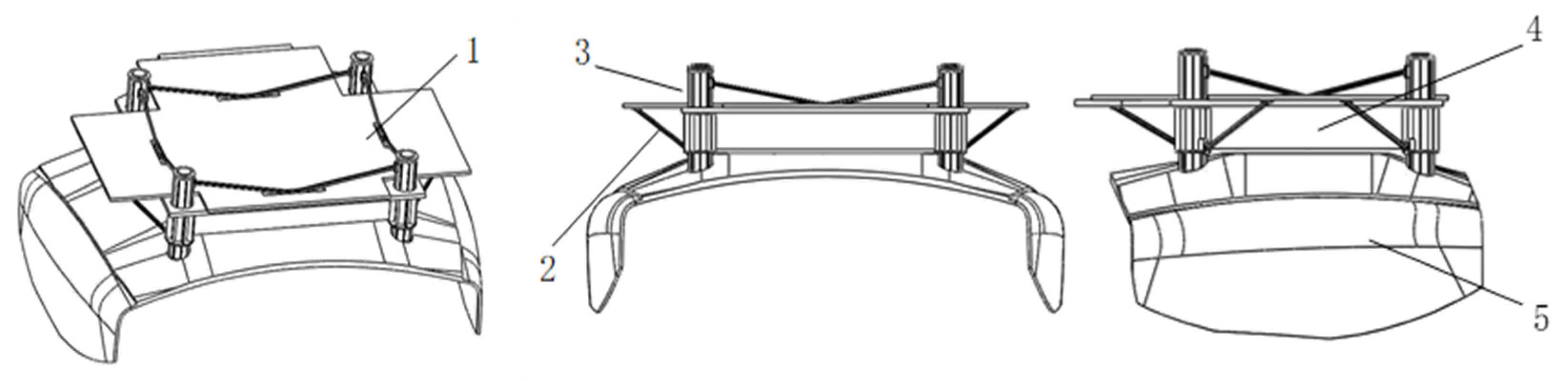
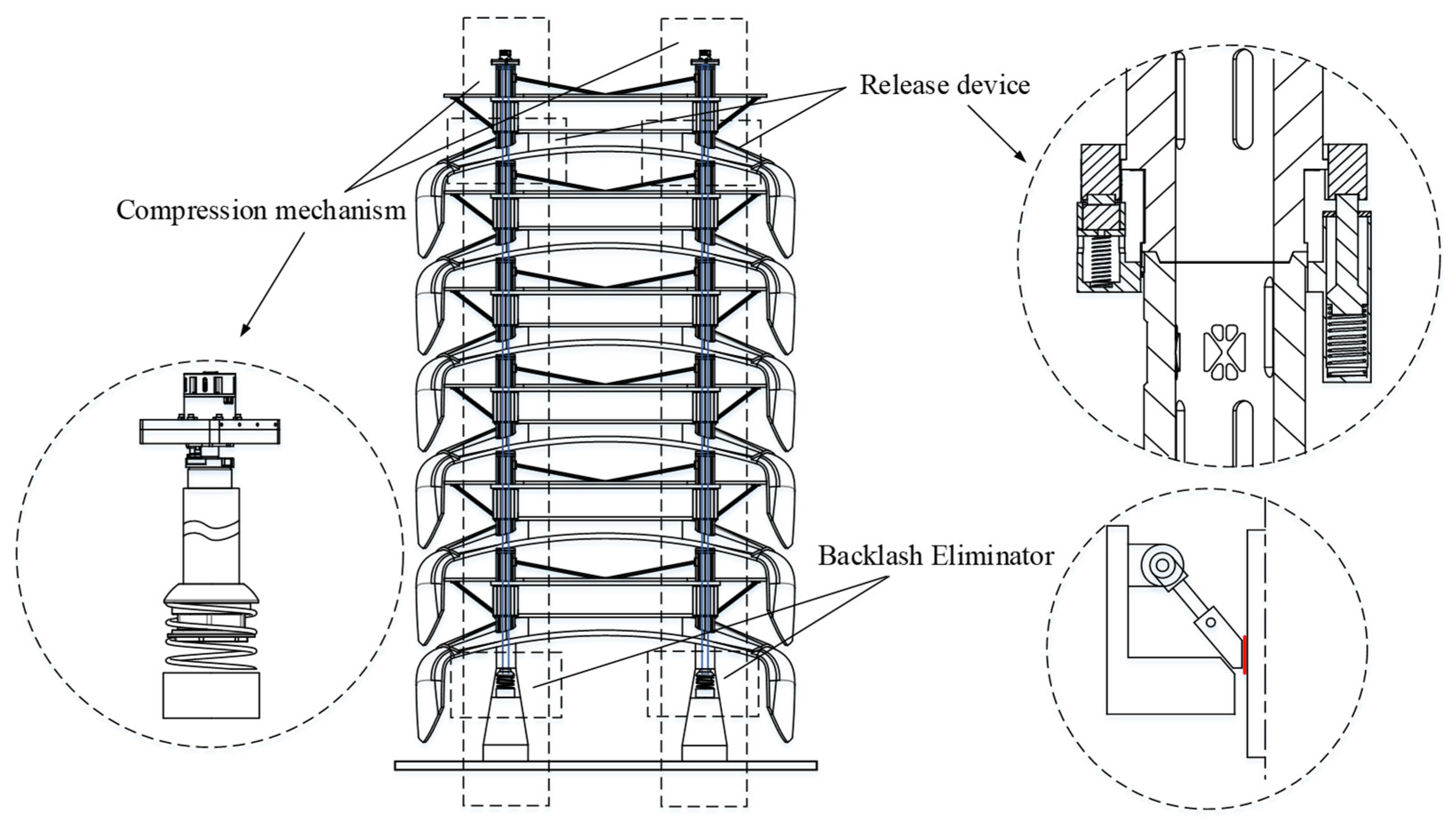
2. Structure and Working Principle
2.1. System Composition
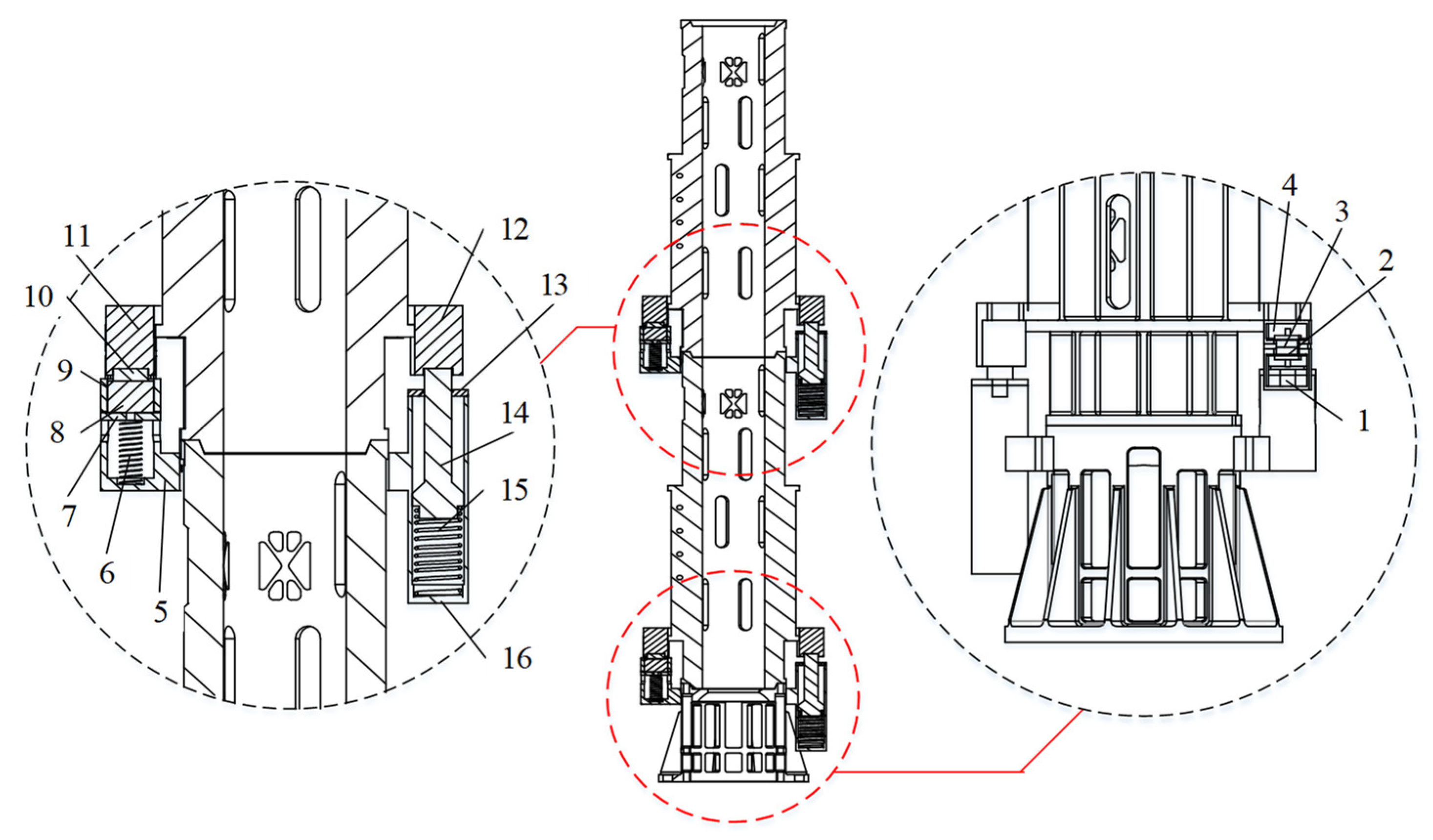
2.2. Compression Mechanism
2.3. Separation Mechanism
3. Dynamic Model
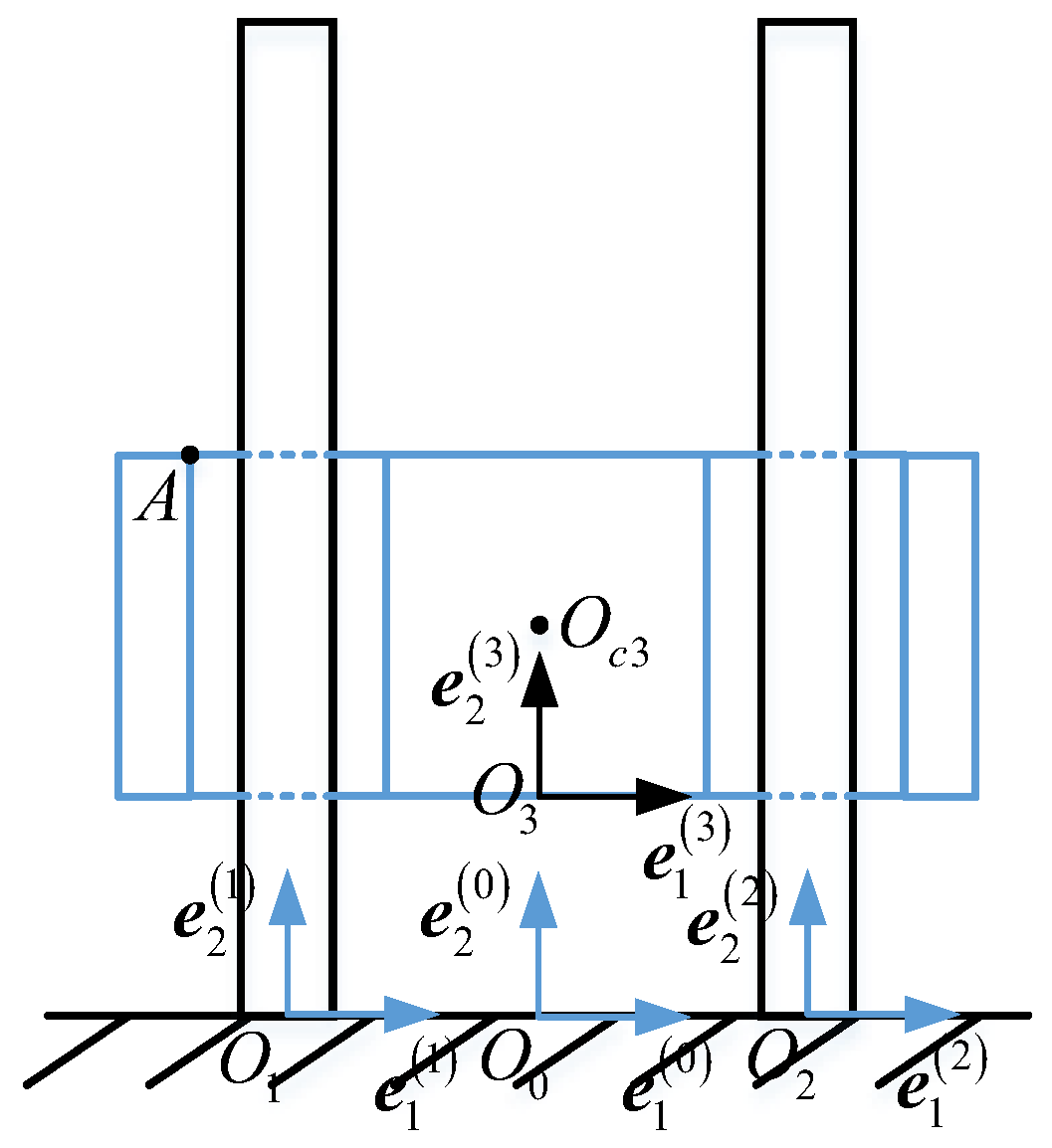
3.1. Natural Coordinate Method Based Rigid Body Satellite Dynamic Model
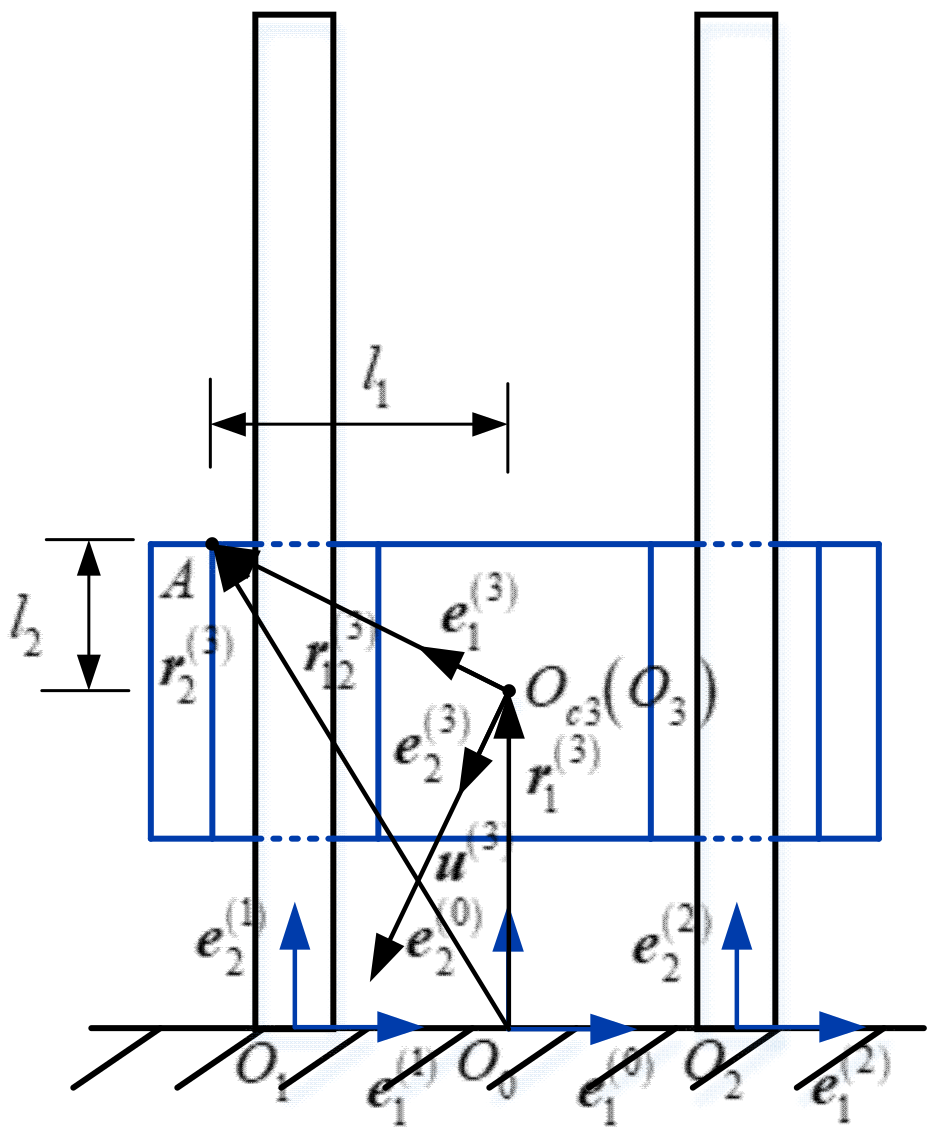
3.2. Dynamic Model of Flexible Guide Bar Based on Floating Coordinate System Method
3.3. Contact Force Model
3.3.1. Contact Form of Rigid Body Satellite and Guide Bars
- No contact between the two elements in the radial direction;
- Point contact occurring between the side of the guide bar and one endpoint of the satellite guide hole;
- Point contact occurring between the sides of two guide bars and two endpoints of the satellite guide hole;
- The sides of the two guide bars overlap with the sides of the satellite guide holes leading to line contact;
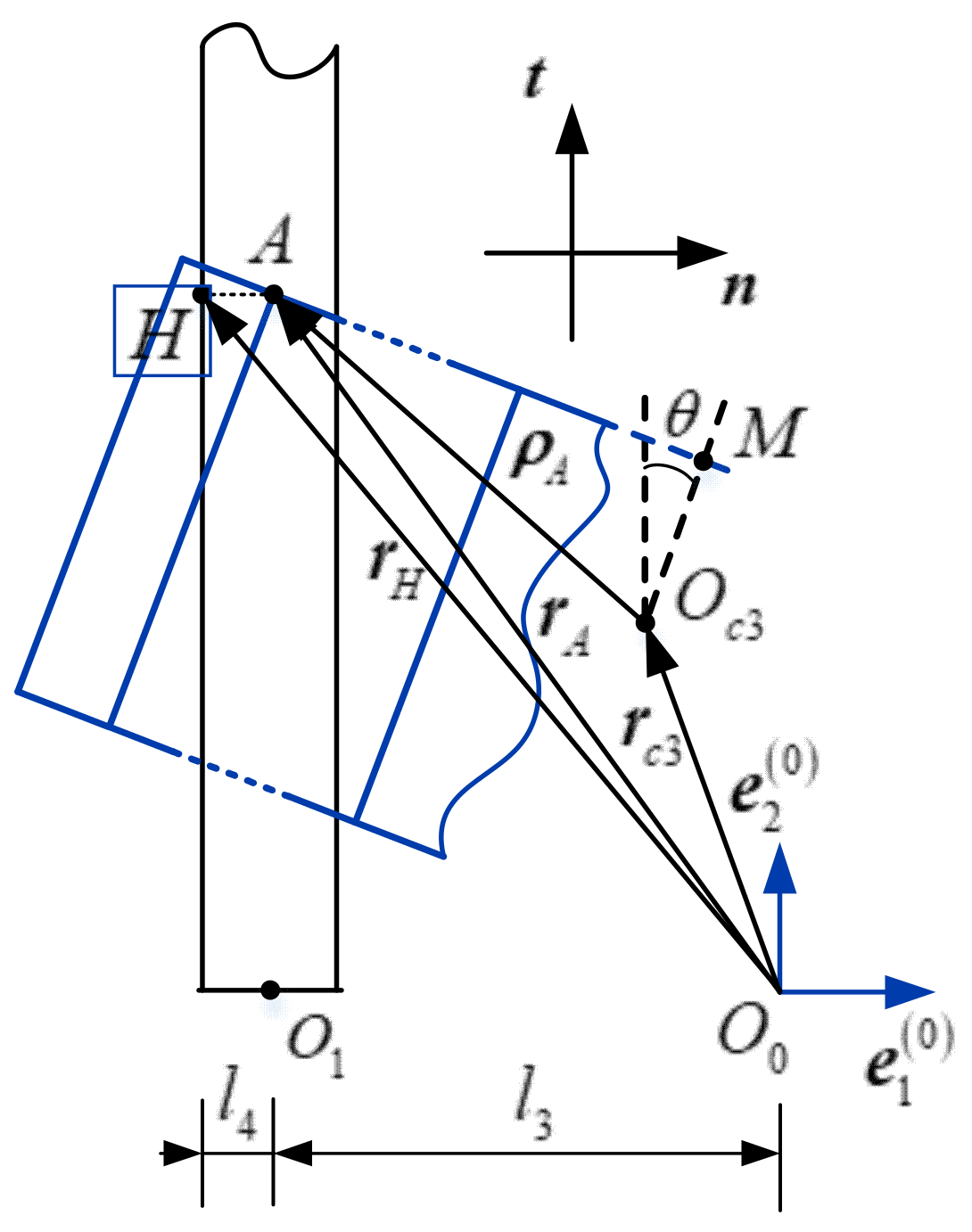
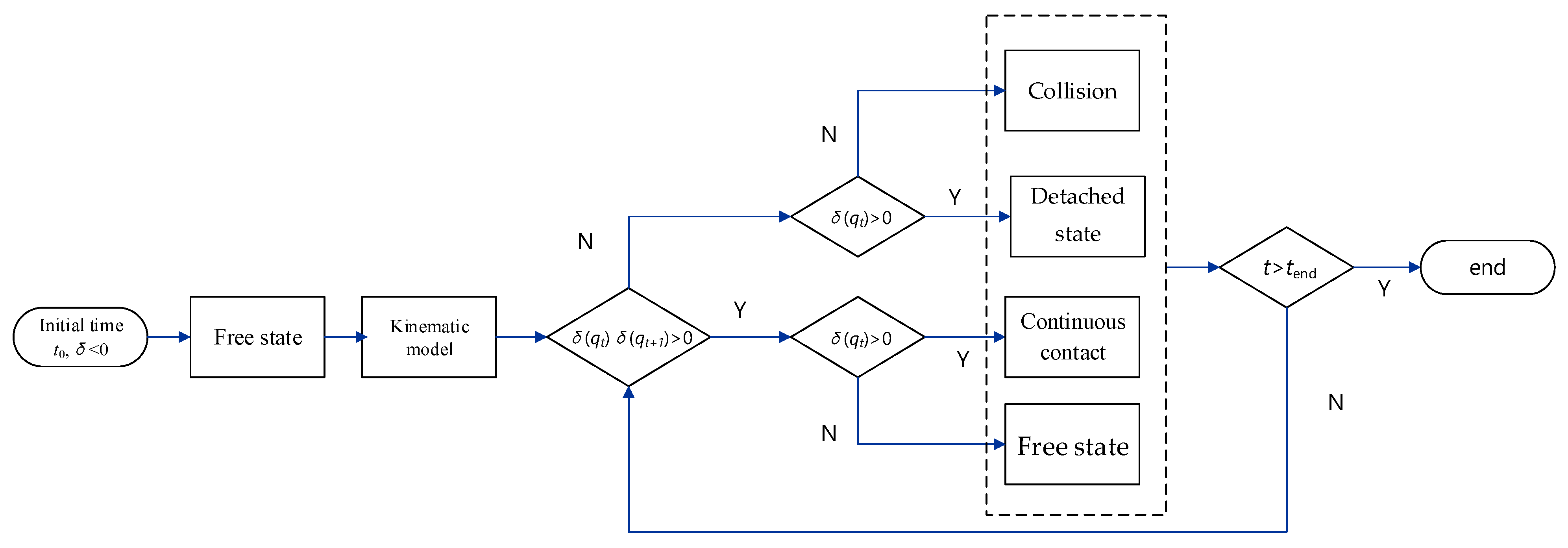
3.3.2. Judgment Basis of Contact State
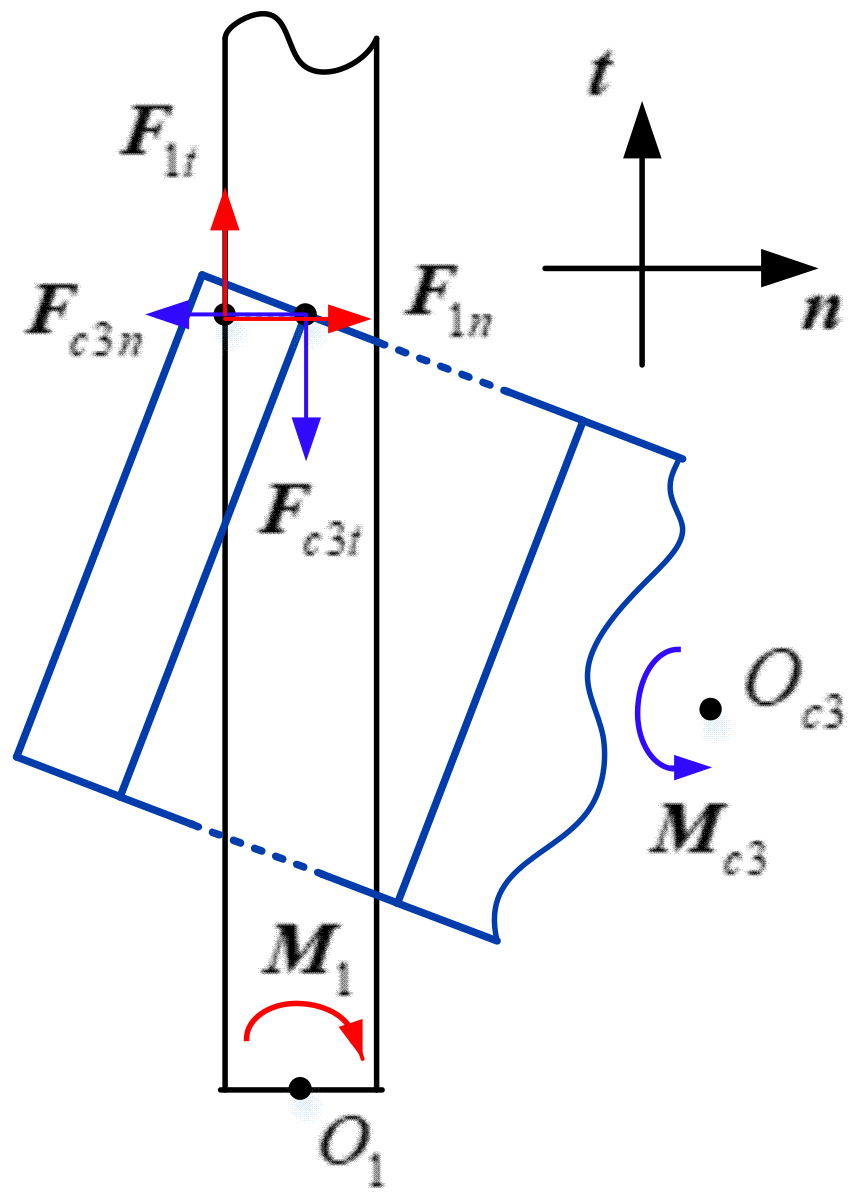
3.4. Separation Dynamic Model with Contact Collisions
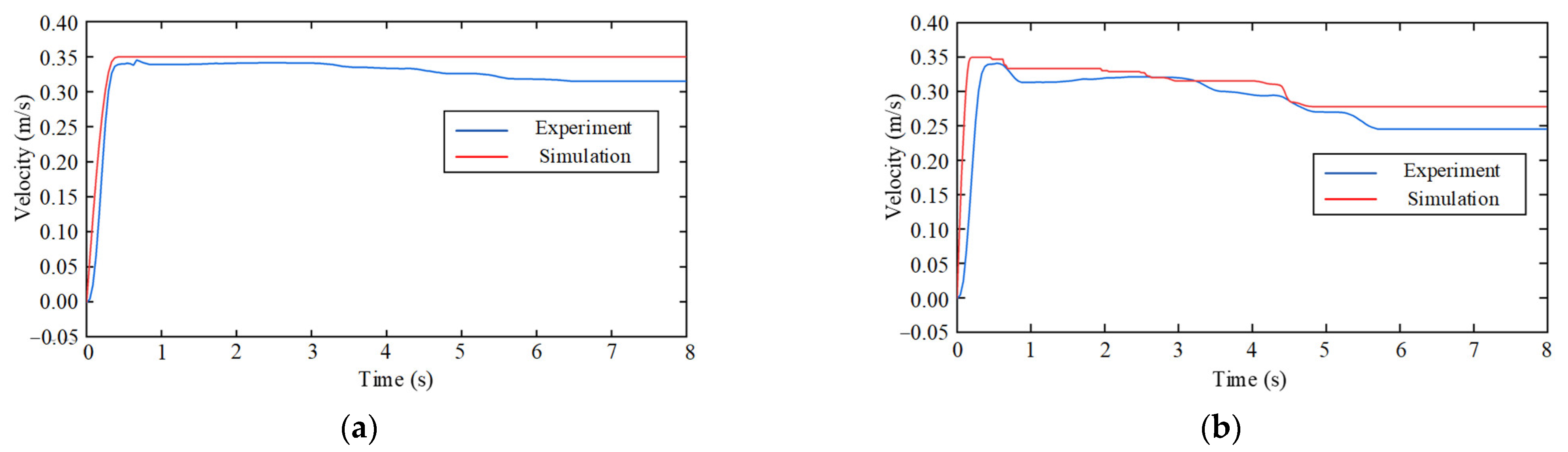
4. Separation Characteristics Simulation
5. Experiment Investigation
5.1. Compression and Unlocking Characteristics Experiment
5.1.1. Compression Test
5.1.2. Unlocking Experiment
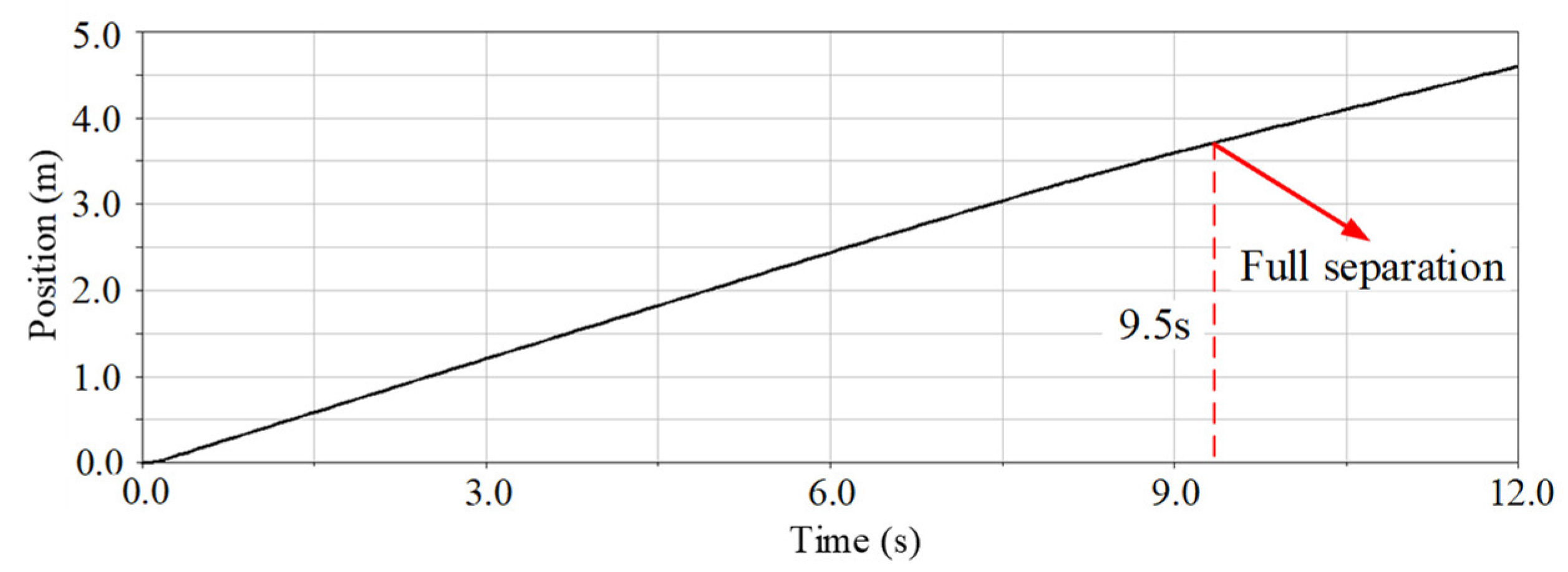
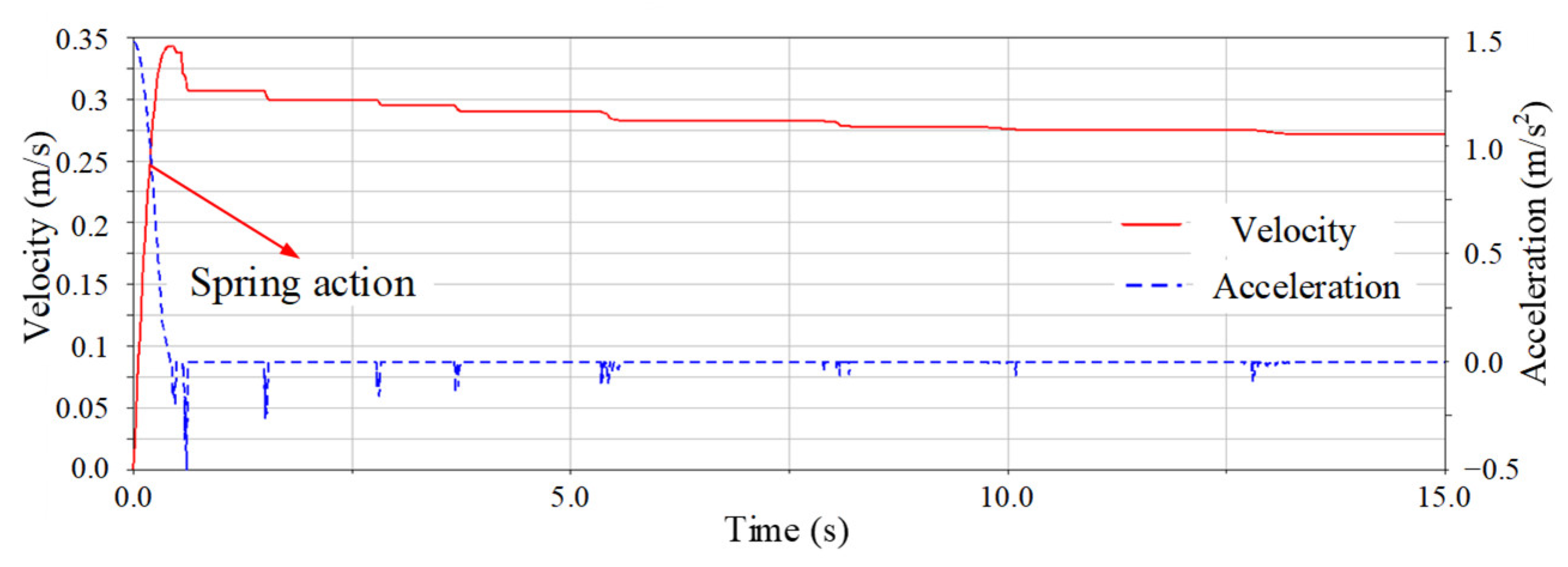
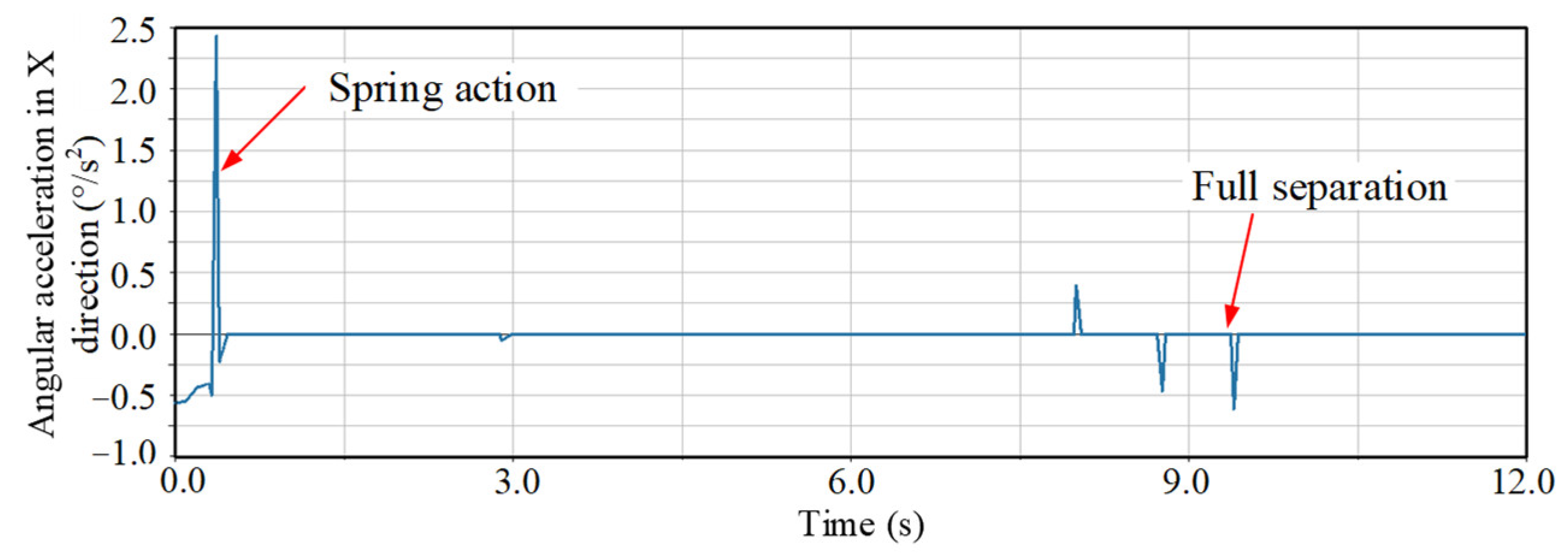
5.2. Separation Characteristics Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, L.; Zhang, Y.; Yu, J.; Wang, X. Design of Mega-Constellations for Global Uniform Coverage with Inter-Satellite Links. Aerospace 2022, 9, 234. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, L.; Feng, J.; Chang, L.; Li, D.; Qin, Y. A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft. Aerospace 2022, 9, 362. [Google Scholar] [CrossRef]
- Luo, Y.; Jiang, X.; Zhong, S.; Ji, Y.; Sun, G. Multisatellite Task Allocation and Orbit Planning for Asteroid Terminal Defence. Aerospace 2022, 9, 364. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, C.; Li, J.; Guan, Y.; Chen, S.; Zhang, L. Research on Design, Simulation, and Experiment of Separation Mechanism for Micro-Nano Satellites. Appl. Sci. 2022, 12, 5997. [Google Scholar] [CrossRef]
- Yang, F.; Yue, H.; Wang, G.; Tu, Q.; Wang, W. The design and analysis of picosatellite deployer with controllable release function. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macao, China, 18–20 July 2017; pp. 548–554. [Google Scholar] [CrossRef]
- Zhao, Y.; Yue, H.; Yang, F.; Zhu, J. A High Thrust Density Voice Coil Actuator with a New Structure of Double Magnetic Circuits for CubeSat Deployers. IEEE Trans. Ind. Electron. 2022, 69, 13305–13315. [Google Scholar] [CrossRef]
- Kwon, S.-C.; Son, J.-H.; Song, S.-C.; Park, J.-H.; Koo, K.-R.; Oh, H.-U. Innovative Mechanical Design Strategy for Actualizing 80 kg-Class X-Band Active SAR Small Satellite of S-STEP. Aerospace 2021, 8, 149. [Google Scholar] [CrossRef]
- SXRS-3_Mission at-a-glance [EB/OL]. Available online: https://spaceflight.com/sp-missions/sxrs-3/ (accessed on 4 August 2022).
- Krebs, G.-D. “Orbital Launches of 2021”. Gunter’s Space Page. Available online: https://space.skyrocket.de/doc_chr/lau2021.htm (accessed on 4 August 2022).
- Niccolai, L.; Bassetto, M.; Quarta, A.A.; Menggali, G. A review of Smart Dust architecture, dynamics, and mission applications. Prog. Aerosp. Sci. 2019, 106, 1–14. [Google Scholar] [CrossRef]
- Filippi, E.; Attouoman, H.; Conti, C. Pyroshock simulation using the alcatel etca test facility. In Proceedings of the First European Conference on Launcher Technology, Toulouse, France, 14–16 December 1999. [Google Scholar]
- Drossel, W.G.; Kunze, H.; Bucht, A.; Weisheit, L.; Pagel, K. Smart3-Smart materials for smart applications. Procedia Cirp 2015, 36, 211–216. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L.; Zhu, Y.; Huang, H.; Cai, W. An investigation of on-orbit release with inter-satellite electromagnetic force. Aerosp. Sci. Technol. 2015, 45, 309–315. [Google Scholar] [CrossRef]
- Yang, F.; Yue, H.; Zhang, Y.; Peng, J.; Deng, Z. Research on a low-impact unlocking trigger device of heavy load based on shape memory alloy fiber. Adv. Mech. Eng. 2017, 9, 1687814017724089. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, X.; Yang, Q. Design and Experimental Validation of Compact, Quick-Response Shape Memory Alloy Separation Device. J. Mech. Des. 2013, 136, 011009. [Google Scholar] [CrossRef]
- Bongers, E.; Koning, J.; Konink, T. Robustness improvement of ARA Kevlar Holddown restraint cables. In Proceedings of the 15th European Space Mechanisms & Tribology Symposium ESMATS, Noordwijk, The Netherlands, 25–27 September 2013. [Google Scholar]
- Peffer, A.; Denoyer, K.; Fosness, E.; Sciulli, D. Development and transition of low-shock spacecraft release devices. In Proceedings of the 2000 IEEE Aerospace Conference, Proceedings (Cat. No. 00TH8484), Big Sky, MT, USA, 25 March 2000; IEEE: New York, NY, USA, 2000; Volume 4, pp. 277–284. [Google Scholar]


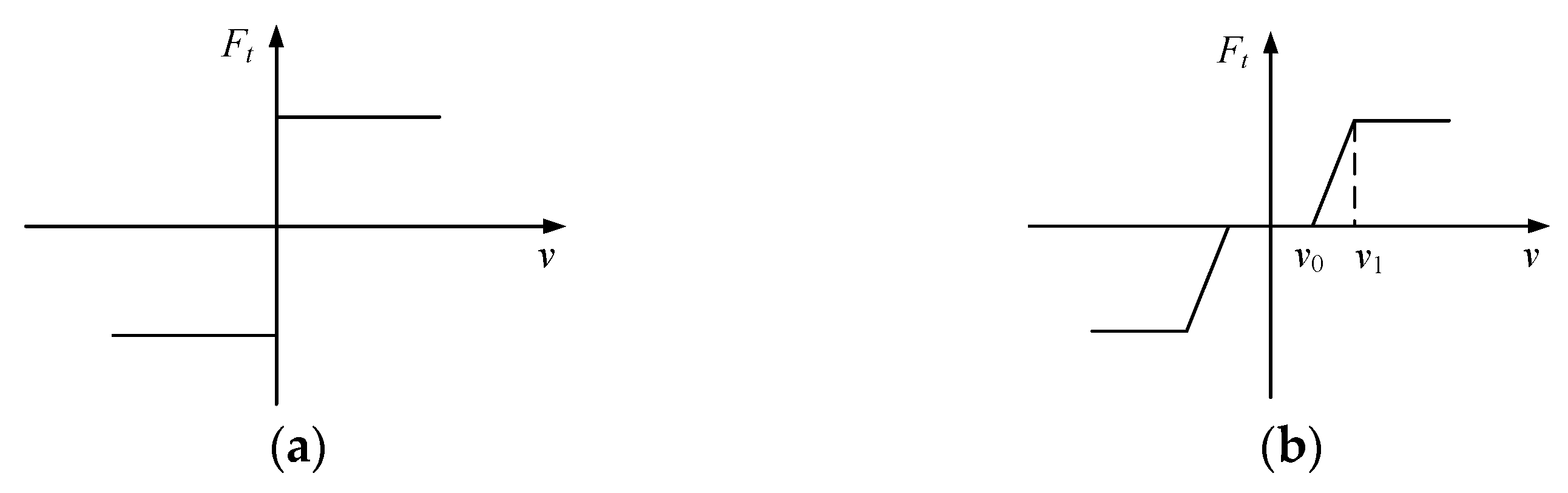


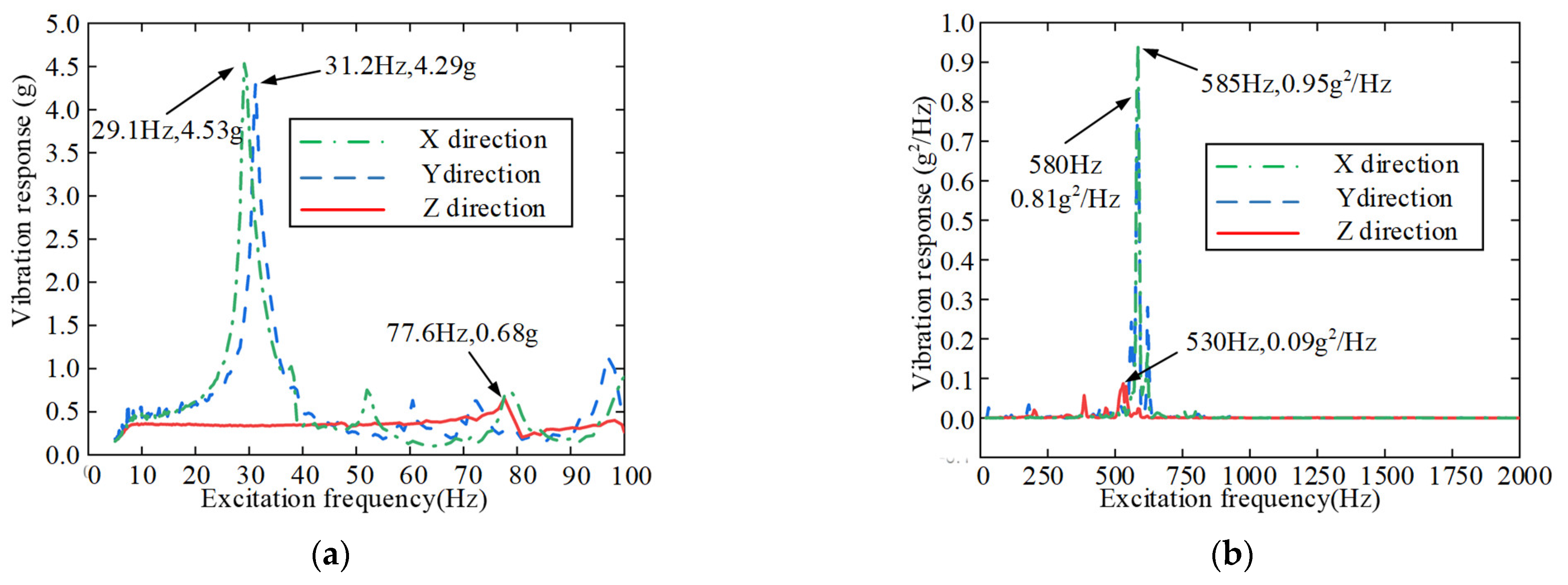



| i | ||||||
|---|---|---|---|---|---|---|
| 3 |
| Frequency Range (Hz) | Experimental Parameters | |
|---|---|---|
| 10~150 | +3 dB/oct (ratio) | +3 dB/oct |
| 150~600 | 0.00126 g2/Hz (density) | 0.00126 g2/Hz |
| 600~2000 | −9 dB/oct | −9 dB/oct |
| GRMS value | 1 grms | 1 grms |
| Load time (min) | 1 min | 1 min |
| Load direction | vertical | horizontal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhao, Q.; Yang, F.; Yue, H.; Yang, X.; Li, H. Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment. Aerospace 2022, 9, 446. https://doi.org/10.3390/aerospace9080446
Zhao Y, Zhao Q, Yang F, Yue H, Yang X, Li H. Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment. Aerospace. 2022; 9(8):446. https://doi.org/10.3390/aerospace9080446
Chicago/Turabian StyleZhao, Yong, Qingguang Zhao, Fei Yang, Honghao Yue, Xiaoze Yang, and Huaiyu Li. 2022. "Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment" Aerospace 9, no. 8: 446. https://doi.org/10.3390/aerospace9080446
APA StyleZhao, Y., Zhao, Q., Yang, F., Yue, H., Yang, X., & Li, H. (2022). Design and Analysis of a Compression and Separation Device for Multi-Satellite Deployment. Aerospace, 9(8), 446. https://doi.org/10.3390/aerospace9080446






