Abstract
In view of the multi-source uncertainty disturbance problem during flight control, the attitude autopilot based on fuzzy linear active disturbance rejection control (F-LADRC) was proposed. A second-order linear active disturbance rejection controller was designed to stabilize the attitude angle of the missiles, and the frequency domain characteristics were analyzed. Firstly, it was proved that the linear expansion state observer (LESO) is convergent and can achieve the indifference estimation of the system state variables and total disturbance. Then, it was proved that the linear active disturbance rejection control (LADRC) possesses disturbance rejection characteristics, and the influence of the bandwidth parameter on the disturbance rejection performance of the system was analyzed. The fuzzy control was used to adjust the parameter adaptively. Finally, the tracking, robustness, and anti-disturbance of the F-LADRC attitude autopilot were verified by performing simulations.
1. Introduction
The core task of the missile control system is to ensure that it accurately and robustly tracks the input command, so that the missile can generate control force and torque to achieve stable flight according to the command. The essence of the missile control system design is autopilot. Recently, with the constant development of the new generation of advanced missiles, the modern autopilot was proposed, especially for the multi-functionalization of missiles and the diversification of flight tasks. The main functions of the autopilot include the following: improving the equivalent damping of the missiles, maintaining the stability of system, speeding up the response frequency of the missiles, and improving the anti-disturbance ability. The attitude autopilot is a kind of typical autopilot, which can directly track the attitude angle command of the missile. However, missiles face interference from various uncertainties during the attitude control process. If the anti-interference performance is not good, it will seriously affect the missile’s command tracking accuracy [1,2,3,4,5,6]. Therefore, the designed controller must ensure the performance and stability robustness of the system under strong uncertainty.
In recent years, many advanced control theories have been implemented in control system design, including robust control [7,8], adaptive control [9,10], linear quadratic regulation [11,12], sliding mode control [13,14] and intelligent control algorithm [15,16,17], etc. In [18], a robust adaptive neural network certainty equivalent controller for a quadrotor unmanned aerial vehicle was proposed. The control method can achieve stable tracking commands without precise dynamic model and prior information of disturbances. In [19], the robust backstepping sliding mode control in conjunction with adaptive radial basis function neural network was applied to the non-linear dynamics of a high fidelity aircraft model. In [20], hybrid adaptive negative imaginary—neural-fuzzy control for a quadrotor was proposed, and this paper highlights the effectiveness of a hybrid controller in the face of some parameter variations. In addition, deep neuromorphic controllers represent an active and on-going area of research. Reference [21] demonstrated a deep neuromorphic controller leveraging dynamic topology for both neural network layers and nodes. The approach could learn the changes in the tasks without destabilizing the system. Neuromorphic control based on the divergence of a ventral optic flow field was proposed for the landing problem [22], and the improved controller was employed as an attitude estimator for quadrotors [23]. All of these control methods aimed to stabilize the system quickly and efficiently.
Although PID control has a wide range of application in engineering practice, it has inherent defects, and the robustness of the system is poor when it is disturbed. In addition, the combination of PID and feedforward or cascade control also has limitations and bottlenecks to varying degrees. The main problem is that this passive method of eliminating errors based on error feedback lags behind the influence of disturbances, which may cause system oscillation or severe overshoot due to excessive initial control command. The integral link set in order to eliminate the residual causes lag in the phase angle of the system, the system characteristics worsen when the disturbance disappears, and the inhibition effect on the change disturbance is not obvious. PI feedback control is applied to provide the missile sufficient stability near the equilibrium point while smoothly following the command. However, when the disturbance torque or the command changes rapidly, the system cannot compensate for the rapidly changing disturbance, and the quality of the command tracking deteriorates, which may lead to system divergence in severe cases.
To achieve the goal of stable control and improve the accuracy of disturbance rejection, disturbance observer-based control [24,25,26,27,28] has been widely proposed. Generally speaking, this kind of control method based on the disturbance observer can observe the disturbance on the one hand, and compensate for the disturbance on the other hand, which can effectively improve the tracking stability and disturbance rejection of the flight control. Reference [29] studied state estimation and parameter identification approaches based on the nonlinear sliding mode observer to obtain an approximation of real parameters of a dynamical system. Based on the idea of actively suppressing disturbances and uncertainties, [30] systematically proposed active disturbance rejection control (ADRC). Gao [31] applied the concept of frequency scale, linearized ADRC, and proposed a general linear active disturbance rejection control (LADRC), which also has a good disturbance rejection effect, and reduces the number of parameters to be adjusted which makes parameter tuning easier.
For the parameter tuning of LADRC, the empirical method is currently used more frequently. References [32,33] studied the relationship between the ADRC and the PID control, and the method of mutual conversion was provided. Reference [34] proposed a method with which to directly obtain the initial value of the LADRC parameters through the existing PID parameters. Reference [35] studied the frequency domain analysis method and gave the relationship between the system dynamic characteristics and the control parameters. Reference [36] proposed the application of the step response tuning formula in LADRC, which is convenient to obtain the initial value of the parameters. These methods provide some guidance for the parameter tuning of LADRC. The limitations of these methods are that they still require constant manual tuning, and they are not convenient for engineering popularization and application.
Based on the above discussion, this paper aimed to design attitude autopilot based on fuzzy linear active disturbance rejection control (F-LADRC) suitable for multi-source disturbance, which can effectively improve the anti-disturbance ability of the missile attitude control system. The main contributions of this paper include:
- The suggested control method could be used for the compensation of the total disturbance of the system. The observer can estimate system disturbances without a transducer to stabilize the system trajectory.
- The second-order LADRC attitude autopilot was designed, and the command tracking performance of the system was compared under the condition of multi-source disturbance, which proves the robustness and stable tracking ability of the second-order LADRC attitude autopilot.
- The fuzzy control theory was applied to the LADRC parameter tuning to realize the parameters’ self-adaptive adjustment and improve the tuning efficiency.
The main difficulty in attitude autopilot based on F-LADRC is the controller design and its convergence and disturbance rejection analysis. The rest of the paper is structured as follows. In Section 2, the missile dynamic model and transfer function are provided. In Section 3, the second-order LADRC attitude autopilot control structure is designed. The convergence of the extended state observer (LESO) and the disturbance rejection of LADRC are theoretically analyzed by studying the frequency domain characteristic. In Section 4, the fuzzy control theory is used for parameter tuning online. In the case of multi-source disturbance, simulation analysis is used for the PI and the LADRC attitude autopilot in the case of multi-source disturbance, which verifies the better tracking performance, robustness, and anti-disturbance of LADRC. Lastly in Section 5, conclusions are drawn.
2. Dynamic Model
In this paper, the configuration of the missile adopts an axisymmetric aerodynamic layout. The missile adopts skid-to-turn (STT) control technology during flight. Currently, the coupling of the pitch, yaw, and roll planes are weak, and the control systems can be independently designed. This paper selected the missile pitch panel control as the research object.
To obtain the linearized missile dynamic model, the following assumptions are given:
Assumption A1.
The angle of attack α is a small angle, that is , . The second-order term is ignored, that is .
Assumption A2.
The missile speed changes slowly, and the missile speed is considered to be a constant value, that is .
Based on above assumption, the linearized dynamic model can be obtained [37]:
where, is the pitch angle, is the angle of attack, is the deflection angle, is the pitch rate, is the lift coefficient caused by angle of attack, is the lift coefficient caused by elevator deflection, is the coefficient representing the efficiency of elevator deflection, is the coefficient representing stability, and is the damping coefficient caused by pitch rate.
When the initial value of and are 0, the transfer function can be obtained by Laplace transform of (1):
where, is the input which represents the elevator deflection angle; and is the output which represents pitch rate. is the open loop transfer coefficient from to , and . represents the missile aerodynamic time constant, and . is the time constant of open-loop missile, and ; is damping coefficient of open-loop missile, and .
3. Design and Analysis of Controller
To provide the the missile attitude control system with strong robustness under various uncertain disturbances, the attitude autopilot based on the second-order linear active disturbance rejection control technology was adopted in this paper. In this section, the design process and frequency characteristic analysis of the controller are given as follow.
3.1. Controller Design
In this paper, the attitude autopilot track pitch angle command. From (1), a second order plant can be written as:
where is input, is control gain. f refers to the generalized disturbance, which contains the internal and external uncertainty of the model, that is , and d is external uncertainty disturbance. We selected the following state variables: . Then, is the expansion state containing the disturbance. The plant in (3) is written in the form of the following extended state equation:
We can write Equation (4) as a state space model:
where , , , .
The state space observer can be constructed as the linear extended state observer (LESO) [31]:
where are the observation vector of respectively; is the estimator of total disturbance. are the observer gain. Selecting the appropriate observer gain can assist in the real-time tracking of various variables in (4). We can write (6) as a state space model:
where , . and are the observer input and output respectively. The characteristic equation is:
where, I is the identity matrix. The bandwidth of the observer can be defined as , which refers to assigning all observer eigenvalues at , and making , , and a function of [31]. That is,
make
The observed gain matrix is uniquely related to the bandwidth of the observer, and the parameters in L are all functions of which can be easily adjusted. Selecting the appropriate bandwidth can realize the real-time tracking of the state variables in (4), which simplifies the LESO design.
The linear state error feedback (LSEF) is constructed as:
where r is pitch angle command, is the proportional amplification factor, and is the differential amplification factor. Then, the closed-loop transfer function becomes a pure second-order system without zero. The characteristic polynomial of the closed-loop system is:
Similar to (9), the controller gain parameters are:
where is the LSEF bandwidth. Selecting the appropriate LSEF bandwidth can make the system track the command value stably.
With the state observer properly designed, the controller is given as
According to the above steps, ee designed attitude autopilot based on LADRC, as shown in Figure 1. We studied the fined missile in this paper. In Figure 1, the actuator transfer function is −1, and the plant is missile transfer function (2).
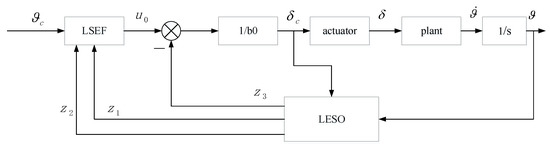
Figure 1.
Attitude autopilot design based on linear active disturbance rejection control.
3.2. Convergence Analysis of LESO
In this section, the convergence of LESO is analyzed. In this paper, the Laplace transform are all carried out under zero initial condition. The Laplace transform of (6) and (9) can be obtained as:
By defining the observation tracking error and the disturbance estimation error , we can obtain from (4). The error function is obtained by substituting (15) in
Assuming that are the step signal with the amplitude of K, then both are . Substitute these values into (16)–(18) to obtain
The error systems in (19)–(21) all have the same characteristic root , that is, the closed-loop poles are all located in the left half-plane of complex plane. The steady state error can be obtained according to the final value theorem.
We can find that LESO has good convergence in the process of the control system response, which can achieve the zero error estimation of system state variables and total disturbance.
3.3. Anti-Disturbance Analysis of LADRC
It can be observed from the LADRC structure that the control system includes two parts, LESO and LSEF, and it is not convenient to directly analyze the anti-disturbance characteristic of the whole system. In this section, we will analyze the frequency domain characteristic of LADRC to determine the ability of LADRC to suppress external disturbance.
We can obtain the Laplace transform of the controller according to (4)
Substitute (25) into (24) to obtain the output of the control system:
where the control system includes the tracking term and the disturbance term. When ignoring the tracking error of , (4) can be simplified to a double-integral series structure:
The simplified system transfer function can be obtained as:
At this time, the system output only contains the tracking item, and the performance of the control system is only determined by . It can be seen from the above analysis that the disturbance term is caused by the dynamic observation error of LESO, which has an important impact on the control performance of the system. Therefore, it is necessary to carry out the anti-disturbance characteristic analysis of LADRC around the system disturbance term.
It can be obtained from (26) that the disturbance rejection characteristic of the system is related to the disturbance terms, which are the bandwidth parameters and . When , the frequency characteristic curve of the disturbance term can be obtained as shown in Figure 2. When , the frequency characteristic curve of the disturbance term can be obtained as shown in Figure 3. From Figure 2 and Figure 3, within a certain range, the amplitude of the system decreases with the increase in and , that is, the disturbance gain decreases, and the system’s ability to suppress disturbance is enhanced.
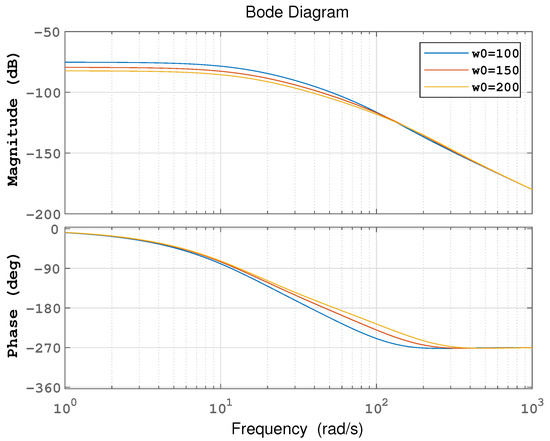
Figure 2.
The frequency characteristic curve of the disturbance term for different .
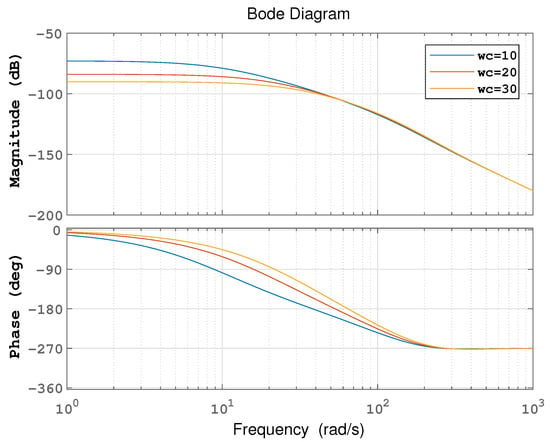
Figure 3.
The frequency characteristic curve of the disturbance term for different .
In particular, assuming that the disturbance f is the unit step signal, the output response of the disturbance term can be obtained:
By applying inverse Laplace transform, we can obtain:
where , , , the limit value can be obtained
that is, if there is step disturbance in the system, the steady state error output response is 0, and LADRC has a good ability to suppress external disturbances. It can be seen from (30) that with the increase in the bandwidth and , the decay speed of increases, and the recovery time of the system shortens after disturbance.
4. Simulation Analysis
In this section, attitude autopilot based on fuzzy linear active disturbance rejection control (F-LADRC) is simulated and analyzed, which is compared with the traditional PI control. Fuzzy control theory is used for adaptive parameters tuning.A simulation analysis is used for the PI and the F-LADRC attitude autopilot in the case of multi-source disturbance, which verifies the better performance of tracking, robustness and anti-disturbance of F-LADRC.
4.1. Tuning of Parameters Based on Fuzzy Control
For LADRC, the key to tune parameters is to select controller gain and observer gain. Through the structural analysis of (23), we can find that the second order LADRC consists of the following three parts: proportion , differentiation and disturbance estimation compensation . To sum up the above analysis, the parameters to be tuned are and , that is, the bandwidth of LSEF and LESO respectively. determines the tracking performance of the control system and determines the system’s ability to compensate for errors. can be set for most common engineering objects [31]. Therefore, choosing an appropriate bandwidth of LSEF becomes the key to parameter tuning. In this section, the fuzzy logic control principle is used to tune the parameter online, and the adaptive ability of the fuzzy control is used to achieve the purpose of automatic tuning. We selected the tracking error E of the pitch angle and the error rate of change as the input of the fuzzy control system, and the bandwidth of LSEF as the output. The schematic diagram of the combination of the fuzzy and LADRC control system is shown in Figure 4.
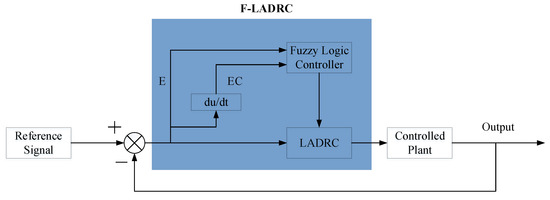
Figure 4.
Schematic diagram of F-LADRC control system.
The main steps of F-LADRC parameters tuning are as follows:
- Select the input and output variables of the fuzzy controller. This paper selected pitch angle error E and pitch rate error as the input variables, and the tuning parameter as the output variable.
- Select fuzzy description of input and output variables and membership function. This paper selected triangle membership function and set the fuzzy description as follows: NB is negative big; NS is negative small; ZO is zero; PS is positive small; PB is positive big.
- Select fuzzy rules. The fuzzy rules are based on the technical knowledge and practical experience of engineers. This paper selected fuzzy rules as shown in Table 1.
 Table 1. fuzzy rules table.
Table 1. fuzzy rules table. - Fuzzy inference. Under the control of the above fuzzy rules, the nonlinear mapping relationship between input and output can be obtained. The fuzzy inference is completed by the fuzzy control toolbox in Matlab software. The inference type chosen in this paper was Mamdani.
- Defuzzification of the fuzzy controller output. After the fuzzy inference is completed, the output is still a fuzzy variable, and we obtain a fixed value. Simulating with the Matlab software, the defuzzification is completed through the fuzzy control toolbox, and the defuzzification method is centroid.
In this paper, we selected the pitch channel of the tail controlled tactical missile as the simulation case. The missile is at the level phase, its angle of attack approximately equal to zero, and its speed is a constant. Aerodynamic data of missile are shown in Table 2 [37]. When tuning parameters of F-LADRC, the basic domains of (E,EC) are , . The parameters of F-LADRC are as follows: , the adjustment range of the fuzzy subset is [30, 40].

Table 2.
Aerodynamic data.
PI controller is widely used in flight controller design [38,39,40]. In this paper, we selected the PI controller to compare with F-LADRC. The parameters of the traditional PI controller were determined using the standard coefficient method [41,42,43]. The parameters of the PI controller were as follows: .
4.2. Simulation Results
In this section, the corresponding simulations are performed to validate the command tracking and disturbance rejection capabilities of F-LADRC. The control systems were built in the Simulink of MATLAB R2020b. The Fuzzy Logic Controller toolbox was used for the written fuzzy algorithm. The simulation had set configuration parameters for automatic solver selection with variable step.
4.2.1. Command Tracking Simulation
Considering the actual flight process, the task of attitude autopilot is to control the attitude. Therefore, the pitch angle command was used as the input signal for simulation. We used three kinds of input signals, namely step signal, sine signal and square wave signal, respectively, and simulation lasted for 5 s, 5 s, and 15 s respectively.The simulation results are shown in Figure 5. Especially in Figure 5a, in the response curve of the input step signal, the adjustment time of F-LADRC is 0.47 s, and the overshoot is 1.6%; the adjustment time of traditional PI control is 1.38 s, and the overshoot is 7.8%. The similar trends can be seen in Figure 5b,c. In order to facilitate the analysis in a visual manner, we employed absolute error (AE) and mean absolute error (MAE) as performance indicators, and the corresponding performance indicators are given in Figure 6. Comparisons of pitch rate response curves are shown in Figure 7.
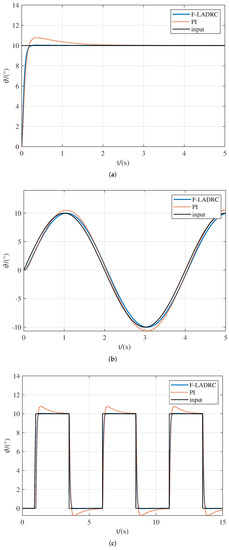
Figure 5.
Comparison of pitch angle response curves in command tracking simulation. (a) Tracking step signal; (b) Tracking sinusoidal signal; (c) Tracking square wave signal.
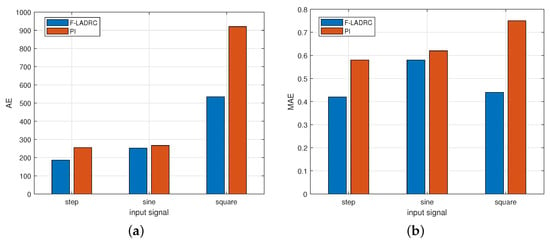
Figure 6.
Comparison of AE and MAE in command tracking simulation. (a) AE; (b) MAE.
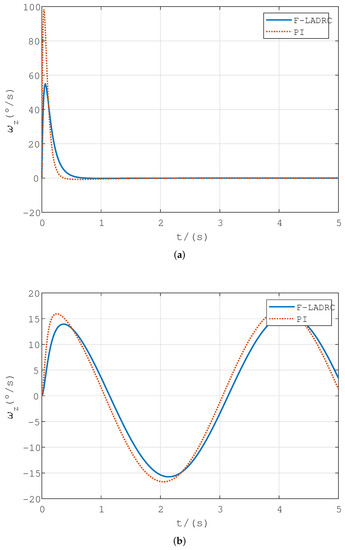
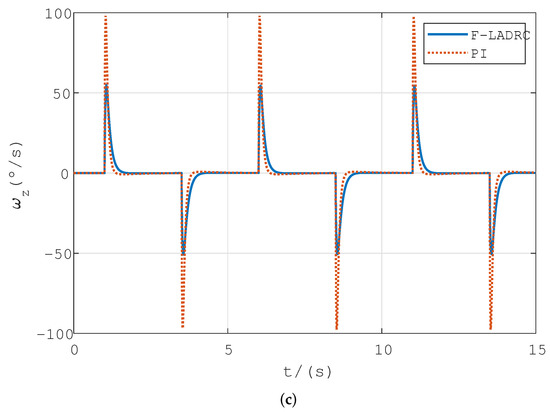
Figure 7.
Comparison of pitch rate response curves in command tracking simulation. (a) Tracking step signal; (b) Tracking sine wave signal; (c) Tracking square wave signal.
According to Figure 5, the adjustment time of F-LADRC is shorter than PI, and there were a few instances of overshoot in F-LADRC. The AE and MAE in Figure 6 show the degree of deviation in the tracking process, and it is obvious that the degree of deviation of F-LADRC is smaller than PI. As can be seen from Figure 7, the floating range of pitch rate of F-LADRC is smaller than PI. Therefore, the F-LADRC designed in this paper demonstrated the best performance in terms of command tracking.
4.2.2. Robustness Simulation
Under the same condition of parameters, a step signal with an amplitude of 10° was used as the input, and simulation lasted for 5s.The aerodynamic data in Table 2 are appropriately drifty, increased 15%, increased 30%, decreased 15%, and decreased 30% respectively, to simulate the uncertainty of aerodynamic parameters during flight. The adjustment time and overshoot corresponding to different floats are shown in Table 3. The simulation results of pitch angle response curves with aerodynamic drift are shown in Figure 8, and the corresponding AE and MAE are shown in Figure 9.

Table 3.
Comparison of response data with different aerodynamic drift.
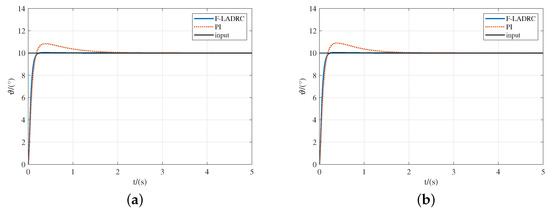
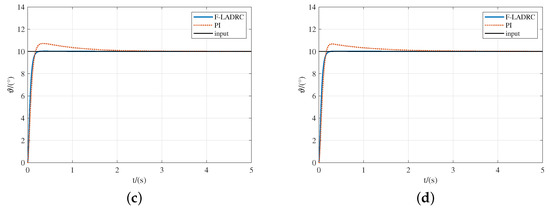
Figure 8.
Pitch angle response curves of aerodynamic drift. (a) Aerodynamic data increased 15%; (b) Aerodynamic data increased 30%; (c) Aerodynamic data reduced 15%; (d) Aerodynamic data reduced 30%.
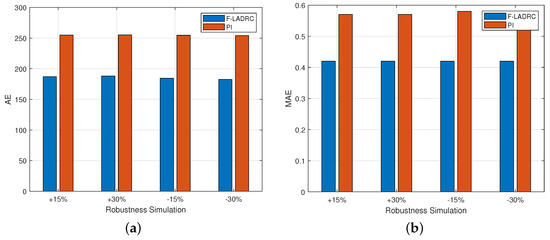
Figure 9.
Comparison of AE and MAE in robustness simulation. (a) AE; (b) MAE.
The simulation results show that even if the aerodynamic data are greatly uncertainty, F-LADRC can keep overshoot small and adjustment time short. It can be seen from Figure 9 that the AE and MAE of the proposed scheme were smaller. Therefore, the proposed scheme has good robustness.
4.2.3. Disturbance Simulation
Under the same condition of parameters, a step signal with an amplitude of 10° was used as input, and simulation lasts for 15 s. At 5s and 10 s, 10°/s and −10°/s step disturbance were added to the pitch rate, respectively, which simulates the disturbance of the external environment such as gusts in actual flight. The pitch angle and pitch rate response curves are shown in Figure 10 and Figure 11. As shown in Figure 12, the AE and MAE of the system are measured as the performance evaluation index. Disturbance estimator of observer is shown in Figure 13.
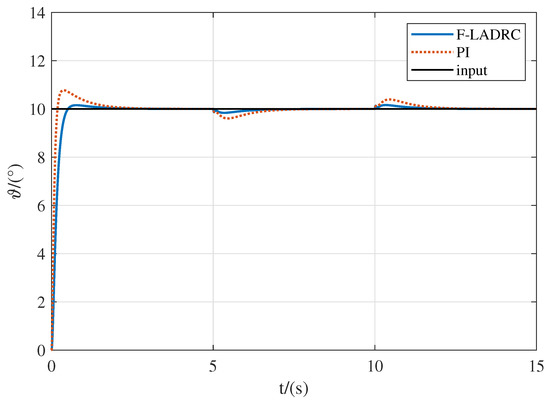
Figure 10.
The pitch angle response curve under gust disturbance.
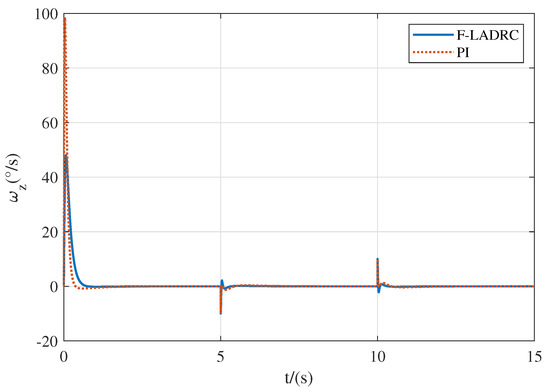
Figure 11.
The pitch rate response curve under gust disturbance.
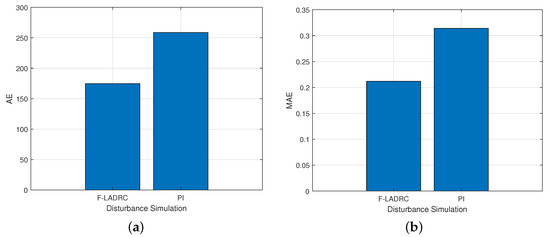
Figure 12.
Comparison of AE and MAE in disturbance simulation. (a) AE; (b) MAE.
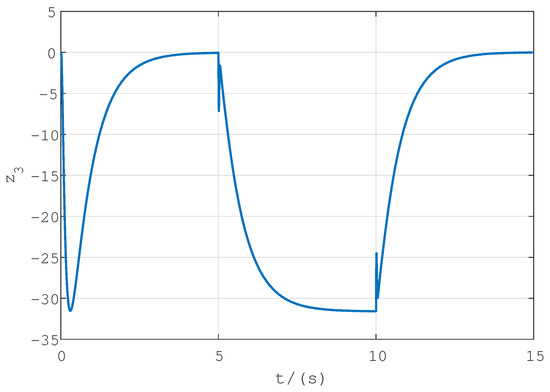
Figure 13.
Disturbance estimator of observer.
As shown in Figure 11 and Figure 12, when the gust of wind disturb the flight, the designed F-LADRC can suppress the disturbance very well, and the pitch angle can quickly converge. As shown in Figure 13, the observer can estimate the disturbance in real time and implement compensation, which ensures that the flight recovers to a steady state in a short time. Therefore, the proposed control scheme has good disturbance compensation ability.
5. Conclusions
In this paper, an attitude autopilot based on fuzzy linear active disturbance rejection control (F-LADRC) was proposed to manage the internal and external multi-source uncertainties during flight. Compared with the conventional active disturbance rejection controller, the linear active disturbance rejection controller realized the linear compensation of uncertain disturbance, and the number of parameters to be adjusted was lower. Applying the fuzzy control theory to the parameter tuning of LADRC can realize online adjustment of feedback gain. The simulation results show that, compared with the traditional PI control, the attitude autopilot using F-LADRC effectively suppressed the multi-source uncertain disturbance and had strong robustness. It is suitable for scenarios such as aerodynamic uncertainty and gust interference during flight, which provides a new idea for solving flight control under the disturbance condition. In future work, we will study the proposed control method based on the nonlinear dynamic model, which can be suitable for more complex flight conditions. Additionally, we will attempt to combine the proposed control method with the simulator for hardware in the loop simulation test.
Author Contributions
Conceptualization, D.H. and C.L.; Data curation, D.H.; Formal analysis, D.H. and Z.S.; Project administration, C.L.; Resources, C.L.; Supervision, C.L.; Validation, D.H.; Visualization, D.H.; Writing—original draft, D.H.; writing—review and editing, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holloway, J.C.; Krstic, M. A predictor observer for seeker delay in the missile homing loop. IFAC-PapersOnLine 2015, 48, 416–421. [Google Scholar] [CrossRef]
- McCourt, M.; Klotz, J.; Mehta, S.S.; Curtis, J.W. Disturbance rejection using micro-jet actuators with a MPC policy. In Proceedings of the AIAA Guidance, Navigation, and Control of the Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1308. [Google Scholar]
- Strub, G.; Theodoulis, S.; Gassmann, V.; Dobre, S.; Basset, M. Gain-scheduled autopilot design and validation for an experimental guided projectile prototype. J. Guid. Control Dyn. 2018, 41, 461–475. [Google Scholar] [CrossRef]
- Theodoulis, S.; Proff, M. Robust flight control tuning for highly agile missiles. In Proceedings of the AIAA Scitech of the Conference, Nashville, TN, USA, 11–15, 19–21 January 2021; p. 1568. [Google Scholar]
- Panchal, B.; Subramanian, K.; Talole, S.E. Robust integrated guidance and control design for tactical missiles. In Proceedings of the AIAA Guidance, Navigation, and Control of the Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1120. [Google Scholar]
- Głębocki, R.; Jacewicz, M. Sensitivity analysis and flight tests results for a vertical cold launch missile system. Aerospace 2020, 7, 168. [Google Scholar] [CrossRef]
- Tang, P.; Dai, Y.H.; Chen, J.F. Nonlinear robust control on yaw motion of a variable-speed unmanned aerial helicopter under multi-Source disturbances. Aerospace 2022, 9, 42. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoğlu, C. Robust autopilot design based on a disturbance/uncertainty/coupling estimator. IEEE Trans. Control Syst. Technol. 2018, 27, 2622–2629. [Google Scholar] [CrossRef]
- Ouda, A.N. A robust adaptive control approach to missile autopilot design. Int. J. Dyn. Control 2018, 6, 1239–1271. [Google Scholar] [CrossRef]
- Guo, J.G.; Gu, X.Y.; Guo, Z.Y. Asymptotic adaptive tracking control for hypersonic vehicles with guaranteeing multi-performance requirements. Aerosp. Sci. Technol. 2020, 105, 106025. [Google Scholar] [CrossRef]
- Devan, V.; Chandar, T.S. Cascaded LQR control for missile roll autopilot. In Proceedings of the International CET Conference on Control, Communication, and Computing (IC4), Trivandrum, India, 5–7 July 2018. [Google Scholar]
- Bużantowicz, W. Tuning of a linear-quadratic stabilization system for an anti-aircraft missile. Aerospace 2021, 8, 48. [Google Scholar] [CrossRef]
- Wang, J.M.; Wu, Y.J.; Dong, X.M. Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer. Nonlinear Dyn. 2015, 81, 1489–1510. [Google Scholar] [CrossRef]
- Gürsoy-Demir, H.; Önder, E.M. A nonlinear disturbance observer-based adaptive integral sliding mode control for missile guidance system. Int. J. Gen. Syst. 2022, 2022, 6978170. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Kim, Y.; Moon, G.; Jun, B. Design of an adaptive missile autopilot considering the boost phase using the SDRE method and neural networks. J. Frankl. Inst. 2018, 355, 9085–9107. [Google Scholar] [CrossRef]
- Elbatal, A.; Elkhatib, M.M.; Youssef, A.M. Intelligent autopilot design based on adaptive neuro-fuzzy technique and genetic algorithm. In Proceedings of the 12th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 7–9 April 2020. [Google Scholar]
- Liu, S.X.; Huang, F.P.; Yan, B.B.; Zhang, T.; Liu, R.F.; Liu, W. Optimal design of multimissile formation based on an adaptive SA-PSO algorithm. Aerospace 2021, 9, 21. [Google Scholar] [CrossRef]
- Doukhi, O.; Lee, D.J. Neural network-based robust adaptive certainty equivalent controller for quadrotor UAV with unknown disturbances. Int. J. Control Autom. Syst. 2019, 17, 2365–2374. [Google Scholar] [CrossRef]
- Singh, P.; Giri, D.K.; Ghosh, A.K. Robust backstepping sliding mode aircraft attitude and altitude control based on adaptive neural network using symmetric BLF. Aerosp. Sci. Technol. 2022, 126, 107653. [Google Scholar] [CrossRef]
- Tran, V.P.; Mabrok, M.A.; Garratt, M.A.; Petersen, I.R. Hybrid adaptive negative imaginary-neural-fuzzy control with model identification for a quadrotor. IFAC J. Syst. Control 2021, 16, 100156. [Google Scholar] [CrossRef]
- Kocer, B.B.; Hady, M.A.; Kandath, H.; Pratama, M.; Kovac, M. Deep neuromorphic controller with dynamic topology for aerial robots. In Proceedings of the Conference on Robotics and Automation, Xi’an, China, 31 May–4 June 2021. [Google Scholar]
- Dupeyroux, J.; Hagenaars, J.J.; Paredes-Vallés, F.; De Croon, G. Neuromorphic control for optic-flow-based landing of MAVs using the Loihi processor. In Proceedings of the Conference on Robotics and Automation, Xi’an, China, 31 May–4 June 2021. [Google Scholar]
- Stroobants, S.; Dupeyroux, J.; De Croon, G. Neuromorphic computing for attitude estimation onboard quadrotors. Neuromorphic Comput. Eng. 2022. [Google Scholar] [CrossRef]
- Liu, X.D.; Huang, W.W.; Yu, C.M. Dynamic surface attitude control for hypersonic vehicle containing extended state observer. J. Astron. 2015, 36, 916–922. [Google Scholar]
- Pu, Z.Q.; Yuan, R.Y.; Tan, X.M.; Yi, J.Q. Active robust control of uncertainty and flexibility suppression for air-breathing hypersonic vehicles. Aerosp. Sci. Technol. 2015, 42, 429–441. [Google Scholar] [CrossRef]
- An, H.; Liu, J.X.; Wang, C.H.; Wu, L.G. Disturbance observer-based antiwindup control for air-breathing hypersonic vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3038–3049. [Google Scholar] [CrossRef]
- Bayrak, A.; Efe, M. A frequency domain comparison of disturbance observer based control schemes. Proc. Inst. Mech. Eng. I-J. Sys. 2022, 236, 244–256. [Google Scholar] [CrossRef]
- Sini, S.; Ananthan, T. A disturbance observer based control for quadrotor aircraft subject to wind gusts. In Proceedings of the IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Trivandrum, India, 10–12 March, 2022; pp. 491–496. [Google Scholar]
- Ordaz, P.; Ramírez, M.; Rodríguez, L.; Cuvas, C.; Romero, H.; Sandre, O. Parameter identification based on nonlinear observer for mechanical systems. J. Comput. Nonlinear Dyn. 2021, 16, 021004. [Google Scholar] [CrossRef]
- Zhang, R.; Han, J.Q. Auto-disturbances rejection controller constructed by cascade extended state observer. Control Decis. 2000, 15, 122–124. [Google Scholar]
- Gao, Z.Q. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Jin, H.Y.; Song, J.C.; Lan, W.Y.; Gao, Z.Q. On the characteristics of ADRC: A PID interpretation. Sci. China Inf. Sci. 2020, 63, 1–3. [Google Scholar] [CrossRef]
- Zhong, S.; Huang, Y.; Guo, L. A parameter formula connecting PID and ADRC. Sci. China Inf. Sci. 2020, 63, 10–13. [Google Scholar] [CrossRef]
- Han, W.J.; Tan, W. Parameter tuning of linear active disturbance rejection control based on PID parameter tuning. Control Decis. 2021, 36, 1592–1600. [Google Scholar]
- Song, J.; Zhao, M.F.; Gao, K.; Su, J.C. Error analysis of ADRC linear extended state observer for the system with measurement noise. IFAC-PapersOnLine 2020, 53, 1306–1312. [Google Scholar] [CrossRef]
- Cui, W.Q.; Tan, W.; Li, D.H.; Wang, Y.T. Tuning of linear active disturbance rejection controllers based on step response curves. IEEE Access 2020, 8, 180869–180882. [Google Scholar] [CrossRef]
- Lin, D.F.; Wang, H.; Wang, J.; Fan, J.F. Autopilot Design and Guidance Law Analysis for Tactical Missiles, 1st ed.; Beijing Institute of Technology: Beijing, China, 2012; pp. 14–20, 57–58. [Google Scholar]
- Mohamed, E.M.; Yan, L. Design and comparison of two-loop with PI and three-loop autopilot for static unstable missile. Int. J. Electr. Comput. Eng. Syst. 2016, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Bahri, S. Longitudinal flight control laws for high aspect ratio light utility aircraft. J. Phys. Conf. Ser. 2018, 1130, 012026. [Google Scholar] [CrossRef]
- Efremov, A.V.; Mbikayi, Z.; Efremov, E.V. Comparative Study of Different Algorithms for a Flight Control System Design and the Potentiality of Their Integration with a Sidestick. Aerospace 2021, 8, 290. [Google Scholar] [CrossRef]
- Hirokawa, R.; Sato, K.; Manabe, S. Autopilot design for a missile with reaction-jet using coefficient diagram method. J. Syst. Eng. Electron. 2001, 4162, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.B.; Chen, X.H. Standard coefficient design method for multi-loops control system and its application. J. Syst. Eng. Electron. 2004, 12, 1852–1855. [Google Scholar]
- Coelho, J.P.; Pinho, T.M.; Boaventura, C.J. Controller system design using the coefficient diagram method. Arab. J. Sci. Eng. 2016, 41, 3663–3681. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).