Anti-Interception Guidance for Hypersonic Glide Vehicle: A Deep Reinforcement Learning Approach
Abstract
:1. Introduction
2. Problem Description
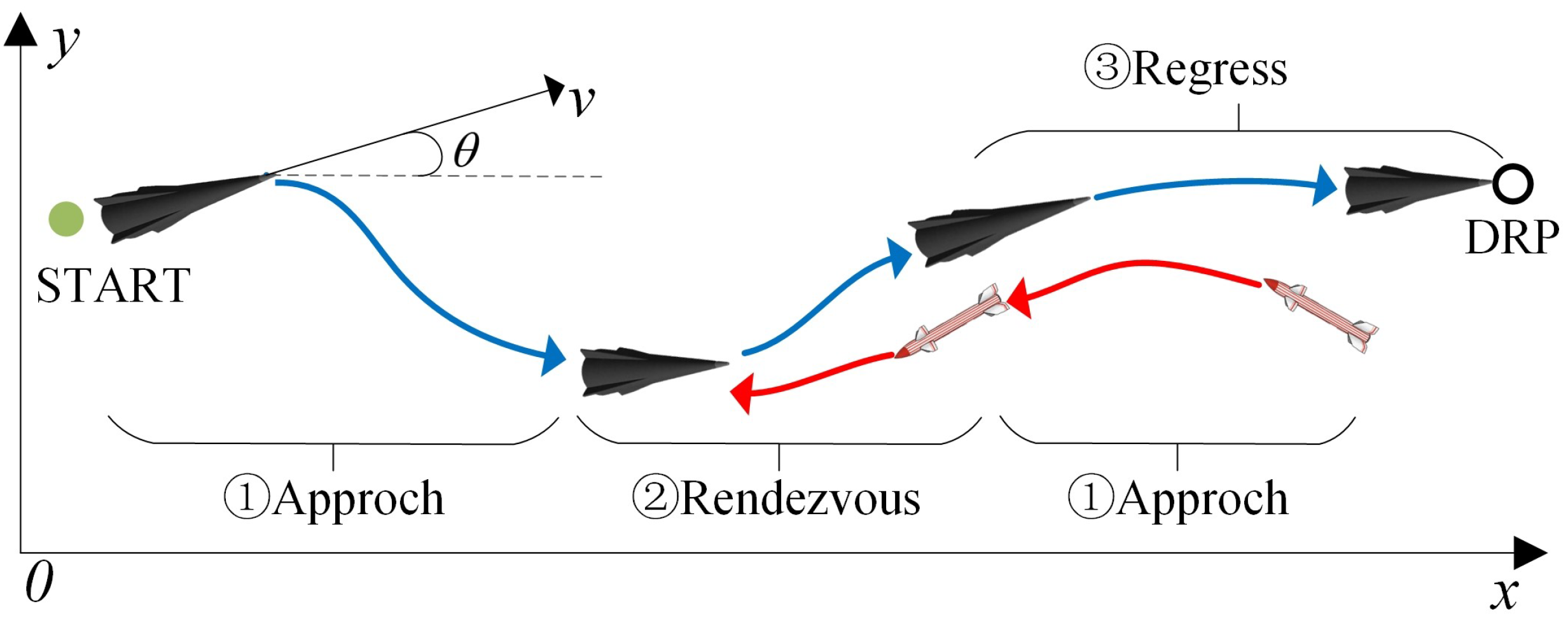
2.1. The Object of Anti-Interception Guidance
2.2. Markov Decision Process
3. Proposed Method
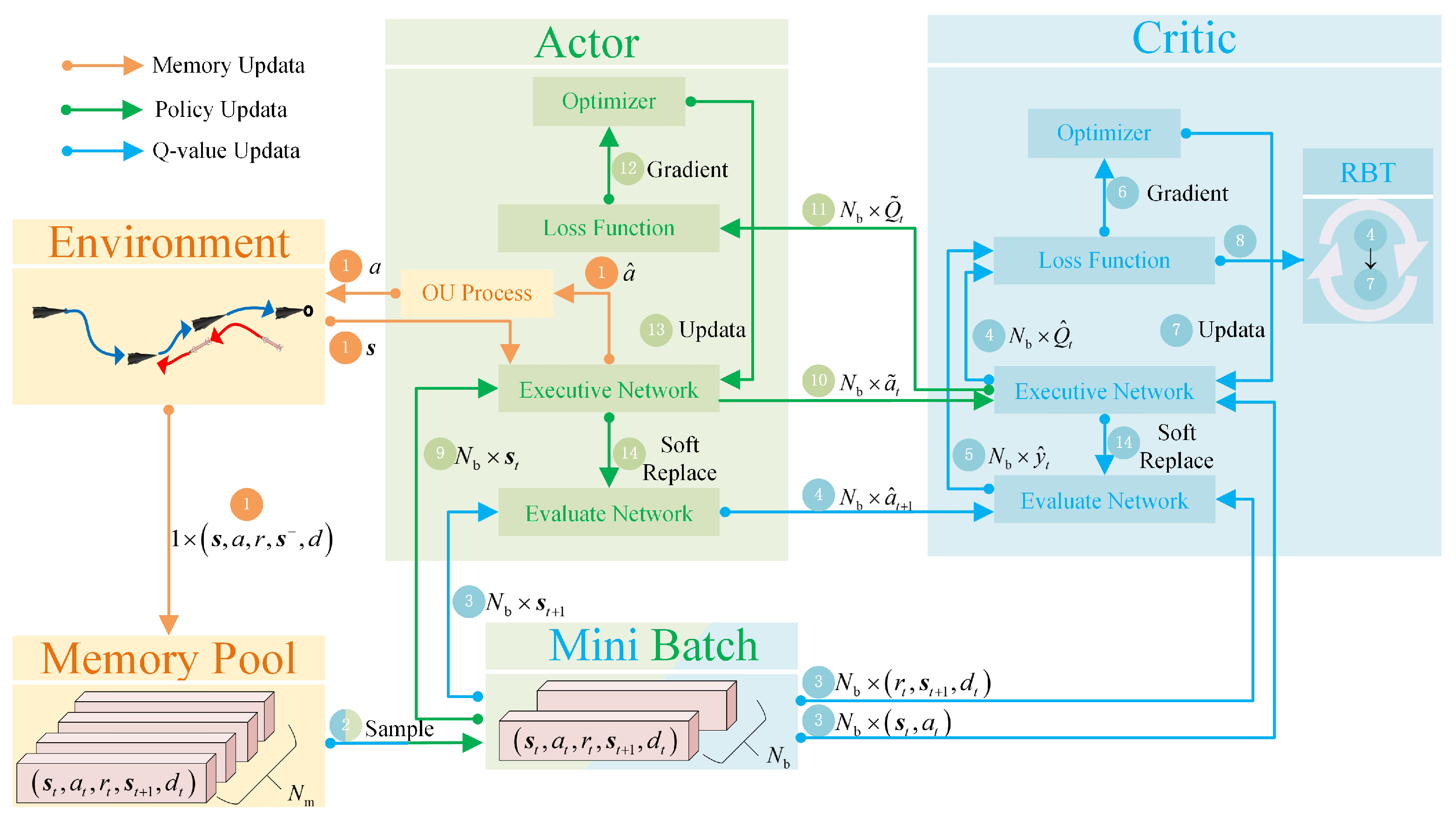
3.1. RBT-DDPG-Based Methods
| Algorithm 1 RBT-DDPG |
|
3.2. Scheme of DRL
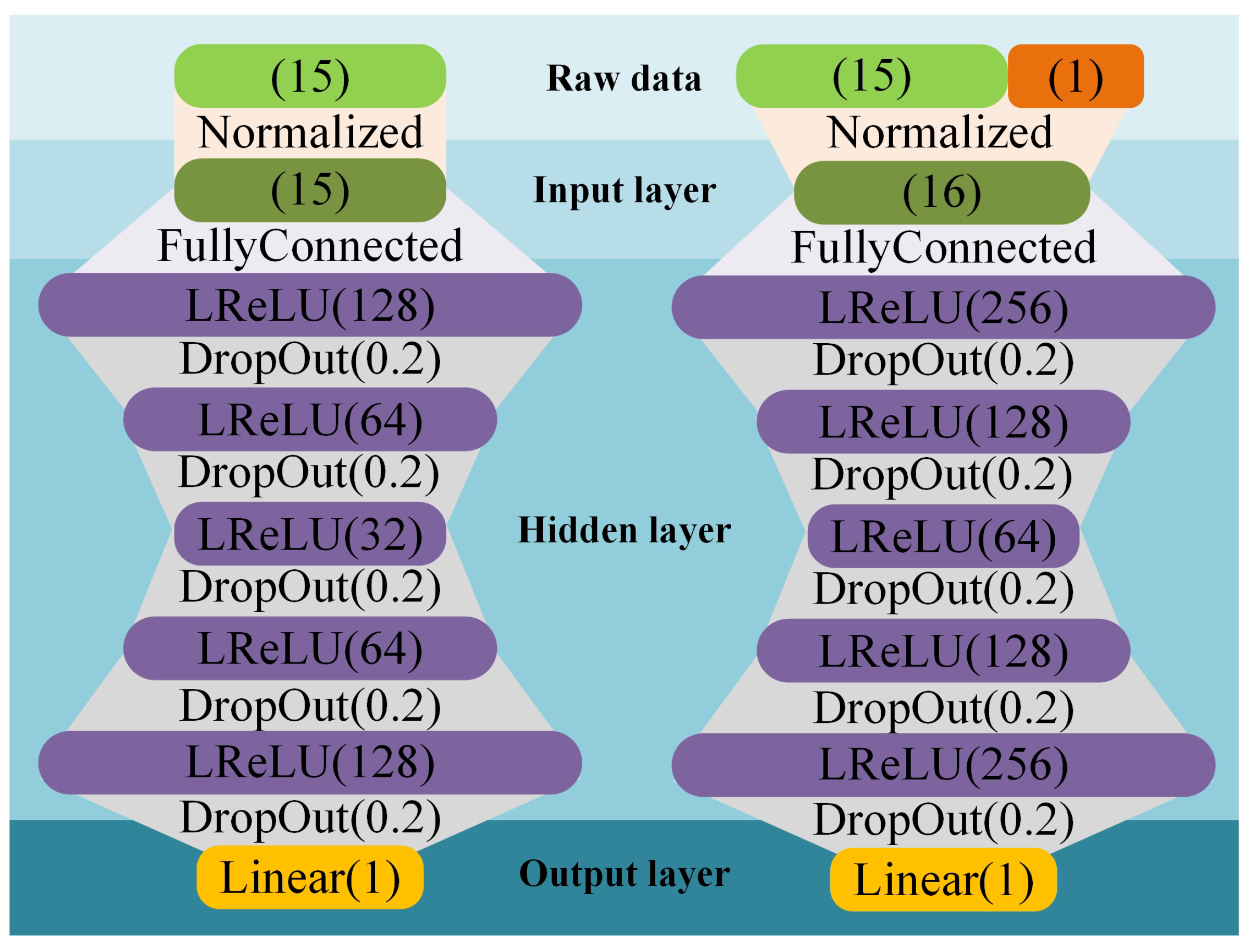
3.2.1. State Space
3.2.2. Action Space
3.2.3. Instant Reward Function
4. Training and Testing
4.1. Settings
4.1.1. Aircraft Settings
4.1.2. Hyperparameter Settings
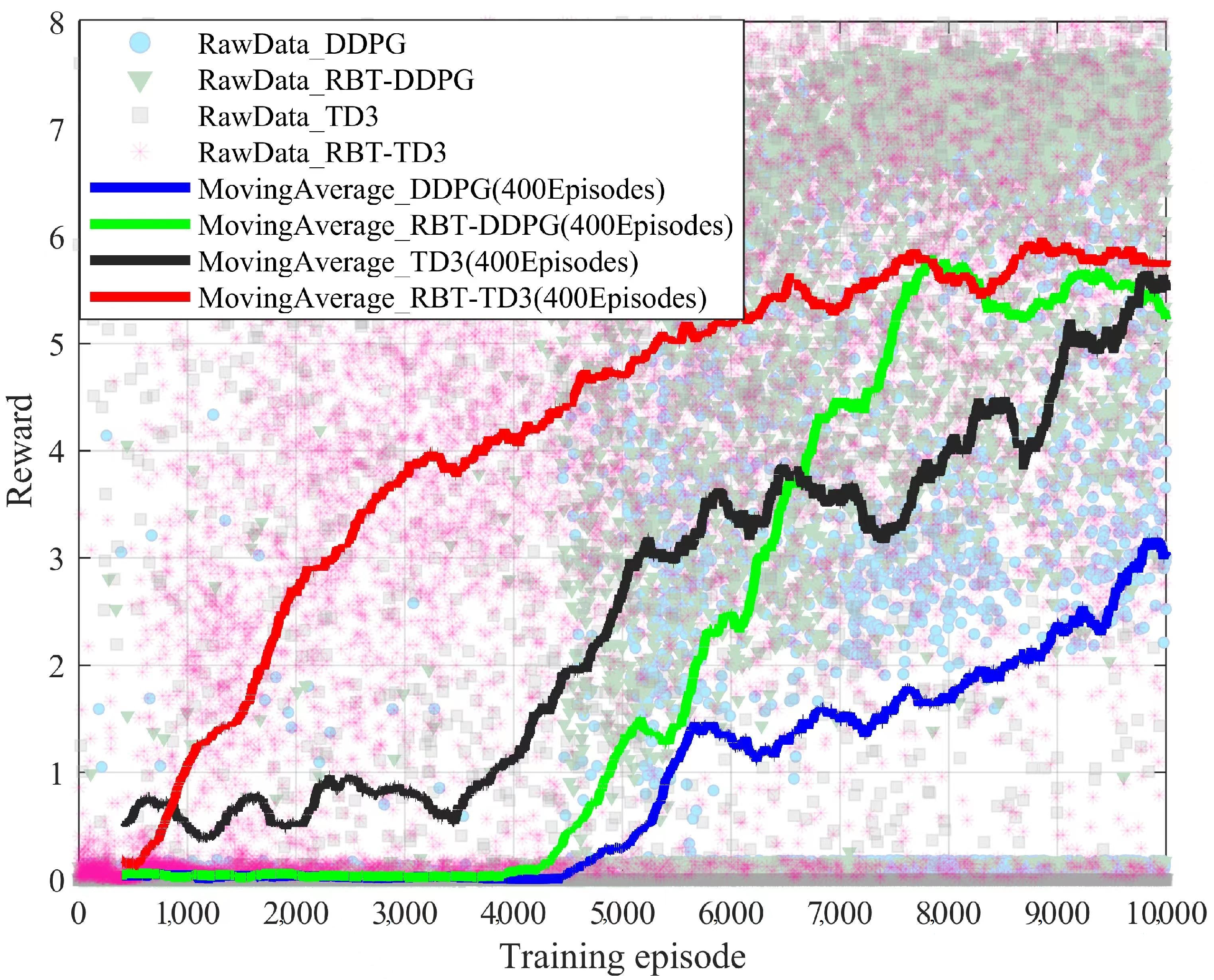
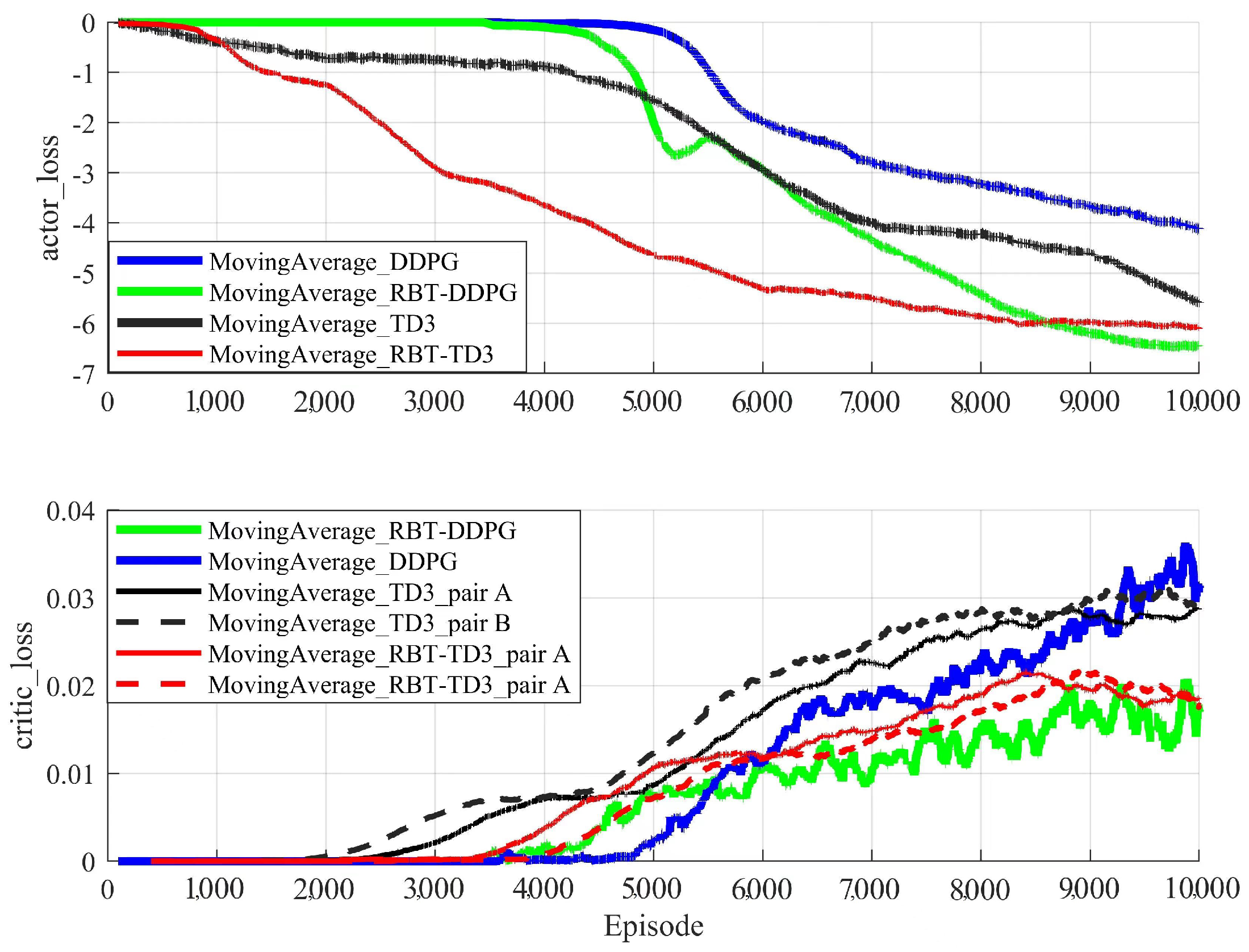
4.2. Training Results and Analysis
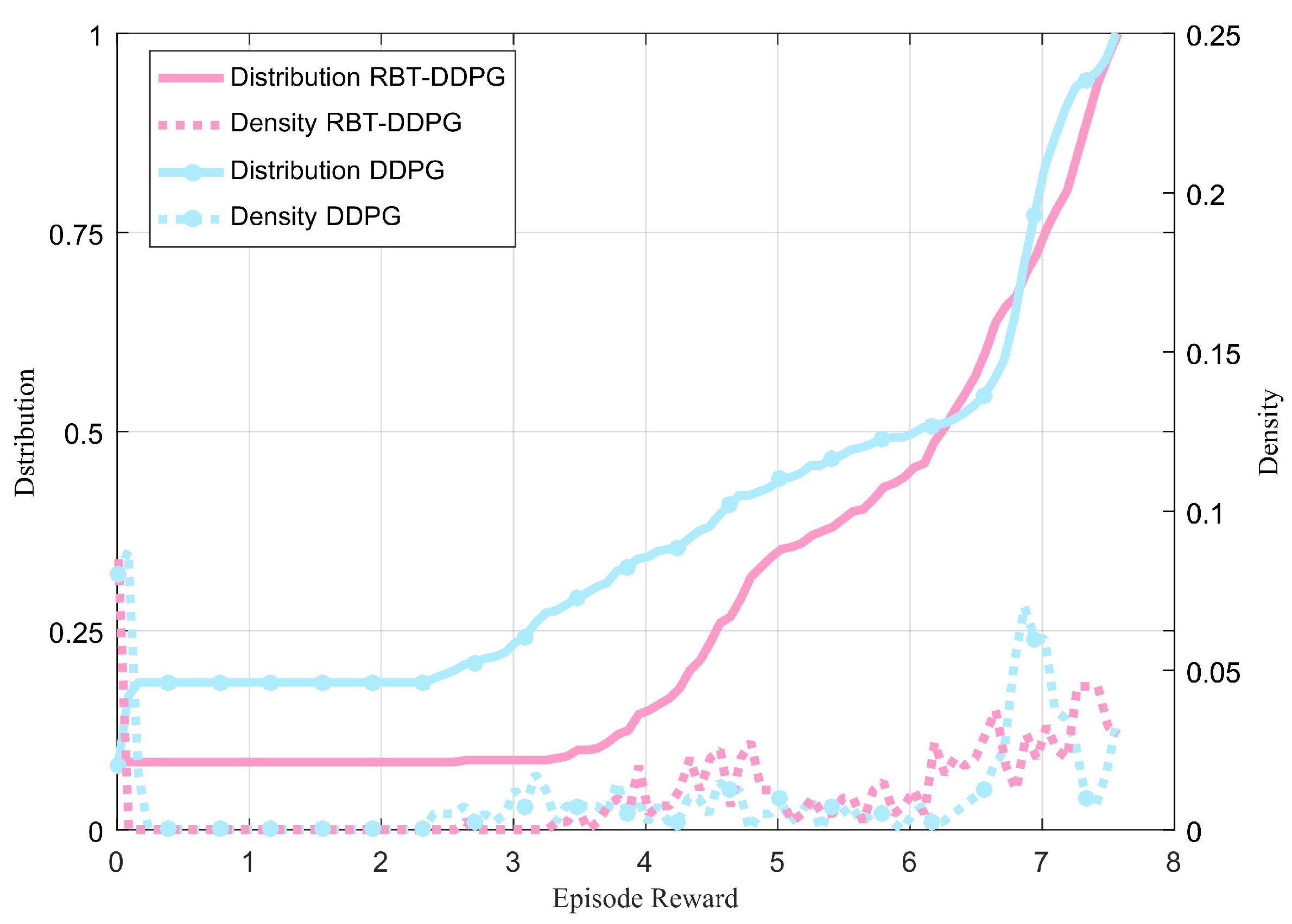
4.3. Test Results and Analysis
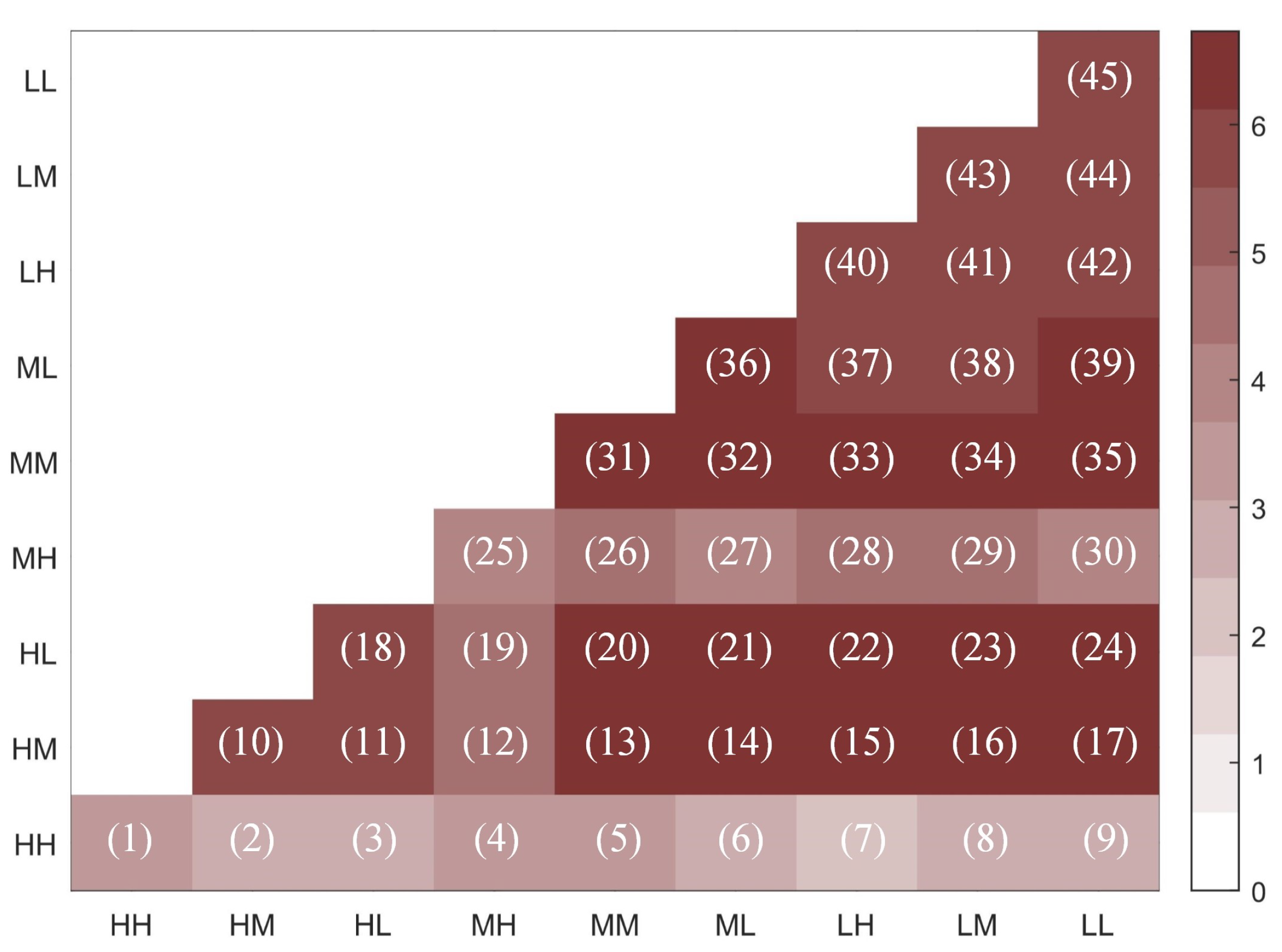
4.3.1. Monte Carlo Test
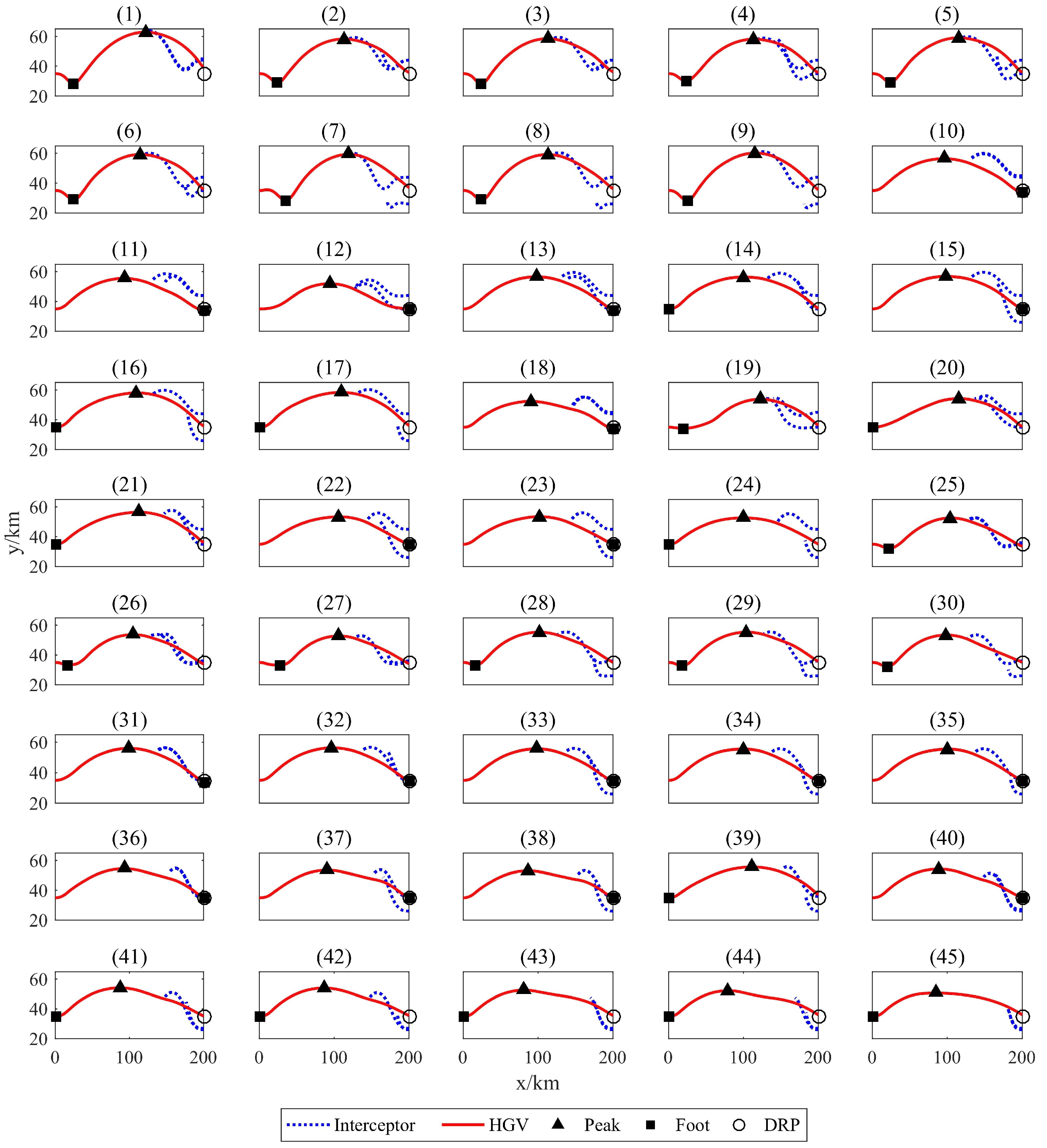
4.3.2. Analysis of Anti-Interception Strategies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Gao, Q.; Xie, J.; Qiao, Y.; Hu, X. Hypersonic vehicles against a guided missile: A defender triangle interception approach. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 2506–2509. [Google Scholar]
- Liu, K.F.; Meng, H.D.; Wang, C.J.; Li, J.; Chen, Y. Anti-Head-on Interception Penetration Guidance Law for Slide Vehicle. Mod. Def. Technol. 2008, 4, 39–45. [Google Scholar]
- Luo, C.; Huang, C.Q.; Ding, D.L.; Guo, H. Design of Weaving Penetration for Hypersonic Glide Vehicle. Electron. Opt. Control 2013, 7, 67–72. [Google Scholar]
- Zhu, Q.G.; Liu, G.; Xian, Y. Simulation of Reentry Maneuvering Trajectory of Tactical Ballistic Missile. Tactical Missile Technol. 2008, 1, 79–82. [Google Scholar]
- He, L.; Yan, X.D.; Tang, S. Guidance law design for spiral-diving maneuver penetration. Acta Aeronaut. Astronaut. Sin. 2019, 40, 188–202. [Google Scholar]
- Zhao, K.; Cao, D.Q.; Huang, W.H. Manoeuvre control of the hypersonic gliding vehicle with a scissored pair of control moment gyros. Sci. China Technol. 2018, 61, 1150–1160. [Google Scholar] [CrossRef]
- Zhao, X.; Qin, W.W.; Zhang, X.S.; He, B.; Yan, X. Rapid full-course trajectory optimization for multi-constraint and multi-step avoidance zones. J. Solid Rocket. Technol. 2019, 42, 245–252. [Google Scholar]
- Wang, P.; Yang, X.L.; Fu, W.X.; Qiang, L. An On-board Reentry Trajectory Planning Method with No-fly Zone Constraints. Missiles Space Vechicles 2016, 2, 1–7. [Google Scholar]
- Fang, X.L.; Liu, X.X.; Zhang, G.Y.; Wang, F. An analysis of foreign ballistic missile manoeuvre penetration strategies. Winged Missiles J. 2011, 12, 17–22. [Google Scholar]
- Sun, S.M.; Tang, G.J.; Zhou, Z.B. Research on Penetration Maneuver of Ballistic Missile Based on Differential Game. J. Proj. Rocket. Missiles Guid. 2010, 30, 65–68. [Google Scholar]
- Imado, F.; Miwa, S. Fighter evasive maneuvers against proportional navigation missile. J. Aircr. 1986, 23, 825–830. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, P.; Tang, Q. The Method of the Impulse Trajectory Transfer in a Different Plane for the Ballistic Missile Penetrating Missile Defense System in the Passive Ballistic Curve. J. Astronaut. 2008, 29, 89–94. [Google Scholar]
- Wu, Q.X.; Zhang, W.H. Research on Midcourse Maneuver Penetration of Ballistic Missile. J. Astronaut. 2006, 27, 1243–1247. [Google Scholar]
- Zhang, K.N.; Zhou, H.; Chen, W.C. Trajectory Planning for Hypersonic Vehicle With Multiple Constraints and Multiple Manoeuvreing Penetration Strategies. J. Ballist. 2012, 24, 85–90. [Google Scholar]
- Xian, Y.; Tian, H.P.; Wang, J.; Shi, J.Q. Research on intelligent manoeuvre penetration of missile based on differential game theory. Flight Dyn. 2014, 32, 70–73. [Google Scholar]
- Sun, J.L.; Liu, C.S. An Overview on the Adaptive Dynamic Programming Based Missile Guidance Law. Acta Autom. Sin. 2017, 43, 1101–1113. [Google Scholar]
- Sun, J.L.; Liu, C.S. Distributed Fuzzy Adaptive Backstepping Optimal Control for Nonlinear Multimissile Guidance Systems with Input Saturation. IEEE Trans. Fuzzy Syst. 2019, 27, 447–461. [Google Scholar]
- Sun, J.L.; Liu, C.S. Backstepping-based adaptive dynamic programming for missile-target guidance systems with state and input constraints. J. Frankl. Inst. 2018, 355, 8412–8440. [Google Scholar] [CrossRef]
- Wang, F.; Cui, N.G. Optimal Control of Initiative Anti-interception Penetration Using Multistage Hp-Adaptive Radau Pseudospectral Method. In Proceedings of the 2015 2nd International Conference on Information Science and Control Engineering, Shanghai, China, 24–26 April 2015. [Google Scholar]
- Liu, Y.; Yang, Z.; Sun, M.; Chen, Z. Penetration design for the boost phase of near space aircraft. In Proceedings of the 2017 36th Chinese Control Conference, Dalian, China, 26–28 July 2017. [Google Scholar]
- Marcus, G. Innateness, alphazero, and artificial intelligence. arXiv 2018, arXiv:1801.05667. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Osband, I.; Blundell, C.; Pritzel, A.; Van Roy, B. Deep Exploration via Bootstrapped DQN. arXiv 2016, arXiv:1602.04621. [Google Scholar]
- Chen, J.W.; Cheng, Y.H.; Jiang, B. Mission-Constrained Spacecraft Attitude Control System On-Orbit Reconfiguration Algorithm. J. Astronaut. 2017, 38, 989–997. [Google Scholar]
- Dong, C.; Deng, Y.B.; Luo, C.C.; Tang, X. Compression Artifacts Reduction by a Deep Convolutional Network. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Fu, X.W.; Wang, H.; Xu, Z. Research on Cooperative Pursuit Strategy for Multi-UAVs based on DE-MADDPG Algorithm. Acta Aeronaut. Astronaut. Sin. 2021, 42, 311–325. [Google Scholar]
- Brian, G.; Kris, D.; Roberto, F. Adaptive Approach Phase Guidance for a Hypersonic Glider via Reinforcement Meta Learning. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Wen, H.; Li, H.; Wang, Z.; Hou, X.; He, K. Application of DDPG-based Collision Avoidance Algorithm in Air Traffic Control. In Proceedings of the ISCID 2019: IEEE 12th International Symposium on Computational Intelligence and Design, Hangzhou, China, 14 December 2020. [Google Scholar]
- Lin, G.; Zhu, L.; Li, J.; Zou, X.; Tang, Y. Collision-free path planning for a guava-harvesting robot based on recurrent deep reinforcement learning. Comput. Electron. Agric. 2021, 188, 106350. [Google Scholar] [CrossRef]
- Lin, Y.; Mcphee, J.; Azad, N.L. Anti-Jerk On-Ramp Merging Using Deep Reinforcement Learning. In Proceedings of the IVS 2020: IEEE Intelligent Vehicles Symposium, Las Vegas, NV, USA, 19 October–13 November 2020. [Google Scholar]
- Xu, X.L.; Cai, P.; Ahmed, Z.; Yellapu, V.S.; Zhang, W. Path planning and dynamic collision avoidance algorithm under COLREGs via deep reinforcement learning. Neurocomputing 2021, 468, 181–197. [Google Scholar] [CrossRef]
- Lei, H.M. Principles of Missile Guidance and Control. Control Technol. Tactical Missile 2007, 15, 162–164. [Google Scholar]
- Cheng, T.; Zhou, H.; Dong, X.F.; Cheng, W.C. Differential game guidance law for integration of penetration and strike of multiple flight vehicles. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 898–909. [Google Scholar]
- Zhao, J.S.; Gu, L.X.; Ma, H.Z. A rapid approach to convective aeroheating prediction of hypersonic vehicles. Sci. China Technol. Sci. 2013, 56, 2010–2024. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Liu, R.Z.; Wang, W.; Shen, Y.; Li, Z.; Yu, Y.; Lu, T. An Introduction of mini-AlphaStar. arXiv 2021, arXiv:2104.06890. [Google Scholar]
- Deka, A.; Luo, W.; Li, H.; Lewis, M.; Sycara, K. Hiding Leader’s Identity in Leader-Follower Navigation through Multi-Agent Reinforcement Learning. arXiv 2021, arXiv:2103.06359. [Google Scholar]
- Xiong, J.-H.; Tang, S.-J.; Guo, J.; Zhu, D.-L. Design of Variable Structure Guidance Law for Head-on Interception Based on Variable Coefficient Strategy. Acta Armamentarii 2014, 35, 134–139. [Google Scholar]
- Jiang, L.; Nan, Y.; Li, Z.H. Realizing Midcourse Penetration With Deep Reinforcement Learning. IEEE Access 2021, 9, 89812–89822. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.P.; Chen, D.Q.; Liang, S.Y.; Ma, H. Maneuvering target tracking of UAV based on MN-DDPG and transfer learning. Def. Technol. 2021, 17, 457–466. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R. Terminal guidance for a hypersonic vehicle with impact time control. J. Guid. Control Dyn. 2018, 41, 1790–1798. [Google Scholar] [CrossRef]
- Ge, L.Q. Cooperative Guidance for Intercepting Multiple Targets by Multiple Air-to-Air Missiles. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2019. [Google Scholar]
- Cruz, F.; Parisi, G.I.; Twiefel, J.; Wermter, S. Multi-modal integration of dynamic audiovisual patterns for an interactive reinforcement learning scenario. In Proceedings of the RSJ 2016: IEEE International Conference on Intelligent Robots & Systems, Daejeon, Korea, 9–14 October 2016. [Google Scholar]
- Bignold, A.; Cruz, F.; Dazeley, R.; Vamplew, P.; Foale, C. Human engagement providing evaluative and informative advice for interactive reinforcement learning. Neural Comput. Appl. 2022. [Google Scholar] [CrossRef]

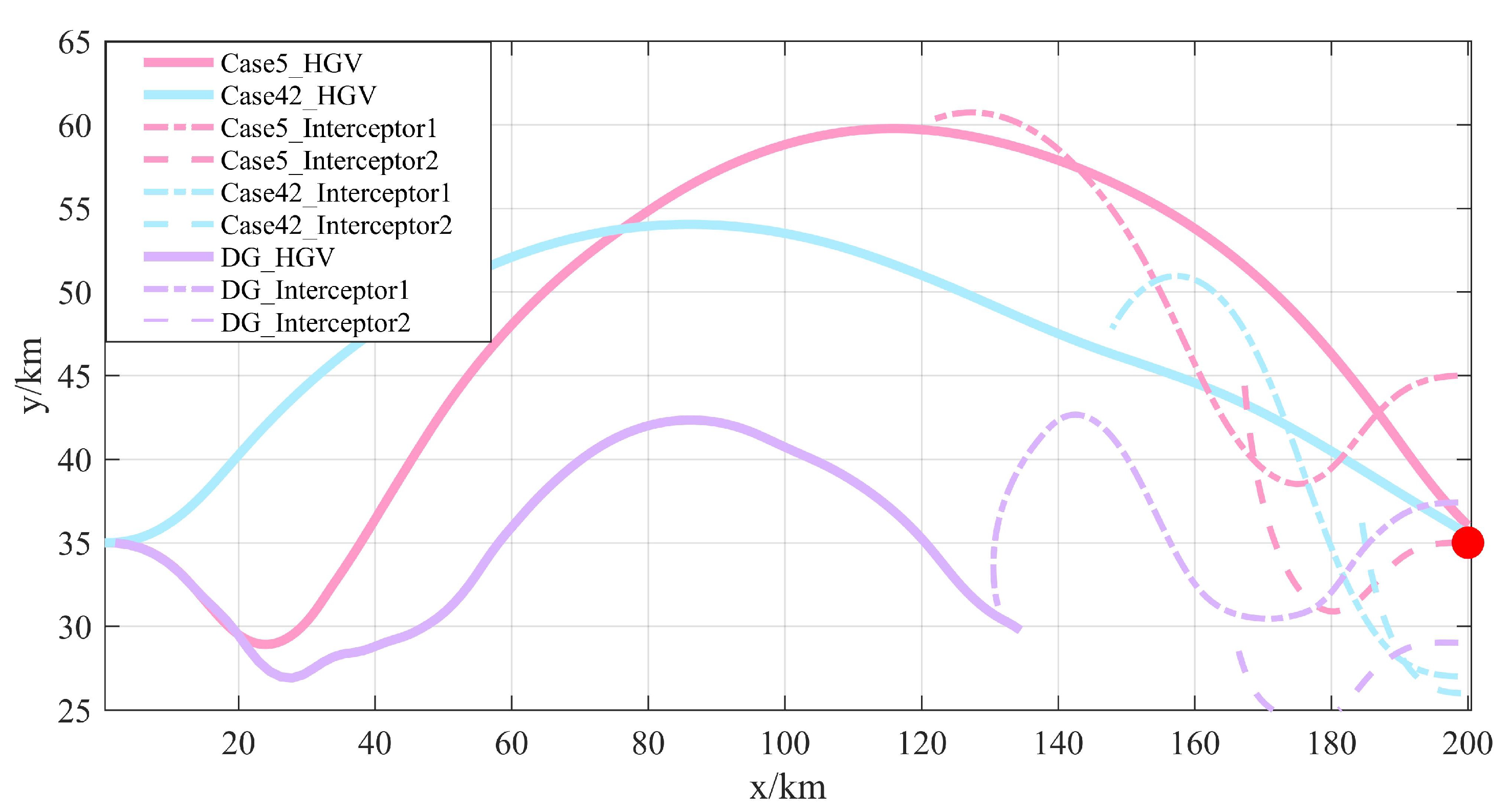
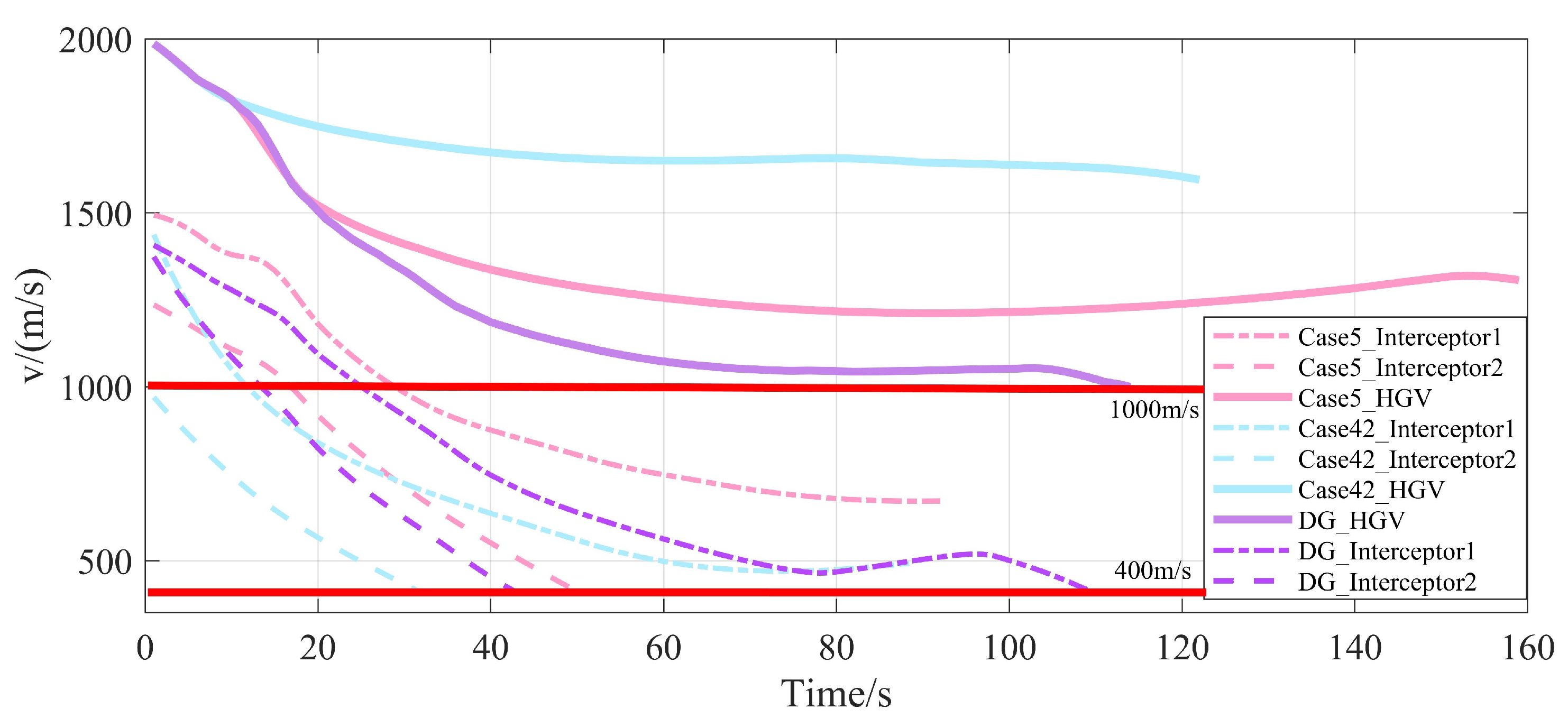

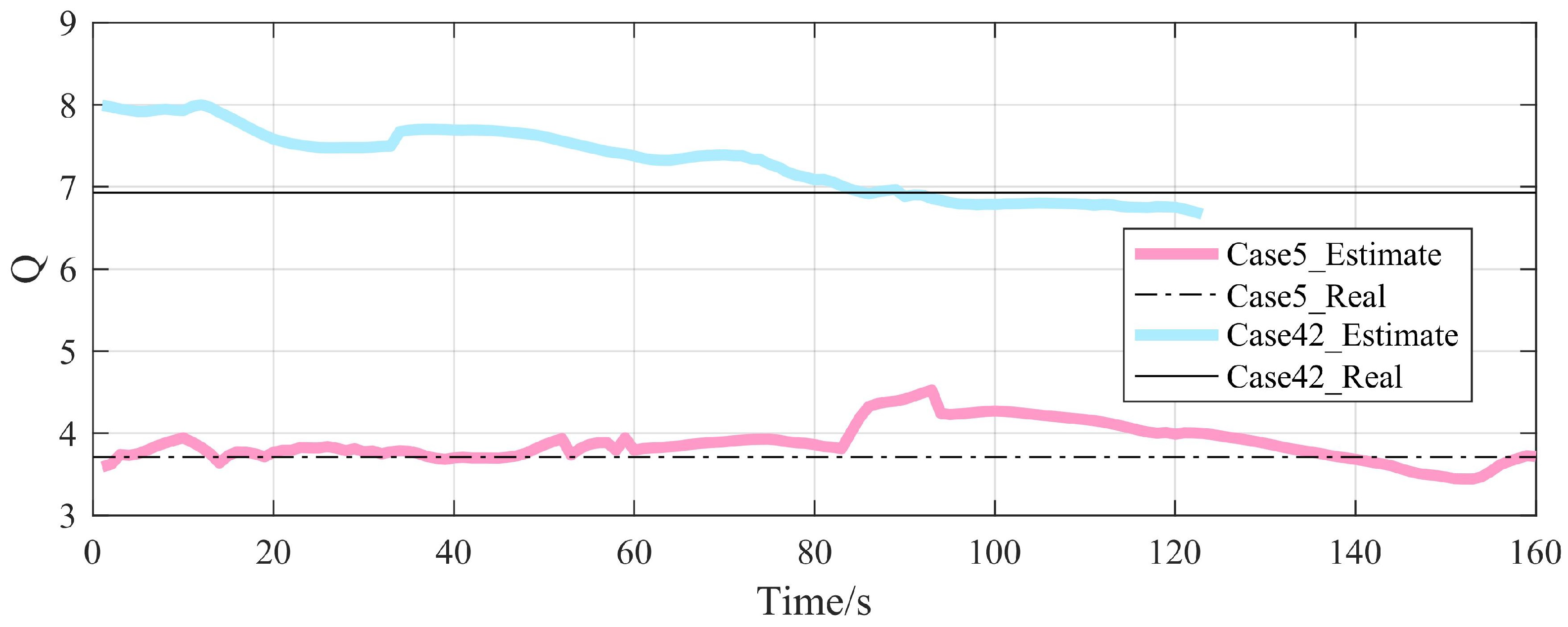

| Parameter | Interceptor | HGV |
|---|---|---|
| Mass/kg | 75 | 500 |
| Reference area/m | 0.3 | 0.579 |
| Minimum velocity/(m/s) | 400 | 1000 |
| Available AoA/° | −20∼20 | −10∼10 |
| Time constant of Attitude Control System/s | 0.1 | 1 |
| Initial coordinate x/km | 200 | 0 |
| Initial coordinate y/km | Random | 35 |
| Initial velocity/(km/s) | Random | 2000 |
| Initial inclination/° | 0 | 0 |
| Coordinate x of the DRP/km | - | 200 |
| Coordinate y of the DRP/km | - | 35 |
| Kill radius/m | 300 | - |
| Parameter | Value |
|---|---|
| /s | |
| /s | 1 |
| 1 | |
| in RBT-DDPG | |
| in RBT-TD3 | |
| in RBT-DDPG | |
| in RBT-DDPG | |
| in RBT-DDPG | |
| in RBT-TD3 | |
| Weight initialization | |
| Bias initialization | |
| Algorithm | Anti-Interception Success Rate | /m | /(m/s) |
|---|---|---|---|
| DDPG | 79.74% | 1425.62 | 1377.17 |
| RBT-DDPG | 91.48% | 1514.44 | 1453.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Nan, Y.; Zhang, Y.; Li, Z. Anti-Interception Guidance for Hypersonic Glide Vehicle: A Deep Reinforcement Learning Approach. Aerospace 2022, 9, 424. https://doi.org/10.3390/aerospace9080424
Jiang L, Nan Y, Zhang Y, Li Z. Anti-Interception Guidance for Hypersonic Glide Vehicle: A Deep Reinforcement Learning Approach. Aerospace. 2022; 9(8):424. https://doi.org/10.3390/aerospace9080424
Chicago/Turabian StyleJiang, Liang, Ying Nan, Yu Zhang, and Zhihan Li. 2022. "Anti-Interception Guidance for Hypersonic Glide Vehicle: A Deep Reinforcement Learning Approach" Aerospace 9, no. 8: 424. https://doi.org/10.3390/aerospace9080424
APA StyleJiang, L., Nan, Y., Zhang, Y., & Li, Z. (2022). Anti-Interception Guidance for Hypersonic Glide Vehicle: A Deep Reinforcement Learning Approach. Aerospace, 9(8), 424. https://doi.org/10.3390/aerospace9080424






