A Prognostic and Health Management Framework for Aero-Engines Based on a Dynamic Probability Model and LSTM Network
Abstract
:1. Introduction
2. PHM Basic Theory
2.1. Probability Modeling
2.1.1. GMM-ADPC Algorithm
2.1.2. Probability Difference Measuring Method
2.2. Long Short-Term Memory Networks
- Information forgetting. The states removed from the previous long-term state are controlled by the forget gate . The can be described by Equation (9).where is the sigmoid function, is the previous current time, is the weight vectors, is the bias term of the forget gate, and “” means matrix multiplication.
- Long-term state updating. The input gate layer determines what values will be updated. The input gate and candidate value vector are expressed by Equations (10) and (11).where are the weight vectors, and are bias terms.
- 3.
- Short-term state updating. The function of the output gate is to change the long-term state to the short-term state. Equation (13) describes the output gate .
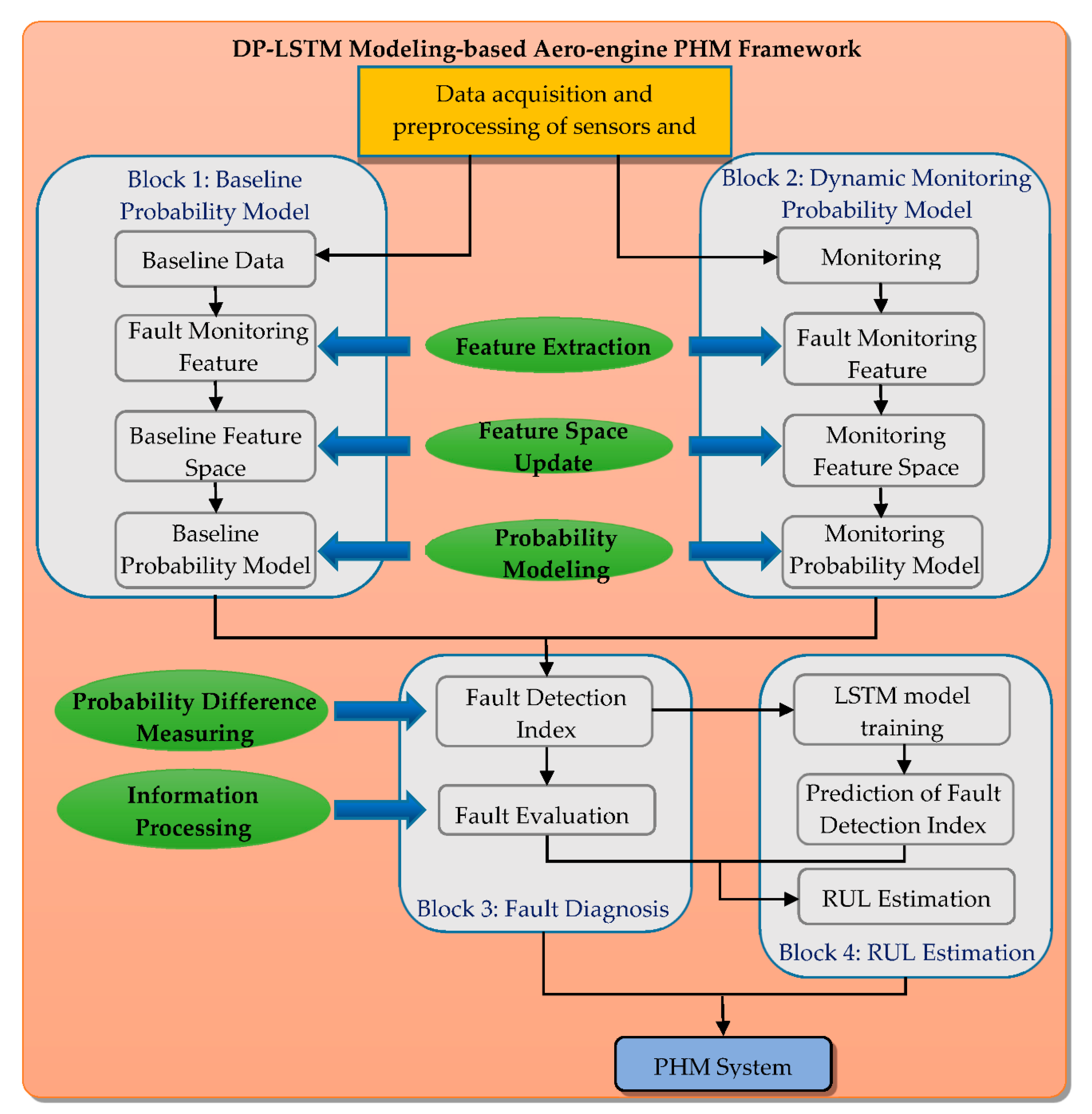
3. Design of the Aero-Engine PHM Framework
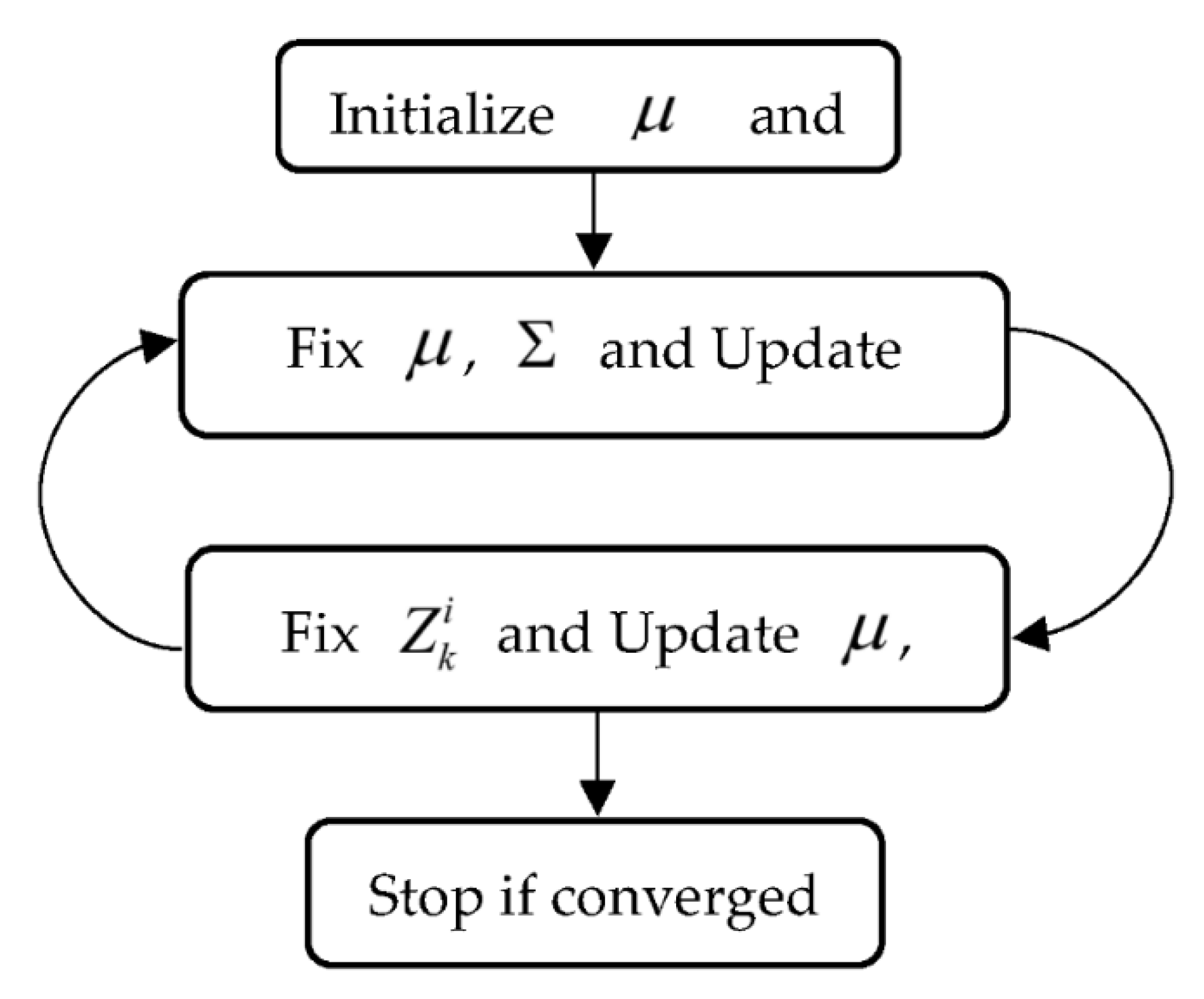
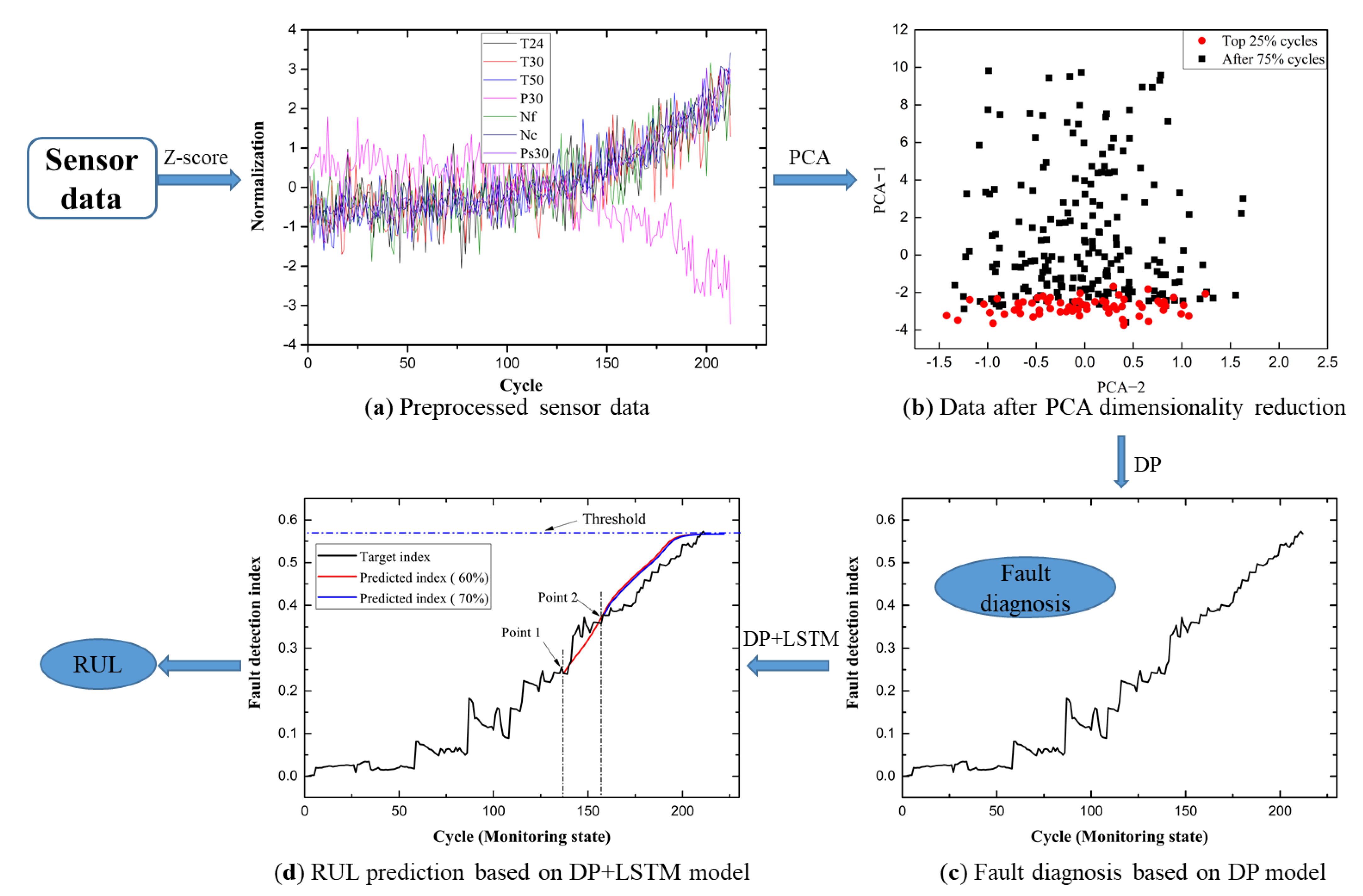
3.1. DP Model for Fault Monitoring
3.2. Combining the DP Model and LSTM for the PHM Framework
4. Results and Discussions
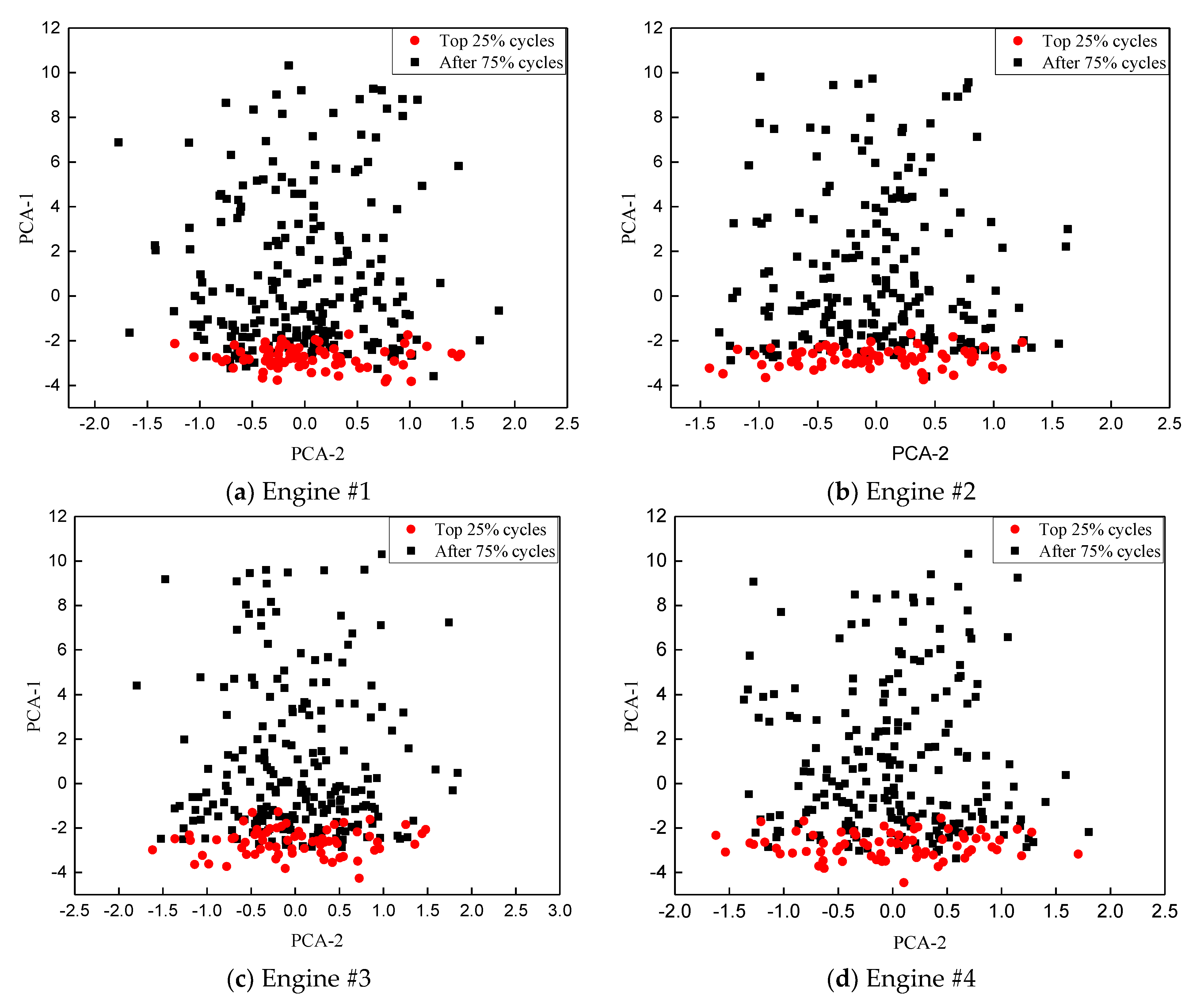
4.1. Data Sets Characterization
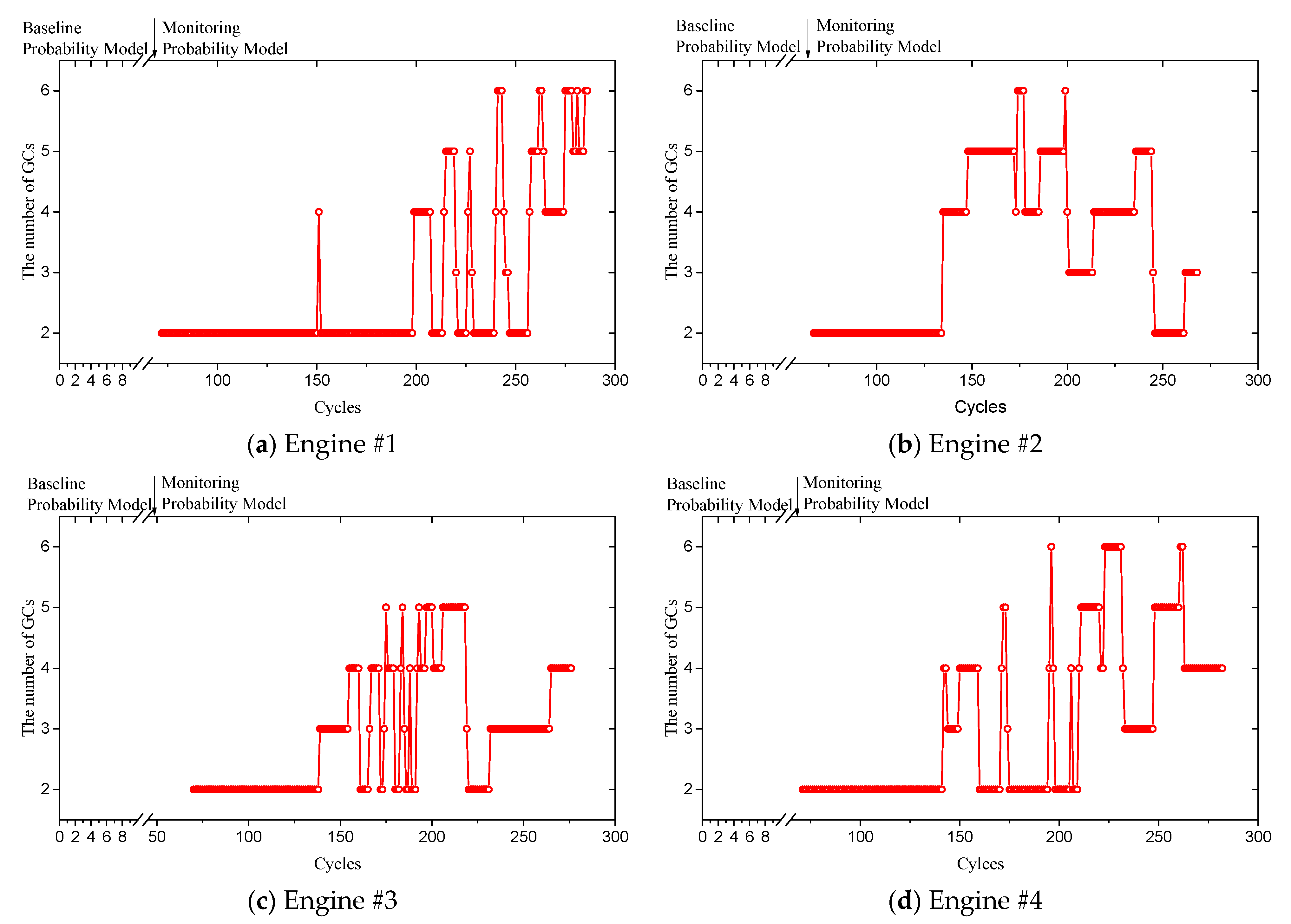
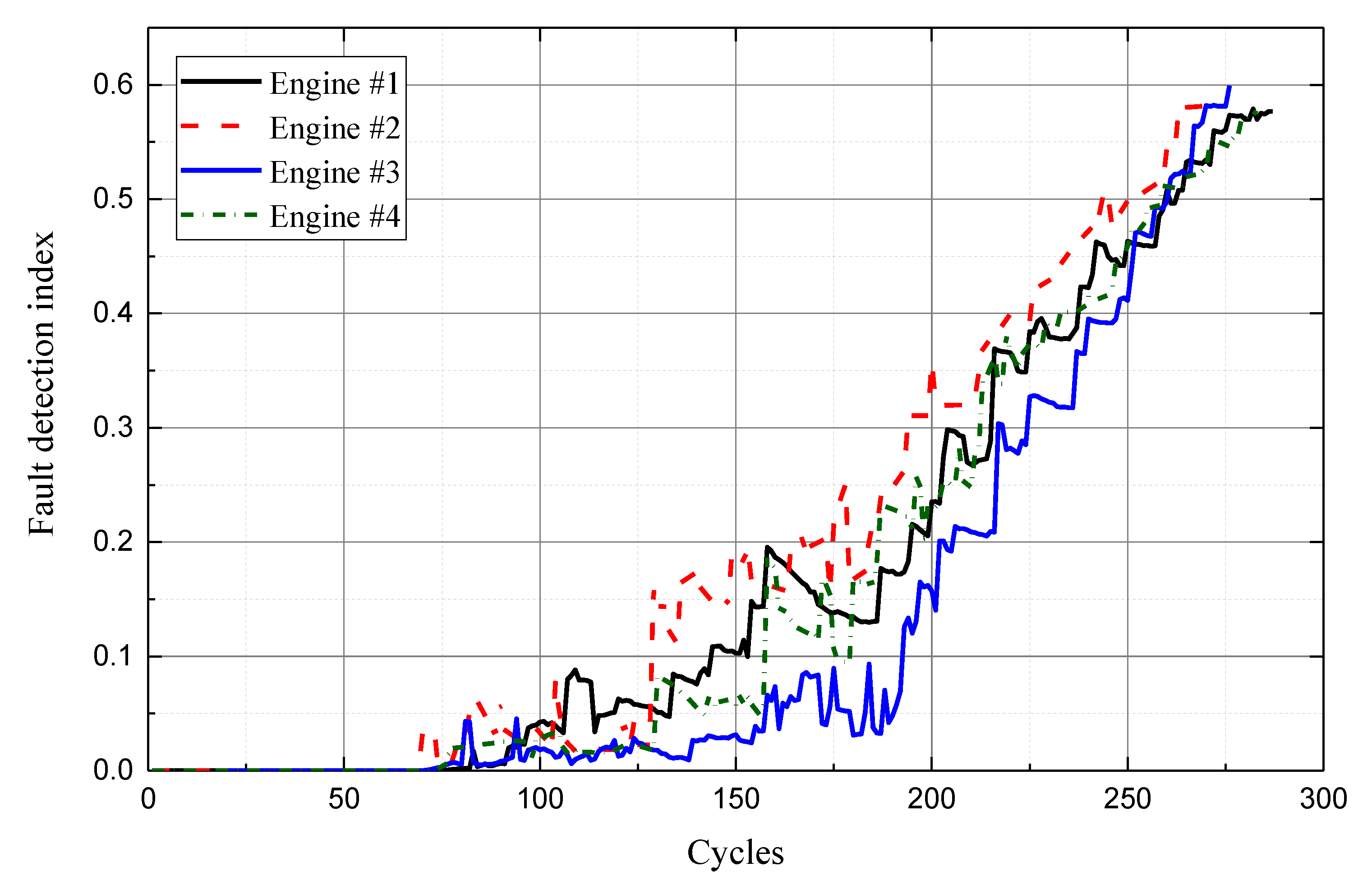
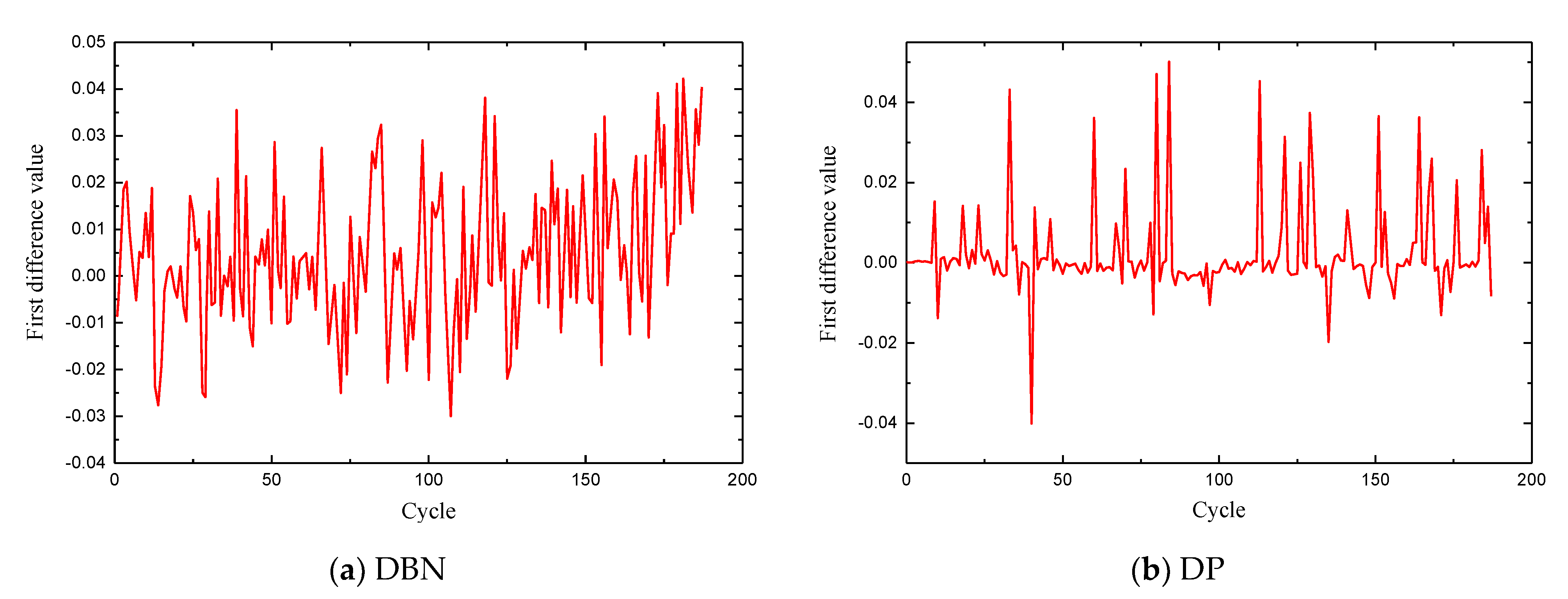
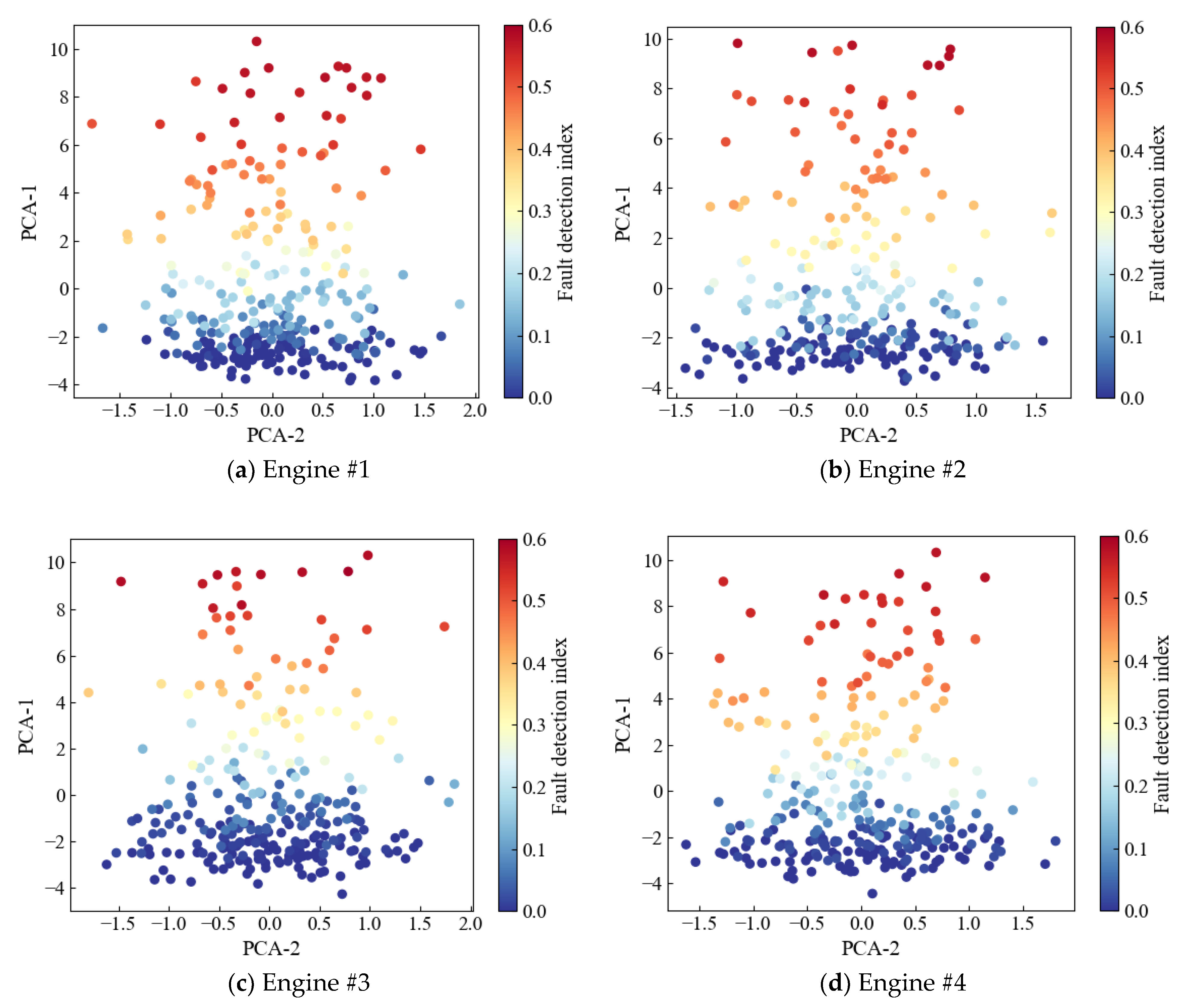
4.2. Fault Diagnosis
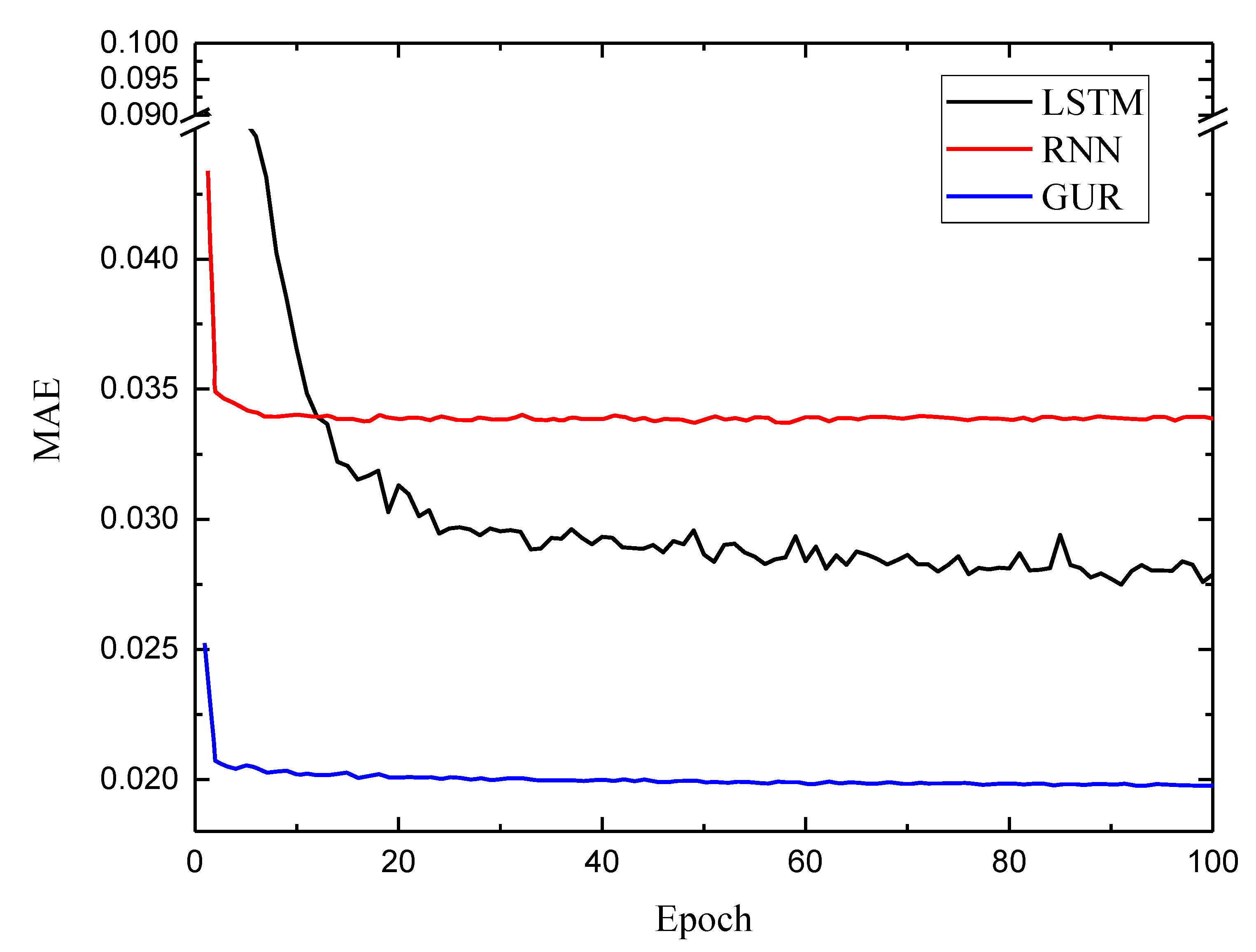
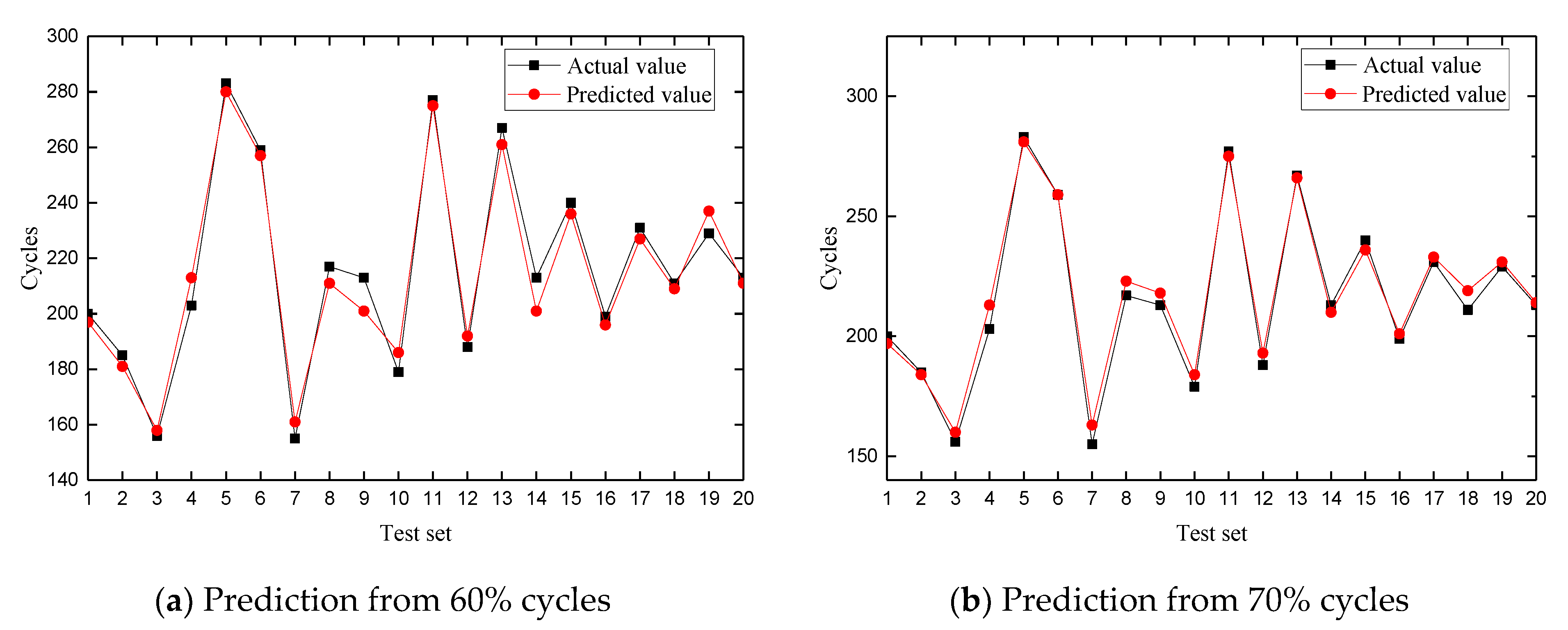
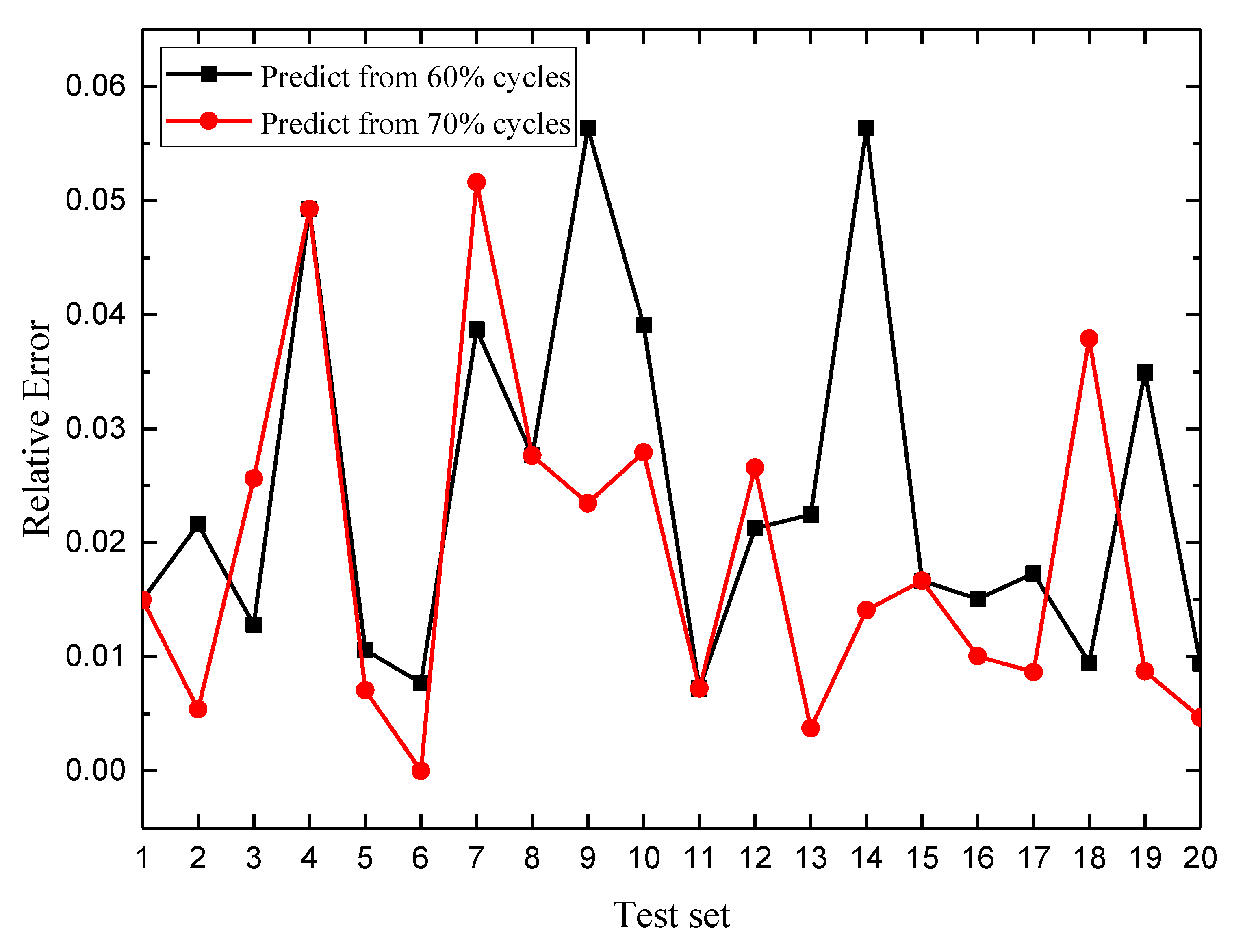
4.3. RUL Estimation
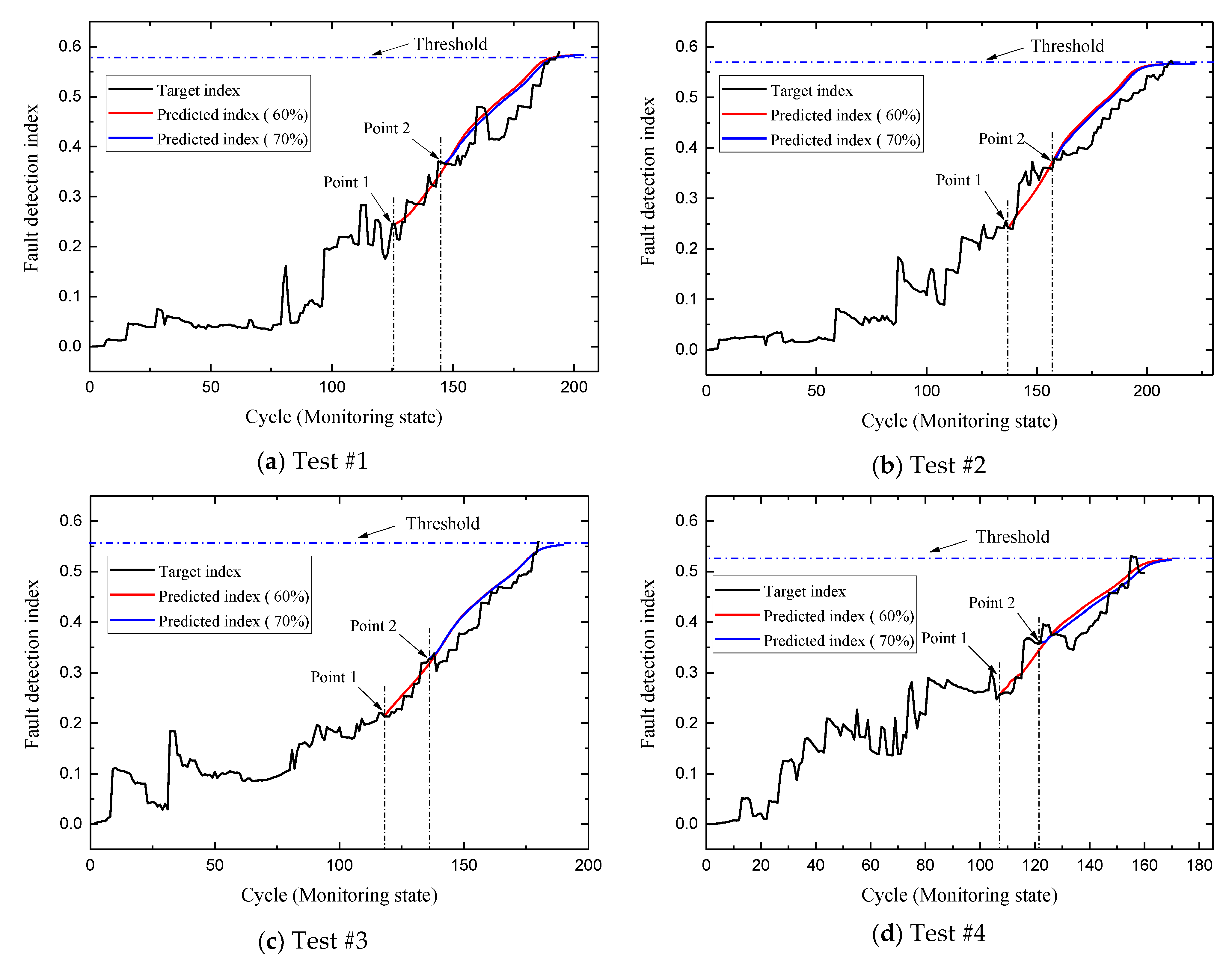
4.4. PHM Application Example
| Algorithm 1. PHM framework process. |
| Input: Aero-engine raw sensor data. Process 1: Data preprocessing
|
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ADPC | adaptive density peaks clustering | HPT | high pressure turbine |
| ANN | artificial neural network | LPC | low pressure compressor |
| BP | back propagation | LPT | low pressure turbine |
| C-MAPSS | commercial modular aero-propulsion system simulation | LSTM | long short-term memory neural network |
| DBN | deep belief network | MAE | mean absolute error |
| DP | dynamic probability | MSE | mean squared error |
| EM | expectation-maximization | PHM | prognostics and health management |
| FMF | fault monitoring feature | PCA | principal component analysis |
| GRU | gated recurrent unit | RNN | recurrent neural network |
| GC | Gaussian component | RUL | remaining useful life |
| GMM | Gaussian mixture model | SHM | structural health monitoring |
| HHT | Hilbert-Huang transform | SVM | support vector machine |
| HPC | high pressure compressor |
References
- Che, C.; Wang, H.; Fu, Q.; Ni, X. Combining multiple deep learning algorithms for prognostic and health management of aircraft. Aerosp. Sci. Technol. 2019, 94, 105423. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, G.; Tao, J.; Hu, Y.; Yuan, L. A modified fusion model-based/data-driven model for sensor fault diagnosis and performance degradation estimation of aero-engine. Meas. Sci. Technol. 2022, 33, 085105. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, C.; Zhang, Q.; Wang, J.; Wang, Y.; Shi, Y.; Lin, C.; Jin, Y. A Method for Aero-Engine Gas Path Anomaly Detection Based on Markov Transition Field and Multi-Lstm. Aerospace 2021, 8, 374. [Google Scholar] [CrossRef]
- Tolani, D.; Yasar, M.; Chin, S.; Ray, A. Anomaly detection for health management of aircraft gas turbine engines. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 459–464. [Google Scholar]
- Fornlöf, V.; Galar, D.; Syberfeldt, A.; Almgren, T. RUL estimation and maintenance optimization for aircraft engines: A system of system approach. Int. J. Syst. Assur. Eng. Manag. 2016, 7, 450–461. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, W.; Huang, J.; Lu, F.; Chen, Z. A Novel Performance Adaptation and Diagnostic Method for Aero-Engines Based on the Aerothermodynamic Inverse Model. Aerospace 2022, 9, 16. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H.; Dong, X.; Zhou, Q.; Chen, H.; Tan, C. Unscented Kalman-filter-based simultaneous diagnostic scheme for gas-turbine gas path and sensor faults. Meas. Sci. Technol. 2021, 9, 49. [Google Scholar] [CrossRef]
- Baumann, M.; Koch, C.; Staudacher, S. Application of Neural Networks and Transfer Learning to Turbomachinery Heat Transfer. Aerospace 2022, 9, 49. [Google Scholar] [CrossRef]
- Zaccaria, V.; Fentaye, A.D.; Stenfelt, M.; Kyprianidis, K.G. Probabilistic Model for Aero-Engines Fleet Condition Monitoring. Aerospace 2020, 7, 66. [Google Scholar] [CrossRef]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Lu, F.; Wu, J.; Huang, J.; Qiu, X. Aircraft engine degradation prognostics based on logistic regression and novel OS-ELM algorithm. Aerosp. Sci. Technol. 2019, 84, 661–671. [Google Scholar] [CrossRef]
- Ochella, S.; Shafiee, M.; Sansom, C. Adopting machine learning and condition monitoring P-F curves in determining and prioritizing high-value assets for life extension. Expert Syst. Appl. 2021, 176, 114897. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Song, F.Q.; Pan, Y.T.; Li, B. Retargeting extreme learning machines for classification and their applications to fault diagnosis of aircraft engine. Aerosp. Sci. Technol. 2017, 71, 603–618. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Ul-Haq Gilani, S.I.; Baheta, A.T.; Li, Y.G. Performance-based fault diagnosis of a gas turbine engine using an integrated support vector machine and artificial neural network method. Proc. Inst. Mech. Eng. Part A J. Power Energy 2019, 233, 786–802. [Google Scholar] [CrossRef]
- Li, Y.; Du, X.; Wan, F.; Wang, X.; Yu, H. Rotating machinery fault diagnosis based on convolutional neural network and infrared thermal imaging. Chin. J. Aeronaut. 2020, 33, 427–438. [Google Scholar] [CrossRef]
- Soualhi, A.; Clerc, G.; Razik, H.; Guillet, F. Hidden Markov Models for the Prediction of Impending Faults. IEEE Trans. Ind. Electron. 2016, 63, 3271–3281. [Google Scholar] [CrossRef]
- Lambert, P.; Eilers, P.H. Bayesian proportional hazards model with time-varying regression coefficients: A penalized Poisson regression approach. Stat. Med. 2005, 24, 3977–3989. [Google Scholar] [CrossRef]
- Ochella, S.; Shafiee, M.; Dinmohanmmadi, F. Artificial intelligence in prognostics and health management of engineering systems. Eng. Appl. Artif. Intel. 2022, 108, 104552. [Google Scholar] [CrossRef]
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef]
- Gao, D.; Wu, Z.; Yang, L.; Zheng, Y.; Yin, W. Structural health monitoring for long-term aircraft storage tanks under cryogenic temperature. Aerosp. Sci. Technol. 2019, 92, 881–891. [Google Scholar] [CrossRef]
- Qiu, L.; Fang, F.; Yuan, S.; Boller, C.; Ren, Y. An enhanced dynamic Gaussian mixture model–based damage monitoring method of aircraft structures under environmental and operational conditions. Struct. Health Monit. 2019, 18, 524–545. [Google Scholar] [CrossRef]
- Fang, F.; Qiu, L.; Yuan, S.; Ren, Y. Dynamic probability modeling-based aircraft structural health monitoring framework under time-varying conditions: Validation in an in-flight test simulated on ground. Aerosp. Sci. Technol. 2019, 95, 105467. [Google Scholar] [CrossRef]
- Aydemir, H.; Zengin, U.; Durak, U. The digital twin paradigm for aircraft—Review and outlook. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–12. [Google Scholar]
- Pernkopf, F.; Bouchaffra, D. Genetic-based EM algorithm for learning Gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing Health Monitoring Based on Hilbert–Huang Transform, Support Vector Machine, and Regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Li, J.; Jing, B.; Dai, H.; Sheng, Z.; Jiao, X.; Liu, X. A remaining useful life prediction method for airborne fuel pump after maintenance. Proc. Inst. Mech. Eng. Part. G J. Aerosp. Eng. 2019, 233, 5660–5673. [Google Scholar] [CrossRef]
- Listou Ellefsen, A.; Bjørlykhaug, E.; Æsøy, V.; Ushakov, S.; Zhang, H. Remaining useful life predictions for turbofan engine degradation using semi-supervised deep architecture. Reliab. Eng. Syst. Safe. 2019, 183, 240–251. [Google Scholar] [CrossRef]
- Li, R.; Verhagen, W.J.C.; Curran, R. Toward a methodology of requirements definition for prognostics and health management system to support aircraft predictive maintenance. Aerosp. Sci. Technol. 2020, 102, 105877. [Google Scholar] [CrossRef]
- Figueiredo Mario, A.T.; Jain Anil, K. Unsupervised learning of finite mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 381–396. [Google Scholar] [CrossRef]
- Chakraborty, D.; Kovvali, N.; Papandreou-Suppappola, A.; Chattopadhyay, A. An adaptive learning damage estimation method for structural health monitoring. J. Intell. Mater. Syst. Struct. 2015, 26, 125–143. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.; Zhou, Y. A Clustering Algorithm with Adaptive Cut-off Distance and Cluster Centers. Data Anal. Knowl. Discov. 2018, 3, 39–48. (In Chinese) [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremos, P. Rényi divergence and kullback-leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Leser Patrick, E.; Warner James, E.; Leser William, P.; Bomarito Geoffrey, F.; Newman John, A.; Hochhalter Jacob, D. A digital twin feasibility study (Part II): Non-deterministic predictions of fatigue life using in-situ diagnostics and prognostics. Eng. Fract. Mech. 2020, 229, 106903. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Yan, R.; Gao, R.X. Long short-term memory for machine remaining life prediction. J. Manuf. Syst. 2018, 48, 78–86. [Google Scholar] [CrossRef]
- Badea, V.E.; Zamfiroiu, A.; Boncea, R. Big Data in the Aerospace Industry. Inform. Econ. 2018, 22, 17–24. [Google Scholar] [CrossRef]
- Li, C.; Mahadevan, S.; Ling, Y.; Choze, S.; Wang, L. Dynamic Bayesian network for aircraft wing health monitoring digital twin. AIAA J. 2017, 55, 930–941. [Google Scholar] [CrossRef]
- Lu, C.; Wang, S.; Makis, V. Fault severity recognition of aviation piston pump based on feature extraction of EEMD paving and optimized support vector regression model. Aerosp. Sci. Technol. 2017, 67, 105–117. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; pp. 1–9. [Google Scholar]
- Vollert, S.; Theissler, A. Challenges of machine learning-based RUL prognosis: A review on NASA’s C-MAPSS data set. In Proceedings of the 2021 26th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vasteras, Sweden, 7–10 September 2021; pp. 1–8. [Google Scholar]
- Li, L.; Shi, W. A fault tolerant model for multi-sensor measurement. Chin. J. Aeronaut. 2015, 28, 874–882. [Google Scholar] [CrossRef]

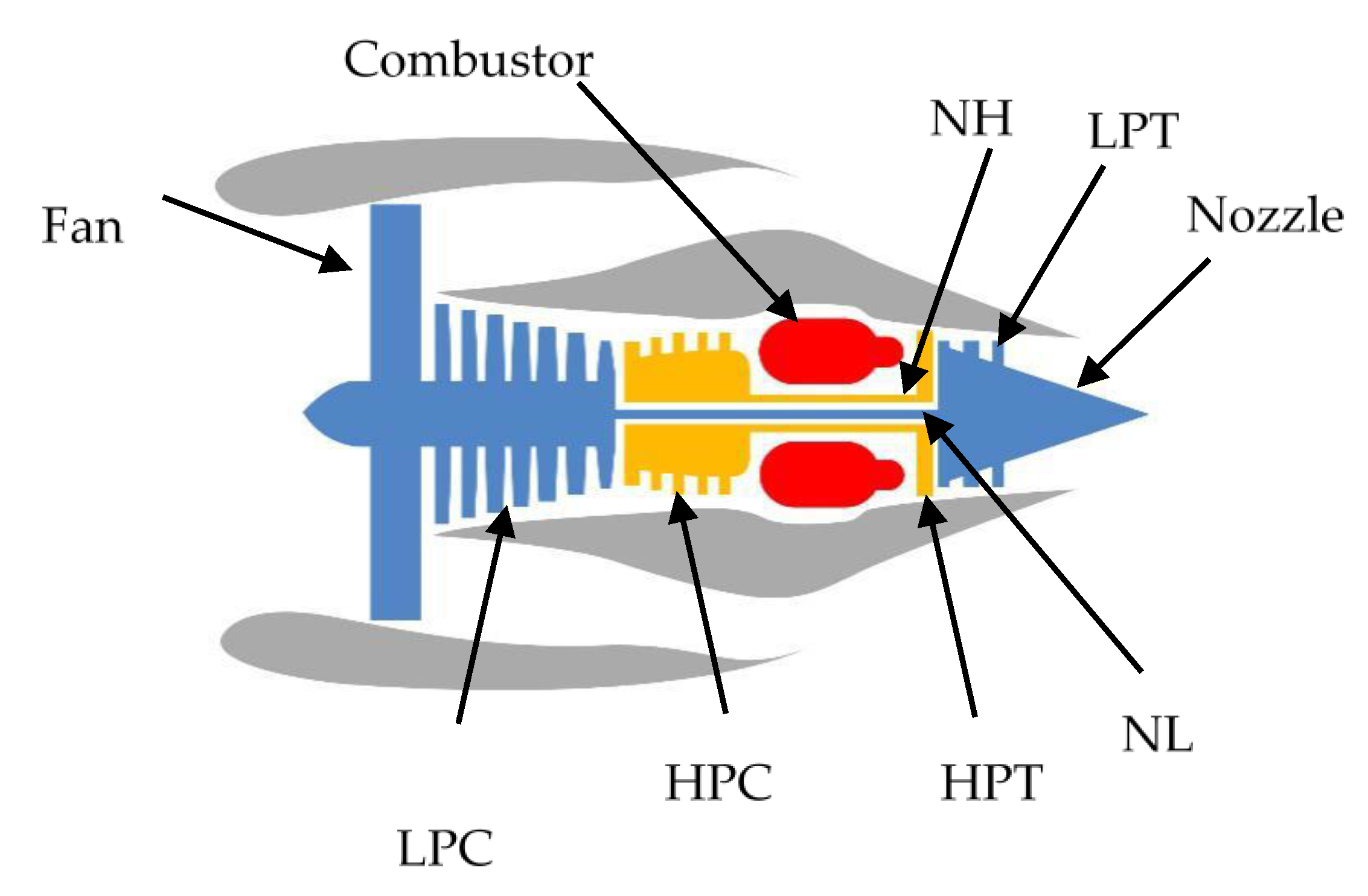

| No. | Sensor Abbreviation | Description | Units |
|---|---|---|---|
| 1 | T24 | Total temperature at low pressure compressor outlet | |
| 2 | T30 | Total temperature at high pressure compressor outlet | |
| 3 | T50 | Total temperature at low pressure turbine outlet | |
| 4 | P30 | Total pressure at high pressure compressor outlet | psia |
| 5 | Nf | Physical fan speed | rpm |
| 6 | Nc | Physical core speed | rpm |
| 7 | Ps30 | Static pressure at high pressure compressor outlet (Ps30) | psia |
| 8 | Phi | Ratio of fuel flow to Ps30 | pps/psi |
| 9 | NRf | Corrected fan speed | rpm |
| 10 | NRc | Corrected core speed | rpm |
| 11 | BPR | Bypass ratio | - |
| 12 | Ht Bleed | Burner fuel–air ratio | - |
| 13 | W31 | High pressure turbine coolant bleed | lbm/s |
| 14 | W32 | Low pressure turbine coolant bleed | lbm/s |
| Engine No. | Full Life Cycle | Fault Detection Index at the End of the Cycle |
|---|---|---|
| Engine #1 | 287 | 0.5768 |
| Engine #2 | 269 | 0.5814 |
| Engine #3 | 276 | 0.5885 |
| Engine #4 | 283 | 0.5747 |
| Model | Difference Variance (10−2) |
|---|---|
| BP | 3.5 |
| DBN | 2.4 |
| DP | 1.5 |
| Model Parameters | Value |
|---|---|
| Layer | 3 |
| Hidden units | [128, 64, 64] |
| Dropout | [0.3, 0.3, 0] |
| Batch size | 100 |
| Epoch | 100 |
| Input shape | [10, 1] |
| Output shape | [1, 1] |
| Model | Point 1 (Cycles) | Point 2 (Cycles) | Average (Cycles) |
|---|---|---|---|
| DP + LSTM | 5.1 | 3.7 | 4.4 |
| DBN + LSTM | 6.9 | 4.4 | 5.6 |
| LSTM | 8.2 | 6.8 | 7.5 |
| RNN | 10.2 | 7.9 | 9.0 |
| GRU | 10.0 | 7.0 | 8.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Tao, J.; Sun, G.; Zhang, H.; Hu, Y. A Prognostic and Health Management Framework for Aero-Engines Based on a Dynamic Probability Model and LSTM Network. Aerospace 2022, 9, 316. https://doi.org/10.3390/aerospace9060316
Huang Y, Tao J, Sun G, Zhang H, Hu Y. A Prognostic and Health Management Framework for Aero-Engines Based on a Dynamic Probability Model and LSTM Network. Aerospace. 2022; 9(6):316. https://doi.org/10.3390/aerospace9060316
Chicago/Turabian StyleHuang, Yufeng, Jun Tao, Gang Sun, Hao Zhang, and Yan Hu. 2022. "A Prognostic and Health Management Framework for Aero-Engines Based on a Dynamic Probability Model and LSTM Network" Aerospace 9, no. 6: 316. https://doi.org/10.3390/aerospace9060316
APA StyleHuang, Y., Tao, J., Sun, G., Zhang, H., & Hu, Y. (2022). A Prognostic and Health Management Framework for Aero-Engines Based on a Dynamic Probability Model and LSTM Network. Aerospace, 9(6), 316. https://doi.org/10.3390/aerospace9060316







