Abstract
In the multi-satellite and multi-ground station downlink task scheduling problem, the waiting time from the proposal of the task to the execution will affect its validity. If the satellite has multiple communicable ground stations when the downlink task is proposed, the selection problem needs to be solved first. After the selection, since the available time conflict between tasks of different satellites for the same ground station, the specific start time should be determined. To reduce the waiting time, a simulated annealing algorithm with a tabu list and start time decision (SATLD) is proposed. This method uses a two-stage scheduling strategy. In the first stage, the improved simulated annealing algorithm based on a tabu list is used to select the downlink ground station. The second stage combines downlink scheduling algorithm based on task arrival time (DSA-AT) method and downlink scheduling algorithm based on task requirement time (DSA-RT) method to determine the specific start time of each task of a single ground station. Simulation analysis prove the method has better selection efficiency of downlink task and shorter total task waiting time, and has practical value.
1. Introduction
With the development of aerospace technology, there are kinds of spacecraft provide excellent opportunities to gather data from space. They are used for obtaining information specifically requested by users or storing data that has been obtained during transmission. No matter what the mission is, it is essential to obtain the data down to the ground station through the downlink. For instance, the earth observation satellite (EOS) is a satellite equipped with various sensors. The main task of EOS is to detect the target area proposed by the user, and then download the detected data to the ground station through the downlink and then deliver it to the user. However, the capacity of the ground station (GS) is very limited compared with the large number of spacecraft and the data waiting to be transmitted. At the same time, some special tasks (e.g., fire spot detection in large-scale wildfires, etc.) need to deliver observation results to users with the shortest possible delay. Taking low-latency data transmission and resource utilization into account, there is a growing need for efficient satellite and ground station data downlink schedule methods.
According to the satellite database of the Union of Concerned Scientist [1], as of 1 January 2022, there are 4852 satellites orbiting the Earth over the world. Although the number of satellites continues to increase, it is still unable to meet the increasing user demand. One possible way is to develop low-cost small satellite, which present some technical limitations [2]. The main technical limitation considered in this paper is the inability to maintain the inter-satellite link (ISL) due to its low attitude control accuracy. This prevents it from using ISL and relay satellites to send data down to a ground station, which means that they can only deliver the results of mission to users by communicating with the ground station. More importantly, some special requests have to be satisfied as soon as possible. For example, EOS is always used to observe and photograph specific areas in the task of natural disaster rescue. Observations are required to reach decision makers as quickly as possible. This first challenge is the multi-satellite observation mission scheduling. Additionally, after the completion of observation, the results should be transmitted to the ground station in the shortest time. Due to the conflict in the visible time window between multi-satellite and limited ground stations, an efficient scheduling method is of great significance for timely completion of missions.
There have been increasing research attentions on satellites mission scheduling problem in recent decades [3]. Beak et al. considered various constraints in the EOS problem, including energy and priority. They proposed a planning method based on genetic algorithm and tested it on three different types of satellites [4]. Wang et al. studied the multi-satellite redundant target planning problem and proposed a fast solution method based on complex networks [5]. Chu et al. proposed a mode of high and low resolution payload satellites working together to solve the problem of multi-satellite cooperative observation [6]. He et al. extended the adaptive large neighborhood search algorithm to the multi-agile satellite planning problem [7,8]. As for area targets, the regional targets are usually divided first, and then arrange the observation tasks of each satellite [9].
The ground station scheduling(GSS) is a crucial part in satellite control and data delivery [10]. Once the satellite completes its mission, taking into account factors, such as data timeliness and onboard memory, the results need to be transmitted to ground users in a timely manner. GSS problem is extremely complex and has been proven to be NP-hard [11]. Xhafa et al. considered the utilization rate of ground stations in the GSS problem and solved it with genetic algorithm [12]. Karapetyan et al. divided downlink requests into ordinary and urgent requests, using fast planning strategy to deal with emergency request first, then use the remaining resources to process ordinary requests [13]. Chen et al. proposed two types of solution construction graphs with the number of tasks completed as the main objective, which improved the performance of the ant colony optimization algorithm by limiting the search neighborhood [14]. Yan et al. considered the inter-satellite bandwidth capacity and solved it using iterative tree search algorithm based on the integer programming model [15]. Zhang et al. proposed a planning method combining SVM and NSGA-II based on the idea of classification for satellite data transmission planning [16]. Luo et al. proposed a conflict resolution technique for satellite downlink scheduling by constructing elite initial schedule [17]. Li et al. solved the satellite range scheduling problem with priority constraints by designing coding and selection methods in genetic algorithm [18]. Li et al. proposed the conflict degree of data transmission and solved it by combining tabu search and genetic algorithm [19]. Li et al. proposed a K-shortest path genetic algorithm for the balance between response time and resource utilization [20]. Hou et al. optimized the ground-satellite link planning with respect to three aspects: link switching frequency, routing update frequency, and relay satellite configuration [21]. Chen et al. designed a rote genetic algorithm operator to guide the algorithm for the problem of data transmission window collisions in the transmission of satellite cluster data transmission [22]. Xiang et al. established a global scheduling optimization model, including satellite ground transmission and ground transmission, including conflict resolution model in the process of satellite ground transmission and data transmission model in the process of ground transmission [23].
Integrated satellite scheduling is to schedule satellite observation and data transmission simultaneously. Zhu et al. established a mixed integer linear programming model for the integrated satellite scheduling problem using a directed acyclic graph for determining candidate solution options [24]. Cho et al. described a two-step binary linear programming formula considering energy consumption, which solved the downlink scheduling sub-problem first and, then, the constellation task scheduling problem [25]. Song et al. considered that all observation data in the same area need to be downloaded to the same ground station, and proposed the construction heuristic algorithm and downlink scheduling algorithm [26]. Xiao et al. considered the impact of weather uncertainty on mission success to ensure the maximum reliability of mission scheduling, proposed two planning modes based on periodic triggering and event triggering, and adopted a two-stage scheduling scheme to optimize observation and downlink operation simultaneously [27]. Zhang et al. proposed a solution method based on quantum genetic algorithm considering the model of energy constraint and storage capacity constraint [28]. Zhang et al. modeled the integrated satellite scheduling problem as a mixed integer programming model and proposed the concept of conflict request set to improve the performance of genetic algorithm [29].
This article focuses on the low latency requirements of users in the multi-satellite and ground stations scheduling problem (MGSS). In this paper, the calculation process of the visible time window between the satellite and the ground station is firstly presented. Then, model the problem as a resource-constrained heterogeneous vehicle routing problem with time window (RC-HVRPTW) according to the characteristics of MGSS. The primary optimization objective is to minimize task delay in MGSS. A simulated annealing algorithm with a tabu list and start time decision (SATLD) is proposed to solve this problem. SATLD assigns the corresponding ground station to each downlink task firstly, and then determines the specific start time of each downlink task. The SATLD algorithm proposed in this paper is a method that balances profit and efficiency. First, the problem of resource allocation in the MGSS problem is solved. Second, according to the characteristics that some specific tasks need to be transmitted to the ground station in a short time, a method for determining the exact start time of the task considering the waiting time is given.
The remainder of this paper is organized as follows. In Section 2, a mathematical model of the MGSS problem is proposed. Section 3 presents the main scheme of the SATLD. Experimental results are presented in Section 4 to verify the efficiency of the model and the effectiveness of the proposed algorithm. The last section offers conclusions and directions for future research.
2. Problem Description and Formulation
There are two critical things that need to be completed between receiving a user request and completing a task. The first one is observation scheduling, which arranges the observation scheme according to the relationship between the available satellite resources and the observation target requested by the user. The second one is downlink scheduling, which transfers observation results from multiple satellites to ground stations as quickly as possible. In many observation tasks, multiple satellites will obtain a large amount of observation data once the observation task completed. Nevertheless, restricted to the number and location of ground stations, it is necessary to schedule the multi-satellite downlink to complete the delivery of the observation results.
2.1. Problem Description
The satellite can establish a downlink with the ground station to transmit the data stored on itself to the ground when it can gain access to a ground station. According to the visible time of different satellites and ground stations conflict with each other, ground station scheduling is needed to complete the data transmission task of each satellite. The MGSS is the last step in the satellite scheduling workflow, which has a great impact on user satisfaction and data timeliness. This problem is mainly caused by the insufficient number and the limited geographical distribution of ground stations. Due to the limitation of the curvature of the earth and the communication capability of the satellite antenna, it is impossible for the satellite and the ground station to maintain a connection state at any time, but can only communicate and transmit data within a specific time window. Additionally, the ground station usually can keep downlink with only one specific satellite simultaneously. As shown in Figure 1, the GS-1 can access to SAT-2, SAT-3 simultaneously, and GS-2 can access to SAT-1 and SAT-2. SAT-2 needs to choose between ground station 1 and ground station 2 as the downlink target. As shown in Figure 2, there are overlaps in the same ground station with different satellites.
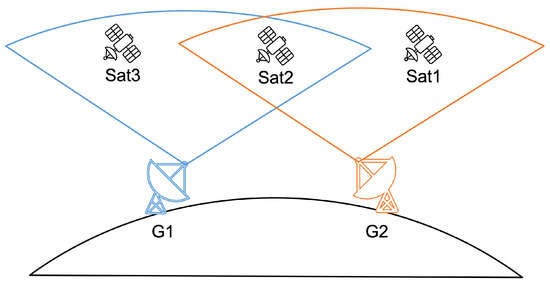
Figure 1.
Example of MGSS problem.
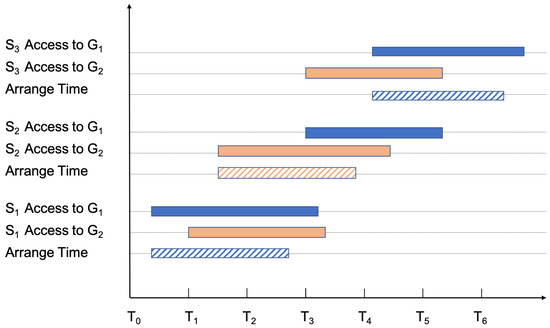
Figure 2.
Schedule example.
After the observation scheduling proposed by the user is completed, the executing satellite of each target, the start time of observation, the time of task completion, and the consumption rate of on-board storage can be calculated. Additionally, then, the problem is transformed into multi-satellite downlink scheduling, and a download plan is arranged for each datum. A downlink task can be described as (1), each task t contains a unique id, sat is the satellite number of the current downlink task, tArrival is the specific time of the current task, tDur is the time required for data transmission, and priority stands for the importance of the task.
Task set T contains all downlink task for all satellites. A subset is selected after executing the downlink scheduling. The exact execution time of each t is determined to ensure that the downlink task has the shortest waiting time while meeting all the constraints of the tasks in . The access time conflict should also be solved.
2.2. The RC-HVRPTW Model
In multi-satellite ground station scheduling, the ground station communication time is scheduled as cargo to multiple satellites with the shortest task waiting time. The relationship between satellite orbits and the geographic location distribution of ground stations determines that there are different visible windows between satellites and ground stations, which means that each satellite is associated with a specific ground station set. As shown in Figure 1, the ground station set for SAT-3 is , and the ground station set for SAT-1 is . According to the urgency of the data, it is necessary to reduce the waiting time of the downlink task as much as possible. In order to facilitate downlink and reduce waiting time, the communication time of the ground station should be allocated to the corresponding downlink request. An alternative representation can be used to represent customer-based graphics and road networks. A customer-based multiple graph, which contains multiple links between two vertexes, which represent different paths in the graph based on different vehicle. In other words, there is no longer a single path between two vertices, but there are multiple alternative paths provided by different vehicles. There are always different routes between nodes, and each route means a different travel cost. The choice of a different route for each node will affect its next route.
RC-HVRPTW arising in the multi-satellite ground station scheduling can be defined on the directed graph where is the vertex set, , is the arc set. Downlink requests are regarded as customers, and ground stations are regarded as vehicle resources for providing kinds of services. The downlink request i has a service time tDur and open window and the arrival time tArrival. In order to ensure the integrity of information, each downlink request is executed only once. Customers with different requests should be served by different kind of vehicles. Arc contains the cost of task transformation from i to j using vehicle k. A fleet of heterogeneous vehicles are used to deliver variety of products to the customers. The objective of cost minimization takes into account customer waiting cost and travel cost. The decision variable is a binary variable. It is set to 1 when vehicle k provide service j before i, 0 for others. is the service start time of customer i.
2.3. Formulation
2.3.1. Downlink Latency Cost (DC)
The downlink latency cost is determined by the scheduled solution. Each downlink request has a request submission time, and the time from the submission time to the completion time of the request is called the downlink latency time. The downlink latency cost can be calculated as follows,
2.3.2. Energy Consumption Cost(EC)
The energy consumption cost includes two part: the cost in attitude maneuver () and the cost in data download (). The and EC refers to the on-board energy required from issuing a downlink request to completing the mission. represents the energy consumption of the satellite maneuvering its attitude to communicate with the ground. Additionally, is the energy consumption of satellite data transmission. The energy consumption cost can be calculated by,
where
The mathematical model of RC-HVRPTW is defined as follows.
subject to:
Equation (4) is the optimization objective function. Equation (5) means that observation is made for a target at most once. Equation (6) stands for that means that the end time of each access window is greater than the start time. Equations (7) and (8) require the service start time for each request. Equation (10) requires energy consumption to be within the total energy range on-board. Equation (11) means that only when there is a request longer than the duration can be served. Equations (12) and (13) represents that the mission execution plan of each ground station has a dummy request at the beginning and end Table 1 and Table 2.

Table 1.
Parameters.

Table 2.
Decision variables.
3. SATLD for MGSS Considering Waiting Time
In this section, we introduce a simulated annealing algorithm with a tabu list and start time decision (SATLD) to efficiently solve the RC-HVRPTW. The origin SA algorithm is upgraded by the use of TL and two deterministic algorithm. The SA is used to explore diversity solution to achieve a more applicable solution. As discussed above, the waiting time of the request increased by that multiple satellites need to use the same ground station in overlapping access windows. The main method to solve the problem is to reduce the conflict by arranging the downlink requests with conflict access windows to different ground stations.
In the proposed algorithm, a greedy strategy with the least conflict ground station first is applied to construct the initial solution. The initial solution constructs a better solution by assigning the ground stations with the least time conflict firstly. In each iteration of SA, a variety of downlink request scheduling methods are used for a single ground station to obtain the appropriate downlink plan. It is observed that the algorithm adopts a multi-start strategy achieving diversification to obtain high quality solutions.
The remainder of this section introduces the proposed solution methodology. Section 3.1 introduces how to solve RC-HVRPTW by exact methods. Additionally, Section 3.2 presents the components of the optimization process.
3.1. Determination Method of Start Time
First-come-first service and short-job first methods are commonly used in operating system process scheduling. However, different from the process scheduling in the operating system, the request may appear at any time in the single ground station downlink scheduling period. If the arrival time of the current request is beyond the whole planning period, it must wait until the cycle starts, and the ground station has a visible window for the current request.
Inspired by the FCFS, we propose a downlink scheduling algorithm based on the arrival time (DSA-AT) of downlink requests. As shown in Figure 3, DSA-AT arranges all requests in ascending order according to their arrival time, and arranges the access window time first according to the order of tasks. In order to reduce the waiting time of the downlink request as much as possible, the specific start time of the request is arranged as early as possible in its visible window. The algorithm is described in detail in Algorithm 1. The input of DSA-AT includes a set of downlink links, a set of ground stations, a set of satellites, and a set of visible windows between the ground station and the satellite. The output is a scheme that includes all the ground stations allocated for the downlink request and the corresponding specific start time. Firstly, arrange the downlink request set in ascending order of arrival time. Then, downlink resource allocation is performed on each request in sequence. Determine all the access windows of the satellite that emit the current request r. Arrange all access windows in ascending order of the start time of the window, and check whether they meet the requirements of the current request. If it is satisfied, the specific execution time is determined, and the waiting time from the request arrival time to the execution time is recorded.
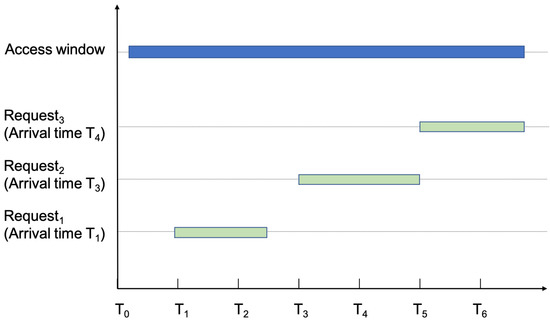
Figure 3.
DSA-AT processing example.
Additionally, then, the access window update algorithm is applied to , as shown in Algorithm 2. The input includes the access window set , the current request r, the chosen ground station number g, the specific start time of request r . The output is the updated access window set. The first step is to select all the access window sets that need to be updated from the ground station numbers currently allocated. Because the arrangement of the current request will only affect the access window with the same ground station number. For each visible window, according to the time occupation interval assigned to downlink request r by the ground station, it can be known that there are at most four relationships between each window and the occupied time. As shown in Figure 4, the four types are subset, left-overlapping, right-overlapping, and inclusion. The first type of relationship is , and window a is completely occupied, so remove it from . In the next two cases, and overlap the left part and the right part, respectively, and move the start time of the window backward and the end time of the window forward. The last case is that is a subset of , and needs to be divided into two visible windows, and then is updated.
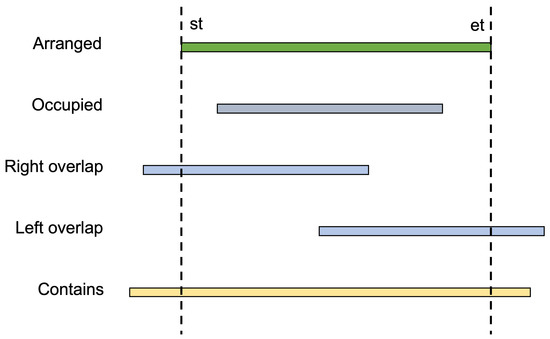
Figure 4.
Time window conflict type.
Inspired by the SJF, we propose the downlink scheduling algorithm based on the requirement time(DSA-RT) of downlink requests. As shown in Figure 5, in some specific scenarios, the use of DSA-AT will cause some tasks with late arrival time to wait too long. Based on the idea of SJF, prioritizing the downlink requests with short demand time can effectively reduce the waiting time of the whole process. The DSA-RT is described as Algorithm 3, it also uses the window update Algorithm 2. The main difference between DSA-RT and DSA-AT lies in the first line of the algorithm, where the time required for each downlink request is used for ascending order.
| Algorithm 1: Downlink scheduling based on arrival time |
 |
| Algorithm 2: Access window update for DSA-RT and DSA-AT |
 |
| Algorithm 3: Downlink scheduling based on requirement time |
 |
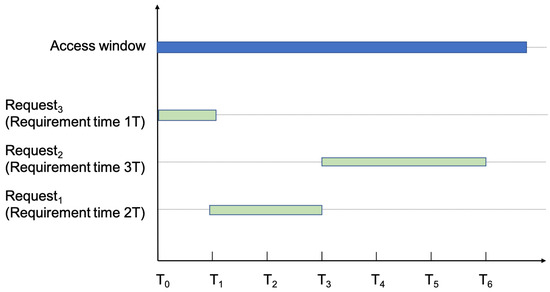
Figure 5.
DSA-RT processing example.
3.2. Simulated Annealing Algorithm with Tabu List and Start Time Decision
As shown in Algorithm 4, we propose a two-stage optimization algorithm based on simulated annealing and tabu list to solve RC-HVRPTW. The first stage is to use SA and TL to explore. This stage mainly solves the optimization problem caused by the simultaneous existence of access windows between satellites and multiple ground stations. A ground station is allocated for each downlink request through SA and TL. Additionally, then, the RC-HVRPTW can be decomposed into a single ground station scheduling problem. In the single ground station downlink scheduling, what needs to be determined is the specific start time of each downlink request. The purpose of downlink planning is to ensure that the downlink requirements are met while reducing the total wait time for each request. Therefore, downlink requests need to be scheduled as early as possible within the window time that the task can be executed. On the basis of the method in the Section 3.1, two methods for solving the exact start time are proposed. Each solution generated by SA uses FCFS-based and SJF-based to determine its specific start time.
The input of SATLD includes downlink request set R, ground station set G, satellite set S, access window set A, maximum number of iterations , tabu list length . First, an initial solution is obtained by using the initialization function . Additionally, the waitingTime, satisfiedNumber of the initial solution is calculated by fitness calculation function .Update using neighborhood search based on tabu list . Compare the with , and update based on Metropolis guidelines.
| Algorithm 4: Simulated annealing with tabu list and start time decision (SATLD) |
 |
The length of the solution is equal to the number of downlink requests, and each request solution position represents the downlink ground station number of the corresponding request. The initial solution will greatly affect the optimization performance of SATLD. Therefore, we propose three initialization criteria. For request r, the corresponding satellite number is , and the arrival time of the task request r is . For all the ground stations with access window to , the ground station set .
- (1)
- The access window conflict time is the least;
- (2)
- The ground station has the longest access window time for ;
- (3)
- The start time of access window between ground station and has the smallest difference with .
In , the specific start time and fitness of each request will be determined by FCFS-based and SJF-based simultaneously. Additionally, use the greedy strategy to determine the final execution time. In , tabu list is used to explore the solution neighborhood to improve the optimization efficiency. The algorithm maintains a tabu list queue of with length , records the change of solution in each iteration, and checks whether the current neighborhood appears in TL. If it appears, the corresponding element in TL will be moved to the end of the queue. If the current neighborhood does not appear in TL, it will be push to TL, and TL will delete the first element of the queue.
4. Experiment Simulation and Discussion
This section describes the computational experiments carried out to validate the effectiveness of the algorithm presented in Section 3. The algorithm was coded in Python and run on a 1.4 GHz Intel®Core (TM) i5 CPU and 8 GB memory. In Section 4.1, the sets of standard benchmark VRPTW instances from the literature are presented and a new set of HVRPTW-LR instances are also proposed. In Section 4.2, experiments are conducted to demonstrate the effectiveness of SATLD.
4.1. Experiment Cases Construction
Because of the lack of benchmarking examples for downlink scheduling problem aiming at request waiting time, on the base of benchmark for downlink scheduling proposed by [30], we propose a test case to verify the correctness of SATLD. The origin benchmark shown in Table 3, there are 16 benchmark instances for each size. However, this benchmark is not constructed for downlink scheduling considering request waiting time. The reason for not adapting to this problem is that it mainly considers the conventional communication between the satellite and the ground station, and it needs to communicate with the ground station once in each circle. In addition to regular requests, downlink requests also need to be satisfied as soon as possible. The randomness of task requests has not been considered, which means that the arrival time of each request is different. The arrival time of each request may not be within the access range of all the ground stations, or it can access to a certain ground station when the request arrived. Based on this, we made a modification on the basis of the original benchmark. Each satellite considers only one downlink request, and the arrival time of each downlink request in the entire planning cycle is random.

Table 3.
Original benchmark.
4.2. Computational Studies
Experiments were performed using our proposed test case with the number of iterations of SATLD set to 200 and the tabu list length set to 5. In the results shown in Table 4, the SATLD algorithm was run 50 times on each scenario, where represents the median value of the running results, and represents the average value of the running results, and , respectively, represent the percentage of SATLD to DSA-RT and DSA-AT, and represent the relationship between the total waiting time of all requests for the SATLD algorithm planning result and the determination algorithm.

Table 4.
Experiment results for waiting time.
From the small-scale test cases, it can be seen that for different problems, although the satellites and the corresponding available resources are the same, differences in problems are caused by the fact that the asymmetric requests for satellites are issued at different moments and each task requires different durations. DSA-RT had better results than DSA-AT on small-scale scenarios (SC_S_1, 2, 4, 6, 7, 9, 11, 14). DSA-AT had better results than DSA-RT on small-scale scenarios (SC_S_3, 5, 8, 10, 12, 13, 15, 16). It can be seen that the dominant number of the two exact methods in small-scale test scenarios is , respectively. However, it can be seen that, except for scenario 4, when DAS-AT algorithm is dominant, it has a greater impact on the results. For all small-scale scenarios, compared with DSA-AT and DSA-RT, SATLD obtains the best results. Among them, the optimal solution is obtained in SC_S_2, SC_S_10, SC_S_12. It can be seen from the ratio part that SATLD improves DSA-RT even more.
From the medium-scale test cases, it can be seen that the results of DSA-AT are better than DSA-RT, and the optimal solution is obtained in SC_M_8 and SC_M_10. SATLD obtained the optimal solution in SC_M_2, SC_M_8, SC_M_10, SC_M_12, SC_M_13, SC_M_15, and SC_M_16.
From the large-scale test cases, it can be seen that the results of DSA-AT are better than DSA-RT, and the optimal solution is obtained in SC_L_2, SC_L_6, SC_L_8, SC_L_11, and SC_L_16. SATLD obtained the optimal solution in SC_M_2, SC_M_8, SC_M_10, SC_M_12, SC_M_13, SC_M_15, and SC_M_16.
In summary, DSA-AT is generally superior to DSA-RT. Even in small-scale test cases, half of the test cases of DSA-AT and DSA-RT are dominant, but when DSA-AT is dominant, it can reduce more waiting time. In both medium-scale and large-scale test cases, DSA-AT is superior to DSA-RT, and it can obtain the optimal solution in multiple test cases. The SATLD algorithm can obtain the best results in each test case. The number of optimal solutions obtained in small-scale test cases is the least, and the number of optimal solutions obtained in medium-scale test cases is the largest. From the number of optimal solutions, it can be seen that with the increase in the number of ground stations, the access windows between ground stations and satellites increase. Although the number of satellites also increases, compared with the increase in resources, the number of downlink requests increases less, so it is more possible to solve the problem of downlink scheduling.
4.3. Algorithm Performance Comparison and Discussion
Simulations have been carried out in three different size scenarios. Genetic algorithm (GA) and stochastic algorithm are used as a comparison to compare algorithm stability and efficiency. The population size of the genetic algorithm is set to 20, the maximum number of iterations is set to 100, and the crossover probability and mutation probability are adaptive.The crossover operator uses two-point crossover, and the mutation operator uses single-point mutation. The three methods performed 20 experiments on each experimental case.
In the small scenario experimental case, it can be seen from Figure 6 that GA has the strongest stability, and stable results can be obtained in all 15 experimental cases. The stochastic algorithm has the worst stability, with a profit difference of more than 100 in multiple experimental cases (S4, S8, S9, S11), and the average number of outliers is twice that of SATLD. In these experimental cases, the difference in SATLD profit is within 80. The average profit of SATLD is comparable to GA on multiple experimental cases (S2, S3, S5, S6, S10, S12, S13, S14), and it is better than GA on S11. In each experimental case in Figure 7, the average time consumption of GA and SATLD differs by an order of magnitude.
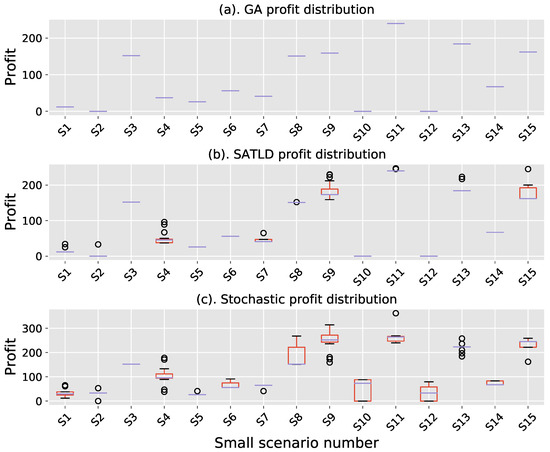
Figure 6.
Distribution in small scenario.
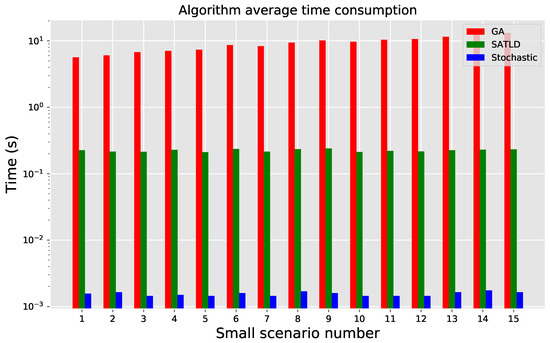
Figure 7.
Average time consumption in small scenario.
In the medium scenario experimental case (Figure 8 and Figure 9), the stability of SATLD is improved compared to the small scenario experimental case, and it is only worse than GA in one-third of the cases (S3, S4, S5, S11, S12). In the large scenario experimental case (Figure 10), SATLD is almost identical to GA. As the problem size increases, from the average time consumption (Figure 7, Figure 9 and Figure 11), the time consumption of GA increases in second order, while the SATLD growth rate is an order of magnitude lower than GA, from the profit and stability point of view SATLD gradually approaching GA.
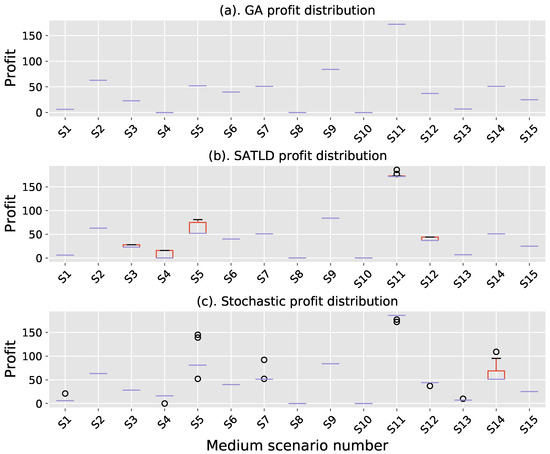
Figure 8.
Distribution in medium scenario.
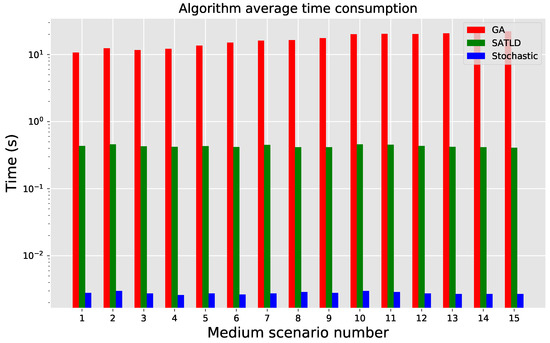
Figure 9.
Average time consumption in medium scenario.
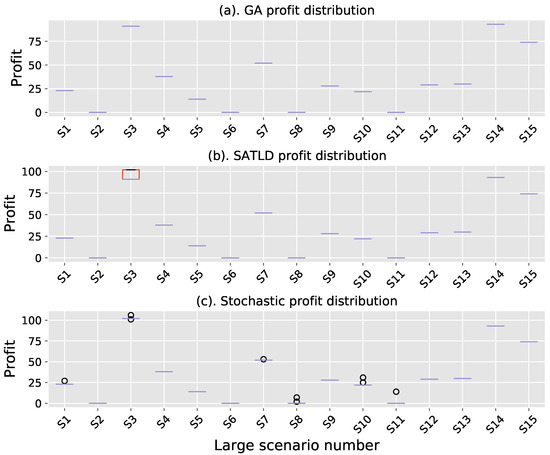
Figure 10.
Distribution in large scenario.
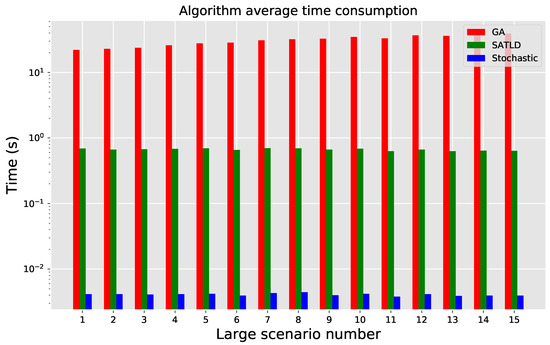
Figure 11.
Average time consumption in large scenario.
The experimental results show that the SATLD algorithm proposed in this paper is a method of balancing profit and efficiency. It achieves the same level of profit as GA with an average time consumption that is an order of magnitude lower than GA, and even outperforms GA in some experimental cases. This efficiency improvement makes it more suitable for running on satellites where hardware performance is insufficient. Compared with the random algorithm with less time consumption, SATLD has stronger stability, which can ensure that there is no large difference between the pros and cons of the planning results of the random algorithm during the running process.
5. Conclusions and Future Work
This study proposes a method for multi-satellite and multi-ground station downlink scheduling problem considering waiting time. Firstly, the simulated annealing algorithm with a tabu table is used to solve the selection problem of multiple satellites and multiple ground stations. Then, two precise algorithms, the downlink scheduling algorithm based on arrival time and the downlink scheduling algorithm based on requirement time, are used to solve the specific start time decision of multiple time conflict downlink tasks in a single ground station.
Calculation and simulation analysis shows this method is a balanced algorithm between profit and efficiency that can efficiently perform ground station selection and mission start time decision. In addition, the constraints considered in this work are mainly geometric visibility and temporal conflicts, without considering uncertain factors, such as communication interruption, and more specific constraints, such as ground station antenna maneuvering, which can be studied in future work. The downlink start time determination method reduces the waiting time of the task, and has practical value for the planning and scheduling of downlink tasks of multi-satellite and multi-ground stations.
Author Contributions
Conceptualization: Y.L. and S.Z.; methodology: Y.L. and S.Z.; supervision: H.H.; writing—review and editing: Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Satellite Database|Union of Concerned Scientists. Available online: https://www.ucsusa.org/resources/satellite-database (accessed on 1 January 2022).
- Meziane-Tani, I.; Métris, G.; Lion, G.; Deschamps, A.; Bendimerad, F.T.; Bekhti, M. Optimization of Small Satellite Constellation Design for Continuous Mutual Regional Coverage with Multi-Objective Genetic Algorithm. Int. J. Comput. Intell. Syst. 2016, 9, 627–637. [Google Scholar] [CrossRef]
- Wolfe, W.; Sorensen, S. Three Scheduling Algorithms Applied to the Earth Observing Domain. Manag. Sci. 2000, 46, 148–166. [Google Scholar] [CrossRef]
- Baek, S.W.; Han, S.M.; Cho, K.R.; Lee, D.W.; Yang, J.S.; Bainum, P.M.; Kim, H.D. Development of a Scheduling Algorithm and GUI for Autonomous Satellite Missions. Acta Astronaut. 2011, 68, 1396–1402. [Google Scholar] [CrossRef]
- Wang, X.; Han, C.; Zhang, R.; Gu, Y. Scheduling Multiple Agile Earth Observation Satellites for Oversubscribed Targets Using Complex Networks Theory. IEEE Access 2019, 7, 110605–110615. [Google Scholar] [CrossRef]
- Chu, X.; Chen, Y.; Tan, Y. An Anytime Branch and Bound Algorithm for Agile Earth Observation Satellite Onboard Scheduling. Adv. Space Res. 2017, 60, 2077–2090. [Google Scholar] [CrossRef]
- He, L.; Liu, X.; Laporte, G.; Chen, Y.; Chen, Y. An Improved Adaptive Large Neighborhood Search Algorithm for Multiple Agile Satellites Scheduling. Comput. Oper. Res. 2018, 100, 12–25. [Google Scholar] [CrossRef]
- Liu, X.; Laporte, G.; Chen, Y.; He, R. An Adaptive Large Neighborhood Search Metaheuristic for Agile Satellite Scheduling with Time-Dependent Transition Time. Comput. Oper. Res. 2017, 86, 41–53. [Google Scholar] [CrossRef]
- Zhibo, E.; Shi, R.; Gan, L.; Baoyin, H.; Li, J. Multi-Satellites Imaging Scheduling Using Individual Reconfiguration Based Integer Coding Genetic Algorithm. Acta Astronaut. 2021, 178, 645–657. [Google Scholar] [CrossRef]
- Xhafa, F.; Ip, A.W. Optimisation Problems and Resolution Methods in Satellite Scheduling and Space-Craft Operation: A Survey. Enterp. Inf. Syst. 2019, 15, 1022–1045. [Google Scholar] [CrossRef]
- Barkaoui, M.; Berger, J. A New Hybrid Genetic Algorithm for the Collection Scheduling Problem for a Satellite Constellation. J. Oper. Res. Soc. 2020, 71, 1390–1410. [Google Scholar] [CrossRef]
- Xhafa, F.; Sun, J.; Barolli, A.; Biberaj, A.; Barolli, L. Genetic Algorithms for Satellite Scheduling Problems. Mob. Inf. Syst. 2012, 8, 351–377. [Google Scholar] [CrossRef][Green Version]
- Karapetyan, D.; Mitrovic Minic, S.; Malladi, K.T.; Punnen, A.P. Satellite Downlink Scheduling Problem: A Case Study. Omega 2015, 53, 115–123. [Google Scholar] [CrossRef]
- Chen, X.G.; Wu, X. ACO algorithm of satellite data transmission scheduling based on solution construction graph. J. Syst. Eng. Electron. 2010, 32, 592–597. [Google Scholar]
- Yan, J.; Xing, L.; Li, C.; Zhang, Z. Multicommodity Flow Modeling for the Data Transmission Scheduling Problem in Navigation Satellite Systems. Complex Syst. Model. Simul. 2021, 1, 232–241. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, L.; Peng, G.; Yao, F.; Chen, C. A Large-Scale Multiobjective Satellite Data Transmission Scheduling Algorithm Based on SVM+NSGA-II. Swarm Evol. Comput. 2019, 50, 100560. [Google Scholar] [CrossRef]
- Luo, K.; Wang, H.; Li, Y.; Li, Q. High-Performance Technique for Satellite Range Scheduling. Comput. Oper. Res. 2017, 85, 12–21. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Liu, Y.; Xu, M. Satellite Range Scheduling with the Priority Constraint: An Improved Genetic Algorithm Using a Station ID Encoding Method. Chin. J. Aeronaut. 2015, 28, 789–803. [Google Scholar] [CrossRef]
- Li, L.X.; Ma, W.Z.; Liu, X.L. Research on TSGA Algorithm Satellite Data Transmission Scheduling. In Proceedings of the 2014 International Conference on Management Science Engineering 21th Annual Conference Proceedings, Helsinki, Finland, 17–19 August 2014; pp. 56–61. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Chen, H.; Jing, N. A Data Transmission Scheduling Algorithm for Rapid-Response Earth-Observing Operations. Chin. J. Aeronaut. 2014, 27, 349–364. [Google Scholar] [CrossRef]
- Hou, Z.; Yi, X.; Zhang, Y.; Kuang, Y.; Zhao, Y. Satellite-Ground Link Planning for LEO Satellite Navigation Augmentation Networks. IEEE Access 2019, 7, 98715–98724. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, Y.; Du, C.; Li, J. A Satellite Cluster Data Transmission Scheduling Method Based on Genetic Algorithm with Rote Learning Operator. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 5076–5083. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhang, W.; Tian, M. Satellite data transmission integrated scheduling and optimization. Syst. Eng. Electron. 2018, 40, 1288–1293. [Google Scholar] [CrossRef]
- Zhu, W.; Hu, X.; Wei, X.; Peng, J. A Two-Phase Genetic Annealing Method for Integrated Earth Observation Satellite Scheduling Problems. Soft Comput. 2019, 23, 181–196. [Google Scholar] [CrossRef]
- Cho, D.H.; Kim, J.H.; Choi, H.L.; Ahn, J. Optimization-Based Scheduling Method for Agile Earth-Observing Satellite Constellation. J. Aerosp. Inf. Syst. 2018, 15, 611–626. [Google Scholar] [CrossRef]
- Song, Y.J.; Zhang, Z.S.; Sun, K.; Yao, F.; Chen, Y.W. A Heuristic Genetic Algorithm for Regional Targets’ Small Satellite Image Downlink Scheduling Problem. Int. J. Aerosp. Eng. 2019, 2019, 1371852. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, S.; Yang, P.; You, M.; Huang, J. A Two-Stage Flow-Shop Scheme for the Multi-Satellite Observation and Data-Downlink Scheduling Problem Considering Weather Uncertainties. Reliab. Eng. Syst. Saf. 2019, 188, 263–275. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.; Zhu, W.; Jin, P. Solving the Observing and Downloading Integrated Scheduling Problem of Earth Observation Satellite with a Quantum Genetic Algorithm. J. Syst. Sci. Inf. 2018, 6, 399–420. [Google Scholar] [CrossRef]
- Zhang, J.; Xing, L. An Improved Genetic Algorithm for the Integrated Satellite Imaging and Data Transmission Scheduling Problem. Comput. Oper. Res. 2022, 139, 105626. [Google Scholar] [CrossRef]
- Xhafa, F.; Barolli, A.; Takizawa, M. Steady State Genetic Algorithm for Ground Station Scheduling Problem. In Proceedings of the 2013 IEEE 27th International Conference on Advanced Information Networking and Applications (AINA), Barcelona, Spain, 25–28 March 2013; pp. 153–160. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).