The Flying and Adhesion Robot Based on Approach and Vacuum
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Main Contributions
- We analyzed the reasons for adsorption failure or overturning, and optimized the structure of the flying and adhesion robot.
- In this paper, the approach-adsorption model of the flying and adhesion robot was established, which solves the optimization-velocity problem when the system model parameters change. To the author’s knowledge, this model is proposed for the first time.
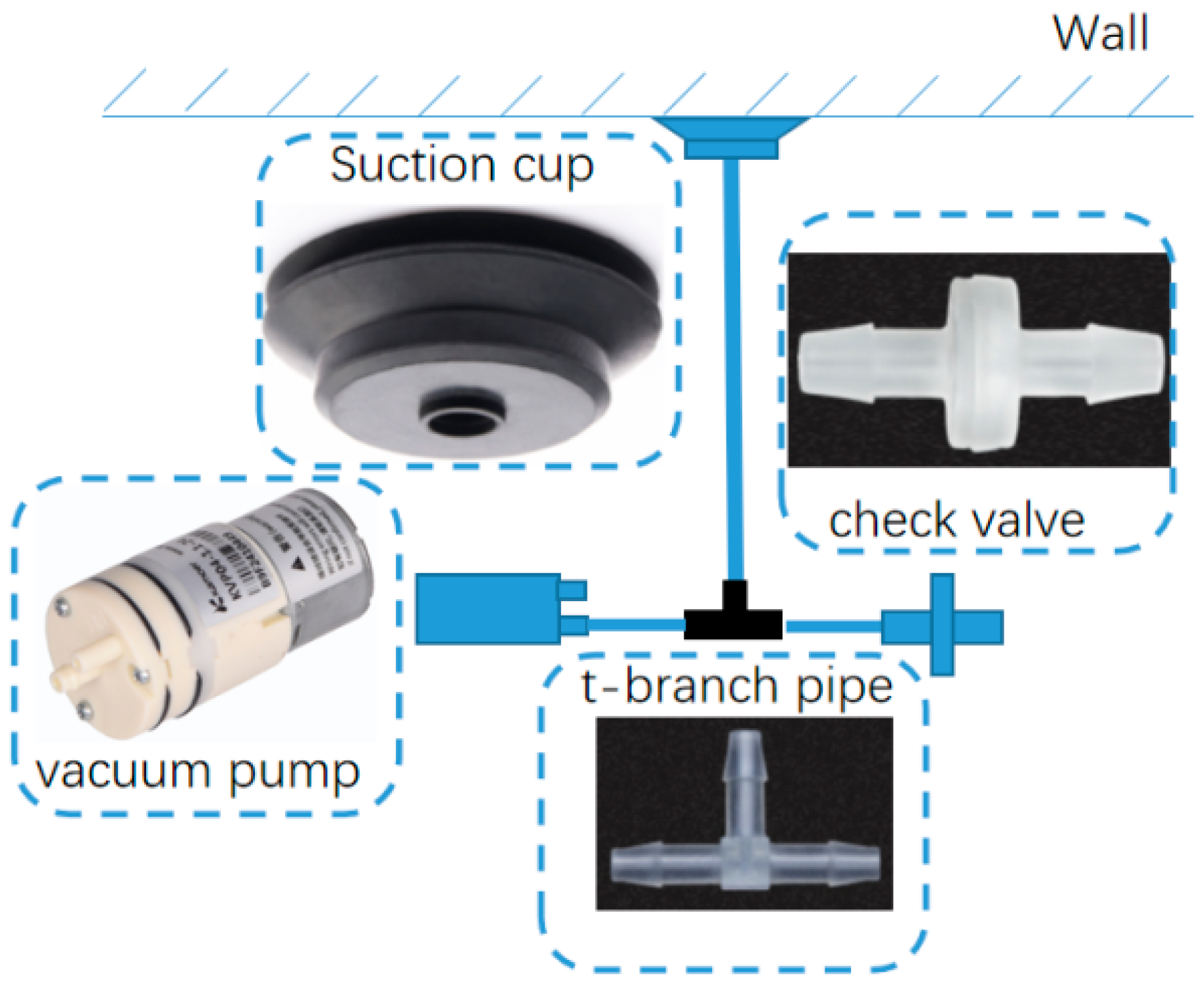
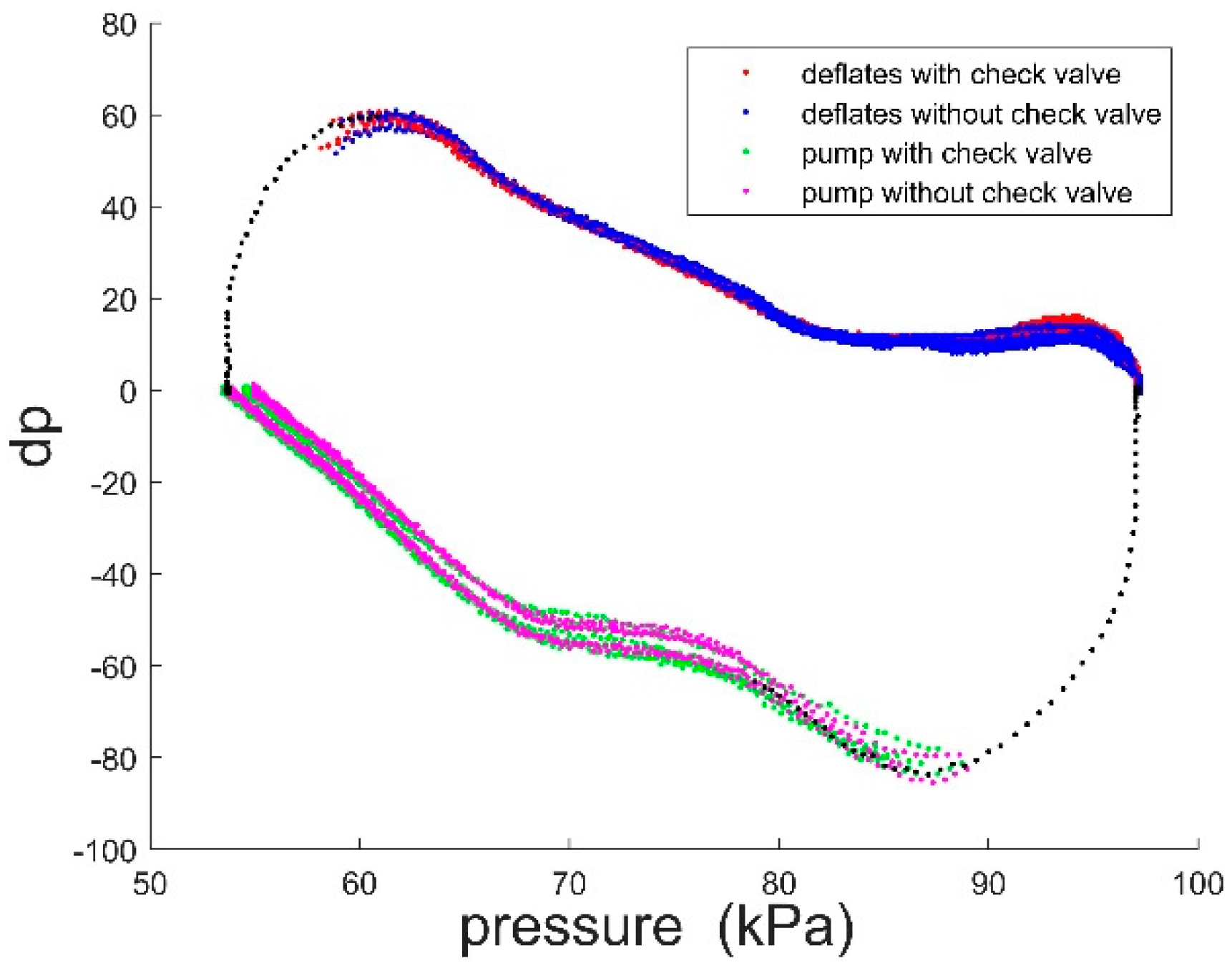
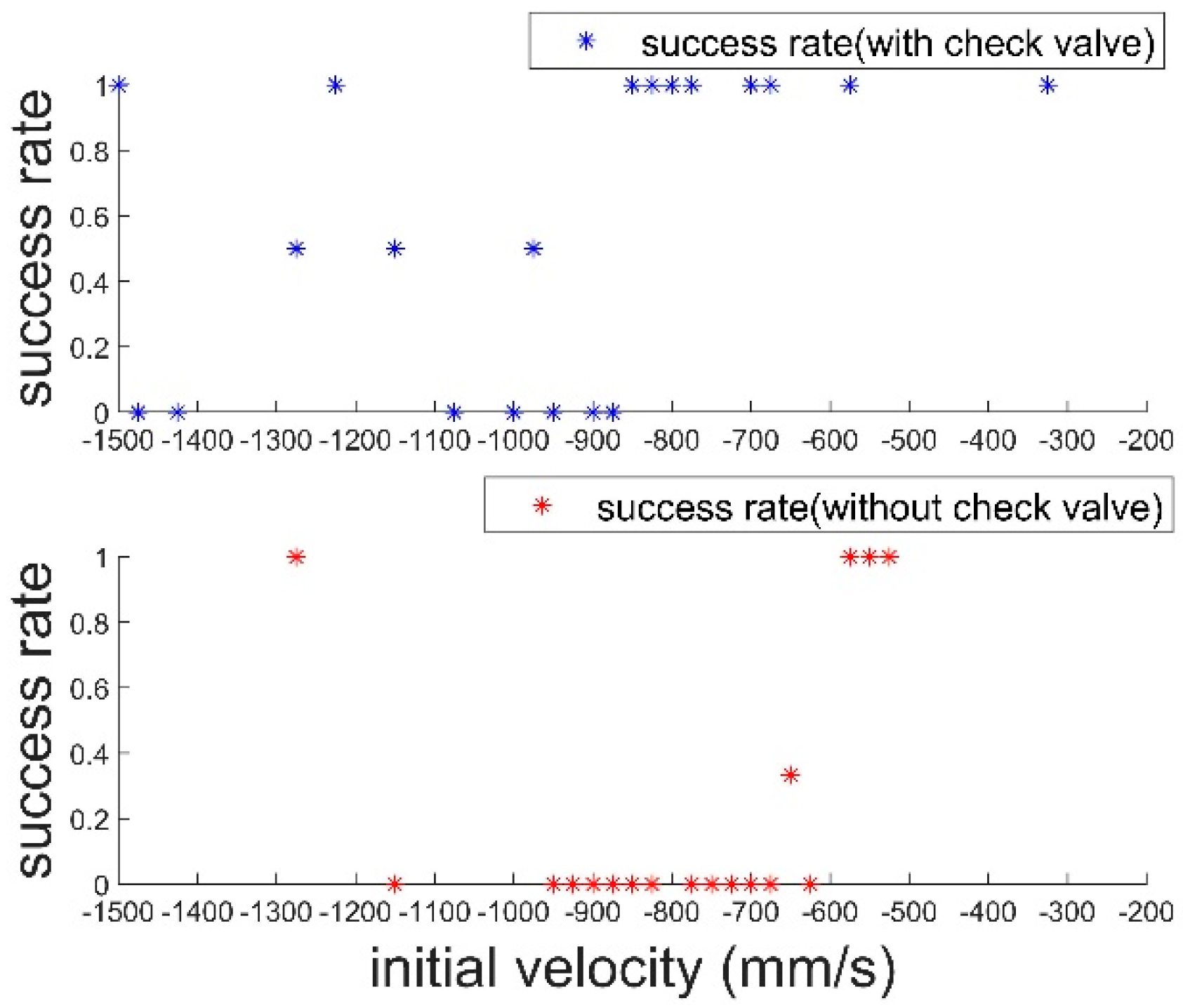
- In order to solve the necessity of the suction cups vertically facing the wall during the approach-adsorption control, a low-cost wall-angle measurement was employed and fed forward the angle to the heading controller. The threshold range of the approach velocity was improved using a check valve.
1.4. Outline
2. Dynamics Model
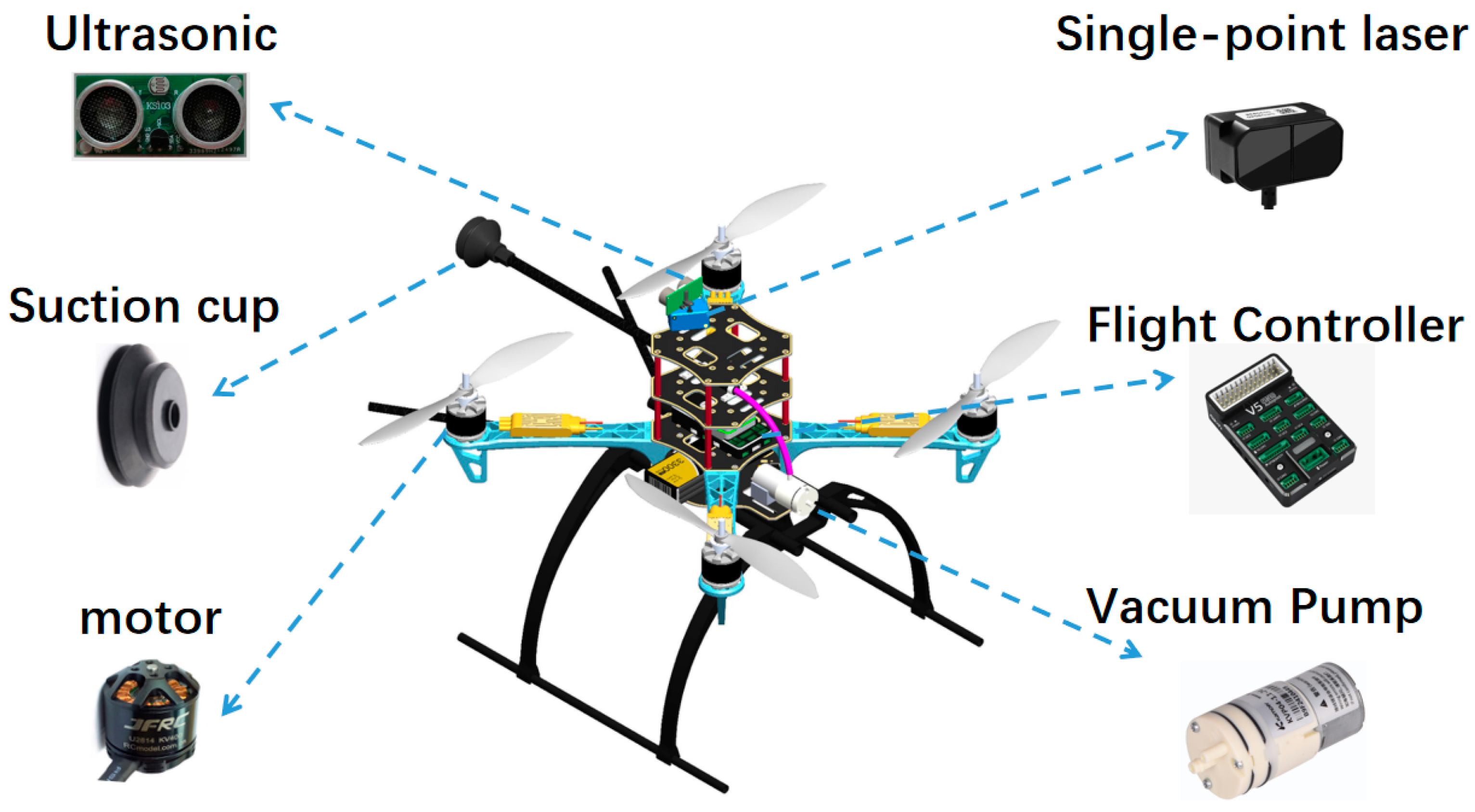
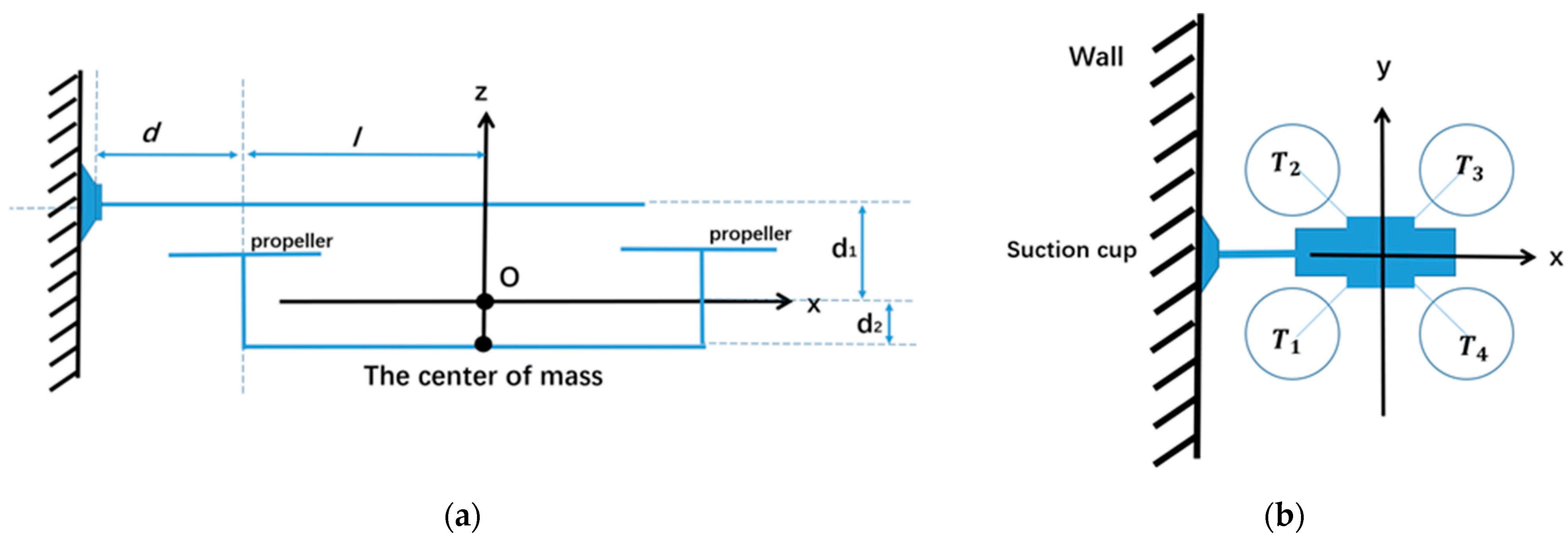
2.1. Overall Structural Design of the Flying and Adhesion Robot
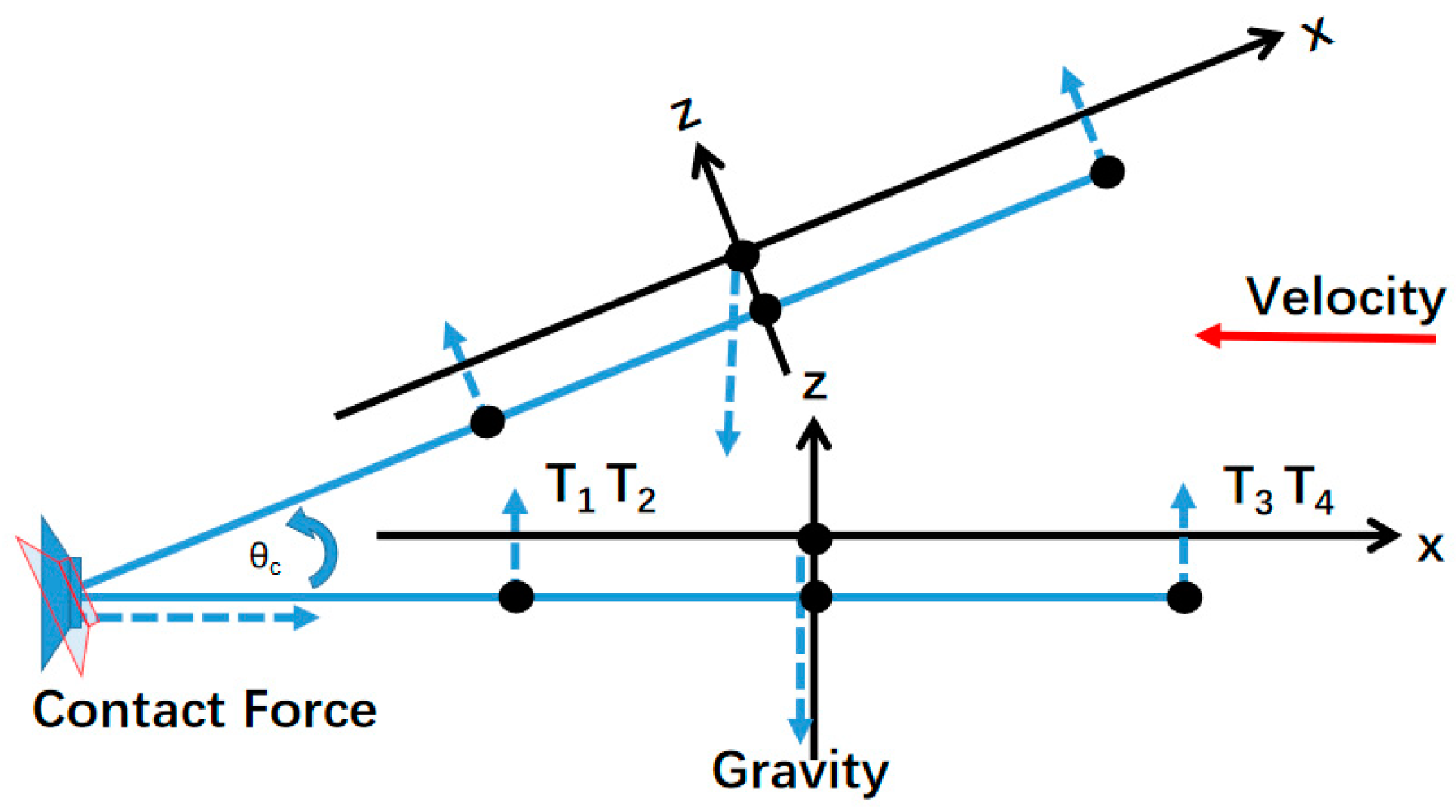
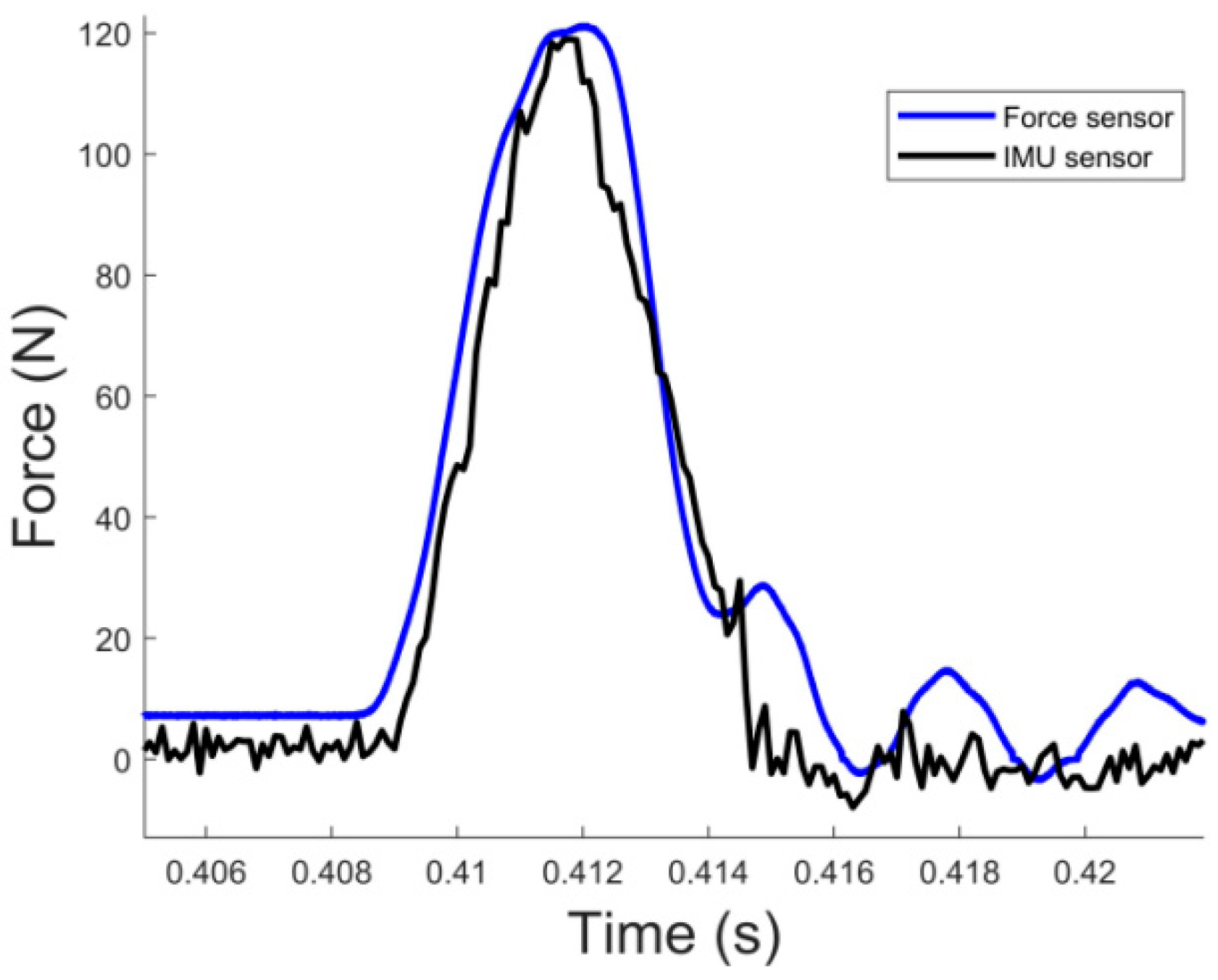
2.2. Modeling and Impact-Factor Analysis of Collision
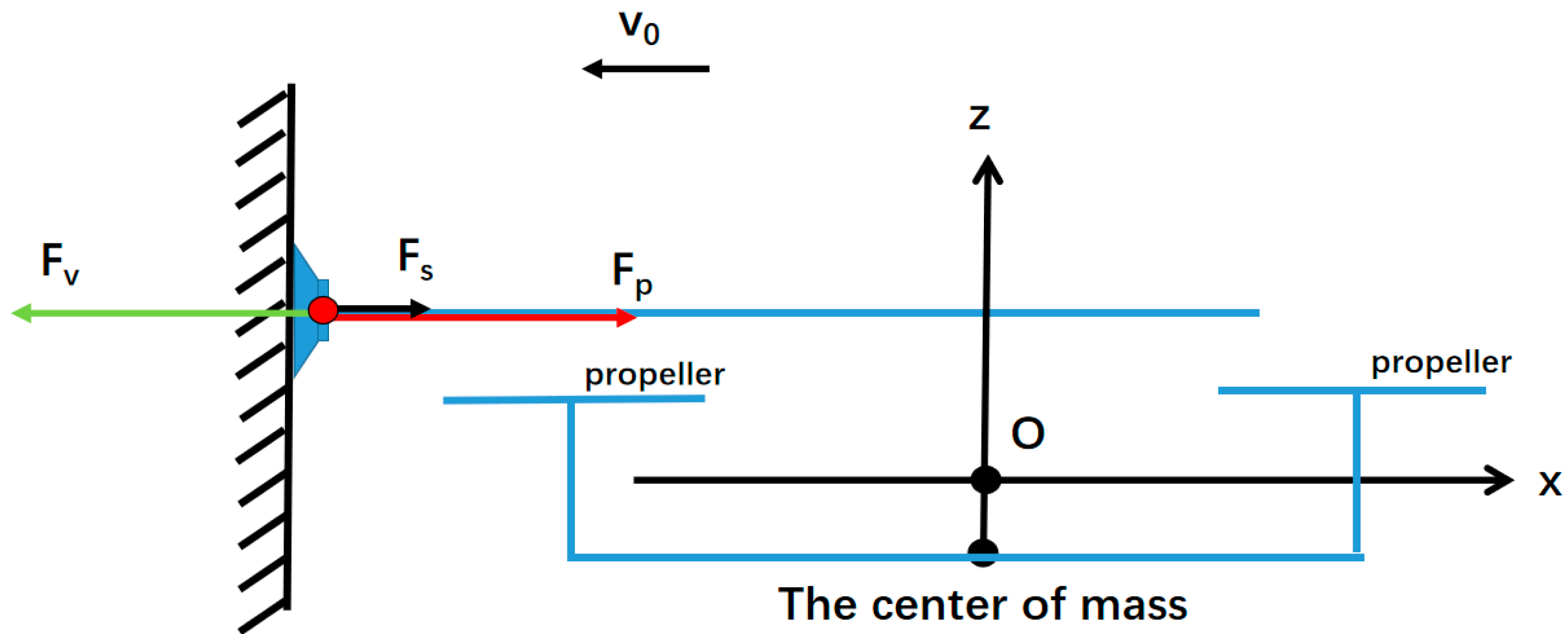
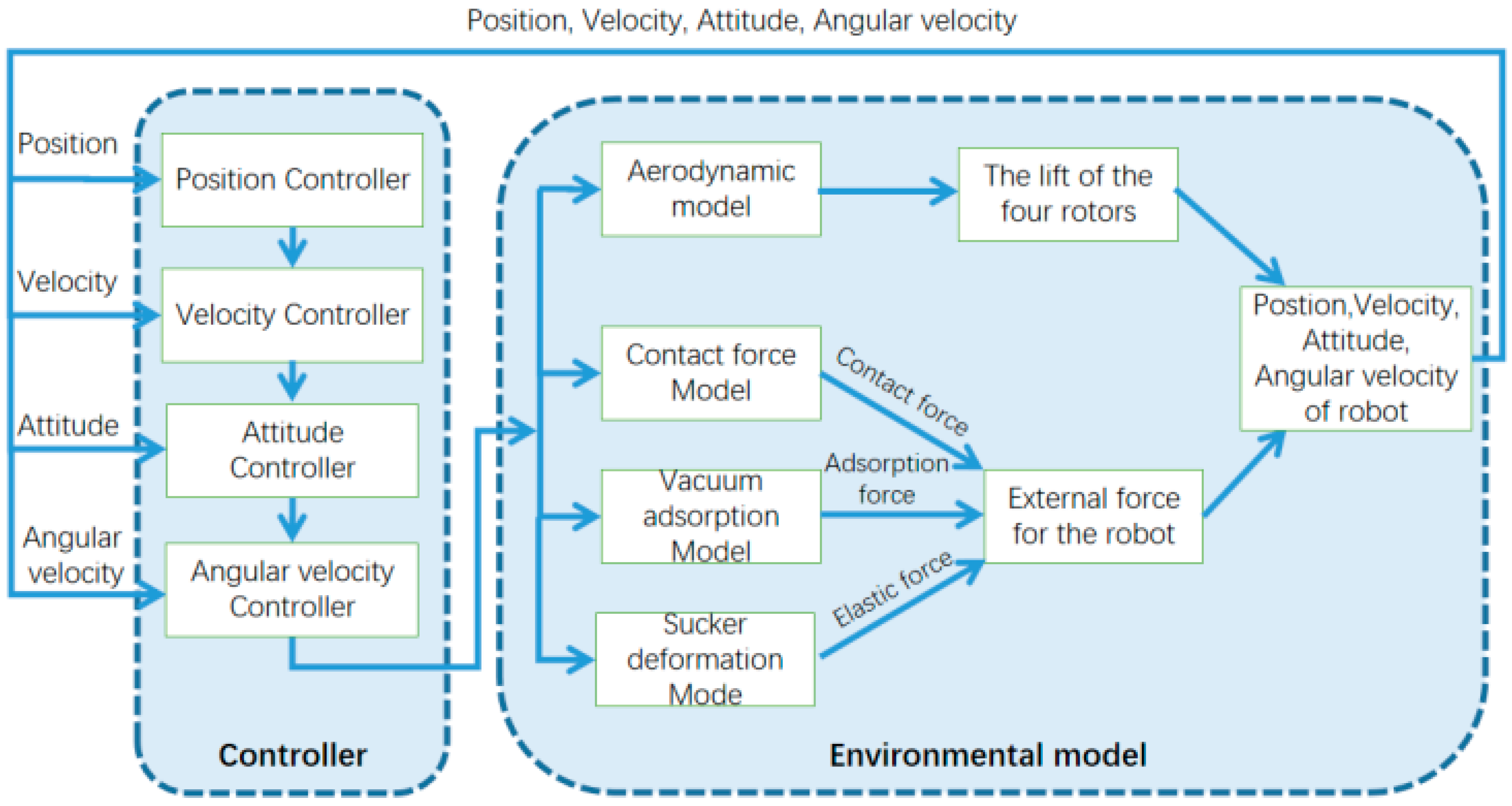
2.3. Approach-Process Modeling and Control
3. Simulation
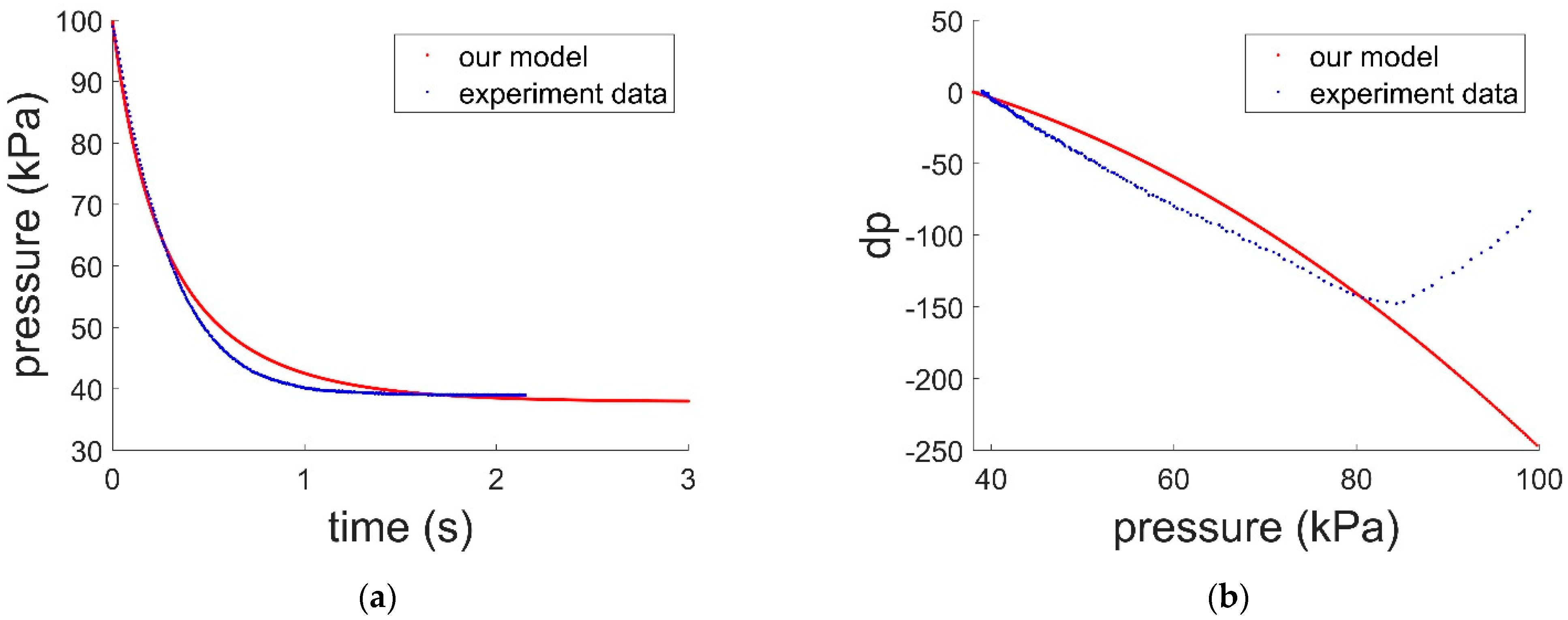
3.1. Determining the Elasticity Coefficient of the Suction Cup
3.2. Determining the Leakage Rate of the Suction Cup
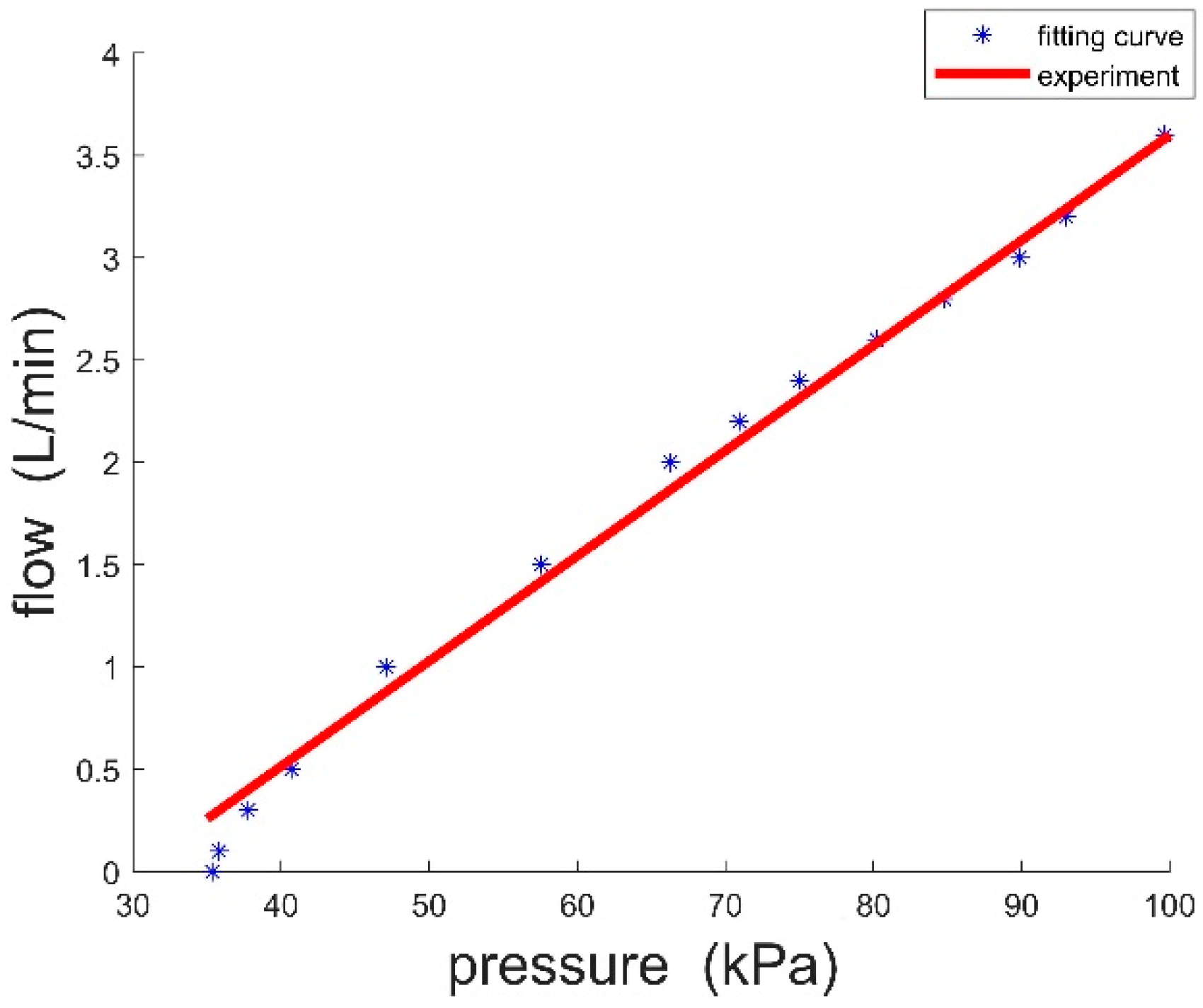
3.3. Determining the Curve between Air Pressure and Flow
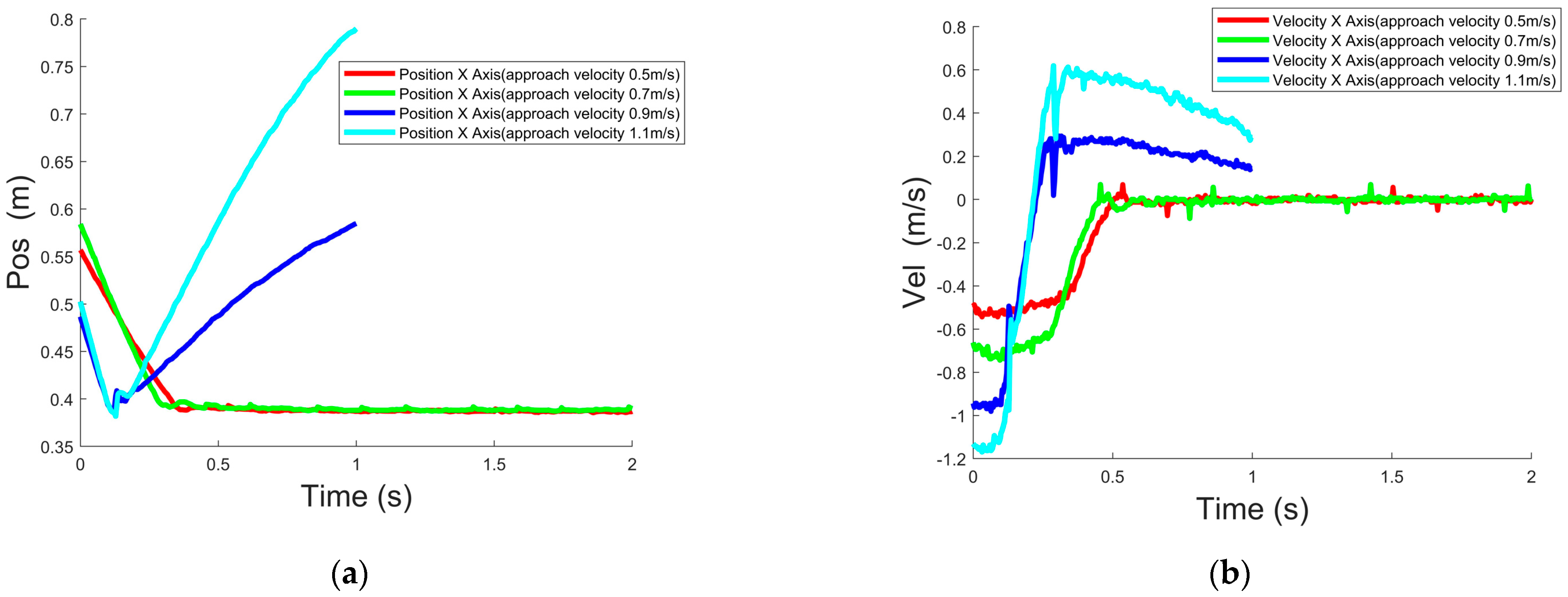
3.4. Simulation of Collision Flight-Adsorption System under Matlab at Different Velocity
4. Experiment
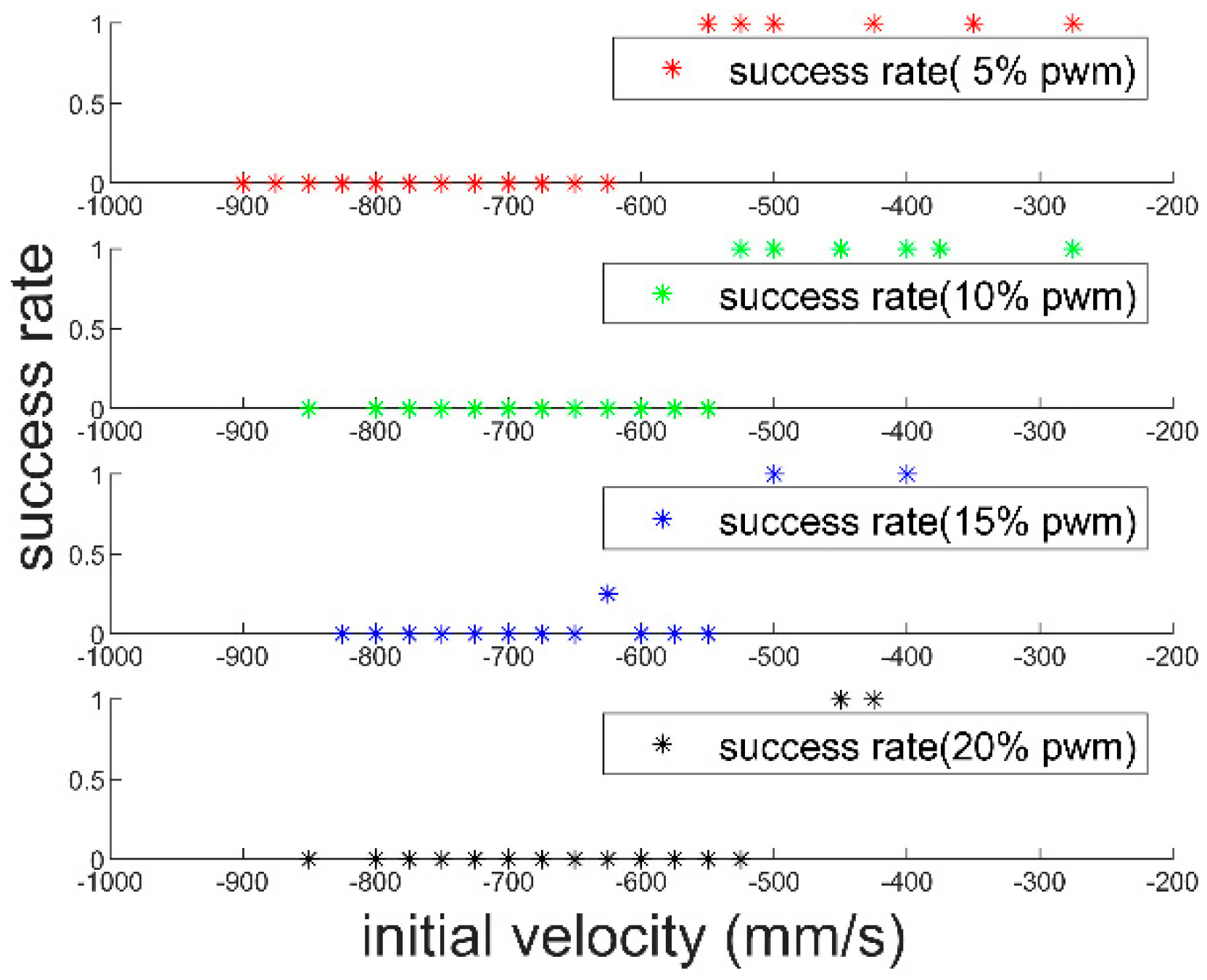
4.1. Rail Experiment
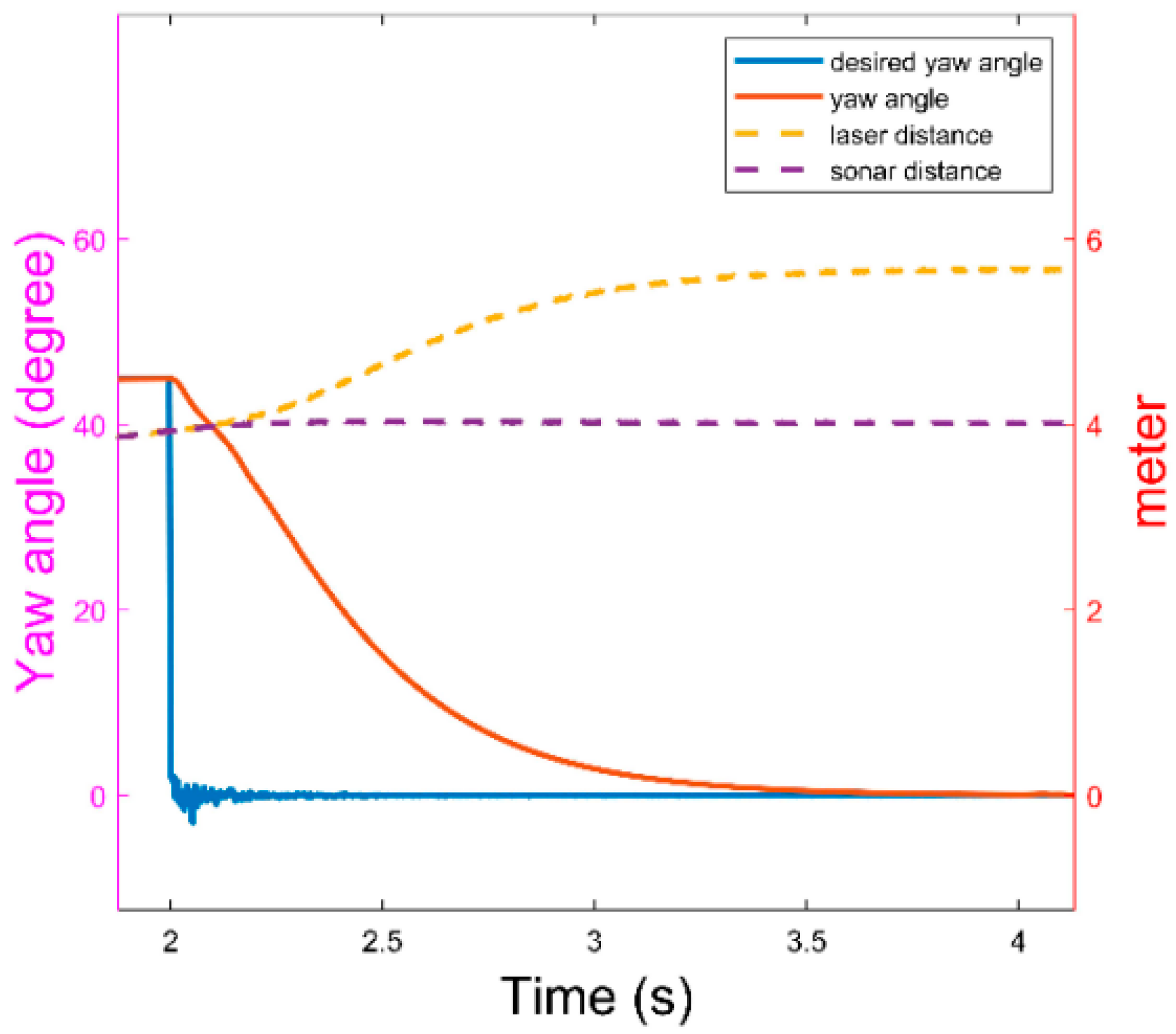
4.2. Heading-Control Experiment
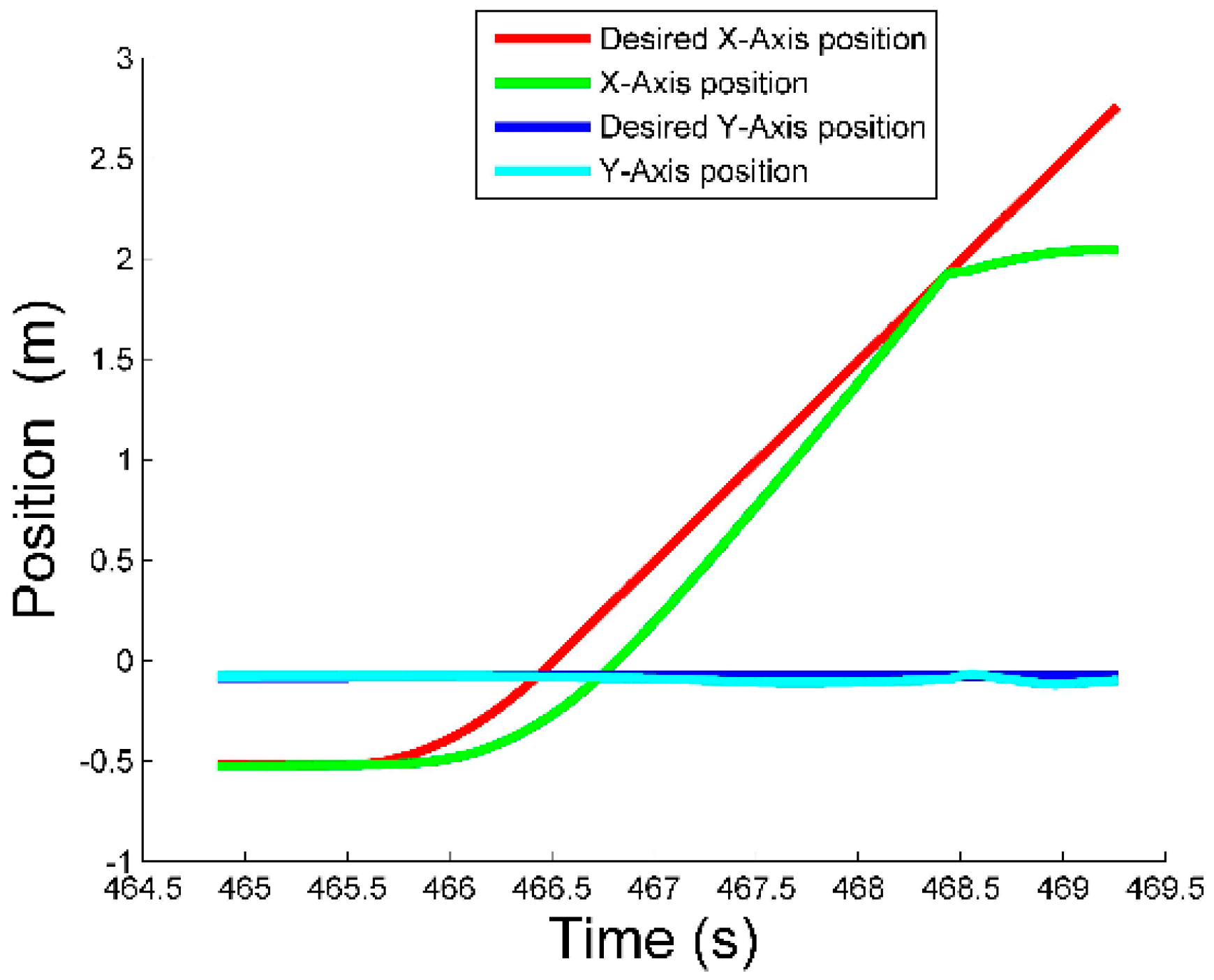
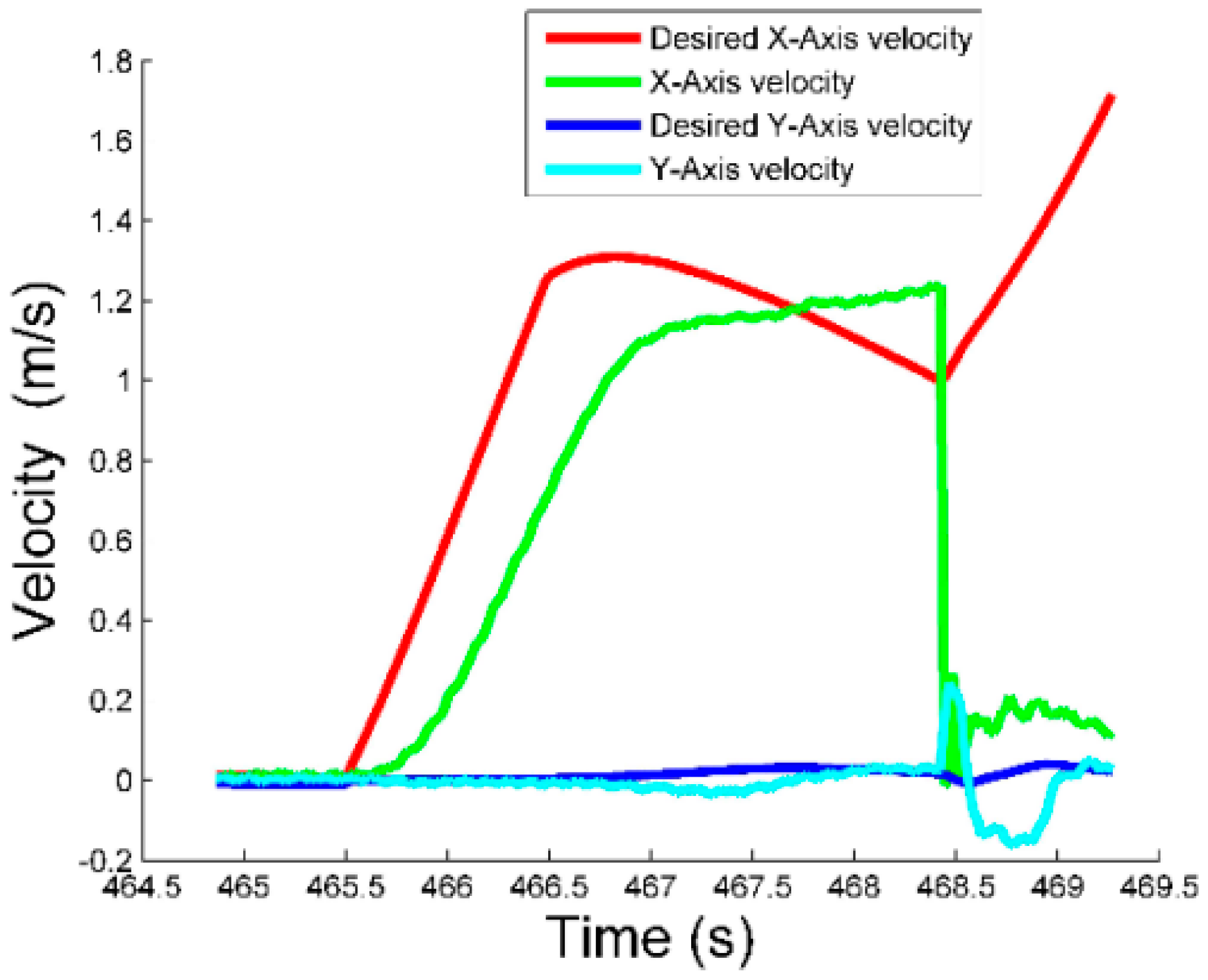
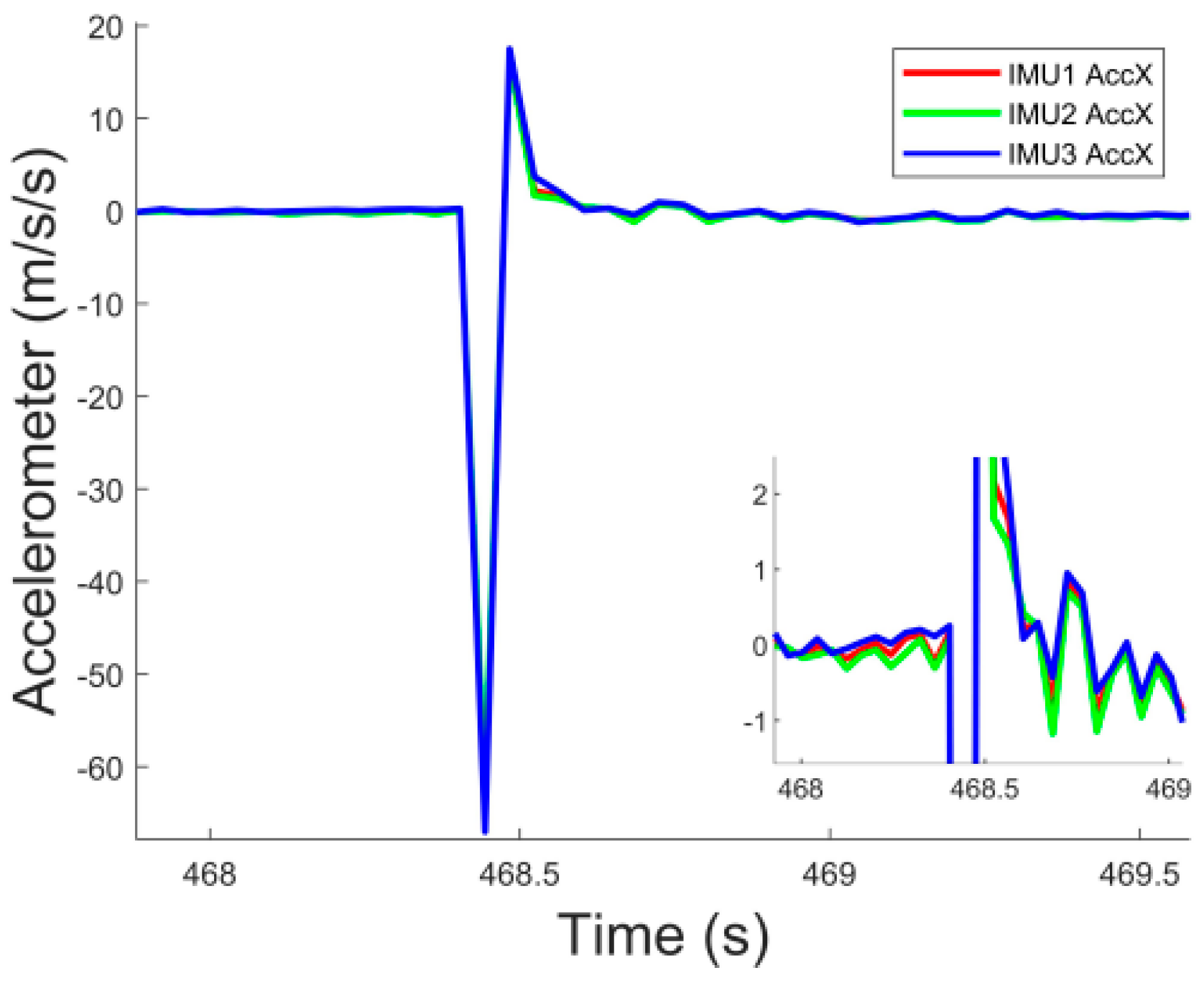
4.3. Actual Flight Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Chen, H.; Tang, Z.; Sun, G. A bat-like switched flying and adhesive robot. In Proceedings of the 2012 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Bangkok, Thailand, 27–31 May 2012; pp. 92–97. [Google Scholar]
- Liu, Y.; Sun, G.; Chen, H. Impedance control of a bio-inspired flying and adhesion robot. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3564–3569. [Google Scholar]
- Albers, A.; Trautmann, S.; Howard, T.; Nguyen, T.; Frietsch, M.; Sauter, C. Semi-autonomous flying robot for physical interaction with environment. In Proceedings of the 2010 IEEE International Conference on Robotics, Automation and Mechatronics (RAM), Singapore, 28–30 June 2010; pp. 441–446. [Google Scholar]
- Nguyen, H.; Lee, D. Hybrid force/motion control and internal dynamics of quadrotors for tool operation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Bellens, S.; De Schutter, J.; Bruyninckx, H. A hybrid pose/wrench control framework for quadrotor helicopters. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2269–2274. [Google Scholar]
- Mersha, A.Y.; Stramigioli, S.; Carloni, R. Variable impedance control for aerial interaction. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Jung, S. An Impedance Force Control Approach to a Quad-Rotor System Based on an Acceleration-Based Disturbance Observer. J. Intell. Robot. Syst. 2014, 73, 175–185. [Google Scholar] [CrossRef]
- Kalantari, A.; Mahajan, K.; Ruffatto, D.; Spenko, M. Autonomous perching and take-off on vertical walls for a quadrotor micro air vehicle. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Liu, Z.; Karydis, K. Toward Impact-resilient Quadrotor Design, Collision Characterization and Recovery Control to Sustain Flight after Collisions. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Chui, F.; Dicker, G.; Sharf, I. Dynamics of a quadrotor undergoing impact with a wall. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016. [Google Scholar]
- Dicker, G.; Chui, F.; Sharf, I. Quadrotor collision characterization and recovery control. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017. [Google Scholar]
- Battiston, A.; Sharf, I.; Nahon, M. Attitude estimation for normal flight and collision recovery of a quadrotor UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017. [Google Scholar]
- Dicker, G.; Sharf, I.; Rustagi, P. Recovery Control for Quadrotor UAV Colliding with a Pole. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Wang, S.; Anselmo, N.; Garrett, M.; Remias, R.; Trivett, M.; Christoffersen, A.; Bezzo, N. Fly-Crash-Recover: A Sensor-based Reactive Framework for Online Collision Recovery of UAVs. In Proceedings of the 2020 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 24 April 2020. [Google Scholar]
- Liu, J.; Tanaka, K.; Bao, L.M.; Yamaura, I. Analytical modelling of suction cups used for window-cleaning robots. Vacuum 2006, 80, 593–598. [Google Scholar] [CrossRef]
- Wang, K.; Wang, W.; Zhang, H.; Fang, J. Suction force of vibrating suction method based on pi theorem: Analysis and experiment. Vacuum 2012, 86, 1783–1788. [Google Scholar] [CrossRef]
- Ge, D.; Matsuno, T.; Sun, Y.; Ren, C.; Tang, Y.; Ma, S. Quantitative study on the attachment and detachment of a passive suction cup. Vacuum 2015, 116, 13–20. [Google Scholar] [CrossRef]
- Mao, J.; Li, G.; Nogar, S.; Kroninger, C.; Loianno, G. Aggressive Visual Perching with Quadrotors on Inclined Surfaces. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Wang, X.; Liu, Y.; Huang, C. Research on Finite Ground Effect of a Rotor. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 6935–6940. [Google Scholar]
- Da, D. Vacuum Design Manual; National Defense Industry Press: Beijing, China, 2004. [Google Scholar]
- Yan, Z.; Huang, S. A Study of Relation to Leak Rate and Pressure. Chin. Space Sci. Technol. 1999, 2, 42–46. [Google Scholar]



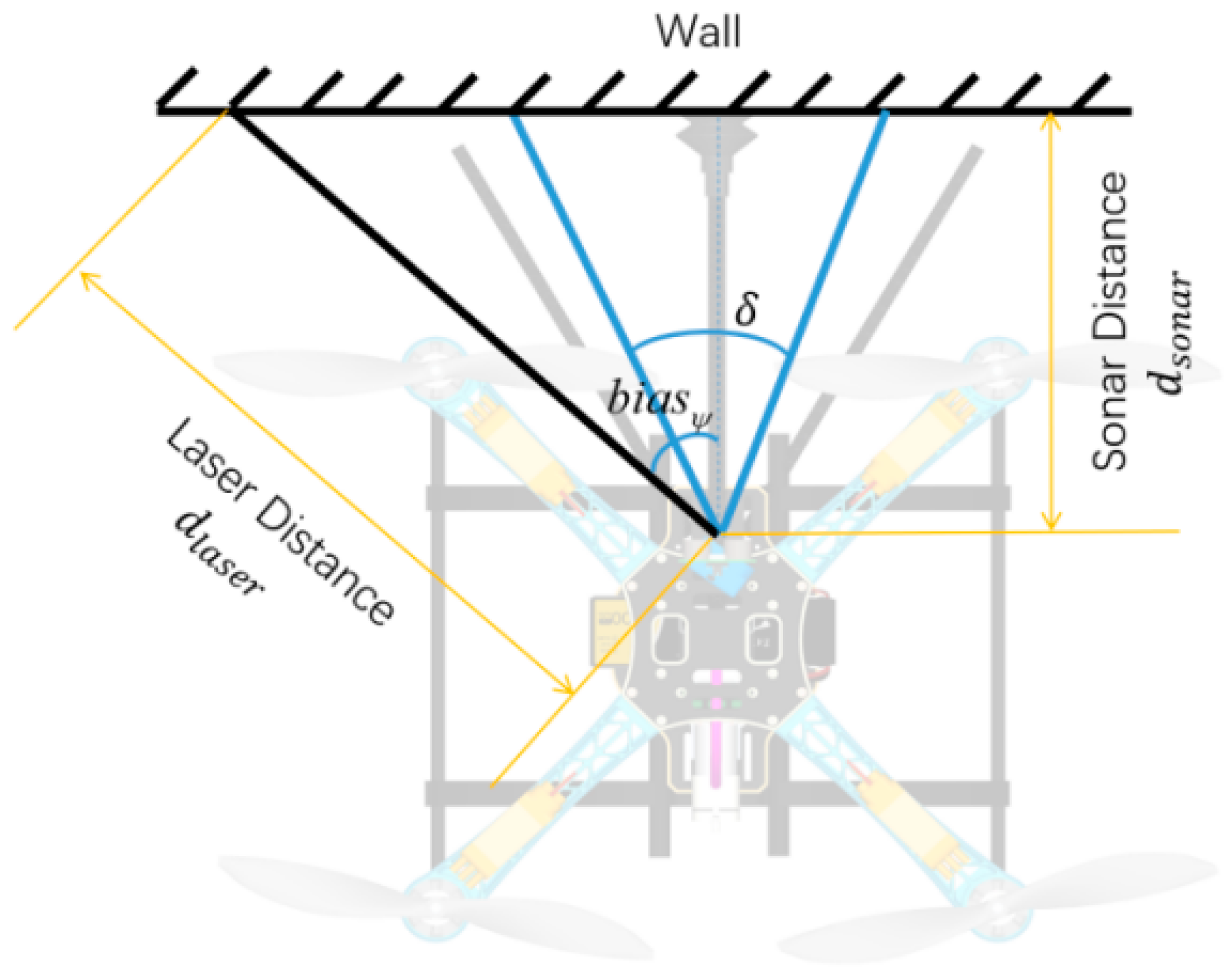

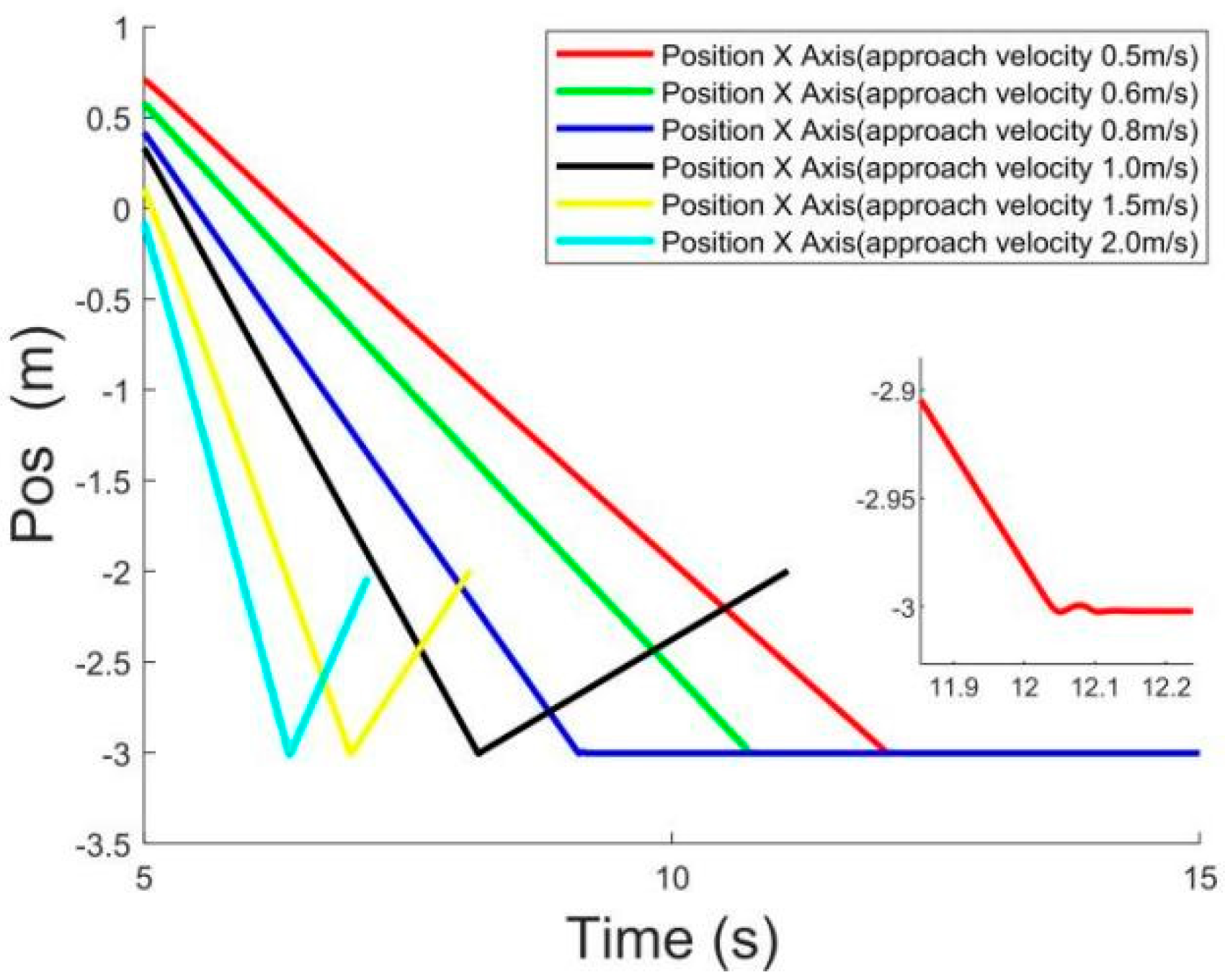

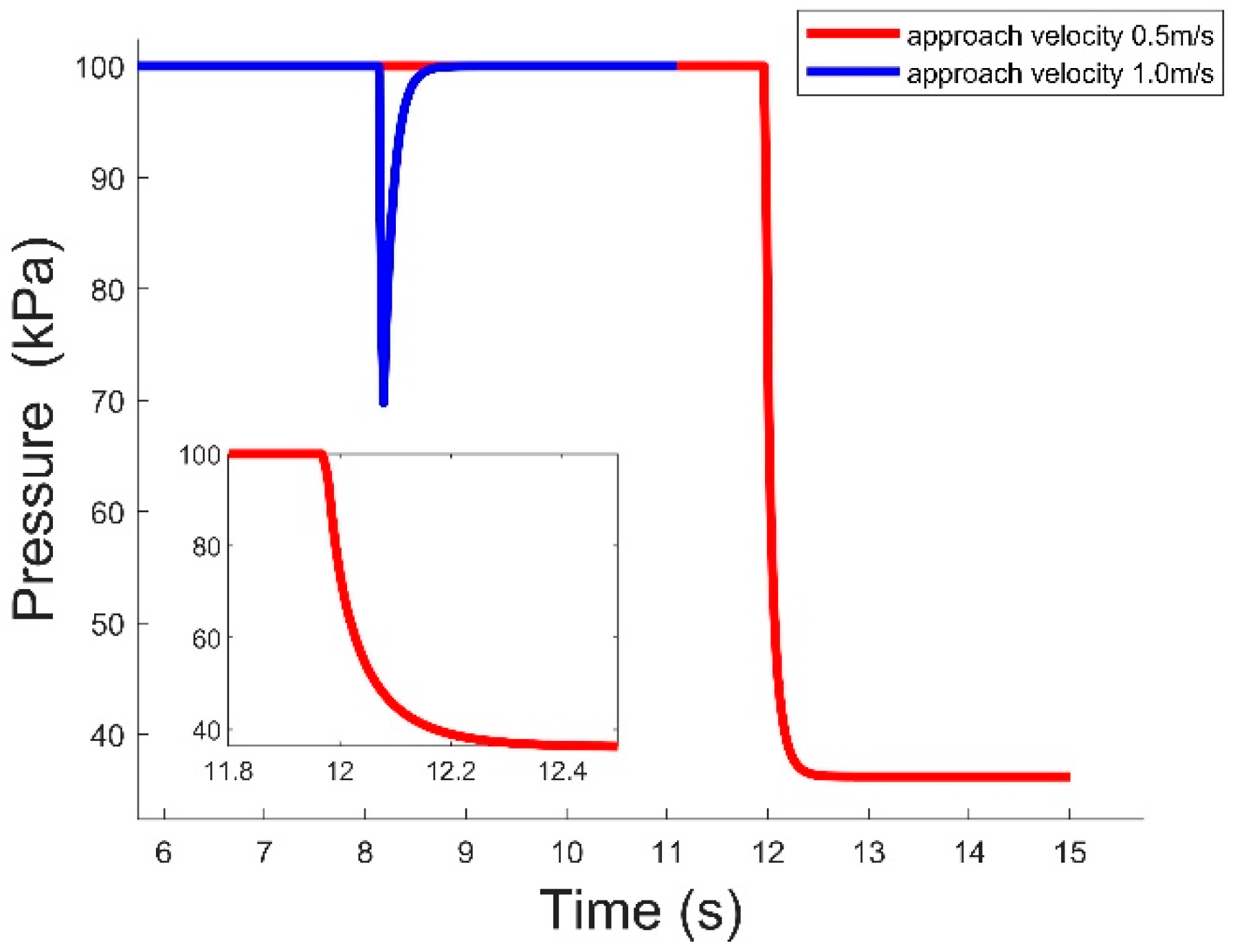
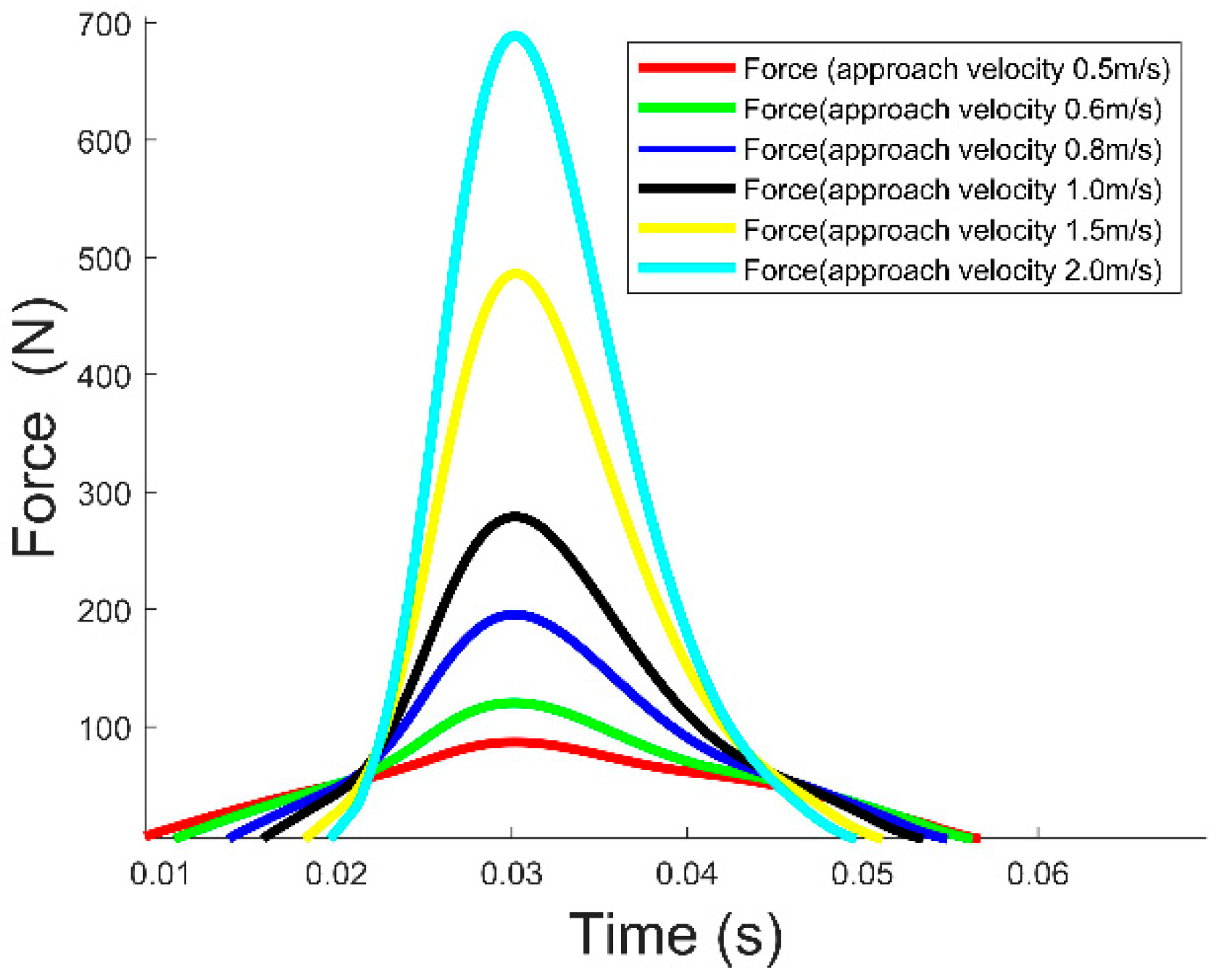

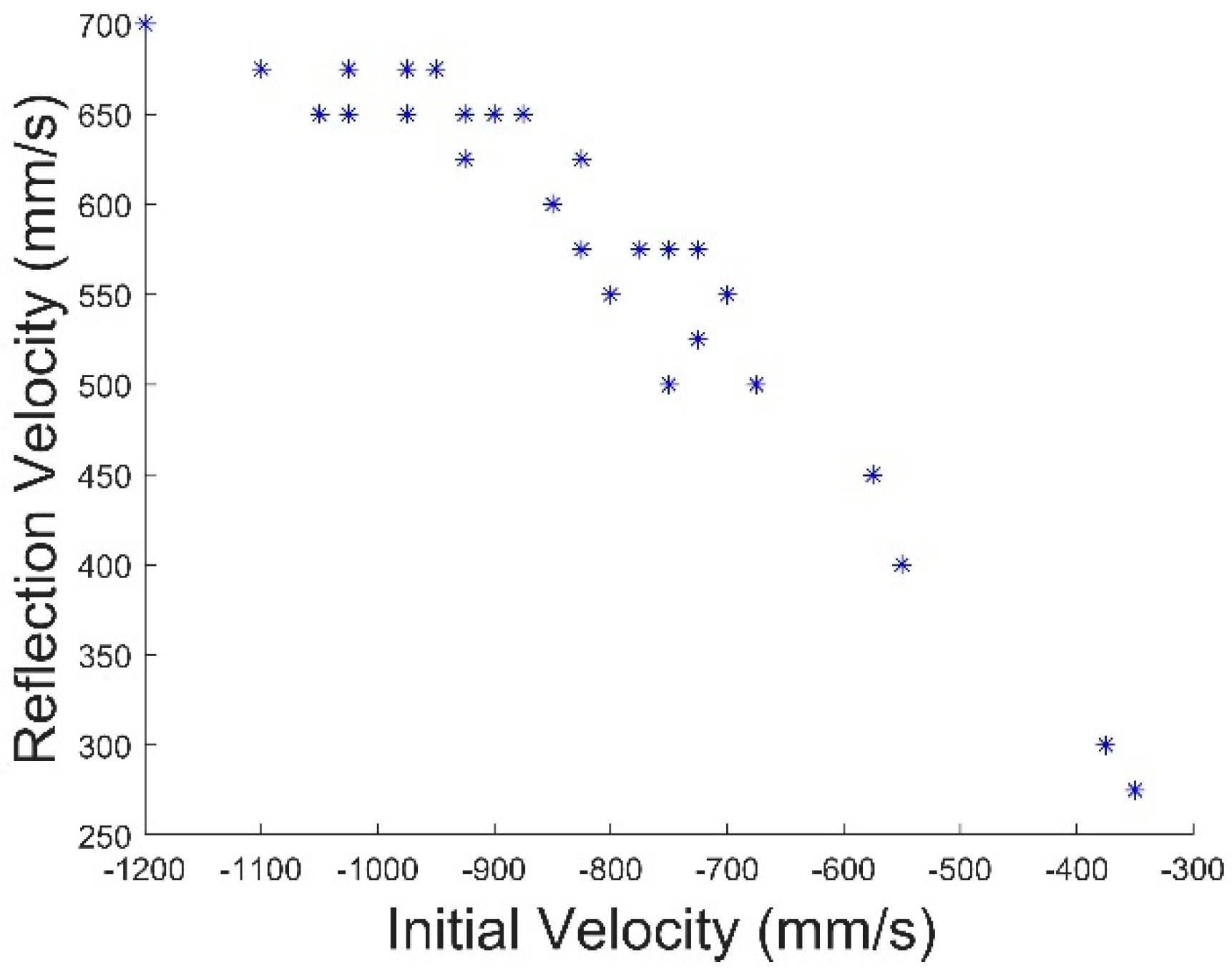




| Laser Distance (mm) | Sonar Distance (mm) | Angle from Equation (Degree) | Angle from Optitrack (Degree) | Error Angle (Degree) |
|---|---|---|---|---|
| 1335 | 997 | 0.00 | 0 | 0.00 |
| 1451 | 1004 | −4.53 | −5 | −0.47 |
| 1598 | 1008 | −9.21 | −10 | −0.79 |
| 1827 | 1021 | −14.34 | −15 | −0.66 |
| 1229 | 1005 | 6.54 | 5 | −1.54 |
| 1157 | 1002 | 11.69 | 10 | −1.69 |
| 1099 | 993 | 16.31 | 15 | −1.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Liu, Y.; Bai, B.; Wang, K. The Flying and Adhesion Robot Based on Approach and Vacuum. Aerospace 2022, 9, 228. https://doi.org/10.3390/aerospace9050228
Huang C, Liu Y, Bai B, Wang K. The Flying and Adhesion Robot Based on Approach and Vacuum. Aerospace. 2022; 9(5):228. https://doi.org/10.3390/aerospace9050228
Chicago/Turabian StyleHuang, Chengwei, Yong Liu, Bing Bai, and Ke Wang. 2022. "The Flying and Adhesion Robot Based on Approach and Vacuum" Aerospace 9, no. 5: 228. https://doi.org/10.3390/aerospace9050228
APA StyleHuang, C., Liu, Y., Bai, B., & Wang, K. (2022). The Flying and Adhesion Robot Based on Approach and Vacuum. Aerospace, 9(5), 228. https://doi.org/10.3390/aerospace9050228






