Gust Alleviation and Wind Tunnel Test by Using Combined Feedforward Control and Feedback Control
Abstract
:1. Introduction
2. Aeroelastic System Modeling and Gust Model
2.1. Aeroelastic System Modeling
2.2. System Output
2.3. State-Space Model of Actuator
2.4. Gusts Modeling
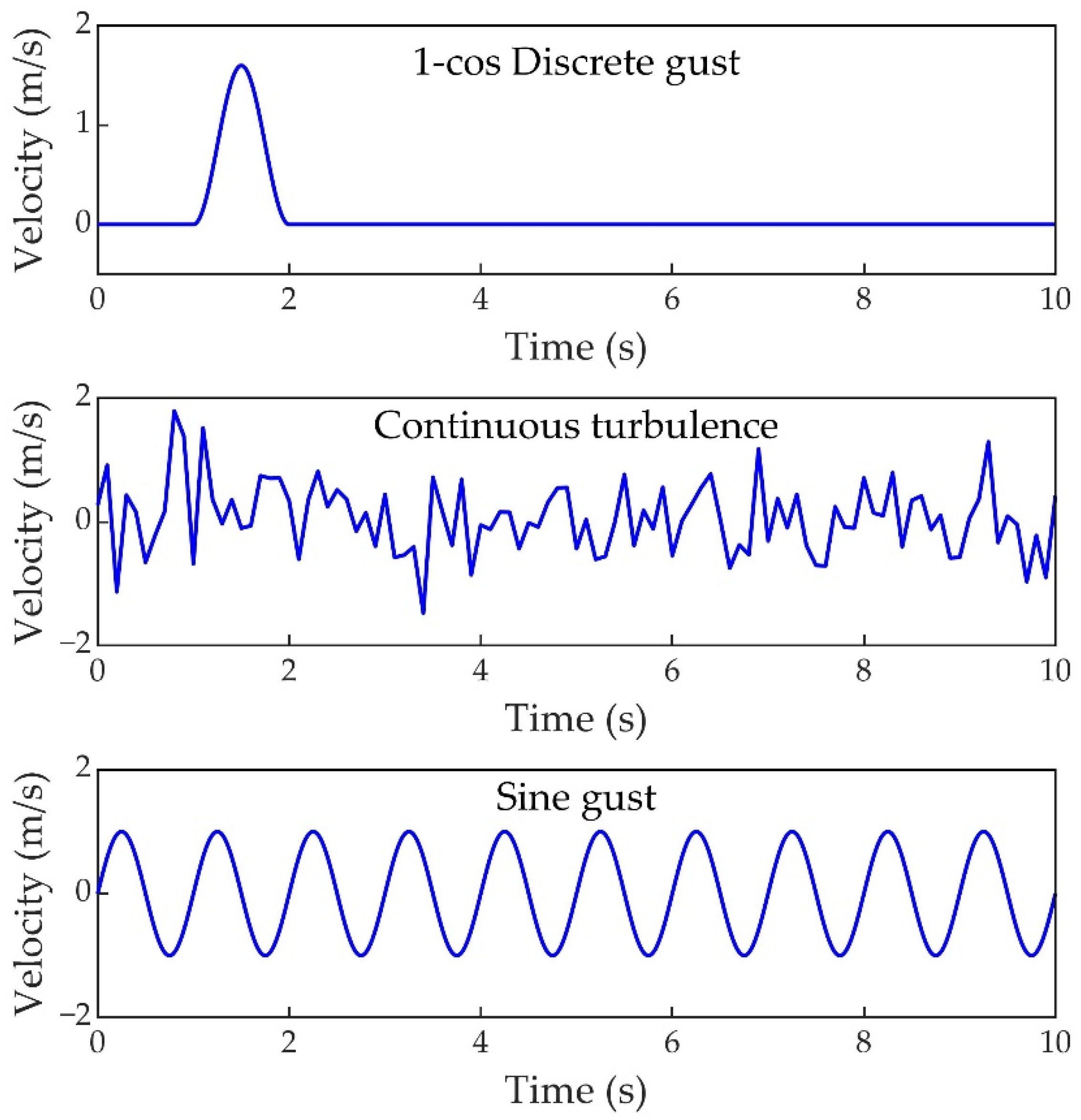
2.4.1. 1-Cos Discrete Gust
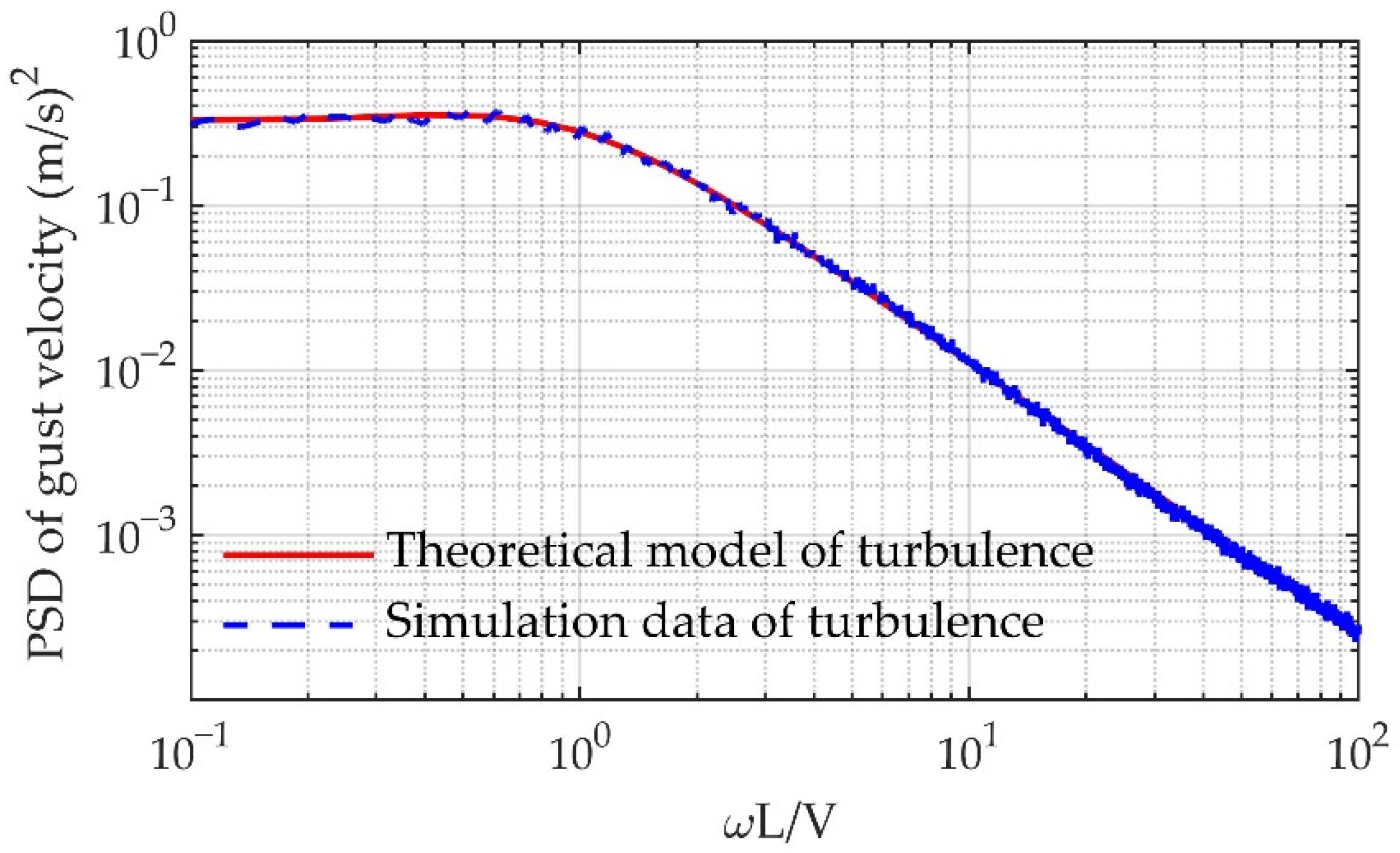
2.4.2. Continuous Turbulence
2.4.3. Sine Gust
3. Controller Design Method
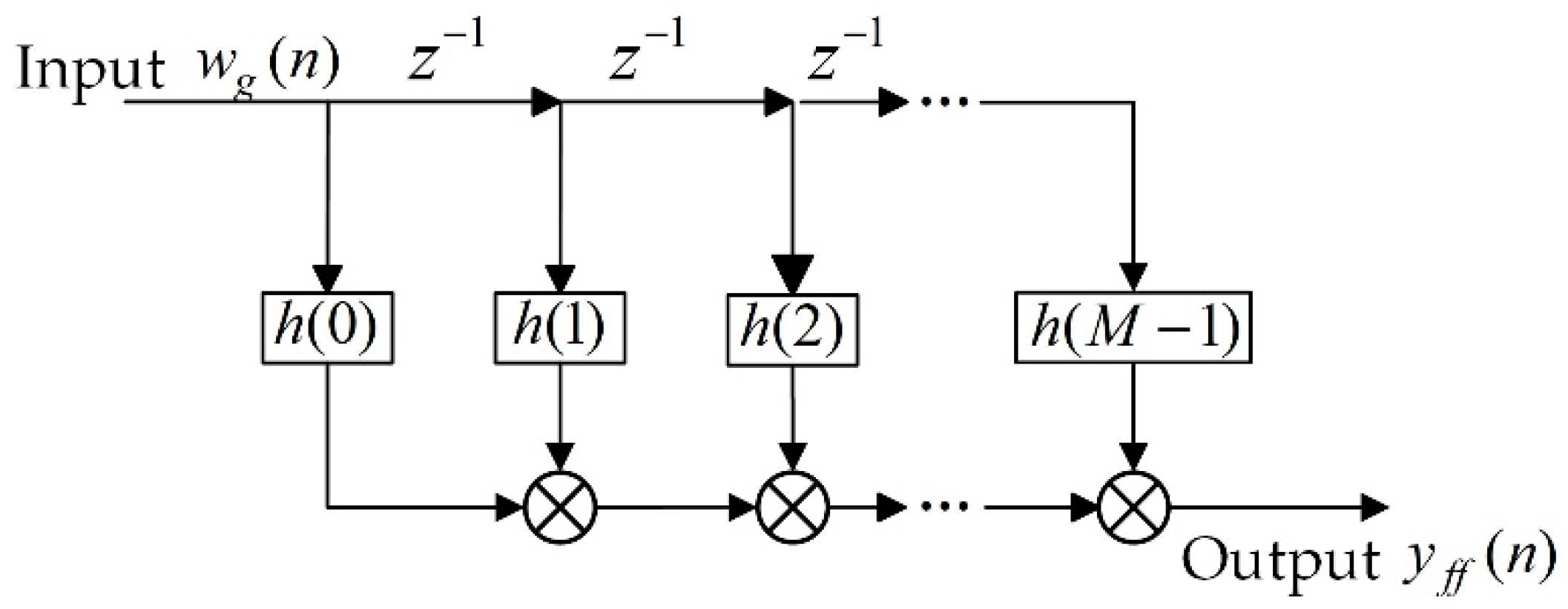
3.1. Adaptive Feedforward Controller
3.2. PID Feedback Controller
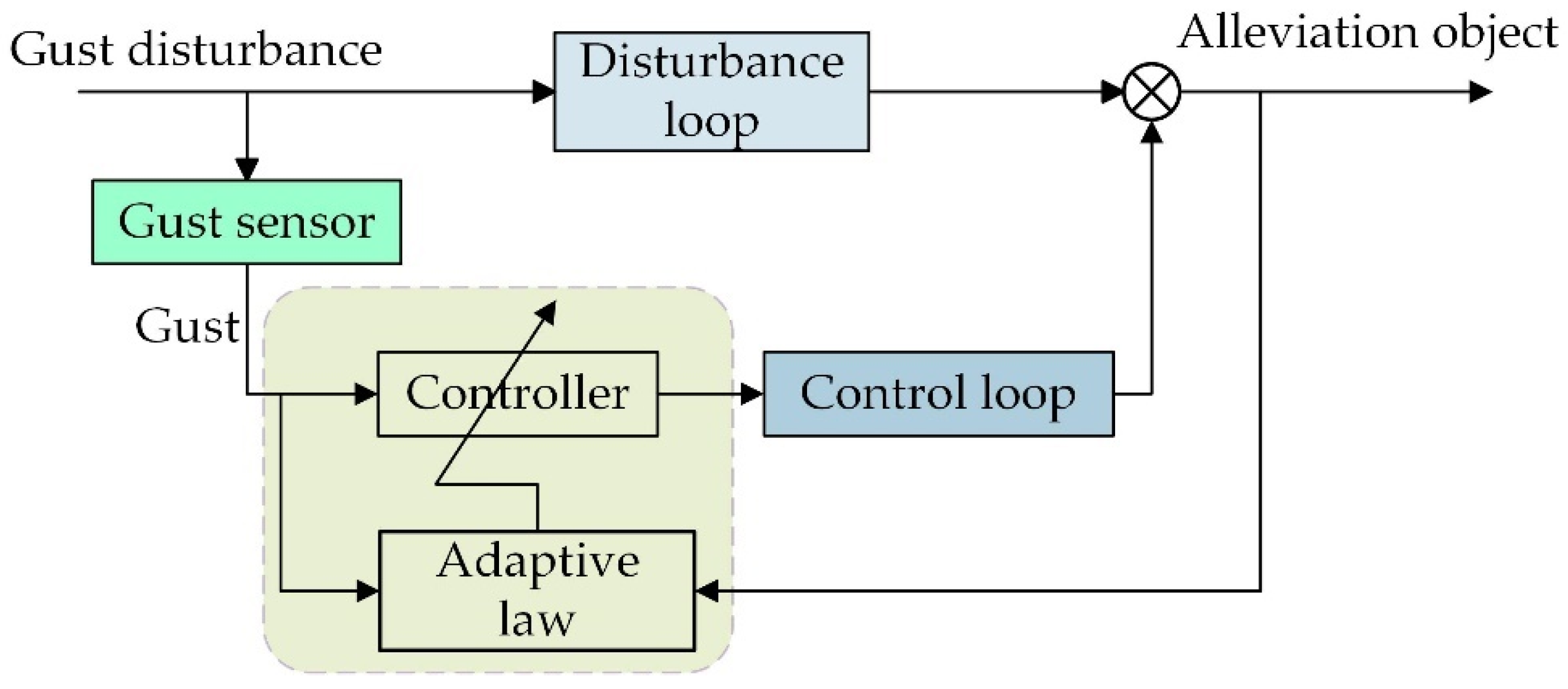
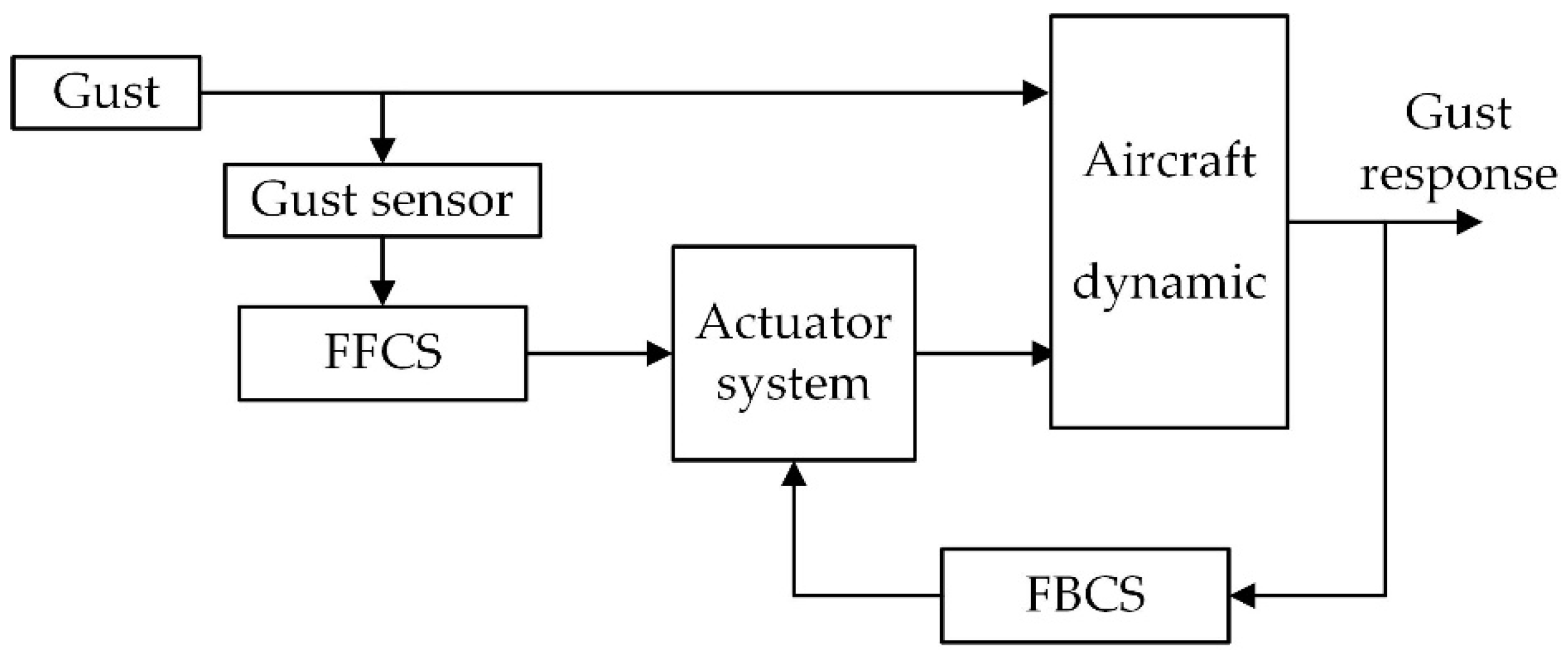
3.3. Combine Feedforward Control and Feedback Control
4. Numerical Simulation
4.1. Wing Model Description
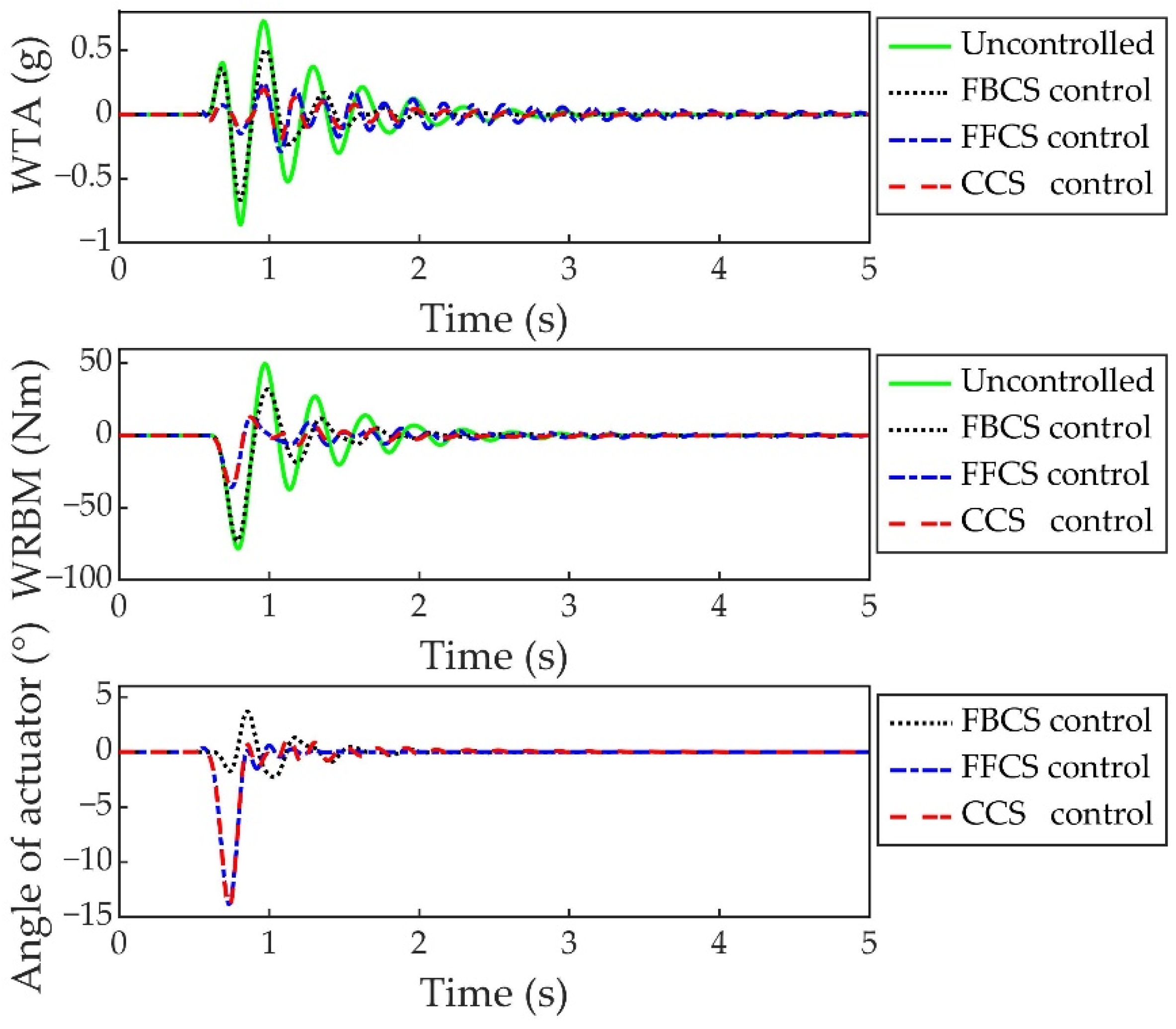
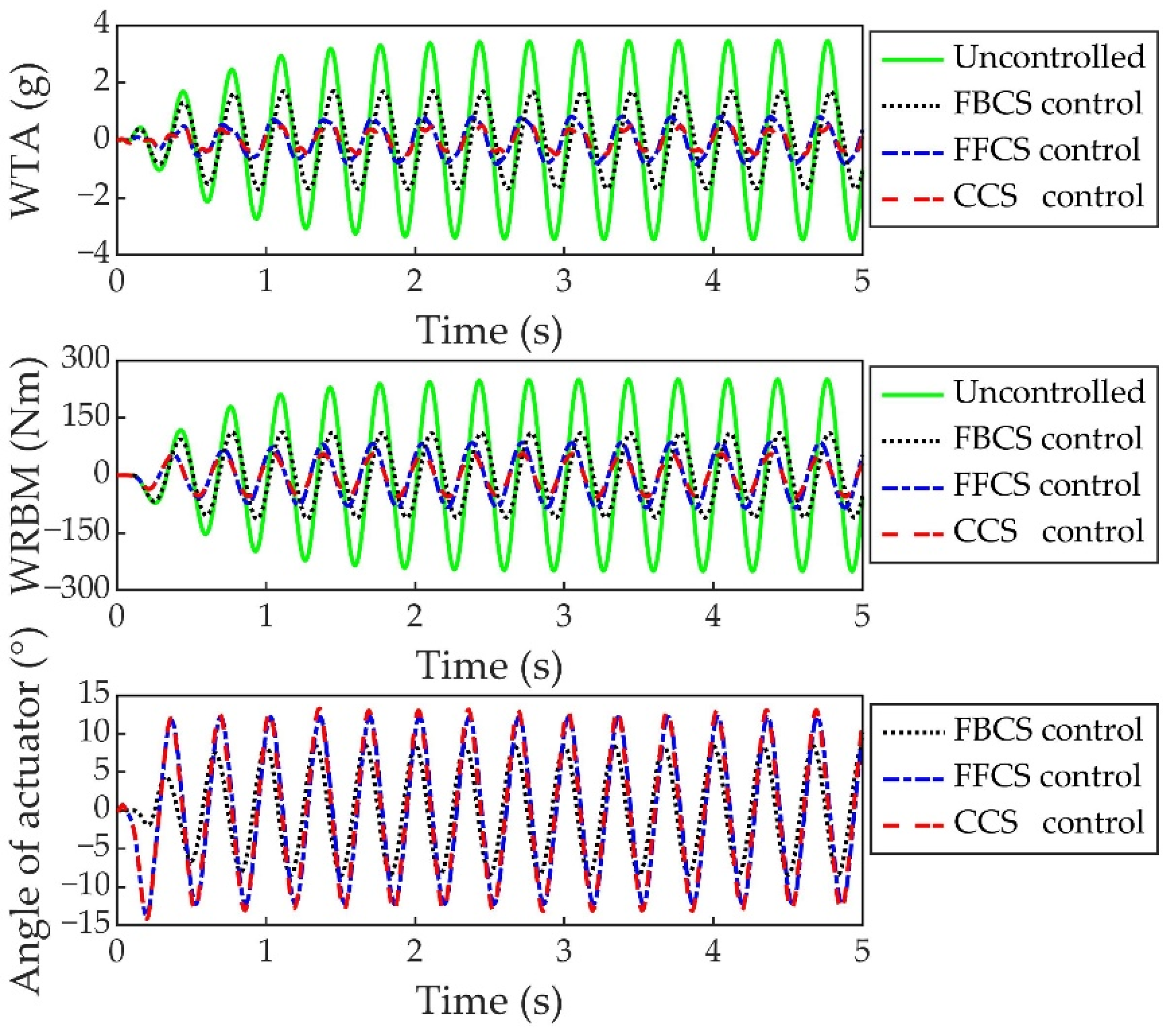
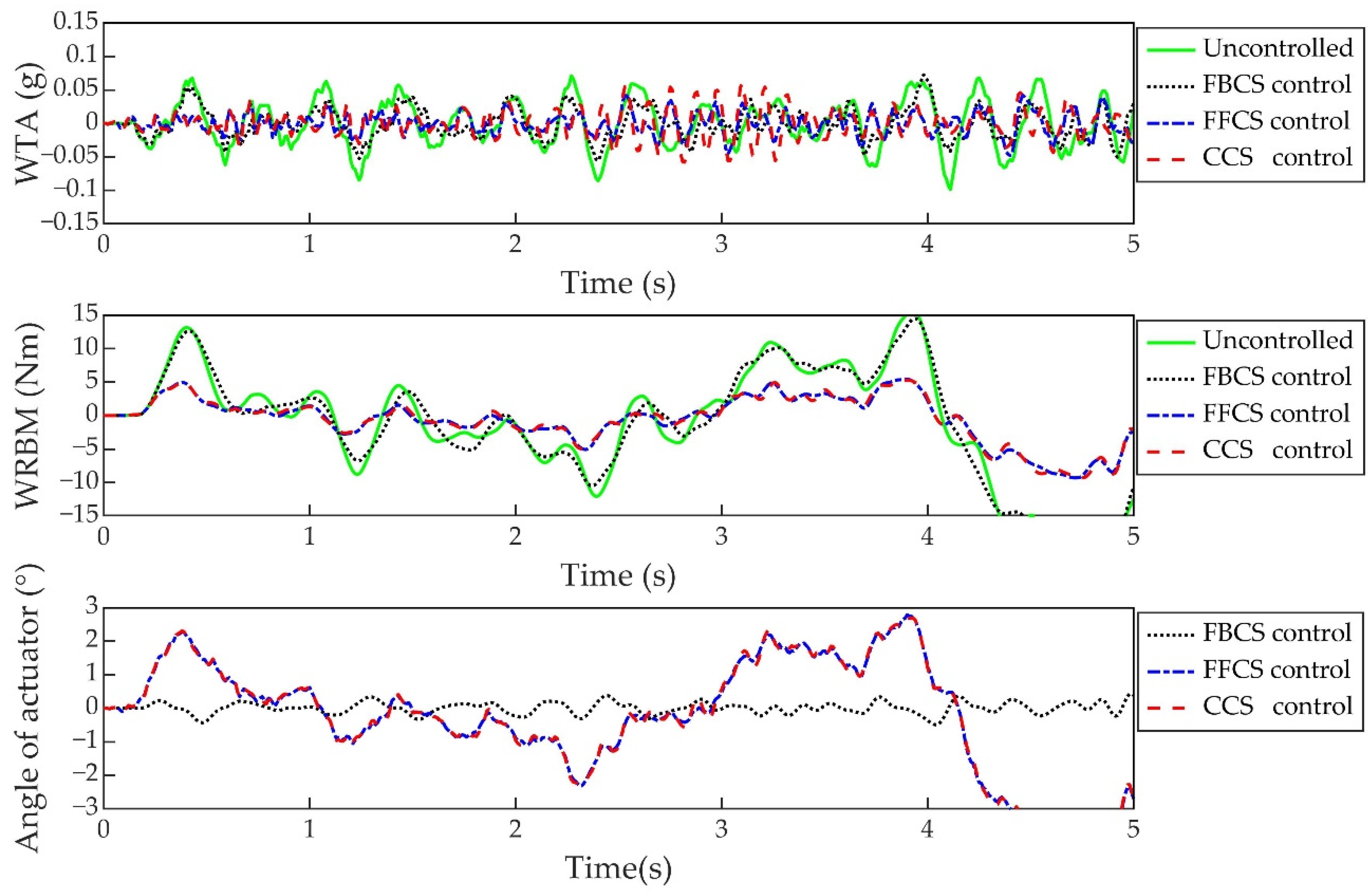
4.2. Simulation and Results Analysis
5. Wind Tunnel Test Design
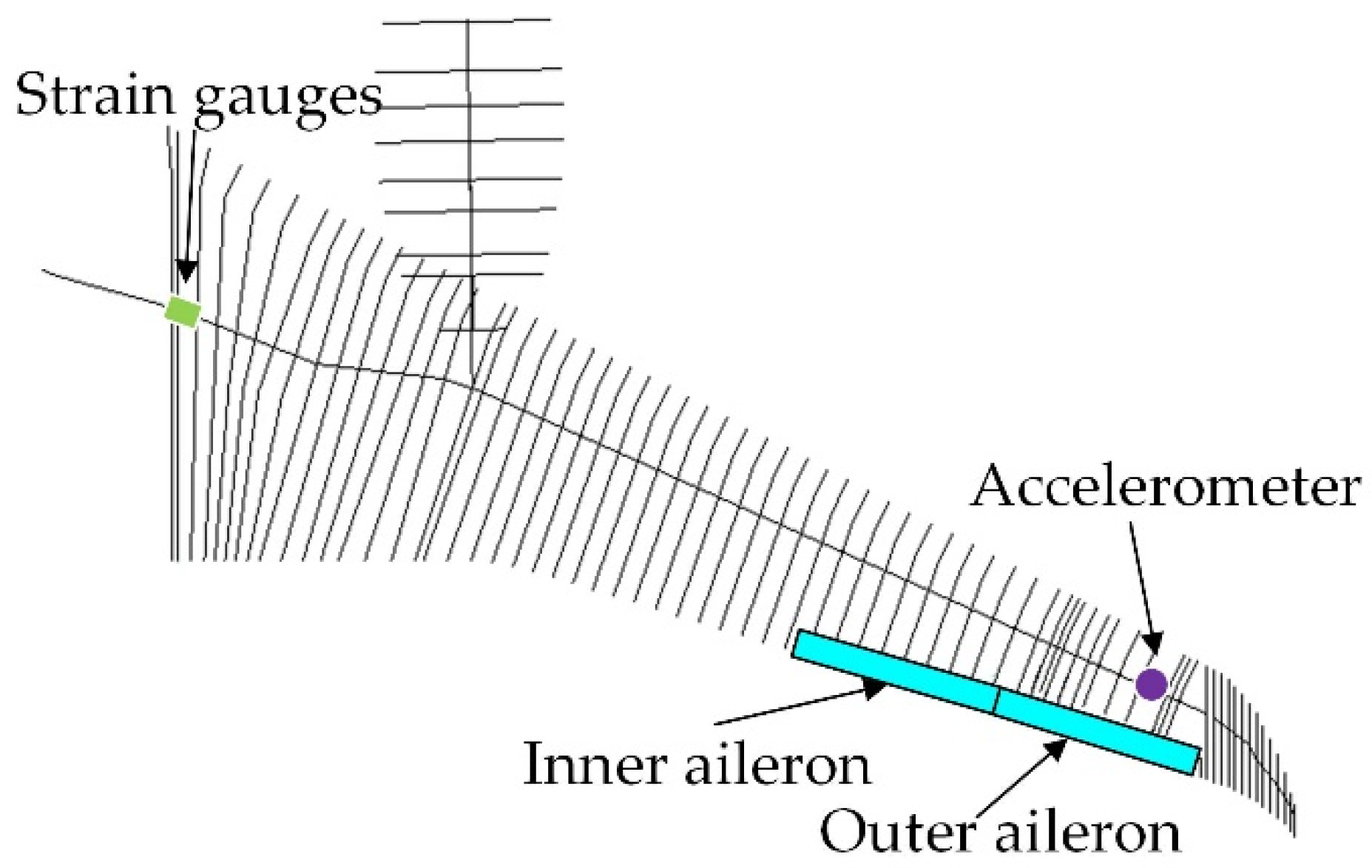
5.1. Test Model and Gust Generator
5.2. Gust Detection
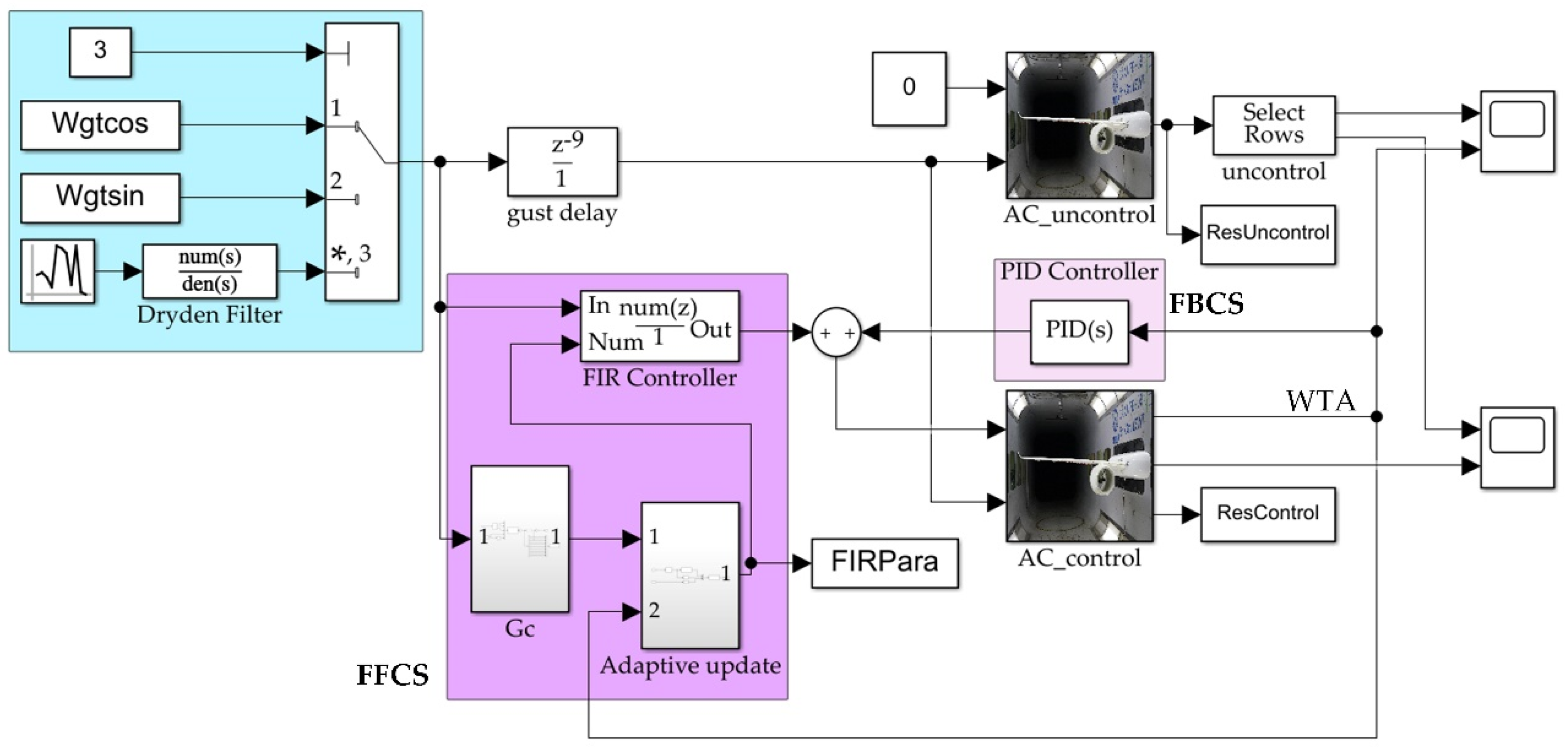
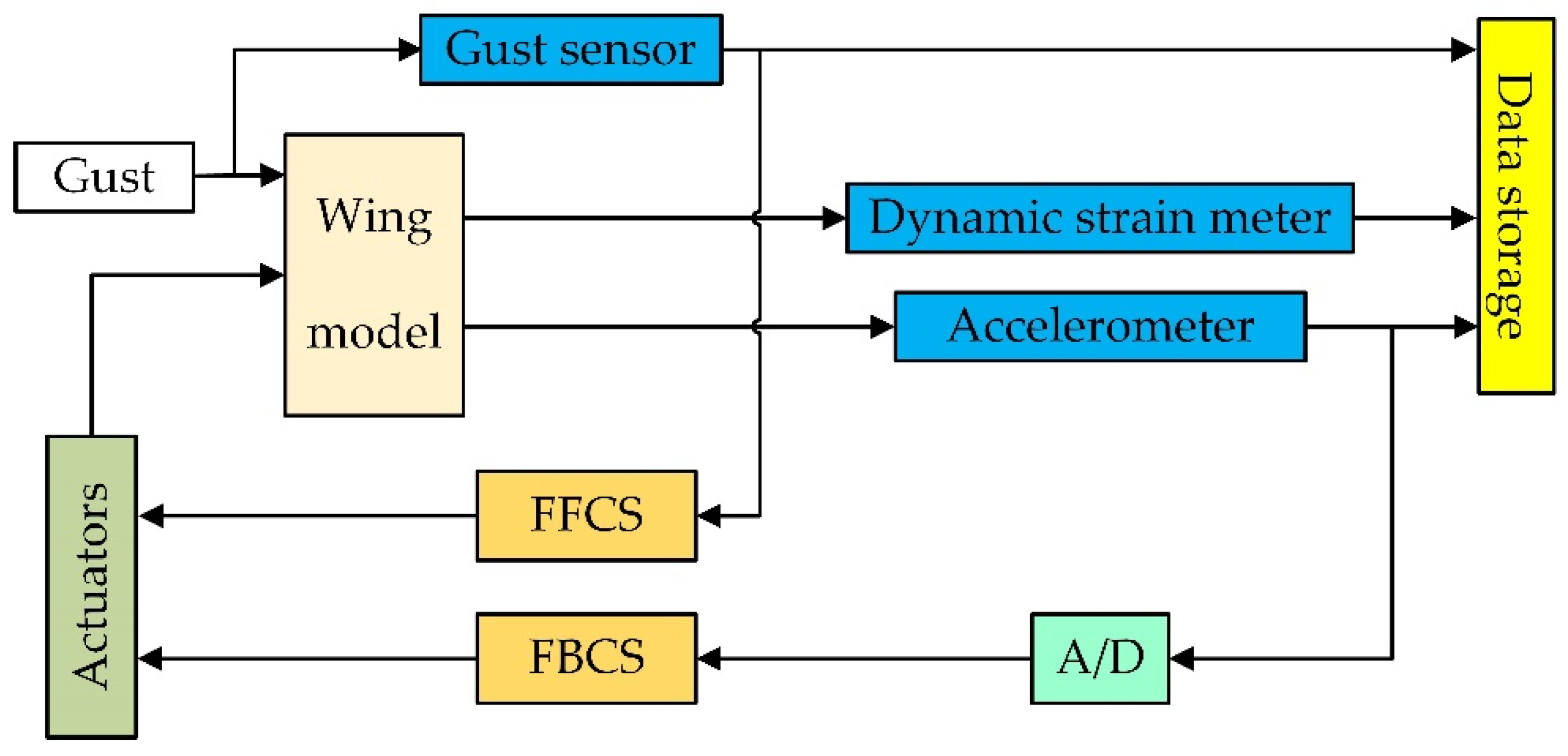
5.3. Measurement and Control System Description
6. Wind Tunnel Results and Discussion
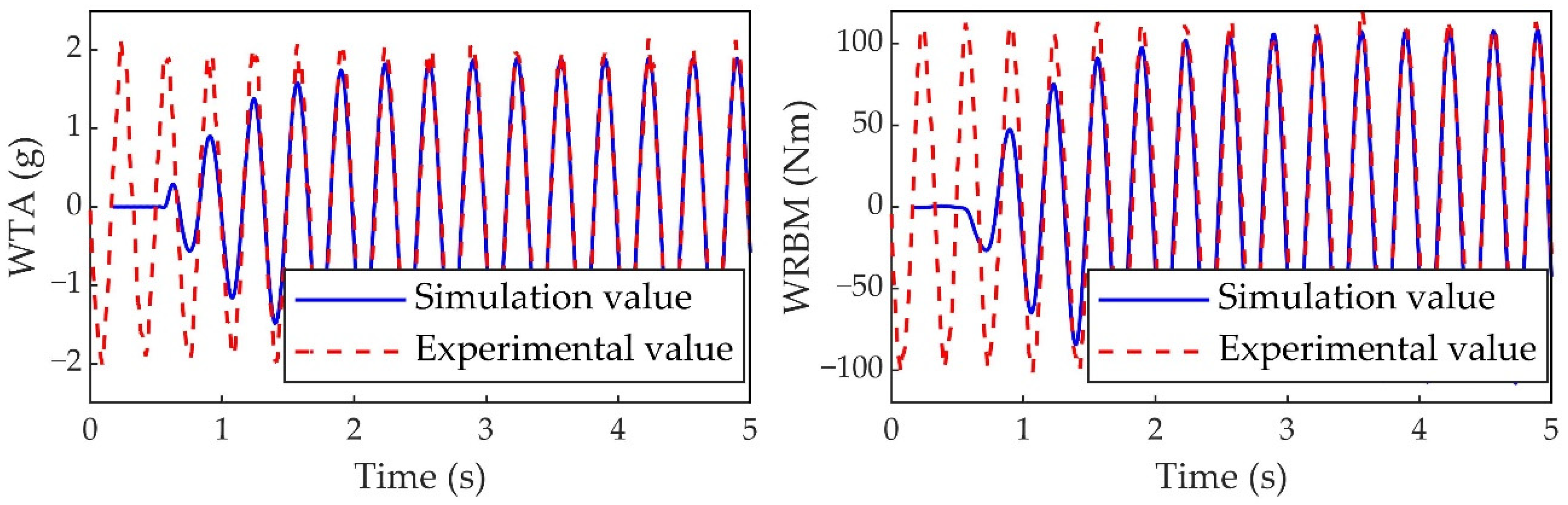
6.1. Comparison between Experiment and Numerical Simulation
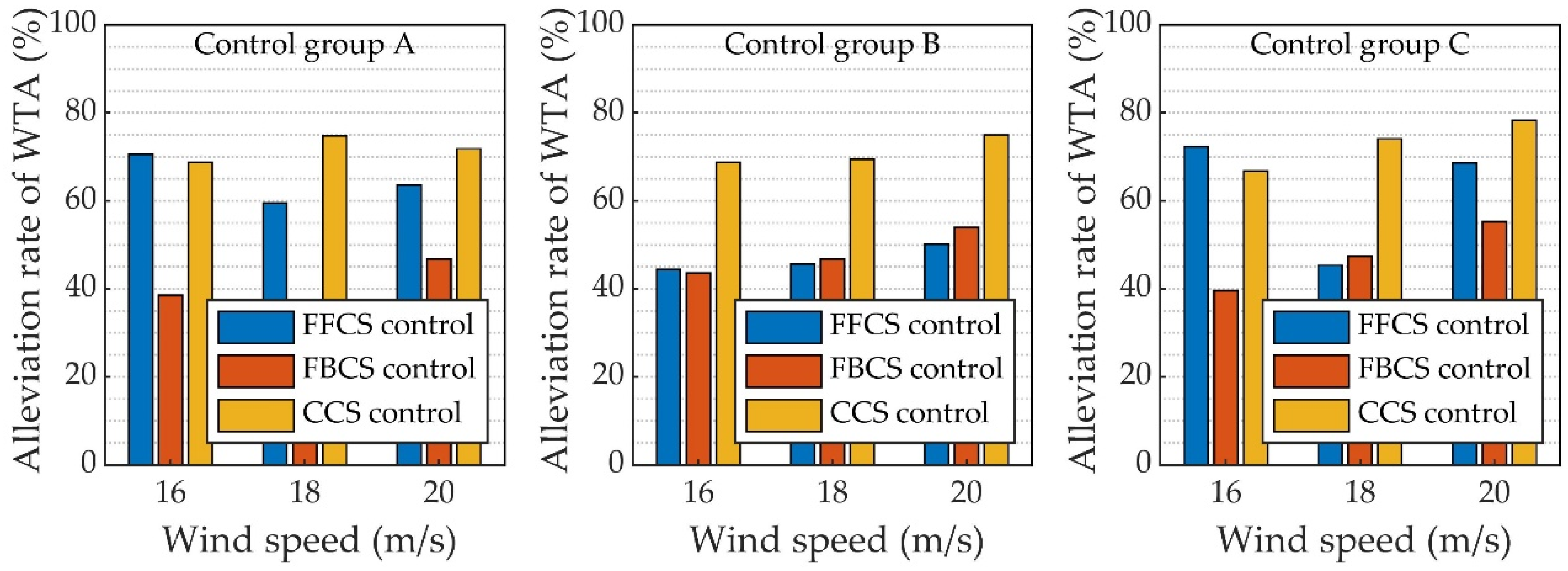
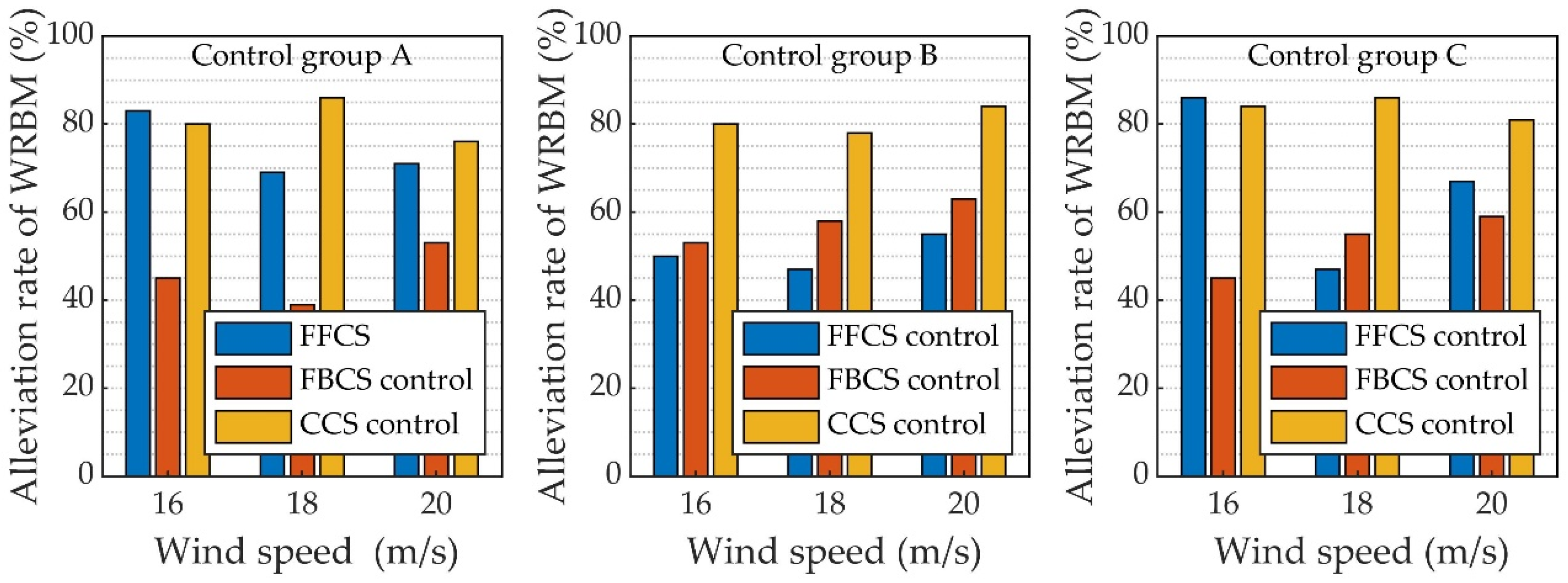
6.2. Wind Tunnel Test Results at Different Wind Speeds and Key Frequency
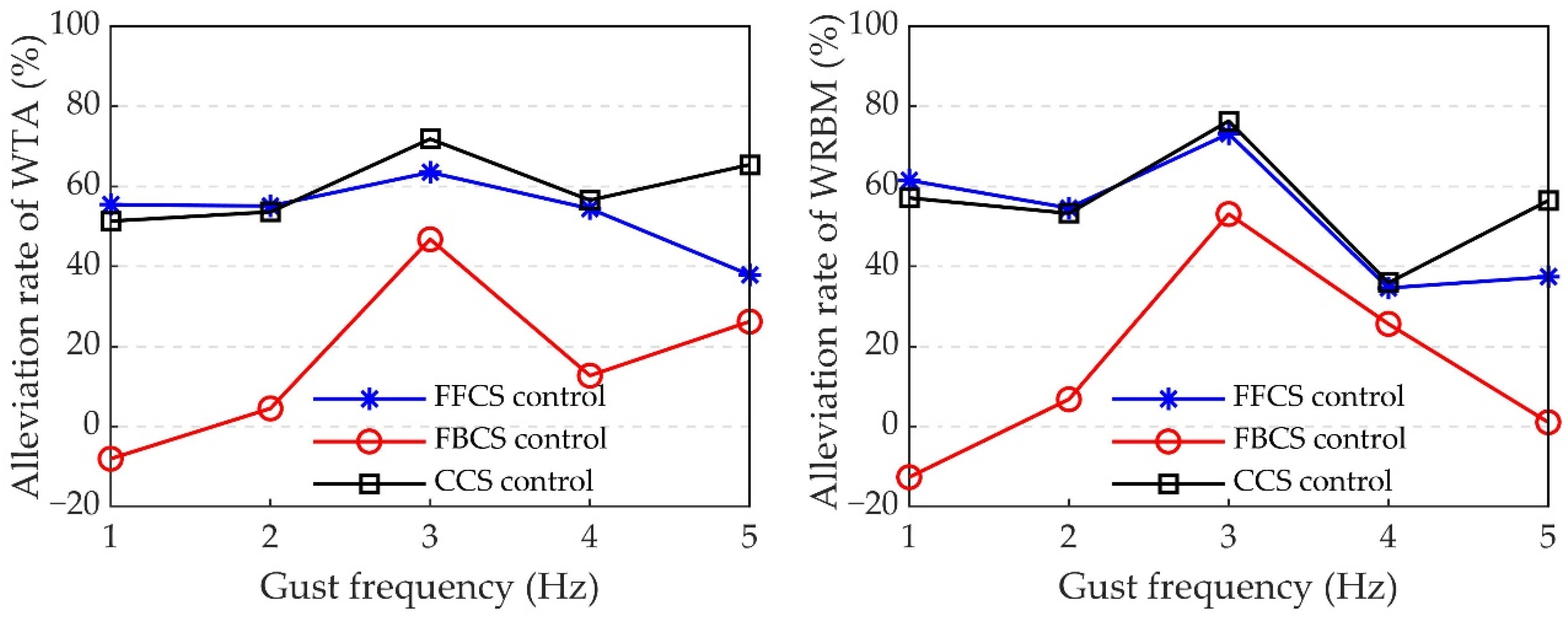
6.3. Wind Tunnel Test Results with The Same Wind Speed and Different Gust Frequencies
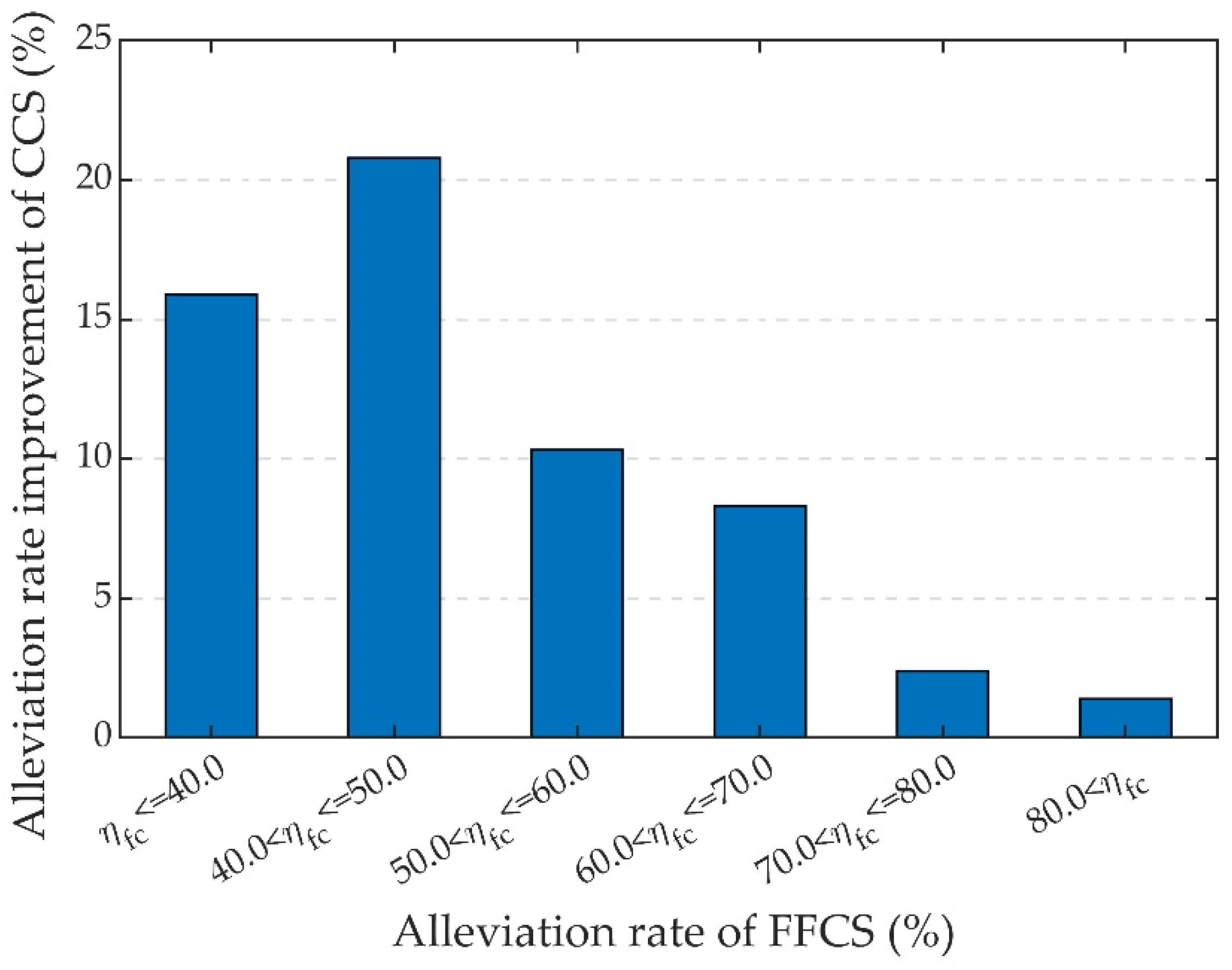
6.4. Improvement of Alleviation Rate by Combining Feedforward and Feedback Control
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Gust response value with control | Gust response value without control | ||
| Damping matrix | Fitting polynomial coefficient matrix | ||
| Weighted cross-correlation vector | Fitting polynomial coefficient matrix | ||
| Gust frequency | Internal force | ||
| Transfer function from control surface deflection angle to aircraft | Gust shaping filter | ||
| Transfer function of control system | Control system weight coefficient vector | ||
| Objective function | Element stiffness matrix | ||
| Stiffness matrix | Control system gain | ||
| Kalman gain vector | Reduced frequency | ||
| Gust scale | Mass matrix | ||
| Inverse autocorrelation matrix | Generalized aerodynamic matrix | ||
| Yaw angle rate | Lag root coefficient matrix | ||
| Laplace variable | Input vector of the adaptive algorithm | ||
| Flight speed | Gusts velocity | ||
| Gust amplitude | Aerodynamic state function | ||
| State vector | Distance from center of gravity to AOA sensor | ||
| Distance from center of gravity to AOS sensor | Response caused by control system | ||
| Response caused by gust | Transform operator | ||
| Gust angle | Angle of attack | ||
| Angle of sideslip | Control surface deflection angle | ||
| Alleviation rate | Pitch angle | ||
| Weight coefficient | Air density | ||
| Roll angle | PSD of gust | ||
| Modal vector |
Abbreviations
| AOA | Angle of attack |
| AOS | Angle of sideslip |
| CCS | Combined control system |
| CCLMS | Circular leaky least mean square |
| GAS | Gust alleviation system |
| FBCS | Feedback control system |
| FFCS | Feedforward control system |
| FIR | Finite impulse response |
| LMS | Least mean square |
| LIDAR | Light detection and ranging |
| RLS | Recursive least square |
| WRBM | Wing root bending moment |
| WTA | Wing tip acceleration |
References
- Katnam, K.B.; Da Silva, L.F.M.; Young, T.M. Bonded repair of composite aircraft structures: A review of scientific challenges and opportunities. Prog. Aeosp. Sci. 2013, 61, 26–42. [Google Scholar] [CrossRef]
- Alam, M.; Hromcik, M.; Hanis, T. Active gust load alleviation system for flexible aircraft: Mixed feedforward/feedback approach. Aerosp. Sci. Technol. 2015, 41, 122–133. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, L.; Yang, C.; Tang, C. Gust response modeling and alleviation scheme design for an elastic aircraft. Sci. China-Technol. Sci. 2010, 53, 3110–3118. [Google Scholar] [CrossRef]
- Karpel, M. Design for active flutter suppression and gust alleviation using state-space aeroelastic modeling. J. Aircr. 1982, 19, 221–227. [Google Scholar] [CrossRef]
- Liebst, B.S.; Garrard, W.L.; Farm, J.A. Design of a multivariable flutter suppression/gust load alleviation system. J. Guid. Control Dyn. 1988, 11, 220–229. [Google Scholar] [CrossRef]
- Dillsaver, M.J.; Cesnik, C.E.S.; Kolmanovsky, I.V. Gust load alleviation control for very flexible aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference 2011, Portland, OR, USA, 8–11 August 2011. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Sun, Q. Improved LQG method for active gust load alleviation. J. Aerosp. Eng. 2017, 30. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Zhan, M.; Gao, Y. Application of LQG theory to gust load alleviation system. Flight Dyn. 2007, 61–64. [Google Scholar] [CrossRef]
- Cook, R.G.; Palacios, R.; Goulart, P. Robust gust alleviation and stabilization of very flexible aircraft. AIAA J. 2013, 51, 330–340. [Google Scholar] [CrossRef]
- Aouf, N.; Boulet, B.; Botez, R.M. Robust gust load alleviation for a flexible aircraft. Can. Aeronaut. Space J. 2000, 46, 131–139. [Google Scholar]
- Fu, J.; Wan, J.; Ai, J. Robust control of flexible aircraft for gust alleviation. Fudan J. 2016, 55, 329–335. [Google Scholar] [CrossRef]
- Haghighat, S.; Liu, H.H.T.; Martins, J.R.R.A. Model-predictive gust load alleviation controller for a highly flexible aircraft. J. Guid. Control Dyn. 2012, 35, 1751–1766. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Z.; Zhang, W.; Xu, L.; He, Q. A MPC and control allocation method for gust load alleviation. J. Northwest. Polytech. Univ. 2017, 35, 259–266. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Cooper, J.E. LQG based model predictive control for gust load alleviation. Aerosp. Sci. Technol. 2017, 71, 499–509. [Google Scholar] [CrossRef] [Green Version]
- Shao, K.; Wu, Z.; Yang, C.; Chen, L. Theoretical and experimental study of gust response alleviation using neuro-fuzzy control law for a flexible wing model. Chin. J. Aeronaut. 2010, 23, 290–297. [Google Scholar] [CrossRef]
- Shao, K.; Yang, C.; Wu, Z.; H, L.; B, W. Design of a gust-response-alleviation online control system based on neuro-fuzzy theory. J. Aircr. 2013, 50, 599–609. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, L.; Yang, C. Study on gust alleviation control and wind tunnel test. Sci. China-Technol. Sci. 2013, 56, 762–771. [Google Scholar] [CrossRef]
- Matsuzaki, Y.; Ueda, T.; Miyazawa, Y.; Matsushita, H. Gust load alleviation of a transport-type wing: Test and analysis. J. Aircr. 1989, 26, 322–327. [Google Scholar] [CrossRef]
- Scott, R.C.; Castelluccio, M.A.; Coulson, D.A.; Heeg, J. Aeroservoelastic wind-tunnel tests of a free-flying, Joined-Wing SensorCraft model for gust load alleviation. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011; p. 1960. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wu, Z.; Dai, Y.; Ma, C.; Yang, C. Wind tunnel test of gust alleviation active control for flying wing configuration aircraft. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 184–192. [Google Scholar] [CrossRef]
- Disney, T.E. C-5A active load alleviation system. J. Spacecr. Rocket. 1977, 14, 81–86. [Google Scholar] [CrossRef]
- Johnston, J.; Urie, D. Development and flight evaluation of active controls in the L-1011. In Proceedings of the Proceedings of CTOL Transport Technology Conference, Hampton, VA, USA, 28 February–3 March 1978; pp. 647–685. [Google Scholar]
- Britt, R.T.; Jacobson, S.B.; Arthurs, T.D. Aeroservoelastic analysis of the B-2 bomber. J. Aircr. 2000, 37, 745–752. [Google Scholar] [CrossRef]
- Regan, C.D.; Jutte, C.V. Survey of Applications of Active Control Technology for Gust Alleviation and New Challenges for Lighter-Weight Aircraft; NASA/TM-2012-216008; NASA—Dryden Flight Research Center: Edwards, CA, USA, 2012.
- Schmitt, N.P.; Rehm, W.; Pistner, T.; Zeller, P.; Diehl, H.; Navé, P. The AWIATOR airborne LIDAR turbulence sensor. Aerosp. Sci. Technol. 2007, 11, 546–552. [Google Scholar] [CrossRef]
- Wildschek, A.; Maier, R.; Hahn, K.-U.; Leissling, D.; Preß, M.; Zach, A. Flight test with an adaptive feed-forward controller for alleviation of turbulence excited wing bending vibrations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6118. [Google Scholar] [CrossRef]
- Wildschek, A.; Maier, R.; Hoffmann, F.; Jeanneau, M.; Baier, H. Active wing load alleviation with an adaptive feed-forward control algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; p. 6054. [Google Scholar] [CrossRef]
- Zhao, Y.; Yue, C.; Hu, H. Gust load alleviation on a large transport airplane. J. Aircr. 2016, 53, 1932–1946. [Google Scholar] [CrossRef]
- Zeng, J.; Moulin, B.; de Callafon, R.; Brenner, M.J. Adaptive feedforward control for gust load alleviation. J. Guid. Control Dyn. 2010, 33, 862–872. [Google Scholar] [CrossRef]
- Fournier, H.; Massioni, P.; Pham, M.T.; Bako, L.; Vernay, R.; Colombo, M. Robust gust load alleviation of flexible aircraft equipped with lidar. J. Guid. Control Dyn. 2022, 45, 58–72. [Google Scholar] [CrossRef]
- Hamada, Y. Flight test results of disturbance attenuation using preview feedforward compensation. IFAC-PapersOnLine 2017, 50, 14188–14193. [Google Scholar] [CrossRef]
- Li, F.; Wang, Y.; Ronch, A.D. Flight testing adaptive feedback/feedforward controller for gust loads alleviation on a flexible aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Washington, DC, USA, 13–17 June 2016; p. 3100. [Google Scholar] [CrossRef]
- Wildschek, A.; Maier, R.; Hoffmann, F.; Steigenberger, J.; Kaulfuss, K.-H.; Breitsamter, C.; Allen, A.; Adams, N.; Baier, H.; Giannopoulos, T. Wind tunnel testing of an adaptive control system for vibration suppression on aircraft. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6331. [Google Scholar] [CrossRef]
- Hamada, Y.; Saitoh, K.; Kobiki, N. Gust alleviation control using prior gust information: Wind tunnel test results. Ifac Pap. 2019, 52, 128–133. [Google Scholar] [CrossRef]
- Karpel, M.; Moulin, B.; Chen, P.C. Dynamic response of aeroservoelastic systems to gust excitation. J. Aircr. 2005, 42, 1264–1272. [Google Scholar] [CrossRef]
- Karpel, M. Time-domain aeroservoelastic modeling using weighted unsteady aerodynamic forces. J. Guid. Control Dyn. 1990, 13, 30–37. [Google Scholar] [CrossRef]
- Moulin, B.; Karpel, M. Gust loads alleviation using special control surfaces. J. Aircr. 2007, 44, 17–25. [Google Scholar] [CrossRef]
- Rhode, R.V.; Lundquist, E.E. Preliminary Study of Applied Load Factors in Bumpy Air; NACA TN 374; NACA: Washington, DC, USA, 1931. [Google Scholar]
- Pratt, K.G. A Revised Formula for the Calculation of Gust Loads; NACA TN 2964; NACA: Washington, DC, USA, 1953. [Google Scholar]
- Von Kármán, T.; Lin, C.C. On the statistical theory of isotropic turbulence. Adv. Appl. Mech. 1951, 2, 1–19. [Google Scholar] [CrossRef]
- Liepmann, H.W. On the application of statistical concepts to the buffeting problem. J. Aeronaut. Sci. 1952, 19, 793–800. [Google Scholar] [CrossRef]
- Houbolt, J.C.; Steiner, R.; Pratt, K.G. Dynamic Response of Airplanes to Atmospheric Turbulence Including Flight Data on Input and Response; NASA TR R-199; NASA: Washington, DC, USA, 1964.
- Hoblit, F.M. Gust Loads on Aircraft: Concepts and Applications; AIAA: Washington, DC, USA, 1988. [Google Scholar]
- Haykin, S.S. Adaptive Filter Theory, 5th ed.; Pearson Education India: London, UK, 2014. [Google Scholar]
- Hahn, K.-U.; Schwarz, C. Alleviation of atmospheric flow disturbance effects on aircraft response. In Proceedings of the 26th Congress of the International Council of the Aeronautical Sciences, Anorchorage, AK, USA, 14–19 September 2008. [Google Scholar]
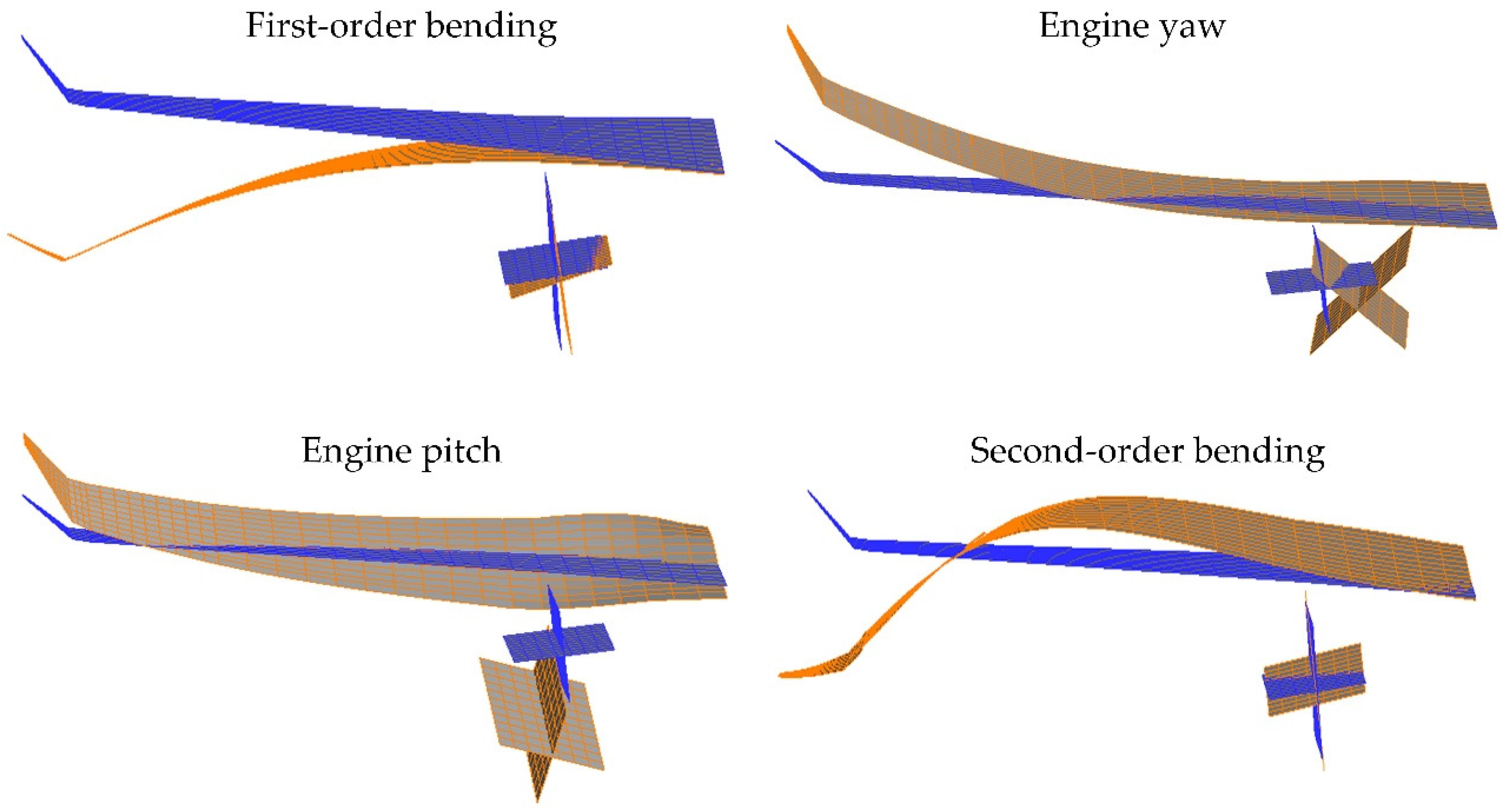



| Modal Name of Flexible Wing | Modal Frequency (Hz) | |
|---|---|---|
| Experimental Value | Theoretical Value | |
| First-order bending | 2.59 | 2.63 |
| Engine yaw | 4.97 | 4.99 |
| Engine pitch | 5.75 | 5.79 |
| Second-order bending | 8.29 | 7.82 |
| Type of Control System | Alleviation Rate of WTA (%) Alleviation Rate of WRBM (%) | |||||
|---|---|---|---|---|---|---|
| 1-Cos | Sine | Dryden | 1-Cos | Sine | Dryden | |
| FBCS | 22.31 | 54.46 | 27.48 | 6.62 | 50.79 | 0.16 |
| FFCS | 67.04 | 66.00 | 52.31 | 54.17 | 75.74 | 60.45 |
| CCS | 76.45 | 77.19 | 55.11 | 53.49 | 85.98 | 60.46 |
| Comparative Variables | Experiment | Numerical Simulation |
|---|---|---|
| WTA (g) | 1.95 | 1.88 |
| WRBM (Nm) | 110.00 | 107.05 |
| FFCS alleviation rate of WTA (%) | 52.11 | 80.80 |
| FFCS alleviation rate of WRBM (%) | 63.40 | 80.84 |
| FBCS alleviation rate of WTA (%) | 53.93 | 64.49 |
| FBCS alleviation rate of WRBM (%) | 63.45 | 60.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wu, Z.; Yang, C. Gust Alleviation and Wind Tunnel Test by Using Combined Feedforward Control and Feedback Control. Aerospace 2022, 9, 225. https://doi.org/10.3390/aerospace9040225
Zhou Y, Wu Z, Yang C. Gust Alleviation and Wind Tunnel Test by Using Combined Feedforward Control and Feedback Control. Aerospace. 2022; 9(4):225. https://doi.org/10.3390/aerospace9040225
Chicago/Turabian StyleZhou, Yitao, Zhigang Wu, and Chao Yang. 2022. "Gust Alleviation and Wind Tunnel Test by Using Combined Feedforward Control and Feedback Control" Aerospace 9, no. 4: 225. https://doi.org/10.3390/aerospace9040225
APA StyleZhou, Y., Wu, Z., & Yang, C. (2022). Gust Alleviation and Wind Tunnel Test by Using Combined Feedforward Control and Feedback Control. Aerospace, 9(4), 225. https://doi.org/10.3390/aerospace9040225






