Abstract
Flow control methods for aerodynamic drag reduction have been a field of interest to aircraft designers, who seek to minimize fuel consumption and increase the aircraft’s aerodynamic performance. Various flow control techniques, applied to aeronautical applications ranging from large airliners to small hand-launched unmanned aerial vehicles (UAVs), have been conceptualized, designed and tested in the past. Among others, the concept of riblets, inspired by the shark’s skin morphology, has been proposed and evaluated for airliners. In this work, the implementation of riblets on a medium-altitude long-endurance UAV (MALE) is investigated. The riblets can offer drag reduction due to the decrease in total skin friction, by altering the boundary layer characteristics in the near-wall region. The riblets are implemented on specific locations on the UAV (main wing, fuselage and empennage) and appropriately selected, on which the boundary layer becomes transitional from the laminar to the turbulent flow regime. For this reason, computational fluid dynamics modelling is performed by solving the Reynolds-averaged Navier–Stokes equations, incorporating the k-ω SST eddy viscosity turbulence model. The effect of the riblets in the near-wall region is modelled with the use of an appropriate wall boundary condition for the specific turbulence dissipation rate transport equation. It is shown that a drag reduction benefit, for both the loiter and the cruise flight segments of the UAV mission, can be obtained, and this is clearly presented by the drag polar diagrams of the air vehicle. Finally, the potential benefit to flight performance in terms of endurance and payload weight increase is also evaluated.
1. Introduction
In recent years, the use of unmanned aerial vehicles (UAVs) around the globe has steadily increased due to their inherent advantages compared to manned alternatives, such as the low operating cost, increased endurance and, most notably, their ability to operate under hazardous conditions. Additionally, the demand and availability of UAV systems has also seen a dramatic increase, mainly because of their reduced purchase cost and the advanced autopilot systems that allow novice operators/pilots to operate them successfully. Currently, the market value of UAV-related applications is estimated at over USD 127 billion, with UAV sales between 2016 and 2021 seeing a growth rate of 7.6%, and over 100,000 new jobs are expected to be created by 2025 [1]. The different UAV designs vary, from small hand-launched UAVs weighing under 1 kg, to high-altitude long-endurance (HALE) systems of several tons. The systems are currently used in a wide range of missions, from security and border monitoring, to precision farming and photogrammetry.
One of the main targets for future UAV designs is to improve their flight endurance. In the case of small electrically powered UAVs, the research is focused on battery technology, aiming to achieve an increased capacity and a reduced weight [1]. Larger tactical, or MALE UAVs, are mainly powered by an internal combustion engine, which has limited optimization prospects in terms of engine efficiency. The majority of these UAV designs are based on the tube-and-wing configuration, with a large number of exposed parts (e.g., cameras and landing gear), while the so-far-adopted UAV design strategies mainly focus on data-link capabilities, autopilot functionality and safety aspects, with aerodynamic performance having been overlooked until recently [2]. The overall UAV design strategy can be enhanced with design methodologies that also aim to reduce the weight, optimize the aerodynamic layout or improve the performance of these configurations [3].
Since UAV layouts are not expected to change dramatically and some limitations regarding exposed parts cannot be overcome, it is necessary to investigate technologies and strategies that result in performance enhancement for current designs. In this context, passive flow control techniques that reduce the overall drag of an aerial vehicle seem appealing. An example of such a technology that is already implemented on commercial airliners is the natural laminar flow airfoils used on the main wings of aircrafts in order to delay the boundary layer transition to the turbulent regime and, thus, reduce the skin friction drag component.
For the regions of the flow where the boundary layer is turbulent, the use of the passive flow control technique based on the usage of riblets can provide an additional skin friction reduction. The riblets are microgroove geometries, with sizes in the range of a few hundred μm depending on the flow friction velocity. The riblets interact with the small scale vortical structures in the near wall region and alter the flow inside the boundary layer, with three distinct mechanisms; consequently, leading to the reduction in skin friction [4]. More specifically, riblets (a) elevate upwards the cross-flow motion in their crests and displace streamwise vortices and streaks away from the wall, (b) weaken the near-wall turbulence regeneration cycle and (c) dampen the spanwise flow fluctuations [5].
In recent decades, a significant amount of research has been performed focusing on the riblets’ geometry and size, in applications where aerodynamic drag reduction is needed. Early experiments on flat plates showed that by using mainly V-shaped riblets, a maximum total drag reduction of 8–10% could be achieved [6,7,8]. In several other studies, various riblet geometries, such as sinusoidal, U-shaped, blade-shaped and trapezoidal grooved riblets (Figure 1), were investigated and showed the aforementioned percentage of drag reduction. From the available literature, it can be concluded that blade-shaped riblets provide the optimum performance in terms of the aerodynamic drag reduction, though they are prone to damage and are difficult to fabricate. Bechert et al. [9] carried out extensive oil channel experiments on blade-shaped and trapezoidal grooved riblets, and concluded that the latter, though inferior in terms of efficiency, was overall the best compromise between actual performance and practical application in engineering aerodynamic problems.
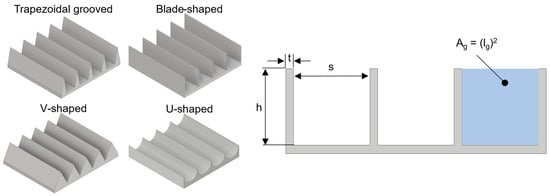
Figure 1.
Different riblet geometries that have previously been investigated (left) and basic geometric parameters (right).
To correlate the relationship between the drag reduction effect of riblets and the Reynolds number, Walsh and Linderman [6] first used the non-dimensional riblet spacing, expressed in wall units , where s is the riblet spacing, u* is the friction velocity and is the kinematic viscosity, with the optimal riblet size corresponding to a relatively constant value of for a large number of riblet geometries and sizes. Based on the experimental results of Bechert et al. [10], for triangular, trapezoidal, blade and scalloped riblets, Garcia-Mayoral and Jimenez [4] showed that for different types of riblets, the optimum value of the non-dimensional square root of the groove cross section had a smaller variation compared to and, thus, was more representative of the riblets performance.
In the past, research focused on the application of riblets in commercial airliners, where the viscous drag component can be as high as 50% of the aircraft’s total drag [11], and their benefit can be correlated to significant savings in fuel costs. As the number of globally operating UAVs is increasing, the interest in the effect of riblets for these applications also increases, since the issues related to riblet applicability are relatively easier to solve. This is due to the fact that the areas covered by riblets are orders of magnitude smaller compared to commercial airliners, while their benefits remain significant [3]. In both cases, several additional parameters influence the performance of riblets compared to a flat plate case, because the boundary layer developing on the surface of aircraft wings is affected by adverse and favorable streamwise pressure gradients, as well as three dimensional effects and spanwise gradients due to sweep. There have been experimental investigations on the influence of the pressure gradient [11,12,13] and sweep angle on the performance of riblets [14]. In a concise manner, Viswanath [11] presented many results of earlier works in that area and concluded that the viscous drag reduction in airfoils at zero and low incidence is comparable to that of a zero-pressure gradient flow over a flat plate. Results from the application of riblets on actual aircraft, such as the main wing of a T-33 [15] and, more recently, the fuselage of a JAXA experimental aircraft [16], were very encouraging, as shown by the measurements performed in experimental wind tunnels.
Additionally, the similar passive flow control technique of vortex generators (VGs) has been investigated and implemented on various aircrafts [17,18]. The VGs are generally small thin geometrical structures that are mainly used for lift enhancement and separation control. Conventional VGs have a height of roughly the same order of magnitude as the airfoil’s boundary layer thickness (), while low-profile VGs have a height between 10–50% of and have demonstrated enhanced performance [17]. The latter are even more similar to the riblet geometries in terms of dimensions, and experiments have shown that they can provide a drag decrease, though this is mainly associated with separation control [17,19]. Their main disadvantage is that their exact placement is highly critical compared to conventional VGs and must be reasonably close upstream from the expected separation location. These VGs create streamwise vortices in the near-wall region, and are capable of overcoming separation but dissipate further downstream when the flow attachment is achieved; thus, enhancing their performance. Depending on the type of flow separation that is expected, counter-rotating VGs are ideal for mitigating 2D flow separation, such as in the case of a low-sweep aircraft wing, while co-rotating VGs are mainly used for 3D flow separation (duct inlets and high-sweep wings). The use of VGs though not providing any significant benefit in low angles of attack (AoA) where no flow separation is expected, could be used synergistically with riblets, so the aerial vehicle’s performance is improved during take-off and landing, as well as the cruise and loiter phases.
From the computational point of view, several researchers have simulated riblets using high-fidelity techniques such as large eddy simulations (LES) [20,21] and direct numerical simulations (DNS) [22]. Due to the high computational cost, a short range of cases has been investigated, limited to flows around a simple flat plate or airfoil geometries, corresponding to Reynolds numbers around 180 for flat plates based on the friction velocity and 180,000 for airfoils based on the freestream velocity. This range of Reynolds numbers is at least one order of magnitude smaller than the ones corresponding to currently operational UAVs or other practical applications. These two factors combined, prohibit the use of such high-fidelity techniques for most industrial applications and, hence, they are primarily used for fundamental studies of the physics involved in the flow development in areas close to the surface, where riblets are installed as flow controllers, and to acquire a better understanding of the mechanisms that result in the overall drag reduction [4].
In the present work, the potential benefit from the use of riblets is investigated on a medium-altitude long-endurance (MALE) UAV, in terms of the aerodynamic performance and fuel consumption reduction and, thus, the endurance and payload capability increase. The existence of the riblets on solid surfaces (e.g., wings and fuselage surfaces) is modelled using an appropriate boundary condition on the less computationally expensive CFD modeling approaches with the adoption of the RANS equations approach. This boundary condition is specifically designed for application on the k-ω family turbulence models, by altering the value of the specific turbulence dissipation rate ω at the wall, mimicking the existence of riblets and their impact on flow development.
The overall benefit of the riblets is examined for three specific areas of application on the external surface of the UAV (i.e., main wing, empennage and fuselage) and for the most critical flight segments of a typical mission profile.
2. Materials and Methods
2.1. The UAV Platform
The unmanned aerial vehicle (UAV) platform on which riblets were applied was developed by the Laboratory of Fluid Mechanics and Turbomachinery under the Hellenic Civil Unmanned Aerial Vehicle research project codenamed HCUAV RX-1 [23]. The HCUAV RX-1 is a medium-altitude Long-endurance (MALE) fixed-wing UAV prototype developed to perform civil operations in Greece. The UAV is designed for long day and night surveillance operations. It is equipped with a variety of cameras, necessary for each type of mission, with a total payload weight of 35 kg. The UAV has a pusher propeller configuration powered by a two-stroke 25 hp reciprocating internal combustion engine, and features a boom-mounted inverted V-tail (Figure 2). Some of the specifications of the HCUAV RX-1 required for the present study are given in Table 1, as presented by Panagiotou et al. [23,24].
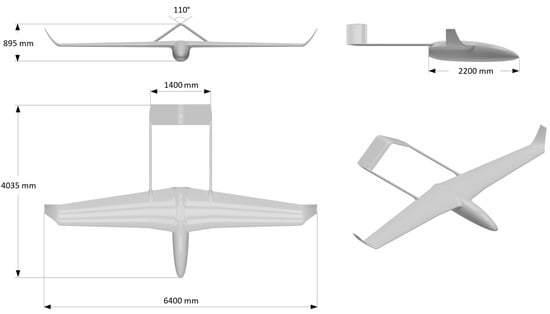
Figure 2.
The HCUAV RX-1 dimensions.

Table 1.
Specification of the HCUAV RX-1.
Its mission profile (Figure 3) includes a loiter phase of 11 h, which constitutes the largest part of the overall flight time. Hence, to obtain the maximum benefit from the application of riblets, they must be designed to operate optimally at loiter conditions, namely, a flight velocity of 140 km/h and an operating altitude of 2000 m. Though the cruise segment of the mission is relatively small compared to loiter, the effect of riblets was also investigated in that phase in an effort to examine their behavior in a wider range of important off-design conditions. It must be noted that both the loiter and cruise segments of the UAV’s mission were at the same operating altitude (2000 m) and only differed in the flight velocity, namely, 140 km/h and 160 km/h, respectively, without any change in the aircraft’s geometry (e.g., flap deflection).
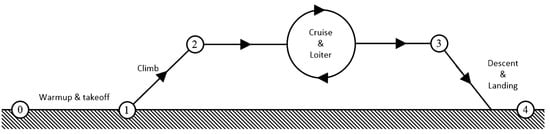
Figure 3.
Mission profile of the HCUAV RX-1 [23].
2.2. Modeling of Riblets and CFD Methodology
The evaluation of the riblets’ drag reduction was performed using computational fluid dynamic (CFD) methods by solving the steady Reynolds-averaged Navier–Stokes (RANS) equations, since the UAV’s operational angles of attack were relatively small, and no stalling or other unsteady phenomena were present. Based on the mechanisms that riblets use to interact with the flow in the near-wall region, it was observed that their presence induced a shift on the velocity profile. This shift is given by the value in the logarithmic law of the wall equation (Equation (1)) that could also describe the influence of wall roughness in turbulent flows.
where κ is the Von-Kármán constant and B represents the influence of the wall on the velocity profile and is usually equal to 5 for smooth walls. Negative values of are associated with the presence of well-designed riblets that produced a skin friction reduction, while positive values are related to poor riblet designs or equally to wall roughness that induced a skin friction increase [25].
The effect of riblets in the flow field was modelled as a singular roughness problem, as was originally proposed by Mele and Tognaccini [26]. More specifically, a dedicated boundary condition for the specific turbulence dissipation rate ω was implemented, which modified the original boundary condition (Equation (2)) proposed by Saffman [27] for the k-ω models.
where and are the density and dynamic viscosity of the fluid, and SR is a function that depends only on the nature of the wall and can model either roughness (as a function of the roughness Reynolds number ) or riblets (as a function of any riblet geometric parameter expressed in wall units, e.g., , ). Based on that and on the original work of Mele and Tognaccini [26], Catalano et al. [28] proposed and implemented on airfoils and a regional airliner an improved algebraic relationship (Equation (3)) to model the effect of riblets in the near-wall region. This equation adopted for the value of SR a function of the non-dimensional square root of the groove cross section , which better represented the influence of riblets compared to other riblet geometric parameters (i.e., , ) [4].
where C1 = 2.5 × 108, C2 = 10.5, C3 = 10−3 and n = 3, are the results of numerical experiments performed by Mele and Tognaccini [26] attempting to match the experimental data presented by Garcia-Mayoral and Jimenez [4]. The value of C2 was set equal to the corresponding to the optimum riblet effect.
The proposed modelling method is limited to applications involving ω-based turbulence models. In the present study, the two-equation shear stress transport (SST) k-ω model of Menter [29], which is widely used in aeronautical applications, was employed. This model can capture the turbulence effects with greater clarity compared to other widely used turbulence models, especially in flows with adverse pressure gradients [30,31].
All computational meshes were generated by the BETA ANSA pre-processing software (v21.0.1, Root, Switzerland). Each unstructured mesh consisted of a structure-like mesh in the boundary layer regions on solid surfaces, with 25 cells in the normal to the wall direction (Figure 4) and an appropriate first cell height that ensured that everywhere there was a value below unity and at least 5 computational cells were lying within the viscous sublayer. To determine the appropriate mesh size, a thorough grid independency study was performed for the loiter flight conditions using the lift and viscous drag coefficients as the primary monitor variables, while the y+ value was maintained below unity for all the different meshes examined. The results of this study were indicatively presented in Figure 5, where it can be observed that the solution was practically grid-independent for mesh sizes larger than 21 × 106 cells, and this mesh was finally selected to reduce the computational cost. The Reynolds number was about 1.9 × 106 based on the UAV’s mean aerodynamic chord, for the loiter flight condition. The solution was performed with the ANSYS Fluent 2020R2 (Academic Multiphysics Campus Solution) software (Canonsburg, PA, USA) using a coupled pressure-based solver and a second-order spatial discretization scheme for all the transport equations that were solved, with the double-precision option enabled.
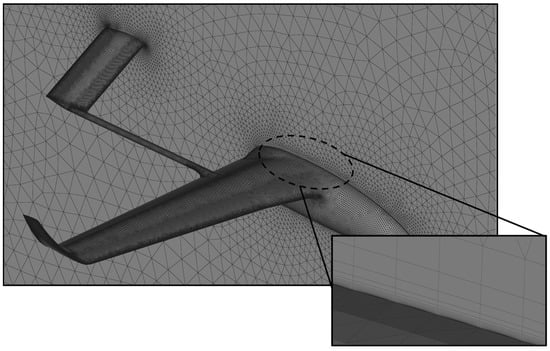
Figure 4.
The computational mesh on the surface of the HCUAV RX-1 and detail of the structure-like region.
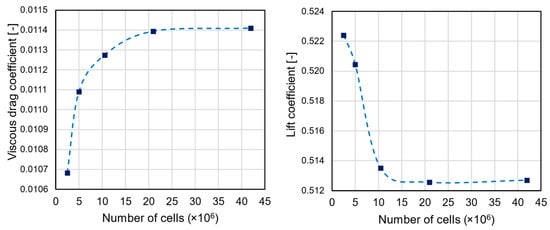
Figure 5.
Grid independency study for the HCUAV RX-1 at loiter conditions.
The specific turbulence dissipation rate boundary condition on the wall surfaces was implemented on the CFD solver by using a programmed user defined function (UDF). As described earlier, the value of , and, thus, , could be described as a function of solely (Equation (3)). More specifically, on the three selected surface areas of the UAV onto which the riblets were applied, an optimal average value of was computed using Equation (4), which corresponded to = 10.5, using the mean wall shear stress on each surface. These values described the riblets size applied on each surface (Table 2). Then, based on that average value of , a local was computed on each wall cell face, this time using the local wall shear stress values. This served as an input to Equation (3) and, thus, the local boundary condition was defined for each wall cell face. The above-described procedure of the UDF on each surface area where riblets were applied is summarized in the flowchart of Figure 6.

Table 2.
Size of riblets applied on each surface area of the UAV.
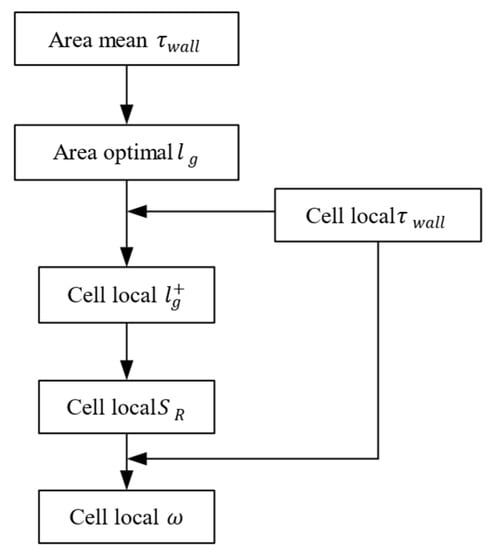
Figure 6.
Flowchart of the UDF operation on each surface area.
2.3. The UAV Selected Surfaces for the Riblet Installation
The riblets were applied on specific areas of the UAV and showed drag reduction potential. Figure 7 (left) shows the drag breakdown of the UAV during loiter based on the results of CFD modeling, with friction accounting for 30% of the total UAV’s drag. The larger part of friction drag was attributed to the main wing (Figure 7, right), with the empennage and fuselage also having a non-negligible contribution. These three surfaces of the UAV were identified as potential areas for riblet application. To define the exact extent of these areas, it was necessary to examine the boundary layer development and identify the region in which transition occurred and a turbulent boundary layer was present. The skin friction reduction mechanisms of riblets were closely associated with the presence of turbulent structures. Riblets have no effect on the laminar component of skin friction [5] and, therefore, they should be applied on areas where the boundary layer had transitioned to turbulent. The empennage was designed with a symmetrical NACA airfoil, while the main wing, and to some extent the fuselage, mainly used the NLF1015 natural laminar airfoil [3]. The use of an NLF airfoil conflicted with the application of riblets, since the flow was expected to remain laminar on a large part of the wing; thus, reducing the possible area on which riblets can be applied.
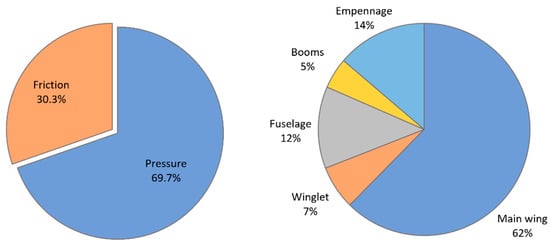
Figure 7.
Breakdown of the UAV’s total drag (left) and contribution of each component to the friction drag (right).
To predict the position of boundary layer transition more accurately, dedicated RANS CFD computations were performed, as described in Section 2.2, and the three-equation k-kL-ω transition turbulence model of Walters and Cokljat [32] was used. The k-kL-ω turbulence model, along with the equations for the turbulent kinetic energy and specific turbulence dissipation rate , includes the transport equation for the energy of non-turbulent fluctuations . This approach has previously been compared and validated with experimental results on both flat plates and airfoils [33]. The computations were performed for the mid-loiter conditions at a 0° AoA, which also served as the design point for the definition of the riblet size. The selection of this design point was based on the fact that the UAV operates for a large portion of its mission near these AoA, and, thus, such were the conditions for which the maximum riblet performance was desired.
The flow conditions in four planes of interest were examined (Figure 8) and, more specifically, those that corresponded to the position of the mean aerodynamic chord (MAC) and wingtip of the main wing, the mean aerodynamic chord of the empennage and the plane of the maximum length of the fuselage.
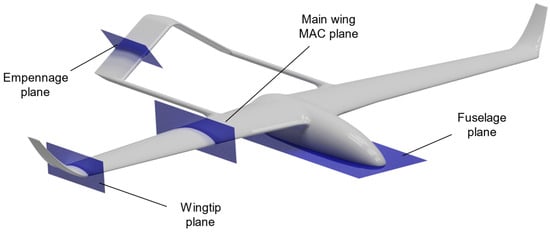
Figure 8.
Planes on which boundary layer transition was investigated.
To identify the point on which the boundary layer had transitioned to fully turbulent, the shape factor , which is the ratio of boundary layer displacement thickness over the boundary layer momentum thickness , was computed using Equations (5)–(7) on specific location points along each surface. In each plane, 20 positions were selected, equally spaced on the suction side of each surface.
The integration was performed on the normal to the wall direction , with being the boundary layer thickness, the velocity inside the boundary layer and the freestream velocity at the edge of the boundary layer.
In Figure 9, the distribution of the boundary layer shape factor along the chord of each airfoil in the four planes is presented. Initially, for all planes, the shape factor was relatively constant, with a value around 2.4, indicating that the boundary layer was still in the laminar regime. At different positions, the shape factor started decreasing and approached a value around 1.4, where the boundary layer was considered to be fully turbulent. More specifically, on the main wing, this was achieved at the position of for the MAC plane and for the wingtip plane. On the empennage and fuselage, the turbulent region existed downstream of the and positions, respectively. Based on these observations, the areas on which riblets were applied were those downstream of the aforementioned positions (summarized in Table 3) and are presented in Figure 10. On the main wing, the riblet application area had a trapezoidal shape, with the upstream edge following the straight line connecting the transition points of the MAC and wingtip planes.
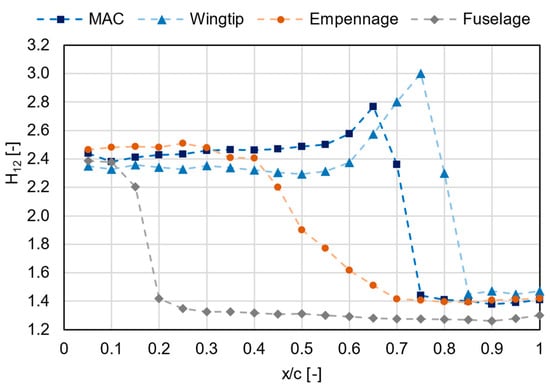
Figure 9.
Shape factor distribution on selected planes.

Table 3.
Boundary layer transition points to fully turbulent for the examined planes of the UAV.
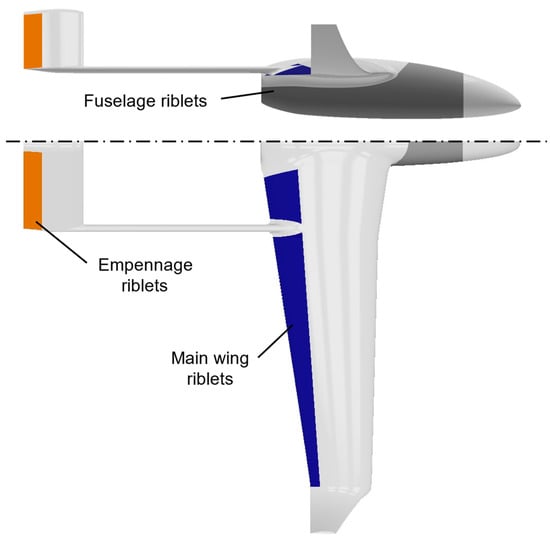
Figure 10.
Areas of riblet application.
3. Results and Discussion
Initially, the contribution of each of the three areas covered with riblets was examined. In loiter conditions, the riblets were applied both separately on the main wing, fuselage and empennage, as well as simultaneously on all three areas, as described in Section 2.3, and were assessed for their contribution to the overall drag reduction on the UAV compared to the case with no riblets using Equation (8).
The results presented in Table 4 refer to loiter conditions at a 0° AoA and indicated that the riblets applied on the fuselage had the greatest drag-reducing effect, while those on the empennage had the least. The lift and drag coefficients presented in Table 4 refer to the whole aircraft and not each individual component. More specifically, due to the larger riblet-covered area on the fuselage (Figure 10) compared to the other two surfaces, the aerodynamic drag reduction benefits were noticeable. Riblets influenced both the skin friction and pressure distributions on the surfaces they were applied to; hence, they also had a small positive effect on the produced lift [34]. Most importantly, it was observed that the drag reduction benefit from the simultaneous application of riblets on all three area of the UAV was somewhat lesser than the corresponding sum of drag reduction if the riblets were applied on the three surfaces separately. This indicated that the presence of riblets on one area of the UAV altered the flow field, mainly the velocity field and turbulence generation due to riblet presence, in a way that affected the downstream UAV parts where riblets were applied and their performance was reduced. All three areas were interlinked, but the greatest interference existed between the riblets applied on the front part of the UAV (fuselage and main wing) and the empennage, because the flowfield alteration from the first was propagated downstream and reduced the performance of the latter. In Figure 11, the velocity profiles on the empennage plane at the position are presented. The cases examined refer to riblets applied only on the empennage and on the whole UAV, respectively. The observed small difference between the two was indicative of the downstream propagated interference and riblet performance degradation.

Table 4.
Influence of riblet application on specific areas of the UAV at 0° AoA and loiter conditions.

Figure 11.
Velocity profiles on the empennage plane at with riblet application only on the empennage and on the whole UAV.
Additionally, it must also be noted that the small increase in CL due to riblets did not result in any significant increase in induced drag; therefore, it did not reduce the actual riblet performance.
To investigate the benefit of riblets on the overall loiter phase, a series of CFD computations was performed, with and without riblets in a range of angles of attack between −8° and 8°, within which the UAV nominally operates during a typical mission. Additionally, the effect of riblets during cruise was also investigated for the same range of angles of attack. The results of the computations were presented in the form of drag polars in Figure 12, with the riblets offering a 4.8% total drag reduction at their design point (i.e., loiter conditions at 0° AoA). For the loiter phase, in the off-design points of higher AoA, the drag reduction due to the riblets quickly diminished to around 0.5% at 4° and became negligible at 8°. In negative AoA, there was initially a drag reduction comparable to 0°, up until the minimum value of , from which point forward it quickly became a drag increase as the angles decreased further. The ±8° AoA cases examined were mostly presented in order to demonstrate the high degradation of riblet performance that resulted from the AoA variation. Additionally, they indicated that the use of poorly designed riblets or riblets designed for very different flight conditions could also possibly result in a drag penalty. Moreover, since the riblets were designed for the loiter conditions (), the cruise conditions ( were considered an off-design point for all angles of attack. The results showed a similar behavior as in the loiter cases, though the overall riblet effectiveness was reduced in the whole AoA range. Based on these results, the poorer performance of riblets in the case of cruise conditions resulted in a separate drag polar curve.
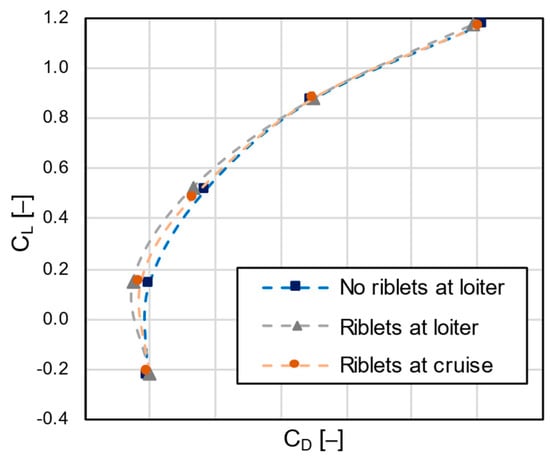
Figure 12.
Drag polar of the HCUAV RX-1 with and without riblets at loiter and cruise conditions.
In Figure 13, the skin friction coefficient on the surface of the UAV was presented for the cases with and without the applied riblets. It was observed that skin friction reduction was present in all the areas where riblets were applied (i.e., main wing, fuselage and empennage). The increased effect of riblets could be seen clearly on the front side of the fuselage and the rear side of the empennage, where the skin friction reduction was obvious (in the order of 12–15%). Regarding the main wing, the skin friction reduction was observable near the trailing edge, where the area of lower skin friction (deep blue color) was increased.
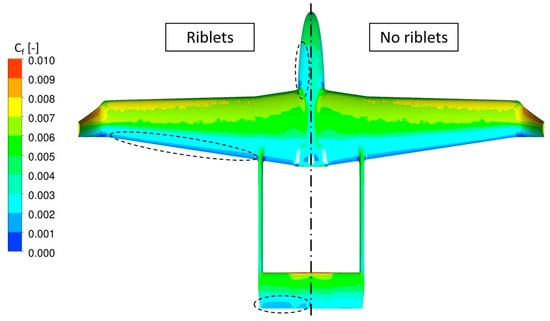
Figure 13.
Skin friction coefficient distribution on the surface of the RX-1 HCUAV with riblets (left) and without (right).
The effect of riblet application on the main wing was presented more clearly in Figure 14, where the skin friction coefficient on the mean aerodynamic chord of the main wing was plotted for the 0° and 8° AoA at loiter conditions. The riblets reduced the skin friction in the region between and the trailing edge of the airfoil, though the skin friction reduction was not equally distributed. The greater part of skin friction reduction was located in the area close to the initial riblet application point (i.e., ) and diminished towards the trailing edge. This unequal skin friction distribution was even more evident at the 8° AoA (Figure 14 Right), where only a small part of the riblet application area offered a drag reducing effect. In the work of Bliamis et al. [35], the same procedure for riblet implementation using an ω boundary condition was applied on an NACA0012 airfoil for a constant value on the whole airfoil. Comparing these results with Figure 14, the highly unequal distribution in the reduction in skin friction (roughly between and ) observed in the present case could be attributed to the use of a constant riblet size over the whole main wing. The specific riblet characteristics in this work were selected based on the mean wall shear stress value of each application area (main wing, empennage and fuselage). Since the wall shear stress varies along an airfoil, the riblets were not expected to operate optimally at all locations of each given area. Therefore, it was expected that the benefit from the installation of riblets on the UAV’s surfaces could be increased if the surfaces where they were applied were broken down to smaller areas and a larger number of riblet sizes was used to ensure that a greater part of them operated in the optimal conditions at a given time.
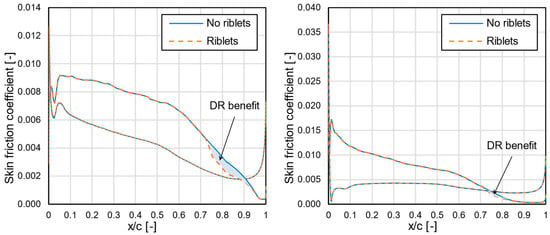
Figure 14.
Skin friction on the MAC airfoil for loiter conditions at 0° (left) and 8° (right) AoA.
In Figure 15, Figure 16 and Figure 17, the velocity profiles on the MAC, fuselage and empennage planes are presented for different positions along the longitudinal axis, at design conditions (loiter at 0° AoA). These positions covered the whole extent of the area in which riblets were applied. In all three planes, it was observed that the effect of riblets was small near the start of the riblet areas (left diagrams) and became greater downstream. The results presented in these figures agreed with the previously determined observations (Figure 14) and, thus, supported the conclusion that the benefit from riblet use could be improved with a further breakdown of each individual area of application into smaller ones.
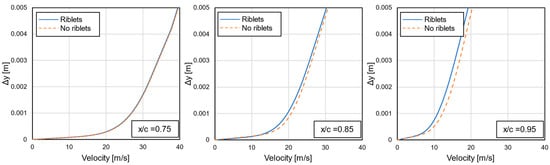
Figure 15.
Velocity profiles on the MAC plane in selected positions, at design conditions.
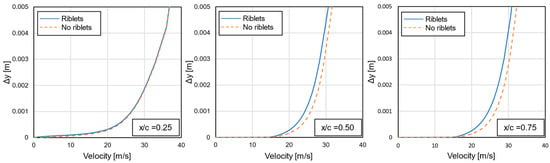
Figure 16.
Velocity profiles on the fuselage plane at selected positions, at design conditions.
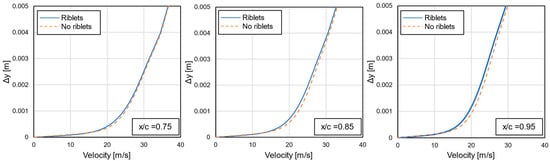
Figure 17.
Velocity profiles on the empennage plane at selected positions at design conditions.
Regarding the effect of riblets on the performance of the UAV, the endurance for the loiter phase was examined, since the latter constituted the largest segment of its mission. Typically, the endurance of a propeller-driven aerial vehicle could be calculated using Equation (9). To achieve the maximum endurance time, the aerial vehicle needs to operate at the maximum CL3/2/CD value. In this form of the endurance equation, the loiter velocity was removed from the equation and a constant flight altitude was assumed [36].
In the present work, the HCUAV RX-1 performed its loiter segment with a predefined fixed velocity value (). In this case, the endurance equation could be written in the form of Equation (10), where the UAV’s loiter velocity was introduced as a variable [36,37].
where the Wi and Wf are the UAV’s weight at the start and end of the loiter phase, respectively, Cbhp is for the engine brake horsepower, np is the propeller efficiency, is the air density at the loitering altitude, is the UAV’s reference area and ( and are the lift and drag forces (coefficients) of the UAV in the loiter segment. Two different scenarios were examined, on both of which the gross take-off weight (GTOW) of the UAV was kept constant. Regarding the benefit in endurance, the fraction of the UAV’s weight during loiter in Equation (10) was held constant (i.e., the same amount of fuel was burned); hence, only the lift-to-drag-ratio was increased. This resulted in an endurance increase of 7% (about 45 min). The second scenario examined the potential payload weight increase for the initially specified endurance (i.e., the reduction in fuel requirement was directly translated into a payload increase). This could result in a 5% payload weight increase (about 2 kg) for an endurance of 11 h. The results of the two scenarios are summed up in Table 5.

Table 5.
Performance improvement of the HCUAV RX-1 due to riblets implementation.
4. Conclusions
In the present study, the effectiveness of riblets on the performance of a MALE UAV was examined. The investigation was performed with RANS CFD computations using the k-ω SST turbulence model for the closure of the equations and the riblets were modelled with the implementation of a dedicated boundary condition for the specific turbulence dissipation rate. The areas on which the riblets were applied were carefully selected using the shape factor to ensure that the boundary layer had become turbulent in order to obtain the maximum riblet effect on the boundary layer development. Additionally, different riblet sizes were appropriately used in each surface area of application on the UAV to maximize their performance. The contribution of each specific surface area (on which the riblets were applied) to the overall drag reduction was examined and the drag polars for the loiter and cruise flight phases were compared against the case without the adoption of riblets. A total drag reduction of approximately 5% was achieved in the design conditions. Regarding the off-design conditions during cruise, the riblets operated beneficially, though the drag reduction percentage was smaller. Finally, regarding the performance of the UAV with the applied riblets, the study indicated that a 7% increase in endurance or a 5% increase in payload could be achieved, while maintaining the gross take-off weight constant. The implemented boundary condition for the specific turbulence dissipation rate showed great potential for modelling the riblet surfaces in industrial applications with complex geometries. The major advantage of this method lies in the implementation of the boundary condition in the RANS equations and, as such, taking into consideration the riblet effect on the flow development without the need of highly refined computational meshes; thus, allowing relatively quick and accurate computations. The performance of the UAV could have potentially been improved further if each surface area of riblet application was divided into smaller areas, and an optimal riblet size based on the boundary layer characteristics was used on each one of them. This, however, must be performed in a multidisciplinary optimization framework to include constraints related to the applicability of multiple different sized riblets on the actual surface of the UAV. Additionally, the results of the numerical analysis presented in this work should be evaluated using future flight-testing campaigns performed in the framework of the RADAERO research project.
Author Contributions
Conceptualization, C.B., Z.V. and D.M.; methodology, C.B. and Z.V.; validation, C.B., Z.V., D.M. and K.Y.; investigation, C.B., Z.V. and D.M.; resources, K.Y.; data curation, C.B. and Z.V.; writing—original draft preparation, C.B. and Z.V.; writing—review and editing, D.M. and K.Y.; visualization, C.B.; supervision, Z.V. and K.Y.; project administration, K.Y.; funding acquisition, Z.V. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was implemented within the project “RADAERO-Innovative Composite Materials for the Drag and Electromagnetic Signature Reduction for Applications in Aviation” (project code: T6ΥΒΠ-00042), which was financially supported by the European Regional Development Fund, Partnership Agreement for the Development Framework (2014–2020), co-funded by Greece and the European Union in the framework of the OPERATIONAL PROGRAMME: “Competitiveness, Entrepreneurship and Innovation 2014–2020 (EPAnEK)”, Nationwide Action: “Industrial Materials”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shakhatreh, H.; Sawalmeh, A.H.; Al-fuqaha, A.L.A.; Member, S.; Dou, Z. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Götten, F.; Finger, D.F.; Havermann, M.; Braun, C.; Marino, M.; Bil, C. Full configuration drag estimation of short-to-medium range fixed-wing UAVs and its impact on initial sizing optimization. CEAS Aeronaut. J. 2021, 12, 589–603. [Google Scholar] [CrossRef]
- Panagiotou, P.; Yakinthos, K. Aerodynamic efficiency and performance enhancement of fixed-wing UAVs. Aerosp. Sci. Technol. 2019, 99, 105575. [Google Scholar] [CrossRef]
- García-Mayoral, R.; Jiménez, J. Drag reduction by riblets. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1412–1427. [Google Scholar] [CrossRef] [Green Version]
- Bannier, A.; Garnier, É.; Sagaut, P. Riblet Flow Model Based on an Extended FIK Identity. Flow Turbul. Combust. 2015, 95, 351–376. [Google Scholar] [CrossRef]
- Walsh, M.J.; Lindemann, A. Optimization and application of riblets for turbulent drag reduction. In Proceedings of the AIAA 22nd Aerospace Sciences Meeting; American Institute of Aeronautics and Astronautics, Reno, NV, USA, 9–12 January 1984. [Google Scholar]
- Walsh, M.J. Riblets. In Viscous Drag Reduction in Boundary Layers; Bushnell, D.M., Hefner, J.N., Eds.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1990; pp. 203–262. [Google Scholar]
- Bruse, M.; Bechert, D.; van der Hoeven, J.G.; Hage, W.; Hoppe, G. Experiments with conventional and with novel adjustable drag-reducing surfaces. In Near Wall Turbulent Flows; So, R.M.C., Speziale, C.G., Launder, B.E., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; pp. 719–739. [Google Scholar]
- Bechert, D.; Bruse, M.; Hage, W.; Meyer, R.D. Biological surfaces and their technological application—Laboratory and flight experiments on drag reduction and separation control. In Proceedings of the AIAA 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar]
- Bechert, D.W.; Bruse, M.; Hage, W.; Van Der Hoeven, J.G.T.; Hoppe, G. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 1997, 338, 59–87. [Google Scholar] [CrossRef]
- Viswanath, P.R. Aircraft viscous drag reduction using riblets. Prog. Aerosp. Sci. 2002, 38, 571–600. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, S.; Viswanath, P.R.; Rudrakumar, S. Viscous drag reduction using riblets on NACA 0012 airfoil to moderate incidence. AIAA J. 1996, 34, 676–682. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M.; Wolthers, W.; Leijdens, H.; Krishna Prasad, K.; Schwarz-van Manen, A. The reduction of skin friction by riblets under the influence of an adverse pressure gradient. Exp. Fluids 1993, 15, 17–26. [Google Scholar] [CrossRef]
- Sundaram, S.; Viswanath, P.R.; Subaschandar, N. Viscous drag reduction using riblets on a swept wing. AIAA J. 1999, 37, 851–856. [Google Scholar] [CrossRef]
- McLean, J.D.; George-Falvey, D.N.; Sullivan, P.P. Flight-Test of Turbulent Skin-Friction Reduction by Riblets. In Proceedings of the Turbulent Drag Reduction by Passive Means, London, UK, 15–17 September 1987. [Google Scholar]
- Kurita, M.; Iijima, H.; Koga, S.; Nishizawa, A.; Kwak, D.; Iijima, Y.; Takahashi, H.; Abe, H. Flight test for paint-riblet. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Lin, J.C. Review of Research on Low-Profile Vortex Generators to Control Boundary-Layer Separation; Elsevier: Amsterdam, The Netherlands, 2002; Volume 38, ISBN 1757864555. [Google Scholar]
- Zhen, T.K.; Zubair, M.; Ahmad, K.A. Experimental and numerical investigation of the effects of passive vortex generators on Aludra UAV performance. Chin. J. Aeronaut. 2011, 24, 577–583. [Google Scholar] [CrossRef] [Green Version]
- Kehro, M.; Hutcherson, S.; Liebeck, R.M.; Blackwelder, R.F.; Liebeck, R.H. Vortex generators used to control laminar separation bubbles. J. Aircr. 1993, 30, 315–319. [Google Scholar] [CrossRef]
- Jahanmiri, M.; Bahraini, A. Large Eddy Simulation of Turbulent Drag Reduction by V-Shaped Riblets. Int. J. Latest Res. Sci. Technol. 2015, 4, 42–46. [Google Scholar]
- Mele, B.; Tognaccini, R.; Catalano, P.; Rosa, D. Analysis of riblets performance in pressure gradient flow by large eddy simulation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–11. [Google Scholar]
- Choi, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 1993, 255, 503–539. [Google Scholar] [CrossRef]
- Panagiotou, P.; Kaparos, P.; Salpingidou, C.; Yakinthos, K. Aerodynamic design of a MALE UAV. Aerosp. Sci. Technol. 2016, 50, 127–138. [Google Scholar] [CrossRef]
- Panagiotou, P.; Kaparos, P.; Yakinthos, K. Winglet design and optimization for a MALE UAV using CFD. Aerosp. Sci. Technol. 2014, 39, 190–205. [Google Scholar] [CrossRef]
- Luchini, P.; Manzo, F.; Pozzi, A. Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 2012, 228, 87–109. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R. Numerical simulation of riblets on airfoils and wings. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Saffman, P.G. Model for Inhomogeneous Turbulent Flow. Proc. R. Soc. London. A Math. Phys. Sci. 1970, 317, 417–433. [Google Scholar] [CrossRef]
- Catalano, P.; de Rosa, D.; Mele, B.; Tognaccini, R.; Moens, F. Effects of riblets on the performances of a regional aircraft configuration in NLF conditions. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Kontogiannis, S.G.; Ekaterinaris, J.A. Design, performance evaluation and optimization of a UAV. Aerosp. Sci. Technol. 2013, 29, 339–350. [Google Scholar] [CrossRef]
- Narayan, G.; John, B. Effect of winglets induced tip vortex structure on the performance of subsonic wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A three-equation eddy-viscosity model for reynolds-averaged navier-stokes simulations of transitional flow. J. Fluids Eng. Trans. ASME 2008, 130, 1214011–12140114. [Google Scholar] [CrossRef]
- Fürst, J.; Straka, P.; Příhoda, J.; Šimurda, D. Comparison of several models of the laminar/turbulent transition. EPJ Web Conf. 2013, 45, 01032. [Google Scholar] [CrossRef]
- Mele, B.; Tognaccini, R.; Catalano, P. Performance Assessment of a Transonic Wing-Body Configuration with Riblets Installed. J. Aircr. 2016, 53, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Bliamis, C.; Vlahostergios, Z.; Misirlis, D.; Yakinthos, K. Modeling Surface Riblets Skin Friction Reduction Effect with the Use of Computational Fluid Dynamics. Chem. Eng. Trans. 2020, 81, 595–600. [Google Scholar] [CrossRef]
- Roskam, J. Airplane Design, Part VII: Determination of Stability, Control and Performance Characteristics: FAR and Military Requirements; Roskam Aviation and Engineering Corp: Ottawa, ON, Canada, 2006. [Google Scholar]
- Raymer, D. Aircraft Design: A Conceptual Approach, Sixth Edition, 6th ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).