Probability Analysis of Widespread Fatigue Damage in LY12-CZ Aluminum Alloy Single-Row Seven-Hole Plate
Abstract
:1. Introduction
2. Fatigue Test of Single-Detail Perforated Plate
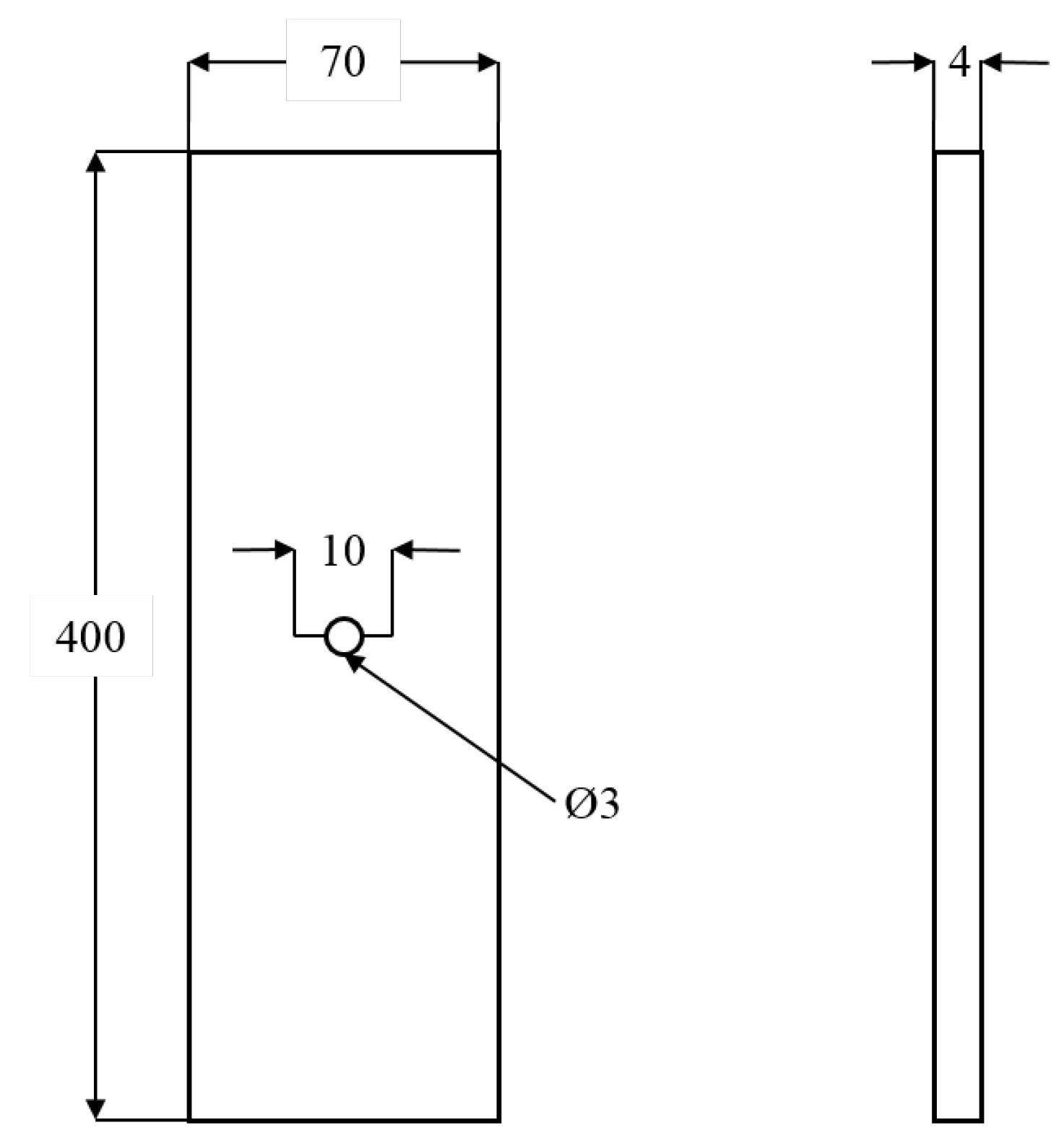
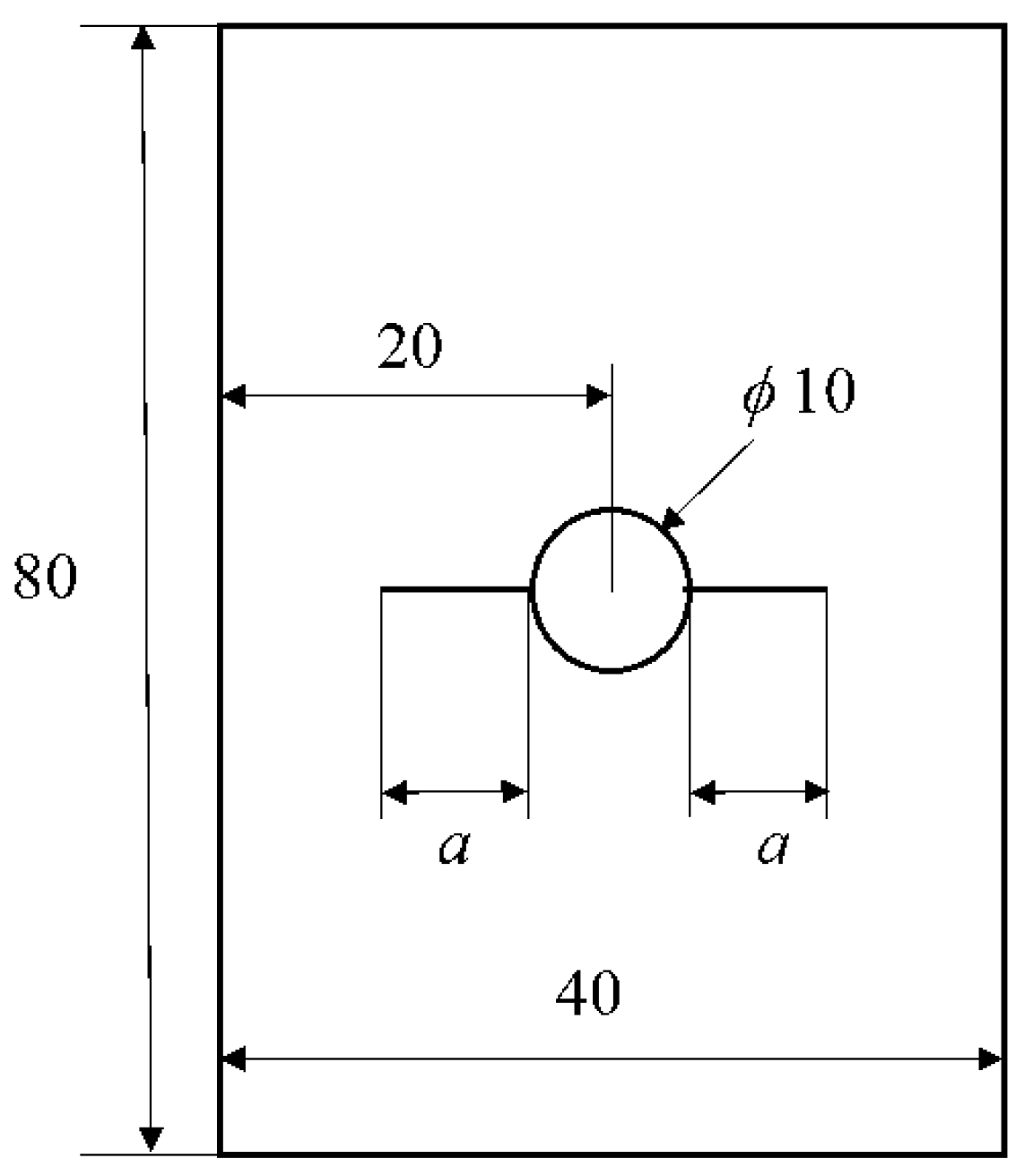
2.1. Test Piece Preparation
2.2. Test Procedure
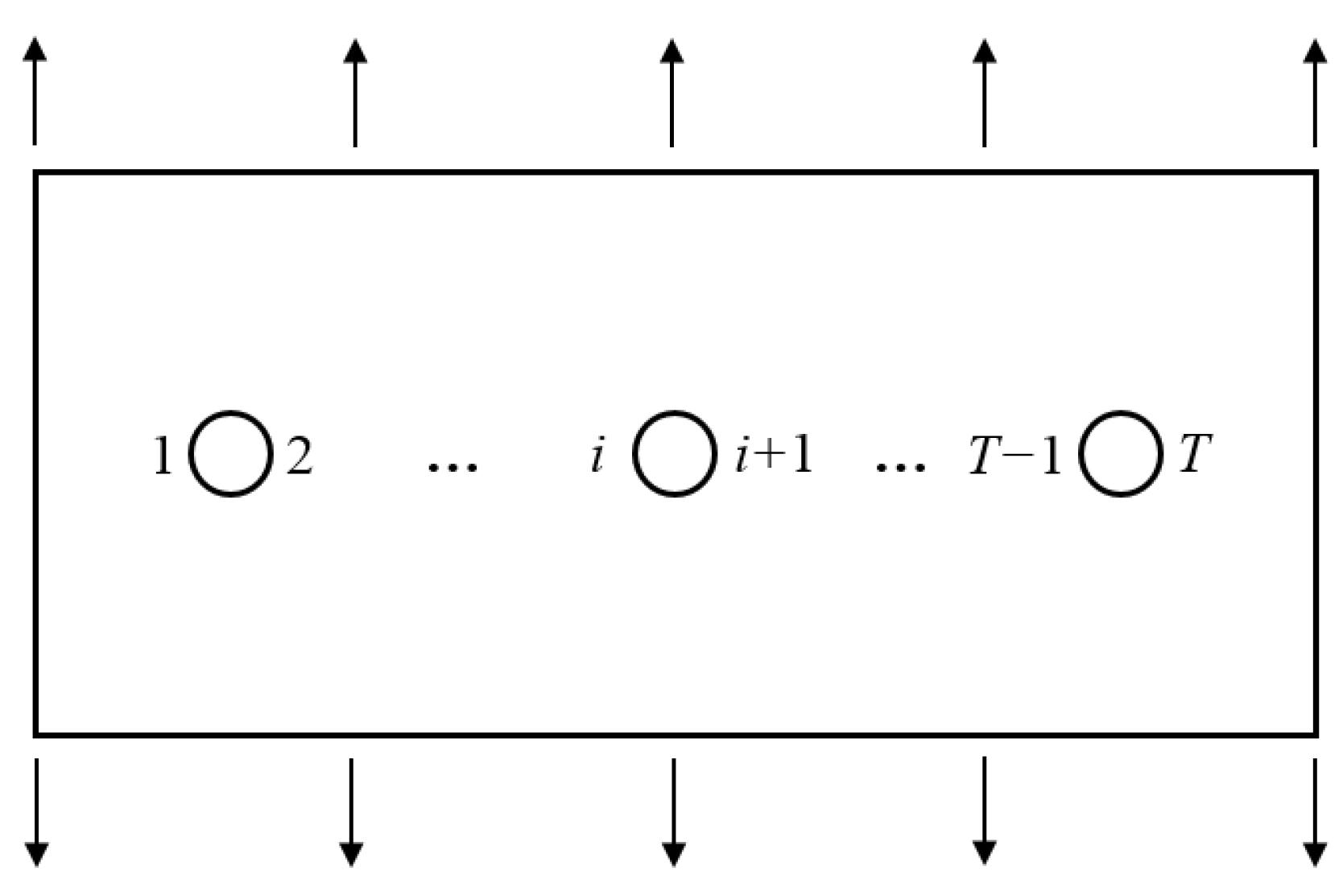
3. Random Crack Initiation Model of MSD Structure
4. Random Crack Propagation in MSD Structure
4.1. Crack Propagation Model Based on Random Variables
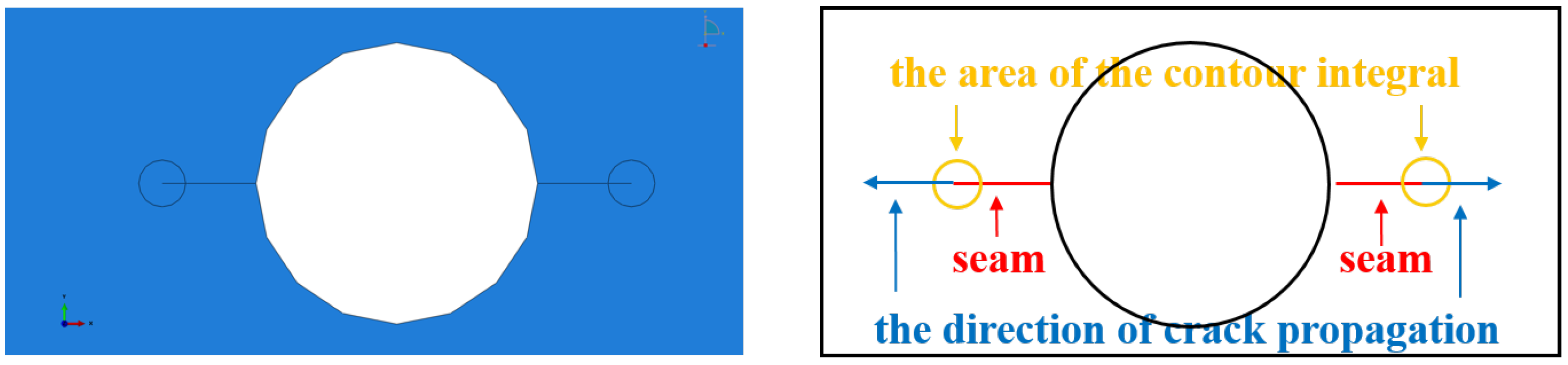
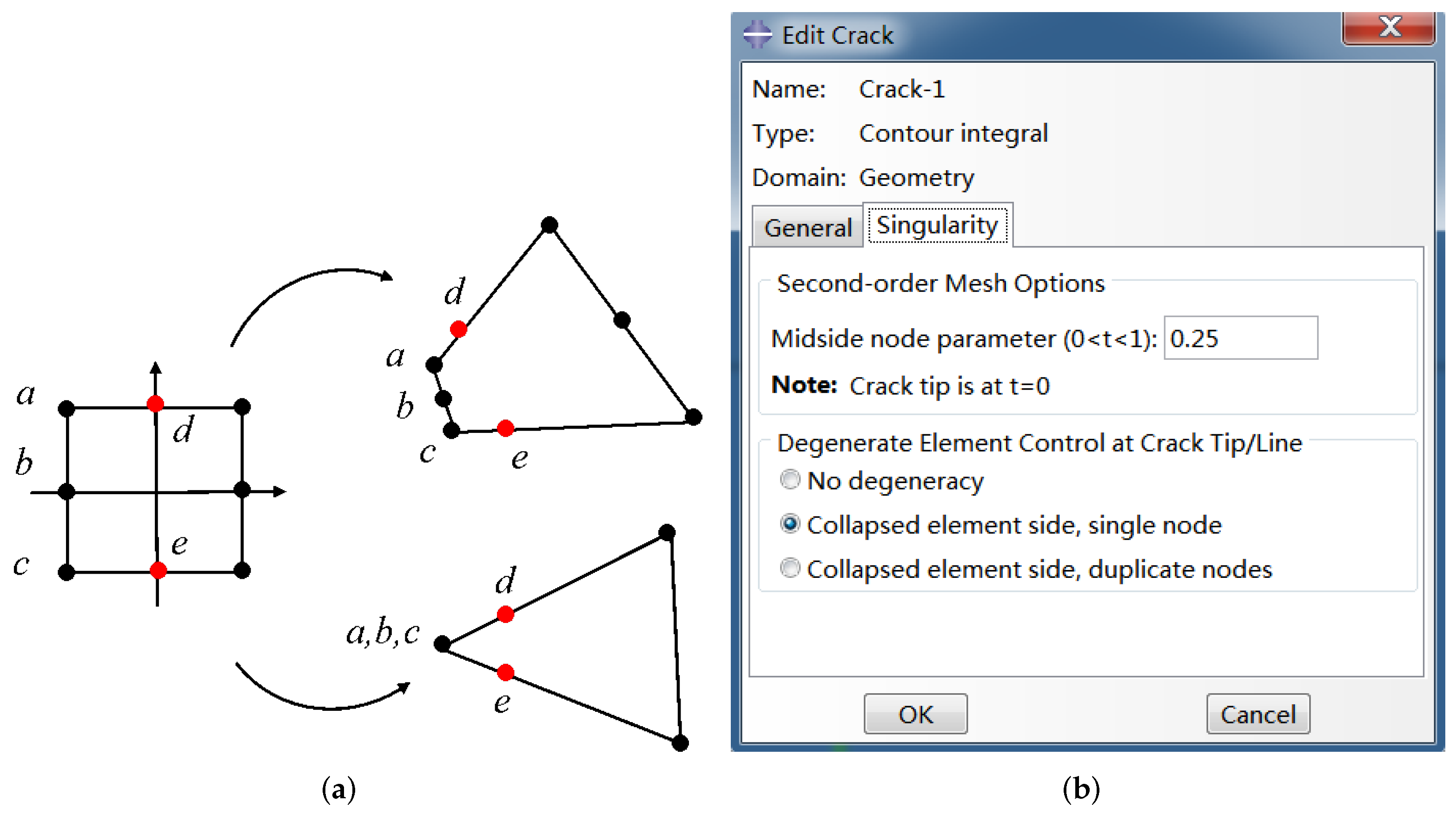
4.2. Calculation of Stress Intensity Factor by FEM
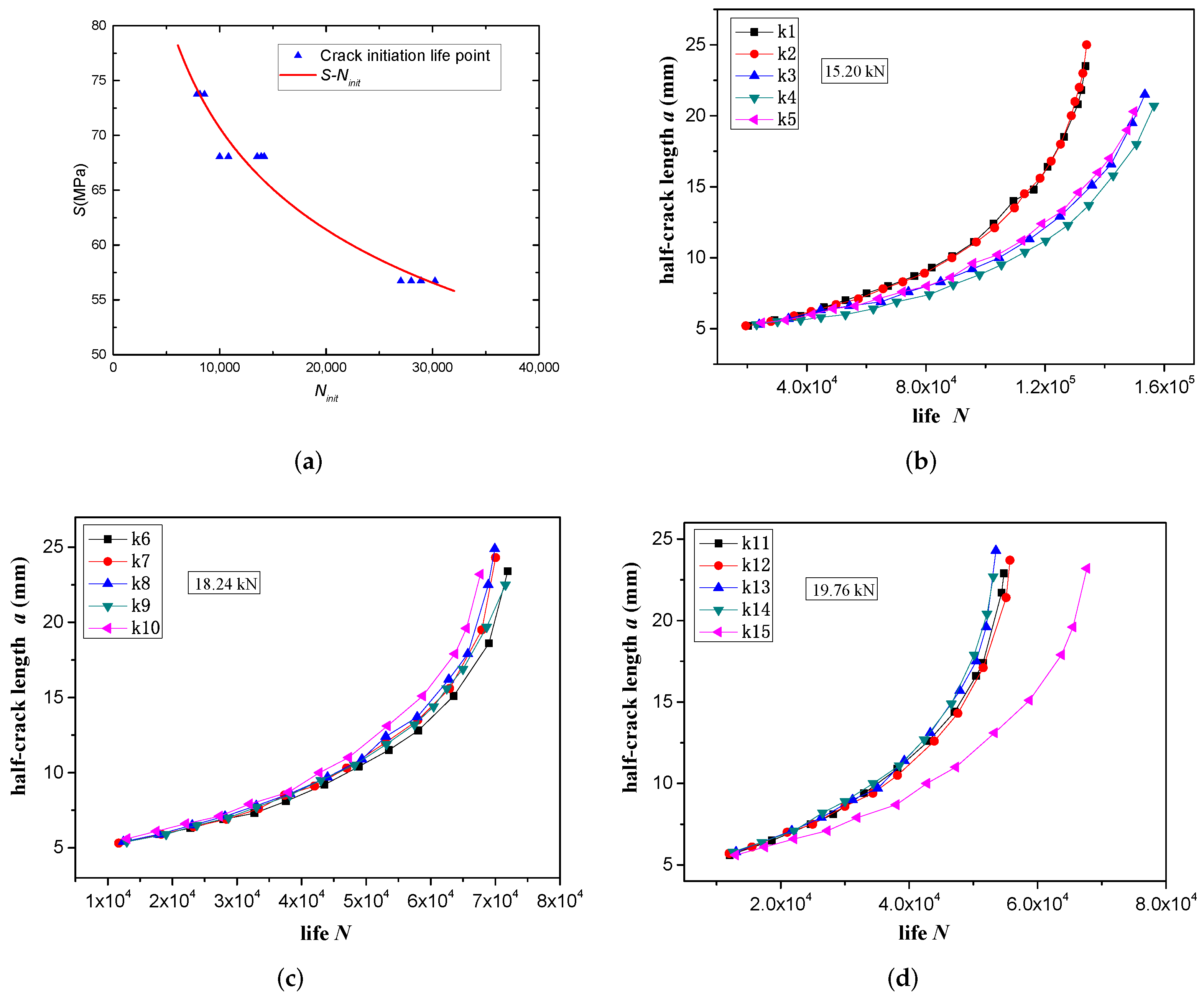
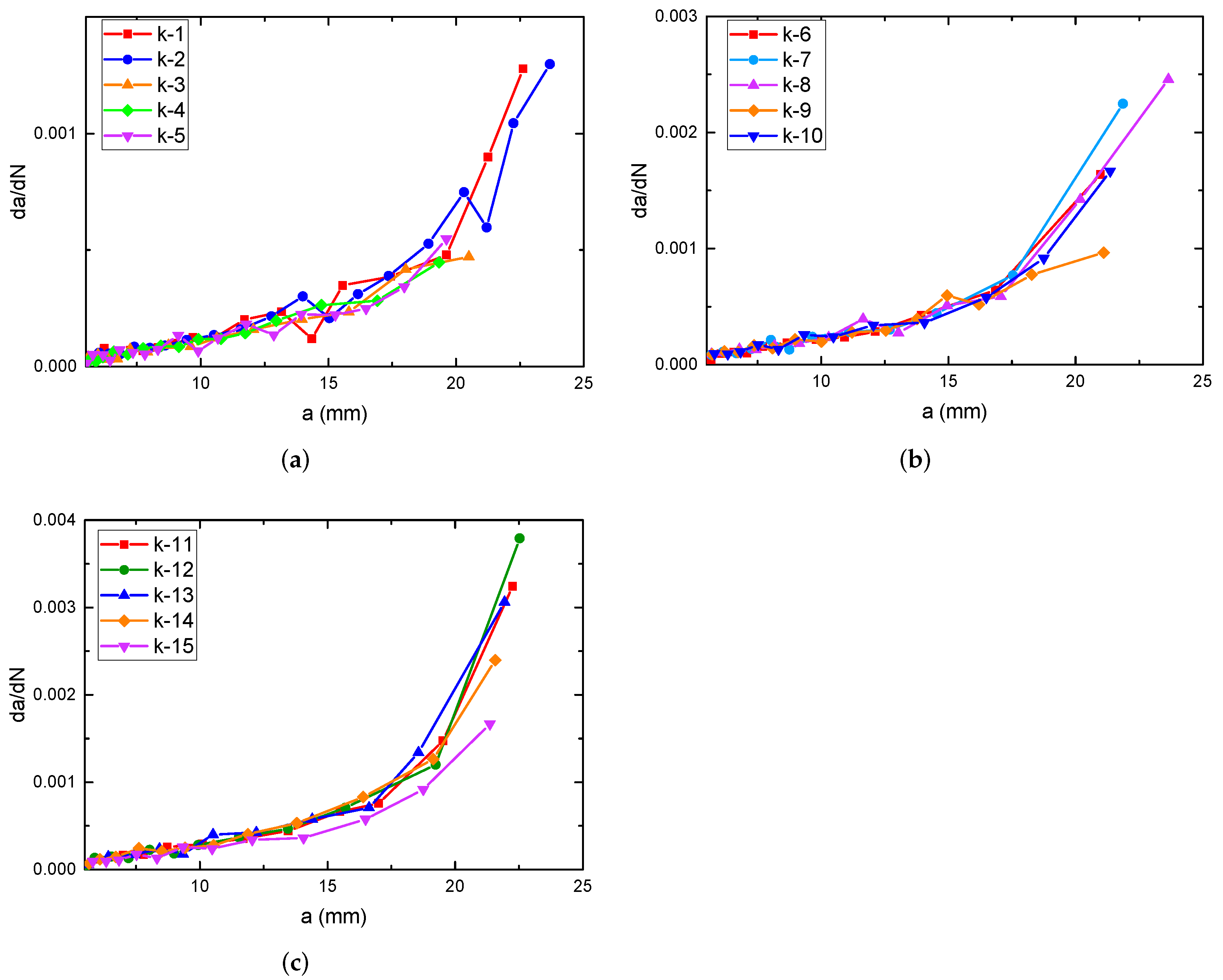
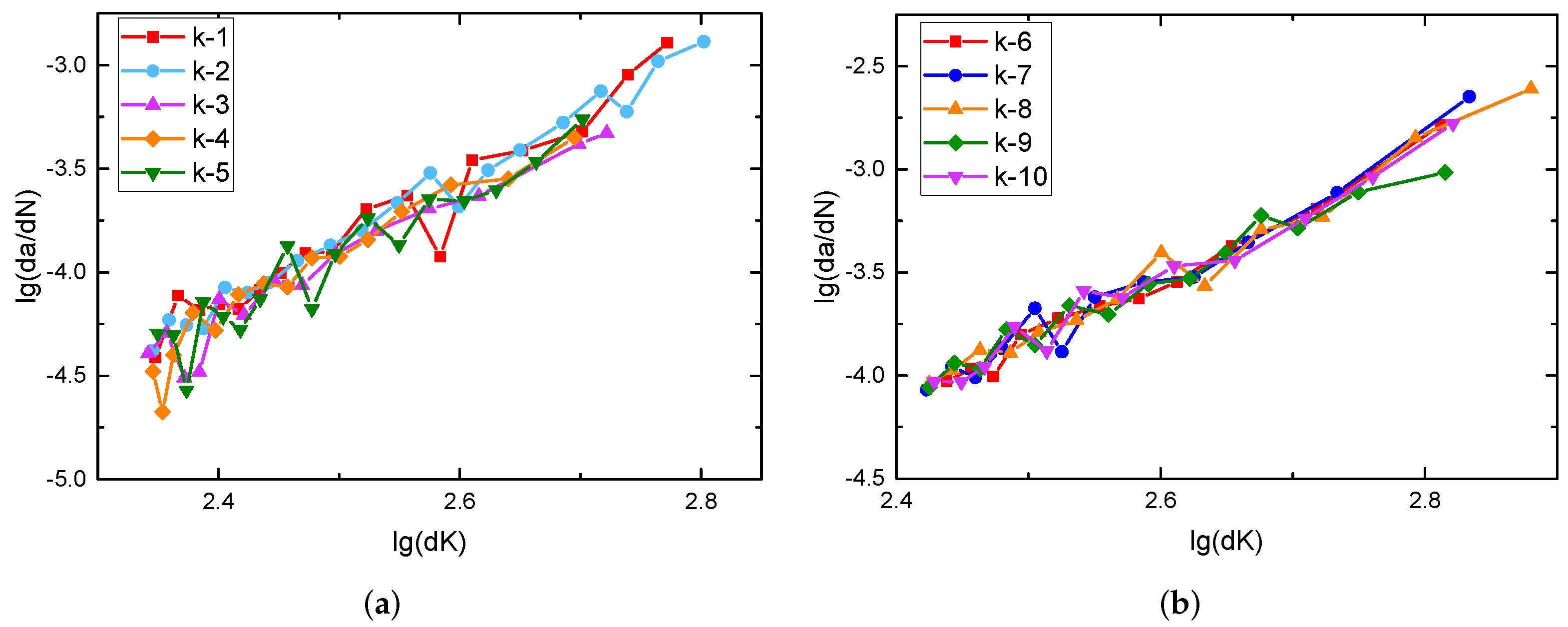
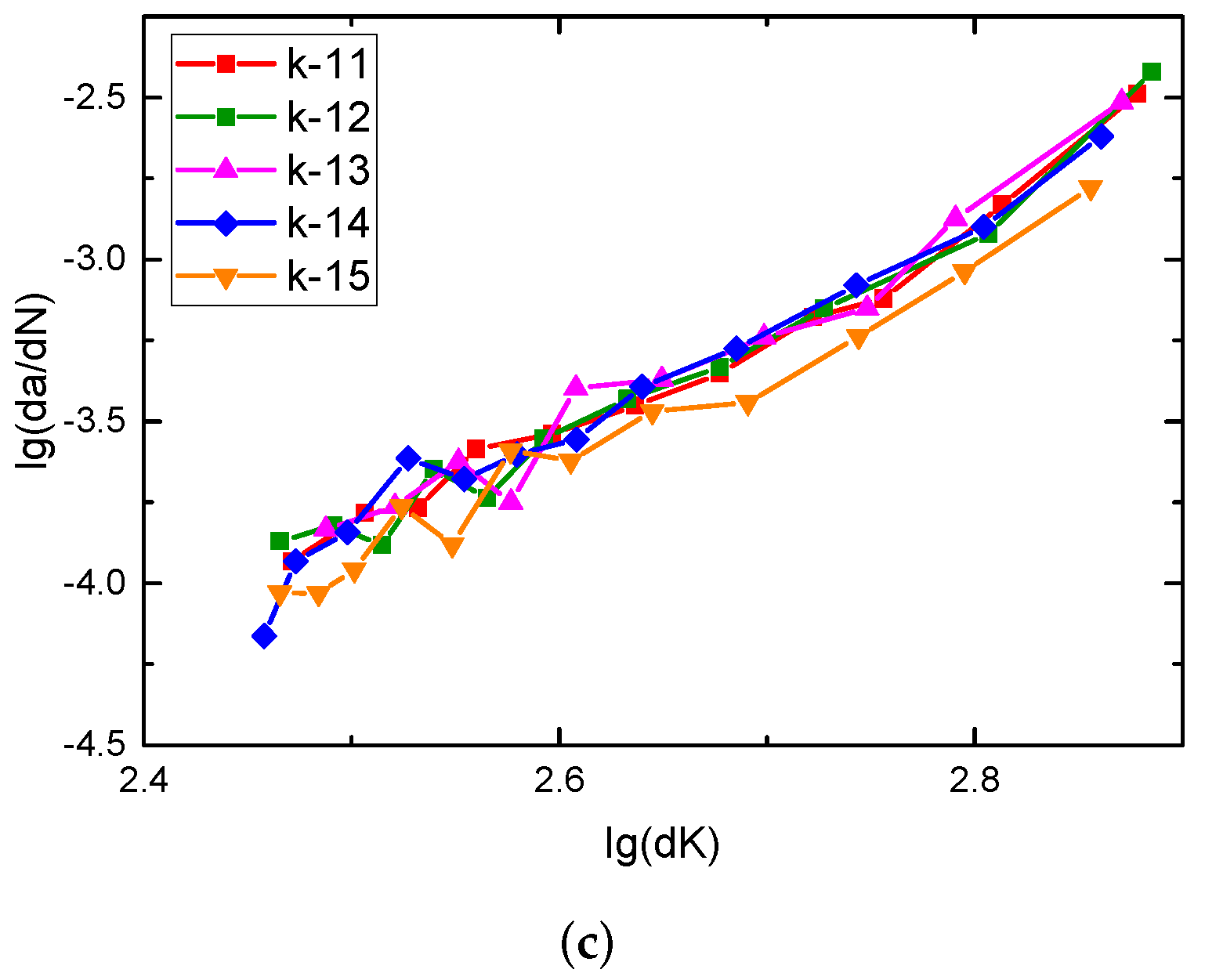
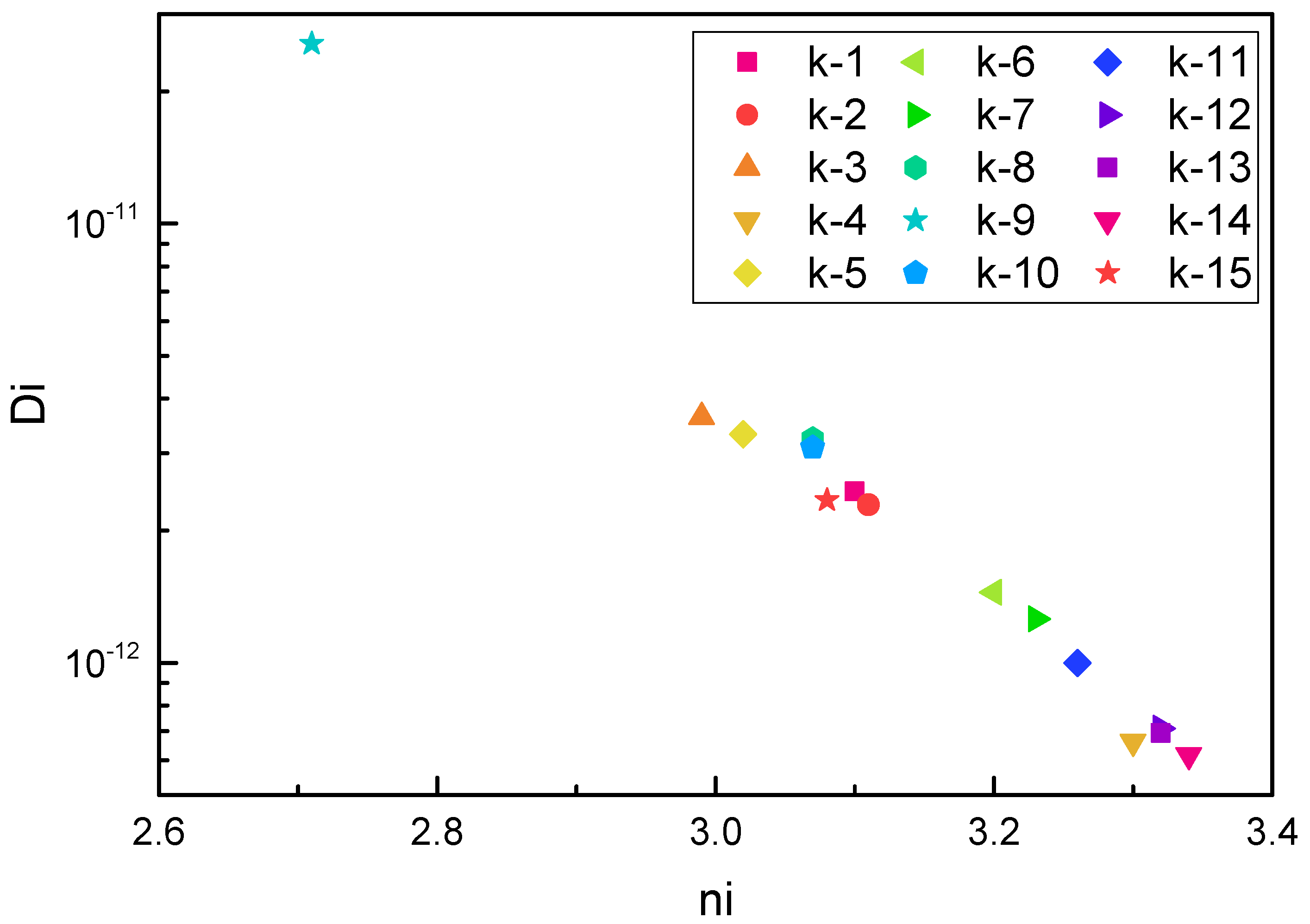
4.3. Processing and Statistics of Crack Propagation Test Results
5. Residual Strength Analysis of MSD Structure
5.1. Plastic Zone Connectivity Criterion
5.2. Structural Failure Criterion
6. Prediction of Structural Life by Monte Carlo Method
- Determine basic properties such as geometric configuration, material properties, initial crack size, and load spectrum size.
- According to the test data, obtain the distribution of the parameters describing the dispersion in the random crack initiation and random crack growth models, and estimate the parameters that satisfy the distribution.
- Use a random number generator to generate a set of random numbers that obey the standard normal distribution. The random number simulating the dispersion of crack initiation is obtained by Equation (3). The initiation life and initiation sequence of cracks at each position are obtained by Equations (3) and (6).
- For the non-initiation position, fatigue damage will continue to accumulate until the cumulative damage value is 1. For the location of the initiated crack, the random crack propagation analysis is carried out.
- The random number generator is used to generate a group of random numbers that obey the standard normal distribution. The random parameters and describing the crack growth rate are obtained by Equations (12) and (13), respectively. Then, the value of each crack tip is obtained by the finite element solution, and the crack growth increment for a given cycle life is obtained by substituting into Equation (8).
- Add to the original crack length a, update the crack size a, and then give and find , and keep cycling. In the process of this cycle, it is continuously determined whether the connectivity criterion and failure criterion are met. If the connectivity criterion is met, the two adjacent cracks are connected. If the failure criterion is met, the structure breaks and fails, and the calculation stops. The simulated structural life is obtained .
- Calculate L times of the above process, i.e., complete L times of Monte Carlo sampling to obtain the results of L structural lives . Through statistical analysis of the calculation results, the logarithmic life mean and logarithmic life standard deviation of the structure can be obtained.
7. Analysis Examples
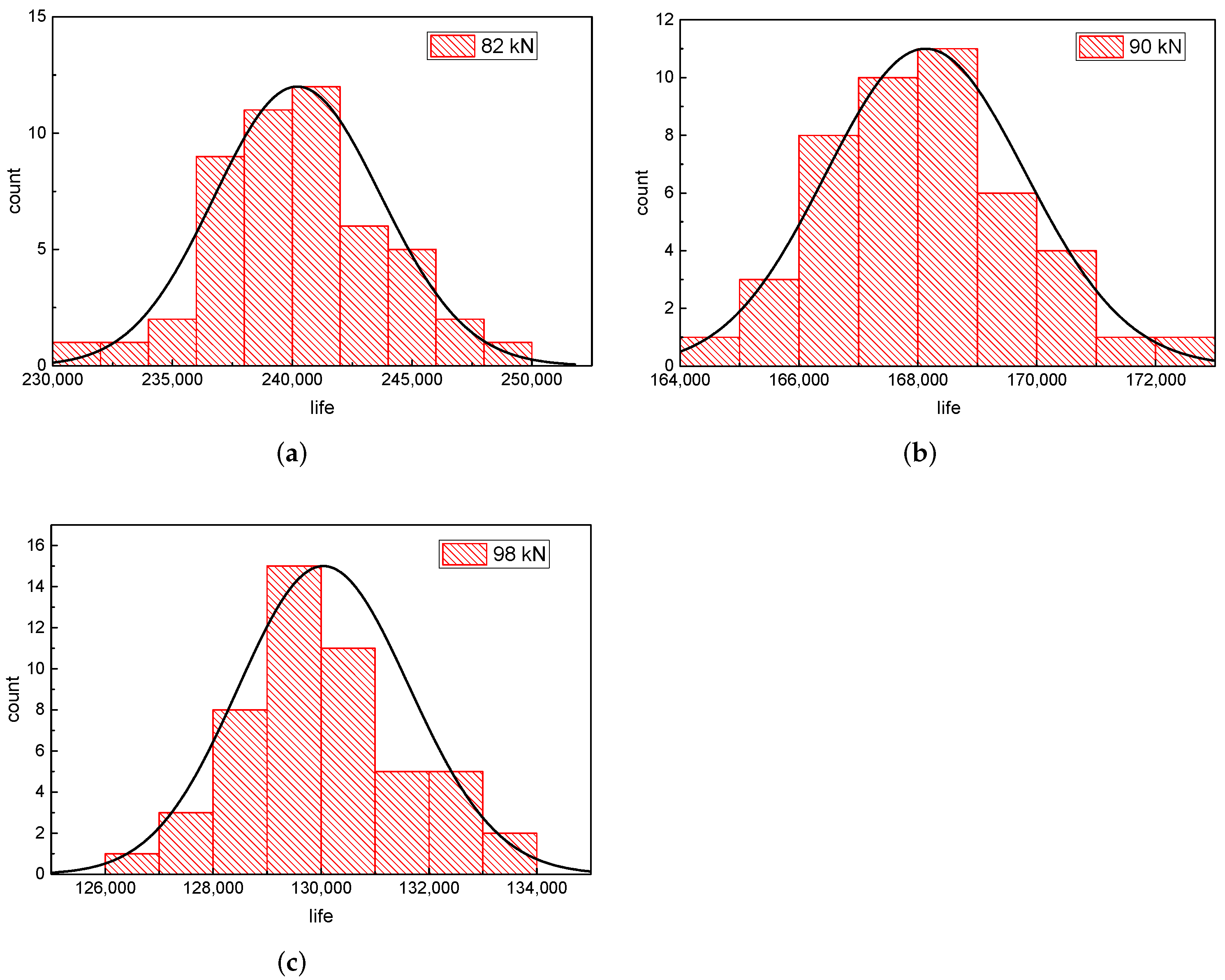
7.1. Seven-Hole Collinear Plate Test
7.2. Simulation Calculation
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horst, P. Widespread fatigue damage—An issue for aging and new aircraft. In Key Engineering Materials; Trans Tech Publications Ltd.: Schwyz, Switzerland, 2006; Volume 324, pp. 1–8. [Google Scholar]
- Federal Aviation Administration. Aging aircraft program: Widespread fatigue damage, proposed rule. Fed. Regist. 2006, 74, 19927–19951. [Google Scholar]
- Xi, W.; Zhao, J.J.; Yao, W.X. Probability distribution analysis model of crack initiation life for widespread fatigue damage. China Sci. 2016, 11, 576–580. [Google Scholar]
- Yan, X.Z.; Wang, S.N.; Huang, H.C. Probability analysis method for aircraft structures containing multiple site damage. J. Mech. Strength 2012, 34, 881–885. [Google Scholar]
- Ai, Y.; Zhu, S.P.; Liao, D.; Correia, J.A.F.O.; Souto, C.; De Jesus, A.M.P.; Keshtegar, B. Probabilistic modeling of fatigue life distribution and size effect of components with random defects. Int. J. Fatigue 2019, 126, 165–173. [Google Scholar] [CrossRef]
- Jung-Hoon, K.; Thanh, C.D.; Goangseup, Z. Probabilistic fatigue integrity assessment in multiple crack growth analysis associated with equivalent initial flaw and material variability. Eng. Fract. Mech. 2016, 156, 182–196. [Google Scholar]
- Wang, S.; Liu, M.B.; Wang, G.l. Experimental study and finite element analysis of widespread damage. Acta Aeronaut. Astronaut. Sin. 2010, 31, 1578–1583. [Google Scholar]
- Ray, A.; Patankar, R. A stochastic model of fatigue crack propagation under variable amplitude loading. Eng. Fract. Mech. 1999, 62, 477–493. [Google Scholar] [CrossRef]
- Riahi, H.; Bressolette, P.; Chateauneuf, A. Random fatigue crack growth in mixed mode by stochastic collocation method. Eng. Fract. Mech. 2010, 77, 3292–3309. [Google Scholar] [CrossRef]
- Edson, D.L.; André, T.B.; Wilson, S.V. On the performance of response surface and direct coupling approaches in solution of random crack propagation problems. Struct. Saf. 2011, 33, 261–274. [Google Scholar]
- Salimi, H.; Kiad, S.; Pourgol-Mohammad, M. Stochastic Fatigue Crack Growth Analysis for Space System Reliability. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2017, 4, 1–31. [Google Scholar] [CrossRef]
- Pyo, C.R.; Okada, H.; Atluri, S.N. An elastic-plastic finite element alternating method for analyzing wide-spread fatigue damage in aircraft structures. Comput. Mech. 1995, 16, 62–68. [Google Scholar] [CrossRef]
- Wu, L.; Sun, Q. Study on semi analytical numerical algorithm of stress intensity factor of structure with MSD. J. Northwestern Polytech. Univ. 2003, 21, 214–217. [Google Scholar]
- Swift, T. Damage tolerance capability. Int. J. Fatigue 1994, 16, 75–94. [Google Scholar] [CrossRef]
- Ge, S.; Li, Z.; Zhang, J.G. Residual strength of unreinforced aluminum alloy panel with multiple damages. Acta Aeronaut. Astronaut. Sin. 2008, 29, 411–415. [Google Scholar]
- Bert, L.S.; Perry, A. Strength of 2024-T3 Aluminum Panels with Multiple Site Damage. J. Aircr. 2000, 37, 325–331. [Google Scholar]
- Wang, C.S.; Zhang, J.Y.; Bao, R. Test study on residual strength of aluminum alloy plate containing MSD. J. Aeronaut. Mater. 2007, 27, 346–350. [Google Scholar]
- Sergey, S.; Roman, K. Probabilistic mothod for the analysis of widespread fatigue damage in structures. Int. J. Fatigue 2005, 27, 223–234. [Google Scholar]
- Gao, Z. Fatigue Applied Statistics, 3rd ed.; National Defense Industry Press: Beijing, China, 1986. [Google Scholar]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. ASM Trans. J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Sun, H.; Dong, D.; Chen, L. Prediction of Random Crack Propagation Life of Multi-damaged Pore Structures. Sci. Technol. Eng. 2019, 19, 278–283. [Google Scholar]
- Kou, K.P.; Cao, J.L.; Yang, Y. Weight Function Method for Stress Intensity Factors of Semi-Elliptical Surface Cracks on Functionally Graded Plates Subjected to Non-Uniform Stresses. Materials 2020, 13, 3155. [Google Scholar] [CrossRef]
- Hsin, J.H.; John, H.L.P.; Kin, S.T. Stress intensity factors for fatigue analysis of weld toe cracks in a girth-welded pipe. Int. J. Fatigue 2016, 87, 279–287. [Google Scholar]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. ASME J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 279–287. [Google Scholar] [CrossRef]
- Grandt, A.F. Stress intensity factors for some through-cracked fastener holes. Int. J. Fract. 1975, 11, 283–294. [Google Scholar] [CrossRef]
- Kebir, H.; Roelandt, J.M.; Gaudin, J. Monte Carlo simulations of life expectancy using the dual boundary element method. Eng. Fract. Mech. 2001, 68, 1371–1375. [Google Scholar] [CrossRef]


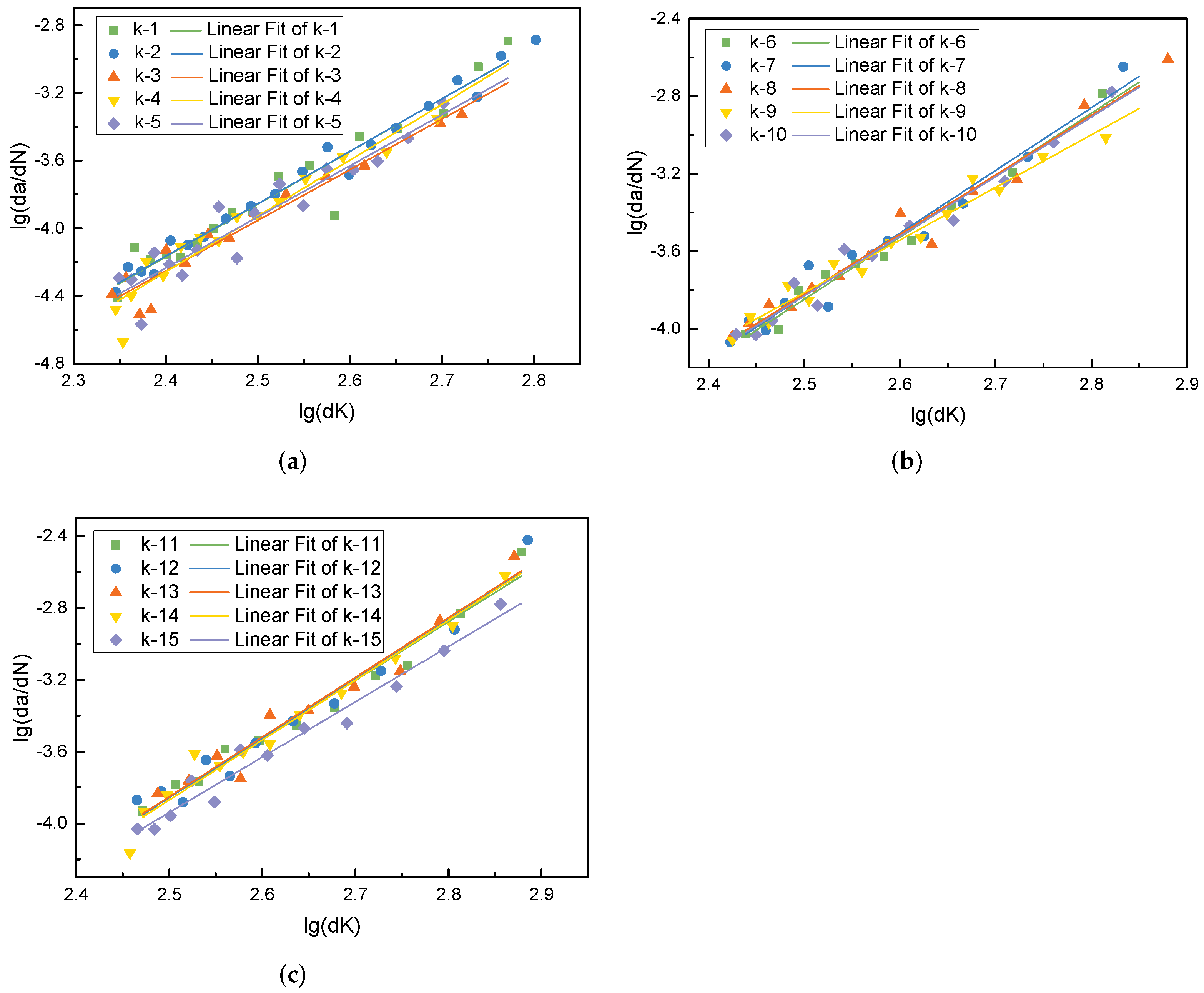






| E/MPa | μ | /MPa | |
|---|---|---|---|
| 0.33 | 100 | 339 |
| R | f | Number | Number of Test Pieces | |
|---|---|---|---|---|
| 15.20 | 0.1 | 5 Hz | k1–k5 | 5 |
| 18.24 | 0.1 | 5 Hz | k6–k10 | 5 |
| 19.76 | 0.1 | 5 Hz | k11–k15 | 5 |
| m | ||
|---|---|---|
| 4.93 | 13.12 | 0.05 |
| a (mm) | ABAQUS | Handbook | Error (%) |
|---|---|---|---|
| 2 | 554.4 | 548.7 | 1.04 |
| 5 | 721.7 | 717.4 | 0.60 |
| 10 | 1179.0 | 1173.9 | 0.43 |
| F/kN | ||||
|---|---|---|---|---|
| 82 | 5.381 | 0.006 | 5.390 | 0.014 |
| 90 | 5.225 | 0.004 | 5.208 | 0.027 |
| 98 | 5.114 | 0.005 | 5.101 | 0.030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Wang, F.; Pan, W.; Yang, L.; Bai, S.; Zhu, Q.; Tong, M. Probability Analysis of Widespread Fatigue Damage in LY12-CZ Aluminum Alloy Single-Row Seven-Hole Plate. Aerospace 2022, 9, 215. https://doi.org/10.3390/aerospace9040215
Liu K, Wang F, Pan W, Yang L, Bai S, Zhu Q, Tong M. Probability Analysis of Widespread Fatigue Damage in LY12-CZ Aluminum Alloy Single-Row Seven-Hole Plate. Aerospace. 2022; 9(4):215. https://doi.org/10.3390/aerospace9040215
Chicago/Turabian StyleLiu, Kai, Fangli Wang, Wei Pan, Le Yang, Shuwei Bai, Qiang Zhu, and Mingbo Tong. 2022. "Probability Analysis of Widespread Fatigue Damage in LY12-CZ Aluminum Alloy Single-Row Seven-Hole Plate" Aerospace 9, no. 4: 215. https://doi.org/10.3390/aerospace9040215
APA StyleLiu, K., Wang, F., Pan, W., Yang, L., Bai, S., Zhu, Q., & Tong, M. (2022). Probability Analysis of Widespread Fatigue Damage in LY12-CZ Aluminum Alloy Single-Row Seven-Hole Plate. Aerospace, 9(4), 215. https://doi.org/10.3390/aerospace9040215





