Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation
Abstract
:1. Introduction
2. Problem Statement and Guidance Model Analysis
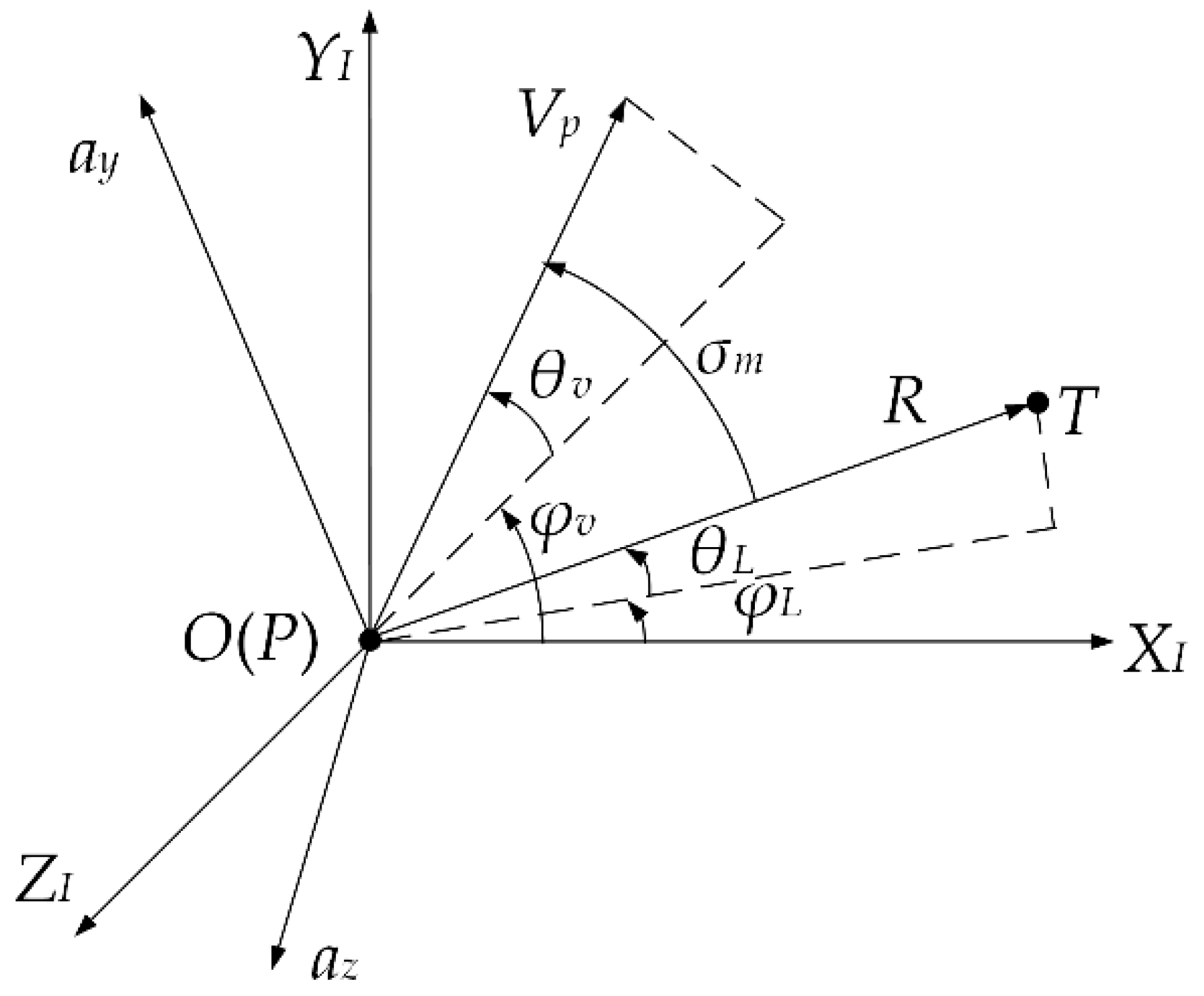
2.1. Problem Statement
2.2. Guidance Model Analysis
3. Three-Dimensional Time-to-Go Estimation under Time-Varying Velocity
4. Three-Dimensional ITCG Law Design
4.1. Analysis of the Biased Term
- (1)
- If fd > 0, the biased term Δaym can increase the flight time of the projectile;
- (2)
- If fd = 0, the biased term Δaym does not affect the flight time of the projectile;
- (3)
- If fd < 0, the biased term Δaym can decrease the flight time of the projectile.
4.2. ITCG Law Design
5. Numerical Simulation Analysis
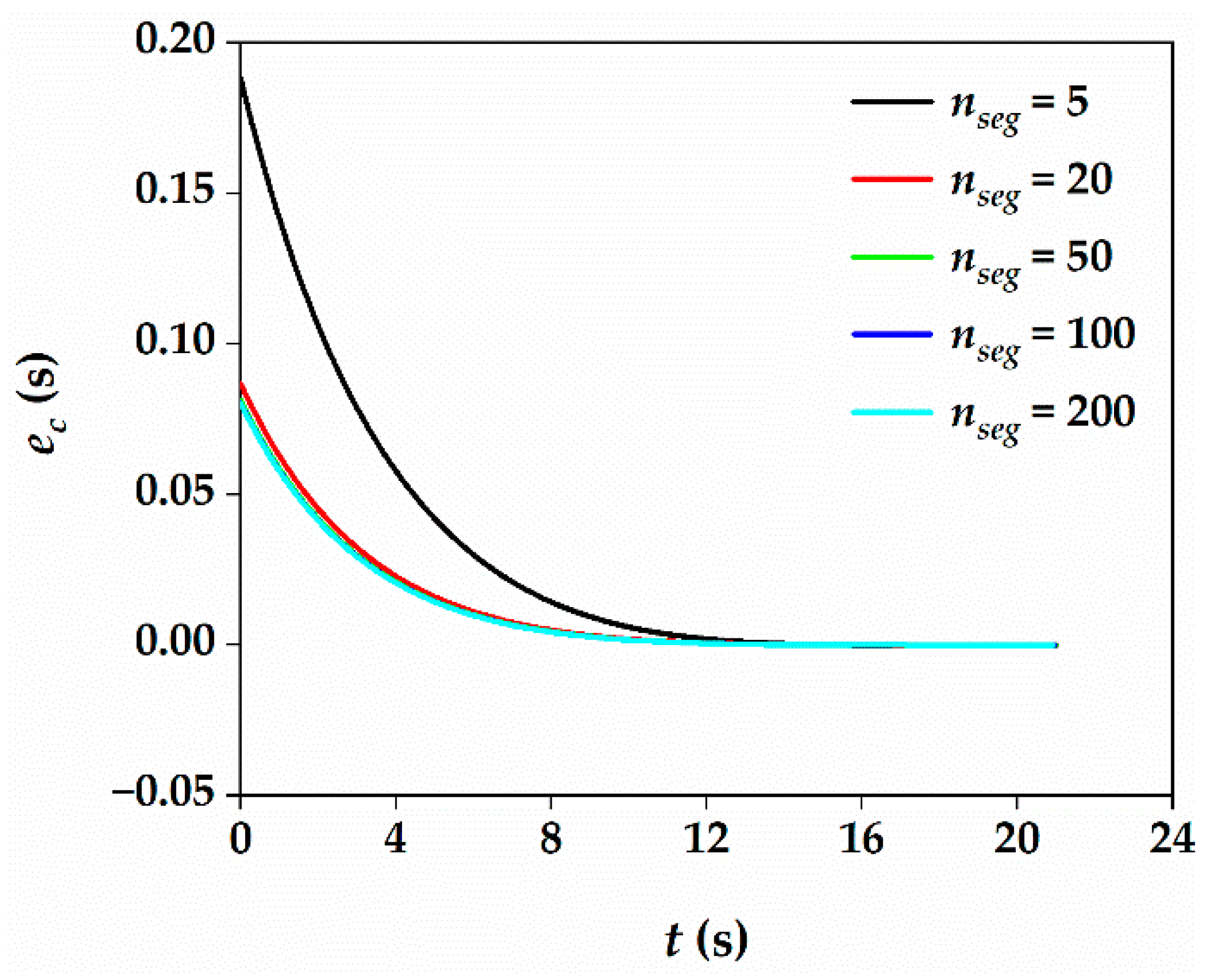
5.1. Verification of Three-Dimensional Tgo Estimation Algorithm
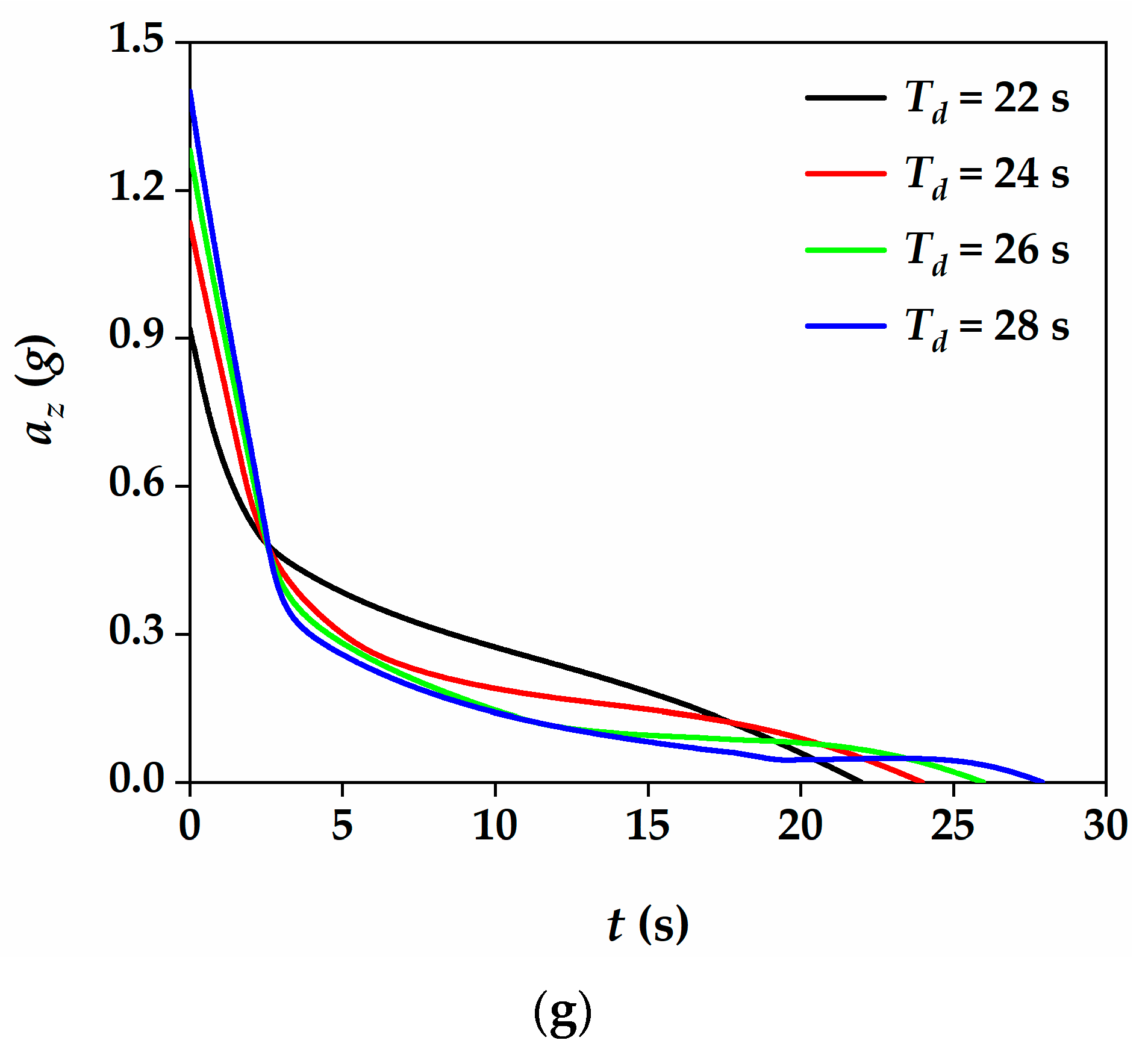
5.2. Performance of the Three-Dimensional ITCG Law under Different Designated Times
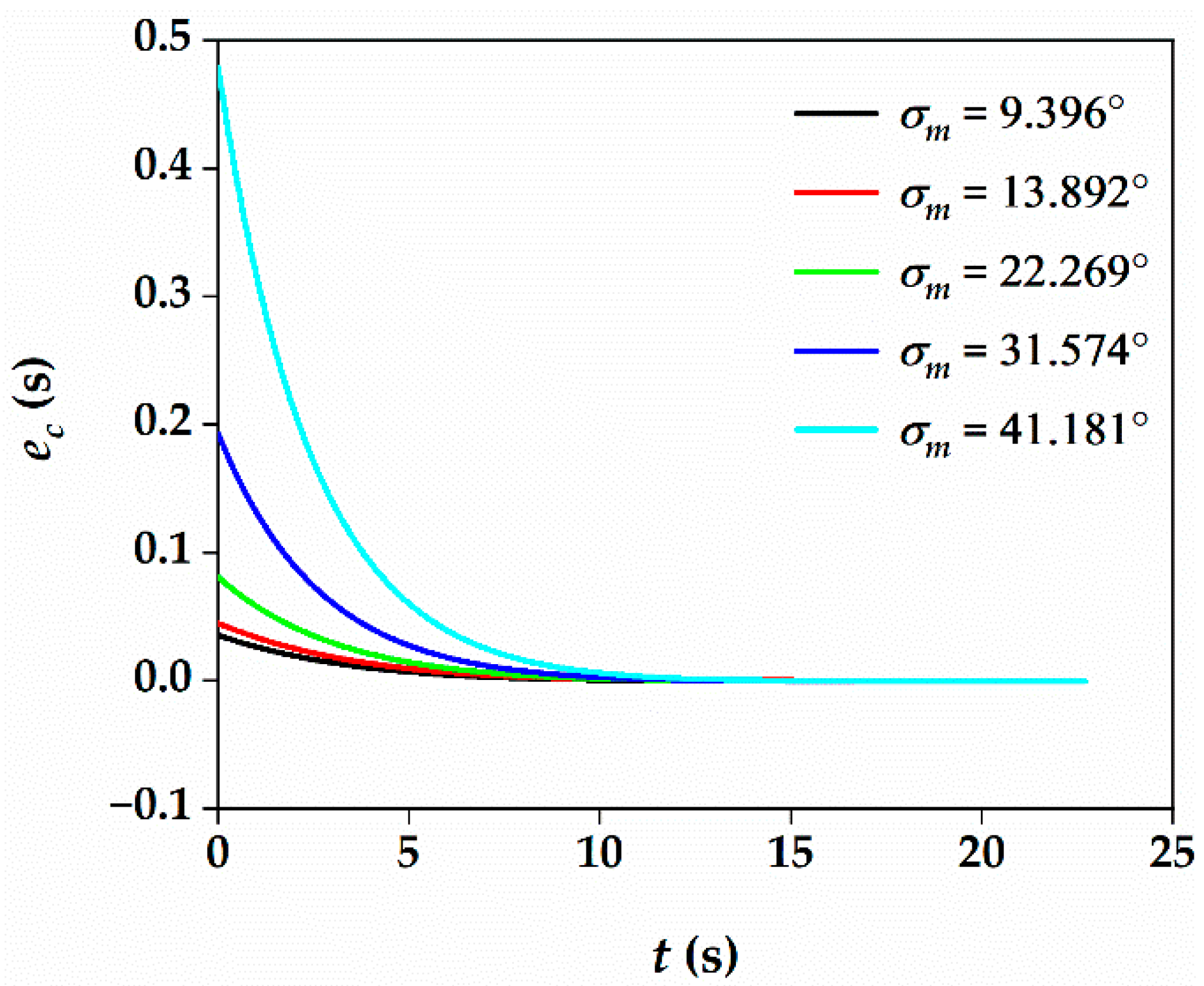
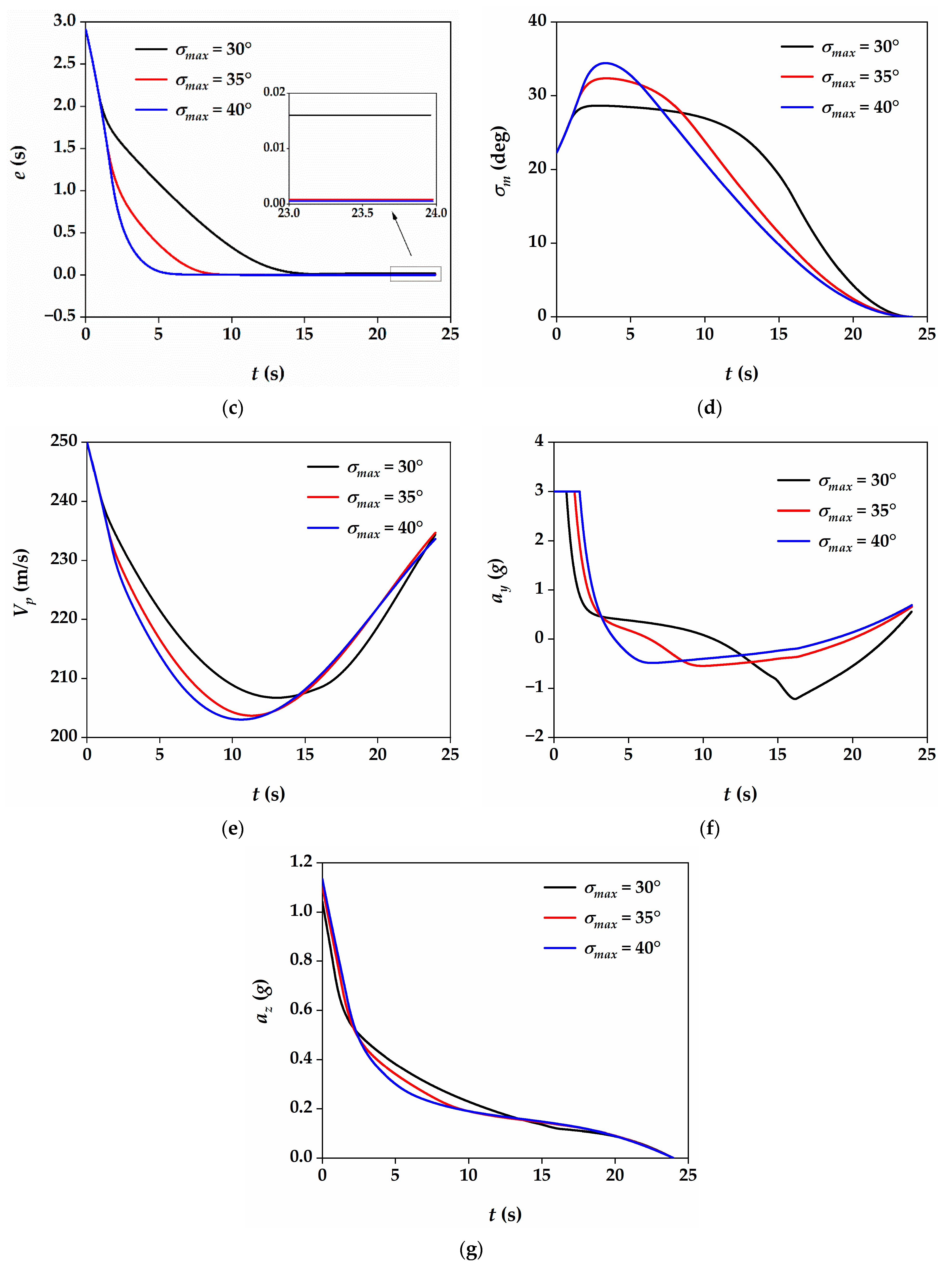
5.3. Performance of the Three-Dimensional ITCG Law under Different FOV Constraints
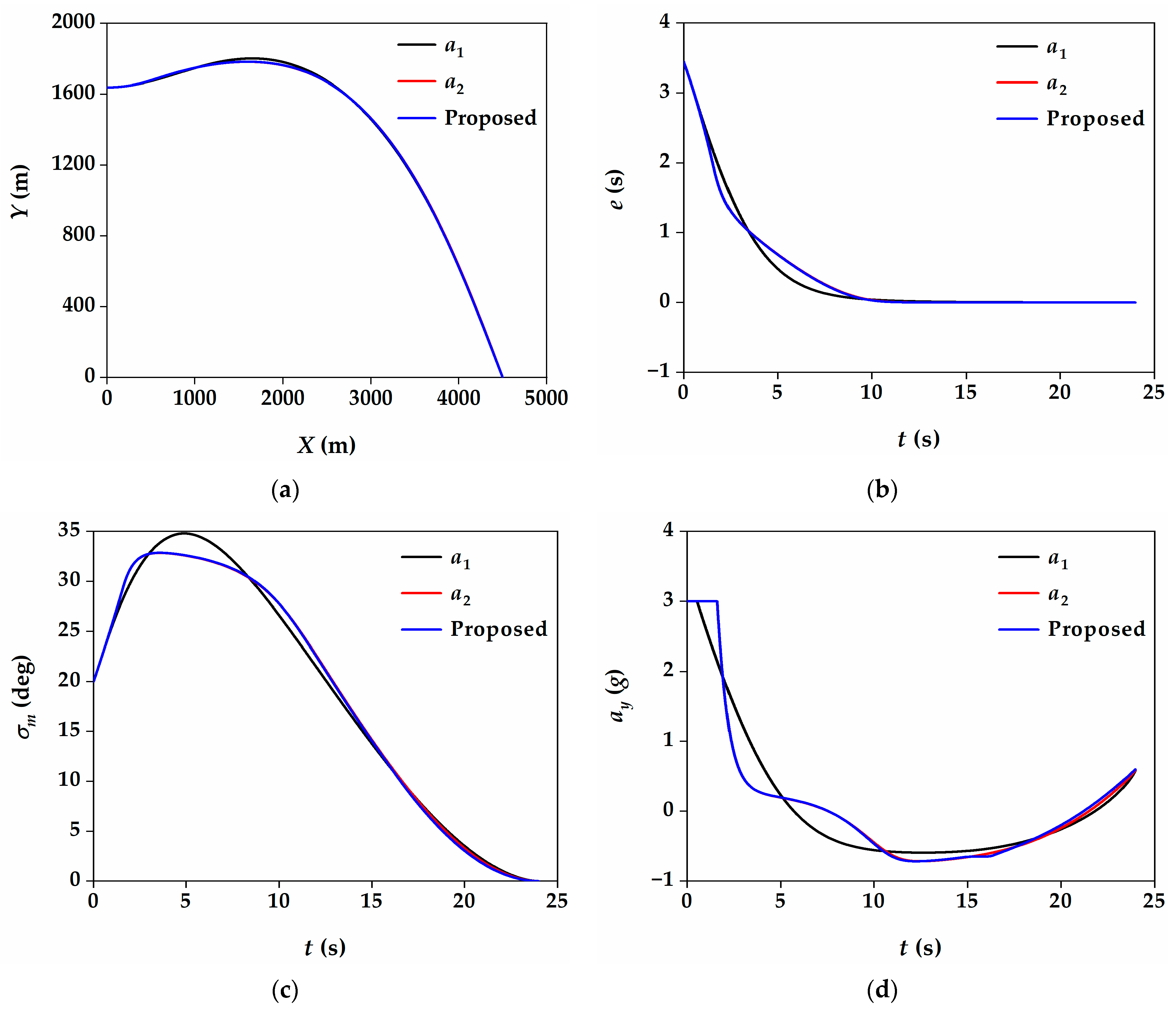
5.4. Compared with Other Guidance Laws
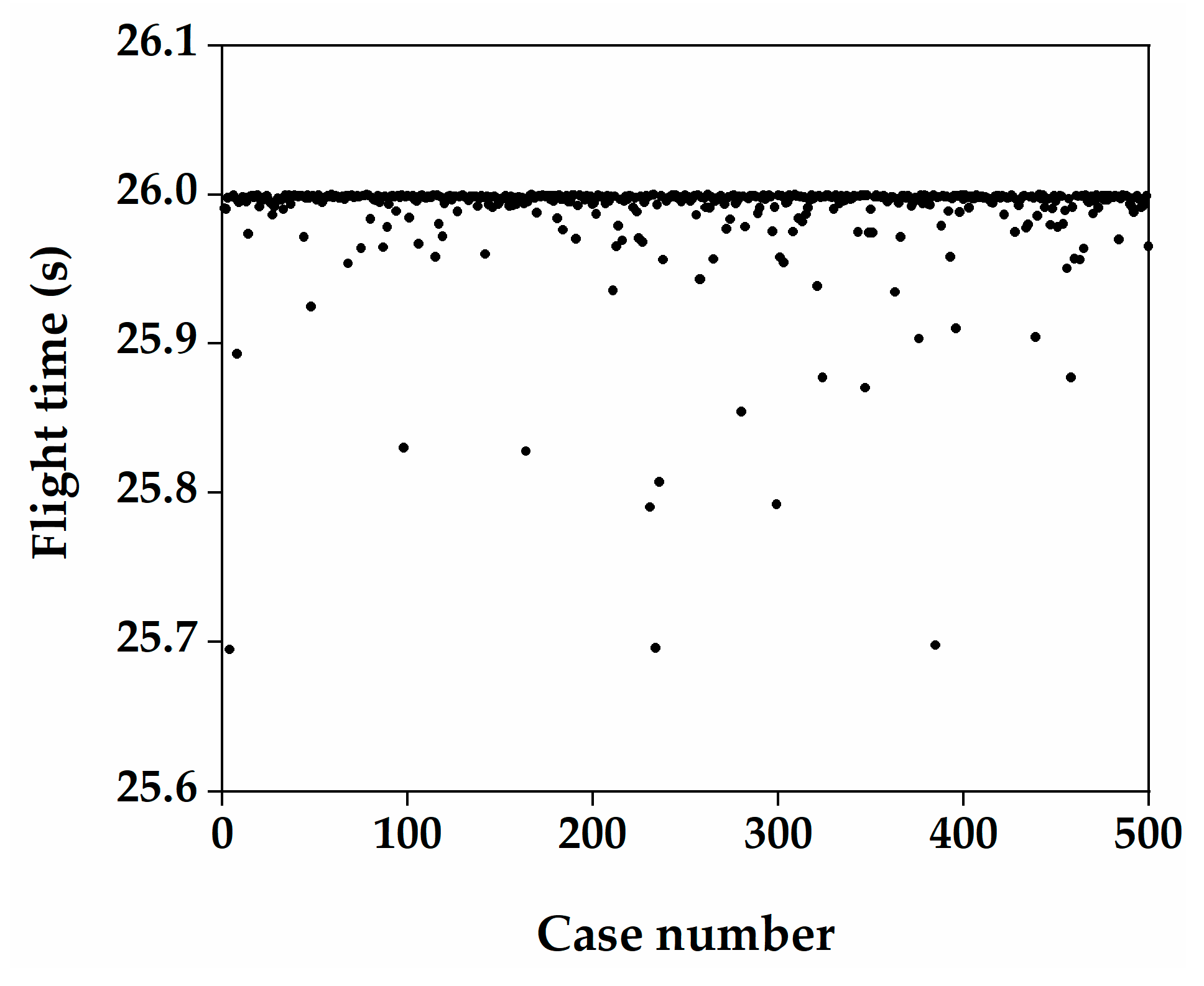
5.5. Monte Carlo Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control. Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Homing Guidance Law for Cooperative Attack of Multiple Missiles. J. Guid. Control. Dyn. 2010, 33, 275–280. [Google Scholar] [CrossRef]
- Harl, N.; Balakrishnan, S.N. Impact Time and Angle Guidance With Sliding Mode Control. IEEE Trans. Control. Syst. Technol. 2012, 20, 1436–1449. [Google Scholar] [CrossRef]
- Zhu, J.W.; Su, D.L.; Xie, Y.; Sun, H.F. Impact time and angle control guidance independent of time-to-go prediction. Aerosp. Sci. Technol. 2019, 86, 818–825. [Google Scholar] [CrossRef]
- Chen, Y.D.; Wang, J.N.; Wang, C.Y.; Shan, J.Y.; Xin, M. Three-Dimensional Cooperative Homing Guidance Law with Field-of-View Constraint. J. Guid. Control. Dyn. 2020, 43, 389–397. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Chen, W.C.; Liu, X.M.; Cheng, J. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint. Aerosp. Sci. Technol. 2021, 110, 106523. [Google Scholar] [CrossRef]
- Zhang, Y.A.; Wang, X.L.; Wu, H.L. Impact time control guidance law with field of view constraint. Aerosp. Sci. Technol. 2014, 39, 361–369. [Google Scholar] [CrossRef]
- Chen, X.T.; Wang, J.Z. Nonsingular Sliding-Mode Control for Field-of-View Constrained Impact Time Guidance. J. Guid. Control. Dyn. 2018, 41, 1214–1222. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, J.Y.; Kim, H.J.; Kwon, H.H.; Park, J.S. Look-Angle-Shaping Guidance Law for Impact Angle and Time Control With Field-of-View Constraint. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1602–1612. [Google Scholar] [CrossRef]
- Lee, S.; Cho, N.; Kim, Y. Impact-Time-Control Guidance Strategy with a Composite Structure Considering the Seeker’s Field-of-View Constraint. J. Guid. Control. Dyn. 2020, 43, 1566–1574. [Google Scholar] [CrossRef]
- Mukherjee, D.; Kumar, S.R. Field-of-View Constrained Impact Time Guidance Against Stationary Targets. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3296–3306. [Google Scholar] [CrossRef]
- Ma, S.; Wang, X.G.; Wang, Z.Y. Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace 2021, 8, 251. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Zhao, B. Impact-Time-Control Guidance Law for Missile with Time-Varying Velocity. Math. Probl. Eng. 2016, 2016, 7951923. [Google Scholar] [CrossRef]
- Wen, L.; Ping, L.; Liang, W.; Huabin, L.; Jie, G. Three-dimensional guidance law of impact-time-control under time-varying velocity. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Yan, X.H.; Kuang, M.C.; Zhu, J.H. A Geometry-Based Guidance Law to Control Impact Time and Angle under Variable Speeds. Mathematics 2020, 8, 1029. [Google Scholar] [CrossRef]
- Zhu, C.H.; Xu, G.D.; Wei, C.Z.; Cai, D.Y.; Yu, Y. Impact-Time-Control Guidance Law for Hypersonic Missiles in Terminal Phase. IEEE Access 2020, 8, 44611–44621. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Ge, J.Q.; Xu, Q.Q.; Yang, T. Impact Time Control Cooperative Guidance Law Design Based on Modified Proportional Navigation. Aerospace 2021, 8, 231. [Google Scholar] [CrossRef]
- Snyder, M.; Qu, Z.H.; Hull, R.; Prazenica, R. Quad-Segment Polynomial Trajectory Guidance for Impact-Time Control of Precision-Munition Strike. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 3008–3023. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Adaptive Impact Time Control Via Look-Angle Shaping Under Varying Velocity. J. Guid. Control. Dyn. 2017, 40, 3247–3255. [Google Scholar] [CrossRef]
- Guo, Y.H.; Li, X.; Zhang, H.J.; Cai, M.; He, F. Data-Driven Method for Impact Time Control Based on Proportional Navigation Guidance. J. Guid. Control. Dyn. 2020, 43, 955–966. [Google Scholar] [CrossRef]
- Wang, J.W.; Zhang, R. Terminal Guidance for a Hypersonic Vehicle with Impact Time Control. J. Guid. Control. Dyn. 2018, 41, 1790–1798. [Google Scholar] [CrossRef]
- Sun, G.X.; Wen, Q.Q.; Xu, Z.Q.; Xia, Q.L. Impact time control using biased proportional navigation for missiles with varying velocity. Chin. J. Aeronaut. 2020, 33, 956–964. [Google Scholar] [CrossRef]
- Wang, X.H.; Tan, C.P. 3-D impact angle constrained distributed cooperative guidance for maneuvering targets without angular-rate measurements. Control. Eng. Pract. 2018, 78, 142–159. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Z.; Chang, S.; Fu, J. Multiphase trajectory optimization for gun-launched glide guided projectiles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 995–1010. [Google Scholar] [CrossRef]
- Song, S.-H.; Ha, I.-J. A Lyapunov-like approach to performance analysis of 3-dimensional pure PNG laws. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 238–248. [Google Scholar] [CrossRef]
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Optimal three-dimensional impact time guidance with seeker’s field-of-view constraint. Chin. J. Aeronaut. 2021, 34, 240–251. [Google Scholar] [CrossRef]
- Zhang, D.C.; Xia, Q.L.; Wen, Q.Q.; Zhou, G.Q. An Approximate Optimal Maximum Range Guidance Scheme for Subsonic Unpowered Gliding Vehicles. Int. J. Aerosp. Eng. 2015, 2015, 389751. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m (kg) | 37.27 | S (m2) | 0.0133 |
| CD0 | 0.352 | CLα | 13.365 |
| Ccβ | −13.365 | kb | 35.0 |
| g (m/s2) | 9.8 | amax (g) | 3 |
| N | 3 | H (s) | 0.001 |
| nseg | Tf (s) | Te (s) | ecm (s) | ecm/Tf (%) |
|---|---|---|---|---|
| 5 | 21.007 | 21.196 | 0.189 | 0.900 |
| 20 | 21.007 | 21.094 | 0.087 | 0.414 |
| 50 | 21.007 | 21.088 | 0.081 | 0.386 |
| 100 | 21.007 | 21.088 | 0.081 | 0.386 |
| 200 | 21.007 | 21.087 | 0.080 | 0.381 |
| θv (°) | σm (°) | Tf (s) | Te (s) | ecm (s) | ecm/Tf (%) |
|---|---|---|---|---|---|
| −20 | 9.396 | 20.594 | 20.630 | 0.036 | 0.175 |
| −10 | 13.892 | 20.644 | 20.689 | 0.045 | 0.218 |
| 0 | 22.269 | 21.007 | 21.088 | 0.081 | 0.386 |
| 10 | 31.574 | 21.692 | 21.885 | 0.193 | 0.890 |
| 20 | 41.181 | 22.719 | 23.198 | 0.479 | 2.108 |
| ITCG Laws | Scenario 1 | Scenario 2 |
|---|---|---|
| a1 | k1 = 20, k3 = 5 | k1 = 20, k3 = 5 |
| a2 | k1 = 50, k2 = 5, k3 = 5 | k1 = 50, k2 = 5, k3 = 5 |
| Proposed | k1 = 50, k2 = 0.15, k3 = 5 | k1 = 80, k2 = 0.15, k3 = 5 |
| ITCG Laws | Scenario 1 | Scenario 2 | ||
|---|---|---|---|---|
| Tf (s) | E (m2/s3) | Tf (s) | E (m2/s3) | |
| a1 | 23.995 | 1982 | 25.995 | 3040 |
| a2 | 23.998 | 2078 | 25.863 | 4543 |
| Proposed | 23.997 | 2090 | 25.899 | 3542 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m (kg) | 37.27 ± 0.1 | CD0 | 0.352 ± 0.035 |
| CLα | 13.365 ± 1.337 | Vp (m/s) | 250 ± 10 |
| θv (°) | 0 ± 5 | φv (°) | 0 ± 5 |
| θL (°) | −20 ± 5 | φL (°) | −10 ± 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Wang, Z.; Wang, X.; Chen, Q. Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation. Aerospace 2022, 9, 202. https://doi.org/10.3390/aerospace9040202
Ma S, Wang Z, Wang X, Chen Q. Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation. Aerospace. 2022; 9(4):202. https://doi.org/10.3390/aerospace9040202
Chicago/Turabian StyleMa, Shuai, Zhongyuan Wang, Xugang Wang, and Qi Chen. 2022. "Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation" Aerospace 9, no. 4: 202. https://doi.org/10.3390/aerospace9040202
APA StyleMa, S., Wang, Z., Wang, X., & Chen, Q. (2022). Three-Dimensional Impact Time Control Guidance Considering Field-of-View Constraint and Velocity Variation. Aerospace, 9(4), 202. https://doi.org/10.3390/aerospace9040202





