A Beam Search-Based Channel Allocation Method for Interference Mitigation of NGSO Satellites with Multi-Beam Antennas
Abstract
:1. Introduction
2. System Model of NGSO Satellites Equipped with Multi-Beam Antennas
2.1. Downlink Analysis Model
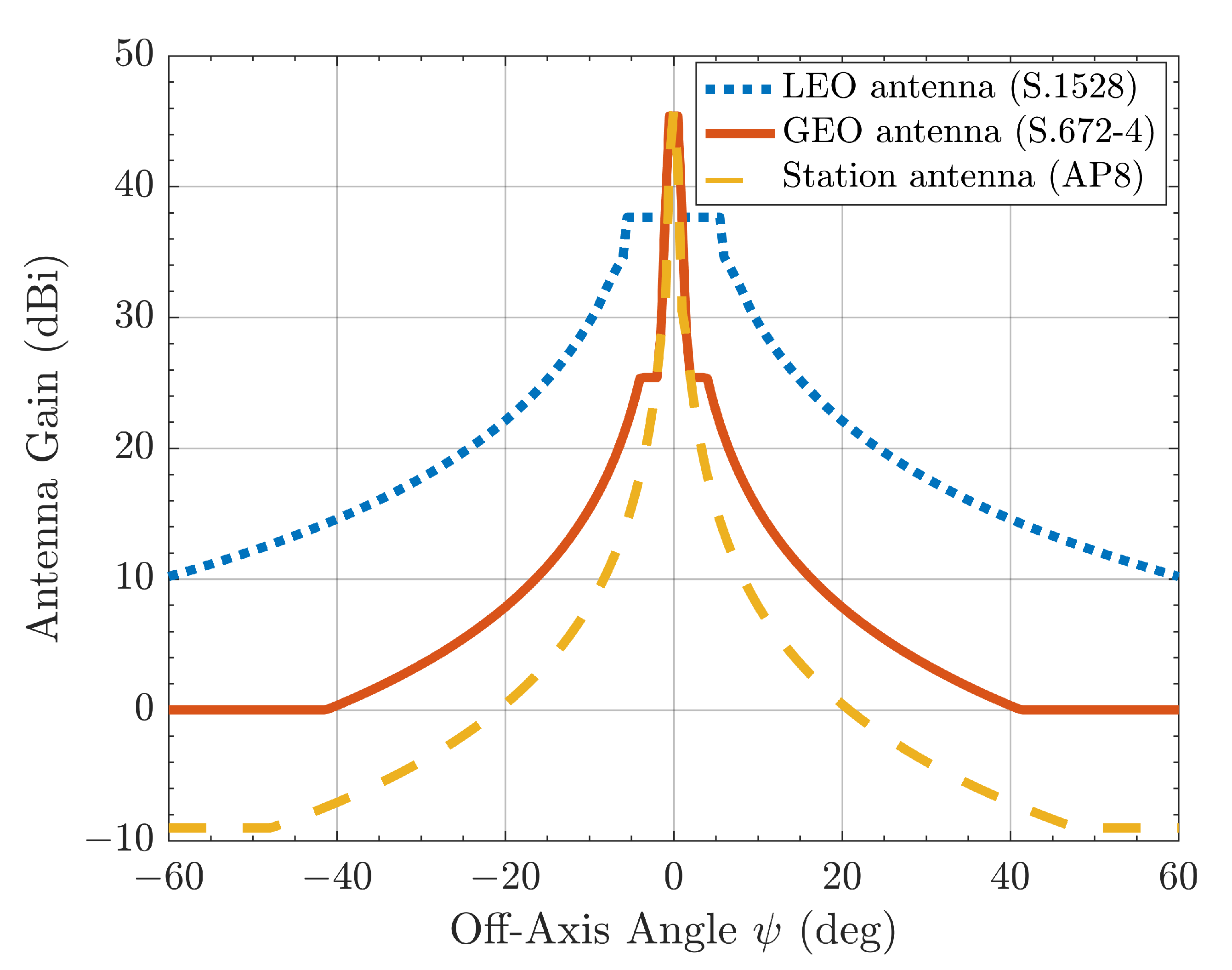
2.2. Interference Evaluation Index and Antenna Radiation Patterns
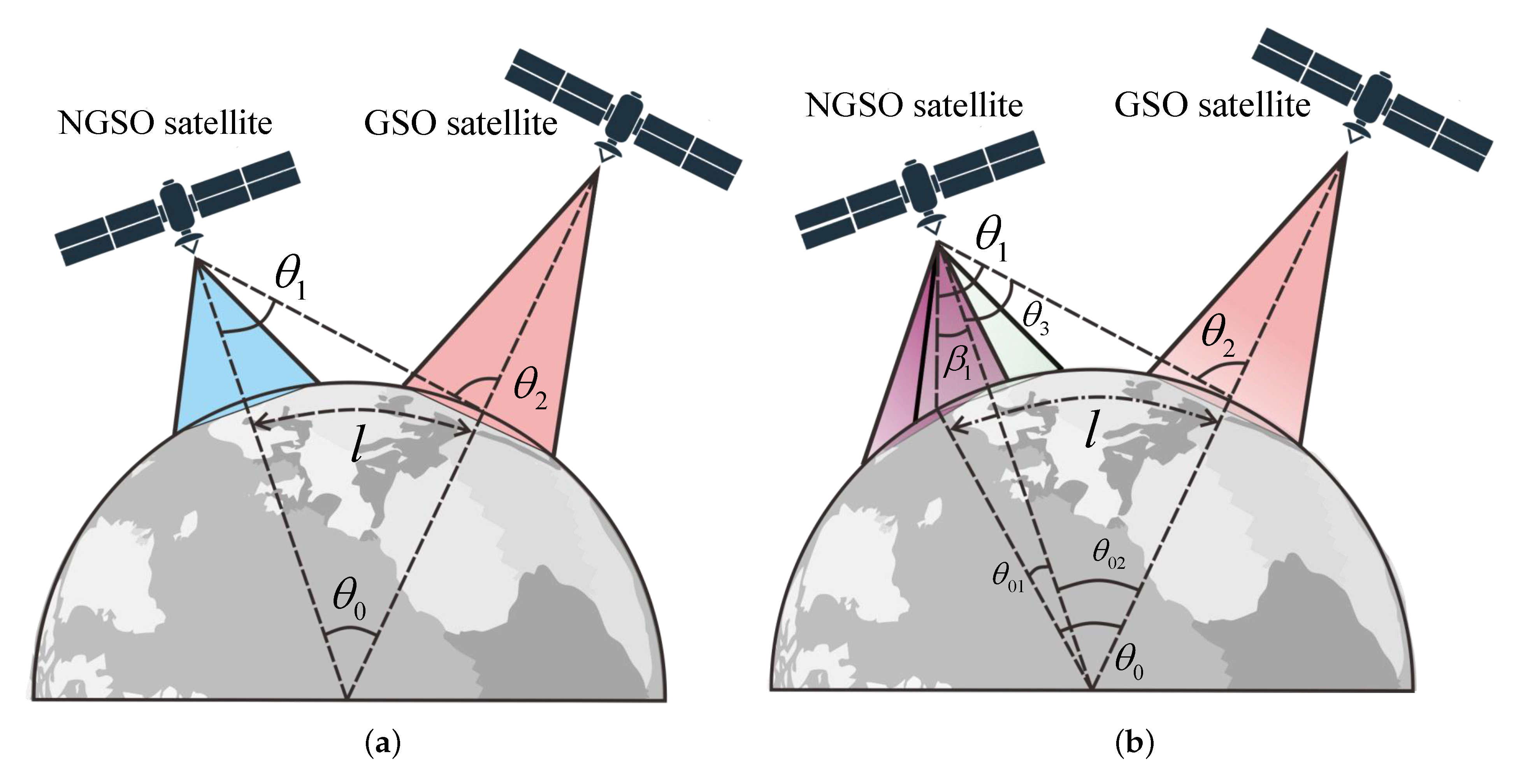
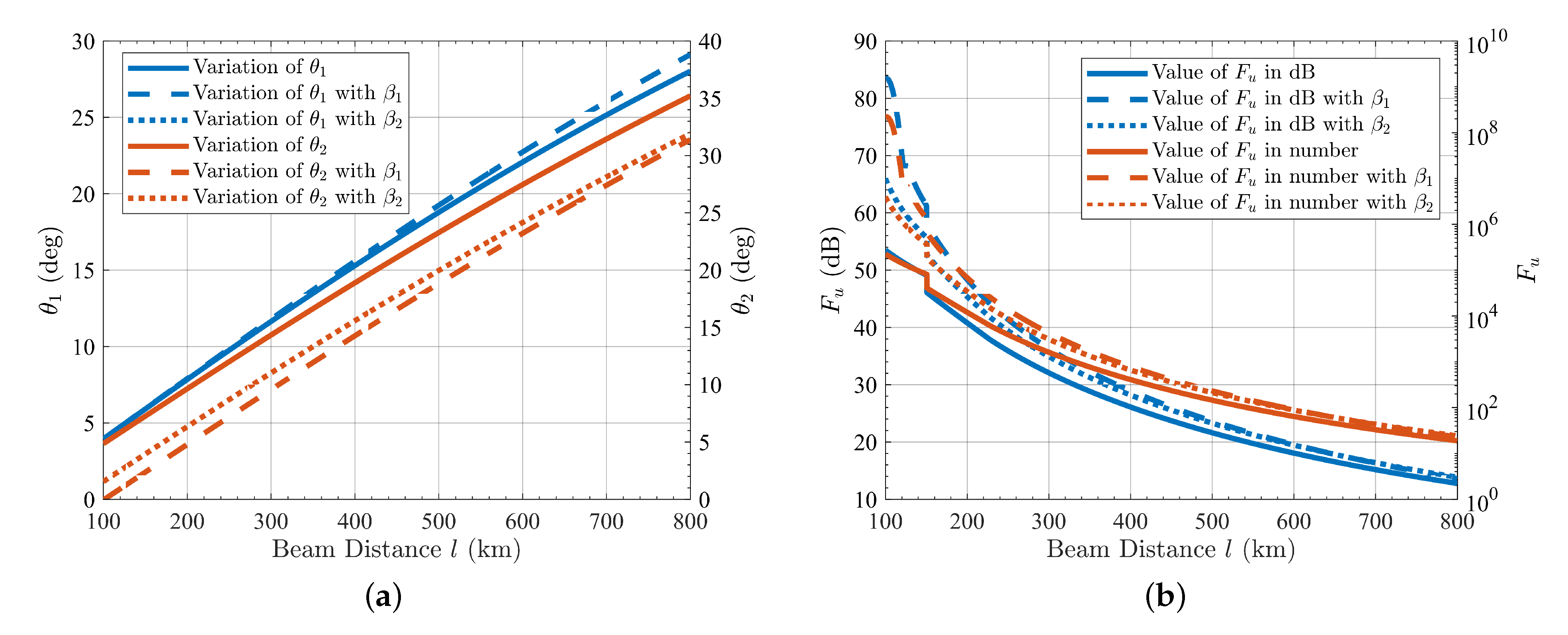
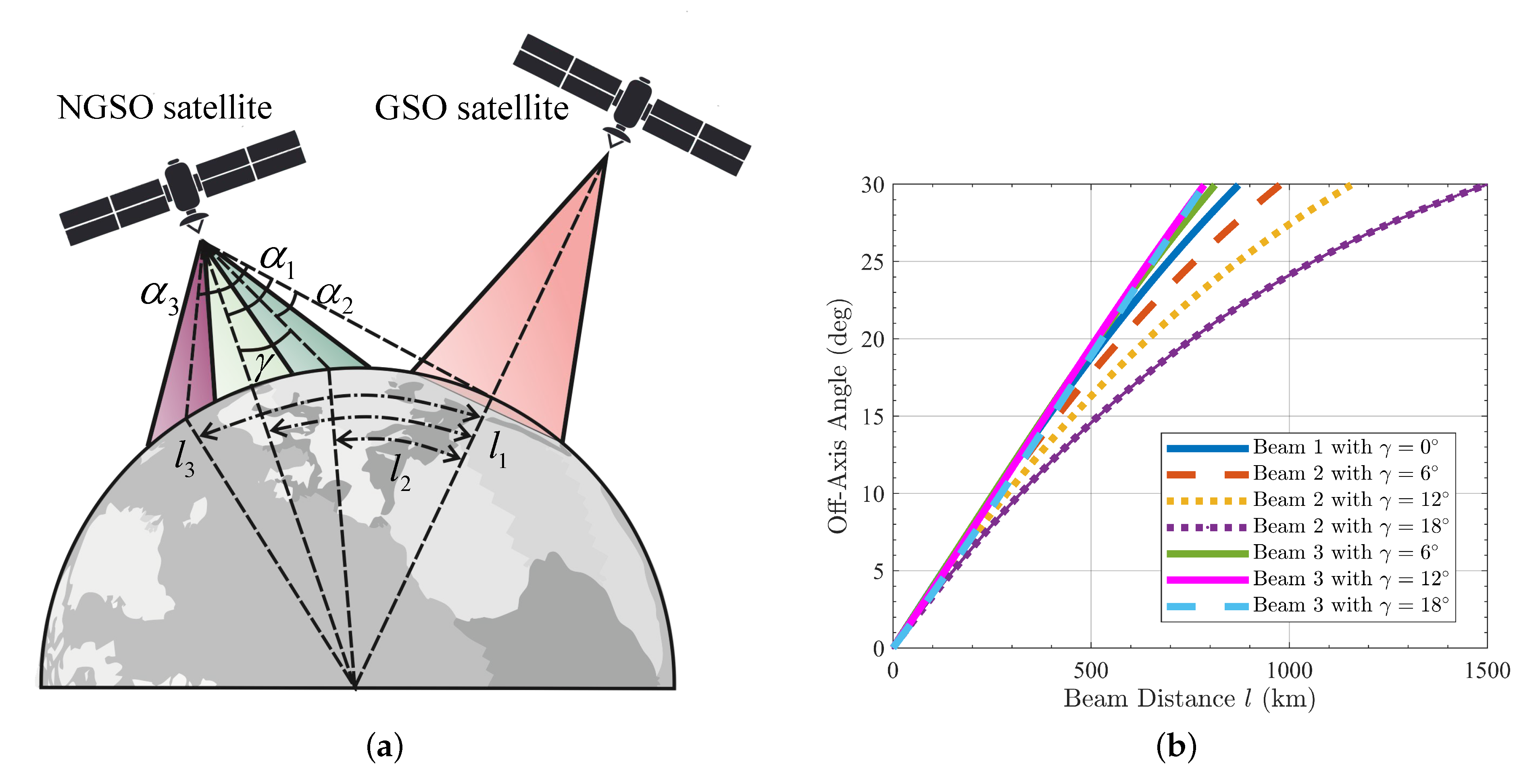
2.3. Analysis of Interference Based on Off-Axis Angle and Beam Distance
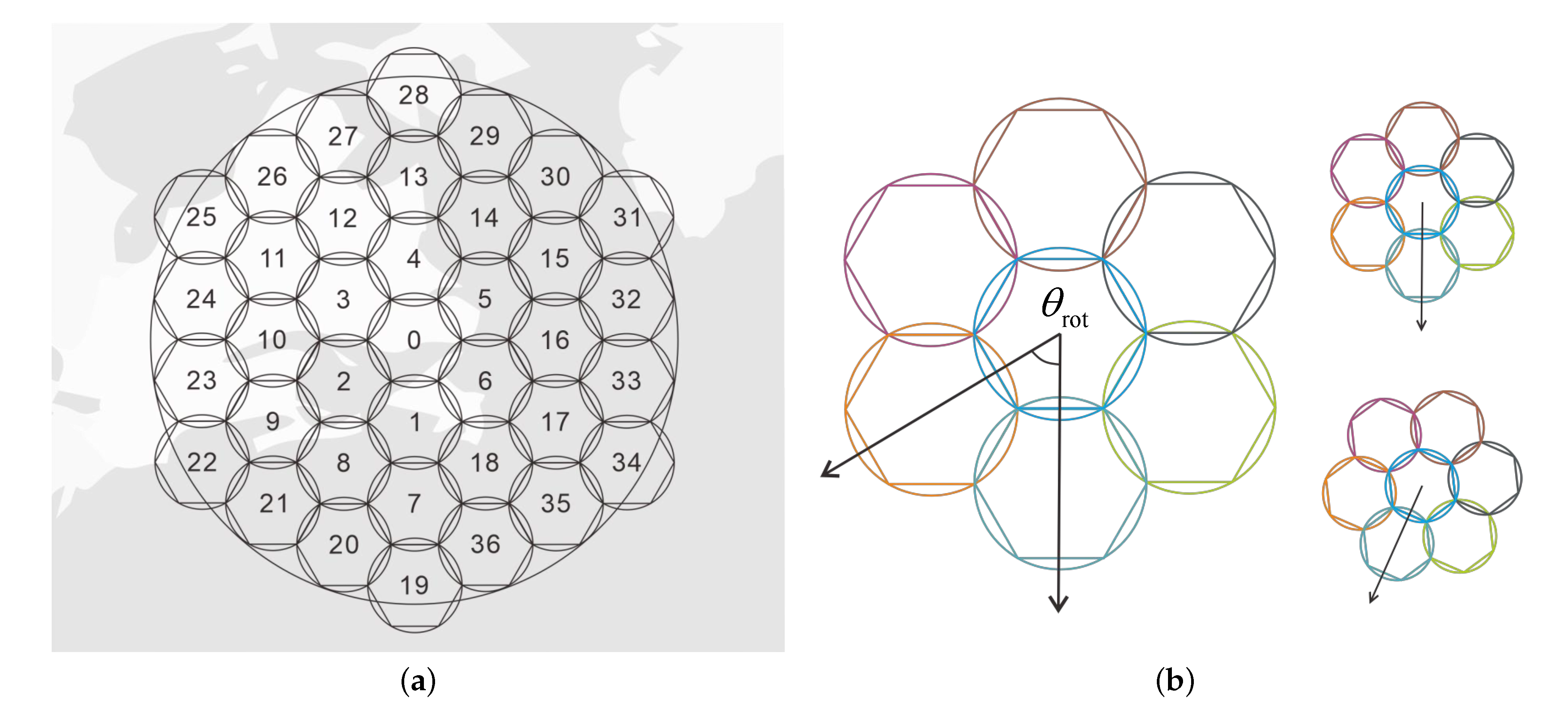
2.4. Channel Allocation Method
| Algorithm 1: Beam search-based channel allocation method. |
Input: Ephemeris of satellites Output: Allocation matrix initialization; whilenot at end of simulation instantdo  end |
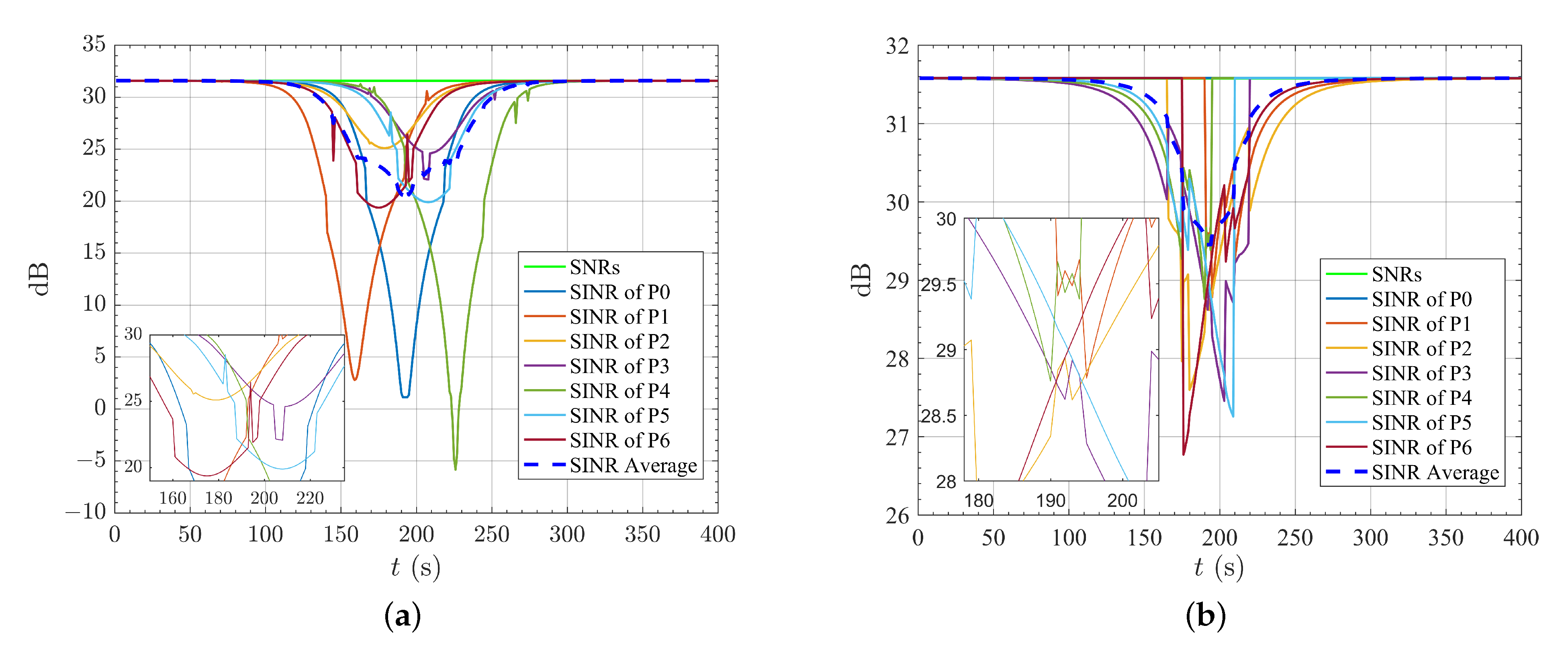
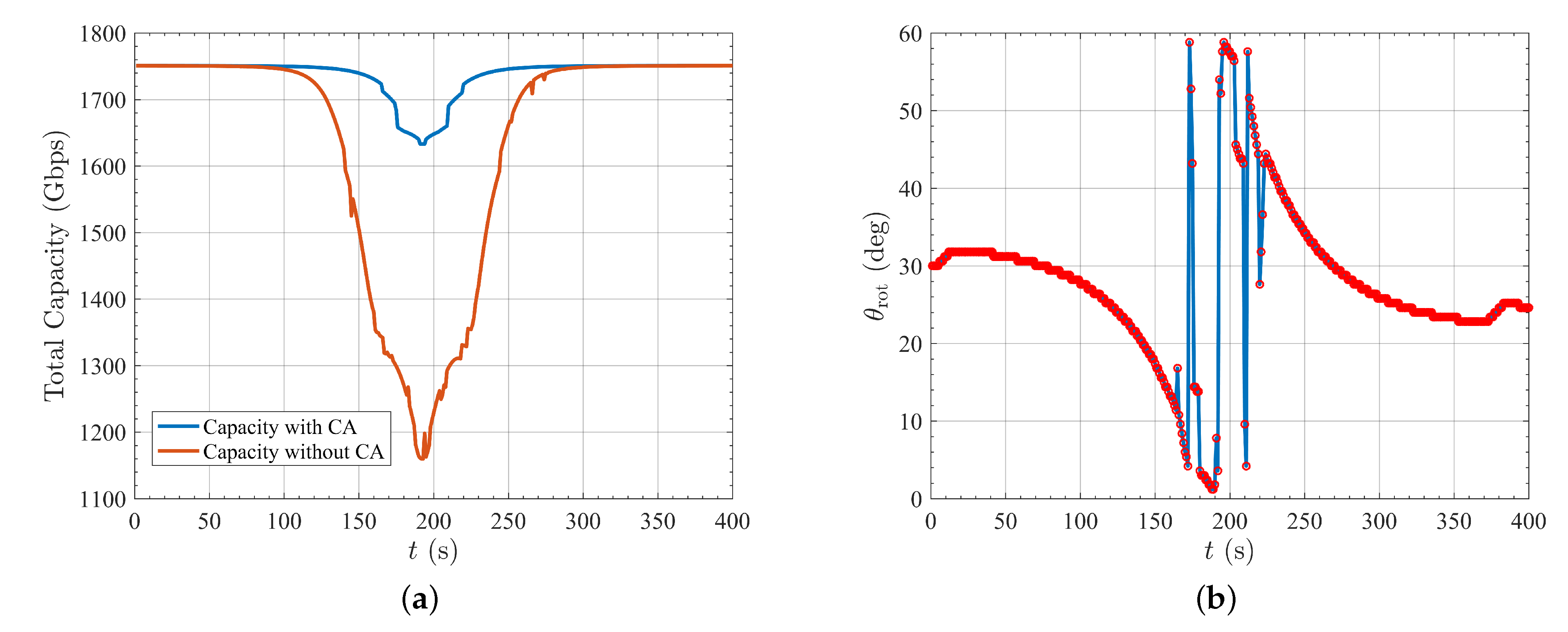
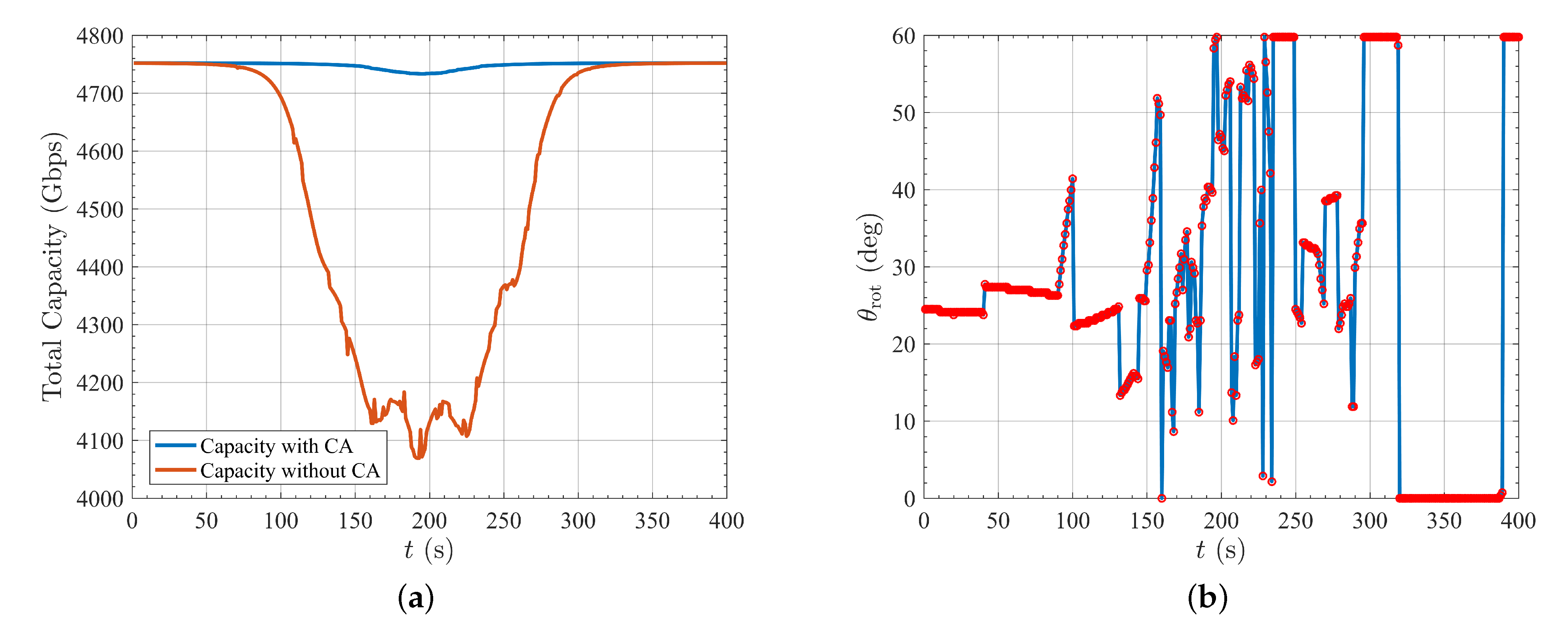
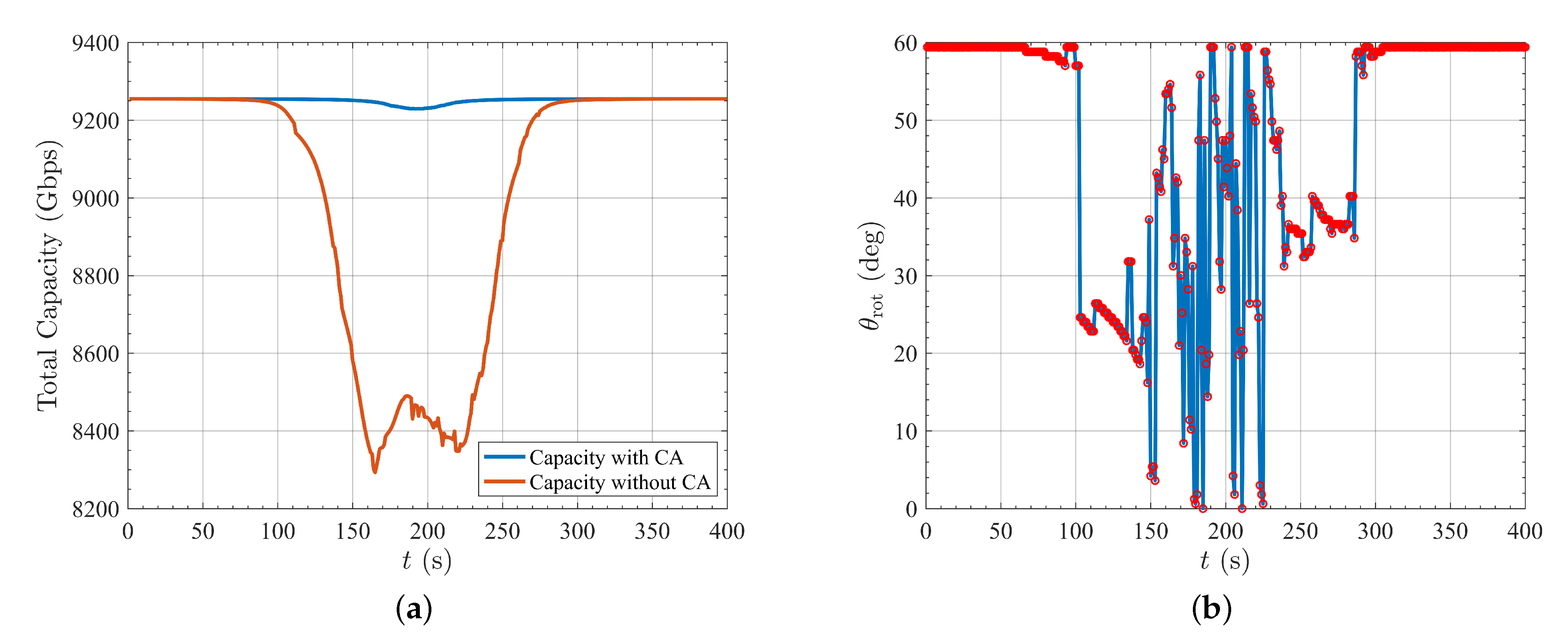
3. Simulation and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NGSO | Non-geostationary orbit |
| GSO | Geostationary orbit |
| LEO | Low Earth orbit |
| HTS | High throughput satellite |
| CA | Channel allocation |
| ITU | International Telecommunication Union |
| SNR | Signal to noise ratio |
| SINR | Signal to interference plus noise ratio |
| NP | Non-deterministic polynomial |
| RAAN | Right ascension of the ascending node |
References
- Wu, W.W.; Miller, E.F.; Pritchard, W.L.; Pickholtz, R.L. Mobile satellite communications. Proc. IEEE 1994, 82, 1431–1448. [Google Scholar] [CrossRef]
- Evans, J.V. Satellite systems for personal communications. Proc. IEEE 1998, 86, 1325–1341. [Google Scholar] [CrossRef]
- Hanson, W. A global Internet: The next four billion users. New Space 2015, 3, 204–207. [Google Scholar] [CrossRef]
- Curran, J.; Fenton, N.; Freedman, D. Misunderstanding the Internet; Routledge: London, UK, 2016. [Google Scholar]
- Internet World Stats. World Internet Usage and Population Statistics 2020. Internet World Stats: 2020. Available online: https://www.internetworldstats.com/stats.htm (accessed on 1 February 2022).
- Lu, Y.; Zheng, X. 6G: A survey on technologies, scenarios, challenges, and the related issues. J. Ind. Inf. Integr. 2020, 19, 100158. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A Comprehensive Survey. IEEE Internet Things J. 2021, 9, 359–383. [Google Scholar] [CrossRef]
- Zhen, L.; Bashir, A.K.; Yu, K.; Al-Otaibi, Y.D.; Foh, C.H.; Xiao, P. Energy-efficient random access for LEO satellite-assisted 6G internet of remote things. IEEE Internet Things J. 2020, 8, 5114–5128. [Google Scholar] [CrossRef]
- Jones, H. Much Lower Launch Costs Make Resupply Cheaper Than Recycling for Space Life Support. In Proceedings of the 47th International Conference on Environmental Systems, Charleston, SC, USA, 16–20 July 2017. [Google Scholar]
- Federal Communications Commission. Application For Approval for Orbital Deployment and Operating Authority for the SpaceX NGSO Satellite System; Federal Communications Commission: Washington, DC, USA, 2016.
- Federal Communications Commission. Application for Modification of Authorization for the SpaceX NGSO Satellite System; Federal Communications Commission: Washington, DC, USA, 2018.
- Barnett, R. Oneweb Non-Geostationary Satellite System: Technical Information to Supplement Schedules—Attachment to Fcc Application Sat-loi-20160428-00041; Tech. Rep. SAT-LOI-20160428-00041; Federal Communications Commission: Washington, DC, USA, 2016. [Google Scholar]
- Barnett, R. Oneweb Non-Geostationary Satellite System: Attachment a—Technical Information to Supplement Schedule S; Tech. Rep. SAT-MOD-20180319-00022; Federal Communications Commission: Washington, DC, USA, 2018. [Google Scholar]
- Ashford, E.W. Non-Geo systems—Where have all the satellites gone? Acta Astronaut. 2004, 55, 649–657. [Google Scholar] [CrossRef]
- Su, Y.; Liu, Y.; Zhou, Y.; Yuan, J.; Cao, H.; Shi, J. Broadband LEO satellite communications: Architectures and key technologies. IEEE Wirel. Commun. 2019, 26, 55–61. [Google Scholar] [CrossRef]
- Bhattacherjee, D.; Aqeel, W.; Bozkurt, I.N.; Aguirre, A.; Chandrasekaran, B.; Godfrey, P.B.; Laughlin, G.; Maggs, B.; Singla, A. Gearing up for the 21st century space race. In Proceedings of the 17th ACM Workshop on Hot Topics in Networks, Redmond, WA, USA, 15–16 November 2018; pp. 113–119. [Google Scholar]
- Butash, T.; Garland, P.; Evans, B. Non-geostationary satellite orbit communications satellite constellations history. Int. J. Satell. Commun. Netw. 2021, 39, 1–5. [Google Scholar] [CrossRef]
- Tang, J.; Bian, D.; Li, G.; Hu, J.; Cheng, J. Resource Allocation for LEO Beam-Hopping Satellites in a Spectrum Sharing Scenario. IEEE Access 2021, 9, 56468–56478. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, J.; Zhang, H.; Li, T. Spectral coexistence between LEO and GEO satellites by optimizing direction normal of phased array antennas. China Commun. 2018, 15, 18–27. [Google Scholar] [CrossRef]
- Nelson, R.A.; Pritchard, W. Interference between satellite systems in non-geostationary orbits. Int. J. Satell. Commun. 1994, 12, 95–105. [Google Scholar] [CrossRef]
- Wang, A. Optimization on constellation design for spectrum sharing among satellite networks. In Proceedings of the 17th AIAA International Communications Satellite Systems Conference and Exhibit, Yokohama, Japan, 23–27 February 1998; p. 1202. [Google Scholar]
- Lin, Z.; Jin, J.; Yan, J.; Kuang, L. Fast Calculation of the Probability Distribution of Interference Involving Multiple Mega-Constellations. In Proceedings of the International Conference on Space Information Network; Springer: Singapore, 2020; pp. 18–34. [Google Scholar]
- Del Portillo, I.; Cameron, B.G.; Crawley, E.F. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband. Acta Astronaut. 2019, 159, 123–135. [Google Scholar] [CrossRef]
- Xia, S.; Jiang, Q.; Zou, C.; Li, G. Beam coverage comparison of LEO satellite systems based on user diversification. IEEE Access 2019, 7, 181656–181667. [Google Scholar] [CrossRef]
- Li, R.; Gu, P.; Hua, C. Optimal beam power control for co-existing multibeam GEO and LEO satellite system. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–25 October 2019; pp. 1–6. [Google Scholar]
- Shen, K.; Yu, W. Fractional programming for communication systems—Part I: Power control and beamforming. IEEE Trans. Signal Process. 2018, 66, 2616–2630. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Hu, X.; Wang, W. Deep reinforcement learning based dynamic channel allocation algorithm in multibeam satellite systems. IEEE Access 2018, 6, 15733–15742. [Google Scholar] [CrossRef]
- Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Cognitive beamhopping for spectral coexistence of multibeam satellites. Int. J. Satell. Commun. Netw. 2015, 33, 69–91. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.; Jin, J.; Li, W.; Zhan, Y. Intelligent Action Selection for NGSO Networks with Interference Constraints: A Modified Q-Learning Approach. IEEE Trans. Aerosp. Electron. Syst. 2021. [Google Scholar] [CrossRef]
- Wang, C.; Bian, D.; Zhang, G.; Cheng, J.; Li, Y. A novel dynamic spectrum-sharing method for integrated wireless multimedia sensors and cognitive satellite networks. Sensors 2018, 18, 3904. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Bian, D.; Shi, S.; Xu, J.; Zhang, G. A novel cognitive satellite network with GEO and LEO broadband systems in the downlink case. IEEE Access 2018, 6, 25987–26000. [Google Scholar] [CrossRef]
- ITU-R. Satellite aNtenna Radiation Patterns for Non-Geostationary Orbit Satellite Antennas Operating in the Fixed-Satellite Service below 30 GHz: ITU-R S. 1528, 2001. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/s/R-REC-S.1528-0-200106-I!!PDF-E.pdf (accessed on 1 February 2022).
- ITU-R. Satellite Antenna Radiation Pattern for Use as a Design Objective in the Fixed-Satellite Service Employing Geostationary Satellites: ITU-R S. 672 4. [Sl: Sn] 1997. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/s/R-REC-S.672-4-199709-I!!PDF-E.pdf (accessed on 1 February 2022).
- ITU-R. ITU Radio Regulations; ITU-R: Geneva, Switzerland, 2016. [Google Scholar]
- Curtis, H. Orbital Mechanics for Engineering Students: Revised Reprint; Butterworth-Heinemann: Oxford, UK, 2020. [Google Scholar]
- Lee, J.; Leyffer, S. Mixed Integer Nonlinear Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 154. [Google Scholar]
- Lageweg, B.; Lenstra, J.; Rinnooy Kan, A. Job-shop scheduling by implicit enumeration. Manag. Sci. 1977, 24, 441–450. [Google Scholar] [CrossRef]
- Zhang, T.J.; Wolz, D.; Shen, H.X.; Luo, Y.Z. Spanning tree trajectory optimization in the galaxy space. Astrodynamics 2021, 5, 27–37. [Google Scholar] [CrossRef]
- Vince, A. A framework for the greedy algorithm. Discret. Appl. Math. 2002, 121, 247–260. [Google Scholar] [CrossRef] [Green Version]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Huang, A.Y.; Yan, B.; Li, Z.Y.; Shu, P.; Luo, Y.Z.; Yang, Z. Orbit design and mission planning for global observation of Jupiter. Astrodynamics 2021, 5, 39–48. [Google Scholar] [CrossRef]
- Sabuncuoglu, I.; Bayiz, M. Job shop scheduling with beam search. Eur. J. Oper. Res. 1999, 118, 390–412. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, J.; Kuang, L.; Yan, J. LEO constellation design methodology for observing multi-targets. Astrodynamics 2018, 2, 121–131. [Google Scholar] [CrossRef]
- Yang, H.; Tang, G.; Jiang, F. Optimization of observing sequence based on nominal trajectories of symmetric observing configuration. Astrodynamics 2018, 2, 25–37. [Google Scholar] [CrossRef]

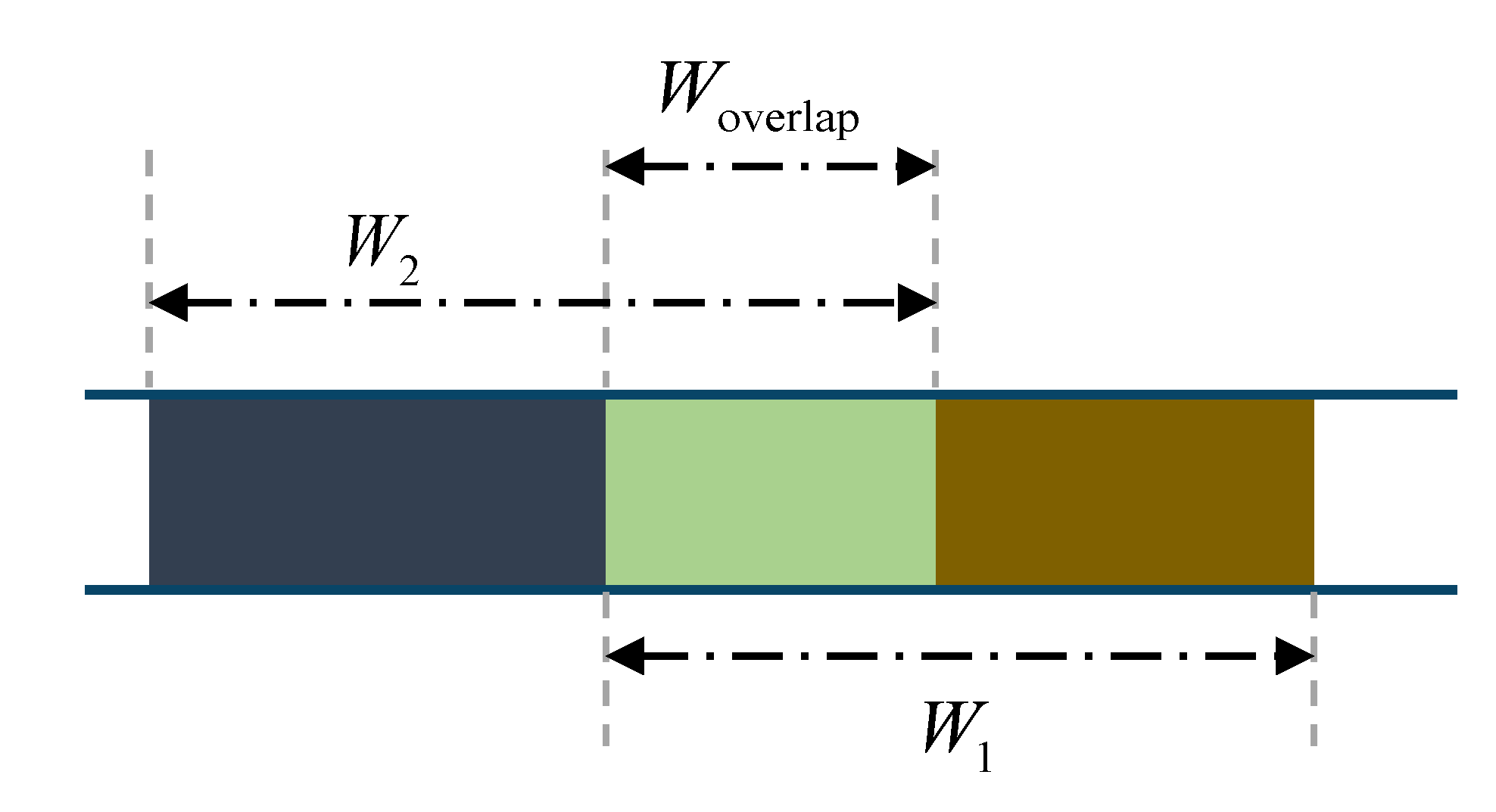



| Parameters | Value |
|---|---|
| Downlink carrier frequency, f | 20 GHz |
| GSO satellite | |
| GSO maximum transmit gain, | 45.39 dBi |
| GSO 3 dB beamwidth | 1.259 |
| Radio of major axis to minor axis, z | 1.5 |
| near-in-side-lobe level, | dB |
| NGSO satellite | |
| NGSO maximum transmit gain, | 37.65 dBi |
| NGSO 3 dB beamwidth | 11.58 |
| GSO ground station | |
| Antenna diameter, D | 1.2 m |
| Maximum receive gain, | 45.76 dBi |
| Simulation Parameters | Value |
|---|---|
| Simulation UTC begin time, | 1 May 2030 04:00:00 |
| Simulation UTC end time, | 1 May 2030 04:06:40 |
| Time step, | 1 s |
| Earth equatorial radius, | 6378 km |
| Boltzmann constant, | W/(HzK) |
| Downlink carrier frequency, f | 20 GHz |
| Bandwidth of each beam, | 25 MHz |
| GSO satellite | |
| Latitude of GSO center beam, | 0 |
| Longitude of GSO center beam, | 21.26 |
| Transmit power of GSO satellite, | 18.57 dBW |
| GSO maximum transmit gain, | 45.39 dBi |
| GSO 3 dB beamwidth for 7 and 19 beams | 1.259 |
| GSO 3 dB beamwidth for 37 beams | 0.6295 |
| Radio of major axis to minor axis, z | 1.5 |
| near-in-side-lobe level, | dB |
| Number of GSO beams | 7, 19, 37 |
| NGSO satellite | |
| Transmit power of NGSO satellite, | 12.55 dBW |
| NGSO maximum transmit gain, | 37.65 dBi |
| NGSO 3 dB beamwidth for 7 and 19 beams | 11.58 |
| NGSO 3 dB beamwidth for 37 beams | 5.79 |
| Number of NGSO beams | 7, 19, 37 |
| GSO ground station | |
| Noise temperature of receive antenna, | 210 K |
| Antenna diameter, D | 1.2 m |
| Maximum receive gain, | 45.76 dBi |
| Orbital Parameters | GSO | NGSO |
|---|---|---|
| Orbital altitude, h | 35,786.14 km | 1450 km |
| Eccentricity, e | 0 | 0 |
| RAAN, | 0 | 301 |
| Orbital inclination, i | 0 | 87.5 |
| Argument of perigee, | 0 | 0 |
| True anomaly, | 300 | 350 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ren, D.; Jiang, F. A Beam Search-Based Channel Allocation Method for Interference Mitigation of NGSO Satellites with Multi-Beam Antennas. Aerospace 2022, 9, 177. https://doi.org/10.3390/aerospace9040177
Zhang H, Ren D, Jiang F. A Beam Search-Based Channel Allocation Method for Interference Mitigation of NGSO Satellites with Multi-Beam Antennas. Aerospace. 2022; 9(4):177. https://doi.org/10.3390/aerospace9040177
Chicago/Turabian StyleZhang, Haojie, Di Ren, and Fanghua Jiang. 2022. "A Beam Search-Based Channel Allocation Method for Interference Mitigation of NGSO Satellites with Multi-Beam Antennas" Aerospace 9, no. 4: 177. https://doi.org/10.3390/aerospace9040177
APA StyleZhang, H., Ren, D., & Jiang, F. (2022). A Beam Search-Based Channel Allocation Method for Interference Mitigation of NGSO Satellites with Multi-Beam Antennas. Aerospace, 9(4), 177. https://doi.org/10.3390/aerospace9040177







