1. Introduction
Electrification has been at the forefront of sustainable aviation research for the last 10 years. Projects such as the European Union’s FlightPath 2050 seek to reduce the
and
emissions of the commercial fleet by 75% and 90%, respectively, compared to the best-of-class in 2000 [
1]. These goals fall within a global trend of aviation de-carbonification measures proposed by the ICAO [
2]. One type of electrified aircraft concept is the hybrid-electric aircraft (HEA), where the power required for propulsion is supplied by more than one type of energy source, usually fuel and batteries [
3,
4]. Hybrid propulsion is proposed as a stepping stone towards full electrification, as future electric technologies are expected to be inadequate for achieving enough range to be competitive with conventional commercial aircraft [
5].
Unlike other propulsion systems, HEAs have multiple energy sources and power distribution paths. An Energy Management Strategy (EMS) can be introduced to find the optimal use of the available energy for a defined mission. EMS is a function of the degree of hybridisation (DoH) [
6] of the power over time, where DoH is the ratio of the power that is supplied by the electric source over the overall power required by the aircraft at that point in time. This single parameter is sufficient if there are only two power paths. Otherwise, multiple non-dimensional parameters have to be specified for each path, such as how much energy is provided by batteries over the total electrical power production if the system has multiple electrical power sources [
3,
4].
The problem of specifying an optimal EMS is complicated by how unpredictable its operational conditions can be. The HEA can operate between any airports within its maximum range and service ceiling. The approaches to solve this problem are divided into two families: offline methods and online methods [
7,
8]. The offline approaches find the optimal strategy by simulating the vehicle’s operational life and tuning the parameters of the EMS. Some examples include heuristic rules [
9], fuzzy control [
10] and global optimisation algorithms such as dynamic programming [
11]. On the contrary, online methods tune the EMS during the vehicle operation, such as Pontryagin’s Maximum Principle [
12].
However, few studies have been published where the EMS and HEPS sizing are coupled [
13,
14,
15,
16]. Indeed, the EMS of an HEA has to address the change in power requirements from the change in aircraft mass during its operation, which is not present in HE land vehicles. In this respect, two opposite approaches are generally adopted. The first one consists of considering a fixed energy management strategy, usually a uniform degree of hybridisation over cruise and climb, and the size of the aircraft according to the energy requirements. This approach is usually selected to study and compare different HE architectures and can be found in Pornet [
13] and Zamboni [
14]. The other approach is to iteratively couple the energy management optimisation with the system sizing. Trawick [
15] implemented a global optimisation methodology where dynamic programming is used to construct the optimal EMS and sequentially size the system. This approach is more flexible since it does not assume any analytical form of the power schedule but calculates the optimal schedule by starting from the end state of the aircraft and searching backwards the optimal power setting that minimises the objective function. The drawback is the high memory and computational cost, as the algorithm has to evaluate
states when searching for the optimal path, assuming a single-setting discretised
M times over
N time steps.
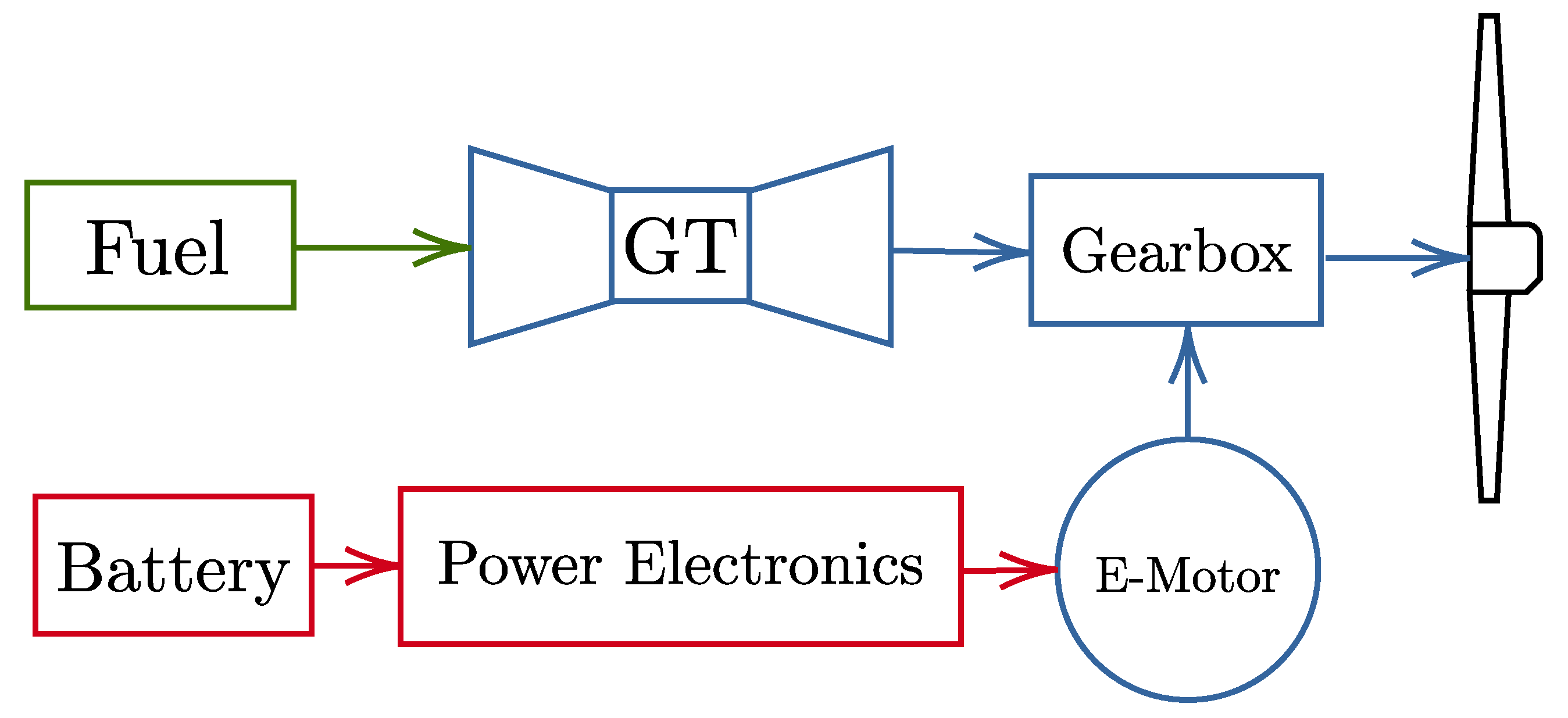
The presented work tries to implement a new design space exploration methodology to study the coupling between the EMS and the HEPS. For this reason we selected an architecture that is well-studied in the literature [
17,
18,
19,
20,
21,
22,
23,
24,
25] and is the most mature within the
FutPrint50 project. Regarding the modelling of the EMS, an intermediate approach is adopted where the class of possible DoH functions are restricted within the set of polynomial functions. Then, the design space methodology searches for the parameters that minimise fuel consumption and
emissions. At each iteration, the evaluation function sizes the mass of required fuel and batteries, taking into account the power–mass coupling. The goal is to identify an optimal energy management strategy for a given mission and value of maximum take-off mass.
The problem of finding the EMS that satisfies the requirements and constraints of the system under design is an engineering design problem. Hence, the design space exploration and optimisation techniques are required. A significant challenge in this field is handling the complex interactions and feedbacks between multiple subsystems [
26].
Several approaches have been developed, which can be divided into two families: an iterative or point-based approach and a convergent or parallel-based approach. In the first type, a candidate design or solution is selected from an initial trade-off analysis and refined with several iterations with optimisation tools and higher fidelity analysis. This approach is the traditional process of conceptual, preliminary and detail design, often called the “waterfall model” in software engineering. Examples of this approach can be found in Ullman [
27] and Pahl [
28]. In the context of design space exploration, the Margin Value Method [
29] is a point-based approach that, from a starting configuration, identifies excessive margins, any parameter that sub-optimally satisfies the constraints and evaluates the possible improvement by quantifying the trade-off between robustness and performance degradation. Guenov [
30] presents a Margin Allocation method to dynamically assess the effect of margins on performance, other margins and constraint satisfaction, so that the designer can understand the interactions between the system under design, its components and the overall requirements.
Conversely, the second type considers and evolves many candidate designs in parallel, discarding the unfeasible, undesirable or non-robust ones. Design methodologies that fall within this category are the Method of Controlled Convergence of Pugh [
31], the Design–Build–Test cycle of Wheelwright [
32] and Set-Based Design (SBD) [
33,
34].
This paper focuses on Set-Based Design, whose principle is to generate as many configurations and delay critical design decisions as much as possible [
35]. The aim is to avoid problems that often surface at advanced stages of the design process, which would require a major redesign or reversal of early decisions, prompting an increased cost both in terms of time and resources [
36]. Set-Based Design has been recently investigated for the problem of designing products under flexible requirements [
37,
38], and incorporate resilience to unexpected modes of operation [
39]. Furthermore, the large sweeping of the design space combined with a multi-disciplinary model makes SBD principles suitable for design space exploration and trade-off activities of complex systems [
40]. SBD has also been applied in decision analysis, where it has been combined with Value of Information methods, enabling robust design selection [
41,
42].
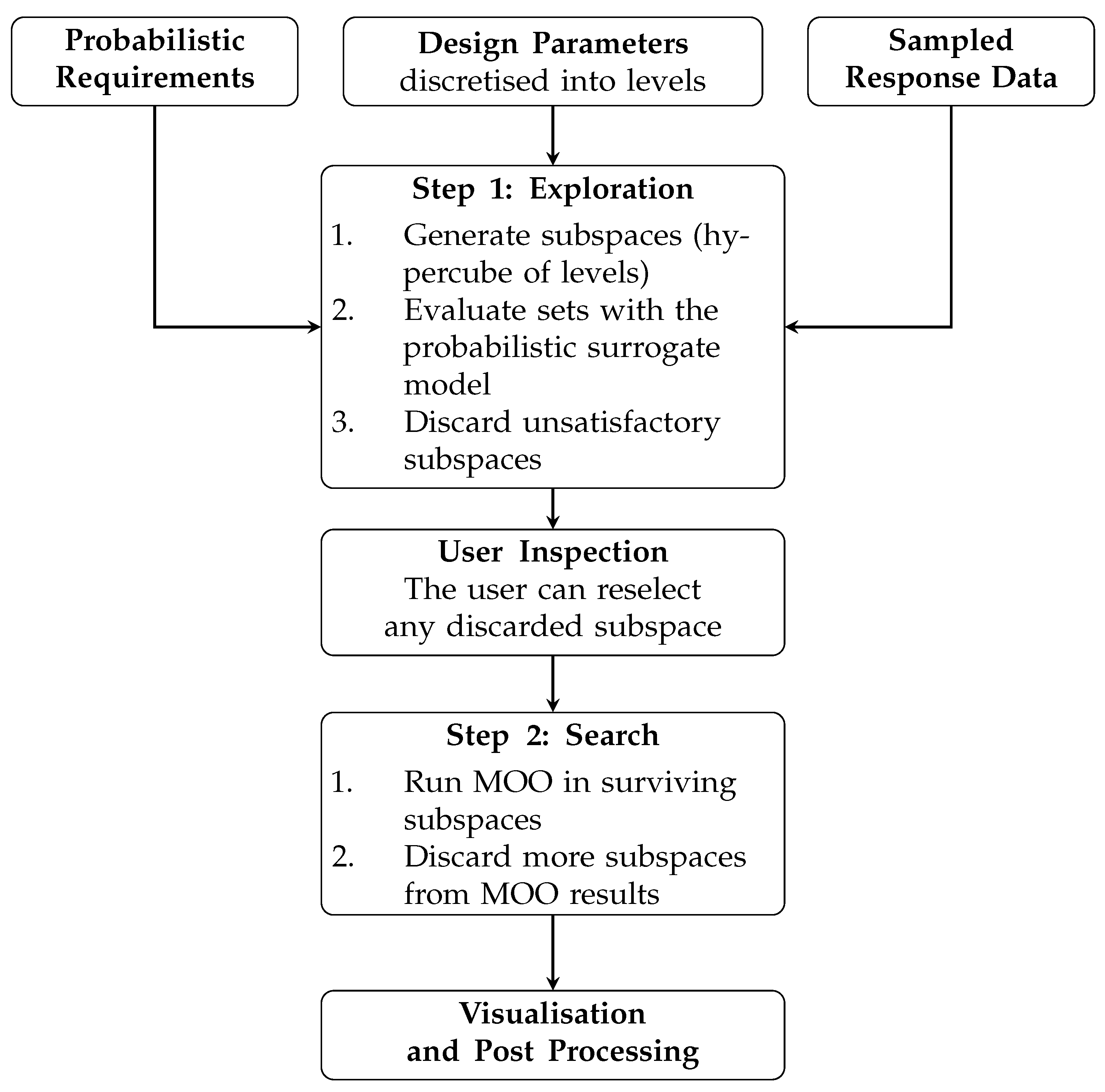
The framework developed for this study combines set-based design with multi-objective optimisation. Most optimisation methods are point-based in nature, where single designs are optimised; hence, several authors have attempted to extend these for design sets.
Some authors use a multi-objective optimiser to search for the optimal set or family of solutions without exploring the individual designs. Sets are evaluated based on abstract quantities such as general optimality, variability, robustness [
43], hypervolume size and imprecision [
44]. Trade-off studies are performed. Some examples of this general approach are the Set-Based Concept method [
43,
45], the Set Swarm Optimisation [
46] and the Set-Based Genetic Algorithm [
44].
In contrast, others use SBD principles to reduce the searchable design space before introducing the optimiser. These approaches evaluate sets by mapping their input parameters to the optimisation objectives [
47]. The final result expresses multiple individual designs that belong to the surviving sets.
Some examples are the Set-Based MDO of Hannapel [
48], the Technology Charaterization Models method [
47] and the ADOPT framework [
49]. The last one was chosen as it allows us to study the interaction between the input parameters and the design requirements. Furthermore, it allows us to identify and reject areas of the design space which are unable to satisfy the top-level requirements. However, the major drawback of this framework is the necessity of expertise on the problem under design for constructing if–else expert rules capable of filtering out unfeasible and undesirable configurations. Otherwise, even with a moderate number of parameters, the combinatorial explosion makes the entire methodology impractical to use. In fact, one major challenge in SBD methodologies is identifying the sets or subspaces out of all the possible combinations of discretised inputs that satisfy the requirements and discarding those that do not. Previous approaches can be divided into three main categories:
Algorithmic approaches which classify the sets by propagating constraints. Examples include Constraint Satisfaction solvers [
50,
51] and Fuzzy Set theory [
52].
Machine Learning classification which constructs a decision boundary based on samples responses. Examples include Bayesian network classifiers [
53], Support Vector Machines [
47] and k-Means Clustering [
54].
Decision-based approaches which model the restriction of the design space as a transition between states. Examples include Markov Decision Processes [
55] and Reinforcement Learning [
56].
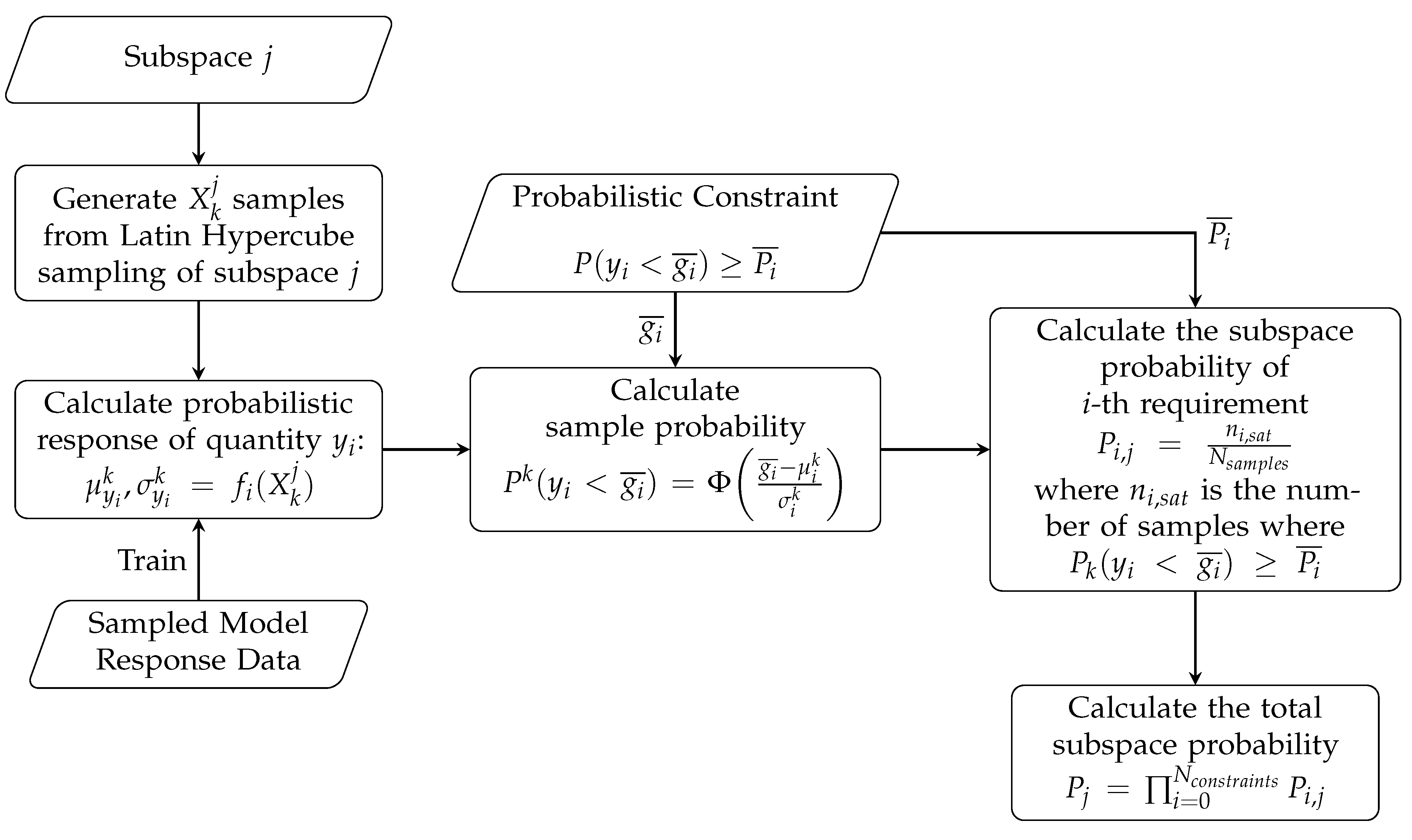
These approaches offer a deterministic classification of desirability of each design space subset. In the methodology presented in this paper the quantification of the uncertainty of the mapping procedure is considered. A Gaussian Process Regression was adopted to evaluate the capability of each set to satisfy the requirements and constraints. While this mathematical tool falls within the family of Machine Learning approaches, it provides an estimation of the variance of its response [
57], hence enabling a probabilistic assessment of the design space [
58].
While the application of probability theory has been widely used for the propagation of uncertainties on system performance [
59,
60], robust optimisation [
61] and sensitivity analysis [
62], it has been rarely used to assess the uncertainty of top level design requirements satisfaction. The previous use of probabilities in the context of top-level requirements satisfaction has been found recently in Guenov [
30] and Di Bianchi [
63]. Both authors use probabilities to estimate the ability of a design to satisfy the constraints, given some uncertainty: specifically on the margin for Guenov and on the constraint values for Di Bianchi. We seek to explore this approach and apply it in the context of Set-Based Design Optimisation.
In this paper,
Section 2 describes the modeling and methodologies adopted for this study with
Section 2.1, focusing on the new design exploration framework, while
Section 2.2 and
Section 2.3 describe the parametrisation of the energy management schedule and the overall sizing and analysis of the hybrid-electric propulsion system.
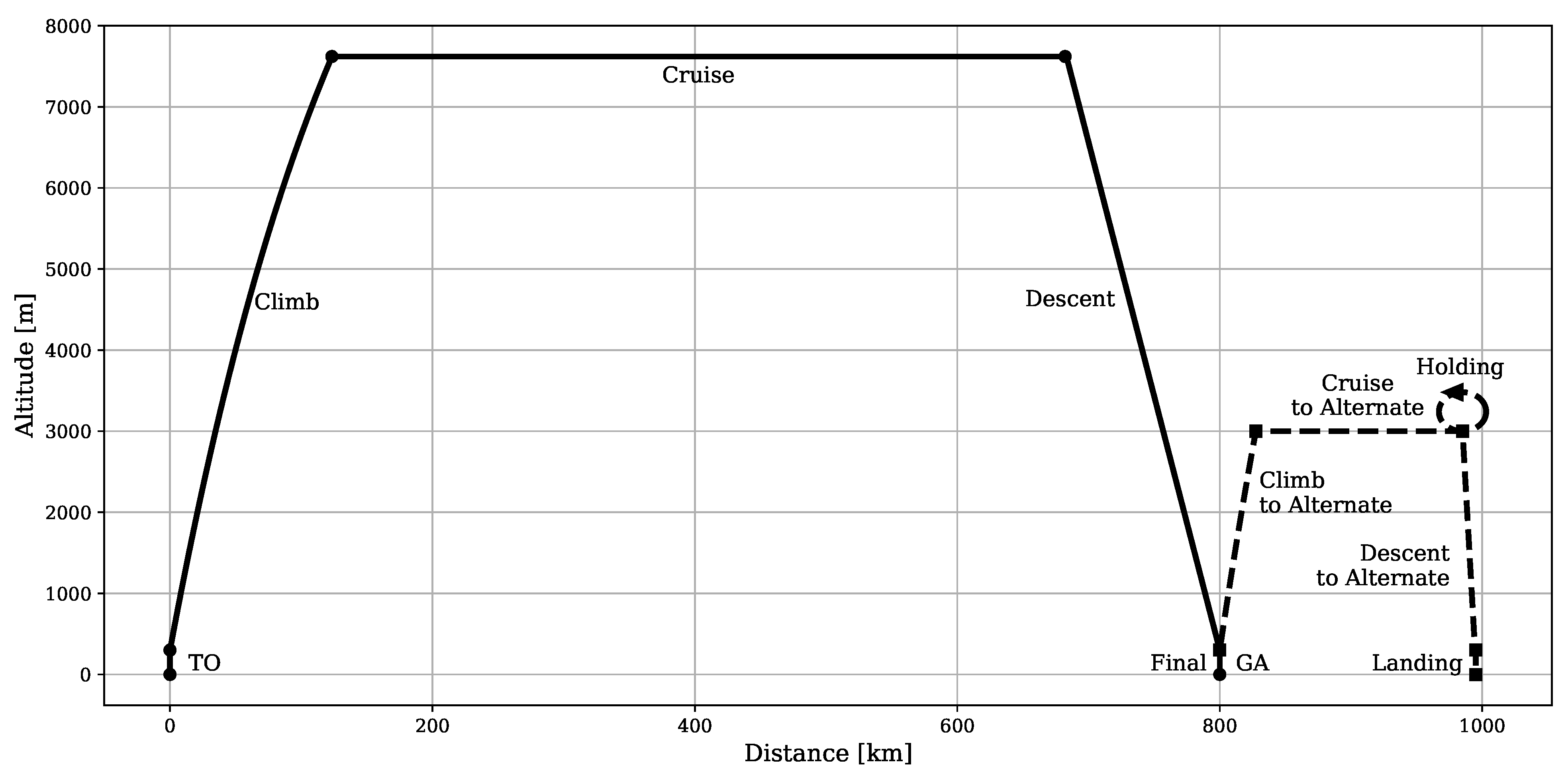
Section 3 presents the baseline aircraft, the sizing mission, the selected hybrid-electric propulsion architecture and the matrix of experiments performed in this study.
Section 4 presents the results of these experiments, both from the perspective of the methodology (
Section 4.1) and the energy management scheduling problem (
Section 4.2,
Section 4.3 and
Section 4.4). These are discussed in
Section 5.1,
Section 5.2,
Section 5.3, and
Section 5.4, respectively. Finally, three families of energy management strategies were recommended in
Section 5.5, and the findings are summarised in
Section 6.
6. Conclusions
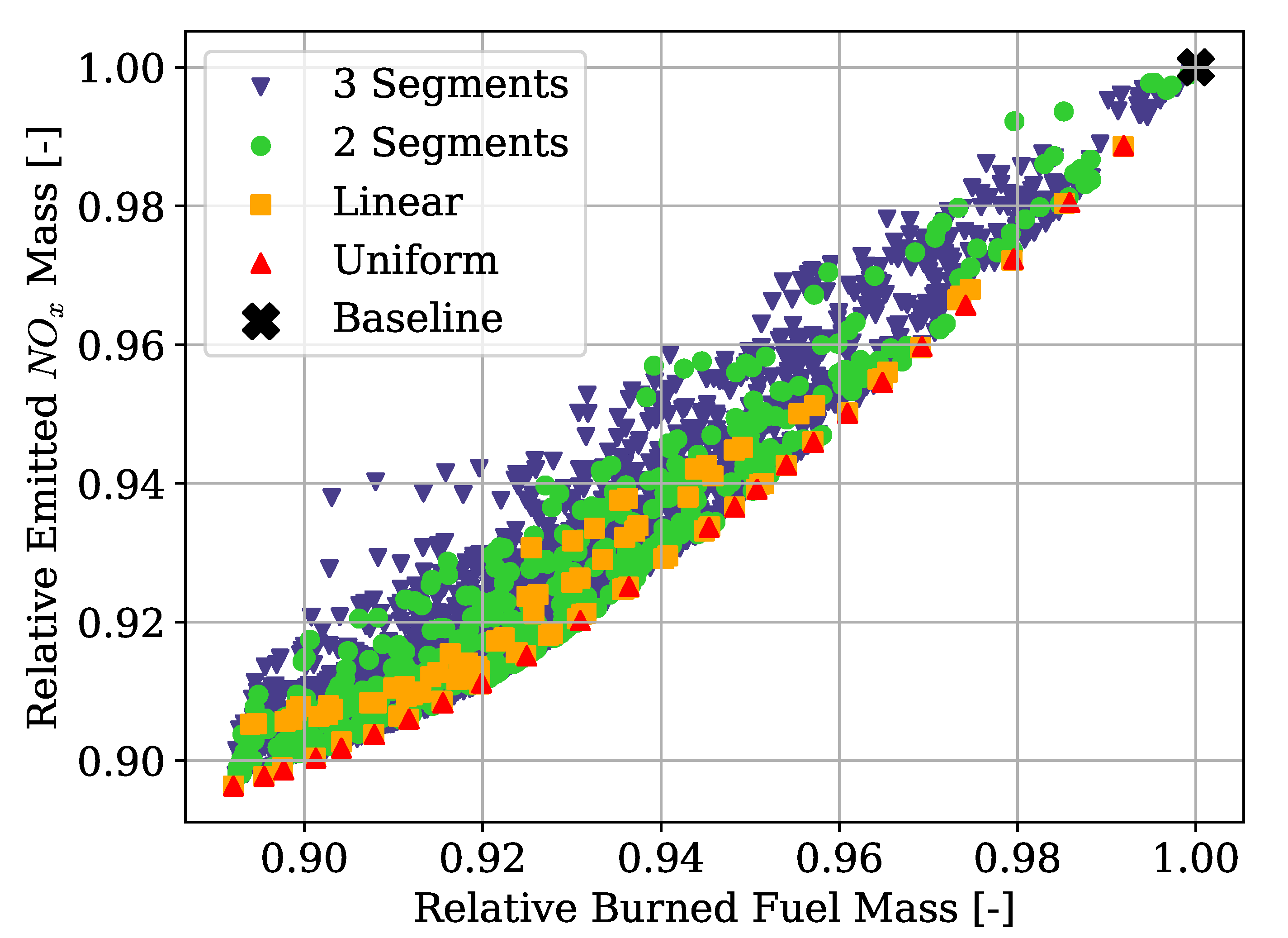
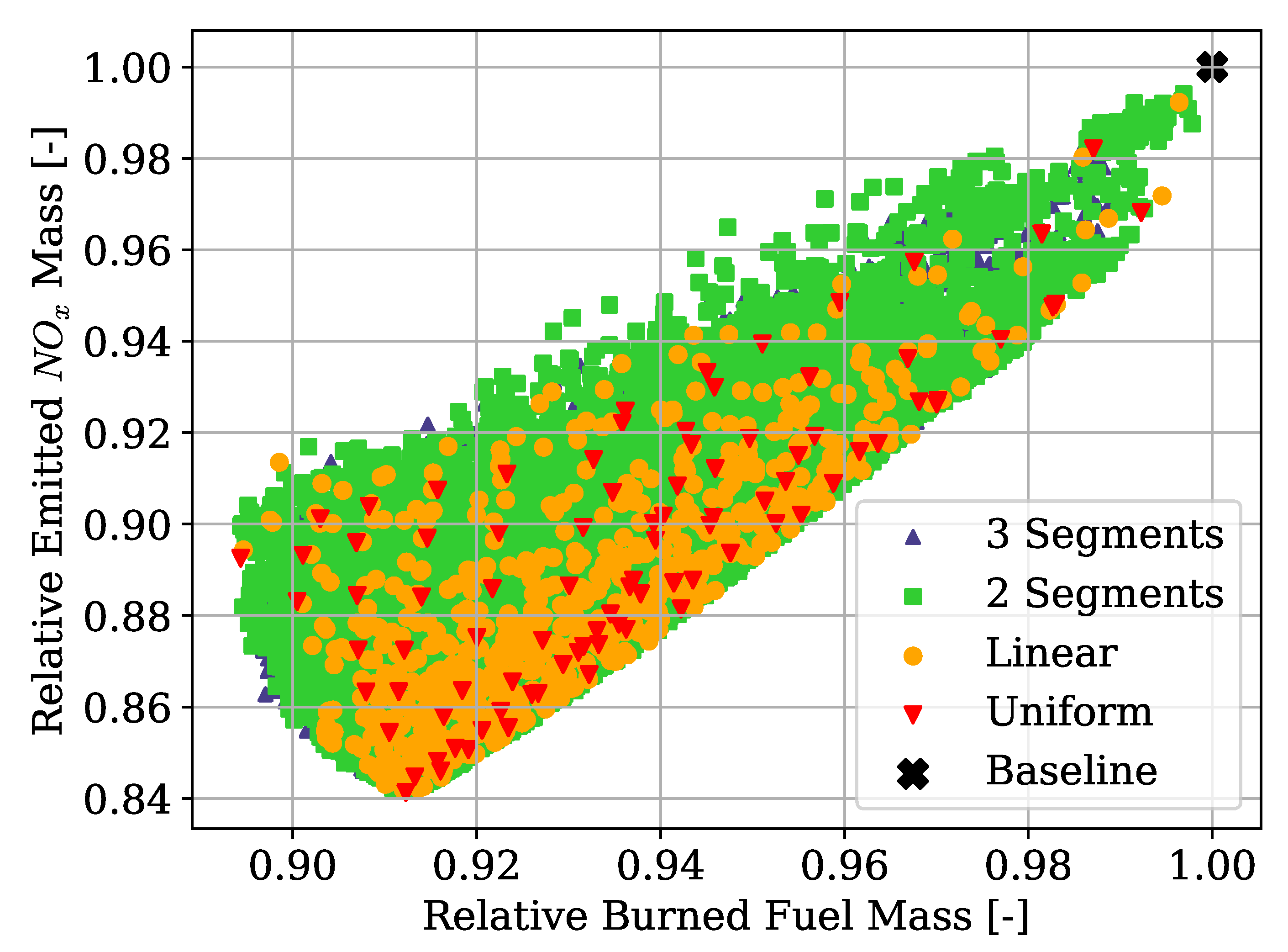
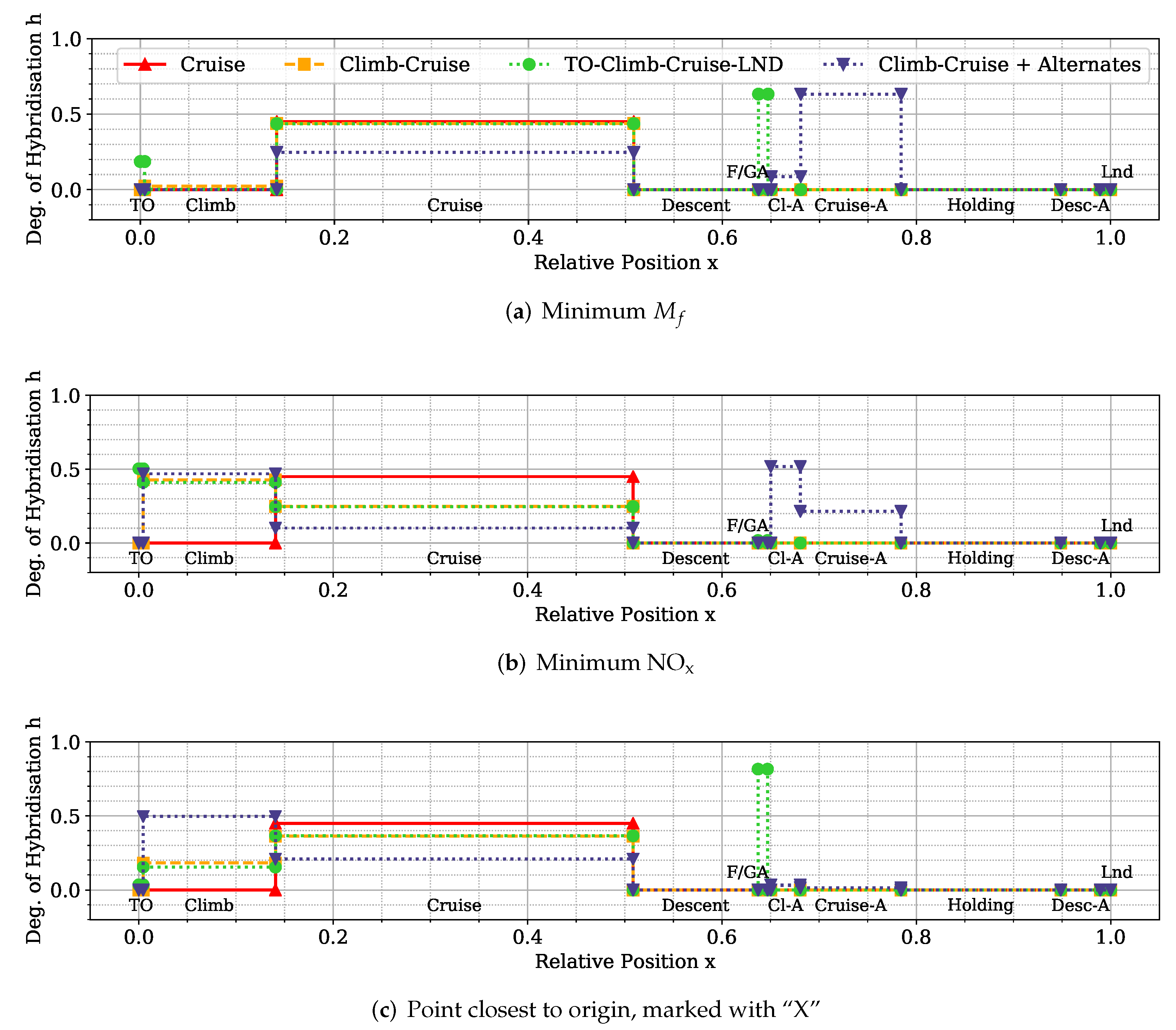
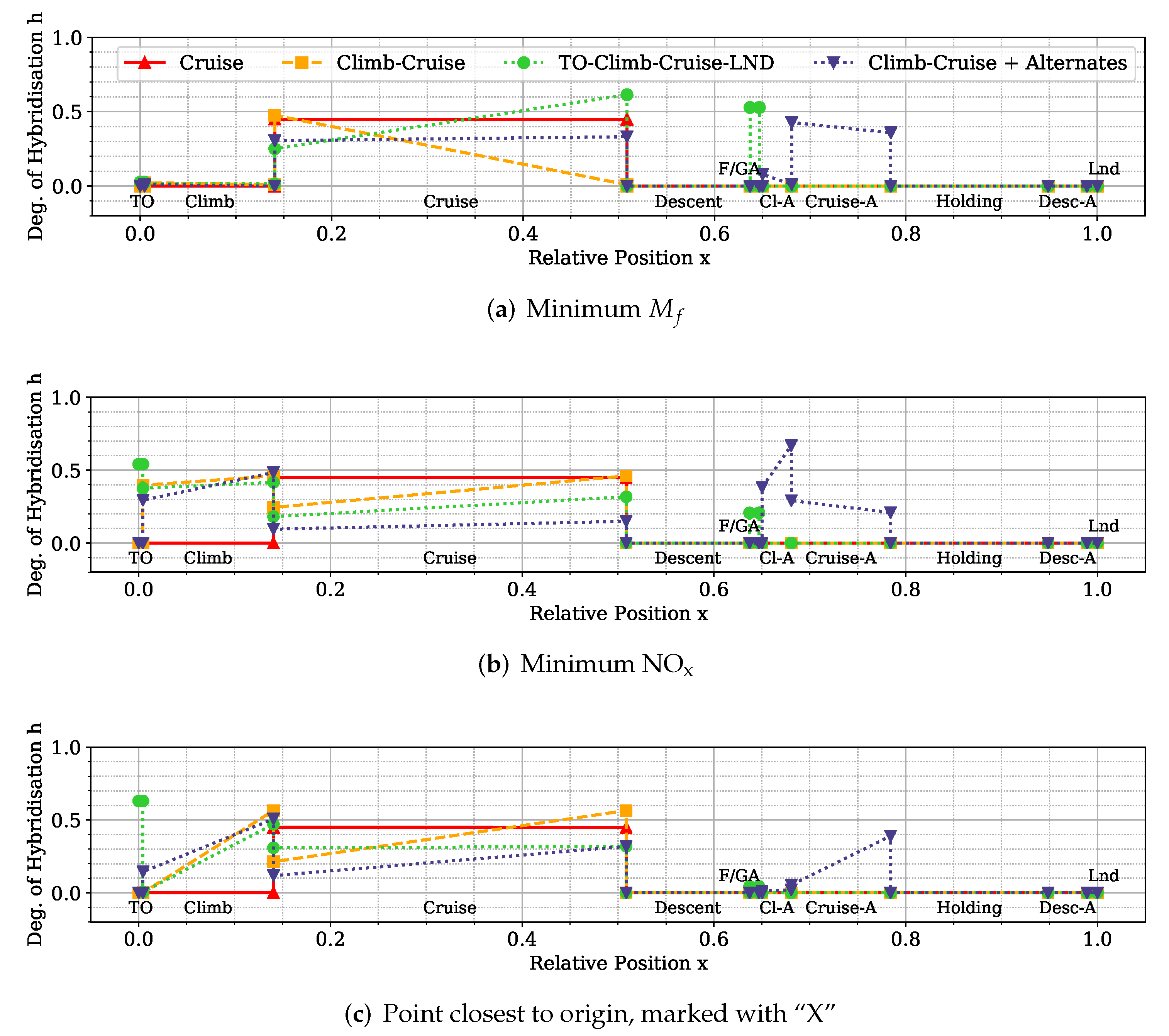
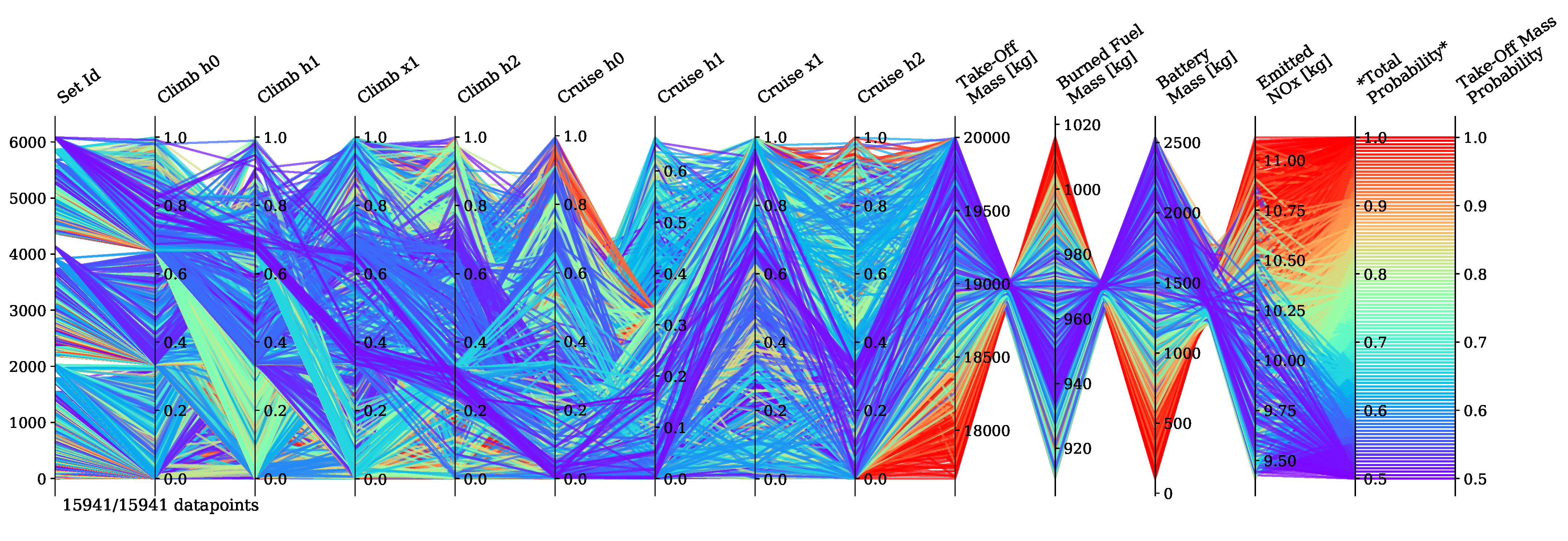
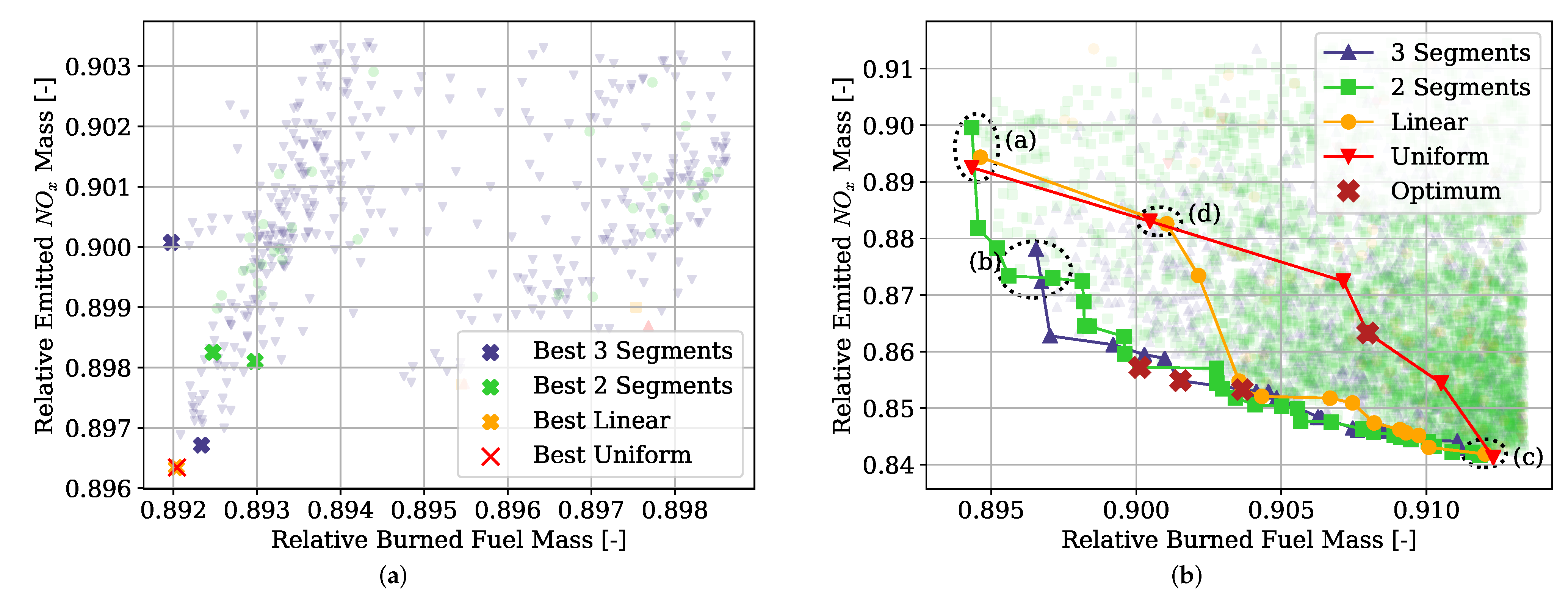
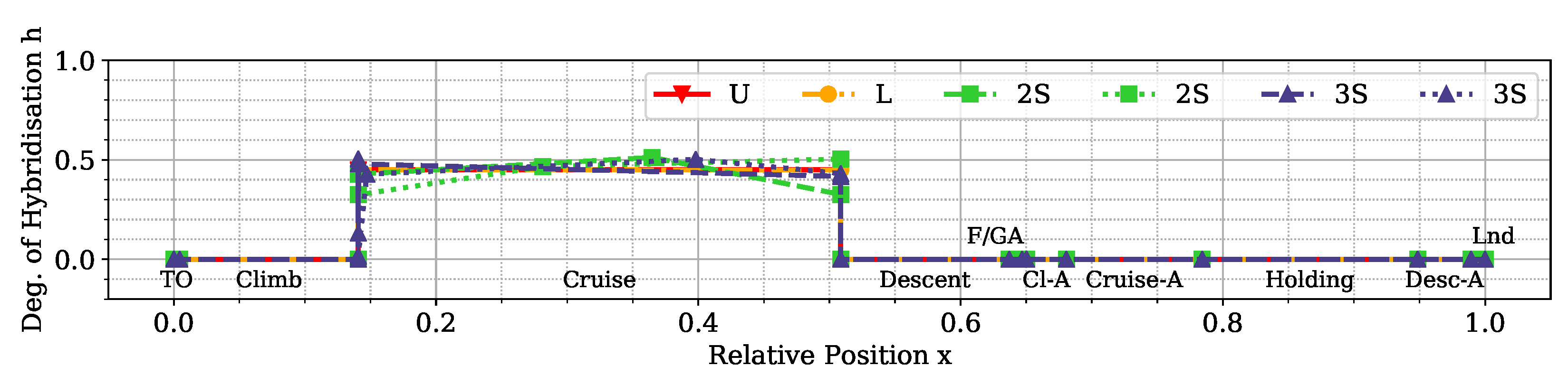
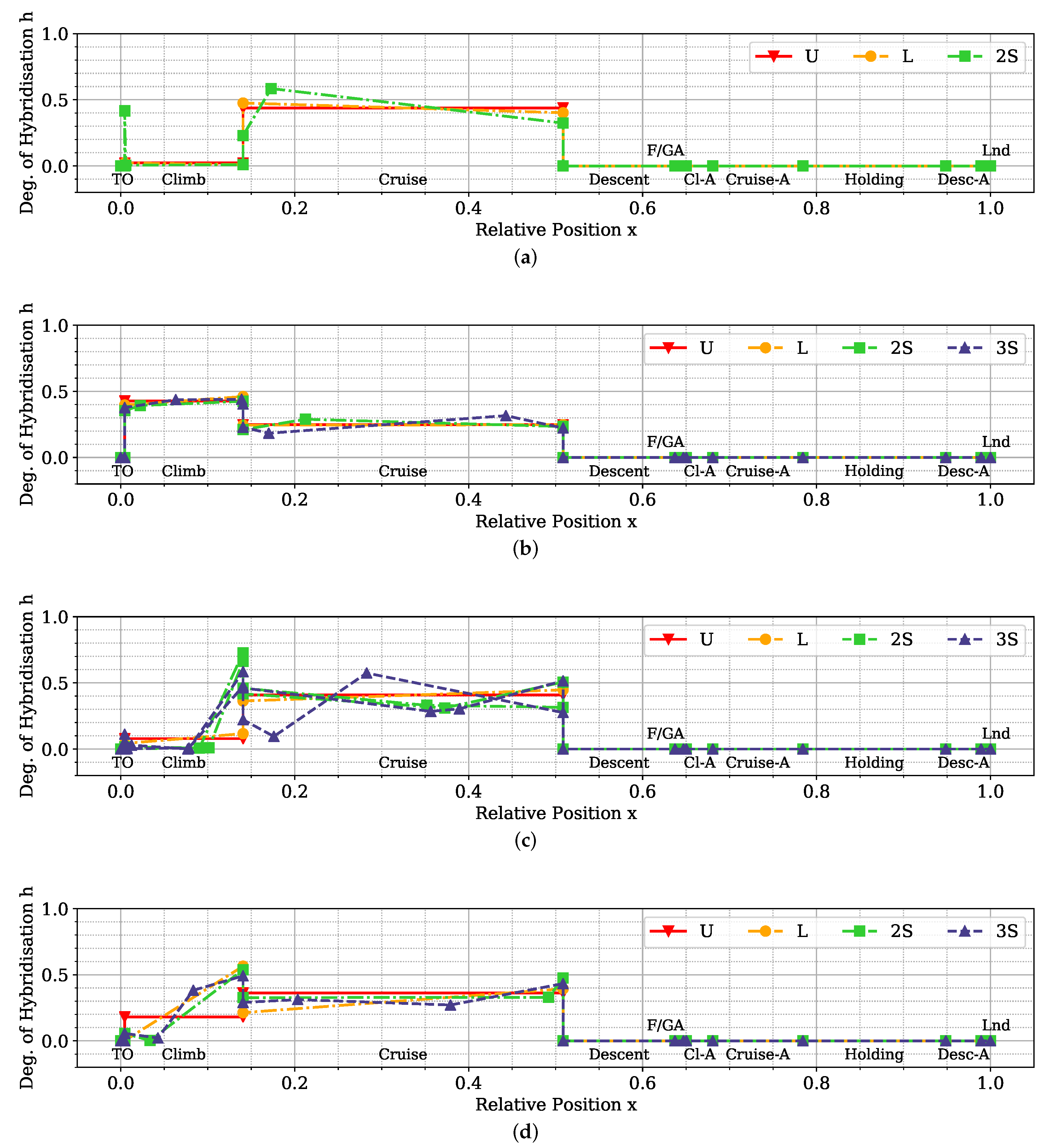
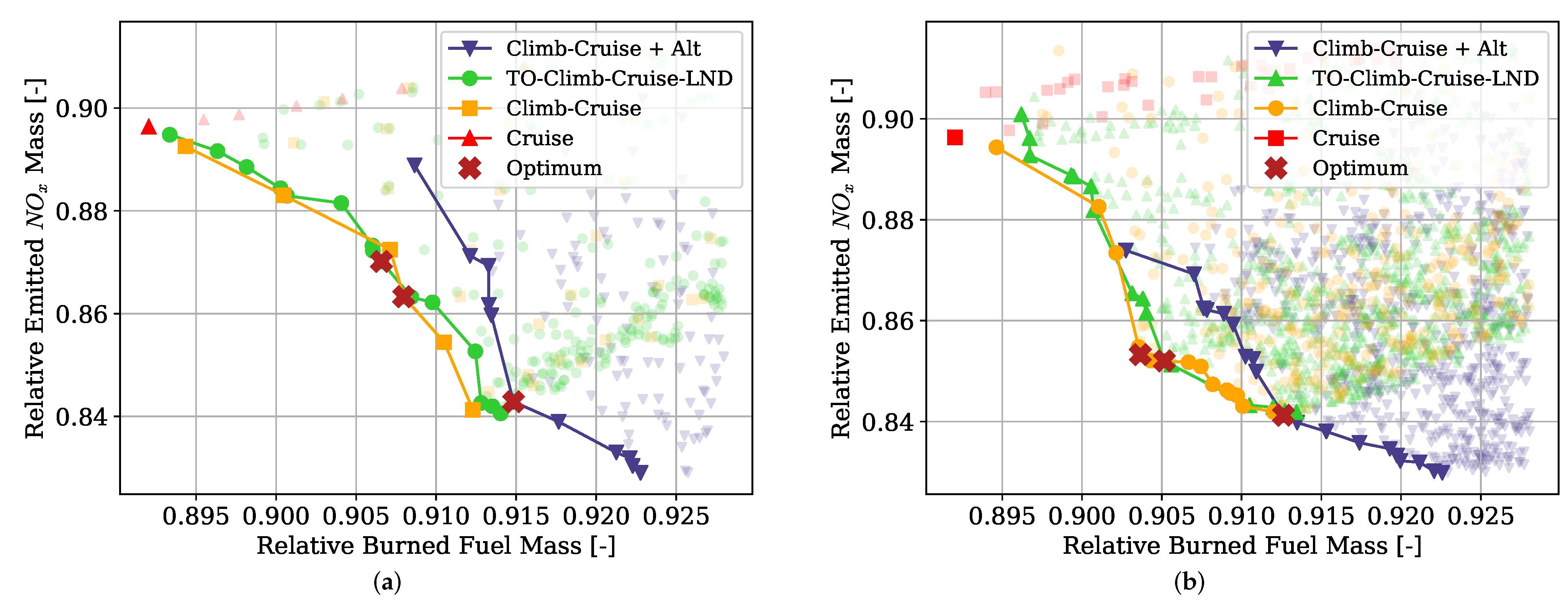
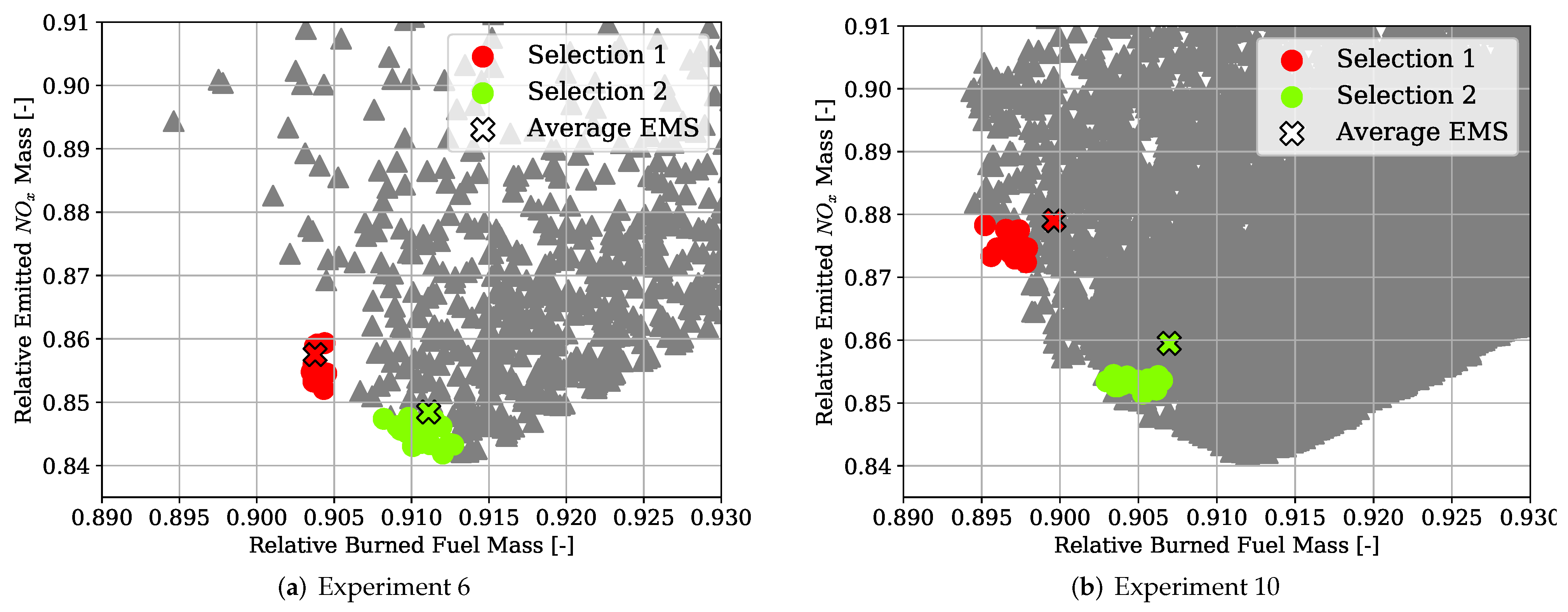
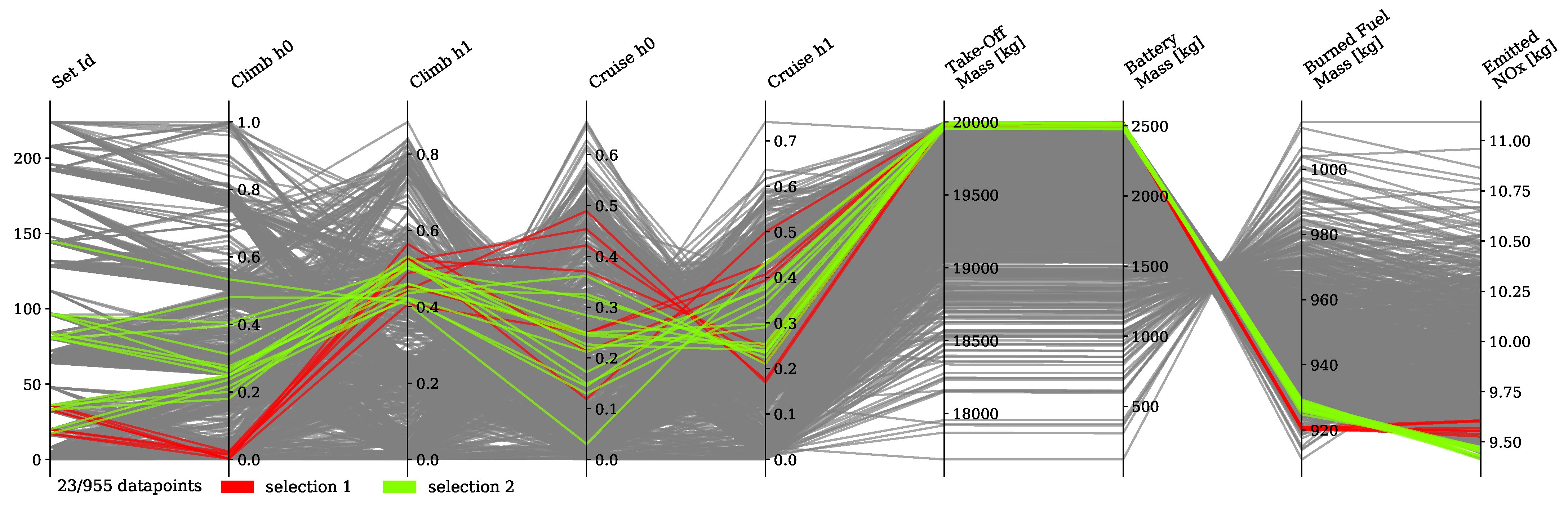
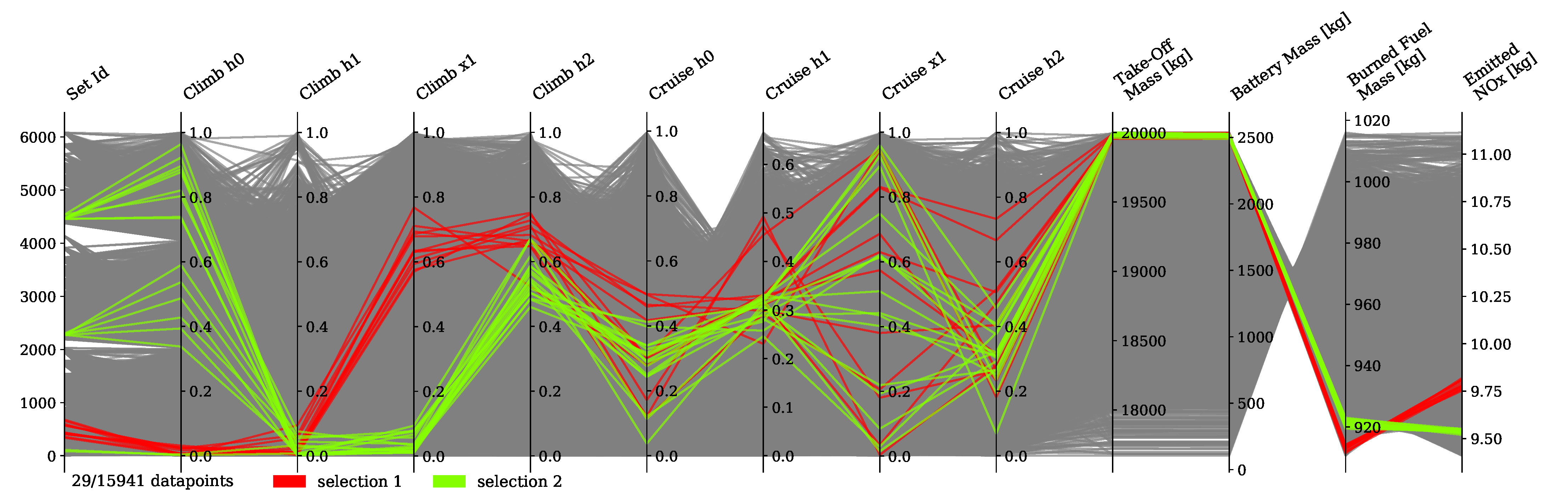
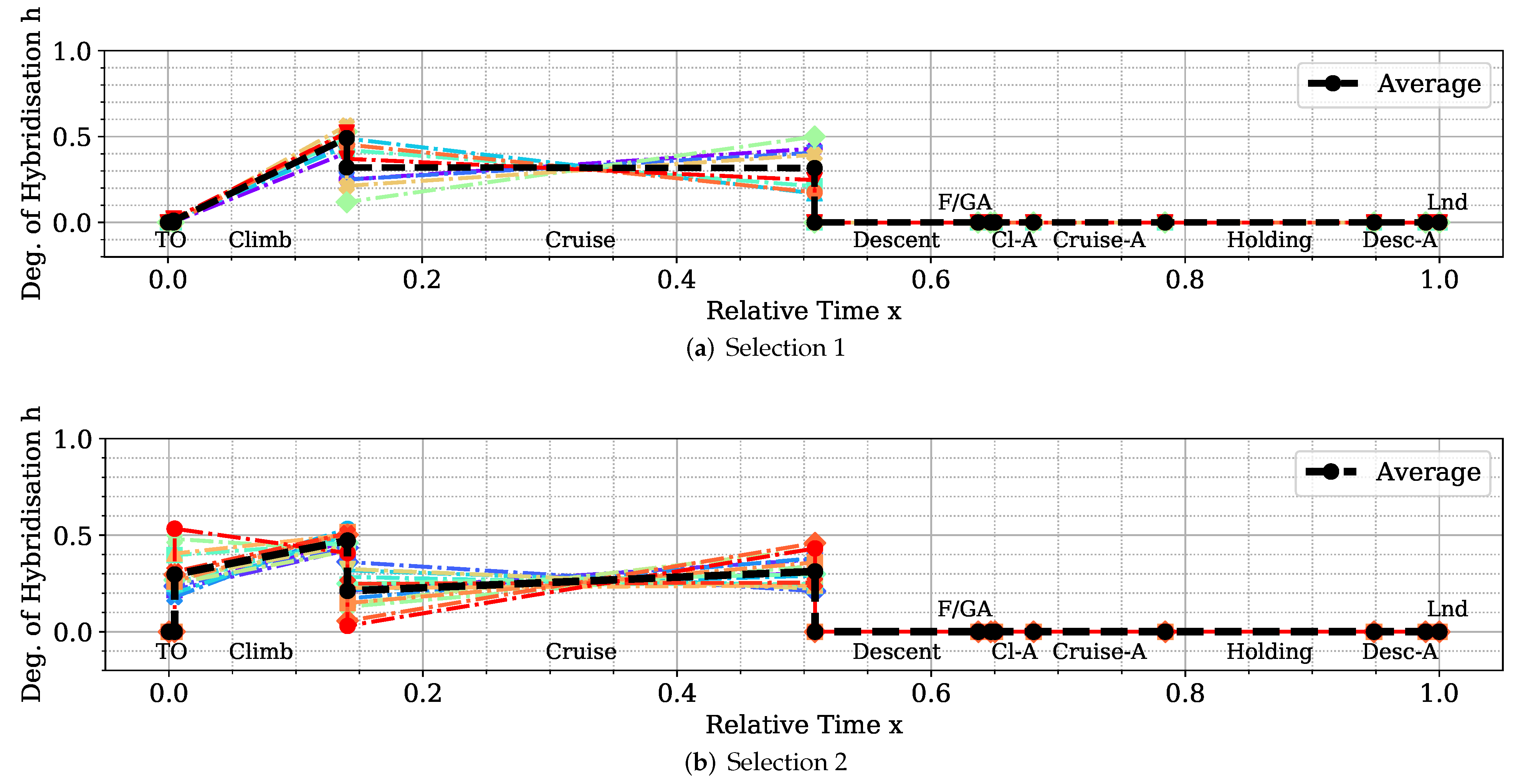
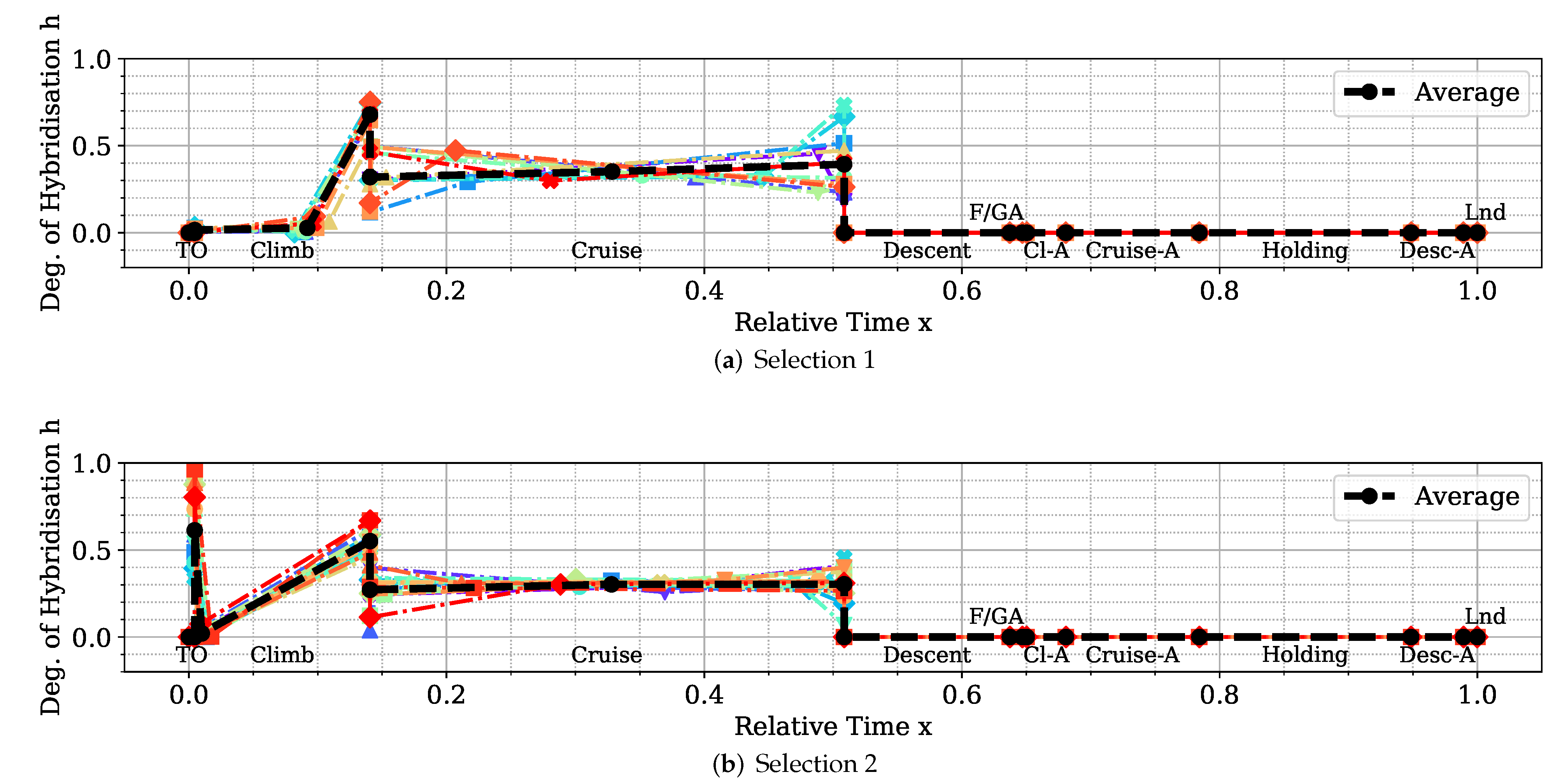
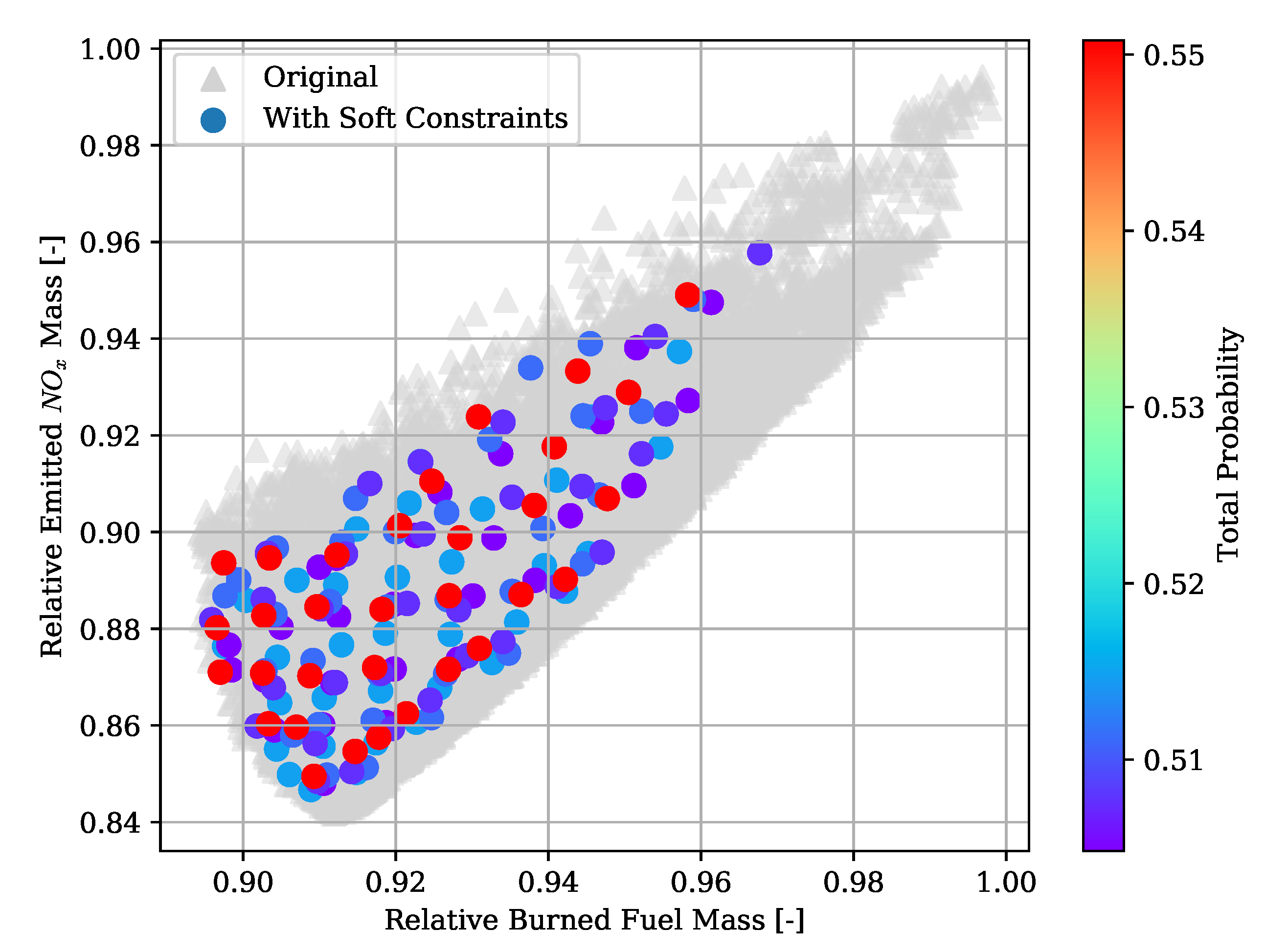
Hybrid-electric vehicles are characterised by providing propulsive power from more than a single energy source. Finding the optimal energy schedule is a common issue that affects hybrid-electric aircraft, albeit with the added complexity of take-off mass limitations. This study presented the problem of finding the optimal energy management scheduling for a hybrid-electric aircraft combined with its battery sizing. An ATR-42 class aircraft retrofitted with a hybrid-electric parallel propulsion system was modelled, and a piecewise linear parametrisation of the degree of hybridisation was introduced for flexibly defining any energy management strategy. A new design space exploration methodology based on the principles of Set-Based Design was introduced, enhanced by a probabilistic approach, which is capable of discarding design subspaces unable to satisfy the requirements set by the designer. This methodology allowed the optimisation algorithm to focus on areas of the design space without constraint violations and, when specified, closer to the global Pareto front. Indeed, the presented test cases had a large portion of the design space unable to satisfy the constraints. The framework was capable of identifying it and discarding it, reducing the number of configurations to evaluate by 75% on average. Furthermore, the optimisation results obtained with this approach allowed us to reveal the behaviour of the system. Nevertheless, a set of tuning hyperparameters of this framework was identified, the granularity of the subspaces and the minimum satisfaction probability, which affect the number of possible results. Tuning studies will be performed to benchmark the proposed methodology and define best practice hyperparameters. Several experiments were performed by changing the complexity of the parametrisation and the number of hybridised mission phases, from which several lessons were learned. The complexity of the energy management parametrisation has diminishing returns on the objectives. The piecewise two-segment topology was found to be enough for identifying the Pareto front. Introducing more phases did not improve the objective significantly to justify the increased computational cost. Furthermore, points in the same area of the objective space have similar energy management strategies, regardless of how complex and flexible their parametrisation is. Indeed, the parametrisation itself was not responsible for the trade-off between the objectives.
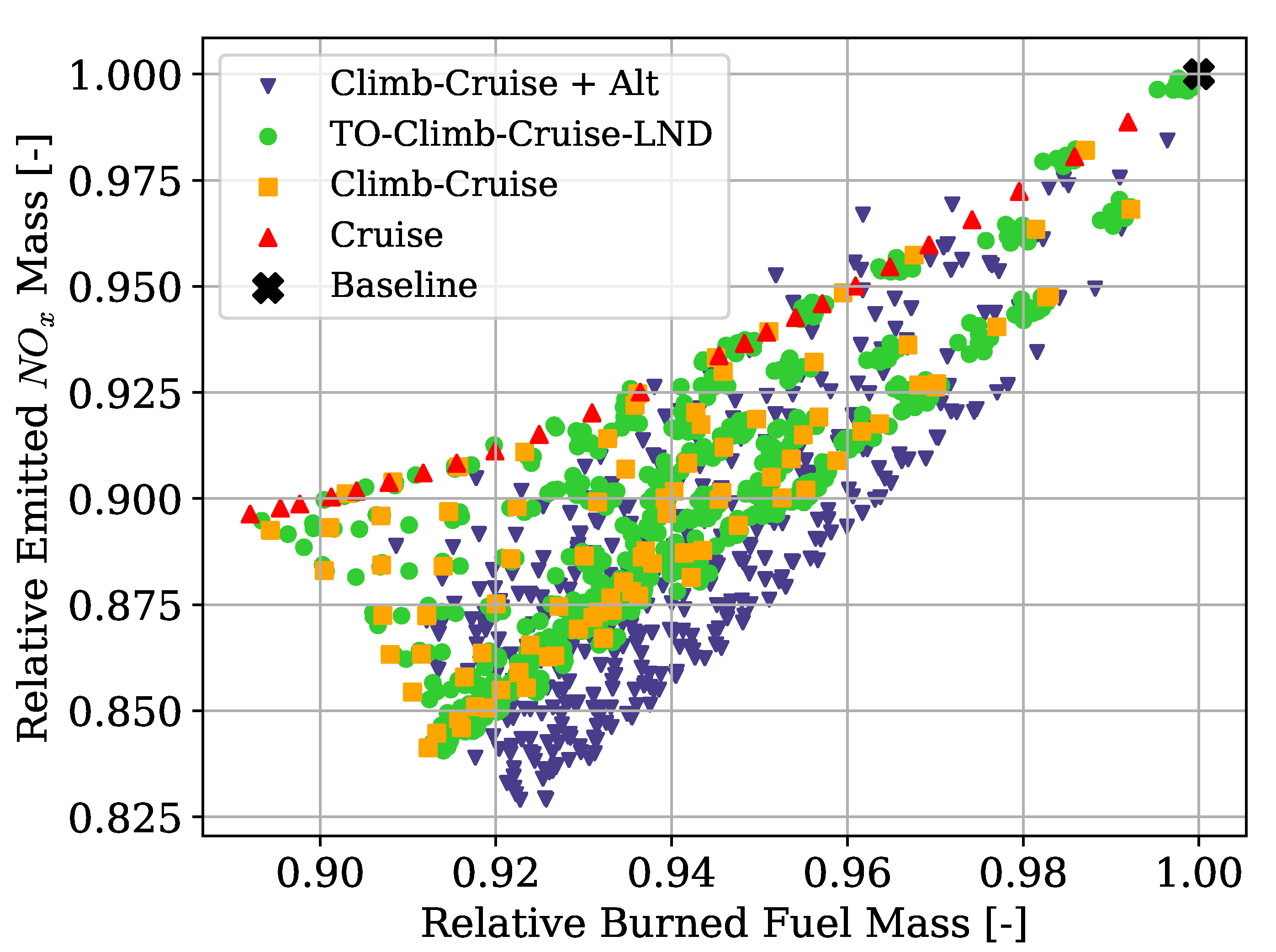
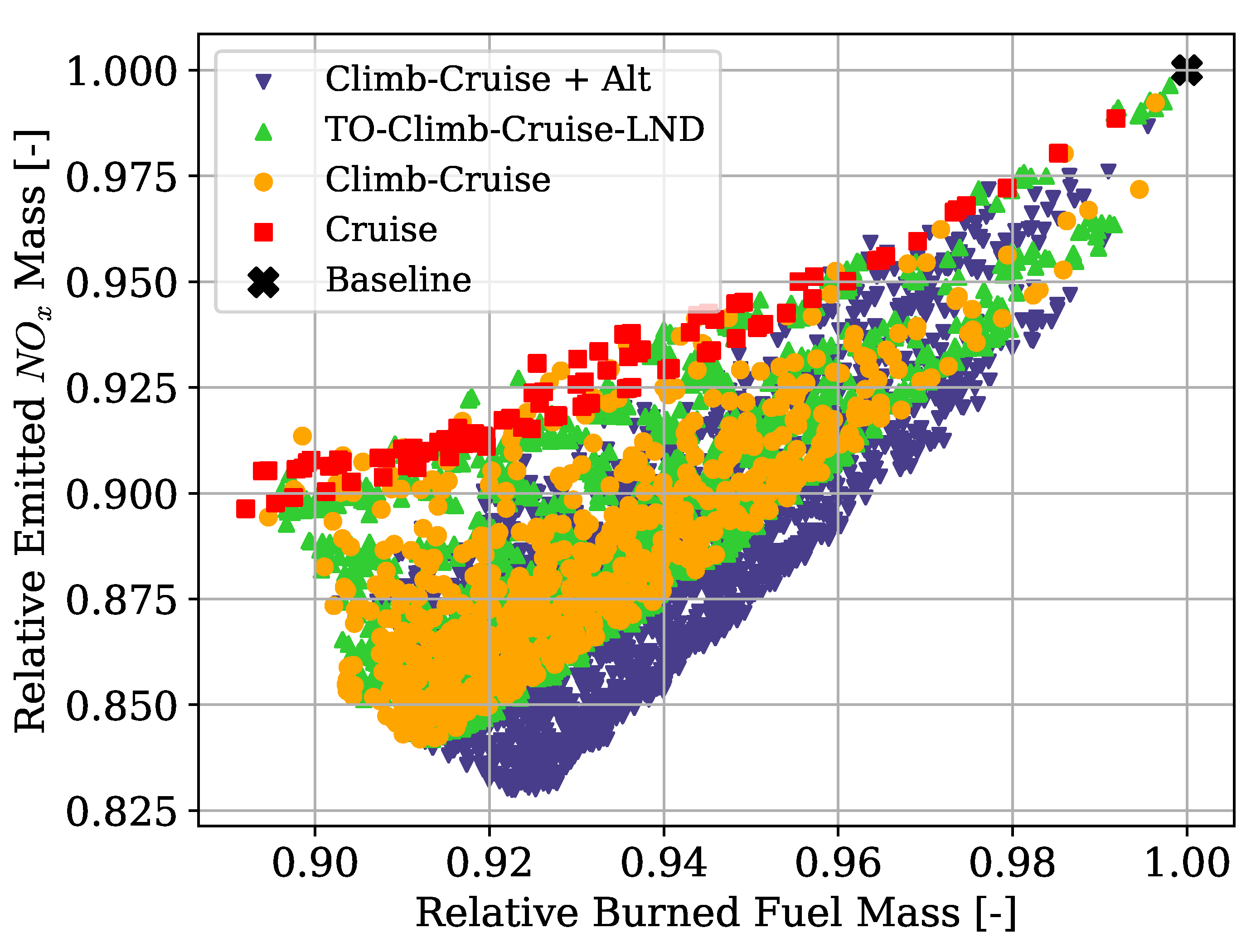
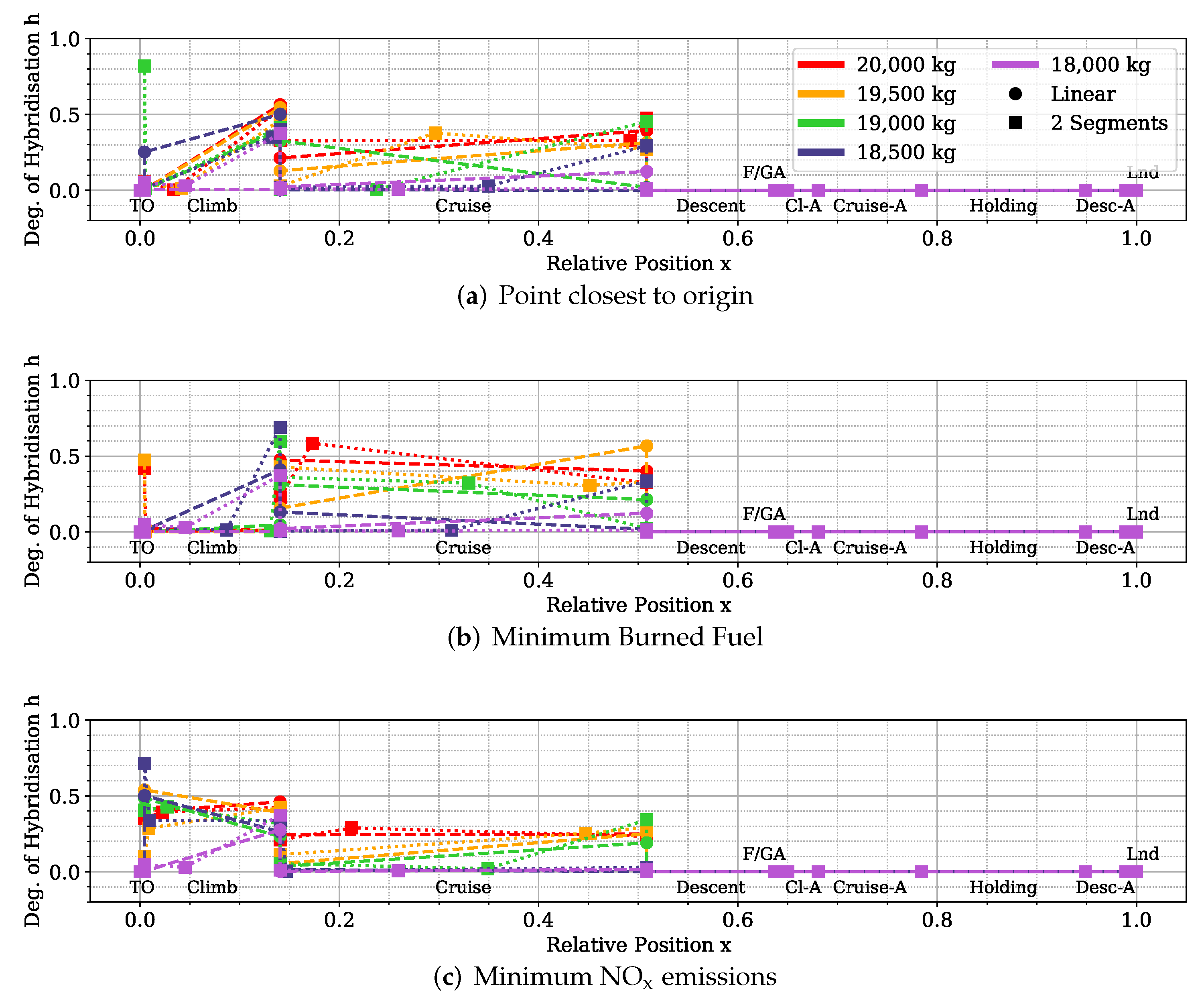
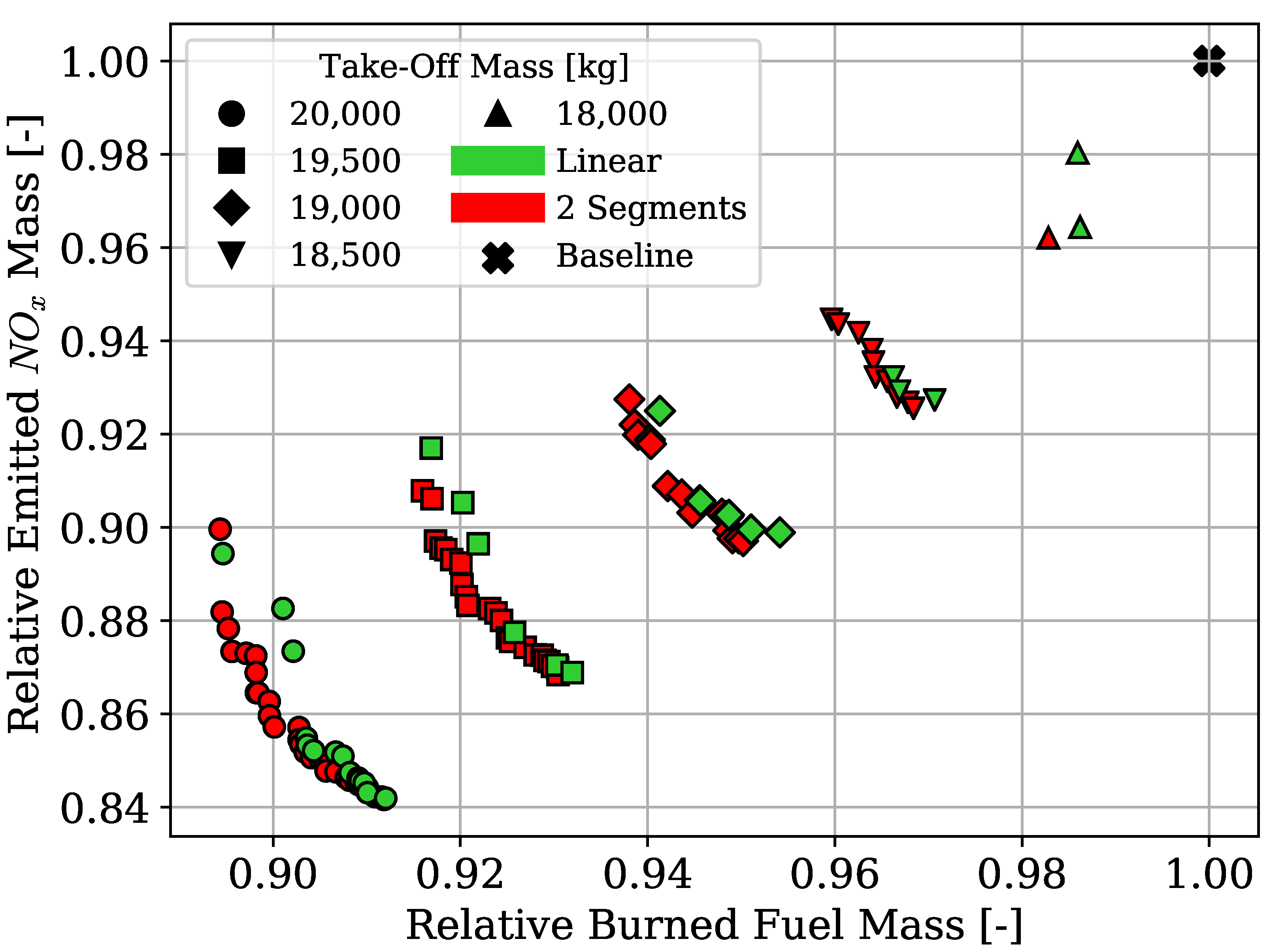
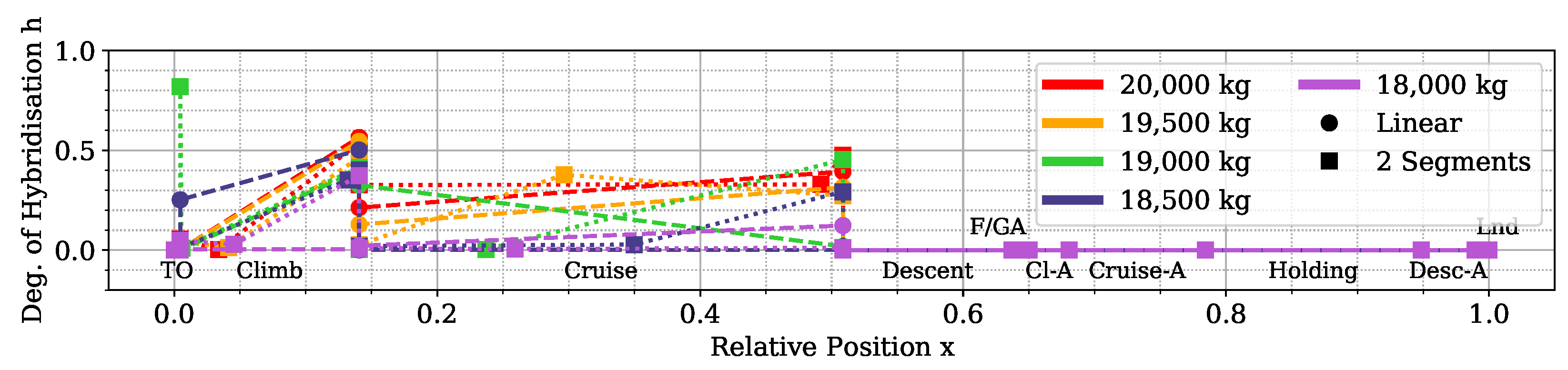
Instead, the length and number of the hybridised mission phases affected the shape and presence of a Pareto front. The results clearly showed that, while the longest mission phases contributed the most to the reduction of fuel consumption, if most mission phases were hybridised, the emissions would go down together with an increment in the overall propulsive efficiency. Moreover, the maximum take-off mass limit affects how much trade-off is present between the objectives. These phenomena can be explained in the limited amount of available electric energy due to the limited amount of battery mass. If this energy is distributed over more mission phases, on average, less gas turbine power is used, and therefore, less is emitted as it runs at a lower combustion temperature. However, the DoH would be lower on the longer mission phases, requiring most fuel burned. Indeed, if the electric energy is used only on the longest mission phase, cruise, the mission fuel consumption is minimised.
Lastly, the maximum take-off mass determines how much battery mass is distributed over the mission phases. While this might suggest increasing this limit indefinitely, the increment in the battery mass and the higher amount of electric power to manage would greatly impact the aircraft’s structural and systems mass, increasing the aircraft’s cost and complexity and ultimately reducing the fuel efficiency benefits.
This aspect was not included in this study but will be included in future work. Furthermore, from this study, the thermal management aspect of the hybrid-electric propulsion system was ignored, which is one of the current challenges in the design and production of HEA. Future studies will introduce the sizing of the thermal management system (TMS) from the electric system lost energy and its effects on aircraft mass and available power.
Finally, a critical aspect in the study and development of HE and Electric propulsion is the uncertainty of future technology. In this study, a fixed value of battery energy density was selected for a 2050 scenario. However, future studies will introduce an uncertainty into the presented methodology for studying different technological scenarios and their impact on the design parameters and requirements at the same time.