1. Introduction
This research work is framed within the European research project named IRON. The research program is addressed to the performance improvement of regional aircraft within the 90–150 passenger segment. Even if the market forecasts made by the most important manufactures at the beginning of 2020 have been completely changed by the unexpected COVID-19 outbreak [
1], when a full recovery from this pandemic disease will be reached most of the major airlines will still have to face a key factor influencing the regional market scenario, which is represented by the need to replace several hundred heritage aircrafts and the world demand for new aircrafts in the segment of 20–150 seats [
2,
3,
4,
5,
6]. This segment is characterized by the predominance of regional jets. Despite their success, turboprop engines are 10–30% more efficient in terms of fuel consumption [
7]. Thus, the introduction of a large turboprop should help in reducing the aviation environmental impact.
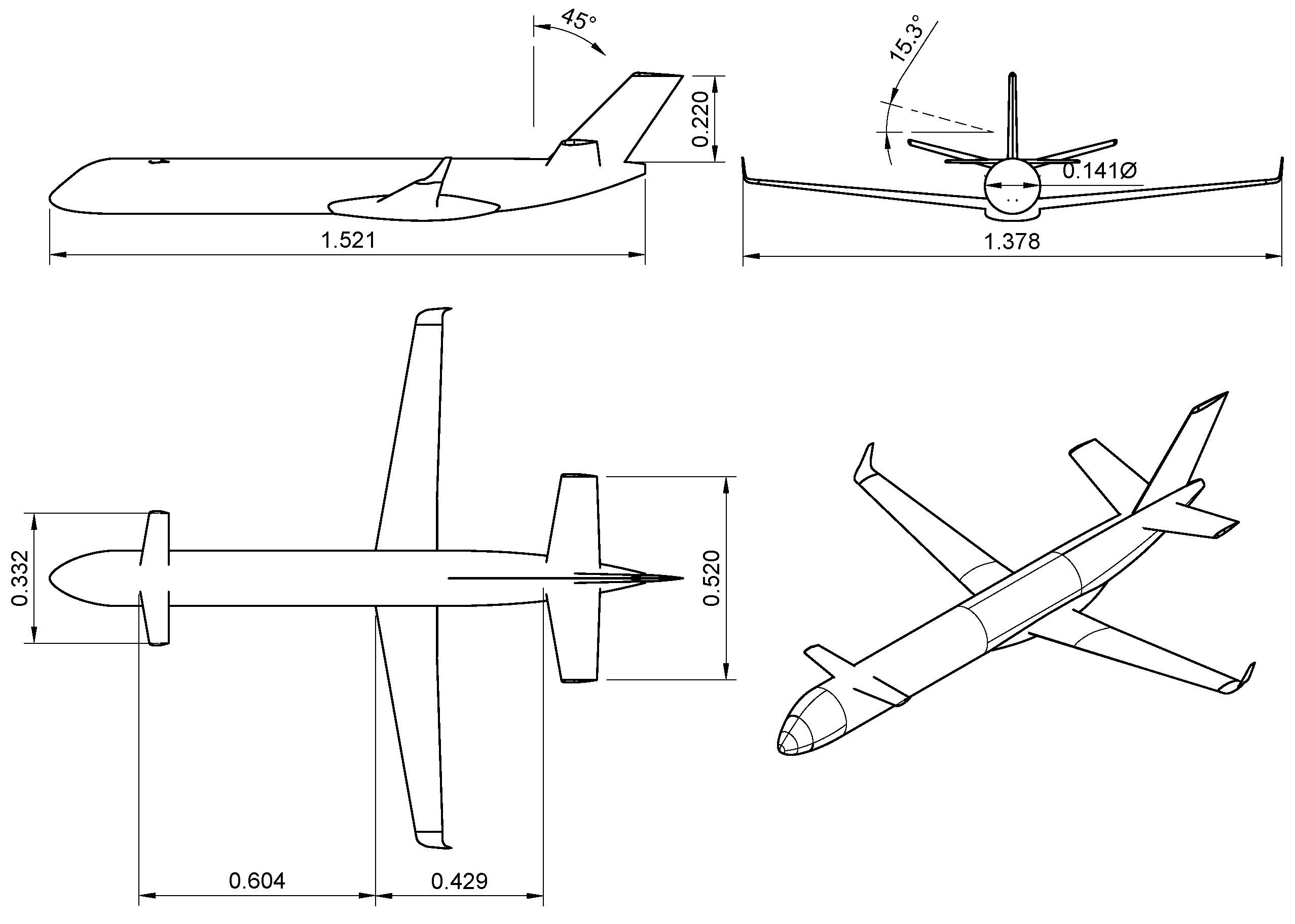
The aircraft configuration object of this work has been designed and optimized through two different design loops with increasingly level of fidelity. Starting from a baseline with the classic wing-tailplane configuration but with rear-mounted turboprop engines, a Multi-Disciplinary Analysis and Optimization (MDAO) has identified in the three-lifting surfaces layout the most promising configuration, being compliant at the same time with the aerodynamic targets to be competitive with regional jets and the aircraft weight-and-balance issues due to the rear engines installation. Details about the design considerations and optimization process of such an innovative aircraft have been provided by the authors in Refs. [
8,
9,
10]. At the end of the first design loop, a scaled model has been manufactured to evaluate the aircraft static stability with wind tunnel tests and to assess the quality of preliminary design. The three-view of the wind tunnel model is illustrated in
Figure 1.
The first experimental test campaign ended with some concerns about aircraft stability. In fact, the design of a three-lifting surfaces airplane with a reduced vertical stagger between wings involves several aerodynamic issues coming from the combined downwash of both canard and wing, as well as the canard wake interference on the lifting capabilities of the horizontal tailplane and consequently on the aircraft longitudinal stability. Apparently, the complicated interactions among the wakes of the lifting surfaces was not well predicted by the MDAO process of Refs. [
8,
11]. Thus, from the results of the first test campaign, the canard and the tailplane group were re-designed and a second test campaign on the updated scaled model, shown in
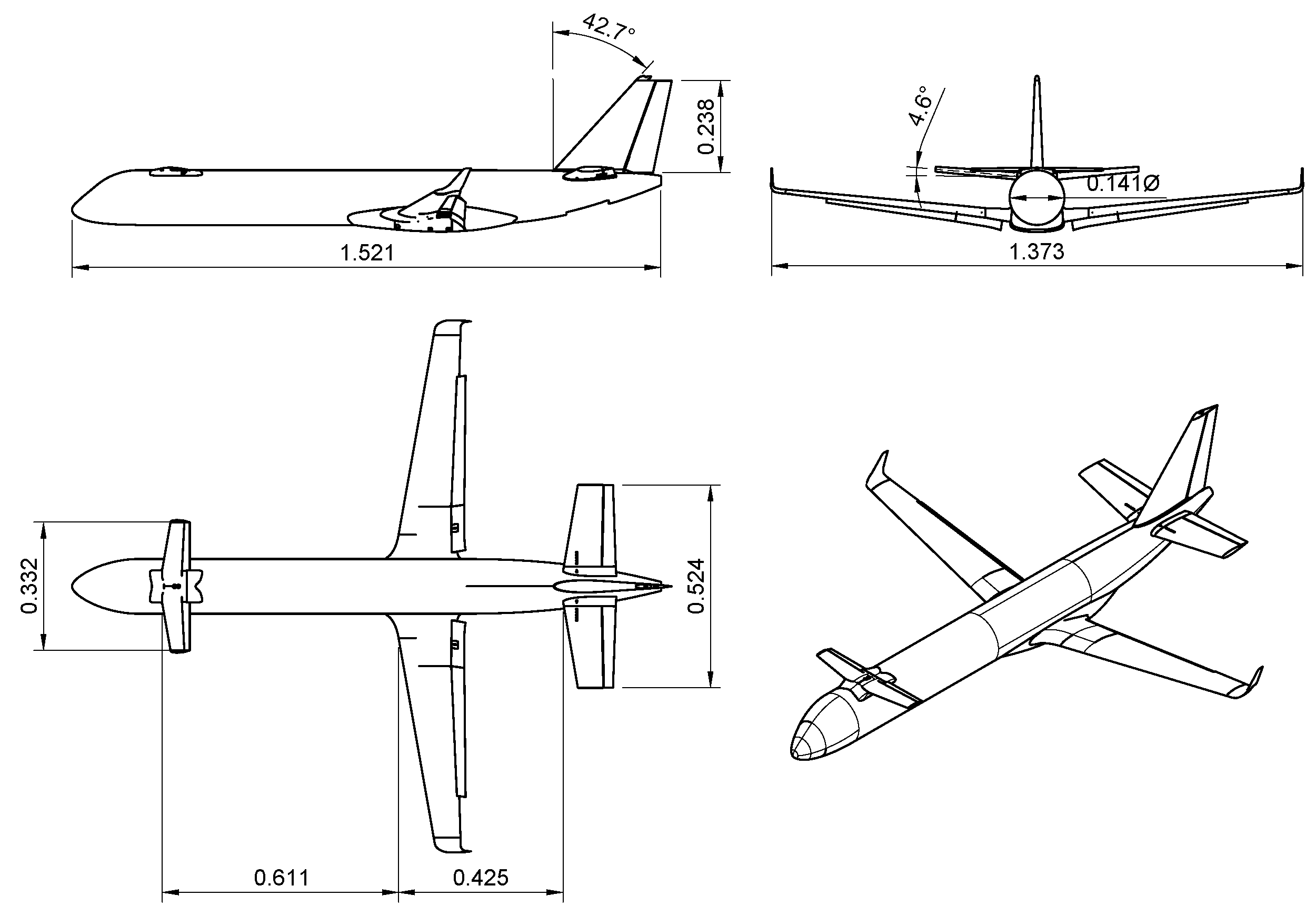
Figure 2, was performed. This constitutes the output of the design loop 2.
This paper discusses the aircraft evolution from the first to the second design loop and describes, in detail, the complex aerodynamic interference and wake phenomena among the lifting surfaces on the last configuration. A literary review of the three-lifting surfaces aircraft configuration follows this first part of the introduction.
A crucial issue for the aerodynamic assessment of this innovative configuration is an accurate estimation of the canard downwash. In literature, various references present the downwash phenomenon and methods to estimate its effects on an aft lifting surface. These methods include linear approaches as proposed by Roskam [
12], Silverstein [
13,
14], and DATCOM [
15], and the non-linear approach presented by Slingerland [
16]. However, these works emphasize the case where an aft tail has a much smaller span than the main wing. The influence of the wing on the tail is calculated by first estimating the downwash gradient in the plane of symmetry at the longitudinal and vertical location of the tail and then correcting for the spanwise variation across the tail. However, the data in Roskam [
12] and Silverstein [
13,
14] are limited to a span ratio equal to 0.4 and to a relatively small change of downwash gradient with tail span, leading to a single value for the downwash derivative for a conventional tailplane.
In case of a canard configuration, where the forward wing has a smaller span than the main wing, the above-cited methods do not work properly since the spanwise variation of the downwash gradient becomes quite significant. A first attempt to provide a method to evaluate the downwash for a canard configuration is proposed by Philips. He evaluated the downwash in the plane of symmetry for an elliptically loaded wing [
17] and then calculated the integral downwash gradient effect [
18]. This method approximated a generic wing as an elliptical one, not accounting for the actual planform parameters. Moreover, Philips’ method did not account for wing span loading distribution, avoiding any design indication for the twist angle distribution.
A method was subsequently proposed by Levy [
19] where a vortex lattice approach was used to build up a simplified methodology to account for both downwash in the symmetry plane and spanwise attenuation factor. However, it only investigated the case with wing and canard having the same aspect ratio.
An optimization study about the longitudinal aerodynamic load distribution resulting in the minimum trim drag in level, steady state flight for airplanes with three or more lifting surfaces and propulsive control effects was performed by Goodrich et al. by means of classical linearised flight mechanics equations [
20]. They were able to identify the best solution in terms of trim drag, but nothing is stated about the interference phenomena among lifting surfaces or downwash effects. The third lifting surface could be also adopted to improve the flying qualities of an aircraft by including an additional elevator on the canard surface as shown in [
21]. The evaluation of flying qualities of a three-lifting surface aircraft has been also evaluated through experimental flight tests of a scaled model [
22]. However, they took into account a configuration similar to the Piaggio P-180, where the canard, wing, and tailplane are conveniently staggered, contrary to the IRON configuration where the tail and wing positions are imposed by design constraints such as number of passengers, propeller clearance, and landing gear height.
So far as it concerns this research, a fundamental role concerns the feasibility study conducted by the authors in [
11]. In this work, the authors investigated three possible high-capacity turboprop configurations conceived to be competitive with regional jets on short/medium haul and providing, at the same time, a lower environmental impact. The three possible layouts are: a high-wing arrangement with under-wing engine installation; and two- and three-lifting surfaces designs, both with low wing and rear engines installed at the tail tips. All of the proposed concepts went through an MDAO process to achieve the minimum block fuel on a design range of 1600 NM. By comparing the proposed concepts with both an existing regional jet as the Airbus A220-300 operating on such a range and with a jet platform specifically designed for the same range, the three-lifting surfaces aircraft has been identified as the solutions having the maximum potential fuel saving, about 17% with respect to the reference regional jet [
11]. This work also highlights that a reliable prediction of the downwash gradient at the horizontal tail is of a primary importance to perform a correct sizing of the horizontal tailplane in order to provide sufficient longitudinal static stability. The downwash gradient at the tailplane in a three-lifting surfaces aircraft is a result of mutual, non-linear aerodynamic interference between the canard and the wing wakes.
The design and optimization of a canard for a three-surface aircraft (TSA) was the objective of Strohomeyer’s research with a higher-order panel method [
23]. Primary aim of the canard study was the preliminary design of an optimum canard geometry for the DLR-F11 TSA wind-tunnel model under the design constraints of a realistic aircraft. Based on the conventional design for the wind tunnel model, the retrofit of the geometrically fixed aircraft with a canard was simulated. The analyses show that a sweptback canard in low position, located downstream to the divergent nose part of the body, with a high aspect ratio, low taper ratio, and moderate span, promises optimum performance. In addition, the canard lift of the TSA configuration allows one to achieve higher cruise lift coefficients for an improved induced drag at transonic speeds, without the risk of additional wave drag. However, the static margin decreases significantly with the integration of the canard. Actually, this was expected to occur also in IRON case, despite the fact low-fidelity studies did not reveal any problems in this respect.
The canard effect on longitudinal stability and trim requirements was also examined by McGeer and Kroo [
24] using methods based on the lifting line theory for the aerodynamic calculations. In particular, they compared the relative efficiency of canard and conventional aft-tailed aircraft configurations in terms of trimmed maximum lift coefficient, drag, and structural weight. They conclude the paper by stating that:
The clear inferiority of the two-surface systems is just the price that one pays for a moderate amount of stability and control.
This sentence invokes two valuable concepts for this paper: (i) the possible aerodynamic and performance advantages of a three-lifting surface configuration; and (ii) the arising of stability issues related to distribution of the lift among the surfaces to balance the system.
Most of the references described so far dealt with low-fidelity analyses. As concerns experimental investigations, wind-tunnel tests of a model of an advanced general aviation aircraft with canard were conducted in the Langley 30- by 60-Foot Tunnel [
25]. The objective of the tests was to determine the aerodynamic stability and control characteristics of the test article for a large range of angles of attack and sideslip for several power conditions. For forward center-of-gravity locations, the model did not exhibit any stability and control characteristics that would be viewed as unsafe. The results also indicate that the configuration would be extremely stall-resistant. This highly desirable stall-resistance characteristic resulted from the fact that the canard was designed to stall prior to the wing. Stalling of the canard resulted in increased longitudinal stability and decreased elevator effectiveness. Both effects limited the maximum achievable trim angle of attack to values below those required for wing stall for all power conditions tested. For aft center-of-gravity locations and high-power, low-speed conditions, the combined effects of nose-up trim changes due to power and reduced longitudinal stability overpowered the stall resistance provided by the canard. Large nose-up elevator control inputs in this condition could result in stalling of the wing, which in turn yield to longitudinal instability and large nose-up moments, which would tend to further increase angle of attack to a deep-stall condition. The findings of this work were held in high regard because similar results on longitudinal stability were expected on the IRON wind tunnel model for aft center-of-gravity locations, despite the difference between the two models.
An aircraft configuration similar to IRON was tested by Ostowari and Naik [
26]. Their paper presents measurements of aerodynamic forces and moments from a series of wind tunnel experiments using a modular airplane configuration to ascertain how non-elliptical lift distributions affect the lift, drag, and static longitudinal stability for a three-surfaces configuration. Among the several outcomes of the work, the change of neutral point position for configuration with low tailplane position—more or less in line with wing and canard—is particularly of interest because it is a sign of stability reduction.
As concerns the evaluation of lateral-directional characteristics of three-lifting surfaces configuration, some experimental data are available for a fighter aircraft. Grafton and Croom in [
25] have studied the low-speed, high-angle-of-attack stability characteristics of a three-surfaces fighter concept based on the F-15 configuration. They have measured static force data over the angle of attack and sideslip range of 0° to 85° and −10° to 10°, respectively. Their results have highlighted that the canard adversely affects both static directional and lateral stability at high angles of attack. According to the authors, this loss is due to the canard causing a large flow separation on the windward fuselage region in sideslip.
Similar results have been also highlighted by Agnew et al. in [
27]. In this work, they have provided detailed understanding of the aerodynamics of a close-coupled horizontal canard in a three-lifting configuration (canard-wing-tail) for a fighter aircraft. This study has highlighted that the vortex interaction phenomenon has a beneficial effect in terms of extending the angle of attack range for the aerodynamic linearity since the vortex interaction maintains the flow attached over large areas that would be normally separated. The abrupt nature of the breakdown of this vortex system causes an adverse effect in terms of lateral-directional characteristics.
However, it is worth to underline that the last two works considering military applications are very far from the passenger aircraft herein considered. It is also true that very poor data are available concerning a three-lifting surfaces configuration for a high-capacity passenger aircraft. The innovation of this work is properly intended in this direction. The aerodynamics of this kind of a three-lifting surfaces aircraft are such that only high-fidelity investigations could lead to a deep comprehension of the above-mentioned interactions phenomena, especially when the vertical separation among the lifting surfaces is small. The aerodynamic characteristics relevant to the static stability of a three-lifting surface turboprop aircraft are investigated and discussed. The results of this paper enhance the comprehension of crucial aspects in terms of stability and aerodynamic interference among aircraft components for this kind of innovative turboprop configuration.
The rest of this paper is organized as follows.
Section 2 describes the experimental apparatus, the wind tunnel test setup, and the procedures used to derive the key aerodynamic characteristics of interest.
Section 3 shows the experimental results of the first wind tunnel test campaign, highlighting all issues introduced by the canard wake interference on the aircraft stability characteristics. A short discussion about the evolution from the first to the second design loop is also made.
Section 4 gives details on the aerodynamic interference effects on the last aircraft configuration, with a focus on the evaluation of downwash gradients. Here, it is discussed how the longitudinal and directional stability change with the canard. Conclusions are drawn in
Section 5.
3. Design Evolution
The design loop 1 configuration has been shown in
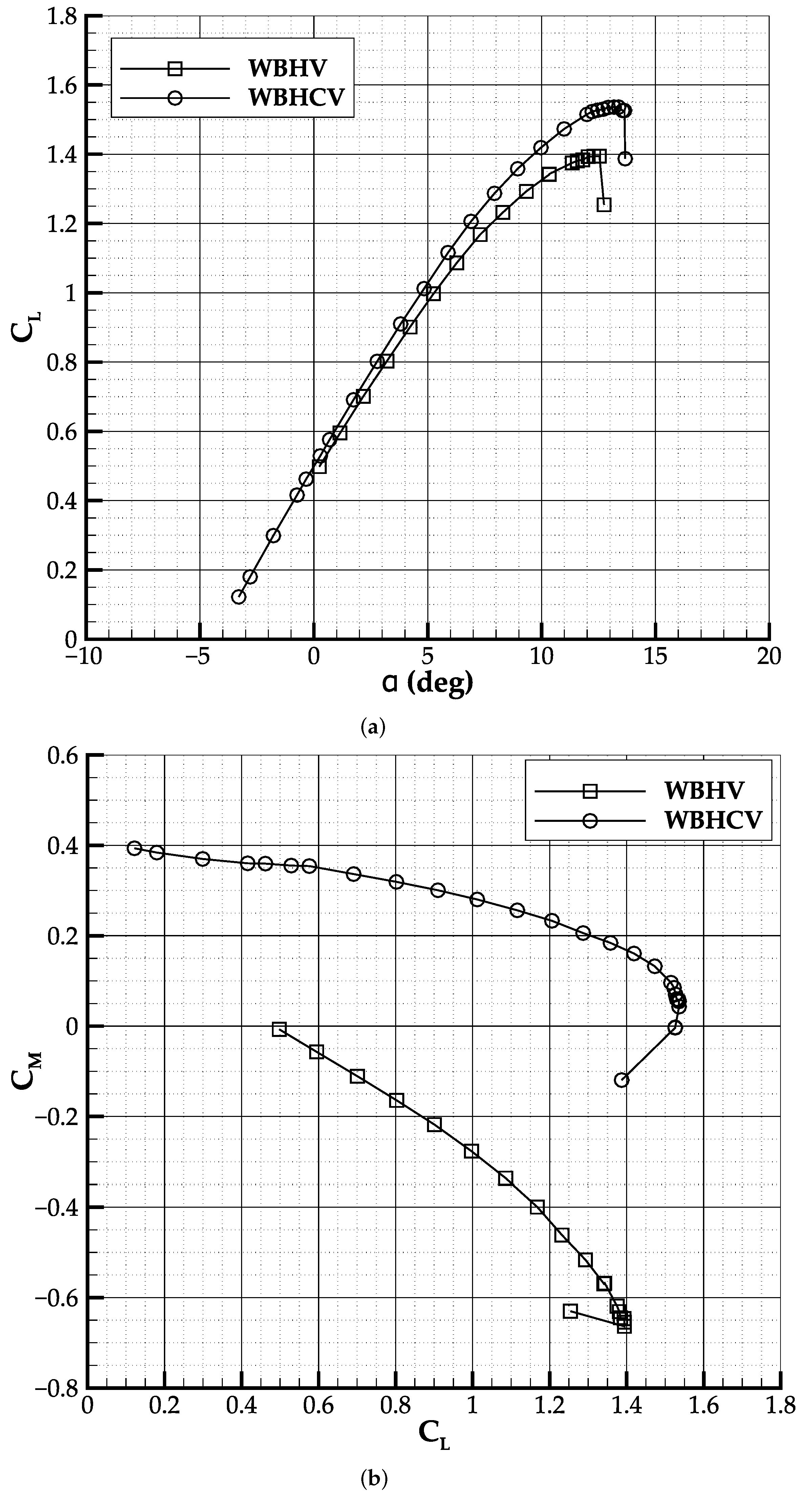
Figure 1. Wind tunnel data highlighted unsatisfactory static stability characteristics, leading to a design review of the canard position and of the empennage layout. In fact, the interaction of the wing and canard wakes was such to provide a neutral longitudinal stability at low lift coefficients, with a tendency to instability at moderate lift coefficients.
To keep the aircraft naturally stable in pitch, it was decided to increase the vertical stagger between the canard and the wing. By design constraint imposed by the IRON project leader, the only way to purse this was to shift the canard as high as possible. This shift was about 8.5% of the fuselage maximum diameter, and it is shown in
Figure 5. This position is slightly above the fuselage; hence, an additional fairing was provided. At the same time, to counteract the longitudinal stability reduction introduced by the canard downwash and its wake at low attitude angles, the horizontal tailplane dihedral angle was reduced from 15° to 5.5°, increasing its planform area. The comparison between the main geometric characteristics is shown in
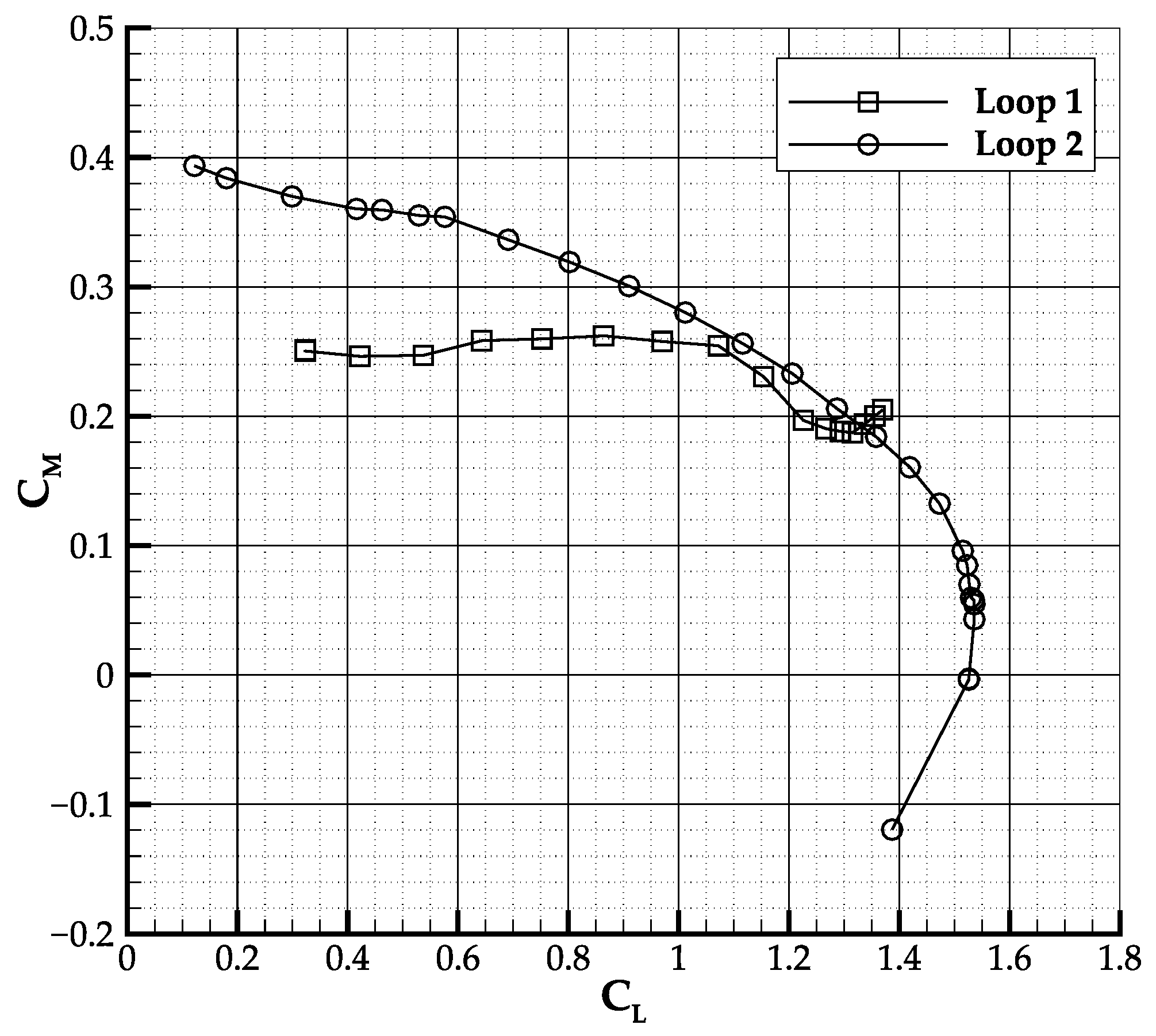
Table 5. The effect of canard re-positioning and horizontal tailplane dihedral change on the pitching moment coefficient is shown in
Figure 6. The increased longitudinal stability is evident, and the stability derivative in the range of lift coefficient from 0.5 up to 1.0 changes from +0.011 (unstable) to −0.16 (stable).
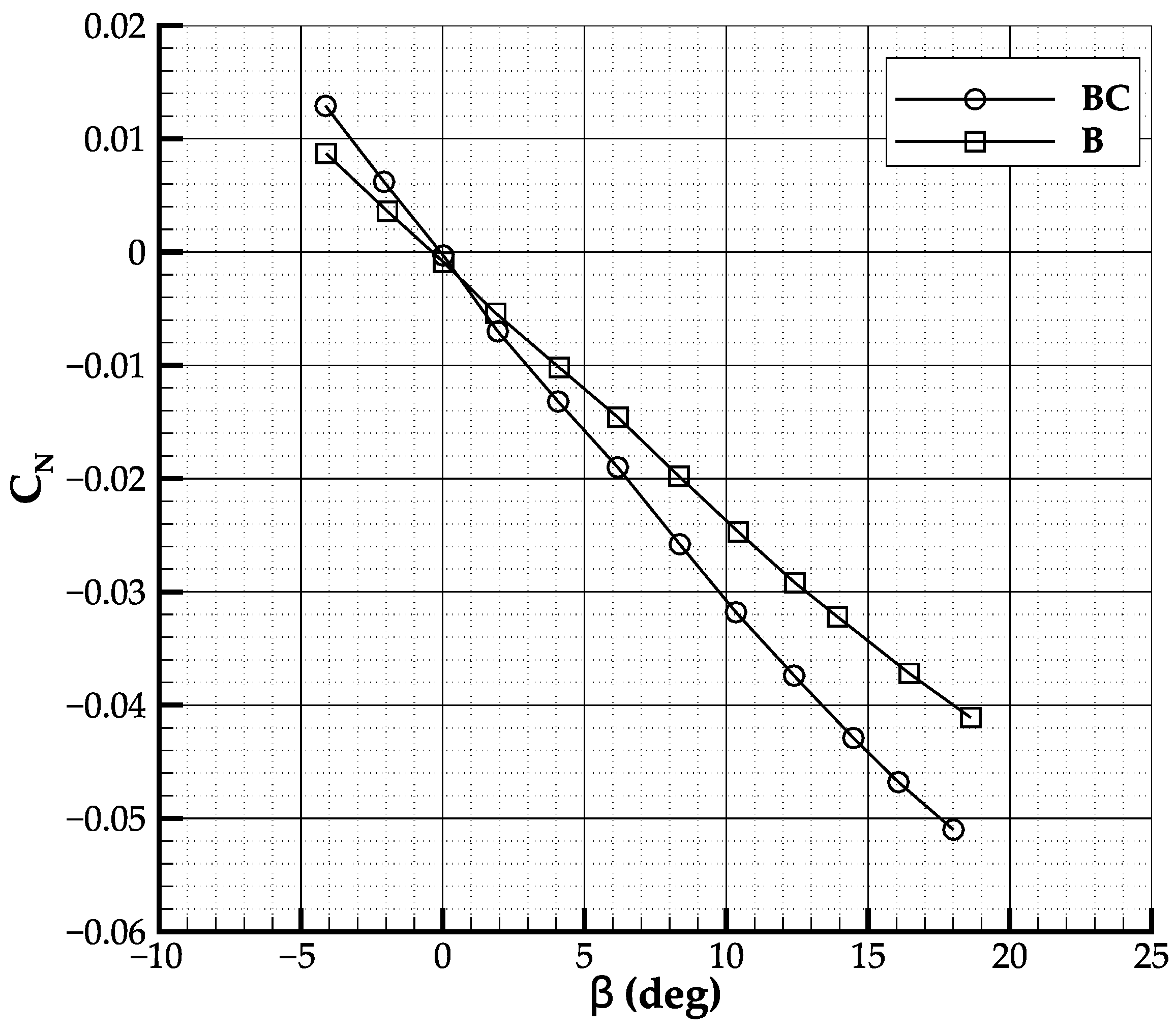
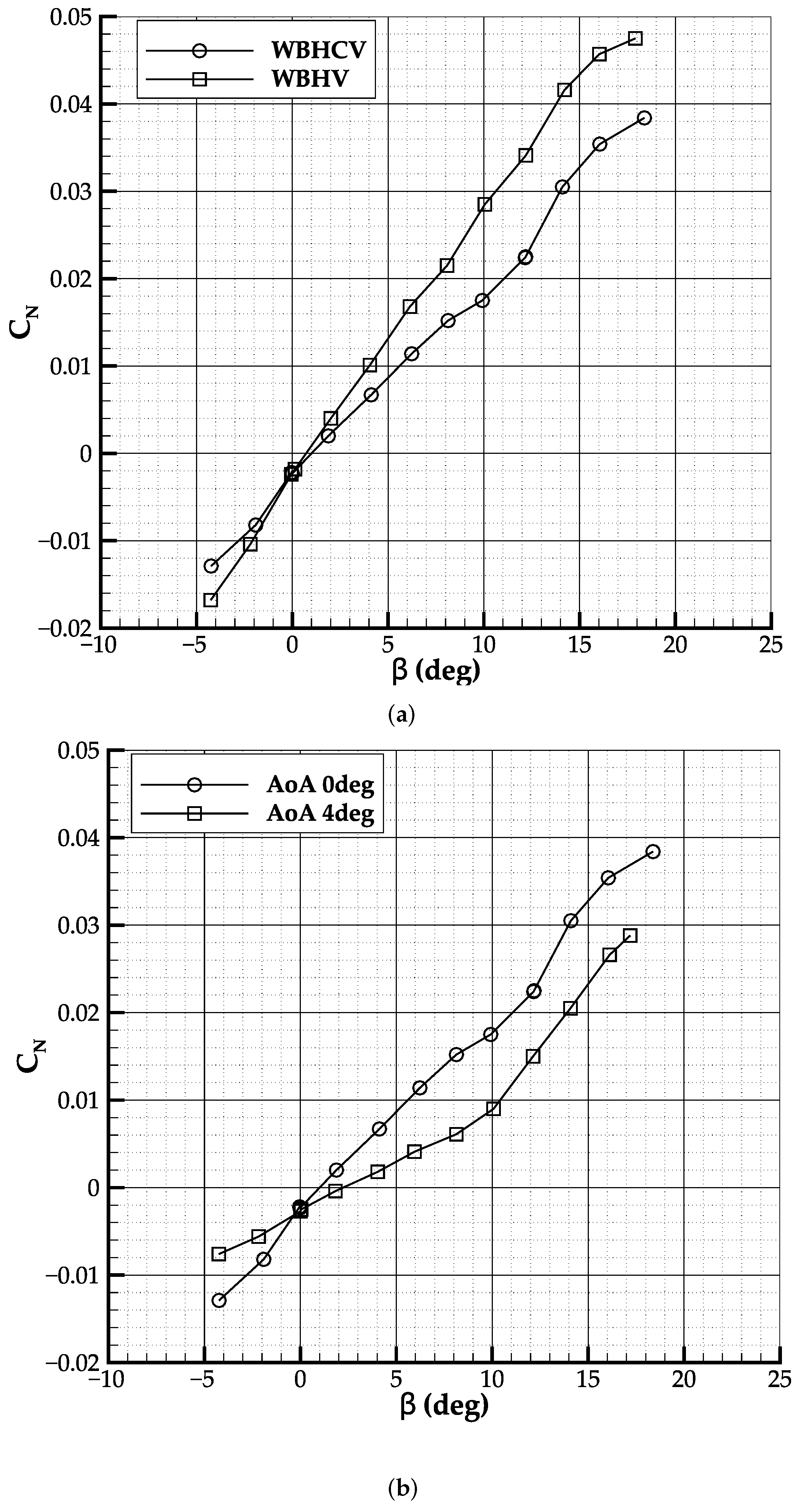
As concerns the sideslip, the application of wool yarns on the canard has shown that its tip vortex interacts with the vertical stabilizer at low and moderate angles of sideslip. As the sideslip angle increases, the tip vortex generated by the canard approaches and leaps over the vertical tailplane, as shown in
Figure 7. From the flow visualization, it can be observed that at a low sideslip angle, the canard tip vortex is impinging the windward side of the vertical tail, reducing its capability to produce sideforce. As the sideslip angle increases, the tip vortex moves across the vertical tail, and when it reaches the leeward side, the vertical tail lifting capabilities are suddenly recovered. This latter occurs at sideslip angles higher than 10°. This is particularly detrimental for aircraft directional stability in the range 5–10° of sideslip, and it is expected to be worse at higher angles of attack. A similar phenomenon has been also observed by Agnew et al. in [
27] on a three-surfaces fighter aircraft.
To mitigate the effect of the canard tip vortex in sideslip, the vertical tailplane planform has been re-designed, see
Figure 8. The planform area has been increased by 6%, a taper ratio of 0.35 has been introduced, and the sweep angle at half-chord has been lowered. These modifications increase the lift curve slope of the vertical tailplane [
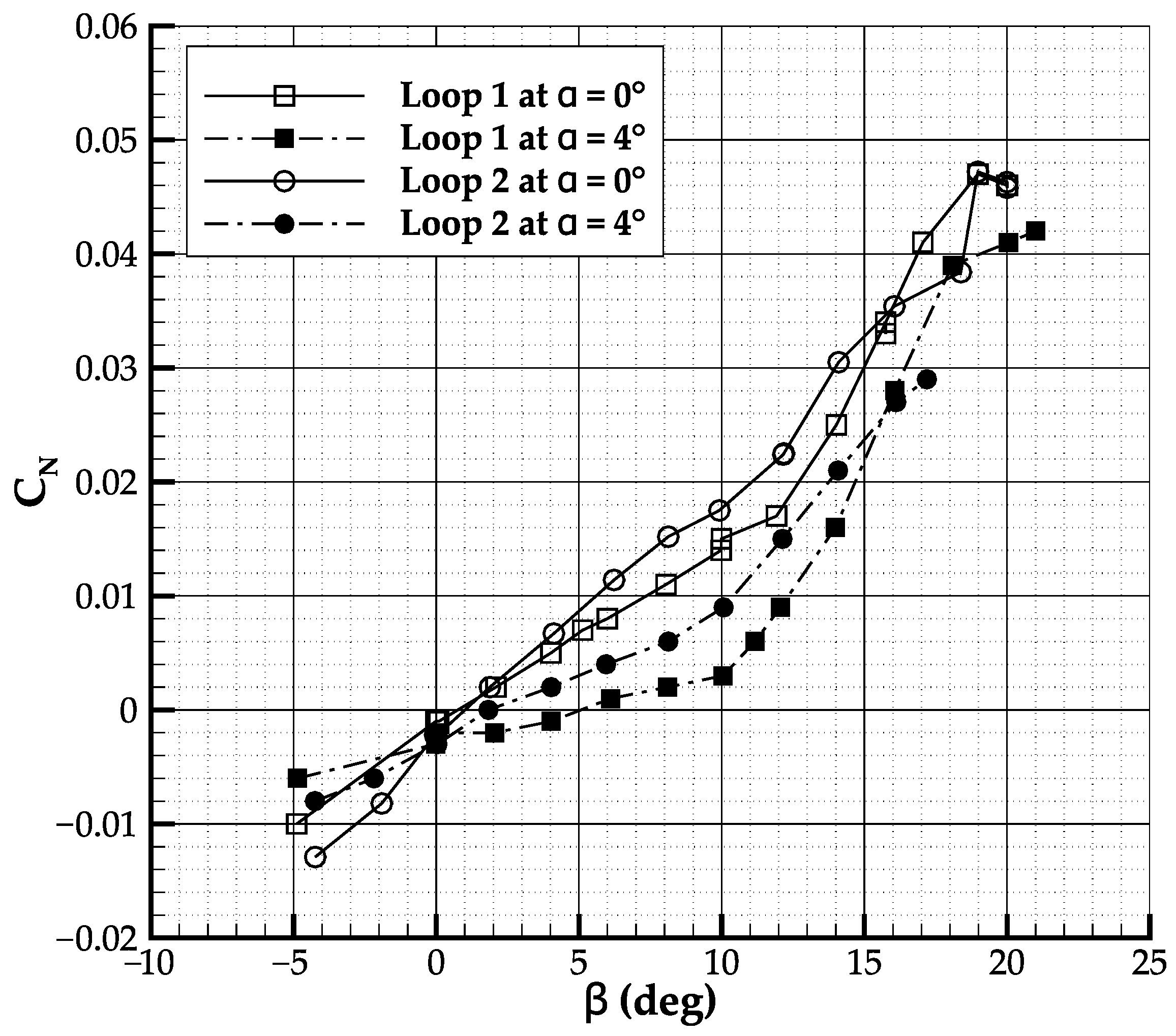
32] The actual configuration is much more similar to the vertical stabilizer of a jet aircraft than the one of a conventional turboprop. This has improved the directional stability characteristics as shown in
Figure 9, where at
the sideslip stability derivative about
changes from
deg
−1 to
deg
−1.
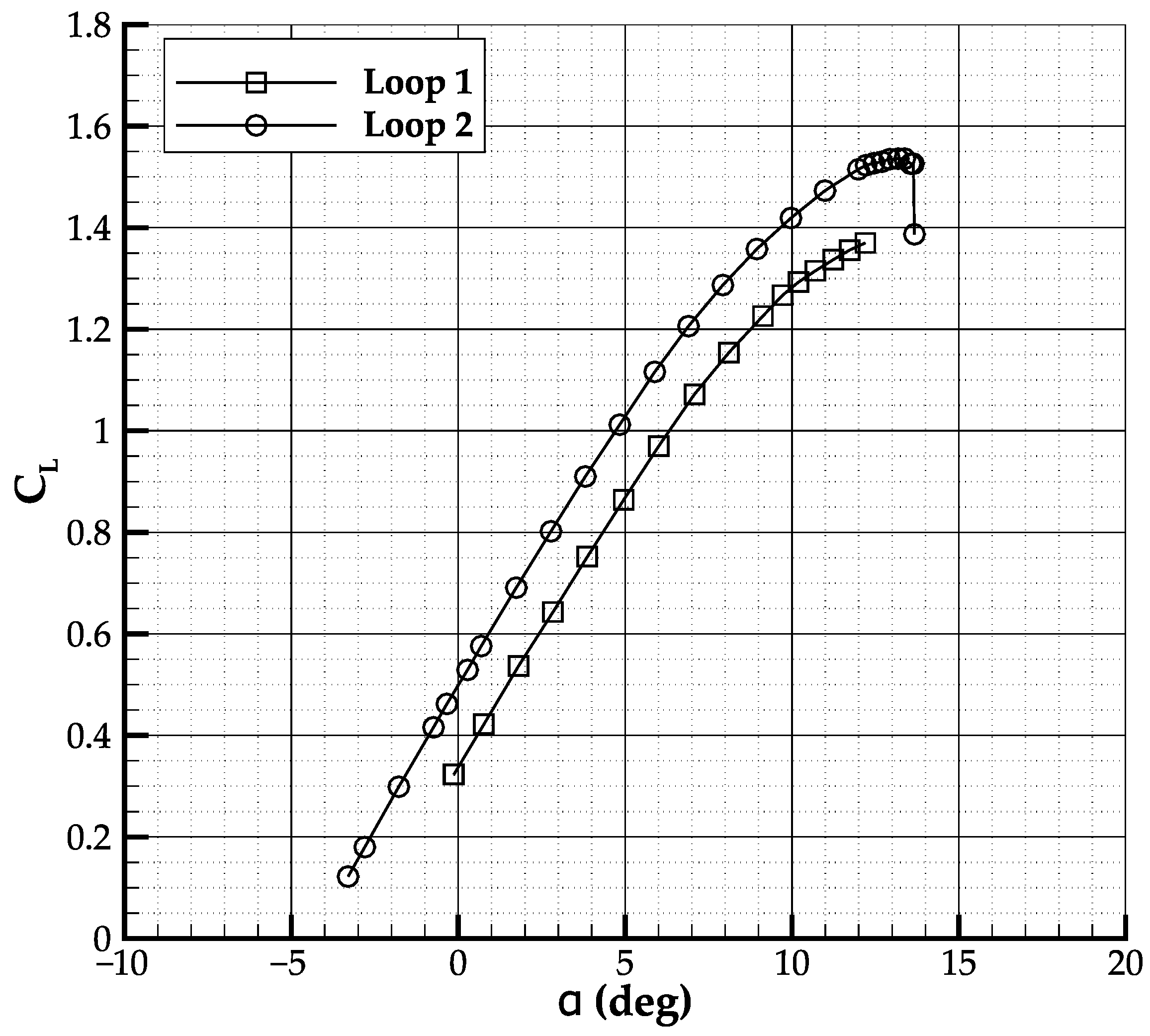
Finally, a non-critical change was also made on the wing root incidence angle and fairing [
33], which shifted up the lift curve, achieving an increase of
of 0.2, as shown in
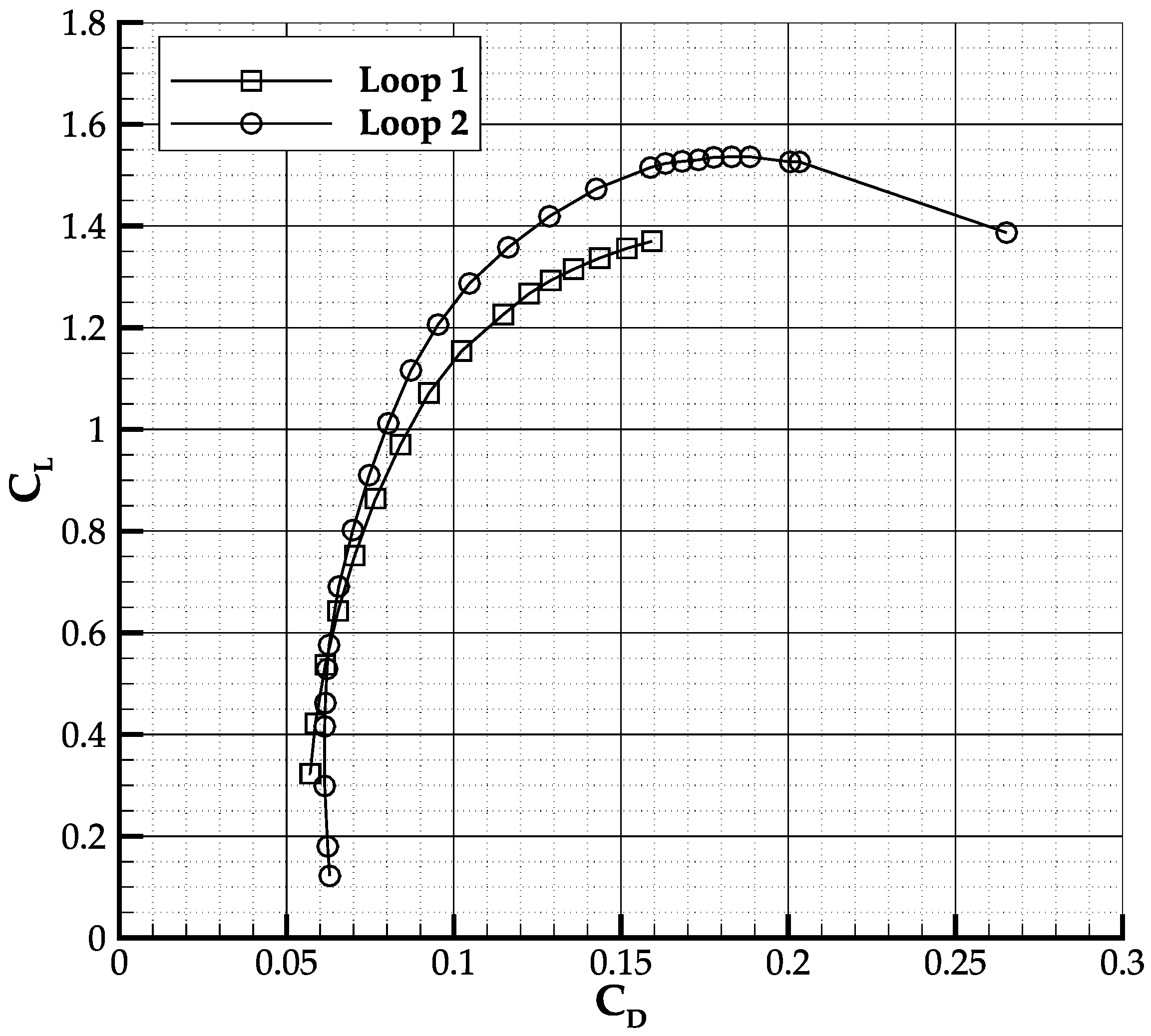
Figure 10. As concerns the drag polars shown in
Figure 11, it is here remarked that the drag coefficient values attained in low Reynolds wind tunnels are usually higher than those in full-scale conditions. Nonetheless, the maximum aerodynamic efficiency achieved by the test article is about 13. The main changes in aerodynamic coefficients, efficiency, and stability derivatives are resumed in
Table 6.
5. Conclusions
This paper dealt with the experimental assessment of the aerodynamic characteristics of an innovative high-capacity turboprop aircraft, a three-lifting surfaces configuration with rear-engines installation. It is believed that such innovative configuration—capable of transporting 130 passengers—could mitigate the pollutant emissions impact of the aircraft, remaining competitive with respect to short- and medium-haul regional jets. Indeed, both aircraft manufacturers and airlines foresee that the 100–149 seat aircraft segment will experience major fleet transformation with the entry-into-service of new clean-sheet aircraft designs powered by new-technology engines, especially with regard to the Asian and North-American markets.
Because of the inherent complexity of the three-lifting surfaces configuration, some aerodynamic interference issues were not anticipated in the preliminary design phase and were highlighted only during the first wind tunnel test campaign. In fact, the first test article—output of the design loop 1 process—provided unsatisfactory longitudinal and directional stability characteristics. After re-designing some of the lifting surfaces, a second test campaign was performed on the updated model. On this last configuration—output of the design loop 2 process—the SSM of the complete aircraft is 7.8% MAC, ensuring that the aircraft is longitudinally stable, even if the canard still exhibits a detrimental effect on both longitudinal and directional stability.
Once the static stability issues were solved, the focus of the tests moved on the above mentioned aerodynamic interference effects. In particular, most of the experimental investigations on the updated model were performed with the aim to detail how the combined downwash coming from both canard and wing, together with their wakes, affect the tail aerodynamics and consequently the aircraft static stability. Several configurations were tested in the wind tunnel to investigate the mutual effects among the aircraft components (wing, fuselage, tail, and canard) in both longitudinal and directional motions.
While tests on configurations without canard showed a larger SSM, no effective benefit could be inferred. In fact, if the innovative large turboprop were to be designed with a conventional configuration—wing and aft tail—it would have a completely different layout: the wing would have a larger area, and it would be placed more forward, while the horizontal tail would be larger to face a completely different center of gravity excursion range. Therefore, the curves relative to the canard-off configurations presented in the paper represent only a partial result that is useful to break down the contributions to downwash. Furthermore, tests confirmed that updated design achieves a higher maximum lift coefficient, splitting the lift force among the three lifting surfaces.
As concerns directional stability, wind tunnel tests have highlighted the detrimental effects of the canard on the vertical tailplane capability of generating sideforce. The canard tip vortex moves across the windward and the leeward side of the empennage, introducing non-linearity to the directional response of the aircraft, even at moderate angles of sideslip. The re-design of the vertical tailplane has mitigated but not canceled this effect.
In conclusion, this paper has provided a deep insight into the aerodynamic interference effects and stability derivatives on a three-lifting surfaces regional-transport aircraft, which is scarcely found in literature. The initial wind tunnel tests have highlighted insufficient stability margins for the aircraft. Despite all the aerodynamic issues and design constraints, the authors managed to solve the most critical problems, re-designed some of the aerodynamic surfaces, and proved the final aircraft to be statically stable.
Designers and aerodynamicists may exploit the high-fidelity data from this paper to check their analyses on a similar configuration, which are scarcely found in the literature, at least regarding trends on aerodynamic coefficients and stability derivatives.