Effect Mechanism and Performance Evaluation of Flange Contact Thermal Resistance in an Aero-Engine
Abstract
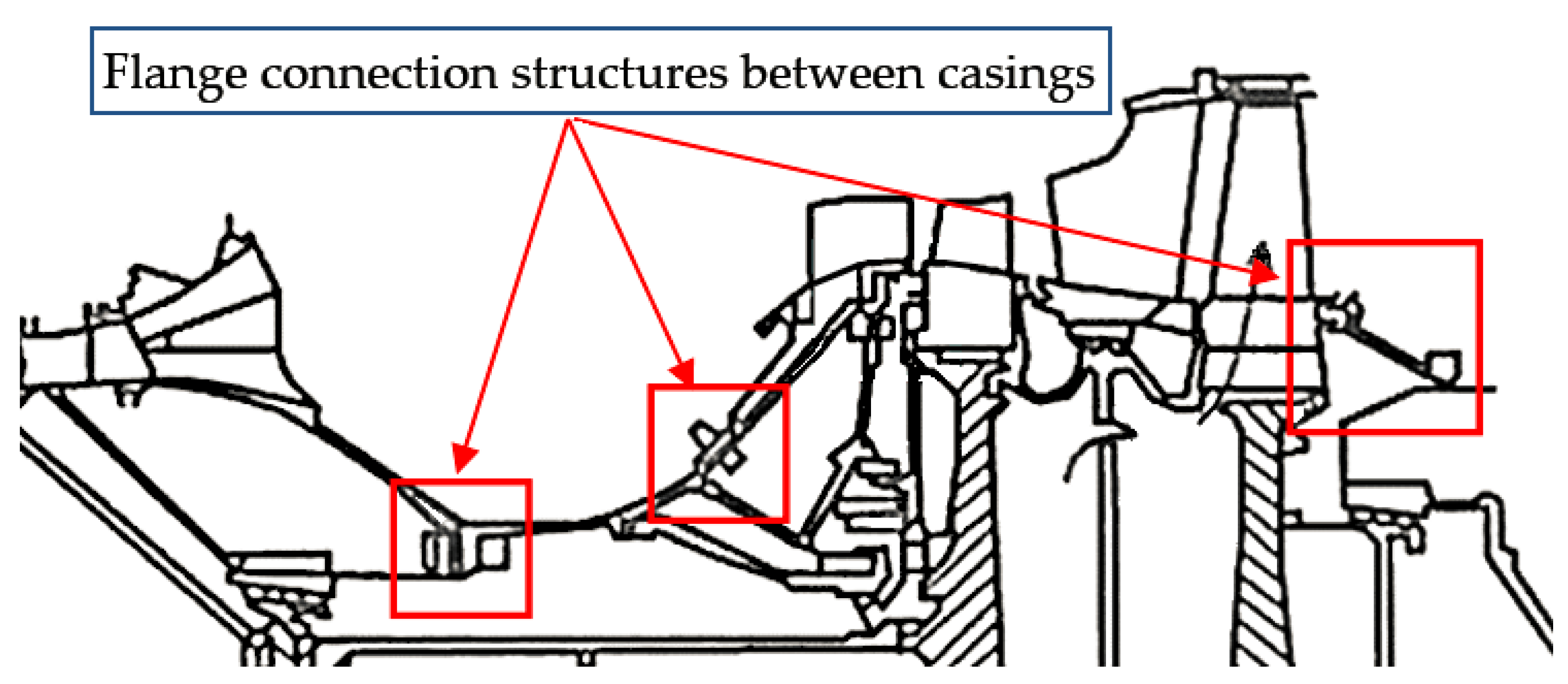
:1. Introduction
2. The Measurement Method of Contact Thermal Resistance
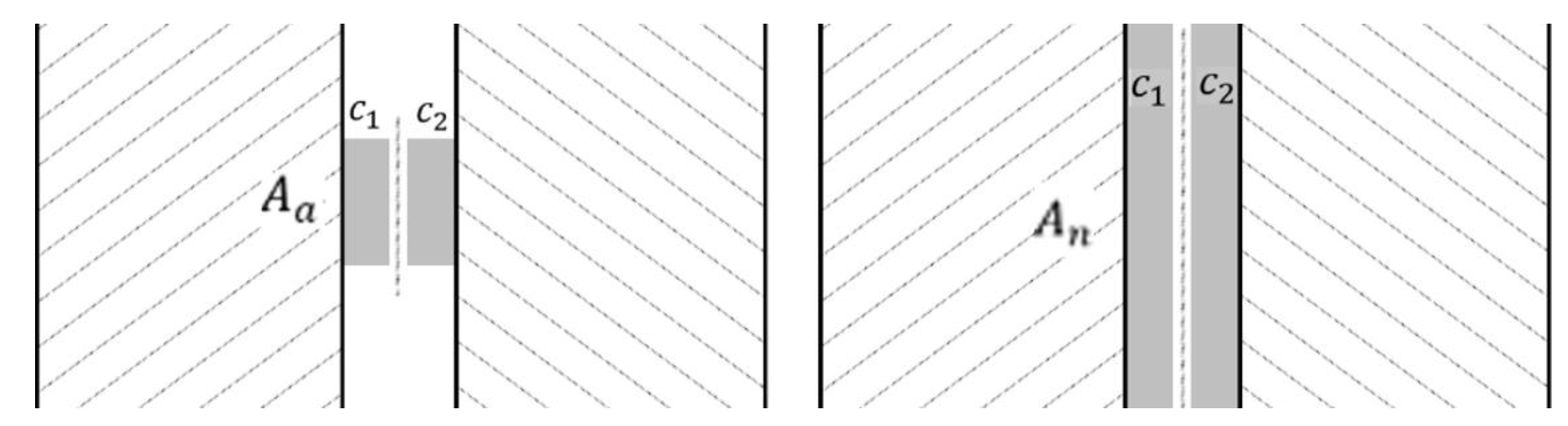
2.1. Mechanics Principles of Contact Thermal Resistance
- (a)
- The contact between the micro-convex body is elastic, i.e., the problem is the Hertz contact problem, and the radius of curvature at the contact point is the same;
- (b)
- There is no heat flux loss during the contact process; all heat flux is conducted through the contact between solids;
- (c)
- The physical parameters of the contact body remain unchanged during the contact heat transfer process;
- (d)
- The contact points are under the same interface temperature, and there is no heat exchange between them.
2.2. Calculation of Contact Thermal Resistance
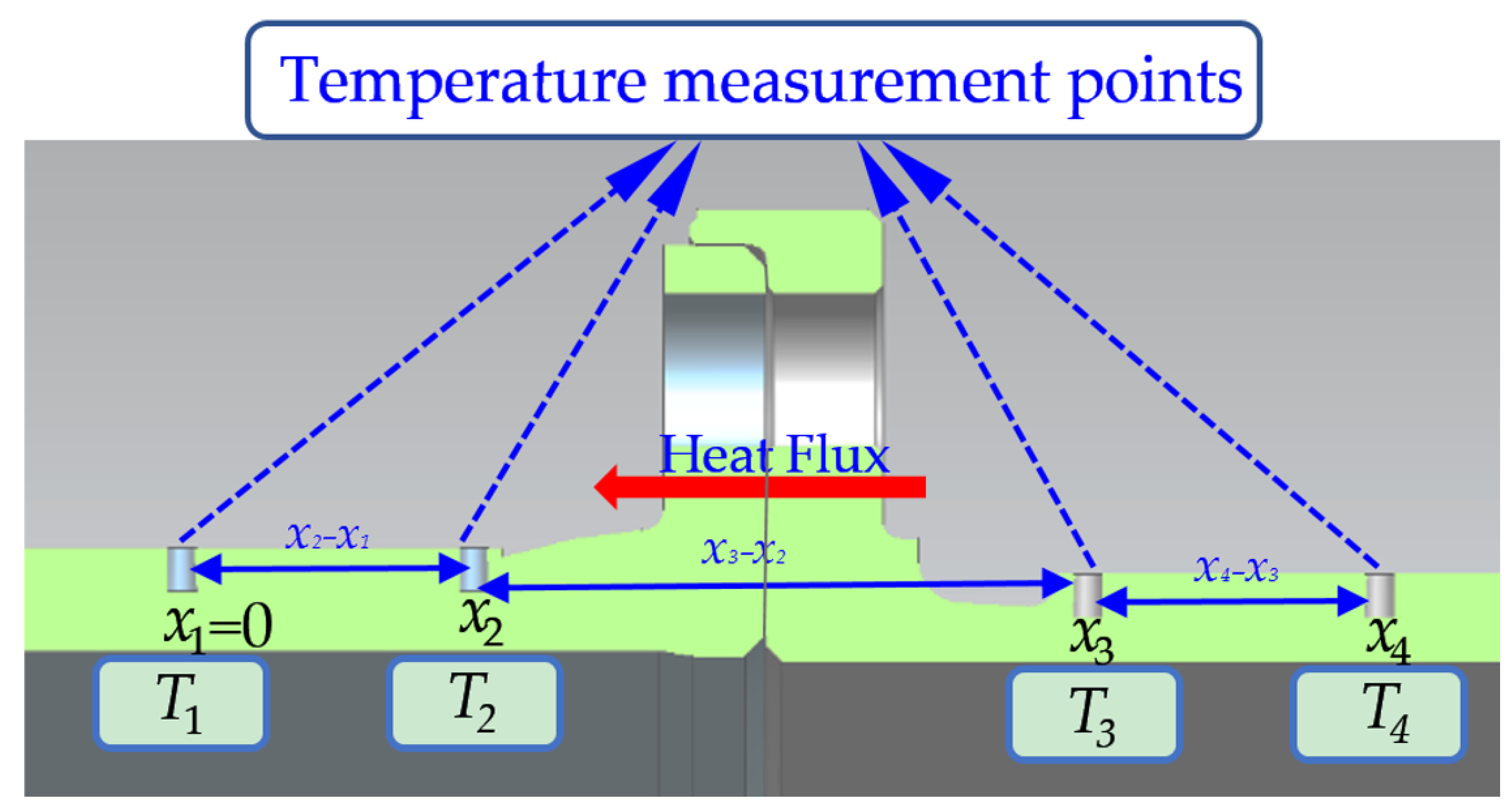
2.3. Principles of Contact Thermal Resistance Measurement
3. Experimental Rig and Method
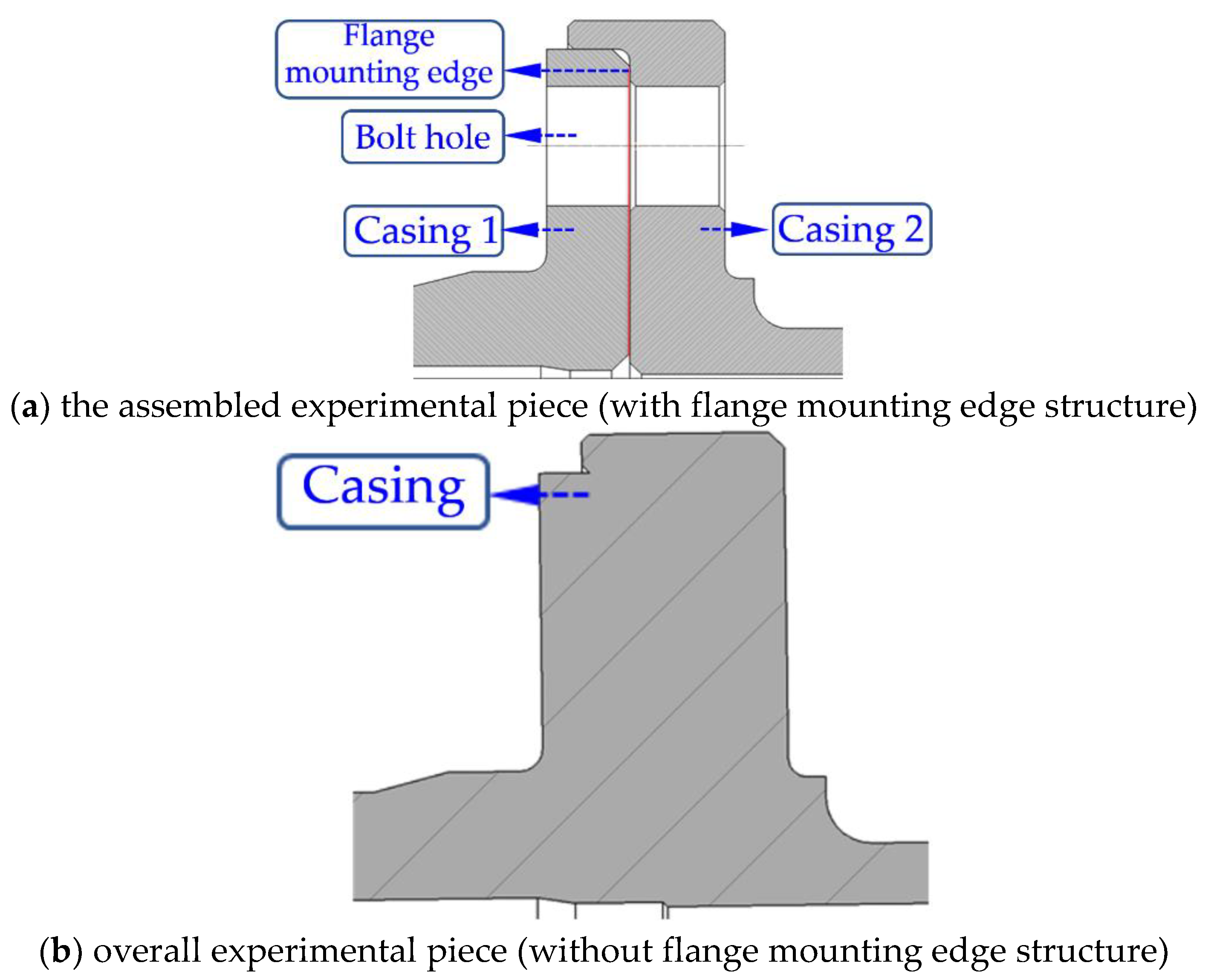
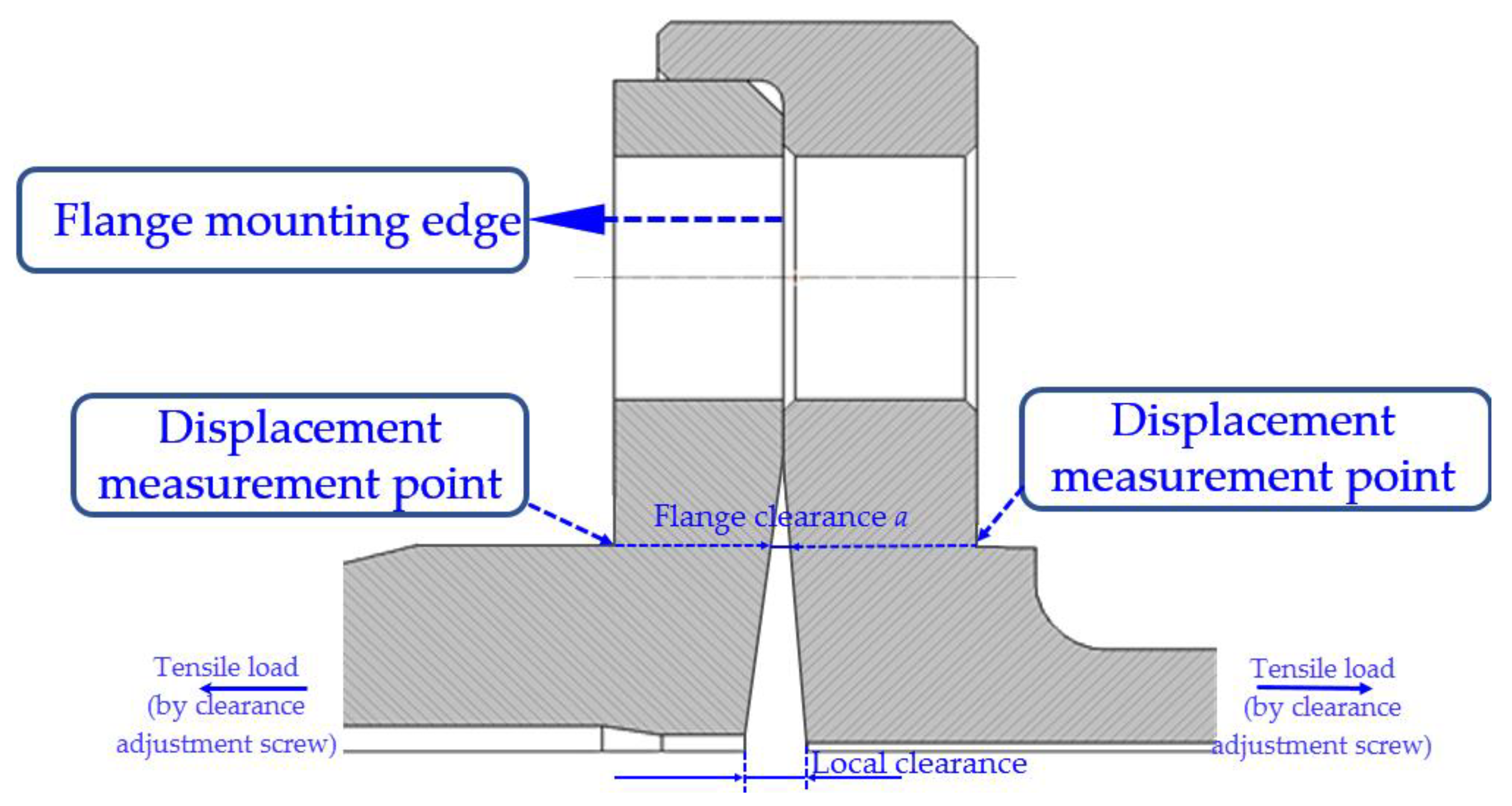
3.1. Research Object and Experimental System
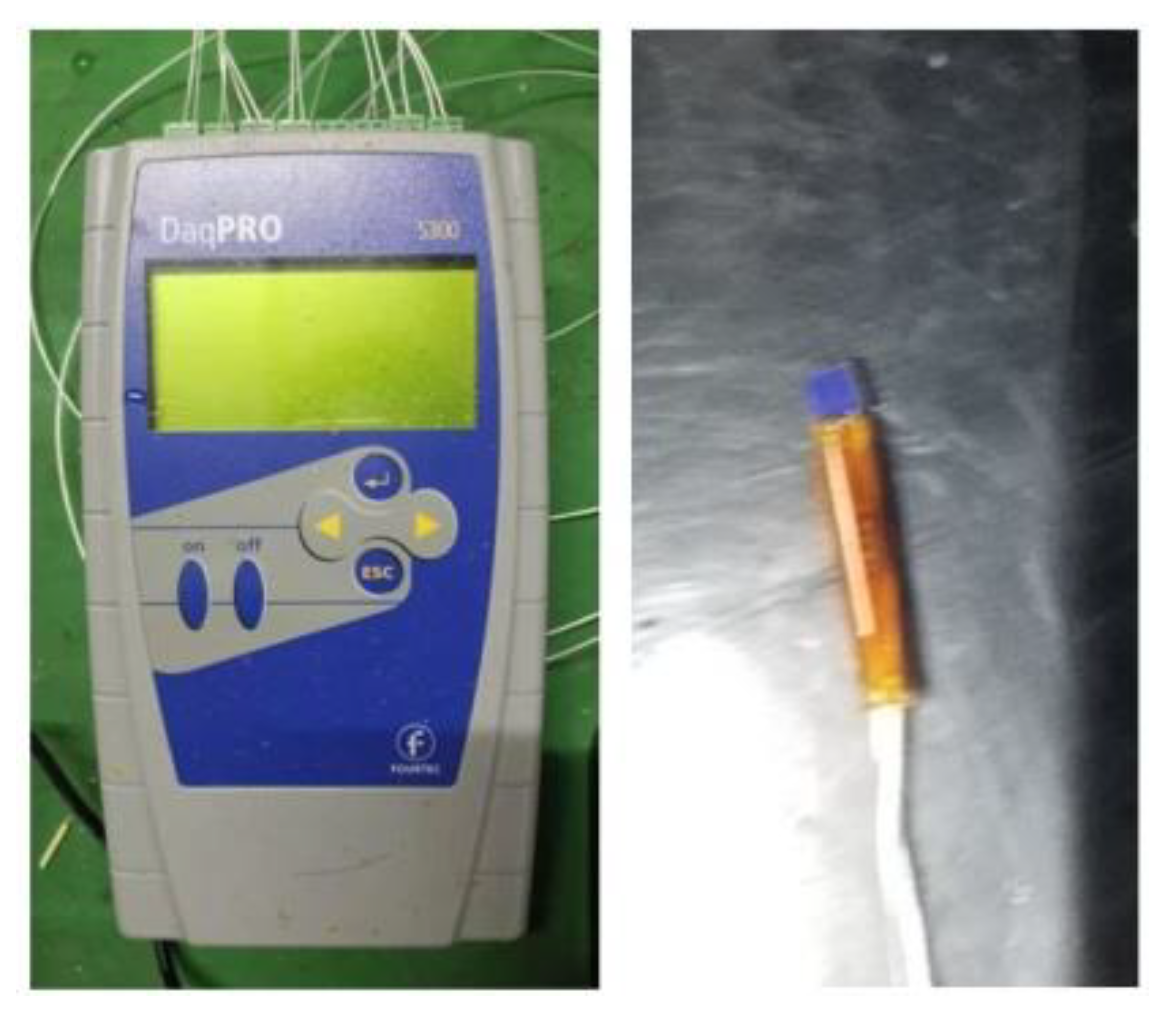
3.2. Experimental Parameter Measurement
3.3. Experimental Conditions
3.4. Error Analysis
4. Results and Analysis
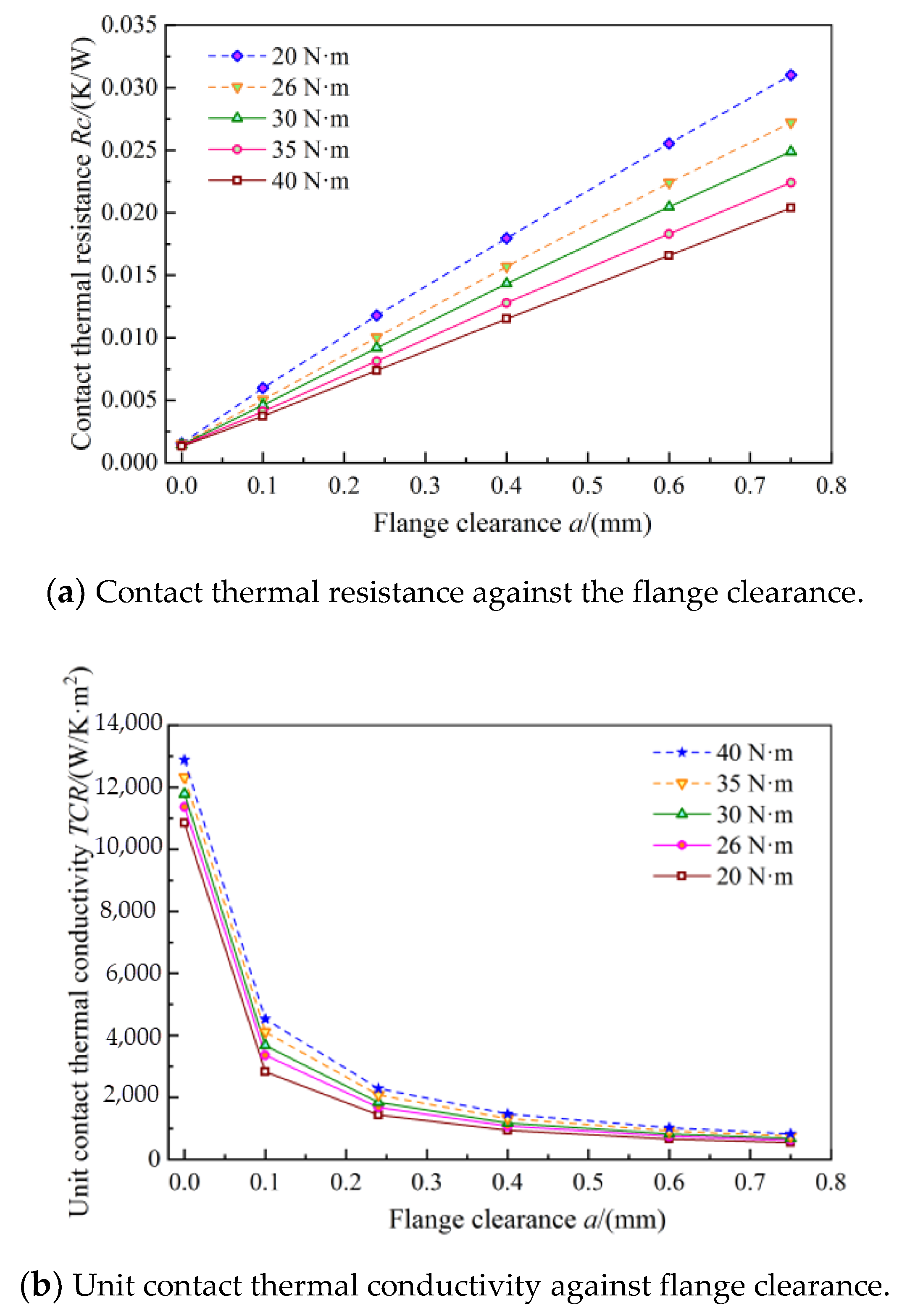
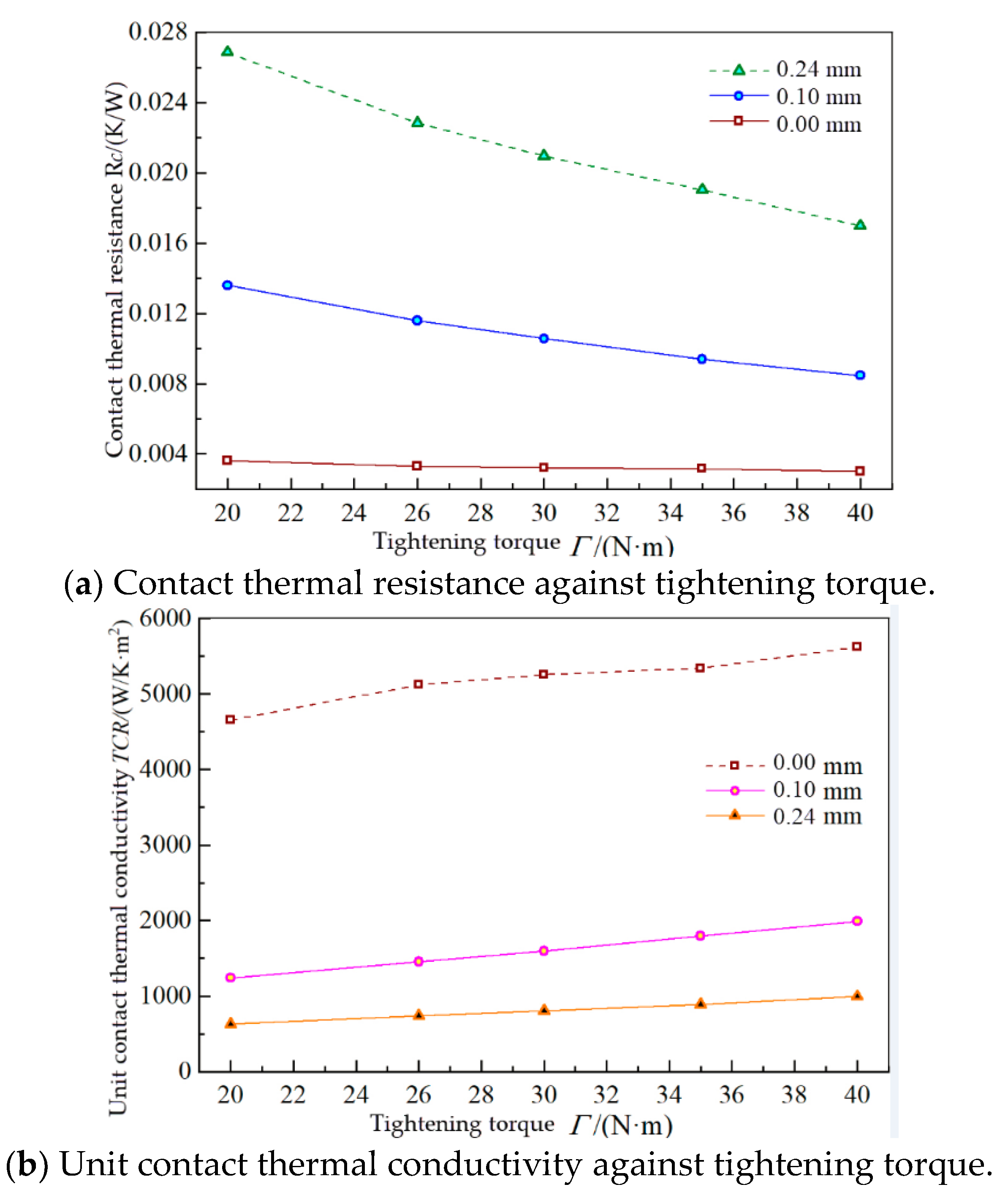
4.1. Analysis of Contact Thermal Resistance Characteristics of Q345R–Q345R Materials
4.2. Conversion of Experimental Data and Actual Unit Contact Thermal Conductivity
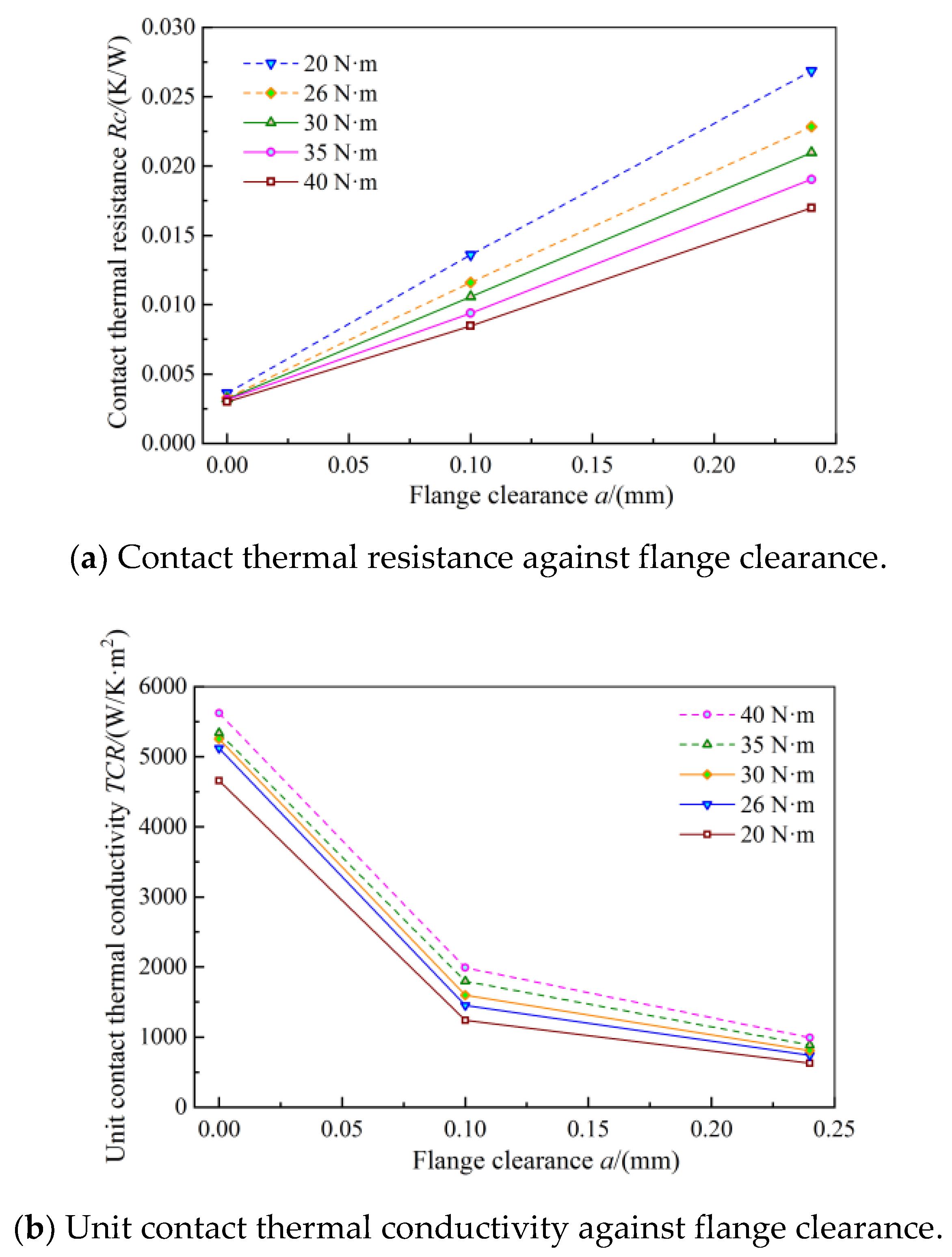
4.3. Characteristics Analysis of Contact Thermal Resistance for the Stainless Steel–Q345R Material
4.4. Verification of the Material Independence of the Experiment to the Unit Contact Thermal Conductivity
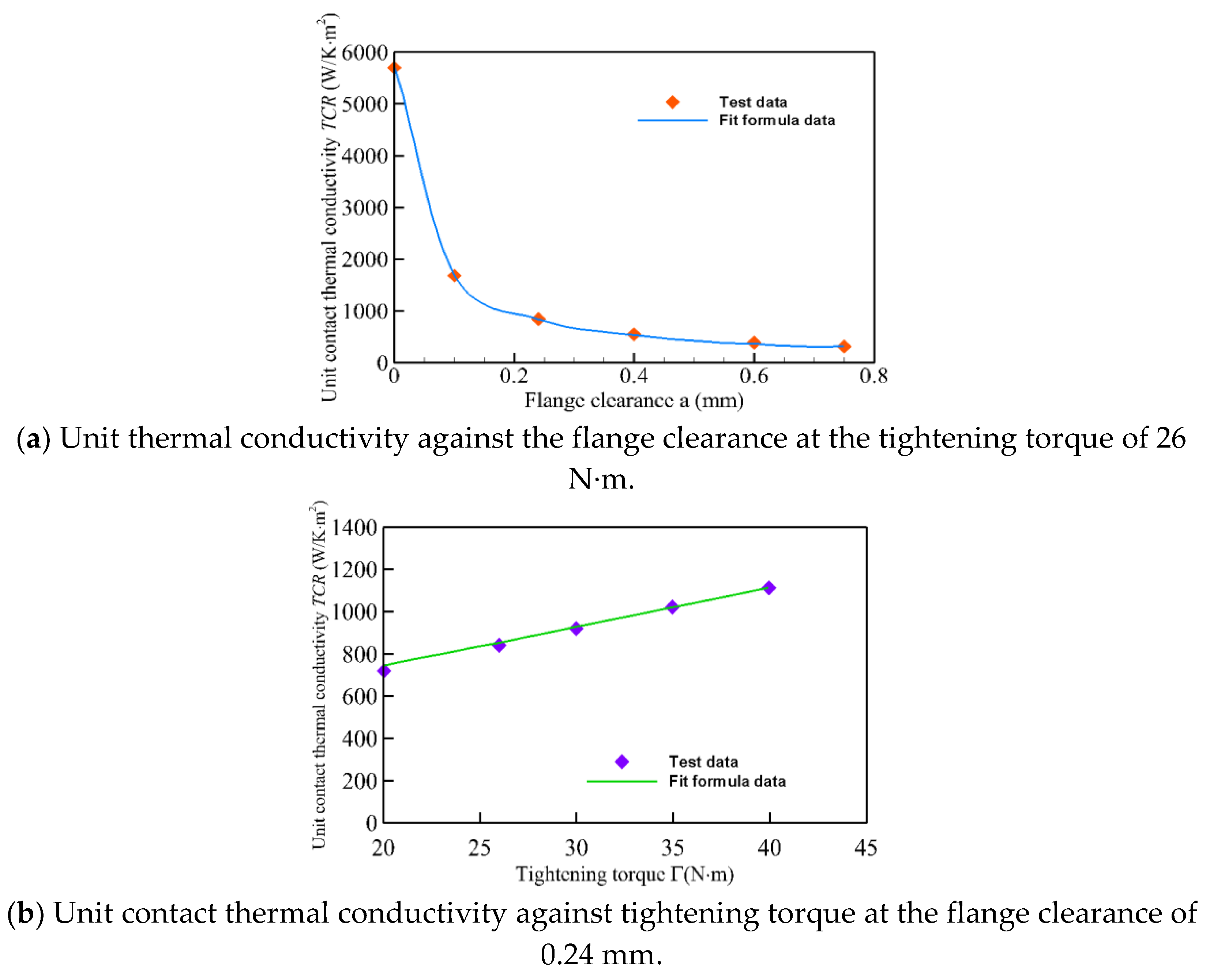
5. Prediction of Contact Thermal Conductivity for Typical Flange Mounting Edges
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lai, C. Research on Sealing Characteristics of Typical Flanged Casing Structure. Master’s Thesis, Shenyang Aerospace University, Shenyang, China, 2018. [Google Scholar]
- Mir-Haidari, S.; Behdinan, K. Nonlinear effects of bolted flange connections in aeroengine casing assemblies. Mech. Syst. Signal Process. 2022, 166, 108433. [Google Scholar] [CrossRef]
- Boeswald, M.; Link, M.; Meyer, S. Experimental and analytical investigations of non-linear cylindrical casing joints using base excitation testing. In Proceedings of the 21st IMAC Conference and Exposition 2003 (IMAC XXI), Kissimmee, FL, USA, 3–6 February 2003. [Google Scholar]
- Zang, C.; Ma, S.; Friswell, M. Finite element model updating of an assembled aero-engine casing. Topics in Model Validation and Uncertainty Quantification; Springer: Berlin/Heidelberg, Germany, 2013; pp. 199–212. [Google Scholar]
- Cao, Z.; Zhang, F.; Zhang, D.; Yu, Y.; Li, L.; Guo, X. Failure mechanisms of bolted flanges in aero-engine casings subjected to impact loading. Chin. J. Aeronaut. 2021, 34, 125–144. [Google Scholar] [CrossRef]
- Peng, H.; Liu, Z.; Huang, F. Study of elastic plastic contact of statistical rough surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 1076–1089. [Google Scholar] [CrossRef]
- Lin, A.; Liu, G.; Chen, Y.; Feng, Q.; Zhang, H. Evaluation and analysis of evaporation cooling on thermodynamic and pressure characteristics of intake air in a precooled turbine engine. Int. J. Hydrog. Energy 2021, 46, 24410–24424. [Google Scholar] [CrossRef]
- Liu, G.; Lei, Z.; Lin, A.; Chen, Y.; Feng, Q. Effect of pre-swirl nozzle closure modes on unsteady flow and heat transfer characteristics in a pre-swirl system of aero-engine. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021. [Google Scholar] [CrossRef]
- Liu, G.; Wang, X.; Gong, W.; Lin, A. Prediction of the sealing flow effect on the temperature drop characteristics of a pre-swirl system in an aero-engine. Appl. Therm. Eng. 2021, 189, 116717. [Google Scholar] [CrossRef]
- Wang, A.; Zhao, J. Review of prediction for thermal contact resistance. Sci. China Technol. Sci. 2011, 41, 545–556. (In Chinese) [Google Scholar] [CrossRef]
- Fukuoka, T.; Nomura, M.; Shino, K. Analysis of heat flow around bolted joints and variations of axial bolt force. In Proceedings of theASME 2007 Pressure Vessels and Piping Conference, ASME Paper PVP2007-26383. San Antonio, TX, USA, 22–26 July 2007; ASME: New York, NY. [Google Scholar]
- Lin, A.; Liu, G.; Wang, X.; Feng, Q. Comprehensive evaluations on performance and energy consumption of pre-swirl rotor–stator system in gas turbine engines. Energy Convers. Manag. 2021, 244, 114440. [Google Scholar] [CrossRef]
- Liu, G.; Gong, W.; Wu, H.; Pang, L.; Lin, A. Theoretical and experimental evaluation of temperature drop and power consumption in a cover-plate pre-swirl system for gas turbine cooling. Case Stud. Therm. Eng. 2021, 27, 101221. [Google Scholar] [CrossRef]
- Fukuoka, T. Finite element analysis of the thermal and mechanical behaviors of a bolted joint. J. Press. Vessel Technol. 2005, 127, 402–407. [Google Scholar] [CrossRef]
- Beaudoin, M.; Behdinan, K. Analytical lump model for the nonlinear dynamic response of bolted flanges in aero-engine casings. Mech. Syst. Signal Process. 2019, 115, 14–28. [Google Scholar] [CrossRef]
- Joseph, R.; Kumar, N.; Kumar, S. Effect of interstitial compounds in controlling thermal contact conductance across pressed joints at cryogenic temperature and low contact pressure. Appl. Therm. Eng. 2021, 194, 117073. [Google Scholar] [CrossRef]
- Greenwood, J.; Williamson, J. Contact of nominally Flat Surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Yovanovich, M. Four decades of research on thermal contact, clearance, and joint resistance in microelectronics. IEEE Trans. Compon. Packag. Technol. 2005, 28, 182–206. [Google Scholar] [CrossRef]
- Yovanovich, M.; Culham, J.; Teertstra, P. Calculating interface resistance. Electron. Cool. 1997, 3, 24–29. [Google Scholar]
- Yuncu, H. Thermal contact conductance of nominaly flat surface. Heat Mass Transf. 2006, 43, 1–5. [Google Scholar] [CrossRef]
- Bahrami, M.; Yovanovich, M.; Culham, J. Thermal joint resistances of conforming rough surfaces with gas filled caps. J. Thermophys. Heat Transf. 2004, 18, 318–325. [Google Scholar] [CrossRef]
- Sridhar, M.; Yovanovich, M. Review of elastic and plastic contact conductance models: Comparison with experiment. J. Thermophys. Heat Transf. 1994, 8, 633–640. [Google Scholar] [CrossRef]
- Madhusudana, C.; Fletcher, L. Contact heat transfer-The last decade. AIAA J. 1986, 34, 510–521. [Google Scholar] [CrossRef]
- Ling, D.; Wang, F.; Zeng, F. Finite element simulation method of contact thermal resistance. Eng. Mech. 2012, 9, 375–379. [Google Scholar]
- Archard, J.F. Elastic Deformation and the laws of friction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 243, 190–205. [Google Scholar]
- Zhang, T.; Xu, L.; Xiong, W.; Zhao, L. Comparison and analysis of theoretical models in the research of thermal contact conductance. Cryog. Supercond. 1998, 26, 58–64. [Google Scholar]
- Zhao, L.; Xu, L.; Li, Z.; Sun, H. Research on the relationship between thermal contact conductance of solid interfaces and cycling load at low Temperatures. Cryog. Supercond. 2000, 28, 5l–54. [Google Scholar]






| Flange clearance a/mm | 0.00, 0.10, 0.24, 0.40, 0.60, 0.75 |
| Bolt tightening torque Γ/N·m | 20, 26, 30, 35, 40 |
| Flange Clearance mm | Tightening Torque 20 N∙m | Tightening Torque 26 N∙m | Tightening Torque 30 N∙m | Tightening Torque 35 N∙m | Tightening Torque 40 N∙m |
|---|---|---|---|---|---|
| 0.00 | 7.65 × 10−4 | 8.02 × 10−4 | 8.32 × 10−4 | 8.70 × 10−4 | 9.09 × 10−4 |
| 0.10 | 2.00 × 10−4 | 2.37 × 10−4 | 2.59 × 10−4 | 2.90 × 10−4 | 3.20 × 10−4 |
| 0.24 | 1.01 × 10−4 | 1.19 × 10−4 | 1.30 × 10−4 | 1.47 × 10−4 | 1.61 × 10−4 |
| 0.40 | 0.66 × 10−4 | 0.76 × 10−4 | 0.83 × 10−4 | 0.93 × 10−4 | 1.03 × 10−4 |
| 0.60 | 0.47 × 10−4 | 0.53 × 10−4 | 0.58 × 10−4 | 0.65 × 10−4 | 0.72 × 10−4 |
| 0.75 | 0.38 × 10−4 | 0.44 × 10−4 | 0.48 × 10−4 | 0.53 × 10−4 | 0.58 × 10−4 |
| Flange Clearance mm | Tightening Torque 20 N∙m | Tightening Torque 26 N∙m | Tightening Torque 30 N∙m | Tightening Torque 35 N∙m | Tightening Torque 40 N∙m |
|---|---|---|---|---|---|
| 0.00 | 7.35 × 10−4 | 8.08 × 10−4 | 8.29 × 10−4 | 8.42 × 10−4 | 8.87 × 10−4 |
| 0.10 | 1.96 × 10−4 | 2.29 × 10−4 | 2.52 × 10−4 | 2.83 × 10−4 | 3.14 × 10−4 |
| 0.24 | 0.99 × 10−4 | 1.16 × 10−4 | 1.27 × 10−4 | 1.40 × 10−4 | 1.57 × 10−4 |
| Flange Clearance mm | Tightening Torque 20 N∙m | Tightening Torque 26 N∙m | Tightening Torque 30 N∙m | Tightening Torque 35 N∙m | Tightening Torque 40 N∙m |
|---|---|---|---|---|---|
| 0.00 | 4.0% | 0.7% | 0.3% | 3.1% | 2.5% |
| 0.10 | 1.9% | 3.2% | 2.8% | 2.3% | 1.8% |
| 0.24 | 2.0% | 1.8% | 2.2% | 4.7% | 3.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Chen, L.; Chu, W. Effect Mechanism and Performance Evaluation of Flange Contact Thermal Resistance in an Aero-Engine. Aerospace 2022, 9, 121. https://doi.org/10.3390/aerospace9030121
Chen Y, Chen L, Chu W. Effect Mechanism and Performance Evaluation of Flange Contact Thermal Resistance in an Aero-Engine. Aerospace. 2022; 9(3):121. https://doi.org/10.3390/aerospace9030121
Chicago/Turabian StyleChen, Yan, Liyuan Chen, and Wuli Chu. 2022. "Effect Mechanism and Performance Evaluation of Flange Contact Thermal Resistance in an Aero-Engine" Aerospace 9, no. 3: 121. https://doi.org/10.3390/aerospace9030121
APA StyleChen, Y., Chen, L., & Chu, W. (2022). Effect Mechanism and Performance Evaluation of Flange Contact Thermal Resistance in an Aero-Engine. Aerospace, 9(3), 121. https://doi.org/10.3390/aerospace9030121




