Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems
Abstract
:1. Introduction
2. Demand Analysis of Electromagnetic Dampers for Shimmy Reduction Performance
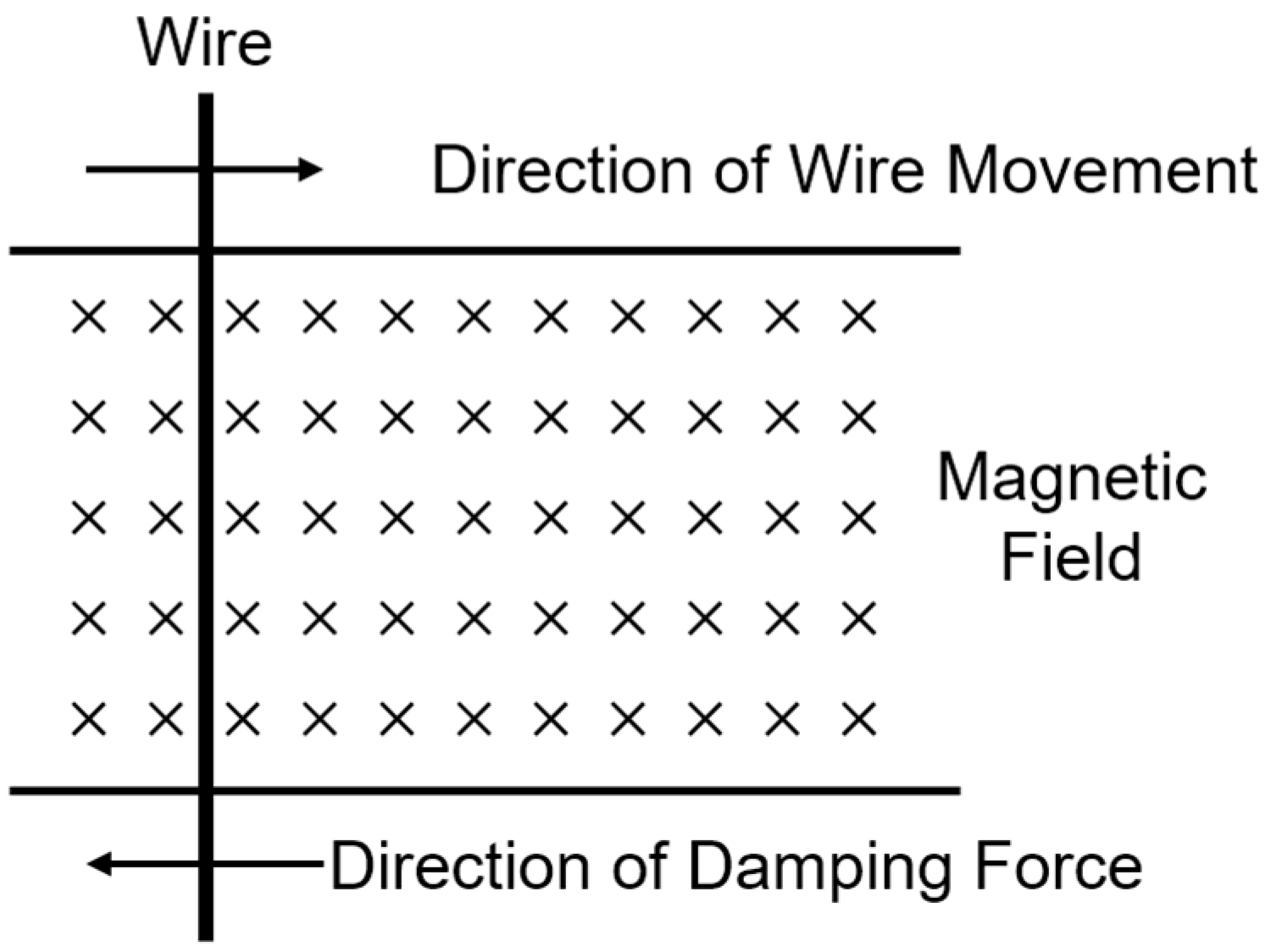
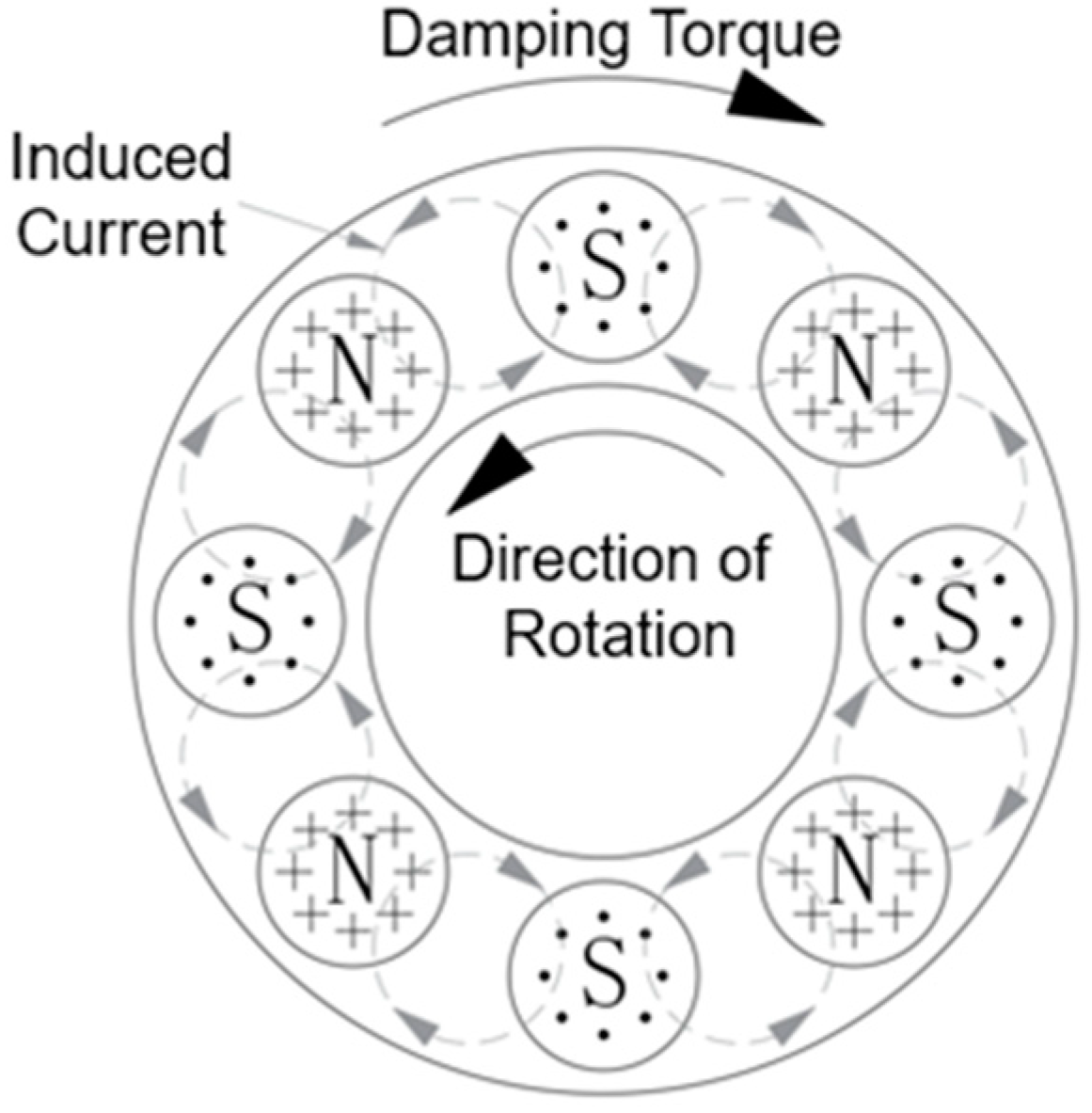
2.1. Operating Principle
2.2. Analysis of Shimmy Motion Parameters
2.3. Damping Requirements for Shimmy Reduction
3. Research on Electromagnetic Damping and Shimmy Reduction Scheme of Electrically Actuated Nose Wheel Steering Systems
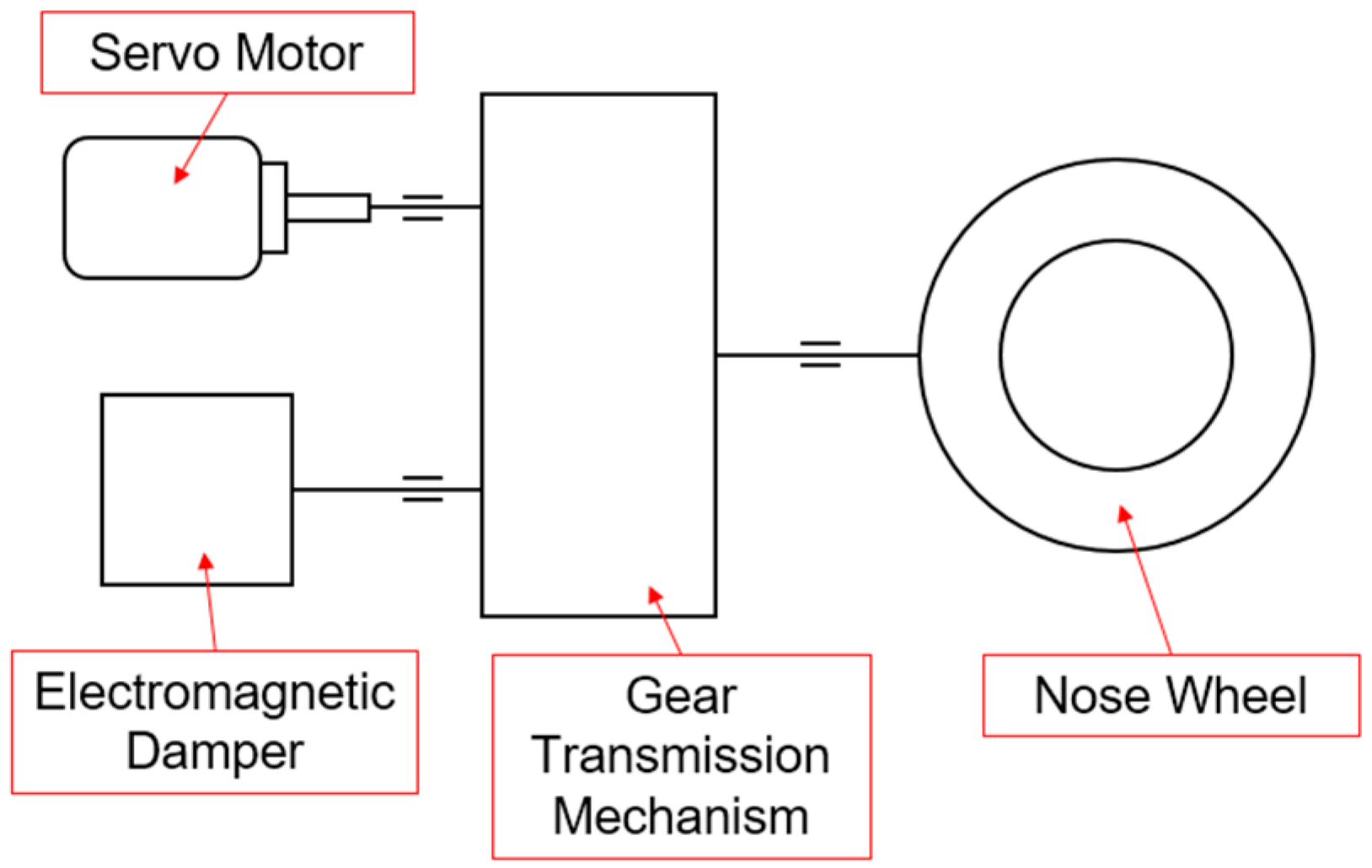
3.1. Structural Scheme Design of the Electrically Actuated Nose Wheel Steering System
3.2. Mathematical Modeling of the Electromagnetic Damper
3.2.1. Calculation of Eddy Current Skin Depth
3.2.2. Calculation of Damping Torque
3.2.3. Calculation of Damping Coefficient
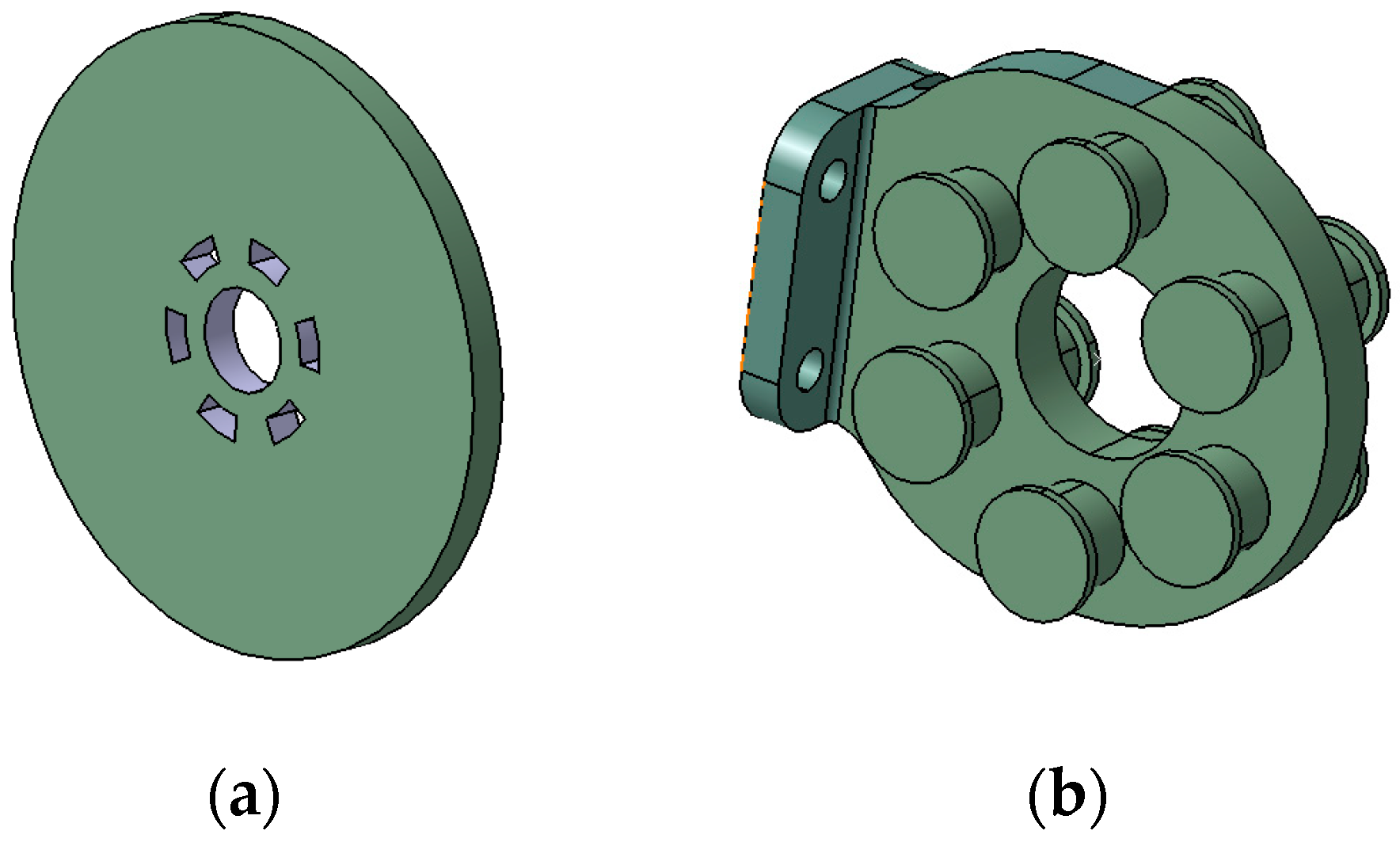
3.3. Design of the Electromagnetic Damper
4. Electromagnetic Field Simulation of the Electromagnetic Damper
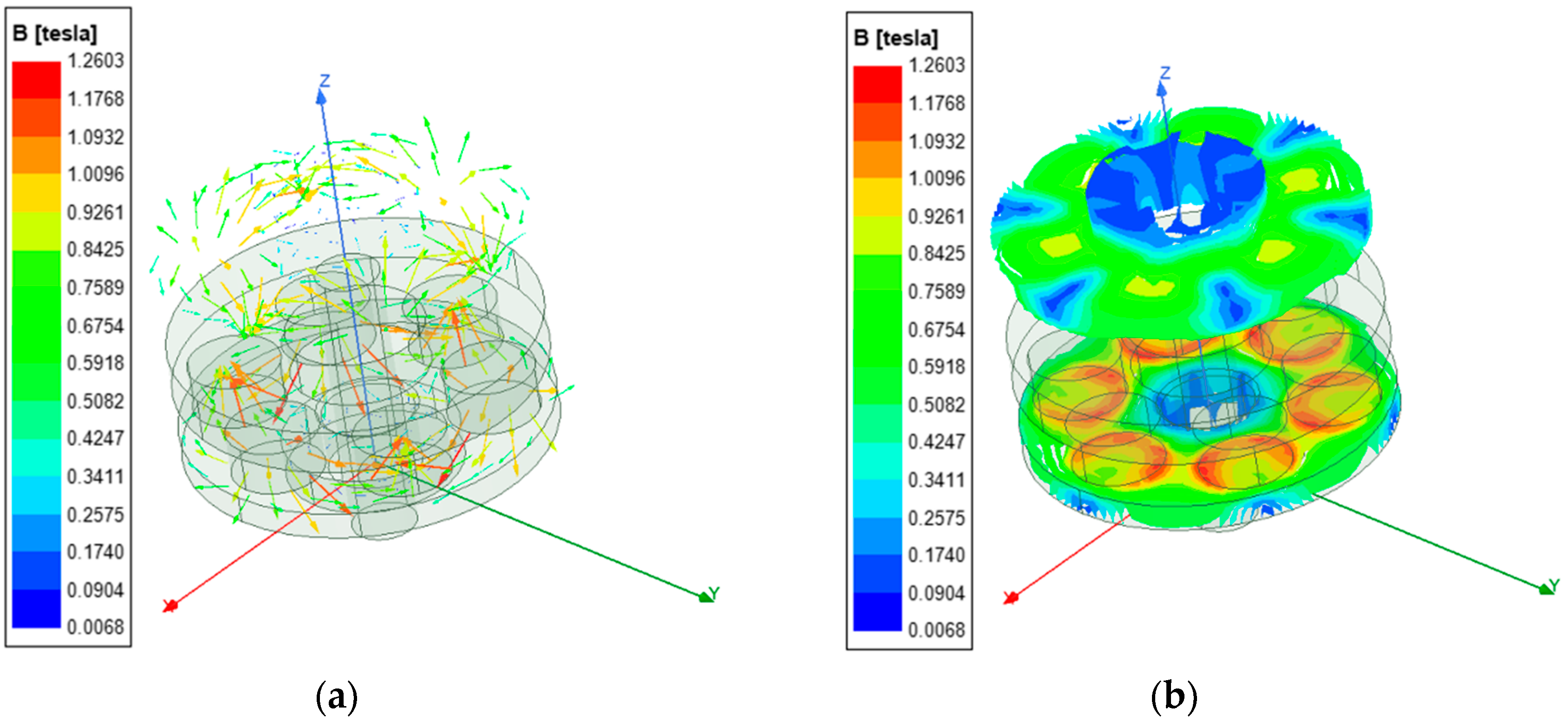
4.1. Static Simulation Results and Analysis of the Electromagnetic Damper
- Static electric fields, forces, torques, and capacitances caused by voltage distributions and charges;
- Static magnetic fields, forces, torques, and inductances caused by DC currents, static external magnetic fields, and permanent magnets;
- Time-varying magnetic fields, forces, torques, and impedances caused by AC currents and oscillating external magnetic fields;
- Transient magnetic fields caused by electrical sources and permanent magnets.
- (1)
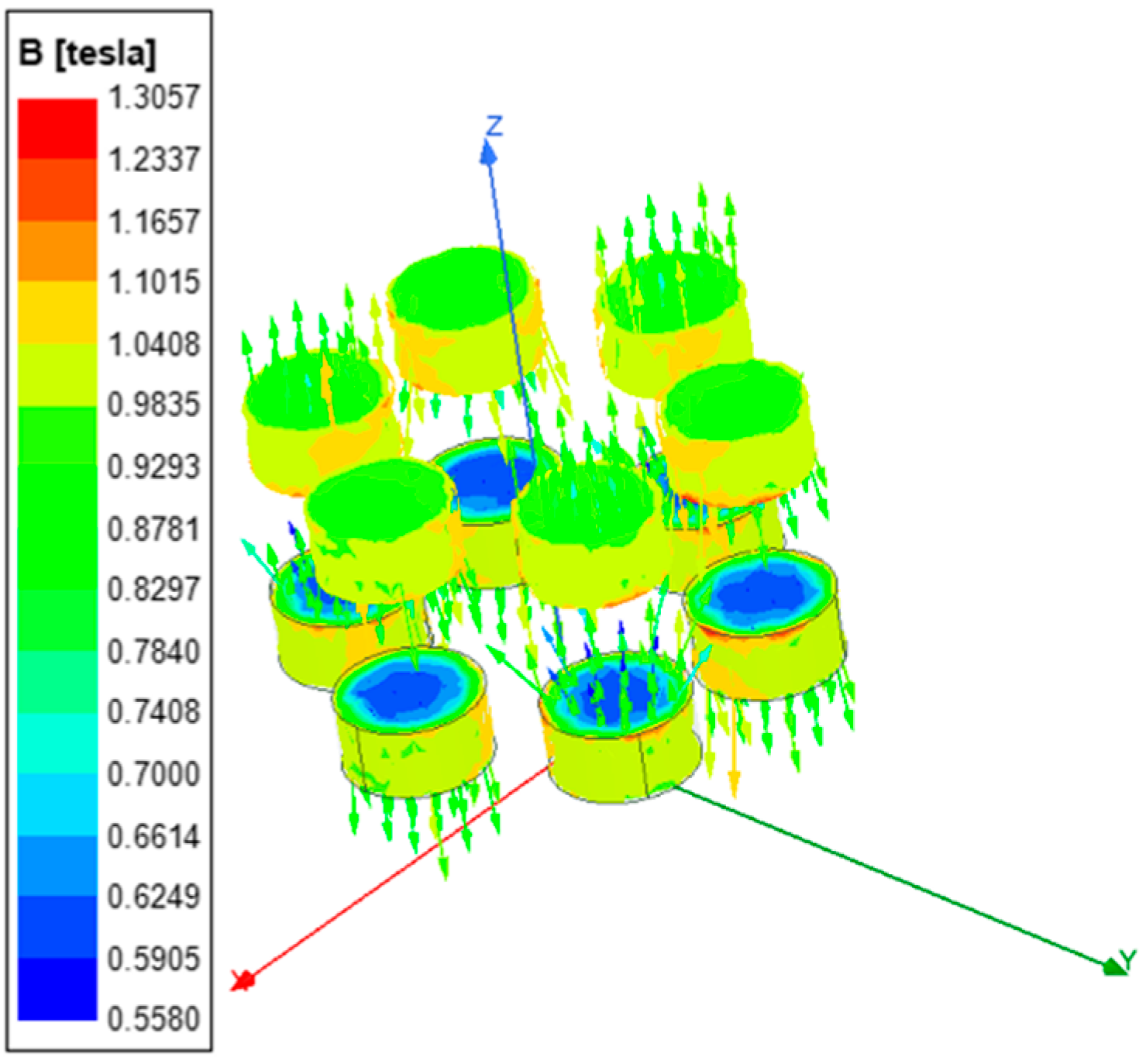
- In the two areas of the rotor disk below the adjacent poles, the magnetic flux densities are in opposite directions but they are equal in values.
- (2)
- The magnetic field superposition at the circumferential edge of the area corresponding to the magnetic poles leads to the maximum magnetic flux density, which can reach 1.26T, and gradually decays in all directions.
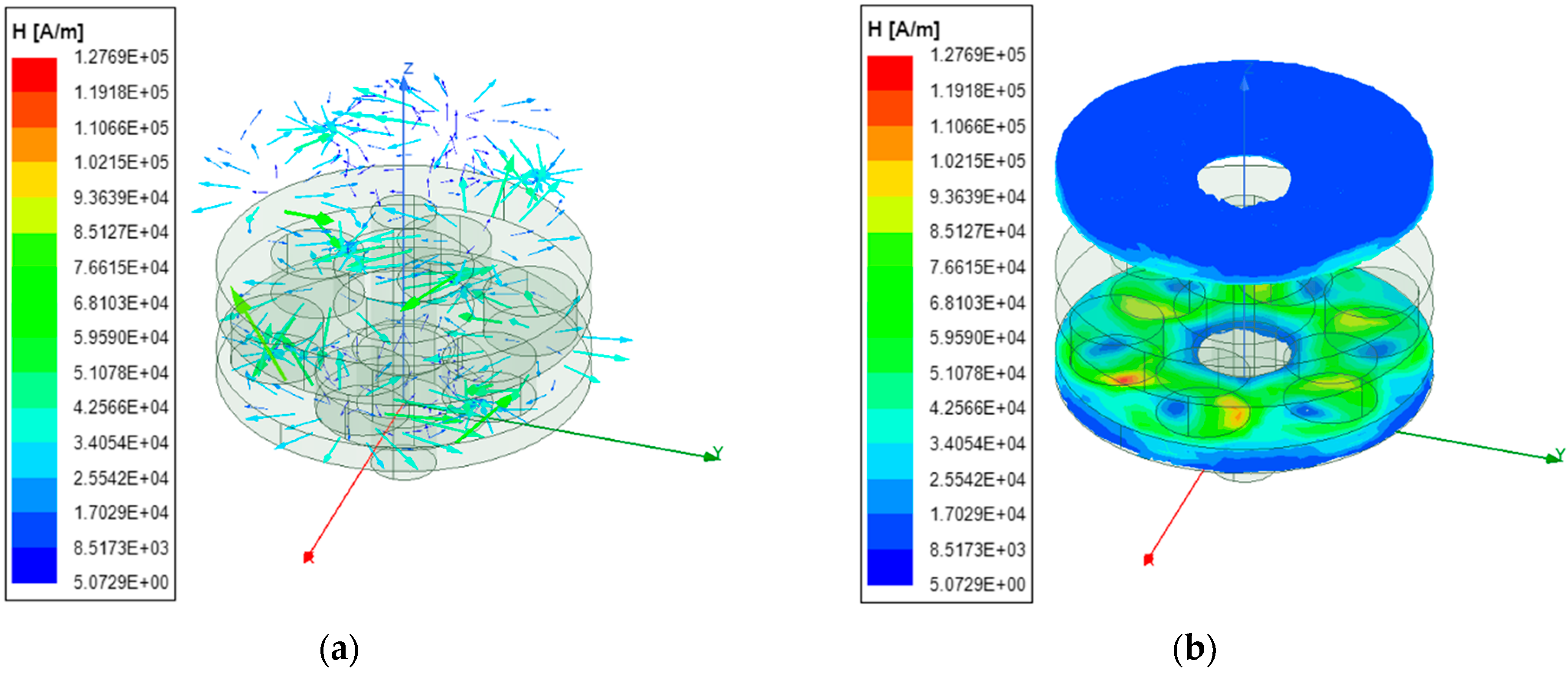
4.2. Dynamic Simulation Results and Analysis of the Electromagnetic Damper
- (1)
- The mathematical model of the electromagnetic damper is reasonable;
- (2)
- The application of electromagnetic dampers to the shimmy reduction function of electrically actuated nose wheel steering systems is also feasible, but there are some differences in the values at some data points and the slopes of the two curves are not identical, because:
- When calculating the output damping torques of the electromagnetic damper using Equation (18), the magnetic flux density of the permanent magnet source is assumed to be the magnetic flux density on the surface of the rotor disks, and the magnetic losses caused by the air gap and resistance and the induced magnetic field generated by the rotor disks themselves during rotation are ignored;
- The magnetic permeability of the permanent magnet material is simply taken as a constant value in the numerical calculation. However, from the hysteresis curve of the permanent magnet material in the finite element simulation, the magnetic field strength is not linearly related to the magnetic flux density, and the relative permeability is also not linear;
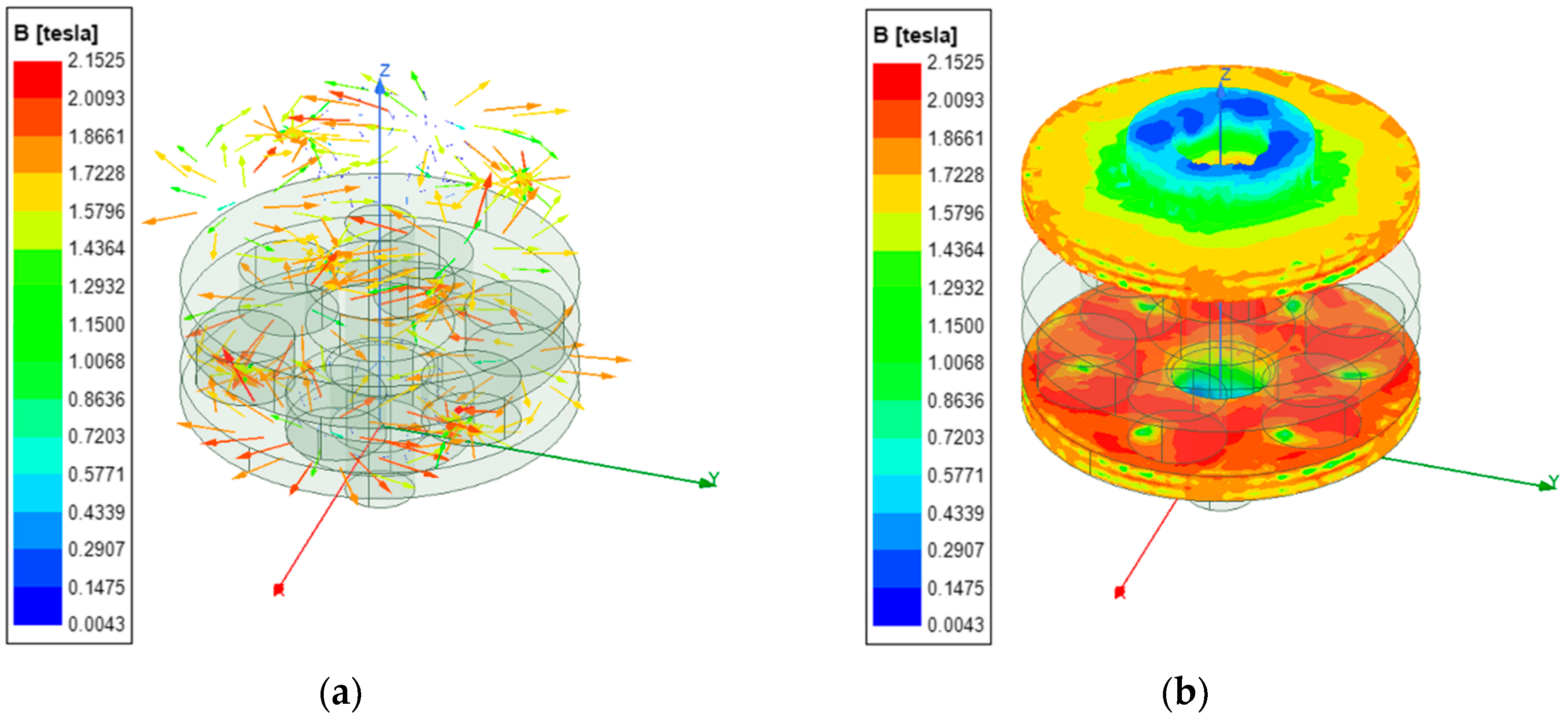
- The demagnetization effect of the permanent magnet is not taken into account in the whole mathematical modeling process of the electromagnetic damper, while the experimental results in the literature [21] show that the demagnetization effect is actually real. The magnetic flux density distribution of the permanent magnet magnetic pole at the relative angular velocity of 1034.14 rad/s is shown in Figure 17, and comparing the static magnetic flux density distribution of the pole in Figure 10, it can be found that the finite element simulation takes this demagnetization effect into account;
4.3. Effect of Various Factors on the Performance of Electromagnetic Dampers
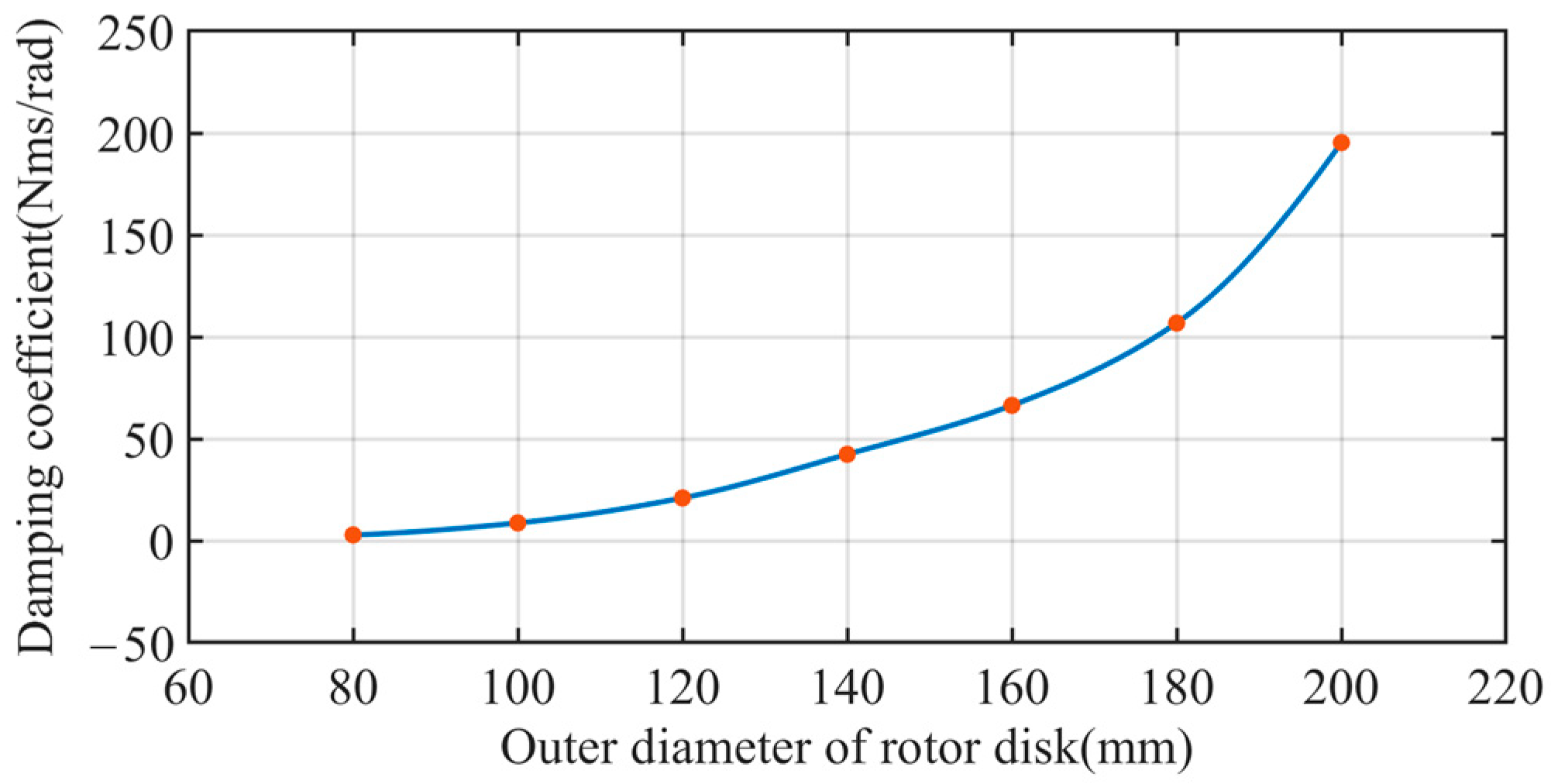
4.3.1. Study of the Effect of Rotor Disks’ Dimensions R2 and R1 on Electromagnetic Damping
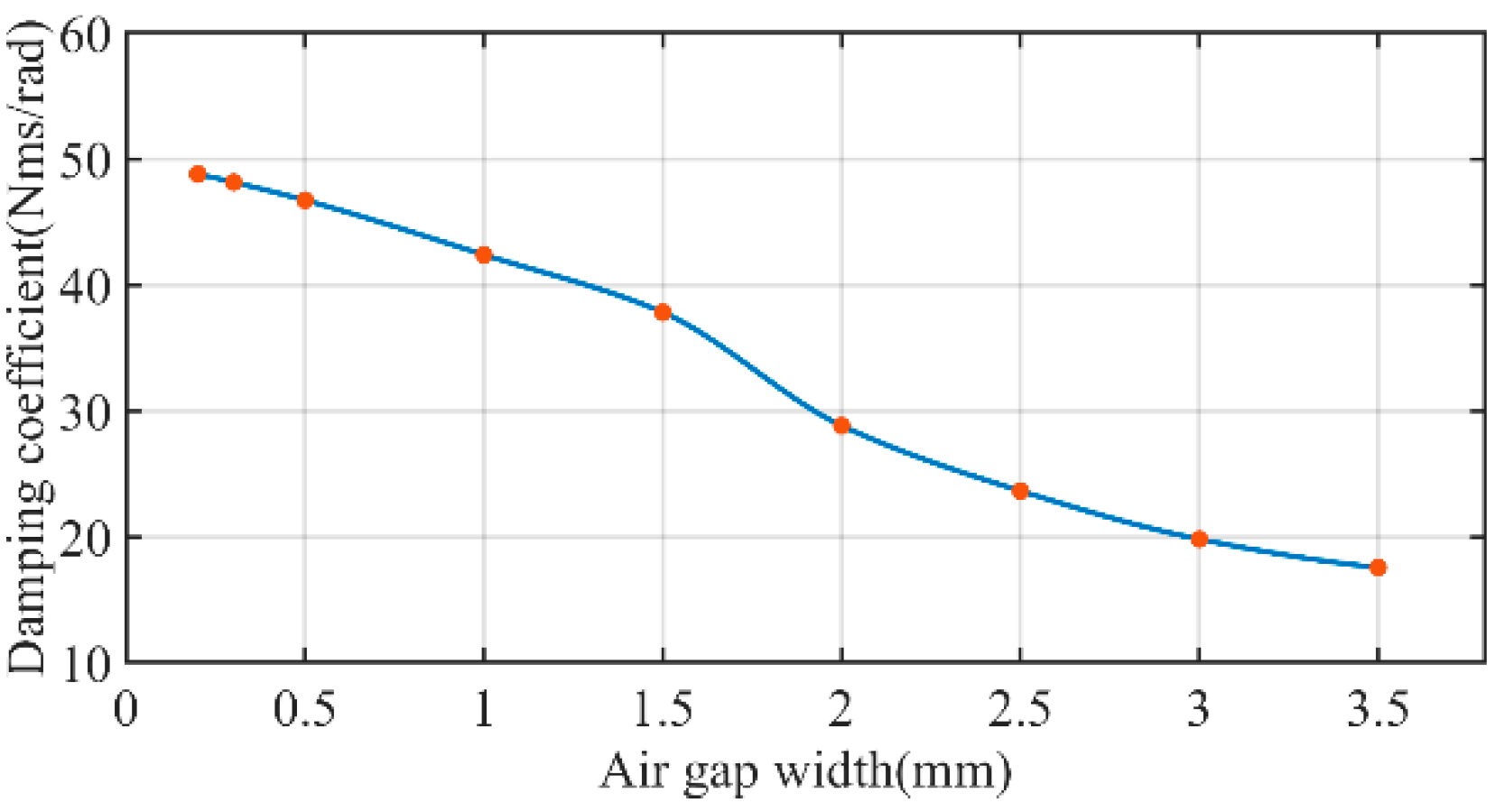
4.3.2. Study of the Effect of Air Gap Width δ on Electromagnetic Damping
5. Conclusions
- (1)
- After correcting the assumption that the rotor disk is located in the uniform magnetic field, which was commonly used in the previous derivation process, and combining the calculation of the skin depth, the derived equation for the output damping torque of the electromagnetic damper is closer to the simulated value;
- (2)
- The electromagnetic damper designed in this paper can provide a damping coefficient of not less than 40 Nms/rad under the conditions of shimmy amplitude between 2–20° and frequency between 5–30 Hz, which not only meets the requirements of the index, but also overcomes the disadvantages of relying on the hydraulic power source compared with the traditional oleo dampers. It also has the advantages of higher reliability, lower maintenance cost and faster response;
- (3)
- There is an approximate quadratic relationship between the dimensions R2 and R1 of the rotor disks and the damping coefficient. The preliminary structural design of electromagnetic dampers’ dimensions can be based on this relationship when the shimmy reduction index requirements are given;
- (4)
- The air gap width δ of the electromagnetic damper designed in this paper can be adjusted to obtain a range of 17.55–49.79 Nms/rad for the damping coefficient. In the actual engineering application, the required damping coefficient can be obtained by adjusting the air gap width δ of the electromagnetic damper for different shimmy conditions.
- (5)
- The application of electromagnetic damping technology to strut damping is the first comprehensive and systematic study of this technology at the theoretical and simulation levels, which can be applied not only to the design of electrically actuated nose wheel steering systems for various types of aircraft, but also to other impact cushioning and vibration energy recovery fields.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Nose wheel shimmy amplitude |
| f | Nose wheel shimmy frequency |
| α | Nose wheel shimmy angle |
| ωNW | Angular velocity of nose wheel shimmy |
| ωmax | Max angular velocity of the nose wheel shimmy |
| ω | Angular frequency of the eddy current |
| μ | Magnetic permeability of the rotor disk material |
| γ | Electrical conductivity of the rotor disk material |
| h | Vertical depth from the surface of the rotor disk |
| Δ | Penetration depth of skin effect |
| ωn | Rotation angular velocity of the rotor disk |
| TRotor | Rotation period of the rotor disk |
| fRotor | Rotation frequency of the rotor disk |
| TEc | Alternating period of the eddy current |
| fEc | Frequency of the eddy current |
| B | Magnetic flux density of a single magnet passing through a rotor disk |
| V | Rotation linear velocity of the rotor disk |
| dε | Induced electromotive force of the micro-ring |
| dl | Width of the micro-ring |
| dR | Resistance of the micro-ring |
| IdR | Current value flowing along the radial direction of the micro-ring |
| ρ | Resistivity of the rotor disk material |
| dF | Damping force of the micro-ring |
| dT | Damping torque of the micro-ring |
| R2 | Outer radius of the rotor disk |
| R1 | Inner radius of the rotor disk |
| T1 | Damping torque of a single rotor disk |
| rMag | Radius of the magnet cross section |
| Tn | Damping torque of the electromagnetic damper |
| i | Transmission ratio |
| ηGear | Transmission efficiency of the 8-grade cylindrical spur gear |
| ηBearing | Transmission efficiency of the bearing |
| η | Total transmission efficiency |
| ωStrut | Angular velocity of the nose landing gear strut |
| TStrut | Damping torque of the nose landing gear strut |
| hn | Damping coefficient of the electromagnetic damper |
| hStrut | Damping coefficient of the nose landing gear strut |
| Magnetic field strength | |
| Magnetic flux density | |
| Conduction current density | |
| Permanent magnetization | |
| μ0 | Permeability of vacuum |
| μr | Relative permeability |
References
- Cláudio, A.L.; James, C.; Kamran, E.S. Rotor Position Synchronization in Central-Converter Multi-Motor Electric Actuation Systems. Energies 2021, 14, 7485. [Google Scholar] [CrossRef]
- George, I.; Stephane, D. Dress: Distributed and Redundant Electro-Mechanical Nose Wheel Steering System. Sae Int. J. Aerosp. 2009, 2, 46–53. [Google Scholar]
- Bennett, C.; William, J. Fault Tolerant Electromechanical Actuators for Aircraft. Ph.D. Thesis, Newcastle University, Newcastle, UK, 2010. [Google Scholar]
- Liao, P.; Zhang, X.; Li, W. Design of Electrical Swerve Control System for Small Aircraft Undercarriages. Small Spec. Electr. Mach. 2010, 38, 4. [Google Scholar]
- Feng, F.; Nie, H.; Zhang, M.; Peng, Y. Effect of Torsional Damping on Aircraft Nose Landing-Gear Shimmy. J. Aircr. 2014, 52, 561–568. [Google Scholar] [CrossRef]
- Zhu, P. Shimmy Theory and Anti-Shimmy Measures, 1st ed.; National Defense Industry Press: Beijing, China, 1984; pp. 9–23. [Google Scholar]
- Luong, Q.-V.; Jo, B.-H.; Hwang, J.-H.; Jang, D.-S. A Supervised Neural Network Control for Magnetorheological Damper in an Aircraft Landing Gear. Appl. Sci. 2022, 12, 400. [Google Scholar] [CrossRef]
- Jo, B.-H.; Jang, D.-S.; Hwang, J.-H.; Choi, Y.-H. Experimental Validation for the Performance of MR Damper Aircraft Landing Gear. Aerospace 2021, 8, 272. [Google Scholar] [CrossRef]
- Chen, D.; Gu, H.; Wu, D. Semi-active Control of Landing Gear Shimmy Based on Magneto-rheological (MR) Damper. China Mech. Eng. 2010, 21, 1401–1405. [Google Scholar]
- Zhu, S.; Wang, G. Design and Experimental Research of External Coil Type Magnetorheological Shimmy Damper. Mach. Tool Hydraul. 2019, 47, 12–17. [Google Scholar]
- Jia, C.; Xia, Y.; Chu, M.; Zhang, X. Post-capture Angular Momentum Management of Space Robot with Controllable Damping Joints. In Proceedings of the 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 22–24 November 2019; pp. 638–642. [Google Scholar]
- Kou, B.; Li, L.; Jin, Y.; Pan, D. System for Testing Linear Motor Characteristics. CN Patent 102096042B, 13 February 2013. [Google Scholar]
- Ebrahimi, B. Development of Hybrid Electromagnetic Dampers for Vehicle Suspension Systems. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2009. [Google Scholar]
- Liu, C.; Jiang, K.; Zhang, Y. Design and Use of an Eddy Current Retarder in an Automobile. Int. J. Automot. Technol. 2011, 12, 611–616. [Google Scholar] [CrossRef]
- Heald, D.; Mark, A. Magnetic Braking: Improved Theory. Am. J. Phys. 1988, 56, 521–522. [Google Scholar] [CrossRef]
- Kou, B.; Jin, Y.; Zhang, H.; Zhang, L.; Zhang, H. Development and Application Prospects of the Electromagnetic Damper. Proc. Chin. Soc. Electr. Eng. 2015, 35, 3132–3143. [Google Scholar]
- Gay, S.E.; Ehsani, M. Parametric Analysis of Eddy-Current Brake Performance by 3-D Finite-Element Analysis. IEEE Trans. Magn. 2006, 42, 319–328. [Google Scholar] [CrossRef]
- Fujita, T.; Kitade, K.; Yokoyama, T. Development of Original End Point Detection System Utilizing Eddy Current Variation Due to Skin Effect in Chemical Mechanical Polishing. Jpn. J. Appl. Phys. 2011, 50, 05–09. [Google Scholar] [CrossRef]
- Jow, H.-M.; Ghovanloo, M. Design and Optimization of Printed Spiral Coils for Efficient Transcutaneous Inductive Power Transmission. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 193. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Yi, F.; He, J. A Computation Method for Braking Torque of Eddy Current R19etarder. Automot. Eng. 2004, 26, 197–200. [Google Scholar]
- Baranski, M.; Szelag, W.; Lyskawinski, W. Experimental and simulation studies of partial demagnetization process of permanent magnets in electric motors. IEEE Trans. Energy Convers. 2021, 99, 1. [Google Scholar] [CrossRef]
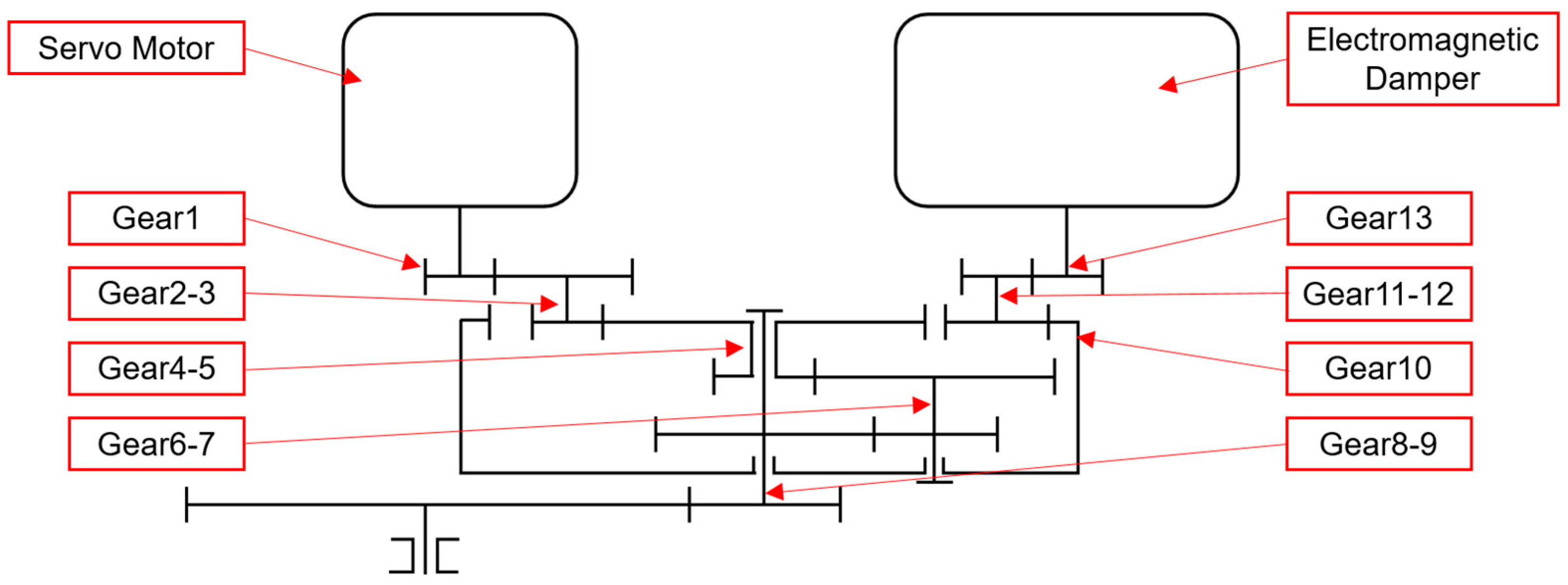
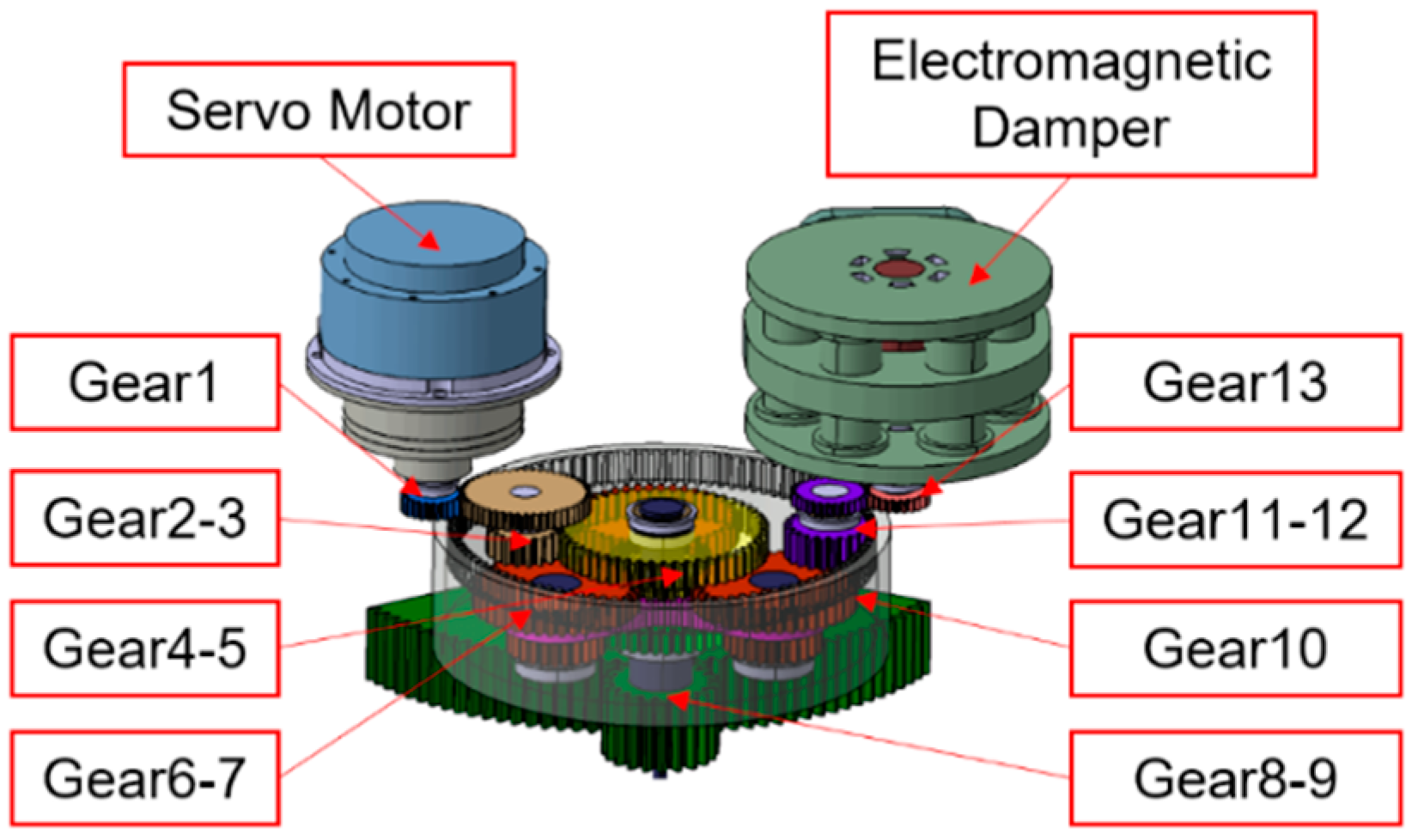
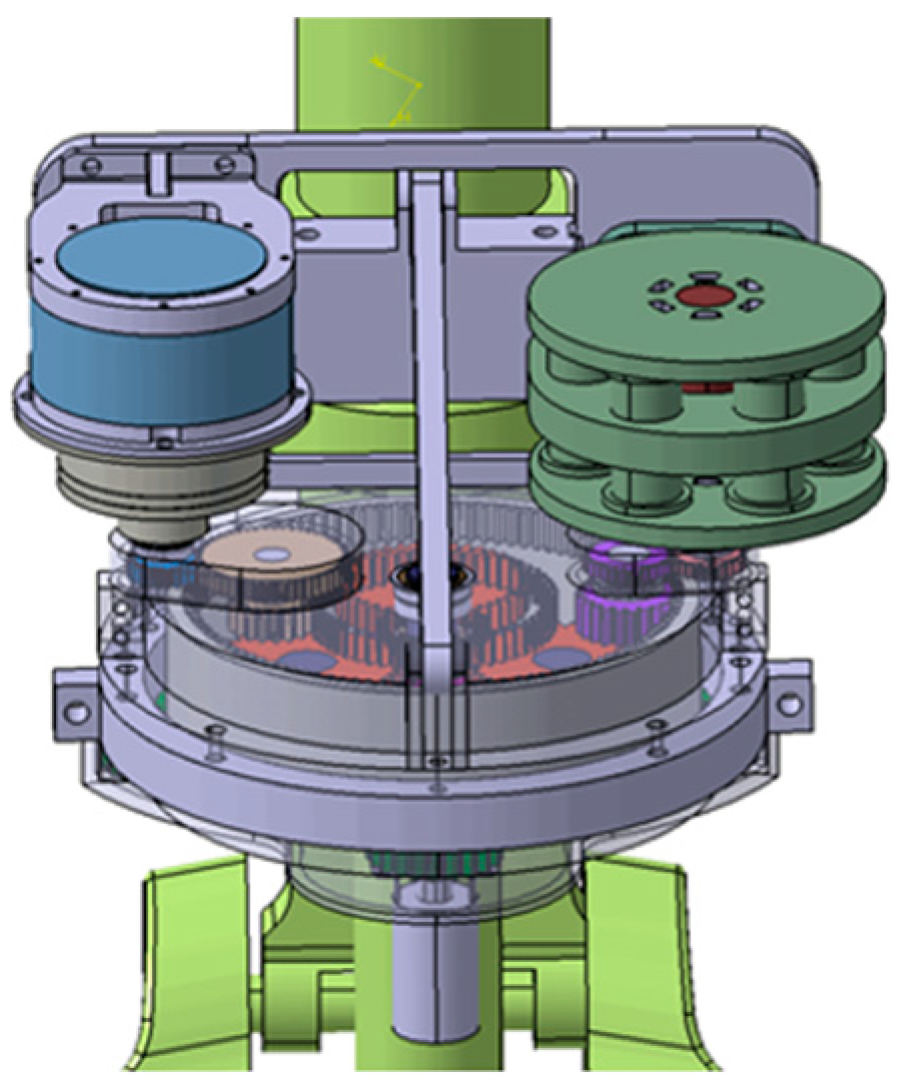
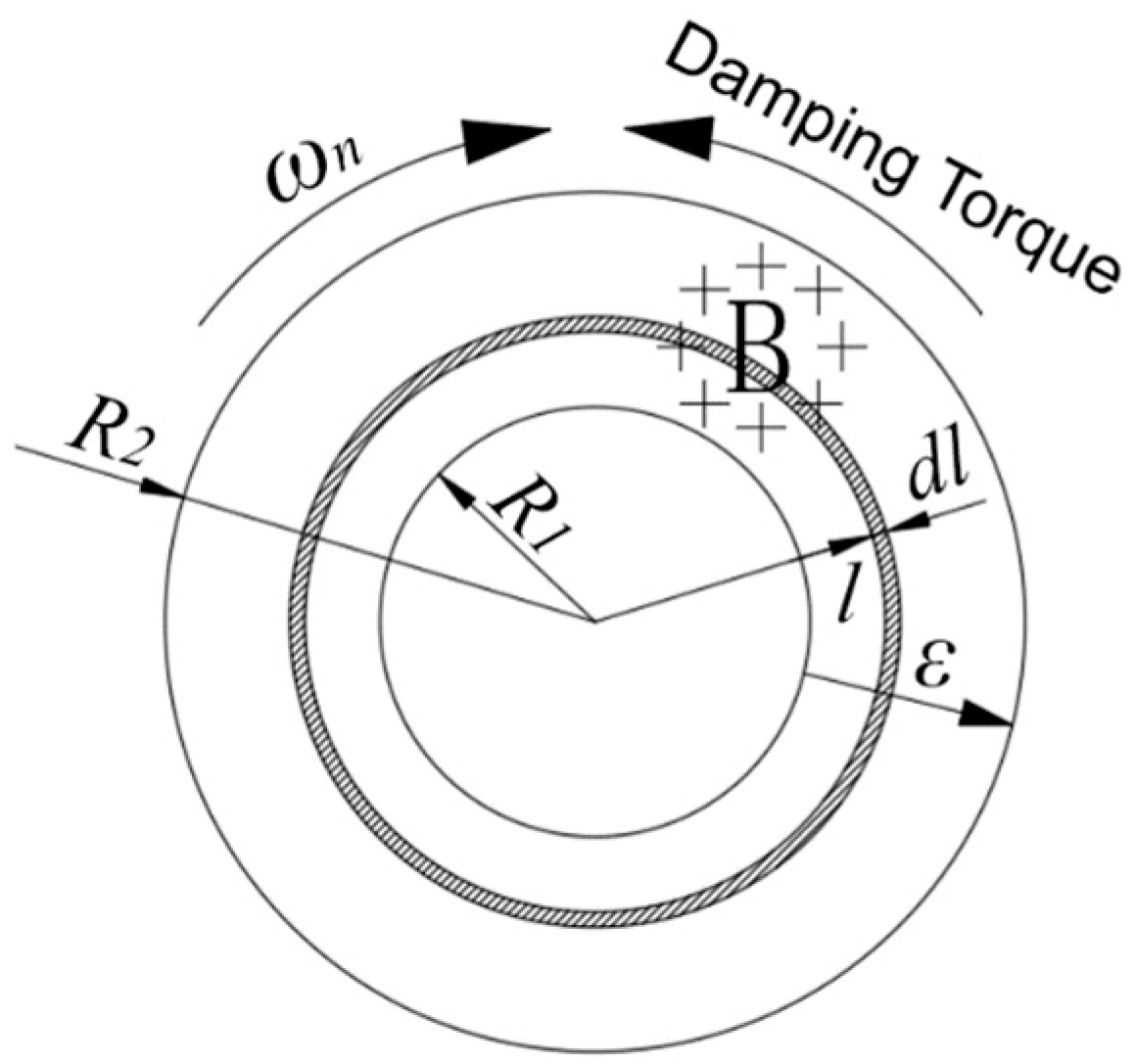






| A (°) | F (Hz) | Angular Velocity of Strut (rad/s) |
|---|---|---|
| 2.0 | 30.00 | 6.58 |
| 4.0 | 27.22 | 11.94 |
| 6.0 | 24.44 | 16.08 |
| 8.0 | 21.67 | 19.01 |
| 10.0 | 18.89 | 20.71 |
| 11.8 | 16.39 | 21.21 |
| 12.0 | 16.11 | 21.20 |
| 14.0 | 13.33 | 20.47 |
| 16.0 | 10.56 | 18.52 |
| 18.0 | 7.78 | 15.35 |
| 20.0 | 5.00 | 10.97 |
| Component | Material |
|---|---|
| Permanent magnet | NdFe35 |
| Stator disk | Steel stainless |
| Rotor disk | Steel 1010 |
| Component | Diameter (mm) | Height (mm) | |
|---|---|---|---|
| Outer Diameter | Inner Diameter | ||
| Permanent magnet | 35 | 18 | |
| Stator disk | 140 | 52 | 18 |
| Rotor disk | 140 | 35 | 10 |
| ωn (rad/s) | ωStrut (rad/s) | Tn (Nm) | TStrut (Nm) | hStrut (Nms/rad) |
|---|---|---|---|---|
| 357.95 | 6.58 | 11.45 | 504.34 | 76.65 |
| 649.54 | 11.94 | 15.42 | 679.39 | 56.90 |
| 874.75 | 16.08 | 17.89 | 788.41 | 49.03 |
| 1034.14 | 19.01 | 19.45 | 857.25 | 45.09 |
| 1126.62 | 20.71 | 20.31 | 894.76 | 43.20 |
| 1153.82 | 21.21 | 20.55 | 905.49 | 42.69 |
| 1153.28 | 21.20 | 20.54 | 905.28 | 42.70 |
| 1113.57 | 20.47 | 20.19 | 889.56 | 43.46 |
| 1007.49 | 18.52 | 19.20 | 846.13 | 45.69 |
| 835.04 | 15.35 | 17.48 | 770.32 | 50.18 |
| 596.77 | 10.97 | 14.78 | 654.21 | 59.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
She, C.; Zhang, M.; Ge, Y.; Tang, L.; Yin, H.; Peng, G. Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems. Aerospace 2022, 9, 113. https://doi.org/10.3390/aerospace9020113
She C, Zhang M, Ge Y, Tang L, Yin H, Peng G. Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems. Aerospace. 2022; 9(2):113. https://doi.org/10.3390/aerospace9020113
Chicago/Turabian StyleShe, Chenfei, Ming Zhang, Yibo Ge, Liming Tang, Haifeng Yin, and Gang Peng. 2022. "Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems" Aerospace 9, no. 2: 113. https://doi.org/10.3390/aerospace9020113
APA StyleShe, C., Zhang, M., Ge, Y., Tang, L., Yin, H., & Peng, G. (2022). Design and Simulation Analysis of an Electromagnetic Damper for Reducing Shimmy in Electrically Actuated Nose Wheel Steering Systems. Aerospace, 9(2), 113. https://doi.org/10.3390/aerospace9020113






