Nonlinear Tunability of Elastic Waves in One-Dimensional Mass-Spring Lattices Attached with Local Resonators
Abstract
1. Introduction
2. Dispersion Relation of One-Dimensional Elastic Metamaterials
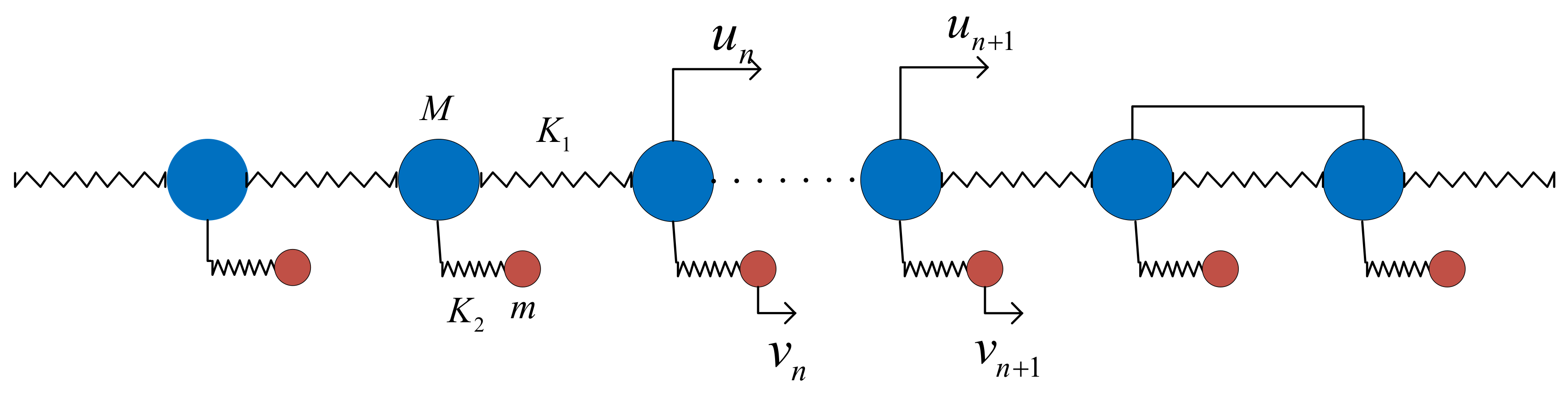
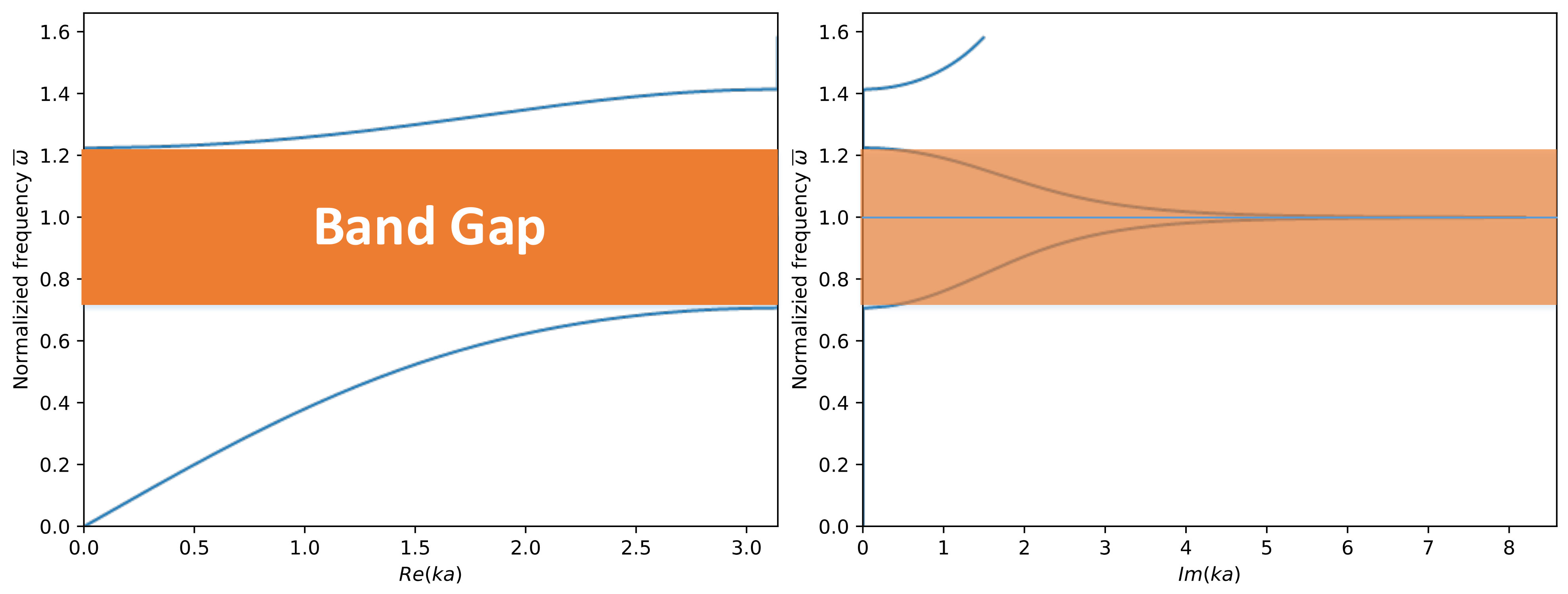
2.1. Linear Case
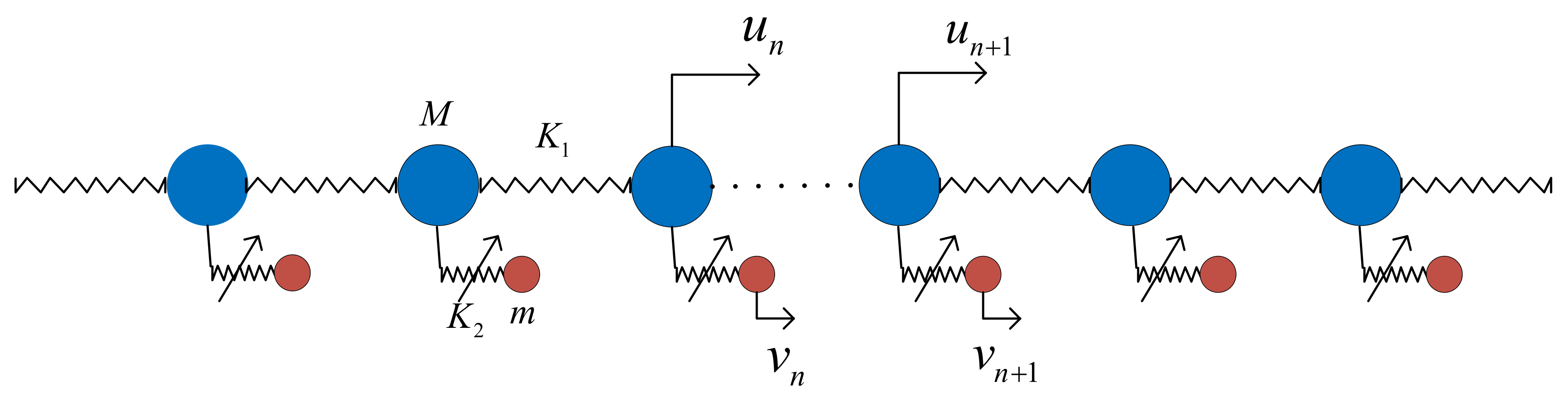
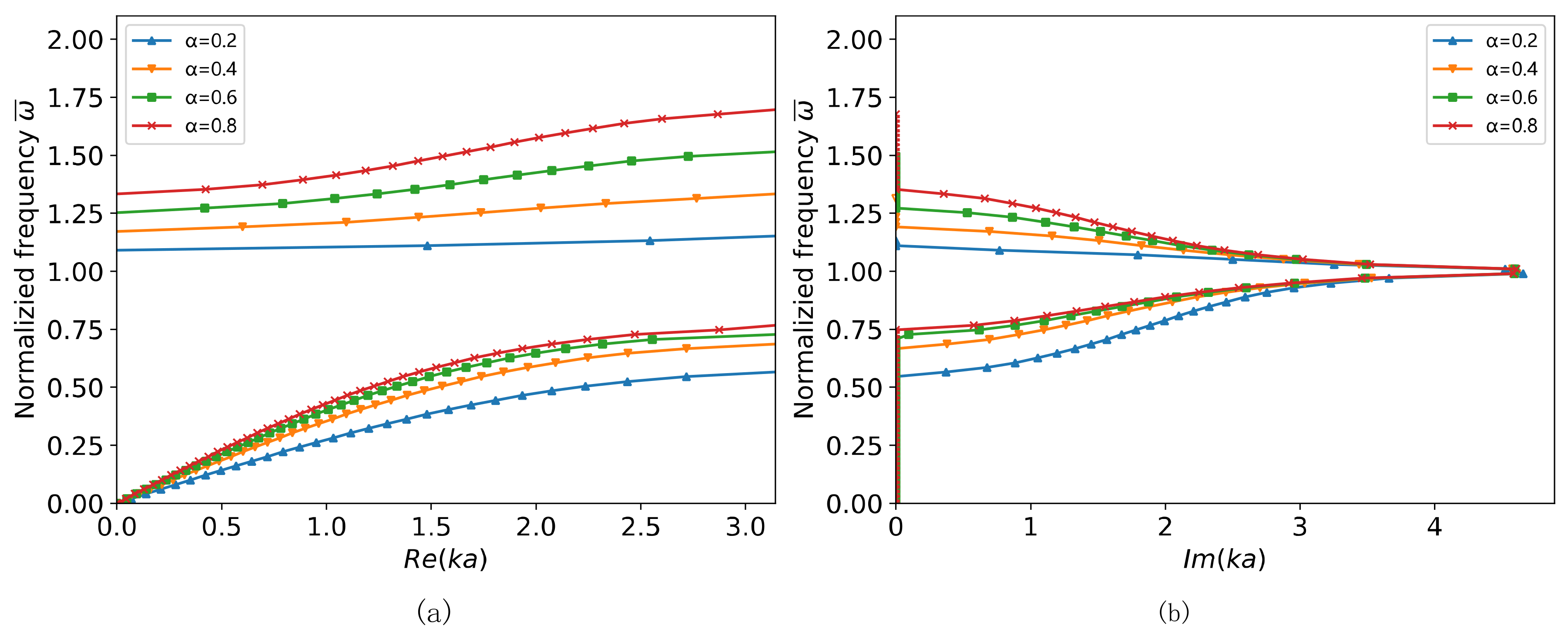
2.2. Nonlinear Case
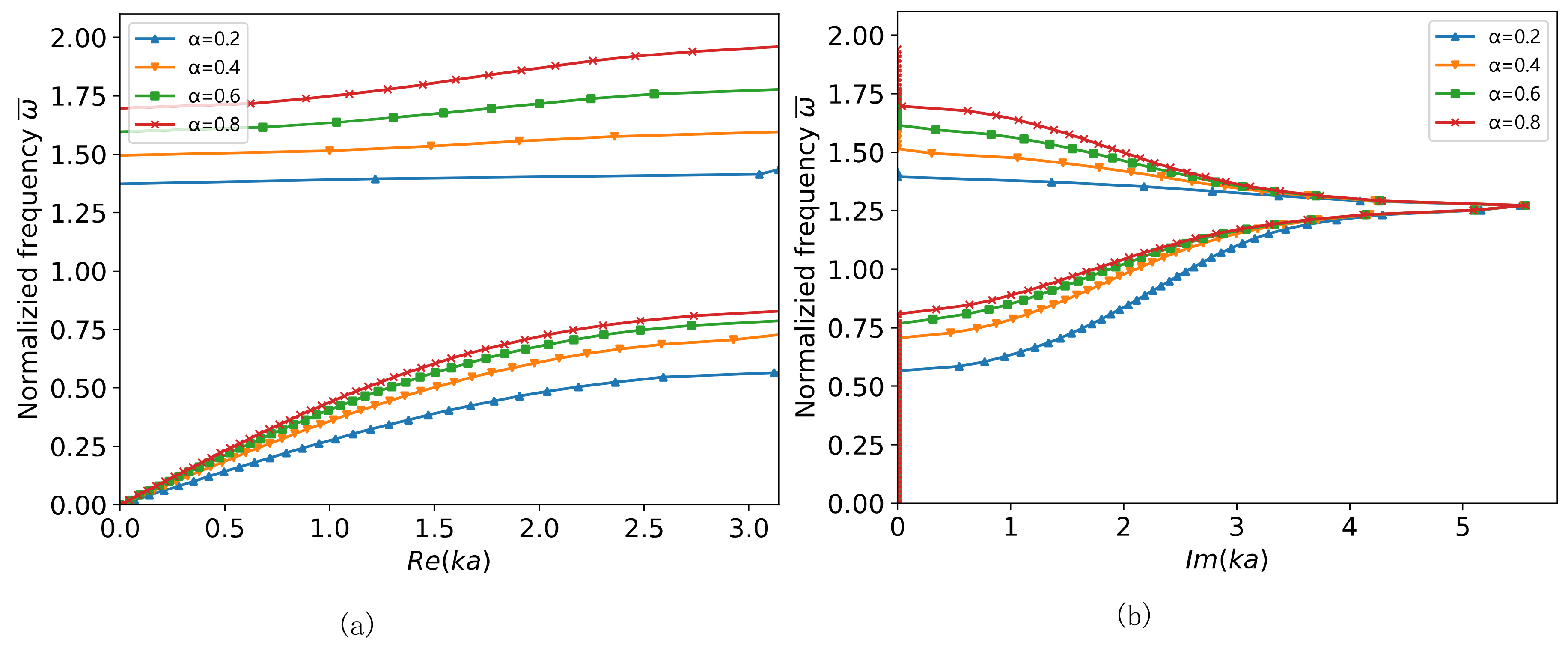
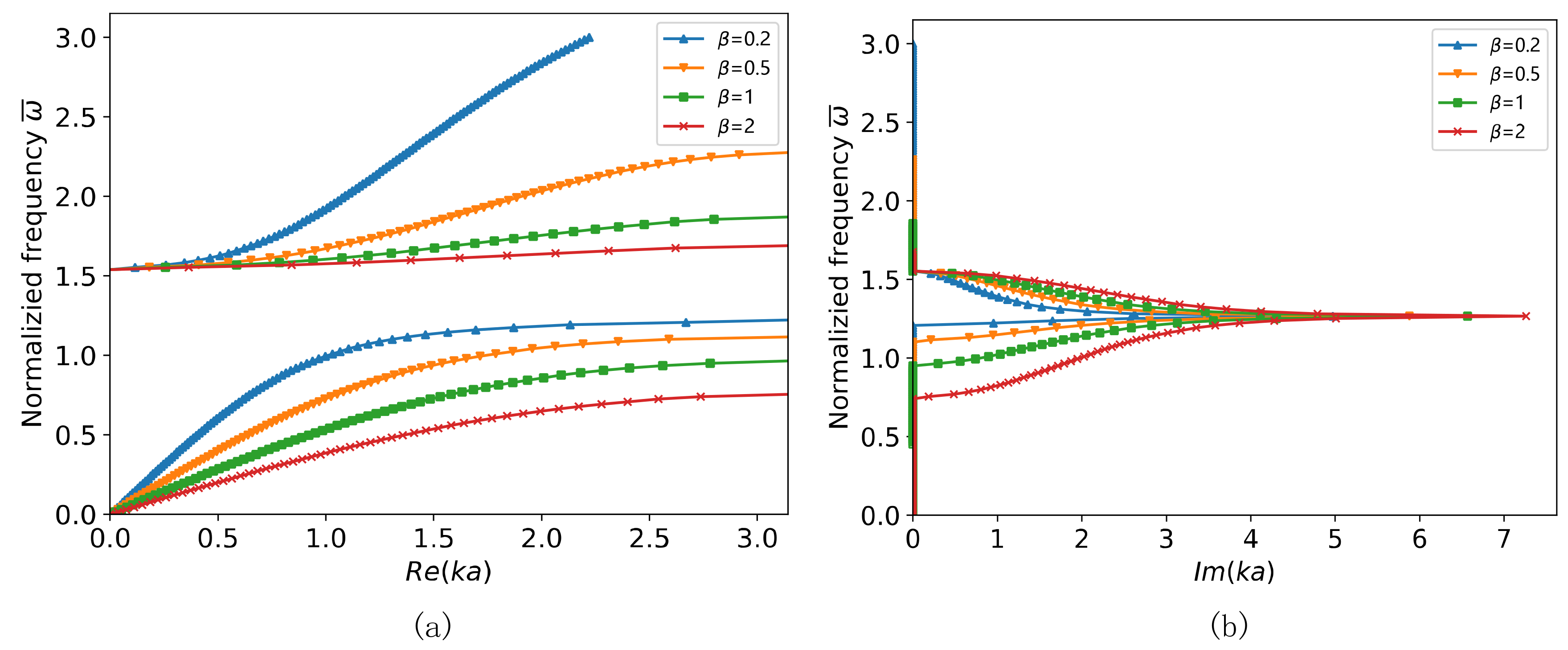
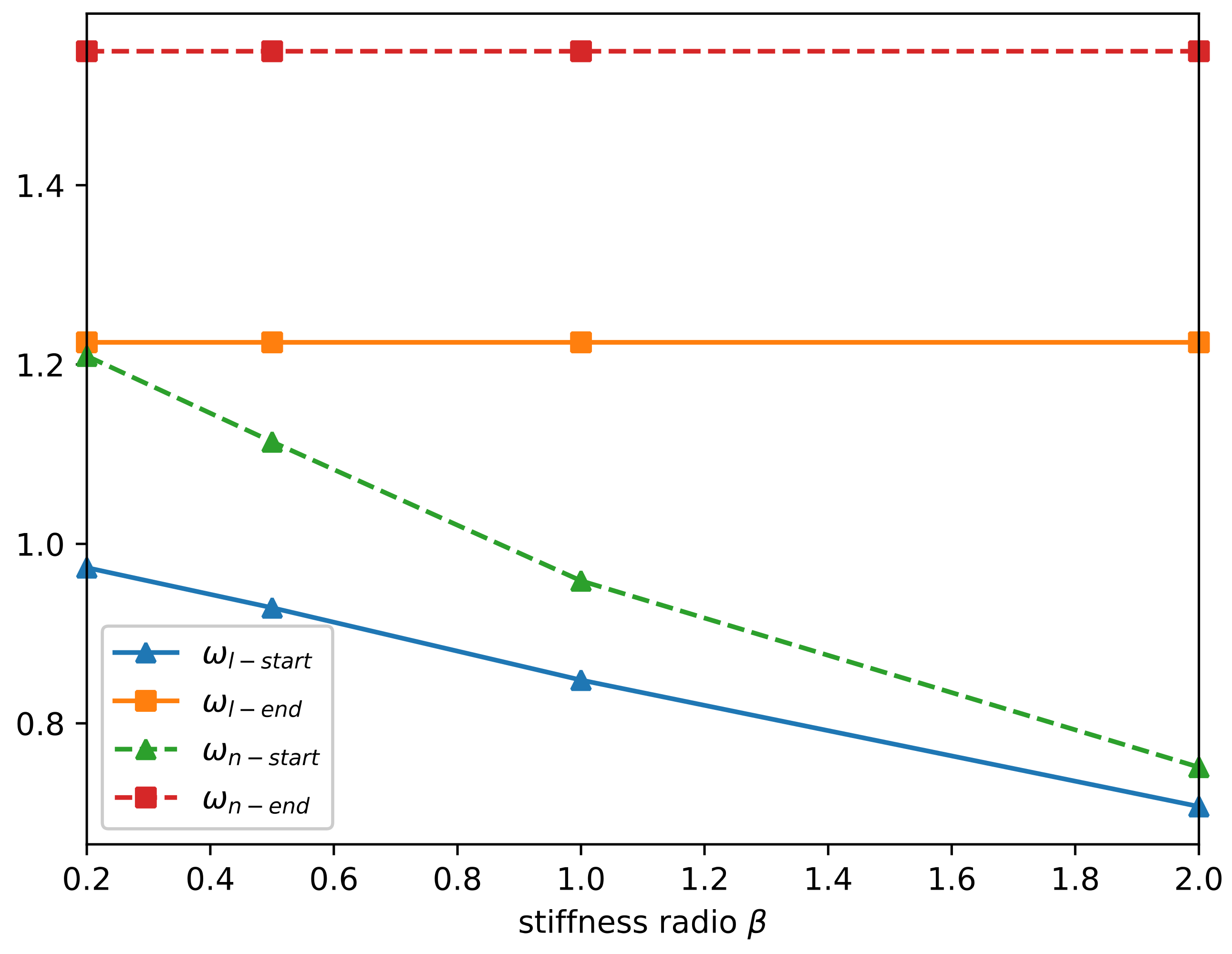
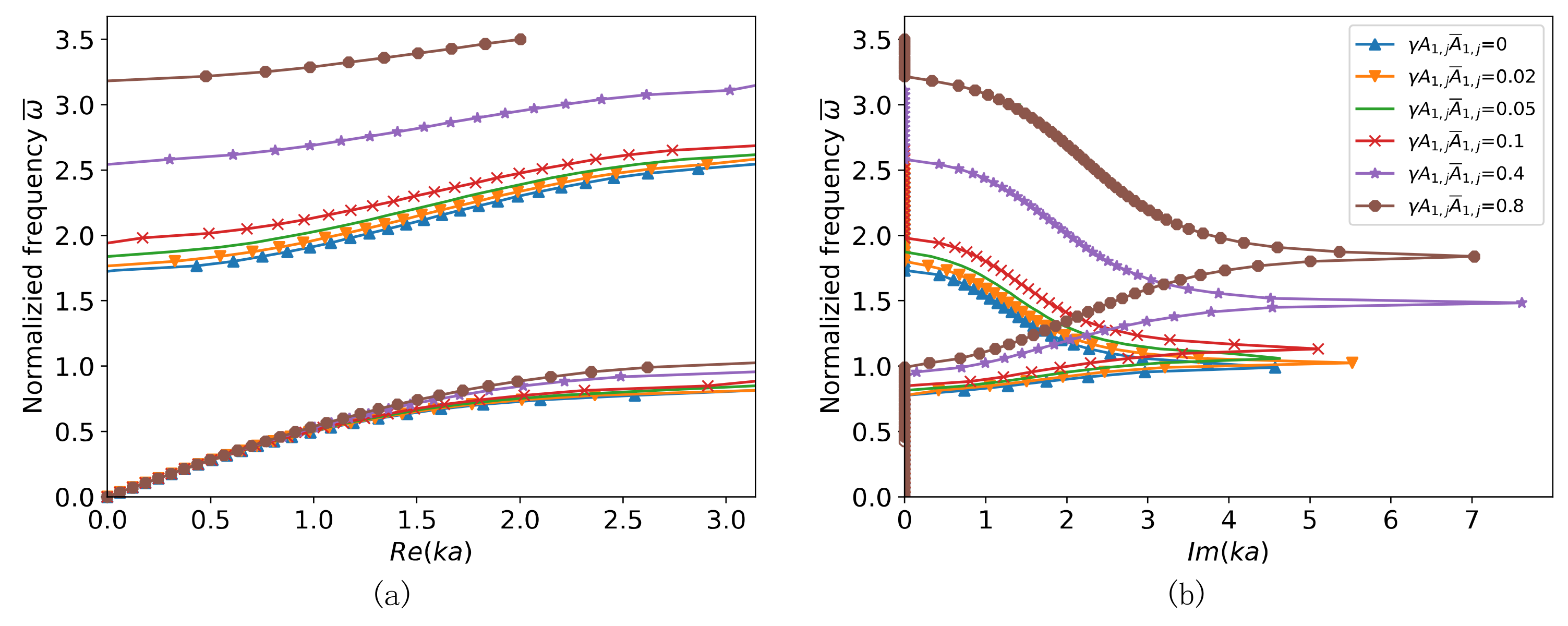
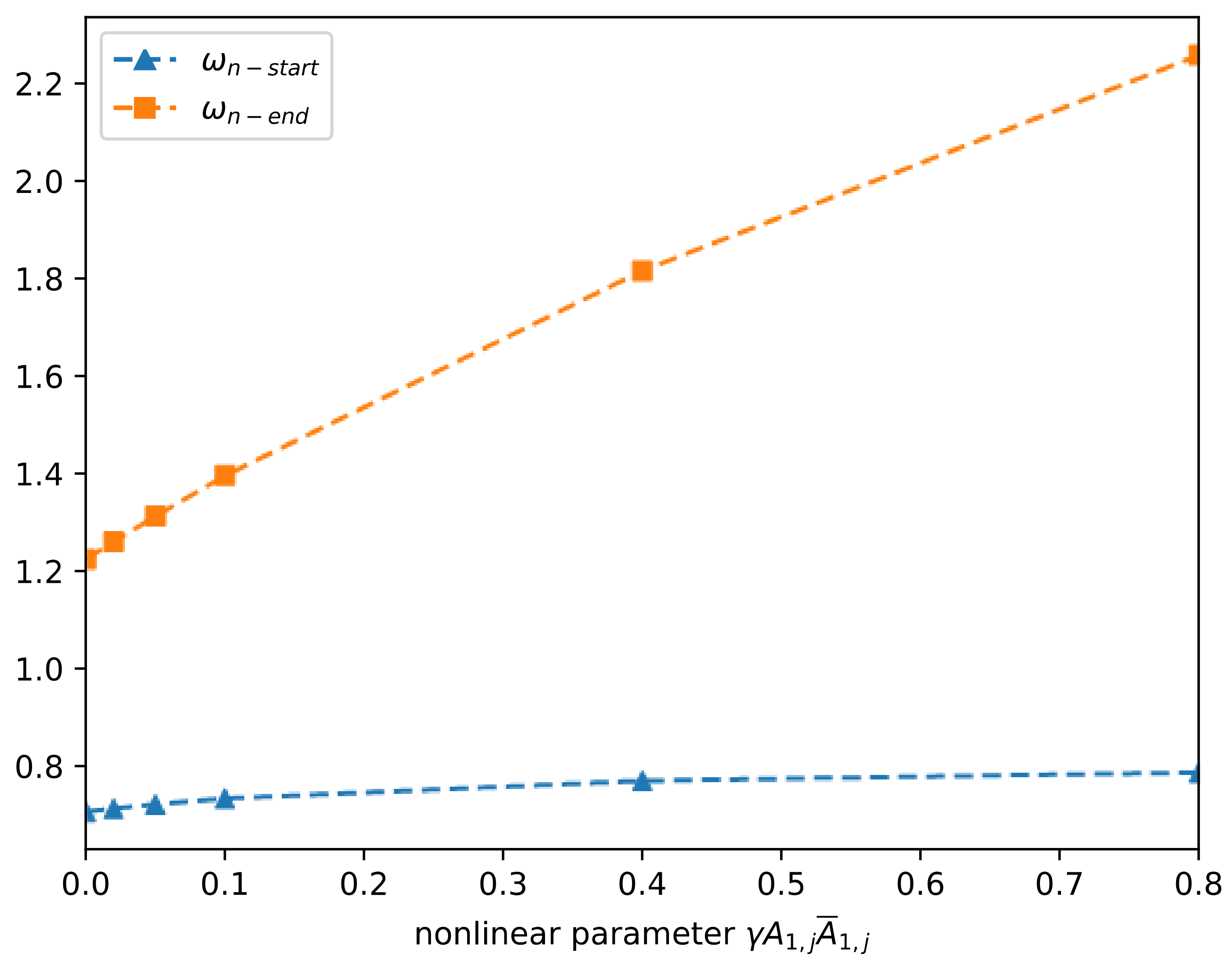
3. Tuning on the Nonlinear Band Gap
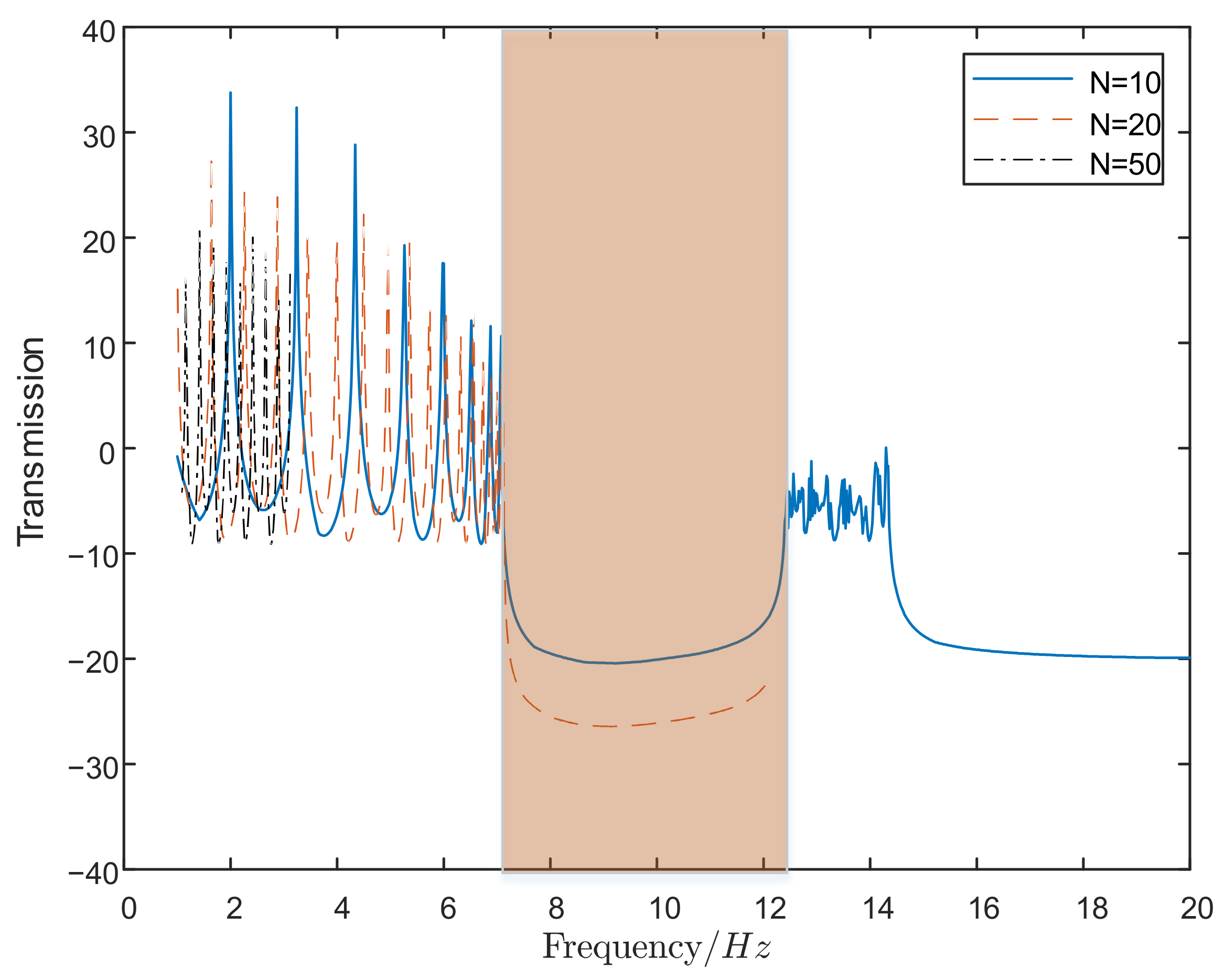
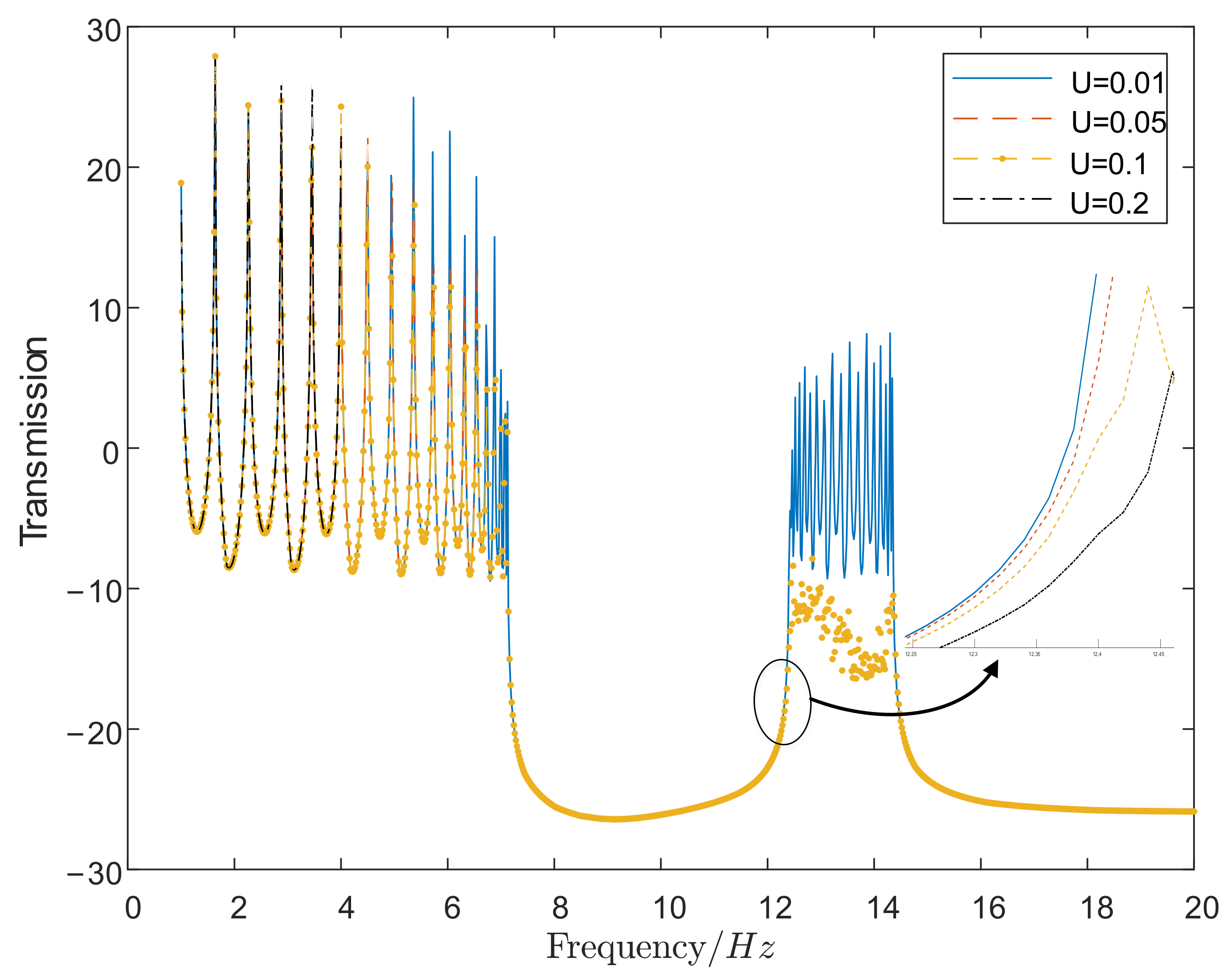
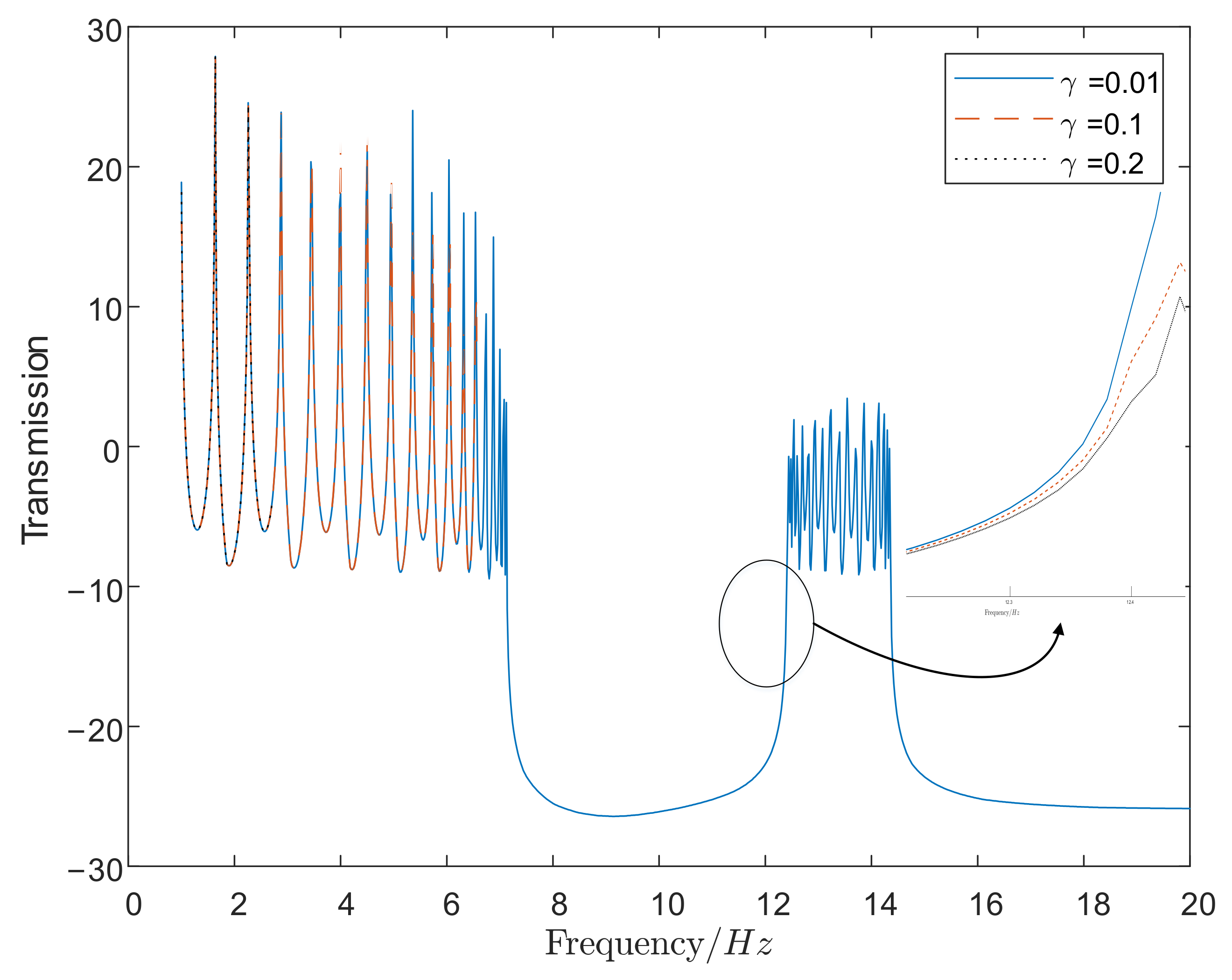
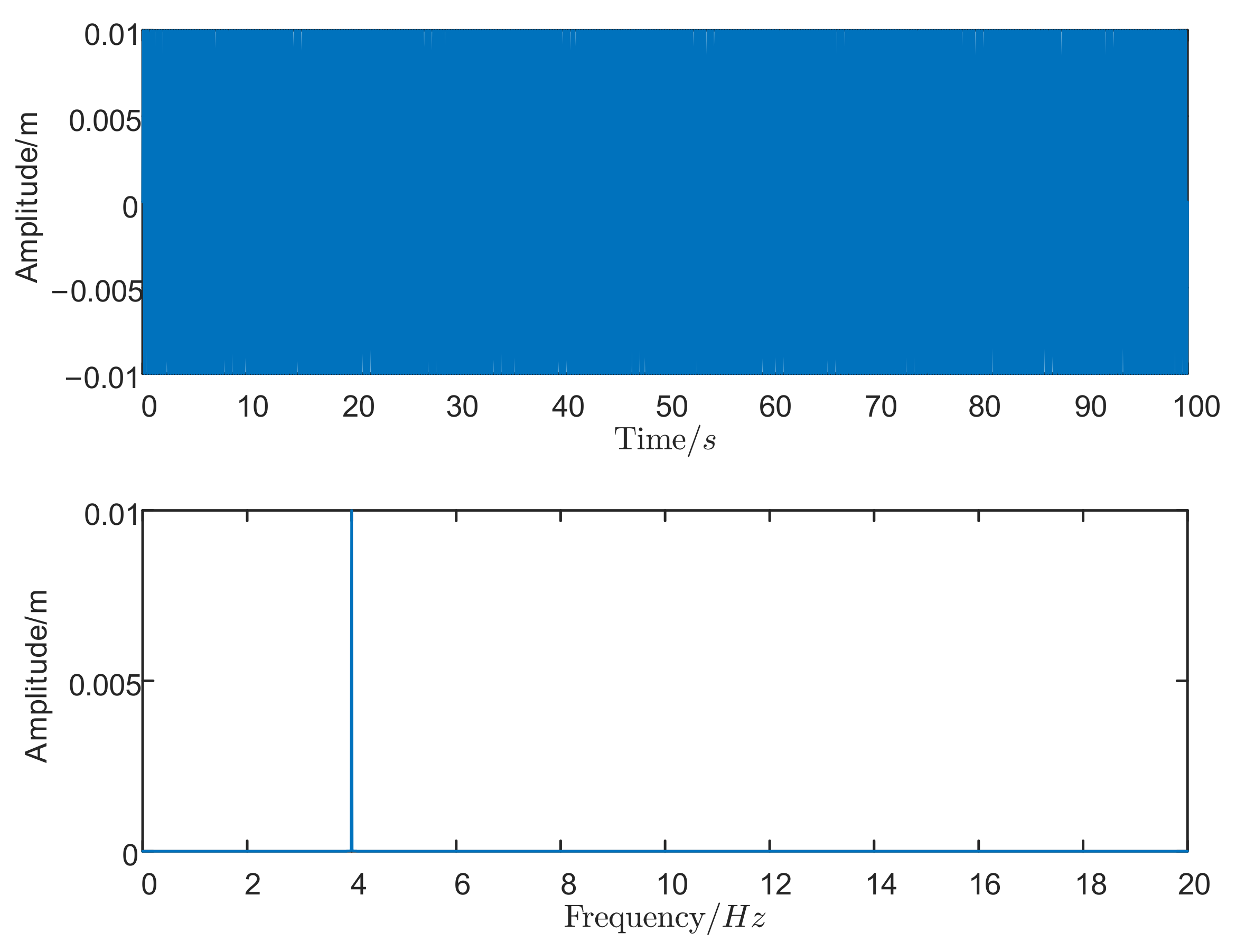
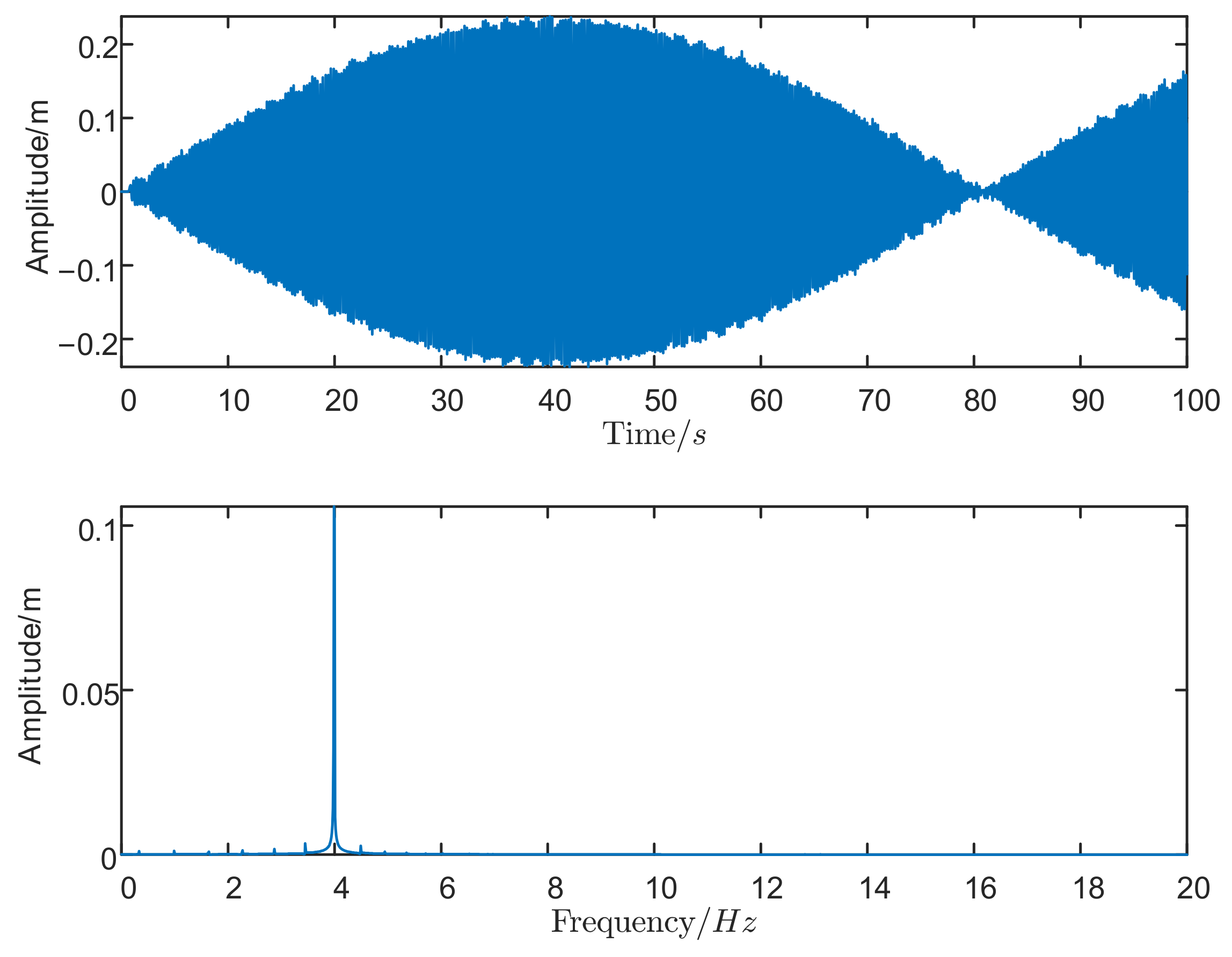
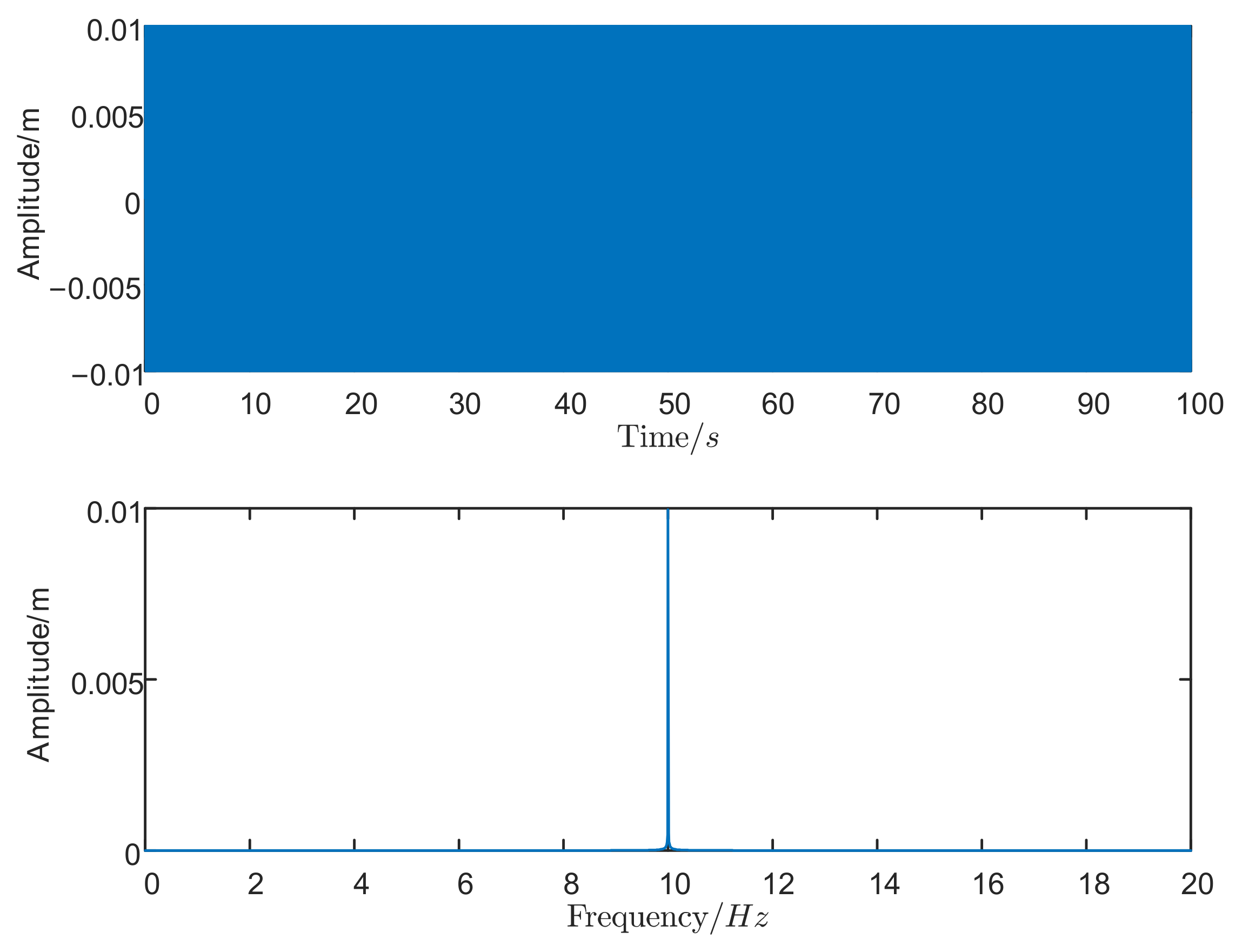
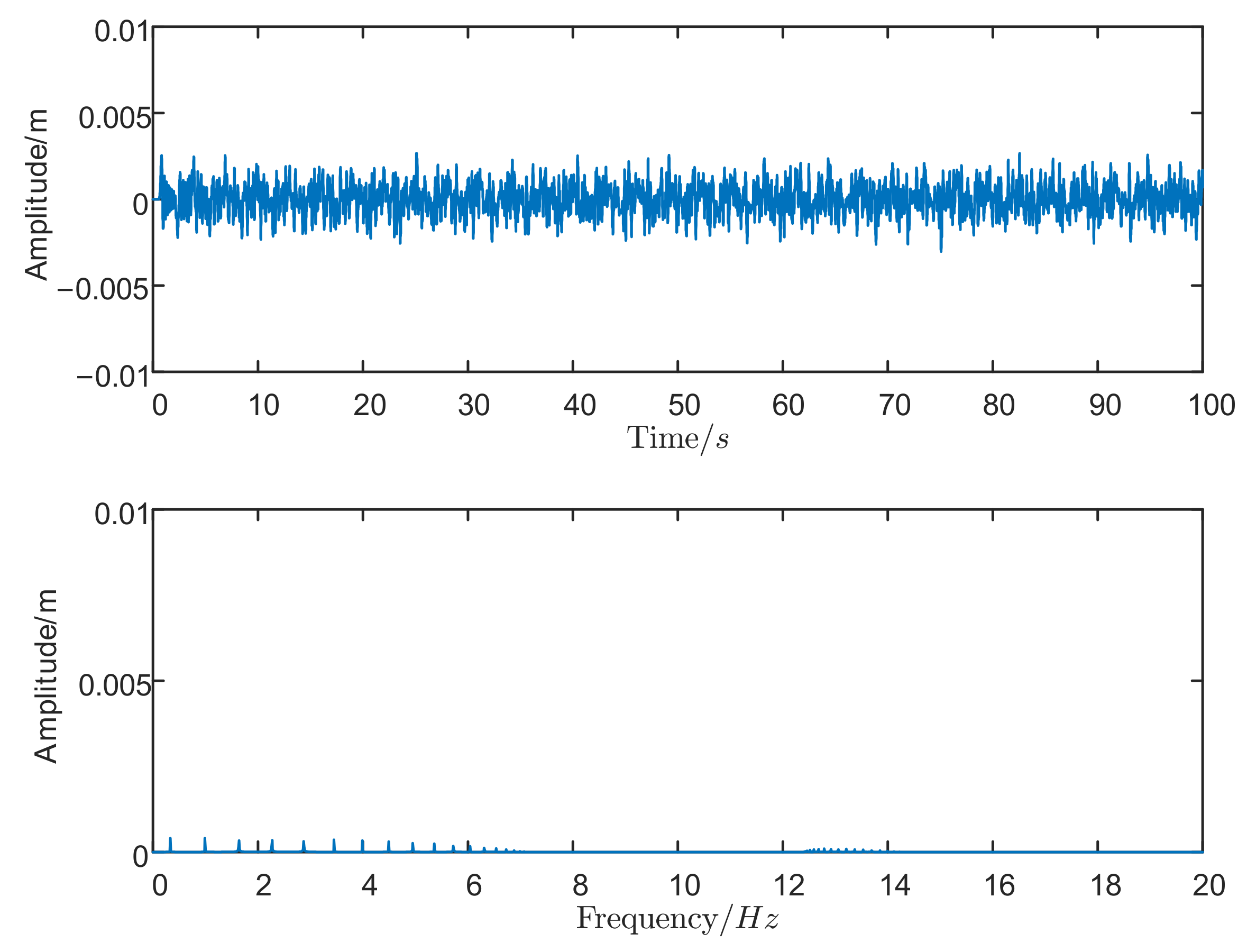
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, C.; Zhang, F.; Jiang, J. Adaptive Boundary Control of Flexible Manipulators with Parameter Uncertainty Based on RBF Neural Network. Shock Vib. 2020, 2020, 8261423. [Google Scholar] [CrossRef]
- Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Baravelli, E.; Ruzzene, M. Internally resonating lattices for bandgap generation and low-frequency vibration control. J. Sound Vib. 2013, 332, 6562–6579. [Google Scholar] [CrossRef]
- Madeo, A.; Collet, M.; Miniaci, M.; Billon, K.; Ouisse, M.; Neff, P. Modeling Phononic Crystals via the Weighted Relaxed Micromorphic Model with Free and Gradient Micro-Inertia. J. Elast. 2018, 130, 59–83. [Google Scholar] [CrossRef]
- Witarto, W.; Nakshatrala, K.B.; Mo, Y.-L. Global sensitivity analysis of frequency band gaps in one-dimensional phononic crystals. Mech. Mater. 2019, 134, 38–53. [Google Scholar] [CrossRef]
- Mo, C.; Singh, J.; Raney, J.R.; Purohit, P.K. Cnoidal wave propagation in an elastic metamaterial. Phys. Rev. E 2019, 100, 013001. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; Wang, T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 2020, 10, 305. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H. Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances. Crystals 2020, 10, 686. [Google Scholar] [CrossRef]
- Choi, C.; Bansal, S.; Münzenrieder, N.; Subramanian, S. Fabricating and Assembling Acoustic Metamaterials and Phononic Crystals. Adv. Eng. Mater. 2021, 23, 2000988. [Google Scholar] [CrossRef]
- He, C.; Lim, K.-M.; Zhang, F.; Jiang, J.-H. Dual-tuning mechanism for elastic wave transmission in a triatomic lattice with string stiffening. Wave Motion Int. J. Report. Res. Wave Phenom. 2022, 112, 102951. [Google Scholar] [CrossRef]
- He, C.; Lim, K.M.; Liang, X.; Zhang, F.; Jiang, J. Tunable band structures design for elastic wave transmission in tension metamaterial chain. Eur. J. Mech. A/Solids 2022, 92, 104481. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, F.; Jiang, J. Ultra-wideband outward-hierarchical metamaterials with graded design. Int. J. Mech. Mater. Des. 2022, 18, 169–184. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, T.-T.; Liang, J.-W.; Wang, Y.-S.; Laude, V. Channeled spectrum in the transmission of phononic crystal waveguides. J. Sound Vib. 2018, 437, 410–421. [Google Scholar] [CrossRef]
- Chen, Z.-G.; Zhao, J.; Mei, J.; Wu, Y. Acoustic frequency filter based on anisotropic topological phononic crystals. Sci. Rep. 2017, 7, 15005. [Google Scholar] [CrossRef]
- Zigoneanu, L.; Popa, B.-I.; Cummer, S.A. Three-dimensional broadband omnidirectional acoustic ground cloak. Nat. Mater. 2014, 13, 352–355. [Google Scholar] [CrossRef]
- Casadei, F.; Beck, B.S.; Cunefare, K.A.; Ruzzene, M. Vibration control of plates through hybrid configurations of periodic piezoelectric shunts. J. Intell. Mater. Syst. Struct. 2012, 23, 1169–1177. [Google Scholar] [CrossRef]
- Wu, X.; Sun, L.; Zuo, S.; Liu, P.; Huang, H. Vibration reduction of car body based on 2D dual-base locally resonant phononic crystal. Appl. Acoust. 2019, 151, 1–9. [Google Scholar] [CrossRef]
- Brooke, D.C.; Umnova, O.; Leclaire, P.; Dupont, T. Acoustic metamaterial for low frequency sound absorption in linear and nonlinear regimes. J. Sound Vib. 2020, 485, 115585. [Google Scholar] [CrossRef]
- Chen, J.; Xiao, J.; Lisevych, D.; Shakouri, A.; Fan, Z. Deep-subwavelength control of acoustic waves in an ultra-compact metasurface lens. Nat. Commun. 2018, 9, 4920. [Google Scholar] [CrossRef] [PubMed]
- Kaina, N.; Lemoult, F.; Fink, M.; Lerosey, G. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature 2015, 525, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Miniaci, M.; Gliozzi, A.S.; Morvan, B.; Krushynska, A.; Bosia, F.; Scalerandi, M.; Pugno, N.M. Proof of Concept for an Ultrasensitive Technique to Detect and Localize Sources of Elastic Nonlinearity Using Phononic Crystals. Phys. Rev. Lett. 2017, 118, 214301. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-N.; Wang, Y.-Z.; Wang, Y.-S. Nonreciprocal phenomenon in nonlinear elastic wave metamaterials with continuous properties. Int. J. Solids Struct. 2018, 150, 125–134. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K. Effects of the initial stress on the propagation and localization properties of Rayleigh waves in randomly disordered layered piezoelectric phononic crystals. Acta Mech. 2011, 216, 291–300. [Google Scholar] [CrossRef]
- Kherraz, N.; Haumesser, L.; Levassort, F.; Benard, P.; Morvan, B. Controlling Bragg gaps induced by electric boundary conditions in phononic piezoelectric plates. Appl. Phys. Lett. 2016, 108, 093503. [Google Scholar] [CrossRef]
- Li, G.-H.; Ma, T.-X.; Wang, Y.-Z.; Wang, Y.-S. Active control on topological immunity of elastic wave metamaterials. Sci. Rep. 2020, 10, 9376. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, K.; Yang, L.; Zhao, R.; Shi, X.; Tian, K. Effect of thermal stresses on frequency band structures of elastic metamaterial plates. J. Sound Vib. 2018, 413, 101–119. [Google Scholar] [CrossRef]
- Bordiga, G.; Cabras, L.; Piccolroaz, A.; Bigoni, D. Prestress tuning of negative refraction and wave channeling from flexural sources. Appl. Phys. Lett. 2019, 114, 041901. [Google Scholar] [CrossRef]
- Xu, X.; Wu, Q.; Chen, H.; Nassar, H.; Chen, Y.; Norris, A.; Haberman, M.R.; Huang, G. Physical Observation of a Robust Acoustic Pumping in Waveguides with Dynamic Boundary. Phys. Rev. Lett. 2020, 125, 253901. [Google Scholar] [CrossRef]
- Banerjee, A.; Das, R.; Calius, E.P. Waves in Structured Mediums or Metamaterials: A Review. Arch. Comput. Methods Eng. 2018, 26, 1029–1058. [Google Scholar] [CrossRef]
- Fang, X.; Wen, J.; Yu, D.; Huang, G.; Yin, J. Wave propagation in a nonlinear acoustic metamaterial beam considering third harmonic generation. New J. Phys. 2018, 20, 123028. [Google Scholar] [CrossRef]
- Yu, M.; Fang, X.; Yu, D. Combinational design of linear and nonlinear elastic metamaterials. Int. J. Mech. Sci. 2021, 199, 106422. [Google Scholar] [CrossRef]
- Bae, M.H.; Oh, J.H. Amplitude-induced bandgap: New type of bandgap for nonlinear elastic metamaterials. J. Mech. Phys. Solid 2020, 139, 103930. [Google Scholar] [CrossRef]
- Fang, X.; Wen, J.; Bonello, B.; Yin, J.; Yu, D. Ultra-low and ultra-broad-band nonlinear acoustic metamaterials. Nat. Commun. 2017, 8, 1288. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Wen, J.; Bonello, B.; Yin, J.; Yu, D. Wave propagation in one-dimensional nonlinear acoustic metamaterials. New J. Phys. 2017, 19, 53007. [Google Scholar] [CrossRef]
- Vakakis, A.F.; King, M.E. Nonlinear wave transmission in a monocoupled elastic periodic system. J. Acoust. Soc. Am. 1995, 98, 1534–1546. [Google Scholar] [CrossRef]
- Silva, P.B.; Leamy, M.J.; Geers, M.G.D.; Kouznetsova, V.G. Emergent subharmonic band gaps in nonlinear locally resonant metamaterials induced by autoparametric resonance. Phys. Rev. E 2019, 99, 063003. [Google Scholar] [CrossRef]
- Manktelow, K.L.; Leamy, M.J.; Ruzzene, M. Weakly nonlinear wave interactions in multi-degree of freedom periodic structures. Wave Motion 2014, 51, 886–904. [Google Scholar] [CrossRef]
- Wei, L.-S.; Wang, Y.-Z.; Wang, Y.-S. Nonreciprocal transmission of nonlinear elastic wave metamaterials by incremental harmonic balance method. Int. J. Mech. Sci. 2020, 173, 105433. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]


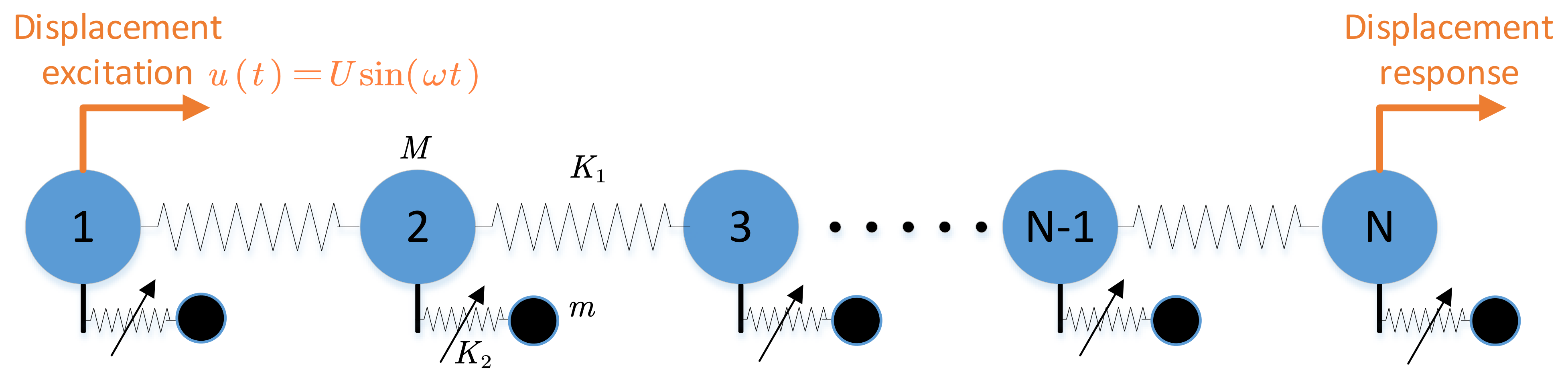
| K1 | K2 | M | m |
|---|---|---|---|
| 1000 N/m | 2000 N/m | 1 kg | 0.5 kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, N.; Jiang, J.; Zhang, F.; Ding, M. Nonlinear Tunability of Elastic Waves in One-Dimensional Mass-Spring Lattices Attached with Local Resonators. Aerospace 2022, 9, 818. https://doi.org/10.3390/aerospace9120818
Shen N, Jiang J, Zhang F, Ding M. Nonlinear Tunability of Elastic Waves in One-Dimensional Mass-Spring Lattices Attached with Local Resonators. Aerospace. 2022; 9(12):818. https://doi.org/10.3390/aerospace9120818
Chicago/Turabian StyleShen, Nansun, Jinhui Jiang, Fang Zhang, and Ming Ding. 2022. "Nonlinear Tunability of Elastic Waves in One-Dimensional Mass-Spring Lattices Attached with Local Resonators" Aerospace 9, no. 12: 818. https://doi.org/10.3390/aerospace9120818
APA StyleShen, N., Jiang, J., Zhang, F., & Ding, M. (2022). Nonlinear Tunability of Elastic Waves in One-Dimensional Mass-Spring Lattices Attached with Local Resonators. Aerospace, 9(12), 818. https://doi.org/10.3390/aerospace9120818







