Frequency Domain Design Method of the Aeroengine Fuel Servo Constant Pressure Difference Control System with High Performance
Abstract
1. Introduction
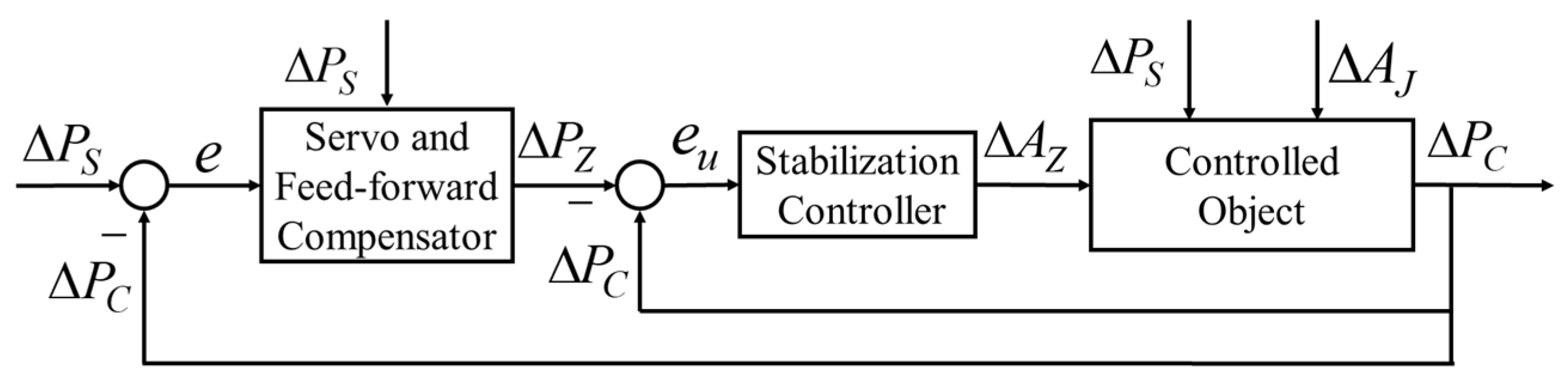
- Firstly, this paper adopts the linear incremental analysis method, which is based on the state space theory, and this method successfully reveals the design theory of the constant pressure difference regulating mechanism. The results clearly show that the system has three elements: the controlled object, the stabilization controller, and the servo and feed-forward compensator.
- Secondly, the precise state space models and frequency domain models of the system are established. On the basis concerning the advantage of frequency domain analysis methods, the accurate influences of the design parameters on the dynamic performance and stability of the system are analyzed, and the effective guidance measures are provided.
- Finally, a frequency domain design method of the core parameters is proposed, which includes the stabilization control gain and the servo control gain, and the method is proven to solve the design work efficiently and accurately.
2. Design Theory and Dynamic Equations
2.1. Design Theory
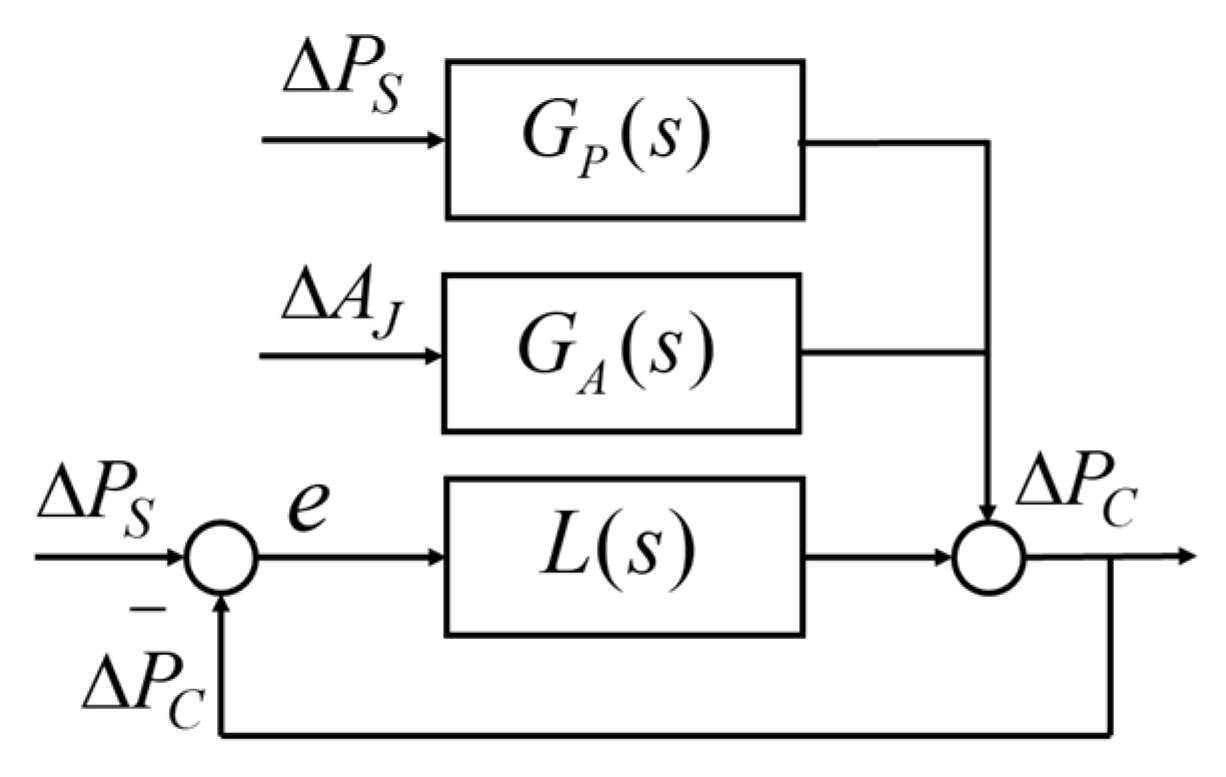
- Firstly, and are the disturbance inputs, and the disturbances caused by them are rejected through the regulation function of the stabilization controller.
- Secondly, is the reference input, and the controlled pressure increment servo tracks it through the regulation function of the servo compensator.
- Thirdly, is the feed-forward input, and the regulation ability of the system is improved, and the steady error is reduced.
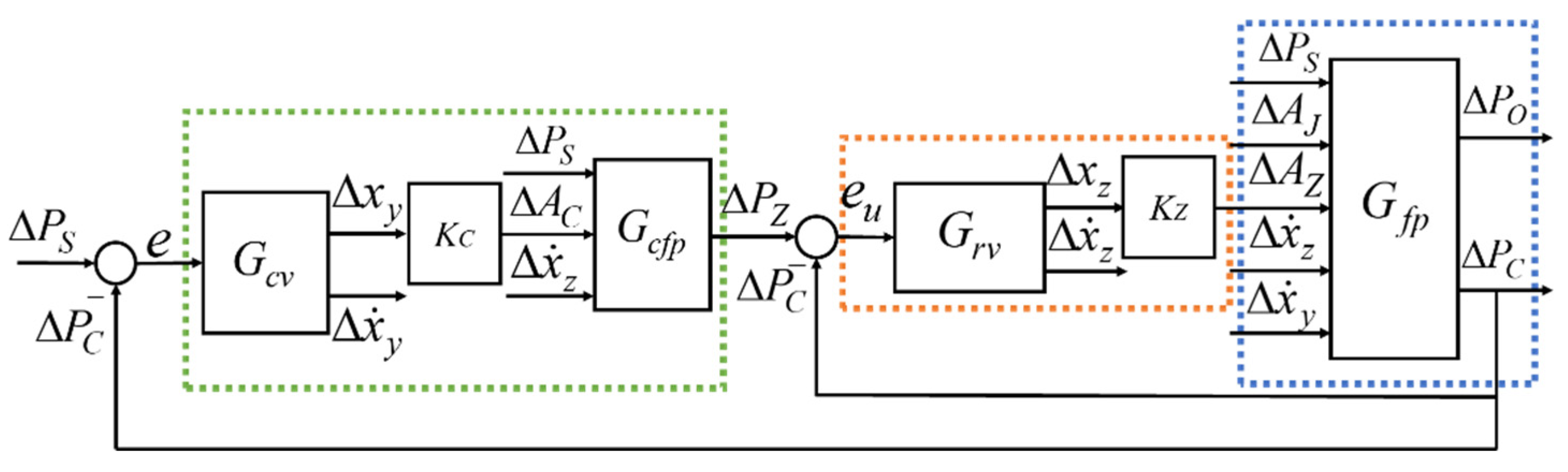
2.2. Composition of the Controllers
- is the dynamic matrix of the controlled object.
- is the dynamic matrix of the regulating motion valve, and is the generalized stabilization control gain, and they construct the stabilization controller.
- is the dynamic matrix of the compensated motion valve, is the generalized servo control gain, and is the dynamic matrix of the feed-forward compensated flow path, and they construct the servo and feed-forward compensator.
2.2.1. Controlled Object
2.2.2. Stabilization Controller
2.2.3. Servo and Feed-Forward Compensator
3. Frequency Domain Analysis
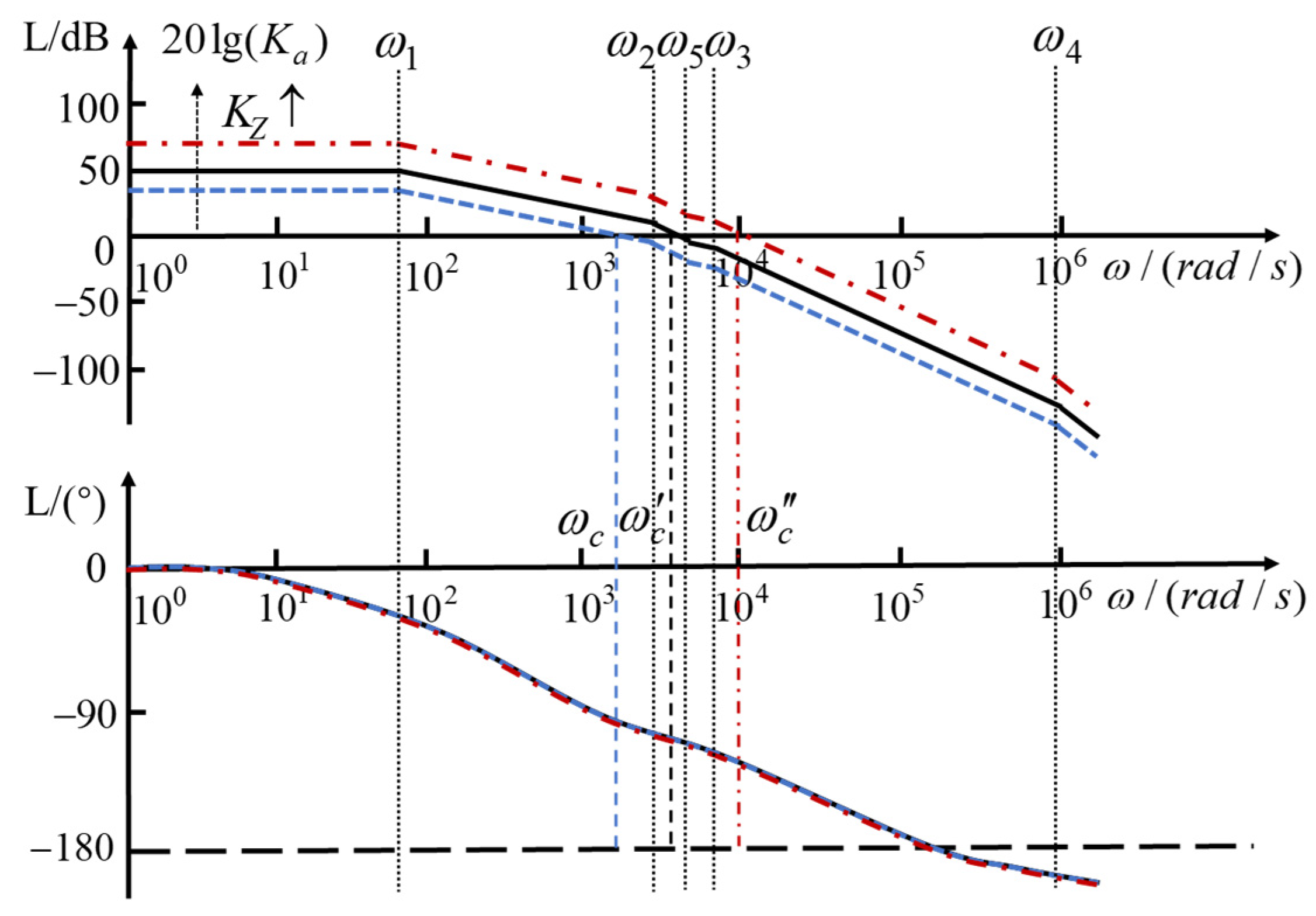
3.1. Design Analysis of the Stabilization Controller
3.1.1. Calculation of the Open-Loop Transfer Function
3.1.2. Calculation of the Corner Frequencies
- If , the second-order section is an underdamped oscillation link, and its poles are:The corner frequencies are defined as:
- If , the second-order section is an overdamped nonoscillation link, and its poles are:The corner frequencies are defined as:The third and fourth poles are:The corner frequencies are defined as:The zero is:The corner frequency is defined as:The open-loop gain of the inner loop is:
- The stabilization control gain only affects the open-loop gain;
- The spring stiffness affects , , and the open-loop gain,
- The volume of the controlled chamber and the volume of the ejection chamber affect , , and .
- Increasing the stabilization control gain ;
- Reducing the spring stiffness ;
- Increasing the pressure-bearing area .
3.1.3. Influence of the Stabilization Control Gain on the Frequency Domain Performance
- The steady-state gain increases according to Equation (32), and the steady error caused by disturbances is reduced, bringing a better disturbance rejection performance;
- The crossover frequency increases, and the settling time is reduced, bringing a faster response performance;
- The slope of the magnitude curve at the crossover frequency increases, and the damping ratio decreases, bringing a bigger overshoot;
- The phase margin decreases, bringing a worse robustness performance.
3.1.4. Stability Analysis
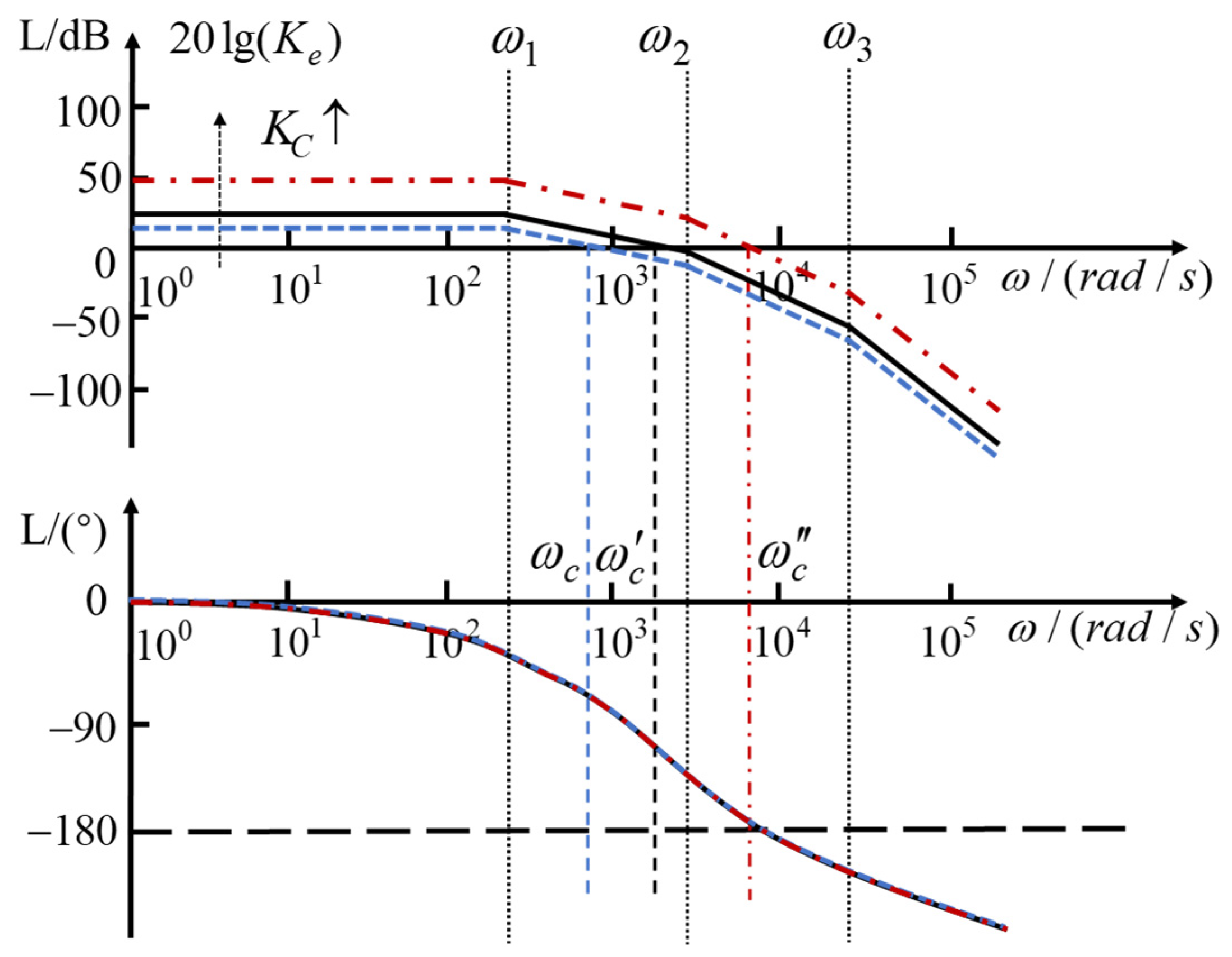
3.2. Design Analysis of the Servo and Feed-Forward Compensator
3.2.1. Calculation of the Open-Loop Transfer Function
3.2.2. Calculation of the Corner Frequencies
- If , the second-order section is an underdamped oscillation link, and its poles are:The corner frequencies are defined as:
- If , the second-order section is an overdamped nonoscillation link, and its poles are:The corner frequencies are defined as:The third pole is:The corner frequency is defined as:The open-loop gain of the servo compensator is:
- The control gain only affects the open-loop gain;
- The spring stiffness affects , , and the open-loop gain;
- The volume of the regulating chamber affects .
- Increasing the control gain ;
- Reducing the spring stiffness ;
- Increasing the pressure-bearing area ;
- Increasing the compensated flow area .
- Reducing the mass of the compensated motion valve;
- Increasing the viscous friction coefficient of the compensated motion valve.
3.2.3. Influence of the Servo Control Gain on the Frequency Domain Performance
- The open loop gain increases according to Equation (46), and the steady error caused by reference input is reduced, bringing a better servo tracking performance;
- The crossover frequency increases, and the settling time is reduced, bringing a faster response performance;
- The slope of the magnitude curve at the crossover frequency increases, and the damping ratio decreases, bringing a bigger overshoot;
- The phase margin decreases, bringing a worse robustness performance.
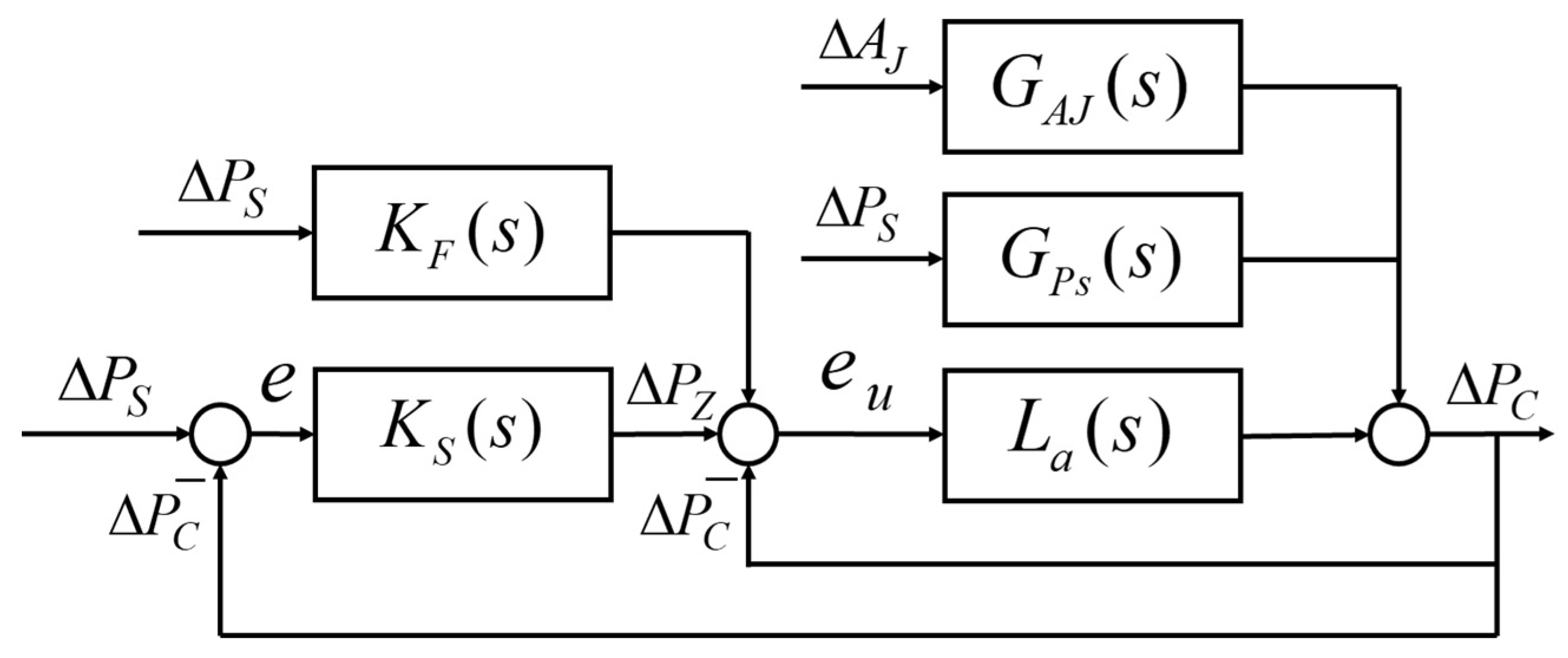
3.3. Calculation of the Transfer Functions
- The open-loop transfer function from to is .
- The open-loop transfer function from to is .
4. Frequency Domain Design Method
- Steady-state performance: the designed pressure difference is , and the phase margin is more than N °.
- Dynamic performance: the regulating time is not more than , and the overshoot is not more than .
4.1. Calculation of the Control Gains
4.1.1. Calculation of the Stabilization Control Gain
4.1.2. Calculation of the Servo Control Gain
- There is a servo control gain extremum that makes the system asymptotically stable, expressed as , then it has:
- There is a minimum control gain value that makes the system within the phase margin constraint, expressed as , then it has:
- There is a control-gain working range that makes the system within the dynamic performance constraint expressed as , then it has:
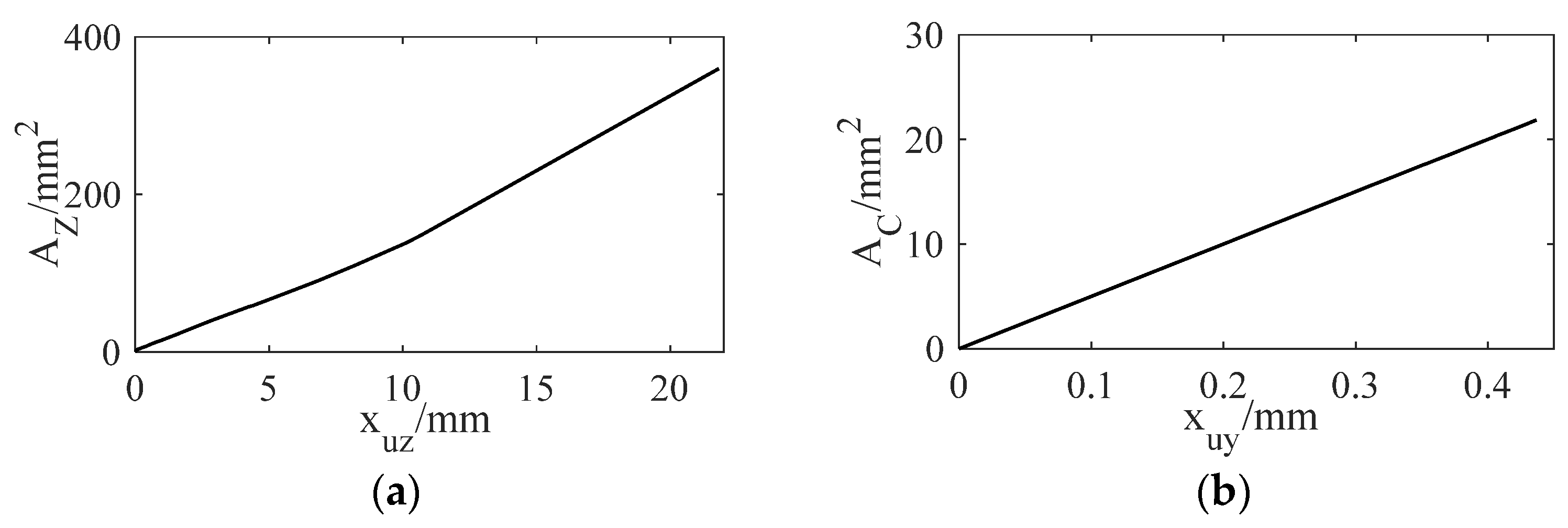
4.2. Geometry Design of the Orifices
4.2.1. The Regulating Motion Valve Orifice
4.2.2. The Compensated Motion Valve Orifice
4.3. Parameters Design of the Motion Valves
4.3.1. The Regulating Motion Valve
4.3.2. The Compensated Motion Valve
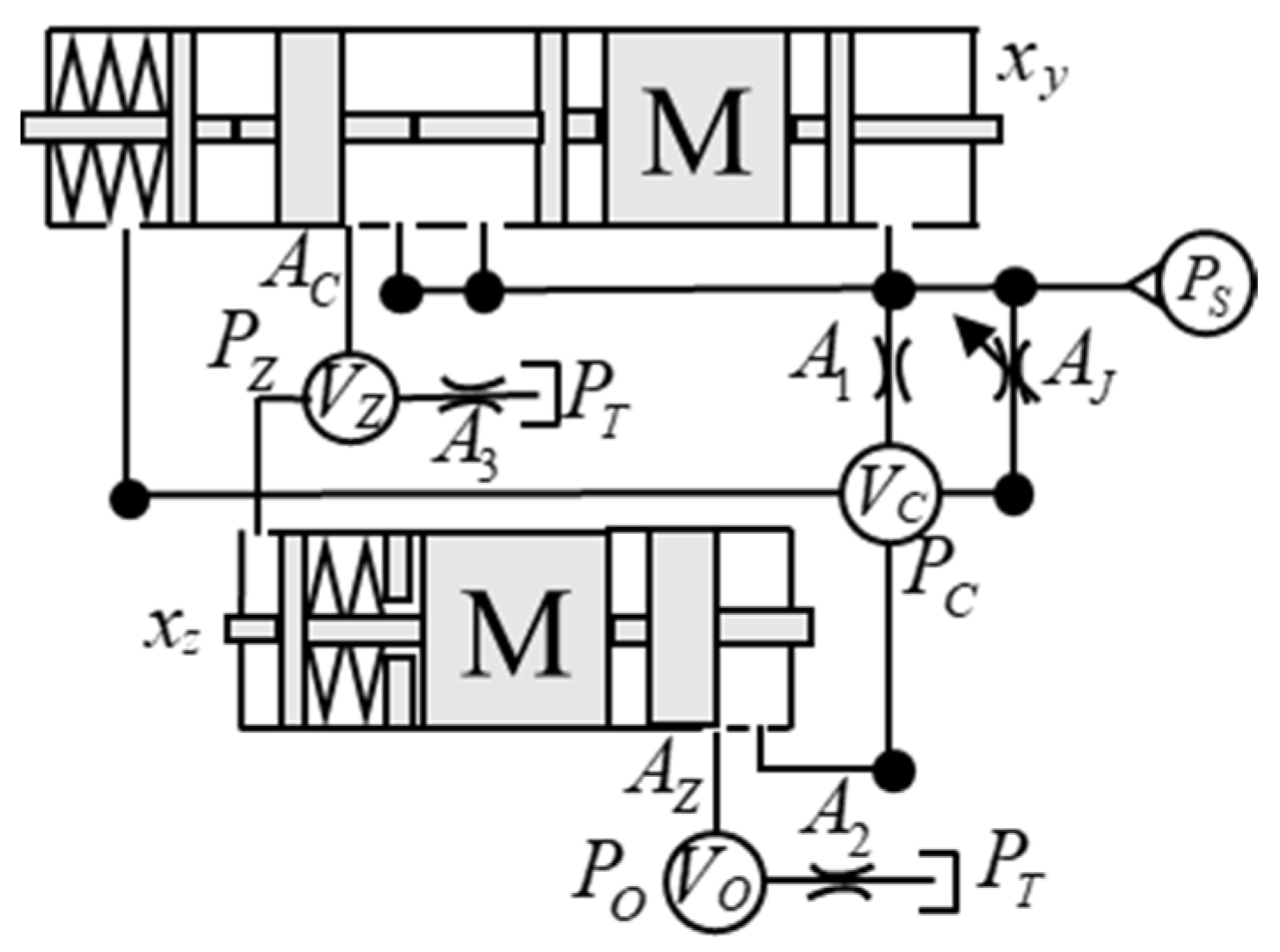
5. Design Example
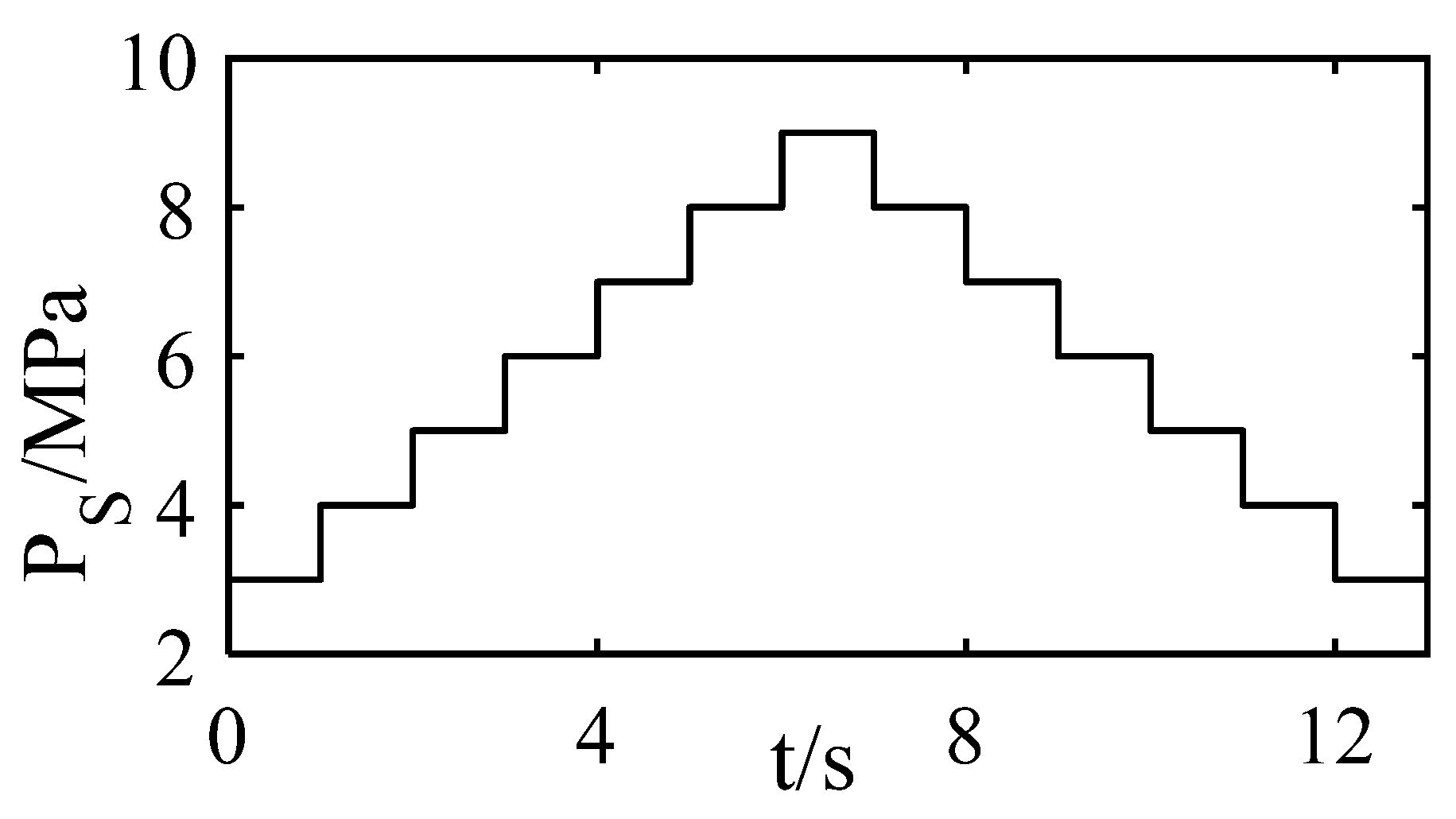
- The working range of the inlet pressure is [3, 9] MPa;
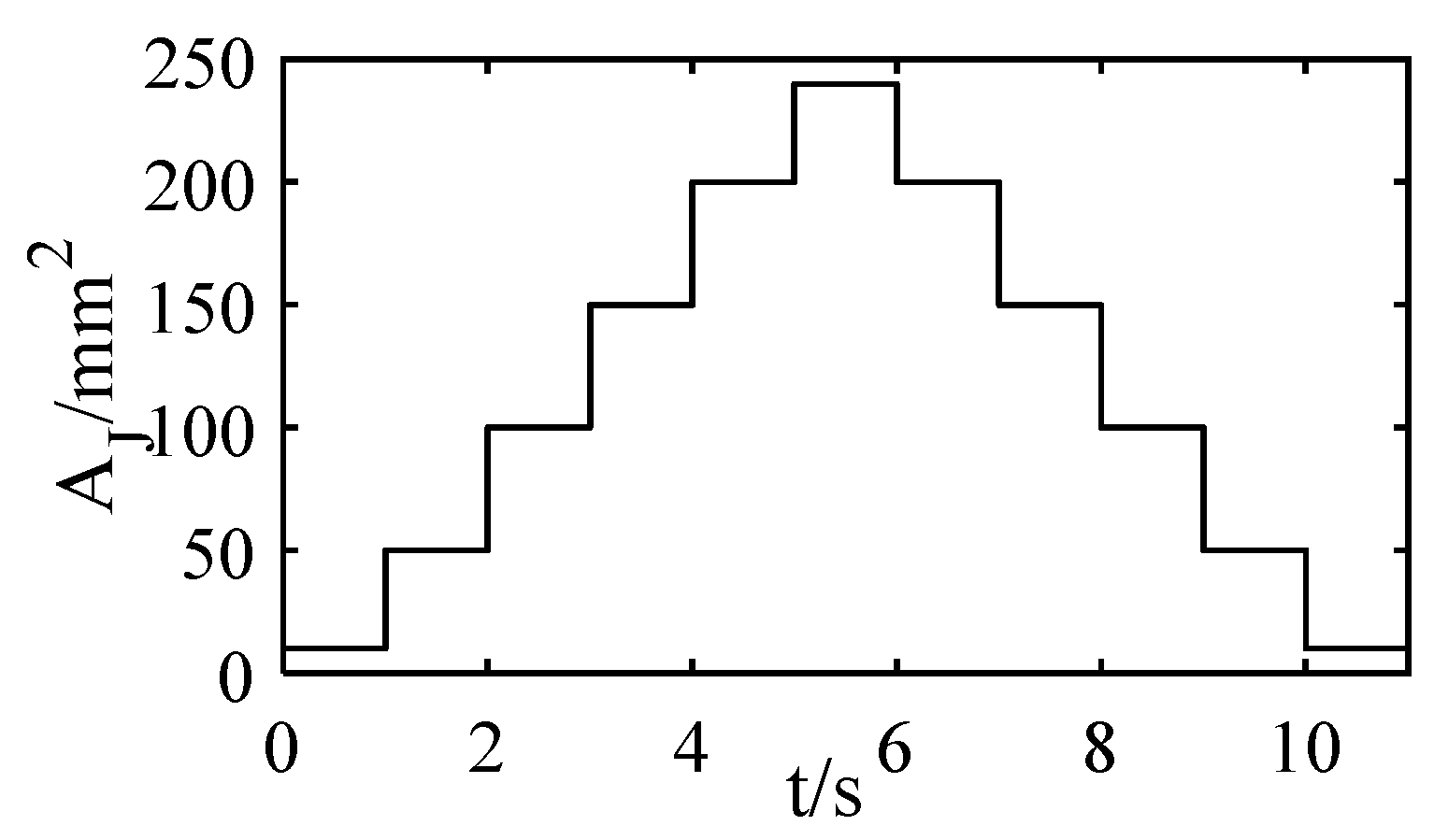
- The working range of the variable inlet flow area is [10, 240] × 10−6 m2.
- The designed pressure difference is 0.92 ± 0.01 MPa, and the phase margin is more than 70°;
- The regulating time is not more than 0.01 s, and the overshoot is not more than 10%.
- Design the stabilization control law ;
- Design the servo control law .
5.1. Dynamic Design of the First Working Point
5.1.1. Calculation of the Stabilization Control Gain
5.1.2. Calculation of the Servo Control Gain
5.2. Dynamic Design of Other Working Points
- The stabilization control gain extrema that make the inner loop system stable are shown in Table 3.
- The design processes in Section 4.1 are executed; then, the value pair can be obtained, as shown in Table 4.
- The design processes in Section 4.1 are executed; then, the value pair can be obtained, as shown in Table 5.
5.3. Parameters Design of the Valves
5.3.1. Parameters Design of the Regulating Motion Valve
5.3.2. Parameters Design of the Compensated Motion Valve
5.3.3. Geometry Design of the Orifices
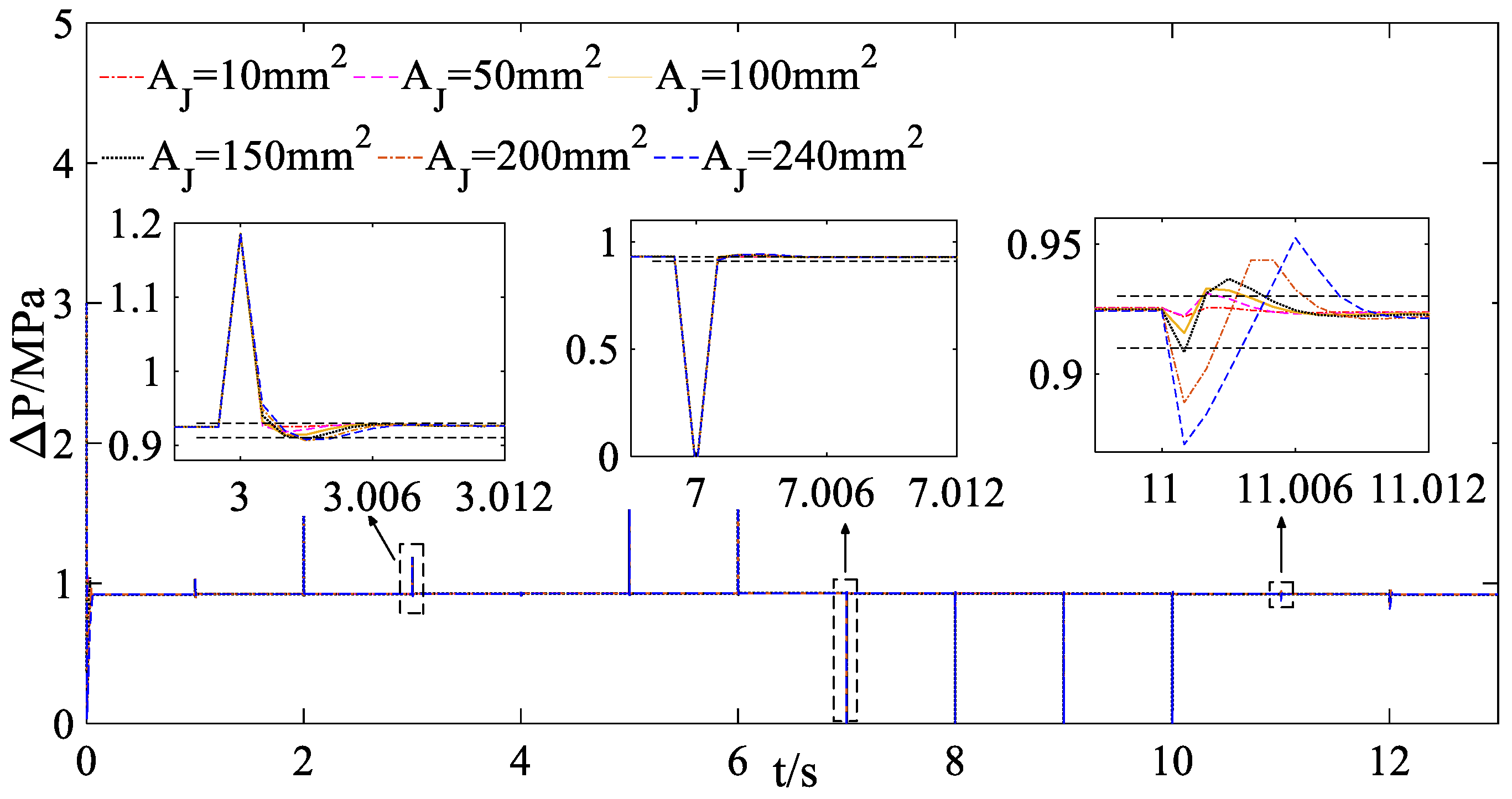
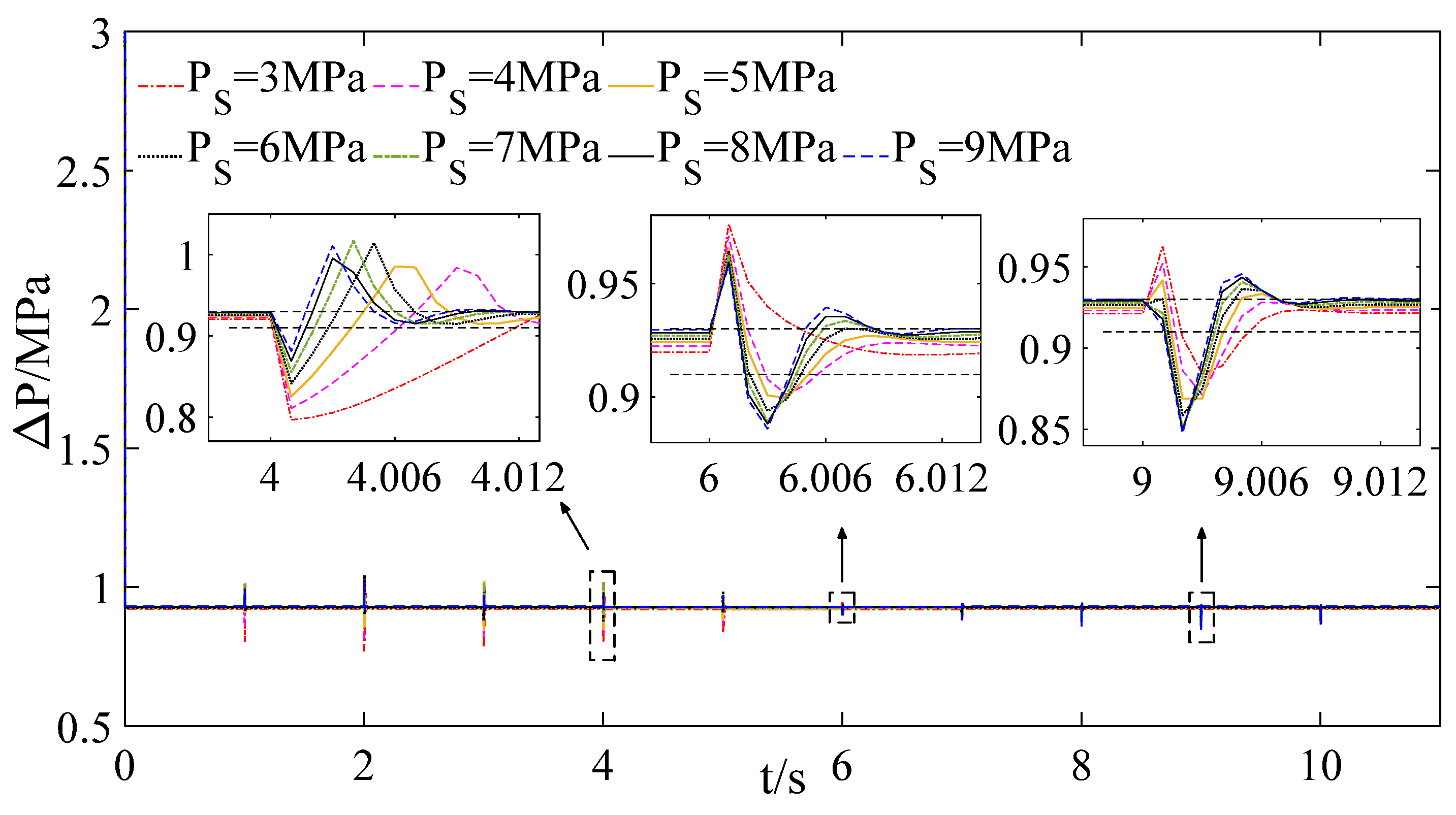
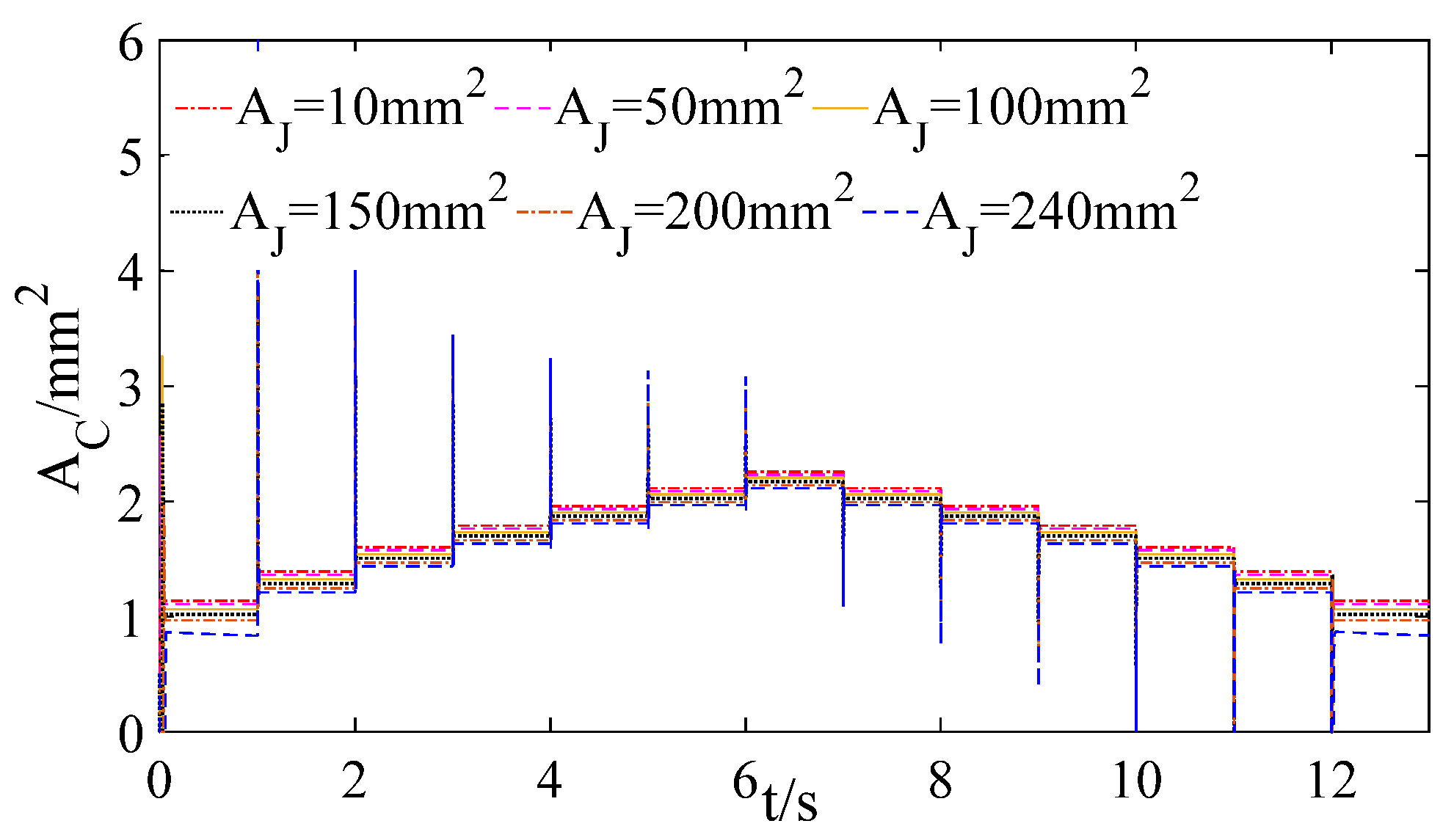
5.4. Simulation and Discussion
5.4.1. Simulation
5.4.2. Discussion
6. Conclusions
- Compared with the classic analysis method based on direct transfer function transformation, the linear incremental method is based on the state space, and it is clearer to reveal the design theory of the constant pressure difference regulating mechanism. Furthermore, the analysis method also clarifies the key design parameters, including the stabilization control gain and the servo control gain, which was not involved in previous research.
- Concerning the advantage of the explicit description between the designed parameters and the performance when analyzed by the loop transfer functions, the frequency domain analysis method clearly describes the quantitative influence of the control gains on the frequency domain performance of the closed-loop system and provides more correct guidance for the design of the performance parameters, avoiding trial and error in simulation research.
- The simulation results show that the steady and dynamic performance all meet the design requirements when utilizing the proposed frequency domain design method; especially, the steady-state error is very small, and the phase margin is very large, which are beyond the design requirements. Evidently, the proposed design methods are correct and accurate and can be widely applied in the analysis and predesign of other components of the fuel metering system, such as the constant pressure control system and the position control system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, F.; Wang, X.; Cheng, T.; Liu, X. Dynamic characteristics analysis of a pressure differential valve. Aeroengine 2015, 41, 44–50. [Google Scholar] [CrossRef]
- Ma, C.Y. The analysis and design of hydraulic pressure-reducing valves. J. Eng. Ind. 1967, 89, 301. [Google Scholar] [CrossRef]
- Fan, R.; Zhang, M. The establishment of pilot-operated relief valve’s dynamic mathematic model and the dynamic properties analysis. J. Zheng Zhou Text. Inst. 1997, 3, 58–61. [Google Scholar]
- Wu, D.; Burton, R.; Schoenau, G.; Bitner, D. Analysis of a pressure—Compensated flow control valve. J. Dyn. Syst. Meas. Control. 2007, 129, 203–211. [Google Scholar] [CrossRef]
- Wen, Y.J. Analysis of characteristics of oil return differential pressure valve with EASY5. In Proceedings of the 11th Symposium on Automatic Engine Control of CAA, Beijing, China, 8–10 November 2002; pp. 21–26. [Google Scholar]
- Hong, W.; Liu, H.L.; Wang, G.Z.; Qin, J. Research on pressure characteristics of relief valve without pressure overshoot. Chin. Hydraul. Pneum. 2012, 10, 104–106. [Google Scholar] [CrossRef]
- Shang, Y.; Guo, Y.Q.; Wang, L. Study of impact of design parameter of differential pressure controller on fuel metering system. Aeronaut. Manuf. Technol. 2013, 6, 89–91. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y.Y.; Yang, L.M.; Li, Y.H. Design and Simulation of Large Flowrate Fuel Metering Valve of Aero engine Based on AMESim. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, H.C.; Ye, Z.F. AMESim simulation of afterburning metering unit for fuel system. Aeroengine 2014, 40, 62–66. [Google Scholar] [CrossRef]
- Zeng, D.T.; Wang, X.; Tan, D.L.; Xu, M. Fuel scavenger contour performance analysis of fuel metering devices. Aeroengine 2010, 36, 38. [Google Scholar] [CrossRef]
- Zeng, D.T.; Wang, X. Design and analysis of characteristics of damping hole for a fuel metering valve. In Proceedings of the 2010 International Conference on Mechanical and Electrical Technology, Kyoto, Japan, 1–3 August 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Zeng, D.T.; Wang, X.; Tan, D.L. Effects of fuel returned shape on metering devices characteristics. Aeroengine 2012, 38, 46. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Wang, H.Y.; Miao, W.B. Analysis on modeling of constant pressure difference valve for a turboshaft engine. Aeroengine 2014, 40, 75–78. [Google Scholar] [CrossRef]
- Maiti, R.; Pan, S.; Bera, D. Analysis of a load sensing hydraulic flow control valve. Proc. JFPS Int. Symp. Fluid Power 1996, 1996, 307–312. [Google Scholar] [CrossRef][Green Version]
- Amirante, R.; Vescovo, G.D.; Lippolis, A. Evaluation of the flow forces on an open centre directional control valve by means of a computational fluid dynamic analysis. Energy Convers. Manag. 2006, 47, 1748–1760. [Google Scholar] [CrossRef]
- Okungbowa, B.; Stanley, N. CFD Analysis of Steady State Flow Reaction Forces in a Rim Spool Valve. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2006. [Google Scholar]
- Amirante, R.; Vescovo, G.D.; Lippolis, A. Flow forces analysis of an open center hydraulic directional control valve sliding spool. Energy Convers. Manag. 2006, 47, 114–131. [Google Scholar] [CrossRef]
- Valdes, J.R.; Miana, M.J.; Nunez, J.L. Reduced order model for estimation of fluid flow and flow forces in hydraulic proportional valves. Energy Convers. Manag. 2008, 49, 1517–1529. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Y.Q.; Liao, G.H. Structure design and performance calculation of a differential pressure measuring device. In Proceedings of the 12th Engine Automatic Control Academic Conference of CAAC, Hong Kong, China, 1–5 November 2004; pp. 158–162. [Google Scholar]
- Deng, Z.J.; Guo, L.Y. Analysis of speed fluctuation in bench test of aero-engine numerical control system. China Sci. Technol. Overv. 2020, 15, 63–65. [Google Scholar]
- Wang, Y.; Fan, D.; Zhang, C.; Peng, K.; Shi, D.Y. Design and analysis of the variable pressure-drop fuel metering device. In Proceedings of the 36th Chinese Control Conference, Dalian, China, 26–28 July 2017; pp. 6434–6439. [Google Scholar]
- Yuan, Y.; Zhang, T.H.; Lin, Z.L.; Zhang, J.M. An investigation into factors determining the metering performance of a fuel control unit in an aero engine. Flow Meas. Instrum. 2020, 71, 1–6. [Google Scholar] [CrossRef]
- Agh, S.M.; Pirkandi, J.; Mahmoodi, M.; Jahromi, M. Optimum design simulation and test of a new flow control valve with an electronic actuator for turbine engine fuel control system. Flow Meas. Instrum. 2019, 65, 65–77. [Google Scholar] [CrossRef]
- Merritt, H.E. Hydraulic Control Systems; John Wiley: New York, NY, USA, 1967; pp. 360–374. [Google Scholar] [CrossRef]
- Fitch, E.C.; Hong, I.T. Hydraulic Component Design and Selection; Bardyn Incorporation: Etobicoke, ON, Canada, 2004; pp. 205–213. [Google Scholar]
- Li, C.G.; He, Y.M. Modeling and Simulation Analysis of Hydraulic System; Aviation Industry Press: Beijing, China, 2008; pp. 2–11. [Google Scholar]
- Wang, X.; Yang, S.B.; Zhu, M.Y.; Kong, X.X. Aeroengine Control Principles; Science Press: Beijing, China, 2021; pp. 128–257. [Google Scholar]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control with Aerospace Applications; Springer: London, UK, 2012; pp. 27–72. [Google Scholar] [CrossRef]
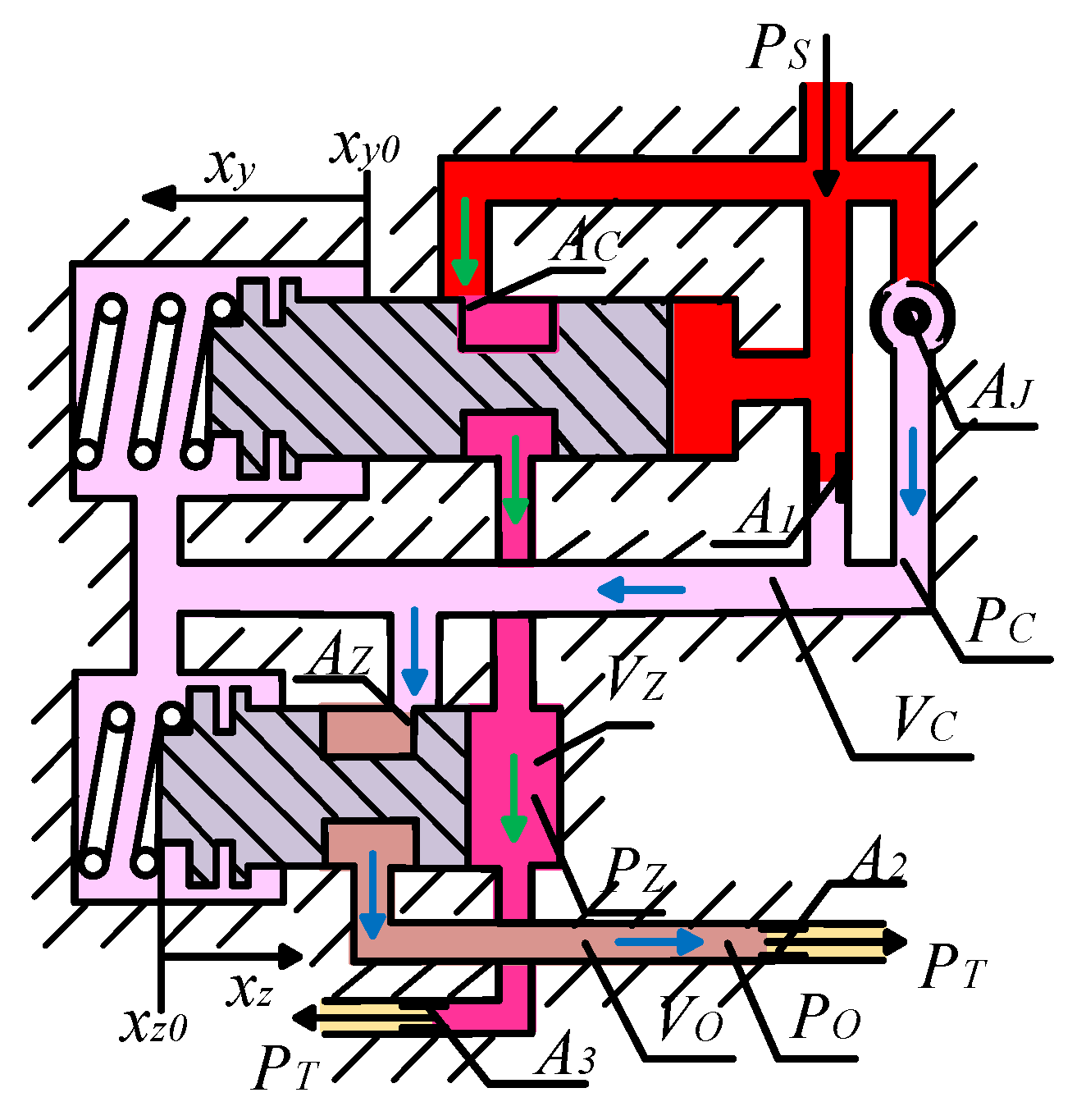
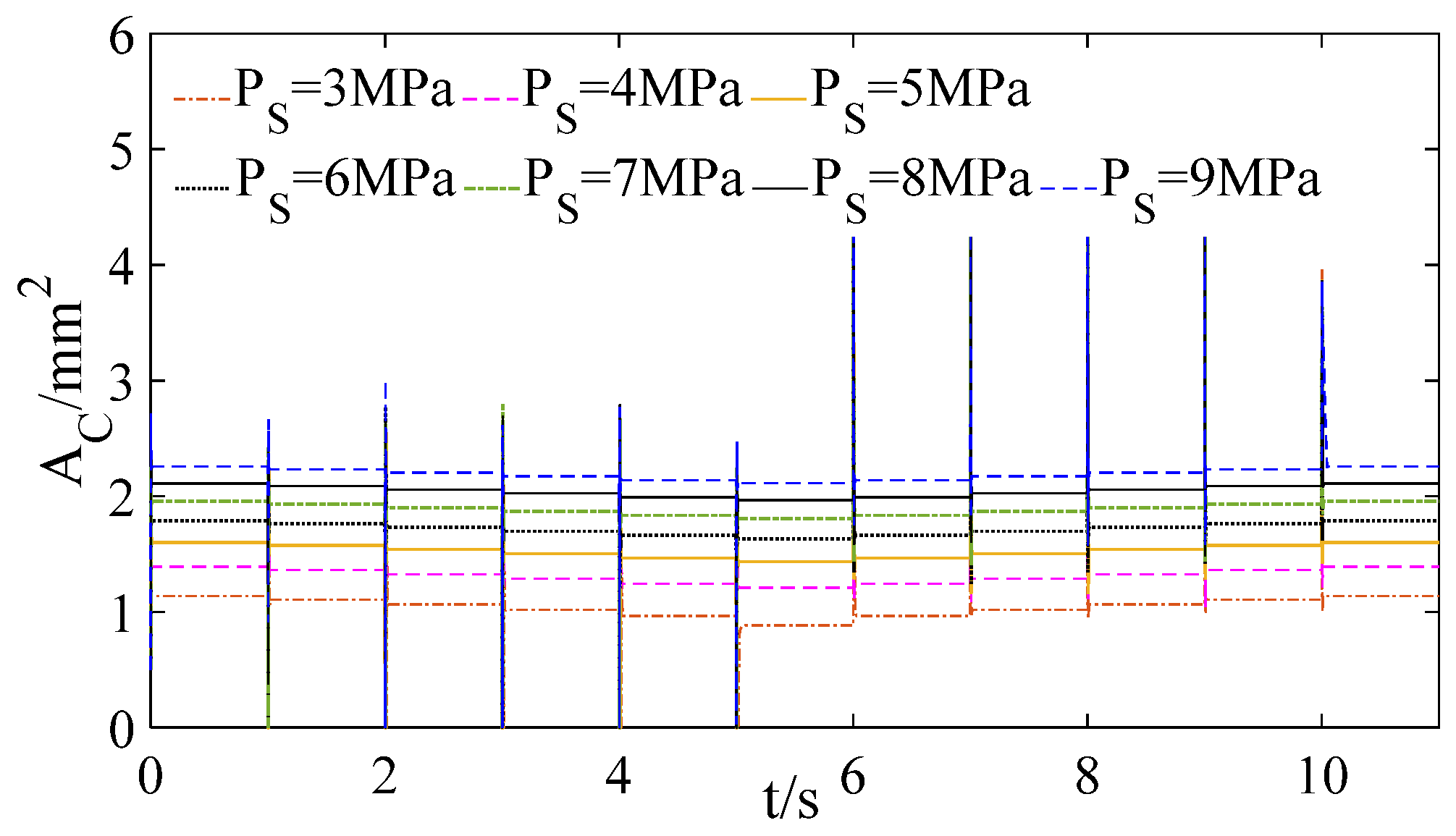
| Parameter/Unit | Value | Parameter/Unit | Value |
|---|---|---|---|
| /Kg | 0.08 | /Kg | 0.05 |
| /(N/m) | 40,000 | /(N/m) | 15,000 |
| /(N/(m/s)) | 200 | /(N/(m/s)) | 200 |
| /m | 0.036 | /m | 0.036 |
| /m2 | 2.827433 × 10−7 | /m3 | 2 × 10−6 |
| /m2 | 1.900664 × 10−4 | /m3 | 2 × 10−6 |
| /m2 | 6.2831852 × 10−6 | /m3 | 4.908739 × 10−4 |
| /(Kg/m3) | 780 | /bar | 17,000 |
| /Pas | 0.051 | 1000 | |
| 0.7 | /bar | 2 |
| 0.0005 | 4.61 | (0.06, 3.30) | 0.49 |
| 0.001 | 4.60 | (0.03, 3.20) | 0.49 |
| 0.005 | 4.56 | (0.02, 3.20) | 0.50 |
| 0.010 | 4.50 | (0.02, 3.20) | 0.50 |
| 0.015 | 4.44 | (0.02, 3.20) | 0.50 |
| 0.020 | 4.38 | (0.01, 3.20) | 0.50 |
| MPa | mm2 | mm2 | |
|---|---|---|---|
| 3 | 10 | 7.1413178 | 0.276 |
| 30 | 21.258905 | 2.560 | |
| 80 | 58.720918 | 26.510 | |
| 160 | 138.75330 | 239.530 | |
| 240 | 359.53286 | 5574.50 | |
| 5 | 10 | 4.9691655 | 0.1328 |
| 30 | 14.750547 | 1.188 | |
| 80 | 39.904931 | 10.328 | |
| 160 | 85.546194 | 59.495 | |
| 240 | 148.38949 | 235.570 | |
| 7 | 10 | 4.0360839 | 0.0944 |
| 30 | 11.969912 | 0.834 | |
| 80 | 32.175269 | 6.792 | |
| 160 | 67.213819 | 34.532 | |
| 240 | 109.70300 | 107.490 | |
| 9 | 10 | 3.4862689 | 0.07609 |
| 30 | 10.334703 | 0.668 | |
| 80 | 27.693258 | 5.255 | |
| 160 | 57.160884 | 25.153 | |
| 240 | 90.995231 | 71.128 |
| No. | mm2 | mm | mm2 | |
|---|---|---|---|---|
| 1 | 3.4862689 | 0.0100 | 0 | 20.252534 |
| 2 | 4.0360839 | 0.0115 | 0.054981500 | 17.559553 |
| 3 | 4.9691655 | 0.0130 | 0.136119030 | 14.367214 |
| 4 | 7.1413178 | 0.0145 | 0.303207669 | 10.215733 |
| 5 | 10.334703 | 0.0130 | 0.523441131 | 20.364172 |
| 6 | 11.969912 | 0.0120 | 0.649226439 | 17.672847 |
| 7 | 14.750547 | 0.0130 | 0.880946022 | 14.490336 |
| 8 | 21.258905 | 0.0140 | 1.381588945 | 10.363465 |
| 9 | 27.693258 | 0.0130 | 1.841185588 | 20.652604 |
| 10 | 32.175269 | 0.0135 | 2.185955665 | 17.974697 |
| 11 | 39.904931 | 0.0125 | 2.758523220 | 14.812128 |
| 12 | 57.160884 | 0.0110 | 4.138999460 | 21.182637 |
| 13 | 58.720918 | 0.0125 | 4.280820733 | 10.781931 |
| 14 | 67.213819 | 0.0130 | 4.960252813 | 18.554773 |
| 15 | 85.546194 | 0.0135 | 6.370435505 | 15.482255 |
| 16 | 90.995231 | 0.0140 | 6.774067876 | 21.837585 |
| 17 | 109.70300 | 0.0150 | 8.110337090 | 19.275786 |
| 18 | 138.75330 | 0.0175 | 10.04702376 | 11.723734 |
| 19 | 148.38949 | 0.0190 | 10.59766319 | 16.368022 |
| 20 | 359.53286 | 0.0200 | 21.71047213 | 14.305249 |
| MPa | mm2 | mm2 | Margin/° | ||||
|---|---|---|---|---|---|---|---|
| 3 | 10 | 10.215733 | 3.79 | (0.02, 1.50) | 0.41 | 0.05 | 96.6 |
| 30 | 10.363465 | 3.55 | (0.02, 0.75) | 0.25 | 0.05 | 96.9 | |
| 80 | 10.781931 | 3.74 | (0.02, 0.55) | 0.17 | 0.05 | 102.0 | |
| 160 | 11.723734 | 3.56 | (0.03, 0.45) | 0.15 | 0.05 | 107.0 | |
| 240 | 14.305249 | 2.74 | (0.04, 0.50) | 0.20 | 0.05 | 117 | |
| 5 | 10 | 14.367214 | 4.06 | (0.02, 2.10) | 0.46 | 0.05 | 101.0 |
| 30 | 14.490336 | 3.40 | (0.02, 1.55) | 0.27 | 0.05 | 98.3 | |
| 80 | 14.812128 | 3.28 | (0.02, 1.25) | 0.18 | 0.05 | 102.0 | |
| 160 | 15.482255 | 3.47 | (0.03, 1.10) | 0.15 | 0.05 | 106.0 | |
| 240 | 16.368022 | 3.36 | (0.03, 0.85) | 0.13 | 0.05 | 93.7 | |
| 7 | 10 | 17.559553 | 4.29 | (0.02, 3.10) | 0.49 | 0.05 | 104.0 |
| 30 | 17.672847 | 3.34 | (0.02, 2.55) | 0.28 | 0.05 | 99.9 | |
| 80 | 17.974697 | 2.97 | (0.02, 2.10) | 0.17 | 0.05 | 103.0 | |
| 160 | 18.554773 | 3.12 | (0.03, 2.05) | 0.14 | 0.05 | 104.0 | |
| 240 | 19.275786 | 3.24 | (0.03, 1.75) | 0.12 | 0.05 | 87.0 | |
| 9 | 10 | 20.252534 | 4.50 | (0.02, 3.20) | 0.50 | 0.05 | 106.0 |
| 30 | 20.364172 | 3.27 | (0.02, 2.95) | 0.29 | 0.05 | 102.0 | |
| 80 | 20.652604 | 2.79 | (0.02, 2.25) | 0.17 | 0.05 | 104.0 | |
| 160 | 21.182637 | 2.94 | (0.03, 2.15) | 0.14 | 0.05 | 105.0 | |
| 240 | 21.837585 | 2.97 | (0.03, 2.05) | 0.10 | 0.05 | 79.6 |
| mm | mm2 | mm | mm2 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.1 | 3.4862689 | 0.20431466 | 10.215733 |
| 0.154981500 | 4.0360839 | 0.2072693 | 10.363465 |
| 0.236119030 | 4.9691655 | 0.21563862 | 10.781931 |
| 0.403207669 | 7.1413178 | 0.23447468 | 11.723734 |
| 0.623441131 | 10.334703 | 0.28610498 | 14.305249 |
| 0.749226439 | 11.969912 | 0.28734428 | 14.367214 |
| 0.980946022 | 14.750547 | 0.28980672 | 14.490336 |
| 1.481588945 | 21.258905 | 0.29624256 | 14.812128 |
| 1.941185588 | 27.693258 | 0.3096451 | 15.482255 |
| 2.285955665 | 32.175269 | 0.32736044 | 16.368022 |
| 2.858523220 | 39.904931 | 0.35119106 | 17.559553 |
| 4.238999460 | 57.160884 | 0.35345694 | 17.672847 |
| 4.380820733 | 58.720918 | 0.35949394 | 17.974697 |
| 5.060252813 | 67.213819 | 0.37109546 | 18.554773 |
| 6.470435505 | 85.546194 | 0.38551572 | 19.275786 |
| 6.874067876 | 90.995231 | 0.40505068 | 20.252534 |
| 8.210337090 | 109.70300 | 0.40728344 | 20.364172 |
| 10.14702376 | 138.75330 | 0.41305208 | 20.652604 |
| 10.69766319 | 148.38949 | 0.42365274 | 21.182637 |
| 21.81047213 | 359.53286 | 0.4367517 | 21.837585 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Wang, X.; Long, Y.; Zhou, Z.; Tian, L. Frequency Domain Design Method of the Aeroengine Fuel Servo Constant Pressure Difference Control System with High Performance. Aerospace 2022, 9, 775. https://doi.org/10.3390/aerospace9120775
Zhao W, Wang X, Long Y, Zhou Z, Tian L. Frequency Domain Design Method of the Aeroengine Fuel Servo Constant Pressure Difference Control System with High Performance. Aerospace. 2022; 9(12):775. https://doi.org/10.3390/aerospace9120775
Chicago/Turabian StyleZhao, Wenshuai, Xi Wang, Yifu Long, Zhenhua Zhou, and Linhang Tian. 2022. "Frequency Domain Design Method of the Aeroengine Fuel Servo Constant Pressure Difference Control System with High Performance" Aerospace 9, no. 12: 775. https://doi.org/10.3390/aerospace9120775
APA StyleZhao, W., Wang, X., Long, Y., Zhou, Z., & Tian, L. (2022). Frequency Domain Design Method of the Aeroengine Fuel Servo Constant Pressure Difference Control System with High Performance. Aerospace, 9(12), 775. https://doi.org/10.3390/aerospace9120775






