Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage
Abstract
1. Introduction
2. Model and Methods
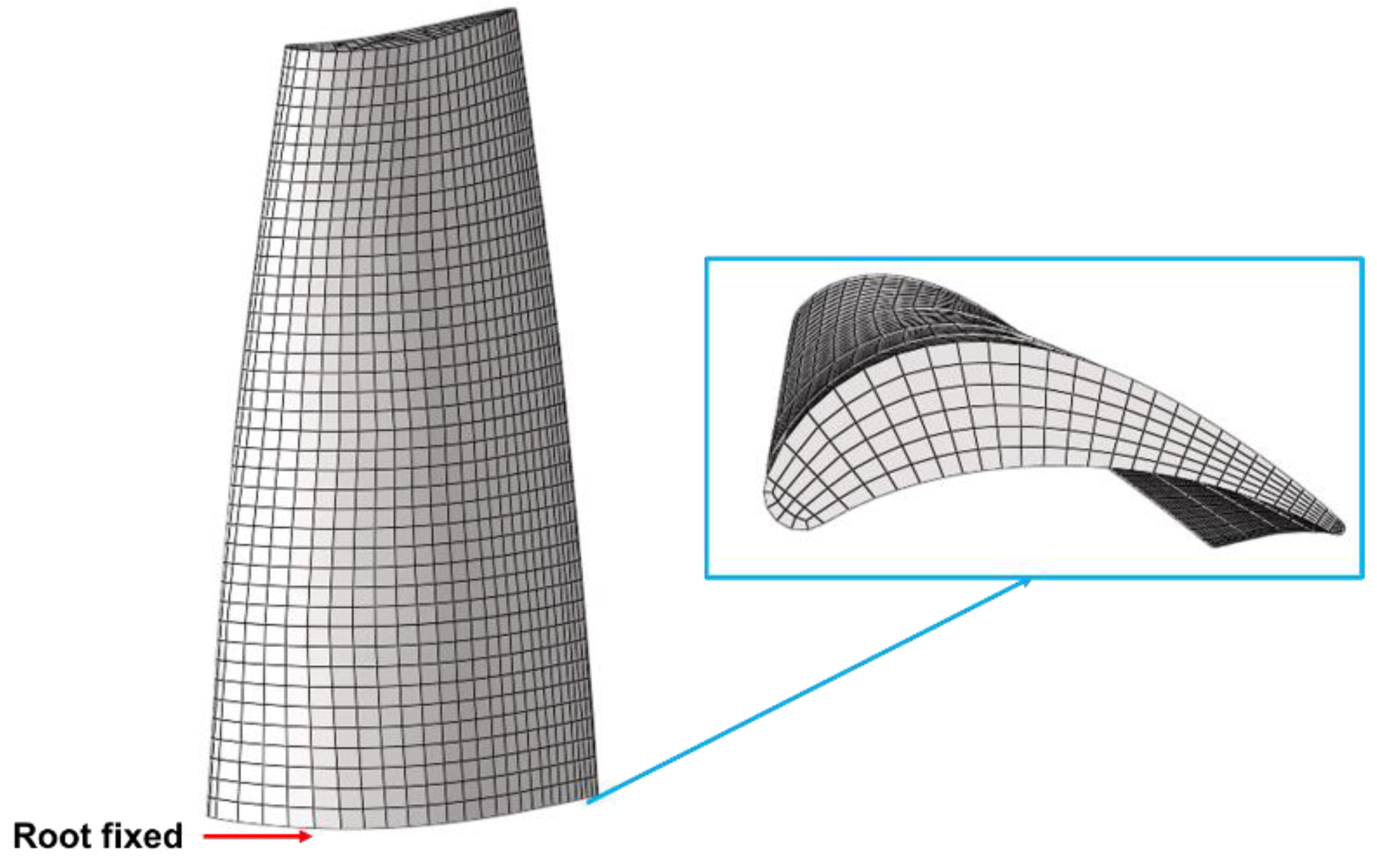
2.1. Geometric Model
2.2. Numerical Methodology
2.2.1. Aerodynamic Models
2.2.2. Structural Model
3. Computational Mesh and Code Verification
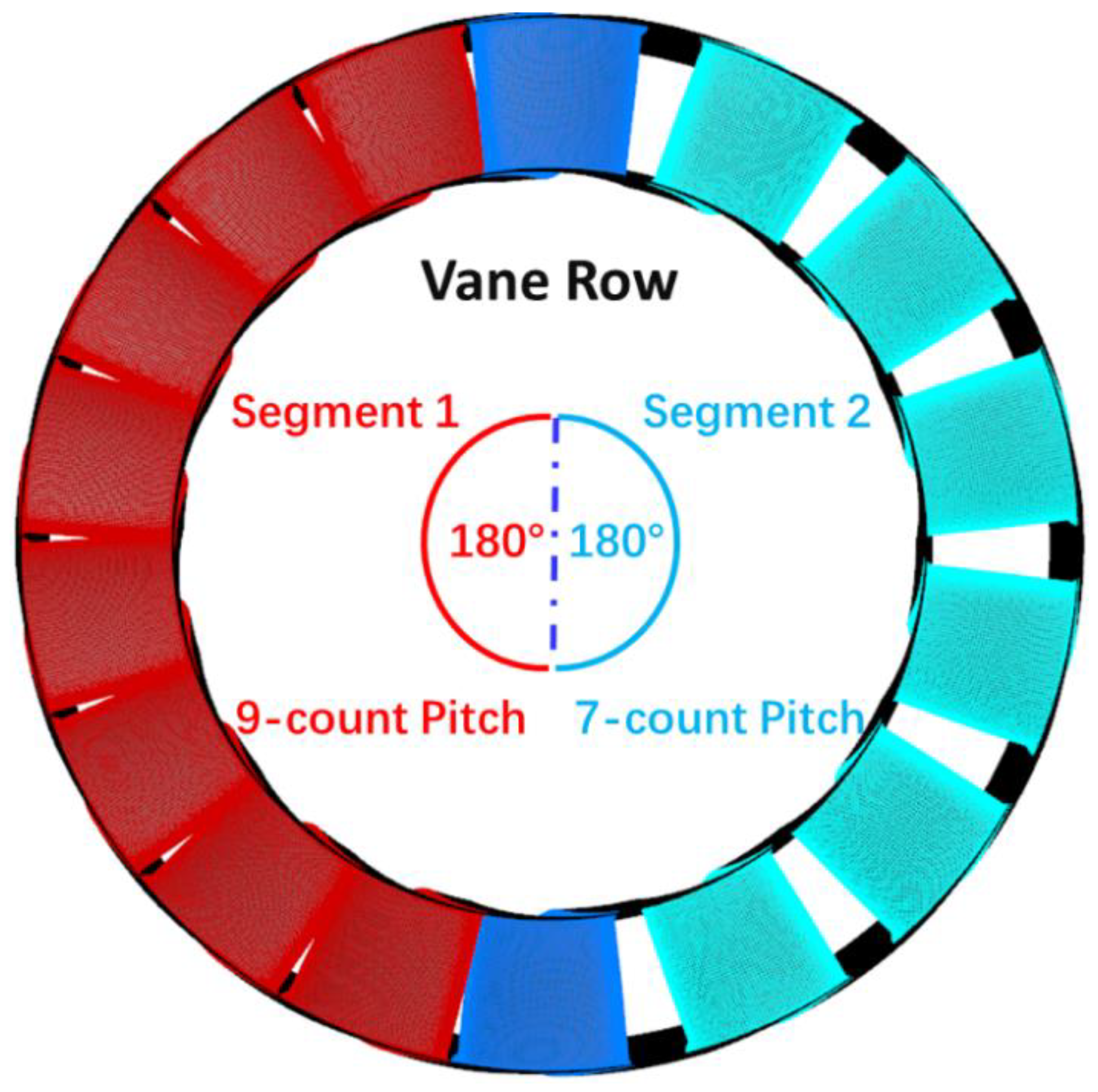
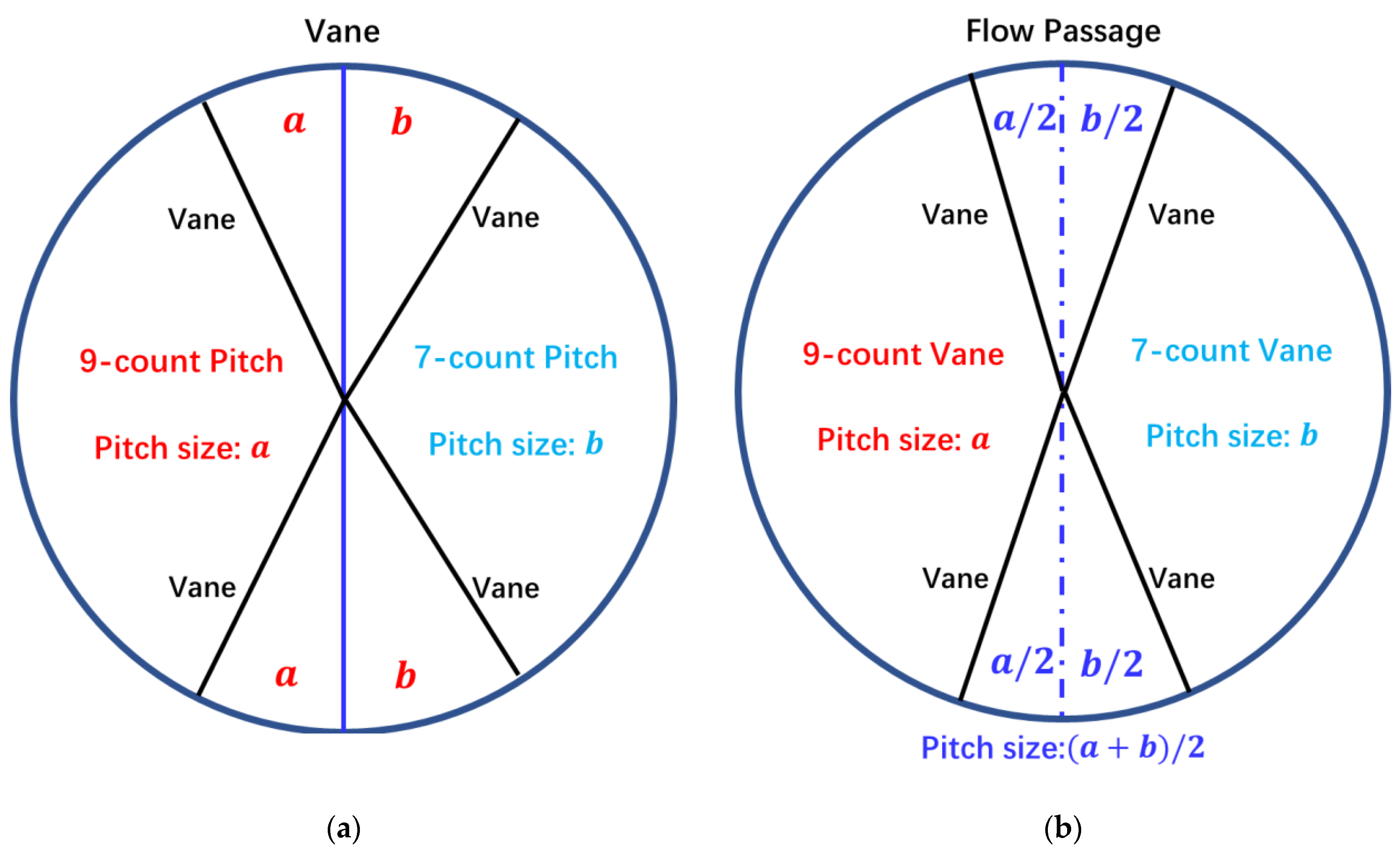
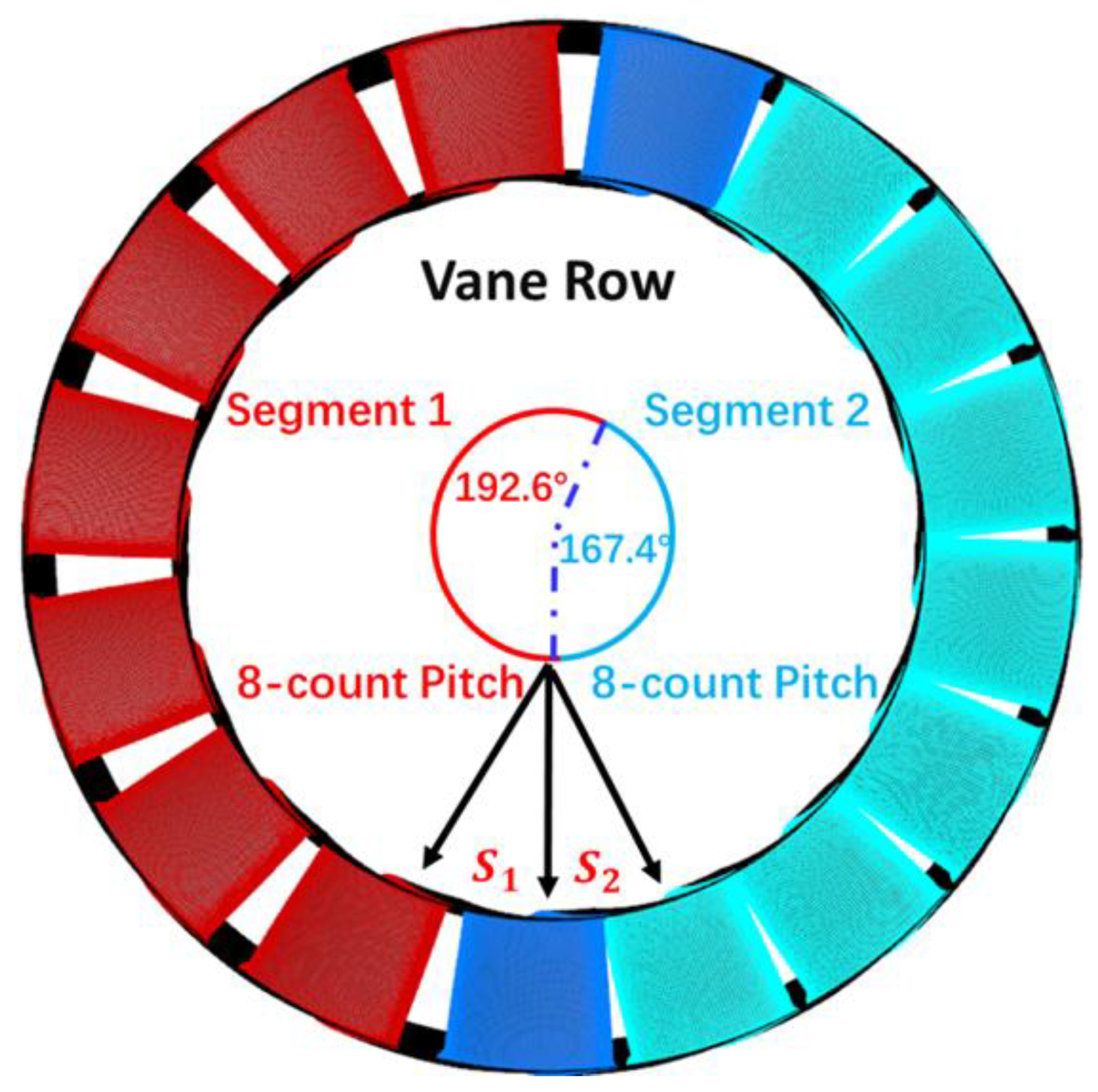
4. Asymmetric Vane Configuration (Half-and-Half Layout)
5. Results and Discussion
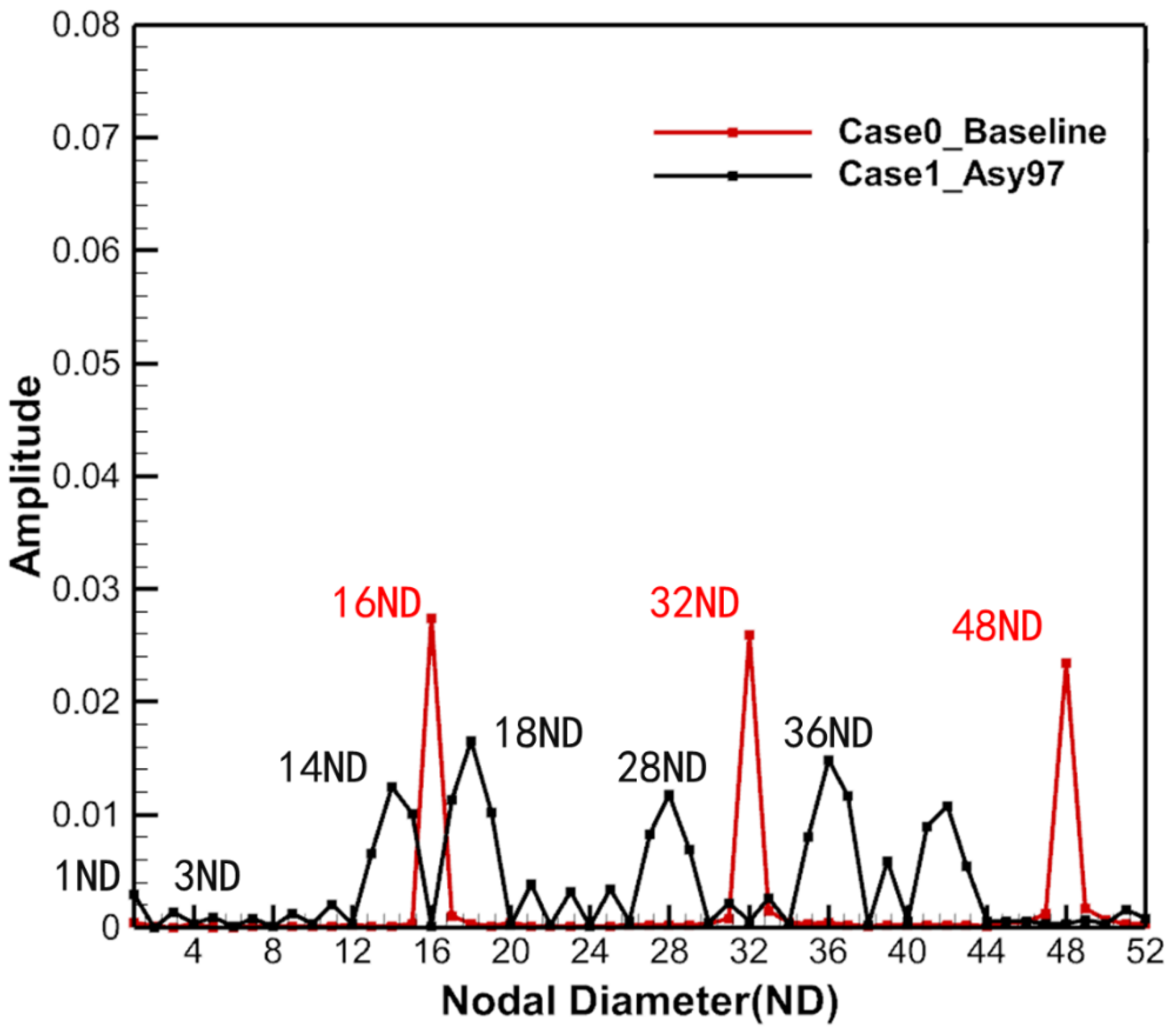
5.1. Campbell Diagram
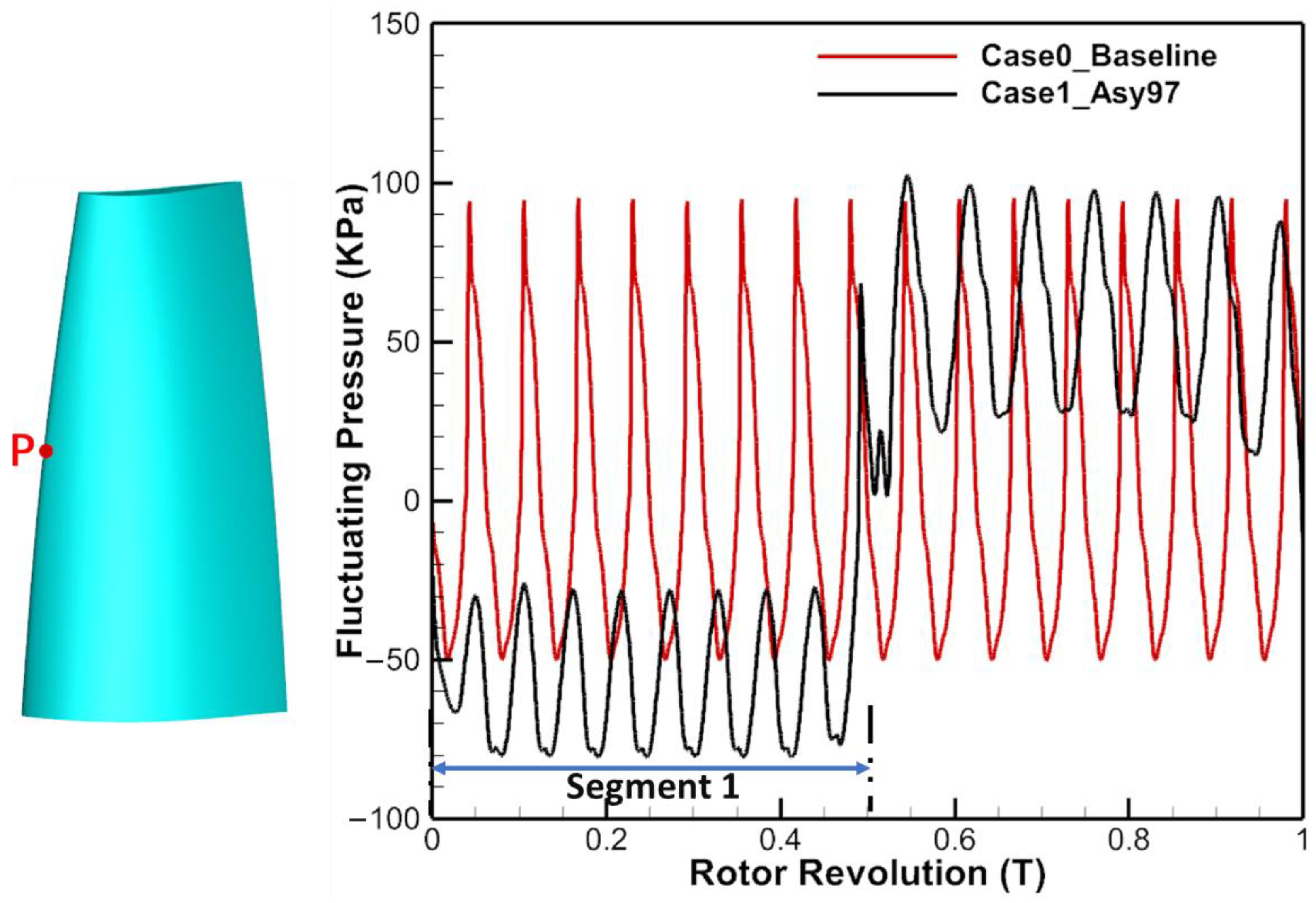
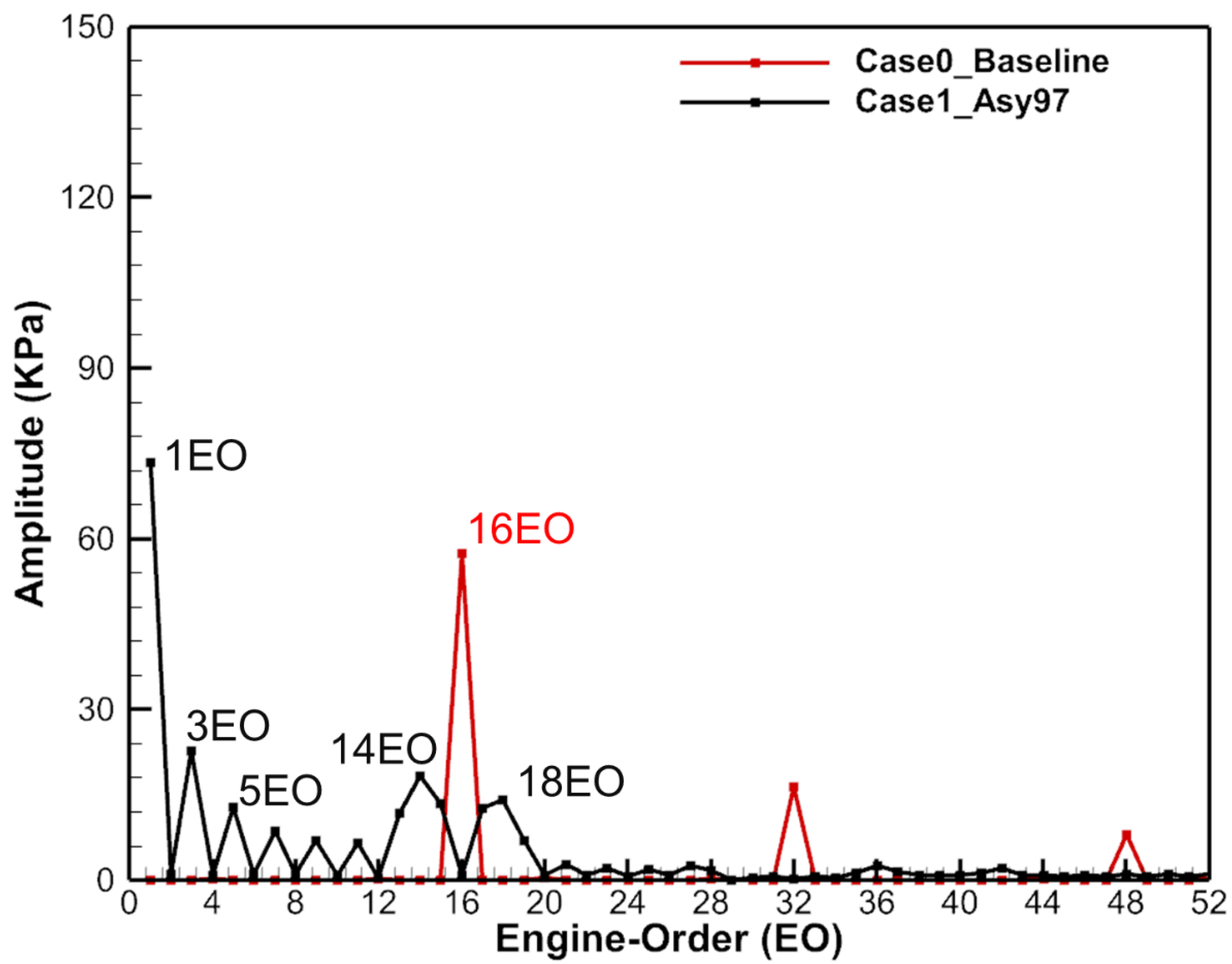
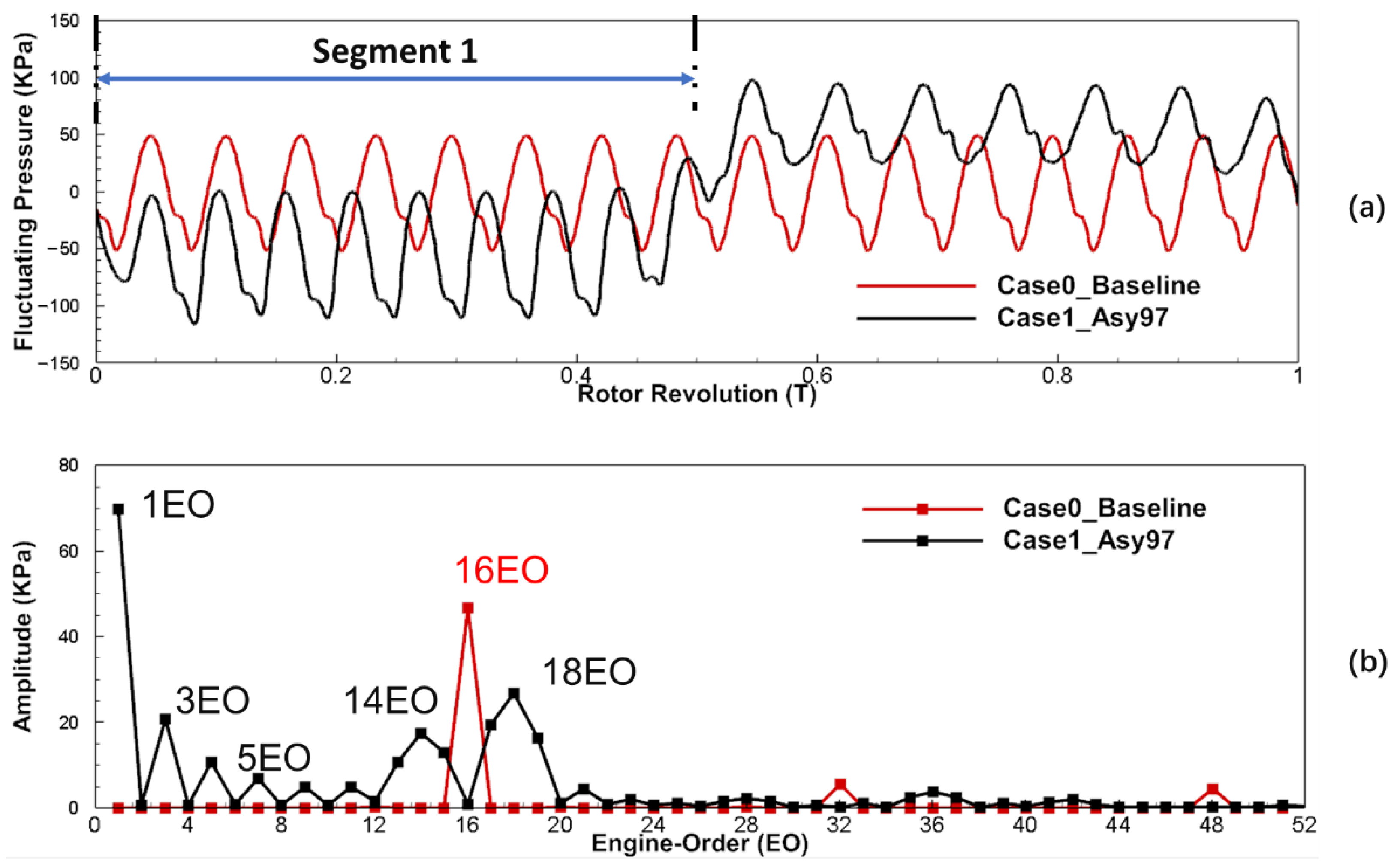
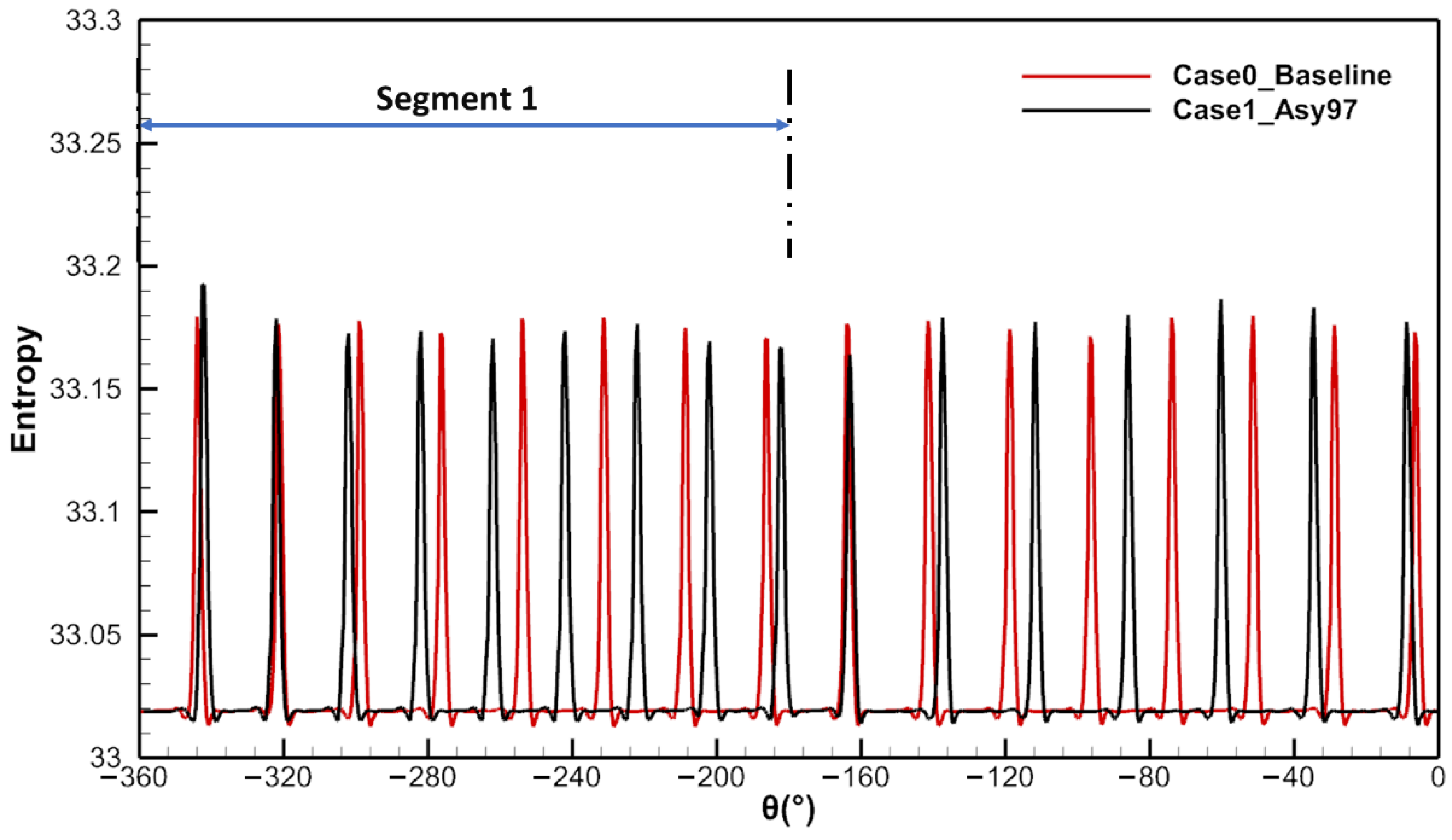
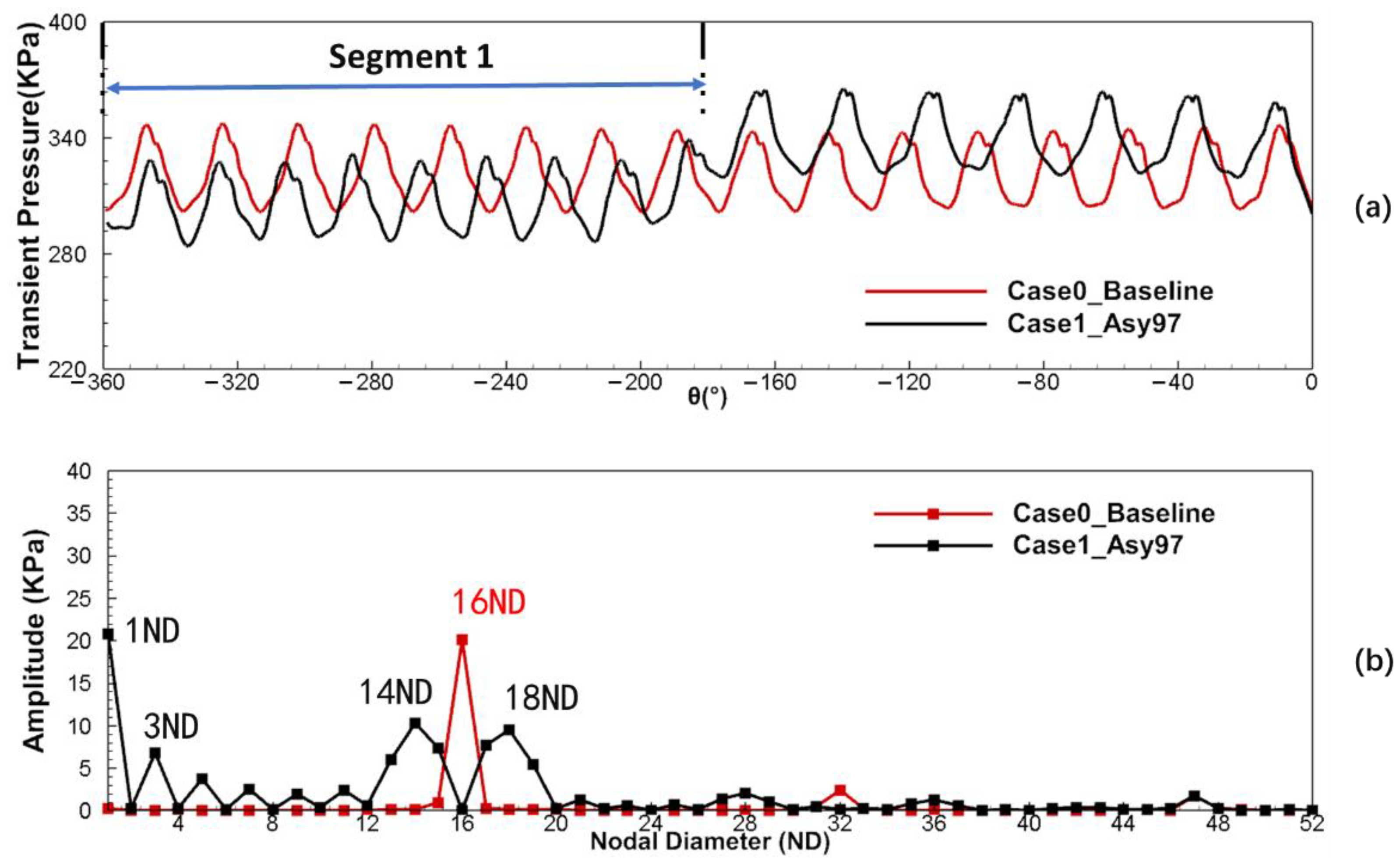
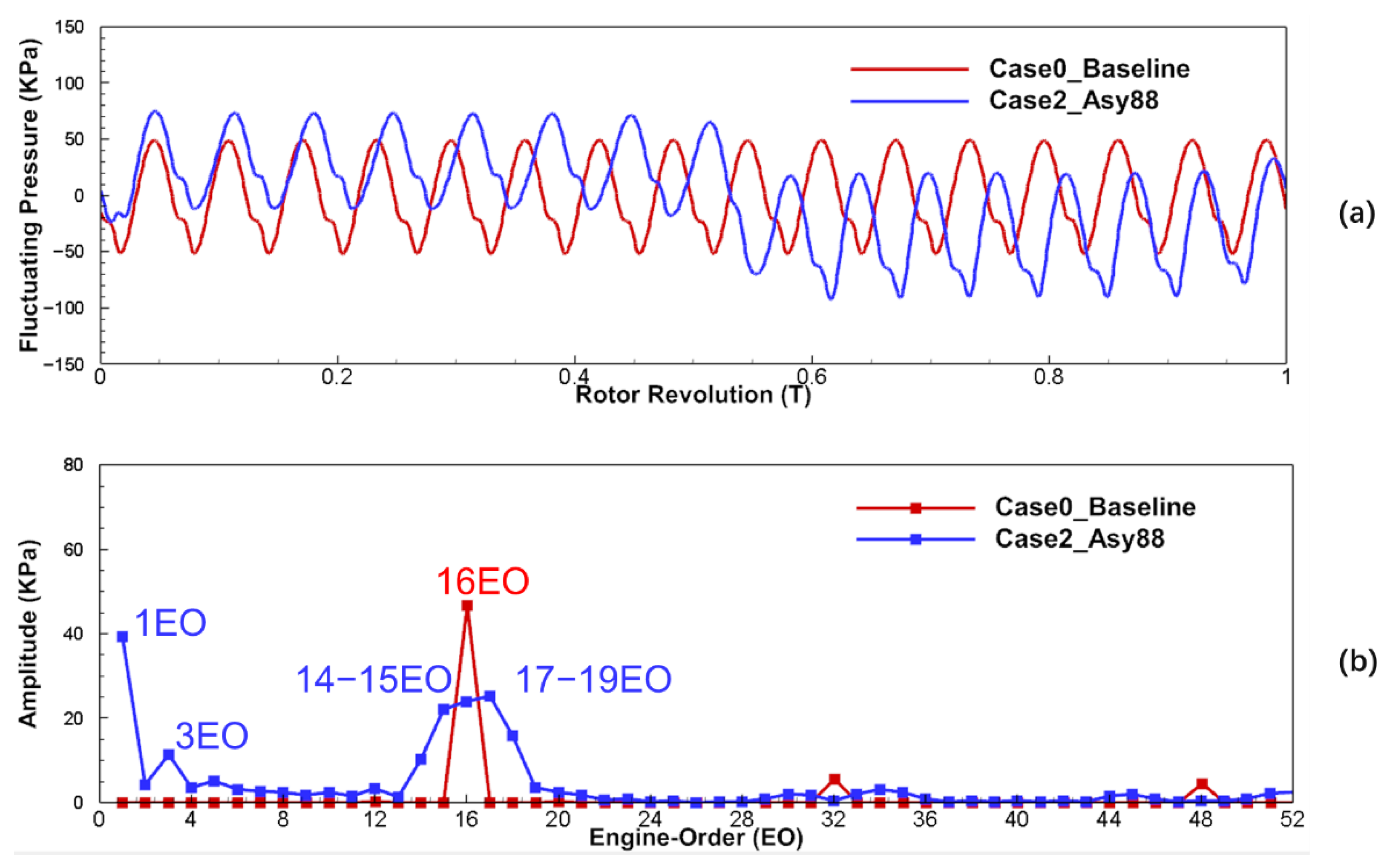
5.2. Aerodynamic Excitation on Rotor Blades
5.3. Maximum Vibrational Amplitude of rotor blades
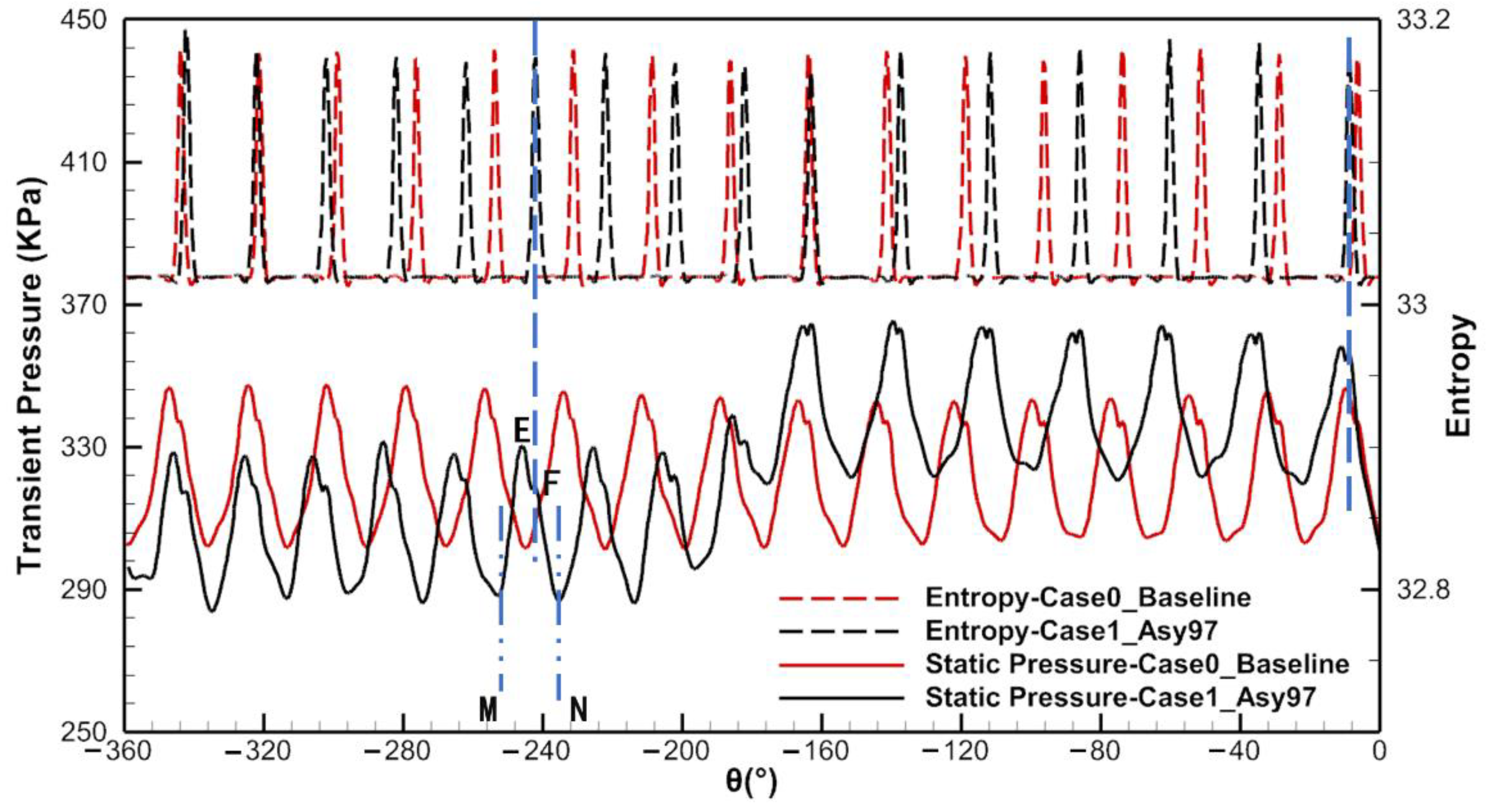
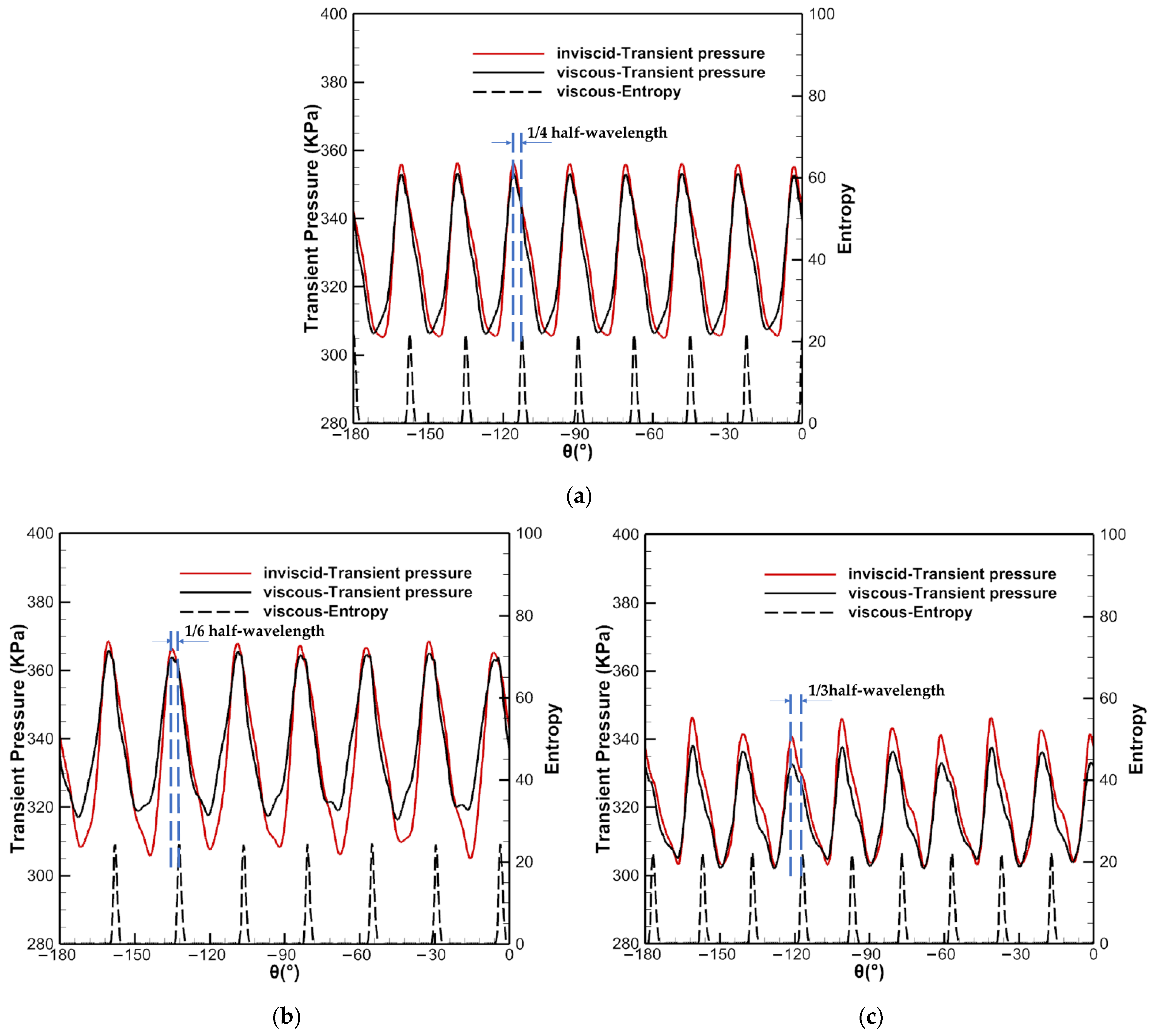
5.4. Flow Mechanism of Asymmetric Vane Pitch
5.5. Analysis of Non-Half Two-Segment Layout
5.5.1. Non-Half Two-Segment Layout
5.5.2. Aerodynamic Excitation and Maximum Vibrational Amplitude
5.5.3. Aerodynamic Performance
6. Conclusions
- The asymmetric vane configuration (half-and-half layout) can effectively reduce the amplitude of the VPF excitation by shifting energy from VPF to neighboring frequencies but introduces high amplitude LEO excitations, such as 1EO and 3EO, which reached 129% and 45% of the amplitude of the 16EO excitation in the uniformly spaced vane configuration, respectively, thus increasing the risk of blade failure;
- The potential field is the main source of LEO excitations for the rotor blade, which was determined for the first time, and the vane wake and potential field jointly affect the difference in the average pressure amplitude between the two segments. The larger the difference, the higher the strength of LEO excitations on the rotor blade. Furthermore, the strength of the potential field and the joint effect of the vane wake and potential field are affected by the vane pitch. Therefore, the vane pitch difference can be used to reduce the strength of the LEO excitation in asymmetric vane configurations;
- The non-half two-segment layout was proposed and the results under this configuration showed that the amplitude of VPF was reduced by 48.32% compared to the uniformly spaced vane configuration. Furthermore, the maximum vibrational amplitude of the 3ND response of the rotor blade at the 3EO crossing operating condition was decreased by 45.49% compared to the half-and-half layout, thus effectively reducing the LEO excitation resonance response. In addition, compared to the uniformly spaced vane configuration, the aerodynamic performance was reduced by more than 0.2% under the half-and-half layout, while the change in aerodynamic performance with the non-half two-segment layout was less than 0.1%. The negative effect of the half-and-half layout on aerodynamic performance was, therefore, significantly alleviated by using the non-half two-segment layout.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fransson, T. Aeroelasticity in Axial Flow Turbomachines; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1999. [Google Scholar]
- Lindenburg, C. Investigation into Rotor Blade Aerodynamics; ECN Wind Energy: Peten, Guatemala, 2003. [Google Scholar]
- Danforth, C.E. Designing to avoid fatigue in long life engines. SAE Trans. 1967, 75, 248–262. [Google Scholar]
- Greitzer, E.M.; Tan, C.S.; Wisler, D.C.; Adamczyk, J.J. Unsteady flow in turbomachines: Where’s the beef? In Proceedings of the ASME Winter Annual Meeting, Chicago, IL, USA, 6–11 November 1994. [Google Scholar]
- Wisler, D.C.; Shin, H.W. Blade row interaction and unsteady effects in axial-flow compressors and fans. Lec. Ser. Van Kareman Inst. Flu. Dyn. 1998, 2, G1–G54. [Google Scholar]
- Snyder, L.E.; Burns, D.W. Forced Vibration and Flutter Design Methodology; AGARD-AG-298-VOL-2; Detroit Diesel Allison: Indianapolis, IN, USA, 1988. [Google Scholar]
- Srinivasan, A.V. Flutter and resonant vibration characteristics of engine blades. J. Eng. Gas Turbines Power 1997, 119, 742–775. [Google Scholar] [CrossRef]
- Kielb, R.; Chiang, H.W. Recent Advancements in Turbomachinery Forced Response Analyses. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12 January 1992. [Google Scholar]
- Chiang, H.W.D.; Kielb, R.E. An analysis system for blade forced response. J. Turbomach. 1993, 115, 762–770. [Google Scholar] [CrossRef]
- Sayma, A.I.; Vahdati, M.; Imregun, M. Turbine forced response prediction using an integrated non-linear analysis. Proc. Inst. Mech. Eng., Part K 2000, 214, 45–60. [Google Scholar] [CrossRef]
- Waite, J.J.; Kielb, R.E. The impact of blade loading and unsteady pressure bifurcations on low-pressure turbine flutter boundaries. J. Turbomach 2016, 138, 041002. [Google Scholar] [CrossRef]
- Corral, R.; Greco, M.; Vega, A. Effective clearance and differential gapping impact on seal flutter modeling and validation. J. Turbomach 2022, 144, 071010. [Google Scholar] [CrossRef]
- Jareland, M.H.; Csaba, G. Friction Damper Mistuning of a Bladed Disk and Optimization with Respect to Wear. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000. [Google Scholar]
- Petrov, E.P. Stability analysis of multiharmonic nonlinear vibrations for large models of gas turbine engine structures with friction and gaps. J. Eng. Gas Turbines Power 2017, 139, 022508. [Google Scholar] [CrossRef]
- Hüls, M.; Panning-von Scheidt, L.; Wallaschek, J. Influence of geometric design parameters onto vibratory response and high-cycle fatigue safety for turbine blades with friction damper. J. Eng. Gas Turbines Power 2019, 141, 041022. [Google Scholar] [CrossRef]
- Hancock, B.J.; Clark, J.P. Reducing shock interactions in a transonic turbine via three-dimensional aerodynamic shaping. J. Propul. Power 2014, 30, 1248–1256. [Google Scholar] [CrossRef]
- Niu, X.; Wang, L.; Li, D.; Du, Q. Reduction of Turbine Blade Unsteady Forces by Shape Modification of Vanes for Industrial Gas Turbines. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Giel, P.W.; Shyam, V.; Juangphanich, P.; Clark, J.P. Effects of Trailing Edge Thickness and Blade Loading Distribution on the Aerodynamic Performance of Simulated CMC Turbine Blades. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Online, 21–25 September 2020. [Google Scholar]
- Kemp, R.H.; Hirschberg, M.H.; Morgan, W.C. Theoretical and Experimental Analysis of The Reduction of Rotor Blade Vibration in Turbomachinery through the Use of Modified Stator Vane Spacing; NACA: Washington, DC, USA, 1958. [Google Scholar]
- Kaneko, Y.; Mori, K.; Okui, H. Study on the Effect of Asymmetric Vane Spacing on Vibratory Stress of Blade. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Sun, T.; Hou, A.; Zhang, M.; Niu, Y.; Gao, J.; Guo, H. Analysis on the Reduction of Rotor Blade Vibration Using Asymmetric Vane Spacing. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Crall, D.W.; Manwaring, S.R. Periodic stator airfoils. U.S. Patent 6,439,838, 27 August 2002. [Google Scholar]
- Leng, Y.; Key, N.L. Effects of nonuniform blade spacing on compressor rotor flutter stability. J. Propul. Power 2021, 37, 682–692. [Google Scholar] [CrossRef]
- Niu, Y.; Hou, A.; Zhang, M.; Sun, T.; Wang, R.; Guo, H. Investigation on the Effect of Asymmetric Vane Spacing on the Reduction of Rotor Blade Vibration. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Senn, S.M. Nozzle ring with non-uniformly distributed airfoils and uniform throat area. U.S. Patent 14/190,814, 25 September 2014. [Google Scholar]
- Simpson, A.J. Gas turbine engine stator vane asymmetry. U.S. Patent 10,443,391, 15 October 2019. [Google Scholar]
- Clark, J.P.; Aggarwala, A.S.; Velonis, M.A.; Gacek, R.E.; Magge, S.S.; Price, F.R. Using CFD to Reduce Resonant Stresses on a Single-Stage, High-Pressure Turbine Blade. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002. [Google Scholar]
- Clark, J.P.; Anthony, R.J.; Ooten, M.K.; Finnegan, J.M.; Dean Johnson, P.; Ni, R.H. Effects of downstream vane bowing and asymmetry on unsteadiness in a transonic turbine. J. Turbomach 2018, 140, 101006. [Google Scholar] [CrossRef]
- Meng, Y.; Li, L.; Li, Q. Asymmetry stator mistuned blade design and research. J. Aerosp. Power 2007, 22, 2083–2088. [Google Scholar]
- Monk, D.J.; Key, N.L.; Fulayter, R.D. Reduction of aerodynamic forcing through introduction of stator asymmetry in axial compressors. J. Propul. Power 2016, 32, 134–141. [Google Scholar] [CrossRef]
- Bréard, C.; Green, J.S.; Imregun, M. Low-engine-order excitation mechanisms in axial-flow turbomachinery. J. Propul. Power 2003, 19, 704–712. [Google Scholar] [CrossRef]
- Trafford, T.; Stapelfeldt, S.; Puente-Rico, R.; Kulkarni, D. A Computational Study of Burner Failure Related Low Engine Order Forced Response Mechanisms in A High Pressure Turbine. In Proceedings of the 16th International Symposium on Unsteady Aerodynamics, Toledo, Spain, 19–23 September 2022. [Google Scholar]
- Schoenenborn, H.; Wohlfahrt, C.; Grosgurin, T.; Widera, T.; Jeschke, P. Forced-Response Measurements and CFD-Analysis of Higher Vibration Modes in a 2.5-stage Axial Compressor Rig. In Proceedings of the 16th International Symposium on Unsteady Aerodynamics, Toledo, Spain, 19–23 September 2022. [Google Scholar]
- Gambitta, M.; Beirow, B. Modeling method for aeroelastic low engine order excitation originating from upstream vanes geometrical variability. In Proceedings of the 16th International Symposium on Unsteady Aerodynamics, Toledo, Spain, 19–23 September 2022. [Google Scholar]
- Zheng, Y. Computational aeroelasticity with an unstructured grid method. J. Aerosp. Power 2009, 24, 2069–2077. [Google Scholar]
- Zheng, Y.; Yang, H. Full assembly fluid/structured flutter analysis of a transonic fan. J. Beijing Univ. Aeronaut. Astronaut 2013, 39, 626. [Google Scholar]
- Zheng, Y.; Jin, X.; Yang, H.; Gao, Q.; Xu, K. Effects of Circumferential Nonuniform Tip Clearance on Flow Field and Performance of a Transonic Turbine. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 21–25 September 2020. [Google Scholar]
- Zheng, Y. Computational Aerodynamics on Unstructed Meshes. Ph.D. Thesis, Durham University, Durham, UK, 2004. [Google Scholar]
- Zheng, Y.; Hui, Y. Coupled fluid-structure flutter analysis of a transonic fan. Chin. J. Aeronaut 2011, 24, 258–264. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. J. Comput. Phys. 1997, 135, 229–248. [Google Scholar] [CrossRef]
- Jameson, A. Time Dependent Calculations Using Multigrid, with Applications to Unsteady Flows Past Airfoils and Wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Marshall, J.G.; Imregun, M. A review of aeroelasticity methods with emphasis on turbomachinery applications. J. Fluids Struct. 1996, 10, 237–267. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. Piezoelectric Aeroelastic Energy Harvesting; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Bréard, C.; Vahdati, M.; Sayma, A.I.; Imregun, M. An integrated time-domain aeroelasticity model for the prediction of fan forced response due to inlet distortion. J. Eng. Gas Turbines Power 2002, 124, 196–208. [Google Scholar] [CrossRef]
- Vahdati, M.; Sayma, A.I.; Imregun, M.; Simpson, G. Multibladerow forced response modeling in axial-flow core compressors. J. Turbomach 2007, 129, 412–420. [Google Scholar] [CrossRef]
- Li, J.; Aye-Addo, N.; Kormanik, N., III; Matthews, D.; Key, N.; Kielb, R. Mistuned Higher-Order Mode Forced Response of an Embedded Compressor Rotor: Part I—Steady and Unsteady Aerodynamics. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- He, L. Unsteady Flow and Aeroelasticity; CRC Press: Boca Raton, FL, USA, 2003; pp. 257–308. [Google Scholar]
- Korakianitis, T. On the prediction of unsteady forces on gas turbine blades: Part 2–Analysis of the results. J. Turbomach 1992, 114, 123–131. [Google Scholar] [CrossRef]
- Korakianitis, T. Influence of stator-rotor gap on axial-turbine unsteady forcing functions. AIAA J. 1993, 31, 1256–1264. [Google Scholar] [CrossRef]





| Parameter | Vane Row | Rotor Row |
|---|---|---|
| Airfoil count | 16 | 47 |
| Axial chord (midspan) (mm) | 97 | 33 |
| Airfoil height (mm) | 75 | 74 |
| Aspect ratio (exit height/chord) | 0.77 | 2.24 |
| Rotor tip clearance (mm) | / | 1 |
| Elasticity Modulus (GPa) | Poisson’s Ratio | Density (g/cm3) |
|---|---|---|
| 155 | 0.31 | 8.44 |
| Parameter | Aerodynamic Efficiency | Expansion Ratio |
|---|---|---|
| HGAE | 0.8954 | 1.7616 |
| NUMECA | 0.8988 | 1.7587 |
| Error | 0.378% | 0.165% |
| Case (NDs) | EO Excitation | Resonant Speed (rpm) | Maximum Vibrational Amplitude (mm) | Change Rate |
|---|---|---|---|---|
| Case0_Baseline (16 NDs) | 16EOs | 10,535.1 | 0.174 | —— |
| Case1_Asy97 (18 NDs) | 18EOs | 9460.22 | 0.053 | −69.91% |
| Case1_Asy97 (14 NDs) | 14EOs | 11,742.5 | 0.085 | −51.20% |
| Case1_Asy97 (16 NDs) | 14EOs | 11,742.5 | 0.003 | −98.15% |
| Case1_Asy97 (16 NDs) | 18EOs | 9460.22 | 0.002 | −98.64% |
| Case1_Asy97 (3 NDs) | 3EOs | 14,928.4 | 2.018 | 10.55 |
| Case | (mm) | (mm) | (mm) |
|---|---|---|---|
| Case0_Baseline | 88.309 | 88.309 | 0 |
| Case1_Asy97 | 78.497 | 100.93 | 22.43 |
| Case2_Asy88 | 82.128 | 94.491 | 12.36 |
| Case (NDs) | EO Excitation | Resonant Speed (rpm) | Maximum Vibrational Amplitude (mm) | Change Rate |
|---|---|---|---|---|
| Case1_Asy97 (3 NDs) | 3 EOs | 14,928.4 | 2.018 | —— |
| Case2_Asy88 (3 NDs) | 3 EOs | 14,928.4 | 1.100 | −45.49% |
| Case | Aerodynamic Efficiency | Expansion Ratio |
|---|---|---|
| Case0_Baseline | 0.89498 | 1.755 |
| Case1_Asy97 | 0.89305 | 1.750 |
| Case2_Asy88 | 0.89453 | 1.754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Jin, X.; Yang, H. Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage. Aerospace 2022, 9, 694. https://doi.org/10.3390/aerospace9110694
Zheng Y, Jin X, Yang H. Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage. Aerospace. 2022; 9(11):694. https://doi.org/10.3390/aerospace9110694
Chicago/Turabian StyleZheng, Yun, Xiubo Jin, and Hui Yang. 2022. "Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage" Aerospace 9, no. 11: 694. https://doi.org/10.3390/aerospace9110694
APA StyleZheng, Y., Jin, X., & Yang, H. (2022). Effects of Asymmetric Vane Pitch on Reducing Low-Engine-Order Forced Response of a Turbine Stage. Aerospace, 9(11), 694. https://doi.org/10.3390/aerospace9110694






