An Uncertainty Weighted Non-Cooperative Target Pose Estimation Algorithm, Based on Intersecting Vectors
Abstract
1. Introduction
- (1)
- We propose a two-step relative pose estimation algorithm, based on the uncertainty analysis of the line extraction. The method fully considers the uncertainty of the straight-line extraction to weigh the error term of the objective function, and is more robust in a space environment than the feature-point-based method.
- (2)
- A novel distance error model for the reprojection of a line, in which the mean value of the distance sum from the two ends of the original direct comparison line segment to the line error, is transformed into the sum of the distance between the two points in the parameter space, which is more reasonable, in theory.
- (3)
- The proposed approach was verified on a ground test simulation environment and has been extensively evaluated in experimental and simulation analyses.
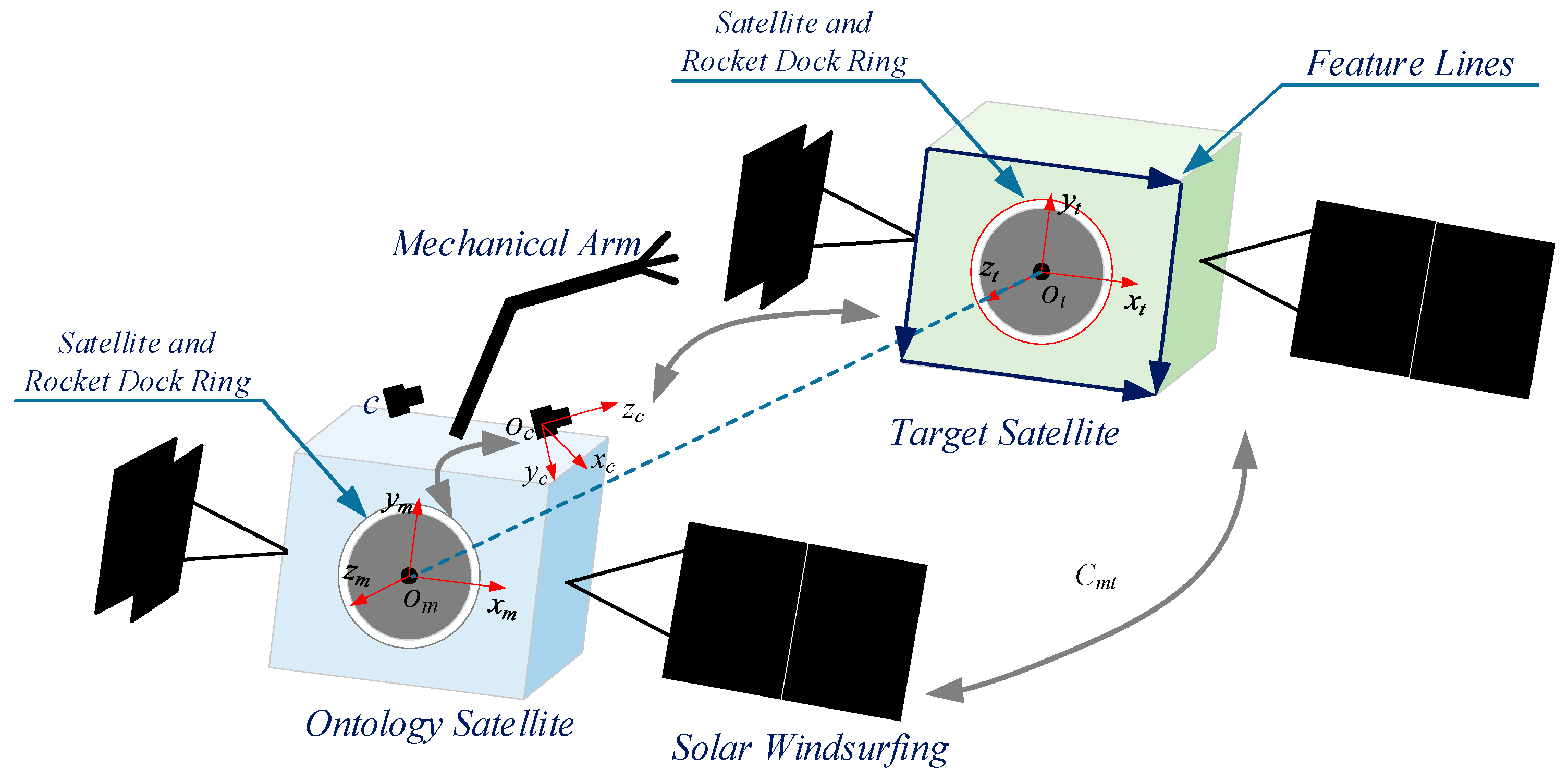
2. Principle of the Non-Cooperative Target Relative to the Pose Estimate
2.1. Problem Description of the Relative Pose Estimation
2.2. Relative Pose Estimation between Spacecrafts
2.2.1. Initial Value Solution of the Relative Pose Estimation, based on the Intersection Vector
2.2.2. Nonlinear Optimization of the Pose Estimation
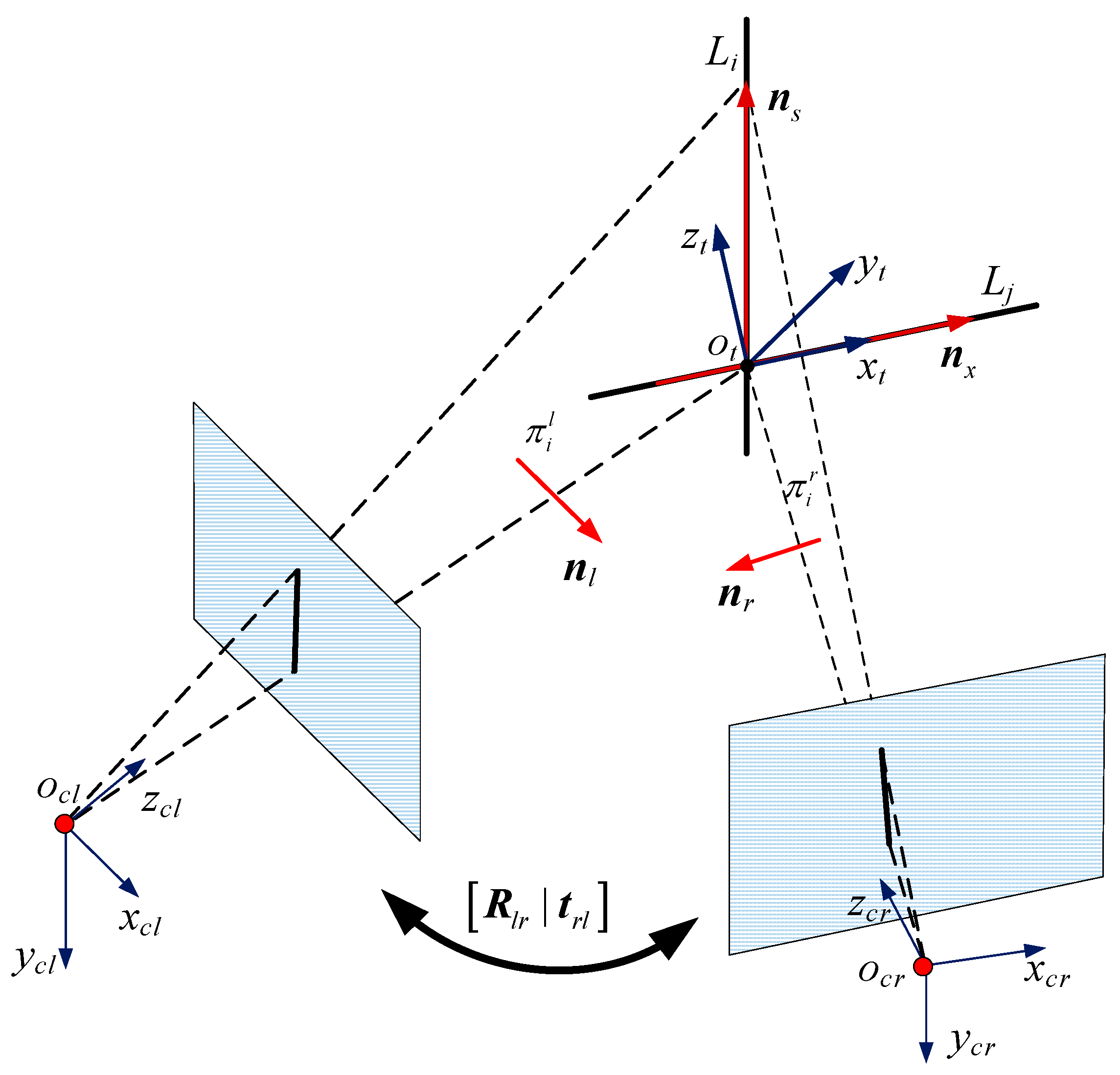
3. Line Features Reconstruction and the Uncertainty Analysis
3.1. Solving the 3D Space Straight Line and Its Intersection
3.2. Uncertainty Analysis of the Straight Line Extraction
3.2.1. Uncertainty Modeling of the Straight Line
3.2.2. Linear Filtering based on the Uncertainty Size
3.3. Line Reprojection Error Analysis
- (1)
- When the detection line segment and the reprojection line are in the situation, as shown in (a) and (b), the error means the two lines are completely inconsistent with the length being equal.
- (2)
- When the detection line segment and the directional projection line are in the situation, as shown in (c) and (d), its position on the line directly affects the error when the direction vector of the line remains unchanged.
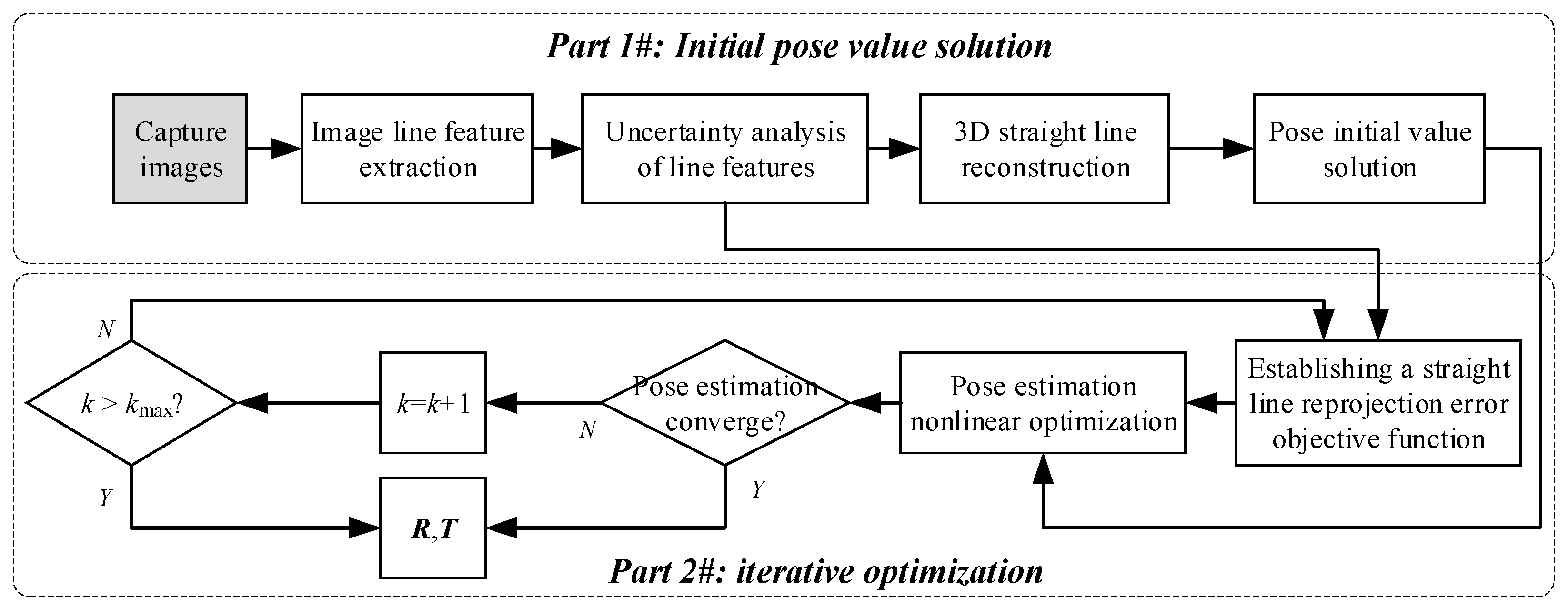
4. Experiments and Analysis
4.1. Simulation and Analysis
4.1.1. Analysis of the Relationship between the Measurement Accuracy and the Measurement Frequency
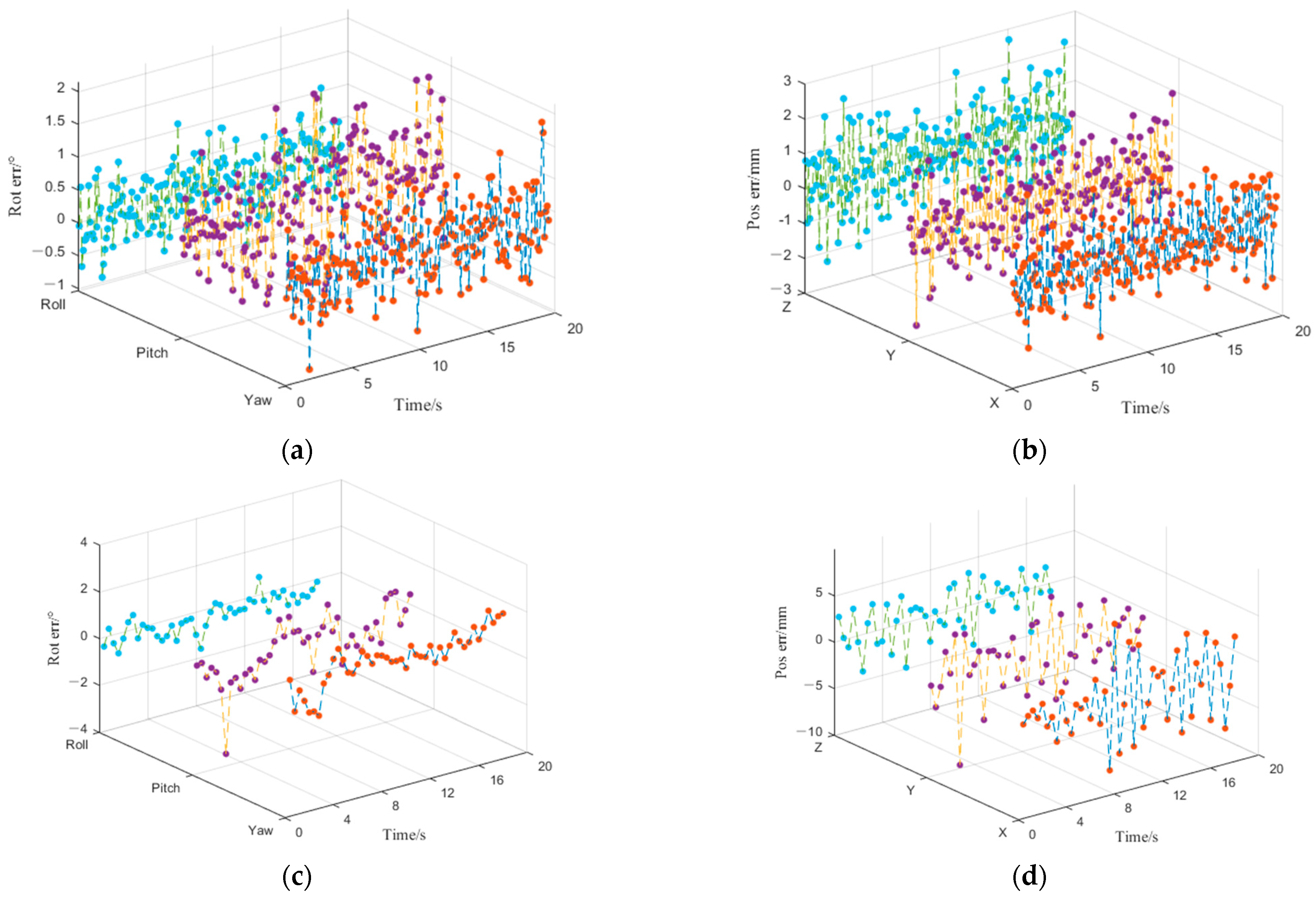
- (1)
- When the simulation data acquisition frequency is 10 Hz, the pose measurement results are shown in Figure 7a,b, the maximum measurement error of the attitude angle is less than 1° (3δ) and that of the position measurement is less than 2 mm (3δ), and the simulation results meet the pose measurement requirements.
- (2)
- When the data acquisition frequency is 2.5 Hz, the position and pose calculation results of the numerical simulation are shown in Figure 7c,d, the attitude measuring results had divergent trends in the shade, but the measurement error is bigger, this is due to the non-cooperative targets in space for the non-linear movement, and the amount of data collected is less, resulting in fewer constraints involved in the optimization using the linear model.
- (3)
- For the position measurement, it can be seen from Figure 7b,d that the position measurement is basically consistent with the theoretical setting value, and the position measurement results. By comparing the position measurement and attitude measurement results, the attitude measurement results are more sensitive to the 3D positioning accuracy, and the attitude measurement accuracy decreases significantly, compared with that when the sampling frequency is 10 Hz. This is mainly because the estimation hysteresis error, caused by the corresponding optimization algorithm, increases significantly with the decrease of the measurement data.
4.1.2. Algorithm Measurement Error Statistics and Analysis
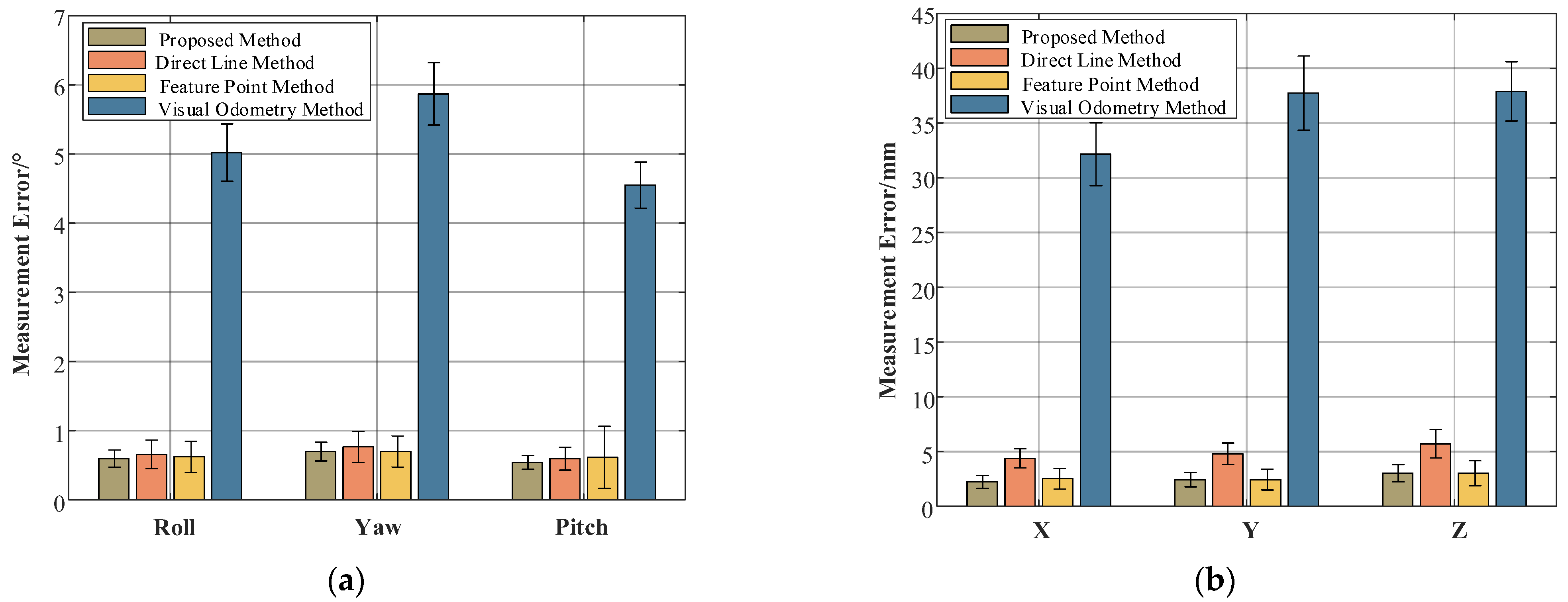
- (1)
- By comparing the measurement results of the four methods, the accuracy of the pose estimation algorithm of the visual odometry method is the worst, reaching the maximum attitude angle of 5.8° and the maximum position error of 37 mm. This is mainly because the visual odometer method has a cumulative error, so its error will become larger and larger as time goes by.
- (2)
- According to the attitude error of the measurement result, the measuring accuracy of the proposed algorithm, and based on the measuring accuracy of the feature point is quite up to 0.6°, the position is 2.2 mm, but this article proposed a smaller algorithm of the attitude angle variance, this is mainly because the participation attitude angle calculating the straight linear feature uses the linear reconstruction uncertainty size selection.
- (3)
- In the measurement results of the attitude angle, the errors of the pitch and yaw angles are large, and the z-axis errors of the position error are large, which is mainly caused by the great uncertainty of the vision measurement in the z-axis direction.
4.1.3. Comparison Experiment of the Algorithm Robustness
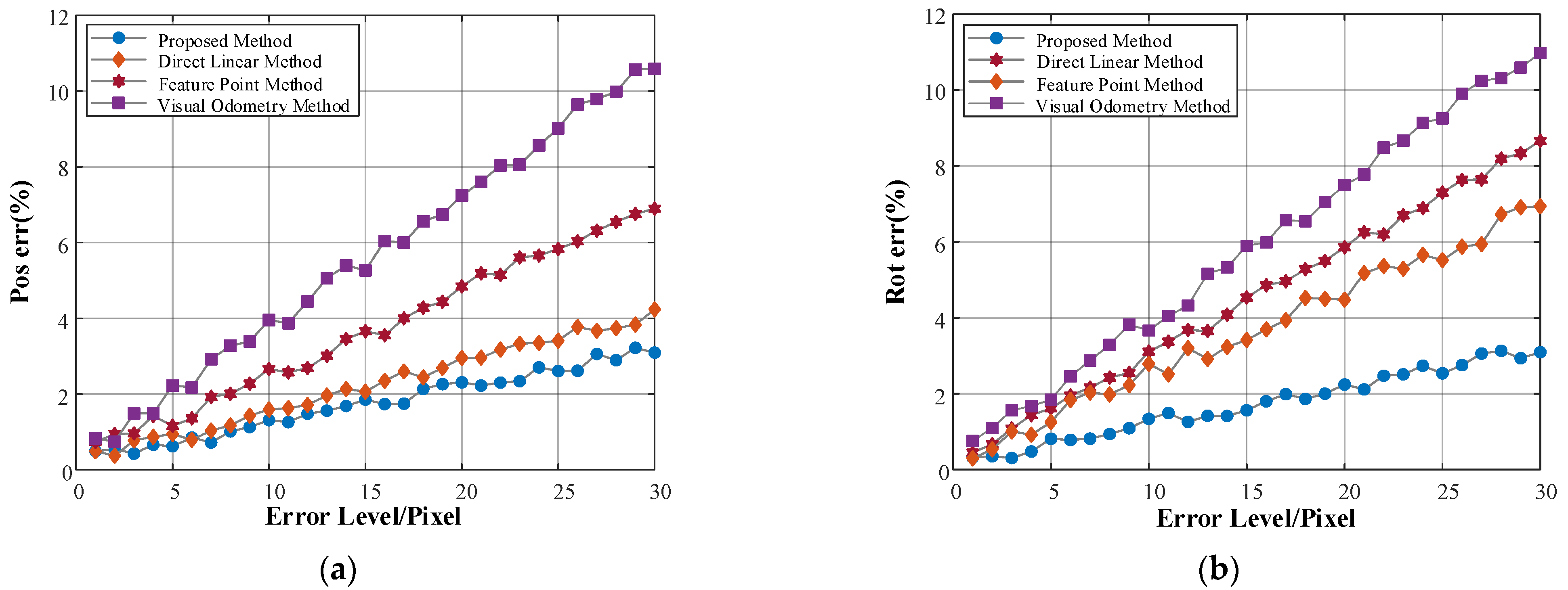
- (1)
- The measurement errors of the attitude and position points increase with the increase of the feature extraction errors, and the proposed calibration algorithm has the highest accuracy, compared with other algorithms participating in the comparison.
- (2)
- The algorithm proposed has a smaller error growth slope, compared with other algorithms, therefore this method has stronger robustness compared with other methods.
- (3)
- The position accuracy of the proposed algorithm is equivalent to that of the feature point method, mainly because it is equivalent, in theory, when the error level is the same. However, the algorithm proposed in this paper filters the straight lines involved in the pose estimation, so the positioning accuracy is slightly higher.
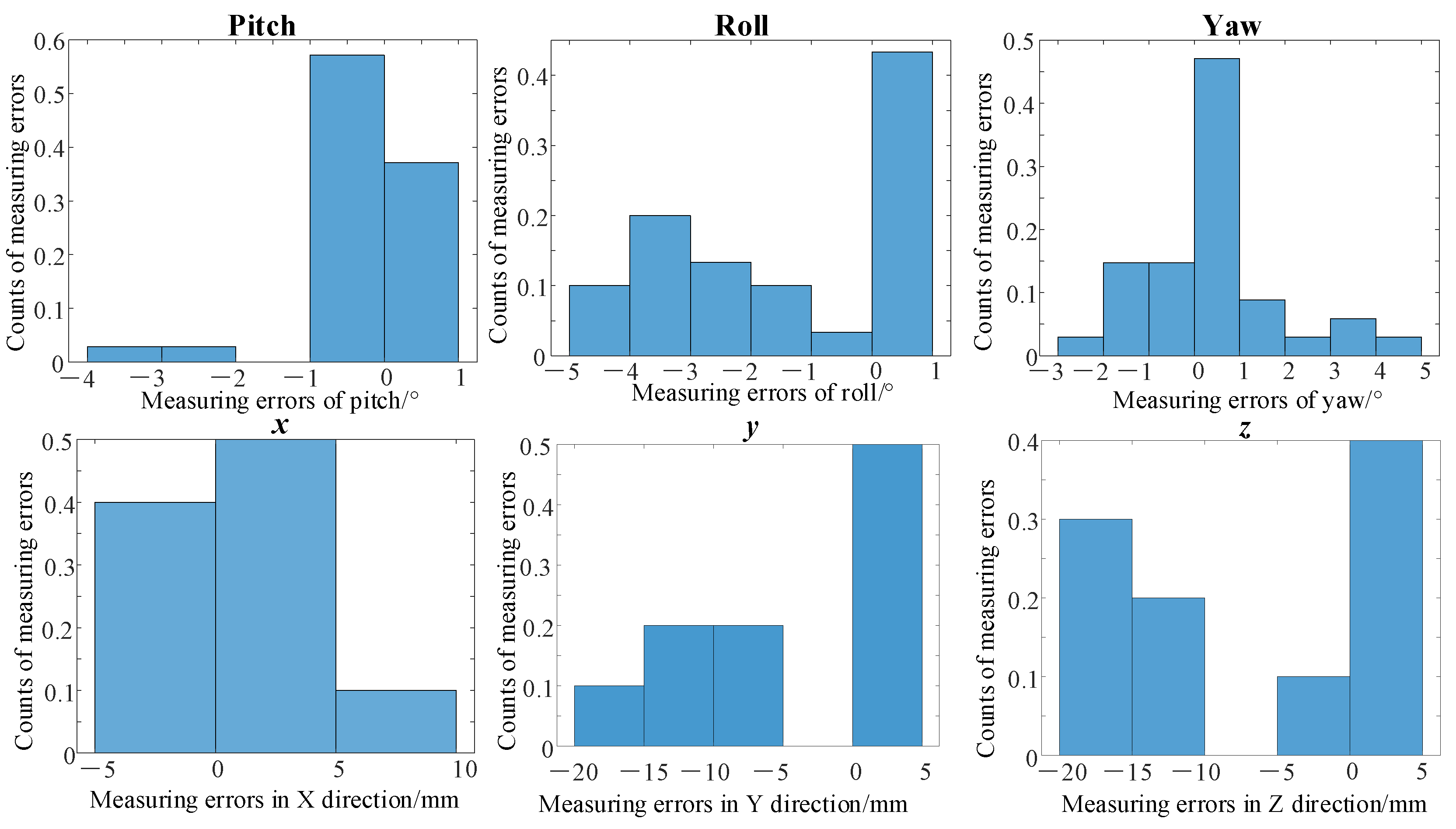
4.2. Actual Experiment and Analysis
4.2.1. Static Pose Estimation Experiment
4.2.2. Dynamic Pose Estimation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, B.; Du, X.; Li, C.; Xu, W. Advances in Space Robot On-orbit Servicing for Non-cooperative Spacecraft. ROBOT 2012, 34, 242–256. [Google Scholar] [CrossRef]
- He, Y.; Liang, B.; He, J.; Li, S. Non-cooperative spacecraft pose tracking based on point cloud feature. Acta Astronaut. 2017, 139, 213–221. [Google Scholar] [CrossRef]
- Cougnet, C.; Gerber, B.; Heemskerk, C.; Kapellos, K.; Visentin, G. On-orbit servicing system of a GEO satellite fleet. In Proceedings of the 9th ESA Workshop on Advanced Space Technologies for Robotics and Automation ‘ASTRA 2006’ ESTEC, Noordwijk, The Netherlands, 28–30 November 2006. [Google Scholar]
- Ibrahim, S.K.; Ahmed, A.; Zeidan, M.A.E.; Ziedan, I.E. Machine Learning Methods for Spacecraft Telemetry Mining. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1816–1827. [Google Scholar] [CrossRef]
- Woods, J.O.; Christian, J.A. Lidar-based relative navigation with respect to non-cooperative objects. Acta Astronaut. 2016, 126, 298–311. [Google Scholar] [CrossRef]
- Fan, B.; Du, Y.; Wu, D.; Wang, C. Robust vision system for space teleoperation ground verification platform. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations. Prog. Aerosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- Terui, F.; Kamimura, H.; Nishida, S.I. Motion estimation to a failed satellite on orbit using stereo vision and 3D model matching. In Proceedings of the 9th International Conference on Control, Automation, Robotics and Vision, Singapore, 5–8 December 2006. [Google Scholar]
- Terui, F.; Kamimura, H.; Nishida, S. Terrestrial experiments for the motion estimation of a large space debris object using image data. In Proceedings of the Intelligent Robots and Computer Vision XXIII: Algorithms, Techniques, and Active Vision, Boston, MA, USA, 23–25 October 2005. [Google Scholar]
- Sharma, S.; Beierle, C.; D’Amico, S. Pose estimation for non-cooperative spacecraft rendezvous using convolutional neural networks. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018. [Google Scholar]
- Sharma, S.; D’Amico, S. Systems, Neural network-based pose estimation for noncooperative spacecraft rendezvous. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4638–4658. [Google Scholar] [CrossRef]
- Du, X.; He, Y.; Chen, L.; Gao, S. Pose estimation of large non-cooperative spacecraft based on extended PnP model. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016. [Google Scholar]
- Li, Y.; Huo, J.; Yang, M.; Cui, J. Non-cooperative target pose estimate of spacecraft based on vectors. In Proceedings of the Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019. [Google Scholar]
- Pan, H.; Huang, J.; Qin, S. High accurate estimation of relative pose of cooperative space targets based on measurement of monocular vision imaging. Optik 2014, 125, 3127–3133. [Google Scholar] [CrossRef]
- De Jongh, W.; Jordaan, H.; Van Daalen, C. Experiment for pose estimation of uncooperative space debris using stereo vision. Acta Astronaut. 2020, 168, 164–173. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, L.; Cheng, L.; Koch, R. Pose Estimation from Line Correspondences: A Complete Analysis and a Series of Solutions. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1209–1222. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xu, G.; Cheng, Y. A novel algebraic solution to the perspective-three-line pose problem. Comput. Vis. Image Underst. 2020, 191, 102711. [Google Scholar] [CrossRef]
- Wang, P.; Xu, G.; Cheng, Y.; Yu, Q. A simple, robust and fast method for the perspective-n-point Problem. Pattern Recognit. Lett. 2018, 108, 31–37. [Google Scholar] [CrossRef]
- Mirzaei, F.M.; Roumeliotis, S.I. Globally optimal pose estimation from line correspondences. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Li, X.; Zhang, Y.; Liu, J. A direct least squares method for camera pose estimation based on straight line segment correspondences. Acta Opt. Sin. 2015, 35, 0615003. [Google Scholar]
- Liu, Y.; Xie, Z.; Zhang, Q.; Zhao, X.; Liu, H. A new approach for the estimation of non-cooperative satellites based on circular feature extraction. Robot. Auton. Syst. 2020, 129, 103532. [Google Scholar] [CrossRef]
- He, Y.; Zhao, J.; Guo, Y.; He, W.; Yuan, K. PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features. Sensors 2018, 18, 1159. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Li, Y.; Huo, J.; Yang, M.; Wang, Y.; Li, C. A measurement method of motion parameters in aircraft ground tests using computer vision. Measurement 2021, 174, 108985. [Google Scholar] [CrossRef]
- Wang, Y. Research on Motion Parameters Measuring System based on Intersected Planes. Harbin Inst. Technol. 2015. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201601&filename=1015982210.nh (accessed on 18 September 2022).
- Cui, J.; Min, C.; Feng, D. Research on pose estimation for stereo vision measurement system by an improved method: Uncertainty weighted stereopsis pose solution method based on projection vector. Opt. Express 2020, 28, 5470–5491. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]


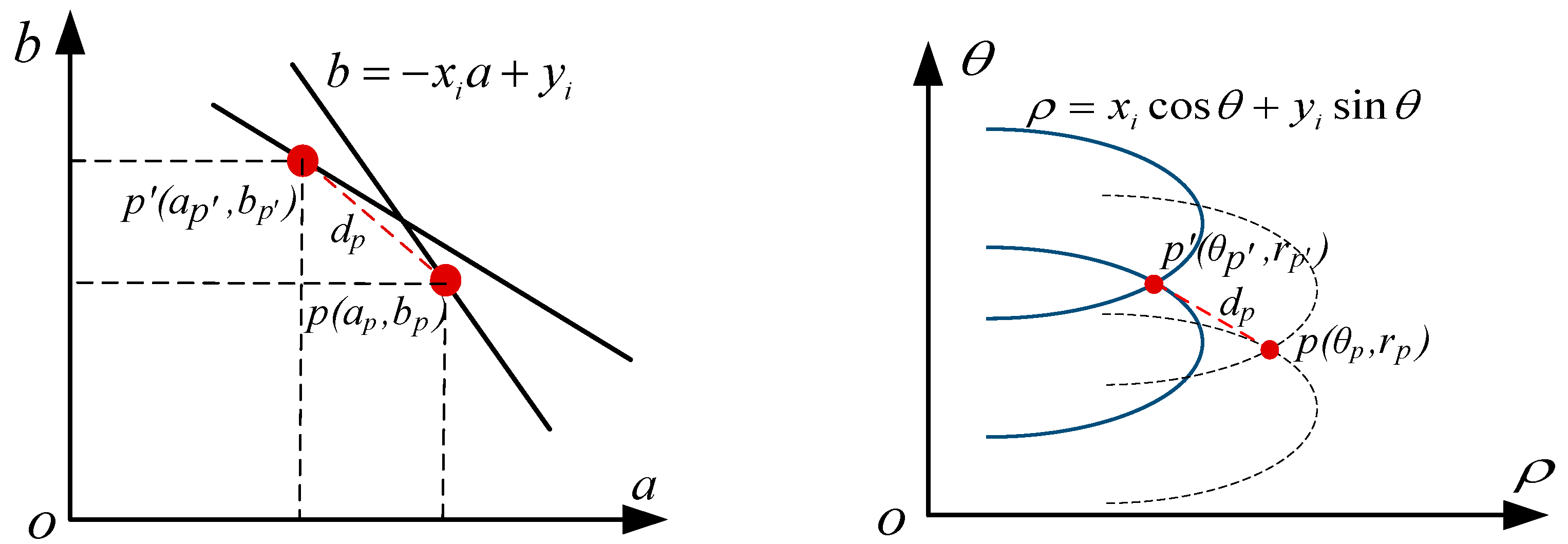

| Position/mm | Pose/° | ||||
|---|---|---|---|---|---|
| tx | ty | tz | Yaw | Roll | Pitch |
| 10 sin(0.2πt) | 525 t | 10 sin(0.2πt) | 10 sin(0.2πt) | 10 sin(0.2πt) | 10 sin(0.2πt) |
| External parameter | Baseline/mm | 1224.98 | |
| rotate/° | (120.92, −14.55, −27.04) | ||
| Intrinsic parameter | radial distortion l,r | (−0.219, 0.072) | (−0.240, 0.129) |
| focal l,r/mm | (10.37, 10.37) | (10.37, 10.37) | |
| principal point l,r/mm | (5.84, 5.47) | (5.48, 5.63) | |
| Average Error | Maximum Error | |||
|---|---|---|---|---|
| Rotation Error (°) | Translation Error (mm) | Rotation Error (°) | Translation Error (mm) | |
| Feature Point method | 1.22 | 9.35 | 2.75 | 25.85 |
| Visual Odometry method | 5.51 | 15.15 | 4.85 | 55.38 |
| Direct Linear method | 1.30 | 12.12 | 2.58 | 39.25 |
| Proposed method | 1.19 | 9.24 | 2.35 | 18.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yan, Y.; Xiu, X.; Miao, Z. An Uncertainty Weighted Non-Cooperative Target Pose Estimation Algorithm, Based on Intersecting Vectors. Aerospace 2022, 9, 681. https://doi.org/10.3390/aerospace9110681
Li Y, Yan Y, Xiu X, Miao Z. An Uncertainty Weighted Non-Cooperative Target Pose Estimation Algorithm, Based on Intersecting Vectors. Aerospace. 2022; 9(11):681. https://doi.org/10.3390/aerospace9110681
Chicago/Turabian StyleLi, Yunhui, Yunhang Yan, Xianchao Xiu, and Zhonghua Miao. 2022. "An Uncertainty Weighted Non-Cooperative Target Pose Estimation Algorithm, Based on Intersecting Vectors" Aerospace 9, no. 11: 681. https://doi.org/10.3390/aerospace9110681
APA StyleLi, Y., Yan, Y., Xiu, X., & Miao, Z. (2022). An Uncertainty Weighted Non-Cooperative Target Pose Estimation Algorithm, Based on Intersecting Vectors. Aerospace, 9(11), 681. https://doi.org/10.3390/aerospace9110681







