Analysis of NO Formation and Entropy Generation in a Reactive Flow
Abstract
1. Introduction
2. Numerical Details
2.1. Governing Equations
2.2. Radiation Modeling
2.3. Calculation of Entropy Generation
2.4. NO Modeling
2.5. Solution Procedures
3. Model Combustor and Boundary Conditions
4. Results and Discussion
5. Conclusions
- I.
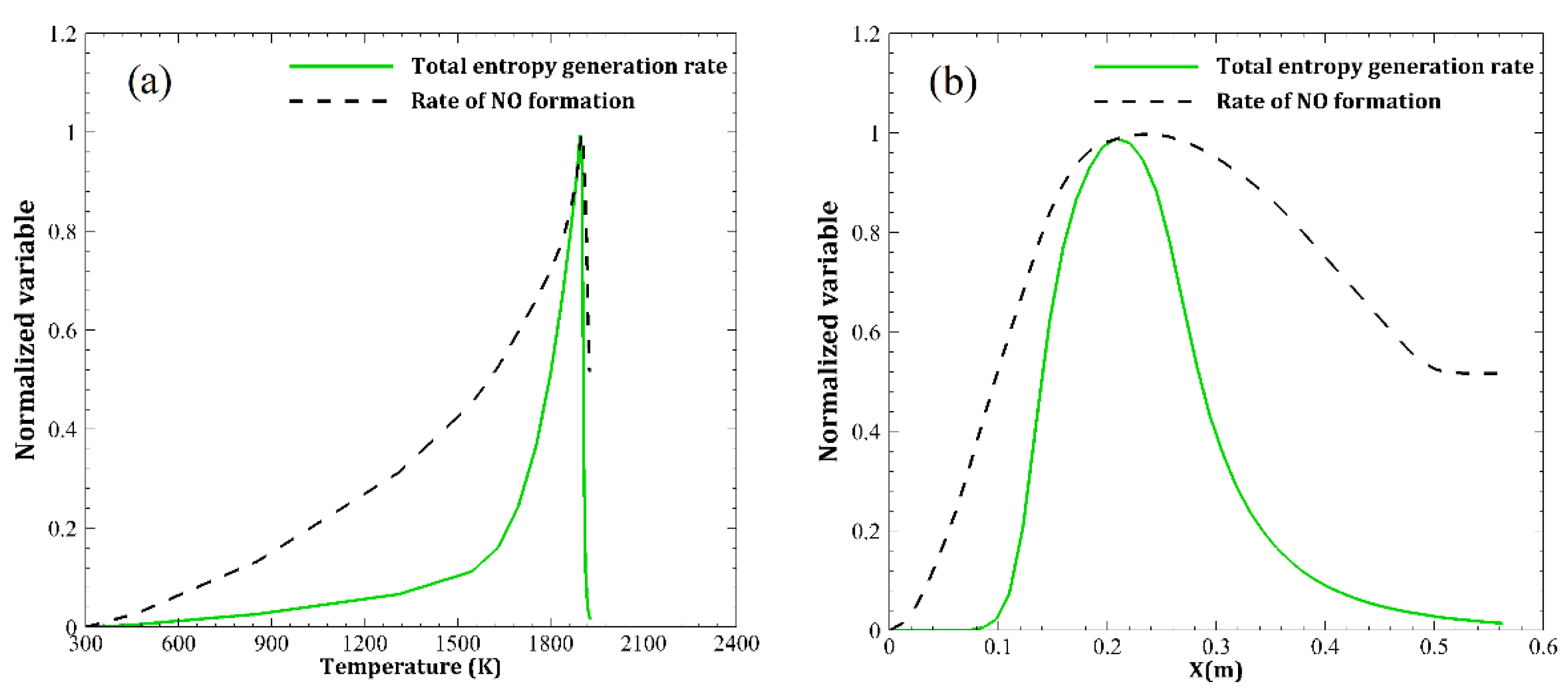
- The prompt NO is mostly produced before the combustion zone, where the air jets of high velocity enter and entropy starts to generate.
- II.
- The main region of NO formation is within the range of , in which the maximum total entropy rate of generation and the maximum temperature are also reported.
- III.
- The total entropy generation rate is more sensitive to high temperature (1500–1930 K) than the NO formation rate. With an increase of 28.7% in temperature, entropy generation and NO formation rates augment by 900% and 127%, respectively.
- IV.
- The chemical reactions process is the major cause of the generation of entropy. Moreover, the contribution of other processes toward entropy generation can be arrayed, such as heat conduction, diffusion of mass, and viscous dissipation.
- V.
- The generation of entropy owing to chemical reactions depends on each species, and therefore, NO formation directly affects the entropy generation rate.
- VI.
- The results prove that, in a reactive flow, the distributions of the total entropy generation rate and temperature are defined in practice by the chemical reactions process. The NO formation rate and total entropy generation rate are dependent on temperature. Therefore, by realizing the distribution of each of these three parameters (i.e., entropy generation), the approximate distributions of the other two (i.e., NO concentration and temperature) along with the combustion formation zone, can be predicted.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| List of symbols | |||
| Surface area of particle | Greek symbols | ||
| Mass diffusion coefficient of species | Absorption coefficient | ||
| Particle diameter | Equivalent absorption coefficient | ||
| Internal energy | Species chemical potential(J/kg K) | ||
| Equivalent emission | Coefficient of diffusion | ||
| Body force per unit volume of species | Kinetic energy dissipation rate | ||
| Radiation intensity | Particle emissivity | ||
| Mass flux of species | Solid angle | ||
| Reaction rate constant | Density () | ||
| Kinetic energy of turbulence | Stefan-Boltzmann constant | ||
| Coefficient of thermal conductivity (W/m K) | Equivalent particle scattering factor | ||
| n | Refractive index | Particle scattering factor | |
| P | Pressure (Pa) | Viscous stress (N/m2) | |
| Reference pressure | Dependent variable | ||
| Conduction heat flux | Production rate from chemical reaction | ||
| r | Position vector | Equivalence ratio | |
| Gas constant (J/kg K) | Phase function | ||
| Cylindrical coordinates system | Viscous dissipation function | ||
| Scattering direction vector | Subscripts | ||
| Direction vector | Effective | ||
| Specific entropy of species | · | Dot product (Multiplication) | |
| Source term | Vector differential operator | ||
| Volumetric generation rate of entropy (W/m3 K) | k | Variable type in Equation (1) | |
| Time () | Abbreviations | ||
| Mean temperature () | CO2 | Carbon dioxide | |
| Velocity component () | DOM | Discrete ordinate model | |
| V | Volume | EDM | Eddy dissipation model |
| Species mole fraction | EGR | Exhaust gas recirculation | |
| Coordinates of Cartesian system | FGR | Flue gas recirculation | |
| Coordinates of Cartesian system | FVM | Finite volume method | |
| Non-dimensional distance | OH | hydroxyl radical | |
| Species mass fraction | MD | Mean deviation | |
| Velocity components () | NO | Nitrogen oxide | |
| Mean temperature () | NOX | Nitrogen oxides | |
| Presumed density function | |||
| WGSSM | Weighted sum of gray gases model | ||
References
- Jiang, L.-Y.; Campbell, I. A Critical Evaluation of NOx Modeling in a Model Combustor. In ASME Turbo Expo 2004: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2004; pp. 403–414. [Google Scholar]
- Meunier, P.; Costa, M.; Carvalho, M. On NOx emissions from turbulent propane diffusion flames. Combust. Flame 1998, 112, 221–230. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Abedinejad, M.S.; Yazdani-Ahmadabadi, H. Influence of Variable Air Distribution on Pollutants Emission in a Model Wall Jet Can Combustor. Heat Transf. Res. 2018, 49, 1667–1688. [Google Scholar] [CrossRef]
- Watanabe, H.; Suwa, Y.; Matsushita, Y.; Morozumi, Y.; Aoki, H.; Tanno, S.; Miura, T. Spray combustion simulation including soot and NO formation. Energy Convers. Manag. 2007, 48, 2077–2089. [Google Scholar] [CrossRef]
- Guo, H.; Smallwood, G.J. The interaction between soot and NO formation in a laminar axisymmetric coflow ethylene/air diffusion flame. Combust. Flame 2007, 149, 225–233. [Google Scholar] [CrossRef]
- Saqr, K.M.; Aly, H.S.; Sies, M.M.; Wahid, M.A. Effect of free stream turbulence on NOx and soot formation in turbulent diffusion CH4-air flames. Int. Commun. Heat Mass Transf. 2010, 37, 611–617. [Google Scholar] [CrossRef]
- Gascoin, N.; Yang, Q.; Chetehouna, K. Thermal effects of CO2 on the NOx formation behavior in the CH4 diffusion combustion system. Appl. Therm. Eng. 2017, 110, 144–149. [Google Scholar] [CrossRef]
- Prakash, V.; Steimes, J.; Roekaerts, D.; Klein, S. Modelling the Effect of External Flue Gas Recirculation on NOx and CO Emissions in a Premixed Gas Turbine Combustor with Chemical Reactor Networks. In ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V04BT04A027. [Google Scholar]
- Peng, L.; Zhang, J. Simulation of turbulent combustion and NO formation in a swirl combustor. Chem. Eng. Sci. 2009, 64, 2903–2914. [Google Scholar] [CrossRef]
- Xu, Q.; Shen, M.; Shi, K.; Liu, Z.; Akkurt, N.; Xiong, Y.; Liu, L.; Feng, J.; Wang, J. Effect of the Mixing Structure Parameters of a Self-reflux Burner on Combustion Characteristics and NOx Emission. J. Therm. Sci. 2021, 30, 1224–1236. [Google Scholar] [CrossRef]
- Xu, Q.; Akkurt, N.; Yang, G.; Zhu, L.; Shi, K.; Wang, K.; Zou, Z.; Liu, Z.; Wang, J.; Du, Z. Effects of optimized operating parameters on combustion characteristics and NOx emissions of a burner based on orthogonal analysis. J. Therm. Sci. 2021, 30, 1212–1223. [Google Scholar] [CrossRef]
- Xu, M.; Fan, Y.; Yuan, J.; Sheng, C.; Yao, H. Modelling NOx emissions during staged combustion. Int. J. Energy Res. 1999, 23, 683–693. [Google Scholar] [CrossRef]
- Yuan, J.; Naruse, I. Modeling of combustion characteristics and NOx emission in highly preheated and diluted air combustion. Int. J. Energy Res. 1998, 22, 1217–1234. [Google Scholar] [CrossRef]
- Briones, A.M.; Mukhopadhyay, A.; Aggarwal, S.K. Analysis of entropy generation in hydrogen-enriched methane–air propagating triple flames. Int. J. Hydrogen Energy 2009, 34, 1074–1083. [Google Scholar] [CrossRef]
- Wang, L.; Karimi, N.; Sutardi, T.; Paul, M.C. Numerical modelling of unsteady transport and entropy generation in oxy-combustion of single coal particles with varying flow velocities and oxygen concentrations. Appl. Therm. Eng. 2018, 144, 147–164. [Google Scholar] [CrossRef]
- Gholamalizadeh, E.; Alimoradi, A.; Saee, A.D.; Amiri, A.; Moghaddam, M.G. Study of the heat transfer characteristics and entropy generation rate for the reacting flows inside tubes. Appl. Therm. Eng. 2019, 149, 1435–1444. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Zuo, Z.; Yang, W. Entropy generation analysis of unsteady premixed methane/air flames in a narrow channel. Appl. Therm. Eng. 2017, 126, 929–938. [Google Scholar] [CrossRef]
- Chen, S. Analysis of entropy generation in counter-flow premixed hydrogen–air combustion. Int. J. Hydrogen Energy 2010, 35, 1401–1411. [Google Scholar] [CrossRef]
- Jejurkar, S.Y.; Mishra, D.P. Numerical analysis of entropy generation in an annular microcombustor using multistep kinetics. Appl. Therm. Eng. 2013, 52, 394–401. [Google Scholar] [CrossRef]
- Yang, W.; Jiang, D.; Chua, K.Y.K.; Zhao, D.; Pan, J. Combustion process and entropy generation in a novel microcombustor with a block insert. Chem. Eng. J. 2015, 274, 231–237. [Google Scholar] [CrossRef]
- Hunt, G.; Karimi, N.; Torabi, M. Analytical investigation of heat transfer and classical entropy generation in microreactors—The influences of exothermicity and asymmetry. Appl. Therm. Eng. 2017, 119, 403–424. [Google Scholar] [CrossRef]
- Mohammadi, I.; Ajam, H. A theoretical study of entropy generation of the combustion phenomenon in the porous medium burner. Energy 2019, 188, 116004. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Abedinejad, M.S. Influence of incoming air conditions on fuel spray evaporation in an evaporating chamber. Chem. Eng. Sci. 2018, 189, 233–244. [Google Scholar] [CrossRef]
- Alemi, E.; Zargarabadi, M.R. Effects of jet characteristics on NO formation in a jet-stabilized combustor. Int. J. Therm. Sci. 2017, 112, 55–67. [Google Scholar] [CrossRef]
- Lu, H.; Liu, F.; Wang, Y.; Fan, X.; Liu, C.; Xu, G. The effect of different reaction mechanisms on combustion simulation of a reverse-flow combustor. J. Therm. Sci. 2020, 29, 793–812. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Teymoori, A.; Ghiyasi, M. Sensitivity Analysis of Pollutants and Pattern Factor in a Gas Turbine Model Combustor due to Changes in Stabilizing Jets Characteristics. J. Therm. Sci. 2022, 31, 1622–1641. [Google Scholar] [CrossRef]
- Ganji, H.B.; Ebrahimi, R. Numerical estimation of blowout, flashback, and flame position in MIT micro gas-turbine chamber. Chem. Eng. Sci. 2013, 104, 857–867. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Abedinejad, M.S.; Mohammadi, M. Analysis of Relationship between Entropy Generation and Soot Formation in Turbulent Kerosene/Air Jet Diffusion Flames. Energy Fuels 2019, 33, 9184–9195. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Strokach, E.; Zhukov, V.; Borovik, I.; Sternin, A.; Haidn, O.J. Simulation of a GOx-GCH4 Rocket Combustor and the Effect of the GEKO Turbulence Model Coefficients. Aerospace 2021, 8, 341. [Google Scholar] [CrossRef]
- Yu, C.; Shrotriya, P.; Li, X.; Maas, U. Reduced modeling of the NOx formation based on the reaction-diffusion manifolds method for counterflow diffusion flames. Proc. Combust. Inst. 2022, in press. [Google Scholar] [CrossRef]
- Torkzadeh, M.; Bolourchifard, F.; Amani, E. An investigation of air-swirl design criteria for gas turbine combustors through a multi-objective CFD optimization. Fuel 2016, 186, 734–749. [Google Scholar] [CrossRef]
- Yao, Q.; Zhang, Y.; Wang, X.; Tian, Z.; Hu, G.; Du, W. Investigation of NOx emission under different burner structures with the optimized combustion model. Neurocomputing 2022, 482, 224–235. [Google Scholar] [CrossRef]
- Pitsch, H.; Peters, N. A consistent flamelet formulation for non-premixed combustion considering differential diffusion effects. Combust. Flame 1998, 114, 26–40. [Google Scholar] [CrossRef]
- Hjertager, L.K.; Hjertager, B.H.; Solberg, T. CFD modelling of fast chemical reactions in turbulent liquid flows. Comput. Chem. Eng. 2002, 26, 507–515. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.; Kelley, A.; Law, C. Hierarchical and comparative kinetic modeling of laminar flame speeds of hydrocarbon and oxygenated fuels. Prog. Energy Combust. Sci. 2012, 38, 468–501. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Abedinejad, M.S.; Bazdidi-Tehrani, F.; Mirzaei, S. Investigation of turbulent flow structures in a wall jet can combustor: Application of large eddy simulation. Eur. Phys. J. Plus 2021, 136, 665. [Google Scholar] [CrossRef]
- Sarlak, R.; Shams, M.; Ebrahimi, R. Numerical simulation of soot formation in a turbulent diffusion flame: Comparison among three soot formation models. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 1290–1301. [Google Scholar] [CrossRef]
- Bidabadi, M.; Dizaji, H.B.; Dizaji, F.F.; Ghahsareh, M.S. Effect of thermal radiation on initiation of flame instability in moisty organic dust combustion. In Proceedings of the 20th Annual International Conference on Mechanical Engineering (ISME), Ropar, India, 19–21 May 2012; Shiraz University: Shiraz, Iran, 2012. [Google Scholar]
- Bidabadi, M.; Beidaghy Dizaji, H.; Faraji Dizaji, F.; Mostafavi, S.A. A parametric study of lycopodium dust flame. J. Eng. Math. 2015, 92, 147–165. [Google Scholar] [CrossRef]
- Bidabadi, M.; Mostafavi, S.; Beidaghy Dizaji, H.; Faraji Dizaji, F. Lycopodium dust flame characteristics considering char yield. Sci. Iran. 2013, 20, 1781–1791. [Google Scholar]
- Fiveland, W. Discrete-ordinates solutions of the radiative transport equation for rectangular enclosures. J. Heat Transf. 1984, 106, 699–706. [Google Scholar] [CrossRef]
- Bazdidi-Tehrani, F.; Mirzaei, S.; Abedinejad, M.S. Influence of Chemical Mechanisms on Spray Combustion Characteristics of Turbulent Flow in a Wall Jet Can Combustor. Energy Fuels 2017, 31, 7523–7539. [Google Scholar] [CrossRef]
- Smith, T.; Shen, Z.; Friedman, J. Evaluation of coefficients for the weighted sum of gray gases model. J. Heat Transf. 1982, 104, 602–608. [Google Scholar] [CrossRef]
- Rahmanpour, M.; Ebrahimi, R.; Shams, M. Numerically gas radiation heat transfer modeling in chemically nonequilibrium reactive flow. Heat Mass Transf. 2011, 47, 1659–1670. [Google Scholar] [CrossRef]
- Howell, J.R.; Menguc, M.P.; Siegel, R. Thermal Radiation Heat Transfer; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Dressler, L.; Nicolai, H.; Agrebi, S.; Ries, F.; Sadiki, A. Computation of Entropy Production in Stratified Flames Based on Chemistry Tabulation and an Eulerian Transported Probability Density Function Approach. Entropy 2022, 24, 615. [Google Scholar] [CrossRef] [PubMed]
- Ismail, N.C.; Abdullah, M.Z.; Mazlan, N.M.; Mustafa, K.F. Entropy Generation and Exergy Analysis of Premixed Fuel-Air Combustion in Micro Porous Media Burner. Entropy 2020, 22, 1104. [Google Scholar] [CrossRef]
- Sadiki, A.; Agrebi, S.; Ries, F. Entropy Generation Analysis in Turbulent Reacting Flows and Near Wall: A Review. Entropy 2022, 24, 1099. [Google Scholar] [CrossRef]
- Korpyś, M.; Gancarczyk, A.; Iwaniszyn, M.; Sindera, K.; Jodłowski, P.J.; Kołodziej, A. Analysis of Entropy Production in Structured Chemical Reactors: Optimization for Catalytic Combustion of Air Pollutants. Entropy 2020, 22, 1017. [Google Scholar] [CrossRef]
- Miller, J.A.; Bowman, C.T. Mechanism and modeling of nitrogen chemistry in combustion. Prog. Energy Combust. Sci. 1989, 15, 287–338. [Google Scholar] [CrossRef]
- Tarokh, A.; Lavrentev, A.; Mansouri, A. Numerical investigation of effect of porosity and fuel inlet velocity on diffusion filtration combustion. J. Therm. Sci. 2021, 30, 1278–1288. [Google Scholar] [CrossRef]
- Hampartsoumian, E.; Nimmo, W.; Pourkashanian, M.; Williams, A.; Missaghi, M. The prediction of NOx emissions from spray combustion. Combust. Sci. Technol. 1993, 93, 153–172. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Chemical kinetic modeling of hydrocarbon combustion. Prog. Energy Combust. Sci. 1984, 10, 1–57. [Google Scholar] [CrossRef]
- De Soete, G.G. Overall reaction rates of NO and N2 formation from fuel nitrogen. Symp. (Int.) Combust. 1975, 15, 1093–1102. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Ashgriz, N.; Mostaghimi, J. An introduction to computational fluid dynamics. In Fluid Flow Handbook; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Davidson, L. Fluid Mechanics, Turbulent Flow and Turbulence Modeling; Chalmers University of Technology: Goteborg, Sweden, 2011. [Google Scholar]
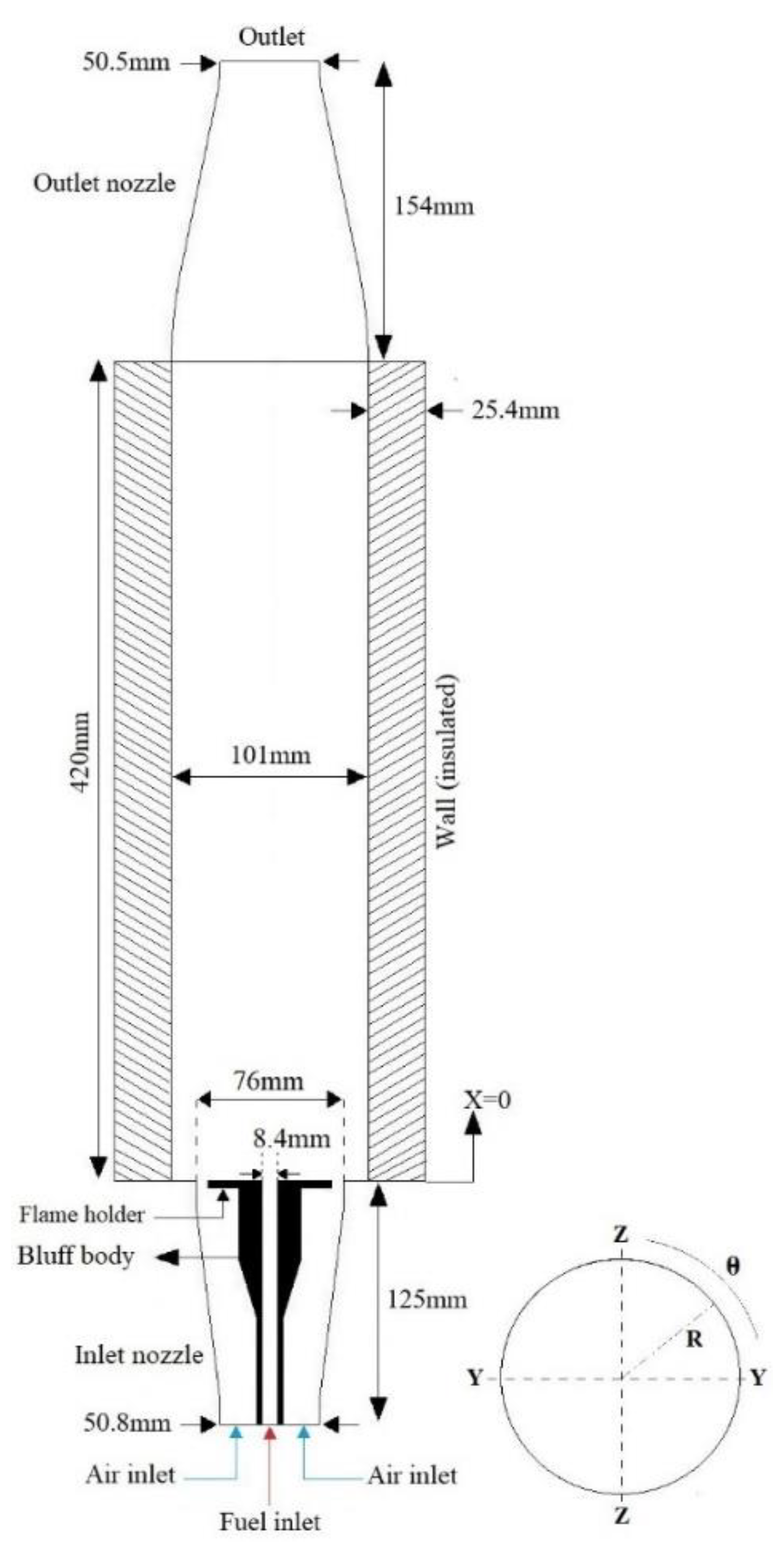
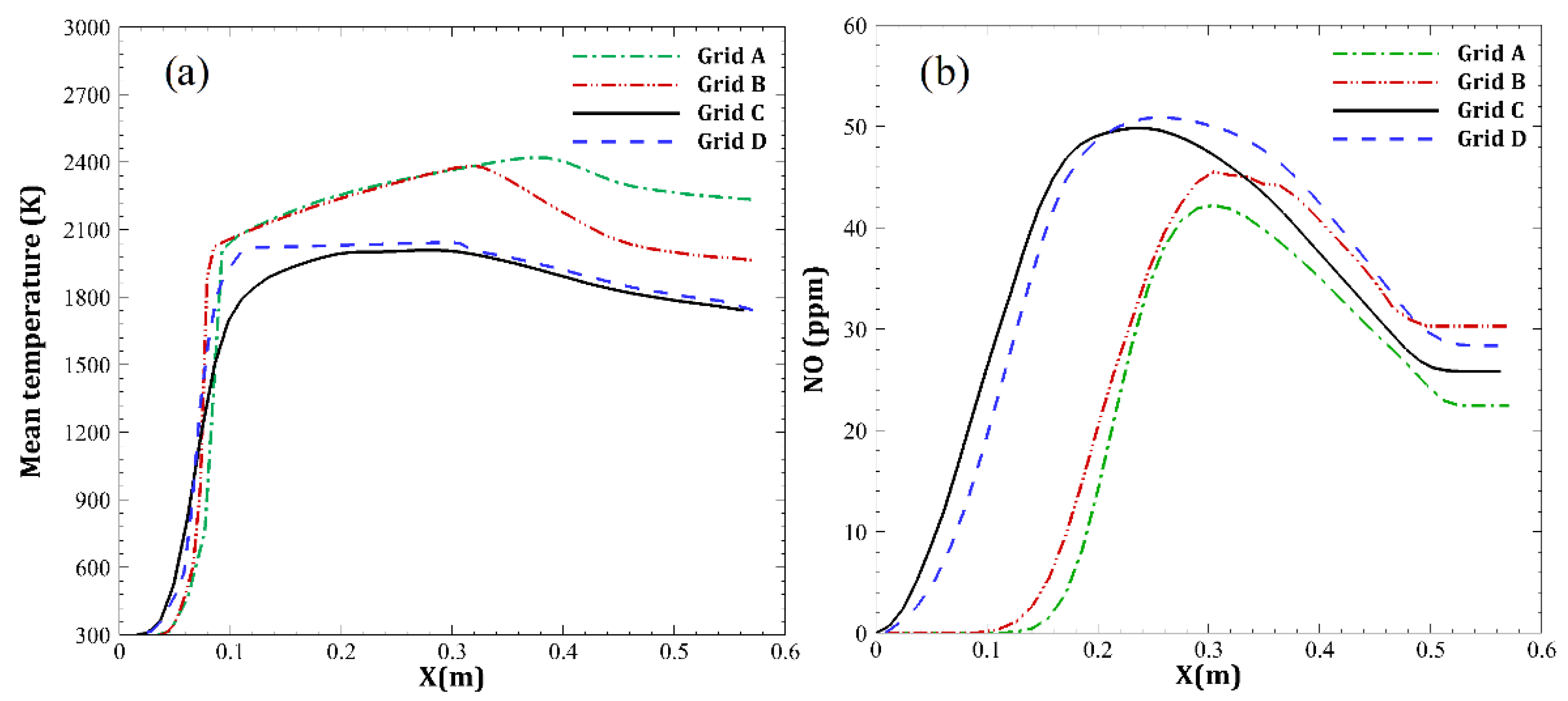
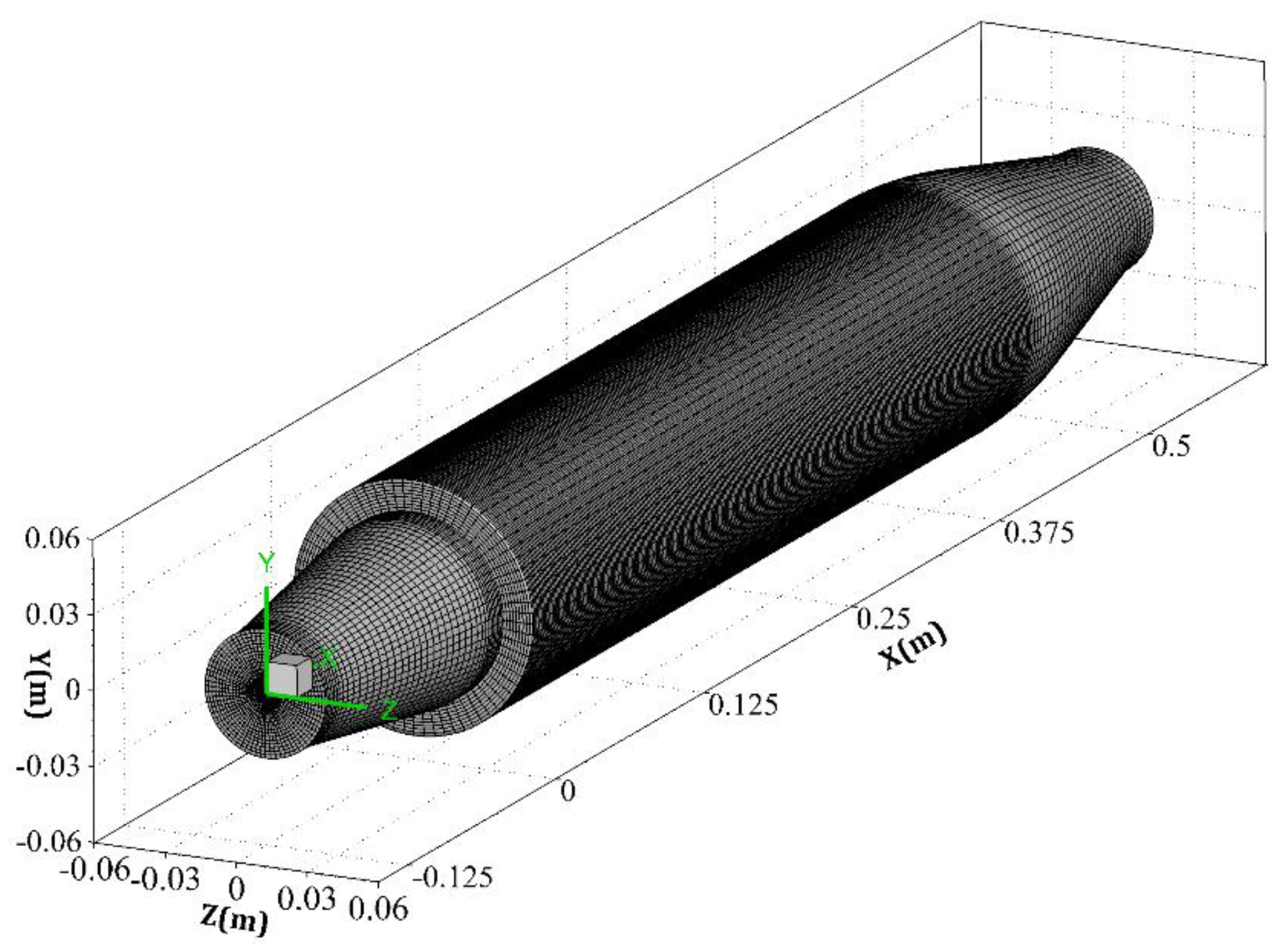
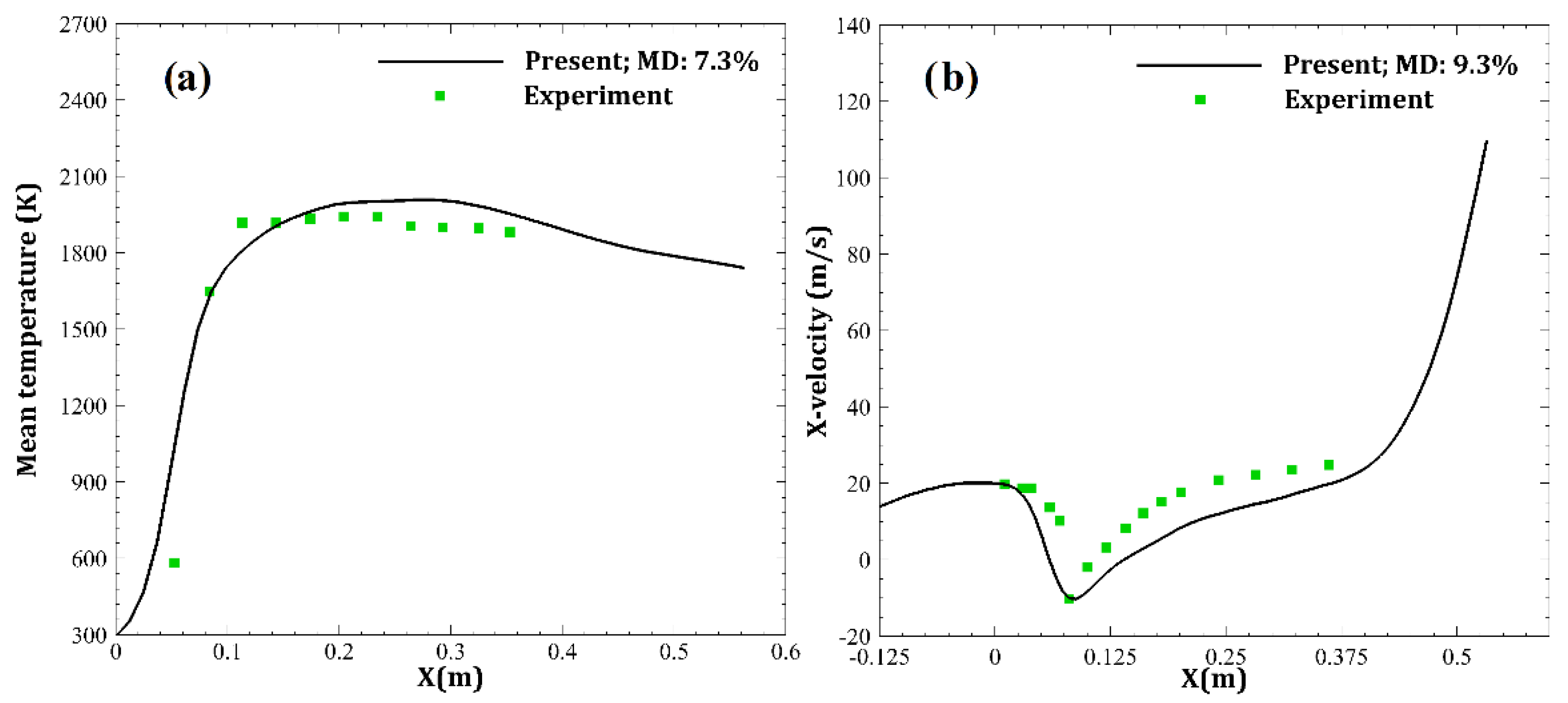
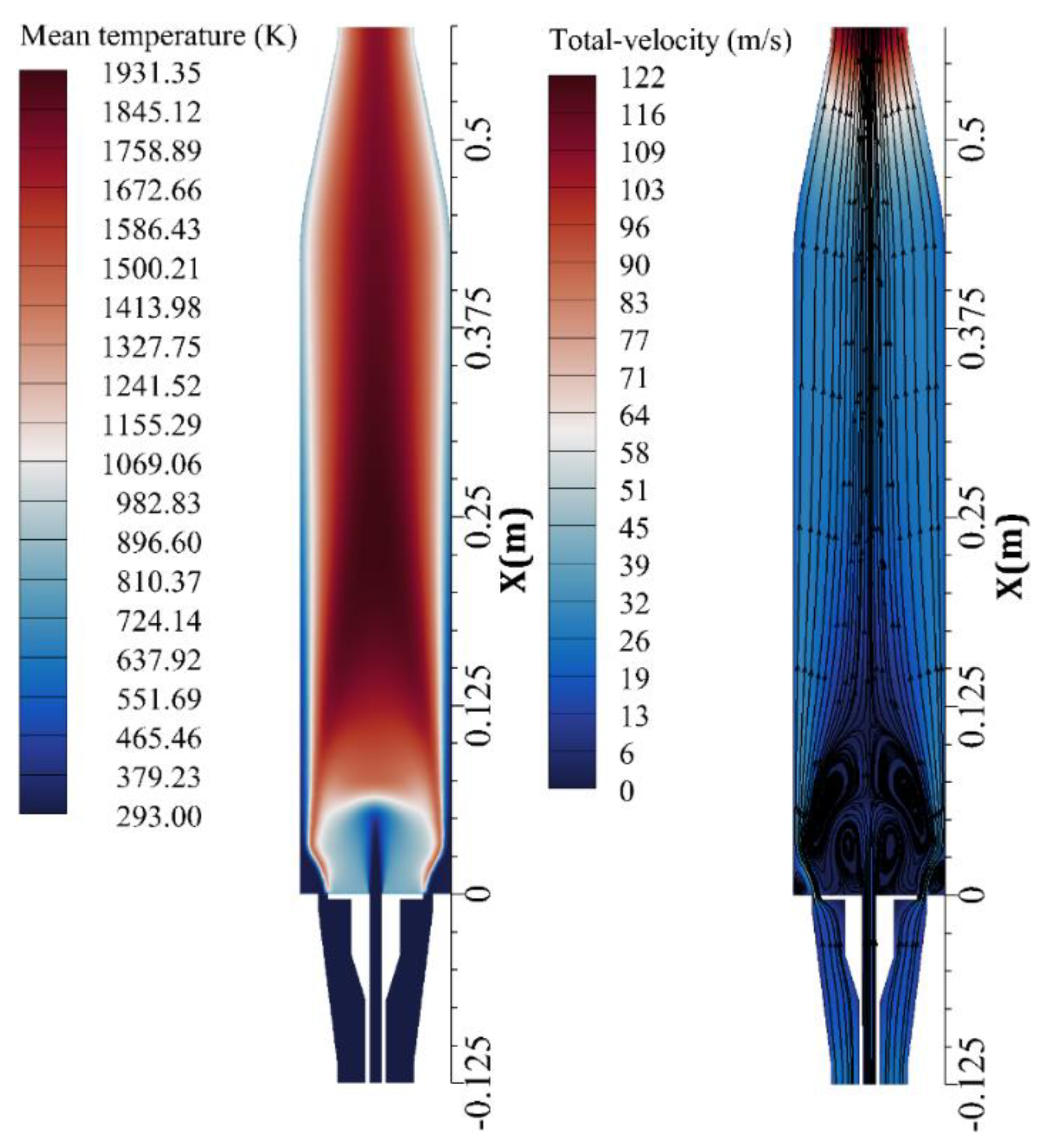
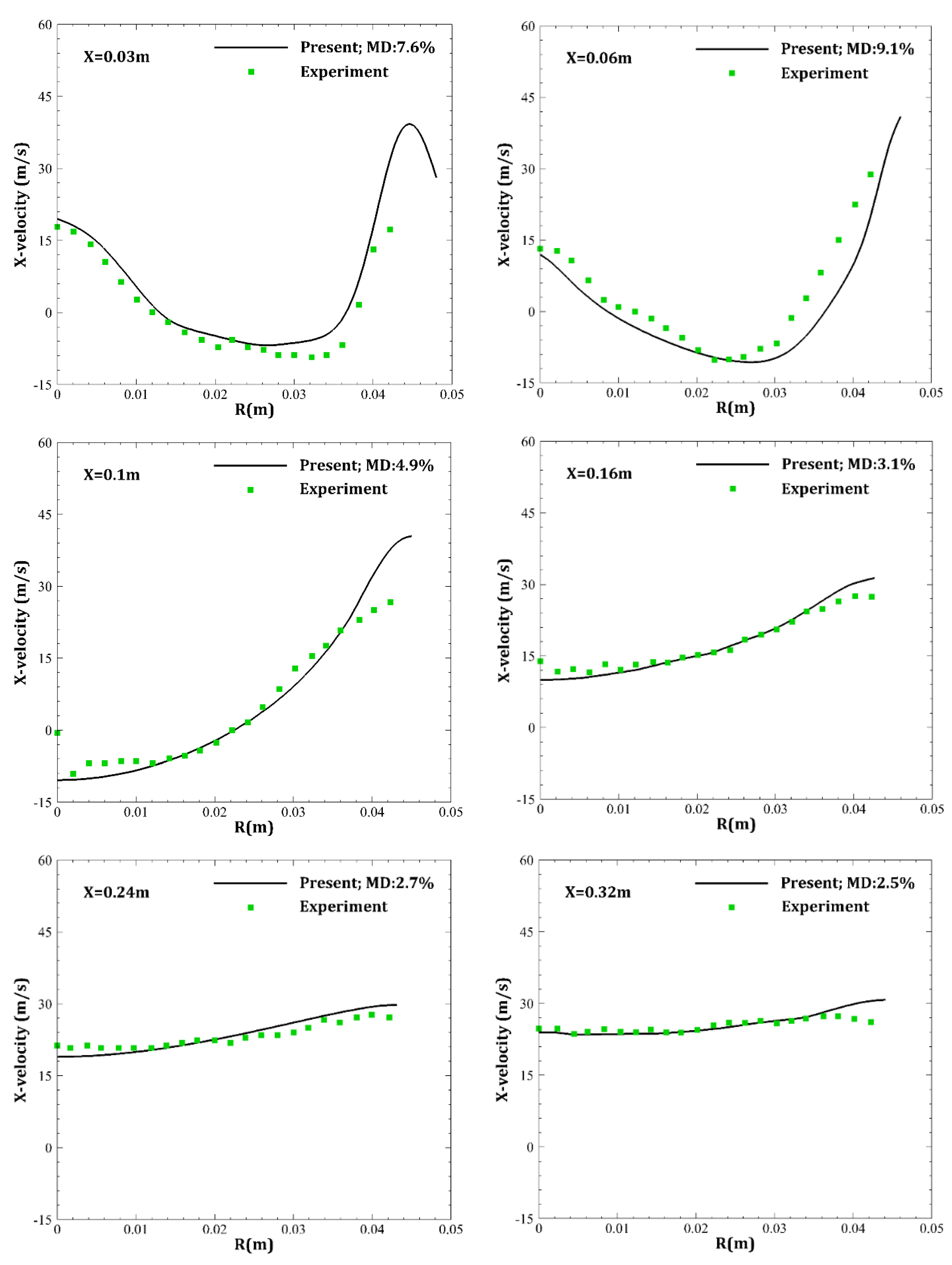
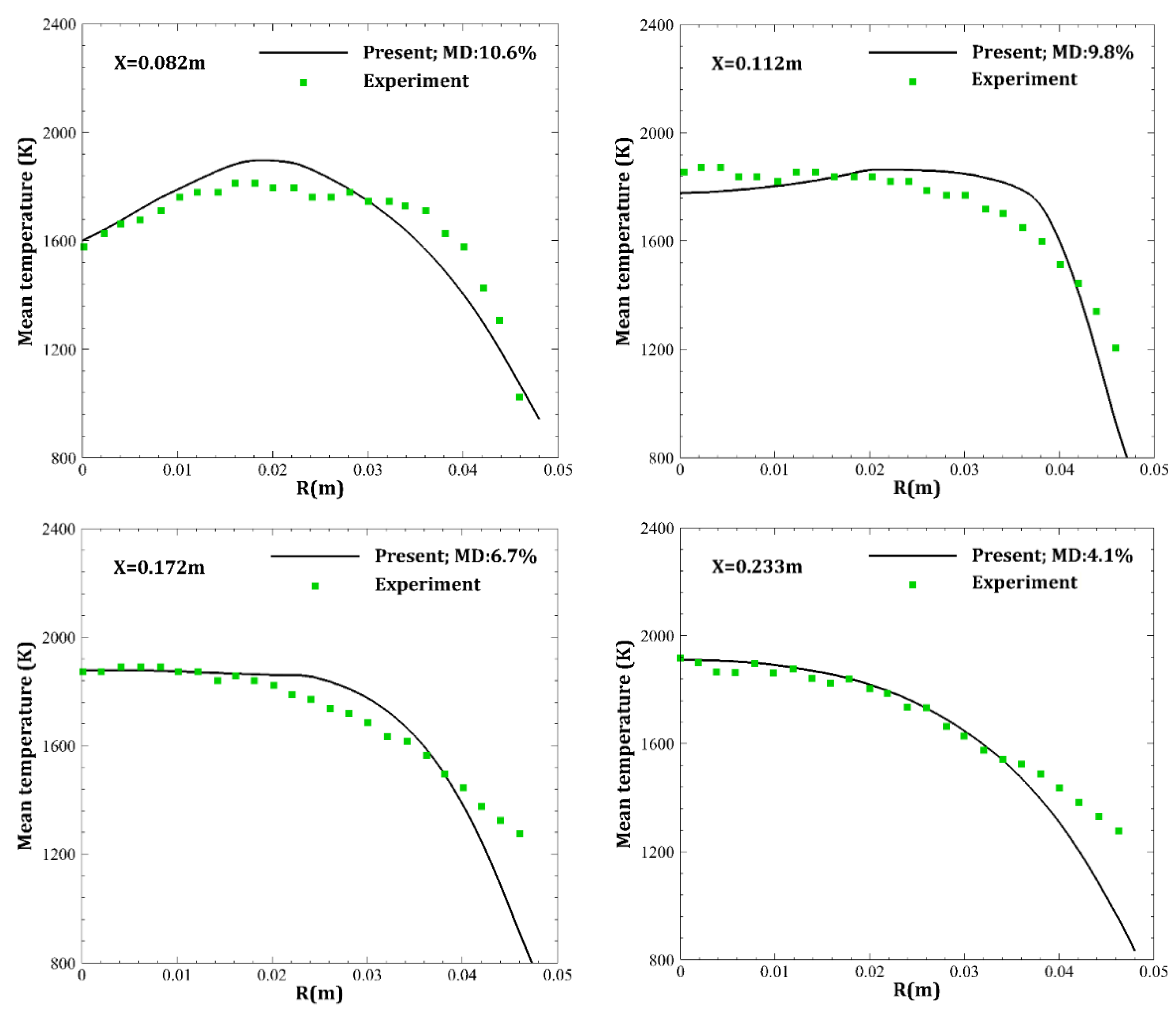

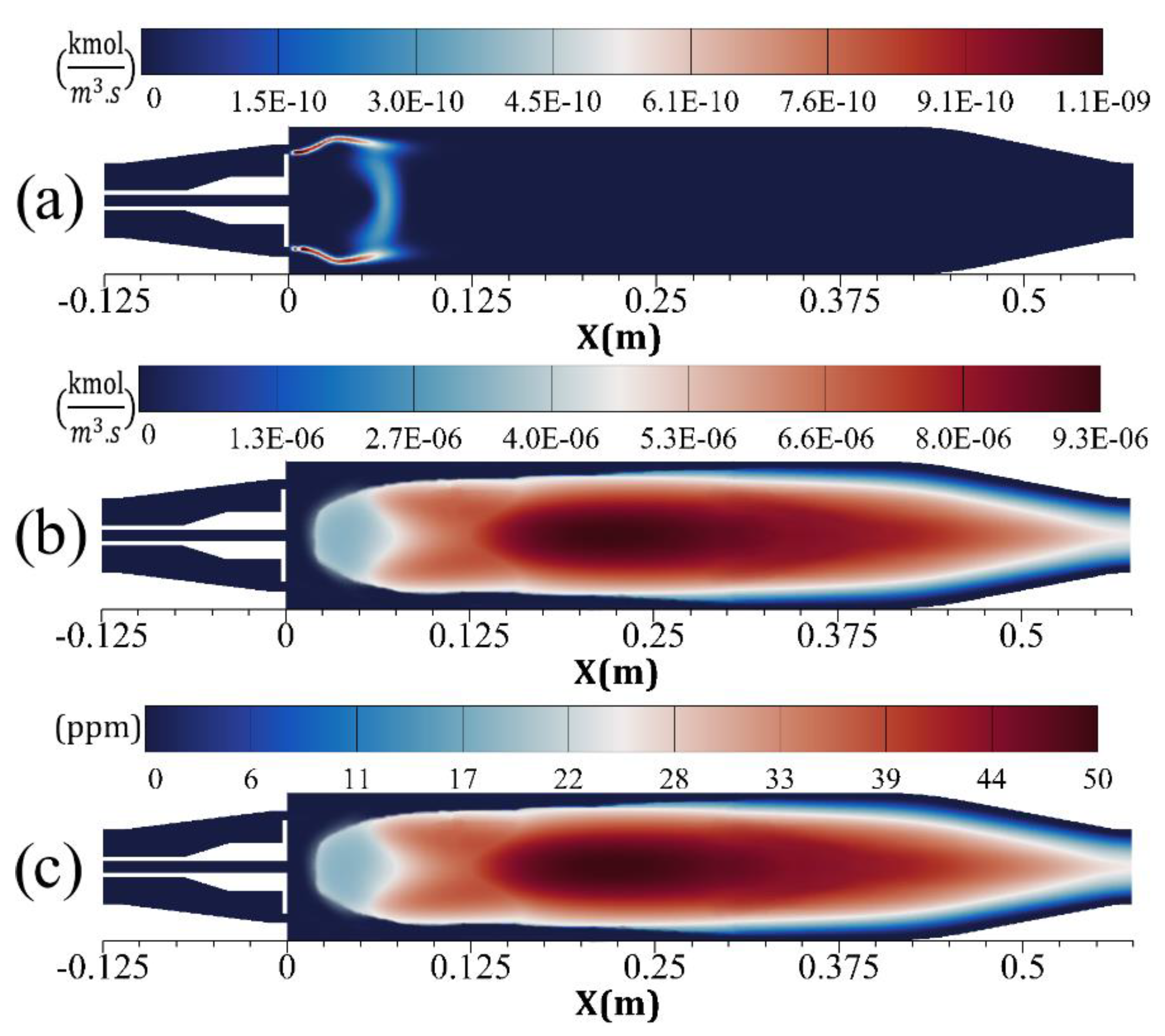
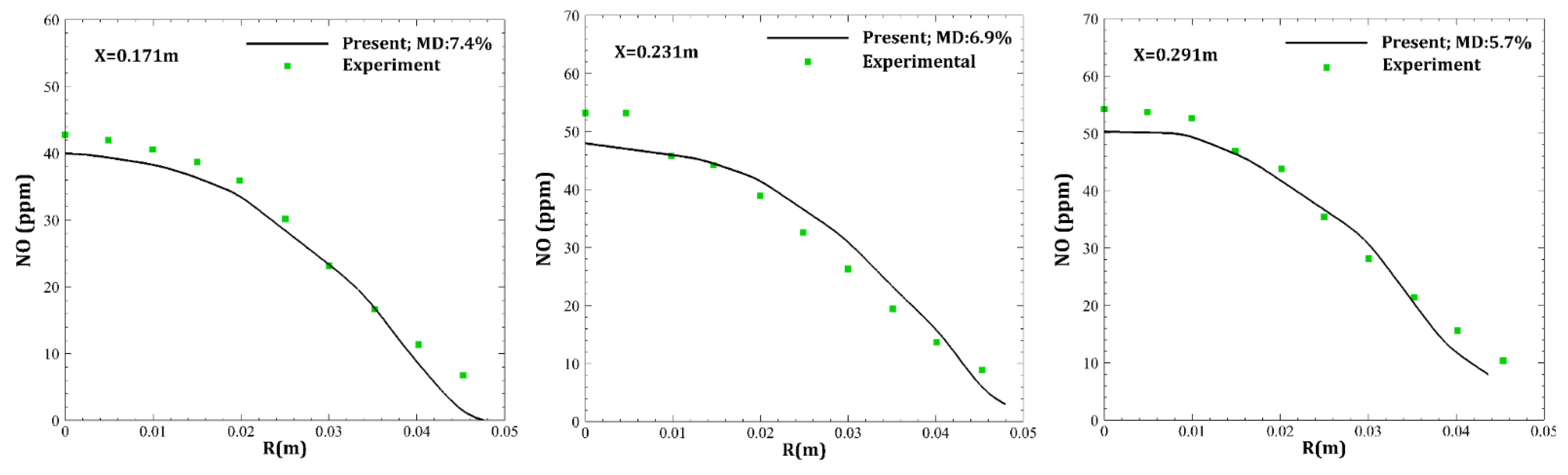
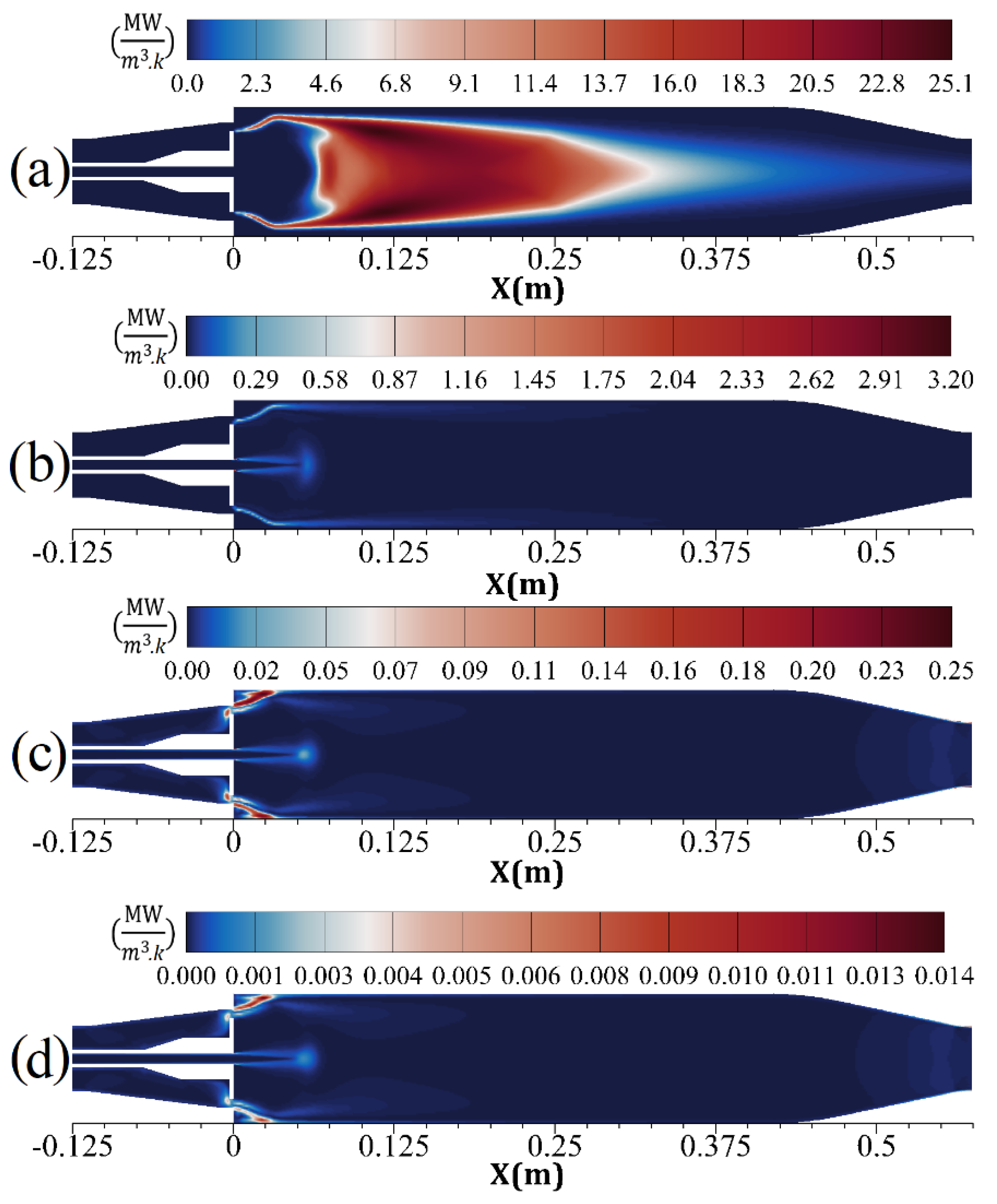
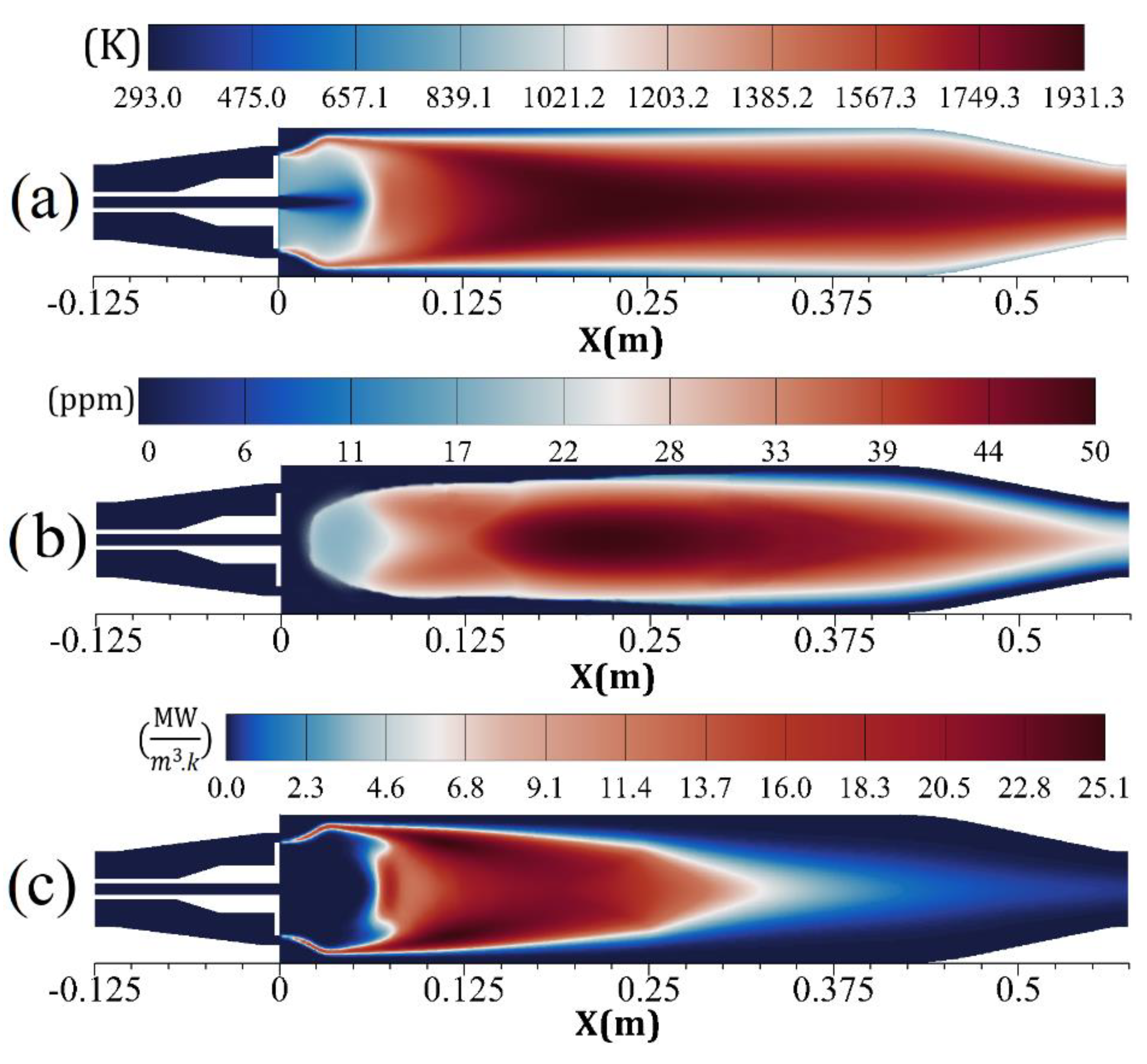
| Parameter | Amount |
|---|---|
| Diameter of inlet air () | 50.8 |
| Diameter of Fuel inlet () | 8.4 |
| Flow rate of air () | 0.55 |
| Flow rate of fuel () | 0.0162 |
| Inlet Air temperature () | 293 |
| Inlet fuel temperature () | 293 |
| Fuel (gas) | Propane (C3H8) |
| Conditions of walls | No-slip |
| Exit pressure () | 1.0 |
| Outlet diameter () | 50.5 |
| Name of Grid | Size | |
|---|---|---|
| (A) | 165 | |
| (B) | 215 | |
| (C) | 298 | |
| (D) | 338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, M.; Abedinejad, M.S. Analysis of NO Formation and Entropy Generation in a Reactive Flow. Aerospace 2022, 9, 666. https://doi.org/10.3390/aerospace9110666
Mohammadi M, Abedinejad MS. Analysis of NO Formation and Entropy Generation in a Reactive Flow. Aerospace. 2022; 9(11):666. https://doi.org/10.3390/aerospace9110666
Chicago/Turabian StyleMohammadi, Milad, and Mohammad Sadegh Abedinejad. 2022. "Analysis of NO Formation and Entropy Generation in a Reactive Flow" Aerospace 9, no. 11: 666. https://doi.org/10.3390/aerospace9110666
APA StyleMohammadi, M., & Abedinejad, M. S. (2022). Analysis of NO Formation and Entropy Generation in a Reactive Flow. Aerospace, 9(11), 666. https://doi.org/10.3390/aerospace9110666








