Multi-Domain Based Computational Investigations on Advanced Unmanned Amphibious System for Surveillances in International Marine Borders
Abstract
1. Introduction
1.1. Innovations of This Work
1.2. Literature Survey
1.3. Author Observation and Finalization
2. Proposed Methodology—Computational Hydrodynamic Analysis
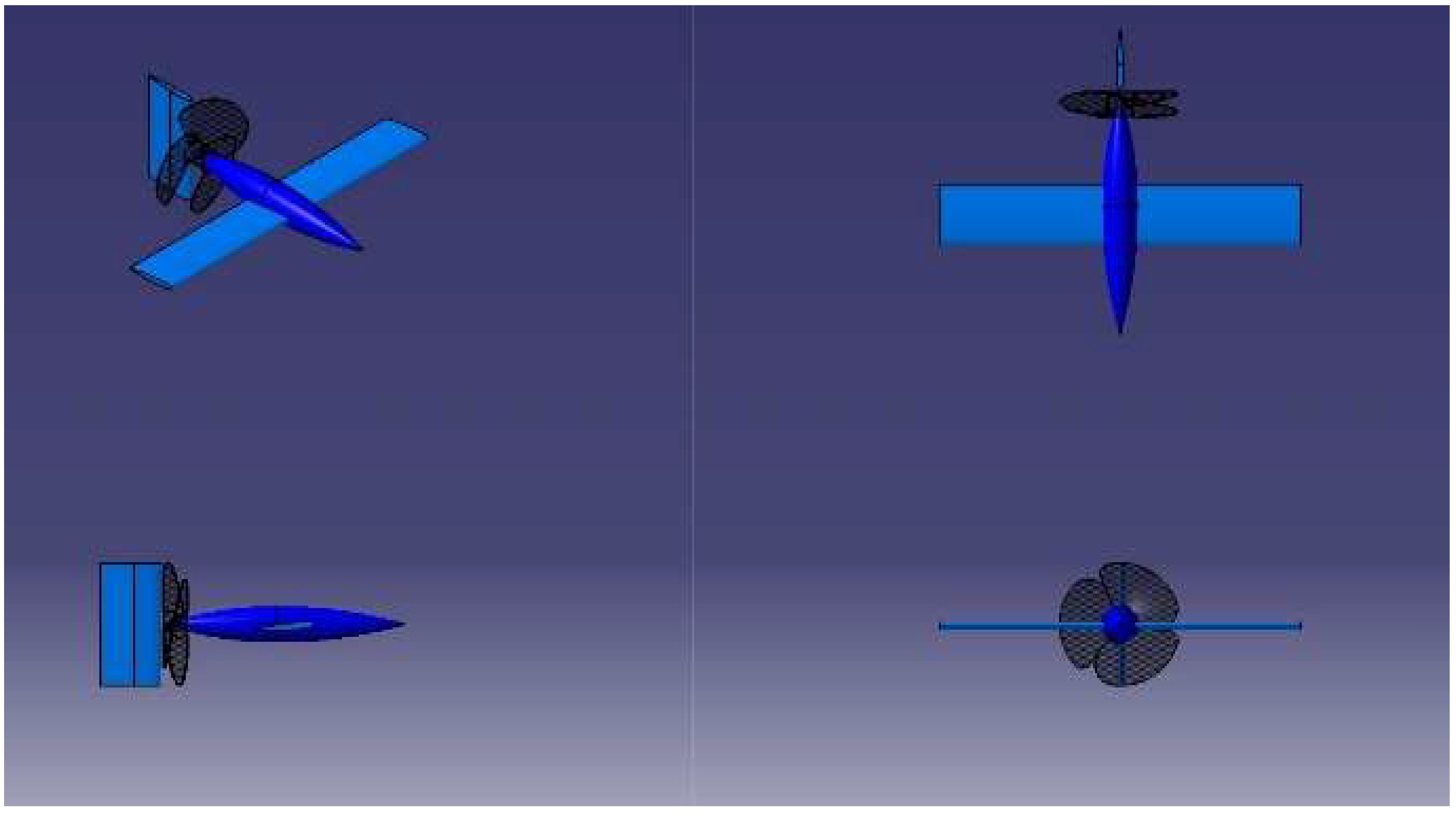
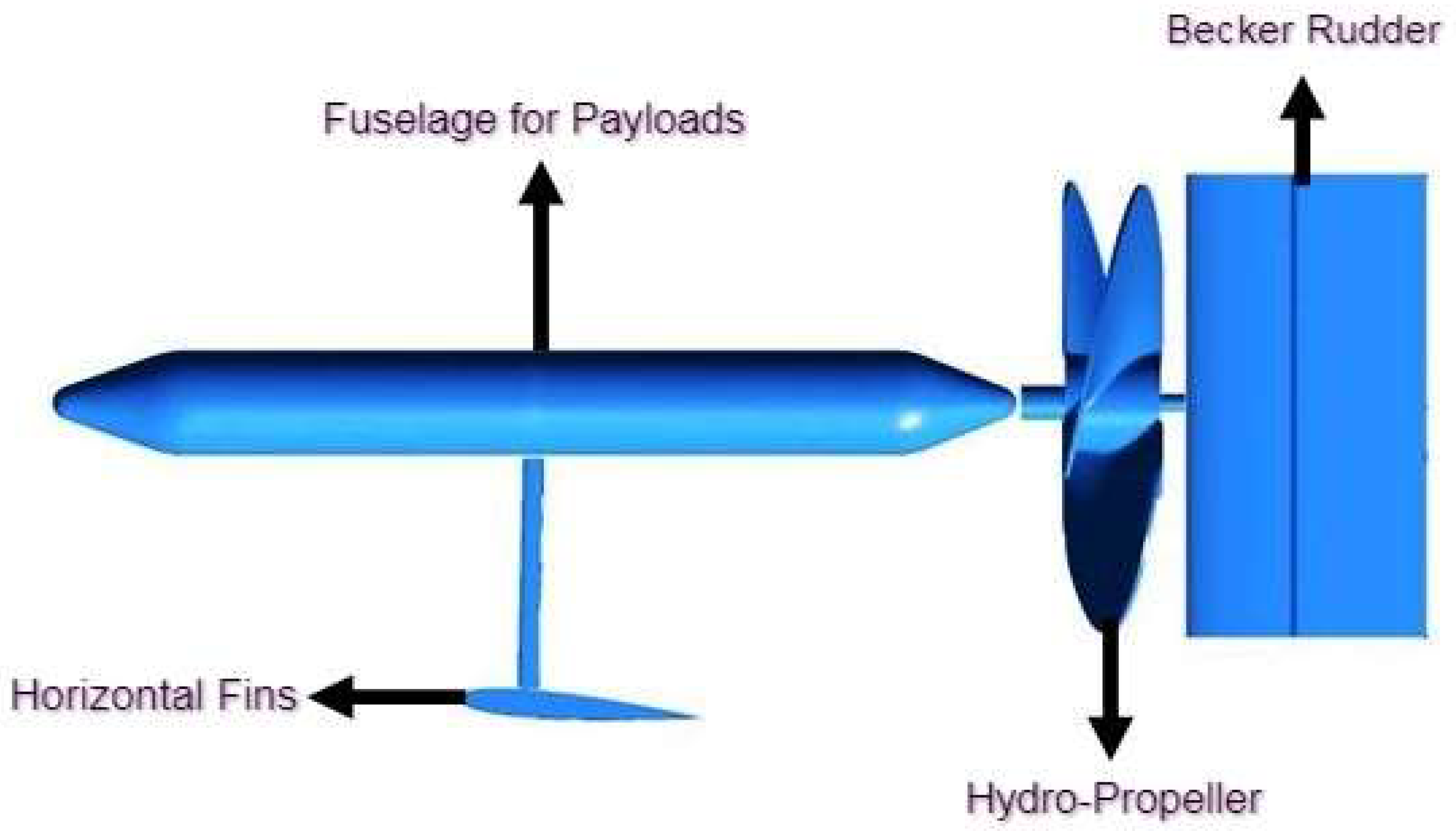
2.1. Design of Unmanned System
2.1.1. Design of Preliminary Calculations of Flexible Rectangular Wing
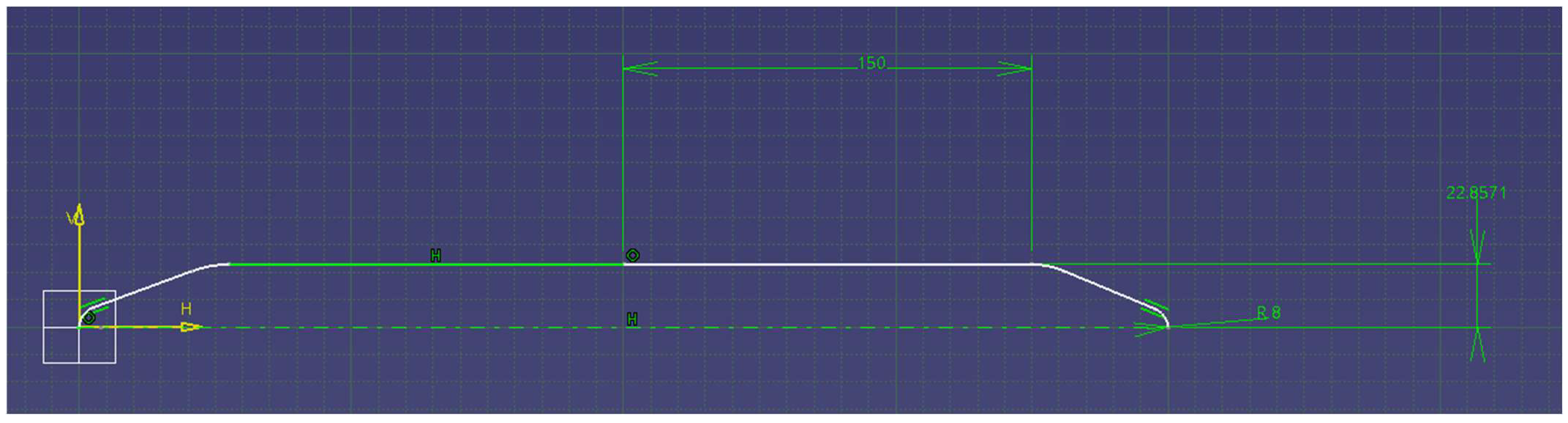
2.1.2. Design of Vertical Stabilizer with Becker Rudder
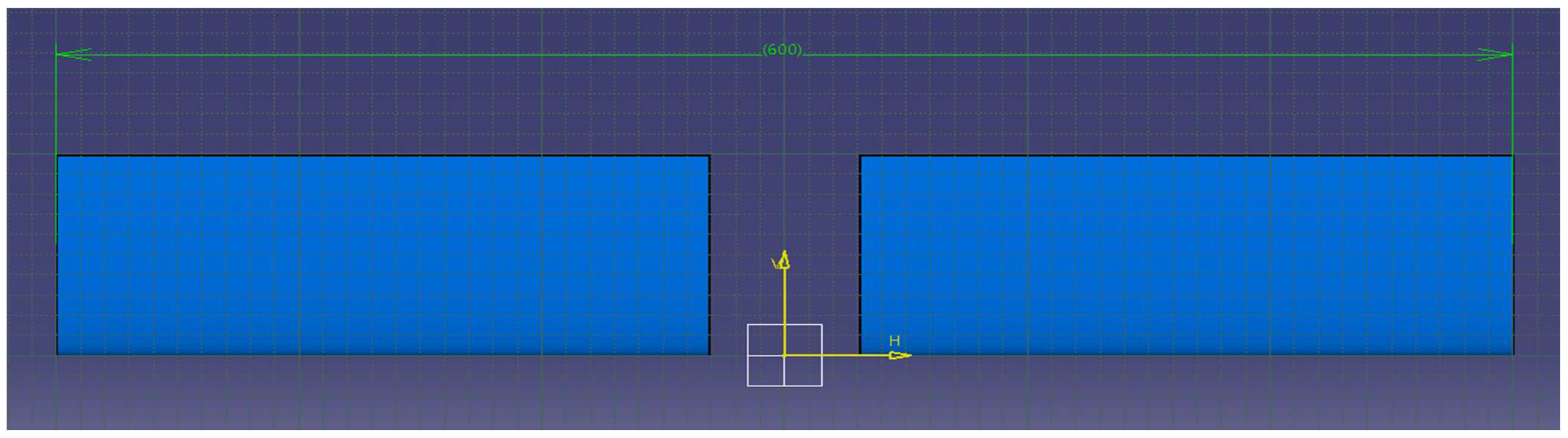
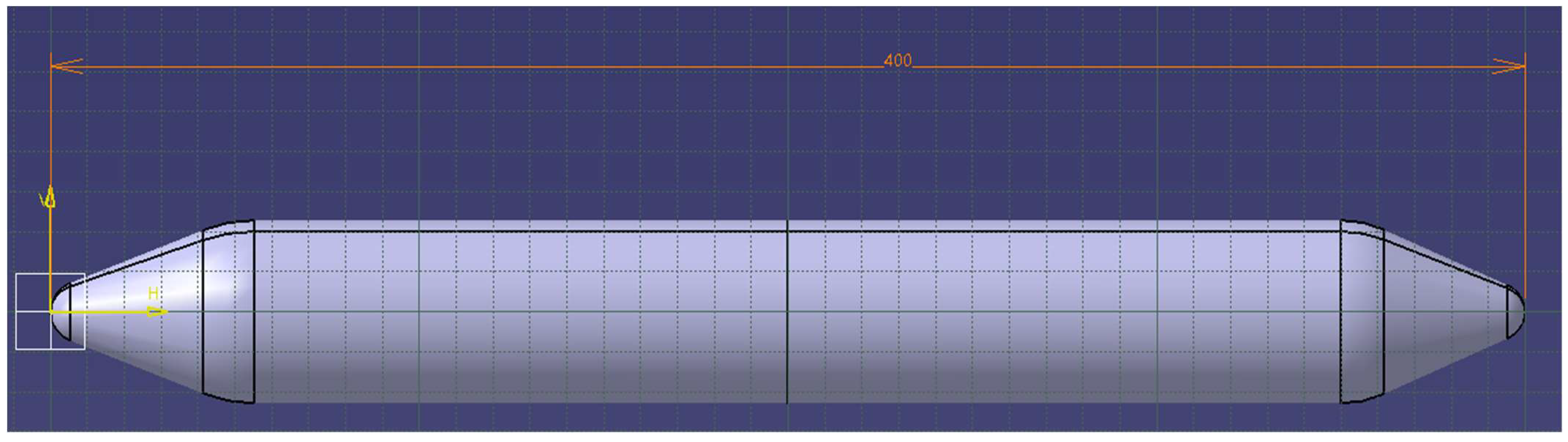
2.1.3. Fuselage Design
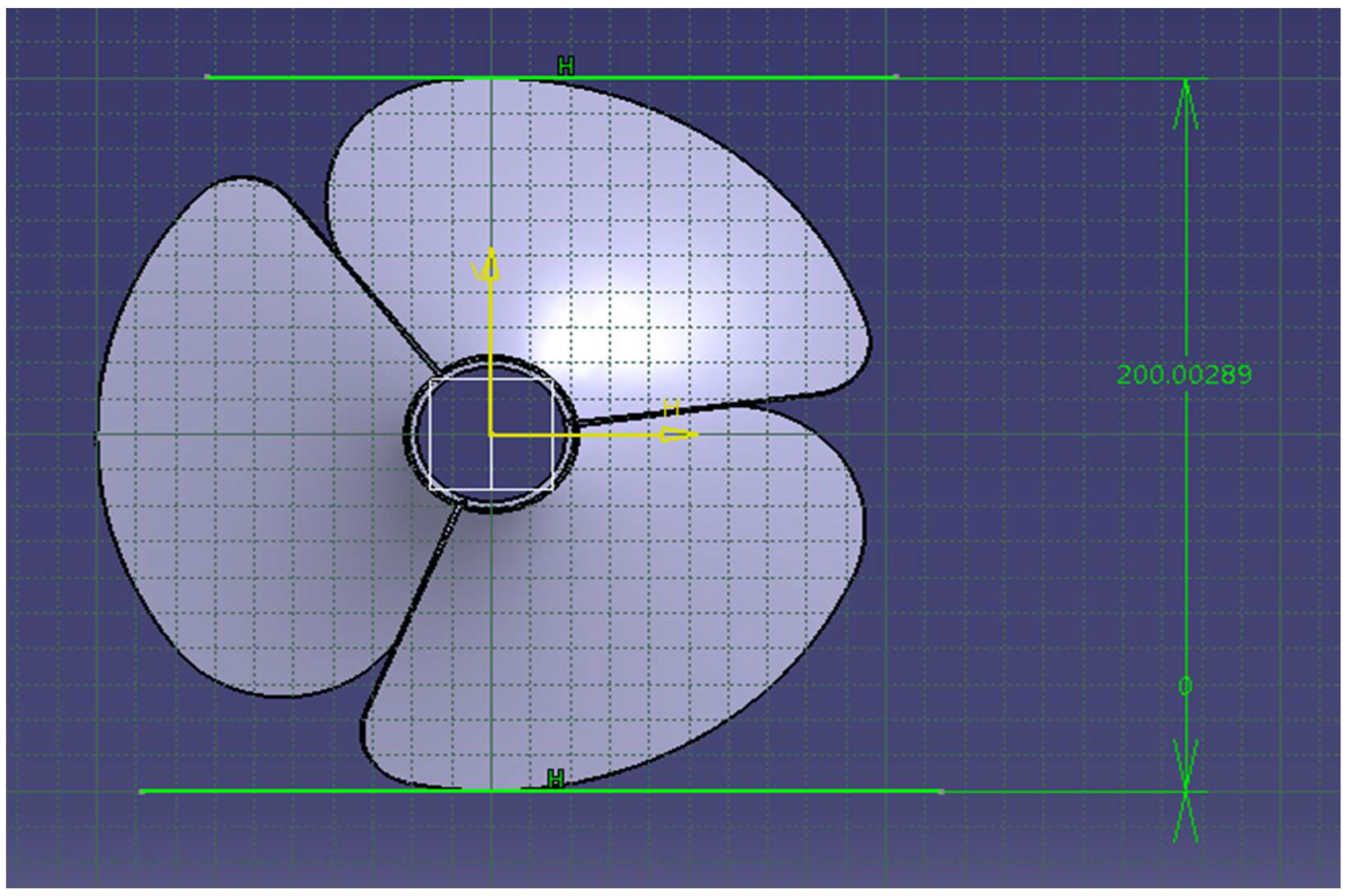
2.1.4. Propulsive System Design
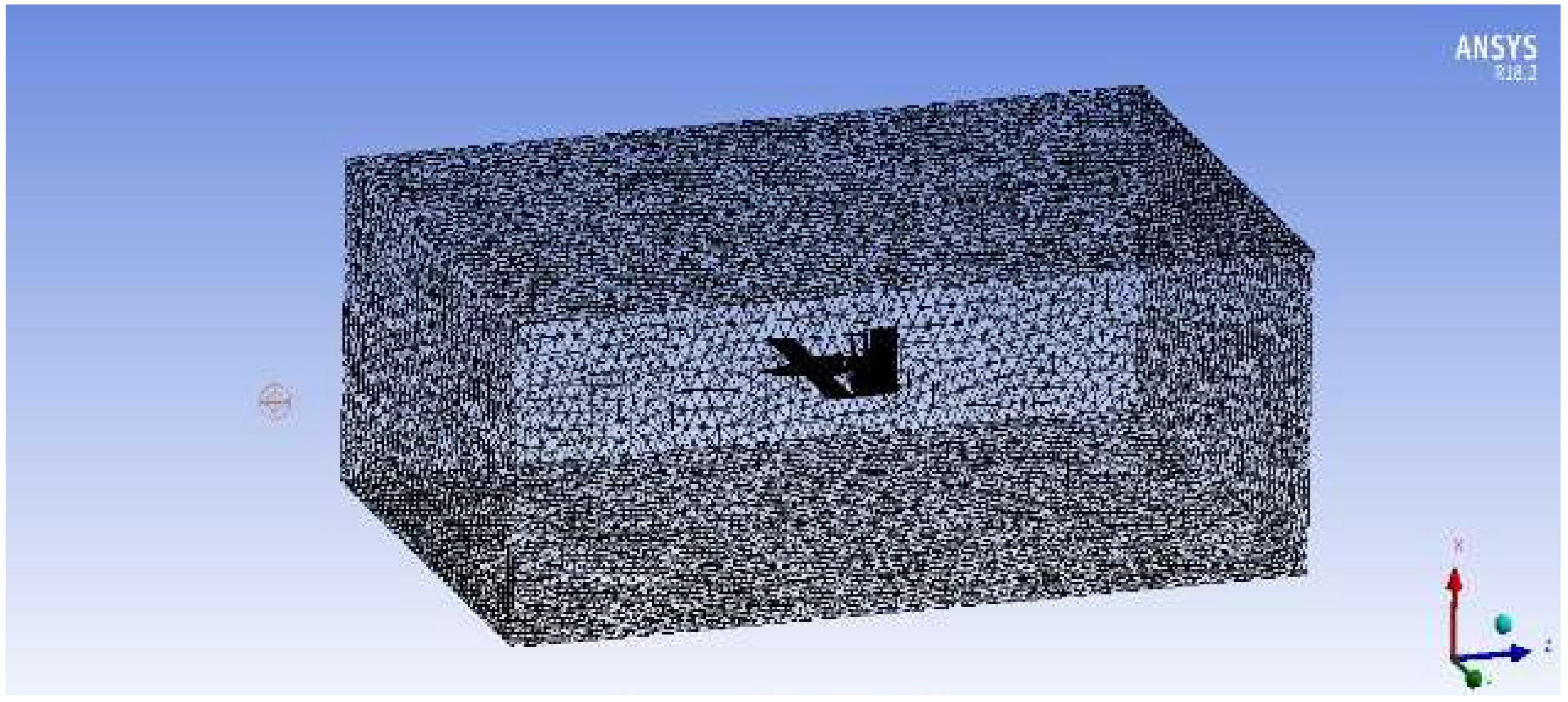
2.2. Discretization
2.3. Boundary Conditions
2.4. Governing Equation
2.5. Validational Study on the Imposed Methodology
3. Results and Discussions
3.1. Computational Hydrodynamic Results of Propeller
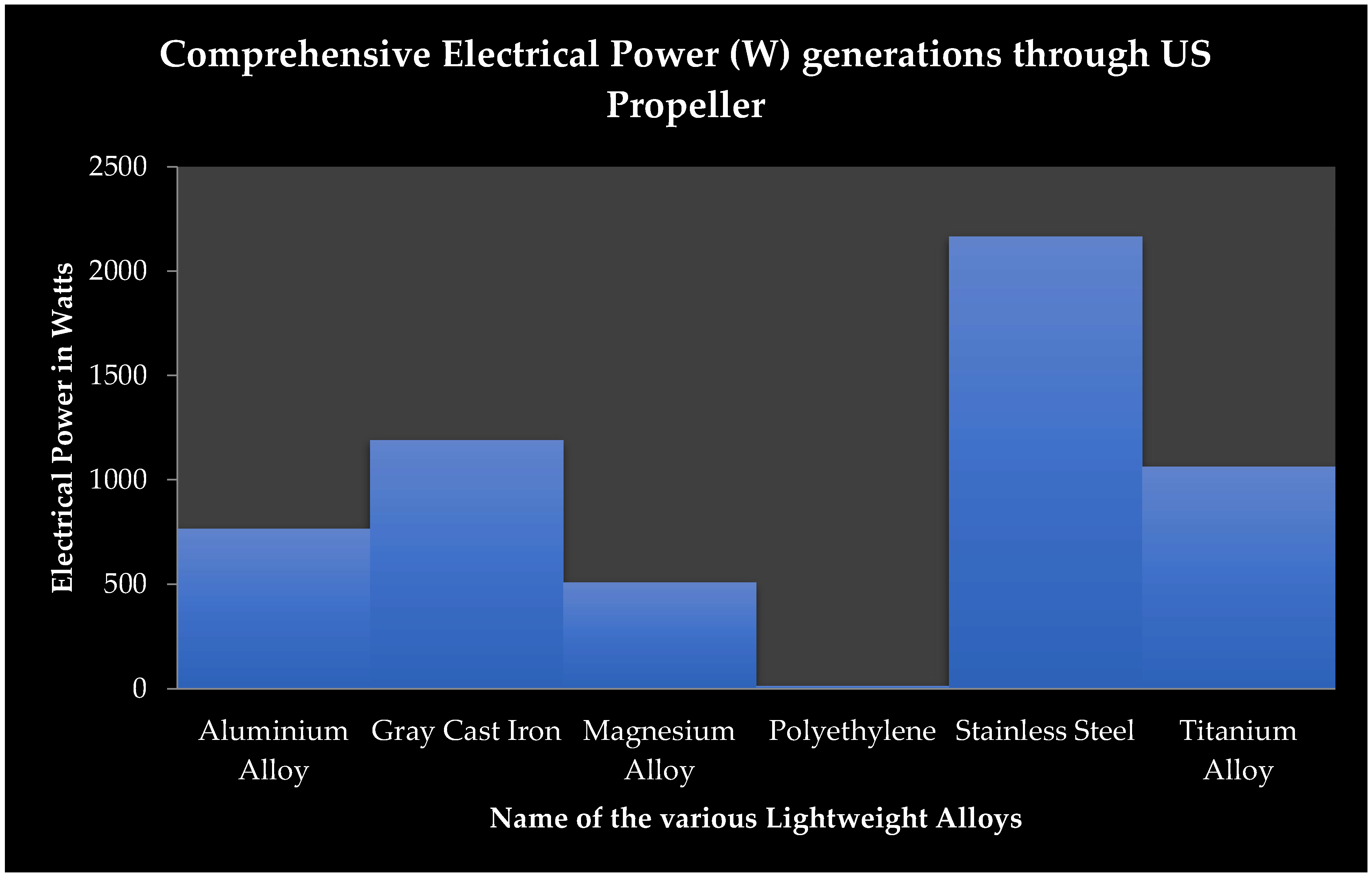
3.2. Material Optimization for the US
3.3. Results of US at Steady Level Flight
3.4. Results of US at Climb in and on the Water Surface
3.5. Execution of Pitching and Yawing Manuverings through Additional Control Surfaces
3.6. Deployment Test on US through CFD-SMRF Coupled Approaches—Execution State of Surveillance
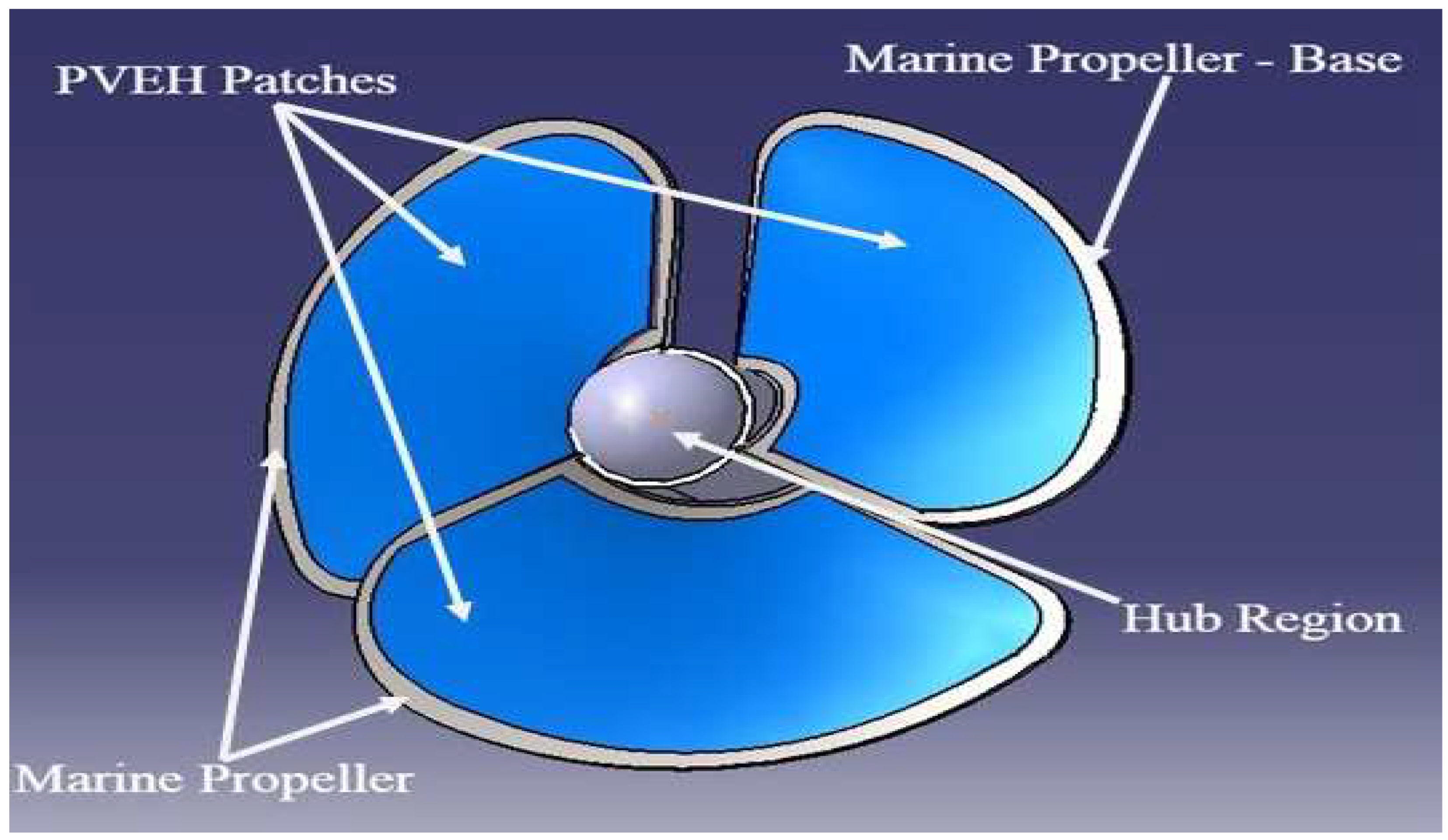
4. Self Energized Hydro Propeller for US
4.1. Hydrodynamic Results
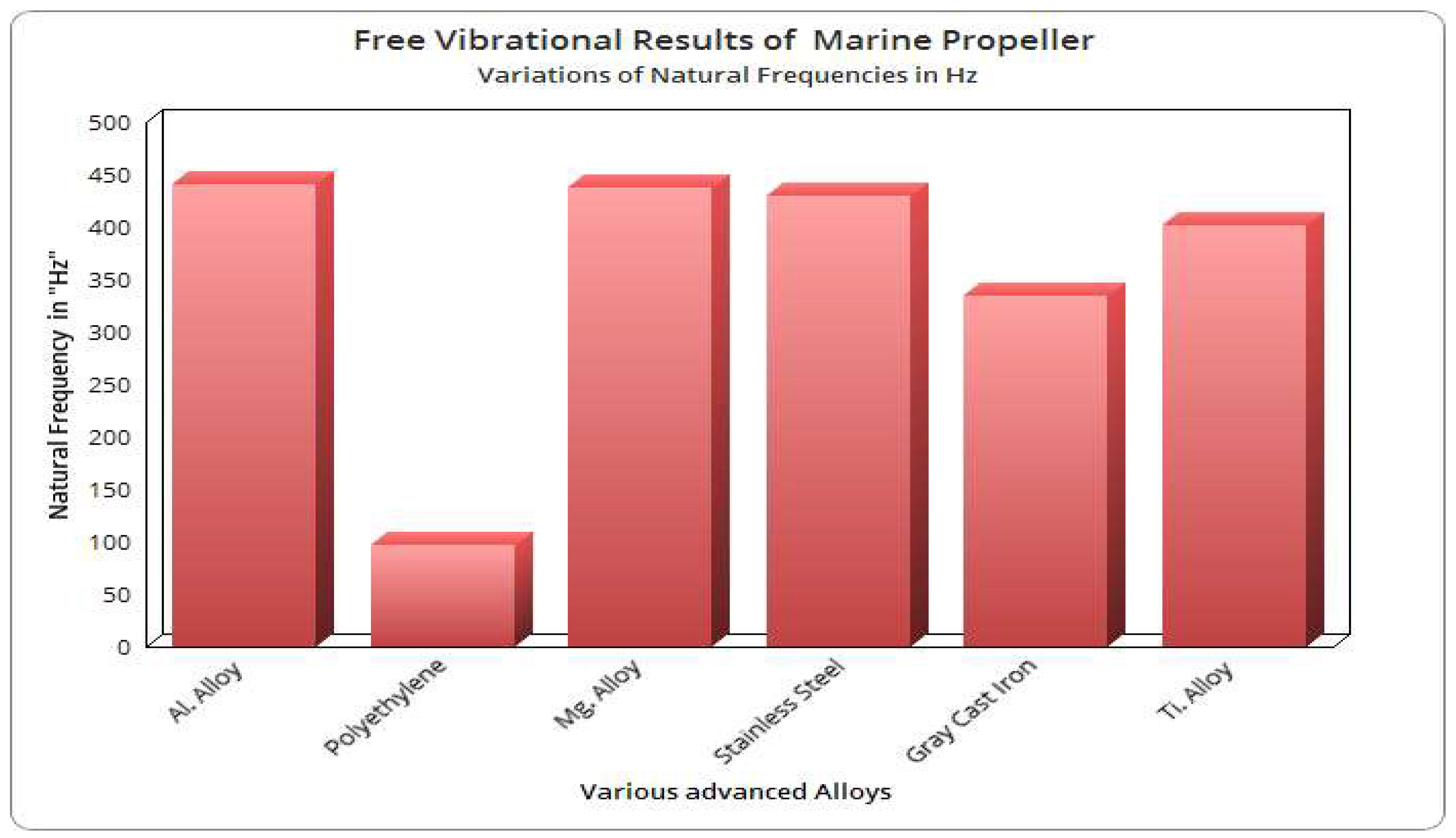
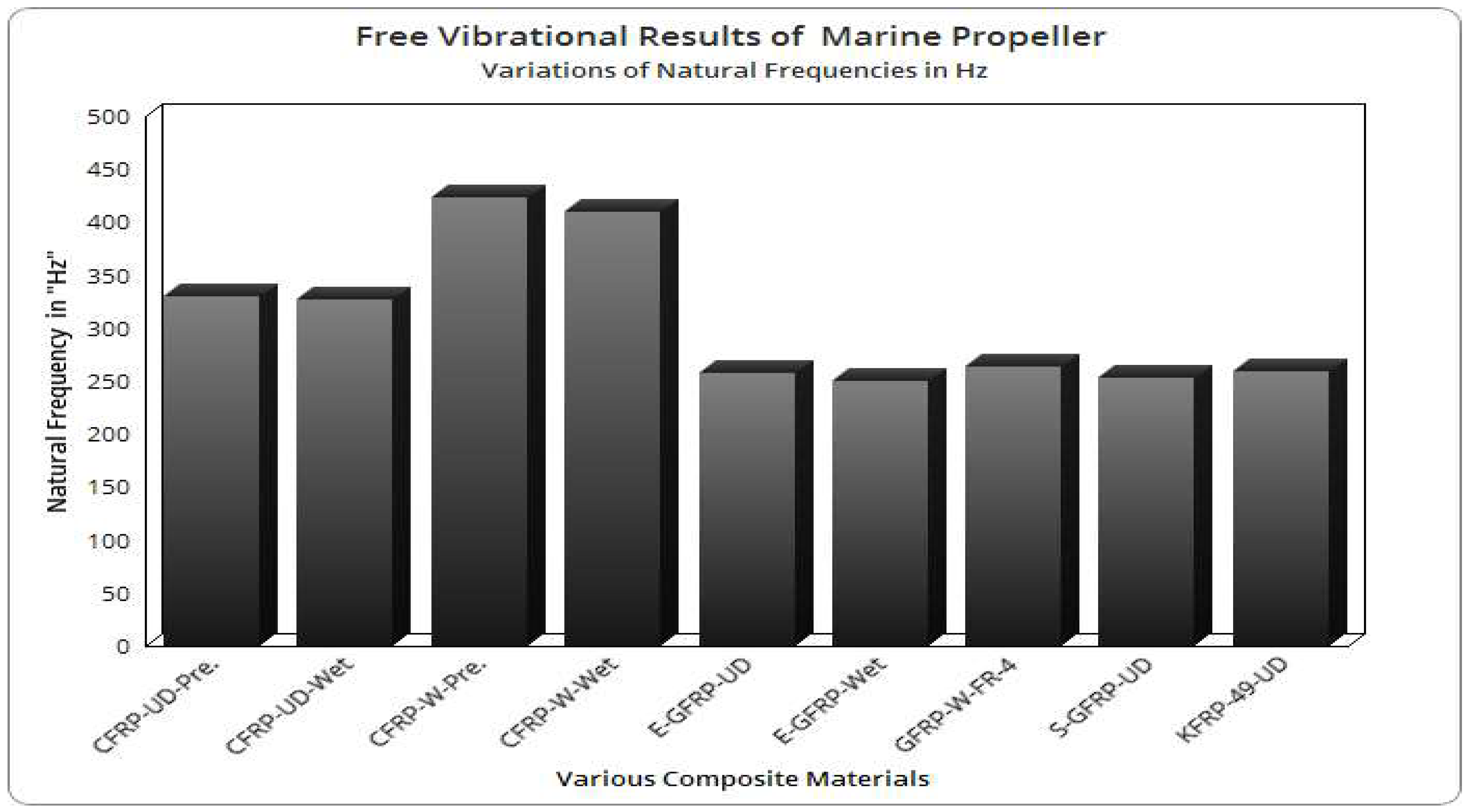
4.2. Free Vibrational Results
4.3. Comparative Analysis
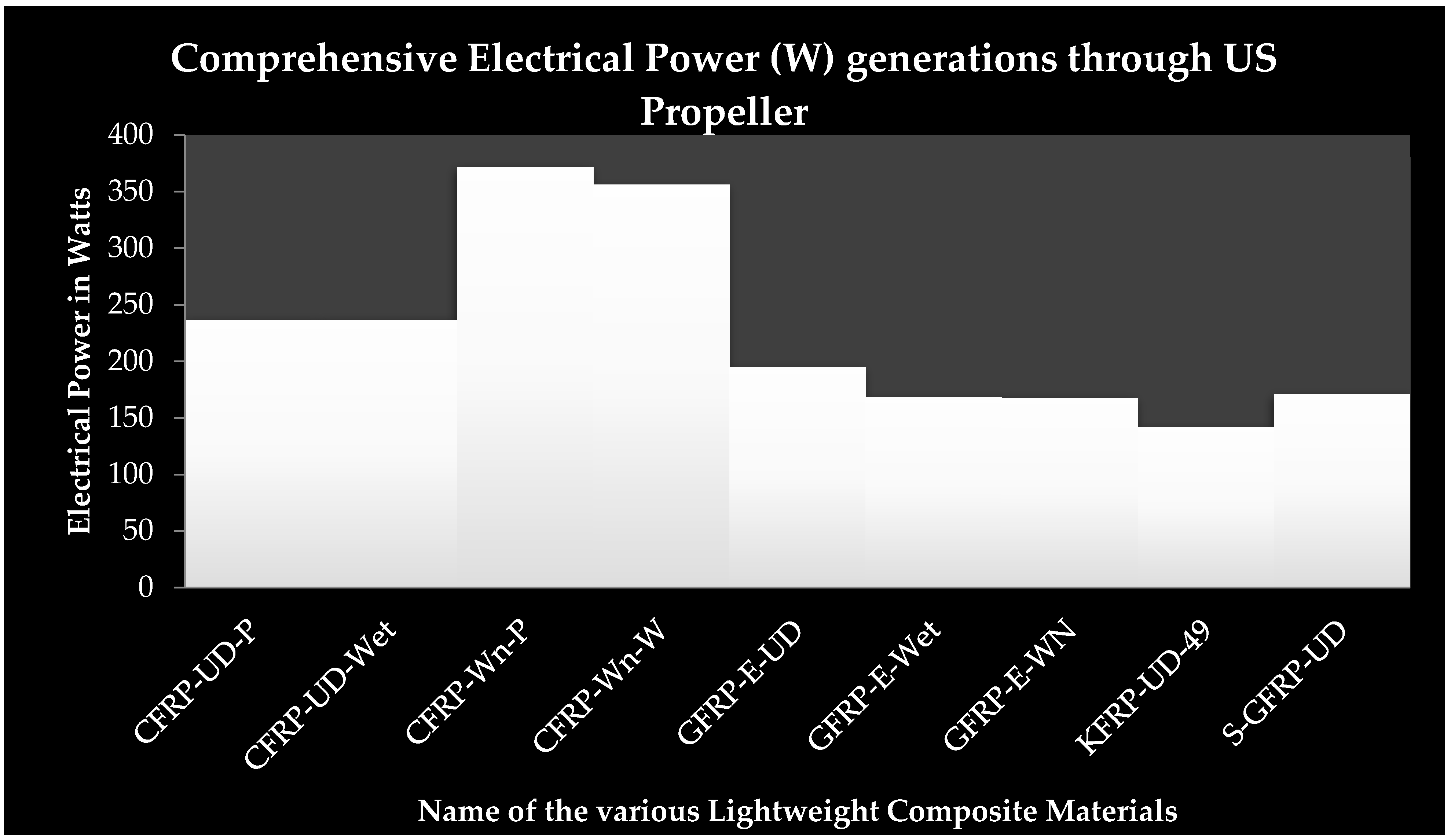
4.4. PVEH Based Electricity Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description |
| Weight of the payloads (kg) | |
| Total weight of the US (kg) | |
| Wing loading of this US’s rectangular wing (kg/m2) | |
| Planform area of the US’s rectangular wing (m2) | |
| Wingspan of the rectangular wing (m) | |
| Root chord of the rectangular wing (m) | |
| Length of the US fuselage (m) | |
| Aspect ratio of the rectangular wing | |
| Design efficiency | |
| Diameter of US Fuselage (m) | |
| Taper ratio of lifting platform | |
| Planform area of the vertical stabilizer (m2) | |
| Tail-span of the vertical stabilizer (m) | |
| Root chord of the vertical stabilizer (m) | |
| Maximum diameter of the US fuselage (m) | |
| Length of the uniform cross section of the US fuselage (m) | |
| Length of the varying cross section of the US fuselage (m) | |
| Diameter of the varying cross section of the US fuselage (m) | |
| m | Slope of the linearized curvy position of fuselage |
| b | Constant of the linearized curvy position of fuselage |
| Required thrust of the US propeller (N) | |
| Optimum tip speed ratio of US propeller | |
| Thrust coefficient of US propeller | |
| Forward velocity of the US (m/s) | |
| Diameter of the US fuselage (m) | |
| Design constants involved in the estimation of various radius and pitch of the US propeller | |
| Radius of the US fuselage (m) | |
| Fluid dynamic velocity (m/s) | |
| Fluid dynamic velocities in different directions (m/s) | |
| Density of the working fluid (kg/m3) | |
| Change in fluid dynamic pressure with respect to direction | |
| Bulk viscosity (Pa-s) | |
| Thermal conductivity (W/mK) | |
| Temperature (K) | |
| Specific gas constant (J/(kgK)) | |
| Averaged force acting on the control volume in CFD (N) | |
| Averaged velocity acting on the control volume in CFD (m/s) | |
| piezoelectric material constant | |
| fluid dynamic load (N) | |
| free vibrational natural frequency (Hz) | |
| US’s propeller width (m) | |
| piezoelectric patch length (m) | |
| US’s propeller thickness (m) | |
| piezoelectric patch thickness (m) | |
| density of the lightweight material (kg/m3) | |
| ε | permittivity of the same lightweight materials |
References
- Wang, Q.; Wu, S.; Hong, W.; Zhuang, W.; Wei, Y. Submersible Unmanned Aerial Vehicle: Configuration Design and Analysis Based on Computational Fluid Dynamics. MATEC Web Conf. 2017, 95, 07023. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Zhao, Q.; Pan, Z.; Ma, Z. Hydrodynamic Performance of Autonomous Underwater Gliders with Active Twin Undulatory Wings of Different Aspect Ratios. J. Mar. Sci. Eng. 2020, 8, 476. [Google Scholar] [CrossRef]
- Tangorra, J.L.; Davidson, S.N.; Hunter, I.W.; Madden, P.G.A.; Lauder, G.V.; Dong, H.; Bozkurttas, M.; Mittal, R. The Development of a Biologically Inspired Propulsor for Unmanned Underwater Vehicles. IEEE J. Ocean. Eng. 2007, 32, 533–550. [Google Scholar] [CrossRef]
- Joung, T.-H.; Sammut, K.; He, F.; Lee, S.-K. Shape optimization of an autonomous underwater vehicle with a ducted propeller using computational fluid dynamics analysis. Int. J. Nav. Arch. OceanEng. 2012, 4, 44–56. [Google Scholar] [CrossRef]
- Xuel, G.; Liu, Y.; Chen, Z.; Li, S. Motion Model of Fish-like Underwater Vehicle and its Effect on Hydrodynamic Performance. In Proceedings of the 2018 11th International Symposium on Mechatronics and its Applications (ISMA), Sharjah, United Arab Emirates, 4–6 March 2018. [Google Scholar] [CrossRef]
- Gao, A.; Techet, A.H. Design considerations for a robotic flying fish. In Proceedings of the OCEANS’11MTS/IEEEKONA, Waikoloa, HI, USA, 19–22 September 2011. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Wang, A.; Wang, X. Flying Wing Underwater Glider: Design, Analysis, and Performance Prediction. In Proceedings of the 2015 International Conference on Control, Automation and Robotics, Singapore, 20–22 May 2015. [Google Scholar] [CrossRef]
- Mathaiyan, V.; Murugesan, R.; Madasamy, S.K.; Gnanasekaran, R.K.; Sivalingam, S.; Jung, D.W. Conceptual Design and Numerical analysis of an Unmanned Amphibious Vehicle. AIAA Scitech 2021 Forum 2021, 1285. [Google Scholar] [CrossRef]
- Javaid, M.Y.; Ovinis, M.; Hashim, F.B.; Maimun, A.; Ahmed, Y.M.; Ullah, B. Effect of wing form on the hydrodynamic characteristics and dynamic stability of an underwater glider. Int. J. Nav. Arch. Ocean Eng. 2017, 9, 382–389. [Google Scholar] [CrossRef]
- Alam, K.; Ray, T.; Anavatti, S.G. Design and construction of an autonomous underwater vehicle. Neurocomputing 2014, 142, 16–29. [Google Scholar] [CrossRef]
- Kumar, V.P.; Kumar, S.K.; Pandian, K.S.; Ashraf, E.; Selvan, K.T.T.; Vijayanandh, R. Conceptual Design and Hydrodynamic Research On Unmanned Aquatic Vehicle. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 121–127. [Google Scholar] [CrossRef]
- Vasudev, K.L. Review of Autonomous Underwater Vehicles, Autonomous VehiclesBook; Intech Open Limited: London, UK, 2018; ISBN 978-1-83968-191-2. [Google Scholar] [CrossRef]
- Amin, O.M.; Karim, A.; Saad, A.H. Development of a highly maneuverable unmanned underwater vehicle on the basis ofquad-copter dynamics. AIP Conf. Proceed. 2017, 1919, 020009. [Google Scholar]
- Pandian, R.S.; Vijayanandh, R.; Kumar, S.K.; Kumar, V.P.; Ramesh, M.; Kumar, M.S.; Kumar, G.R. Comparative Hydrodynamic Investigations on Unmanned Aquatic Vehicle for Ocean Applications. In Recent Trends in Mechanical Engineering; Lecture Notes in Mechanical Engineering Book Series(LNME); Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-981-16-2086-7. [Google Scholar] [CrossRef]
- Nesteruk, I.; Passoni, G.; Redaelli, A. Shape of Aquatic Animals and Their Swimming Efficiency. J. Mar. Biol. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Bettle, M.C.; Gerber, A.G.; Watt, G.D. Using reduced hydrodynamic models to accelerate the predictor–corrector convergenceofimplicit6-DOFURANS submarine manoeuvring simulations. Comput. Fluids 2014, 102, 215–236. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Zhang, M.; Yang, Z.; Wu, Z. Design and flight performance of hybrid underwater glider with controllable wings. Int. J. Adv. Robot. Syst. 2017, 14, 1–12. [Google Scholar] [CrossRef]
- Qiu, S.; Cui, W. An Overview on Aquatic Unmanned Aerial Vehicles. Ann. Rev. Res. 2019, 5, 555663. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Nie, Z.-Q.; Li, J.-X.; Ma, Y. Conceptual Design of a Water-air Amphibious Unmanned Vehicle. DES techTrans. Comput. Sci. Eng. 2019, 2018, 000781–000786. [Google Scholar] [CrossRef]
- Uiblein, F.; Cruz, N.A. Deep-Sea Fish Behavioral Responses to Underwater Vehicles: Differences among Vehicles, Habitats and Species; Autonomous Underwater Vehicles; Cruz, N., Ed.; IntechOpen: London, UK, 2011; ISBN 978-953-307-432-0. [Google Scholar]
- Bozkurttas, M.; Tangorra, J.; Lauder, G.; Mittal, R. Understanding the Hydrodynamics of Swimming from Fish Fins to Flexible Propulsors for Autonomous Underwater Vehicles. Adv. Sci. Technol. 2008, 58, 193–202. [Google Scholar] [CrossRef]
- Fish, F.E. Wing design and scaling of flying fish with regard to flight performance. J. Zoöl. 1990, 221, 391–403. [Google Scholar] [CrossRef]
- Wang, J.; Wainwright, D.K.; Lindengren, R.E.; Lauder, G.V.; Dong, H. Tuna locomotion: A computational hydrodynamic analysis of finlet function. J. R. Soc. Interface 2020, 17, 20190590. [Google Scholar] [CrossRef]
- Ignacio, L.C.; Victor, R.R.; Del Rio, R.; Pascoal, A. Optimized design of an autonomous underwater vehicle, for exploration in the Caribbean Sea. Ocean Eng. 2019, 187, 106184. [Google Scholar] [CrossRef]
- Park, H.; Choi, H. Aerodynamic characteristics of flying fish in gliding flight. J. Exp. Biol. 2010, 213 Pt 19, 3269–3279. [Google Scholar] [CrossRef] [PubMed]
- Allotta, B.; Costanzi, R.; Monni, N.; Pugi, L.; Ridolfi, A.; Vettori, G. Design and Simulation of an Autonomous Underwater Vehicle. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering ECCOMAS, Vienna, Austria, 10–14 September 2012. [Google Scholar]
- Gao, T.; Wang, Y.; Pang, Y.; Cao, J. Hull shape optimization for autonomous underwater vehicles using CFD. Eng. Appl. Comput. Fluid Mech. 2016, 10, 599–607. [Google Scholar] [CrossRef]
- Vijayanandh, R.; Senthil Kumar, M.; Rahul, S.; Thamizhanbu, E.; Durai Isaac Jafferson, M. Conceptual Design and Comparative CFD Analyse son Unmanned Amphibious Vehicle for Crack Detection. Proceedings of UASG 2019, Roorkee, India, 6–7 April 2019; Lecture Notes in CivilEngineering. Springer: Cham, Switzerland, 2019. ISBN 978-3-030-37393-1. [Google Scholar] [CrossRef]
- Raja, V.; Solaiappan, S.K.; Kumar, L.; Marimuthu, A.; Gnanasekaran, R.K.; Choi, Y. Design and Computational Analyses of Nature Inspired Unmanned Amphibious Vehicle for Deep Sea Mining. Minerals 2022, 12, 342. [Google Scholar] [CrossRef]
- Vijayanandh, R.; Venkatesan, K.; Kumar, R.R.; Kumar, M.S.; Jagadeeshwaran, P. Theoretical and Numerical Analyses on Propulsive Efficiency of Unmanned Aquatic Vehicle’s Propeller. J. Phys. Conf. Ser. 2020, 1504, 012004. [Google Scholar] [CrossRef]
- Vijayanandh, R.; Venkatesan, K.; Kumar, M.S.; Kumar, G.R.; Jagadeeshwaran, P. Comparative fatigue life estimations of Marine Propeller by using FSI. J. Phys. Conf. Ser. 2020, 1473, 012018. [Google Scholar] [CrossRef]
- Jiang, Y.; Raji, A.P.; Raja, V.; Wang, F.; Al-Bonsrulah, H.A.Z.; Murugesan, R.; Ranganathan, S. Multi–Disciplinary Optimizations of Small-Scale Gravitational Vortex Hydropower (SGVHP) System through Computational Hydrodynamic and Hydro–Structural Analyses. Sustainability 2022, 14, 727. [Google Scholar] [CrossRef]
- Raja, V.; Raji, A.P.; Madasamy, S.K.; Mathaiyan, V.; Kandasamy, S.; Subramaniam, I.P.; Kandasamy, K.; Murugesan, R.; Rajapandi, R.; Jayaram, D.K.; et al. Comparative Estimations of Hydrodynamic Analysis on Unmanned Aquatic Vehicle’s Propeller by using an advanced [CFD with MRF] Approach. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. [Google Scholar] [CrossRef]
- Raja, V.; AL-bonsrulah, H.A.Z.; Raji, A.P.; Madasamy, S.K.; Ramaiah, M.; Gnanasekaran, R.K.; Kulandaiyapan, N.K.; Al-Bahrani, M. Design and multi-disciplinary computational investigations on PVEH patches attached horizontal axis hybrid wind turbine system for additional energy extraction in HALE UAVs. IET Renew. Power Gener. 2022, 16, 1–27. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Seshia, A. Maximizing Output Power in a Cantilevered Piezoelectric Vibration Energy Harvester by Electrode Design. J. Phys. Conf. Ser. 2015, 660, 012114. [Google Scholar] [CrossRef]
- Kulandaiyaappan, N.K.; Gnanasekaran, R.K.; Raja, V.; Bernard, F.A.; Murugesan, R.; Madasamy, S.K.; Mathaiyan, V.; Raji, A.P.; K Asher, P.; Ponmariappan, J. Optimization of High Payload Unmanned Aerial Vehicle’s Propellers based on Energy Formation by using Computational Vibrational Analyses. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. [Google Scholar] [CrossRef]
- Osuchukwu, N.; Shpanin, L. Feasibility Study of the Quadcopter Propeller Vibrations for the Energy Product. Int. J. Mech. Mechatron. Eng. 2017, 11, 313–319. [Google Scholar] [CrossRef]
- Anton, S.R.; Inman, D.J. Performance modeling of unmanned aerial vehicles with on-board energy harvesting. Act. Passiv. Smart Struct. Integr. Syst. 2011, 7977, 12–27. [Google Scholar] [CrossRef]
- Anton, S.R.; Erturk, A.; Inman, D.J. Investigation of a Multifunctional energy harvesting and energy-storage wing spar for unmanned aerial vehicles. J. Aircr. 2012, 49, 292–301. [Google Scholar] [CrossRef]
- Mohammadi, S.; Cheraghi, K.; Khodayari, A. Piezoelectric vibration energy harvesting using strain energy method. Eng. Res. Express 2019, 1, 015033. [Google Scholar] [CrossRef]
- Kress, R.; Lorenz, E.L. Marine Propeller Selection; Section 1: Works 700010–700182; SAE Transactions: Warrendale, PA, USA, 1970; Volume 79, pp. 334–345. [Google Scholar]
- Sahoo, S.S.; Singh, V.K.; Panda, S.K. Experimental and simulation study of flexural behaviour of woven Glass/Epoxy laminated composite plate. IOP Conf. Ser. Mater. Sci. Eng. 2015, 75, 012017. [Google Scholar] [CrossRef]
- Rajagurunathan, M.; Raj Kumar, G.; Vijayanandh, R.; Vishnu, V.; Rakesh Kumar, C.; Mohamed Bak, K. The Design Optimization of the Circular Piezoelectric Bimorph Actuators Using FEA. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 410–422. [Google Scholar]
- Kumar, M.S.; Krishnan, A.; Vijayanandh, R. Vibrational Fatigue Analysis of NACA63215 Small Horizontal Axis Wind Turbine blade. Mater. Today Proc. 2018, 5, 6665–6674. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P.A. Review on Mechanisms for Piezoelectric-Based Energy Harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef]
- DeMarqui, C., Jr.; Vieira, W.G.R.; Erturk, A.; Inman, D.J. Modeling and Analysis of Piezoelectric Energy Harvesting From Aeroelastic Vibrations Using the Doublet-Lattice Method. J. Vib. Acoust. 2011, 133, 11003. [Google Scholar] [CrossRef]
- Dobbs, S.; Yu, Z.; Anderson, K.R.; Franco, J.A.; Deravanessian, A.E.; Lin, A.; Ahn, A. Design of an In-flight Power Generation And Storage System for UAVs. In Proceedings of the 2018 IEEE Conference on Technologies for Sustainability, Long Beach, CA, USA, 11–13 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Williams, C.D.; Curtis, T.L.; Doucet, J.M.; Issac, M.T.; Azarsina, F. Effects of Hull Length on the Hydrodynamic Loads on a Slender Underwater Vehicle during Manoeuvres. In Proceedings of the OCEANS2006, Boston, MA, USA, 18–21 September 2006; pp. 1–6. [Google Scholar] [CrossRef][Green Version]
- Sakaki, A.; Kerdabadi, M.S. Experimental and numerical determination of the hydrodynamic coefficients of an autonomous underwater vehicle. Sci. J. Marit. Univ. Szczec. 2020, 62, 124–135. [Google Scholar]
- Barlow, J.B.; Guterres, R.; Ranzenbach, R. Experimentalparametricstudyofrectangularbodieswithradiusededgesingroundeffect. J. Wind Eng. Ind. Aerodyn. 2001, 89, 1291–1309. [Google Scholar] [CrossRef]
- Cory, R.; Tedrake, R. Experiments in fixed-wing UAV perching. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; pp. 1–12. [Google Scholar]
- Xu, G.; Zhang, Y.; Ji, S.; Cheng, Y.; Tian, Y. Research on computer vision-based for UAV autonomous landing on a ship. Pattern Recognit. Lett. 2009, 30, 600–605. [Google Scholar] [CrossRef]
- Pisanich, G.; Morris, S. Fielding an amphibious UAV: Development, results, and lessons learned. In Proceedings of the 21st Digital Avionics Systems Conference, Irvine, CA, USA, 27–31 October 2002; Volume 2, p. 8C4-1-8C4-9. [Google Scholar]
- Siddall, R.; Kovač, M. Launching the Aqua MAV: Bioinspired design for aerial–aquatic robotic platforms. Bioinspir. Biomim. 2014, 9, 031001. [Google Scholar] [CrossRef]
- Schwarzbach, M.; Laiacker, M.; Mulero-Pázmány, M.; Kondak, K. Remote water sampling using flying robots. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 72–76. [Google Scholar]
- Ore, J.P.; Elbaum, S.; Burgin, A.; Detweiler, C. Autonomous aerial water sampling. J. Field Robot. 2015, 32, 1095–1113. [Google Scholar] [CrossRef]
- Yang, X.; Wang, T.; Liang, J.; Yao, G.; Zhao, W. Submersible unmanned aerial vehicle concept design study. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; p. 442. [Google Scholar]





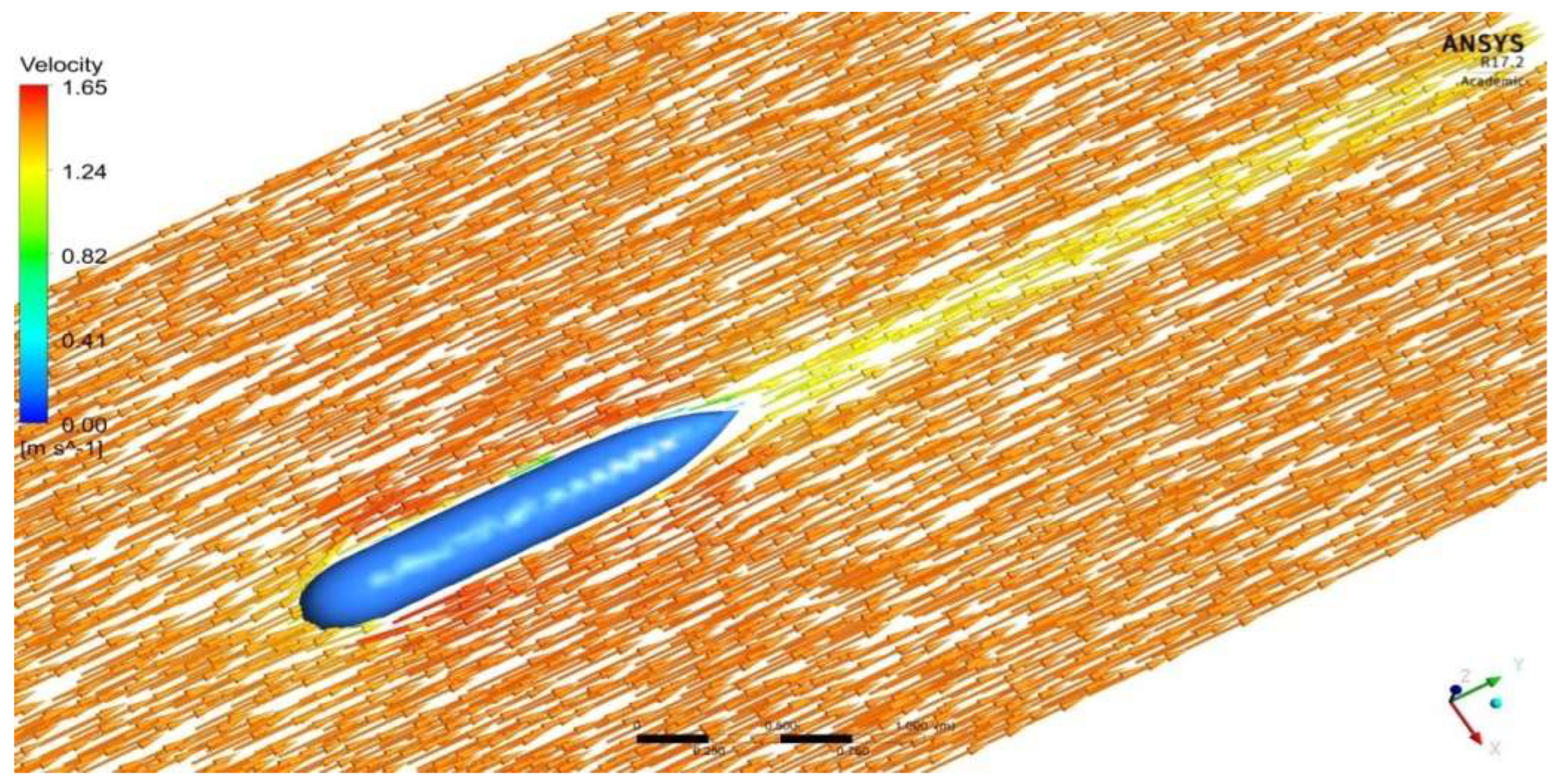


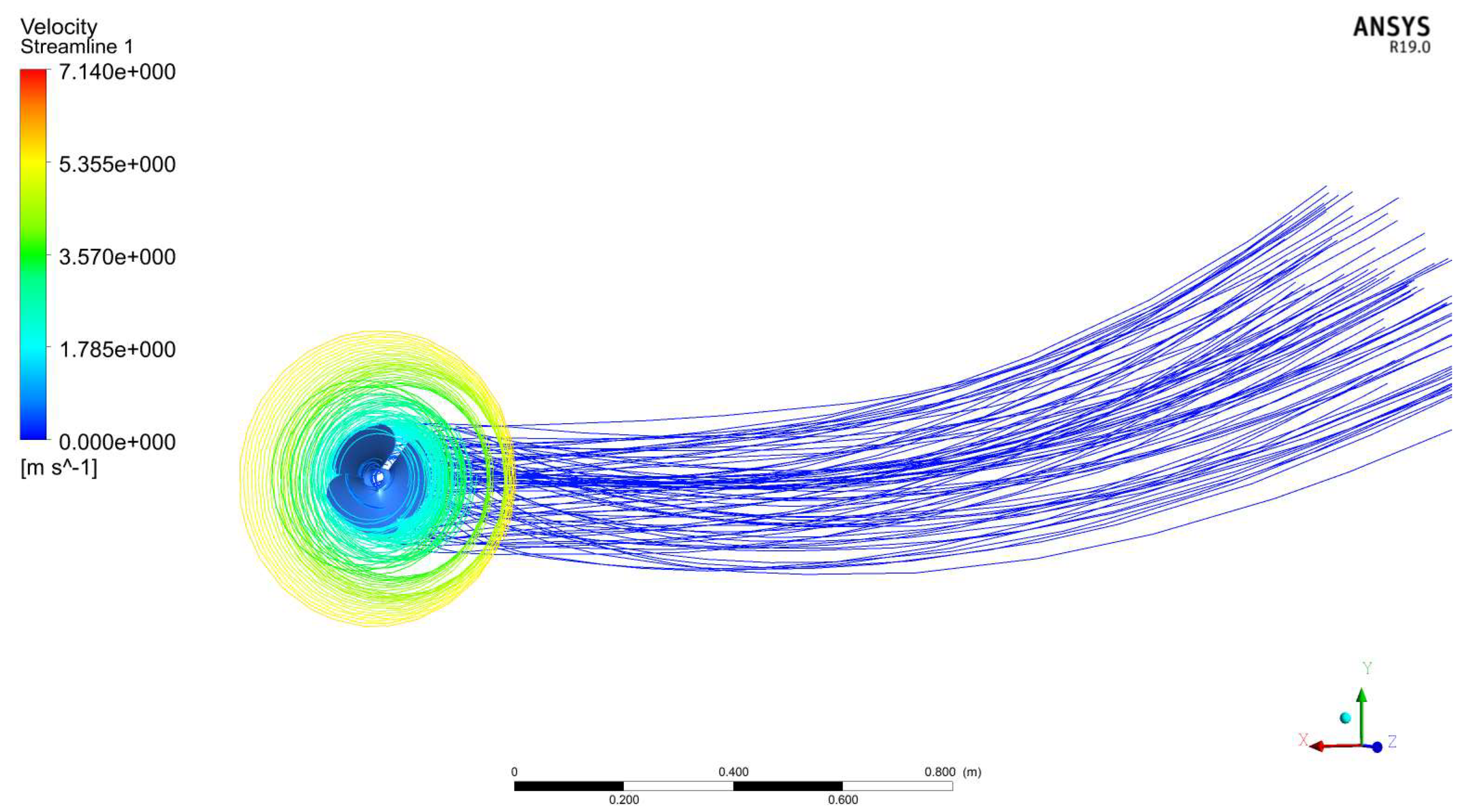
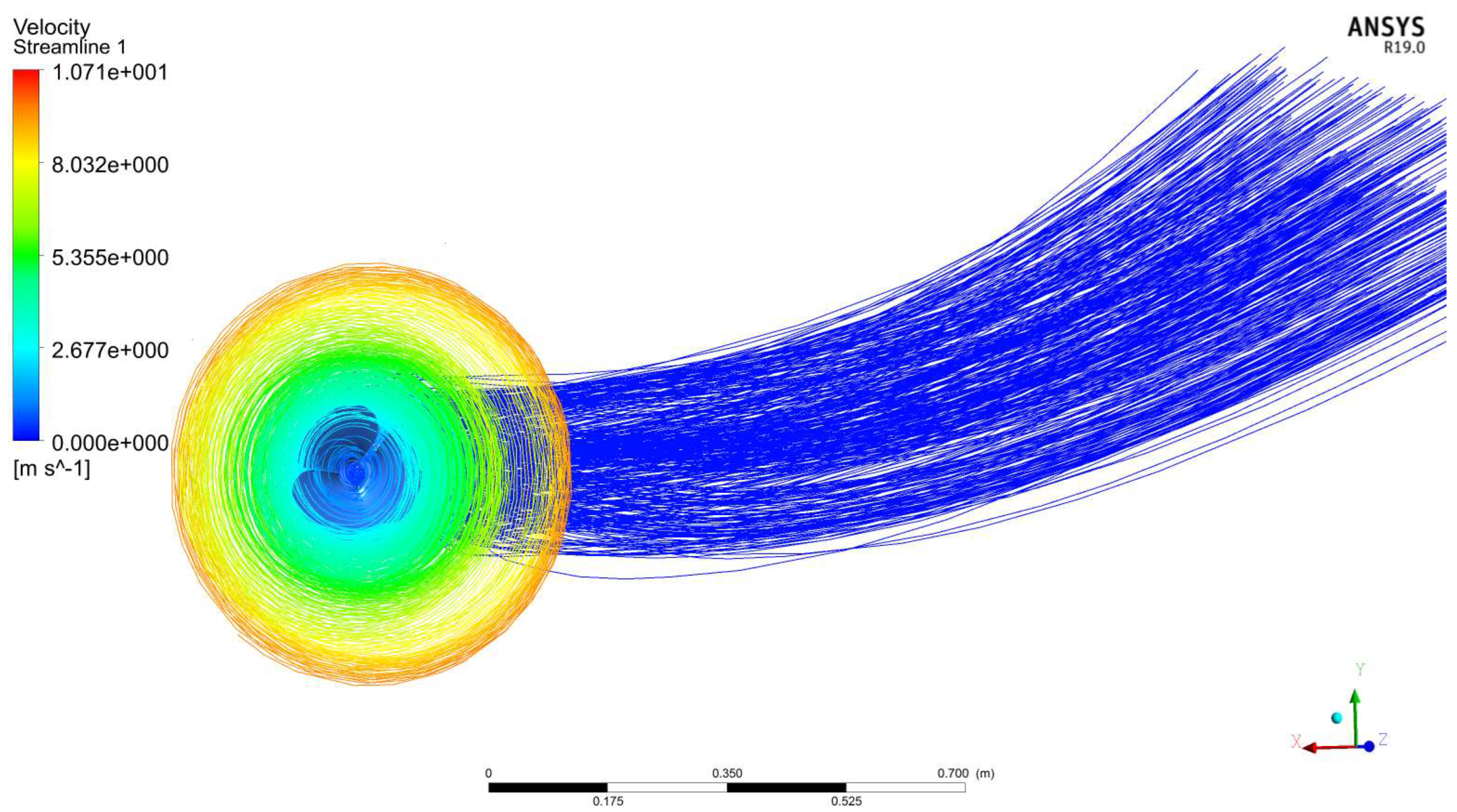

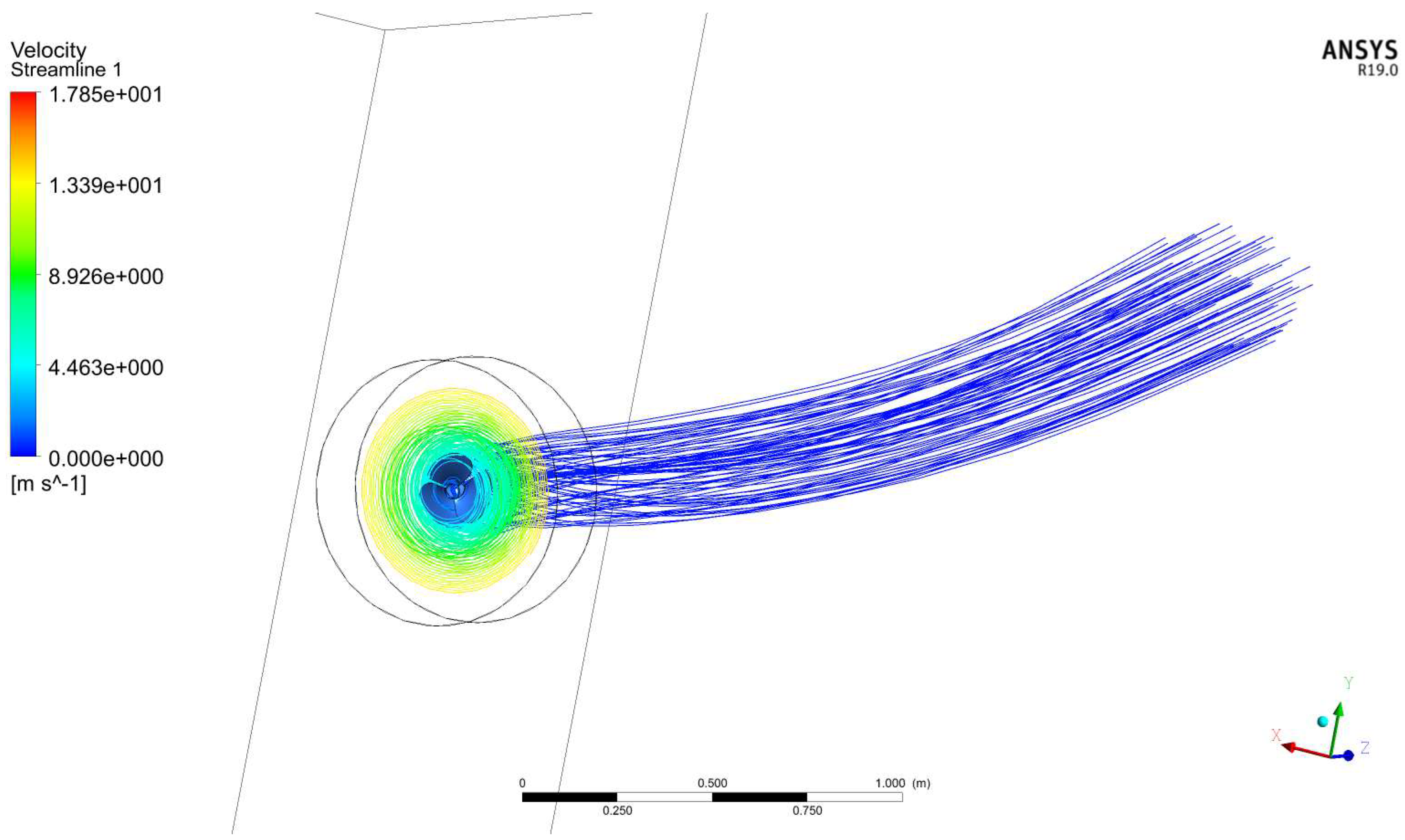
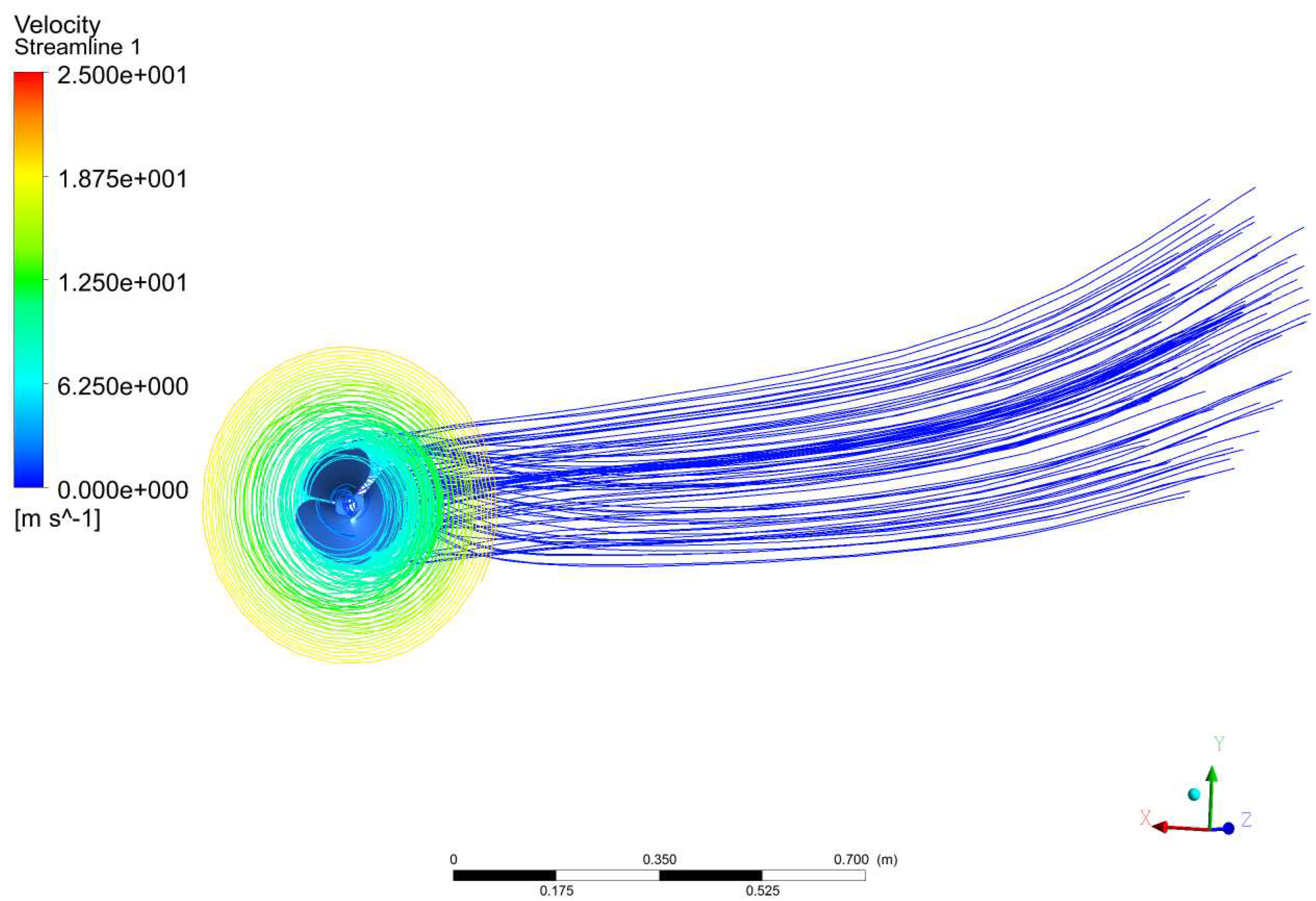
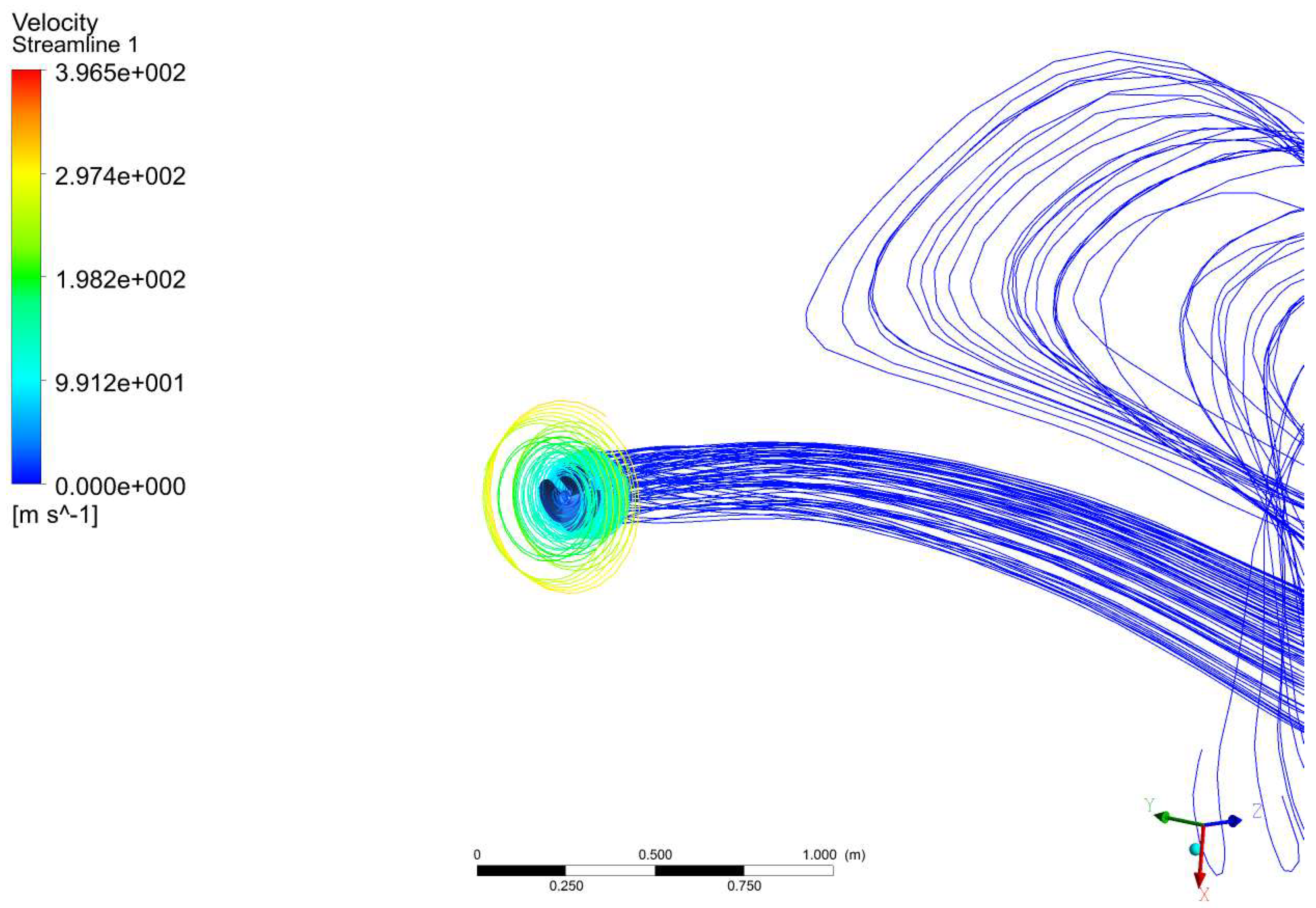

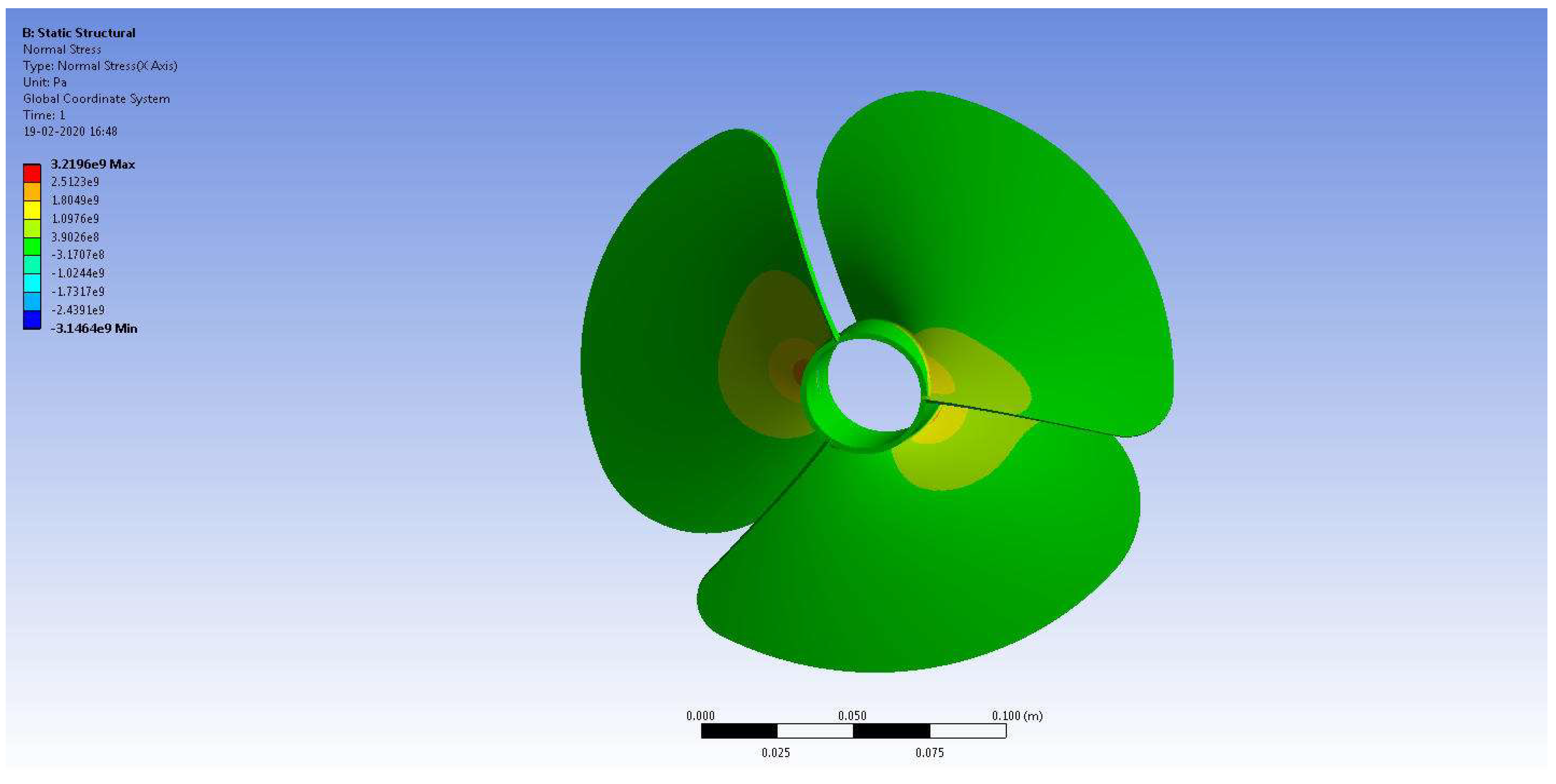



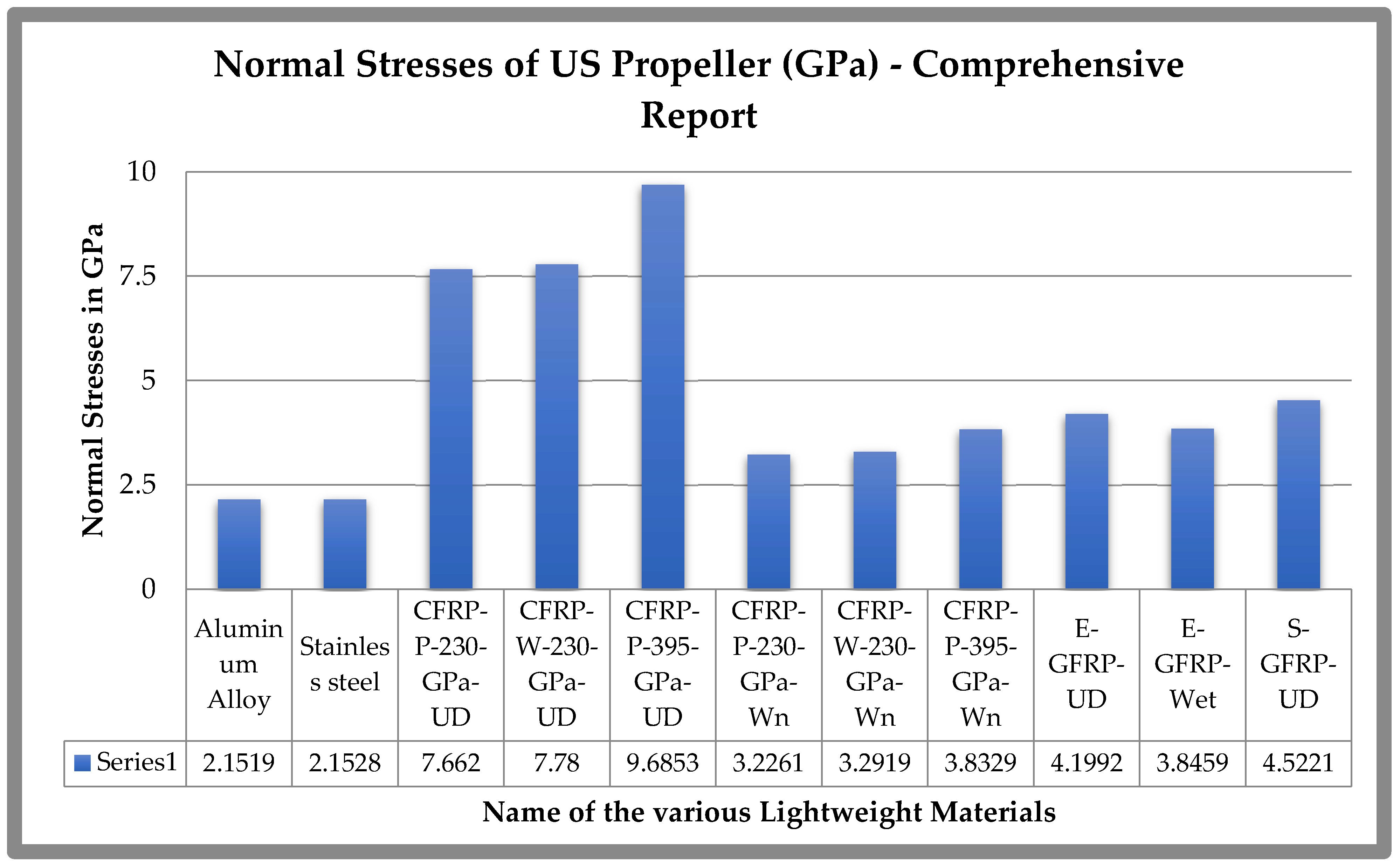
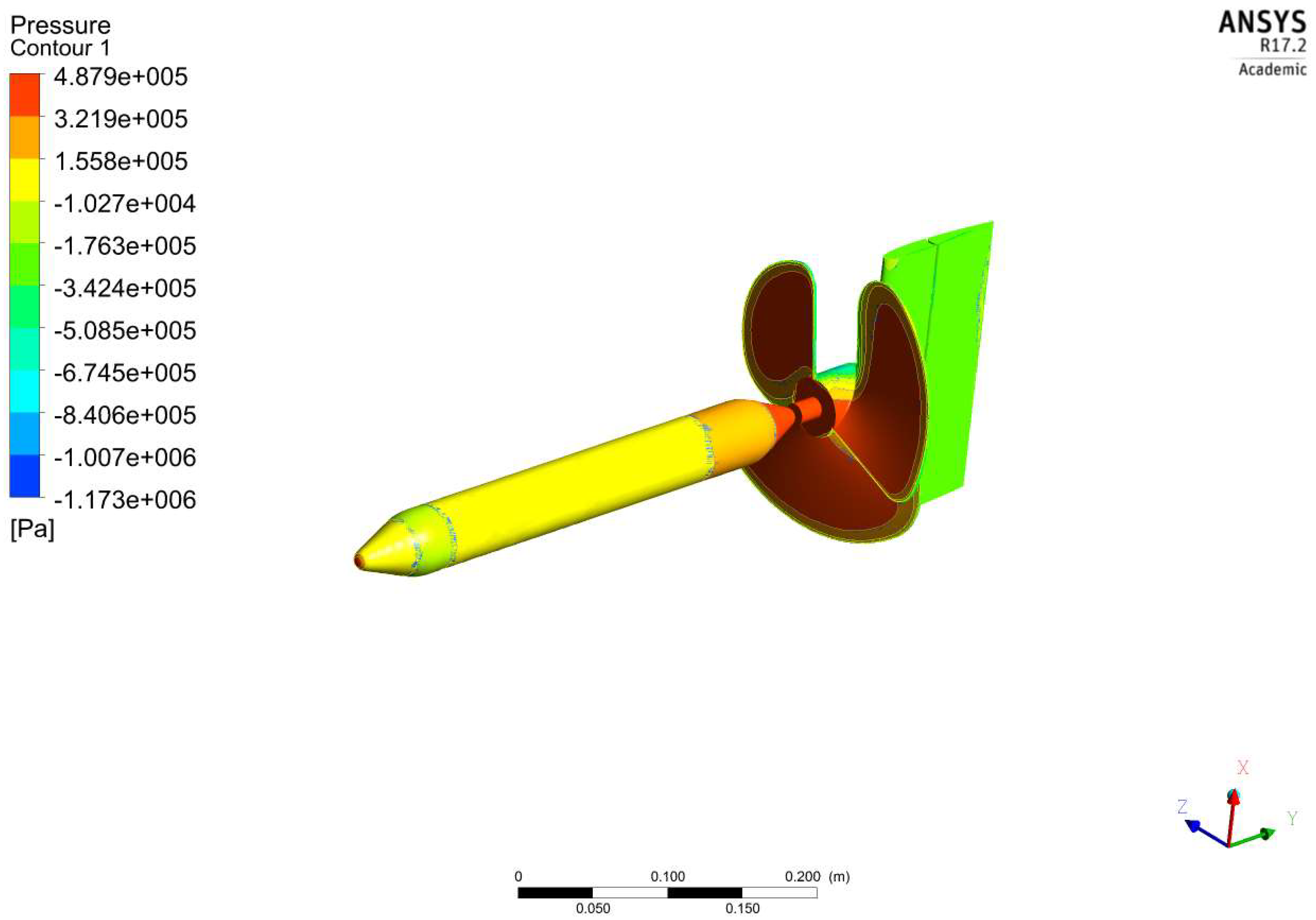
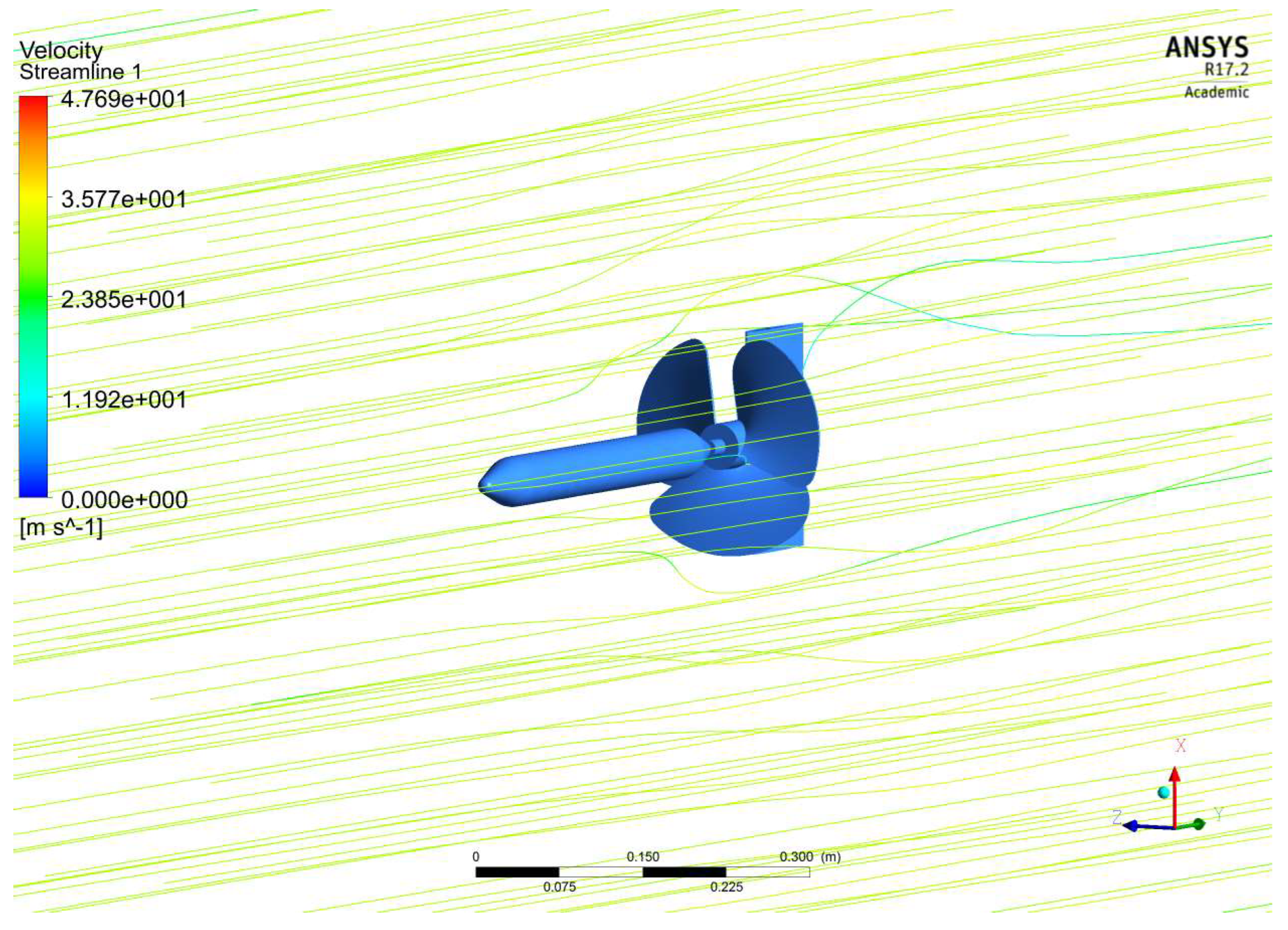
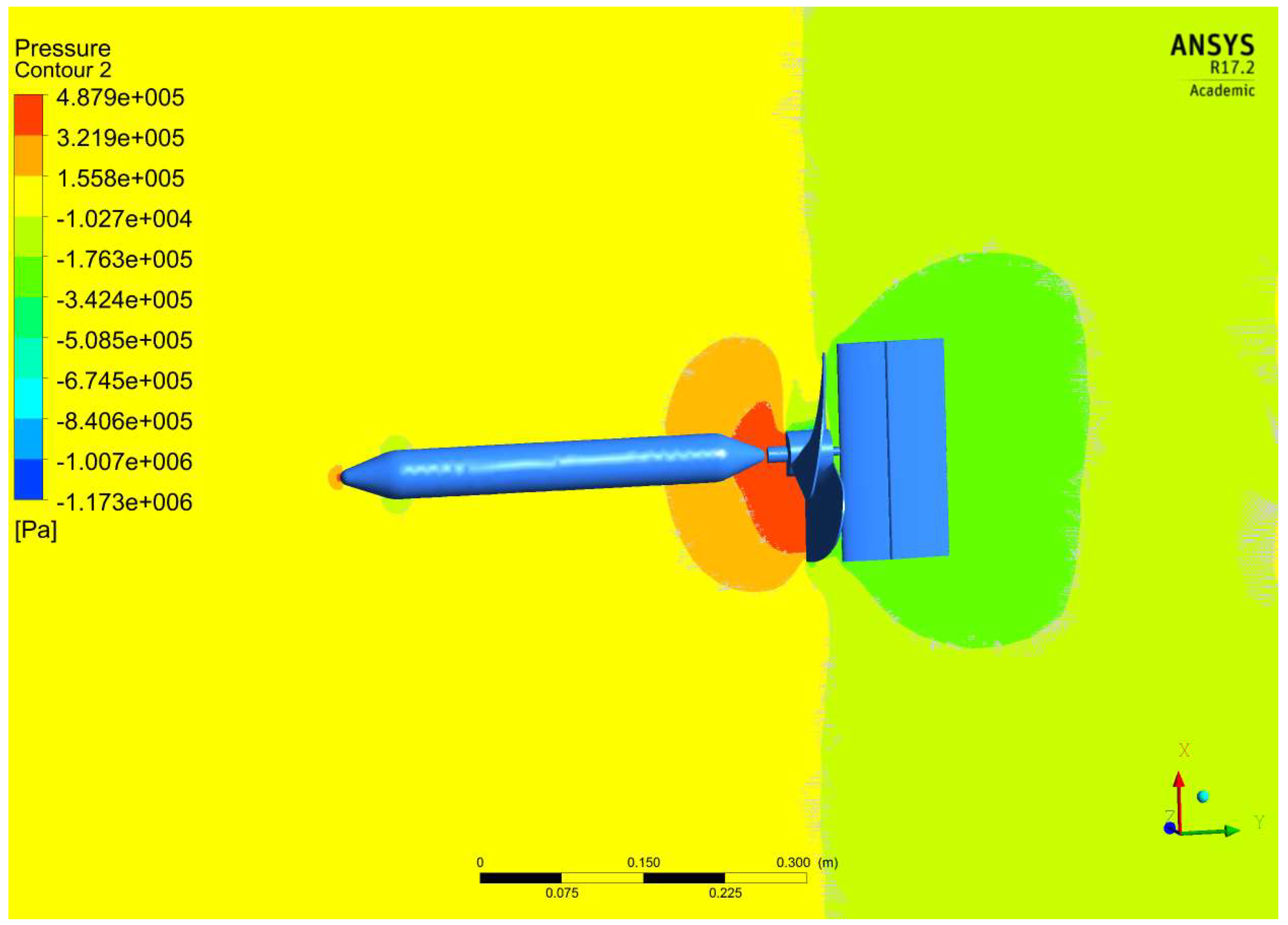
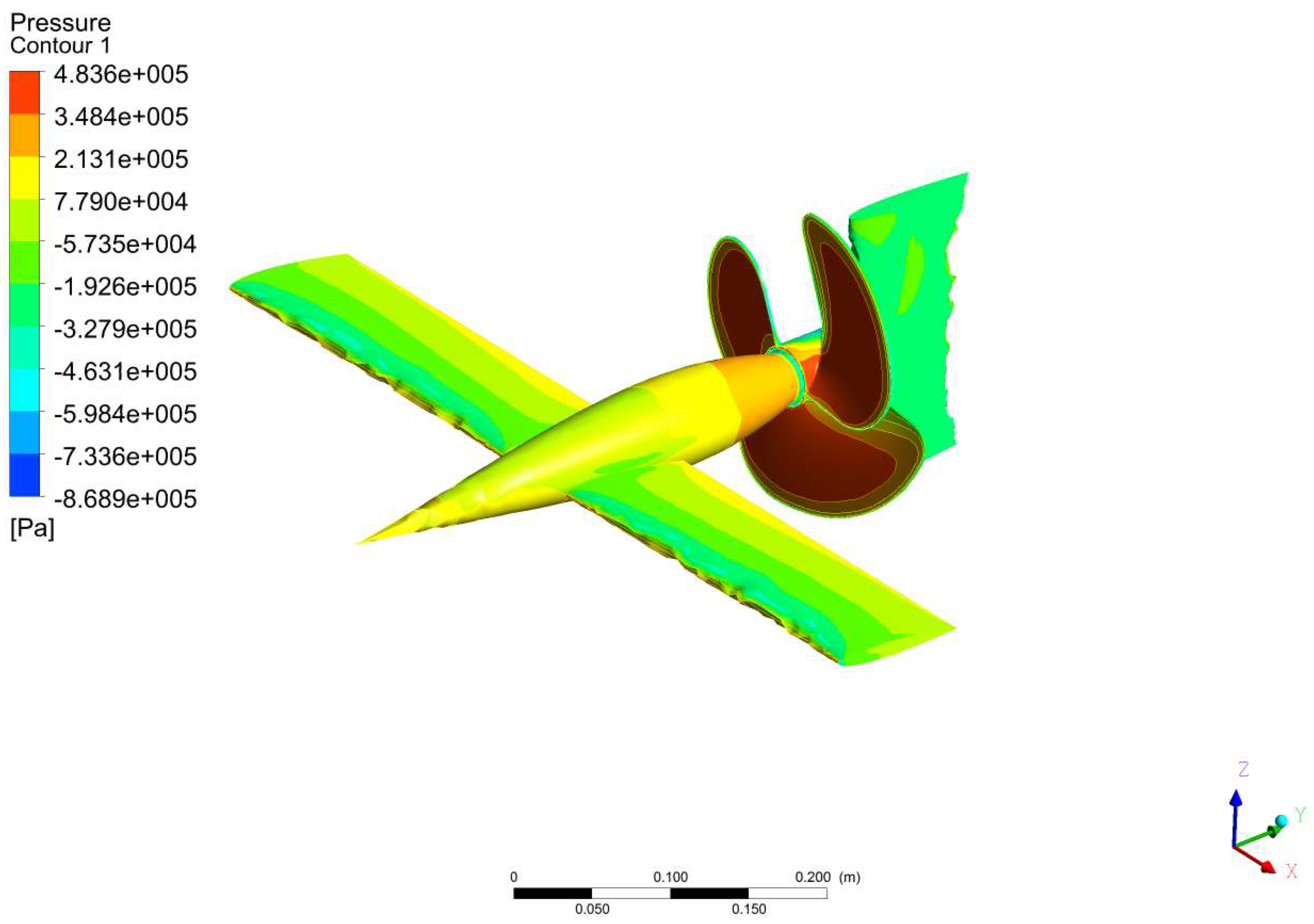
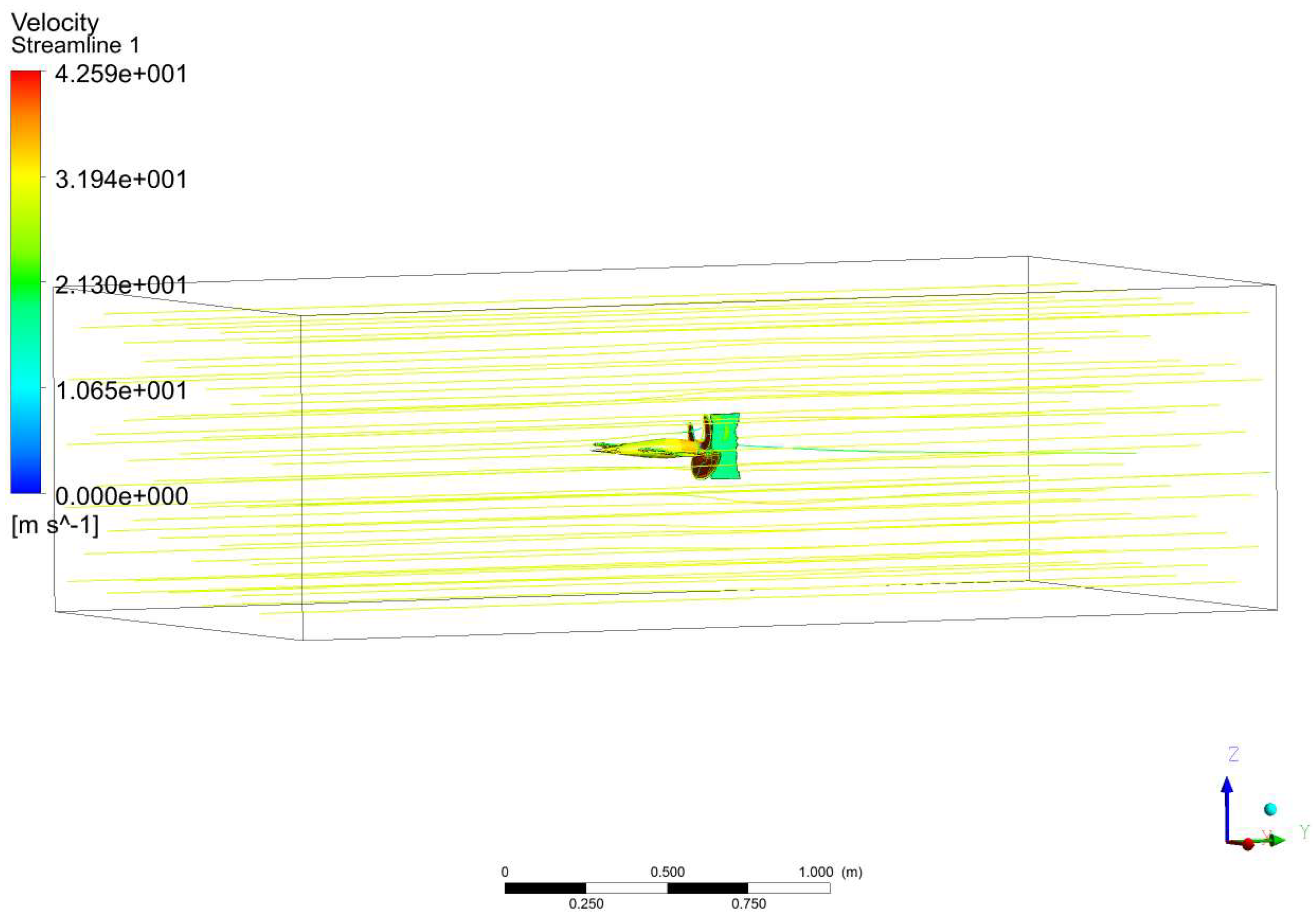
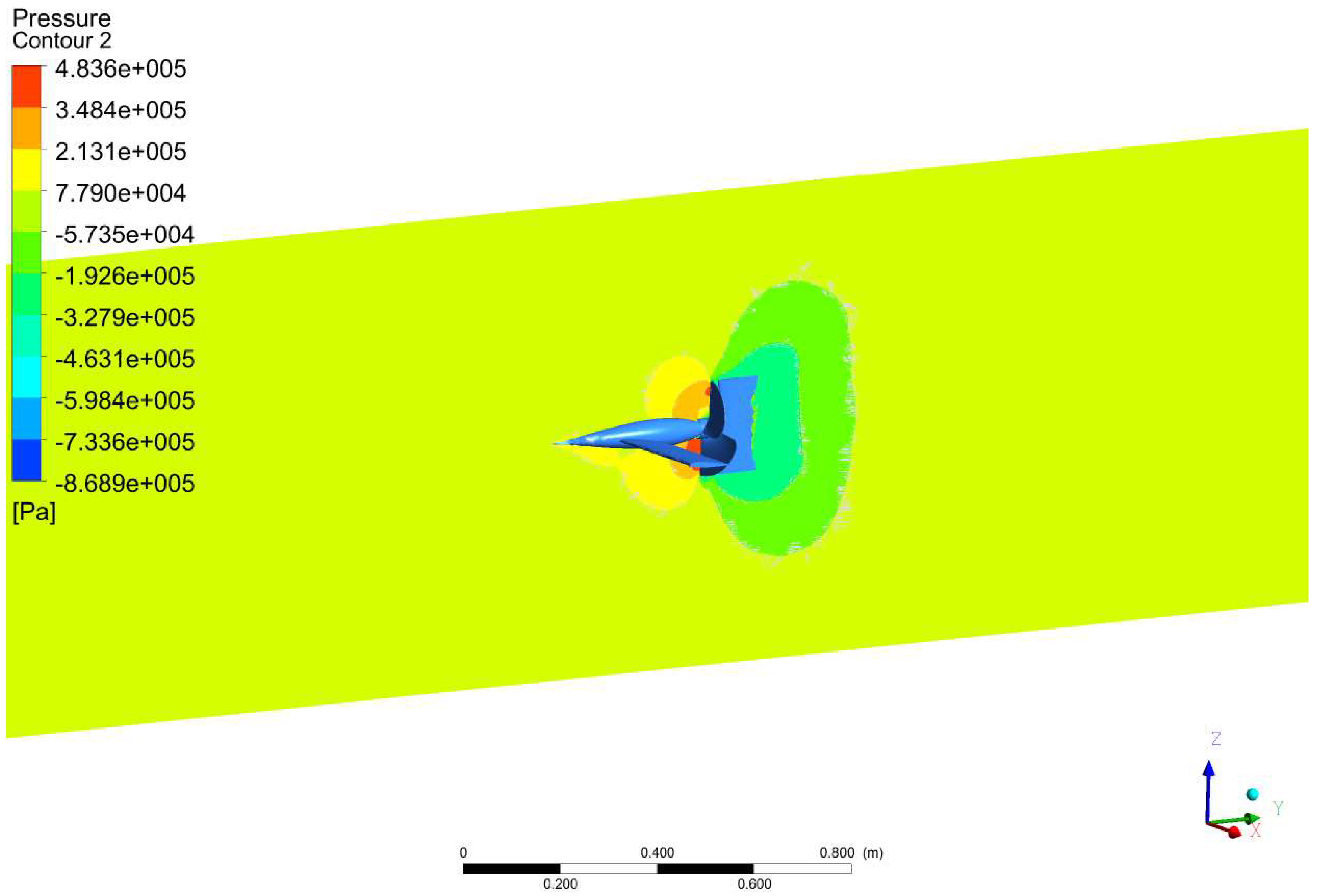

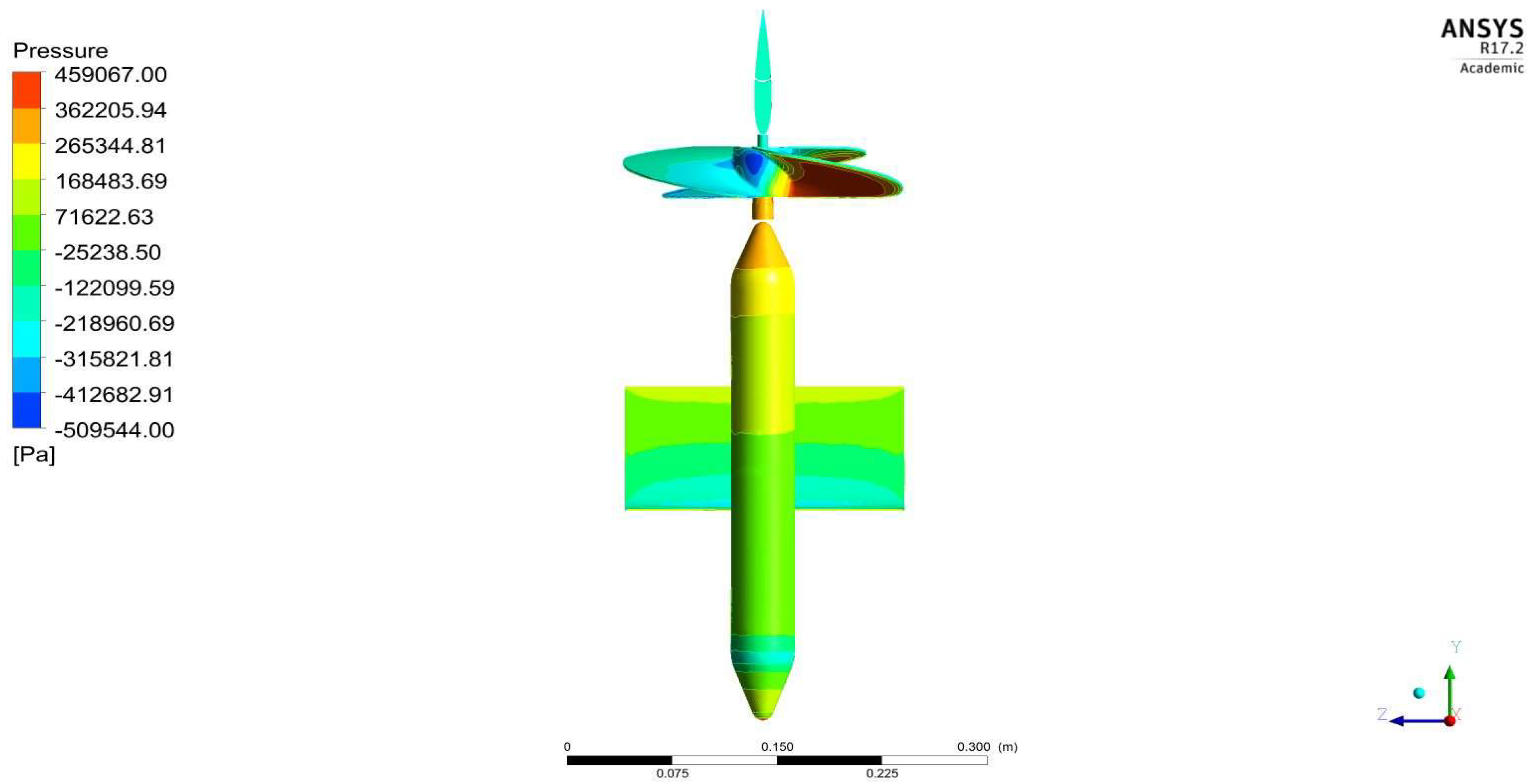

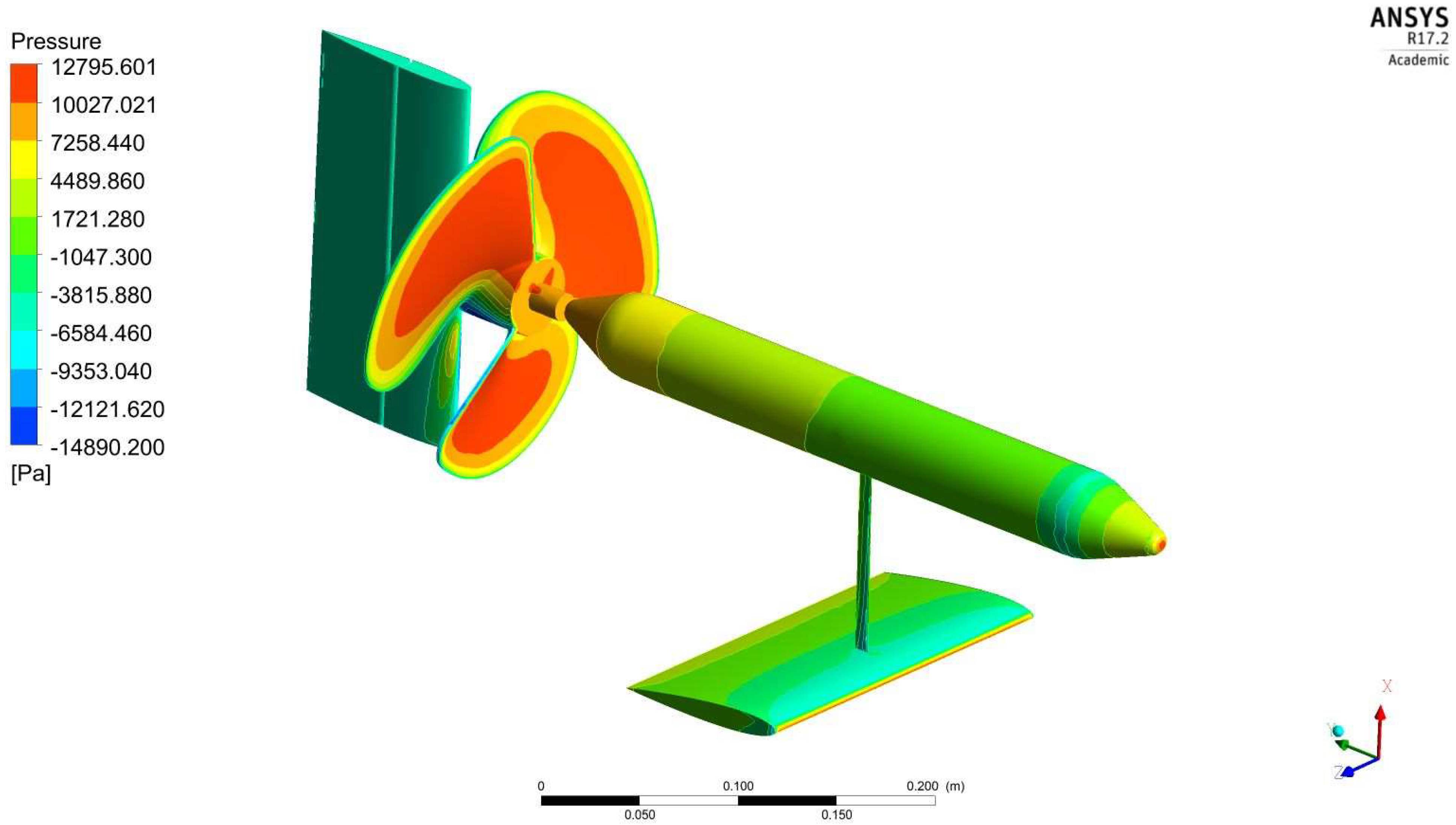


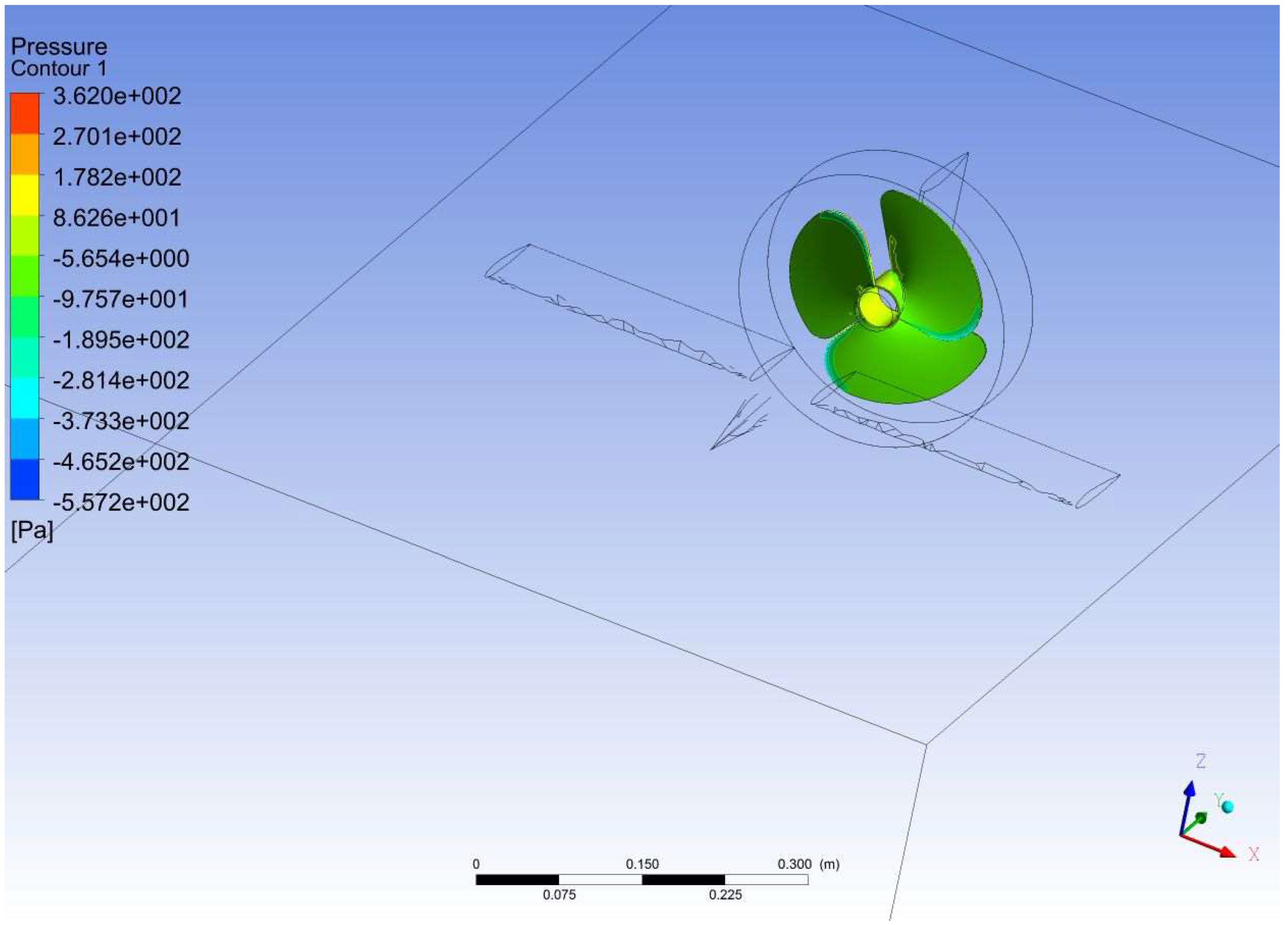
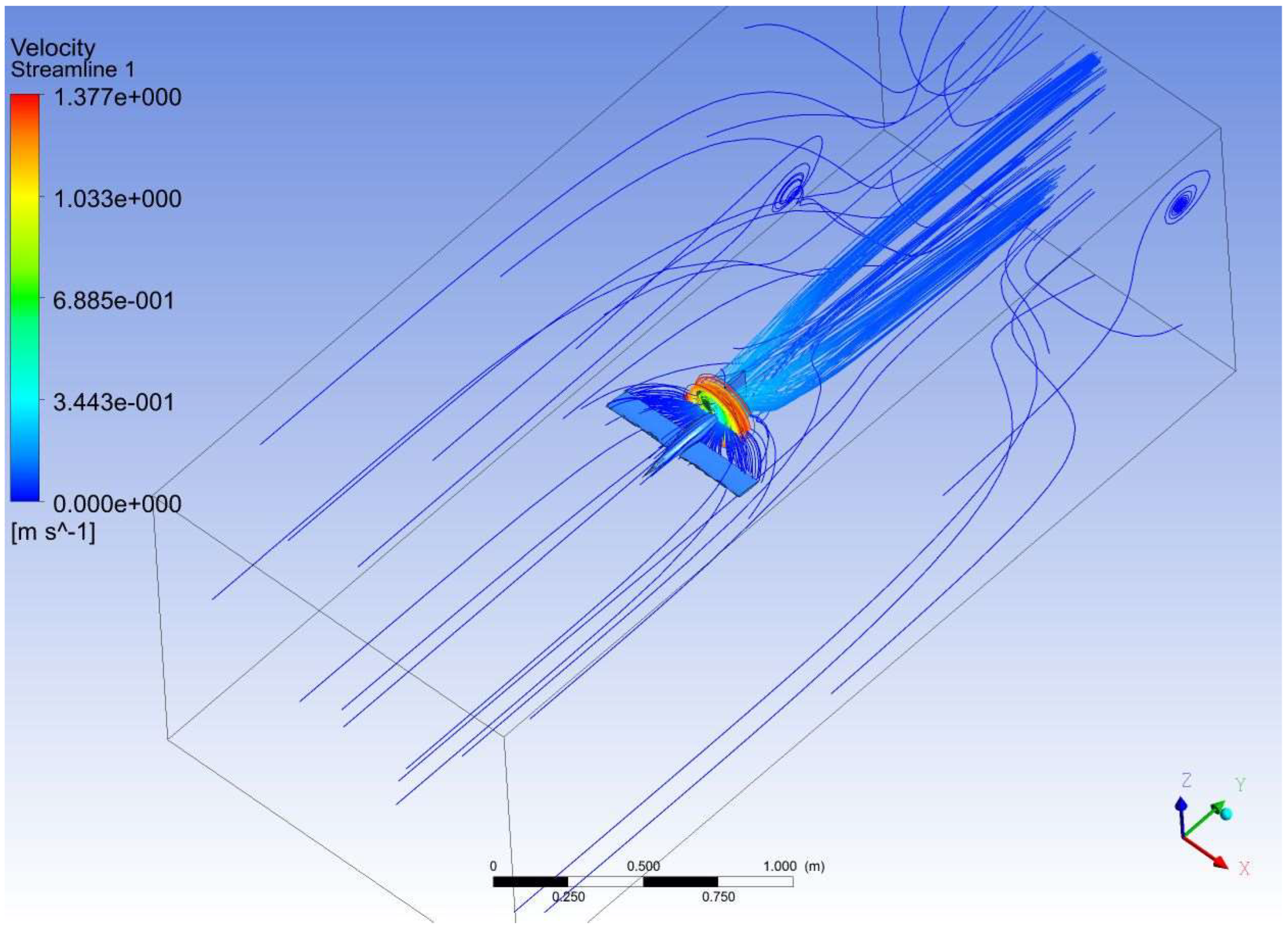

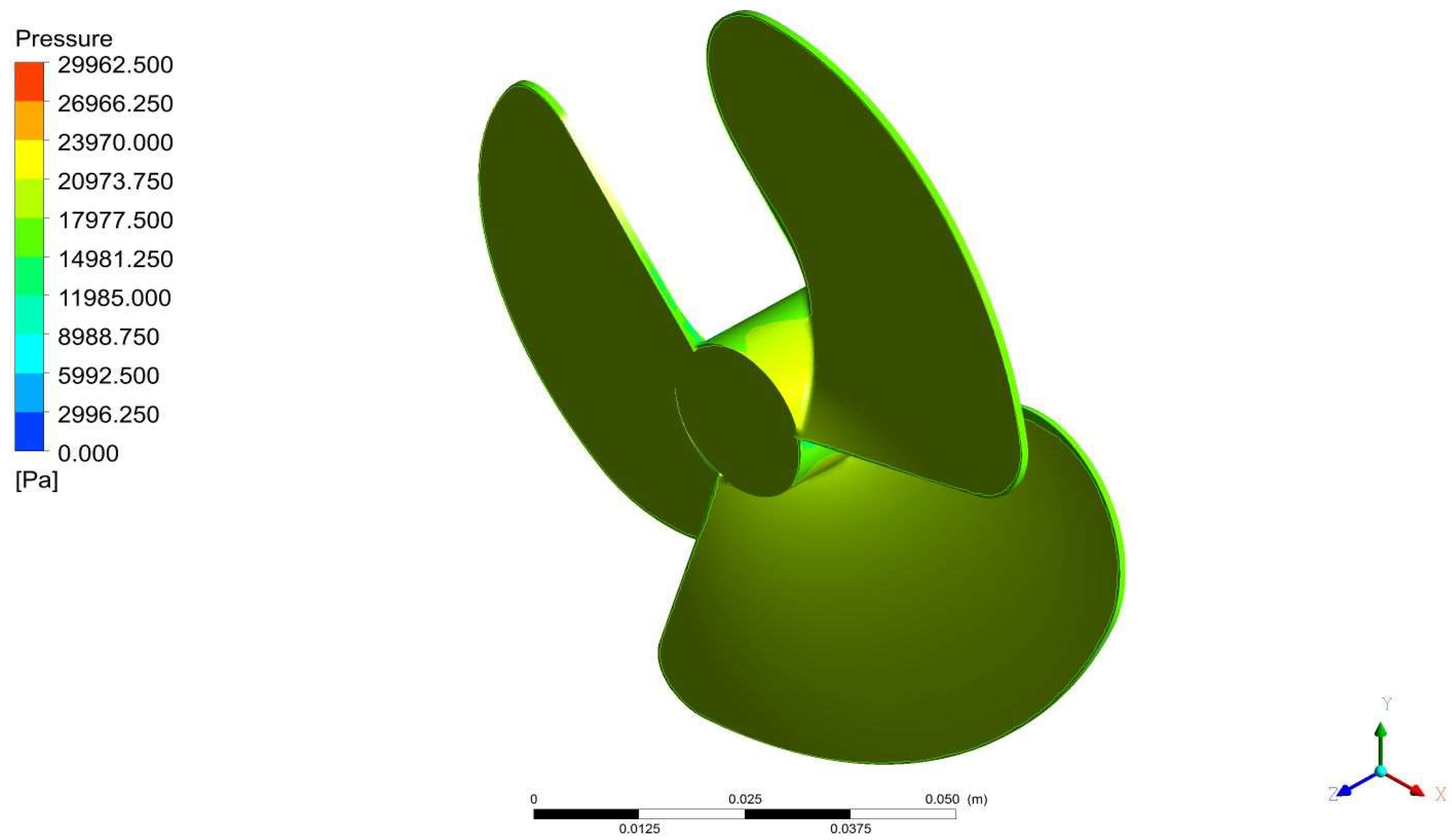

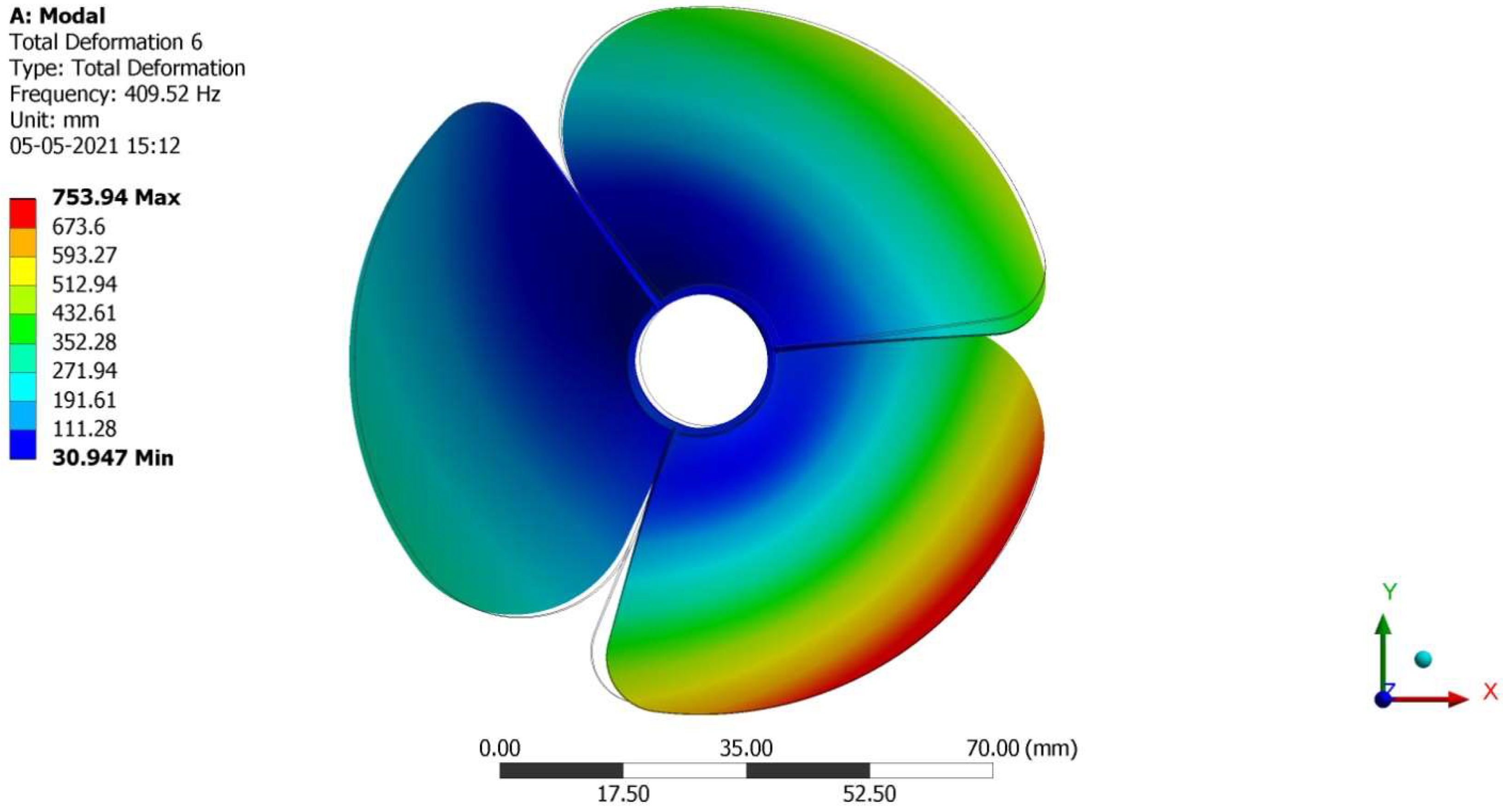
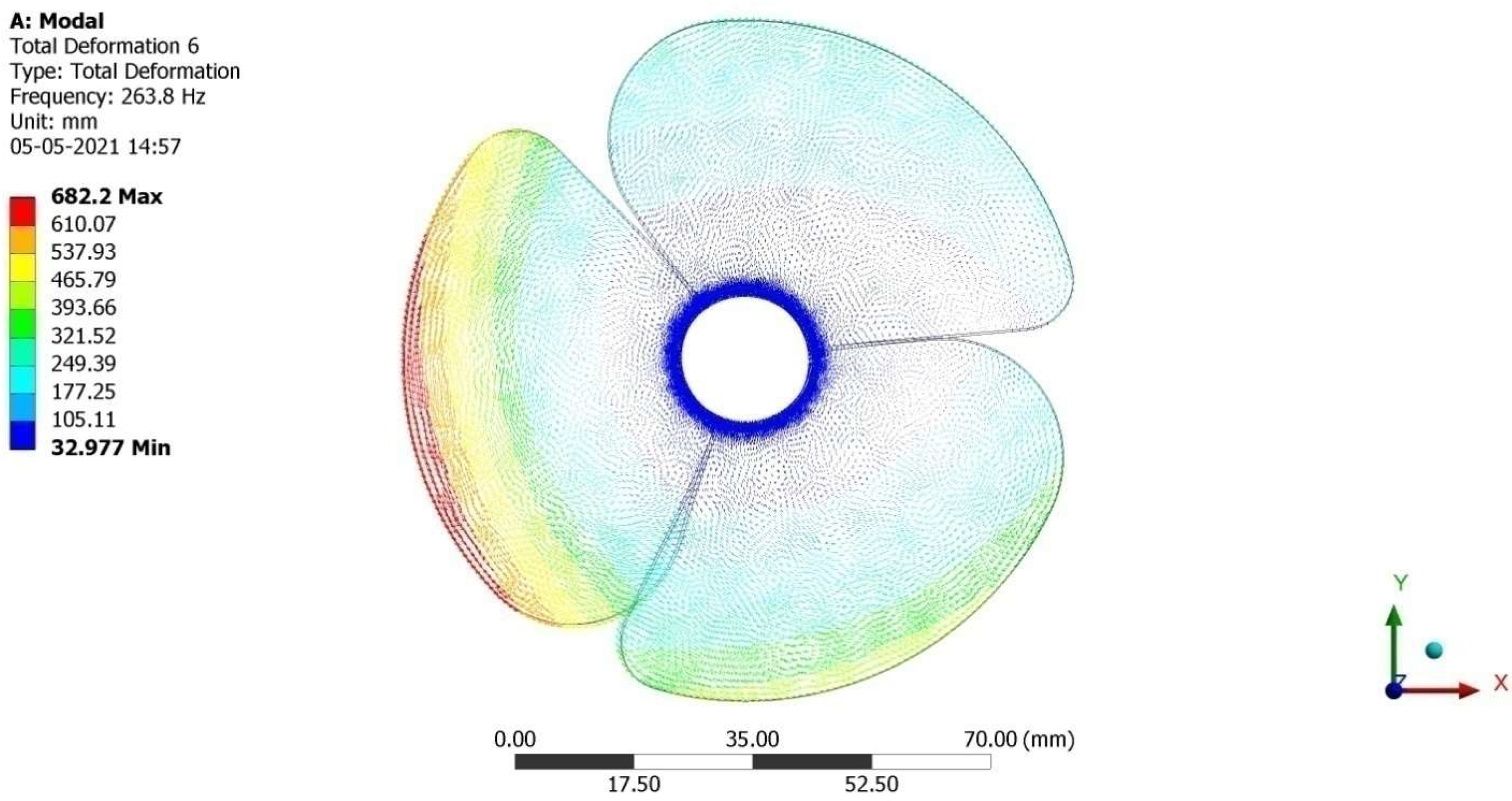


| Experimental Results That Cause Drag on the Fuselage Model [48,49,50] | This Forced Computing Methods Caused Drag on the Fuselage Model | Error (%) |
|---|---|---|
| 9.75 N | 9.56 N | 1.95 |
| RPM | Exit Velocity (m/s) | Thrust (N) |
|---|---|---|
| 25 | 0.8912 | 29.28983369 |
| 50 | 1.784 | 117.3808604 |
| 75 | 2.678 | 264.5064847 |
| 100 | 3.571 | 470.3244203 |
| 200 | 7.14 | 1880.255232 |
| 300 | 10.71 | 4230.578883 |
| 400 | 14.28 | 7521.031994 |
| 500 | 17.85 | 11,751.61456 |
| 600 | 21.42 | 16,922.3266 |
| 700 | 25 | 23,051.60569 |
| 800 | 28.57 | 30,105.21005 |
| 900 | 32.14 | 38,098.94388 |
| 1000 | 35.71 | 47,032.80717 |
| 11,000 | 396.5 | 5,798,392.598 |
| Material | Density (kg/m3) | Volume (m3) | Mass (kg) |
|---|---|---|---|
| Aluminium | 2710 | 0.00124 | 3.6023 |
| Aluminium alloy 2014 | 2800 | 0.00124 | 3.472 |
| Stainless steel | 7860 | 0.00124 | 9.7439 |
| CFRP-UD-230-GPa-Prepreg | 1490 | 0.00124 | 1.8476 |
| CFRP-Wn-230-GPa-Wet | 1451 | 0.00124 | 1.79924 |
| S-GFRP-UD | 2000 | 0.00124 | 2.48 |
| Models | Drag (N) (Force in Y Direction) |
|---|---|
| 1 | 16,900 |
| 2 | 17,250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raja, V.; Murugesan, R.; Rajendran, P.; Palaniappan, S.; AL-bonsrulah, H.A.Z.; Jayaram, D.K.; Al-Bahrani, M. Multi-Domain Based Computational Investigations on Advanced Unmanned Amphibious System for Surveillances in International Marine Borders. Aerospace 2022, 9, 652. https://doi.org/10.3390/aerospace9110652
Raja V, Murugesan R, Rajendran P, Palaniappan S, AL-bonsrulah HAZ, Jayaram DK, Al-Bahrani M. Multi-Domain Based Computational Investigations on Advanced Unmanned Amphibious System for Surveillances in International Marine Borders. Aerospace. 2022; 9(11):652. https://doi.org/10.3390/aerospace9110652
Chicago/Turabian StyleRaja, Vijayanandh, Ramesh Murugesan, Parvathy Rajendran, Surya Palaniappan, Hussein A. Z. AL-bonsrulah, Darshan Kumar Jayaram, and Mohammed Al-Bahrani. 2022. "Multi-Domain Based Computational Investigations on Advanced Unmanned Amphibious System for Surveillances in International Marine Borders" Aerospace 9, no. 11: 652. https://doi.org/10.3390/aerospace9110652
APA StyleRaja, V., Murugesan, R., Rajendran, P., Palaniappan, S., AL-bonsrulah, H. A. Z., Jayaram, D. K., & Al-Bahrani, M. (2022). Multi-Domain Based Computational Investigations on Advanced Unmanned Amphibious System for Surveillances in International Marine Borders. Aerospace, 9(11), 652. https://doi.org/10.3390/aerospace9110652










