A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat
Abstract
:1. Introduction
- (1)
- The first of these is the complexity of modeling the real air combat problem. The huge amount of information in a real air combat environment and the rapidly changing state of it brings problems to those that are conducting accurate modeling.
- (2)
- The second of these is the dimension explosion problem that is caused by the growth of the number of game individuals and the decision-making space. The decision-making problems that occur due to there being a large number of game participants bring huge decision-making space dimensions which will directly affect the efficiency and accuracy of the solution.
- (3)
- Finally, it is difficult to solve the problem with an optimal strategy. In the face of complex and dynamic air combat decision-making problems, it is impossible to obtain the analytical solution of the Nash equilibrium.
- (1)
- To simulate the real air combat environment, this paper establishes a six-degree-of-freedom model of the unmanned combat aircraft, constructs the action library of the unmanned combat aircraft, and establishes the missile attack area and the corresponding probability of damage occurring according to both the enemy and us.
- (2)
- This paper designs a set of comprehensive reward functions according to the angle, height, speed, and distance of the unmanned combat aircraft, and the probability of damage occurring to the missile attack area to overcome the problem of sparse rewards in reinforcement learning and improve the training efficiency.
- (3)
- The multi-agent proximal policy optimization approach is designed to optimize the air combat decision-making algorithm, which adopts the architecture of the centralized training-distributed execution mechanism to improve the decision-making ability of the UCAVs.
- (4)
- A two-to-one battlefield environment is used to simulate and verify the algorithm. The experimental results show that deep reinforcement learning can guide UCAVs to fight, find a way to quickly expand their superiority when they are superior, and find a suitable way to attack to win in an air combat scenario when it is at an absolute disadvantage.
2. Task Scene and Decision Structure Design
3. Air Combat Model of the UCAV under the Decision Structure
3.1. Motion Control Model of the UCAV
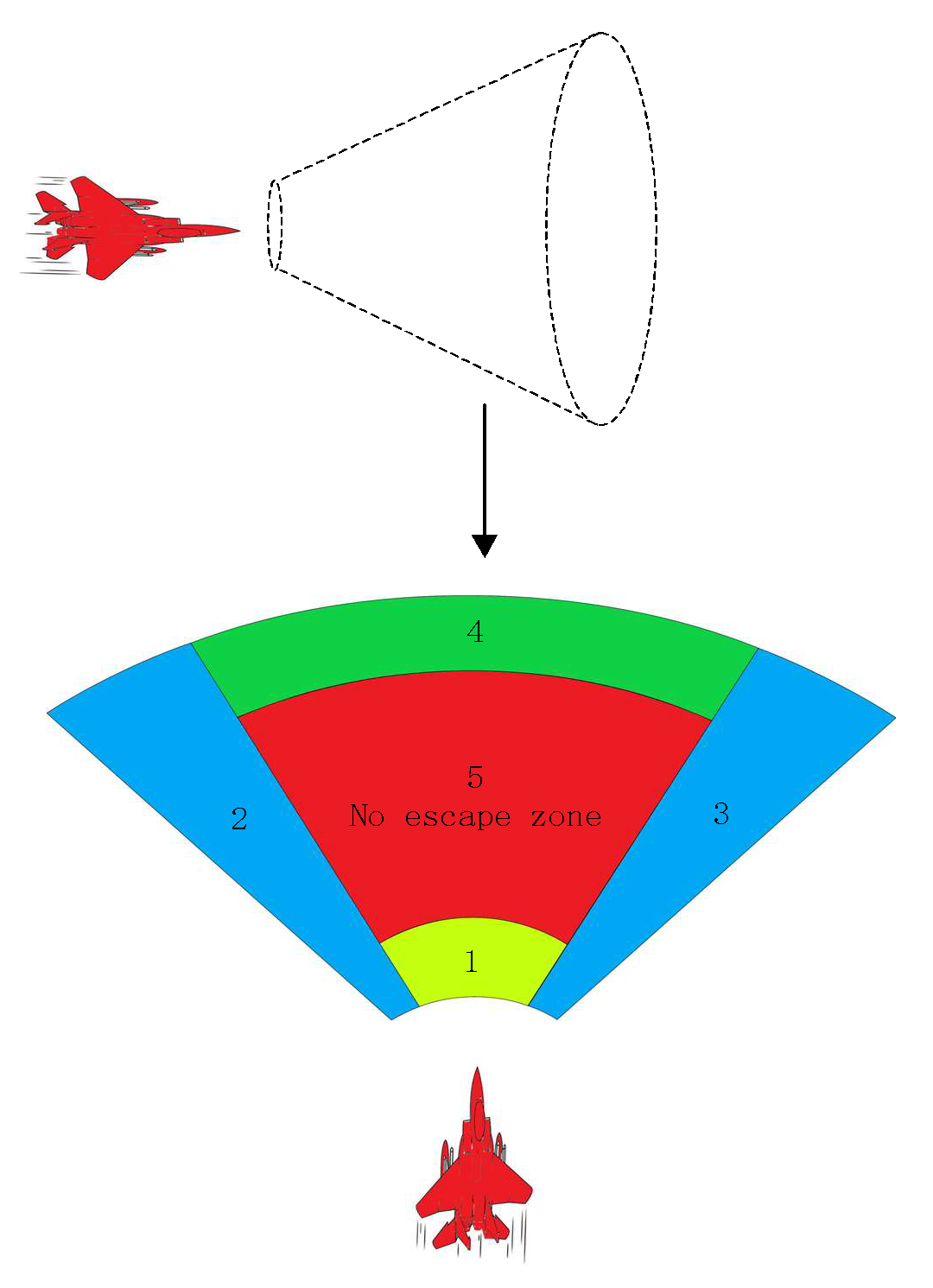
3.2. Modeling of the Missile Attack Zone
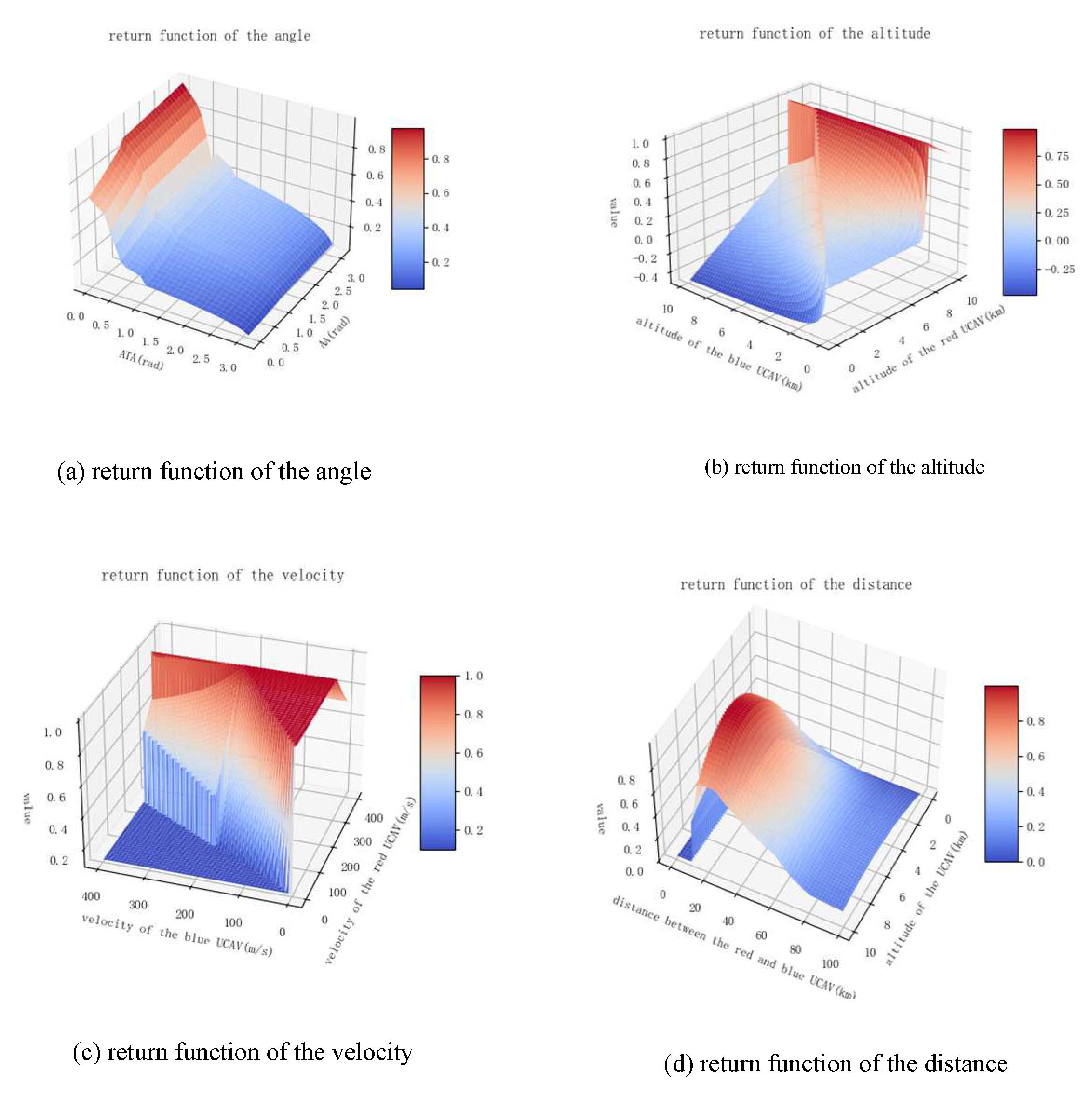
3.3. Design of a Comprehensive Reward Function
4. Algorithm Design of Air Combat Decisions That Are Based on MAPPO
4.1. Algorithm of Proximal Policy Optimization
4.2. Centralized Training and Distribution Execution Strategy
4.3. Network Structure Design of MAPPO
4.4. Algorithm Implementation Flow
| Algorithm 1. Specific implementation steps of the MAPPO algorithm. |
| 1. put UCAV model, aerial combat environment, and missile model 2. initialize hyper-parameters: Training episode E, Incentive discount rate, the Learning rate of actor net work, the Learning rate of critic network, batch_size 3. For each episode 1,2,3,…..E, do 4. For each UCAV, it is normalized according to current private observations 5. Input the normalized to the policy network to selection action , execute the action set in the environment to get the state 6. Input the of UCAV i and the of adversary UCAV j to the target selection module to obtain the primary target and secondary target 7. Input the of UCAV i and the of adversary UCAV j to the missile module, calculate whether the enemy UCAV is in the attack area of its UCAV and the missile hit rate, and obtain the discrete return according to the judgment conditions such as missile hit rate, crash and stall. 8. Obtain continuous rewards according to the main and secondary targets of the UCAV and the angle reward , distance reward , speed reward and high reward of the current state. Add discrete returns and continuous returns to obtain comprehensive returns . 9. When the data in the experience pool reaches the set min_ BATCH_ The normalized joint state, joint action, and joint reward of all agents are input into the value network. 10. For UCAV 11. calculate and update the advantage estimation of each UCAV . 12. Update the value network, and the objective function is: 13. The advantage estimation function of each UCAV is input into the strategy network. Input the private state observation of each UCAV in the experience pool to the strategy network. 14. Calculate the action selection strategy of the policy network. 15. Select the old action strategy and update the new action strategy. 16. The objective function of the policy network is: 17. Regularly update the target critical network. 18. Regularly update the target actor network 19. end for 20. end for |
5. Intelligent Air Combat Decision Simulation Experiment
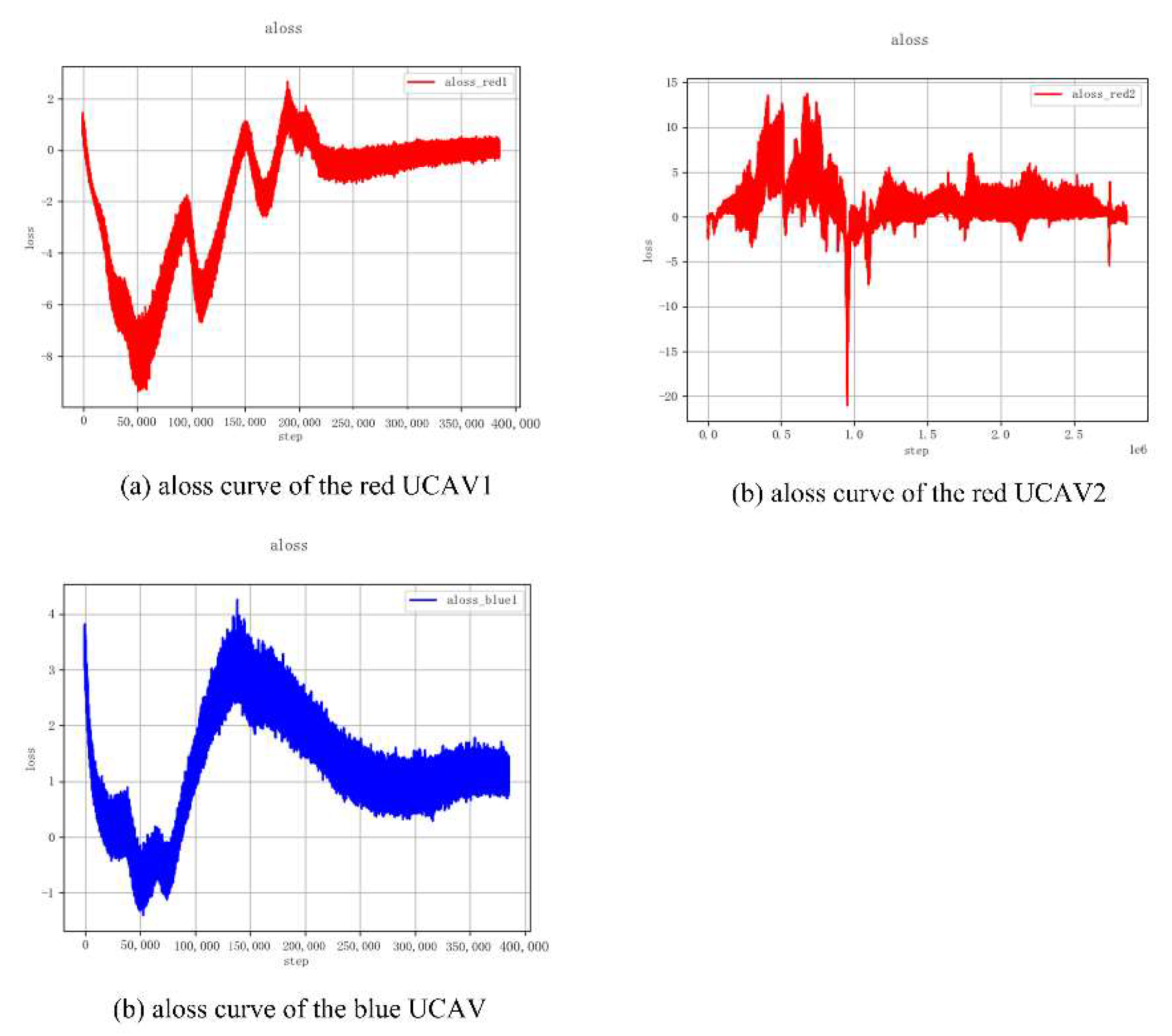
5.1. Training Process
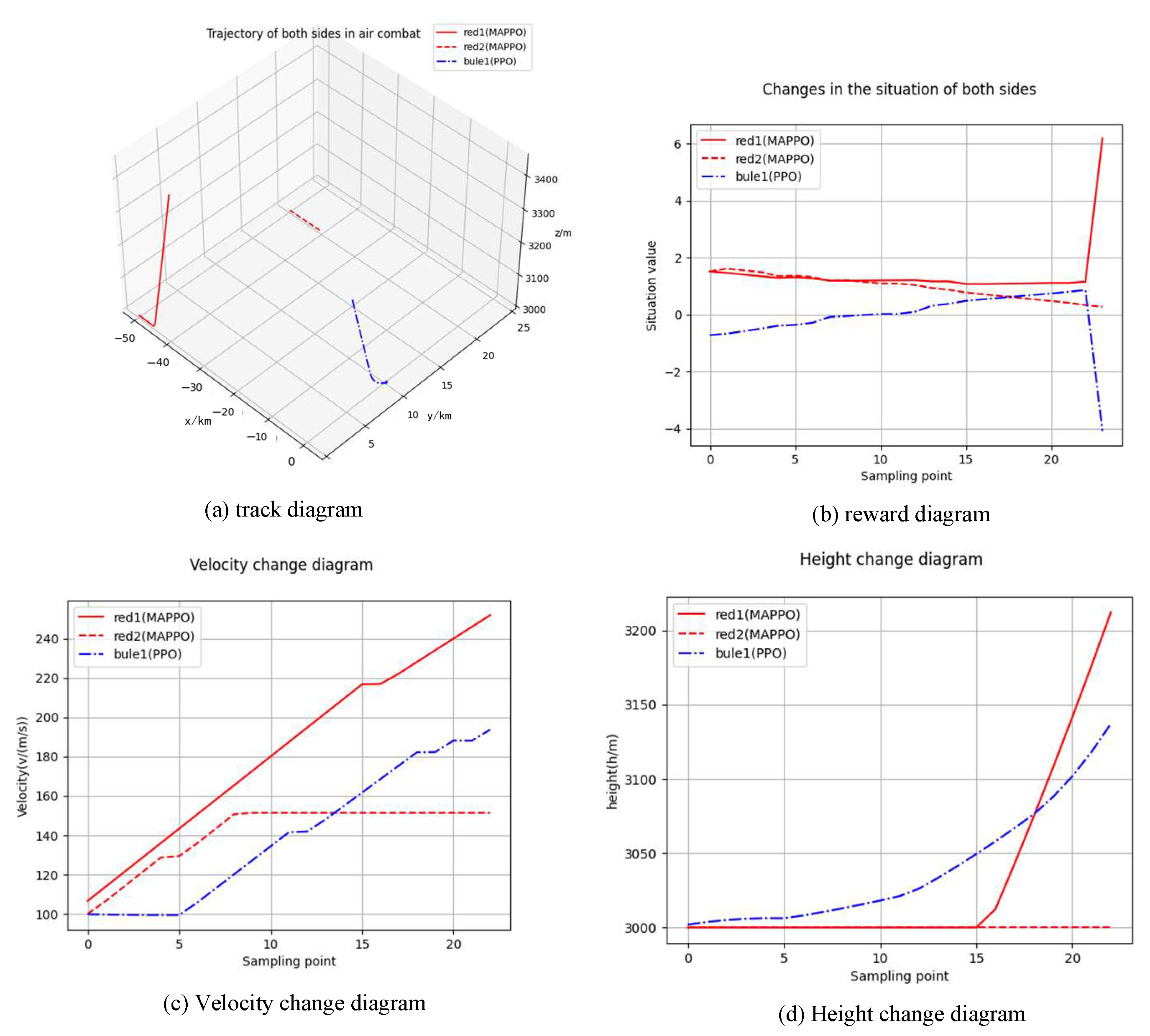
5.2. Simulation Verification
- (1)
- Red 1 hits the blue UCAV.
- (2)
- The blue UCAV hits the red 1.
5.3. Comparison of Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Sun, Z.-X.; Piao, H.-Y.; Huang, J.-C.; Zhou, D.-Y.; Ren, Z. Online hierarchical recognition method for target tactical intention in beyond-visual-range air combat. Def. Technol. 2022, 18, 1349–1361. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, D.; Piao, H.; Zhang, K.; Kong, W.; Pan, Q. Evasive Maneuver Strategy for UCAV in Beyond-Visual-Range Air Combat Based on Hierarchical Multi-Objective Evolutionary Algorithm. IEEE Access 2020, 8, 46605–46623. [Google Scholar] [CrossRef]
- Li, W.-H.; Shi, J.-P.; Wu, Y.-Y.; Wang, Y.-P.; Lyu, Y.-X. A Multi-UCAV cooperative occupation method based on weapon engagement zones for beyond-visual-range air combat. Def. Technol. 2022, 18, 1006–1022. [Google Scholar] [CrossRef]
- Li, S.-Y.; Chen, M.; Wang, Y.-H.; Wu, Q.-X. Air combat decision-making of multiple UCAVs based on constraint strategy games. Def. Technol. 2021, 18, 368–383. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J.; Wang, Z.; Lin, Y.; Li, H. Sub-AVG: Overestimation reduction for cooperative multi-agent reinforcement learning. Neurocomputing 2021, 474, 94–106. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Active target defence differential game: Fast defender case. IET Control Theory Appl. 2017, 11, 2985–2993. [Google Scholar] [CrossRef]
- Park, H.; Lee, B.-Y.; Tahk, M.-J.; Yoo, D.-W. Differential Game Based Air Combat Maneuver Generation Using Scoring Function Matrix. Int. J. Aeronaut. Space Sci. 2016, 17, 204–213. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.; Hu, X.; Luo, H.; Lei, X. Cooperative Occupancy Decision Making of Multi-UAV in Beyond-Visual-Range Air Combat: A Game Theory Approach. IEEE Access 2019, 8, 11624–11634. [Google Scholar] [CrossRef]
- Han, S.-J. Analysis of Relative Combat Power with Expert System. J. Digit. Converg. 2016, 14, 143–150. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, R.; Xu, Z.; Zhang, Q. A Brain like Air Combat Learning System Inspired by Human Learning Mechanism. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, Z.; Liu, H.; Yang, H. Situation Assessment of Far-Distance Attack Air Combat Based on Mixed Dynamic Bayesian Networks. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 4569–4574. [Google Scholar] [CrossRef]
- Fu, L.; Liu, J.; Meng, G.; Xie, F. Research on beyond Visual Range Target Allocation and Multi-Aircraft Collaborative Decision-Making. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 586–590. [Google Scholar] [CrossRef]
- Ernest, N.; Carroll, D.; Schumacher, C.; Clark, M.; Cohen, K.; Lee, G. Genetic Fuzzy based Artificial Intelligence for Unmanned Combat Aerial Vehicle Control in Simulated Air Combat Missions. J. Déf. Manag. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Sathyan, A.; Ernest, N.D.; Cohen, K. An Efficient Genetic Fuzzy Approach to UAV Swarm Routing. Unmanned Syst. 2016, 4, 117–127. [Google Scholar] [CrossRef]
- Ernest, N.D.; Garcia, E.; Casbeer, D.; Cohen, K.; Schumacher, C. Multi-agent Cooperative Decision Making using Genetic Cascading Fuzzy Systems. AIAA Infotech. Aerosp. 2015. [Google Scholar] [CrossRef]
- Crumpacker, J.B.; Robbins, M.J.; Jenkins, P.R. An approximate dynamic programming approach for solving an air combat maneuvering problem. Expert Syst. Appl. 2022, 203. [Google Scholar] [CrossRef]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. A survey and critique of multiagent deep reinforcement learning. Auton. Agents Multi-Agent Syst. 2019, 33, 750–797. [Google Scholar] [CrossRef]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent cooperation and competition with deep reinforcement learning. PLoS ONE 2017, 12, e0172395. [Google Scholar] [CrossRef] [PubMed]
- Heuillet, A.; Couthouis, F.; Díaz-Rodríguez, N. Explainability in deep reinforcement learning. Knowl.-Based Syst. 2020, 214, 106685. [Google Scholar] [CrossRef]
- Li, Y.-F.; Shi, J.-P.; Jiang, W.; Zhang, W.-G.; Lyu, Y.-X. Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm. Def. Technol. 2022, 18, 1697–1714. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, C. Maneuver Decision-Making of Deep Learning for UCAV Thorough Azimuth Angles. IEEE Access 2020, 8, 12976–12987. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Yang, C.; Wu, J. Research on Air Combat Maneuver Decision-Making Method Based on Reinforcement Learning. Electronics 2018, 7, 279. [Google Scholar] [CrossRef]
- Yang, Q.; Zhu, Y.; Zhang, J.; Qiao, S.; Liu, J. UAV Air Combat Autonomous Maneuver Decision Based on DDPG Algorithm. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA), Edinburgh, UK, 16–19 July 2019; pp. 37–42. [Google Scholar] [CrossRef]
- Piao, H.; Sun, Z.; Meng, G.; Chen, H.; Qu, B.; Lang, K.; Sun, Y.; Yang, S.; Peng, X. Beyond-Visual-Range Air Combat Tactics Auto-Generation by Reinforcement Learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, P.; Ma, Y. A Deep Reinforcement Learning Based Intelligent Decision Method for UCAV Air Combat. Commun. Comput. Inf. Sci. 2017, 751, 274–286. [Google Scholar] [CrossRef]
- Hu, D.; Yang, R.; Zuo, J.; Zhang, Z.; Wu, J.; Wang, Y. Application of Deep Reinforcement Learning in Maneuver Planning of Beyond-Visual-Range Air Combat. IEEE Access 2021, 9, 32282–32297. [Google Scholar] [CrossRef]
- Liang, W.; Wang, J.; Bao, W.; Zhu, X.; Wu, G.; Zhang, D.; Niu, L. Neurocomputing Qauxi: Cooperative multi-agent reinforcement learning with knowledge transferred from auxiliary task. Neurocomputing 2022, 504, 163–173. [Google Scholar] [CrossRef]
- Yao, W.; Qi, N.; Wan, N.; Liu, Y. An iterative strategy for task assignment and path planning of distributed multiple unmanned aerial vehicles. Aerosp. Sci. Technol. 2019, 86, 455–464. [Google Scholar] [CrossRef]





| Maneuvering Action | Maneuver Coding | ||
|---|---|---|---|
| Tangential Overload | Normal Overload | Roll Angle | |
| Flat flight with fixed length | 0 | 1 | 0 |
| Accelerate flight | 0.3 | 1 | 0 |
| Deceleration flight | −0.3 | 1 | 0 |
| Turn left | 0 | 1.985 | |
| Turn right | 0 | −1.985 | |
| Pull up | 0 | 1.5 | 0 |
| Dive down | 0 | −1.5 | 0 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Training episode | 1,000,000 | ||
| Incentive discount rate | 0.9 | ||
| Learning rate of actor network | 0.0001 | ||
| Learning rate of critic network | 0.0001 | 350 m/s | |
| Batch_size | 64 | 8000 m | |
| 80km | 25km | ||
| 60km | 15km |
| Situation | Frequency | Winning Probability |
|---|---|---|
| Red 1 hits blue | 314 | 31.4% |
| Red 2 hits blue | 388 | 38.8% |
| Blue hits Red 1 | 146 | 14.6% |
| Blue hits Red 2 | 152 | 15.2% |
| Situation | Frequency | Winning Probability |
|---|---|---|
| Red 1 hits blue | 418 | 41.8% |
| Red 2 hits blue | 439 | 43.9% |
| Blue hits Red 1 | 68 | 6.8% |
| Blue hits Red 2 | 75 | 7.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yin, Y.; Su, Y.; Ming, R. A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat. Aerospace 2022, 9, 563. https://doi.org/10.3390/aerospace9100563
Liu X, Yin Y, Su Y, Ming R. A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat. Aerospace. 2022; 9(10):563. https://doi.org/10.3390/aerospace9100563
Chicago/Turabian StyleLiu, Xiaoxiong, Yi Yin, Yuzhan Su, and Ruichen Ming. 2022. "A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat" Aerospace 9, no. 10: 563. https://doi.org/10.3390/aerospace9100563
APA StyleLiu, X., Yin, Y., Su, Y., & Ming, R. (2022). A Multi-UCAV Cooperative Decision-Making Method Based on an MAPPO Algorithm for Beyond-Visual-Range Air Combat. Aerospace, 9(10), 563. https://doi.org/10.3390/aerospace9100563






