Abstract
Hollow-cup motors are usually used in spacecraft because of their low power consumption and high control accuracy. However, because the air-gap between the permanent magnets (PMs) and the rotor of the hollow-cup motor is uniform, the sinusoidal characteristic of the air-gap magnetic field waveform is inferior and the total harmonic distortion (THD) is large, resulting in torque ripple. For the large air-gap hollow-cup motor, the existing methods for optimizing the sinusoidal characteristics of the air gap magnetic field change the shape of PMs, but the changed PMs are difficult to manufacture and magnetize, resulting in the methods being limited and not being able to achieve the ideal optimization effect for the hollow-cup motor. Based on the characteristics of the inner rotor and outer rotor rotating synchronously during operation, a new structure design of the hollow-cup motor with an eccentric inner rotor is proposed instead of changing the PMs’ shape. Firstly, the mathematical model of the hollow-cup motor is established. Then, the FEM shows that the inner rotor’s eccentricity can bring the air-gap magnetic field waveform closer to the ideal sinusoidal waveform and can effectively reduce the THD. Finally, a prototype with the optimal eccentricity value is made for experimental verification.
1. Introduction
With the rapid development of aerospace technology, more and more spacecraft enter space to perform missions. In order to ensure the functions of high-resolution observation, communication and energy supply, it is necessary to constantly adjust their attitude. At present, the motion of spacecraft along the attitude trajectory mainly depends on magnetically suspended flywheels and magnetically suspended control moment gyro [1,2,3]. The hollow-cup brushless permanent magnet motor has the characteristics of a high energy density, high speed, high precision, long life and no cogging torque ripple; it has been widely used in magnetically suspended flywheel and gyro [4]. In particular, the hollow-cup motor with a sinusoidal air-gap magnetic flux density waveform adopts a cup-shaped stator design, and the inner and outer rotors rotate synchronously during operation, which has the advantages of a convenient speed regulation and fast response speed. However, due to the air-gap width between the PMs and inner rotor being almost uniform, the air-gap magnetic field waveform of the hollow-cup motor is inconsistent with the ideal waveform, resulting in an increased output torque ripple, which affects the smoothness of the motor and the accuracy of the output torque [5].
To solve the above problems, improving the sine wave characteristics of the air-gap magnetic field is an important way to reduce torque ripple [6,7]. Most permanent magnet synchronous motors use a uniform air-gap structure, which results in the air-gap magnetic field containing high-order harmonics. In order to make it be closer to a sine wave, many scholars have studied and optimized the air-gap magnetic field of the motor [8,9,10]. Surface-mounted motors usually adopt the method of an eccentric design to the outer diameter of the PMs. In [11], By eccentric cutting of the outer diameter of the PMs, the influence of the eccentric distance on the harmonic content in the air-gap flux density was analyzed. In [12], through solving Maxwell’s equations and considering different boundary conditions, a mathematical model of the air-gap magnetic density of the Halbach array PMs was constructed, and the height or width of the PMs was changed to reduce the sine wave distortion rate of the air-gap magnetic field. In [13,14], by changing the eccentricity value of the PMs’ profile, the air-gap flux density waveform was sinusoidal. In [15], a new type of segmented Halbach permanent magnet motor was proposed. Through the eccentric design of the outer diameter of the inner and outer segments of the segmented magnetic poles and a finite element analysis, the proportion of harmonics was effectively reduced. In [16], the Carter coefficient was used to correct the uneven variation of radial thickness caused by cogging, and the design parameters for the lowest total harmonic distortion were obtained by the equivalent magnetic circuit method, so that the radial air-gap magnetic flux density waveform was close to sinusoidal. For the built-in permanent magnet motor, in [17], by adjusting the rotor shape, an effective air-gap flux density was achieved, and the fundamental component of the back EMF was optimized to reduce the harmonic content, to minimize the pulsating torque. In [18], an optimization method for the shape of an anisotropic ferrite magnet as proposed, which reduced the torque ripple and THD. In [19], an analytical solution for air-gap magnetic density was obtained by conformal transformation, and the eccentric design of the rotor’s outer diameter reduced the harmonic components of the air-gap magnetic field. In [20,21], an analytical model for calculating the air-gap magnetic field of a U-shaped built-in permanent magnet DC motor was established, and the bottom of the magnet was eccentrically designed to reduce the harmonic content in the air-gap magnetic field.
The existing methods are mainly for surface-mounted or built-in motors with a narrow air-gap width, and they are not applicable to the surface-mounted hollow-cup motor with a large air-gap described in this paper. What is more, many scholars adjusted the parameters of the PMs according to the characteristics of the air-gap magnetic field; because the PMs are thin, this method has a poor optimization effect, as at the same time the adjusted PMs are difficult to process and magnetize. Based on the special structure of the hollow-cup motor, the relative position of the magnet and the inner rotor remains unchanged during operation; this paper proposes a method to optimize the design of the eccentricity of the inner rotor. First, the mathematical model of the air-gap magnetic density of the hollow-cup motor is established by using the equivalent surface current method, and the main factors affecting the air-gap magnetic field waveform are analyzed, which are verified by finite element simulation and experiments. It is proved that the inner rotor eccentric structure proposed in this paper can bring the air-gap magnetic field waveform closer to the sine wave and reduce the harmonic distortion rate of the air-gap magnetic field.
2. Analytical Air-Gap Magnetic Field Modeling of Hollow-Cup Motor
For a sinusoidal waveform, the evaluation index is mainly the total harmonic distortion rate. The air-gap magnetic field waveform is Fourier-decomposed and -transformed to obtain the amplitude of each order of harmonic. The smaller the , the better the sine of the waveform, and the more similar it is to an ideal sine wave. The calculation formula is as follows:
where is the amplitude value of the corresponding nth-order harmonic wave.
This paper focuses on the hollow-cup motor in the magnetically suspended control moment gyro; the hollow-cup motor is mainly composed of an inner rotor core, an outer rotor core, permanent magnets (PMs) and a hollow-cup stator. The PM is mounted inside the outer rotor. In the gyroscope, two rotors are fixed on the flywheel, the cup-shaped stator is fixed on the gyro chamber, and the stator winding part is placed in the air gap between the PM and the inner rotor. The sectional view of the hollow-cup motor is shown in Figure 1a and top view is shown in Figure 1b.

Figure 1.
Model diagram of inner rotor’s eccentric hollow-cup motor: 1—Outer rotor; 2—PMs; 3—Cup stator; 4—Inner rotor; 5—Rotor fixing ring. (a) Axis section drawing of hollow-cup motor; (b) Top view of bow-shaped PMs’ hollow-cup motor.
The static air-gap magnetic field of the motor is excited by the permanent magnet, so the equivalent surface current method can be used. By replacing PMs with surface current, the magnetic field generated by the equivalent surface current is obtained by integration [22,23,24]. This paper mainly analyzes the magnetic field generated by the parallel magnetized magnets in the air gap. Combining the boundary conditions of the air-gap magnetic field and the electromagnetic field theory, the mathematical model of the magnetic field generated by a pair of current-carrying coils is:
For multi-stage coils, the coils can be calculated by the above formula and then superimposed, and the magnetic flux density generated by the combined action of 2p pairs of current-carrying coils in the air gap can be obtained, and its expression is:
Through the equivalent current method, the equivalent current of a PM during parallel charging is shown in Figure 2.
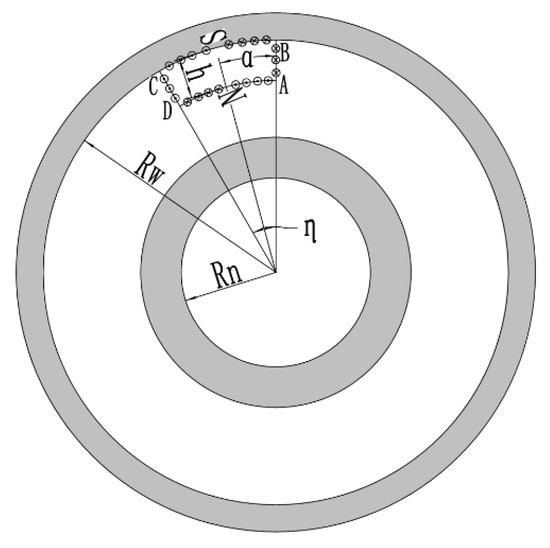
Figure 2.
Equivalent current of a PM during parallel charging.
According to the equivalent surface current method, the surface currents of AB and CD along the surface of the magnet are equal in opposite directions, which is:
The surface currents along the AD side and BC side of the PM surface are in opposite directions and equal in magnitude, which is:
where is the angle of the PM, is the angle of the AD or BC side, and is the coercivity.
Since the AB and CD sides are exactly the same:
The BC edge-to-surface flow micro-elements are:
The AD edge-to-surface flow micro-elements are:
The equivalent coil current micro-element is , the radial length micro-element of the AB and CD sides of the PM is , and the angle micro-element is .
According to the theoretical analysis, the factors that can change the rotor air-gap magnetic field are the permanent magnet thickness , permanent magnet inner diameter , rotor outer diameter , rotor inner diameter and pole pair . Under the same size and pole pair motor parameters, the parameter can change the air-gap magnetic field. In order to make the air-gap magnetic field be closer to the sine wave, PMs can be cut or the outer diameter of the inner rotor can be eccentric. Compared with the design of PMs’ cutting, the eccentricity of the inner rotor is convenient for machining and avoids the difficulty of magnetization after PMs’ cutting.
The eccentric design of the above inner rotor consists in rendering eccentric the part corresponding to the inner rotating outer diameter and each piece of PM. Move the center O of the outer diameter of the inner rotor to O’ along the centerline of PMs, keep the original end position of the outer diameter of the inner rotor unchanged, and draw an arc centered on O’, which is the outer diameter after eccentricity. Figure 3 shows the structural design of the inner rotor based on the eccentricity of the inner rotor. From the above formula, when the size of the motor structure is determined, the air-gap magnetic field is only related to the eccentric value.
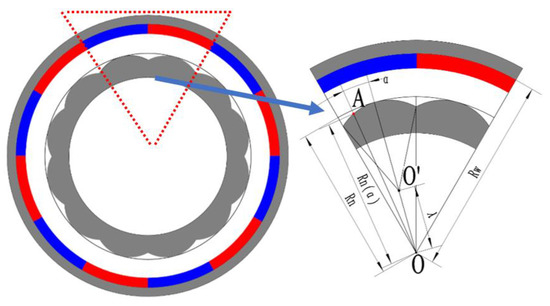
Figure 3.
Structural diagram of the eccentric design of the inner rotor.
The position A of any point on the outer diameter of the inner rotor can be obtained from the geometric relationship, where:
In the above formula, λ is the eccentricity value (the distance between O and O’).
Combining , we can obtain the equivalent currents of p pair PMs on the AB and CD sides, BC sides, and AD sides when the outer diameter of the inner rotor is eccentric. The magnetic field intensity generated at the air gap () is:
Edge :
Edge :
Edge :
The is:
Finally, the above formula is integrated and summed, and the result is the air-gap magnetic density produced by PMs in the air gap of the p pair pole hollow-cup motor:
From the above formula, when the size of the motor structure is determined, the air-gap magnetic field is only related to the eccentric value.
3. Finite Element Simulation Analysis of Hollow-Cup Motor
The parameters of the six pole pairs’ motor model in the laboratory are used for the simulation analysis, and the simulation results of different eccentricity values are compared. The hollow-cup motor’s parameters are shown in Table 1.

Table 1.
Parameters of hollow-cup motor model.
The finite element model of the hollow-cup motor is built through FEA software, and the model under the parameters in Table 1 is simulated under different inner rotor eccentricity values to analyze the influence of inner rotor eccentricity on the air-gap magnetic field waveform of the motor, as shown in Figure 4.
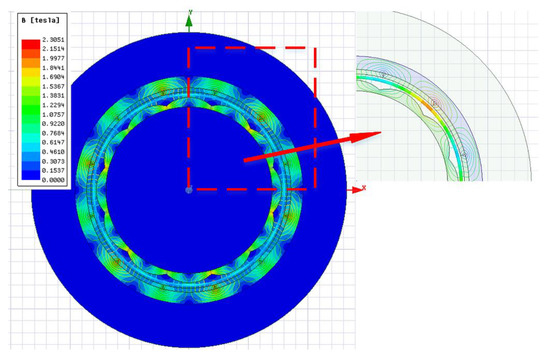
Figure 4.
Magnetic map and magnetic line distribution diagram of the motor under FEA.
The influence of inner rotor eccentricity on the air-gap flux density waveform is analyzed by finite element software. The magnetic field waveform at the midpoint of the air gap under different eccentricities is obtained by taking the eccentricity values () of 10 mm, 20 mm, 30 mm, 40 mm and 50 mm, respectively (the maximum eccentricity value of the inner rotor is 56 mm, but considering the actual machinability and strength, the maximum actual eccentricity value is 50 mm), as shown in Figure 5. The air-gap magnetic field waveforms with different eccentricities are decomposed by Fourier transform. According to the calculation formula of total harmonic distortion (THD), the relationship between THD and eccentricity is shown in Figure 6.
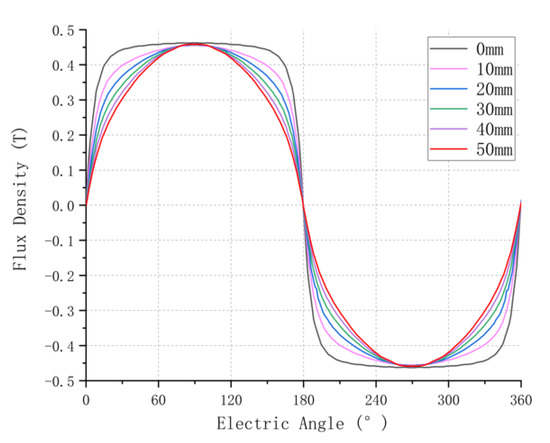
Figure 5.
Air-gap magnetic field waveform with different eccentricity values.
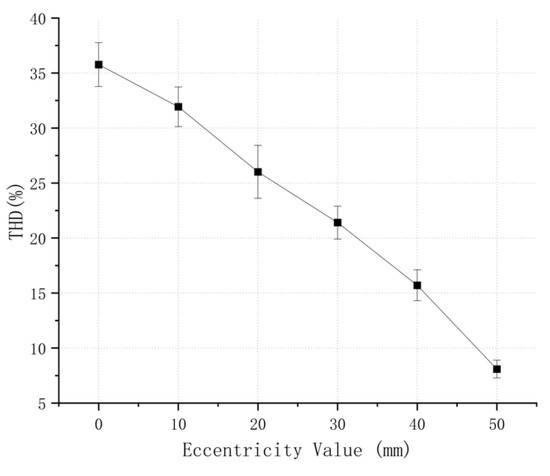
Figure 6.
The THD with the air-gap magnetic field.
From a comprehensive analysis of Figure 5 and Figure 6, it can be seen that the THD gradually decreases with the increase of the eccentric value of the outer diameter of the inner rotor of the motor, indicating that the eccentric structure of the inner rotor can effectively reduce the total harmonic distortion, and the total harmonic distortion decreases with the increase of the eccentric value of the outer diameter of the inner rotor. Therefore, the eccentric value of 50 mm is selected as the optimal solution.
With the increase of eccentricity, the air-gap magnetic field waveform gradually approaches the sine wave, which is due to the increase of magnetic resistance due to the thickening of the air gap caused by the local thinning of the rotor, thus reducing the air-gap magnetic field between the thinning area of the inner rotor and the two sides of each PM. At the same time, due to the special design of the “petal” shape of the inner rotor, the air-gap magnetic field between the inner rotor and the center of each PM remains unchanged and finally brings the air-gap magnetic field waveform closer to the sine wave.
Figure 7 and Figure 8 show the air-gap magnetic field waveform and Fourier spectrum before and after optimization under the condition of an eccentricity value of 50 mm.
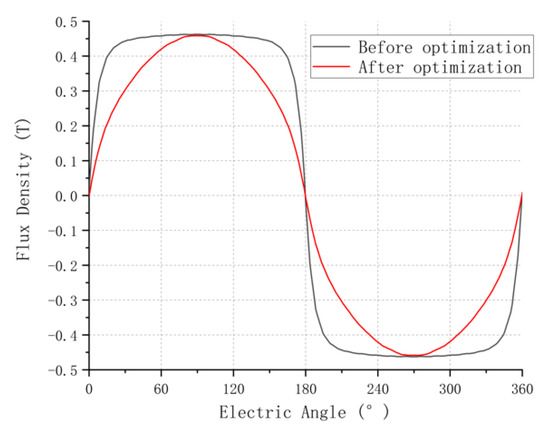
Figure 7.
Comparison of air-gap magnetic field waveform at 50 mm eccentricity.
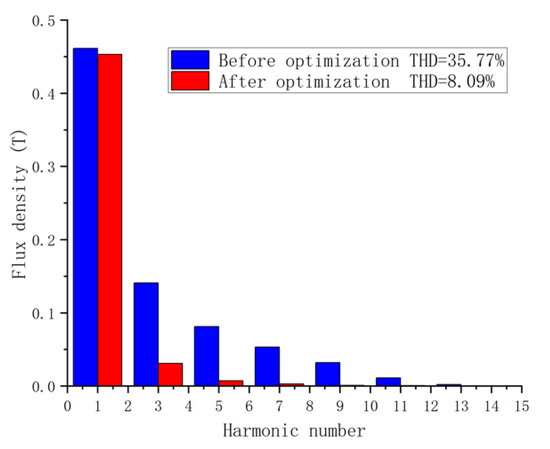
Figure 8.
Comparison of harmonic components at 50 mm eccentricity.
To summarize, when the eccentricity value of the inner rotor is 50 mm, the air-gap magnetic field is closer to a sinusoidal waveform, and the THD is reduced from 35.77% to 8.09%, a decrease of 77.4%. This shows that the eccentric design of the inner rotor of the motor can effectively reduce the THD and make the air-gap magnetic field waveform be closer to a sine wave, thereby improving the performance of the motor. Although the amplitude of the fundamental wave is slightly reduced (1.8%), which has a slight impact on the torque, the sine is significantly improved (77.4%), which is significant for the application of a magnetically suspended control moment gyro. At the same time, compared with the eccentric design based on PMs, it is more convenient for PMs’ magnetization and fabrication.
4. Experimental Validation
An inner rotor prototype under the optimal eccentric value (50 mm) in the finite element simulation is made, along with a prototype before the optimal design. The prototype consists of inner/outer rotors and permanent magnets; the fixtures fix the inner and outer rotor cores and keep the distance between them fixed during the test, and the permanent magnets are attached to the inner side of the outer rotor core. The inner rotor is made of industrial pure iron DT4 commonly used in motors, which has an excellent machining performance. First, the cylindrical material is installed in the CNC (Computerized Numerical Control), then the inner diameter of the inner rotor ring is processed by milling, and finally the outer diameter of the eccentric inner rotor is processed by milling. The parameters of the prototype are shown in Table 1, and the prototype is shown in Figure 9.

Figure 9.
Prototype of inner rotor eccentricity.
The experimental platform, shown in Figure 10, is mainly composed of a rotating platform, a magnetometer, a robotic arm, a waveform display and a control measurement device. During the test, install the experimental sample on the rotating platform, place the magnetometer in the middle of the air gap, start the test and record the data. The detailed test steps are as follows:

Figure 10.
Air-gap magnetic field testing system.
Step 1: the prototype is fixed by a three-jaw chuck, the manipulator clamps the magnetometer and adjusts the probe of the magnetometer to the middle of the air gap, and the rotating motor drives the chuck into rotating.
Step 2: the magnetometer uses the Hall effect to measure the size and direction of the magnetic field, with a measurement accuracy of 1 mT, and 36,000 points are sampled each time the prototype rotates.
Step 3: the measured data is output as a two-dimensional array of angle points and magnetic field intensity values.
The prototype with an inner rotor eccentricity of 50 mm is tested experimentally, and the abnormal periodic data caused by the uneven magnetization of the permanent magnet synchronous motor is eliminated. The comparison of the experimental results, simulation results and analytical results under an eccentricity of 50 mm is shown in Figure 11 and Figure 12.

Figure 11.
Comparison of the waveforms of the analytical result, FE result and experimental result.
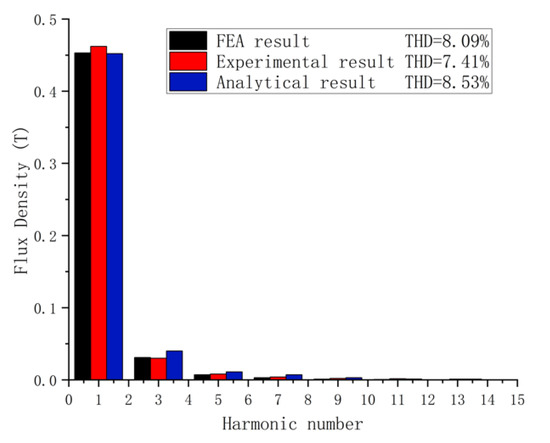
Figure 12.
Comparison of the harmonic components of the analytical result, FE result and experimental result.
According to the results of the air-gap flux density waveform and the harmonic component of the magnetic field waveform, the experimental results, simulation results and analysis results have a high consistency. When the eccentricity value is 50 mm, according to Formula (1), THD is 7.41%, which is −0.68% different from the simulation result. The THD difference is very small, which verifies the correctness of the finite element simulation results.
To summarize, the experimental results show that before the optimal design of the inner rotor, the THD is 34.11%. When the eccentricity of the inner rotor is 50 mm, the THD decreases from 34.11% to 7.41%, which proves that the hollow-cup motor model based on the eccentricity of the inner rotor can effectively improve the shape of the air-gap magnetic field waveform and make it present the sinusoidal waveform more closely. At the same time, compared with the design of the PMs’ eccentric device, it is more convenient for PMs’ magnetization and manufacturing, and has a certain engineering application value.
5. Conclusions
In this paper, the equivalent surface current method is used to establish the mathematical model of the air-gap magnetic field of a hollow-cup permanent magnet motor, and the analytical formula of the air-gap magnetic field after the inner rotor is eccentric is obtained. Motor models with different inner rotor eccentricity values are established by finite element software, and the air-gap magnetic field waveforms are analyzed. Then, based on the variation and trend of the waveform and total harmonic distortion, the optimal eccentricity value for the motor described in this paper is determined. Finally, an experimental prototype is made for verification, and the experimental results are basically consistent with the simulation results. For the six-pair poles’ hollow-cup motor with an inner-rotor outer radius of 78 mm and inner radius of 70 mm, when the inner-rotor outer radius eccentricity value is 50 mm, the FEM results show that after the eccentric design of the inner rotor, the THD value decreases by 77.4%. Through prototype testing, the THD value decreases by 78.27% after optimization. In summary, the eccentric design of the inner rotor of the hollow-cup motor proposed in this paper can effectively improve the sinusoidal characteristics of the air-gap magnetic field waveform and reduce the THD, thus improving the stability of the motor.
Author Contributions
Conceptualization, J.S. and J.R.; methodology, J.S.; software, J.R. and H.W.; validation, J.S., J.R. and Y.L.; formal analysis, J.R.; investigation, Y.L.; resources, J.S.; data curation, J.R. and H.W.; writing—original draft preparation, J.R.; writing—review and editing, Y.L.; visualization, J.S.; supervision, J.S.; project administration, J.S. and Y.L.; funding acquisition, J.S. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China, Grant/Award Numbers: 52075017.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gaude, A.; Lappas, V. Design and Structural Analysis of a Control Moment Gyroscope (CMG) Actuator for CubeSats. Aerospace 2020, 7, 55. [Google Scholar] [CrossRef]
- Han, B.C.; Zheng, S.; Li, H. Weight-Reduction Design Based on Integrated Radial-Axial Magnetic Bearing of A Large Scale MSCMG for Space Station Application. IEEE Trans. Ind. Electron. 2016, 64, 2205–2214. [Google Scholar] [CrossRef]
- Papakonstantinou, C.; Daramouskas, I.; Lappas, V.A. Machine Learning Approach for Global Steering Control Moment Gyroscope Clusters. Aerospace 2022, 9, 164. [Google Scholar] [CrossRef]
- Praveen, R.P.; Ravichandran, M.H.; Sadasivan Achari, V.T. A novel slotless halbach-array permanent-magnet brushless DC motor for spacecraft applications. IEEE Trans. Ind. Electron. 2012, 59, 3553–3560. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S. Two-order Active Disturbance Rejection Control Algorithm for Permanent Magnetic Synchronous Motor. In Proceedings of the Control Conference, Wuhan, China, 26–31 July 2007. [Google Scholar]
- Li, H.; Cui, L.; Ma, Z. Multi-Objective Optimization of the Halbach Array Permanent Magnet Spherical Motor Based on Support Vector Machine. Energies 2020, 13, 5704. [Google Scholar] [CrossRef]
- Yu, Y.; Cong, L.; Tian, X. Simultaneous suppression of torque ripple and flexible load vibration for PMSM under stator current vector orientation. IET Electr. Power Appl. 2019, 13, 359–369. [Google Scholar] [CrossRef]
- Hyok, N.; Kyung, H. A Study on Iron Loss Analysis Method Considering the Harmonics of the Flux Density Waveform Using Iron Loss Curves Tested on Epstein Samples. IEEE Trans. Magn. 2003, 39, 1472. [Google Scholar] [CrossRef]
- Kallaste, A.; Belahcen, A.; Kilk, A.; Vaimann, T. Analysis of the eccentricity in a low-speed slotless permanent-magnet wind generator. In Proceedings of the Electric Power Quality and Supply Reliability Conference (PQ), Tartu, Estonia, 11–13 June 2012. [Google Scholar]
- Zhang, X.; Zhang, C.; Yu, J. Analytical Model of Magnetic Field of a Permanent Magnet Synchronous Motor with a Trapezoidal Halbach Permanent Magnet Array. IEEE Trans. Magn. 2019, 55, 8105205. [Google Scholar] [CrossRef]
- Li, Y.; Xing, J.; Wang, T. Programmable Design of Magnet Shape for Permanent-Magnet Synchronous Motors with Sinusoidal Back EMF Waveforms. IEEE Trans. Magn. 2008, 44, 2163–2167. [Google Scholar]
- Wang, F.; Liao, Y.; Chen, J. Analytical calculation of air-gap magnetic field in permanent magnet linear motors. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications, Siem Reap, Cambodia, 18–20 June 2017. [Google Scholar]
- Zhou, Y.; Li, H.; Meng, G. Analytical Calculation of Magnetic Field and Cogging Torque in Surface-Mounted Permanent-Magnet Machines Accounting for Any Eccentric Rotor Shape. IEEE Trans. Ind. Electron. 2015, 62, 3438–3447. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Ma, H. Optimization and Analysis of Permanent-magnet Synchronous Machine with Eccentric Magnetic Pole Shape. In Proceedings of the 18th International Conference on Electrical Machines and Systems, Pattaya, Thailand, 25–28 October 2015. [Google Scholar]
- Jing, L.; Luo, Z.; Qu, R.; Kong, W.; Gao, Y.; Huang, H.; Shah, M.R. Investigation of a Surface PM Machine With Segmented-Eccentric Magnet Poles. IEEE Trans. Appl. Supercond. 2018, 28, 5204305. [Google Scholar] [CrossRef]
- Hu, P.; Wang, D. Analytical Average Torque Optimization Method of Parallel Magnetized Surface-Mounted Permanent-Magnet Machine with Third-Order Harmonic Shaping Method. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1377–1383. [Google Scholar] [CrossRef]
- Waheed, A.; Ro, J.S. Analytical Modeling for Optimal Rotor Shape to Design Highly Efficient Line-Start Permanent Magnet Synchronous Motor. IEEE Access 2020, 8, 145672–145686. [Google Scholar] [CrossRef]
- Kim, H.; You, Y.M.; Kwon, B. Rotor Shape Optimization of Interior Permanent Magnet BLDC Motor According to Magnetization Direction. IEEE Trans. Magn. 2013, 49, 2193–2196. [Google Scholar] [CrossRef]
- Yu, Z.; Li, H.; Ren, N.; Xue, Z. Analytical Calculation and Optimization of Magnetic Field in Spoke-Type Permanent-Magnet Machines Accounting for Eccentric Pole-Arc Shape. IEEE Trans. Magn. 2017, 53, 8107807. [Google Scholar]
- Hajdinjak, M.; Miljavec, D. Analytical Calculation of the Magnetic Field Distribution in Slotless Brushless Machines With U-Shaped Interior Permanent Magnets. IEEE Trans. Ind. Electron. 2020, 67, 6721–6731. [Google Scholar] [CrossRef]
- Kang, G.H.; Son, Y.D.; Kim, G.T. A Novel Cogging Torque Reduction Method for Interior-Type Permanent-Magnet Motor. IEEE Trans. Ind. Appl. 2009, 45, 161–167. [Google Scholar] [CrossRef]
- Tsai, W.B.; Chang, T.Y. Analysis of Flux Leakage in a Brushless Permanent-magnet Motor with Embedded Magnets. IEEE Trans. Magn. 1999, 35, 543–547. [Google Scholar] [CrossRef]
- Wu, L.J.; Li, Z.K.; Wang, D. On-Load Field Prediction of Surface-Mounted PM Machines Considering Nonlinearity Based on Hybrid Field Model. IEEE Trans. Magn. 2019, 55, 8100911. [Google Scholar] [CrossRef]
- Jang, S.M.; Ko, K.J.; Cho, H.W. Electromechanical Parameters Calculation of Permanent Magnet Synchronous Motor Using the Transfer Relations Theorem. IEEE Trans. Magn. 2007, 43, 2495–2497. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).