Abstract
Landing on a moving platform is an essential requirement to achieve high-performance autonomous flight with various vehicles, including quadrotors. We propose an efficient and reliable autonomous landing system, based on model predictive control, which can accurately land in the presence of external disturbances. To detect and track the landing marker, a fast two-stage algorithm is introduced in the gimbaled camera, while a model predictive controller with variable sampling time is used to predict and calculate the entire landing trajectory based on the estimated platform information. As the quadrotor approaches the target platform, the sampling time is gradually shortened to feed a re-planning process that perfects the landing trajectory continuously and rapidly, improving the overall accuracy and computing efficiency. At the same time, a cascade incremental nonlinear dynamic inversion control method is adopted to track the planned trajectory and improve robustness against external disturbances. We carried out both simulations and outdoor flight experiments to demonstrate the effectiveness of the proposed landing system. The results show that the quadrotor can land rapidly and accurately even under external disturbance and that the terminal position, speed and attitude satisfy the requirements of a smooth landing mission.
1. Introduction
Mainly due to its simple mechanical structure, low cost and relatively high maneuverability, quadrotors are currently of widespread use in multiple commercial and military applications. These include surveillance, transportation, logistics and power inspection, among others [1,2,3]. However, their limited payload capacity and endurance have become an important obstacle to their further development. To tackle these limitations, vehicles and ships are often used as mobile platforms for quadrotors to take off and land, broadening the scope of possible missions and application scenarios [4,5]. For example, when the quadrotor power is low or suffers a malfunction that prevents it from reaching a predefined landing area, it is advantageous to be able to land on a mobile platform for recharging or maintenance. Therefore, it is highly beneficial if the quadrotor has the ability to land on a moving platform autonomously.
A large amount of research has been conducted on autonomous landing technology for quadrotors. However, most applications require the platform to be parked at a pre-selected location, thus allowing the quadrotor can take off and land from such stationary platform [6]. This mode of operation needs considerable logistics, making autonomous landing on a moving platform a better choice for many applications. Aiming at this technology, the works [7,8,9,10] achieve the estimation of the relative position and attitude between quadrotor and platform, and navigation using vision, while the control is carried out using a traditional proportional-integral-derivative (PID) algorithm. However, the quadrotor may be disturbed by ground effects and winds during the landing process. In addition, the strong coupling and nonlinear dynamics of high-speed flight imposes strict requirements on the control system.
To improve the robustness of the quadrotor control system, researchers have applied many nonlinear methods. The authors in [11] introduce a guidance law to generate the desired speed commands, based on the relative distance obtained from global positioning system (GPS) and vision sensors. They also use the L1 adaptive algorithm in the speed controller, which can respond fast and reduce the influence of external disturbances and uncertainty. In [12], an adaptive sliding mode controller (ASMC) is proposed, to track the speed commands directly during the landing process. This is done using a vision system, so as to achieve a real-time compensation of the influence of external disturbances, such as ground effects. The autonomous landing operation in [13] proceeds into three basic phases: the search phase, the homing phase, and the landing phase. Its core task is tracking the virtual target point in the homing phase, by combining backstepping and dynamic surface control. When the relative distance is close enough, the landing phase is initiated, leading to an accurate landing. However, it can be seen from simulation results, that a quadrotor following this strategy will track the virtual target point with a circular motion in the beginning. The latter produces unnecessary consumption of both energy and time. The work in [14] regards the unknown motion of the ship and winds as external disturbances to the process of controlling the quadrotor landing a shipboard. The authors use an uncertainty and disturbance estimator to guess the disturbances and compensate them to the control commands. A new control method with a proportional navigation (PN) guidance law for the approach phase and a PD controller for the terminal landing phase is presented in [15], but this landing system needs to consider the impact of external disturbances on the flight controller, which will affect whether it is able to successfully land on a high-speed ground vehicle. On the other hand, [16] combines model predictive control (MPC) and ASMC to realize the landing of a quadrotor on a moving platform with a speed of 1 m/s, effectively controlling the influence of external interferences.
Moreover, to achieve high performance trajectory tracking and avoid most of the limitations in the tracking problem, a new solution based on iterative learning control (ILC) provides many advantages over conventional feedback controllers in that they develop an element of intelligence by memorizing from previous practice [17]. In [18], the existing ILC approaches in UAVs applications and possible future trends are discussed and reviewed. Reference [19] develops optimal ILC algorithms for a UAV model, which has not only contributed to good trajectory tracking but also to fast convergence speed and the ability to cope with exogenous disturbances. On the other hand, ILC has also been applied to some complicated systems, such as the distributed ILC of multiple flexible manipulators in the presence of uncertain disturbances and actuator dead zones in [20].
In the above-mentioned solution, MPC is active in trajectory planning and tracking, since it considers various software and hardware constraints in the design and can achieve a finite-time online optimization [21,22,23]. The quadrotor should meet the constraints imposed by the control input and the terminal state while autonomously landing, rendering MPC an effective control strategy. The landing system designed by Imperial College London [24] estimates the quadrotor’s position, attitude and relative speed, as well as the trajectory of the moving platform using visual-inertial odometry. Using the information of the estimated state, the position loop designs a linear MPC to generate the landing trajectory and produce attitude control commands based on the identified linear model. The attitude loop directly adopts the Pixhawk Autopilot including a PID controller for tracking. Research groups in other institutions have also studied the autonomous landing of a multirotor using the MPC method, including the University of Bonn [25], ETH Zurich [26] and the Czech Technical University in Prague [27], among others. In [28], a nonlinear MPC is proposed to guide the quadrotor to land on a maneuvering inclined platform, which includes an objective function that can ensure the position, speed, and attitude deviations in the terminal are minimized. Their work also optimizes the desired trajectory and prediction horizon to ensure a fast, autonomous landing. However, this method requires a large number of calculations, including the MPC commands at the ground station, and their continuous transmission of the optimized trajectory to the quadrotor via Wi-Fi. That can be difficult to apply in practical actual landing system. Therefore, it is necessary to consider the limitations of onboard computing efficiency when designing a landing system based on MPC.
Quadrotor flight control is usually affected by various disturbances, especially in the landing process. Incremental nonlinear dynamic inversion (INDI) uses the angular acceleration feedback to replace a part of model information with sensor measurements, to reduce the influence of such disturbances and the overall uncertainty of the system [29]. This control method was proposed in [30] and has been widely employed in the design of quadrotors control systems [31,32,33]. Among them, [31,33] design an INDI controller to track the attitude and position of the quadrotor, to effectively suppress the impact of disturbances and uncertainty. Compared to the accurate model obtained by system identification [34], INDI reduces the dependence on the dynamics model. It complies with the calculation limitations of the onboard computer and is more convenient for practical applications. However, the above-mentioned literature does not analyze and compensate for the remaining uncertainty of the closed-loop system. The incremental sliding mode control (INDI-SMC) has been recently proposed to tackle this problem by combining both INDI and SMC, to make up for the shortcomings and mutual advantage complement; see [35]. Moreover, the authors in [36] use INDI and a disturbance observer to ensure the stability of the quadrotor’s attitude control, while suppressing the chattering in SMC. In [37], INDI and a nonlinear terminal SMC are designed to improve the robustness and rapidity of the trajectory tracking system, although, the authors are conservative when choosing the gain in control mode switching.
Motivated by the observations above, this work proposes an efficient and reliable autonomous system for landing a quadrotor on a moving platform. We firstly use a fast, two-stage algorithm to detect and track the landing marker via a gimbaled camera. Then, we design an MPC controller with variable sampling time to plan the entire landing trajectory, based on the estimated platform information. As the quadrotor approaches the target platform, the sampling time is gradually shortened, and the re-planning prefects the landing trajectory continuously and rapidly, which improves the overall accuracy and calculation efficiency. We select an appropriate objective function for the different landing phases. This way, the quadrotor cannot only land accurately and smoothly, but also the mission time is shortened. At the same time, considering the influence of various disturbances in the landing process, a cascade incremental nonlinear dynamic inversion (INDI) control method [33] is adopted to track the planned trajectory and ultimately increase robustness. We carried out simulations and outdoor flight experiments to demonstrate the effectiveness and disturbance rejection of our proposed landing system. The main contributions of this paper may be summarized as follows:
- (1)
- Upon combining MPC trajectory planning and INDI flight control, a novel vision-based landing system is developed, able to land rapidly and accurately on a maneuvering platform with a certain disturbance rejection capability.
- (2)
- Compared with the previous research on MPC-based trajectory tracking control for quadrotors [16,23,28], the proposed method with variable sampling time reduces the requirements of the onboard computer while ensuring the landing accuracy.
- (3)
- At variance with what is used in other landing systems, we employ distinct objective functions for the different modes correspondingly, to realize the real-time-optimized landing of the quadrotor. The system meets the requirements of terminal position, speed and attitude.
The rest of this paper is organized as follows: The flight dynamics of the quadrotor, modeled in Section 2 and Section 3, describes the landing procedure and system components. Section 4 gives the technical design of the proposed autonomous system for landing a quadrotor on a moving platform. In Section 5, we present the results of both numerical simulations and outdoor flight experiments and then list the main conclusions in Section 6.
2. Dynamic Model of a Quadrotor
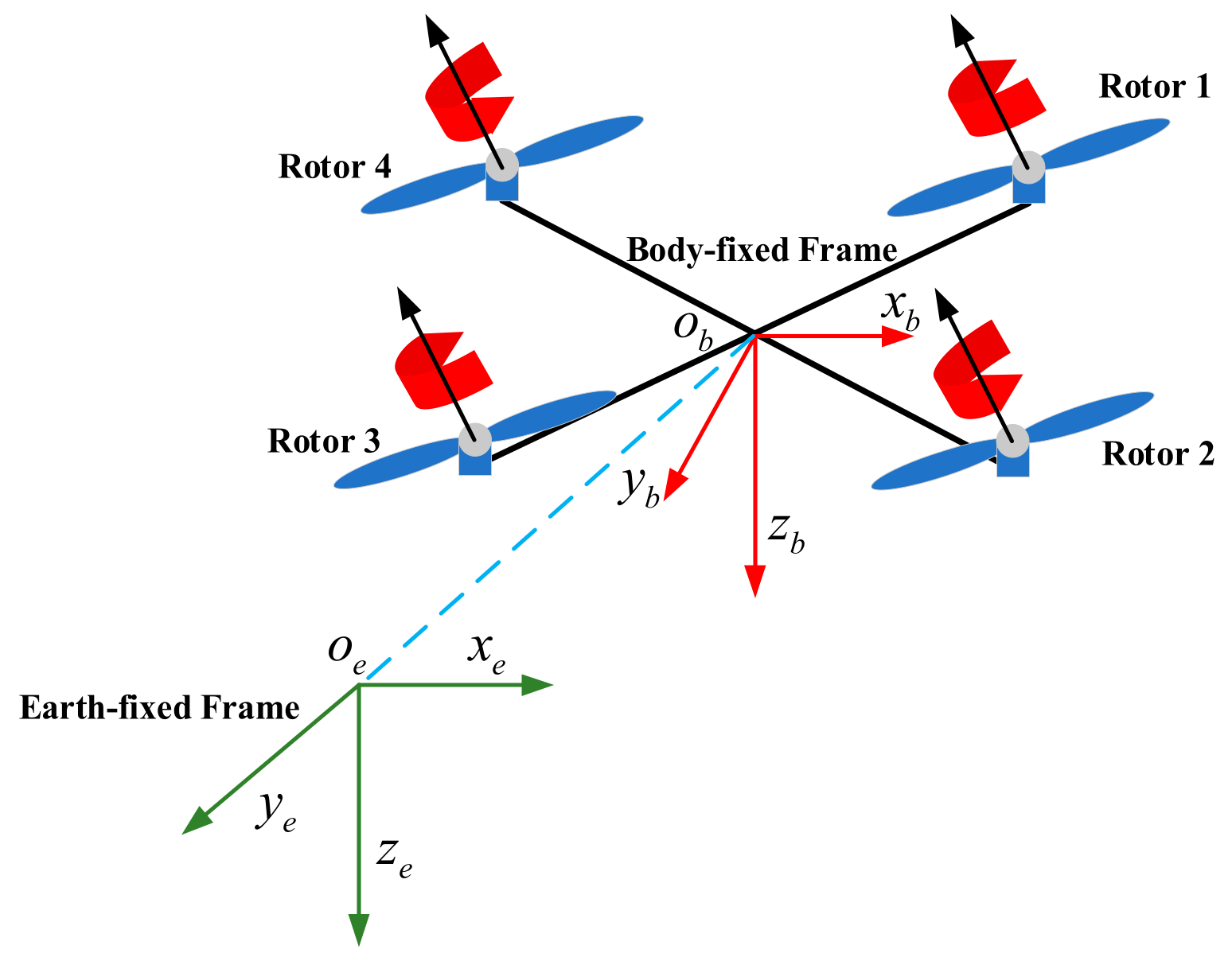
A quadrotor accomplishes translation and rotation by changing the speed of four rotors. To facilitate the description of its dynamic model, two main reference frames need to be introduced: the earth-fixed frame (E) with coordinates and the body-fixed frame (B) with coordinates , as shown in Figure 1.
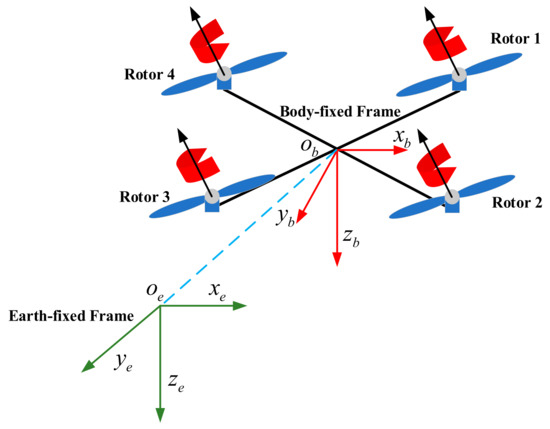
Figure 1.
Basic configuration and reference frames used to model the quadrotor dynamics.
After expressing the quadrotor’s position, velocity and Euler angles in frame E, as well as the angular rates in frame B as , , and , respectively, the kinematic functions of position and attitude may be written as:
where is the conversion relationship between and , namely,
In this work, we use the Newton–Euler method to establish the dynamic model of the quadrotor as follows:
where is the mass, is the inertia matrix, and is an anti-symmetric matrix, that can be expressed as
The resultant forces , integrated on the quadrotor in frame E, include gravity , thrust generated by the four rotors and disturbance forces . Meantime, the total moments include those produced by the four rotors , the gyroscopes and disturbances .
Among them, the gyroscopic moments are related to the rotation speed of the rotors, which is difficult to accurately measure in practice. Therefore, we regard the gyroscopic moments as a kind of disturbance.
3. Autonomous Landing System Architecture
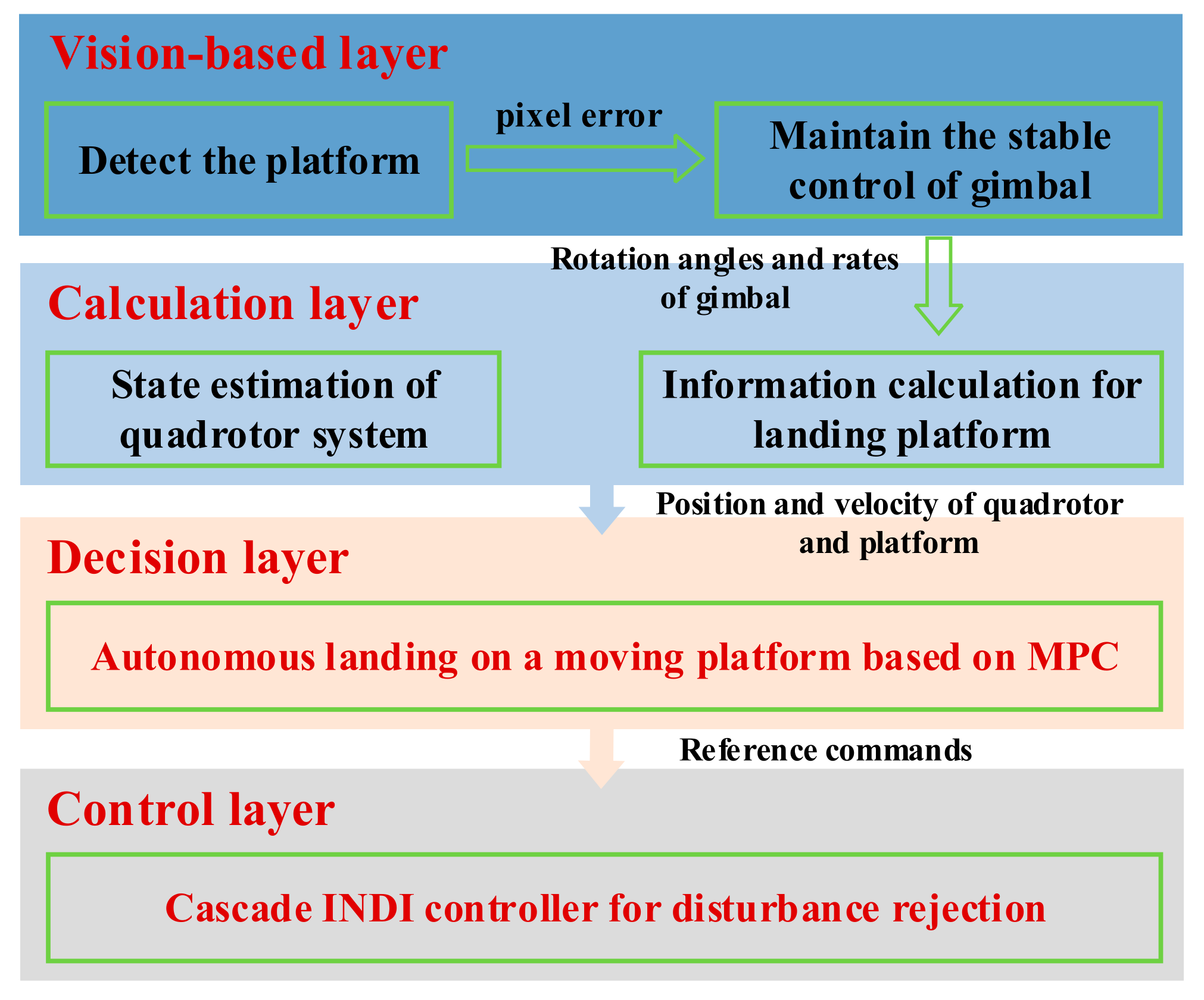
As shown in Figure 2, the autonomous landing system designed in this paper is mainly composed of four layers, namely, vision-based, calculation, decision and control layers. Their respective functioning is described below.
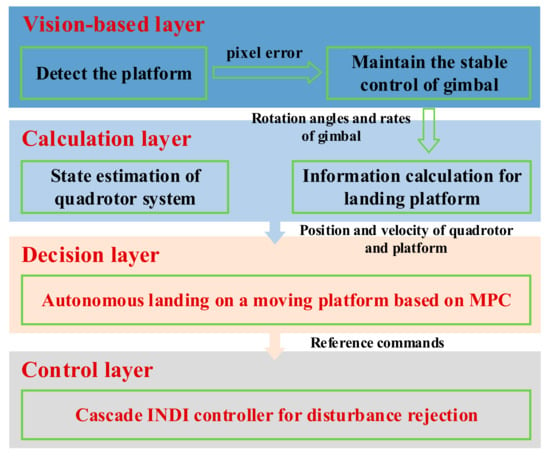
Figure 2.
Four functional layers and the information transmission of the designed landing system.
The vision-based layer includes a camera and a two-axis stabilized gimbal, which are used to detect and track the landing marker on the moving platform. The gimbal measures the angles and angular rates of its rotation via an angle encoder and a gyroscope and transmits this information to the calculation layer.
The calculation layer derives the status information of both quadrotor and landing platform. At different landing phases, this layer uses specific measurements to calculate and export its results to the decision layer.
Considering the flight status and control constraints of the quadrotor, the decision layer utilizes MPC to plan the landing trajectory, so that its position and speed are the same as those of the moving platform at the terminal. Then, the desired trajectory is passed to the control layer for implementation.
The control layer, based on an INDI controller, is responsible for tracking the desired flight trajectory and dealing with the influence of disturbances and uncertainty during this process.
4. Autonomous Landing System Design
4.1. State Machine for the Landing Mission
A well-performing state machine is a basic requirement for a quadrotor to land on a moving platform rapidly and accurately. The entire process of this mission can be completed by a machine with a single state, which involves the following four modes.
- (A)
- Beginning mode: When the quadrotor receives the landing instruction, it starts the programs of each module and drives the rotors to perform the autonomous landing mission. It does not switch to searching mode until all programs are started.
- (B)
- Searching mode: When the quadrotor is far away from the target platform, it will plan the landing trajectory to approach the platform based on GPS information. After the gimbaled camera detects the guide marker, it switches to the landing mode.
- (C)
- Landing mode: The quadrotor uses the platform state information, obtained from vision-based estimation, to predict the landing trajectory and control it to complete the landing. When the relative distance between quadrotor and target platform is less than predefined threshold, it executes the end program.
- (D)
- Ending mode: All rotors of the quadrotor stop, which means landing and recovery has been accomplished.
4.2. Detection and State Estimation of the Landing Platform
During the landing and recovery process, the updated frequency and accuracy of the information provided by the GPS are not sufficient. Therefore, we use a gimbaled camera to detect the landing marker and estimate the maneuvering information of the target platform. In order to improve robustness and versatility, this module applies a fast two-stage detection algorithm. When the quadrotor is far away from the moving platform, we identify the vehicle based on a theoretical minimum cost function that works well at a long-distance and with a large-flied-of-view. As the relative distance decreases, we combine the prior information to detect the guide marker simultaneously. The vision-based layer uses an improved, fast ellipse detection algorithm to detect the ellipse landmark or other elliptical objects. Furthermore, convolution neural networks (CNN) are utilized to verify and obtain the correct one. The detection results during the landing are shown in Figure 3. The target detection algorithm is not the focus of this paper, and you can refer to [38] for extra details.

Figure 3.
Vision-based detection of the moving target during the landing process.
One drawback of the vision sensor described above is its limited detection range. Our state estimation method for the landing platform is similar to [15]. If the quadrotor does not detect the guide marker, we use the position information provided by the differential GPS base on the vehicle.
4.3. MPC Design for Autonomous Landing of a Quadrotor
Since MPC can handle the constraints of the landing mission, it is widely used in the trajectory of unmanned aerial vehicles (UAVs) [39,40], rockets [41,42] and robots [43,44]. Among them, [44] designed an MPC to solve the problem of point-to-point trajectory planning, thereby controlling the manipulator to catch a thrown tennis ball. During the landing process, the quadrotor needs to reach the position of the moving platform from the current position, which can also be regarded as a type of point-to-point trajectory planning problem. Therefore, this section improves on the method introduced in [44] to achieve an accurate and stable landing.
The MPC framework requires defining a model of the system, an objective function, state and input constraints, and a prediction horizon. To accelerate the calculation, we only consider the quadrotor position control in the prediction model and simplify it to a three-order integrator. Although the influence of disturbances is ignored in the simplified model, an auxiliary attitude controller can be used to compensate for them. The vector represents the position, velocity and acceleration of the quadrotor. The control command is the Jerk of it. Therefore, the state space equation of the prediction model can be written as
where matrices and are
The symbol represents a block diagonal matrix, and
The model above can be discretized using a zero-order holder [45], as follows,
where denotes the sampling time and and are
To achieve an accurate and stable landing of the quadrotor, while reducing the mission time, the requirements of the different modes vary. Consequently, a suitable objective function needs to be defined correspondingly. In searching mode, due to the relatively long distance, the quadrotor must spend less time approaching and detecting the landing marker. Let the objective function in this mode be
where is the relative position, and is the estimation of the mission time. The matrices and are the weight coefficients of and . affects the flight speed, and is related to the time required for the entire landing process. The estimation of is derived with the same method used for the calculation of the time-to-go in missile [46], namely,
Among them, denotes the relative speed, and denotes the projection of on the line of sight (from quadrotor to target). Both and were obtained in Section 4.2. Although the curved flight trajectory causes errors in this estimation method, the fast and efficient re-planning based on MPC can compensate for them. As the quadrotor approaches the landing platform, is gradually more accurate.
After the gimbaled camera detects the landing platform, the quadrotor switches to landing mode. At this point, the generated trajectory needs to be as smooth as possible, to prevent the loss of the target marker due to excessive maneuvering. In addition, to avoid tumbling during the rendezvous, the quadrotor terminal Euler angles need to be as small as possible. To guarantee planning a smooth trajectory of the quadrotor, the minimum Jerk indicator is widely used [47,48]. Therefore, we write the objective function of this mode as follows:
where and are the horizontal acceleration of the quadrotor. , and are all constant weighting matrices. Among them, determines the accuracy of the landing position, and can be adjusted to make the generated trajectory smoother. Since we need to reduce the quadrotor Euler angles during the rendezvous, we should tune the weight of the horizontal acceleration, , in landing mode.
After the position and velocity of the landing platform are updated, the MPC re-plans the desired trajectory according to the objective functions in Equations (11) and (13). No new trajectory is calculated until the distance to the target is less than a given threshold. Each step of the planning requires solving the following optimization problem.
where denotes the height of the landing platform, and are the upper boundaries of the quadrotor Jerk and acceleration, respectively, and denotes the prediction horizon. Different from what is done in [28], we employ a fix . On the contrary, we use a variable sampling time , i.e., a variable ratio of and . When the target platform is far, and the accuracy requirements are relatively relaxed, we select a larger to greatly reduce the amount of calculation. As the quadrotor approaches the target, is gradually shortened to improve the accuracy and calculation efficiency of this process.
The constraints in Equation (14) are linear, so the CVXGEN toolbox [49] can be used to solve the optimization problem and reduce the computing load of an online calculation. At the beginning, the control period of the quadrotor controller is much shorter than the sampling time of the MPC. Thus, the linear interpolation shown in Equation (15) is applied to the planned trajectory to improve computing performance.
where and the interpolation interval is determined by the control period of the controller.
Note that the state and control constraints of the quadrotor in Equation (14) can be obtained using differential flatness theory [50]. When the yaw angle is zero, the horizontal accelerations are approximated as and . Their upper boundary can be obtained from the maximum Euler angles and . Moreover, the same method can be used to get the Jerk upper boundary in the horizontal plane.
Our proposed autonomous landing system based on MPC can be summarized as Algorithm 1, shown below.
| Algorithm 1. Autonomous landing algorithm of a quadrotor via MPC |
| Input: discrete state Equation (9) of landing dynamics, , , positions and velocities of the quadrotor and target platform, prediction horizon N in MPC. Output: planned trajectory for tracking. 1: Initialization: current position and velocity of the quadrotor, 2: Repeat 3: Estimate and update the position and velocity of the moving platform, 4. Calculate the mission time TA by (12), and obtain the sampling time h of MPC from the prediction horizon N, 5. Solve the optimization problem (14) and get the planned landing trajectory, 6: Use the designed controller to track the desired waypoints, 7. Update the current flight state x of the quadrotor, . |
4.4. Cascade INDI Controller Design
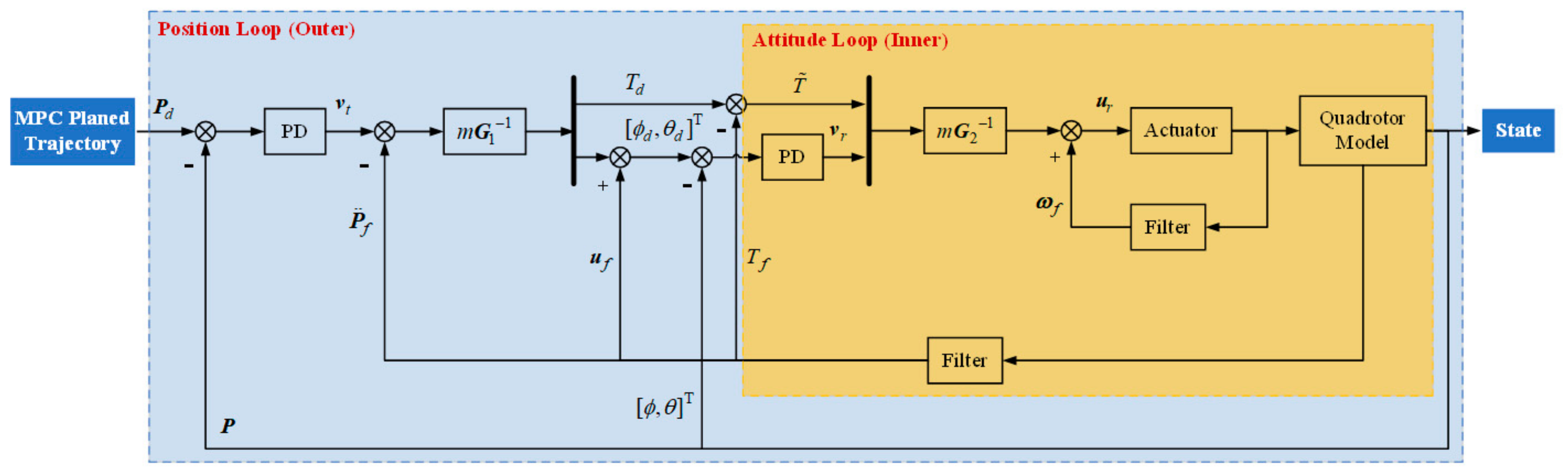
Considering the influence of external disturbances during the landing process, we designed a cascade incremental nonlinear dynamic inversion (INDI) controller; see [33]. The controller allows the quadrotor to track the trajectory planned by the MPC. The INDI method is based on measurements from sensors, which can reduce the dependence on the quadrotor dynamic model and enhance the robustness of the whole system [33]. In addition, it does not need a complex neural network or real-time identification to estimate the model. Thus, it can be easily implemented in a Pixhawk autopilot. We adopt the traditional cascade controller structure depicted in Figure 4.
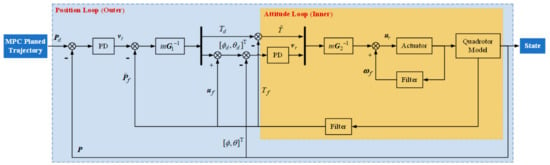
Figure 4.
Block diagram of our quadrotor cascade INDI controller in position and attitude loop.
Combined with Equation (5), the control law of the outer loop is designed as shown in Equation (16).
where denotes the total thrust generated by the rotors and is the reference instructions of the inner loop. Quantities are the filtered values of and the acceleration, respectively. The filter reduces noise in the measured values. Symbol represents the control matrix of the outer loop, which can be derived by the Taylor expansion of Equation (5); see [38]. Finally, is the virtual volume of the position deviation under the action of a proportional-differential (PD) controller, and it can be expressed as follows,
where is the desired position from the MPC planned trajectory, and and are the parameters of the PD controller.
If we regard the gyroscopic moments as a disturbance, the inner-loop controller can be designed as
where represents the rotation speed of the rotors, are the filtered values of , is the control matrix of the inner loop, is the virtual volume with a solution similar to Equation (17), and denotes the filtered angular accelerations that can be obtained by differentiating the gyroscope measurements. We can derive the change of the total thrust , using the outer loop controller.
5. Simulations and Experiments Description and Results
5.1. Simulations
According to the predefined mission requirements and structural parameters, we simulated a quadrotor with a mass of kg and an inertia matrix of kg·m2. The distances between the center of mass and each rotor along the axes are both 0.16 m. We verify the effectiveness of our proposed autonomous landing system using two sets of numerical simulations. The first one assumes the target platform moves along a straight trajectory, and the second one uses an eight-shaped curved trajectory. In MPC, the prediction horizon is . The acceleration constraints during the whole landing process are m/s2 and m/s2, and the Jerk constraints are m/s3 and m/s3, where . Meanwhile, we assume that the disturbance moments can be described as
5.1.1. Simulation A: The Target Platform Moves along a Straight Trajectory
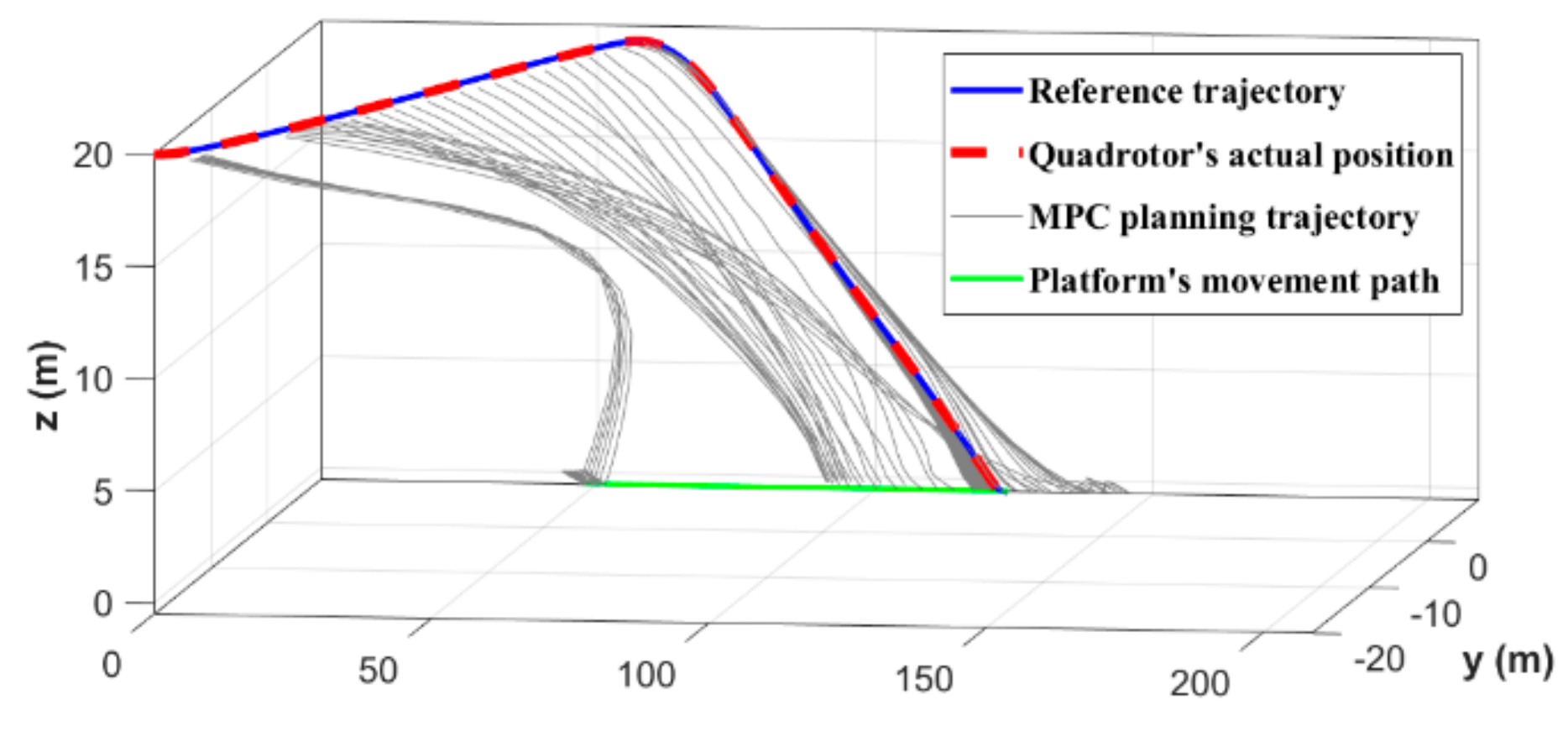
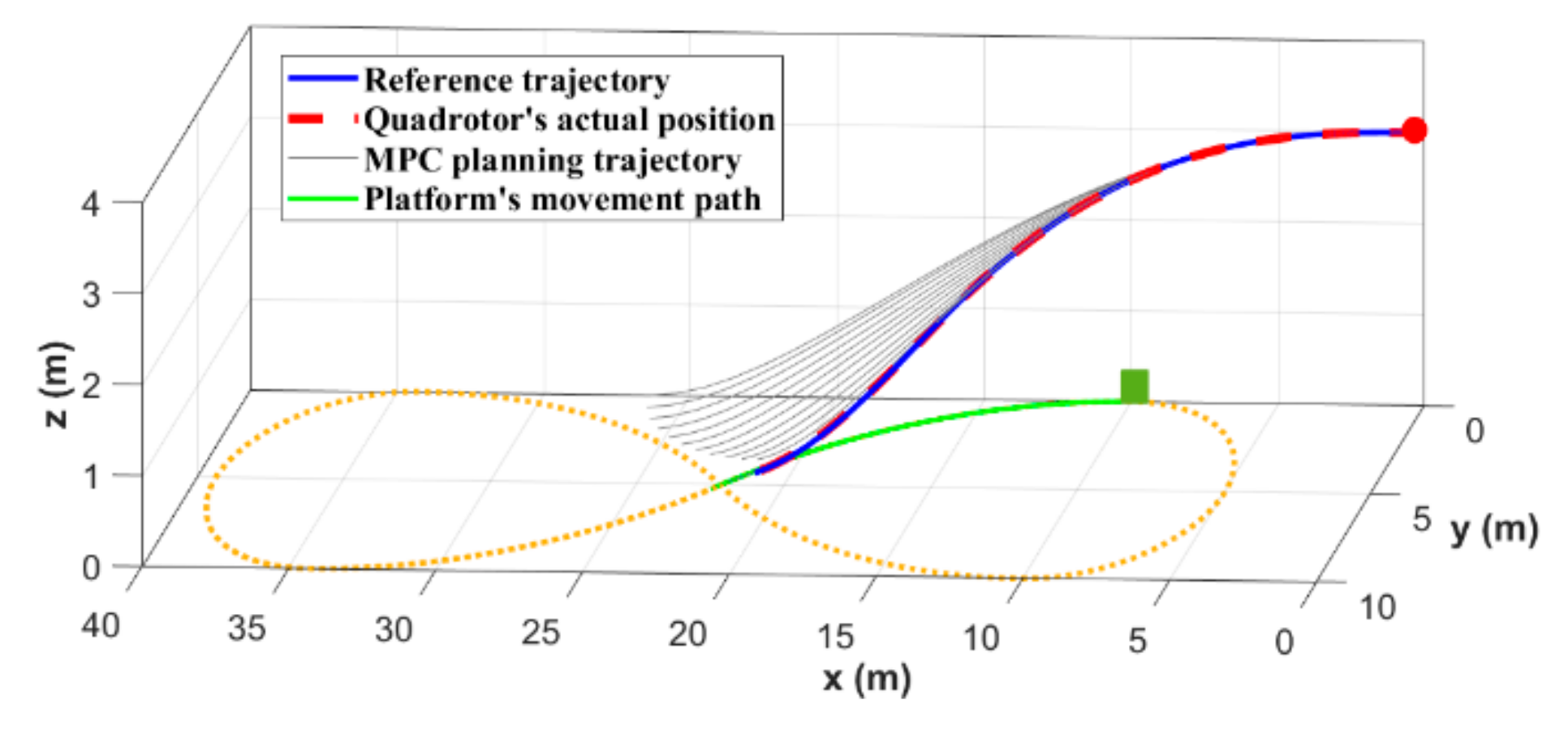
The initial position and velocity assigned to our quadrotor are and . It is assumed that the target platform moves along the axis with a speed of from its initial position . The three-dimensional (3D) landing trajectory of the quadrotor is shown in Figure 5, where the black curves belong to the trajectory cluster planned by MPC during the whole process. It can be seen that the landing accuracy gradually improves as the quadrotor approaches the target. Moreover, under the influence of external disturbances, the quadrotor can accurately track the reference trajectory and complete the mission.
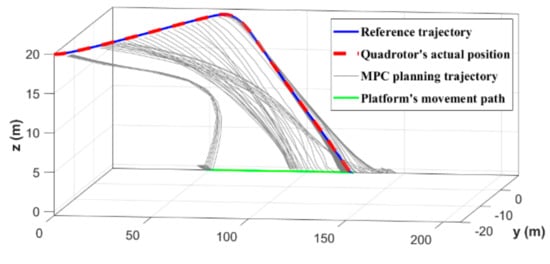
Figure 5.
3D landing trajectory of the quadrotor when the target platform moves along a straight trajectory.
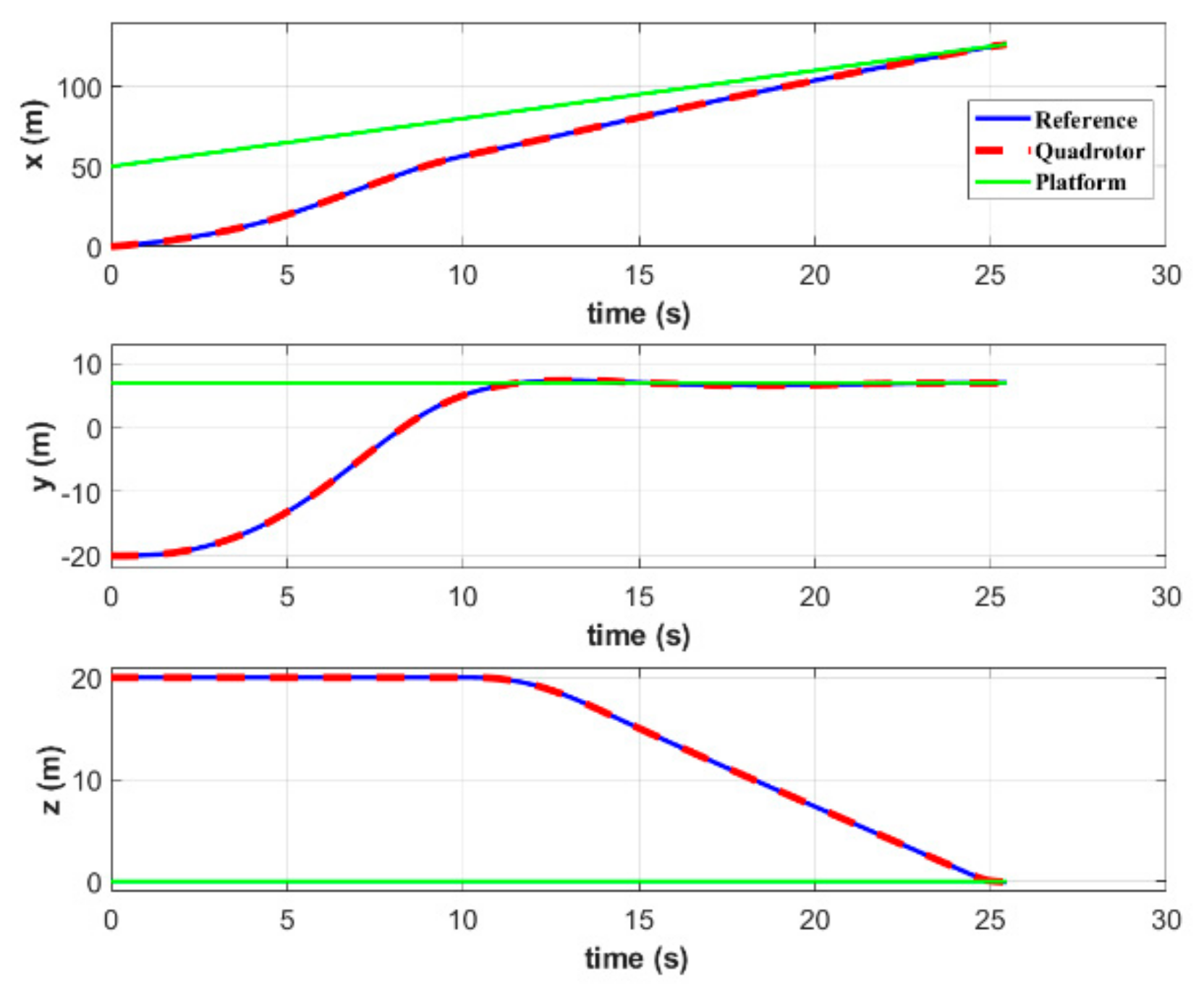
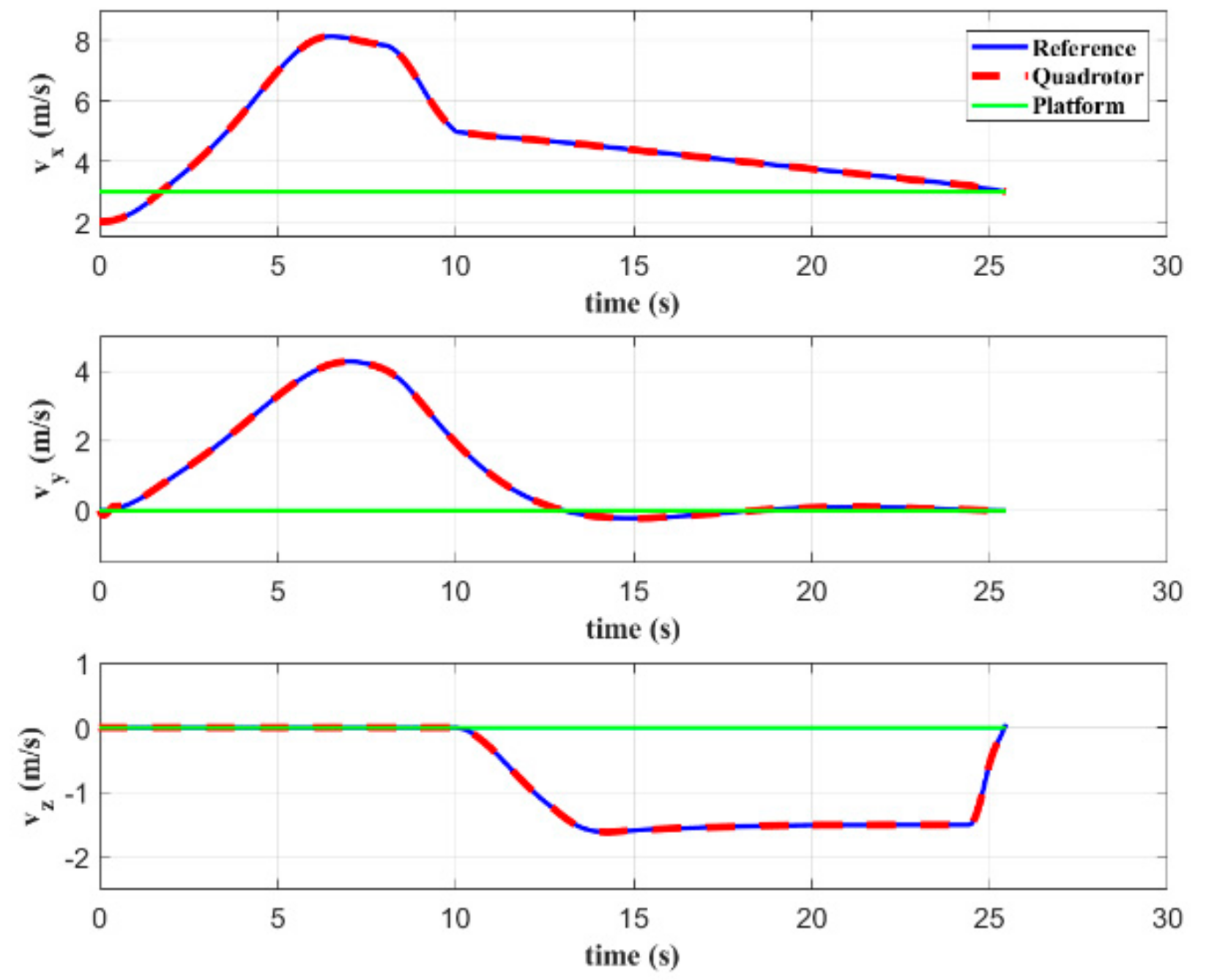
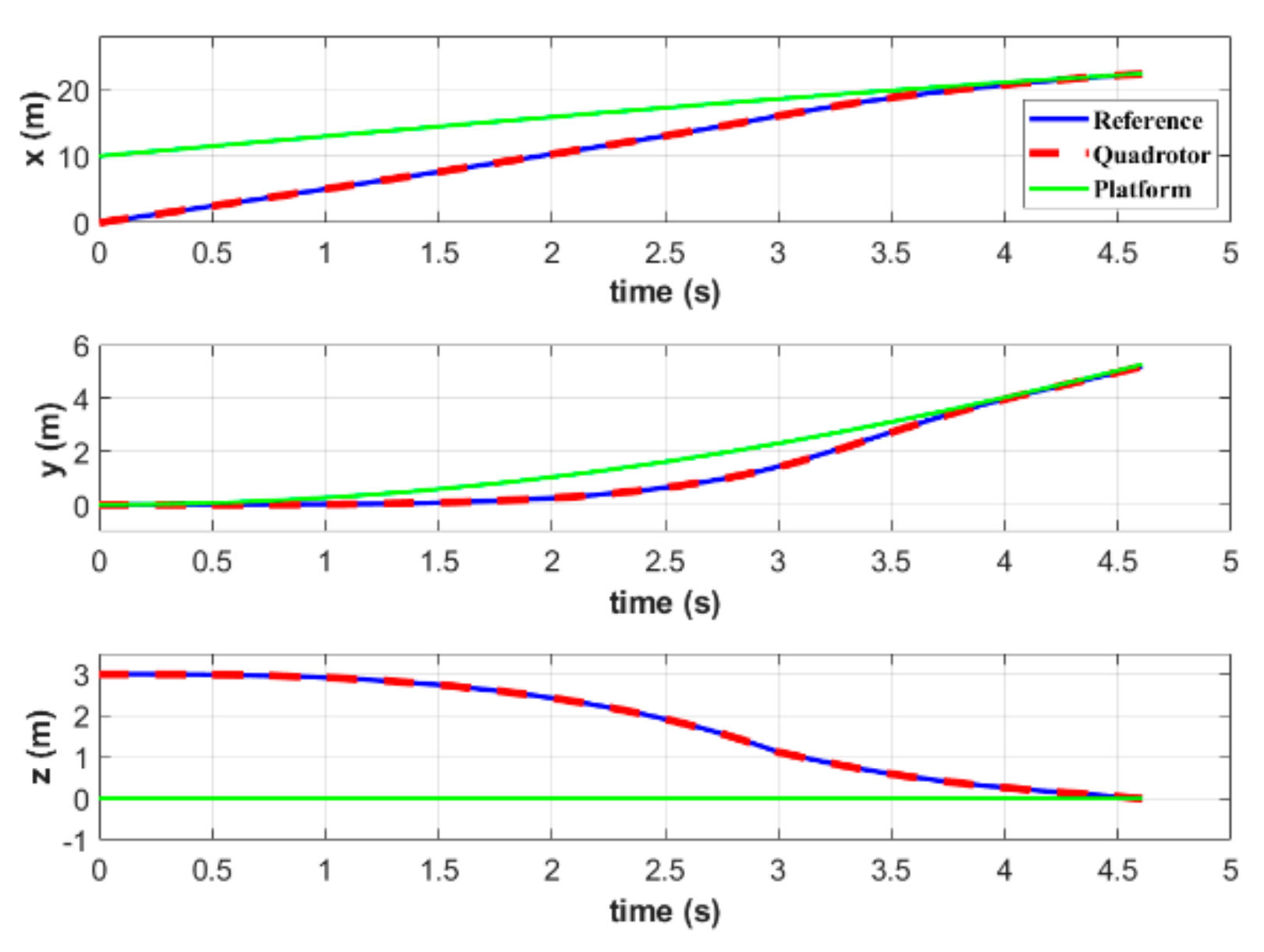
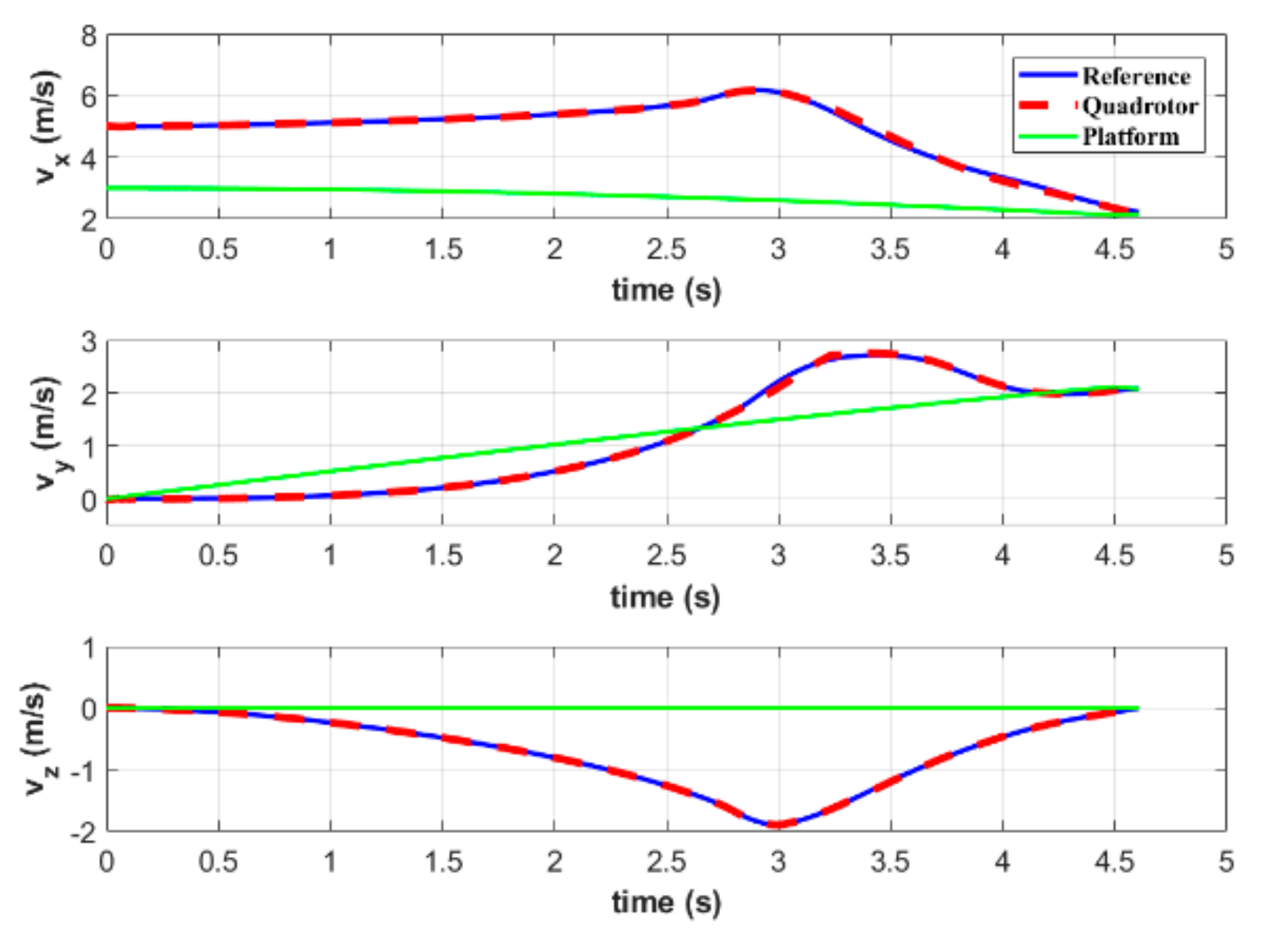
Figure 6 and Figure 7 show the position and velocity, respectively, of both quadrotor and platform. It takes s for the simulated vehicle to land on such a moving platform. During the rendezvous, both position and velocity of the quadrotor and platform are equal, which satisfies the terminal constraints set in MPC. Figure 6 shows that the quadrotor firstly keeps the position and velocity in the direction consistent with the target platform, and then approaches it from other two directions. This method does not require following the platform for too long, thereby reducing the total time required to complete the task.
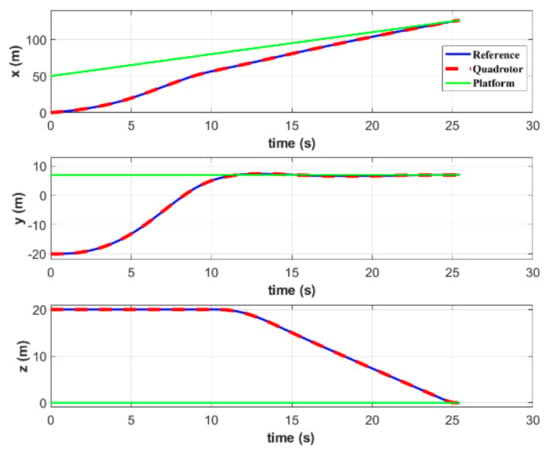
Figure 6.
Positions of the quadrotor and platform in simulation A.
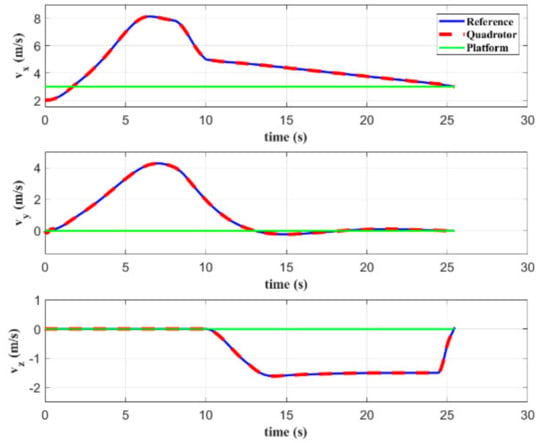
Figure 7.
Velocities of the quadrotor and platform in simulation A.
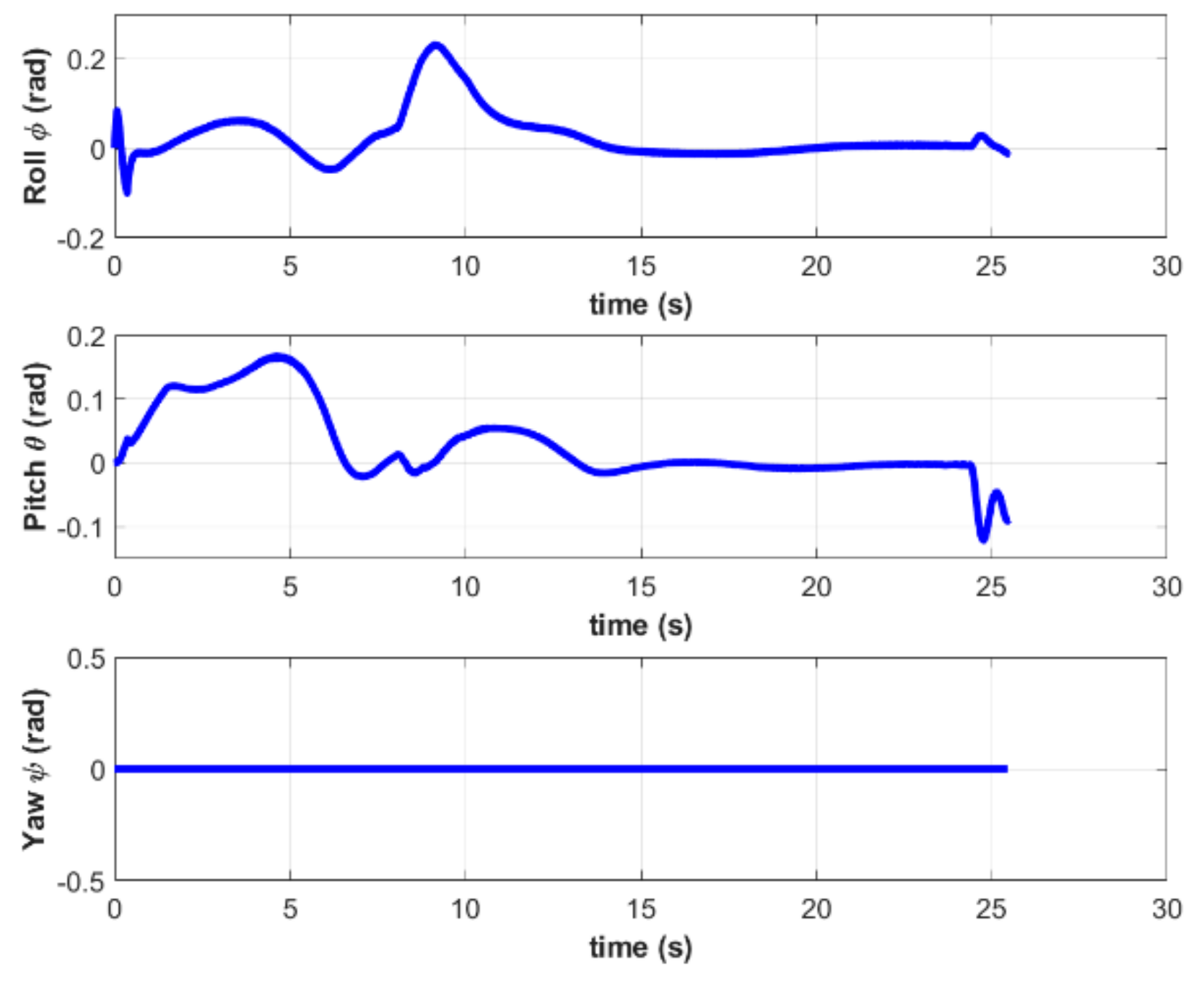
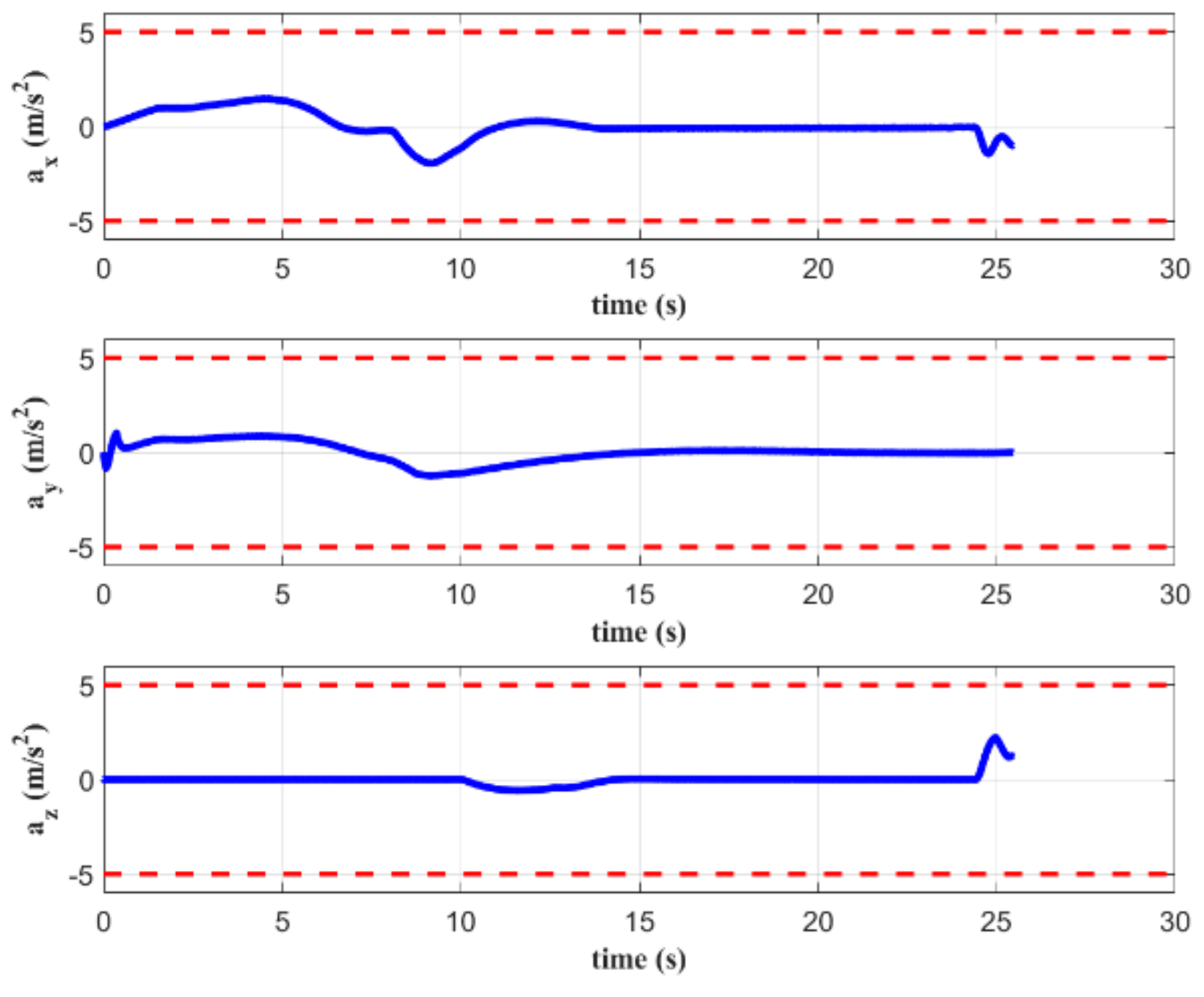
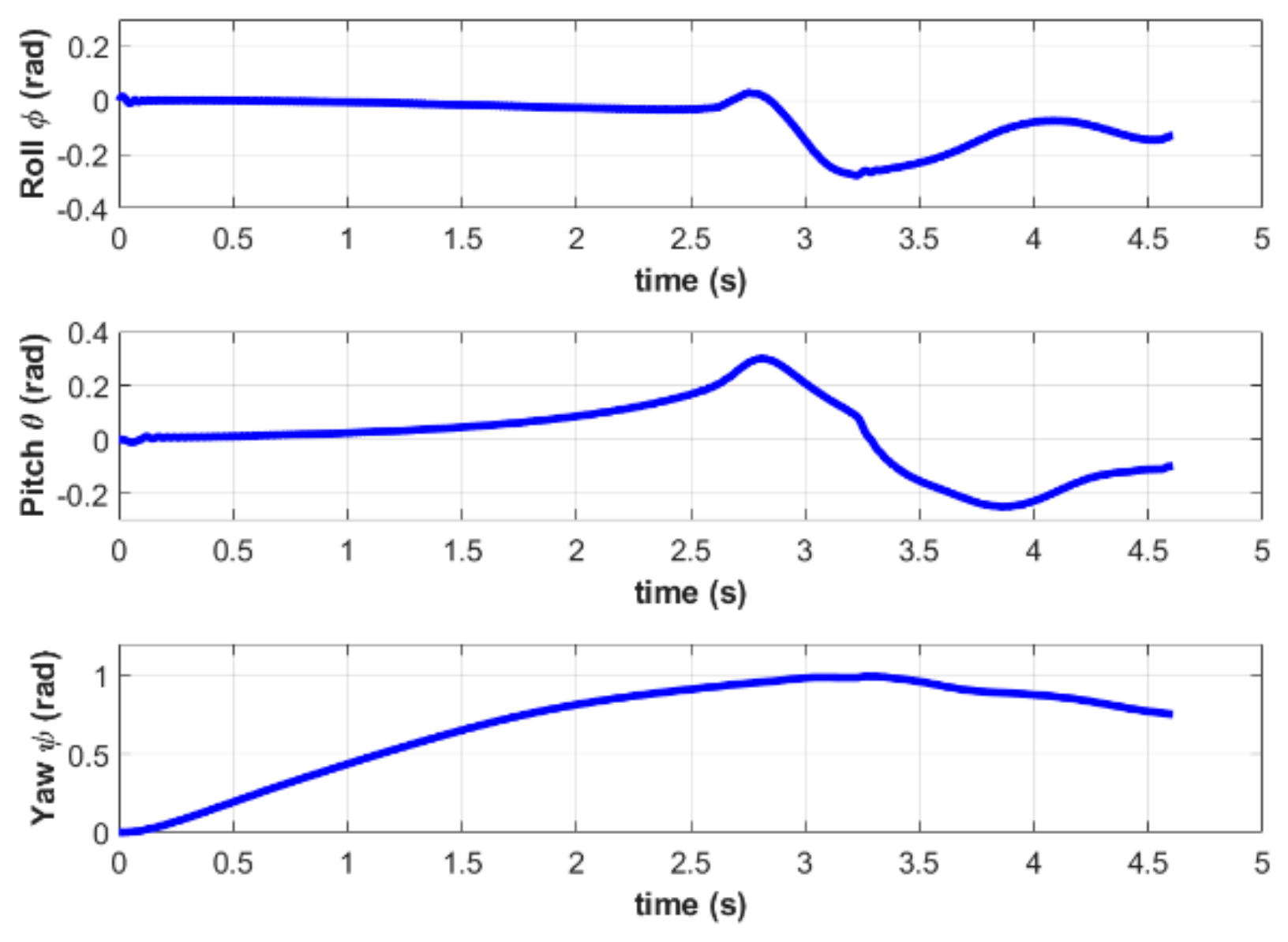
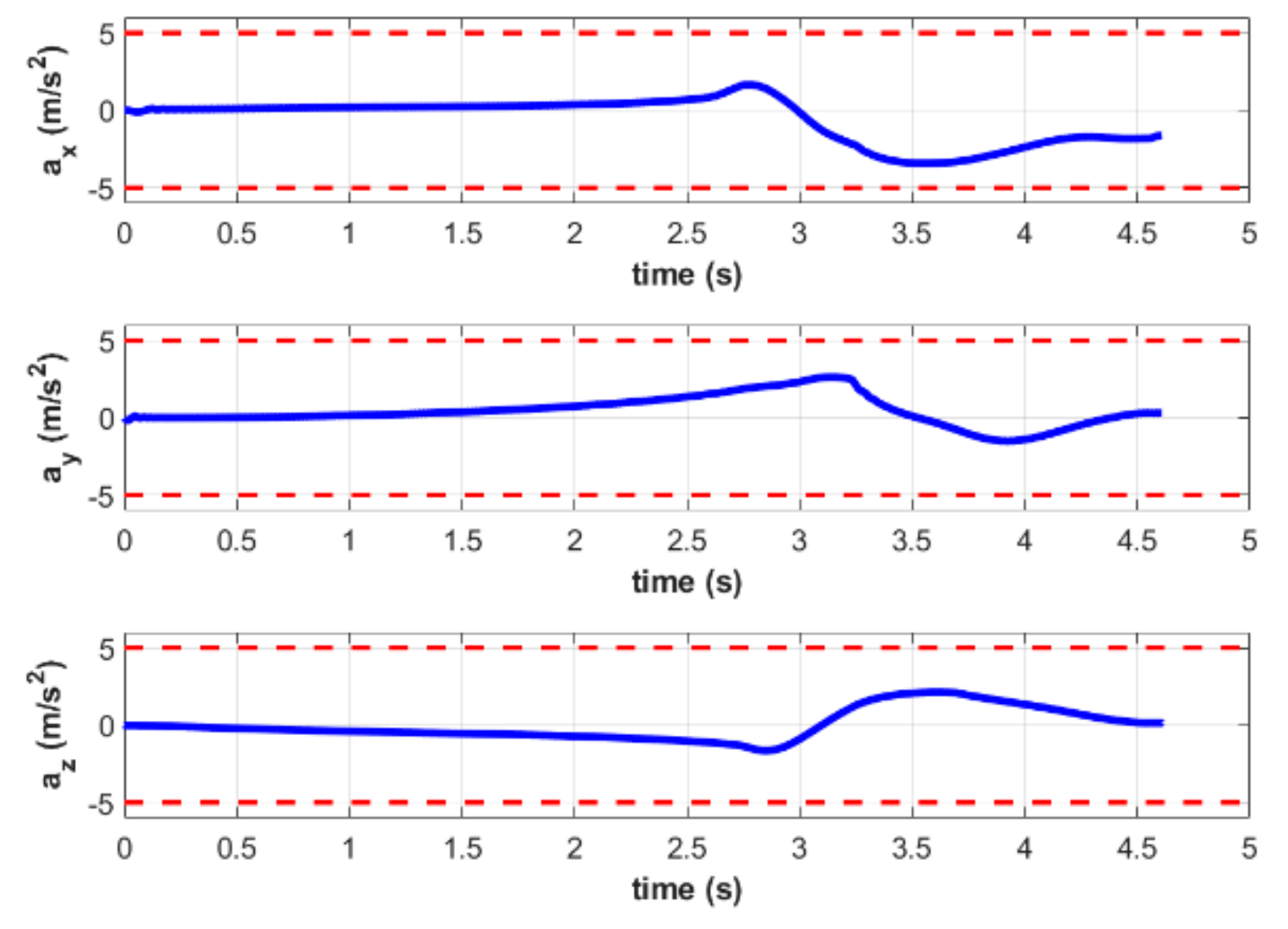
The attitude and acceleration curves of the quadrotor are shown in Figure 8 and Figure 9, respectively. It can be seen that both pitch and roll angles are less than 6 degrees in the terminal state. This demonstrates that the objective function defined in (13) can ensure a safe and stable landing without tumbling due to excessive Euler angles. Additionally, the acceleration of the quadrotor during the entire process satisfies the constraints given in the MPC controller.
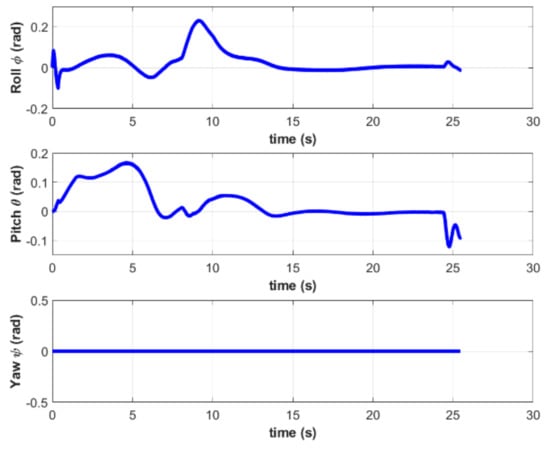
Figure 8.
Attitude of the quadrotor in simulation A.
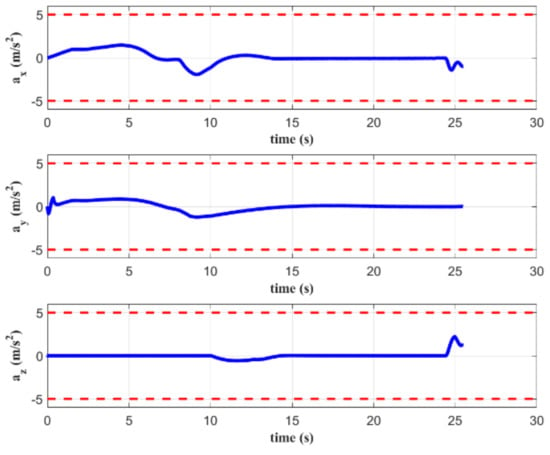
Figure 9.
Acceleration of the quadrotor in simulation A.
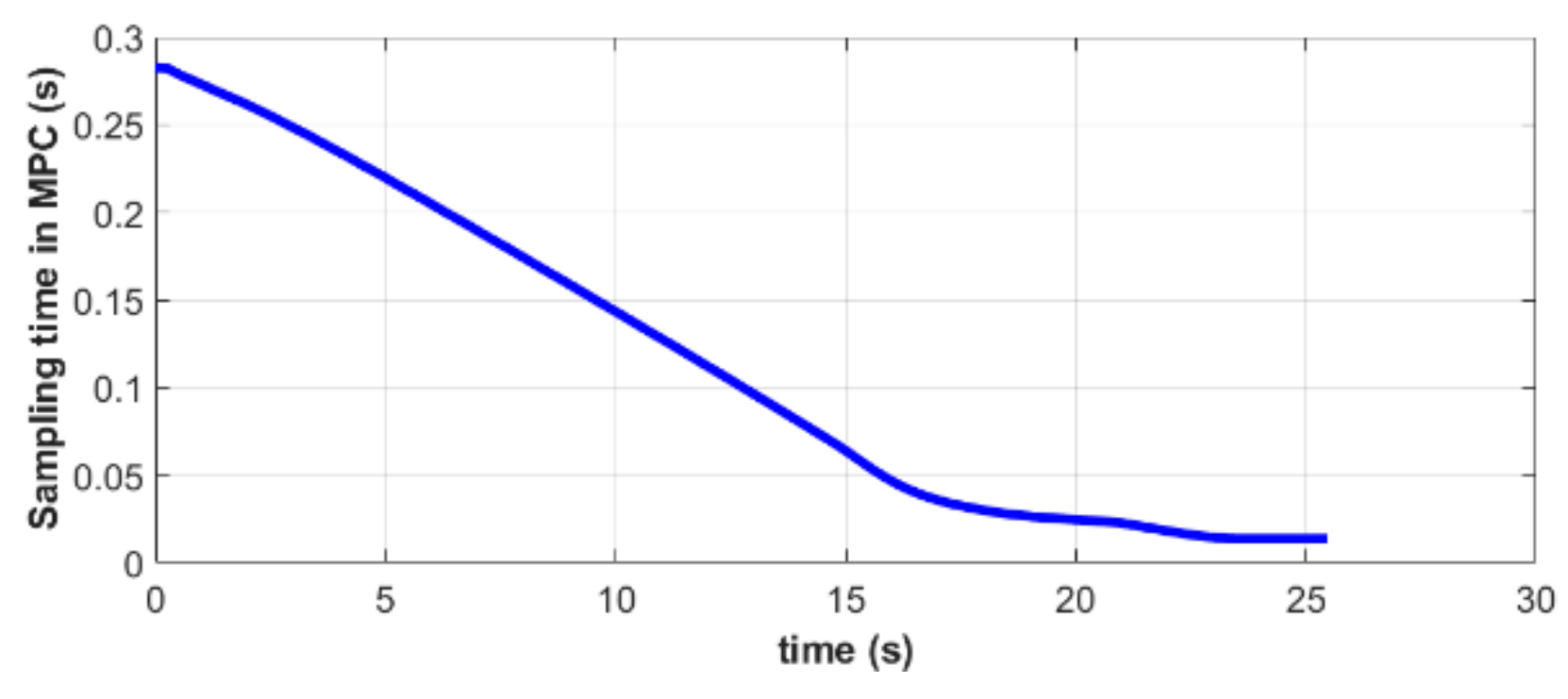
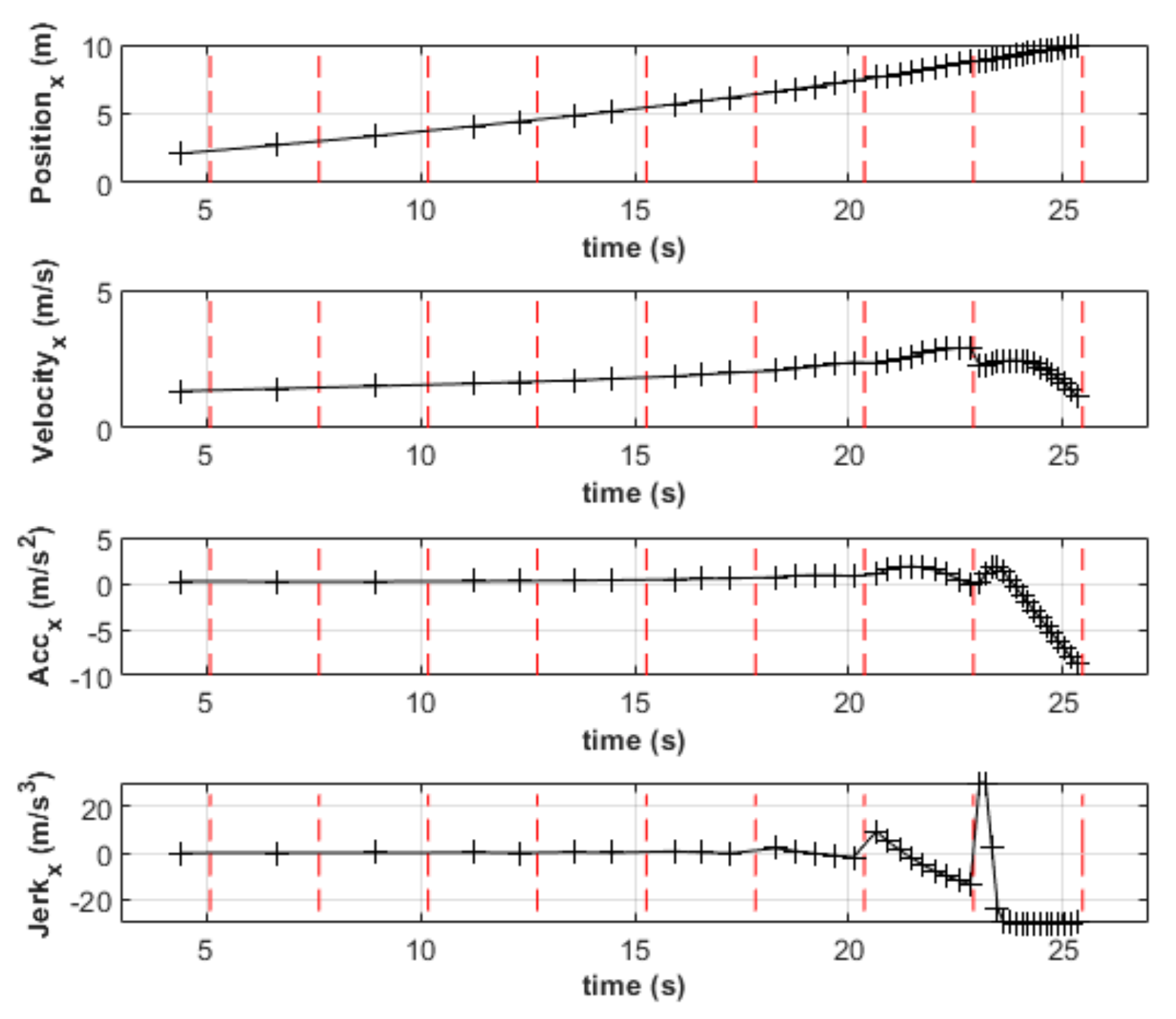
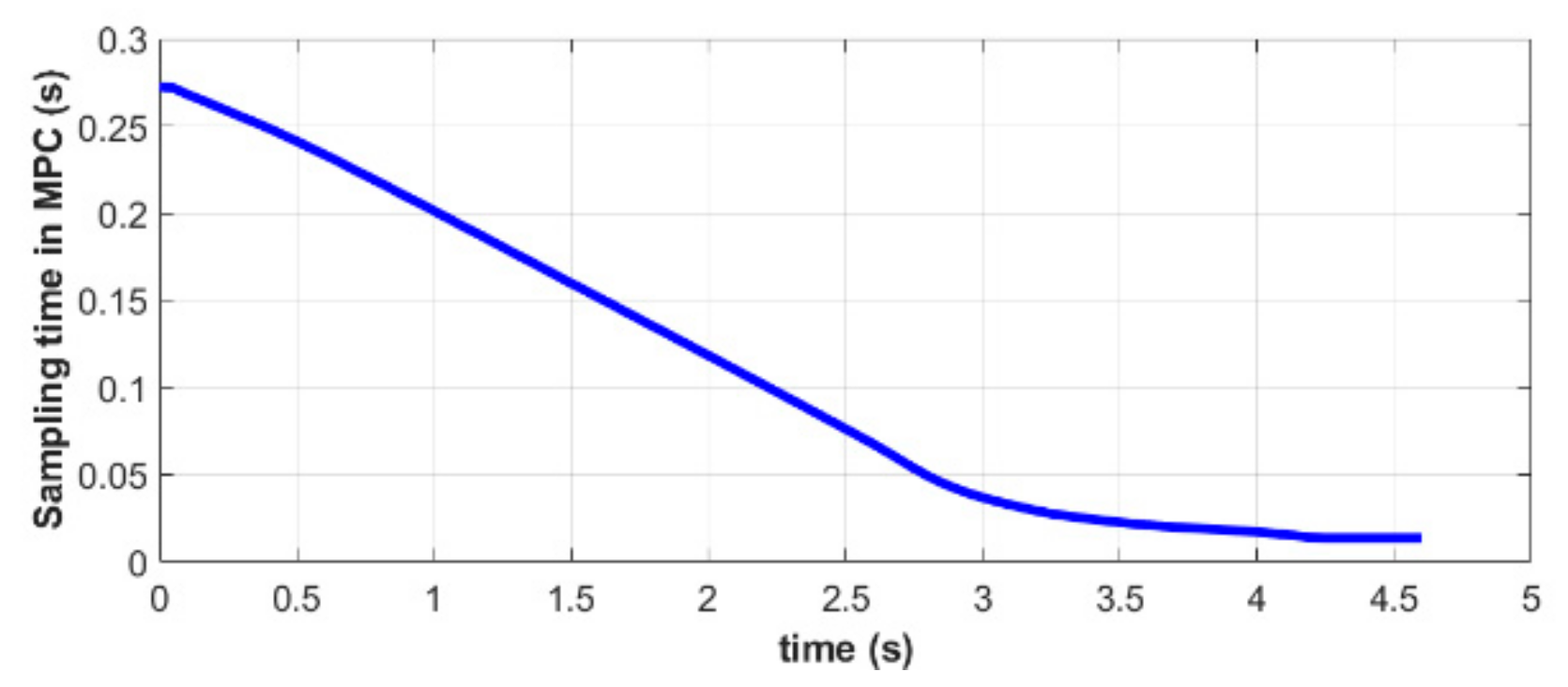
As shown in Figure 10, the sampling time of MPC is indeed decreasing gradually, which is consistent with the proposed control strategy in Section 4.3. When the distance between the quadrotor and the moving platform is large, and the requirements for the landing accuracy of the planned trajectory are relaxed, it is beneficial to adopt a longer sampling time to improve the computational efficiency when solving the MPC optimization problem. As the relative distance decreases, the sampling time is shortened, to continuously correct the planned trajectory and enhance the accuracy of the landing. This method not only optimizes the entire landing process but also constitutes a balanced tradeoff between calculation costs and control accuracy. In Figure 11, the red dotted lines represent the moments when the platform state information is updated, while the black vertical segments are the points where a new trajectory is planned. Every time the target information is updated, MPC will re-plan a path. During the initial stages, the time interval between the adjacent trajectory points is longer. As the relative distance decreases, more trajectories are calculated for the same time interval.
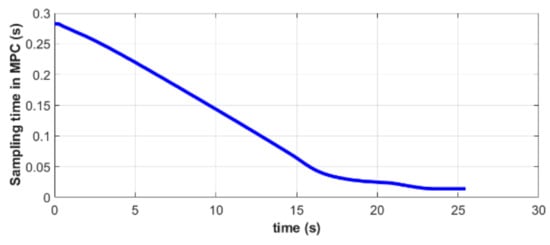
Figure 10.
Sampling time of the MPC controller in simulation A.
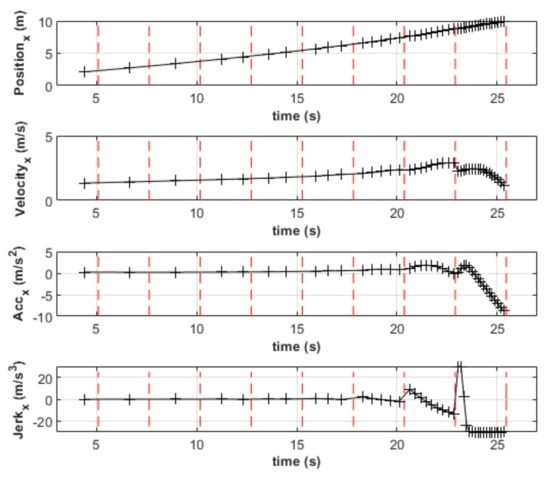
Figure 11.
Planned trajectory of updates during the landing in simulation A.
5.1.2. Simulation B: The Target Platform Moves along an Eight-Shaped Trajectory
The initial position and velocity assigned to the quadrotor are and , respectively. It is assumed that the target platform moves along an eight-shaped trajectory, with a speed of 3 m/s from its initial position . The 3D landing trajectory of the quadrotor is shown in Figure 12, where the black curves belong to the trajectory cluster planned by MPC during the whole process. It can be seen that the initial predictions deviate from the eight-shaped trajectory of the target platform. This is because the predicted rendezvous point is related to the present velocities of both quadrotor and platform. At the beginning, the velocity of the platform does not suggest an eight-shaped trajectory, so the planned quadrotor trajectory is also far away from the actual motion. Fortunately, the fast and efficient re-planning in MPC compensates for these errors. As seen in Figure 12, with the relative distance shortened, the MPC controller modifies and optimizes the planned trajectory continuously.
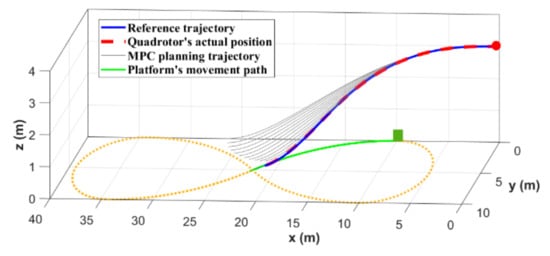
Figure 12.
3D landing trajectory of the quadrotor when the target platform moves along an eight-shaped trajectory.
Figure 13 and Figure 14 show the position and velocity, respectively, of both quadrotor and platform during the landing process. It can be seen that given the terminal constraints in MPC, the quadrotor position and velocity are equal to those of the maneuvering platform during rendezvous. Similar to simulation A, the quadrotor first aligns with the target in the direction and then reduces the relative distance to zero from and directions. This avoids collisions in the landing mission. Moreover, our quadrotor uses the designed INDI control method to accurately track the planned trajectory under the influence of external disturbances.
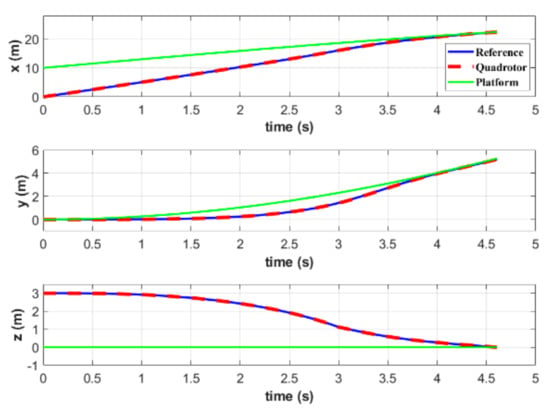
Figure 13.
Positions of the quadrotor and platform in simulation B.
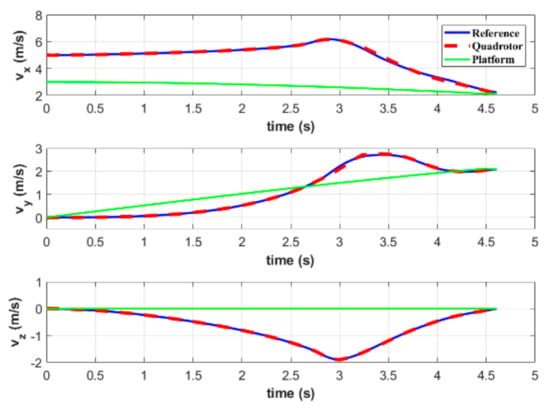
Figure 14.
Velocities of the quadrotor and platform in simulation B.
The attitude and acceleration curves of the quadrotor are shown in Figure 15 and Figure 16, respectively. It can be seen that both pitch and roll angles are small enough to guarantee a smooth landing during rendezvous. Moreover, the acceleration during the entire process meets the requirements set in the MPC controller.
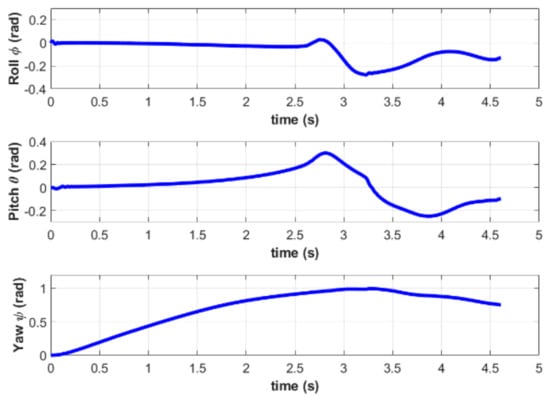
Figure 15.
Attitude of the quadrotor in simulation B.
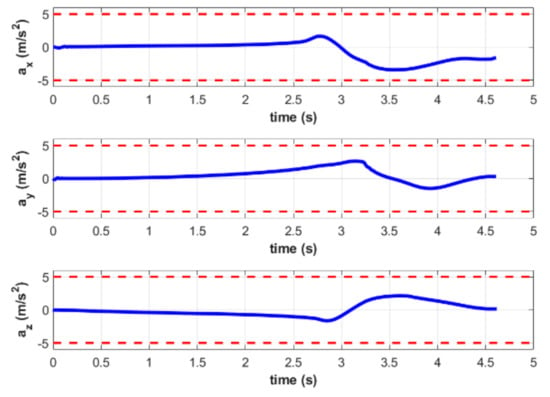
Figure 16.
Acceleration of the quadrotor in simulation B.
Figure 17 shows the variation of the sampling time in our MPC controller. We find that no matter how the landing platform maneuvers, the quadrotor can land accurately and smoothly based on the proposed autonomous system. Neither the trajectory nor the dynamic model of the target platform needs to be estimated in advance. Instead, we use the fast and efficient re-planning of MPC to continuously compensate for the landing error based on the information from the gimbaled camera. Furthermore, the inner autopilot can deal with external disturbances, ensuring the success of the landing and recovery.
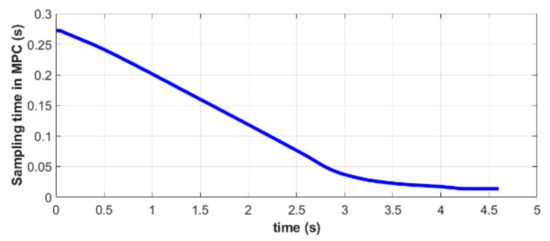
Figure 17.
Sampling time of the MPC controller in simulation B.
5.2. Flight Experiments
In this section, we report on flight experiments carried out to demonstrate the practical effectiveness of the proposed autonomous landing system under realistic conditions. Owing to the limited indoor space, we must take the quadrotor to conduct a landing mission in the outdoor environment. The complex outdoor aerodynamic characteristics require higher system performance on the disturbance rejection. The quadrotor [51] and maneuvering platform used during the flight experiments are shown in Figure 18. The vision-based sensor uses a two-axis electro-optical pod, which is mounted on the front of quadrotor. We use Nvidia Jetson TX2 as the onboard computer to run the designed algorithms, such as image processing, gimbal controlling, information calculation, trajectory planning, etc. After the desired waypoints are generated, the control commands are transmitted to the autopilot. In order to improve the accuracy of the altitude control, a millimeter wave radar (MMWR) sends altitude information to the autopilot, which is integrated with the information coming from the GPS and barometer. The ranging altitude accuracy can reach 0.01 m in the direction. A Pixhawk Cube autopilot is responsible for executing the designed cascade INDI controller to track the planned trajectory. Considering the impact of outdoor aerodynamic disturbances on the fuselage, we include a 3 D-printed, carbon fiber skin to cover our quadrotor, and magnets are installed on the landing gear. The total mass of our quadrotor is measured to be , and its diagonal wheelbase is .

Figure 18.
Quadrotor (a) and landing platform (b) used during landing experiments.
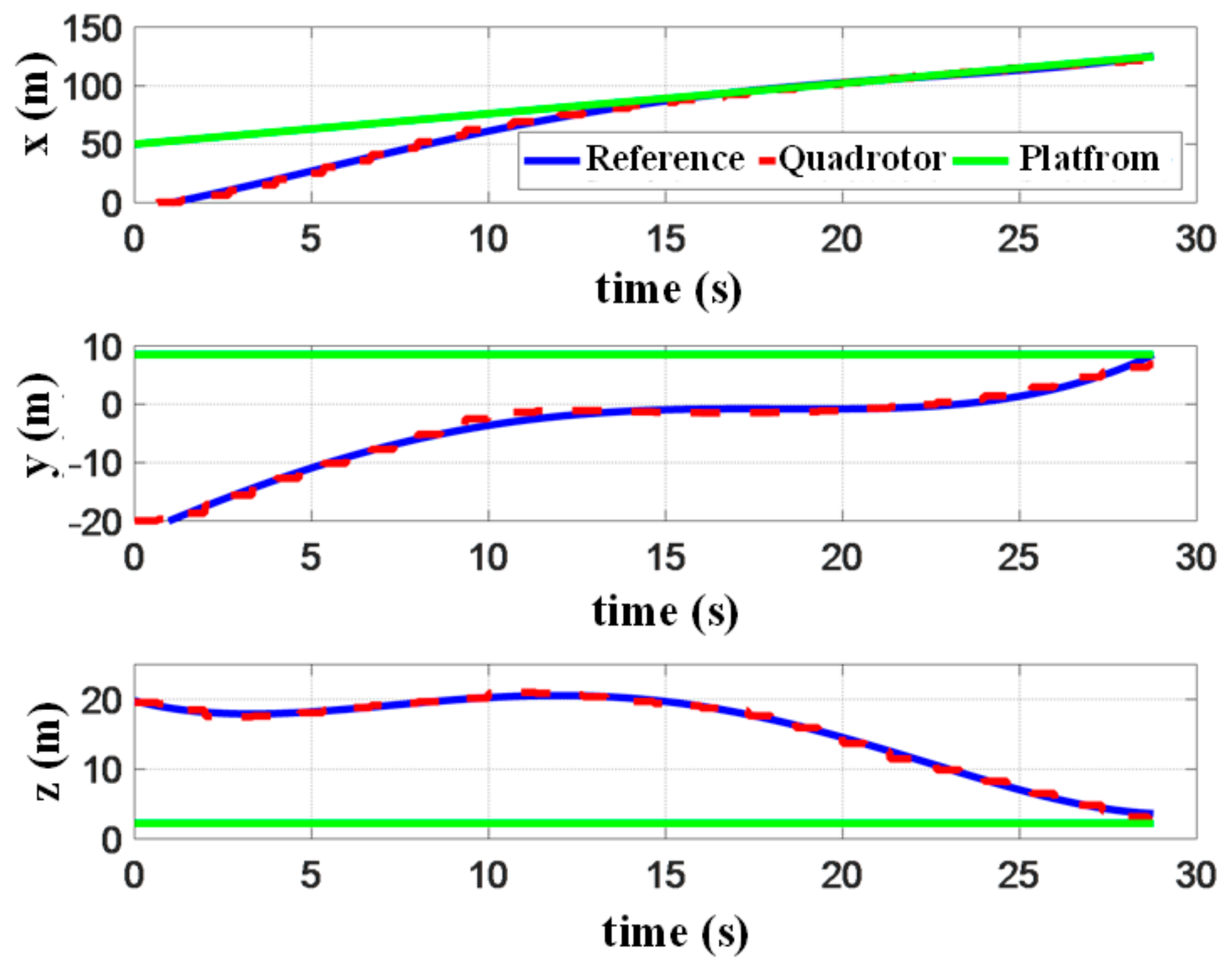
Besides the above-described hardware devices, the host computer also needs to issue instructions to the onboard TX2 via Wi-Fi. The ground station is responsible for monitoring the real-time status of the quadrotor. In an emergency, our operator will directly switch the flight mode and control it to a safe state. During the experiments, the quadrotor initially hovers at the position , and the vehicle platform moves straight from with a speed below . When the relative distance is less than , the gimbaled camera can stably detect the landing marker on the platform. When no target is identified, the measurement information from an equipped differential GPS base is used to plan the landing trajectory.
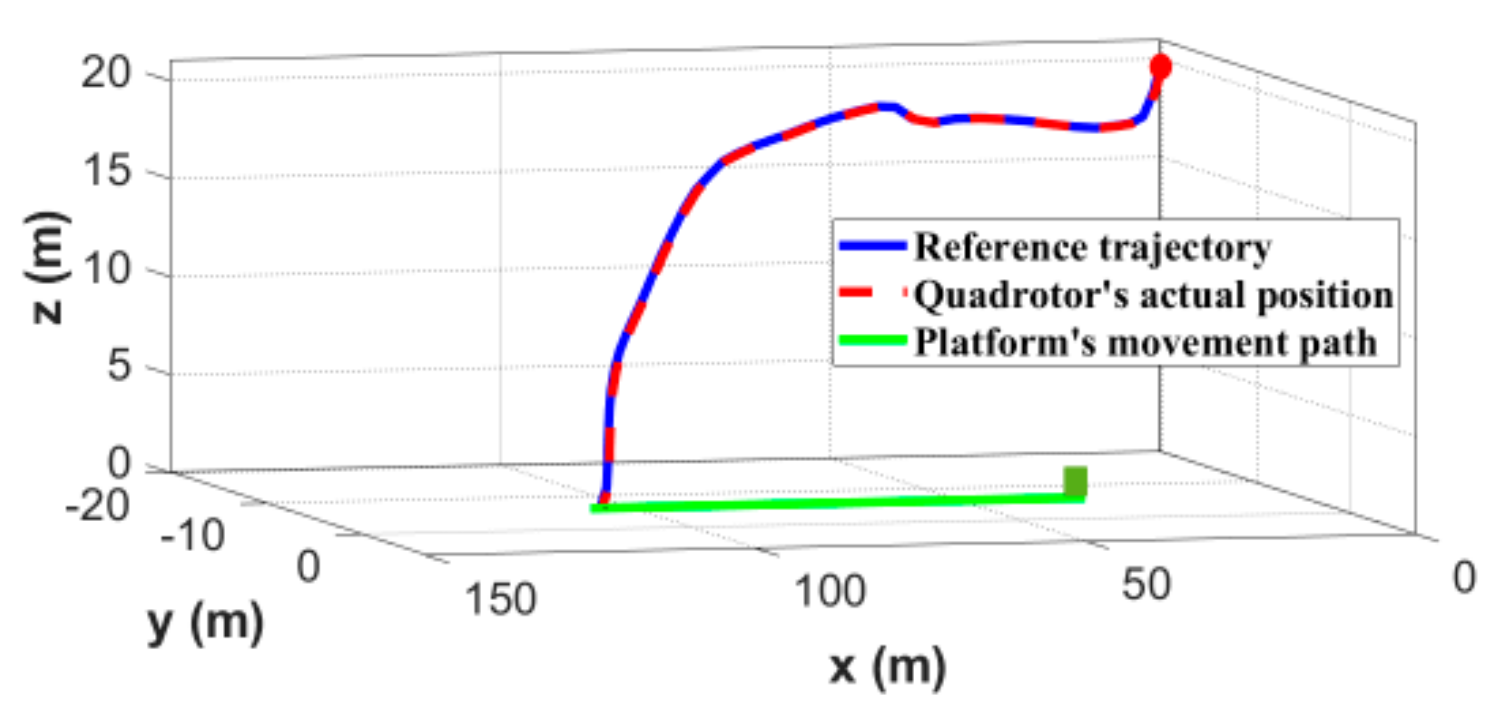
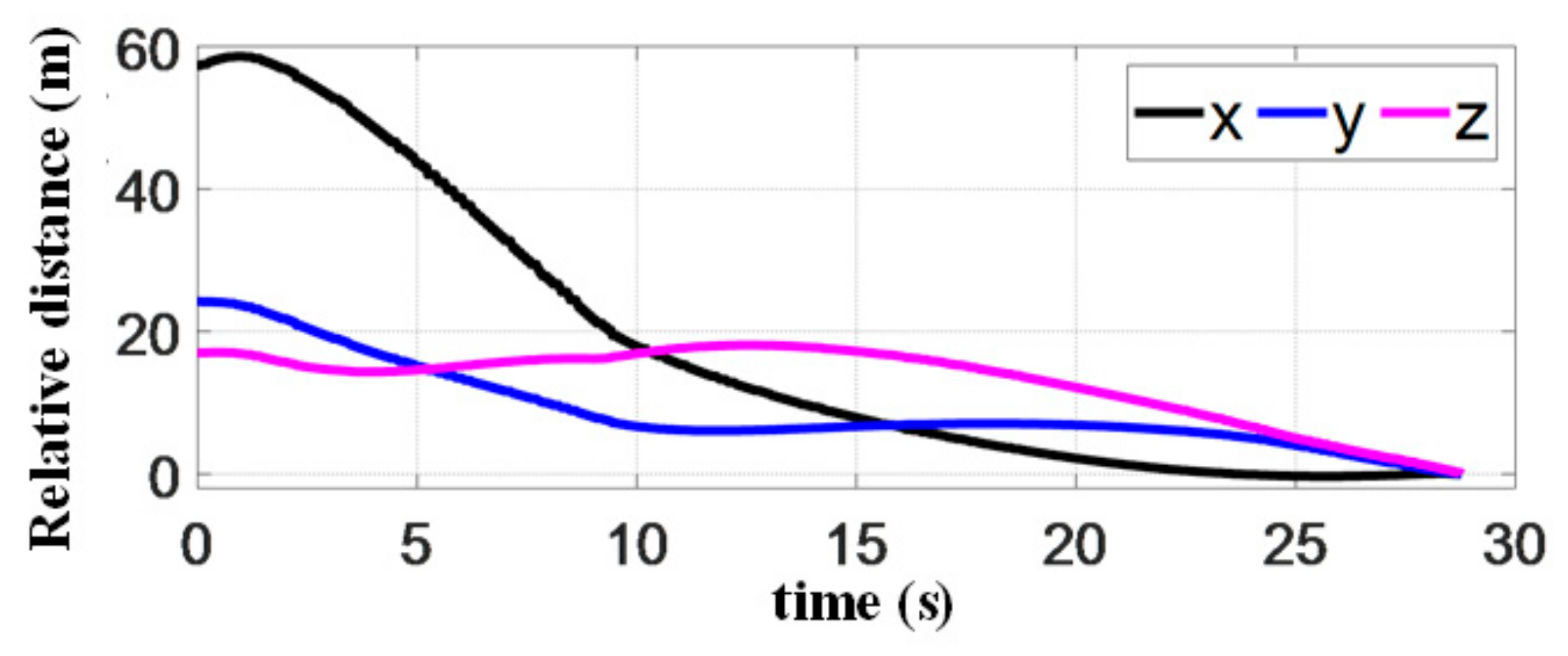
As shown in Figure 19, the 3D landing trajectory of the quadrotor demonstrates the feasibility of our proposed autonomous landing system. The fact that the flight trajectory is almost perpendicular to the platform, is related to the constraints on the terminal horizontal acceleration in the objective function. This ultimately determines the shape of the landing trajectory. Figure 20 shows the positions of both quadrotor and target platform. It can be seen that their final positions are the same, which means the landing mission is successful. Figure 21 shows that the tracking errors in the direction converge to 0 before landing. That is because quadrotor maneuvers along the moving direction of the platform for a period of time, while adjusting the relative distance in the other two directions. The control process is similar to the one observed in the simulations. It can also be seen that the cascade INDI controller proposed in this paper can accurately track the planned trajectory and achieve the landing.
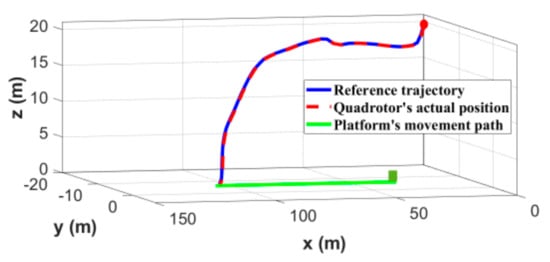
Figure 19.
3D landing trajectory during the experiment.
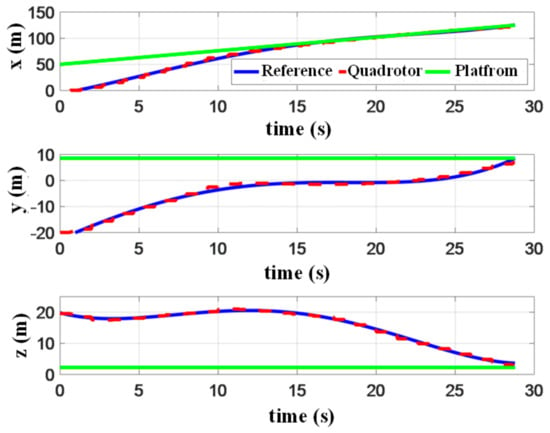
Figure 20.
Position of the quadrotor and platform in the experiment.
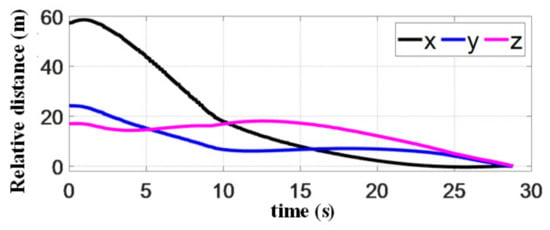
Figure 21.
Relative distance between quadrotor and platform in the experiment.
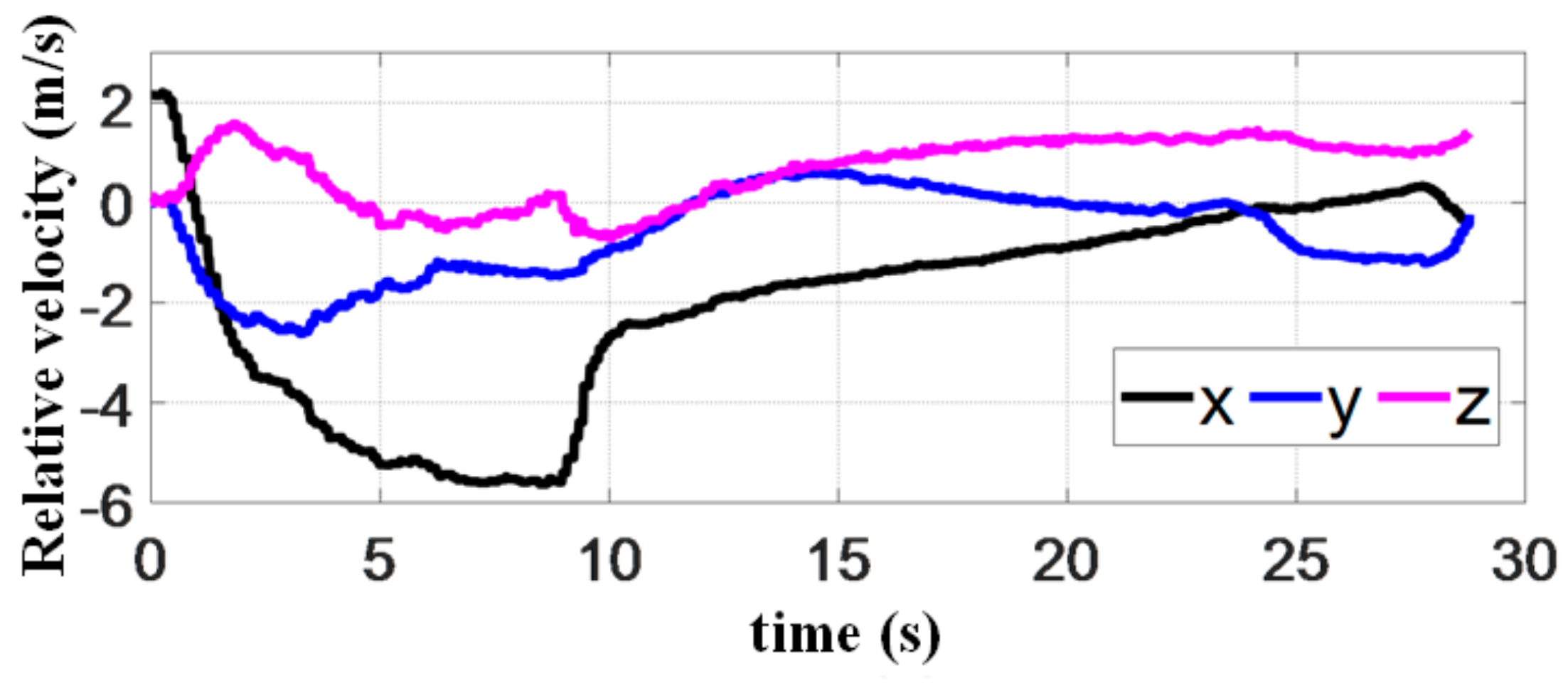
The velocity of quadrotor is given in Figure 22, while the relative velocity of quadrotor and platform is shown in Figure 23. It can be seen in the latter that the velocity difference in and directions during rendezvous is less than . MPC indeed plays an important role in constraining the terminal velocity. Furthermore, the flight speed in direction decreased significantly after the quadrotor recognizes the landing marker, to ensure the same terminal speed as the platform. The vertical speed fight before landing is kept at . In the final stage, the magnets on the landing gear help the quadrotor to reach the roof perpendicularly with no bounces.
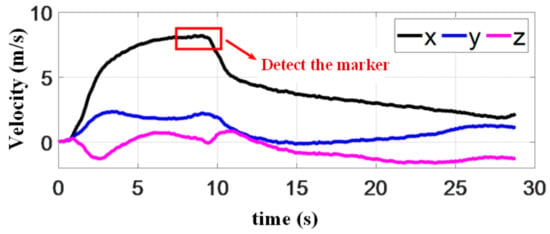
Figure 22.
Velocity of the quadrotor in the experiment.
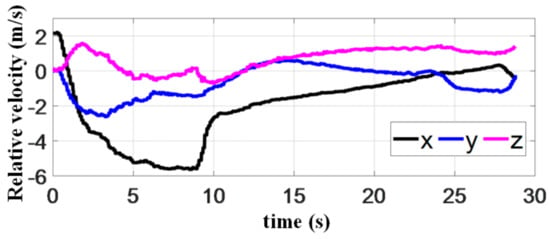
Figure 23.
Relative velocity between quadrotor and platform in the experiment.
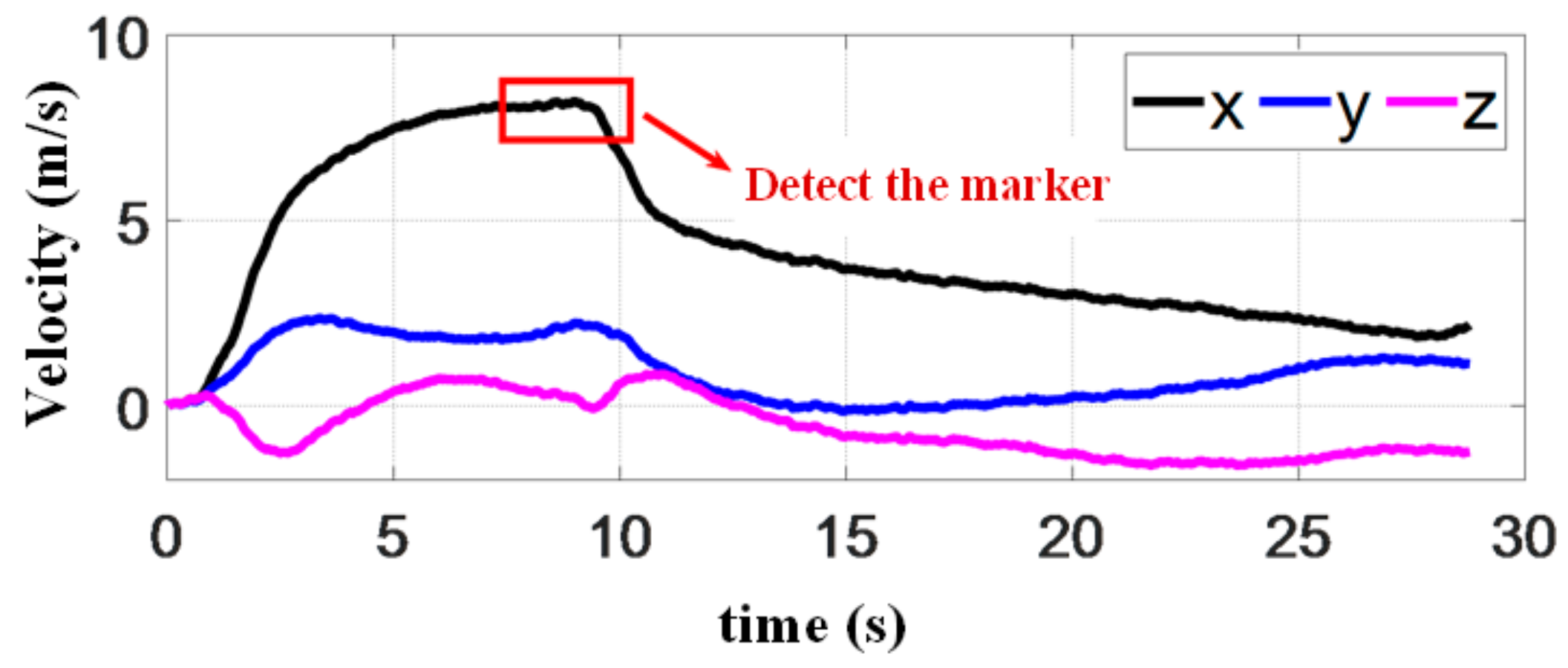
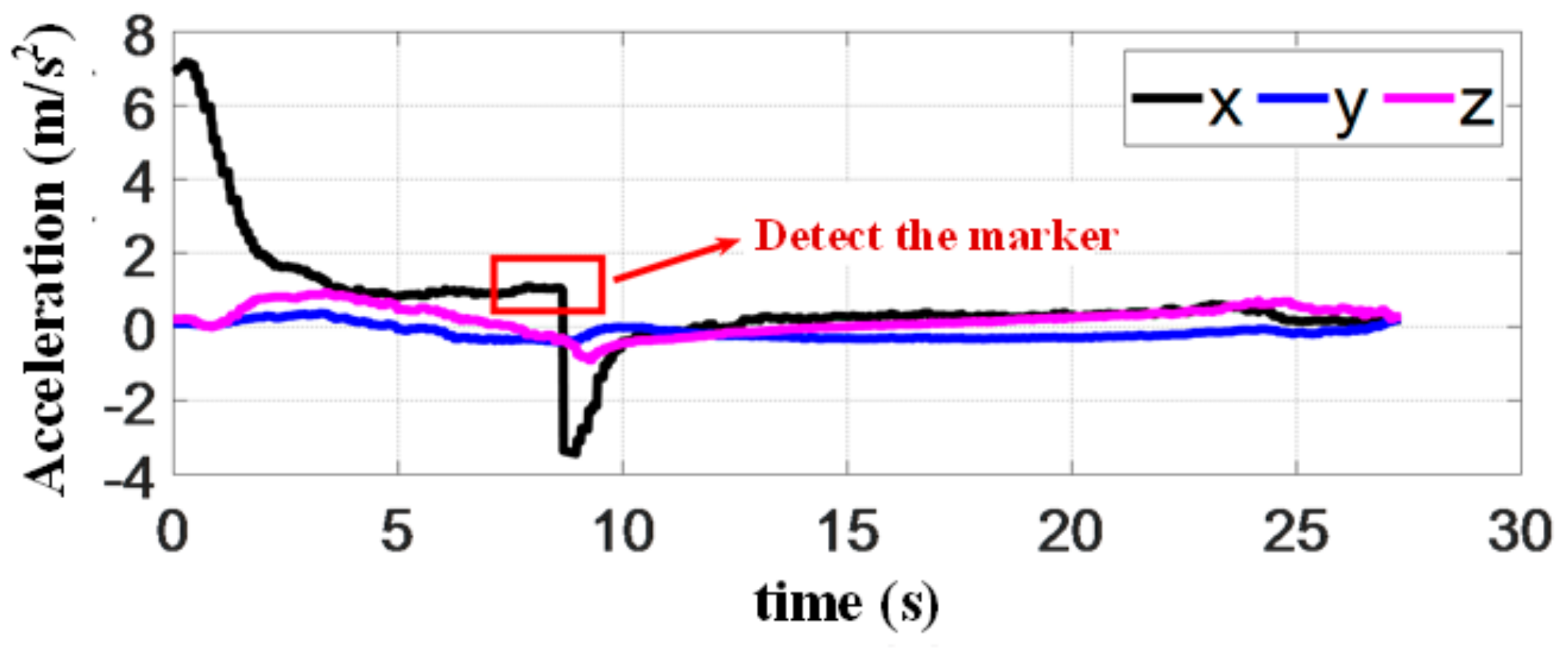
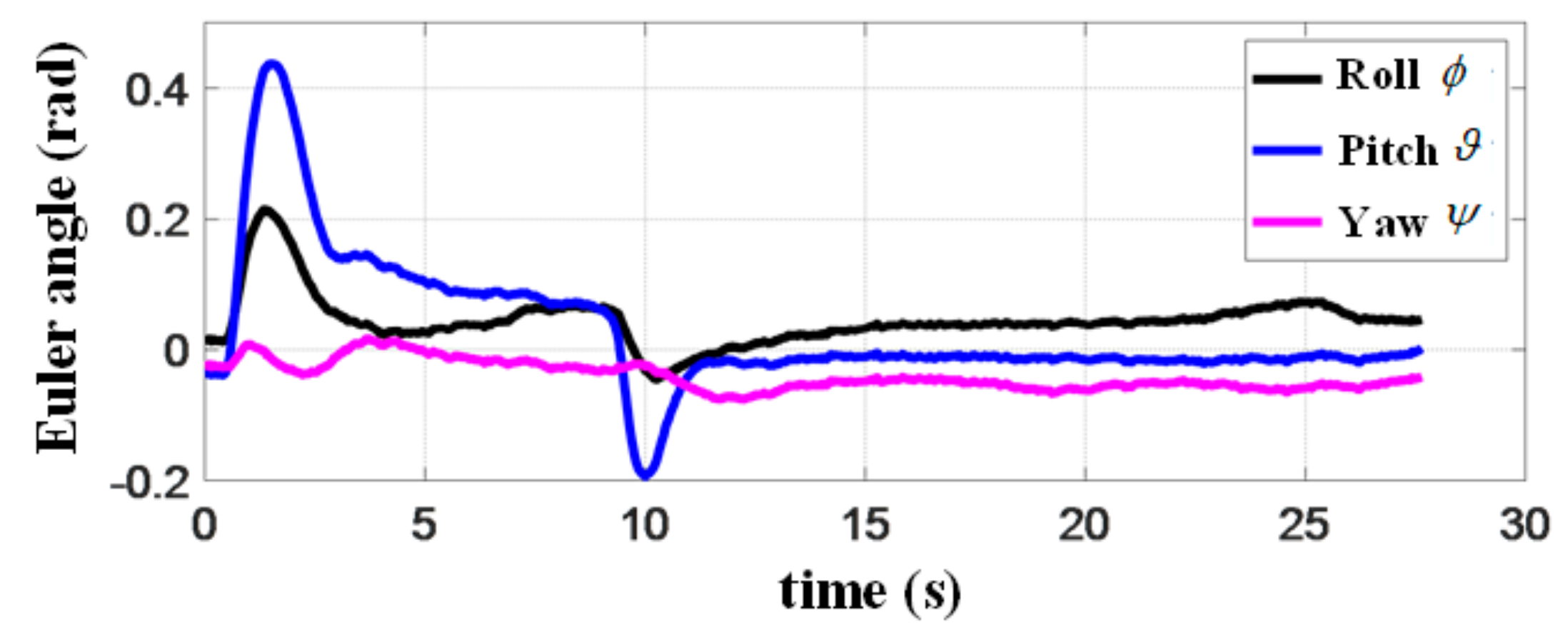
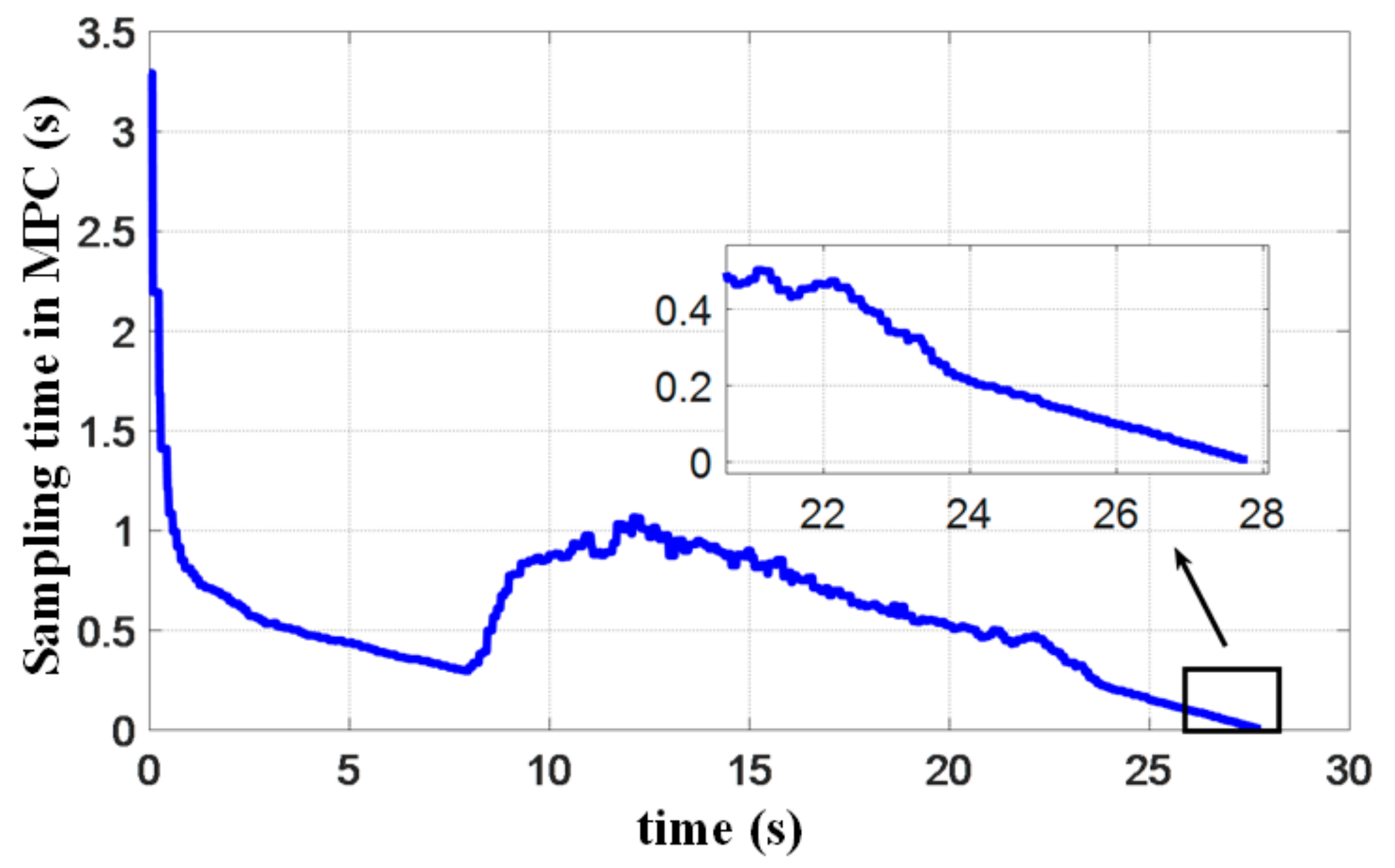
Figure 24 presents the acceleration of the quadrotor in the line of sight (LOS) coordinate during the landing process. When the quadrotor successfully detects the landing marker (see the red square in Figure 24), the acceleration along the LOS suddenly changes to reduce the flight speed. The terminal constraints in MPC require the landing speed to be consistent with that of the target platform, and thus, the acceleration of the quadrotor decreases before rendezvous. According to these results, the acceleration change does not affect the landing accuracy. However, it is still necessary to improve our algorithms and system to avoid the instability of attitude and loss of target platform. In the end, the accelerations along the three axes in the LOS frame converge to 0, indicating that the landing is accomplished. Figure 25 shows the attitude change of the quadrotor. We find that both roll and pitch angles during rendezvous are very small, resulting in a smooth landing, demonstrating the benefits of introducing the objective function (13) in MPC. It can also be seen from this curve that due to the movement of the platform in the direction, the pitch angle of quadrotor changes considerably, reflecting the coupling between position and attitude in the quadrotor forward dynamics. The sampling time of MPC in the experiment is shown in Figure 26, which is gradually shortened when the relative distance decreases. However, it slightly increases at 8 s when the speed of quadrotor decreases abruptly. Since the estimated mission time increases, the system also increases the sampling time.
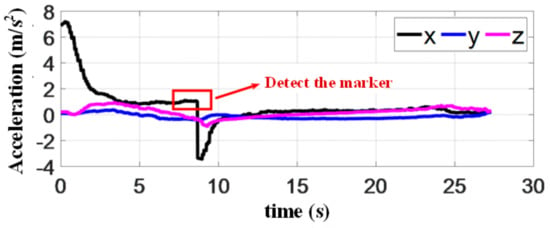
Figure 24.
Acceleration of the quadrotor in the experiment.
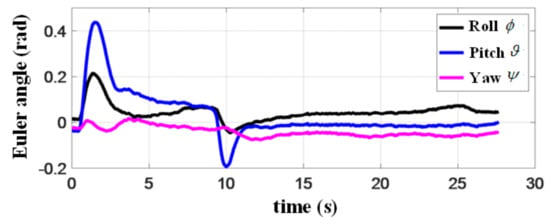
Figure 25.
Attitude of the quadrotor in the experiment.
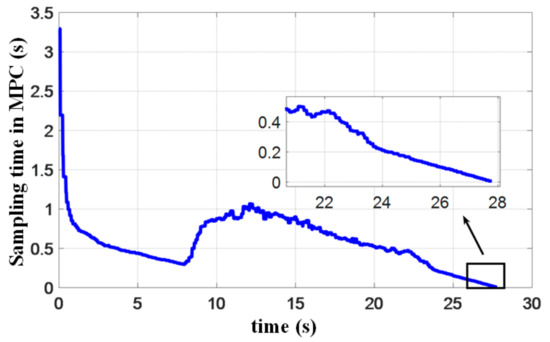
Figure 26.
Sampling time of the MPC controller in the experiment.
6. Conclusions
This paper proposes an autonomous system for landing a quadrotor on a mobile platform using MPC. To detect and track the guide marker on the platform, a fast two-stage algorithm is introduced. The MPC controller is designed to plan the landing trajectory based on the estimated platform information. Based on numerical simulations and outdoor flight experiments, we draw the following conclusions:
The MPC with variable sampling time revises the planned landing trajectory continuously as the relative distance decreases, which improves the onboard computing efficiency. The accuracy of the outdoor landing experiments reached 0.15 m. According to the designed state machine, using different objective functions for the corresponding operation modes helped to land the quadrotor rapidly, while also meeting the requirements regarding its terminal position, speed and attitude. The proposed cascade INDI method improves the disturbance rejection of the landing system, and the quadrotor can still achieve an accurate and stable landing under the influence of external disturbances.
Author Contributions
All authors contributed to the study conception and design. K.G. contributed to methodology, programing, writing, reviewing, editing and validation. P.T. involved in conceptualization, methodology, software and editing the draft. H.W. contributed to programing, software, writing, editing and reviewing. D.L. involved in software, data curation, supervision and project administration. X.C. contributed to visualization, draft preparation, formal analysis and investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Natural Science Foundation of China] grant number [U61827901].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This study was co-supported by the Beijing Key Laboratory of UAV Autonomous Control.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, S.; Hu, Z.; Yin, M.; Ang, K.Z.Y.; Liu, P.; Wang, F.; Dong, X.; Lin, F.; Chen, B.M.; Lee, T.H. A robust real-time vision system for autonomous cargo transfer by an unmanned helicopter. IEEE Trans. Ind. Electron. 2015, 62, 1210–1219. [Google Scholar] [CrossRef]
- John, M.; Robert, L.; Randal, B.; Timothy, M. Analysis of an improved IMU-based observer for multirotor helicopters. J. Intell. Robot. Syst. 2014, 74, 1049–1061. [Google Scholar]
- Bernard, M.; Kondak, K.; Maza, I.; Ollero, A. Autonomous transportation and deployment with aerial robots for search and rescue missions. J. Field Robot. 2011, 28, 914–931. [Google Scholar] [CrossRef] [Green Version]
- Daly, J.M.; Ma, Y.; Waslander, S.L. Coordinated landing of a quadrotor on a skid-steered ground vehicle in the presence of time delays. Auton. Robot. 2015, 38, 179–191. [Google Scholar] [CrossRef]
- Persson, L.; Wahlberg, B. Model predictive control for autonomous ship landing in a search and rescue scenario. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2010. [Google Scholar]
- Ferrandez, S.M.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374–388. [Google Scholar] [CrossRef] [Green Version]
- Respall, V.M.; Sellami, S.; Afanasyev, I. Implementation of autonomous visual detection, tracking and landing for AR.Drone 2.0 quadcopter. In Proceedings of the Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 477–482. [Google Scholar]
- Araar, O.; Aouf, N.; Vitanov, I. Vision based autonomous landing of multirotor UAV on moving platform. J. Intell. Robot. Syst. 2017, 85, 369–384. [Google Scholar] [CrossRef]
- Zhao, T.; Hong, J. Landing system for AR.Drone 2.0 using onboard camera and ROS. In Proceedings of the IEEE Guidance, Navigation Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; IEEE: Piscataway Township, NJ, USA, 2017; pp. 1098–1102. [Google Scholar]
- Herissé, B.; Hamel, T.; Mahony, R.; Russotto, F.X. Landing a VTOL unmanned aerial vehicle on a moving platform using optical flow. IEEE Trans. Robot. 2011, 28, 77–89. [Google Scholar] [CrossRef]
- Lee, H.; Jung, S.; Shim, D.H. Vision-based UAV landing on the moving vehicle. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 1–7. [Google Scholar]
- Lee, D.; Ryan, T.; Kim, H.J. Autonomous landing of a VTOL UAV on a moving platform using image-based visual servoing. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 971–976. [Google Scholar]
- Ghommam, J.; Saad, M. Autonomous landing of a quadrotor on a moving platform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1504–1519. [Google Scholar] [CrossRef]
- Lu, Q.; Ren, B.B.; Parameswaran, S. Shipboard landing control enabled by an uncertainty and disturbance estimator. J. Guid. Control Dyn. 2018, 41, 1502–1520. [Google Scholar] [CrossRef]
- Borowczyk, A.; Nguyen, D.T.; Nguyen, A.P.V.; Nguyen, D.Q.; Saussié, D.; Le Ny, J. Autonomous landing of a quadcopter on a highspeed ground vehicle. J. Guid. Control Dyn. 2017, 40, 2378–2385. [Google Scholar] [CrossRef] [Green Version]
- Paris, A.; Lopez, B.T.; How, J.P. Dynamic landing of an autonomous quadrotor on a moving platform in turbulent wind conditions. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 9577–9583. [Google Scholar]
- Ahn, H.S.; Chen, Y.; Moore, K.L. Iterative learning control: Brief survey and categorization. IEEE Trans. Syst. Man Cybern. Part C 2007, 37, 1099–1121. [Google Scholar] [CrossRef]
- Foudeh, H.A.; Luk, P.C.-K.; Whidborne, J.F. An Advanced Unmanned Aerial Vehicle (UAV) Approach via Learn-ing-Based Control for Overhead Power Line Monitoring: A Comprehensive Review. IEEE Access 2021, 9, 130410–130433. [Google Scholar] [CrossRef]
- Foudeh, H.A.; Luk, P.C.-K.; Whidborne, J.F. Application of norm optimal iterative learning control to quadrotor unmanned aerial vehicle for monitoring overhead power system. Energies 2020, 13, 3223. [Google Scholar] [CrossRef]
- Chen, T.; Shan, J. Distributed control of multiple flexible manipulators with unknown disturbances and dead-zone input. IEEE Trans. Ind. Electron. 2020, 67, 9937–9947. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Abdolhosseini, M.; Zhang, Y.M.; Rabbath, C.A. An Efficient Model Predictive Control Scheme for an Unmanned Quadrotor Helicopter. J. Intell. Robot. Syst. 2013, 70, 27–38. [Google Scholar] [CrossRef]
- Chikasha, P.N.; Dube, C. Adoptive Model Predictive Control of a Quadrotor. In Proceedings of the World Congress of International Federation of Automatic Control, Toulouse, France, 9–14 July 2017; Volume 50, pp. 157–162. [Google Scholar]
- Tzoumanikas, D.; Li, W.; Grimm, M.; Zhang, K.; Kovac, M.; Leutenegger, S. Fully autonomous micro air vehicle flight and landing on a moving target using visual-inertial estimation and model-predictive control. J. Field Robot. 2019, 36, 49–77. [Google Scholar] [CrossRef] [Green Version]
- Beul, M.; Nieuwenhuisen, M.; Quenzel, J.; Rosu, R.A.; Horn, J.; Pavlichenko, D.; Houben, S.; Behnke, S. Team NimbRo at MBZIRC 2017: Fast landing on a moving target and treasure hunting with a team of micro aerial vehicles. J. Field Robot. 2019, 36, 204–229. [Google Scholar] [CrossRef] [Green Version]
- Bähnemann, R.; Pantic, M.; Popović, M.; Schindler, D.; Tranzatto, M.; Kamel, M.; Grimm, M.; Widauer, J.; Siegwart, R.; Nieto, J. The ETH-MAV team in the MBZ International Robotics Challenge. J. Field Robot. 2017, 36, 78–103. [Google Scholar] [CrossRef]
- Baca, T.; Stepan, P.; Spurny, V.; Hert, D.; Penicka, R.; Saska, M.; Thomas, J.; Loianno, G.; Kumar, V. Autonomous landing on a moving vehicle with an unmanned aerial vehicle. J. Field Robot. 2019, 36, 874–891. [Google Scholar] [CrossRef]
- Vlantis, P.; Marantos, P.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Quadrotor landing on an inclined platform of a moving ground vehicle. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2202–2207. [Google Scholar]
- Lu, P.; van Kampen, E.J.; de Visser, C.; Chu, Q. Aircraft fault-tolerant trajectory control using incremental nonlinear dynamic inversion. Control. Eng. Pract. 2016, 57, 126–141. [Google Scholar] [CrossRef] [Green Version]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Smeur, E.J.; Chu, Q.; Croon, G.C. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles. J. Guid. Control Dyn. 2016, 39, 450–461. [Google Scholar] [CrossRef] [Green Version]
- Simplício, P.; Pavel, M.D.; Van Kampen, E.; Chu, Q.P. An acceleration measurements-based approach for helicopter nonlinear flight control using incremental nonlinear dynamic inversion. Control Eng. Pract. 2013, 21, 1065–1077. [Google Scholar] [CrossRef]
- Smeur, E.J.; Croon, G.C.; Chu, Q. Cascaded incremental nonlinear dynamic inversion for MAV disturbance rejection. Control. Eng. Pract. 2018, 73, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Lombaerts, T.J.J.; Chu, Q.P.; Mulder, J.A.; Joosten, D.A. Modular flight control reconfiguration design and simulation. Control. Eng. Pract. 2011, 19, 540–554. [Google Scholar] [CrossRef]
- Wang, X.; Kampen, E.J.V.; Chu, Q.; Lu, P. Incremental sliding-mode fault-tolerant flight control. J. Guid. Control Dyn. 2019, 42, 244–259. [Google Scholar] [CrossRef]
- Wang, X.; Sun, S.; van Kampen, E.J.; Chu, Q. Quadrotor fault tolerant incremental sliding mode control driven by sliding mode disturbance observers. Aerosp. Sci. Technol. 2019, 87, 417–430. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Van Kampen, E.-J.; Chu, Q. Quadrotor fault-tolerant incremental nonsingular terminal sliding mode control. Aerosp. Sci. Technol. 2019, 95, 105514. [Google Scholar] [CrossRef]
- Jin, R.; Owais, H.M.; Lin, D.; Song, T.; Yuan, Y. Ellipse proposal and convolutional neural network discriminant for autonomous landing marker detection. J. Field Robot. 2019, 36, 6–16. [Google Scholar] [CrossRef] [Green Version]
- Manzoor, T.; Xia, Y.Q.; Zhai, D.H.; Ma, D.L. Trajectory tracking control of a VTOL unmanned aerial vehicle using offset-free tracking MPC. Chin. J. Aeronaut. 2020, 33, 2024–2042. [Google Scholar] [CrossRef]
- Yao, P.; Wang, H.L.; Ji, H.X. Multi-UAVs tracking target in urban environment by model predictive control and Improved Grey Wolf Optimizer. Aerosp. Sci. Technol. 2016, 55, 131–143. [Google Scholar] [CrossRef]
- Wang, J.; Cui, N.; Wei, C. Optimal rocket landing guidance using convex optimization and model predictive control. J. Guid. Control Dyn. 2019, 42, 1078–1092. [Google Scholar] [CrossRef]
- Wang, C.; Song, Z.Y. Convex Model Predictive Control for Rocket Vertical Landing. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 9837–9842. [Google Scholar]
- Wang, B.H.; Meng, Z.J.; Jia, C.; Huang, P.F. Anti-tangle control of tethered space robots using linear motion of tether offset. Aerosp. Sci. Technol. 2019, 89, 163–174. [Google Scholar] [CrossRef]
- Ardakani, M.M.G.; Olofsson, B.; Robertsson, A.; Johansson, R. Real-time trajectory generation using model predictive control. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 942–948. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Computer Controlled Systems: Theory and Design; Prentice Hall: Hoboken, NJ, USA, 1997; pp. 32–35. [Google Scholar]
- Wang, H.; Lin, D.; Cheng, Z.; Wang, J. Optimal guidance of extended trajectory shaping. Chin. J. Aeronaut. 2014, 14. [Google Scholar] [CrossRef] [Green Version]
- Phang, S.K.; Lai, S.; Wang, F.; Lan, M.; Chen, B.M. Systems design and implementation with jerk-optimized trajectory generation for UAV calligraphy. Mechatronics 2015, 30, 65–75. [Google Scholar] [CrossRef]
- Yu, J.; Cai, Z.; Wang, Y. Minimum jerk trajectory generation of a quadrotor based on the differential flatness. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Yantai, China, 8–10 August 2014; pp. 832–837. [Google Scholar]
- Mattingley, J.; Boyd, S. CVXGEN: A code generator for embedded convex optimization. Optim. Eng. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Chamseddine, A.; Zhang, Y.; Rabbath, C.A.; Join, C.; Theilliol, D. Flatness-based trajectory planning/ replanning for a quadrotor unmanned aerial vehicle. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2832–2848. [Google Scholar] [CrossRef]
- Guo, K.; Lin, D.; Li, B.; Song, T.; Zang, L.; Yuan, Y. Design of a quadrotor attitude controller and throttle acceleration autopilot based on forward modeling. In Proceedings of the 5th China Aeronautical Science and Technology Conference, Jiaxing, China; 2021; pp. 349–365. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).