Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control
Abstract
:1. Introduction
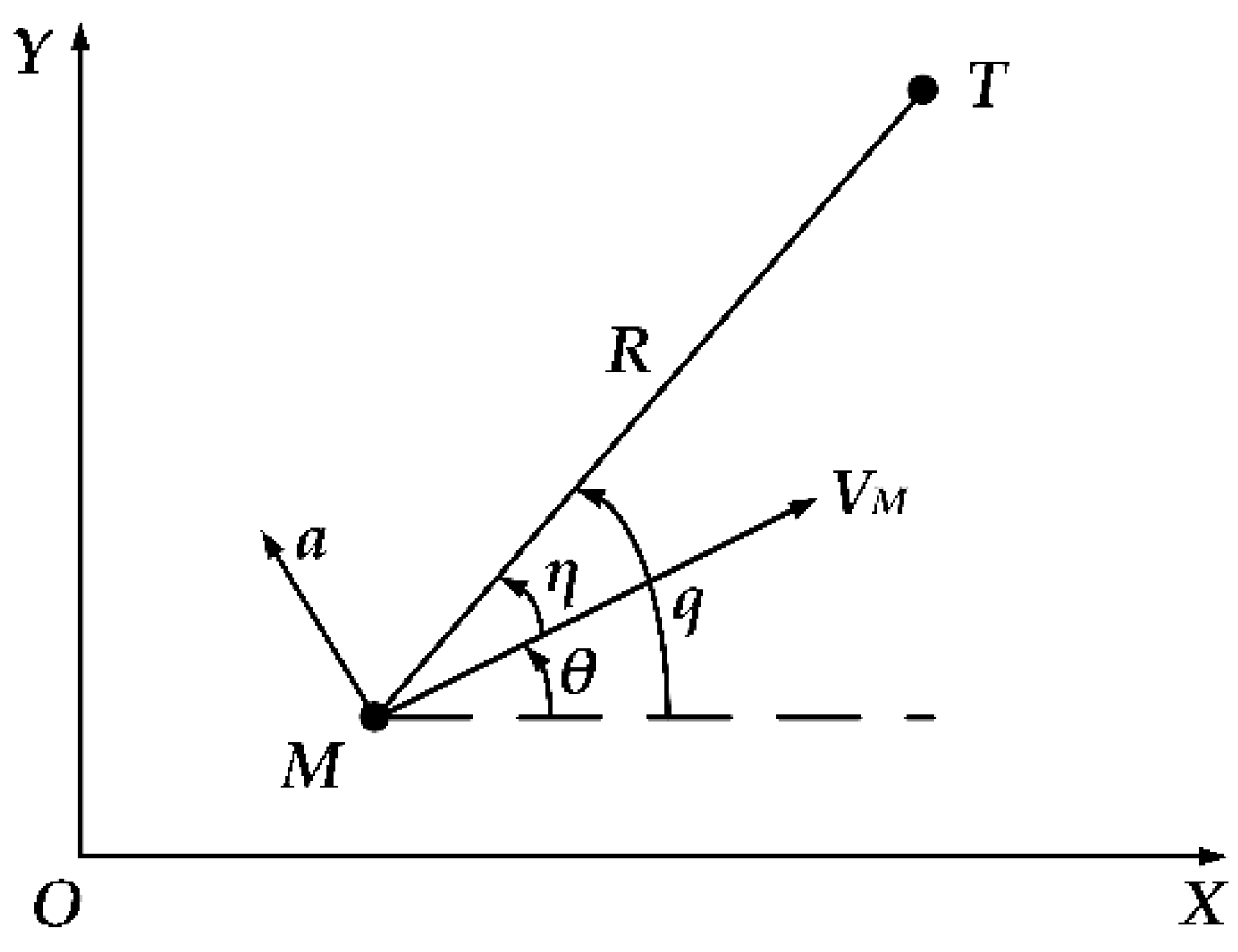
2. Problem Statement
3. Time-Varying Sliding Mode Guidance Law Design
3.1. Impact Time Control Guidance Law Design
- (1)
- A global sliding mode is obtained, i.e., s ≡ 0 for t ∈ [0, tf].
- (2)
- The states x1 and x2 converge to 0 when t approaches tf, i.e., x1(tf) = 0 and x2(tf) = 0.
3.2. FOV Constraint Consideration
- (1)
- tf ≥ tf0. It can be verified that t4 ≤ 0 and for t ∈ [0, tf]. Hence, x2 increases monotonically, and the minimum value of x2 is x2(0). To meet the FOV constraint, x2(0) ≥ x2min should be satisfied.
- (2)
- tf < tf0. In this case, t4 ∈ (0, tf). It can be obtained that for t ∈ [0, t4), and for t ∈ [t4, tf]. Hence, to meet the FOV constraint, x2(t4) ≥ x2min should be satisfied. The value of x2(t4) can be calculated as follows:
3.3. Singularity Analysis
- (1)
- η(0) = 0. The initial value of F(t) in (13) can also be obtained by (19) and can be calculated asIt can be seen that the singularity occurs at η(0) = 0. Therefore, to avoid singularity, the initial lead angle cannot be 0. Remark 2 also gives a reason why the initial lead angle cannot be 0.
- (2)
- η(tf) = 0. According to (19), it can be verified that F(tf) = 0. Taking the derivative of F(t) with respect to t, we obtain
4. Closed-Loop and Maximum FOV Utilization Modification
4.1. Guidance Law Modification
- (1)
- If ts ∈ (0, ts0), then F(x1, x2, ts) > 0 and |η| increases monotonically.
- (2)
- If ts ∈ (ts0, −4x1/x2], then F(x1, x2, ts) < 0 and |η| decreases monotonically.
- (3)
- If ts = ts0, then F(x1, x2, ts) = 0 and .
| Algorithm 1.ts generation process |
| 1: for each time step do |
| 2: Calculate ts0 and ts1. If ts1 ≥ ts0, ts ← ts1, go to 6; if ts1 < ts0, calculate ε, go to 3. |
| 3: If ε ≤ εs, go to 4; if ε > εs, go to 5. |
| 4: ts ← ts0, go to 6. |
| 5: Calculate ts2. ts ← max{ts1, ts2}, go to 6. |
| 6: Substitute ts into guidance law to complete the simulation of this time step. |
| 7: end for |
4.2. Algorithm and Guidance Law Analysis
- (1)
- ts1(0) ≥ ts0(0). This case is shown in Figure 2a, and the coefficient ts = ts1 = tf − t throughout the process. It can be seen that ts is continuous with respect to t, and |η| converges monotonically.
- (2)
- Ts1(0) < ts0(0) and ε(0) ≤ εs. This case is shown in Figure 2b. ts1 = ts0 is satisfied at the time instant t = t1. For t ∈ [0, t1], we take ts = ts0, and the lead angle remains unchanged. For t ∈ (t1, tf], we take ts = ts1, and |η| converges monotonically. It can be observed that the coefficient ts is continuous at the switching point t = t1.
- (3)
- ts1(0) < ts0(0), ε(0) > εs and the value of the lead angle does not increase to ηmax. This case is shown in Figure 2c. For t ∈ [0, t2], we take ts = max{ts1, ts2} < ts0, and |η| increases monotonically. ts1 = ts0 is satisfied at the time instant t = t2. Note that ts = max{ts1, ts2} = ts1 at t = t2 because ts2 < ts0. For t ∈ [t2, tf], we take ts = ts1. It can be seen that the coefficient ts is continuous at the switching point t = t2.
- (4)
- ts1(0) < ts0(0), ε(0) > εs and the value of the lead angle increases to ηmax. This case is shown in Figure 2d. For t ∈ [0, t3], we take ts = max{ts1, ts2}, and |η| increases monotonically. ts1 < ts0 and ts2 ≈ ts0 at the time instant t = t3. For t ∈ (t3, t4], we take ts = ts0, and the lead angle remains unchanged. ts1 = ts0 is satisfied at the time instant t = t4. For t ∈ (t4, tf], we take ts = ts1, and |η| converges monotonically. The coefficient ts is continuous at the switching points t = t3 and t = t4.
5. Simulation and Analysis
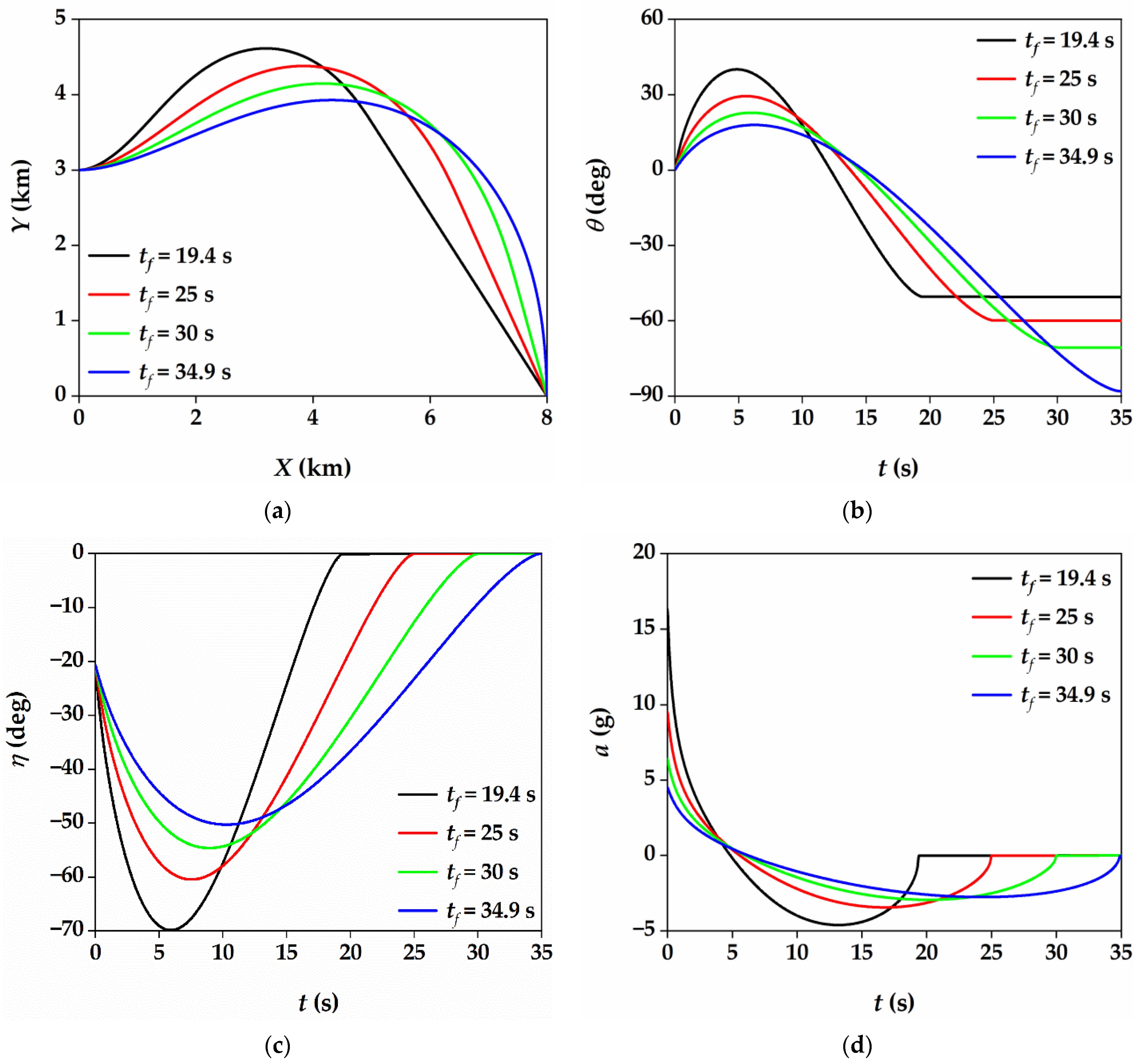
5.1. Performance Analysis of the Proposed Guidance Law
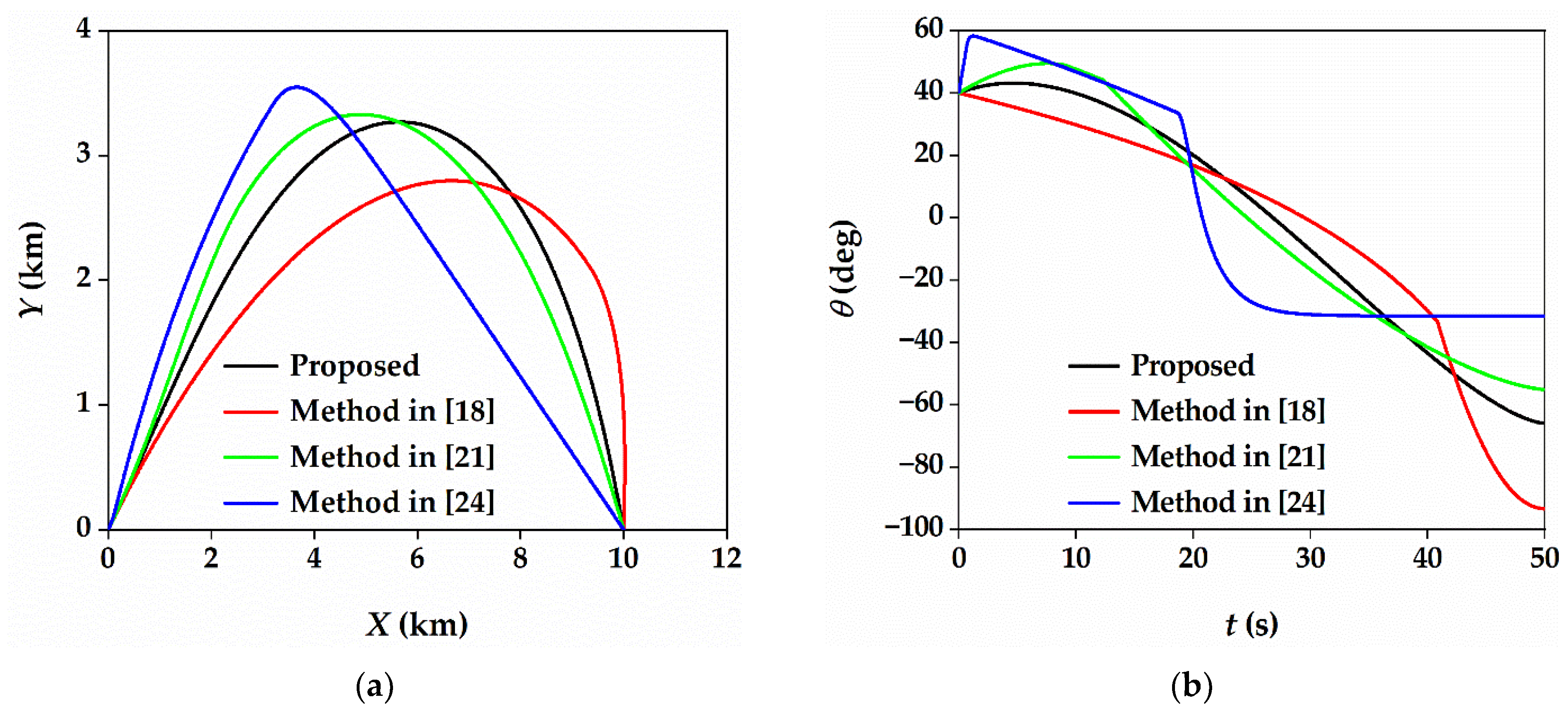
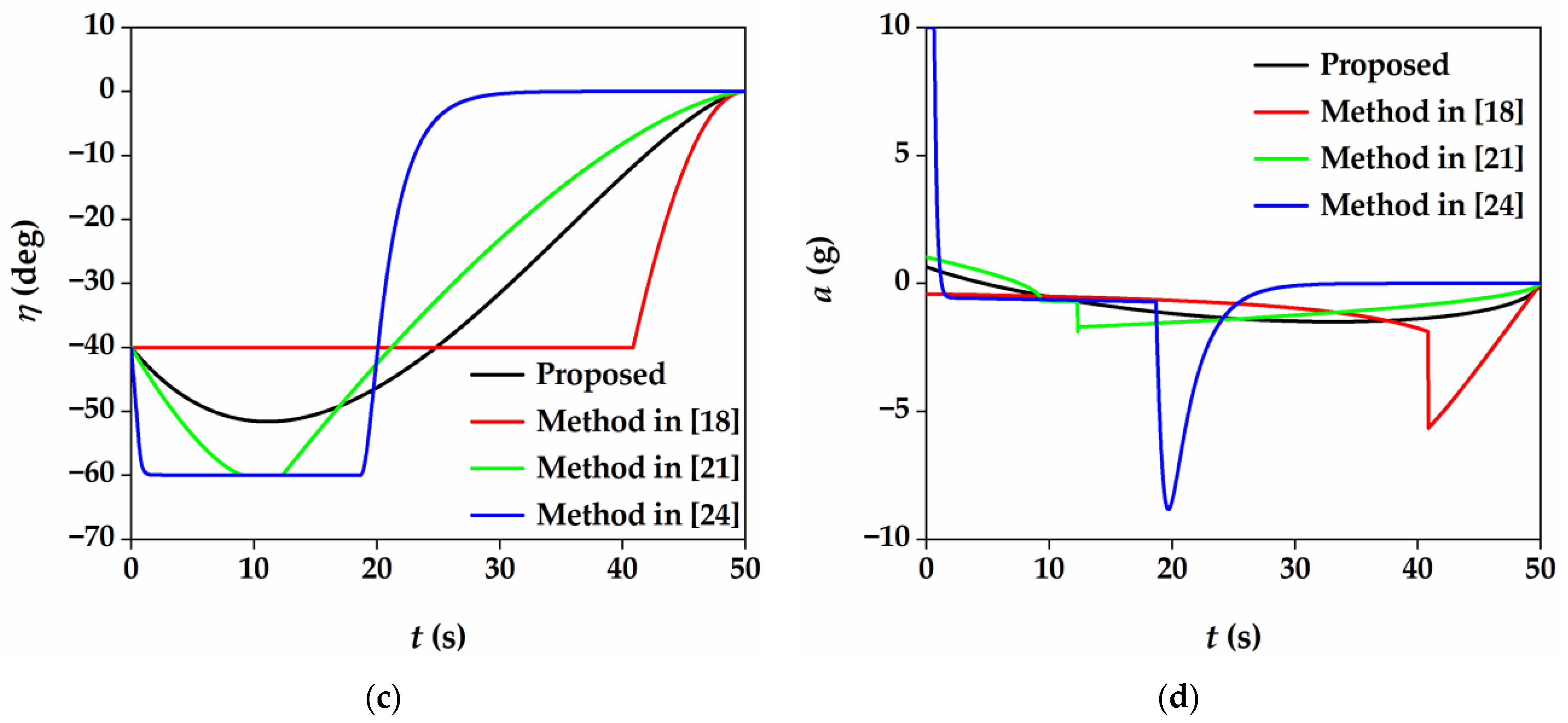
5.2. Comparative Work
5.3. Salvo Attack Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Homing Guidance Law for Cooperative Attack of Multiple Missiles. J. Guid. Control Dyn. 2010, 33, 275–280. [Google Scholar] [CrossRef]
- Chen, Y.D.; Wang, J.A.; Shan, J.Y.; Xin, M. Cooperative Guidance for Multiple Powered Missiles with Constrained Impact and Bounded Speed. J. Guid. Control Dyn. 2021, 44, 825–841. [Google Scholar] [CrossRef]
- Kumar, S.R.; Mukherjee, D. Terminal Time-Constrained Nonlinear Interception Strategies Against Maneuvering Targets. J. Guid. Control Dyn. 2021, 44, 200–209. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R.; Mukherjee, D. Three-Dimensional Guidance with Terminal Time Constraints for Wide Launch Envelops. J. Guid. Control Dyn. 2021, 44, 343–359. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation. J. Guid. Control Dyn. 2016, 39, 1885–1890. [Google Scholar] [CrossRef]
- Cho, D.; Kim, H.J.; Tahk, M.-J. Nonsingular Sliding Mode Guidance for Impact Time Control. J. Guid. Control Dyn. 2016, 39, 61–68. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.; Lin, D.; Zang, L. A New Impact Time and Angle Control Guidance Law for Stationary and Nonmaneuvering Targets. Int. J. Aerosp. Eng. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. New Impact Time and Angle Guidance Strategy via Virtual Target Approach. J. Guid. Control Dyn. 2018, 41, 1755–1765. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Sliding-Mode Guidance for Simultaneous Control of Impact Time and Angle. J. Guid. Control Dyn. 2019, 42, 394–401. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S. Impact Time and Angle Control Against Moving Targets with Look Angle Shaping. J. Guid. Control Dyn. 2020, 43, 1020–1025. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wu, H. Impact time control guidance law with field of view constraint. Aerosp. Sci. Technol. 2014, 39, 361–369. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wu, H. Impact time control guidance with field-of-view constraint accounting for uncertain system lag. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 515–529. [Google Scholar] [CrossRef]
- Shim, S.-W.; Hong, S.-M.; Moon, G.-H.; Tahk, M.-J. Impact Angle and Time Control Guidance Under Field-of-View Constraints and Maneuver Limits. Int. J. Aeronaut. Space Sci. 2018, 19, 217–226. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, J.Y.; Kim, H.J.; Kwon, H.H.; Park, J.S. Look-Angle-Shaping Guidance Law for Impact Angle and Time Control With Field-of-View Constraint. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1602–1612. [Google Scholar] [CrossRef]
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Optimal three-dimensional impact time guidance with seeker’s field-of-view constraint. Chin. J. Aeronaut. 2021, 34, 240–251. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I. Impact-Time-Control Guidance Law With Constraints on Seeker Look Angle. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2621–2627. [Google Scholar] [CrossRef]
- Lee, S.; Cho, N.; Kim, Y. Impact-Time-Control Guidance Strategy with a Composite Structure Considering the Seeker’s Field-of-View Constraint. J. Guid. Control Dyn. 2020, 43, 1566–1574. [Google Scholar] [CrossRef]
- Mukherjee, D.; Kumar, S.R. Nonlinear Impact Time Guidance with Constrained Field-of-View. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 3802–3807. [Google Scholar]
- Mukherjee, D.; Kumar, S.R. Field-of-View Constrained Impact Time Guidance against Stationary Targets. IEEE Trans. Aerosp. Electron. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Nonsingular Sliding-Mode Control for Field-of-View Constrained Impact Time Guidance. J. Guid. Control Dyn. 2018, 41, 1214–1222. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Impact Time Control with Generalized-Polynomial Range Formulation. J. Guid. Control Dyn. 2018, 41, 1190–1195. [Google Scholar] [CrossRef]
- Kim, H.-G.; Kim, H.J. Impact time control guidance considering seeker’s field-of-view limits. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 4160–4165. [Google Scholar]
- Kim, H.-G.; Kim, H.J. Backstepping-Based Impact Time Control Guidance Law for Missiles With Reduced Seeker Field-of-View. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 82–94. [Google Scholar] [CrossRef]
- Ha, I.-J.; Hur, J.-S.; Ko, M.-S.; Song, T.-L. Performance analysis of PNG laws for randomly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 713–721. [Google Scholar] [CrossRef]


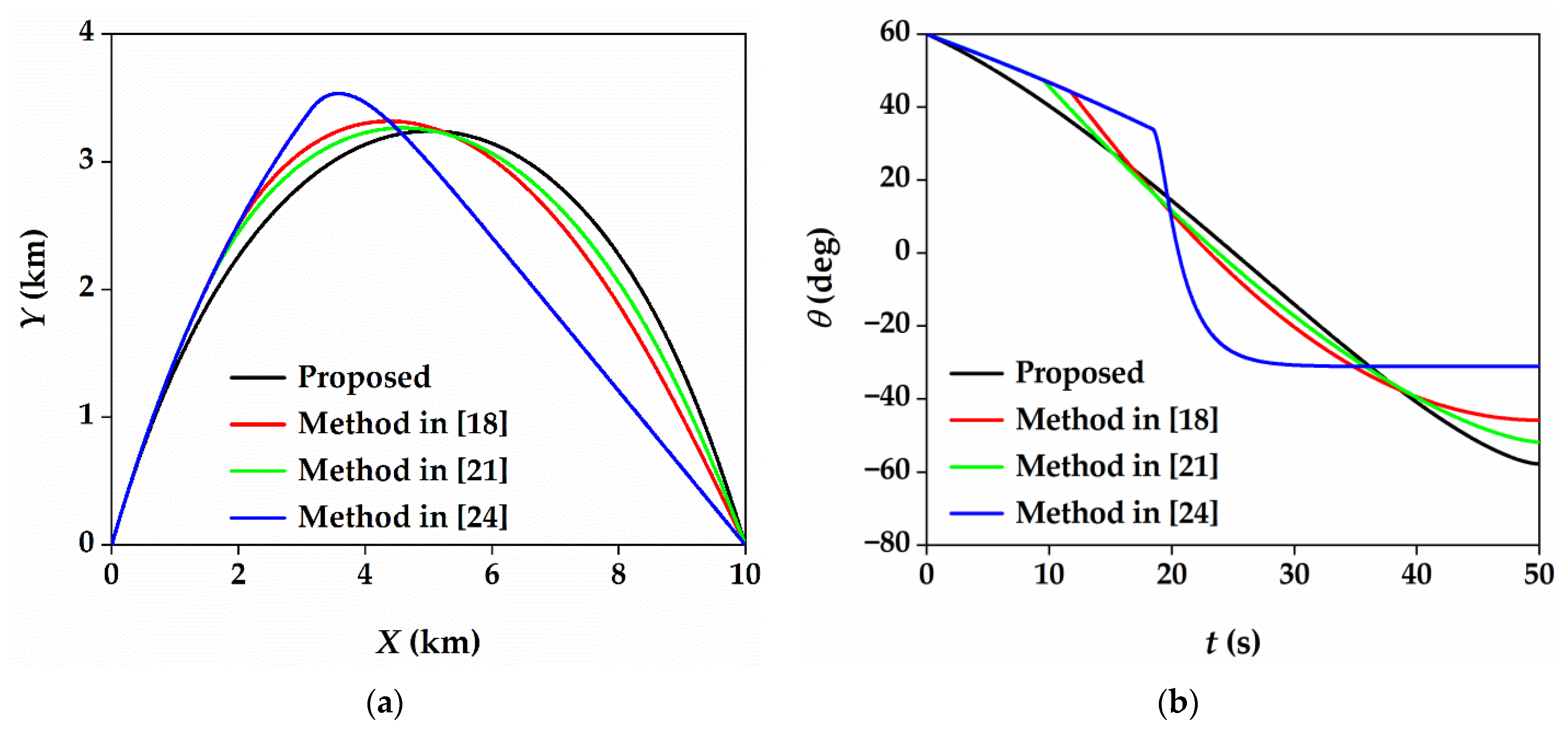
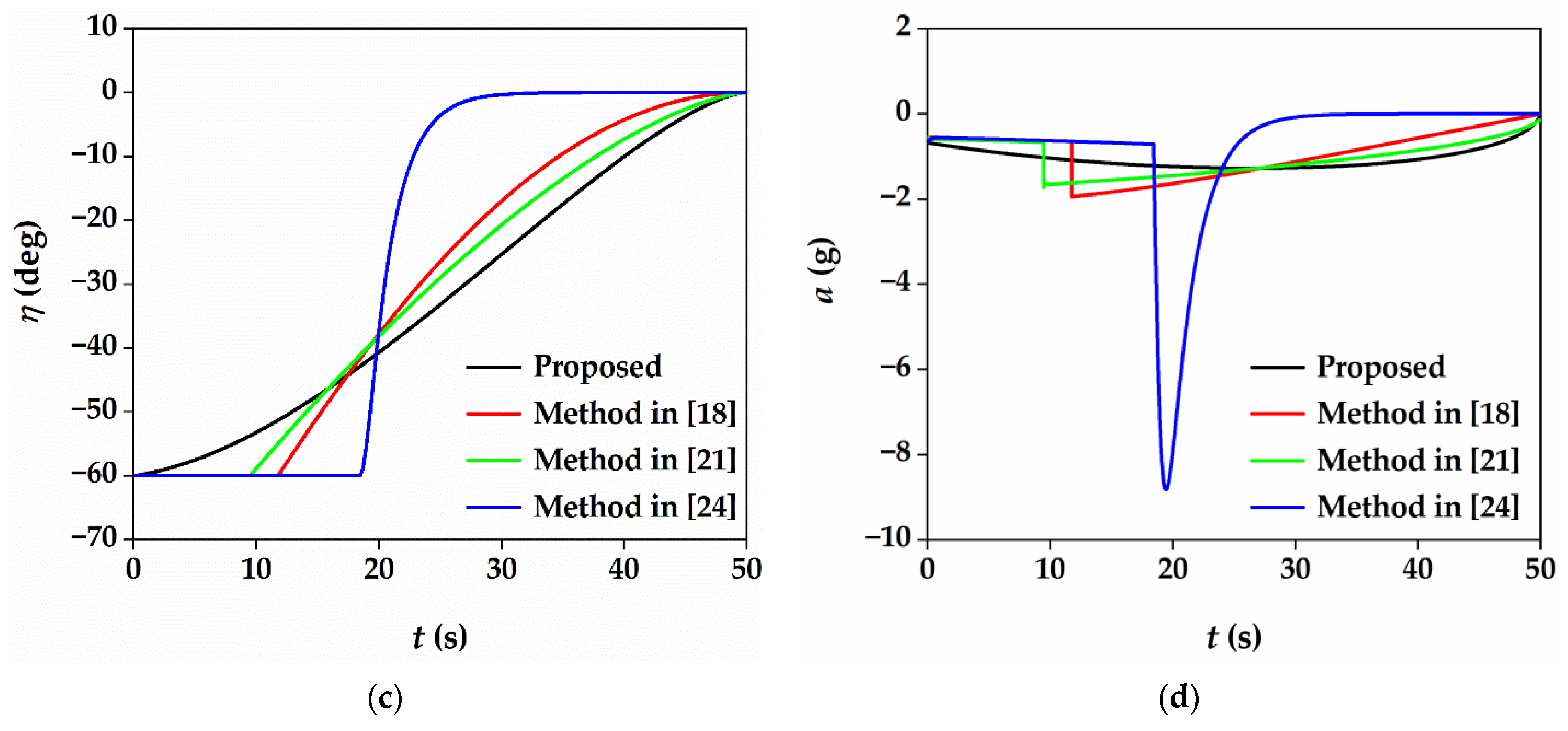

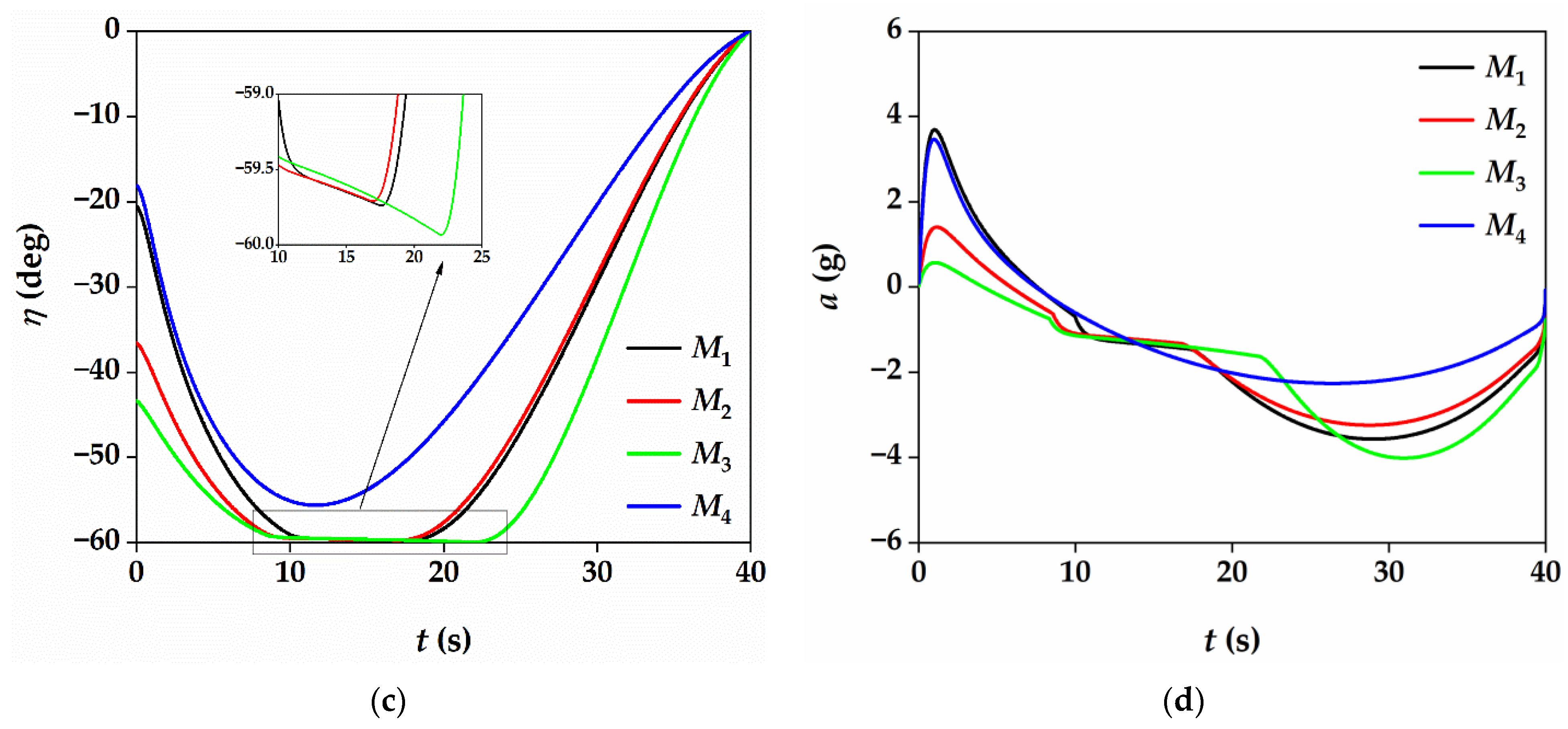
| θ0 = 40° | θ0 = 60° | |||
|---|---|---|---|---|
| tdmin (s) | tdmax (s) | tdmin (s) | tdmax (s) | |
| Proposed | 40.4 | 67.4 | 41.1 | 71.2 |
| Method in [18] | 42.1 | 51.4 | 44.8 | 72.2 |
| Method in [21] | 40.6 | 69.9 | 41.4 | 71.7 |
| Method in [24] | 40.5 | 71.9 | 40.8 | 72.1 |
| X0 (m) | Y0 (m) | VM (m/s) | θ0 (°) | |
|---|---|---|---|---|
| M1 | 0 | 3000 | 300 | 0 |
| M2 | 1000 | 3500 | 280 | 10 |
| M3 | 1500 | 2800 | 270 | 20 |
| M4 | 500 | 3200 | 260 | −5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Wang, X.; Wang, Z. Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace 2021, 8, 251. https://doi.org/10.3390/aerospace8090251
Ma S, Wang X, Wang Z. Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace. 2021; 8(9):251. https://doi.org/10.3390/aerospace8090251
Chicago/Turabian StyleMa, Shuai, Xugang Wang, and Zhongyuan Wang. 2021. "Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control" Aerospace 8, no. 9: 251. https://doi.org/10.3390/aerospace8090251
APA StyleMa, S., Wang, X., & Wang, Z. (2021). Field-of-View Constrained Impact Time Control Guidance via Time-Varying Sliding Mode Control. Aerospace, 8(9), 251. https://doi.org/10.3390/aerospace8090251






