Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump
Abstract
:1. Introduction
2. Numerical Method and Validation
2.1. Numerical Method
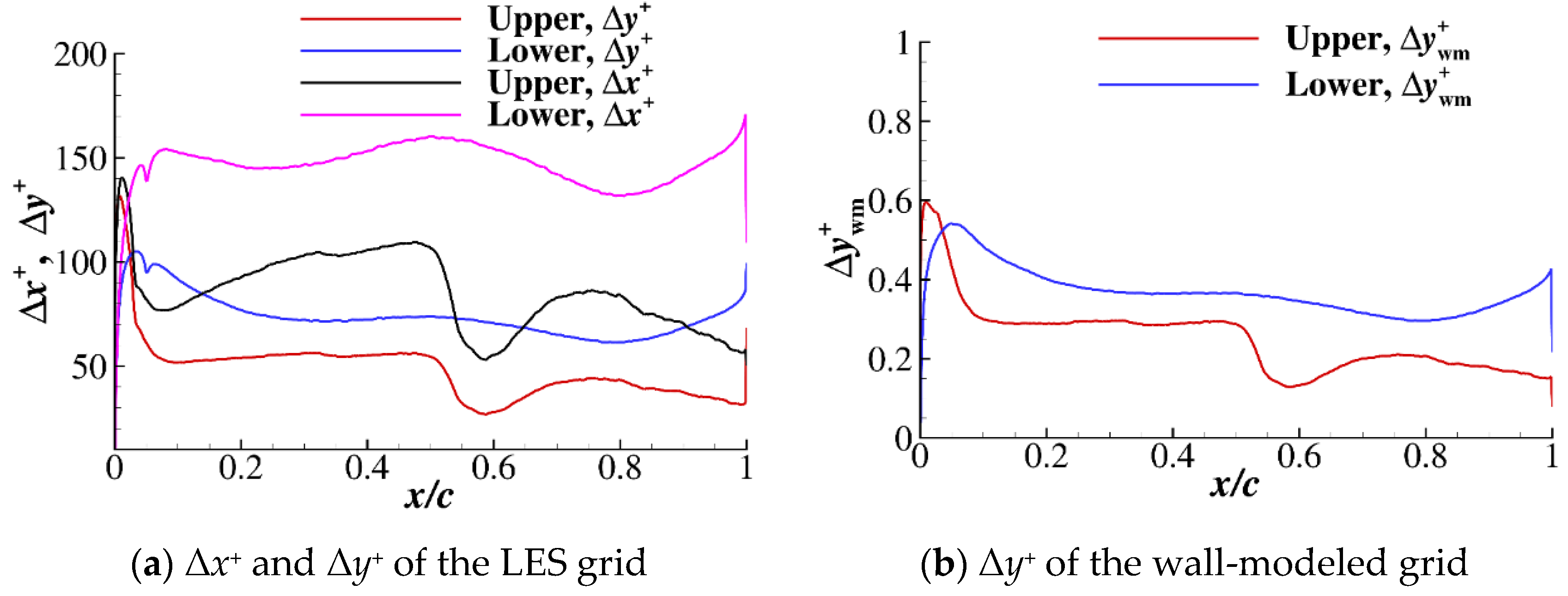
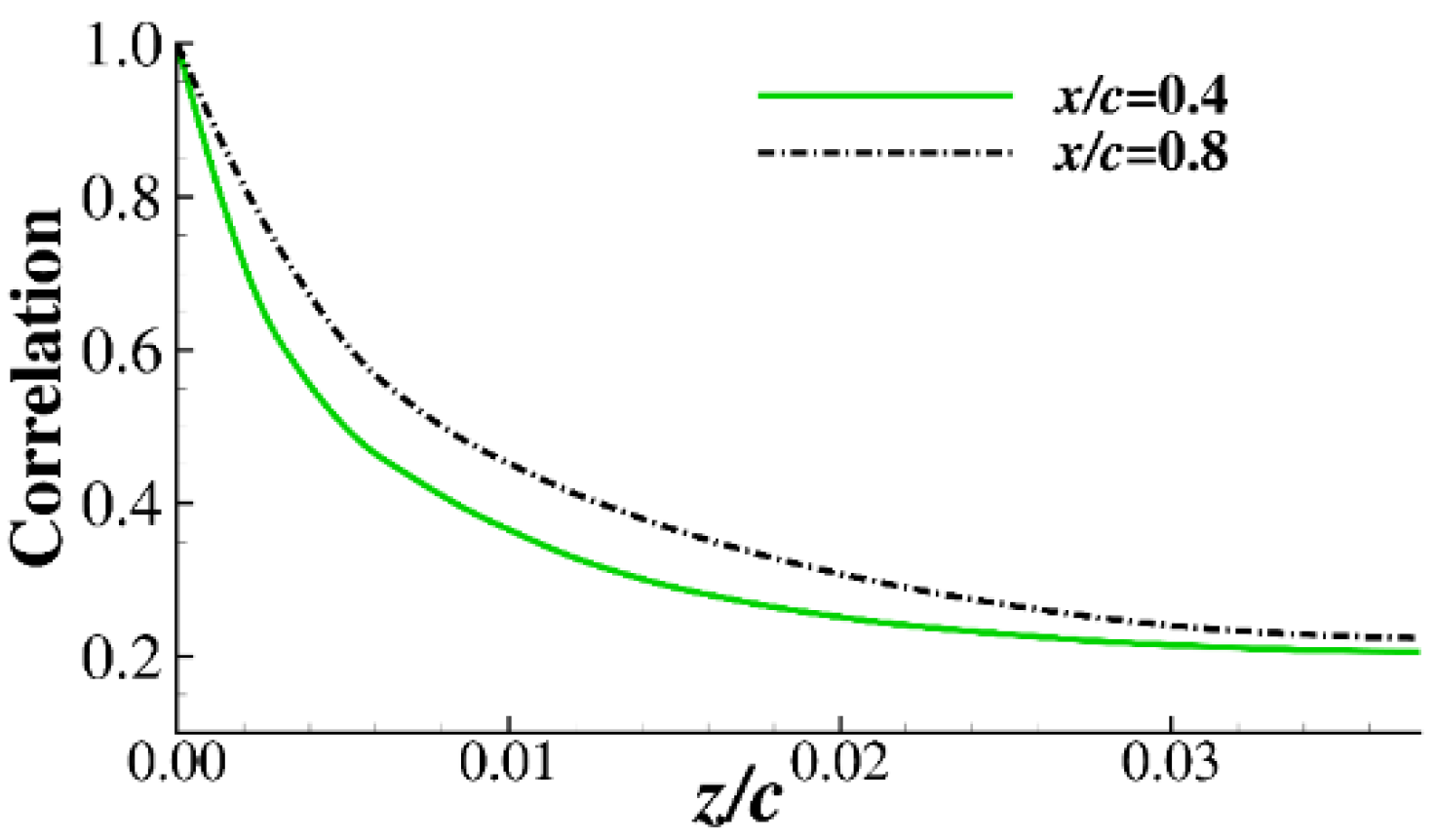
2.2. Computational Grid
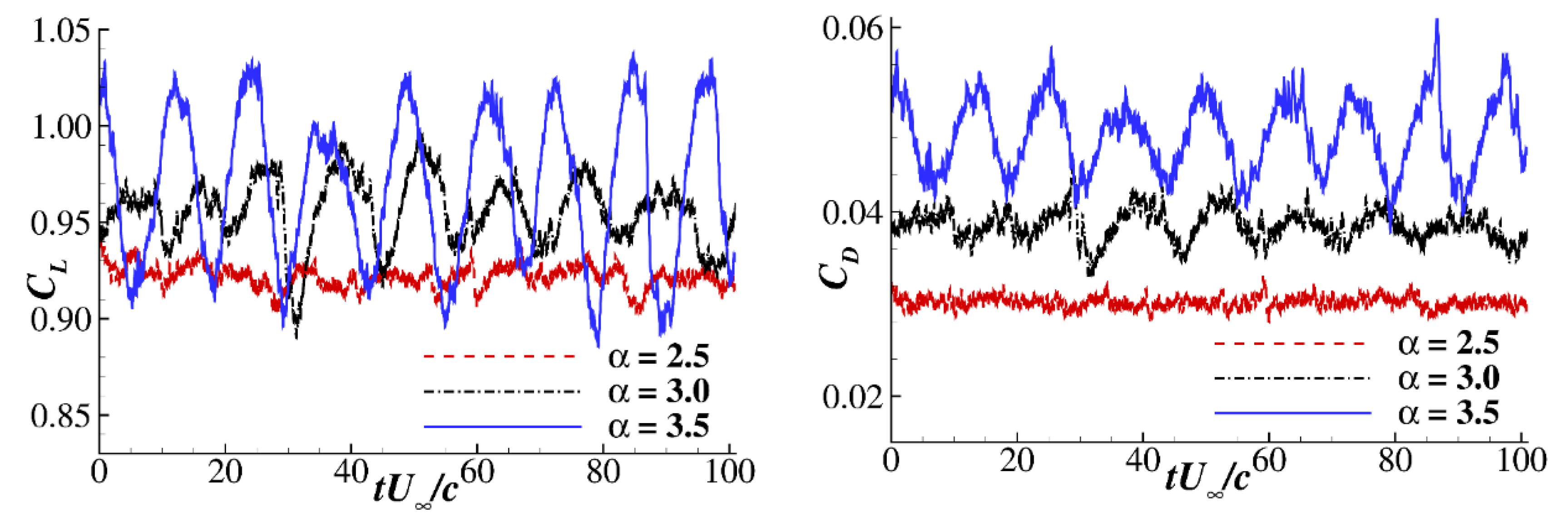
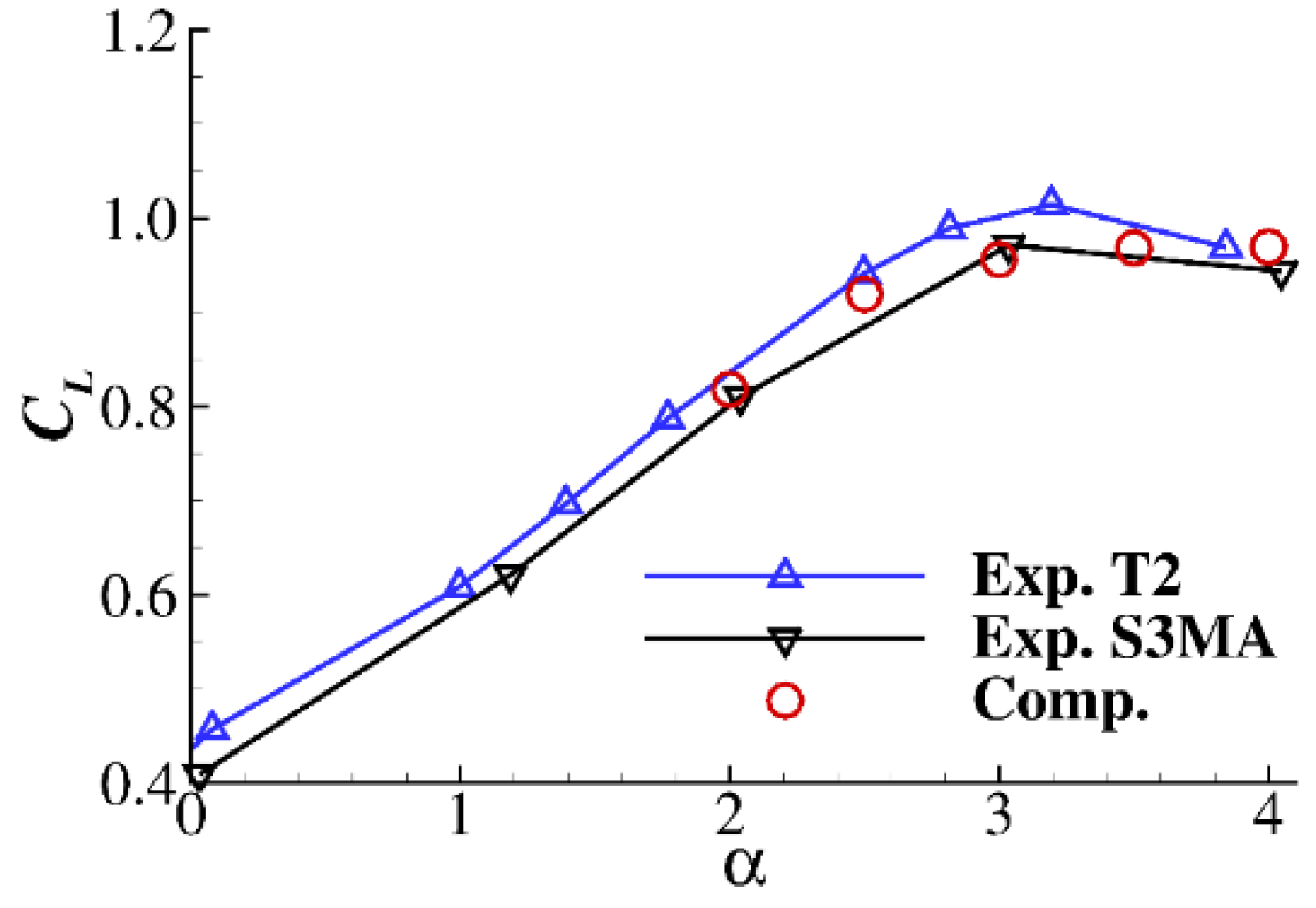
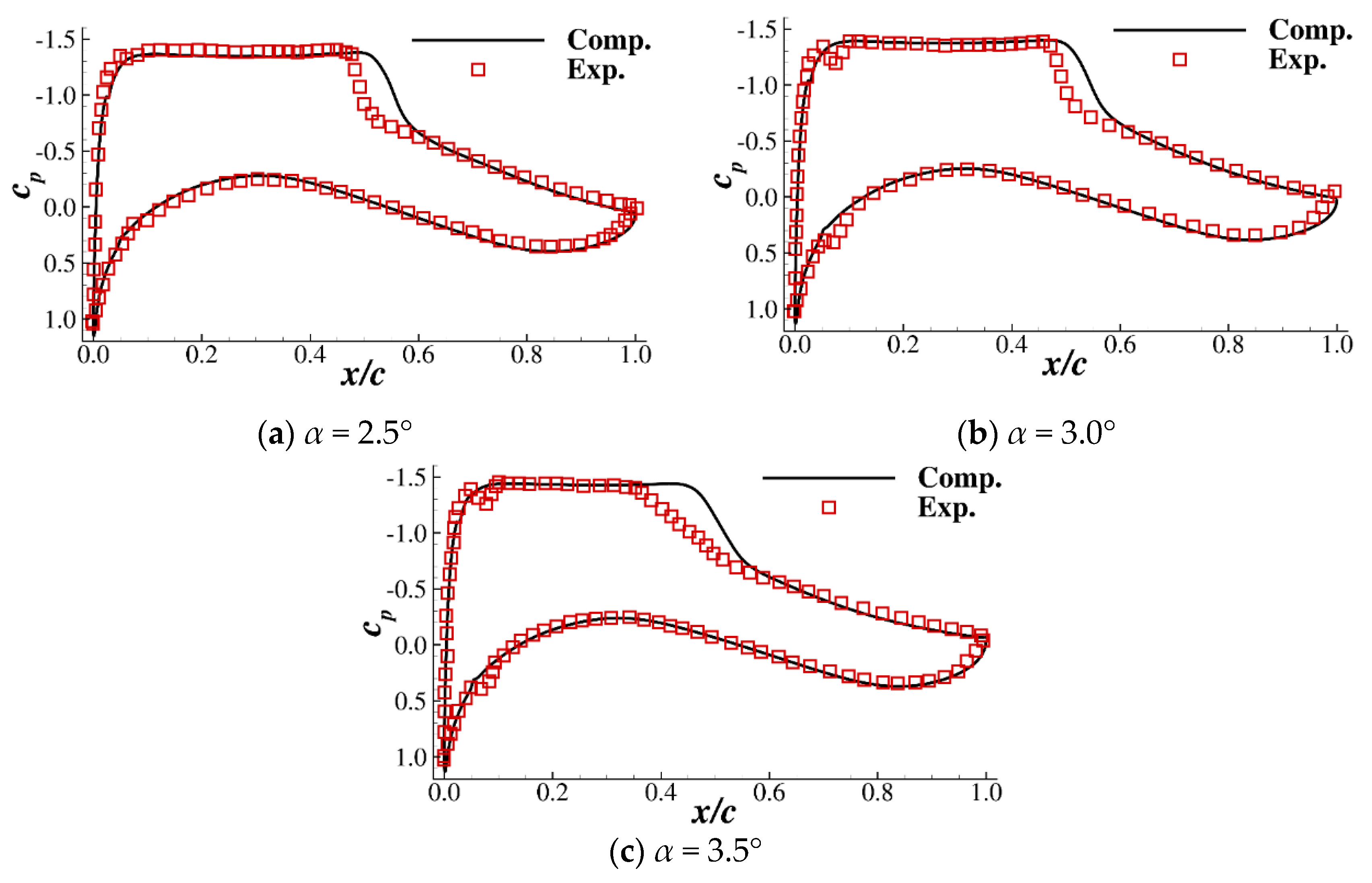
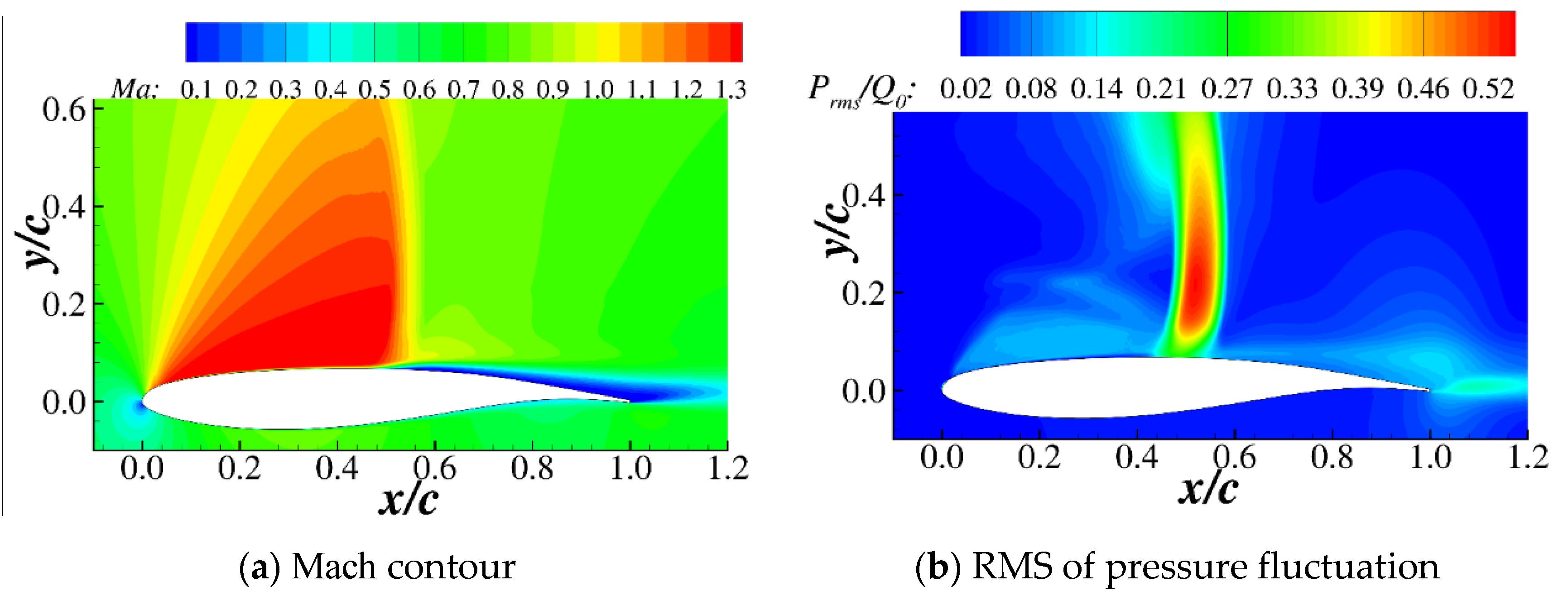
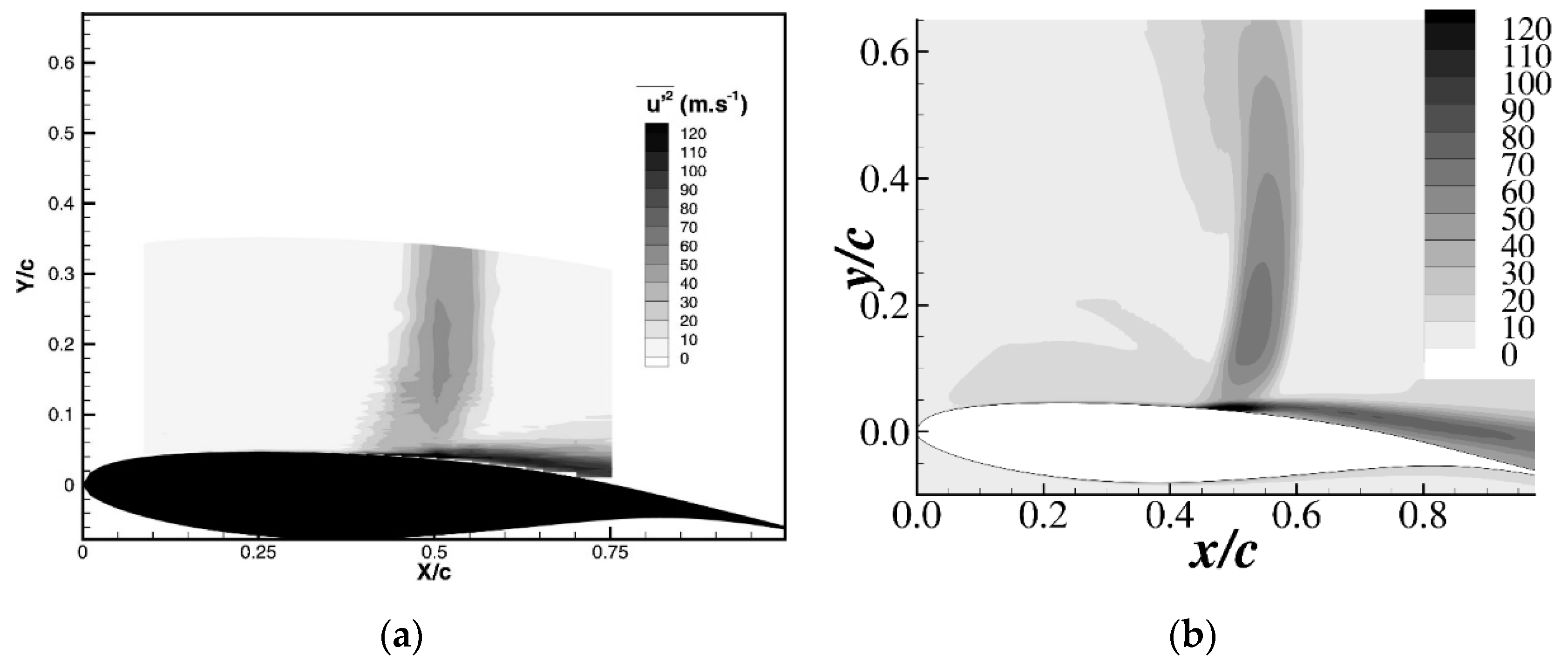
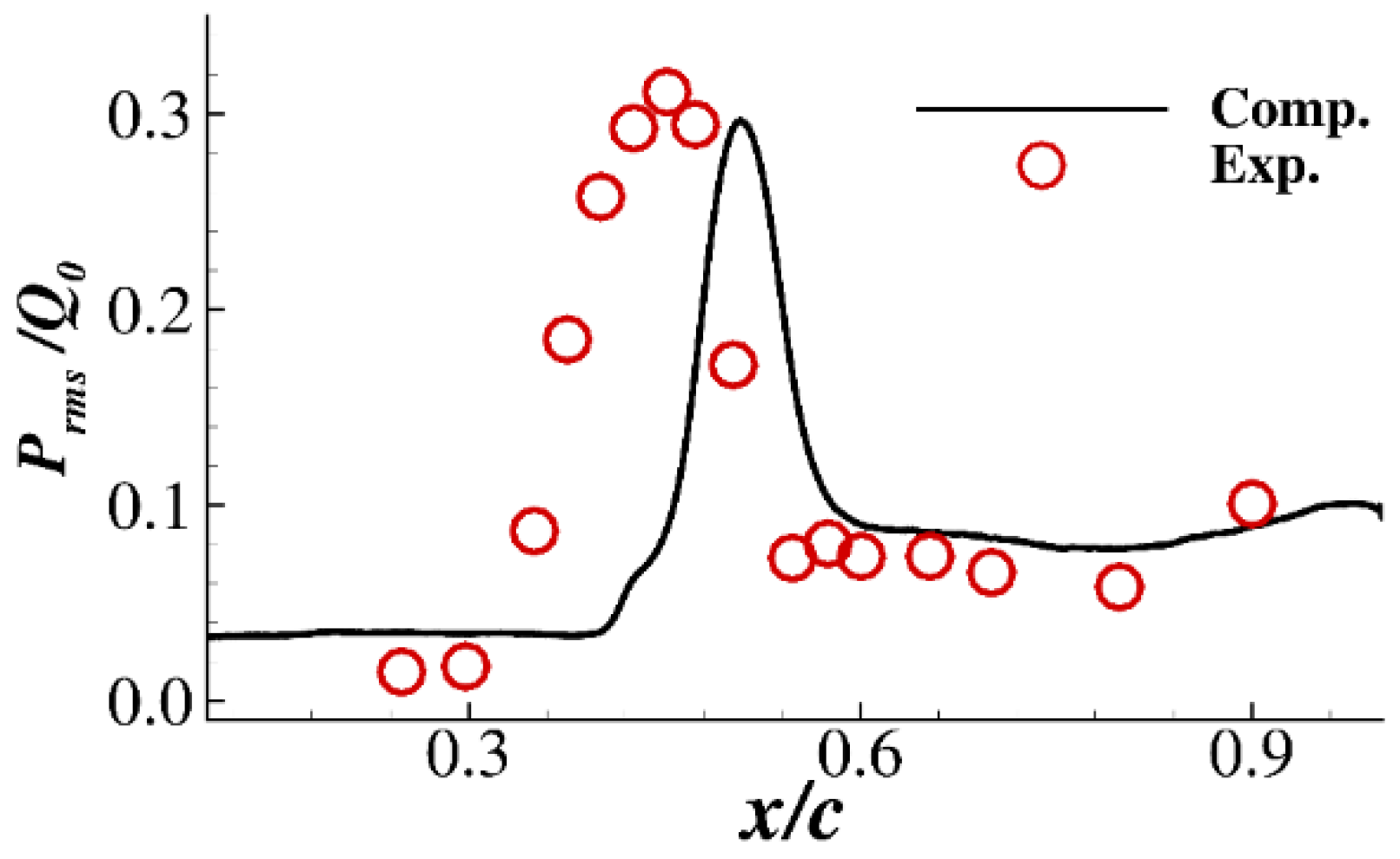
2.3. Validation of the Baseline OAT15A Airfoil
3. Numerical Study of Shock Control Bump
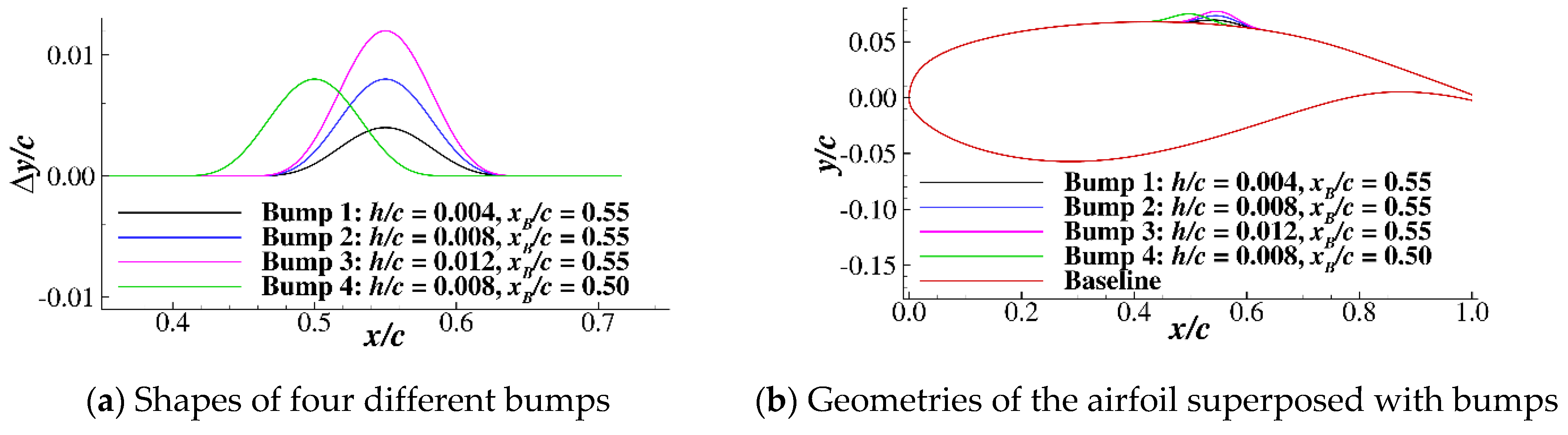
3.1. Shape of the Shock Control Bump
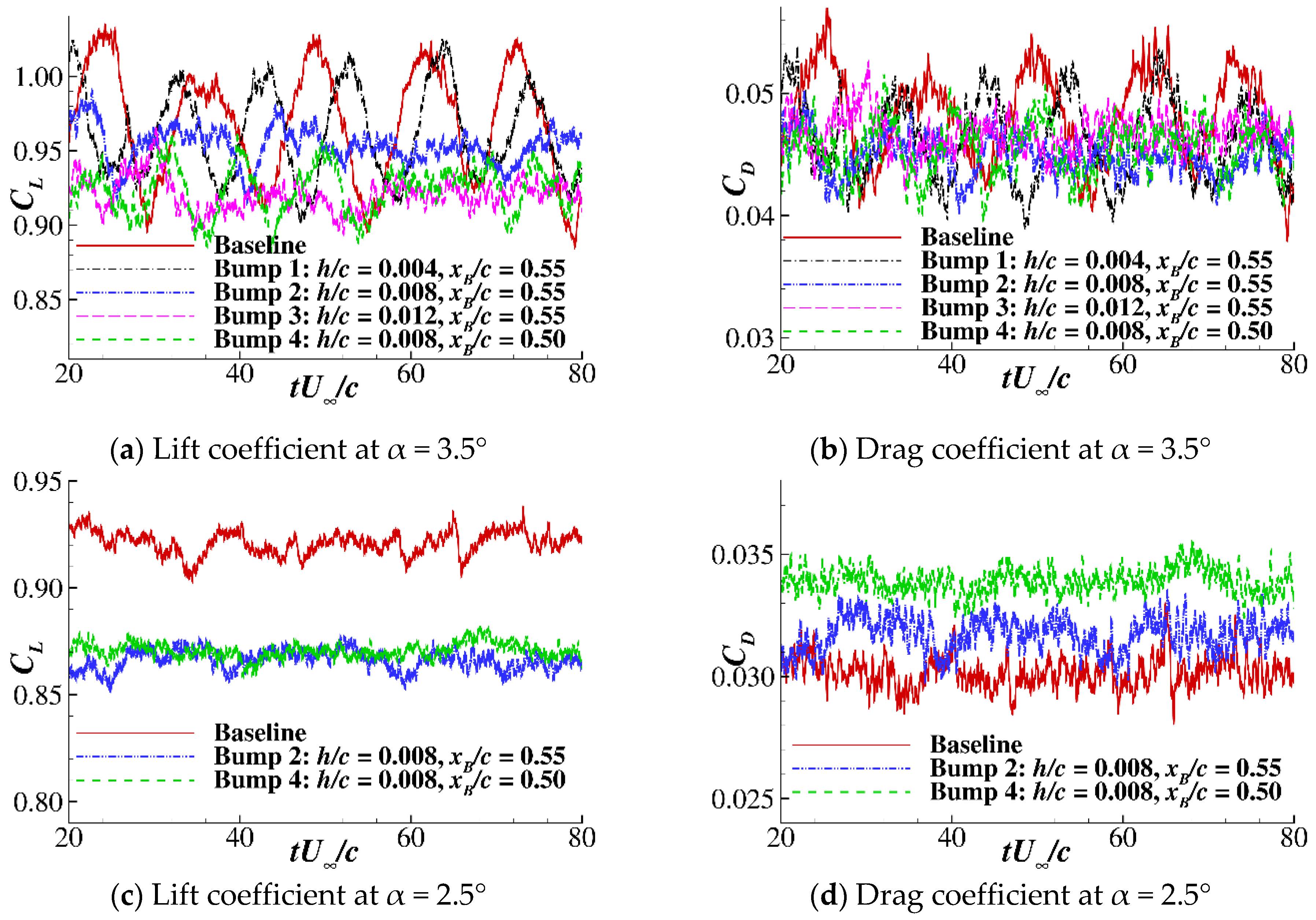
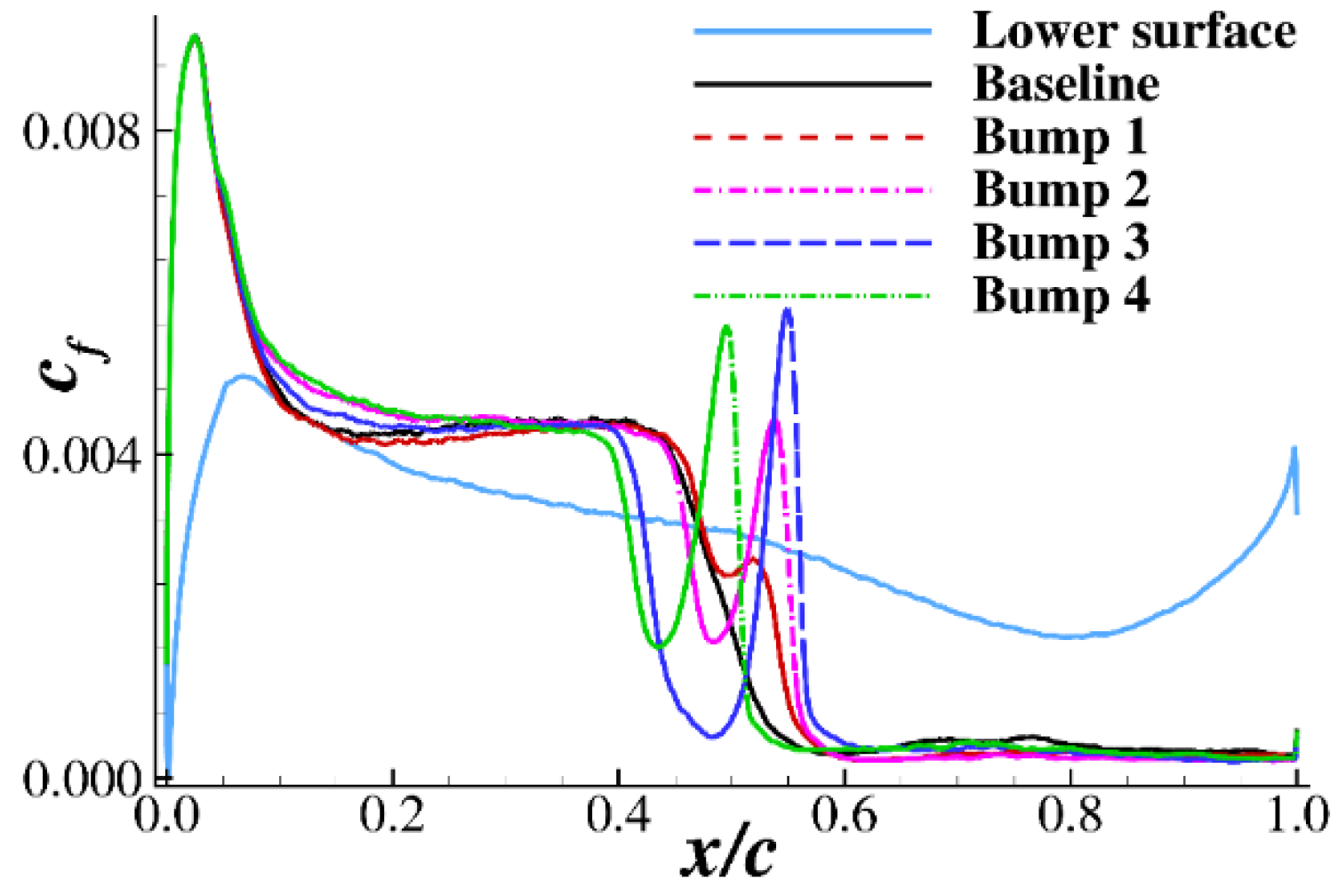
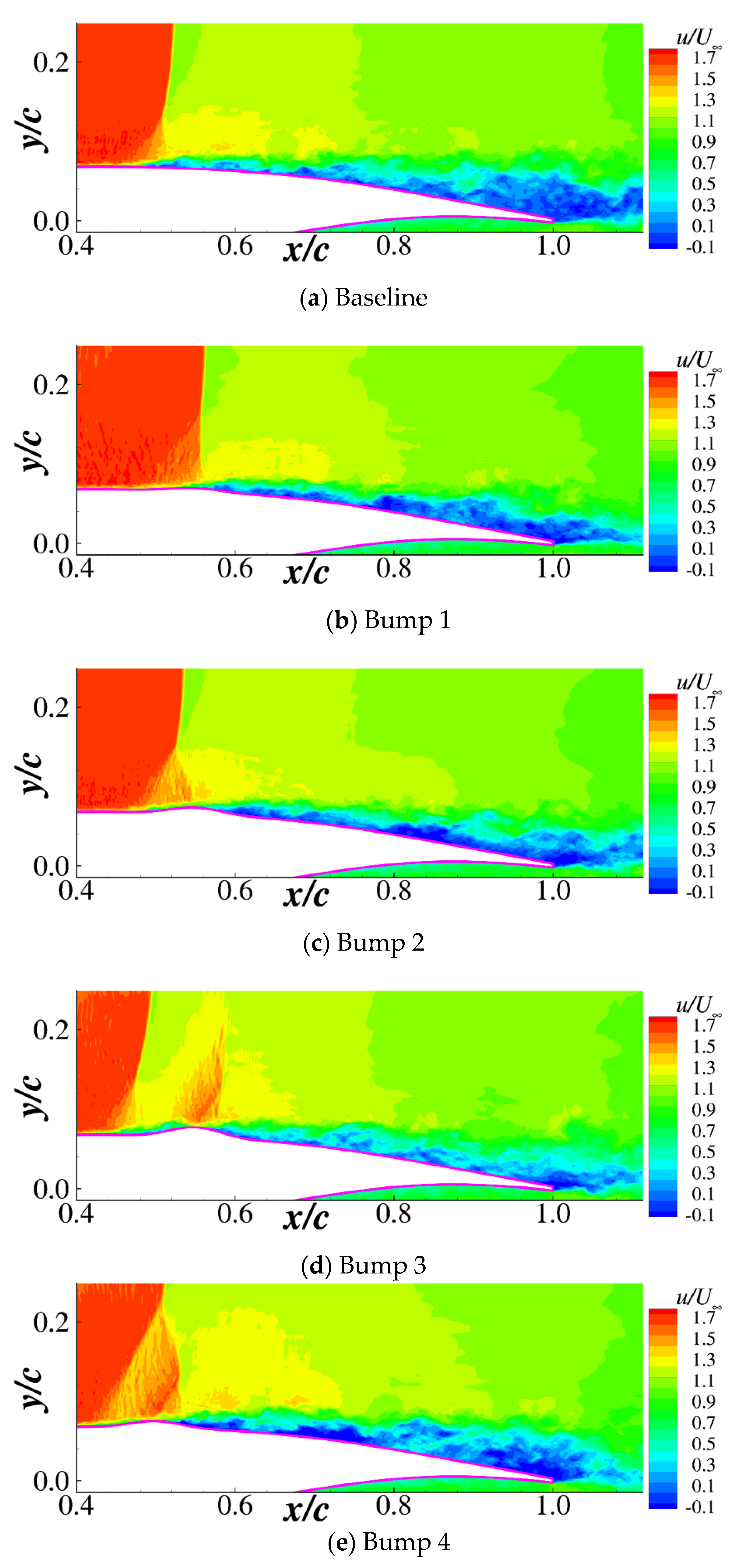
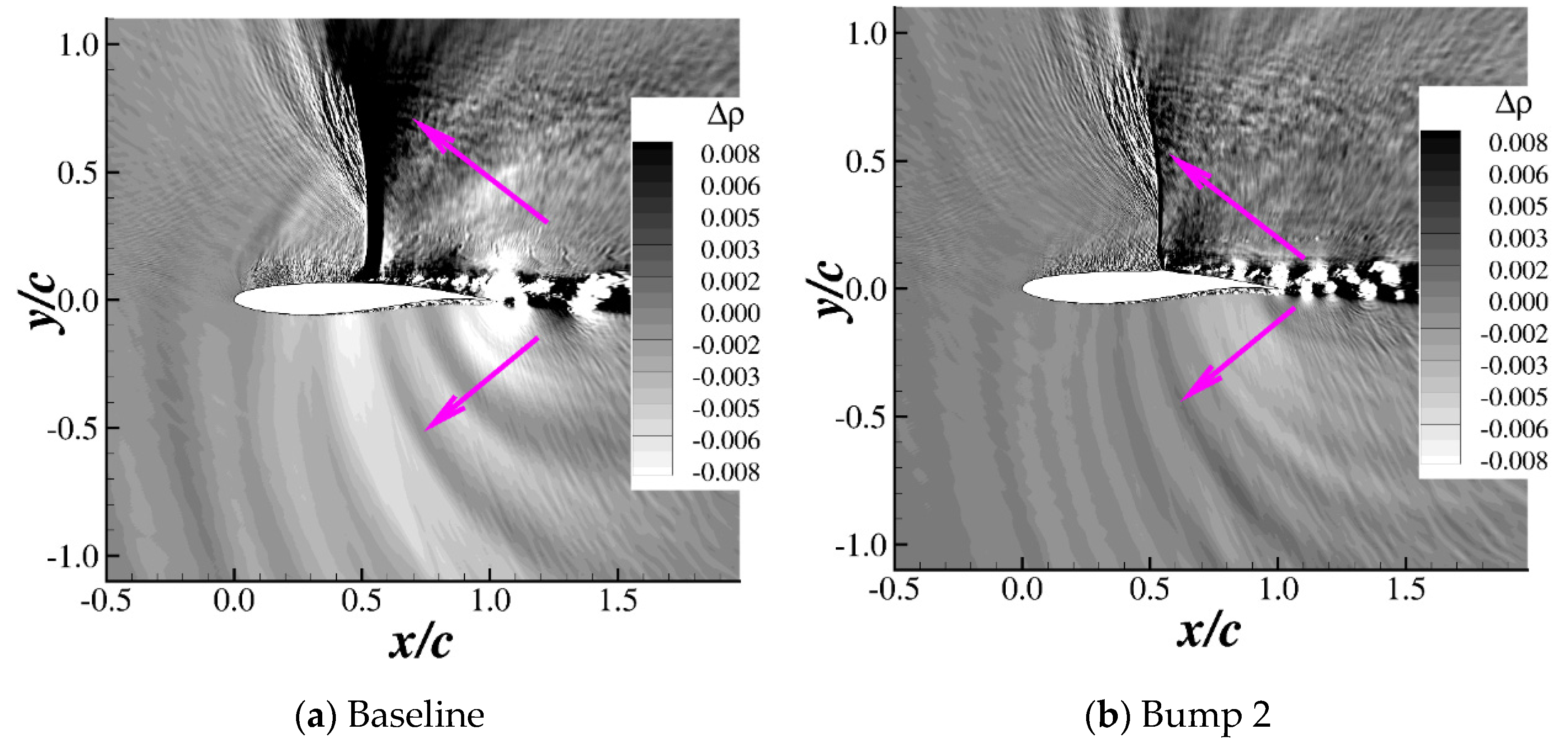
3.2. Time-Averaged Characteristics of the Airfoil with Bumps
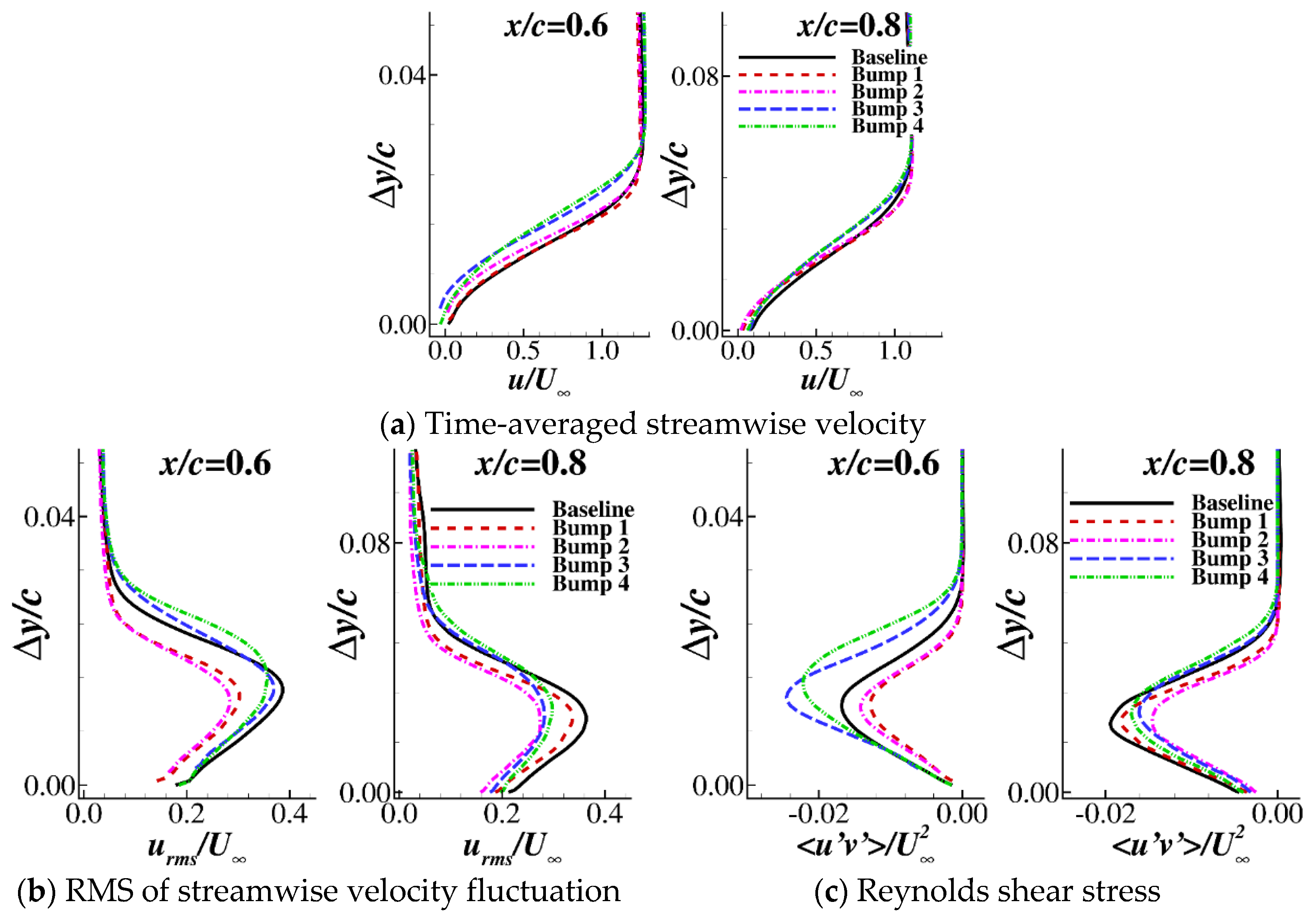
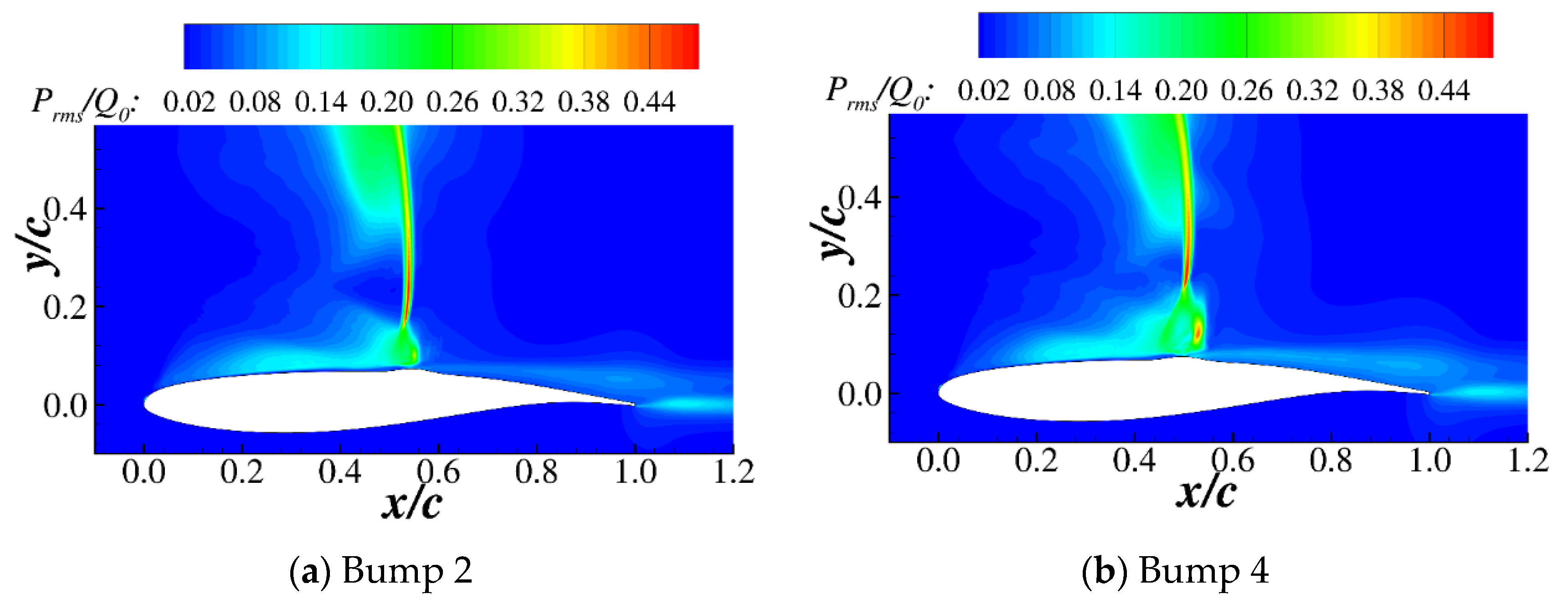
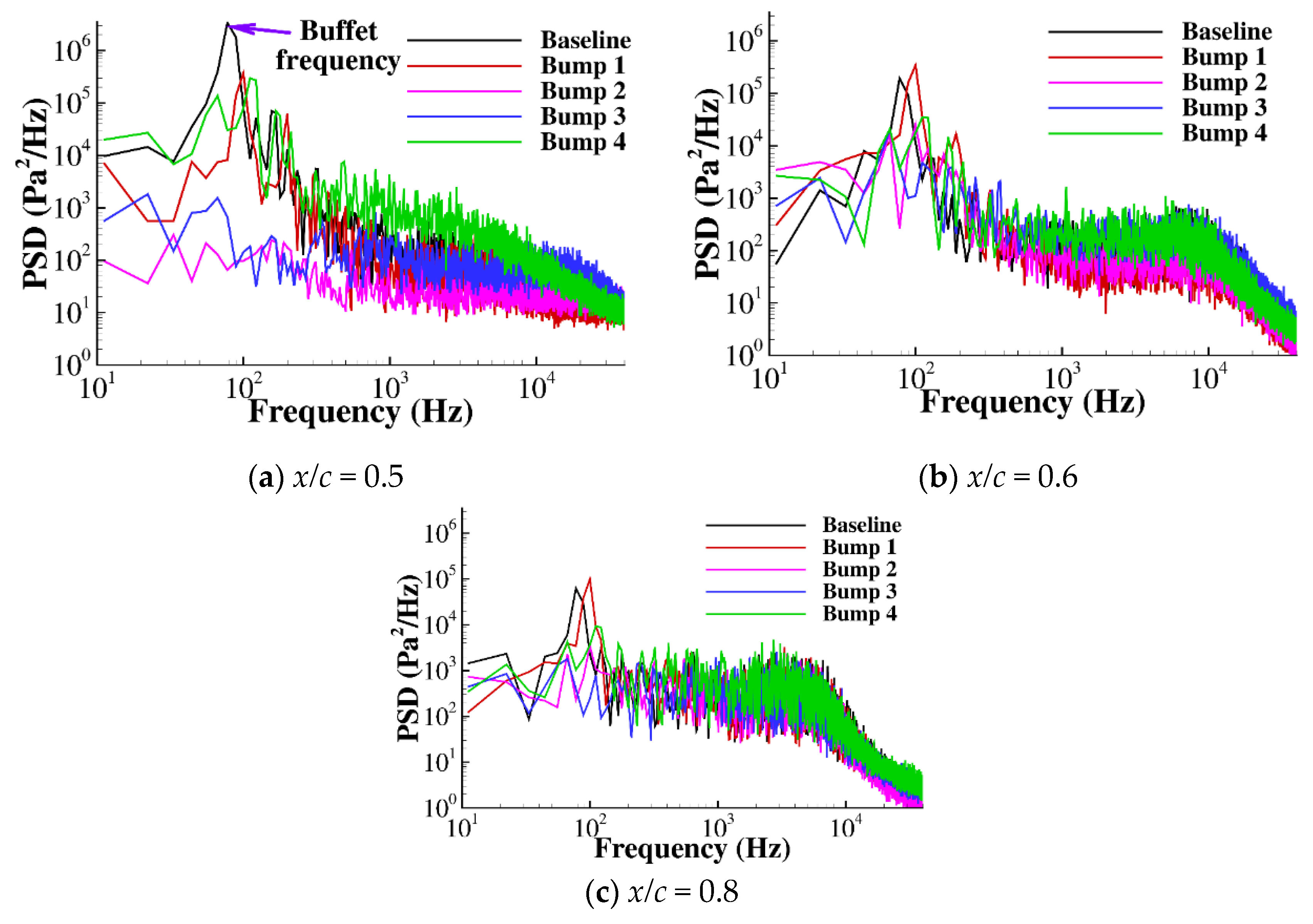
3.3. Fluctuation Characteristics of the Airfoil with Bumps
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niu, W.; Zhang, Y.; Chen, H.; Zhang, M. Numerical study of a supercritical airfoil/wing with variable-camber technology. Chin. J. Aeronaut. 2020, 33, 1850–1866. [Google Scholar] [CrossRef]
- Li, R.; Deng, K.; Zhang, Y.; Chen, H. Pressure distribution guided supercritical wing optimization. Chin. J. Aeronaut. 2018, 31, 1842–1854. [Google Scholar] [CrossRef]
- Lee, B.H.K. Self-sustained shock oscillations on airfoils at transonic speeds. Prog. Aerosp. Sci. 2001, 37, 147–196. [Google Scholar] [CrossRef]
- Kenway, G.K.W.; Martins, J.R.R.A. Buffet-onset constraint formulation for aerodynamic shape optimization. AIAA J. 2017, 55, 1930–1947. [Google Scholar] [CrossRef]
- Hilton, W.F.; Fowler, R.G. Photographs of Shock Wave Movement, NPL R &M No. 2692; National Physical Laboratories: Teddington, UK, 1947. [Google Scholar]
- Iovnovich, M.; Raveh, D.E. Reynolds-averaged Navier-stokes Study of the Shock-buffet Instability Mechanism. AIAA J. 2012, 50, 880–890. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, C.; Ye, Z. Research Advances on Wing/Airfoil Transonic Buffet. Acta Aeronaut. Astronaut. Sin. 2015, 36, 1056–1075. (In Chinese) [Google Scholar]
- Pearcey, H.H.; Osborne, J.; Haines, A.B. The Interaction Between Local Effects at the Shock and Rear Separation—A Source of Significant Scale Effects in Wind-Tunnel Tests on Aerofoils and Wings, AGARD CP-35; Transonic Aerodynamics: Paris, France, 1968; pp. 1–23. [Google Scholar]
- Tijdeman, H.; Seebass, R. Transonic flow past oscillating airfoils. Annu. Rev. Fluid Mech. 1980, 12, 181–222. [Google Scholar] [CrossRef]
- Lee, B.H.K.; Murty, H.; Jiang, H. Role of Kutta waves on oscillatory shock motion on an airfoil. AIAA J. 1994, 32, 789–796. [Google Scholar] [CrossRef]
- Hartmann, A.; Feldhusen, A.; Schröder, W. On the interaction of shock waves and sound waves in transonic buffet flow. Phys. Fluids 2013, 25, 026101. [Google Scholar] [CrossRef]
- Chen, L.; Xu, C.; Lu, X. Numerical investigation of the compressible flow past an aerofoil. J. Fluid Mech. 2009, 643, 97–126. [Google Scholar] [CrossRef] [Green Version]
- Crouch, J.D.; Garbaruk, A.; Strelets, M. Global instability in the onset of transonic-wing buffet. J. Fluid Mech. 2019, 881, 3–22. [Google Scholar] [CrossRef]
- Jacquin, L.; Molton, P.; Deck, S.; Maury, B.; Soulevant, D. Experimental study of shock oscillation over a transonic supercritical profile. AIAA J. 2009, 47, 1985–1994. [Google Scholar] [CrossRef]
- Hartmann, A.; Steimle, P.C.; Klaas, M.; Schröder, W. Time-Resolved Particle Image Velocimetry of Unsteady Shock Wave-Boundary Layer Interaction. AIAA J. 2011, 49, 195–204. [Google Scholar] [CrossRef]
- Zhao, Y.; Dai, Z.; Tian, Y.; Xiong, Y. Flow characteristics around airfoils near transonic buffet onset conditions. Chin. J. Aeronaut. 2020, 33, 1405–1420. [Google Scholar] [CrossRef]
- Grossi, F.; Braza, M.; Hoarau, Y. Prediction of transonic buffet by delayed detached-eddy simulation. AIAA J. 2014, 52, 2300–2312. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, Y.; Kawai, S. Wall-Modeled Large-Eddy Simulation of Transonic Airfoil Buffet at High Reynolds Number. AIAA J. 2018, 56, 2372–2388. [Google Scholar] [CrossRef]
- Caruana, D.; Mignosi, A.; Corrège, M.; Le Pourhiet, A.; Rodde, A. Buffet and buffeting control in transonic flow. Aerosp. Sci. Technol. 2005, 9, 605–616. [Google Scholar] [CrossRef]
- Huang, J.; Xiao, Z.; Liu, J.; Fu, S. Simulation of shock wave buffet and its suppression on an OAT15A supercritical airfoil by IDDES, SCIENCE CHINA Physics. Mech. Astron. 2012, 55, 260–271. [Google Scholar] [CrossRef]
- Deng, F.; Qin, N.; Liu, X.; Yu, X.; Zhao, N. Shock control bump optimization for a low sweep supercritical wing. Sci. China Technol. Sci. 2013, 56, 2385–2390. [Google Scholar] [CrossRef]
- Huang, J.; Xiao, Z.; Fu, S.; Zhang, M. Study of control effects of vortex generators on a supercritical wing. Sci. China Technol. Sci. 2010, 53, 2038–2048. [Google Scholar] [CrossRef]
- Deng, F.; Qin, N. Quantitative comparison of 2D and 3D shock control bumps for drag reduction on transonic wings. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 2344–2359. [Google Scholar] [CrossRef]
- Mazaheri, K.; Nejati, A.; Kiani, K.C. Application of the adjoint multi-point and the robust optimization of shock control bump for transonic aerofoils and wings. Eng. Optim. 2016, 48, 1887–1909. [Google Scholar] [CrossRef]
- Tian, Y.; Gao, S.; Liu, P.; Wang, J. Transonic buffet control research with two types of shock control bump based on RAE2822 airfoil. Chin. J. Aeronaut. 2017, 30, 1681–1696. [Google Scholar] [CrossRef]
- Sabater, C.; Bekemeyer, P.; Görtz, S. Efficient Bilevel Surrogate Approach for Optimization Under Uncertainty of Shock Control Bumps. AIAA J. 2020, 58, 5228–5242. [Google Scholar] [CrossRef]
- Jia, N.; Zhang, Y.; Chen, H. The drag reduction study of the supercritical airfoil with shock control bump considering the robustness. Sci. Sin. Phys. Mech. Astron. 2014, 44, 249–257. (In Chinese) [Google Scholar]
- Jinks, E.; Bruce, P.; Santer, M. Optimisation of adaptive shock control bumps with structural constraints. Aerosp. Sci. Technol. 2018, 77, 332–343. [Google Scholar] [CrossRef]
- Gramola, M.; Bruce, P.J.K.; Santer, M. Experimental FSI study of adaptive shock control bumps. J. Fluids Struct. 2018, 81, 361–377. [Google Scholar] [CrossRef]
- Lutz, T.; Sommerer, A.; Wagner, S. Parallel numerical optimisation of adaptive transonic airfoils. IUTAM Symp. Transsonicum IV 2003, 73, 265–270. [Google Scholar]
- Colliss, S.P.; Babinsky, H.; Nübler, K.; Lutz, T. Vortical Structures on Three-Dimensional Shock Control Bumps. AIAA J. 2016, 54, 2338–2350. [Google Scholar] [CrossRef] [Green Version]
- Mayer, R.; Lutz, T.; Krämer, E. Numerical Study on the Ability of Shock Control Bumps for Buffet Control. AIAA J. 2018, 56, 1978–1987. [Google Scholar] [CrossRef]
- Ogawa, H.; Babinsky, H.; Pätzold, M.; Lutz, T. Shock-Wave/Boundary-Layer Interaction Control Using Three-Dimensional Bumps for Transonic Wings. AIAA J. 2008, 46, 1442–1452. [Google Scholar] [CrossRef]
- Bruce, P.J.K.; Babinsky, H. Experimental Study into the Flow Physics of Three-Dimensional Shock Control Bumps. J. Aircr. 2012, 49, 1222–1233. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Li, Y.; Qin, N.; Huang, Y.; Deng, F.; Wang, Y.; Zhao, N. Shock control of a low-sweep transonic laminar flow wing. AIAA J. 2019, 57, 2408–2420. [Google Scholar] [CrossRef]
- Konig, B.; Pätzold, M.; Lutz, T.; Krämer, E.; Rosemann, H.; Richter, K.; Uhlemann, H. Numerical and experimental validation of three-dimensional shock control bumps. J. Aircr. 2009, 46, 675–682. [Google Scholar] [CrossRef]
- Bruce, P.J.K.; Colliss, S.P. Review of research into shock control bumps. Shock Waves 2015, 25, 451–471. [Google Scholar] [CrossRef] [Green Version]
- Deng, F.; Qin, N. Vortex-generating shock control bumps for robust drag reduction at transonic speeds. AIAA J. 2021. [Google Scholar] [CrossRef]
- Eastwood, J.P.; Jarrett, J.P. Toward designing with three-dimensional bumps for lift/drag improvement and buffet alleviation. AIAA J. 2012, 50, 2882–2898. [Google Scholar] [CrossRef]
- Colliss, S.P.; Babinsky, H.; Nübler, K.; Lutz, T. Joint experimental and numerical approach to three-dimensional shock control bump research. AIAA J. 2014, 52, 436–446. [Google Scholar] [CrossRef]
- Geoghegan, J.A.; Giannelis, N.F.; Vio, G.A. Parametric study of active shock control bumps for transonic shock buffet alleviation. AIAA Pap. 2020, 2020, 1989. [Google Scholar]
- Chen, H.; Li, Z.; Zhang, Y. U or V shape: Dissipation effects on cylinder flow implicit large-eddy simulation. AIAA J. 2017, 55, 459–473. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, C.; Chen, H.; Yin, Y. Study of riblet drag reduction for an infinite span wing with different sweep angles. Chin. J. Aeronaut. 2020, 33, 3125–3137. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Y.; Zhou, F. Numerical study of iced airfoils with horn features using large-eddy simulation. J. Aircr. 2019, 56, 94–107. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Y.; Zhou, F. Numerical investigation of the unsteady flow past an iced multi-element airfoil. AIAA J. 2020, 58, 3848–3862. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24, 011702. [Google Scholar] [CrossRef]
- Advisory Group for Aerospace Research & Development. A Selection of Experimental Test Cases for the Validation of CFD Codes; AGARD Advisory Report No. 303; Advisory Group for Aerospace Research & Development: Dortmund, Germany, 1994; Volume 2. [Google Scholar]
- Deck, S. Numerical simulation of transonic buffet over a supercritical airfoil. AIAA J. 2005, 43, 1556–1566. [Google Scholar] [CrossRef]
- Obert, E. Aerodynamic Design of Transport Aircraft, Chapter 15, The Pressure Distribution on Airfoil Sections; IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]




| Configuration | Angle of Attack | Lift Coefficient | RMS of Lift Coefficient | Drag Coefficient | RMS of Drag Coefficient | Lift-to-Drag Ratio | Pitching Moment |
|---|---|---|---|---|---|---|---|
| Baseline airfoil | 2.5° | 0.919 | 0.006884 | 0.03009 | 0.000724 | 30.54 | −0.1335 |
| 3.5° | 0.968 | 0.037572 | 0.04823 | 0.003737 | 20.07 | −0.1262 | |
| Bump 1 (h/c = 0.004, xB/c = 0.55) | 3.5° | 0.965 (−0.3%) | 0.027828 (−25.9%) | 0.04634 (−3.9%) | 0.003107 (−16.8%) | 20.82 (+3.7%) | −0.1252 (+0.8%) |
| Bump 2 (h/c = 0.008, xB/c = 0.55) | 2.5° | 0.866 (−5.8%) | 0.004527 (−34.2%) | 0.03174 (+5.5%) | 0.000662 (−8.6%) | 27.28 (−10.6%) | −0.1260 (+5.6%) |
| 3.5° | 0.953 (−1.5%) | 0.012188 (−67.6%) | 0.04484 (−7.0%) | 0.001569 (−58.0%) | 21.25 (+5.9%) | −0.1229 (+2.6%) | |
| Bump 3 (h/c = 0.012, xB/c = 0.55) | 3.5° | 0.917 (−5.3%) | 0.008297 (−77.9%) | 0.04642 (−3.8%) | 0.001343 (−64.1%) | 19.75 (−1.6%) | −0.1184 (+6.2%) |
| Bump 4 (h/c = 0.008, xB/c = 0.50) | 2.5° | 0.870 (−5.3%) | 0.003852 (−44.0%) | 0.03395 (+12.8%) | 0.000549 (−24.2%) | 25.63 (−16.1%) | −0.1271 (+4.8%) |
| 3.5° | 0.925 (−4.4%) | 0.016171 (−56.9%) | 0.04559 (−5.5%) | 0.002168 (−42.0%) | 20.29 (+1.1%) | −0.1193 (+5.5%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, P.; Li, R.; Chen, H. Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump. Aerospace 2021, 8, 203. https://doi.org/10.3390/aerospace8080203
Zhang Y, Yang P, Li R, Chen H. Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump. Aerospace. 2021; 8(8):203. https://doi.org/10.3390/aerospace8080203
Chicago/Turabian StyleZhang, Yufei, Pu Yang, Runze Li, and Haixin Chen. 2021. "Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump" Aerospace 8, no. 8: 203. https://doi.org/10.3390/aerospace8080203
APA StyleZhang, Y., Yang, P., Li, R., & Chen, H. (2021). Unsteady Simulation of Transonic Buffet of a Supercritical Airfoil with Shock Control Bump. Aerospace, 8(8), 203. https://doi.org/10.3390/aerospace8080203






