A Survey on Low-Thrust Trajectory Optimization Approaches
Abstract
1. Introduction
2. Concurrent Engineering Requirements
- Flexibility: high versatility to cope with a wide range of scenarios is demanded, as well as the ability to optimize discrete decision-making and mission planning.
- Robustness: the sensitivity to the input parameters has as low as possible.
- Speed: they have to be fast, since it is not possible to spend long computation times during concurrent design studies.
- Accuracy: they must provide meaningful results, yet high-fidelity is not required. An accurate trajectory will be required during the detailed design, once a mission candidate is selected.
- Automation: minimal user-interaction is desired to reduce man-power cost.
- Optimality: near-optimal solutions are deemed acceptable.
3. Multiobjective Hybrid Optimal Control
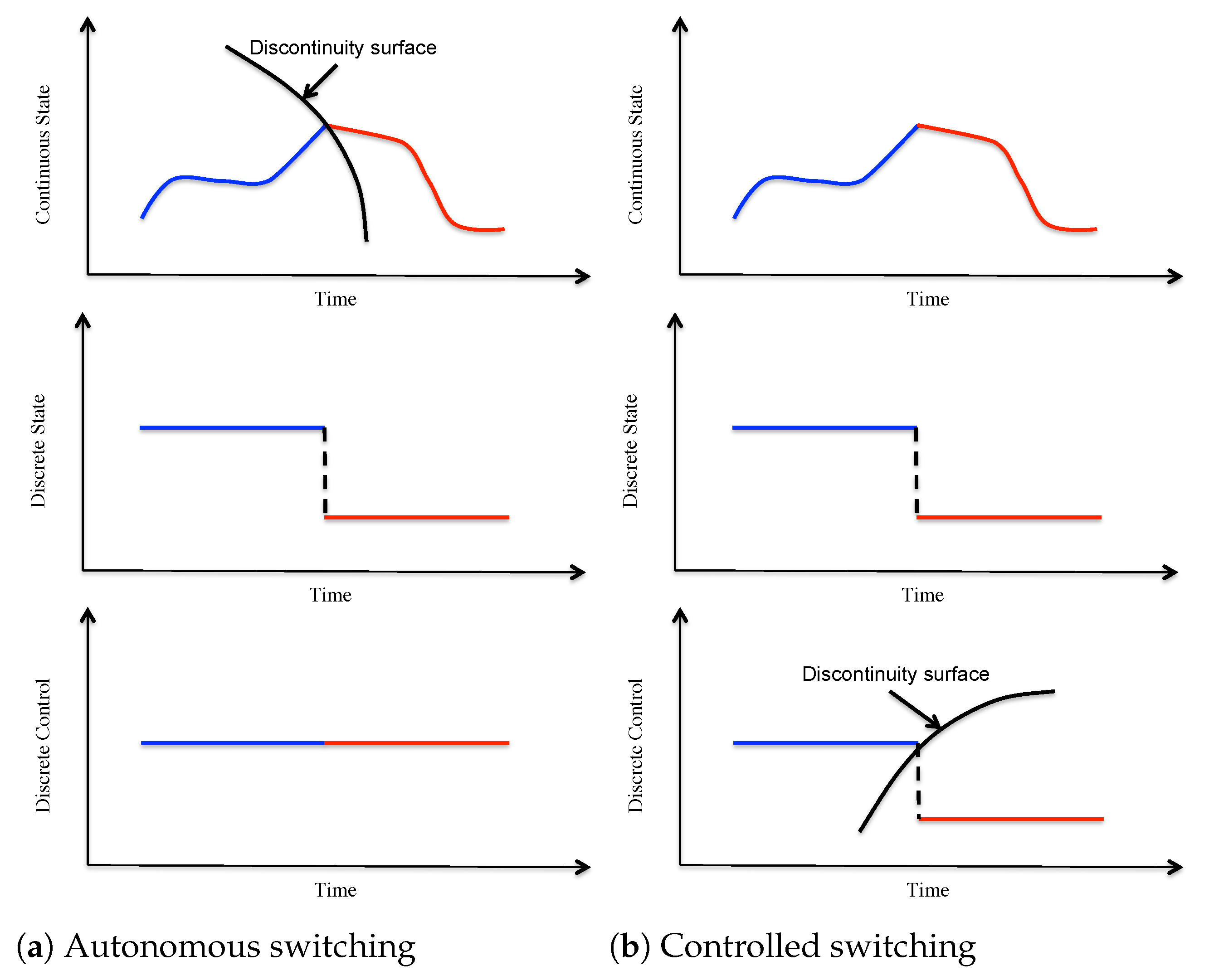
3.1. Hybrid Dynamical System
- Autonomous switching: An autonomous switching occurs when the continuous state trajectory crosses the discontinuity surface in the continuous state-time space (see Figure 1a). In this case, the discontinuity surface depends only on the continuous state and on time, i.e., . The switching causes the discrete state to change, whereas the continuous states before and after the switching are equal, i.e., and . In the new discrete state, the continuous state trajectory follows different equation of motions than in the previous discrete state. In spacecraft systems, autonomous switching occurs, for example, when the electric engine is switched-off due to power availability constraints (e.g., the spacecraft crosses through the Earth-shadow or it is far from the Sun).
- Controlled switchings: Controlled switching differs from autonomous switching in that the discontinuity surface is not a function of the continuous state but it depends on the controls, i.e., . Therefore, the discrete event occurs in the control-time space (see Figure 1b). Controlled switching models logical decisions that can be made at a desired point of time to change the system dynamics, e.g., switching-off the electric engine for propellant savings reasons.
- Autonomous impulses: An autonomous impulse resets the value of the continuous state, when the continuous state trajectory hits the discontinuity surface (see Figure 2a). In a similar fashion than autonomous switching, the discontinuity surface depends only on the continuous state and on time, i.e., . However, after an autonomous impulse, the discrete state, and thus the differential equations, remains unchanged, whereas the continuous state jumps according to the transition maps function, i.e., and . Examples for autonomous impulses in spacecraft dynamics are gravity assisted-maneuvers, since a discrete change is the heliocentric velocity is experienced when it encounters a planet in space and time.
- Controlled impulses: The difference of controlled impulses to autonomous ones is that the impulse is triggered by a discontinuity surface that depends on the controls, i.e., . Similarly to controlled switchings, the event occurs in the control-time space (see Figure 2b). Incrementing the velocity of a spacecraft by an instantaneous firing of a chemical engine is an example of a controlled impulse.
3.2. Problem Statement
4. Dynamical Modeling
4.1. Continuous State Representation
- Cartesian State Vector (CSV): The most common model for describing a spacecraft trajectory refers to its position and velocity vectors. They are typically projected on an inertial Cartesian frame, such that . Here, and are the projections of the position vector, and of the velocity vector , respectively.
- Polar State Vector (PSV): They are mainly used for two-dimensional or planar representations of the problem dynamics. They consists on the following set: , where is the distance to the central body, is the polar angle, is the modulus of the velocity with respect to an inertial frame, and is the flight path angle.
- Classical Orbital Elements (COE): Another form of mathematical model to represent the spacecraft dynamics is in terms of classical orbit elements . They are named as the semimajor axis, eccentricity, inclination, right-ascension of the ascending node, argument of perigee, and mean anomaly, respectively. Instead of the true anomaly, the mean motion, the true anomaly or the eccentric anomaly can be used [18].
- Modified Equinoctial Elements (MEE): The other model for completely defining the state of the spacecraft is by the use of the set of modified equinoctial orbital elements . Here, p is the semilatus rectum and L is named the true longitude. The elements are related to the projection of the eccentricity vector on the inertial frame, while are associated to the inclination of the orbit.
4.2. Continuous Controls
- Blended Control (BC): The optimal thrust steering that maximize the variation (i.e., increase or decrease) of a set of orbital elemenst element independently or each other, are computed as a function of the position in the orbit. They are commonly obtained analytically. Then, the complete control law to simultaneously modify all the elements of the state vector results from the following weighted sum:where are time-varying or static weighting functions that fulfills . Their time-discretized values are the unknowns to be determined. Commonly, BC-based methods are derived for MEE or COE formulations, and allow to naturally reach the target orbit, avoiding the need to impose final boundary constraints. This type of control law is rather used in planetocentric environments, where the rendezvous with a target true anomaly may not be required.
- Calculus of Variations based (COV) The Pontryagin Minimum Principle (PMP) [20] is used to obtain the optimal control history. For a minimum-time continuous optimal control problem, the optimal thrust direction will have the following form:where is state-dependent matrix resulting from solving the PMP. Here, are known as the costates, and represent the new continuous controls. Unfortunately, this approach lack of flexibility since an analytical reformulation of is required every time a new constrained is added or a new-objective function is considered. Beside, if the problem combines hybrid dynamics, the formulation of this control law becomes much more challenging.
- Lyapunov Control (LC): It defines an energy-like (i.e., a positive-definite) scalar Lyapunov function of the state . Here, , and is the target state. The set of constant parameters or static controls are to be determined as part of the solution. The Lyapunov function has to fulfill the following condition:The thrust steering law is then obtained by minimizing the variation of with respect to the control law (i.e., making it as negative as possible) as follows:Notably, this control law naturally drives the spacecraft to the desired final state, avoiding the need to include the final boundary conditions in the problem.
- Shape-based Approaches (SB): In this approach, the state vector , usually the trajectory, is assumed to have a predefined form, e.g., , where are the set of parameters to be determined. The control law is obtained by forcing the EOM to be satisfied:An analytical solution for the control is derived therefrom. Note that the obtained control may not satisfy the constrained related to the maximum thrust available. Thus it may lead to unfeasible trajectories. The solution may not fulfill the boundary constraints, thus they must be included as part of the problem.
- Neurocontroller (NC): The problem of finding an optimal strategy that leads to an optimal trajectory is thus transformed into the determination of the optimal network transfer function . This function acts as a map from the current spacecraft state , the desired final state , and the network’s internal parameters to the instantaneous steering. Thus, it holds that:The controller parameters are to be determined as part of the solution.
- Finite Fourier Series (FFS). The low-thrust steering history is assumed to be represented by a Finite Fourier series expansion, such that:where the time-varying or static coefficients and are the continuous controls. The angle represents the orbit anomaly, and represents the with of the interval in which the Fourier expansion applies. Note that, increasing the number of coefficients will improve the accuracy of the representation at the cost of increasing the number of unknowns and the complexity.
4.3. Discrete States
4.4. Discrete Controls
4.5. Continuous Dynamics
- Analytical solutions: Analytical techniques were at the origin of spacecraft trajectory optimization. They seek to obtain closed-forms solutions for the dynamical systems, such that the EOM do not need to be integrated.These techniques are only available for special cases. Two well-known and widely used analytical solutions are the Kepler and Stark models. A graphical representation of these techniques along with the continuous model is represented in Figure 4.
- -
- Kepler Model (KM): It is a reduced model that uses pure Keplerian arcs connected at nodes with impulsive velocity vector discontinuities that approximate the effect of performing a low-thrust maneuver during the Keplerian arc.
- -
- Stark Model (SM): The Stark model yields exact closed-form solutions for a spacecraft in a two-body gravitational field subject to a thrust acceleration that is inertially constant in both magnitude and direction.
Additionally, analytical solutions can be derived under constant radial or tangential thrust without space perturbations, even including some environmental effects, such as the Earth oblateness. - Asymptotic solutions: The propulsive acceleration is considered as a perturbation effect acting on a well-known or unperturbed trajectory (e.g., a Keplerian orbit). Thus, the perturbed trajectory can be approximated as a series expansion:where is a nondimensional thrust acceleration, and has to fulfill that , is the unperturbed trajectory, and is the first-order perturbation term, which can be obtained analytically under certain circumstances (e.g., constant tangential or radial acceleration). Commonly, second-order terms are not included in the expansion.
- Averaging techniques: The method of averaging consists in the elimination of high-frequency components from the EOM by averaging over a short time scale (typically the orbital period). The averaged equations contains only secular and long-periodic terms.where is the mean state vector, and is the orbital period. This is particularly useful in planetocentric scenarios with multiple-revolutions due to the quasi-periodic nature of the orbits. However, averaging results in a loss of exact position information which may be desired to assess the power availability to the spacecraft or to rendezvous with a celestial body.
4.6. Discrete Dynamics
4.6.1. Flybys
4.6.2. Engine on-off Switchings
5. Objective Functions
- Single-objective: The goal is to search for a solution in the feasible set that provides the minimum value of a scalar-valued function, i.e., . In this case, a single-point solution, under mild regularity assumptions, is obtained. From a mathematical point of view, a feasible solution is optimal if it satisfies the following condition:
- Multiobjective: The aim is to minimize a vector-valued function formed by conflicting criteria, i.e., . The solution in the objective space typically consists of a -dimensional hypersurface [23] known as the Pareto-optimal set (Pareto-optimal set is also known as Pareto front, Pareto frontier, Pareto-efficient set or nondominated front.) [24]. A feasible solution is weak Pareto-optimal if there does not exit another feasible solution that could improve all the objectives simultaneously such that:Otherwise, the point is said to be dominated.
6. Approaches and Solutions for COCPs
6.1. Indirect, Direct, and Dynamic Programming Approaches
- Indirect Approach: In the indirect approach, the goal is to solve the multipoint boundary value problem (MPBVP) that results from applying the PMP [20]. The PMP characterizes the first-order necessary conditions that an optimal solution must satisfy. its derivation involves the determination of the states and costates, which must obey the Euler-Lagrange equation. Notably, the minimum principle allow to obtain the continuous control as a function of the state and costate at each instant, explicitly or numerically. Furthermore, a set of additional constraints, namely transversality, and complementary conditions, must be satisfied [26].
- Direct Approach: The basic idea of direct methods is to transcribe the COCP into a nonlinear programming problem (NLP), where the objective function (Equation (3)) is “directly” optimized. The transcription process requires the discretization of the control variables in a time-grid. The goal of a NLP problem is to determine a vector of unknown decision variables that comply with a set of nonlinear constraints, including equality and inequality restrictions. An optimal solution to the NLP problem has to fulfill first-order necessary optimality conditions. These conditions are known as the Karush-Kuhn-Tucker conditions (KKT) [27,28]. The NLP is then numerically solved using well-known optimization techniques [13].
- Dynamic Programming Approach: The method of Dynamic Programming is based on the Bellman’s principle of optimality [29]: “An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision.” Even though Dynamic Programming was originally developed for discrete-time systems, it was extended to continuous-time problems. The continuous-time equivalent of the Bellman’s principle resulted in the Hamilton-Jacobi-Bellman (HJB) theorem [30]. In this case, a set of partial differential equations must be solved first.
- Single shooting: The trajectory is integrated using time-marching methods from upon reaching the final time . In this case, the initial state (and costates) are unknowns to be determined, and boundary constraints are imposed at the end of the integration.
- Multiple shooting: The time interval is broken up into subintervals. The trajectory is integrated over each subinterval with the initial values of the state (and adjoints) at each subinterval being unknowns that need to be determined. Additionally, continuity conditions have to be enforced at the interface of each subinterval.
- Collocation: The states (and costates) are discretized over a predefined time-grid, such that they are known only at discrete points. The system-governing equations are transformed into discrete defect constraints, which relate the values at the beginning of the subinterval to the values at the end. Different methods are characterized by the choice of quadrature rule to approximate the differential equations between each two subintervals: local and global collocation methods.
6.2. Gradient-Based, Heuristic, and Hybrid Solutions
- Gradient-based: In a gradient-based method, an initial guess is made of the unknown decision vector . At the iteration, a search direction , and a step length , are determined. The search direction provides a direction in along which to change the current value , while the step length provides the magnitude of the change. The update from to has the form: . The iterations proceed until the KKT conditions are met. To compute the search direction, these methods require the user provide information for the gradient of the constraint and the objective function (if necessary). The most widely used methods are classified as sequential quadratic problems (e.g., SNOPT, NPSOL) or interior point methods (e.g., IPOPT, KNITRO). Extensive information about their implementations can be found in Refs. [34,35], respectively.
- Heuristic: The search is performed in a stochastic/metaheuristic manner without requiring gradient information. The most known class of heuristics are evolutionary algorithms. They start by generating a set of candidate solutions or individuals for , termed population. Thereafter, the population is iteratively modified by applying a set of stochastic rules , which may incorporate random processes, such that the population at iteration is computed as , and the iterations proceed until a stopping criteria is met (e.g., max number of iterations). The candidate with the lowest cost is deemed as the solution to the problem. Well known stochastic rules are genetic algorithms (GA) [36], which emulate evolutionary processes in genetics, and particle swarm optimization (PSO) [37], which is based on the idea of swarms of animals.
- Hybrid: Hybrid approaches combine a set of rules exploiting gradient-information and a set of rules based on heuristics searches to iteratively operate over a solution or a set of candidate solutions. Gradient-information is exploited to drive the constraints to zero, while heuristic rules are applied to efficiently explore large design domains or to manage integer variables. They are typically combined on a two-loop approach. The heuristic solver operates over a subset of decision variables in the outer loop. In the inner loop, the remaining subset of design parameters are optimized with the gradient-based method.
6.3. Discussion
7. Approaches and Solutions for HOCPs
8. Existing Low-Thrust Optimization Tools
8.1. Analytical Solutions
8.2. Indirect Methods
8.3. Direct Methods
8.4. Predefined Control Laws
8.5. Dynamic Programming Methods
9. Conclusions
- Optimize alternative objectives: it has been seen that typically, either propellant mass or time-of-flight are optimized. However, mission designer may be interested into minimizing the radiation absorbed during the passage through the Van-Allen radiation belts to reduce the damage into the solar panel, or into minimizing the time-spent in eclipse. Additionally, when including spacecraft design along with the trajectory optimization, other performance indexes, such as spacecraft total mass or target on-station mass may have to be included.
- Reduce computational time: among the presented tools, GA-EMTG is able to automatically find the sequence of gravity assists for an interplanetary mission with respect to multiple-objectives, requiring minimal user-interaction, and providing medium fidelity solutions. However, computational times range from several hours to days. Therefore, faster assessments at the cost of fidelity and optimality are desirable.
- Extend the capability of preliminary design tools to include mission constraints: low-thrust trajectory optimization tools used for the preliminary design due to their speed, such as implementing predefined control laws, do not have the ability to impose important mission constraints, which may imply that the obtained trajectory is not feasible. Thus, advancing into the incorporation of constraints into such tools, either by a penalty function or by a different predefined control law, will significantly enhance the success during the preliminary design.
- Increase the efficiency of searching over wider design spaces: presented hybrid and heuristic tools are able to work for a limited combinatorial complexity of the problem. However, they are not well-suited for solving problems such as asteroid tours, debris-removal missions, or asteroid mining mission, where the are thousands of available options. Improving the capability of searching over this broad spaces will enable the of more ambitious low-thrust missions. A potential approach would be to develop dedicated heuristic algorithms able to efficiently optimize over large sequences os visited bodies (e.g., asteroids, debris), possibly incorporating artificial intelligence into the approach.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aeronautics, N.; Administration, S. NASA Systems Engineering Handbook; U.S. Government Printing Office: Washington, DC, USA, 2008.
- Lawden, D.F. Impulsive Transfer between Elliptical Orbits. In Optimization Techniques; Leitmann, G., Ed.; Elsevier: Amsterdam, The Netherlands, 1962; Volume 5, pp. 323–351. [Google Scholar] [CrossRef]
- Vinh, N.X.; Kuo, S.H.; Marchal, C. Optimal time-free nodal transfers between elliptical orbits. Acta Astronaut. 1988, 17, 875–880. [Google Scholar] [CrossRef]
- Prussing, J.E.; Chiu, J.H. Optimal multiple-impulse time-fixed rendezvous between circular orbits. J. Guid. Control Dyn. 1986, 9, 17–22. [Google Scholar] [CrossRef]
- Jezewski, D.J.; Rozendaal, H.L. An efficient method for calculating optimal free-space n-impulse trajectories. AIAA J. 1968, 6, 2160–2165. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Mortari, D. N-Impulse Orbit Transfer Using Genetic Algorithms. J. Spacecr. Rocket. 2007, 44, 456–460. [Google Scholar] [CrossRef]
- Petropoulos, A.E.; Sims, J.A. A Review of Some Exact Solutions to the Planar Equations of Motion of a Thrusting Spacecraft. In Proceedings of the 2nd International Symposium Low-Thrust Trajectories, Toulouse, France, 18–20 June 2002. [Google Scholar]
- Branicky, M.S.; Borkar, V.S.; Mitter, S.K. A unified framework for hybrid control: Model and optimal control theory. IEEE Trans. Autom. Control 1998, 43, 31–45. [Google Scholar] [CrossRef]
- Buss, M.; Glocker, M.; Hardt, M.; von Stryk, O.; Bulirsch, R.; Schmidt, G. Nonlinear Hybrid Dynamical Systems: Modeling, Optimal Control, and Applications. In Modelling, Analysis, and Design of Hybrid Systems; Engell, S., Frehse, G., Schnieder, E., Eds.; Springer: Berlin/Heidelberg, Germay, 2002; pp. 311–335. [Google Scholar] [CrossRef]
- Chilan, C.M.; Conway, B.A. Automated Design of Multiphase Space Missions Using Hybrid Optimal Control. J. Guid. Control Dyn. 2013, 36, 1410–1424. [Google Scholar] [CrossRef]
- Ross, I.M.; D’Souza, C.N. Hybrid Optimal Control Framework for Mission Planning. J. Guid. Control Dyn. 2005, 28, 686–697. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528. [Google Scholar]
- Conway, B.A. A Survey of Methods Available for the Numerical Optimization of Continuous Dynamic Systems. J. Optim. Theory Appl. 2012, 152, 271–306. [Google Scholar] [CrossRef]
- Shirazi, A.; Ceberio, J.; Lozano, J. Spacecraft trajectory optimization: A review of models, objectives, approaches and solutions. Prog. Aerosp. Sci. 2018. [Google Scholar] [CrossRef]
- Wall, S.D. Use of concurrent engineering in space mission design. In Proceedings of the EuSEC 2000, 2nd European Systems Engineering Conference, Munich, Germany, 13–15 September 2000. [Google Scholar]
- Hintz, G.R. Survey of Orbit Element Sets. J. Guid. Control Dyn. 2008, 31, 785–790. [Google Scholar] [CrossRef]
- McClain, W.; Vallado, D. Fundamentals of Astrodynamics and Applications; Space Technology Library; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Cefola, P. Equinoctial orbit elements—Application to artificial satellite orbits. In Proceedings of the Astrodynamics Conference, Palo Alto, CA, USA, 11–12 September 1972. Number AIAA Paper 72-937. [Google Scholar] [CrossRef]
- Pontryagin, L. Mathematical Theory of Optimization Processes; CRC Press: Boca Raton, FL, USA, 1962. [Google Scholar]
- Olympio, J.T. Optimisation and Optimal Control Methods for Planet Sequence Design of Low-Thrust Interplanetary Transfer Problems with Gravity Assists. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 2008. [Google Scholar]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. Multi-Objective Low-Thrust Interplanetary Trajectory Optimization Based on Generalized Logarithmic Spirals. J. Guid. Control Dyn. 2019, 42, 476–490. [Google Scholar] [CrossRef]
- Hillermeier, C. Generalized Homotopy Approach to Multiobjective Optimization. J. Optim. Theory Appl. 2001, 110, 557–583. [Google Scholar] [CrossRef]
- Pareto, V. Manuale di Economica Politica, Societa Editrice Libraria; Technical Report; MacMillan Press: New York, NY, USA, 1971. [Google Scholar]
- Marler, R.; Arora, J. Survey of Multi-Objective Optimization Methods for Engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C.; Siouris, G.M. Applied Optimal Control: Optimization, Estimation, and Control. Syst. Man Cybern. IEEE Trans. 1979, 9, 366–367. [Google Scholar] [CrossRef]
- Karush, W. Minima of Functions of Several Variables with Inequalities as Side Conditions. Master’s Thesis, Department of Mathematics, University of Chicago, Chicago, IL, USA, 1939. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1951; pp. 481–492. [Google Scholar]
- Bellman, R.; Kalaba, R.E. Dynamic Programming and Modern Control Theory; Academic Press: Cambridge, MA, USA, 1965; Volume 81. [Google Scholar]
- Caputo, M.R. Dynamic Programming and the Hamilton-Jacobi-Bellman Equation. In Foundations of Dynamic Economic Analysis: Optimal Control Theory and Applications; Cambridge University Press: Cambridge, UK, 2005; pp. 511–536. [Google Scholar] [CrossRef]
- Gottlieb, R.G. Rapid convergence to optimum solutions using a Min-H strategy. AIAA J. 1967, 5, 322–329. [Google Scholar] [CrossRef]
- Longmuir, A.G.; Bohn, E.V. Second-variation Methods in Dynamic Optimization. J. Optim. Theory Appl. 1969, 3, 164–173. [Google Scholar] [CrossRef]
- Mayne, D.Q. Differential Dynamic Programming-A Unified Approach to the Optimization of Dynamic Systems. In Control and Dynamic Systems; Academic Press: Cambridge, MA, USA, 1973; Volume 10, pp. 179–254. [Google Scholar] [CrossRef]
- Gill, P.R. User’s Guide for SNOPT Version 7: Software for Large-Scale Nonlinear Programming; Technical Report; Department of Mathematics, University of California: San Diedo, CA, USA, 2008. [Google Scholar]
- Wächter, A.; Biegler, L. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Mitchell, M. Introd. Genet al.gorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle Swarm Optimization: An Overview. Swarm Intell. 2007, 1. [Google Scholar] [CrossRef]
- Passenberg, B. Theory and Algorithms for Indirect Methods in Optimal Control of Hybrid Systems. Ph.D. Thesis, Technische Universitat München, Munich, Germany, 2012. [Google Scholar]
- Rungger, M.; Stursberg, O. Continuity of the Value Function for Exit Time Optimal Control Problems of Hybrid Systems. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 4210–4215. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1990. [Google Scholar]
- Androulakis, I. MINLP: Branch and Bound Global Optimization Algorithm; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Williams, S.N. An Introduction to the Use of VARITOP: A General Purpose Low-Thrust Trajectory Optimization Program; Technical Report jpl d-11475; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1994. [Google Scholar]
- Sauer, C.G.J. Optimization of multiple target electric propulsion trajectories. In Proceedings of the 11th Aerospace Sciences Meeting, Bruges, Belgium, 22–27 June 1973; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1973; p. 11. [Google Scholar]
- Polsgrove, T.; Hopkins, R.; Thomas, D.; Crane, T.M.; Kos, L.D. Comparison of Performance Predictions for New Low-Thrust Trajectory Tools. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Kos, L.; Polsgrove, T.; Hopkins, R.; Thomas, D.; Sims, J. Overview of the Development for a Suite of Low-Thrust Trajectory Analysis Tools. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Mann, F.I.; Horsewood, J.L. Program Manuel for HILTOP, A Heliocentric Interplanetary Low Thrust Trajectory Optimization Program; Technical Report NASA-CR-143894; NASA, Analytical Mechanics Associates Inc.: Hampton, VA, USA, 1974. [Google Scholar]
- Bertrand, R.; Foliard, J. Low-thrust Optimal Trajectories for Rendezvous with Near Earth Asteroids. In Proceedings of the 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11–15 October 2004. [Google Scholar]
- Feistel, A.; Ranieri, C. Modeling perturbations and operational considerations when using indirect optimization with equinotical elements. Adv. Astronaut. Sci. 2009, 134, 1737–1756. [Google Scholar]
- Zhang, C.; Topputo, F.; Bernelli-Zazzera, F.; Zhao, Y.S. Low-Thrust Minimum-Fuel Optimization in the Circular Restricted Three-Body Problem. J. Guid. Control Dyn. 2015, 38, 1501–1510. [Google Scholar] [CrossRef]
- Caillau, J.B.; Gergaud, J.; Noailles, J. TfMin: Short Reference Manual. Technical Report RT/APO/01/3 July 2001. Available online: http://www.optimization-online.org/DB_HTML/2002/07/511.html (accessed on 19 March 2021).
- Kéchichian, J.A. Optimal Low-Earth-Orbit-Geostationary-Earth-Orbit Intermediate Acceleration Orbit Transfer. J. Guid. Control Dyn. 1997, 20, 803–811. [Google Scholar] [CrossRef]
- Dargent, T.; Martinot, V. An integrated tool for low thrust optimal control orbit transfers in interplanetary trajectories. In Proceedings of the 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11–15 October 2004; p. 143. [Google Scholar]
- Mazzini, L.; Cerreto, M. Theory and Applications of Optimal Finite Thrust Orbital Transfers. In Modeling and Optimization in Space Engineering; Springer: Cham, Switzerland, 2019; pp. 233–269. [Google Scholar] [CrossRef]
- Juan, C.; Bastante, P.P. Electro: A Sw Tool for the Electric Propulsion Trajectory Optimisation. In Proceedings of the 7th International Conference on Astrodynamics Tools and Techniques, Oberpfaffenhofen, Germany, 6–9 November 2018. [Google Scholar]
- Geffroy, S.; Epenoy, R. Optimal low-thrust transfers with constraints—Generalization of averaging techniques. Acta Astronaut. 1997, 41, 133–149. [Google Scholar] [CrossRef]
- Sackett, L.L.; Malchow, H.L.; Edelbaum, T.N. Solar Electric Geocentric Transfer With Attitude Constraints: Analysis; Technical Report NASA CR–134927; NASA: Houston, TX, USA, 1975. [Google Scholar]
- Coverstone-Carroll, V.; Hartmann, J.; Mason, W. Optimal multi-objective low-thrust spacecraft trajectories. Comput. Methods Appl. Mech. Eng. 2000, 186, 387–402. [Google Scholar] [CrossRef]
- Krier, G.; Mostaza, D. Fast and robust optimization of high fidelity continuous thrust transfer orbits with constraints. In Proceedings of the 25th International Symposium on Space Flight Dynamics, Munich, Germany, 19–23 October 2015. [Google Scholar]
- Sentinella, M.R.; Casalino, L. Genetic Algorithm and Indirect Method Coupling for Low-Thrust Trajectory Optimization. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar] [CrossRef]
- Pontani, M.; Conway, B.A. Particle Swarm Optimization Applied to Space Trajectories. J. Guid. Control Dyn. 2010, 33, 1429–1441. [Google Scholar] [CrossRef]
- Lee, S.; Finkt, W.; von Allmed, P.; Von Allmen, P.E.; Petropoulos, A.; Terrile, R.J. Evolutionary Computing for Low-Thrust Navigation; American Institute of Aeronautics and Astronautics: New York, NY, USA, September 2005. [Google Scholar] [CrossRef]
- Oberle, H.; Grimm, W. BNDSCO: A Program for the Numerical Solution of Optimal Control Problems. Ph.D. Thesis, Inst. für Angewandte Math. der University, Hamburg, Germany, 2001. [Google Scholar]
- Hermosin, P.; Centouri, S.B.E. LOTNAV: A Low-Thrust Interplanetary Navigation Tool and Cano Juan L. In Proceedings of the International Conference on Astrodynamics Tools and Techniques, Oberpfaffenhofen, Germany, 6–9 November 2018. [Google Scholar]
- Meng, Y.; Zhang, H.; Gao, Y. Low-Thrust Minimum-Fuel Trajectory Optimization Using Multiple Shooting Augmented by Analytical Derivatives. J. Guid. Control Dyn. 2018, 42, 1–16. [Google Scholar] [CrossRef]
- Olympio, J. Algorithm for Low-Thrust Optimal Interplanetary Transfers with Escape and Capture Phases. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, American Institute of Aeronautics and Astronautics, Savannah, GA, USA, 8–12 February 2008. [Google Scholar] [CrossRef]
- Horsewood, J. Program Manual for ASTOP, an Arbitrary Space Trajectory Optimization Program; Technical Report NASA-CR-120660; NASA, Analytical Mechanics Associates, Inc.: Houston, TX, USA, 1975. [Google Scholar]
- Johnson, G.; Munoz, S.; Lehman, J. Copernicus: A Generalized Trajectory Design and Optimization System; Technical Report; University of Texas: Austin, TX, USA, 2003. [Google Scholar]
- Campagnola, S.; Ozaki, N.; Sugimoto, Y.; Yam, C.H.; Hongru, C.; Kawabata, Y.; Ogura, S.; Sarli, B.; Kawakatsu, Y.; Funase, R.; et al. Low-Thrust Trajectory Design and Operations of PROCYON, the First Deep-Space Micro-Spacecraf. In Proceedings of the 25th International Symposium on Space Flight Dynamics, Munich, Germany, 19–23 October 2015. [Google Scholar]
- Vasile, M.; Bernelli-Zazzera, F.; Fornasari, N.; Masarati, P. Design of Interplanetary and Lunar Missions Combining Low Thrust and Gravity Assists; Final Report of esa/esoc Study Contract no. 14126/00/d/cs; ESA/ESOC: Darmstadt, Germany, 2001. [Google Scholar]
- Ricciardi, L.; Vasile, M. Modhoc-Multi Objective Direct Hybrid Optimal Control. In Proceedings of the 7th International Conference on Astrodynamics Tools and Techniques, Oberpfaffenhofen, Germany, 6–9 November 2018. [Google Scholar]
- Zhang, C.; Topputo, F.; Bernelli-Zazzera, F.; Zhao, Y.S. An exploration of numerical methods for low-thrust trajectory optimization in n-body models. In Proceedings of the International Astronautical Congress, Beijing, China, 23–27 September 2013; Volume 7, pp. 4971–4977. [Google Scholar]
- Herman, J.F.C.; Parker, J.S.; Jones, B.A.; Born, G.H. High-speed, high-fidelity low-thrust trajectory optimization through parallel computing and collocation method. Adv. Astronaut. Sci. Spacefl. Mech. 2015, 2015, 15–298. [Google Scholar]
- Grebow, D.J.; Pavlak, T.A. MCOLL: Monte Collocation Trajectory Design Too. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Stevenson, WA, USA, 20–24 August 2017; Volume 162. [Google Scholar]
- Pritchett, R.; Howell, K.; Grebow, D. Low-Thrust Transfer Design Based on Collocation Techniques: Applications in the Restricted Three-Body Problem. Adv. Astronaut. Sci. Astrodyn. 2017, 162, 1–92. [Google Scholar]
- Hughes, S.P.; Qureshi, R.H.; Cooley, S.D.; Parker, J. Verification and Validation of the General Mission Analysis Tool (GMAT). In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014. [Google Scholar] [CrossRef]
- Gallesio, E.; Antipolis, S. STK Reference Manual; Université de Nice: Nice, France, 2000. [Google Scholar]
- Hargraves, C.R.; Paris, S.W. Direct trajectory optimization using nonlinear programming and collocation. J. Guid. Control Dyn. 1987, 10, 338–342. [Google Scholar] [CrossRef]
- Brauer, G.L.; Cornick, D.E.; Stevenson, R. Capabilities and Applications of the Program to Optimize Simulated Trajectories (POST); Program Summary Document; Technical Report NASA-CR-2770; NASA: Washington, DC, USA, 1977. [Google Scholar]
- Betts, J.T. Very low-thrust trajectory optimization using a direct SQP method. J. Comput. Appl. Math. 2000, 120, 27–40. [Google Scholar] [CrossRef]
- Ross, I. User’s Manual for DIDO: A MATLAB Application Package for Solving Optimal Control Problems; TOMLAB Optimization: Vallentuna, Sweden, 2004. [Google Scholar]
- Patterson, M.A.; Rao, A.V. GPOPS–II: A MATLAB Software for Solving Multiple-Phase Optimal Control Problems Using hpAdaptive Gaussian Quadrature Collocation Methods and Sparse Nonlinear Programming. ACM Trans. Math. Softw. 2014, 41. [Google Scholar] [CrossRef]
- Locoche, S. OptElec: An Optimisation Software for Low-Thrust Orbit Transfer Including Satellite and Operation Constraints. In Proceedings of the 7th International Conference on Astrodynamics Tools and Techniques, Oberpfaffenhofen, Germany, 6–9 November 2018. [Google Scholar]
- Schoenmaekers, J. MANTRA—Flight Dynamics Interplanetary Manoeuvre Optimisation Software Specification Document; Technical Report; ESA/ESOC: Darmstadt, Germany, 2005. [Google Scholar]
- Schäff, S. Low-Thrust Multi-Revolution Orbit Transfers; Springer: Berlin/Heidelberg, Germany, 2016; pp. 337–367. [Google Scholar] [CrossRef]
- Ocampo, C. Method of Simultaneously Reducing Inclination and Eccentricity for Geostationary Orbit Transfer. U.S. Patent 6,341,749, 29 January 2002. [Google Scholar]
- McConaghy, T.T.; Debban, T.J.; Petropoulos, A.E.; Longuski, J.M. Design and Optimization of Low-Thrust Trajectories with Gravity Assists. J. Spacecr. Rocket. 2003, 40, 380–387. [Google Scholar] [CrossRef]
- Herman, J.; Zimmer, A.; Reijneveld, J.; Dunlop, K.; Takahashi, Y.; Tardivel, S.; Scheeres, D. Human Exploration of Near Earth Asteroids: Mission Analysis for a Chemical and Electric Propulsion Mission. Acta Astronaut. 2014, 104, 313–323. [Google Scholar] [CrossRef]
- Ozimek, M.; Riley, J.; Arrieta, J. The Low-thrust Interplanetary EXplorer: A Medium-Fidelity Algorithm for Multi-Gravity Assist Low-Thrust Trajectory Optimization. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Maui, HI, USA, 13–17 January 2019. [Google Scholar]
- De Smet, J.S.; Parker, J.H.; Noomen, R. Mission Design for a Crewed Earth-Venus-Mars-Flyby Mission using Solar Electric Propulsion. In Proceedings of the 32nd annual AAS Guidance and Control Conference, South Lake Tahoe, CA, USA, 9–13 August 2015. [Google Scholar]
- Sims, P.J.; Finlayson, E.R.M.V.; Kowalkowski, T. Implementation of a low-thrust trajectory optimization algorithm for preliminary design. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Monterey, CA, USA, 5–8 August 2006. [Google Scholar]
- Englander, J.A.; Vavrina, M.; Ghosh, A.R. Multi-Objective Hybrid Optimal Control for Multiple-Flyby Low-Thrust Mission Design. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Maui, HI, USA, 13–17 January 2015. [Google Scholar]
- Yam, C.; Di Lorenzo, D.; Izzo, D. Low-Thrust Trajectory Design as a Constrained Global Optimization Problem. Part J. Aerosp. Eng. 2011, 225, 1243–1251. [Google Scholar] [CrossRef]
- Vavrina, M.; Howell, K. Multiobjective Optimization of Low-Thrust Trajectories Using a Genetic Algorithm Hybrid. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009. [Google Scholar]
- Zuiani, F.; Vasile, M.; Palmas, A.; Avanzini, G. Direct transcription of low-thrust trajectories with finite trajectory elements. Acta Astronaut. 2012, 72, 108–120. [Google Scholar] [CrossRef][Green Version]
- Coverstone, V.; Williams, S. Optimal low thrust trajectories using differential inclusion concepts. J. Astronaut. Sci. 1994, 42, 379–393. [Google Scholar]
- Rauwolf, G.A.; Coverstone-Carroll, V.L. Near-optimal low-thrust orbit transfers generated by a genetic algorithm. J. Spacecr. Rocket. 1996, 33, 859–862. [Google Scholar] [CrossRef]
- Pontani, M.; Ghosh, P.; Conway, B.A. Particle Swarm Optimization of Multiple-Burn Rendezvous Trajectories. J. Guid. Control Dyn. 2012, 35, 1192–1207. [Google Scholar] [CrossRef]
- Tsien, H. Take-Off from Satellite Orbit. J. Am. Rocket. Soc. 1953, 23. [Google Scholar] [CrossRef]
- Battin, R.H. An Introduction to the Mathematics and Methods of Astrodynamics; American Institute of Aeronautics and Astronautics, Inc.: New York, NY, USA, 1987. [Google Scholar] [CrossRef]
- Izzo, D.; Biscani, F. Explicit Solution to the Constant Radial Acceleration Problem. J. Guid. Control Dyn. 2015, 38, 733–739. [Google Scholar] [CrossRef]
- Bombardelli, C.; Baù, G.; Pelaez, J. Asymptotic solution for the two-body problem with constant tangential thrust acceleration. Celest. Mech. Dyn. Astron. 2011, 110, 239–256. [Google Scholar] [CrossRef]
- Gonzalo, J.L.; Bombardelli, C. Asymptotic solution for the two body problem with radial perturbing acceleration. Adv. Astronaut. Sci. 2014, 152, 359–377. [Google Scholar]
- Prussing, J.E. Constant Radial Thrust Acceleration Redux. J. Guid. Control Dyn. 1998, 21, 516–518. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Escape from Elliptic Orbit Using Constant Radial Thrust. J. Guid. Control Dyn. 2009, 32, 1018–1022. [Google Scholar] [CrossRef]
- Edelbaum, T.N. Propulsion Requirements for Controllable Satellites. ARS J. 1961, 31, 1079–1089. [Google Scholar] [CrossRef]
- Kéchichian, J.A. Reformulation of Edelbaum’s Low-Thrust Transfer Problem Using Optimal Control Theory. J. Guid. Control Dyn. 1997, 20, 988–994. [Google Scholar] [CrossRef]
- Edelbaum, T.N. An asymptotic solution for optimum power limited orbit transfer. AIAA J. 1965, 4, 15. [Google Scholar] [CrossRef]
- Fernandes, S.; Carvalho, F.; Vilhena de Moraes, R. Optimal low-thrust transfers between coplanar orbits with small eccentricities. Comput. Appl. Math. 2015, 641. [Google Scholar] [CrossRef]
- Ilgen, M.R. Hybrid method for computing optimal low thrust OTV trajectories. Adv. Astronaut. Sci. 1994, 87, 941–958. [Google Scholar]
- Gao, Y. Near-Optimal Very Low-Thrust Earth-Orbit Transfers and Guidance Schemes. J. Guid. Control Dyn. 2007, 30, 529–539. [Google Scholar] [CrossRef]
- Yang, G. Direct Optimization of Low-thrust Many-revolution Earth-orbit Transfers. Chin. J. Aeronaut. 2009, 22, 426–433. [Google Scholar] [CrossRef][Green Version]
- Zuiani, F.; Kawakatsu, Y.; Vasile, M. Multi-objective optimisation of many-revolution, low-thrust orbit raising for destiny mission. Adv. Astronaut. Sci. 2013, 148, 783–802. [Google Scholar]
- Kluever, C.A.; Oleson, S.R. Direct Approach for Computing Near-Optimal Low-Thrust Earth-Orbit Transfers. J. Spacecr. Rocket. 1998, 35, 509–515. [Google Scholar] [CrossRef]
- Hudson, J.S.; Scheeres, D.J. Reduction of Low-Thrust Continuous Controls for Trajectory Dynamics. J. Guid. Control Dyn. 2009, 32, 780–787. [Google Scholar] [CrossRef]
- Chang, D.E.; Chichka, D.F.; Marsden, J.E. Lyapunov-Based Transfer Between Elliptic Keplerian Orbits. Discret. Contin. Dyn. Syst. Ser. 2002, 2, 57–67. [Google Scholar] [CrossRef]
- Varga, G.I.; Pérez, J.M.S. Many-revolution Low-Thrust Orbit Transfer Computation Using Equinoctial Q-law Including J2 and Eclipse Effects. In Proceedings of the 6th International Conference on Astrodynamics Tools and Techniques, Darmstadt, Germany, 1–3 March 2016. [Google Scholar]
- Petropoulos, A.E. Low-Thrust Orbit Transfers Using Candidate Lyapunov Functions with a Mechanism for Coasting. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, Rhode Island, 16–19 August 2004. [Google Scholar] [CrossRef]
- Petropoulos, A.E.; Longuski, J.M. Shape-based Algorithm for Automated Design of Low-Thrust, Gravity-Assist Trajectories. J. Spacecr. Rocket. 2004, 41, 787–796. [Google Scholar] [CrossRef]
- Pascale, P.D.; Vasile, M. Preliminary Design of Low-Thrust Multiple Gravity-Assist Trajectories. J. Spacecr. Rocket. 2006, 43, 1065–1076. [Google Scholar] [CrossRef]
- Wall, B.J.; Conway, B.A. Shape-Based Approach to Low-Thrust Rendezvous Trajectory Design. J. Guid. Control Dyn. 2009, 32, 95–101. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Initial three-dimensional low-thrust trajectory design. Adv. Space Res. 2016, 57, 889–903. [Google Scholar] [CrossRef]
- Gondelach, D.; Noomen, R. Analytical low-thrust transfer design based on velocity hodograph. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Vail, CO, USA, 9–13 August 2015. [Google Scholar]
- Roa, J.; Petropoulos, A.E.; Park, R.S. Semi-Analytic Preliminary Design of Low-Thrust Missions. In Proceedings of the Astrodynamics Specialist Conference, Stevenson, WA, USA, 20–24 August 2017. [Google Scholar]
- Morante, D.; Sanjurjo-Rivo, M.; Soler, M.; Sánchez-Pérez, J.M. Hybrid multi-objective orbit-raising optimization with operational constraints. Acta Astronaut. 2020, 175, 447–461. [Google Scholar] [CrossRef]
- Carnelli, I.; Dachwald, B.; Vasile, M. Evolutionary Neurocontrol: A Novel Method for Low-Thrust Gravity-Assist Trajectory Optimization. J. Guid. Control Dyn. 2009, 32, 616–625. [Google Scholar] [CrossRef]
- Whiffen, G. Mystic: Implementation of the Static Dynamic Optimal Control Algorithm for High-Fidelity, Low-Thrust Trajectory Design. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Tampa, FL, USA, 22–26 January 2006. [Google Scholar] [CrossRef]
- Aziz, J.D. Low-Thrust Many-Revolution Trajectory Optimization. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2018. [Google Scholar]
- Lantoine, G.; Russell, R. A Hybrid Differential Dynamic Programming Algorithm for Constrained Optimal Control Problems. Part 1: Theory. J. Optim. Theory Appl. 2013, 154, 382–417. [Google Scholar] [CrossRef]
- Ruggiero, A.; Pergola, P.; Marcuccio, S.; Andrenucci, M. Low-thrust maneuvers for the efficient correction of orbital elements. In Proceedings of the 32nd International Electric Propulsion Conference, Wiesbaden, Germany, 11–15 September 2011; pp. 1–13. [Google Scholar]
- Kéchichian, J.A. Analytic Representations of Optimal Low-Thrust Transfer in Circular Orbit. In Spacecraft Trajectory Optimization; Conway, B.A., Ed.; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2010; pp. 139–177. [Google Scholar] [CrossRef]
- Burt, E. On space manoeuvres with continuous thrust. Planet. Space Sci. 1967, 15, 103–122. [Google Scholar] [CrossRef]
- Pollard, J. Simplified Analysis of Low-Thrust Orbital Maneuvers; Technical Report NTIS Issue Number 200107; NTIS: Springfield, VA, USA, 2000; p. 42. [Google Scholar]
- Di Carlo, M.; Romero Martin, J.M.; Vasile, M. CAMELOT: Computational-Analytical Multi-fidElity Low-thrust Optimisation Toolbox. CEAS Space J. 2017, 10. [Google Scholar] [CrossRef]
- Kéchichian, J.A. Orbit Raising with Low-Thrust Tangential Acceleration in Presence of Earth Shadow. J. Spacecr. Rocket. 1998, 35, 516–525. [Google Scholar] [CrossRef]
- Kluever, C.A. Using Edelbaum’s Method to Compute Low-Thrust Transfers with Earth-Shadow Eclipses. J. Guid. Control Dyn. 2011, 34, 300–303. [Google Scholar] [CrossRef]
- Kechichian, J.A. Low-Thrust Eccentricity-Constrained Orbit Raising. J. Spacecr. Rocket. 1998, 35, 327–335. [Google Scholar] [CrossRef]
- Colasurdo, G.; Casalino, L. Optimal Low-Thrust Maneuvers in Presence of Earth Shadow. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, San Diego, CA, USA, 29–31 July 2004. [Google Scholar] [CrossRef]
- Flandro, G. Asymptotic solution for solar electric low thrust orbit raising witheclipse penalty. In Proceedings of the Mechanics and Control of Flight Conference, Anaheim, CA, USA, 5–9 August 1974; p. 1974-0802. [Google Scholar] [CrossRef]
- Kéchichian, J.A. The streamlined and complete set of the nonsingular J2-perturbed dynamic and adjoint equations for trajectory optimization in terms of eccentric longitude. J. Astronaut. Sci. 2007, 55. [Google Scholar] [CrossRef]
- Kéchichian, J.A. Inclusion of Higher Order Harmonics in the Modeling of Optimal Low-Thrust Orbit Transfer. J. Astronaut. Sci. 2008, 56. [Google Scholar] [CrossRef]
- Edelbaum, T.N.; Sackett, L.; Malchow, H. Optimal low thrust geocentric transfer. In Proceedings of the 10th Electric Propulsion Conference, Lake Tahoe, NV, USA, 31 October–2 November 1973. [Google Scholar] [CrossRef]
- Jehn, R.; García Yárnoz, D.; Schoenmaekers, J.; Companys, V. Trajectory Design for BepiColombo Based on Navigation Requirements. J. Aerosp. Eng. Sci. Appl. 2012, 4. [Google Scholar] [CrossRef]
- Englander, J.A.; Conway, B.A. Automated Solution of the Low-Thrust Interplanetary Trajectory Problem. J. Guid. Control Dyn. 2016, 40, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Beeson, R.; Englander, J.A.; Hughes, S.P.; Schadegg, M. An Automatic Medium To High Fidelity Low-Thrust Global Trajectory Tool-Chain. In Proceedings of the 25th AAS/AIAA Space Flight Mechanics Meeting, Williamsbug, VA, USA, 11–15 January 2015. [Google Scholar]
- Hargens, J.; Coverstone, V. Low-Thrust Interplanetary Mission Design Using Differential Inclusion. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar] [CrossRef]
- Ko, H.C.; Scheeres, D. Essential Thrust-Fourier-Coefficient Set of Averaged Gauss Equations for Orbital Mechanics. J. Guid. Control Dyn. 2014, 37, 1236–1249. [Google Scholar] [CrossRef]
- Kolosa, D.; Hudson, J. A TFC Approach to Low-Thrust Trajectory Optimization in STK. In Proceedings of the 2018 Space Flight Mechanics Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Ilgen, M.R. Low Thrust OTV Guidance Using Lyapunov Optimal Feedback Control Techniques; Advances in the Astronautical Sciences; The Society: Victoria, BC, Canada, 1993; Volume 85, pp. 1527–1545. [Google Scholar]
- Lee, S.; Petropoulos, A.E.; von Allmen, P. Low-Thrust Orbit Transfer Optimization with Refined Q-Law and Multi-Objective Genetic Algorithm. In Proceedings of the 2005 AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA, USA, 7–11 August 2005. [Google Scholar]
- Lee, S.; Von Allmen, P.; Fink, W.E.; Petropoulos, A.J.; Terrile, R. Design and optimization of low-thrust orbit transfers. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005. [Google Scholar]
- Chang, D.; Chichka, D.; Marsden, J. Lyapunov functions for elliptic orbit transfer. In Proceedings of the AAS/AIAA Astrodynamics Specialists Conference, American Astronautical Society, San Antonio, TX, USA, 27–30 January 2002. [Google Scholar]
- Gurfil, P. Nonlinear feedback control of low-thrust orbital transfer in a central gravitational field. Acta Astronaut. 2007, 60, 631–648. [Google Scholar] [CrossRef]
- Forbes, G.F. The trajectory of a powered rocket in space. J. Br. Interplanet. Soc. 1950, 9, 75–79. [Google Scholar]
- Tsu, T.C. Interplanetary Travel by Solar Sail. ARS J. 1959, 29, 422–427. [Google Scholar] [CrossRef]
- Bacon, R.H. Logarithmic spiral: An ideal trajectory for the interplanetary vehicle with engines of low sustained thrust. Am. J. Phys. 1959, 27, 164–165. [Google Scholar] [CrossRef]
- Pinkham, G. Reference Solution for Low Thrust Trajectories. J. Am. Rocket. Soc. 1962, 32, 775–776. [Google Scholar]
- Lawden, D.F. Optimal programming of rocket thrust direction. Acta Astronaut. 1995, 1, 41–56. [Google Scholar]
- Izzo, D. Lambert’s Problem for Exponential Sinusoids. J. Guid. Control Dyn. 2006, 29, 1242–1245. [Google Scholar] [CrossRef][Green Version]
- Vasile, M.; Schütze, O.; Junge, O. Spiral trajectories in global optimization of interplanetary and orbital transfers. Ariadna Study Rep. 2005, 5, 4106. [Google Scholar]
- Wall, B. Shape-Based Approximation Method for Low-Thrust Trajectory Optimization. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Novak, D.M.; Vasile, M. Improved Shaping Approach to the Preliminary Design of Low-Thrust Trajectories. J. Guid. Control Dyn. 2011, 34, 128–147. [Google Scholar] [CrossRef]
- Roa, J.; Peláez, J.; Senent, J. New Analytic Solution with Continuous Thrust: Generalized Logarithmic Spirals. J. Guid. Control Dyn. 2016, 39, 2336–2351. [Google Scholar] [CrossRef]
- Roa, J.; Peláez, J. Introducing a degree of freedom in the family of generalized logarithmic spirals. In Proceedings of the 26th Spaceflight Mechanics Meeting, Springfield, VA, USA, 11–15 January 2015. [Google Scholar]
- Roa, J.; Pelaez, J. Three-dimensional generalized logarithmic spirals. In Proceedings of the 26th AAS/AIAA Space Flight Mechanics Meeting, Napa, CA, USA, 14–18 February 2016. [Google Scholar]
- Dachwald, B. Low-Thrust Trajectory Optimization and Interplanetary Mission Analysis Using Evolutionary Neurocontrol. Ph.D. Thesis, Universität der Bundeswehr München, Munich, Germany, 2004. [Google Scholar]
- Whiffen, G.J.; Sims, J.A. Application of a novel optimal control algorithm to low-thrust trajectory optimization. In Proceedings of the 2001 AAS/AIAA Space Flight Mechanics Meeting, Santa Barbara, CA, USA, 11–15 February 2001. [Google Scholar]
- Whiffen, G.J.; Sims, J. Application of the SDC optimal control algorithm to low-thrust escape and capture trajectory optimization. In Proceedings of the 2002 AAS/AIAA Spaceflight Mechanics Meeting, San Antonio, TX, USA, 27–30 January 2002. [Google Scholar]
- Lantoine, G.; Russell, R. A Hybrid Differential Dynamic Programming Algorithm for Constrained Optimal Control Problems. Part 2: Application. J. Optim. Theory Appl. 2013, 154, 418–442. [Google Scholar] [CrossRef]







| Name | Ref | Company/Org./Author | Approach | Solution | Obj. | Dynamics | States | Transfers |
|---|---|---|---|---|---|---|---|---|
| VARITOP | [42] | JPL | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| SEPTOP | [43] | JPL | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| NEWSEP | [44] | JPL | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| SAIL | [45] | JPL | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| HILTOP | [46] | Space Flight Sol. | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| ETOPH | [47] | CNES | Single Shooting | GB | SO | PR-TBP | CSV | IT |
| ITOP | [48] | Aerospace Corp. | Single Shooting | GB | SO | PR-TBP | MEE | PC |
| LT20 | [49] | Milano Univ. | Single Shooting | GB | SO | PR-TBP | MEE | PC |
| Tfmin | [50] | CNES | Single Shooting | GB | SO | PR-TBP | COE | PC |
| - | [51] | Kéchichian | Single Shooting | GB | SO | PR-TBP | MEE | PC |
| T-3D | [52] | Thales | Single Shooting | GB | SO | PR-TBP + AVG | MEE | G |
| SOFTT | [53] | Thales | Single Shooting | GB | SO | PR-TBP + AVG | - | PC |
| ELECTRO | [54] | OHB | Single Shooting | GB | SO | PR-TBP + AVG | MEE | PC |
| MIPELEC | [55] | CNES | Single Shooting | GB | SO | PR-TBP + AVG | MEE | PC |
| SEPSPOT | [56] | NASA | Single Shooting | GB | SO | PR-TBP + AVG | MEE | PC |
| GA-SEPTOP | [57] | JPL | Single Shooting | HY | MO | PR-TBP | CSV | IT |
| LOTTO | [58] | SES Engineering | Single Shooting | GB | SO | PR-TBP | MEE | PC |
| - | [59] | Torino Univ. | Single Shooting | HS | SO | PR-TBP | CSV | IT |
| - | [60] | Pontani et al. | Single Shooting | HS | SO | PR-TBP | PSV | IT |
| - | [61] | Lee et al. | Single Shooting | HS | MO | PR-TBP | CSV | IT |
| BNDSCO | [62] | Hamburg. Univ | Multiple Shooting | HS | SO | - | - | G |
| LOTNAV | [63] | Deimos Space | Multiple-shooting | GB | SO | CSV | PR-NBP | IT |
| - | [64] | Meng et al. | Multiple-Shooting | GB | SO | PR-TBP | MEE | PC |
| - | [65] | Olympio | Gradient method | - | SO | PR-NBP | PSV | G |
| Name | Ref | Company/Org./Author | Approach | Solution | Obj. | Dynamics | States | Transfers |
|---|---|---|---|---|---|---|---|---|
| ASTOP | [66] | Space Flight Solutions | Single Shooting | GB | SO | PR-NBP | CSV | IT |
| COPERNICUS | [67] | Texas Univ., JSC | Multiple Shooting | GB | SO | PR-NBP | CSV | G |
| jTOP | [68] | Tokio Univ., JAXA | Multiple Shooting | GB | SO | PR-NBP | CSV | G |
| DITAN | [69] | ESA, Milano Univ. | Collocation | GB | SO | PR-NBP | CSV | G |
| MODHOC | [70] | Strathclyde Univ. | Collocation | HY | MO | PR-NBP | CSV | G |
| DIRETTO | [71] | Milano Univ. | Collocation | GB | SO | PR-NBP | CSV | G |
| MAVERICK | [72] | Colorado Boulder Univ. | Collocation | GB | SO | PR-NBP | CSV | G |
| MColl | [73] | NASA. | Collocation | GB | SO | PR-NBP | CSV | G |
| COLT | [74] | Purdue Univ. | Collocation | GB | SO | PR-NBP | CSV | G |
| GMAT | [75] | NASA | Collocation | GB | SO | - | - | G |
| STK | [76] | AGI | Collocation | GB | SO | - | - | G |
| OTIS | [77] | GCR, Boeing | Collocation | GB | SO | - | - | G |
| POST | [78] | NASA | Single Shooting | GB | SO | - | - | G |
| SOCS | [79] | Boeing | Collocation | GB | SO | - | - | G |
| DIDO | [80] | TOMLAB | Collocation | GB | SO | - | - | G |
| GPOPS | [81] | Univ. of Florida | Collocation | GB | SO | - | - | G |
| OPTELEC | [82] | Airbus | Multiple Shooting | GB | SO | PR-TBP | MEE | PC |
| MANTRA | [83] | ESA | Multiple-shooting | GB | SO | PR-NBP | CSV | G |
| LOTOS | [84] | ASTOS Solutions | Collocation | GB | SO | PR-TBP | MEE | PC |
| XIPSTOP | [85] | Boeing | Collocation | GB | SO | PR-TBP | MEE | PC |
| GALLOP | [86] | JPL, Purdue Univ. | Multiple-Shooting | GB | SO | KM | CSV | IT |
| COLTT | [87] | Colorado Boulder | Multiple-Shooting | GB | SO | KM | CSV | IT |
| LInX | [88] | J.H. Univ., Nabla Zero | Multiple-Shooting | GB | SO | KM | CSV | IT |
| BOLTT | [89] | Colorado Boulder | Multiple-Shooting | GB | SO | KM | CSV | IT |
| MALTO | [90] | JPL | Multiple-Shooting | GB | SO | KM | CSV | IT |
| EMTG | [91] | GSFC, Illinois Univ. | Multiple-Shooting | HY | MO | KM | CSV | IT |
| PaGMO | [92] | ESA | Multiple-Shooting | HY | SO | KM | CSV | IT |
| GA-GALLOP | [93] | Purdue Univ. | Multiple-Shooting | HY | MO | KM | CSV | IT |
| - | [94] | Zuiani et al. | Multiple-Shooting | GB | SO | SM | CSV | IT |
| DIFINC | [95] | Coverstone et al. | Differential Inclusion | GB | SO | PR-TBP | CSV | IT |
| - | [96] | Gerald et al. | Single Shooting | HS | SO | PR-TBP | PSV | IT |
| - | [97] | Pontani et al. | Single Shooting | HS | SO | PR-TBP | PSV | IT |
| Name | Ref | Company/Org./Author | Approach | Solution | Obj. | Dynamics | States | Transfers |
|---|---|---|---|---|---|---|---|---|
| HYTOP | [109] | Aerospace Corp. | Blended Control | GB | SO | PR-TBP | MEE | PC |
| - | [110] | Yang Gao | Blended Control | GB | SO | PR-TBP + AN + AVG | COE | PC |
| - | [111] | Yang Gao | COV-Based | GB | SO | PR-TBP + AVG | MEE | PC |
| - | [112] | Strathclyde Univ | Blended Control | HY | MO | SM + AVG | COE | PC |
| SEPDOC | [113] | Kluever et al. | Blended Control | GB | SO | PR-TBP + AVG | COE | PC |
| - | [114] | Hudson et al. | Fourier-Expansion | GB | SO | PR-TBP + AN + AVG | COE | PC |
| - | [115] | Chang et al. | Lyapunov Control | GB | SO | PR-TBP | CSV | PC |
| LATOP | [116] | ESA | Lyapunov Control | HS | MO | PR-TBP | MEE | PC |
| GA-Q-Law | [117] | JPL | Lyapunov Control | HS | MO | PR-TBP | MEE | PC |
| STOUR-LTGA | [118] | JPL, Purdue Univ. | Shape-based | HS | SO | PR-TBP + AN | PSV | IT |
| IMAGO | [119] | Pascale et al. | Shape-based | HS | SO | PR-TBP + AN | MEE | IT |
| - | [120] | Wall et al. | Shape-based | HS | SO | PR-TBP + AN | PSV | IT |
| - | [121] | Taheri et al. | Shape-based | HS | SO | PR-TBP + AN | PSV3 | IT |
| - | [122] | Gondelach et al. | Shape-based | HS | SO | PR-TBP + AN | PSV3 | IT |
| - | [123] | Roa et al. | Shape-based | HS | SO | PR-TBP + AN | PSV | IT |
| MOLTO-IT | [22] | Morante et al. | Shape-based | HY | MO | PR-TBP + AN | PSV | IT |
| MOLTO-OR | [124] | Morante et al. | Lyapunov Control | HS | MO | PR-TBP | MEE | PC |
| InTrance-GA | [125] | DLR | Neural control | HY | SO | PR-TBP | CSV | IT |
| Name | Ref | Company/Org./Author | Approach | Solution | Obj. | Dynamics | States | Transfers |
|---|---|---|---|---|---|---|---|---|
| MYSTIC | [126] | NASA | DDP | - | SO | PR-NBP | CSV | G |
| - | [127] | Colorado Boulder Univ. | DDP | - | SO | PR-TBP | MEE | PC |
| HDDP | [128] | Lantoine et al. | HDDP | - | SO | SM/KM | CSV | G |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morante, D.; Sanjurjo Rivo, M.; Soler, M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace 2021, 8, 88. https://doi.org/10.3390/aerospace8030088
Morante D, Sanjurjo Rivo M, Soler M. A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace. 2021; 8(3):88. https://doi.org/10.3390/aerospace8030088
Chicago/Turabian StyleMorante, David, Manuel Sanjurjo Rivo, and Manuel Soler. 2021. "A Survey on Low-Thrust Trajectory Optimization Approaches" Aerospace 8, no. 3: 88. https://doi.org/10.3390/aerospace8030088
APA StyleMorante, D., Sanjurjo Rivo, M., & Soler, M. (2021). A Survey on Low-Thrust Trajectory Optimization Approaches. Aerospace, 8(3), 88. https://doi.org/10.3390/aerospace8030088








