Configuration Study of Electric Helicopters for Urban Air Mobility

Abstract

There is currently interest in the design of small electric vertical take-off and landing aircraft to alleviate ground traffic and congestion in major urban areas. To support progress in this area, a conceptual design method for single-main-rotor and lift-augmented compound electric helicopters has been developed. The design method was used to investigate the feasible design space for electric helicopters based on varying mission profiles and technology assumptions. Within the feasible design space, it was found that a crossover boundary exists as a function of cruise distance and hover time where the most efficient configuration changes from a single-main-rotor helicopter to a lift-augmented compound helicopter. In general, for longer cruise distances and shorter hover times, the lift-augmented compound helicopter is the more efficient configuration. An additional study was conducted to investigate the potential benefits of decoupling the main rotor from the tail rotor. This study showed that decoupling the main rotor and tail rotor has the potential to reduce the total mission energy required in all cases, allowing for increases in mission distances and hover times on the order of 5% for a given battery size.

1. Introduction and Background

A current area of interest is the development of vehicle designs and infrastructure to enable safe and efficient air transportation within urban settings, known as urban air mobility (UAM) [1,2,3]. A strong driver in this area has been the Uber Elevate program, which seeks to establish a network of small electric vertical take-off and landing (eVTOL) aircraft to alleviate ground traffic and congestion and provide rapid transportation within major urban areas [4].

The design objectives for aircraft for UAM applications include high energy efficiency, low noise, and low costs, among others [4]. As these aircraft represent a potential new large-scale form of urban transportation, they should be environmentally responsible and sustainable. Even electric vehicles, which produce zero emissions in flight, are charged with electricity that is often sourced from fossil-fuel power plants. In addition, less efficient vehicles require greater battery weight to fly a given mission, which further reduces their efficiency. Thus, it is desirable to utilize vehicles with the lowest energy requirements, regardless of their on-board energy source. Aircraft noise also plays a significant role in the design process, as the noise level in urban areas must be acceptable to communities. Finally, to enable an economically feasible and sustainable large-scale transportation service, aircraft acquisition, maintenance, and operational costs must be kept to a minimum.

The conventional helicopter has several potential advantages over more unorthodox configurations for use in UAM applications. First, helicopter technology is mature, both for VTOL applications in general and in particular with respect to urban environments. This provides potential cost benefits in terms of development and certification. Second, as a result of the fact that helicopters are already used in urban areas, there is a clear benefit to the configuration in terms of infrastructure.

There are a few recent eVTOL design and configuration studies for UAM applications worth noting in relation to the current work. McDonald and German [5] compared eVTOL configurations at three set mission profiles and assuming a vehicle gross weight, while varying lift-to-drag ratios and disk loadings of each configuration. Based on these assumptions, a concept trade space was developed in terms of power required in hover and cruise. The conventional helicopter configuration was determined to be along the Pareto frontier of this trade space, indicating potential optimality depending on the battery assumptions and mission requirements.

Brown and Harris [6] applied similar assumptions and expanded on this work by including noise and cost considerations, but considered only one mission profile. This study showed potential noise and efficiency advantages for a compound helicopter configuration over tiltrotor, tiltwing, and lift-and-cruise configurations for UAM applications. It is worth noting, however, that later work by the same authors [7] indicated potential operational cost and weight savings with higher disk loading designs.

Kadhiresan and Duffy [8] compared several configurations (including helicopters) for UAM applications over a range of mission distances (10 miles–100 miles) and speeds (50–150 mph). The driving geometric constraint on the vehicle designs was a requirement to fit within a 50 ft × 50 ft footprint with variations in rotor diameter size and wing loading permitted. The weight of the resulting vehicle with the battery sized to complete a given mission was then determined using a component weight build-up. The optimal vehicle for each mission profile considered was then selected based on that capable of completing the mission with the lowest gross weight. The results of the study indicate that at a battery energy density of 300 Wh/kg, the conventional helicopter is optimal using the lowest gross weight criteria for series of low range/mid-speed missions.

Several additional configuration studies [9,10,11,12,13,14] omitted consideration of a single-main-rotor electric helicopter entirely, with the closest typically considered configuration being a side-by-side helicopter.

While all of these studies certainly have merit, there are some shortcomings evident with respect to the design processes applied. To allow for comparison between very different configurations, the design assumptions employed are typically high level (e.g., varying assumed lift-to-drag ratio and disk loading or forcing a geometry based on the vehicle footprint and assuming all other parameters). Although these assumptions allow for an effective high-level assessment, the approaches lack the detail required to complete a realistic conceptual design of an electric helicopter over a wide variety of UAM mission parameters. By mission parameters, the authors refer to the ability to vary both the mission profile (e.g., distance, hover time, number of passengers, and cruise speed) and the helicopter design itself (e.g., rotor design parameters, inclusion of and design assumptions for a wing, and coupled or decoupled main and tail rotor).

A starting point for the development of a conceptual design approach is to consider those for conventionally fueled helicopters. Conventional methods [15,16] make size, weight, and power estimations accounting for fuel and engine systems. Statistical correlations from historical aircraft are used to estimate the gross weight, which drives the design of the geometric parameters. Power calculations dictate the engine selection and the range and endurance calculations, and the design iteration is based on fuel requirements. To design electric systems, these fuel and engine estimates are no longer applicable, and the battery, motor, and other control systems must be sized and taken into account appropriately.

In light of the current state-of-the-art with respect to design of electric helicopters for UAM applications, there are three main objectives discussed in this paper. First, detailed conceptual design methods for an electric single-main-rotor helicopter and an electric lift-augmented compound helicopter are developed and documented. Second, these methods are used to investigate the design space for a better understanding of what mission profiles are possible based on current technology levels and future forecasts. Third, configuration selection criteria based on a wide range of potential mission profiles were developed.

To accomplish these objectives, the conceptual design approach for a single-main-rotor helicopter laid out in Kee [16] was modified to replace the components used in conventional fuel and engine systems with those necessary for electric propulsion systems. An additional set of modifications were made to account for the addition of a wing to an electric helicopter, resulting in a second configuration in the form of a lift-augmented compound helicopter. The design process was then automated using reasonable assumptions, resulting in a series of helicopters capable of completing a range of defined mission profiles. The results were then compared to determine configuration selection criteria based on the configuration requiring the least energy to complete the mission, or in some cases, the only configuration capable of completing the mission. Earlier work on this project by the authors including preliminary results are documented in Refs. [17,18,19,20].

2. Methods

An overview of the conceptual design method developed for single-main-rotor and lift-compound electric helicopters is provided in this section. The basis of this method is the conventional design approach of Kee [16]. In this paper, emphasis is placed on modifications made to this approach along with assumptions applied for automation of the process. For further details, the reader is referred to Kee [16], Salinger [17], and Rajauski [19].

Two main sections from the approach of Kee [16] were implemented and modified to account for electric systems. In the first section, an initial estimation of gross weight is determined based on historical statistical correlations. This estimated gross weight then drives a first estimation of the basic geometric parameters of the helicopter that are then iterated until a geometry that meets certain constraints is determined. In the second section, a more accurate component-based estimation method is used to predict the weight of the helicopter, and the predicted weight then drives the higher order power estimations in hover and cruise. In the original method, these power estimations are used to drive the required engine size and fuel requirements, and the design is then iterated through until the required engine size and fuel requirements meet those determined through power estimation.

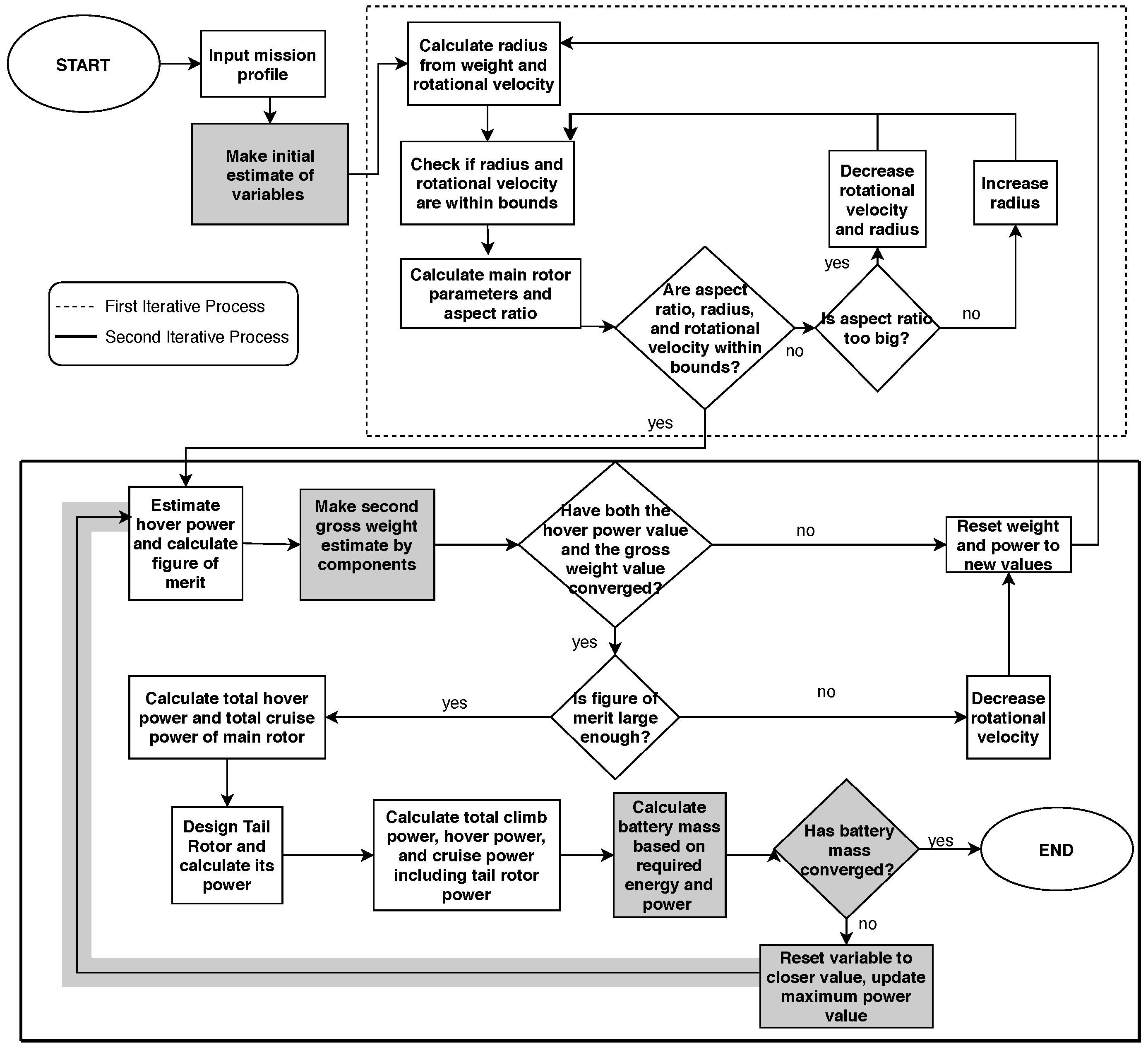
This approach, as modified to account for the electrical systems, is outlined in the flow chart provided in Figure 1. Broad changes to the original approach are highlighted in the figure in gray. In the first iterative process (identified in the figure with a dashed line), the initial estimation of weight and geometric parameters was modified as the conventional statistical regressions for weight are not applicable to helicopters with electrical systems. In the second iterative process (identified in the figure with a solid line), the component weight build-up and the power prediction processes were modified to account for the electrical systems. The process was also changed to iterate on the required energy capacity rather than the fuel requirements.

Within the first main section of the approach, the mission profile is used to drive an initial estimate of the parameters that define the geometry of the helicopter. In this process, the gross weight is estimated based on the payload requirements and is determined using a relation for the gross weight as a function of empty weight. Conventional relations between these parameters are insufficient as there are significant differences in the gross weight and empty weight of conventional versus electric helicopters. The difference between the gross weight and empty weight of a conventional helicopter includes both the fuel and the payload (in this case primarily passengers). Unlike fuel weight, which decreases over the course of a mission as the fuel is used, the battery weight is constant. Thus, the difference between the gross weight and empty weight of an electric helicopter includes only the payload. It was therefore necessary to create a new relation to be able to estimate the gross weight for electric helicopters. This was done by gathering data on existing electric VTOL vehicles and plotting the gross weight as a function of empty weight [21] (this data was gathered from several separate websites at the time that this relationship was developed, but is now compiled at the given reference). The resulting plot and linear relation for the gross weight is shown in Figure 2 with a comparison to the relation for conventional helicopters [16]. From this data, the relationship between the gross weight and empty weight of electric helicopters was determined to be

$$W_g=1.091W_e+251.9$$

(1)

where $W_g$ is the gross weight in lbs and $W_e$ is the empty weight in lbs. Using the payload, this relation can be manipulated to solve for an initial estimate of the gross weight. Based on this initial gross weight estimate, an iterative process is then used to determine the geometry of the helicopter, including blade radius, aspect ratio, and rotational velocity, within the constraints and assumptions provided in the Appendix A.

Within the second main section, a second gross weight estimate is determined using a component build-up that was modernized through use of the U.S. Army aeroflight dynamics directorate (AFDD) weight models [15]. The component build-up was then modified to account for the weights of the electrical components and to remove the conventional engine and fuel system. The assumptions with respect to the electrical components were varied based on three sets of technologies (current technology, conservative future, optimistic future) as generated from Freidrich and Robertson [22] and Kruger et al. [23] and as shown in

Table 1. Battery, motor and inverter technology assumptions [22,23].

Component	Current	Conservative Future 2035	Optimistic Future 2035
Inverter Specific Power (kW/kg)	2.2	9	19
Motor Specific Power (kW/kg)	2	9	16
Battery Power Density (W/kg)	520	745	1200
Battery Specific Energy (Wh/kg)	144	250	400
Electric Component Efficiency	0.95	0.98	0.99

.

Initial estimates are made for the battery, motor, and inverter weights based on the results of the first iterative process and technology assumptions. At the start of the second process, these values are used to drive a component based weight estimate, which is then used to estimate hover power. If the hover power and gross weight are not within tolerances of those assumed in the first iterative process, the design is returned to the first iterative process and resized based on the new assumed gross weight. Alternatively, the method moves on to a higher fidelity estimate of hover power, cruise power, and climb power (including tail rotor power). The power and energy requirements for the full mission are then determined, and the battery mass required to meet those requirements is calculated. If the battery mass is sufficient to complete the mission, the method has converged. If the battery mass is insufficient, the power requirements and new battery mass are then passed into a new gross weight estimate allowing for new motor and inverter sizing, and the process iterates until convergence is reached.

A few details about the sizing of the electric propulsion system are noteworthy. The battery mass is calculated as is necessary based on the technology assumptions to meet both the energy capacity and power requirements to complete a given mission profile. The larger of these two masses is then adopted and adjusted for the assumption that 10% of the battery should not be used to maintain battery longevity [5]. The motor and inverter are sized based on the predicted maximum power required during a given mission. The total weight of the electrical system is estimated by summing the motor, inverter, and battery weights and multiplying by an adjustment factor to account for the additional electrical components.

The design approach for the compound helicopter is an adaptation of the single-main-rotor approach that incorporates the design and performance of an additional lifting surface. It is important to note that in this study, the compound helicopter design involved the addition of a wing only, without the addition of an auxiliary propulsion system. Thus, the vehicles discussed in this section are more precisely described as lift-augmented compound helicopters. The benefit in adding a wing is to reduce the power required by the rotor during cruise. The lift produced by the wing effectively reduces the weight of the helicopter, reducing the required thrust in cruise. The reduction in required thrust decreases the total induced power during the cruise segment. The trade-off to this decrease in power due to the weight offload, however, is that the wing increases the total drag and weight of the vehicle.

Although much of the single-main-rotor approach remains applicable, the geometry of the wing and its additional weight, influence on rotor efficiency, and drag must all be taken into account. After the rotor is sized as outlined previously, the wing is designed using the approach of Raymer [24]. This approach assumes that the drag of the compound helicopter in cruise behaves roughly like a dirty, fixed-gear, propeller-driven fixed-wing aircraft in which the cruise lift coefficient is dictated by the lift being offloaded onto the wing only. The first step in defining the wing geometry is to determine the wing area, S. This is accomplished by enforcing wing loading for maximum range in cruise according to Raymer [24], adjusted for the lift required from the wing as a function of the weight offload in cruise, $X_w$ as

$$S=\frac{X_w{W}_g}{q\sqrt{\pi AR{e}_0{C}_{D,0,ac}}}$$

(2)

where q is the dynamic pressure in cruise, $AR$ is the aspect ratio of the wing, $e_0$ is an estimated Oswald efficiency factor, and $C_{D,0,ac}$ is an estimated zero-lift drag coefficient of the full aircraft. With the wing area set, the full wing geometry is defined based on the assumed aspect ratio and taper ratio. The values of wing offload, aspect ratio, and taper ratio are constant and are provided in the Appendix A. These values were selected for minimum energy requirements based on parametric studies that were run over a series of mission profiles [19]. The weight of the wing is then calculated using the NDARC AFDD model [15] and added to the overall gross weight estimate for the aircraft.

In addition to accounting for the weight of the wing, it is necessary to account for the two main aerodynamic effects of the wing, download in hover and increased drag in cruise. During hover, the wake of the rotor impinges upon the wing. This results in a download on the wing that must be overcome through additional thrust. It also results in a reduction in rotor efficiency, further increasing the hover power required to produce the same amount of thrust as a traditional single-rotor helicopter. The wing also produces drag during cruise that must be overcome by an increase in thrust and be taken into account within the parasite power calculation.

The method of Keys [25] was implemented to account for download effects. In this approach, the wing is broken into sections over which the local velocities are estimated via test measured velocity profiles. Local drag coefficients for each section are then determined using the local velocities and section geometries based on empirical flat plate data. Section drag forces are then calculated and summed to estimate the download, which is given as a percentage of thrust. The calculated download percentage is used to determine the increase in induced power for hover as well as the increase in thrust required. The thrust coefficient and ideal power coefficients are also updated based on the updated thrust. The figure of merit is updated based on the changes to the thrust and power coefficients.

The influence of drag on the helicopter performance is taken into account in two calculations within the method. The first calculation modified is that of the thrust required, which is adjusted to account for the additional drag due to the wing. The wing drag is calculated as

$$D_{wing}=qS\left(C_{D,0,wing}+\frac{C_L^2}{\pi eAR}\right)$$

(3)

where $C_{D,0,wing}$ is the zero-lift drag coefficient of the wing, $C_L$ is the lift coefficient in cruise, and e is an estimation of the span efficiency based on the assumed aspect ratio and taper ratio calculated with a numerical lifting line method [26]. Additional interference drag between the wing and the fuselage in cruise was assumed to be negligible in this study. The increase in thrust required due to the drag of the wing also increases the parasite power and is included accordingly.

To show the benefit of the wing in cruise, the reduction of the gross weight on the rotor due to the percentage of the total weight that is offloaded by the wing during cruise is included in the thrust required, and subsequently through the induced velocity and cruise power. Thus, although the cruise power increases for shorter missions due to the weight of the wing and download considerations, in missions that contain larger segments of cruise, the reduction of power due to the weight offloaded by the wing outweighs the increase in parasite power.

As an example of the sensitivity of the approach to the selected wing design parameters and as justification for the selected aspect ratio and taper ratio provided in the Appendix A, the results of a sweep of the wing aspect ratio and taper ratio for a single mission profile are provided in Figure 3. Based on these results and those gathered from a series of other mission profiles, an aspect ratio between 30 and 40 allows for minimum required energy. These relatively high aspect ratios are driven in part by the inverse dependence of the wing area on aspect ratio (see Equation (2)) and in part by the increase in aerodynamic efficiency resulting from the higher aspect ratio designs (see Equation (3)). Because increasing the aspect ratio results in a larger vehicle footprint if the wing extends beyond the rotor footprint, and to incorporate potential aeroelastic concerns, an aspect ratio of 30 was selected. A sampling of resulting designs over varying mission profiles and technology assumptions showed wing spans on the order of 40–60 ft for rotor diameters on the order of 30–45 ft. Because the results were less sensitive to taper ratio and to prevent Reynolds number concerns with very small tip chords, a taper ratio of 0.5 was selected.

3. Test Cases and Limitations

3.1. Test Cases

To ensure that the design method developed in this study produces designs that are realistic and reasonable for a given input mission profile, publicly available test flights of two existing experimental electric helicopters were converted to notional mission profiles and used to design new electric helicopters. Although use of a design mission profile with the resulting performance and geometry of the prototype aircraft would be ideal for this purpose, the authors were unable to find such information for any electric helicopters in the flight test phase. In lieu of these details, the flight test data was assumed to decently approximate the current performance capabilities of electric helicopter technology. A comparison of the geometry and performance of the experimental test aircraft to the new designed aircraft was then conducted to validate the approach.

The two test cases used for this purpose were that of the Volta [27] and the Tier 1 [28]. The Volta completed a 15 min and 4 s hover with no cruise. The Tier 1 completed a 22 min 18 s cruise, which was rounded up to an assumed 30 min cruise segment for the purpose of sizing. The other given mission parameters for each of the test cases are listed in

Table 2. Mission parameters used in the test cases.

Parameter	Volta	Tier 1
Payload	220 lbs	200 lbs
Hover Time	15 min 4 s	40 s
Cruise Speed	34 kts (loiter)	80 kts
Cruise Time	0 min	30 min
Battery Energy Density	133 Wh/kg	140.6 Wh/kg
Altitude	0 ft	800 ft

. In addition to the provided flight data, it was assumed that both cases included a reserve time of 20 min in the cruise condition as a notional loiter segment. Since the Volta electric helicopter mission only included hover, there was no given velocity to use to calculate the energy for this loiter segment. To determine a loiter velocity, the total energy was calculated over a sweep of velocities. The velocity for minimum energy usage was found to be 34 knots, which was used to calculate the energy due to the reserve requirement.

To account for components of the electric system that are not directly modeled (wiring, cooling systems, etc.), the weight of the electric system is increased by a weight adjustment factor. The two test cases were run with a sweep of this factor from 1 to 1.15 to identify the value that minimizes the difference between the resulting design and the test cases. The absolute value of the percent difference between the test helicopters and the designed helicopters were determined for gross weight, empty weight, battery weight, energy capacity and rotor radius. These values were then averaged for each vehicle and, to ensure that the influence of each vehicle was considered in terms of the magnitude of difference, the average differences were summed. The resulting value is plotted against the adjustment factor in Figure 4. The results of this sweep indicated that an adjustment factor of 1.1 provided the smallest discrepancy between the designed vehicles and test vehicles with a summed average percent different of 20%. The 20% breaks down to an average percent difference for each vehicle of around 10%.

Using a weight adjustment factor of 1.1, the results and comparison to the expected values for the Volta are detailed in

Table 3. Comparison of Volta [27] test aircraft to that designed using the current method.

Parameter	Volta	Designed Vehicle	% Difference
Gross Weight	1146 lbs	1114.9 lbs	2.71%
Empty Weight	926 lbs	894.9 lbs	3.36%
Battery Weight	364 lbs	440 lbs	20.88%
Energy Capacity	22 kWh	26.79 kWh	21.77%
Rotor Radius	11.48 ft	11.04 ft	3.83%

, and the results and comparison for the Tier 1 are detailed in

Table 4. Comparison of Tier 1 [28] test aircraft to that designed using the current method.

Parameter	Tier 1	Designed Vehicle	% Difference
Gross Weight	2500 lbs	2346 lbs	6.16%
Empty Weight	2300 lbs	2146 lbs	6.70%
Battery Weight	1100 lbs	1215.2 lbs	19.47%
Energy Capacity	72 kWh	78.24 kWh	8.68%
Rotor Radius	16 ft	13.04 ft	18.50%

. For most of the outputs, the results differed from the expected values by less than 10%. The major variations were in the battery weight and energy capacity of the Volta which varied by 20.88% and 21.77% respectively, and the radius of the Tier 1 with a difference of 18.50%. This discrepancy could be a result of variations in the actual design missions versus those assumed based on flight tests. It is also important to note that this design method is intended to produce a reasonable and technically feasible (although not necessarily optimal) design that can complete the mission profile. It can be assumed that multiple solutions exist.

3.2. Limitations and Future Work

There are a few limitations of the developed methods that the authors have left for future work. First, although a combination of historical precedent and parametric studies were used to justify the selection of constant values assumed within the design process, the designs have not been fully optimized for each mission profile. Employing optimization techniques within the design process may result in better performance in some cases. Second, quantitative assessment of objectives and constraints driven by logistical (e.g., recharging rates and vehicle footprints), financial, and noise considerations were neglected within this study but are worth considering in a full system design. Improvements to electrical system modeling, including more detailed accounting for wiring/cabling and battery discharge models may also improve the accuracy of the results. Finally, as electric helicopter technology is currently developing at a rapid pace, publicly available information to validate these processes is limited. As such information becomes available, the methods may need to be adjusted accordingly.

4. Results and Discussion

4.1. Design Space Exploration

The design methods were used to explore the design space and develop an understanding of the boundaries of the feasible design space over varying assumed battery energy densities and missions. To gather these results, the baseline mission profile shown in Figure 5 was used along with a 2-passenger payload. This baseline mission profile is based on that provided by McDonald and German [5] with two 120 s hover portions, an altitude of 1000 feet, and a climb rate of 500 feet per minute. A cruise distance of 25 miles, a cruise speed of 100 knots and a two-passenger payload are also assumed in order to produce solutions at the lowest level of technology. Additionally, each passenger is assumed to weigh 200 lbs. A reserve time of 20 min is included according to the FAA standards [29]. A maximum forward velocity of 120 knots is used, which is an assumption that is standard for small helicopters [16]. It is worth noting that this profile consists of a relatively short range and hover time in comparison with the performance of conventional helicopters. Regardless, it is an appropriate baseline for urban air mobility applications with current battery technology.

With these parameters as a baseline, a sweep of the potential design space was performed by varying the cruise speed, the distance, the number of passengers, and the hover time. Each sweep was performed for three varying assumed technology levels, as described in Table 1. For each sweep of variables, the total energy capacity requirement for the mission was plotted versus each parameter, as shown in Figure 6. Additionally, the plots with varying distance and hover time include lines mapping the gross weight to give a notational indication of the size of the designed helicopter.

A clear observation from the upper left plot of Figure 6 is that as technologies improve, the designs become more energy efficient for a set cruise speed. In each case, the maximum velocity was set at 120 knots and the minimum velocity was dictated by the feasible design space. Thus, it can also be seen that for the higher battery energy densities compared to the current technology, there is a wider range of potential cruise speeds and a flatter optimal region. It is worth noting in this result that design weights vary along each line of constant technology assumptions, and between the lines as well. The higher weights of the low energy density designs are drivers for the significantly decreased feasible design space.

In the upper right and lower plots of Figure 6, it is again clear that as technology improves, the energy required to complete the mission decreases. In the upper right plot, the maximum number of passengers was limited to 10 to align with the small helicopter assumptions while maintaining passenger comfort. However, in the lower plots the distances and hover times were varied until no more design solutions were possible for each battery density. As is intuitively evident, there is a significantly wider range of missions that are possible with the better battery technology.

There are other trends that can be observed as well. In the lower plots of Figure 6, there is a rapid increase in energy required as the hover times and cruise distances grow. This can be explained in two ways. First, the percent of the total weight of the vehicle taken up by the battery (or battery mass fraction) will increase with increasing range or endurance for any aircraft. If a constant operational empty weight mass fraction is assumed along with a constant payload (in this case, two passengers), then the payload fraction approaches zero as the gross weight approaches infinity, providing bounds to the design space. A second explanation can be made in that there is feedback between weight and aerodynamic efficiency as manifested in the power required for each mission segment. As the time of the mission increases, the energy required to complete the mission also increases, requiring a larger battery. As a result, an increase in power is needed to lift the battery weight. Since both power and time are increasing, the relationship is nonlinear, and the energy requirement grows substantially on the upper limits of the designs. In contrast, the upper right plot of Figure 6 shows an increase in efficiency (reduction in total energy per passenger) as the number of passengers increases. This is because the increasing the payload affects the gross weight of the helicopter at a much less severe rate within the bounds of the space considered (up to 10 passengers).

One noteworthy aspect of the lower two plots is a seeming discontinuity in the trends, particularly visible in the optimistic future case between the 3000 lb vehicle and 6000 lb vehicle. This is a result of a shift in the driving rotor design constraint and is due to the linear nature of the design process employed (as shown in Figure 1) as opposed to a true optimization for each design point. Because the goal of the study is to consider reasonably feasible designs, this small discontinuity in trends does not have an impact on the overall conclusions.

These same trends were exhibited by the lift-augmented compound helicopters under the same mission profiles as shown in Figure 7, allowing for a direct comparison of each of the variables. The major observable difference when comparing the sets of results was that the lift-augmented compound helicopter designs accommodate traveling slightly further distances, while the single-main-rotor helicopters accommodate longer hover times. To compare the efficiency and benefits of both types of helicopter, the total energy requirement as a function of cruise distance, hover time, cruise speed, and number of passengers was investigated. When comparing the energy requirements based on a sweep of cruise speed and passenger number, there was not as much sensitivity to these two parameters as there was to the cruise distance and hover time. Therefore, cruise distance and hover time were investigated in the comparison between the two configurations.

While investigating the energy efficiency of the helicopters under varying cruise distances, it became clear that there exists a crossover point at which the lift-augmented compound helicopter becomes the more efficient configuration. The location of this crossover point with varying hover time was then investigated. At shorter cruise distances, the benefit of adding the wing to reduce thrust are outweighed by the extra drag created by the wing, making the single-main-rotor helicopter more efficient. However, at longer cruise distances, the increased cruise efficiency dominates, resulting in the lift-augmented compound helicopter being more efficient. The crossover points and design bounds were determined for a range of mission profiles.

A visualization of the most energy efficient helicopter configuration for each mission profile based on this investigation is provided in Figure 8 for current technology and optimistic future technology assumptions. Because decoupling the drive train between the main rotor and tail rotor was found to result in improved performance in all cases (as is detailed in Section 4.2), these results consist of decoupled design solutions. They are also a representation of the mission range and hover time with the baseline mission profile of 2 passengers and a 100 knot cruise speed. The crossover points are visible, as well as the outer bounds of the feasible design space.

While the bounds of the design space vary slightly with selected mission parameters, the general trends do not. This can be seen in Figure 9 and Figure 10, which show the feasible design space for a 2-passenger, 80 knot cruise speed mission and an 8-passenger, 100 knot cruise speed mission respectively.

The visualization of the design space provided in Figure 8 has potential value within the UAM community. For example, if designing or selecting a vehicle out of a fleet of options to be used in a city where the vertiports will require aircraft to hover for longer periods of time, the single-main-rotor helicopter will likely be the more efficient configuration. On the other hand, if longer flights are required to maintain a profitable business model in a given city, the lift-augmented compound helicopter will likely be the more efficient selection.

4.2. Consideration of Drive-Train Decoupling

In conventional gas-powered helicopters, the main rotor and tail rotor are connected by a driveshaft and series of gearboxes, as illustrated in Figure 11. The use of electric components enables the possibility of a decoupled design in which each rotor has its own motor and inverter. This configuration has the potential to be more efficient because of the reduction in aircraft weight resulting from the removal of the large driveshaft.

The components required for a decoupled design differ from those of a conventional coupled design in several ways and must be sized accordingly. In the conventional coupled design, the total maximum power required by the main and tail rotors is supplied by a single motor and inverter. Thus, the motor and inverter are sized according to the maximum power required at any point during the mission (typically during hover) and the assumed efficiencies and specific power technologies as provided in Table 1. In order to model the decoupled design, the maximum power requirement for the main rotor and tail rotor at any point during the mission were determined individually. Then, the mass of both the main rotor and tail rotor motors and inverters is calculated based on the required power and assumed component efficiencies and specific power technologies (again as outlined in Table 1). As the decoupled design does not require the driveshaft and gearbox between the main rotor to the tail rotor, these components are eliminated from the weight buildup. The weight of the additional wiring was assumed to be taken into account through the electrical component weight adjustment factor (as described in Section 3). In other words, because the weight of the electrical system increases due to the additional motor and inverter, the magnitude of the weight adjustment increases as well. Improved accounting for the weight of the wiring due to this configuration are left for future work.

It is noteworthy that the efficiency of the gearboxes and resulting power losses in the transmission of power from the main rotor to the tail rotor in the coupled design were neglected, resulting in a conservative estimate of the benefits of the decoupled design. Inclusion of these losses could be expected to have minimal effect because the power and energy requirements of the tail rotor are significantly less than the main rotor requirements. Regardless of the required mission, the percentage of the total mission energy required that is a result of the tail rotor for either configuration never exceeds 3%. Thus, even with an inefficient mechanical drivetrain, changes to the results are expected to be modest. Including losses would increase the improvement in energy efficiency toward the decoupled rotors even further.

For the single-main-rotor helicopter, plots of mission energy consumption vs. distance and hover time, respectively, are shown in Figure 12. The first noteworthy result is that the decoupled rotor motors are always more energy efficient for the single-main-rotor helicopter than the coupled motors and rotors. For example, decoupling the system assuming a 500 kWh battery results in an increase in mission distance available of 6% for conservative future technology levels, and 5% for optimistic future technology levels. The increases predicted in terms of mission hover time due to decoupling for the conservative future and optimistic future technology levels for the same case are 7% and 5% respectively. Another noteworthy result is the overall expansion of feasible design space in terms of maximum range and hover time. Similar energy savings and mission expansions were found to be present in analysis of the compound helicopter configuration, as shown in Figure 13.

5. Conclusions

The conceptual design process for a single-main-rotor helicopter was effectively modified to account for electric propulsion systems. The main changes were made within the initial gross weight estimate, the component-based weight estimate, and the energy determination, and it was found that the energy capacity and battery weight were the most significant drivers in the design. The process was further modified to include a wing to be able to analyze a lift-augmented compound helicopter configuration. The Volta and Tier 1 test cases showed that this process was able to reproduce reasonable designs.

A sweep of mission parameters was conducted to investigate trends and the limits of the feasible design space. The single-main-rotor helicopter and the lift-augmented compound helicopter produced results with similar trends. From these results, it was evident that mission length variables such as hover time and cruise distance more severely impact the weight of the resulting vehicle as a result of the tradeoff between the weight of the battery and aerodynamic efficiency of the system. Additionally, it was clear that the design space is extremely sensitive to technology assumptions. As such, the comparison between the two configurations focused on the interactions between cruise distance and hover time for varying technology assumptions.

The investigation of the crossover points in a mission where the lift-augmented compound helicopter became more efficient than the single-main-rotor helicopter yielded useful results for configuration selection. In general, for missions with a longer hover time and a shorter range, the single-main-rotor helicopter outperforms the lift-augmented compound helicopter in terms of energy efficiency. For each type of helicopter that was investigated, the design space grows significantly with the battery energy density. Therefore, it is apparent that improvements in this area of technology will greatly expand the capabilities of electric helicopters by increasing the range of mission parameters they are capable of performing.

An investigation into the decoupling of the main and tail rotor was also conducted for both a single-main rotor and lift-augmented compound configuration. This study involved replacing the drive train and gearboxes typically used to divert power from the main rotor to the tail rotor with an individual motor and inverter for the tail rotor. The results of this study showed energy savings in all cases allowing for increases in mission distances and hover times on the order of 5% for a set battery size.