On Probabilistic Risk of Aircraft Collision along Air Corridors
Abstract
1. Introduction
2. Three Alternative Safety Metrics for Collision Risk
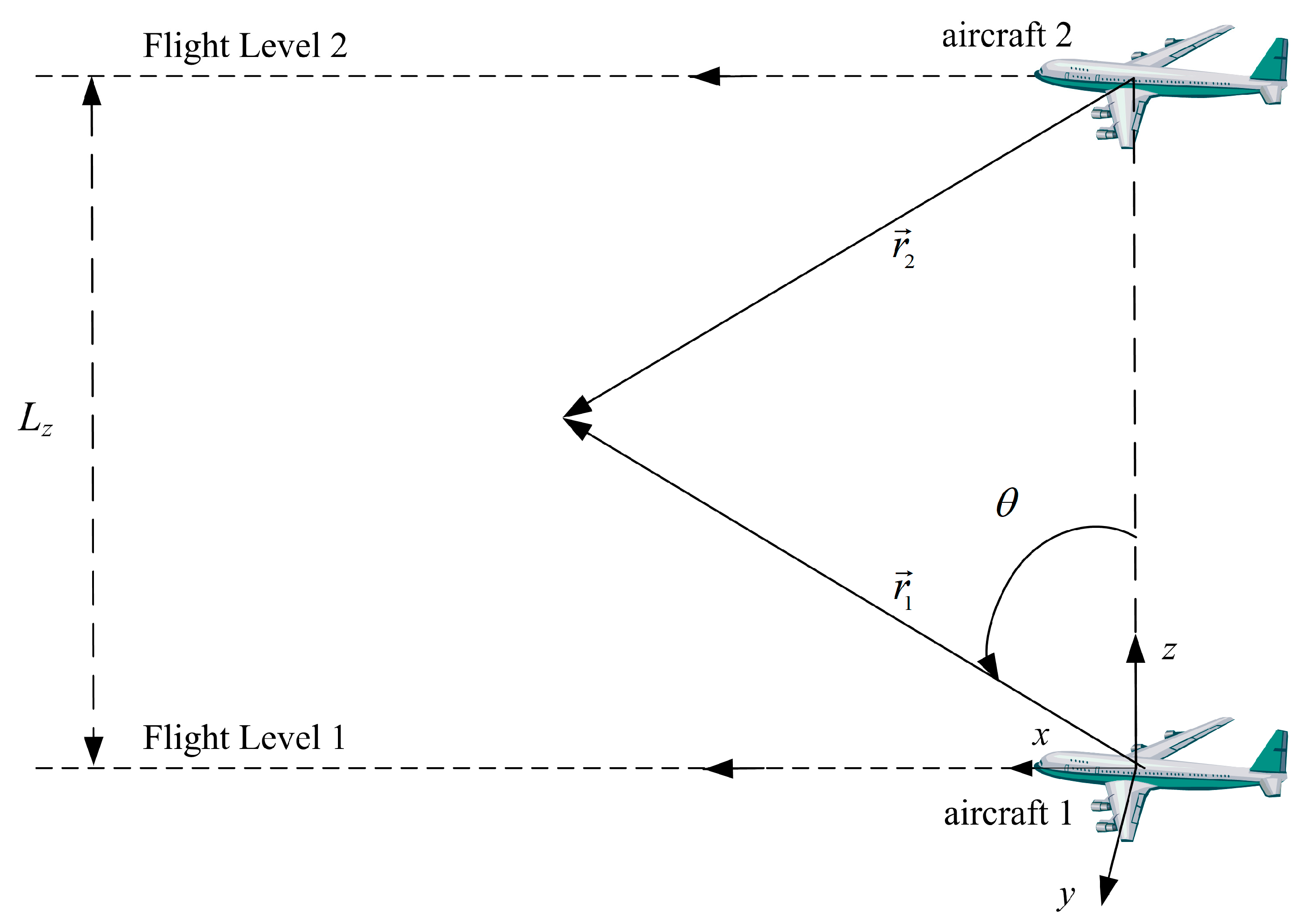
2.1. Maximum of the Joint Probability Density of Coincidence
2.2. Three-Dimensional Cumulative Probability of Coincidence over All Space
2.3. One-Dimensional Marginal Probability of Coincidence
3. Comparison of Safety Metrics in ATM Scenarios
3.1. Application to Standard and Reduced Vertical Separations
3.2. Gaussian and Laplace as Particular Exponential Distributions
3.3. Correction Factor for Generalized Gaussian Distribution
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| constant (56b) in the exponential of the generalized probability distribution (54) | |
| dissimilarity factor (32a) for aircraft with distinct r.m.s. position errors | |
| k | weighting exponent in the generalized exponential probability distribution (54) |
| distance (1b) from aircraft “1” | |
| position vector of the aircraft “i” respectively, (1b) and (2b) for i = 1, 2 | |
| distance of maximum probability of coincidence (7a; 8b) | |
| position (62a) of the minimum in (62b) of the function G in (60) | |
| A | constant factor (56a) in the generalized exponential probability distribution (54) |
| C | correction factor (65) between the Gaussian k = 2.0 and generalized exponential probability distribution with k = 1/2 |
| D | distance flown (47) |
| F | generalized exponential probability distribution (54) with weight k = 1/2 in (57) |
| G | ratio (60) of generalized exponential probability distribution (57) with weight k = 1/2 to the Gaussian distribution (59) with weight k = 2.0 |
| minimum (62b) of the function G in (60) | |
| azimuthal integral (15) appearing in the three-dimensional cumulative probability of coincidence (13,14) | |
| radial integrals (18a) appearing in the evaluation of the three-dimensional cumulative probability of coincidence (13, 17) | |
| separation distance between aircraft (2b), e.g., standard (40a) or reduced (40b) vertical separation | |
| generalized exponential distribution (54; 56a,b) with (57) weight k = 1/2 | |
| two-dimensional marginal probability of coincidence across the fight path (25b) | |
| three-dimensional cumulative probability of coincidence over all space (13) | |
| one-dimensional Gaussian probability distribution (1) of aircraft “i” as a function of position, respectively in (1a) and (2b) for i = 1, 2 | |
| maximum of the joint density of coincidence (11) | |
| Laplace probability distribution (53) | |
| joint probability density of coincidence (3) | |
| alternative ICAO target levels of safety for k = 1, 2, 3 using different units in, respectively, (45), (46) and (47) | |
| two-dimensional probability of coincidence for a great circle tour of the earth (49b) | |
| ICAO Target Level of Safety (43) | |
| modified ICAO TLS (52b) based on the three-dimensional probability of coincidence over all space (13) | |
| modified ICAO TLS (50a) based on maximum probability of coincidence (11) | |
| flight duration in hours (46) | |
| airspeed (45) | |
| maxima probability of coincidence for a great circle tour of the earth (51) | |
| polar angle (1b) in Figure 1 | |
| ratio r.m.s. position errors (33c) | |
| r.m.s. position error of the aircraft “i” appearing respectively in (1a) and (2a) for i = 1, 2 | |
| arithmetic mean of variances (30a) or squares of the r.m.s. position errors | |
| azimuthal angle (1b) in Figure 1 and Figure 2. | |
| azimuthal angle of maximum probability of coincidence (7a) | |
| constant (21b) appearing in the evaluation of the integrals (18a) | |
| change of variable (21a) used to evaluate the integrals (18a) | |
| Subscripts | |
| 1 | first aircraft |
| 2 | second aircraft |
| a | standard vertical separation of 2000 ft |
| b | reduced vertical separation of 1000 ft |
| Abbreviations | |
| r.m.s. | root mean square |
| ATM | Air Traffic Management |
| ICAO | International Civil Aviation Organization |
| TLS | Target Level of Safety |
| RVSM | Reduced Separation Vertical Minima |
| T-CAS | Traffic Collision Avoidance System |
References
- Eurocontrol. EUROCONTROL Seven-Year Forecast February 2018. Available online: https://www.eurocontrol.int/sites/default/files/content/documents/official-documents/forecasts/seven-year-flights-service-units-forecast-2018-2024-Feb2018.pdf (accessed on 20 December 2020).
- Vismari, L.F.; Junior, J.B.C. A safety assessment methodology applied to CNS/ATM-based air traffic control system. Reliab. Eng. Syst. Saf. 2011, 7, 727–738. [Google Scholar] [CrossRef]
- Barnett, A. Free-Flight and en Route Air Safety a First-Order Analysis. Oper. Res. 2000, 48, 833–845. [Google Scholar] [CrossRef]
- Hinton, D.A.; Tatnall, C.R. A Candidate Wake Vortex Strength Definition for Application to the NASA Aircraft Vortex Spacing System (AVOSS); NASA: Hampton, VA, USA, 1997. [Google Scholar]
- Spalart, P.R. Airplane Trailing Vortices. Annu. Rev. Fluid Mech. 1998, 39, 107–138. [Google Scholar] [CrossRef]
- Rossow, V.J. Lift-generated vortex wakes of subsonic transport aircraft. Prog. Aerosp. Sci. 1999, 35, 507–660. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On wake vortex response for all combinations of five classes of aircraft. Aeronaut. J. 2004, 108, 295–310. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On the compensation and damping of roll induced by wake vortices. Aeronaut. J. 2014, 118, 1–23. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On an analytical model of wake vortex separation of aircraft. Aeronaut. J. 2016, 120, 1534–1565. [Google Scholar] [CrossRef]
- ICAO. The Procedures for Air Navigation Services—Air Traffic Management (PANS-ATM), ICAO Doc 4444, 15th ed.; ICAO: Montreal, QC, Canada, 2009. [Google Scholar]
- Ballin, M.G.; Wing, D.J.; Hughes, M.F.; Conway, S.R. Airborne Separation Assurance and Air Traffic Management: Research and Concepts and Technology; AIAA: Reston, VA, USA, 1999. [Google Scholar]
- Anderson, E.W. Principles of Navigation; Hollis & Carter: London, UK, 1966. [Google Scholar]
- Leighton, S.J.; McGregor, A.E.; Lowe, D.; Wolfe, A.; Macaulay, A.A. GNSS Guidance for all Phases of Flight: Pratical Results. J. Navig. 2001, 54, 1–13. [Google Scholar] [CrossRef]
- Tomlin, C.; Pappas, J.; Sastry, S. Conflict Resolution in Air Traffic Management: A Study in Multi-agent Hybrid Systems. IEEE Trans. Autom. Control 1998, 43, 509–521. [Google Scholar] [CrossRef]
- Reich, P.G. Analysis of Long-range Air Traffic Systems: Separation Standards. J. Navig. 1966, 19, 88–98, 169–186, 331–347. [Google Scholar] [CrossRef]
- Eurocontrol. European Studies of Vertical Separation above FL290—Summary Report; Eurocontrol: Brussels, Belgium, 1988. [Google Scholar]
- Harisson, D.; Moek, G. European Studies to Investigate the Feasibility of using 1000 ft Vertical Separation Minima above FL 290: Part I: Overview of Organization, Techniques Employed and Conclusions. J. Navig. 1992, 44, 91–106. [Google Scholar] [CrossRef]
- Harisson, D.; Moek, G. European Studies to Investigate the feasibility of using 1000 ft Vertical Separation Minima above FL 290: Part II: Precision Data Analysis and Collision Risk Assessment. J. Navig. 1992, 45, 91–106. [Google Scholar] [CrossRef]
- Moek, G.; ten Have, J.M.; Harisson, D.; Cox, M.E. European Studies to Investigate the Feasibility of using 1000 ft Vertical Separation Minima above FL 290: Part III: Overview of Organization, Techniques Employed and Conclusions. J. Navig. 1992, 46, 245–261. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. On the probability of collision between aircraft with dissimilar position errors. J. Aircr. 2001, 38, 593–599. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On Safety Metrics Related to Aircraft Separation. J. Navig. 2002, 55, 39–63. [Google Scholar] [CrossRef]
- Shortie, J.F.; Xie, Y.; Chen, C.H.; Dunohue, G.L. Simulating Collision Probabilities of Landing Airplanes at Non-Towered Airports. Simulation 2004, 80, 21–31. [Google Scholar] [CrossRef]
- Houck, S.; Powell, J.D. Assessment of Probability of Mid-Air Collision during an Ultra Closely Spaced Parallel Approach; AIAA: Reston, VA, USA, 2001. [Google Scholar]
- Vidal, R.J.; Curtis, J.T.; Hilton, J.H. The Influence of Two-Dimensional Stream Shear on Airfoil Maximum Lift; Cornell Aeronautical Research Laboratory: Buffalo, NY, USA, 1961. [Google Scholar]
- Clodman, J.; Muller, F.R.; Morrisey, E.G. Wind Regime in the Lowest One Hundred Meters as Related to Aircraft Take-Offs and Landings. In Proceedings of the World Health Organization Conference, London, UK; 1968; pp. 28–43. [Google Scholar]
- Glazunov, V.G.; Guerava, V.Z. A Model of Windshear in the Lower 50 Meter Section of the Glide Path, from Data of Low Inertia Measurements; NLL-M-23036; Mathematical London Library of Science and Technology: London, UK, 1973. [Google Scholar]
- Gerlach, O.H.; Van de Moesdisk, G.A.J.; Van der Vaart, J.C. Progress in Mathematical Modeling of Flight in Turbulence; AGARD: Neuilly sur Seine, France, 1973. [Google Scholar]
- Etkin, B. Turbulent Wind and its Effects on Flight. J. Aircr. 1981, 18, 327–345. [Google Scholar] [CrossRef]
- Schanzer, G. Dynamic Energy Transfer between Wind and Aircraft. In Proceedings of the 13th Congress of the International Council of the Aeronautical, Seattle, WA, USA, 22–27 August 1982. [Google Scholar]
- Campos, L.M.B.C. On the Influence of Atmospheric Disturbances on Aircraft Aerodynamics. Aeronaut. J. 1984, 6, 257–264. [Google Scholar]
- Campos, L.M.B.C. On the Aircraft Flight Performance in a Perturbed Atmosphere. Aeronaut. J. 1986, 10, 301–312. [Google Scholar]
- Campos, L.M.B.C. On a Pitch Control Low for Constant Glide Slope through Windshears and Other Disturbances. Aeronaut. J. 1989, 9, 290–300. [Google Scholar]
- Etkin, B.; Etkin, D.A. Critical Aspect of Trajectory Prediction Flight in a Non-Uniform Wind; AGARD: Neuilly sur Seine, France, 1990. [Google Scholar]
- Pinsker, W.J.G. Critical Flight Conditions and Loads Resulting from Inertia Cross-Coupling and Aerodynamic Deficiencies; Aeronautical Research Council: London, UK, 1958. [Google Scholar]
- Hacker, T.; Oprisiv, C. A discussion of the roll coupling problem. Prog. Aerosp. Sci. 1974, 15, 30–60. [Google Scholar] [CrossRef]
- Schy, A.A.; Hannah, M.E. Prediction of jump phenomena in roll-coupling maneuvers of airplane. J. Aircr. 1975, 14, 100–115. [Google Scholar]
- Campos, L.M.B.C.; Aguiar, A.J.M.N. On the inverse phugoid problem as an instance of non-linear stability in pitch. Aeronaut. J. 1989, 10, 241–253. [Google Scholar]
- Campos, L.M.B.C.; Fonseca, A.A.; Azinheira, J.R.C. Some Elementary Aspects of Non-linear Airplane Speed Stability in Constrained Flight. Prog. Aerosp. Sci. 1995, 31, 137–169. [Google Scholar] [CrossRef]
- Etkin, B.; Reid, L.D. Dynamics of Flight: Stability and Control; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Campos, L.M.B.C.; Azinheira, J.R.C. On the application of special functions to non-linear and unsteady stability. Integral Transform. Spec. Funct. 2003, 14, 149–180. [Google Scholar] [CrossRef]
- Campos, L.M.B.C. On the non-linear longitudinal stability of symmetrical aircraft. J. Aircr. 1997, 36, 360–369. [Google Scholar] [CrossRef]
- Mises, R.V. Theory of Probability and Statistics; Academic Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Lindeberg, J.W. Ueber der Exponential Gezetzes in der Wahrlicheinkalkulus. Z. Math. 1922, 15, 211–225. [Google Scholar] [CrossRef]
- Reiss, R.D.; Thomas, M. Statistical Analysis of Extreme Values: With Applications to Insurance, Finance, Hydrology and Other Fields, 3rd ed.; Birkhäuser Verlag: Basel, Switzerland, 2007. [Google Scholar]
- Johnson, N.L.; Balakrishnan, N. Continuous Univariate Probability Distributions; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Campos, L.M.B.C.; Marques, J.M.G. On the Combination of the Gamma and Generalized Error Distribution with Application to Aircraft Flight Path Deviation. Commun. Stat. Theory Methods 2004, 3, 2307–2332. [Google Scholar] [CrossRef]
- Braff, R.; Shively, C. A Method of Over Bounding Ground Based Augmentation System Heavy Tail Error Distributions. J. Navig. 2005, 58, 83–103. [Google Scholar] [CrossRef]
- Kozubowski, T.J.; Podgórsi, K. Asymmetric Laplace Laws and Modelling of Financial Data. Math. Comput. Model. 2001, 34, 1003–1021. [Google Scholar] [CrossRef]
- Jammalamadaka, S.R.; Kozubowski, T.J. New Families of Wrapped Distributions for Modelling Skew Circular Data. Commun. Stat. Theory Methods 2004, 33, 2059–2074. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. Collision Probabilities, Aircraft Separation and Airways Safety, Aeronautics and Astronautics; Mulder, M., Ed.; InTech: Rijeka, Croatia, 2011; pp. 571–588. [Google Scholar]
- Campos, L.M.B.C. Generalized Calculus with Applications to Matter and Forces; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Abramowitz, M.; Stegun, I. Tables of Mathematical Functions; Dover: Mineola, NY, USA, 1965. [Google Scholar]
- Campos, L.M.B.C.; Marques, J.M.G. On the Probability of Collision Between Climbing and Descending Aircraft. J. Aircr. 2007, 44, 550–557. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On a dimensionless alternative to the ICAO Target Level of Safety. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 9, 1548–1557. [Google Scholar] [CrossRef]
- Pérez-Castán, J.A.; Rodríguez-Sanz, Á.; Pérez Sanz, L.; Arnaldo Valdés, R.M.; Gómez Comendador, V.F.; Greatti, C.; Serrano-Mira, L. Probabilistic Strategic Conflict-Management for 4D Trajectories in Free-Route Airspace. Entropy 2020, 22, 159. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.; Ellerbroek, J.; Hoekstra, J. Review of Conflict Resolution Methods for Manned and Unmanned Aviation. Aerospace 2020, 7, 79. [Google Scholar] [CrossRef]
- Pérez-Castán, J.A.; Comendador, F.G.; Rodríguez-Sanz, A.; Valdés, R.M.A.; Águeda, G.; Zambrano, S.; Torrecilla, J. Decision framework for the integration of RPAS in non-segregated airspace. Saf. Sci. 2020, 130, 104860. [Google Scholar] [CrossRef]
- Pérez-Castán, J.A.; Comendador, F.G.; Rodríguez-Sanz, Á.; Valdés, R.M.A.; Alonso-Alarcon, J.F. Safe RPAS integration in non-segregated airspace. Aircr. Eng. Aerosp. Technol. 2020, 6, 801–806. [Google Scholar] [CrossRef]
- Tabassum, A.; Sabatini, R.; Gardi, A. Probabilistic Safety Assessment for UAS Separation Assurance and Collision Avoidance Systems. Aerospace 2019, 6, 19. [Google Scholar] [CrossRef]
- Zhang, J.; Zou, X.; Wu, Q.; Xie, F.; Liu, W. Empirical study of airport geofencing for unmanned aircraft operation based on flight track distribution. Transp. Res. Part C Emerg. Technol. 2020, 121, 102881. [Google Scholar] [CrossRef]
- Costea, M.-L.; Nae, C.; Apostolescu, N.; Costache, F.; Andrei, I.-C.; Stroe, G.-L.; Semenescu, A. Automatic Aircraft Collisions Algorithm Development for Civil Aircraft. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies, Deggendorf, Germany, 16–18 September 2020; pp. 98–103. [Google Scholar]
- Hashemi, S.M.; Botez, R.M.; Grigorie, T.L. New Reliability Studies of Data-Driven Aircraft Trajectory Prediction. Aerospace 2020, 7, 145. [Google Scholar] [CrossRef]
- Metz, I.C.; Mühlhausen, T.; Ellerbroek, J.; Kügler, D.; Van Gasteren, H.; Kraemer, J.; Hoekstra, J.M. Simulation Model to Calculate Bird-Aircraft Collisions and Near Misses in the Airport Vicinity. Aerospace 2018, 5, 112. [Google Scholar] [CrossRef]
- Campos, L.M.B.C.; Marques, J.M.G. On the probability of collision for crossing aircraft. Aircr. Eng. Aerosp. Technol. 2011, 5, 306–314. [Google Scholar] [CrossRef]


| 1 | 3 | 9 | |
| 1 | 5/3 = 1.6667 | 41/9 = 4.5556 | |
| 1 | 1/3 | 1/9 |
| Arithmetic Mean of Variances (ft) | Maximum of the Joint Probability Density of Coincidence (per Square NM) | 1D Marginal Probability of Coincidence (per NM) | 3D Cumulative Probability of Coincidence (Times NM) | ||||
| 1000 | |||||||
| 500 | |||||||
| 400 | |||||||
| 300 | |||||||
| 200 | |||||||
| 180 | |||||||
| 160 | |||||||
| 140 | |||||||
| 120 | |||||||
| 100 | |||||||
| Arithmetic Mean of Variances (ft) | Maximum of the Joint Probability Density of Coincidence (per Square NM) | 1D Marginal Probability of Coincidence (per NM) | 3D Cumulative Probability of Coincidence (Times NM) | ||||
| 500 | |||||||
| 300 | |||||||
| 200 | |||||||
| 150 | |||||||
| 100 | |||||||
| 90 | |||||||
| 80 | |||||||
| 70 | |||||||
| 60 | |||||||
| 50 | |||||||
| Quantity | Unit | Standard | Reduced |
|---|---|---|---|
| Vertical separation | ft | ||
| r.m.s. altitude error | ft | ||
| One-dimensional marginal probability of coincidence with | (NM)−1 | ||
| Maximum velocity to meet the ICAO TLS | kt | ||
| Probability of coincidence in a great circle tour of the earth | - | ||
| r.m.s. altitude error | ft | ||
| Probability density ofcoincidence with or | (NM)−2 | ||
| Maximum velocity to meet the ICAO TLS (50a) | - | ||
| Probability of coincidence in a great circle tour of the earth | - | ||
| r.m.s. altitude error | ft | ||
| Cumulative probability of coincidence with or | NM | ||
| Maximum velocity to meet the ICAO TLS (49b) | - |
| Arithmetic Mean of Variances (ft) | Correction Factor C | Maximum of the Joint Probability Density of Coincidence (per Square NM) | 2D Marginal Probability of Coincidence (per NM) | 3D Cumulative Probability of Coincidence (Times NM) | ||||
| 1000 | 1.71 × 10−1 | 6.73 | 2.46 | 1.48 | 4.31 × 10−1 | 3.66 × 10−2 | 1.32 × 10−2 | 1.76 × 10−3 |
| 500 | 2.21 × 10−1 | 1.73 | 6.35 × 10−1 | 3.80 × 10−1 | 5.55 × 10−2 | 1.18 × 10−3 | 4.25 × 10−4 | 5.68 × 10−5 |
| 400 | 6.95 × 10−1 | 8.97 × 10−1 | 3.29 × 10−1 | 1.97 × 10−1 | 2.30 × 10−2 | 3.14 × 10−4 | 1.13 × 10−4 | 1.51 × 10−5 |
| 300 | 1.78 × 101 | 3.17 × 10−1 | 1.16 × 10−1 | 6.94 × 10−2 | 6.06 × 10−3 | 4.66 × 10−5 | 1.68 × 10−5 | 2.24 × 10−6 |
| 200 | 1.27 × 106 | 4.71 × 10−2 | 1.72 × 10−2 | 1.03 × 10−2 | 6.02 × 10−4 | 2.05 × 10−6 | 7.38 × 10−7 | 9.89 × 10−8 |
| 180 | 2.00 × 108 | 2.60 × 10−2 | 9.55 × 10−3 | 5.72 × 10−3 | 3.00 × 10−4 | 8.29 × 10−7 | 2.98 × 10−7 | 4.00 × 10−8 |
| 160 | 2.82 × 1011 | 1.28 × 10−2 | 4.69 × 10−3 | 2.81 × 10−3 | 1.31 × 10−4 | 2.85 × 10−7 | 1.03 × 10−7 | 1.38 × 10−8 |
| 140 | 1.41 × 1016 | 5.34 × 10−3 | 1.95 × 10−3 | 1.17 × 10−3 | 4.78 × 10−5 | 7.98 × 10−8 | 2.87 × 10−8 | 3.85 × 10−9 |
| 120 | 3.42 × 1023 | 1.76 × 10−3 | 6.42 × 10−4 | 3.86 × 10−4 | 1.35 × 10−5 | 1.66 × 10−8 | 5.98 × 10−9 | 8.00 × 10−9 |
| 100 | 1.03 × 1036 | 4.09 × 10−4 | 1.50 × 10−4 | 8.98 × 10−5 | 2.62 × 10−6 | 2.23 × 10−9 | 8.02 × 10−10 | 1.08 × 10−10 |
| Arithmetic Mean of Variances (ft) | Correction Factor C | Maximum of the Joint Probability Density of Coincidence (per Square NM) | 2D Marginal Probability of Coincidence (per NM) | 3D Cumulative Probability of Coincidence (Times NM) | ||||
|---|---|---|---|---|---|---|---|---|
| 500 | 1.71 × 10−1 | 2.70 × 10 | 9.84 | 5.91 | 8.61 × 10−1 | 1.83 × 10−2 | 6.60 × 10−3 | 8.84 × 10−4 |
| 300 | 1.47 × 10−1 | 1.09 × 10 | 3.99 | 2.39 | 2.09 × 10−1 | 1.61 × 10−3 | 5.77 × 10−4 | 7.72 × 10−5 |
| 200 | 6.95 × 10−1 | 3.59 | 1.31 | 7.86 × 10−1 | 4.60 × 10−2 | 1.56 × 10−4 | 5.64 × 10−5 | 7.58 × 10−6 |
| 150 | 1.78 × 10 | 1.26 | 4.62 × 10−1 | 2.77 × 10−1 | 1.21 × 10−2 | 2.33 × 10−5 | 8.38 × 10−6 | 1.12 × 10−6 |
| 100 | 1.27 × 106 | 1.89 × 10−1 | 6.89 × 10−2 | 4.13 × 10−2 | 1.20 × 10−3 | 1.03 × 10−6 | 3.70 × 10−7 | 4.94 × 10−8 |
| 90 | 2.00 × 108 | 1.04 × 10−1 | 3.82 × 10−2 | 2.28 × 10−2 | 6.00 × 10−4 | 4.14 × 10−7 | 1.49 × 10−7 | 2.00 × 10−8 |
| 80 | 2.82 × 1011 | 5.11 × 10−2 | 1.8 × 10−2 | 1.12 × 10−2 | 2.63 × 10−4 | 1.43 × 10−7 | 5.14 × 10−8 | 6.89 × 10−9 |
| 70 | 1.41 × 1016 | 2.14 × 10−2 | 7.82 × 10−3 | 4.68 × 10−3 | 9.57 × 10−5 | 3.99 × 10−8 | 1.43 × 10−8 | 1.93 × 10−9 |
| 60 | 3.42 × 1023 | 7.04 × 10−3 | 2.58 × 10−3 | 1.55 × 10−3 | 2.71 × 10−5 | 8.27 × 10−9 | 2.98 × 10−9 | 4.00 × 10−10 |
| 50 | 1.03 × 1036 | 1.63 × 10−3 | 5.89 × 10−4 | 3.60 × 10−4 | 3.82 × 10−6 | 1.11 × 10−9 | 4.02 × 10−10 | 5.37 × 10−11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, L.M.B.C.; Marques, J.M.G. On Probabilistic Risk of Aircraft Collision along Air Corridors. Aerospace 2021, 8, 31. https://doi.org/10.3390/aerospace8020031
Campos LMBC, Marques JMG. On Probabilistic Risk of Aircraft Collision along Air Corridors. Aerospace. 2021; 8(2):31. https://doi.org/10.3390/aerospace8020031
Chicago/Turabian StyleCampos, Luís M. B. C., and Joaquim M. G. Marques. 2021. "On Probabilistic Risk of Aircraft Collision along Air Corridors" Aerospace 8, no. 2: 31. https://doi.org/10.3390/aerospace8020031
APA StyleCampos, L. M. B. C., & Marques, J. M. G. (2021). On Probabilistic Risk of Aircraft Collision along Air Corridors. Aerospace, 8(2), 31. https://doi.org/10.3390/aerospace8020031







