Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation
Abstract
1. Introduction
2. Methodology
2.1. Filtering Approach and Energy Flux
2.2. Subgrid-Scale Turbulence
2.3. Vortex Stretching and Subgrid-Scale Stress
3. Result
3.1. Setup of the Simulations
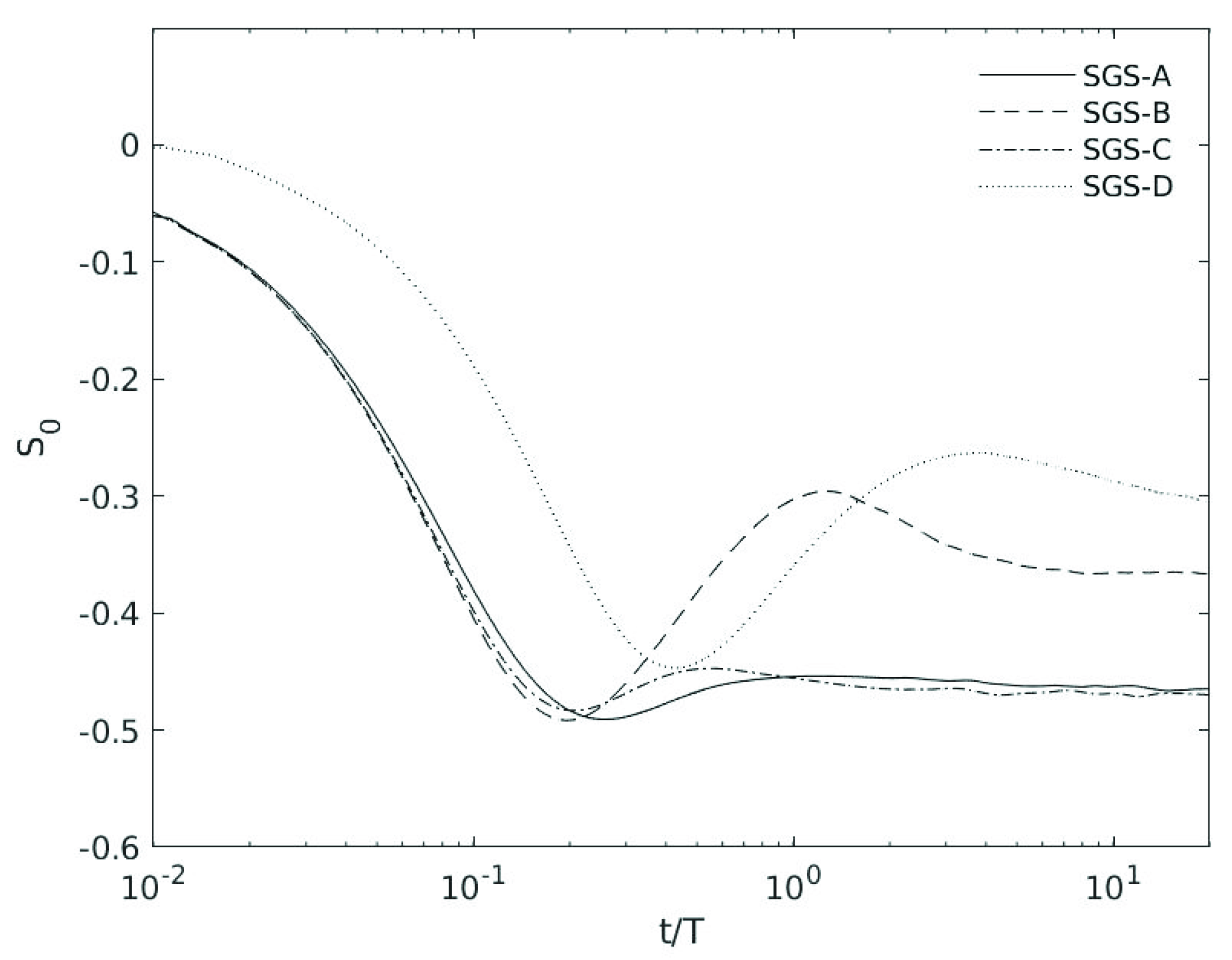
3.2. Skewness and Velocity Gradient Tensor
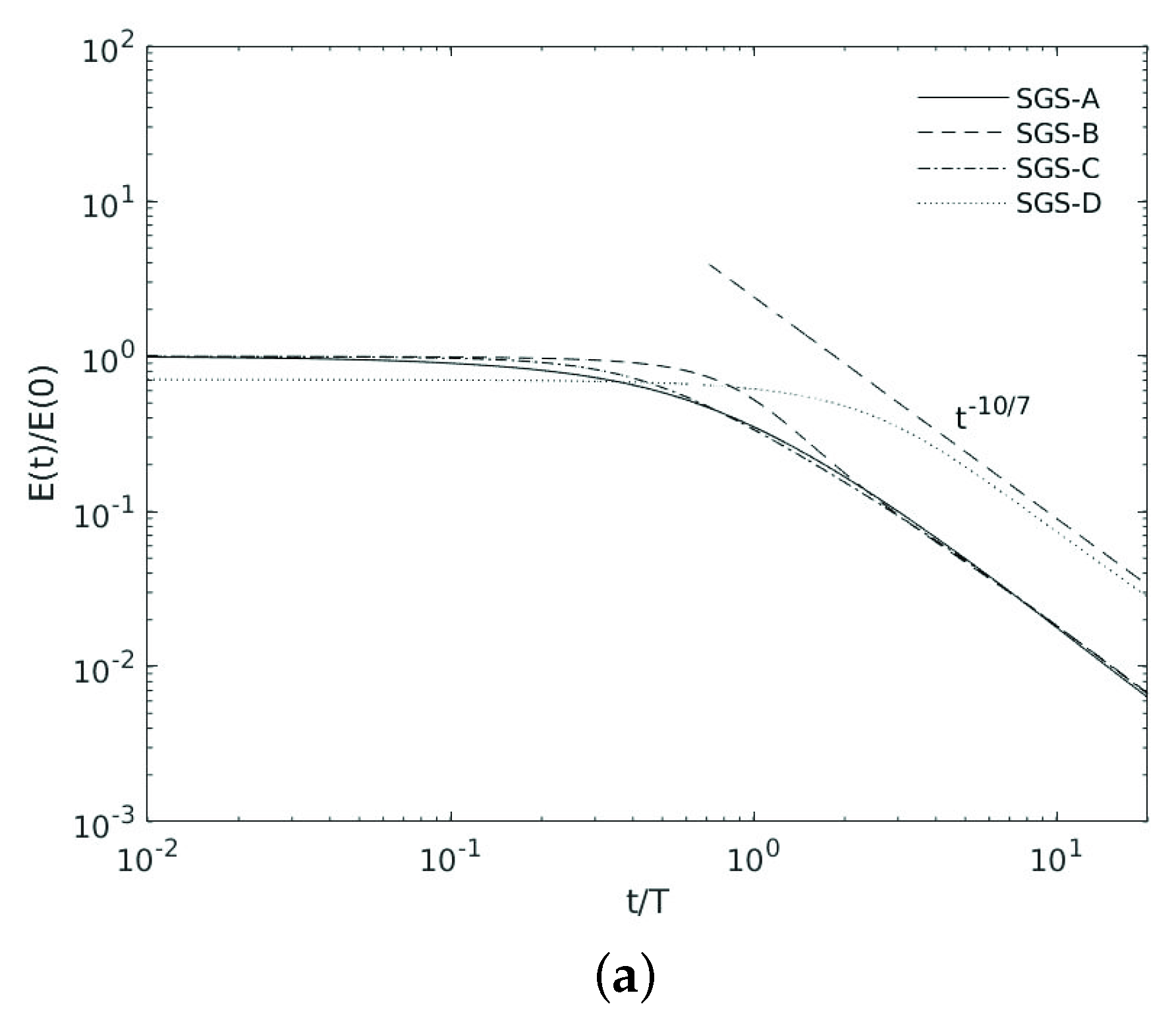
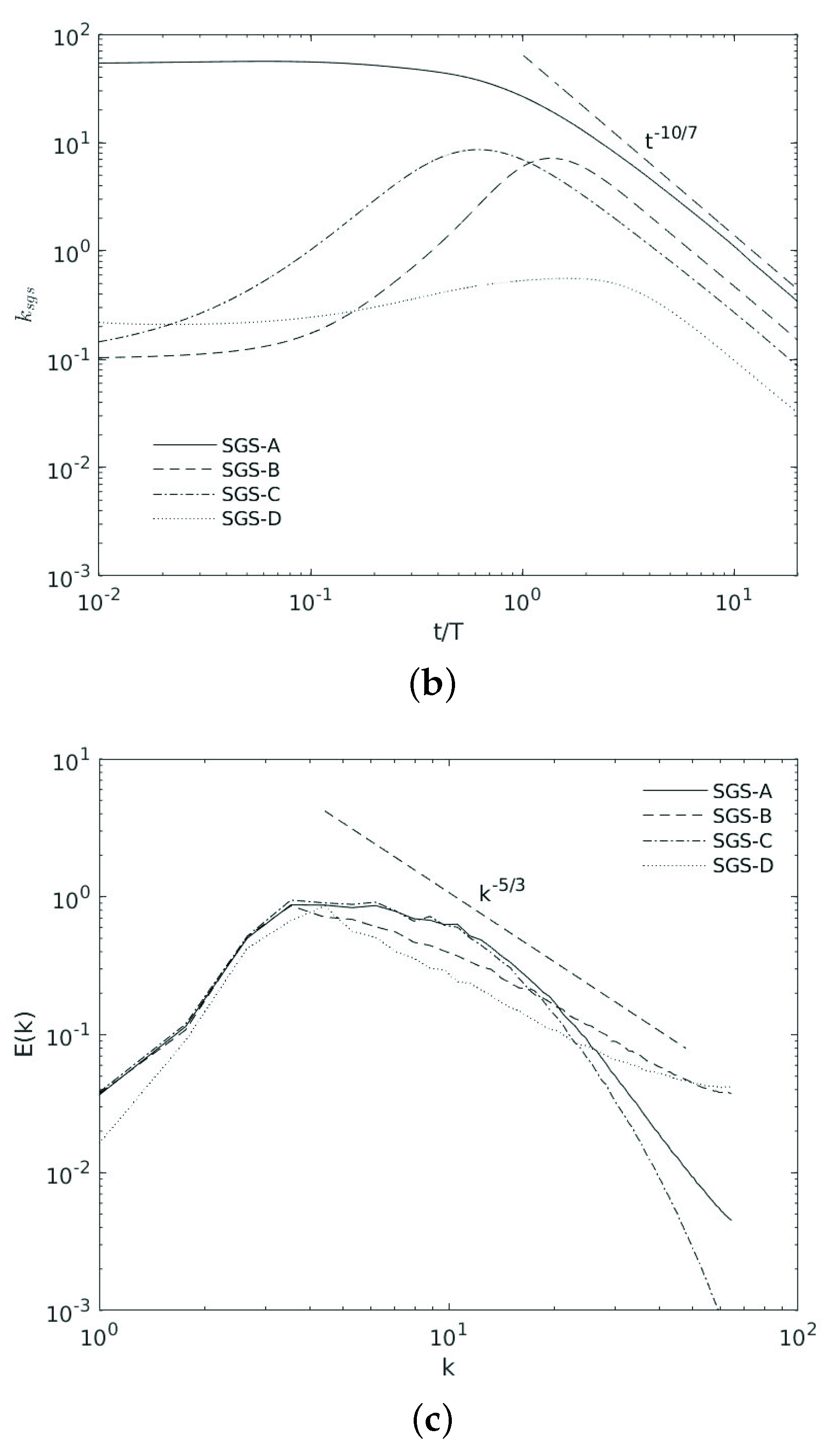
3.3. Second Moment of the Velocity Field
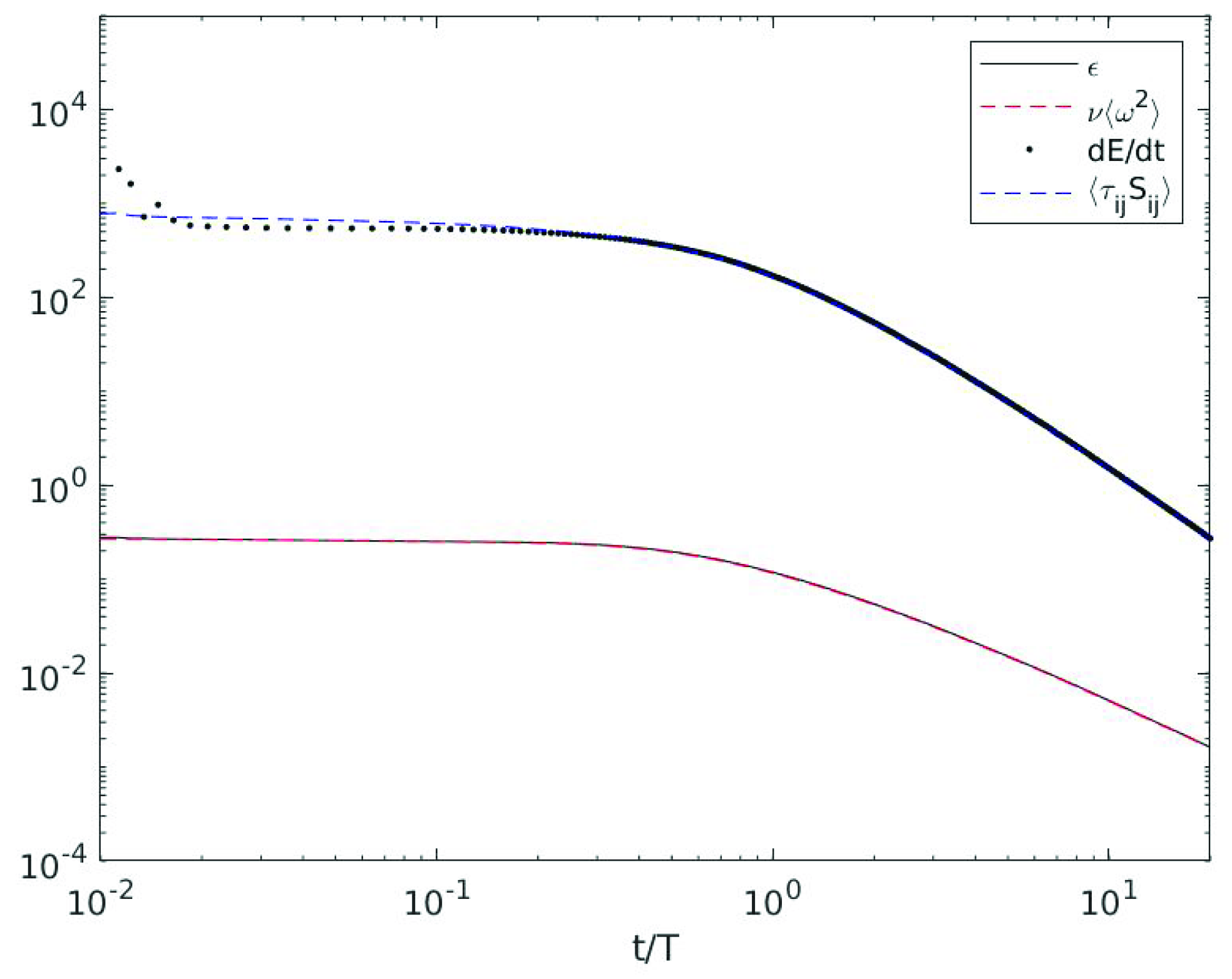
Viscous Dissipation
3.4. Statistics, Vortices, Stretches, and Whirls of Turbulence
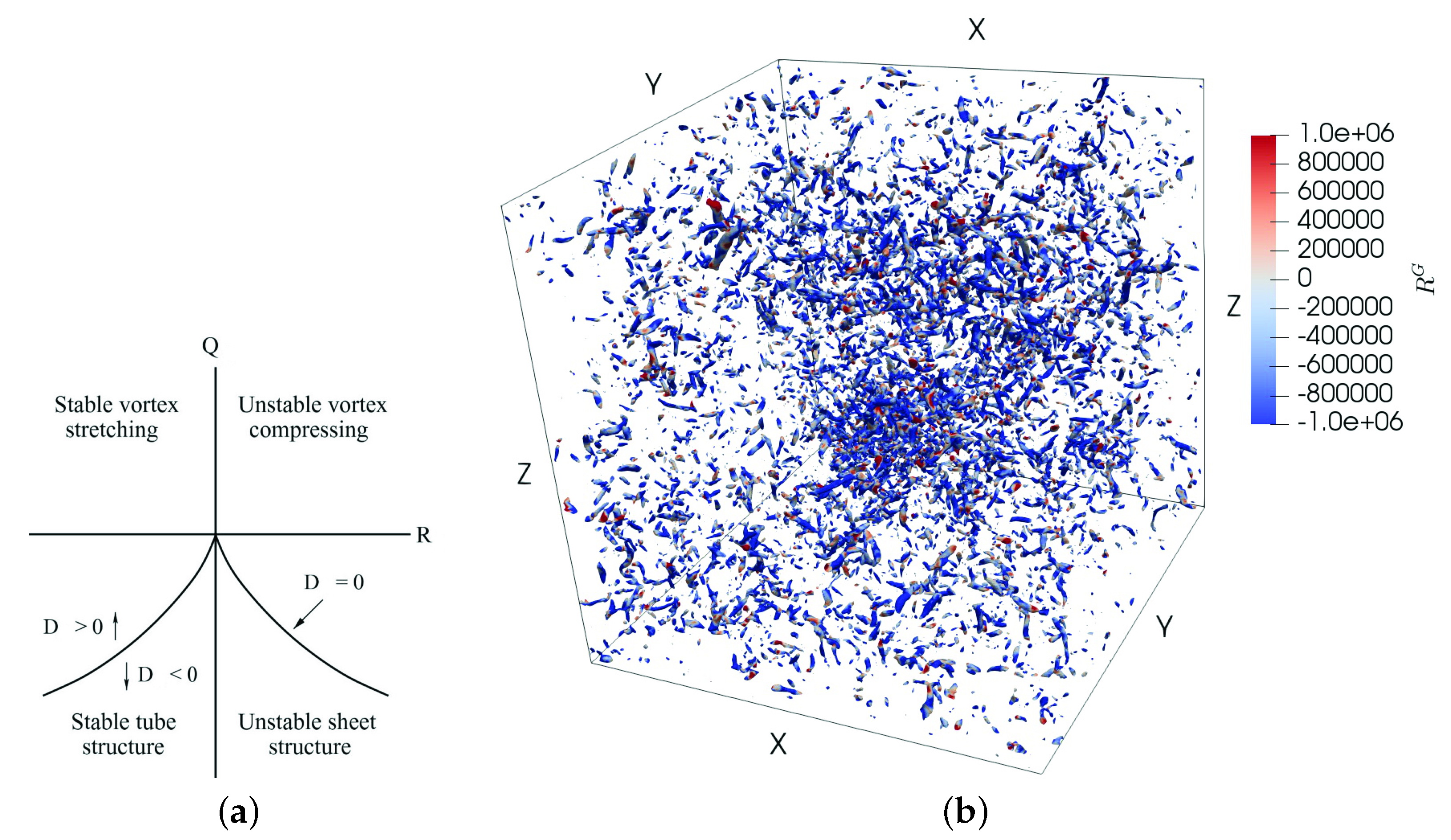
3.4.1. Dynamics of Filtered Velocity Gradients
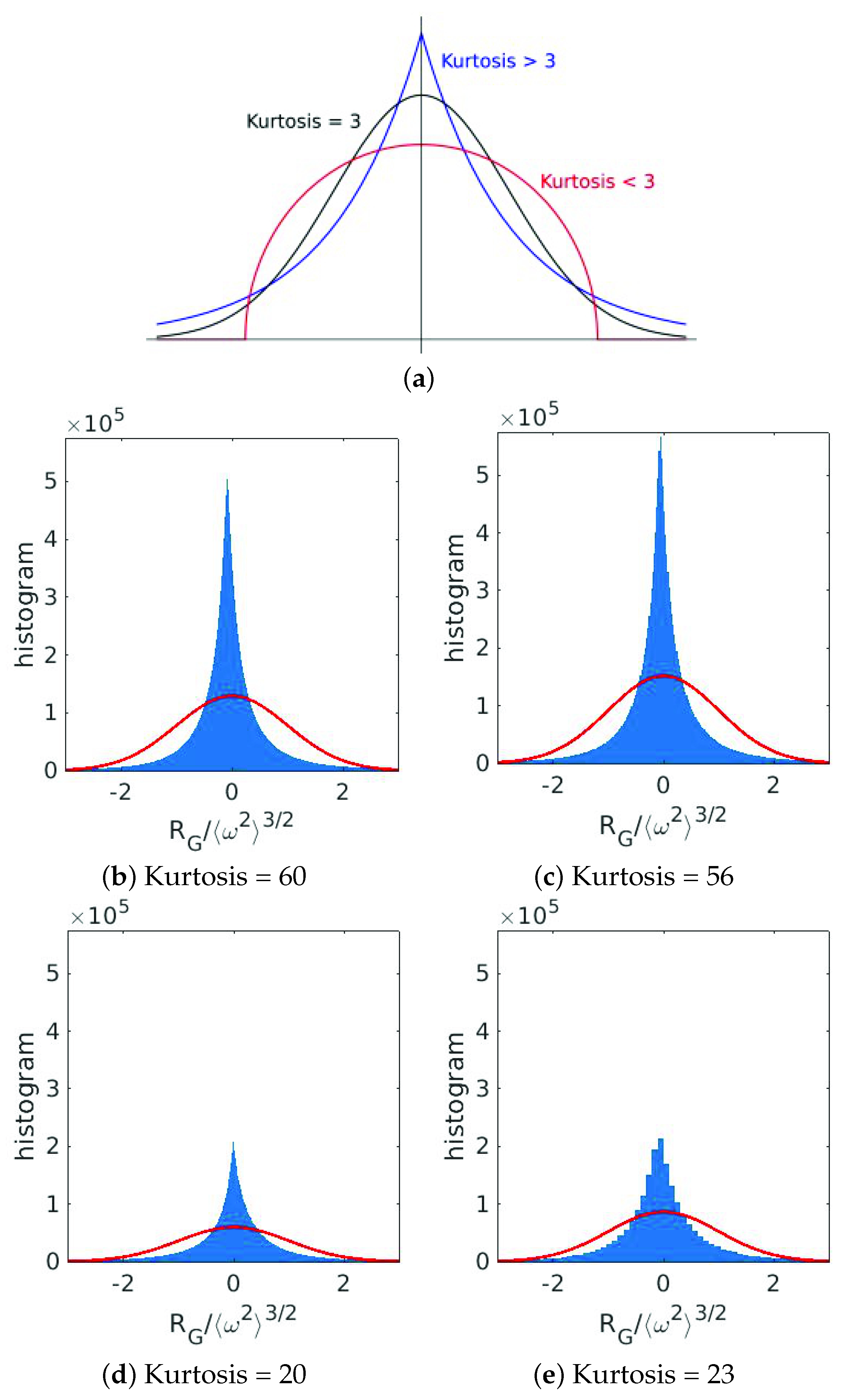
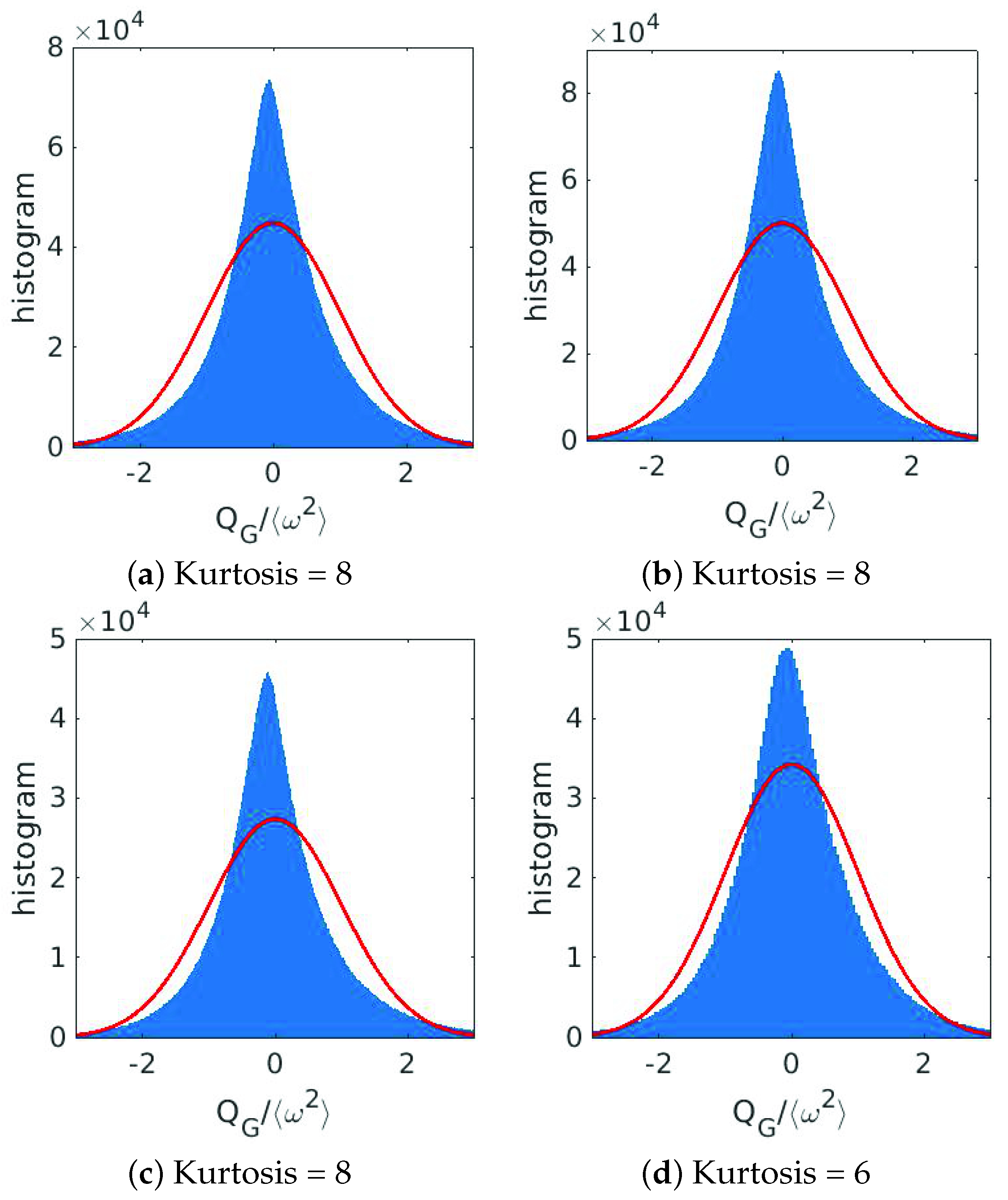
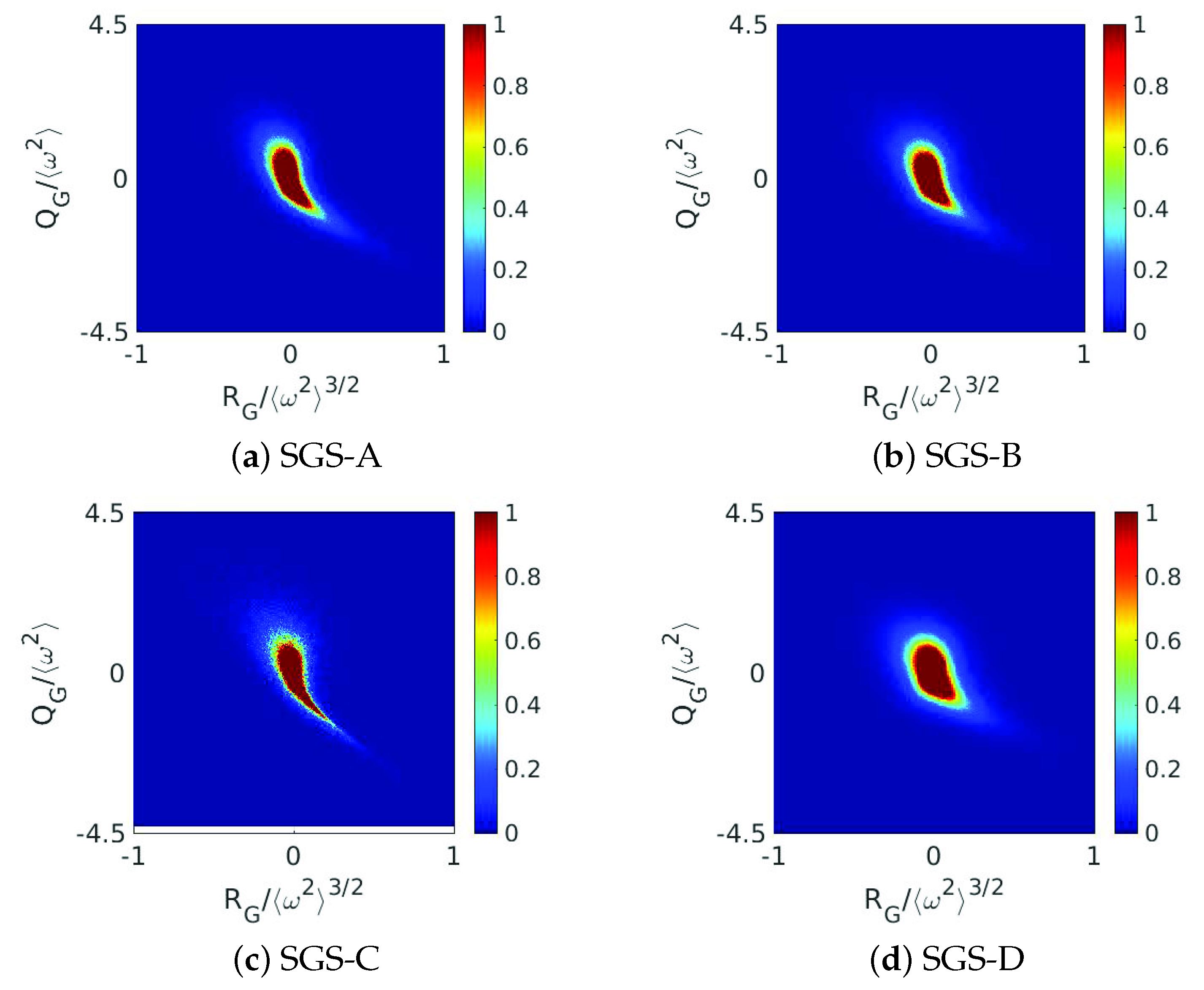
3.4.2. Statistics
3.4.3. Energy Flux, Vortex Stretching, and Strain Skewness
4. Conclusions and Future Direction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| LES | Large Eddy Simulation |
References
- Bradshaw, P. Understanding and prediction of turbulent flow—1996. Int. J. Heat Fluid Flow 1997, 18, 45–54. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Moser, R.D.; Haering, S.W.; Yalla, G.R. Statistical Properties of Subgrid-Scale Turbulence Models. Annu. Rev. Fluid Mech. 2021, 53, 255–286. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent flows; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Meneveau, C.; Lund, T.S.; Cabot, W.H. A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Michler, C.; Calo, V.; Hughes, T. Weak Dirichlet boundary conditions for wall-bounded turbulent flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 4853–4862. [Google Scholar] [CrossRef]
- Golshan, R.; Tejada-Martínez, A.E.; Juha, M.; Bazilevs, Y. Large-eddy simulation with near-wall modeling using weakly enforced no-slip boundary conditions. Comput. Fluids 2015, 118, 172–181. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-Layer Models For Large-Eddy Simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Chung, D.; Pullin, D.I. Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 2009, 631, 281–309. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-Modeled Large-Eddy Simulation for Complex Turbulent Flows. Annu. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef]
- Eyink, G.L. Multi-scale gradient expansion of the turbulent stress tensor. J. Fluid Mech. 2006, 549, 159–190. [Google Scholar] [CrossRef]
- Tsinober, A. An Informal Introduction to Turbulence; Springer: Berlin/Heidelberg, Germany, 2001; Volume 63. [Google Scholar]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: Cambridge UK, 2018. [Google Scholar]
- Carbone, M.; Bragg, A.D. Is vortex stretching the main cause of the turbulent energy cascade? J. Fluid Mech. 2020, 883. [Google Scholar] [CrossRef]
- Meneveau, C. Statistics of turbulence subgrid-scale stresses: Necessary conditions and experimental tests. Phys. Fluids 1994, 6, 815–833. [Google Scholar] [CrossRef]
- Farge, M.; Schneider, K. Coherent Vortex Simulation (CVS), A Semi-Deterministic Turbulence Model Using Wavelets. Flow Turbul. Combust. 2001, 66, 393–426. [Google Scholar] [CrossRef]
- Doan, N.A.K.; Swaminathan, N.; Davidson, P.A.; Tanahashi, M. Scale locality of the energy cascade using real space quantities. Phys. Rev. Fluids 2018, 3, 084601. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.S.; Alam, J.M. Scale-adaptive turbulence modeling for LES over complex terrain. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Alam, J.M.; Fitzpatrick, L.P. Large eddy simulation of flow through a periodic array of urban-like obstacles using a canopy stress method. Comput. Fluids 2018, 171, 65–78. [Google Scholar] [CrossRef]
- Alam, J.M.; Afanassiev, A.; Singh, J. Characterizing Impacts of Atmospheric Turbulence on Wind Farms Through Large Eddy Simulation (LES). In Ocean Renewable Energy, Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, Scotland, UK, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 10. [Google Scholar]
- Borue, V.; Orszag, S.A. Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 1998, 366, 1–31. [Google Scholar] [CrossRef]
- Taylor, G.I. The transport of vorticity and heat through fluids in turbulent motion. Proc. R. Soc. London. Ser. Contain. Pap. Math. Phys. Character 1932, 135, 685–702. [Google Scholar]
- Taylor, G.I. Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. London. Ser. Math. Phys. Sci. 1938, 164, 15–23. [Google Scholar]
- Onsager, L. Statistical hydrodynamics. Il Nuovo C. (1943–1954). 1949, Volume 6, pp. 279–287. Available online: http://fig.if.usp.br/~marchett/fluidos/statistical-hydrodynamics_onsager.pdf (accessed on 28 November 2021).
- Bernard, P.S.; Thangam, S.; Speziale, C.G. The Role of Vortex Stretching in Turbulence Modeling. In Instability, Transition, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1992; pp. 563–574. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D. Fluid Mechanics, 6th ed.; Academic Press: London, UK, 2016. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Betchov, R. An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1956, 1, 497–504. [Google Scholar] [CrossRef]
- Shetty, D.A.; Frankel, S.H. Assessment of stretched vortex subgrid-scale models for LES of incompressible inhomogeneous turbulent flow. Int. J. Numer. Methods Fluids 2013, 73, 152–171. [Google Scholar] [CrossRef][Green Version]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Trias, F.; Folch, D.; Gorobets, A.; Oliva, A. Building proper invariants for eddy-viscosity subgrid-scale models. Phys. Fluids 2015, 27, 065103. [Google Scholar] [CrossRef]
- Martın, J.; Ooi, A.; Chong, M.S.; Soria, J. Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 1998, 10, 2336–2346. [Google Scholar] [CrossRef]
- da Silva, C.B.; Pereira, J.C. Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 2008, 20, 055101. [Google Scholar] [CrossRef]
- Lund, T.S.; Novikov, E. Parameterization of subgrid-scale stress by the velocity gradient tensor. Annu. Res. Briefs 1992, 1992, 27–43. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- McMillan, O.J.; Ferziger, J.H. Direct Testing of Subgrid-Scale Models. AIAA J. 1979, 17, 1340–1346. [Google Scholar] [CrossRef]
- Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Deardorff, J.W. The Use of Subgrid Transport Equations in a Three-Dimensional Model of Atmospheric Turbulence. J. Fluids Eng. 1973, 95, 429–438. [Google Scholar] [CrossRef]
- Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound.-Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
- Stoll, R.; Gibbs, J.A.; Salesky, S.T.; Anderson, W.; Calaf, M. Large-Eddy Simulation of the Atmospheric Boundary Layer. Bound.-Layer Meteorol. 2020, 177, 541–581. [Google Scholar] [CrossRef]
- Yoshizawa, A. Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling. Phys. Fluids 1986, 29, 2152–2164. [Google Scholar] [CrossRef]
- Bardina, J.; Ferziger, J.; Reynolds, W. Improved subgrid-scale models for large-eddy simulation. In Proceedings of the 13th Fluid and Plasma Dynamics Conference, Snowmass, CO, USA, 14–16 July 1980. [Google Scholar]
- Comte-Bellot, G.; Corrsin, S. Simple Eulerian time correlation of full-and narrow-band velocity signals in grid-generated, isotropic turbulence. J. Fluid Mech. 1971, 48, 273–337. [Google Scholar] [CrossRef]
- Dallas, V.; Alexakis, A. Structures and dynamics of small scales in decaying magnetohydrodynamic turbulence. Phys. Fluids 2013, 25, 105106. [Google Scholar] [CrossRef]
- Liu, S.; Meneveau, C.; Katz, J. On the properties of similarity subgrid-scale models as deduced from measurements in a turbulent jet. J. Fluid Mech. 1994, 275, 83–119. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Jiménez, J.; Wray, A.A.; Saffman, P.G.; Rogallo, R.S. The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 1993, 255, 65–90. [Google Scholar] [CrossRef]
- Alam, J.; Islam, M.R. A multiscale eddy simulation methodology for the atmospheric Ekman boundary layer. Geophys. Astrophys. Fluid Dyn. 2015, 109, 1–20. [Google Scholar] [CrossRef]
| Model | Remark | ||||
|---|---|---|---|---|---|
| SGS-A | Nicoud and Ducros [31] | 0.1105 | 5.9719 × 10 | 8837 | 0.0629 |
| SGS-B | Yoshizawa [42] | 0.0796 | 5.0677 × 10 | 6365 | 0.1231 |
| SGS-C | Deardorff [39] | 0.1068 | 5.8718 × 10 | 8546 | 0.0673 |
| SGS-D | Meneveau et al. [5] | 0.0880 | 5.3308 × 10 | 7043 | 0.0991 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossen, M.K.; Mulayath Variyath, A.; Alam, J.M. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace 2021, 8, 375. https://doi.org/10.3390/aerospace8120375
Hossen MK, Mulayath Variyath A, Alam JM. Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace. 2021; 8(12):375. https://doi.org/10.3390/aerospace8120375
Chicago/Turabian StyleHossen, Mohammad Khalid, Asokan Mulayath Variyath, and Jahrul M. Alam. 2021. "Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation" Aerospace 8, no. 12: 375. https://doi.org/10.3390/aerospace8120375
APA StyleHossen, M. K., Mulayath Variyath, A., & Alam, J. M. (2021). Statistical Analysis of Dynamic Subgrid Modeling Approaches in Large Eddy Simulation. Aerospace, 8(12), 375. https://doi.org/10.3390/aerospace8120375






