Dynamic Stability and Flight Control of Biomimetic Flapping-Wing Micro Air Vehicle
Abstract
1. Introduction
2. Materials and Methods
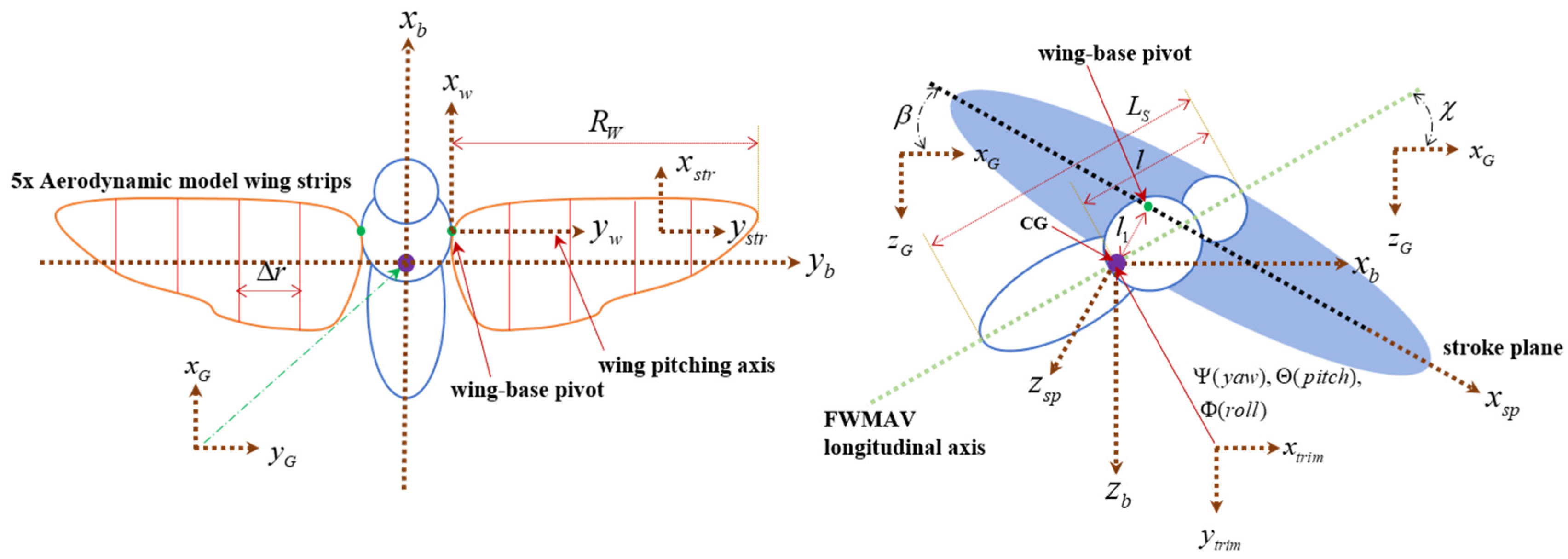
2.1. FWMAV Multibody Model and Coordinate Systems
2.1.1. FWMAV Multibody Modeling
2.1.2. Coordinate Systems
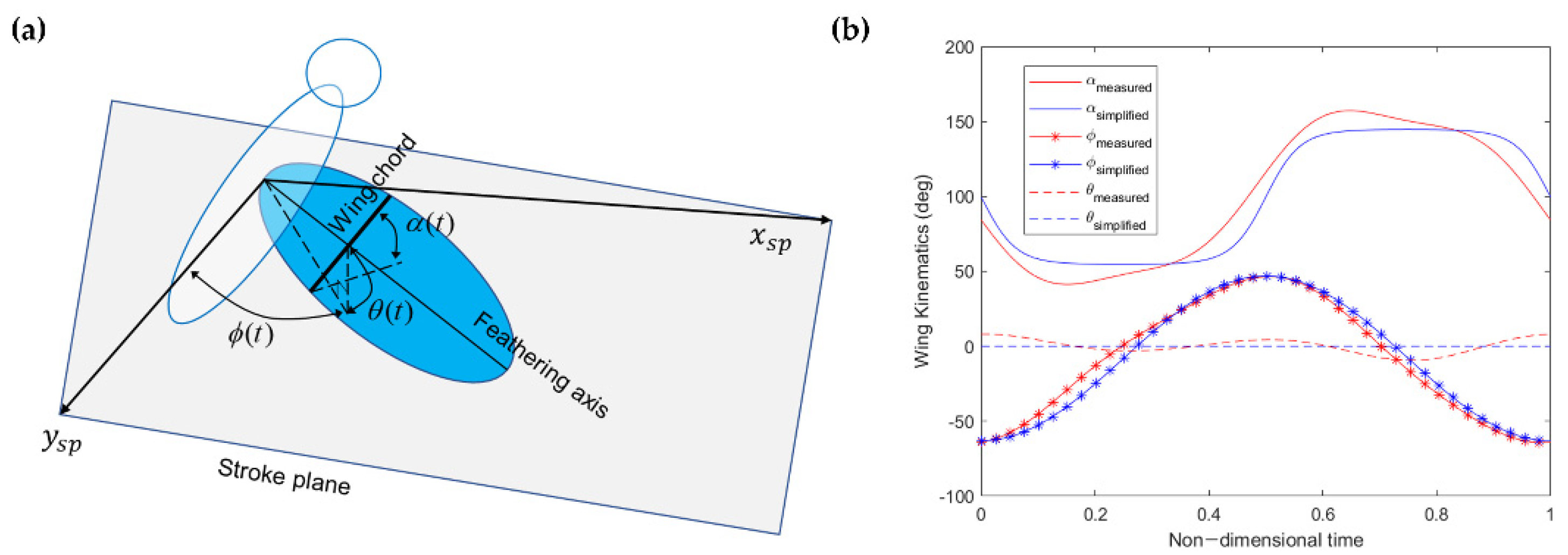
2.2. Wing Kinematics and Aerodynamic Model
2.2.1. FWMAV Wing Kinematics
2.2.2. Quasi-Steady Aerodynamic Model
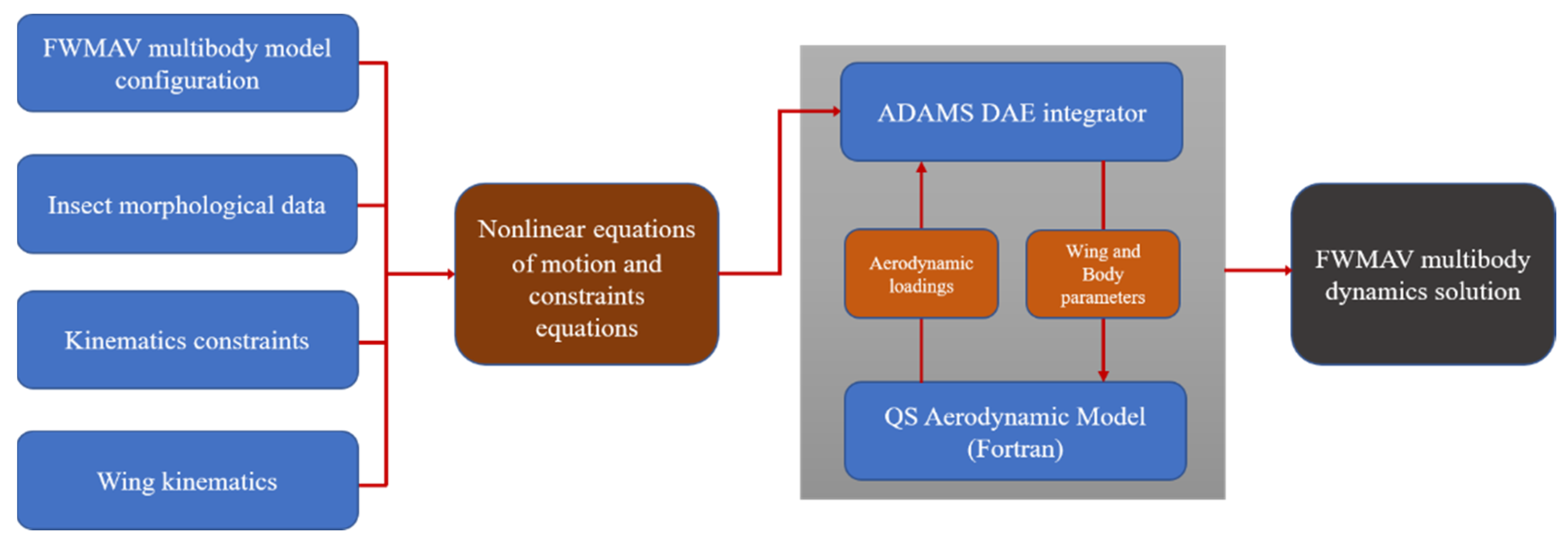
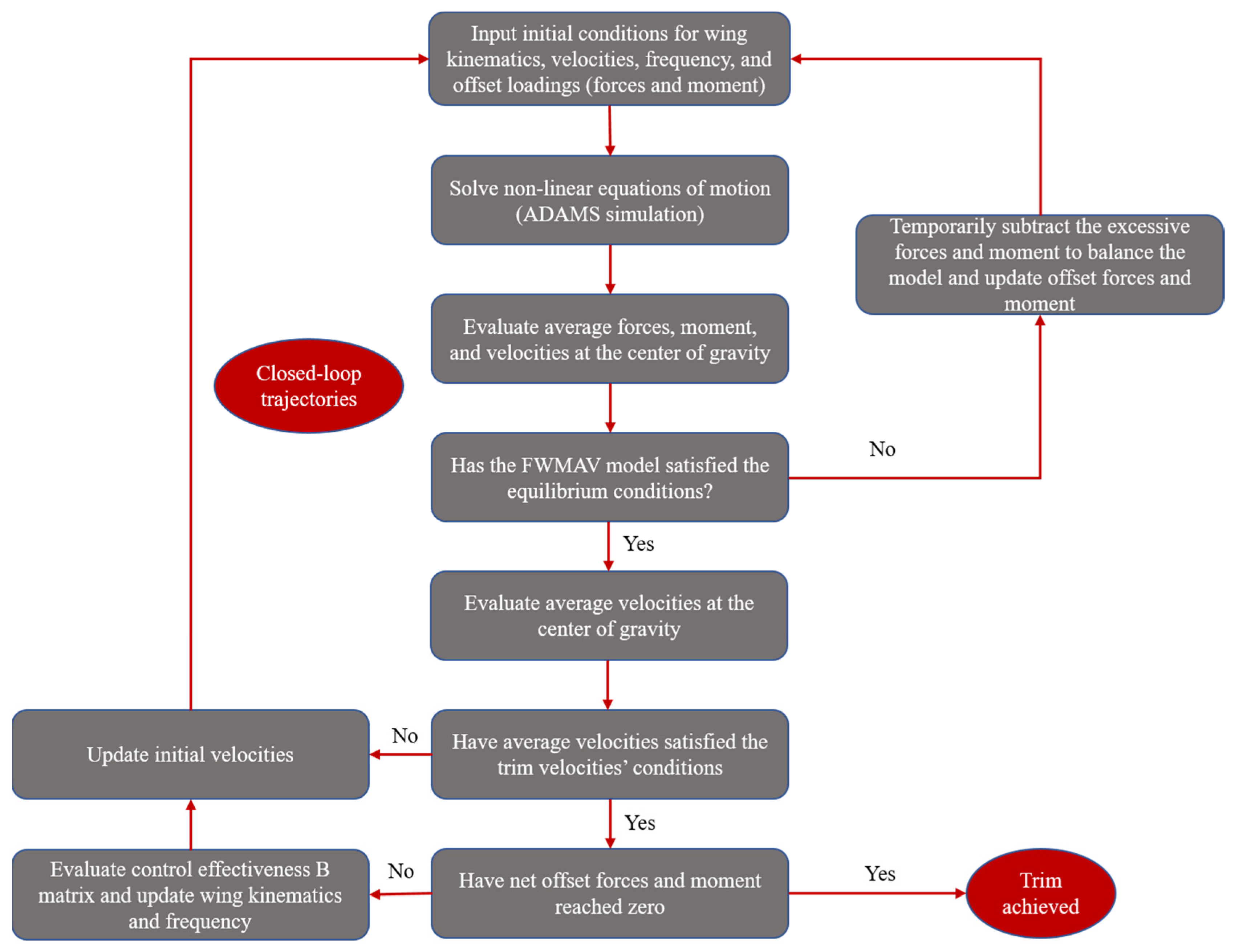
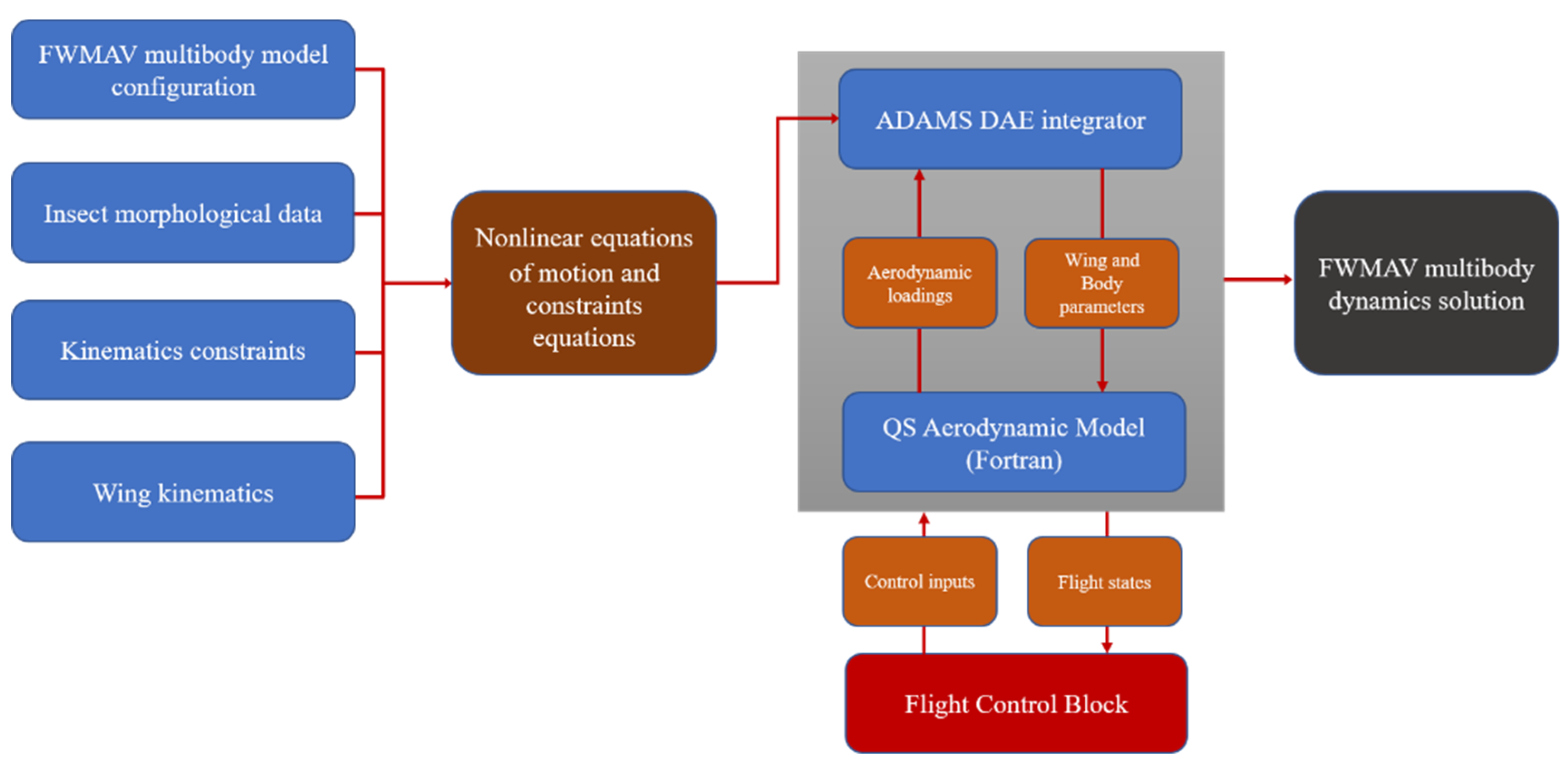
2.3. Multibody Dynamics Simulation Framework and Trim Search Algorithm
2.3.1. FWMAV Multibody Dynamics Simulation Framework
2.3.2. Gradient-Based Trim Search Algorithm
2.4. Equations of Motion and Linearization
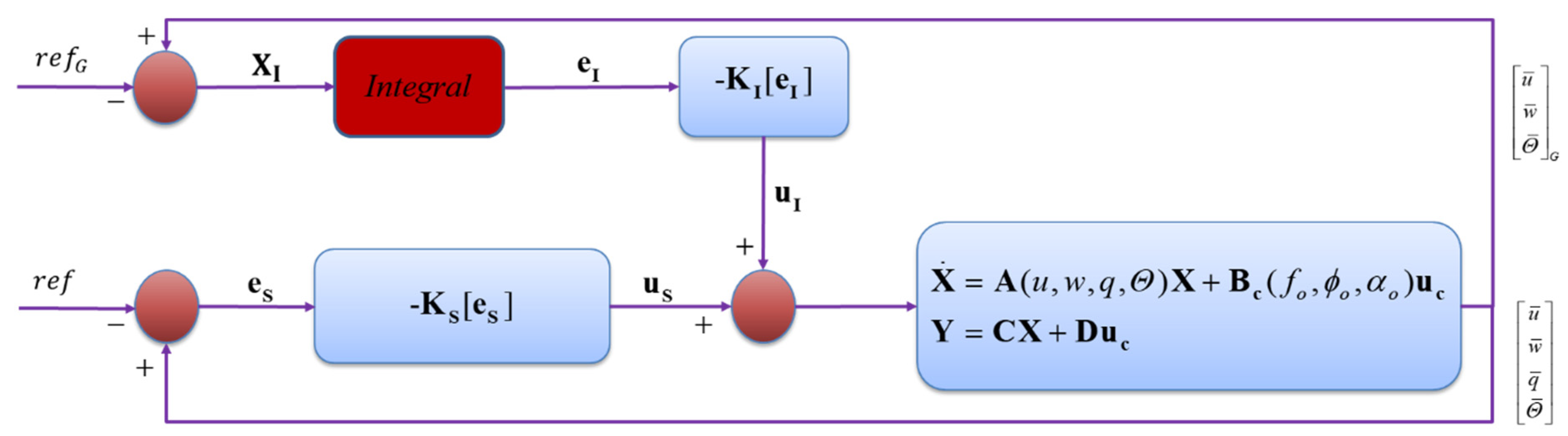
2.5. Augmented LQR Controller Design for Transition Flight Tracking
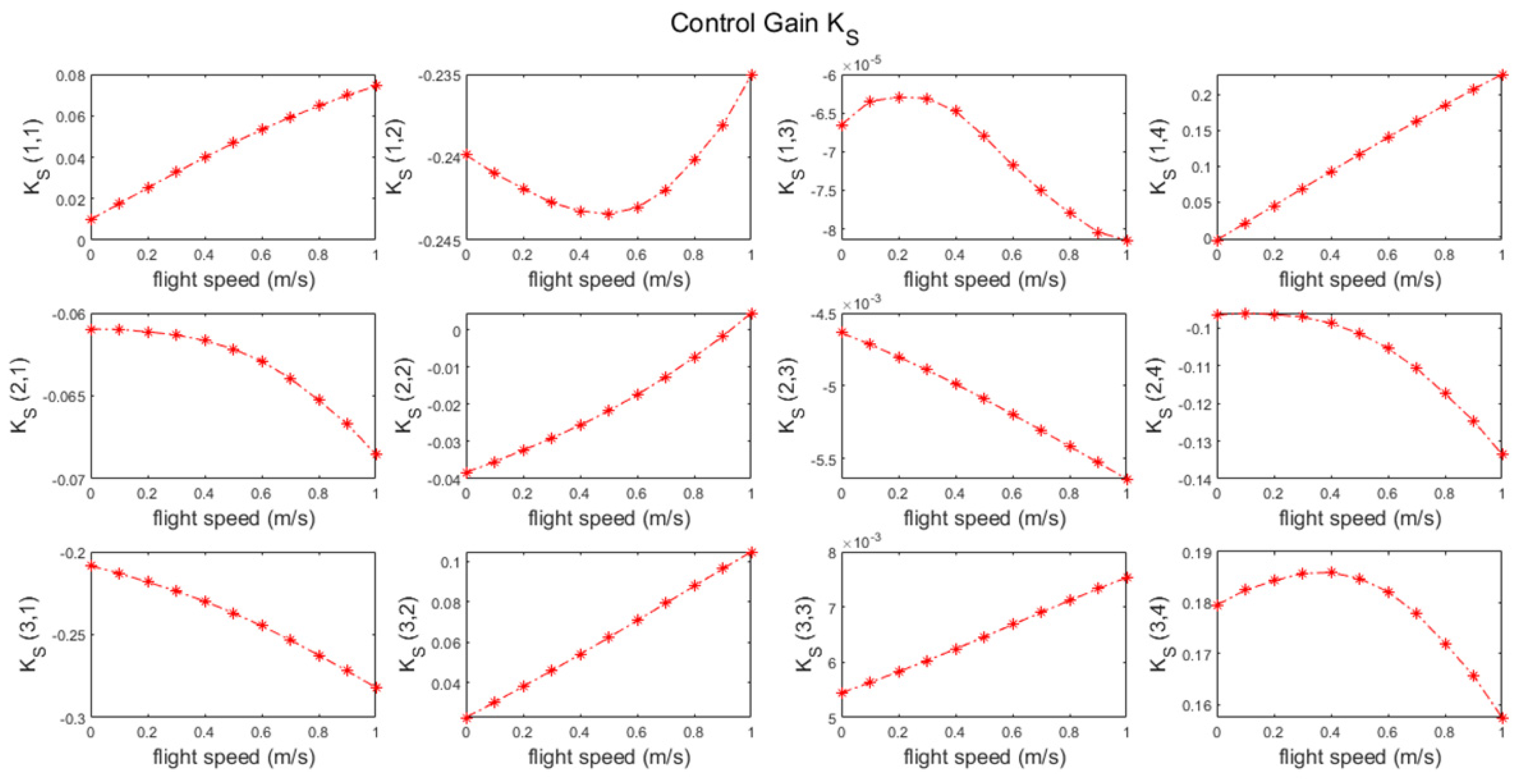
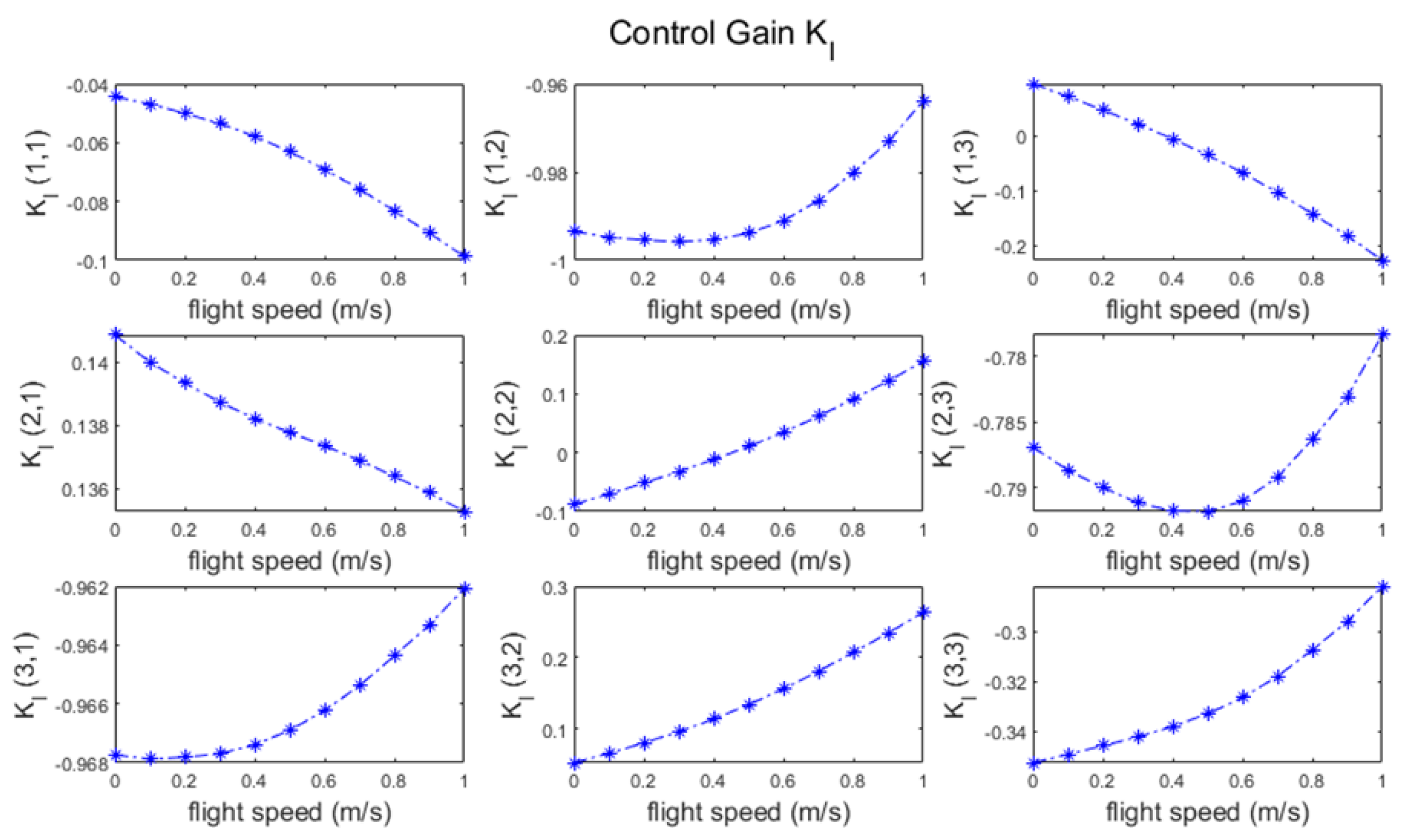
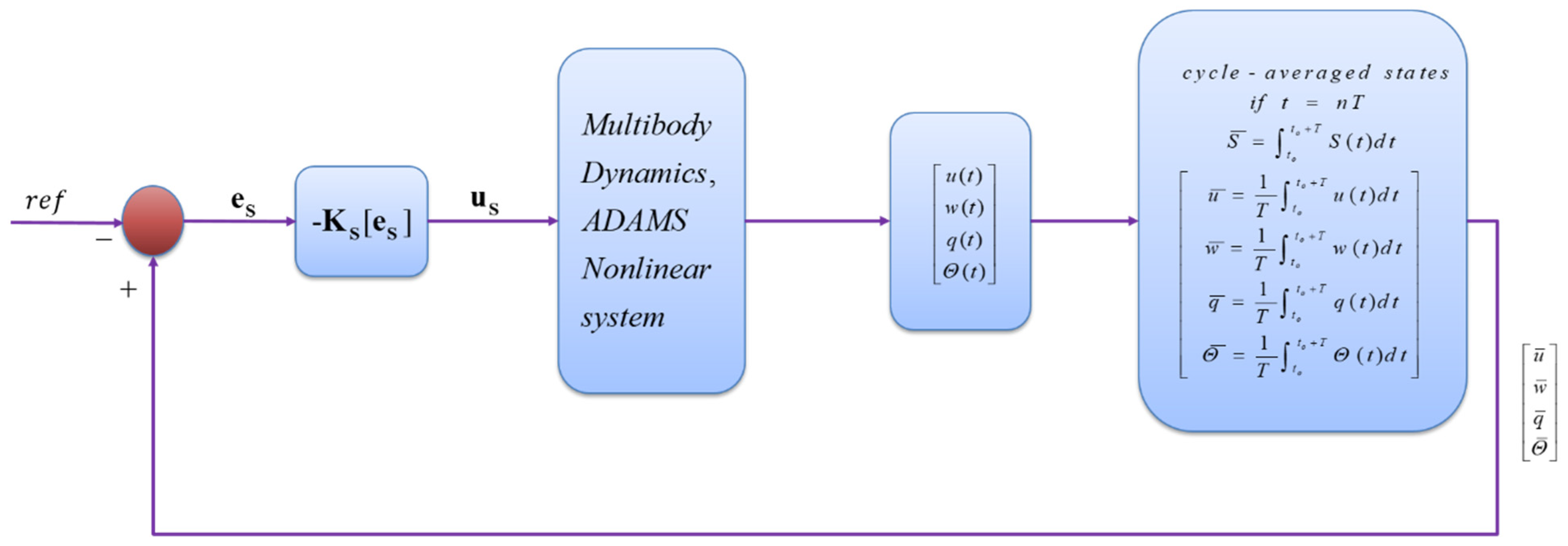
2.5.1. Gain-Scheduled LQR Controller Design for Linear System
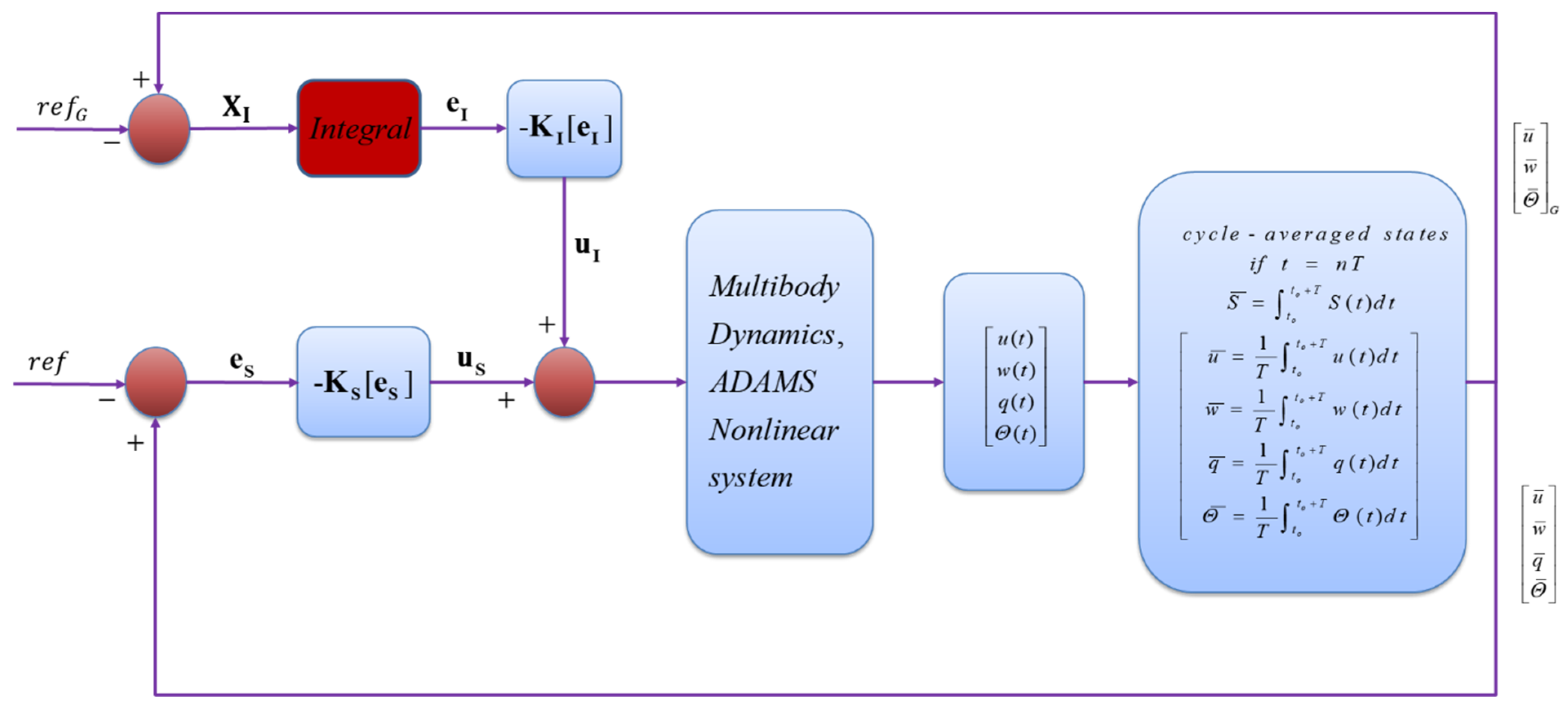
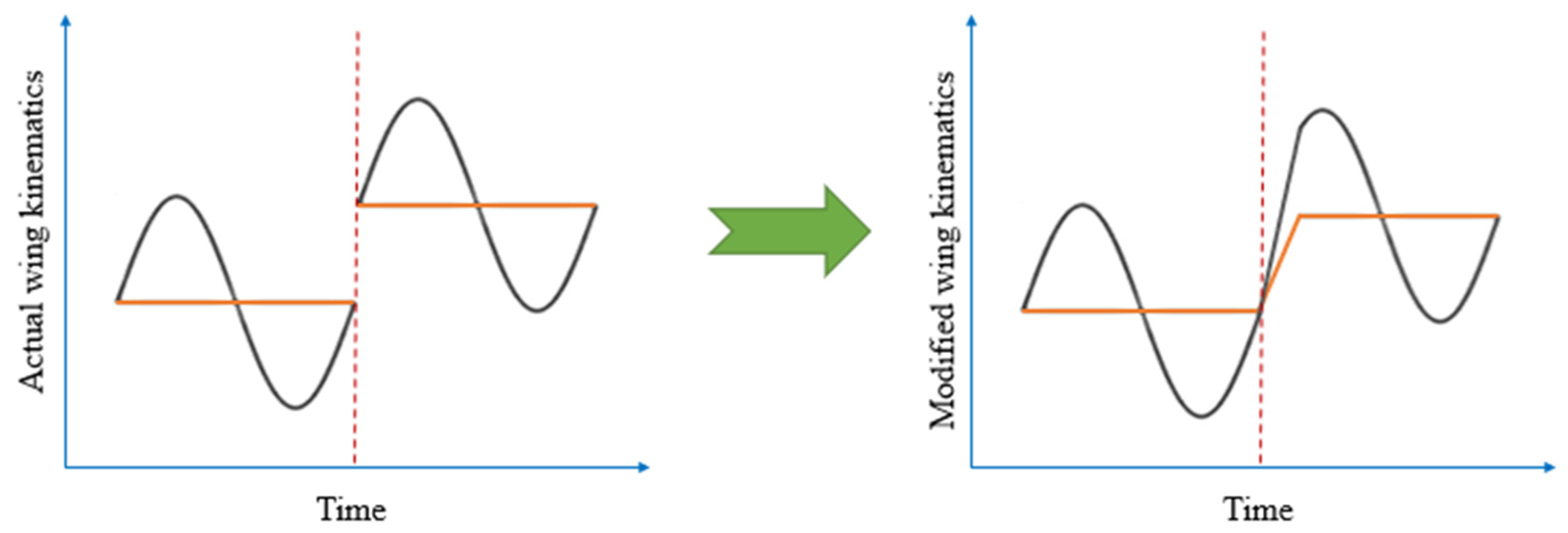
2.5.2. Gain-Scheduled LQR Controller Design for Nonlinear System
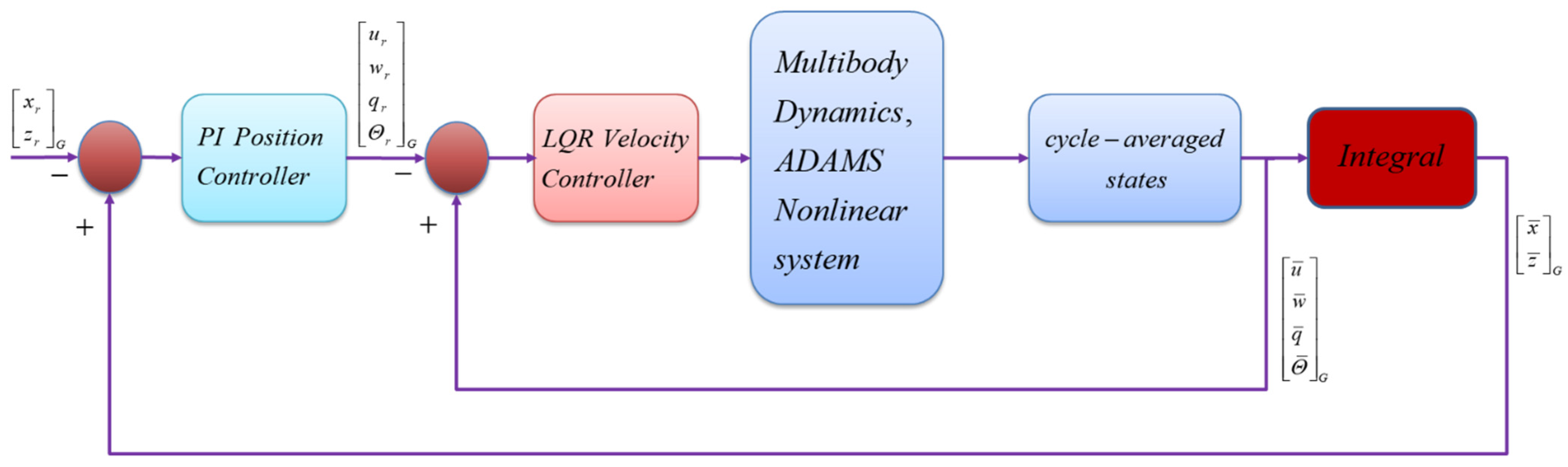
2.6. Trajectory Tracking Controller Design
3. Results and Discussion
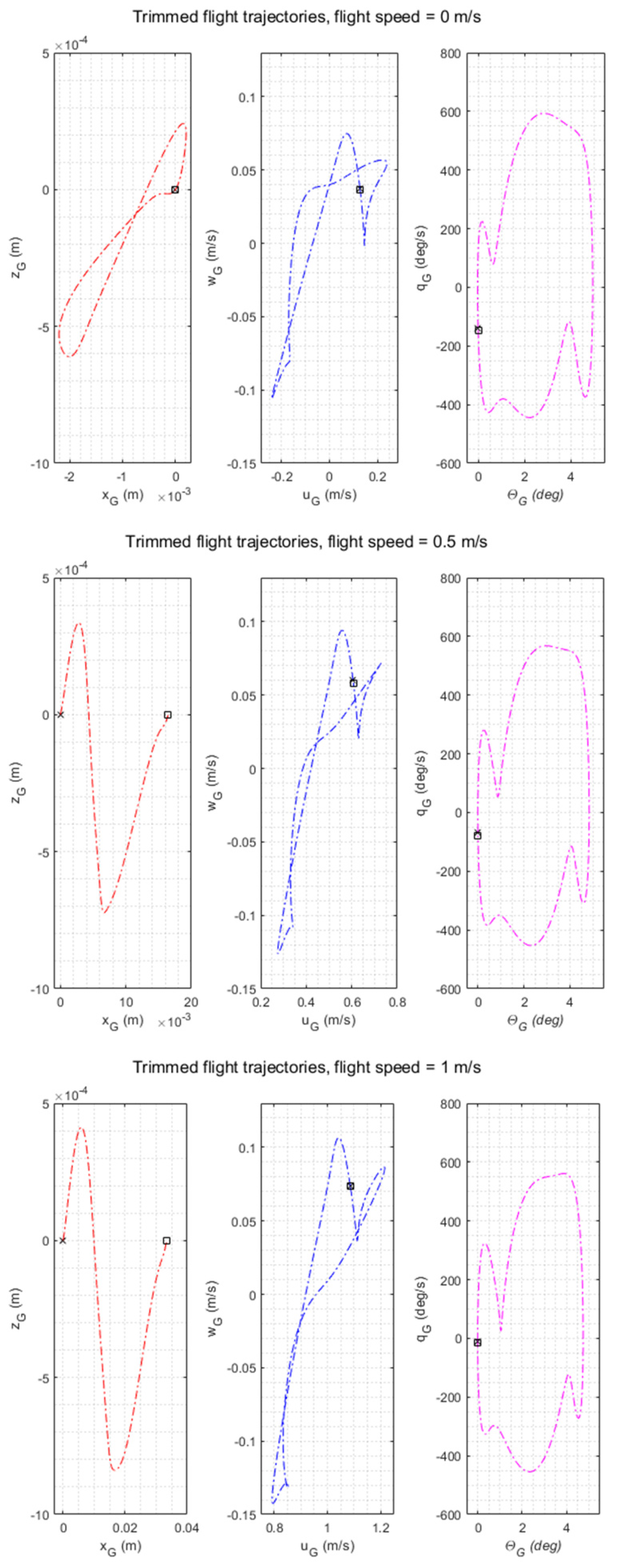
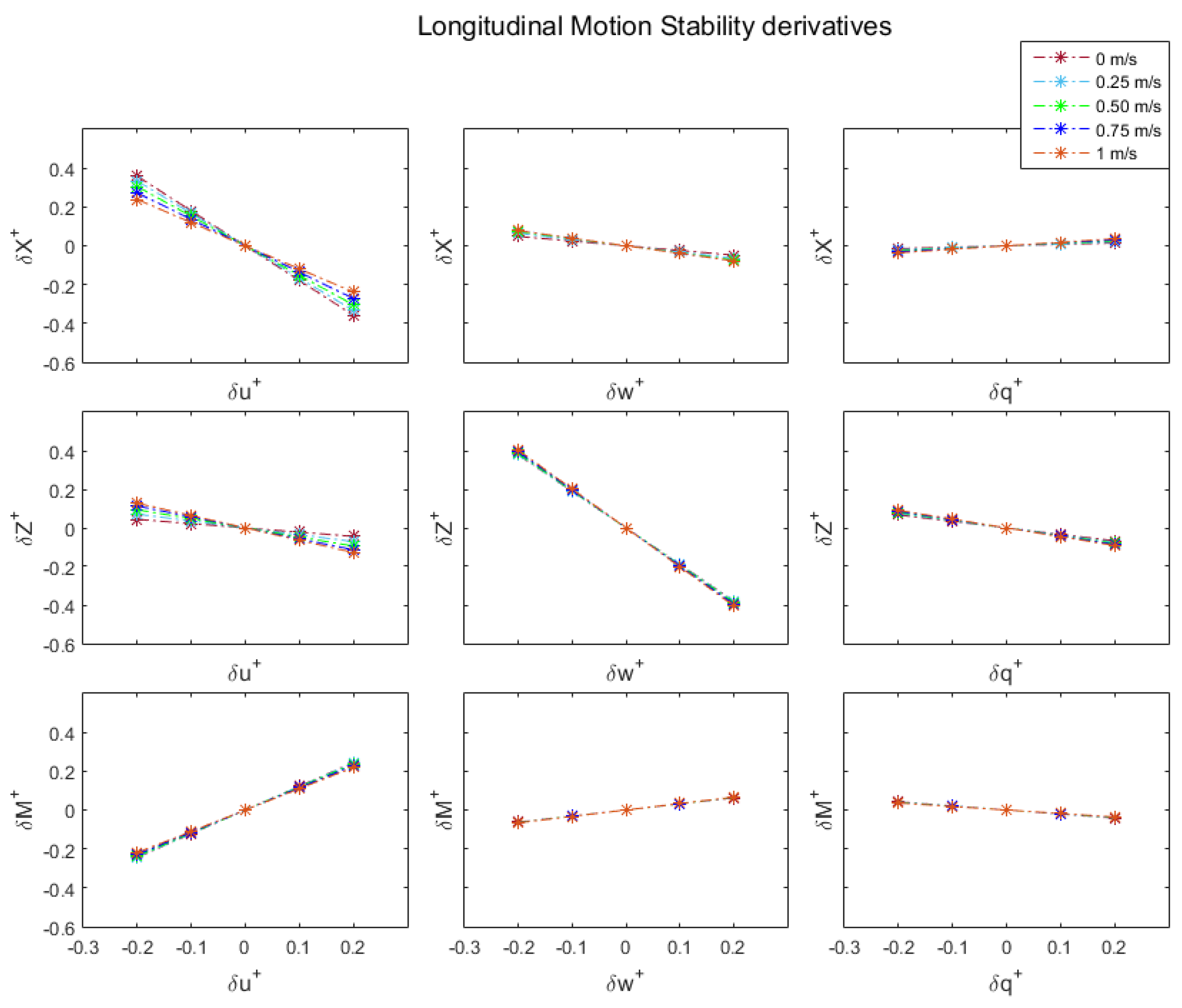
3.1. Stability Characterization of Longitudinal Dynamics
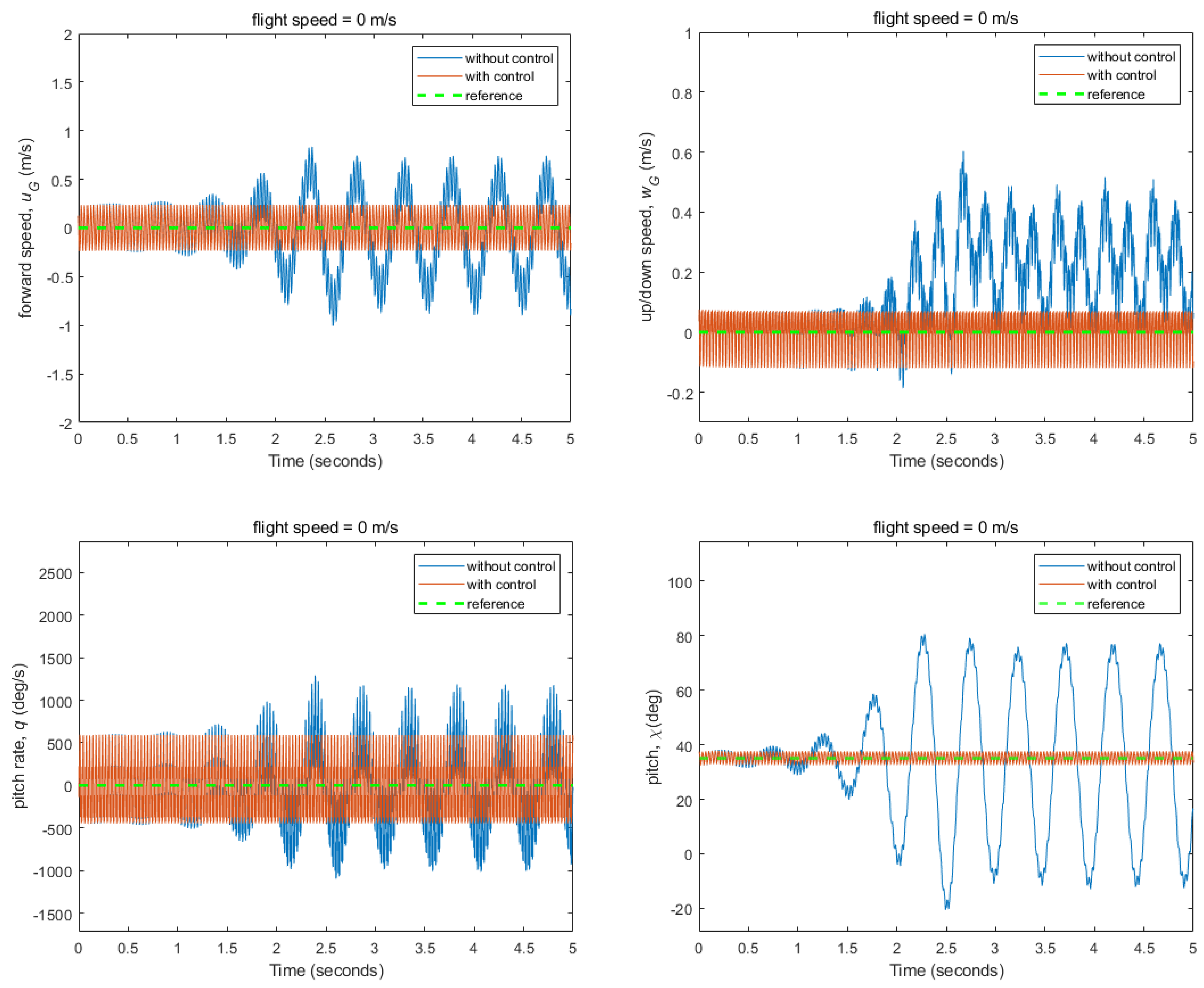
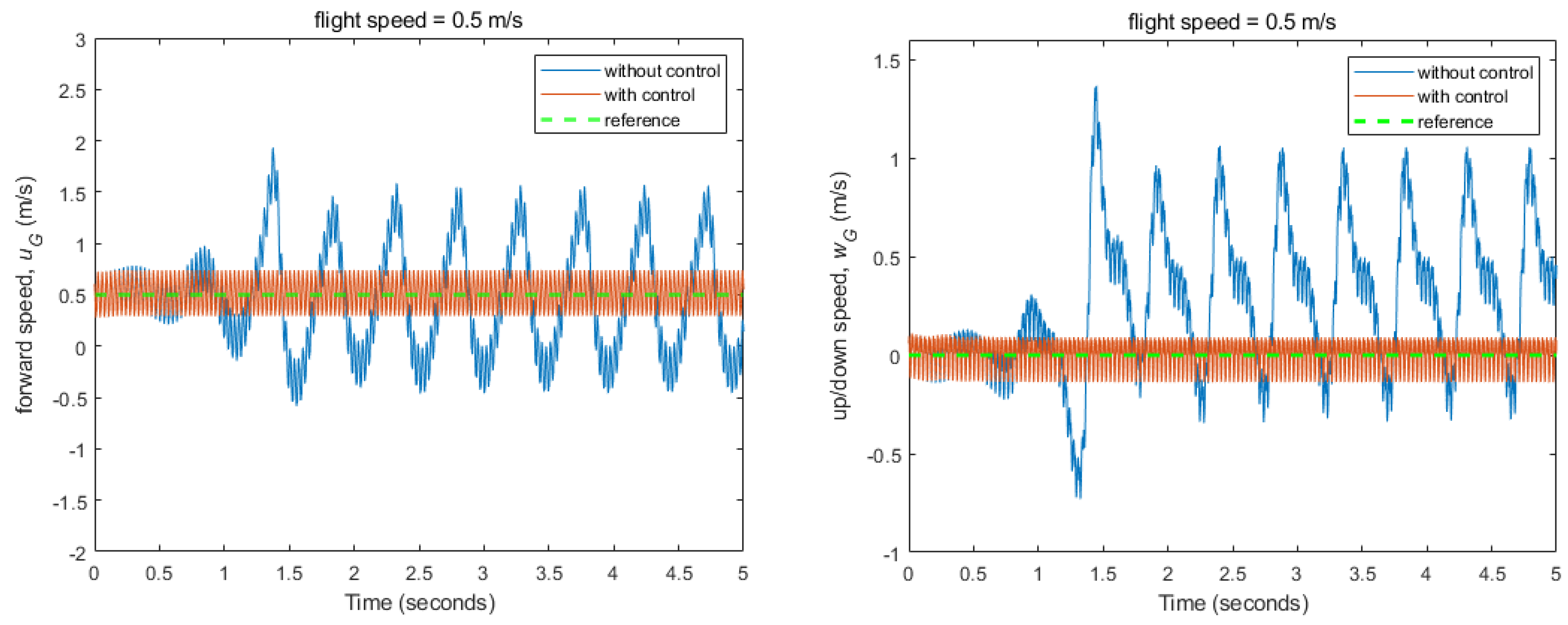
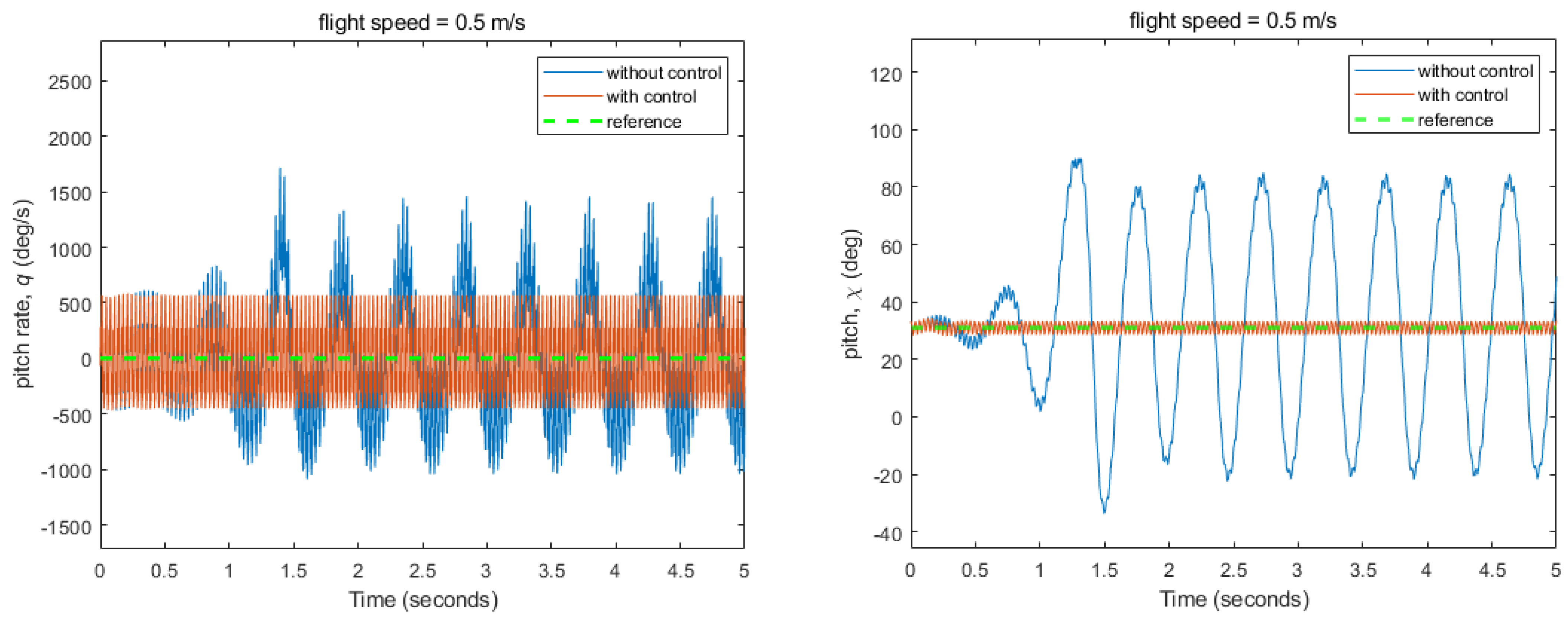
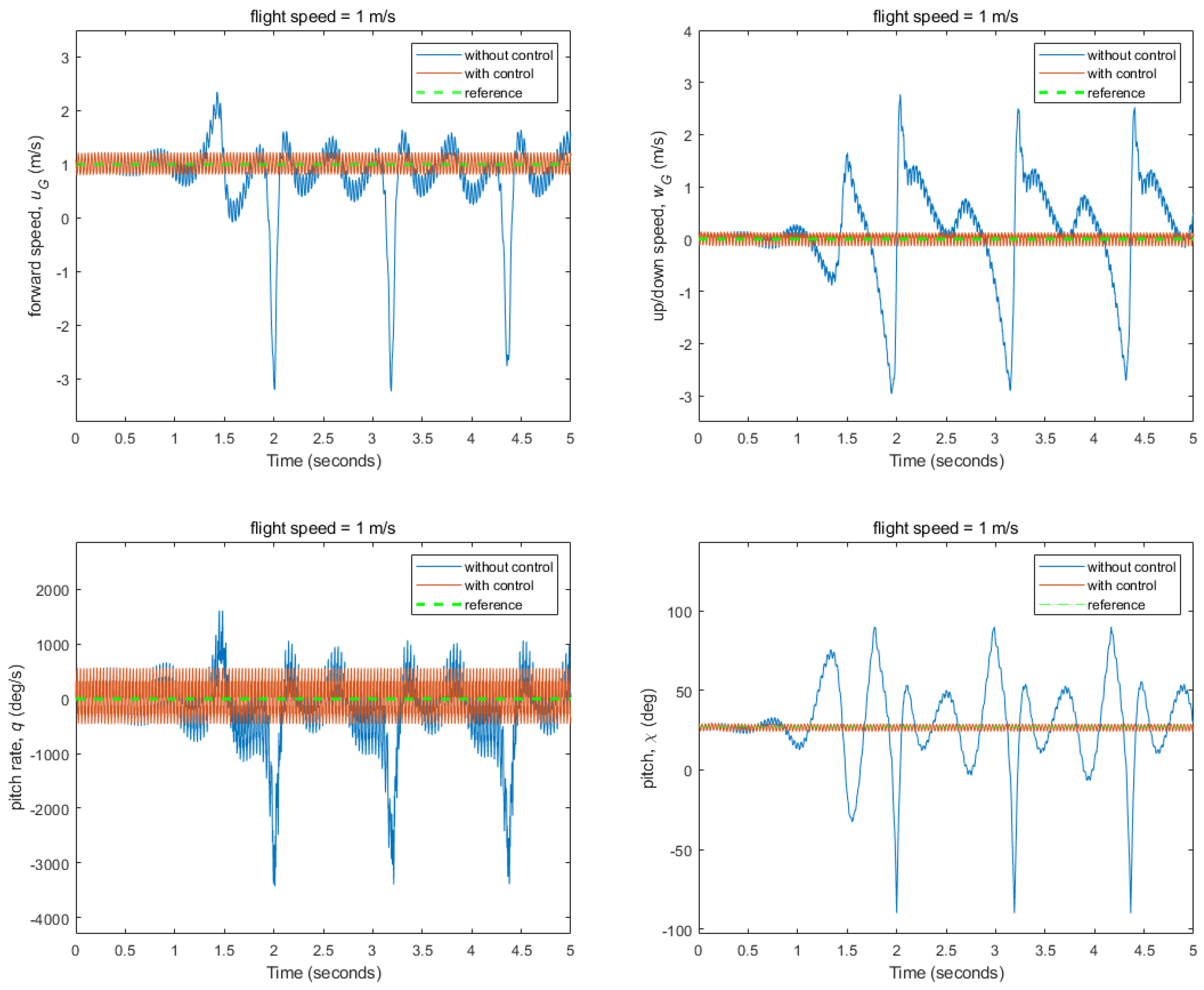
3.2. Flight Control Simulations for Stabilizing Fixed Flight Conditions
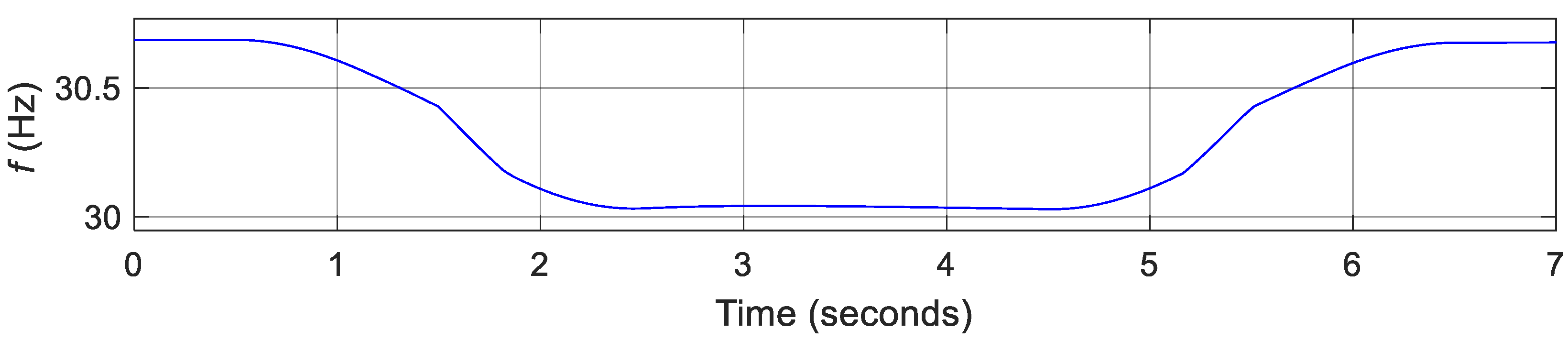
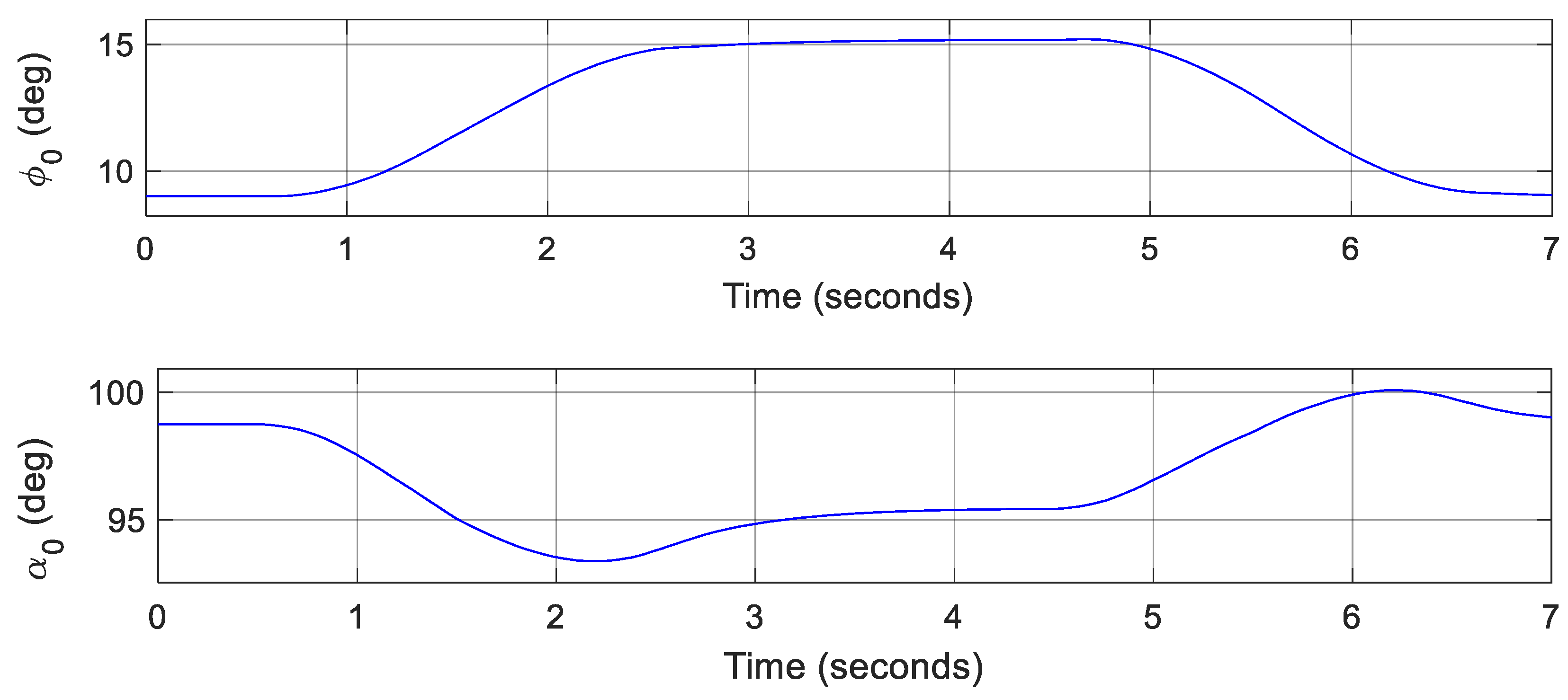
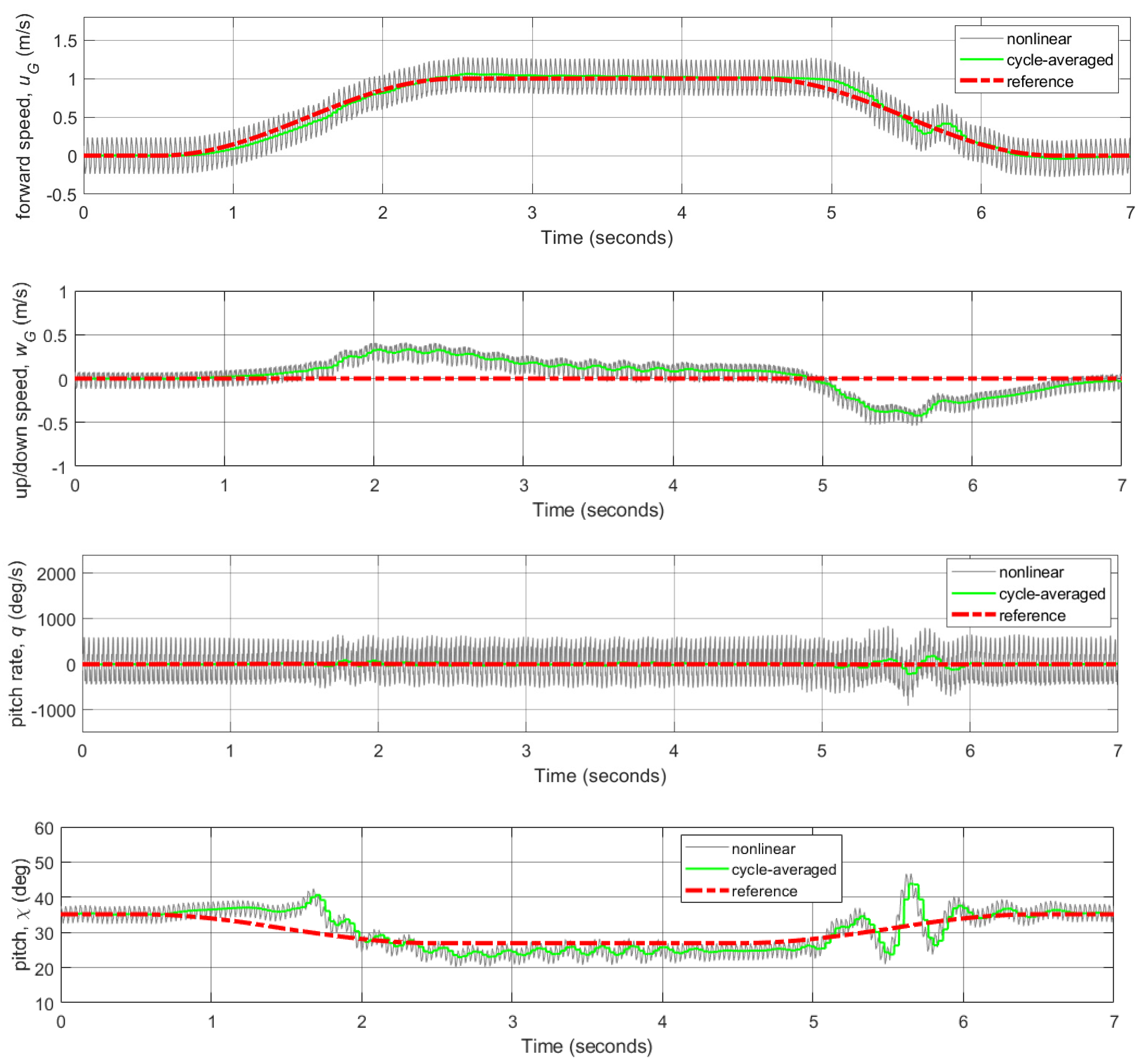
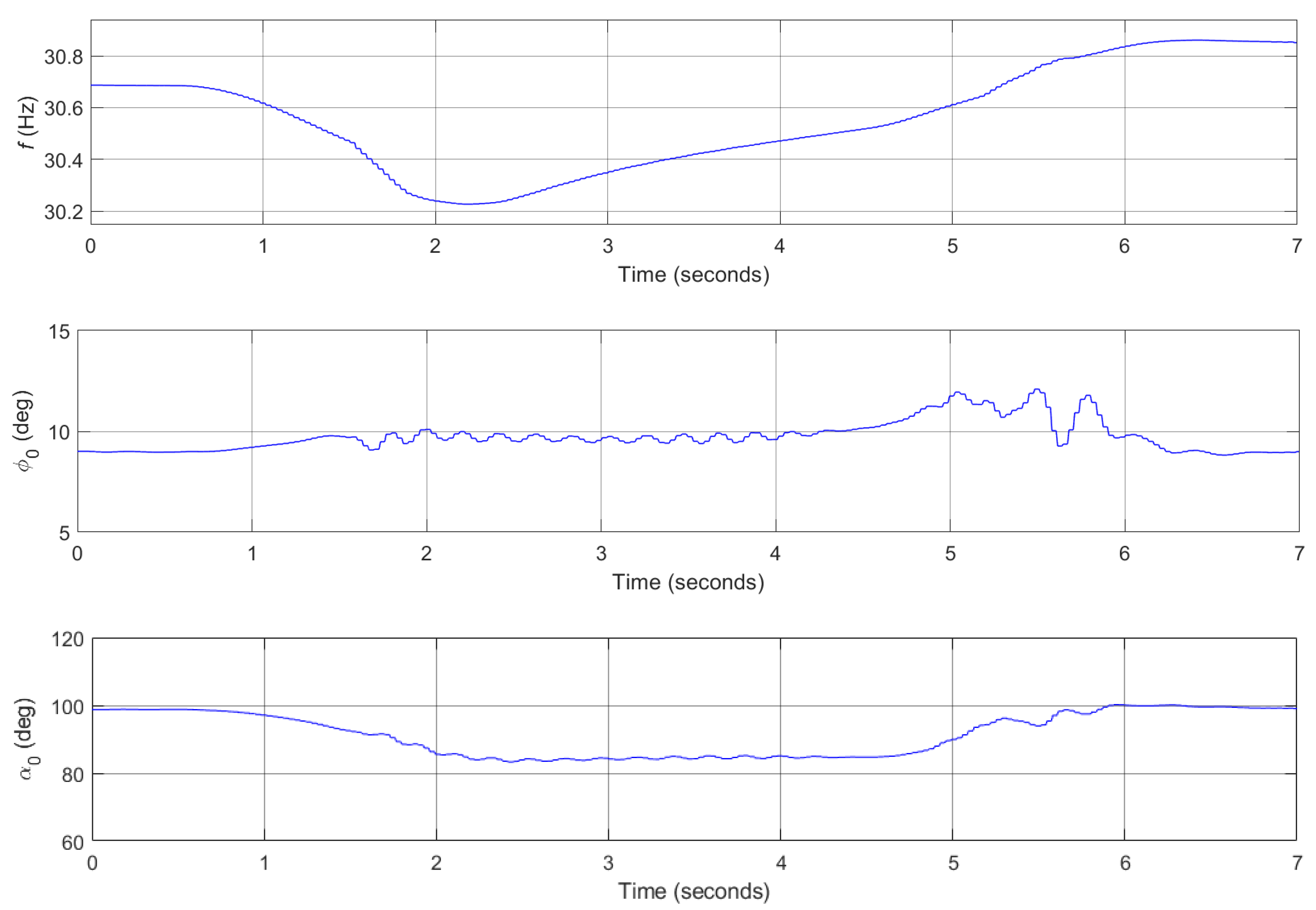
3.3. Flight Control Simulations for Transition Flight Tracking
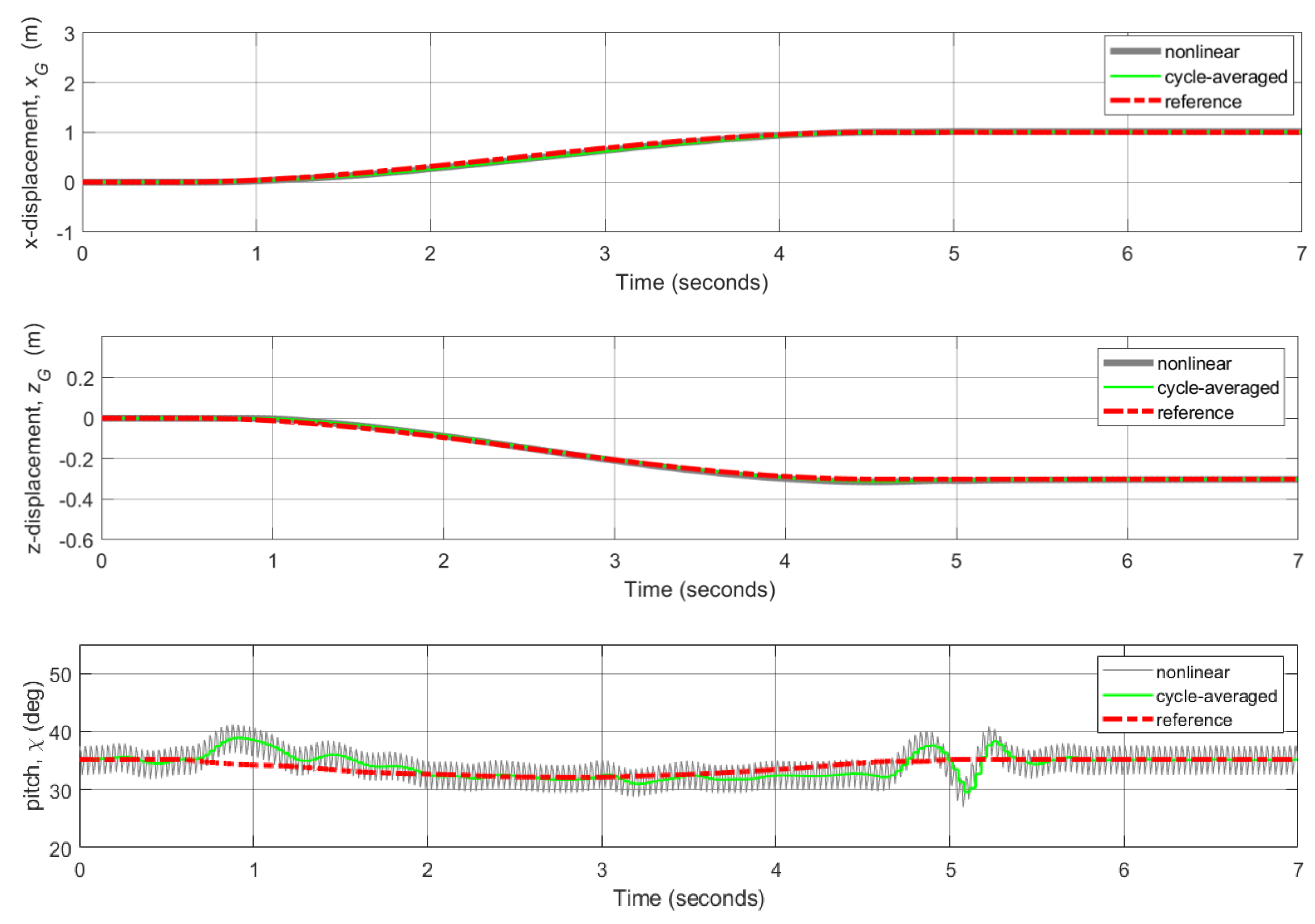
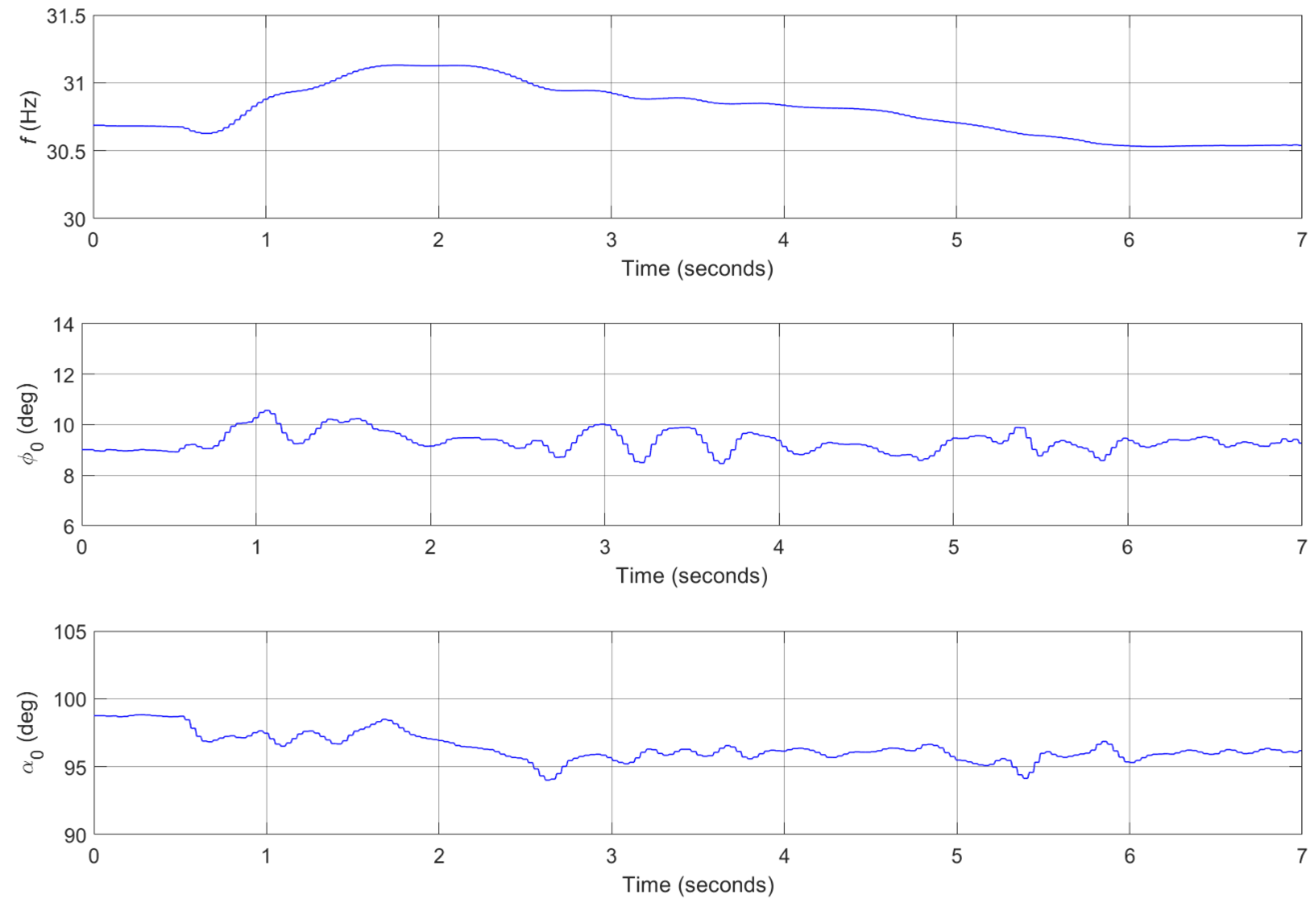
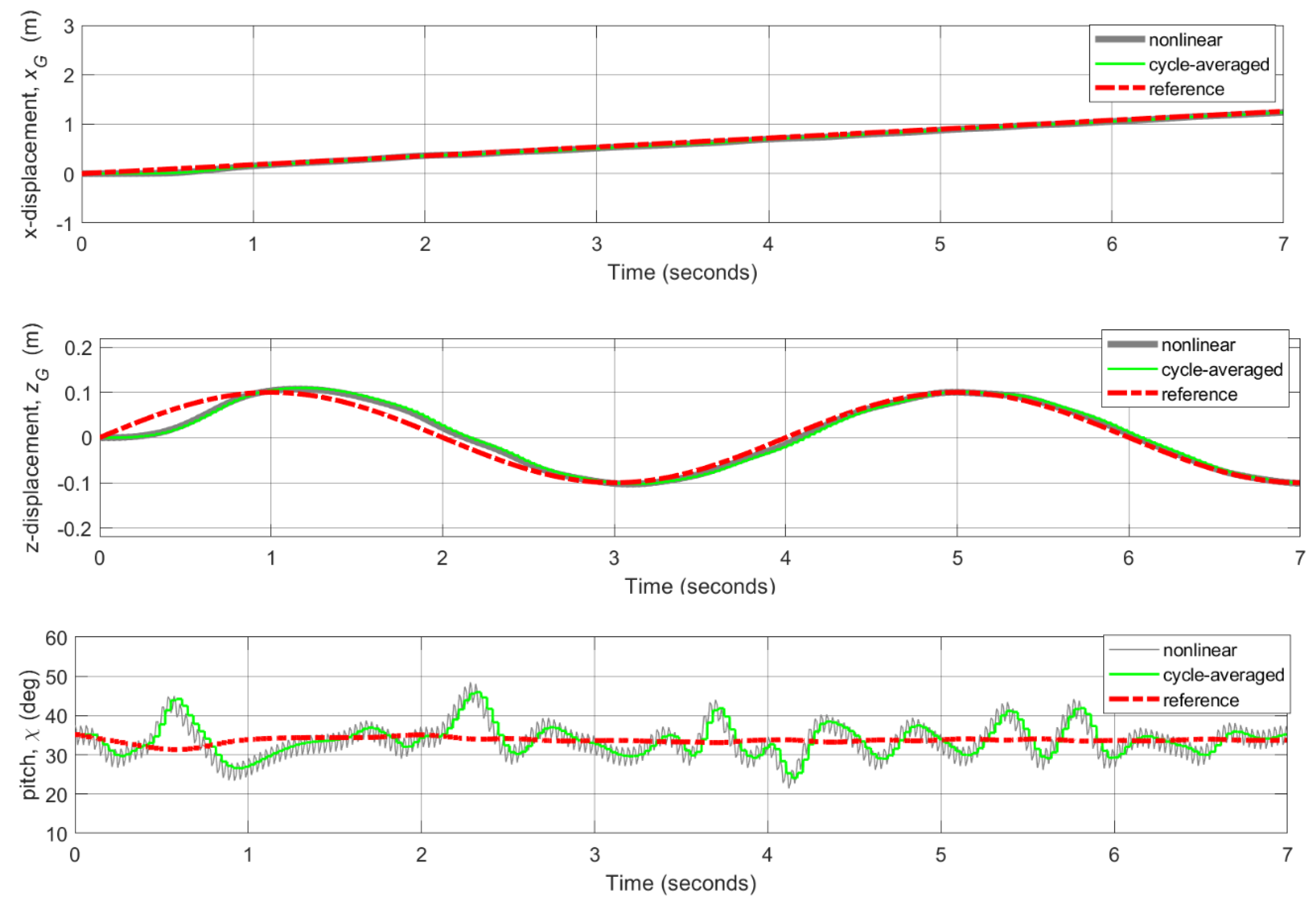
3.4. Flight Control Simulations for Reference Trajectories Tracking
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Phan, H.V.; Aurecianus, S.; Kang, T.; Park, H.C. KUBeetle-S: An insect-like, tailless, hover-capable robot that can fly with a low-torque control mechanism. Int. J. Micro Air Veh. 2019, 11, 1756829319861371. [Google Scholar] [CrossRef]
- Tijmons, S.; De Wagter, C.; Remes, B.; De Croon, G. Autonomous Door and Corridor Traversal with a 20-Gram Flapping Wing MAV by Onboard Stereo Vision. Aerospace 2018, 5, 69. [Google Scholar] [CrossRef]
- Keennon, M.; Klingebiel, K.; Won, H. Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 588. [Google Scholar]
- Pérez-Arancibia, N.O.; Ma, K.Y.; Galloway, K.C.; Greenberg, J.D.; Wood, R.J. First controlled vertical flight of a biologically inspired microrobot. Bioinspir. Biomim. 2011, 6, 036009. [Google Scholar] [CrossRef] [PubMed]
- Ratti, J.; Vachtsevanos, G. A biologically-inspired micro aerial vehicle. J. Intell. Robot. Syst. 2010, 60, 153–178. [Google Scholar] [CrossRef]
- Srigrarom, S.; Chan, W.-L. Ornithopter type flapping wings for autonomous micro air vehicles. Aerospace 2015, 2, 235–278. [Google Scholar] [CrossRef]
- Nguyen, Q.-V.; Park, H.C. Design and demonstration of a locust-like jumping mechanism for small-scale robots. J. Bionic Eng. 2012, 9, 271–281. [Google Scholar] [CrossRef]
- Michelson, R.; Helmick, D.; Reece, S.; Amarena, C. A reciprocating chemical muscle (RCM) for micro air vehicle ‘Entomopter’flight. Proc. Assoc. Unmanned Veh. Syst. 1997, 429–435. [Google Scholar]
- Orlowski, C.T.; Girard, A.R. Modeling and simulation of nonlinear dynamics of flapping wing micro air vehicles. AIAA J. 2011, 49, 969–981. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Han, J.-H. Wing flexibility effects on the flight performance of an insect-like flapping-wing micro-air vehicle. Aerosp. Sci. Technol. 2018, 79, 468–481. [Google Scholar] [CrossRef]
- Taylor, G.K.; Thomas, A.L. Dynamic flight stability in the desert locust Schistocerca gregaria. J. Exp. Biol. 2003, 206, 2803–2829. [Google Scholar] [CrossRef]
- Taylor, G.K.; Żbikowski, R. Nonlinear time-periodic models of the longitudinal flight dynamics of desert locusts Schistocerca gregaria. J. R. Soc. Interface 2005, 2, 197–221. [Google Scholar] [CrossRef]
- Nguyen, A.T. Effects of Body Aerodynamics and Wing Flexibility on Flight Characteristics of Insect-Like Flapping-Wing Micro Air Vehicles. Ph.D. Dissertation, Korea Advanced Institute of Science and Technology, Daejeon, Korea, 2017. [Google Scholar]
- Kalliny, A.N.; El-Badawy, A.A.; Elkhamisy, S.M. Command-filtered integral backstepping control of longitudinal flapping-wing flight. J. Guid. Control Dyn. 2018, 41, 1556–1568. [Google Scholar] [CrossRef]
- Kim, J.-K.; Han, J.-H. A multibody approach for 6-DOF flight dynamics and stability analysis of the hawkmoth Manduca sexta. Bioinspir. Biomim. 2014, 9, 016011. [Google Scholar] [CrossRef][Green Version]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Flight dynamics and control of flapping-wing MAVs: A review. Nonlinear Dyn. 2012, 70, 907–939. [Google Scholar] [CrossRef]
- Taylor, G.; Thomas, A. Animal flight dynamics II. Longitudinal stability in flapping flight. J. Theor. Biol. 2002, 214, 351–370. [Google Scholar] [CrossRef]
- Taylor, G.; Bomphrey, R.; ‘t Hoen, J. Insect flight dynamics and control. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 32. [Google Scholar]
- Sun, M.; Wang, J.; Xiong, Y. Dynamic flight stability of hovering insects. Acta Mech. Sin. 2007, 23, 231–246. [Google Scholar] [CrossRef]
- Dietl, J.M.; Garcia, E. Stability in ornithopter longitudinal flight dynamics. J. Guid. Control Dyn. 2008, 31, 1157–1163. [Google Scholar] [CrossRef]
- Doman, D.; Oppenheimer, M.; Sigthorsson, D. Dynamics and control of a minimally actuated biomimetic vehicle: Part i-aerodynamic model. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6160. [Google Scholar]
- Oppenheimer, M.; Doman, D.; Sigthorsson, D. Dynamics and control of a minimally actuated biomimetic vehicle: Part ii-control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6161. [Google Scholar]
- Hedrick, T.L.; Cheng, B.; Deng, X. Wingbeat time and the scaling of passive rotational damping in flapping flight. Science 2009, 324, 252–255. [Google Scholar] [CrossRef]
- Faruque, I.; Humbert, J.S. Dipteran insect flight dynamics. Part 1 Longitudinal motion about hover. J. Theor. Biol. 2010, 264, 538–552. [Google Scholar] [CrossRef]
- Sun, M.; Xiong, Y. Dynamic flight stability of a hovering bumblebee. J. Exp. Biol. 2005, 208, 447–459. [Google Scholar] [CrossRef]
- Orlowski, C.; Girard, A.; Shyy, W. Derivation and simulation of the nonlinear dynamics of a flapping wing micro-air vehicle. In Proceedings of the European Micro-Air Vehicle Conference and Competition, Delft, The Netherlands, 14–17 September 2009. [Google Scholar]
- Su, W.; Cesnik, C. Flight dynamic stability of a flapping wing micro air vehicle in hover. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011; p. 2009. [Google Scholar]
- Bolender, M. Rigid multi-body equations-of-motion for flapping wing mavs using kane’s equations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; p. 6158. [Google Scholar]
- Gebert, G.; Gallmeier, P.; Evers, J. Equations of motion for flapping flight. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002; p. 4872. [Google Scholar]
- Grauer, J.A.; Hubbard Jr, J.E. Multibody model of an ornithopter. J. Guid. Control Dyn. 2009, 32, 1675–1679. [Google Scholar] [CrossRef]
- Xiong, Y.; Sun, M. Dynamic flight stability of a bumblebee in forward flight. Acta Mech. Sin. 2008, 24, 25–36. [Google Scholar] [CrossRef]
- Wu, J.H.; Sun, M. Floquet stability analysis of the longitudinal dynamics of two hovering model insects. J. R. Soc. Interface 2012, 9, 2033–2046. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering; Westview Press: Boulder, CO, USA, 1994. [Google Scholar]
- Gao, N.; Aono, H.; Liu, H. Perturbation analysis of 6DoF flight dynamics and passive dynamic stability of hovering fruit fly Drosophila melanogaster. J. Theor. Biol. 2011, 270, 98–111. [Google Scholar] [CrossRef] [PubMed]
- Gao, N.; Aono, H.; Liu, H. A numerical analysis of dynamic flight stability of hawkmoth hovering. J. Biomech. Sci. Eng. 2009, 4, 105–116. [Google Scholar] [CrossRef][Green Version]
- Pennycuick, C.J. Power requirements for horizontal flight in the pigeon Columba livia. J. Exp. Biol. 1968, 49, 527–555. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. V. A vortex theory. Philos. Trans. R. Soc. London B Biol. Sci. 1984, 305, 115–144. [Google Scholar]
- Phlips, P.; East, R.; Pratt, N. An unsteady lifting line theory of flapping wings with application to the forward flight of birds. J. Fluid Mech. 1981, 112, 97–125. [Google Scholar] [CrossRef]
- Ansari, S.A. A Nonlinear, Unsteady Aerodynamic Model for Insect-Like Flapping Wings in the Hover with Micro Air Vehicle Applications. Ph.D. Dissertation, Cranfield University, Bedford, UK, 2004. [Google Scholar]
- Xuan, H.; Hu, J.; Yu, Y.; Zhang, J. Recent progress in aerodynamic modeling methods for flapping flight. AIP Adv. 2020, 10, 020701. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [CrossRef]
- Han, J.-S.; Kim, J.-K.; Chang, J.W.; Han, J.-H. An improved quasi-steady aerodynamic model for insect wings that considers movement of the center of pressure. Bioinspir. Biomim. 2015, 10, 046014. [Google Scholar] [CrossRef]
- Taha, H.E.; Hajj, M.R.; Nayfeh, A.H. Longitudinal flight dynamics of hovering MAVs/insects. J. Guid. Control Dyn. 2014, 37, 970–979. [Google Scholar] [CrossRef]
- Au, L.T.K.; Park, H.C. Influence of center of gravity location on flight dynamic stability in a hovering tailless FW-MAV: Longitudinal motion. J. Bionic Eng. 2019, 16, 130–144. [Google Scholar] [CrossRef]
- Kim, J.-K.; Han, J.-S.; Lee, J.-S.; Han, J.-H. Hovering and forward flight of the hawkmoth Manduca sexta: Trim search and 6-DOF dynamic stability characterization. Bioinspir. Biomim. 2015, 10, 056012. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Deng, X. Translational and rotational damping of flapping flight and its dynamics and stability at hovering. IEEE Trans. Robot. 2011, 27, 849–864. [Google Scholar] [CrossRef]
- Oppenheimer, M.W.; Doman, D.B.; Sigthorsson, D.O. Dynamics and control of a biomimetic vehicle using biased wingbeat forcing functions. J. Guid. Control Dyn. 2011, 34, 204–217. [Google Scholar] [CrossRef]
- Loh, K.; Cook, M.; Thomasson, P. An investigation into the longitudinal dynamics and control of a flapping wing micro air vehicle at hovering flight. Aeronaut. J. 2003, 107, 743–753. [Google Scholar]
- Khanmirza, E.; Yousefi-Koma, A.; Tarvirdizadeh, B. Nonlinear trajectory control of a flapping-wing micro aerial vehicle. Aircr. Eng. Aerosp. Technol. 2012, 84, 58–65. [Google Scholar] [CrossRef]
- Banazadeh, A.; Taymourtash, N. Adaptive attitude and position control of an insect-like flapping wing air vehicle. Nonlinear Dyn. 2016, 85, 47–66. [Google Scholar] [CrossRef]
- Wissa, B.E.; Elshafei, K.O.; El-Badawy, A.A. Lyapunov-based control and trajectory tracking of a 6-DOF flapping wing micro aerial vehicle. Nonlinear Dyn. 2020, 99, 2919–2938. [Google Scholar] [CrossRef]
- Khosravi, M.; Novinzadeh, A. A multi-body control approach for flapping wing micro aerial vehicles. Aerosp. Sci. Technol. 2021, 112, 106525. [Google Scholar] [CrossRef]
- Guo, S.; Li, H.; Zhou, C.; Zhang, Y.L.; He, Y.; Wu, J.H. Analysis and experiment of a bio-inspired flyable micro flapping wing rotor. Aerosp. Sci. Technol. 2018, 79, 506–517. [Google Scholar] [CrossRef]
- Wu, J.H.; Zhang, Y.L.; Sun, M. Hovering of model insects: Simulation by coupling equations of motion with Navier–Stokes equations. J. Exp. Biol. 2009, 212, 3313–3329. [Google Scholar] [CrossRef]
- Serrani, A.; Keller, B.; Bolender, M.; Doman, D. Robust control of a 3-dof flapping wing micro air vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 7709. [Google Scholar]
- Schenato, L.; Campolo, D.; Sastry, S. Controllability issues in flapping flight for biomimetic micro aerial vehicles (MAVs). In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No. 03CH37475), Maui, HI, USA, 9–12 December 2003; pp. 6441–6447. [Google Scholar]
- Peng, K.; Lin, F.; Chen, B.M. Modeling and control analysis of a flapping-wing micro aerial vehicle. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 295–300. [Google Scholar]
- Zhu, B.; Zuo, Z. Adaptive model predictive control for set-point tracking of a single-DOF flapping-wing unmanned aerial vehicle. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 861–866. [Google Scholar]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. II. Morphological Parameters. Philos. Trans. R. Soc. B 1984, 305, 17–40. [Google Scholar]
- Hedrick, T.L.; Daniel, T.L. Flight control in the hawkmoth Manduca sexta: The inverse problem of hovering. J. Exp. Biol. 2006, 209, 3114–3130. [Google Scholar] [CrossRef]
- O’Hara, R.P.; Palazotto, A.N. The morphological characterization of the forewing of the Manduca sexta species for the application of biomimetic flapping wing micro air vehicles. Bioinspir. Biomim. 2012, 7, 046011. [Google Scholar] [CrossRef]
- Willmott, A.P.; Ellington, C.P. The mechanics of flight in the hawkmoth Manduca sexta. I. Kinematics of hovering and forward flight. J. Exp. Biol. 1997, 200, 2705–2722. [Google Scholar] [CrossRef]
- Berman, G.J.; Wang, Z.J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 2007, 582, 153–168. [Google Scholar] [CrossRef]
- Faruque, I.; Humbert, J.S. Dipteran insect flight dynamics. Part 2: Lateral–directional motion about hover. J. Theor. Biol. 2010, 265, 306–313. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, A.T.; Lee, J.-S.; Han, J.-H.; Baier, H. Ornithopter Flight Simulation Based on Flexible Multi-Body Dynamics. J. Bionic Eng. 2010, 7, 102–111. [Google Scholar] [CrossRef]
- Lee, J.-S.; Kim, J.-K.; Kim, D.-K.; Han, J.-H. Longitudinal Flight Dynamics of Bioinspired Ornithopter Considering Fluid-Structure Interaction. J. Guid. Control Dyn. 2011, 34, 667–677. [Google Scholar] [CrossRef]
- Gear, C. Simultaneous Numerical Solution of Differential-Algebraic Equations. IEEE Trans. Circuit Theory 1971, 18, 89–95. [Google Scholar] [CrossRef]
- Nelson, R.C. Flight Stability and Automatic Control; WCB/McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Kwakernaak, H.; Sivan, R. Linear Optimal Control Systems; Wiley-Interscience: New York, NY, USA, 1972. [Google Scholar]
- Willmott, A.P.; Ellington, C.P. The mechanics of flight in the hawkmoth Manduca sexta. II. Aerodynamic consequences of kinematic and morphological variation. J. Exp. Biol. 1997, 200, 2723–2745. [Google Scholar] [CrossRef] [PubMed]





| Parameter (Unit) | Description | Value |
|---|---|---|
| ms (mg) | Total system’s mass | 1437.5 |
| mw (mg) | Single wing’s mass | 48.3 |
| Ls (mm) | Total length of the system (anterior tip to posterior tip) | 40.2 |
| Rw (mm) | Wing span | 48.3 |
| r2 (mm) | Radius of second moment of wing area | 24.6 |
| tw (mm) | Wing thickness | 3.7 × 10−2 |
| Sw (mm2) | Single wing area | 879.8 |
| (mm) | Mean aerodynamic chord | 18.1 |
| l1 (mm) | Distance between center of mass (CG) and wing-pivot point | 10.9 |
| l (mm) | Distance between center of mass (CG) and anterior tip | 20.5 |
| Iyy (kg·mm2) | Mass moment of inertia of the system | 0.28 |
| χo (o) | Trimmed body pitch angle | Trimmed result |
| βo (o) | Trimmed stroke plane angle | Trimmed result |
| fo (Hz) | Trimmed flapping frequency | Trimmed result |
| ϕo (o) | Trimmed stroke positional angle | Trimmed result |
| αo (o) | Trimmed feathering angle | Trimmed result |
| f (Hz) | Flapping frequency | Wing kinematics |
| ϕ (o) | Stroke positional angle | Wing kinematics |
| α (o) | Feathering angle | Wing kinematics |
| Flight Speed (m/s) | fo (Hz) | ϕo (deg) | αo (deg) | χo (deg) | βo (deg) |
|---|---|---|---|---|---|
| 0 | 30.687 | 9.013 | 98.749 | 37.506 | 19.496 |
| 0.25 | 30.546 | 10.520 | 97.563 | 35.409 | 21.593 |
| 0.5 | 30.412 | 12.107 | 96.538 | 33.283 | 23.719 |
| 0.75 | 30.141 | 13.613 | 95.867 | 31.203 | 25.796 |
| 1 | 29.976 | 15.178 | 95.3 | 29.112 | 27.889 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, M.Y.; Lee, S.-G.; Han, J.-H. Dynamic Stability and Flight Control of Biomimetic Flapping-Wing Micro Air Vehicle. Aerospace 2021, 8, 362. https://doi.org/10.3390/aerospace8120362
Bhatti MY, Lee S-G, Han J-H. Dynamic Stability and Flight Control of Biomimetic Flapping-Wing Micro Air Vehicle. Aerospace. 2021; 8(12):362. https://doi.org/10.3390/aerospace8120362
Chicago/Turabian StyleBhatti, Muhammad Yousaf, Sang-Gil Lee, and Jae-Hung Han. 2021. "Dynamic Stability and Flight Control of Biomimetic Flapping-Wing Micro Air Vehicle" Aerospace 8, no. 12: 362. https://doi.org/10.3390/aerospace8120362
APA StyleBhatti, M. Y., Lee, S.-G., & Han, J.-H. (2021). Dynamic Stability and Flight Control of Biomimetic Flapping-Wing Micro Air Vehicle. Aerospace, 8(12), 362. https://doi.org/10.3390/aerospace8120362








