A Physics-Based Multidisciplinary Approach for the Preliminary Design and Performance Analysis of a Medium Range Aircraft with Box-Wing Architecture
Abstract
1. Introduction
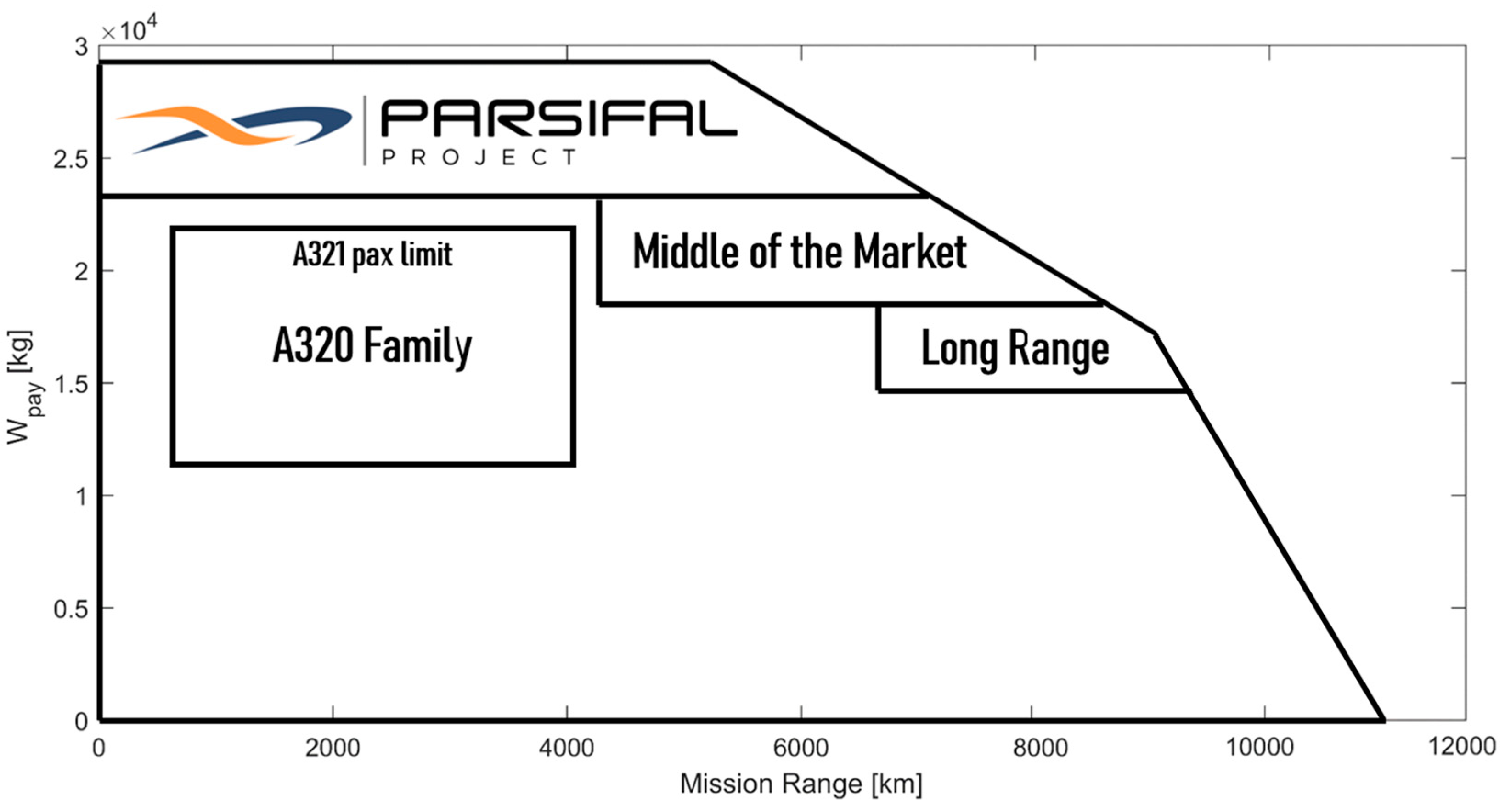
- The transport of a larger number of passengers compared to the present aircraft operating on medium routes, by exploiting the increased lifting capacity of the box-wing system, and using a new fuselage design, in order to increase the number of travellers without increasing the number of flights;
- The exploitation of the increased lifting capacity of the box-wing to design an aircraft with the same overall dimensions, in particular of wingspan, of present aircraft operating on short/medium routes, while improving the passenger capability, in order to avoid the increase in required apron space; namely, this requires the design of a box-wing with wingspan limited to the standard related to short-to-medium-route aircraft, i.e., maximum 36 m (ICAO Aerodrome Code C), to be compliant with the airport infrastructure (aprons, taxiways), but at the same time, to transport a larger payload;
- The exploitation of the box-wing architecture designed according to the “Best Wing System” theory to maximise the aerodynamic efficiency; indeed, a properly designed box-wing aircraft allows one to theoretically minimise the induced drag, by exhibiting Oswald factor efficiencies larger than 1 [45], as well as to increase the lifting capability (i.e., to trim a larger weight), and thus to reduce the fuel consumption per passenger–kilometre compared to conventional aircraft.
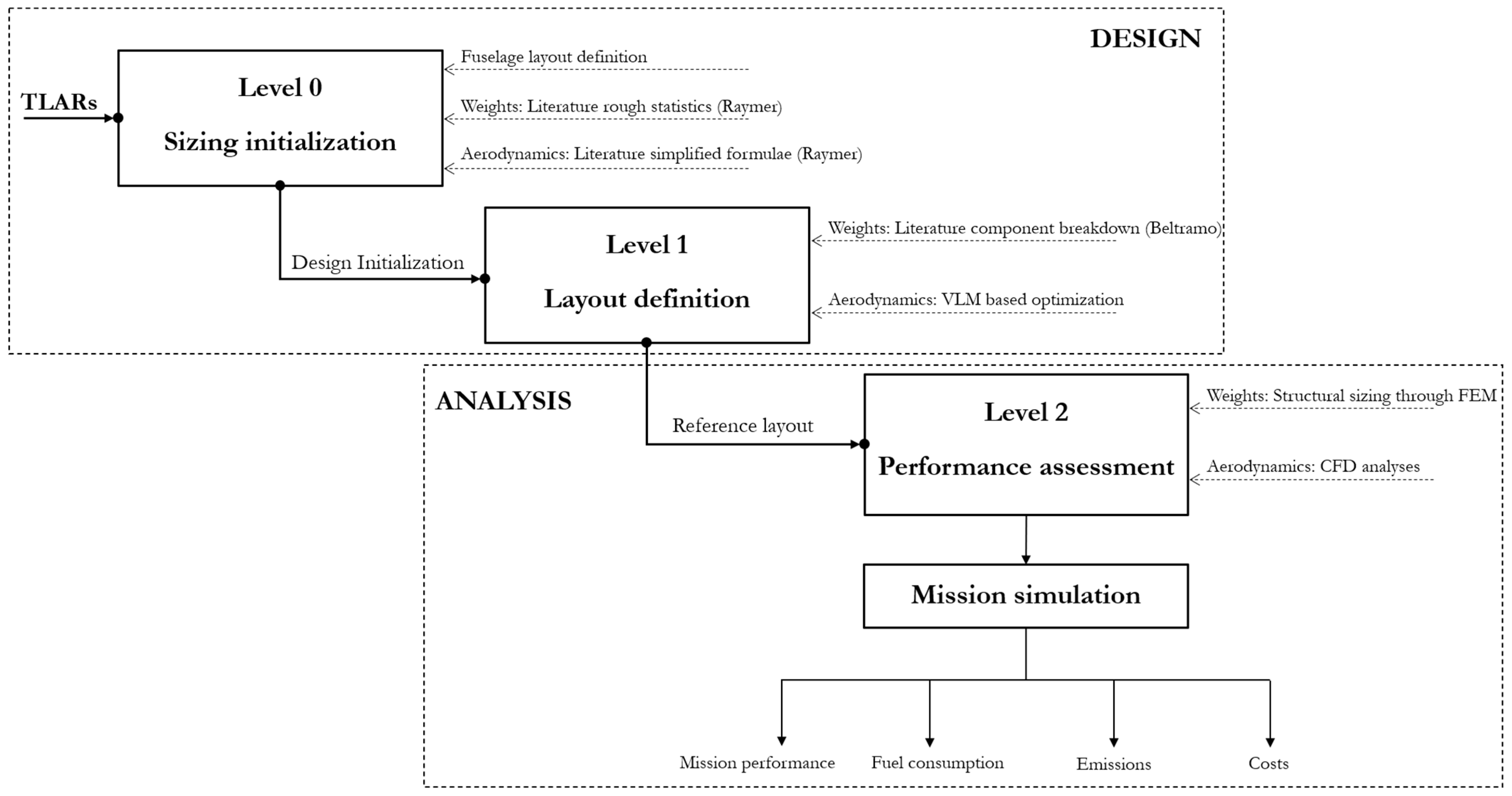
2. Design Methodology Description
2.1. Conceptual Design Initialisation
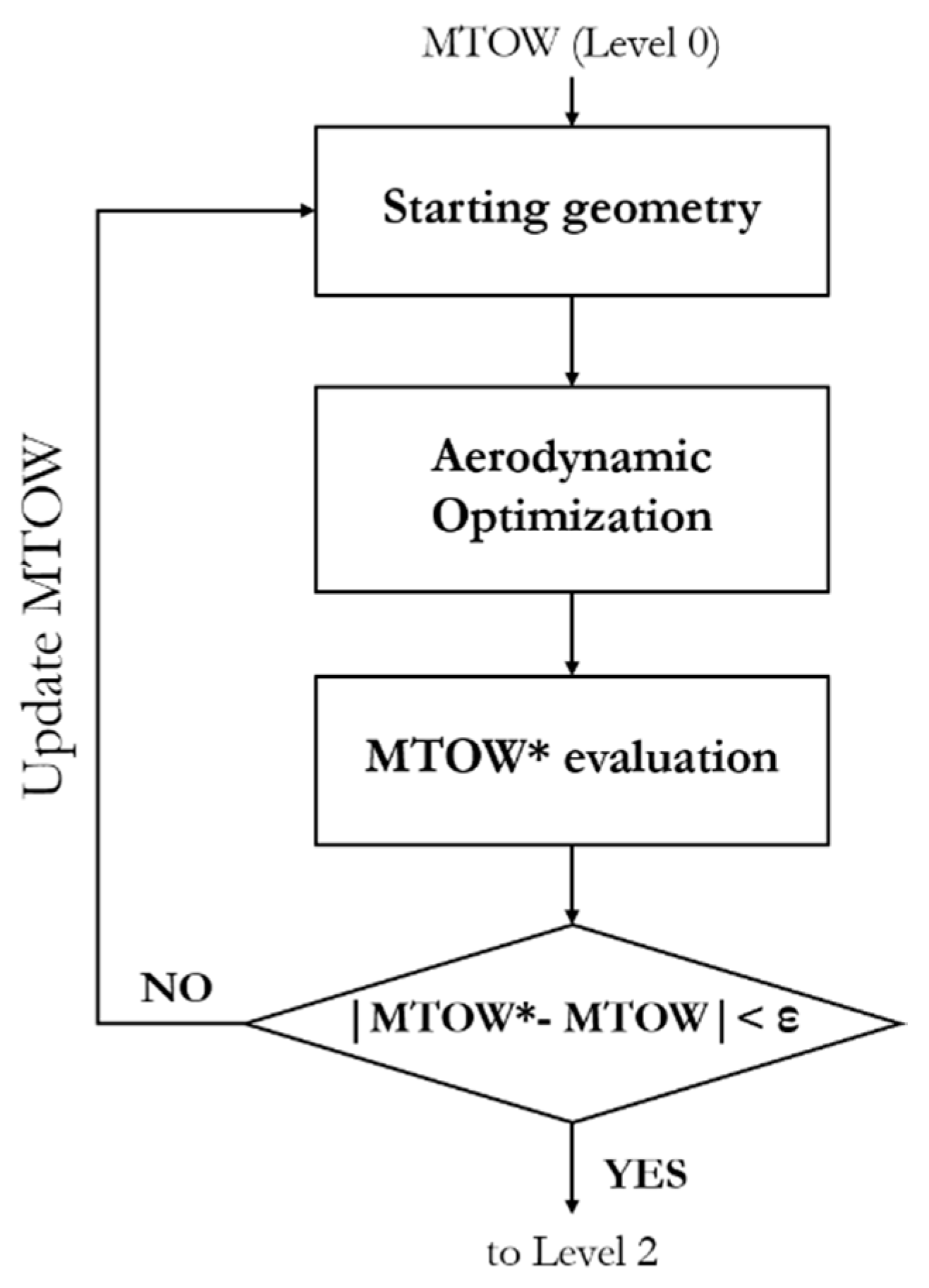
2.2. Optimisation Driven Preliminary Design
- Objective function
- Set of inequality constraints
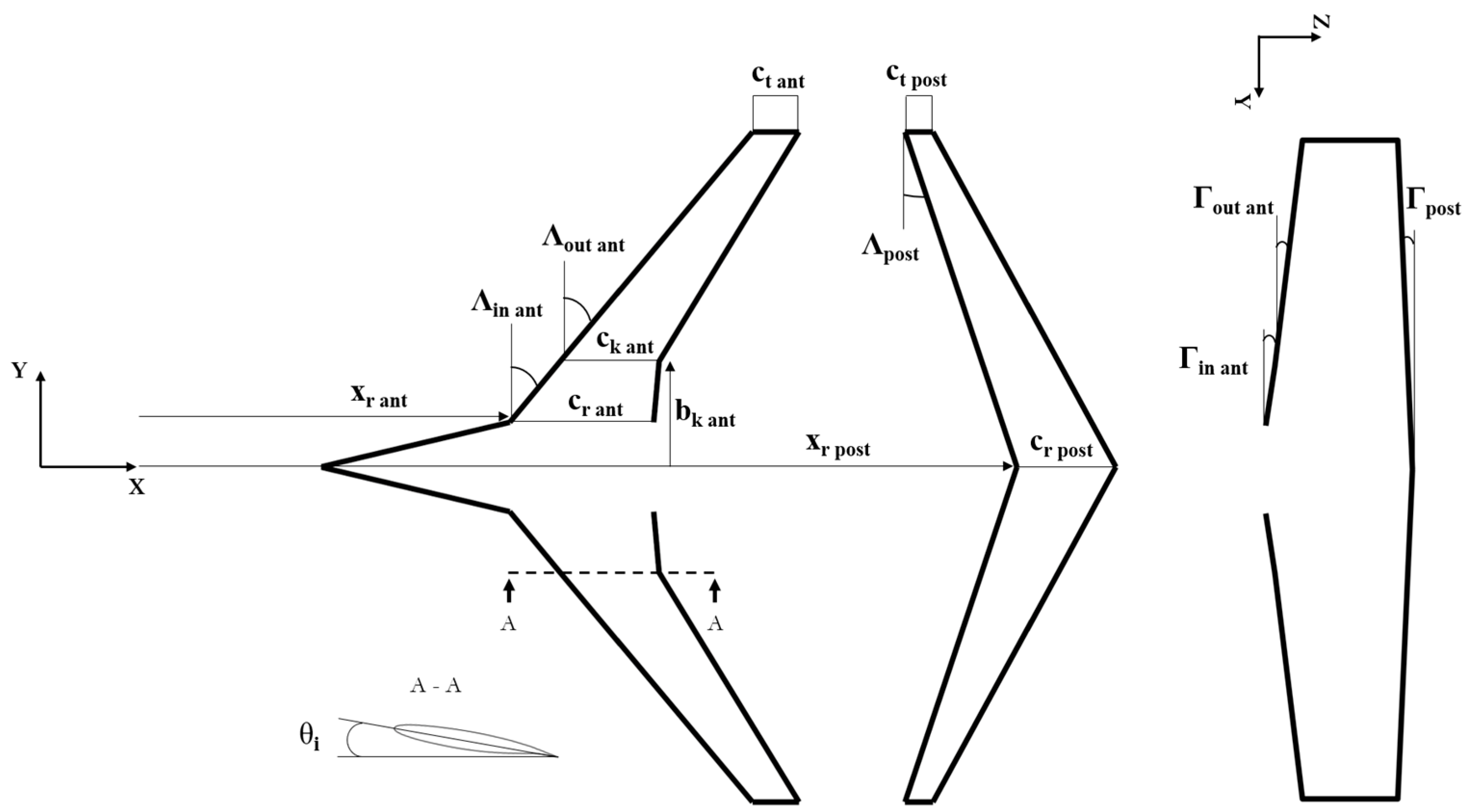
- Design space
- Vertical trim
- Longitudinal static stability
- Pitch trim
- Max local lift coefficient
- Wing loading constraints
- Taper ratio
- Relative wings position
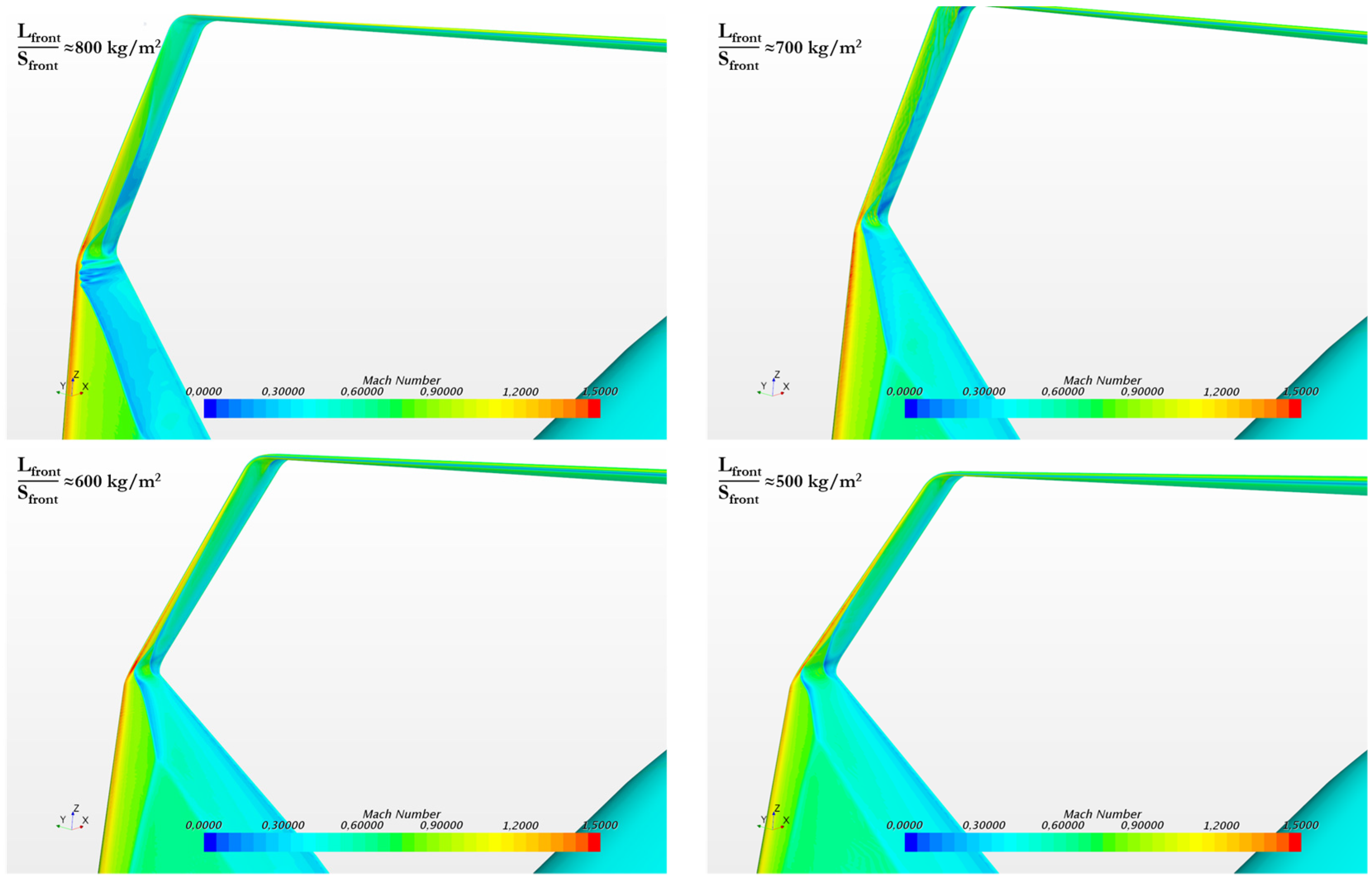
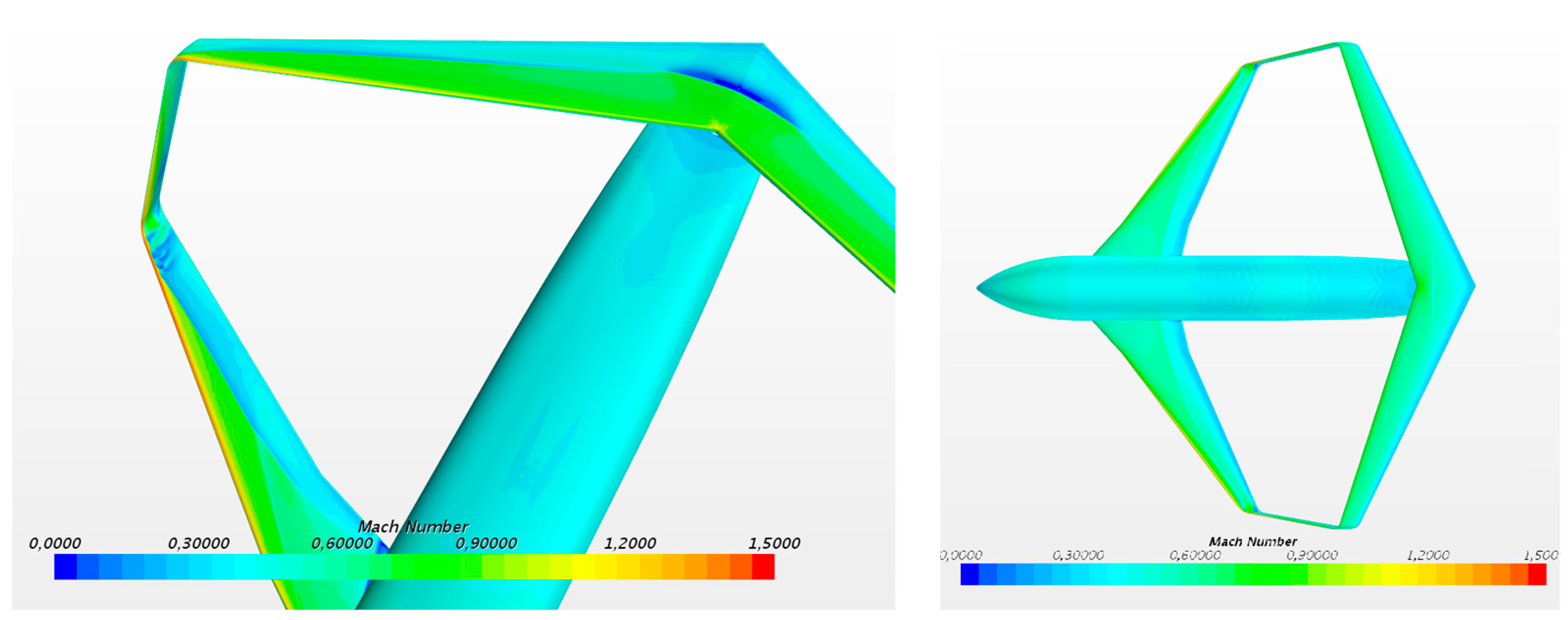
Transonic Aerodynamic Assessment: Level 1 and ½
2.3. High-Fidelity Performance Assessment
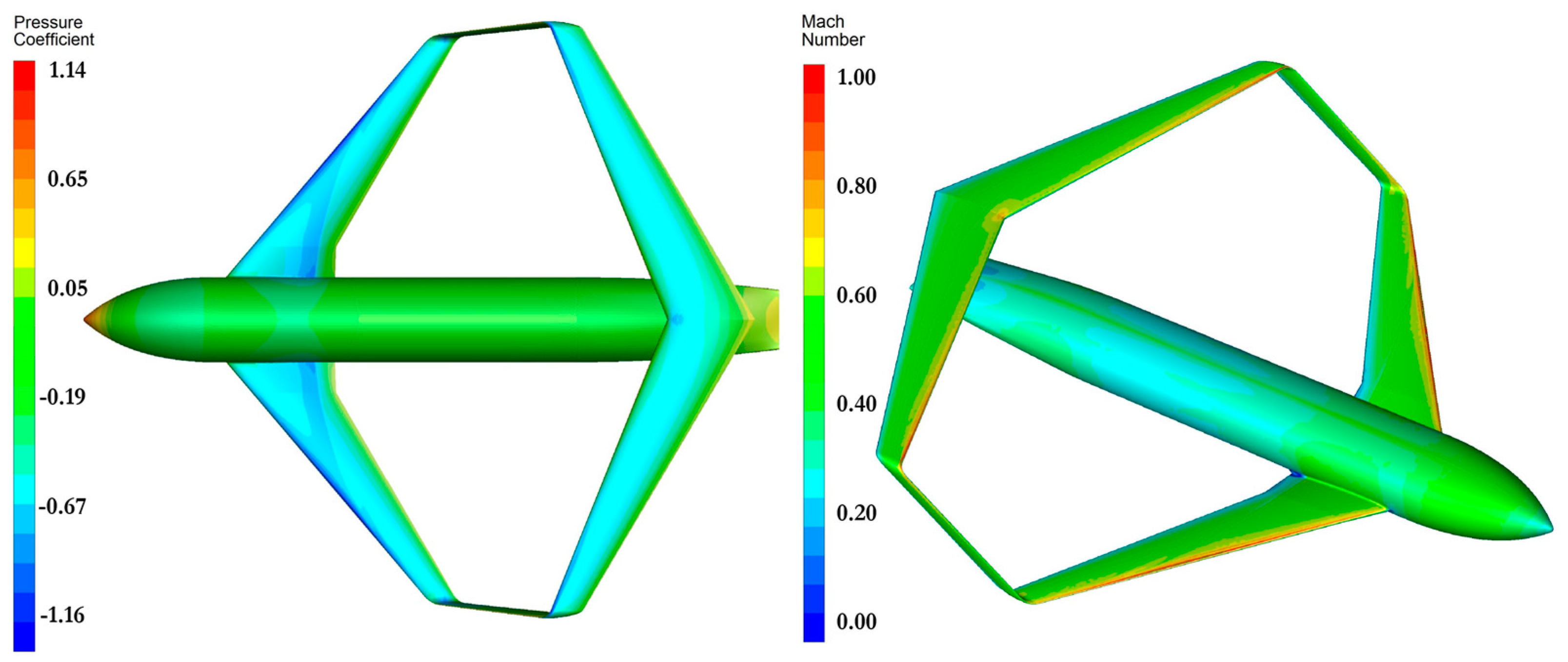
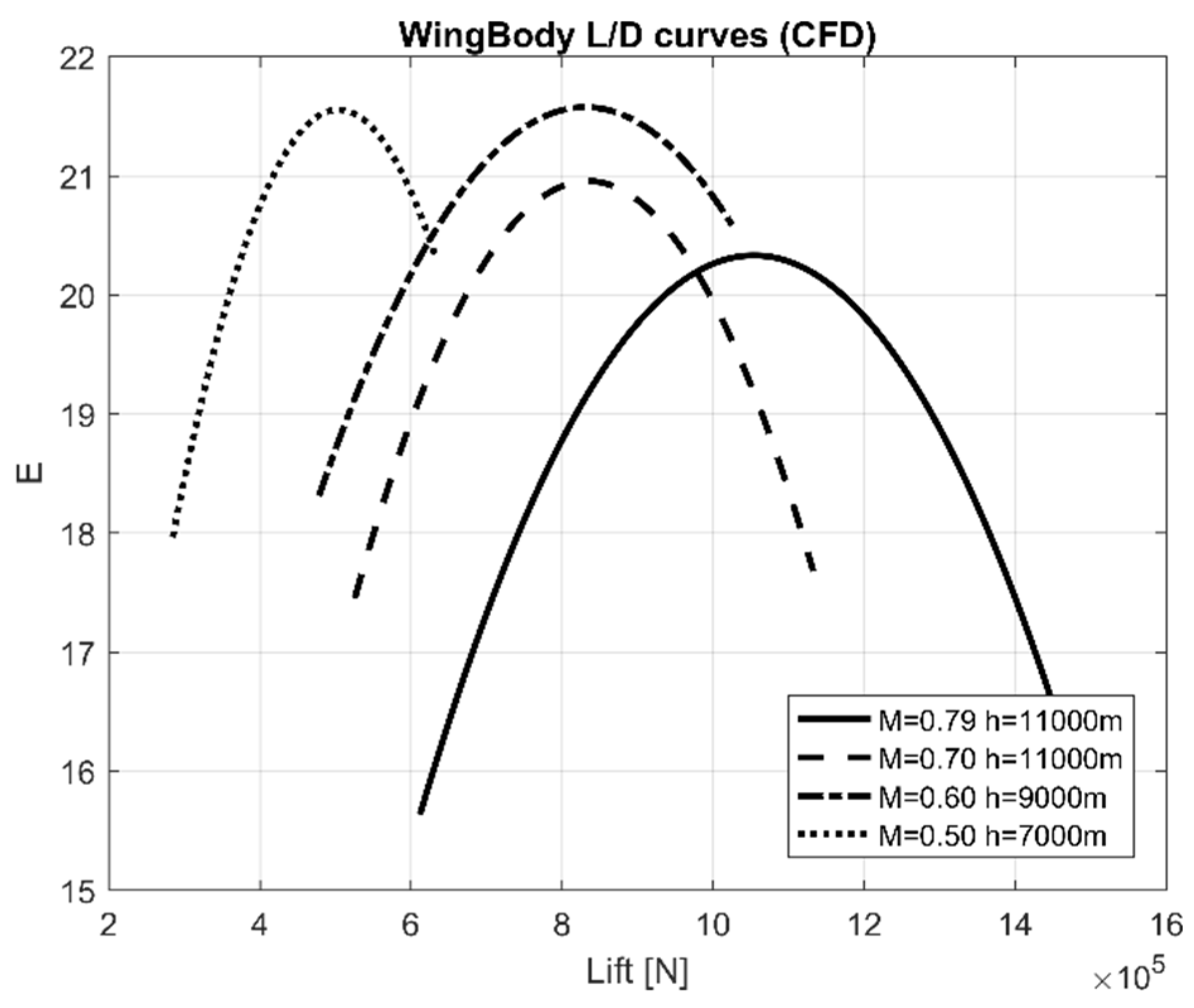
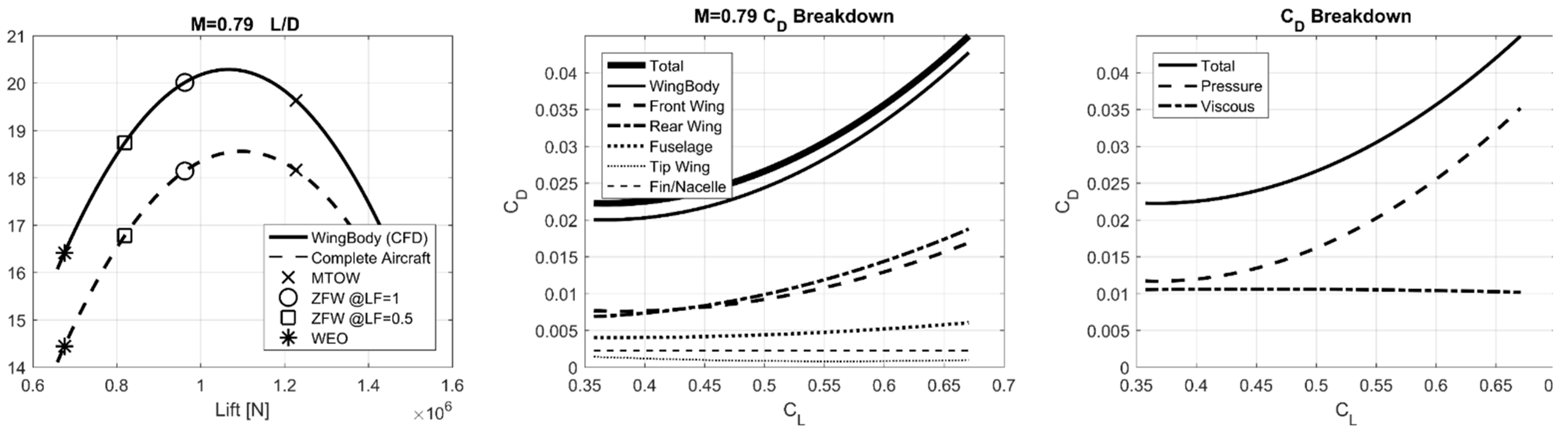
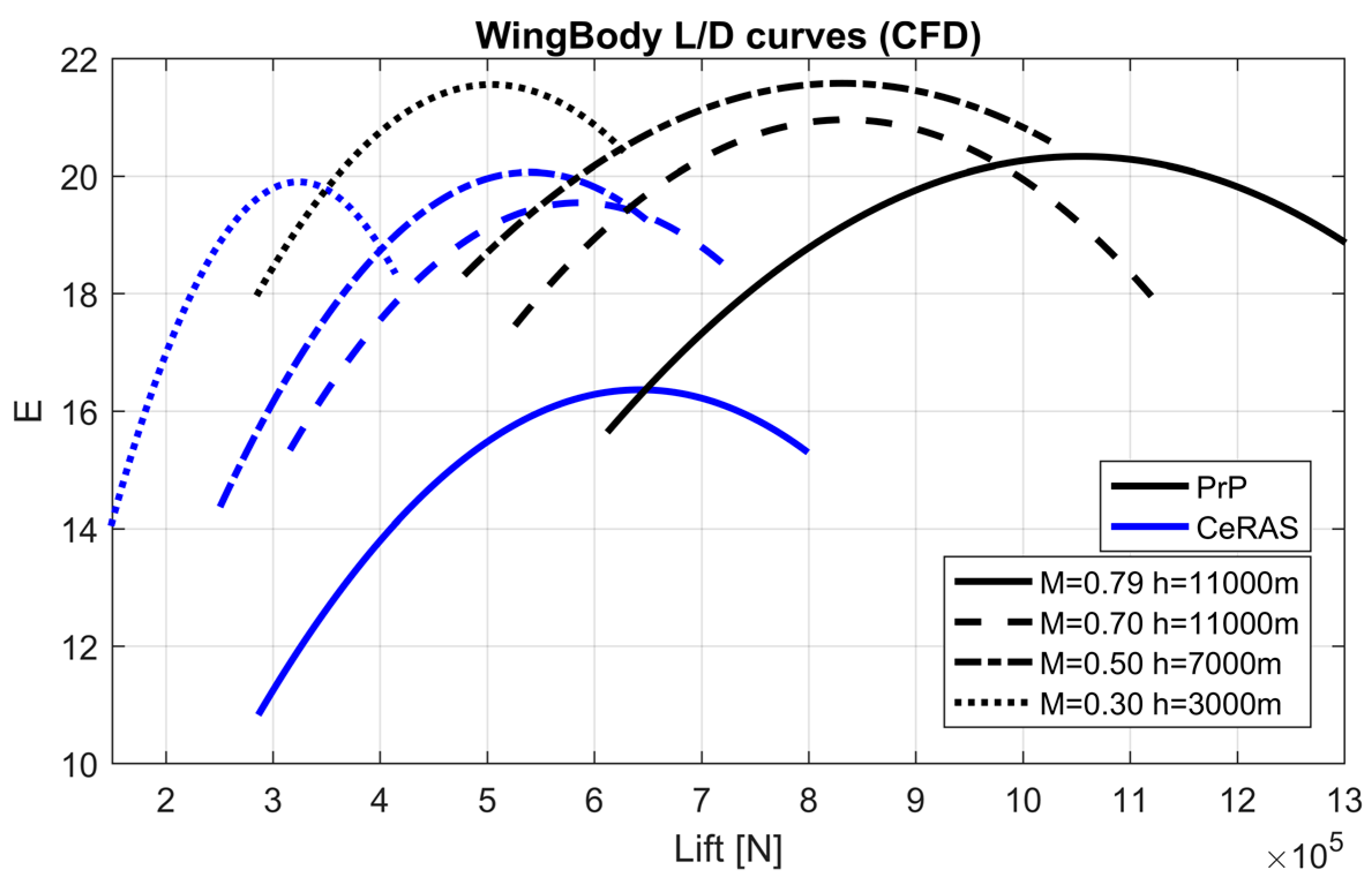
2.3.1. Aerodynamic Performance
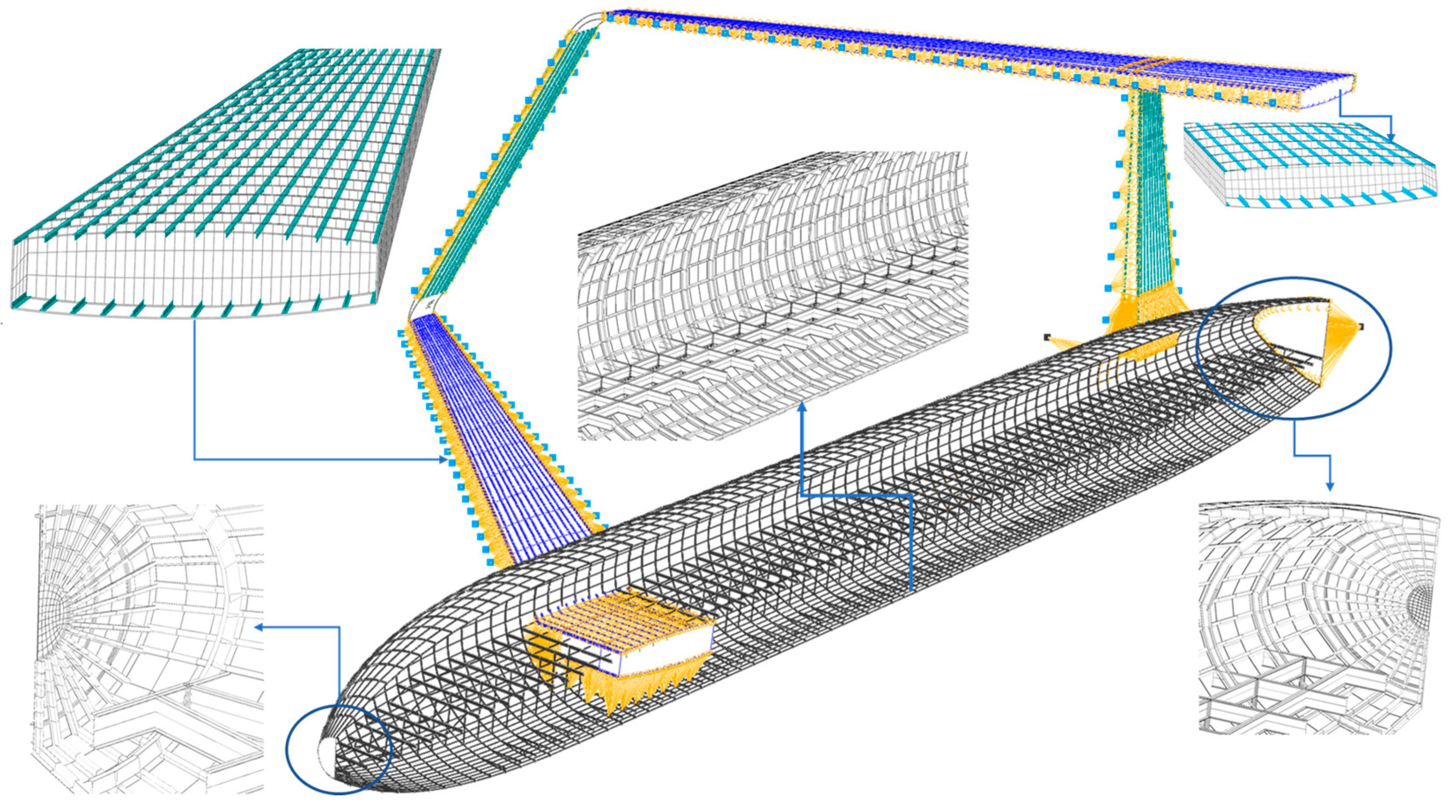
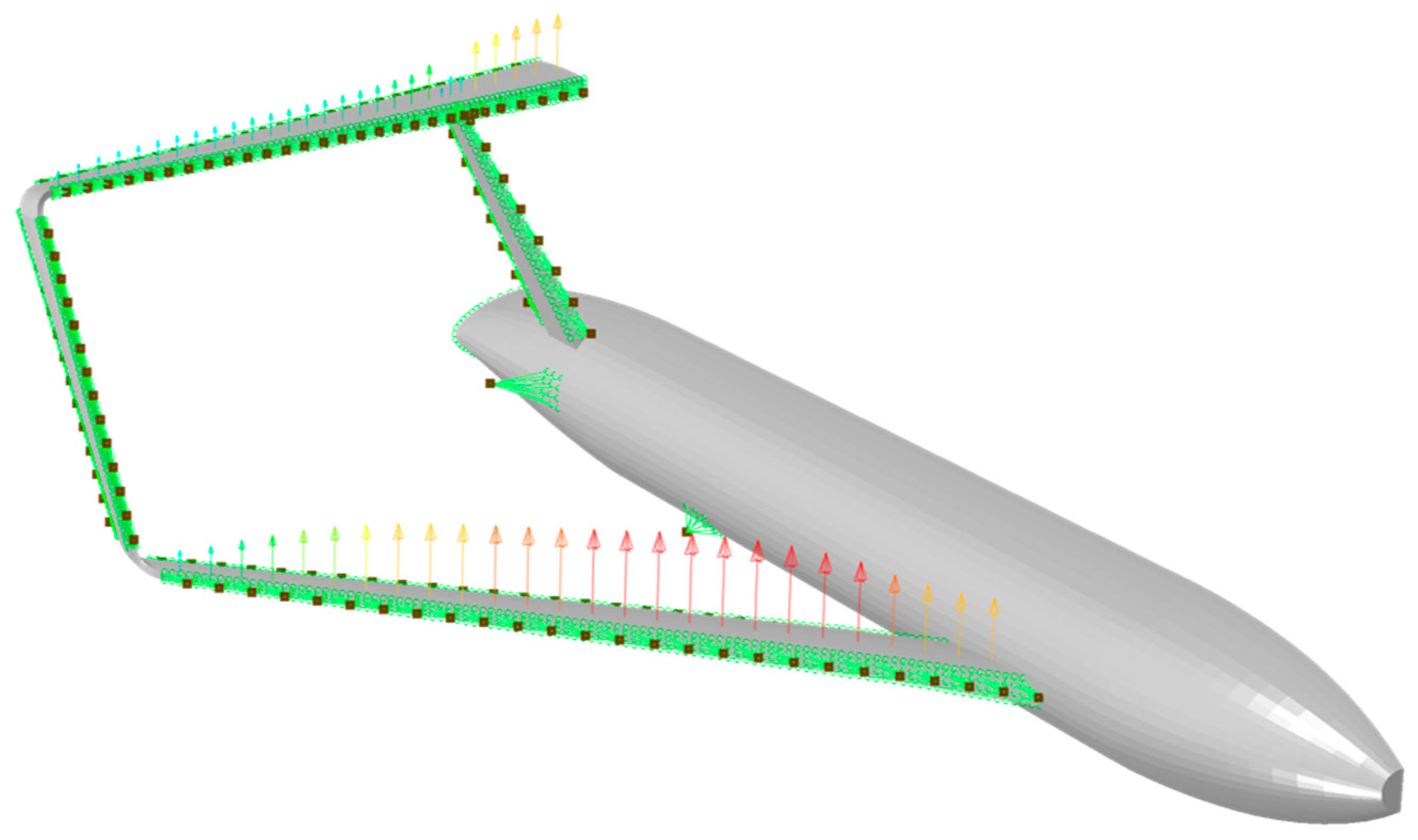
2.3.2. Structural Design and Mass Estimation
- Objective function
- Stiffness constraint
- Strength constraint
- Design variables
- Design space
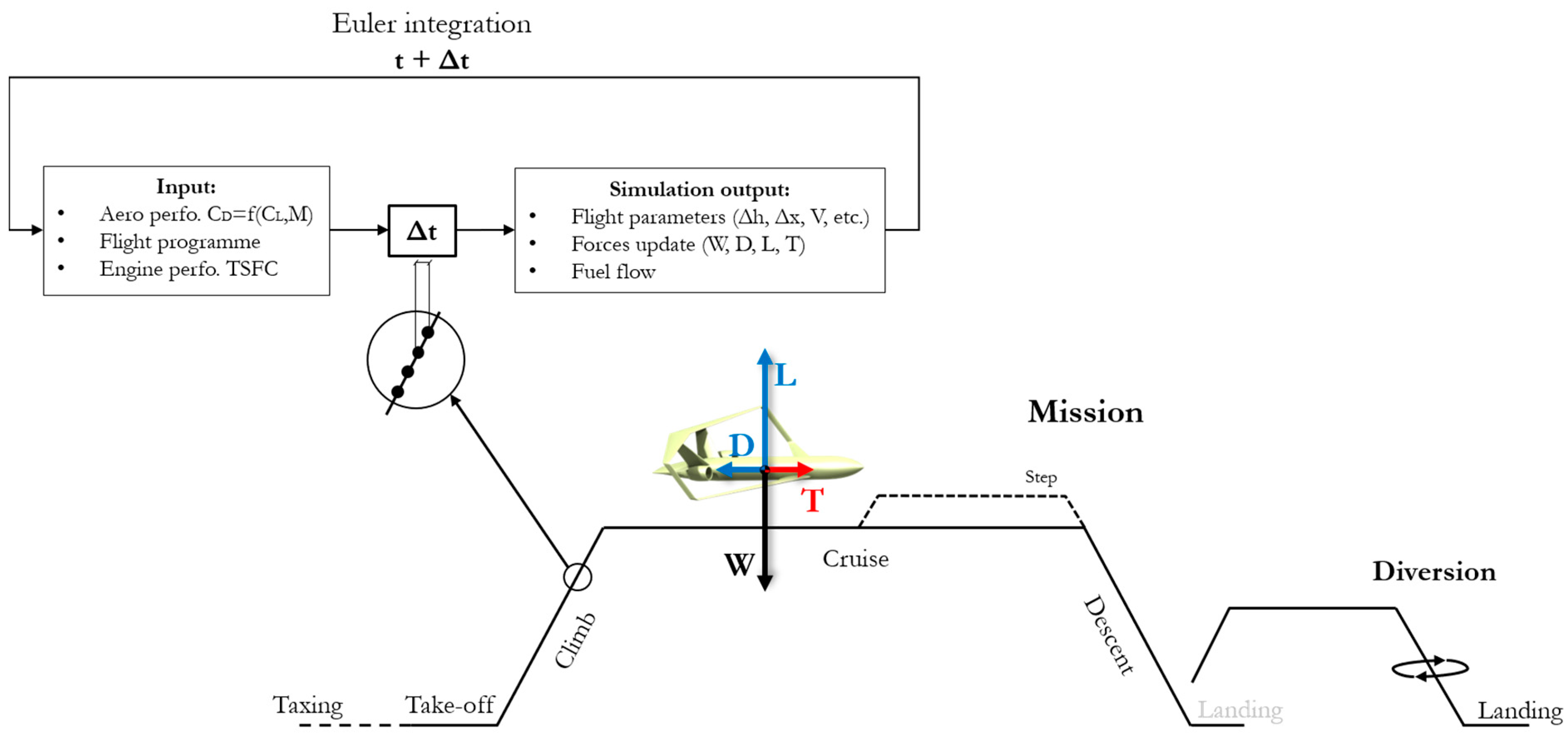
2.3.3. Mission Simulation
- The taxing fuel consumption is extrapolated by the data reported in [84]. The take-off phase was simulated by integrating the equation of motion of the aircraft in the longitudinal plane, also considering its pitch dynamics; the take-off simulation and analysis procedure used in this work is widely described in [85];
- The climb phase was simulated by integrating the equation of motion of the aircraft considered as a point mass in the longitudinal plane:
- The cruise phase was simulated by integrating the equations of steady and level flights for the aircraft point mass model (Equations (33)–(35)); a constant altitude () = 0 and constant speed (= V = constant) flight programme was considered; the simulation, taking aircraft aerodynamic performance and cruise length into account, provided stepped cruise programmes if it resulted in performance gains.
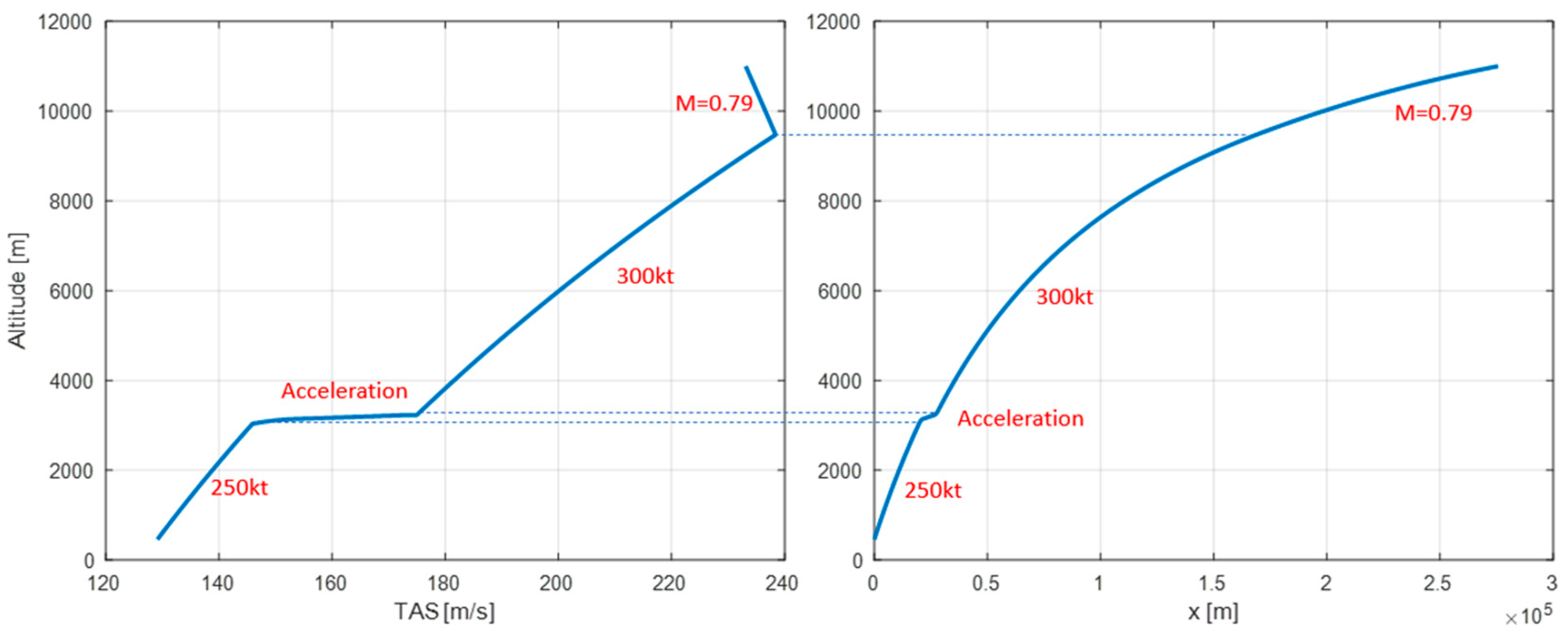
- The descent starts at the cruise altitude and ends at an altitude of 1500 ft; the equations of motion are obtained for the climb, and in the same manner, the flight programme for the descent is made by segments at constant IAS or Mach number [85]; the reference selected programme is “Mcruise/300 kt/250 kt”, namely: (1) the aircraft flies at a constant Mach number from the cruise altitude to the crossover altitude; (2) the aircraft flies at IAS = 300 kt from the crossover altitude to an altitude of 10,000 ft; (3) the aircraft decelerates in an almost level flight until the IAS is 250 kt, and then flies at this IAS until an altitude of 1500 ft is reached.
- Concerning diversion and loiter, analogous considerations about climb, cruise and descent were implemented.
3. Results of the Design Process
3.1. Input Data
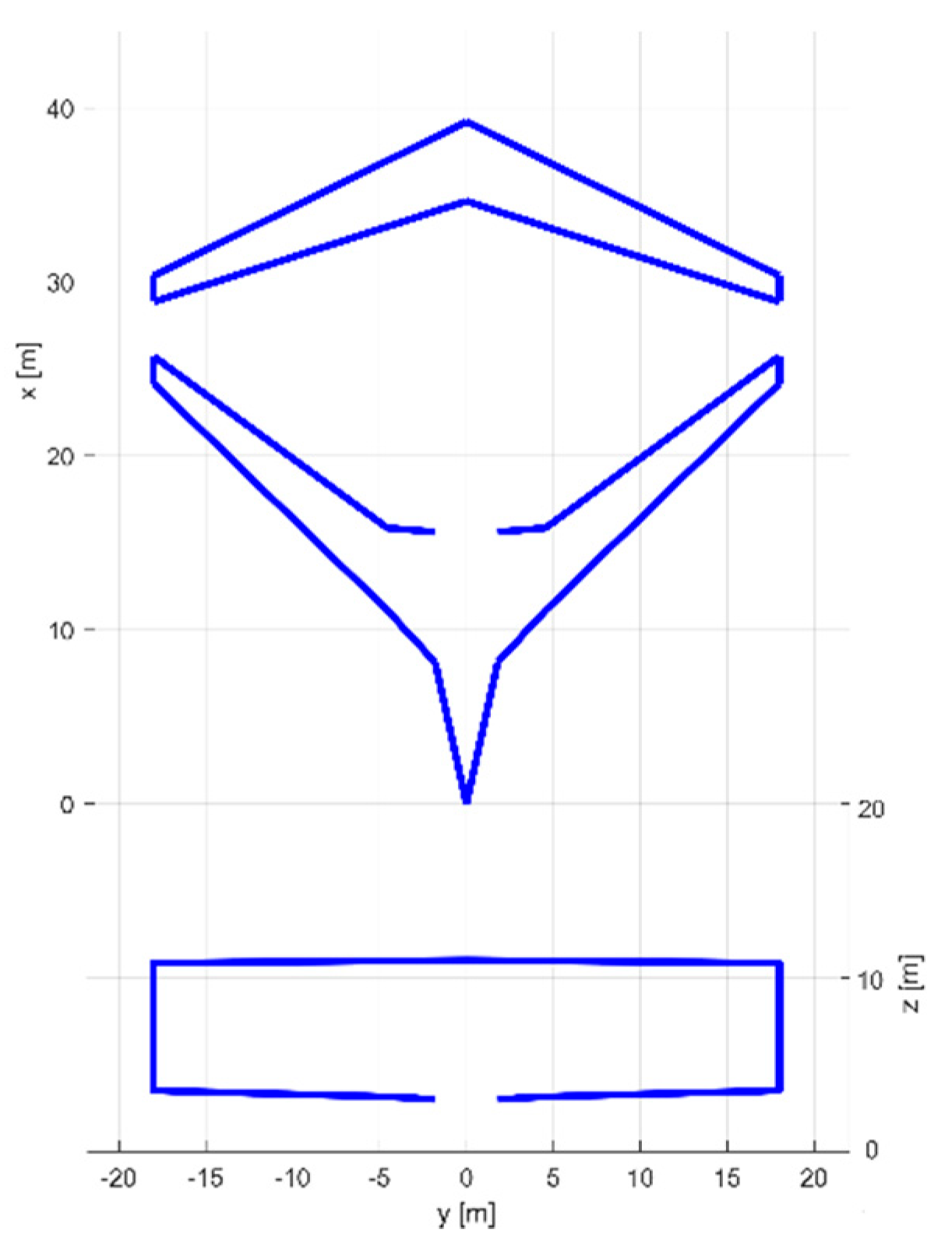
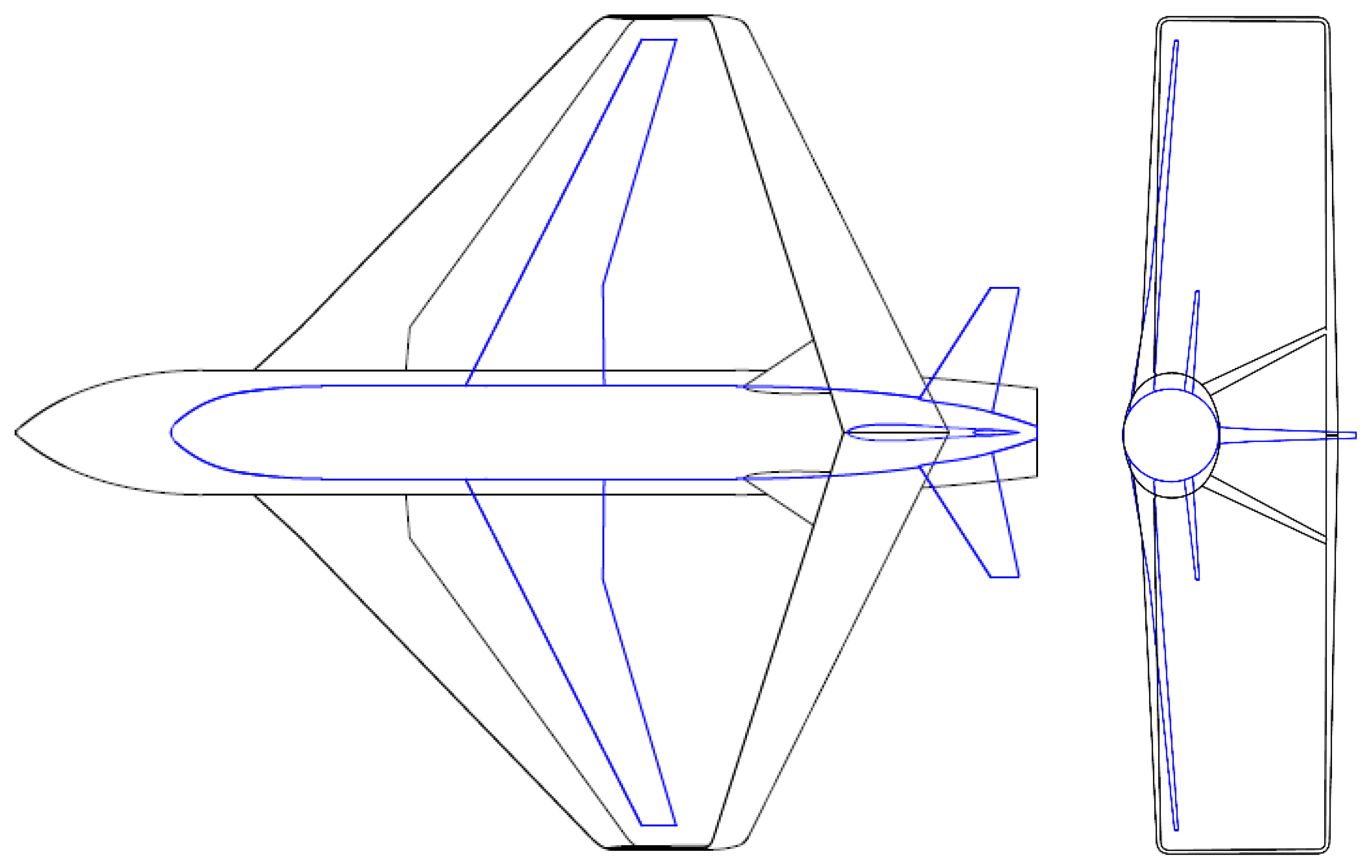
3.2. Conceptual Design and Reference Layout Selection
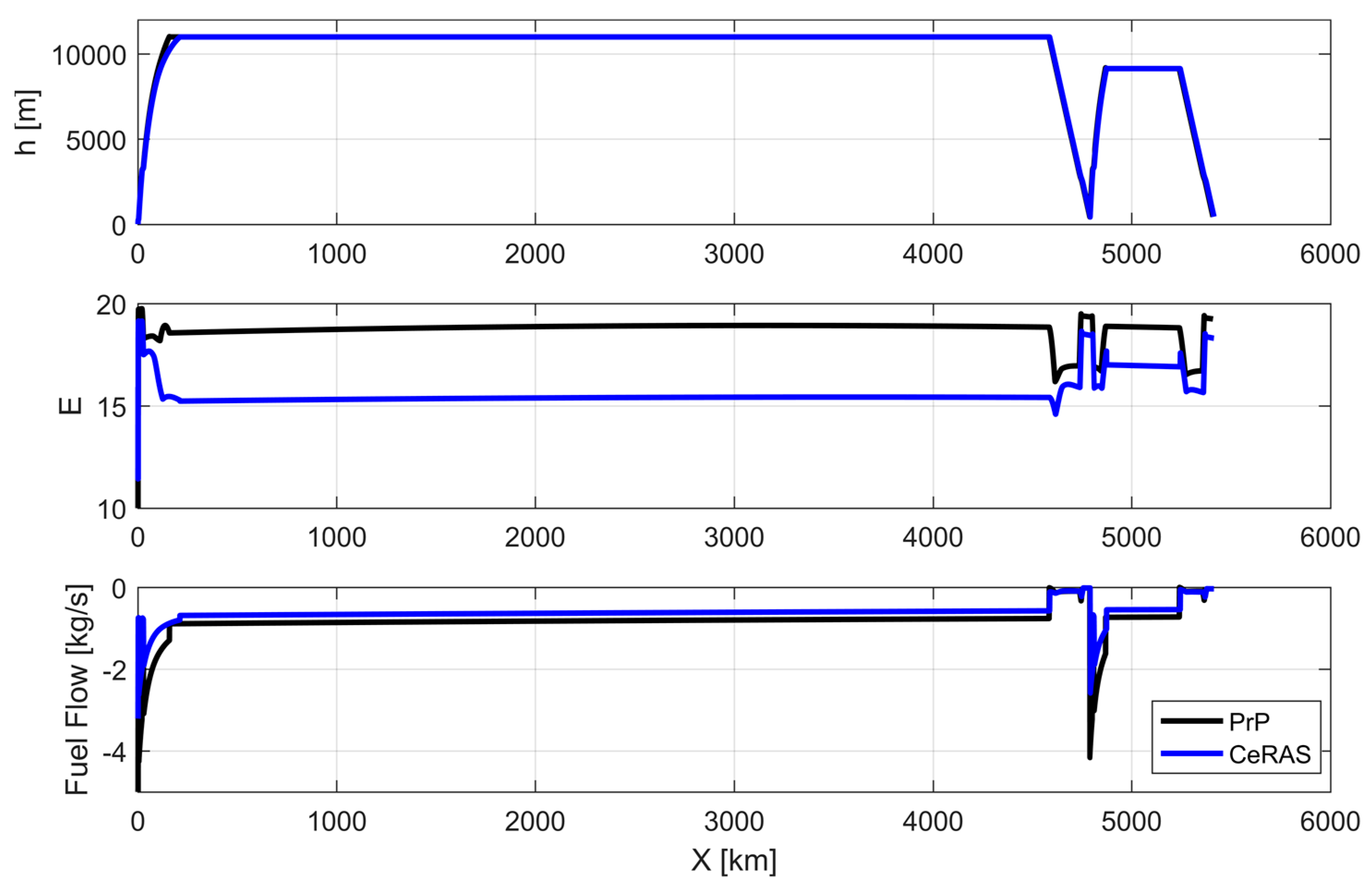
3.3. Mission Performance Analysis
3.4. Box-Wing Performance Comparison with Respect to the Conventional Benchmark
3.5. Box-Wing Operating Performance
3.6. Discussion of the Performance Comparison between the Box-Wing and the Conventional Competitor
- The PARSIFAL PrandtlPlane has a larger pax-range envelope with respect to the CeRAS CSR-01 monoplane; in particular, at the harmonic point, the PrandtlPlane presents +66% more passengers and +19% longer range. Both the aircraft are compliant with the ICAO Aerodrome Reference Code “C” constraint (max wingspan equal to 36 m);
- The PARSIFAL PrandtlPlane can transport the same maximum number of passengers of the CeRAS CSR-01 (186 pax in high density) for about 9350 km, 95% more than the reference aircraft.
- The PARSIFAL PrandtlPlane exhibits a gain in terms of mission fuel per pax km in the relevant area of the pax-range diagram, up to the harmonic range of the CeRAS CSR-01; considering the harmonic ranges, the PrandtlPlane needs 19% less fuel per passenger–kilometre; the reduction in fuel per passenger is relevant, from −13% up to −22%, in the whole operating space considered; this also reflects the aircraft environmental performance: the introduction of the PrandtlPlane configuration allows a reduction in pollutant and greenhouse gas emissions per passenger, as widely discussed in [99,103];
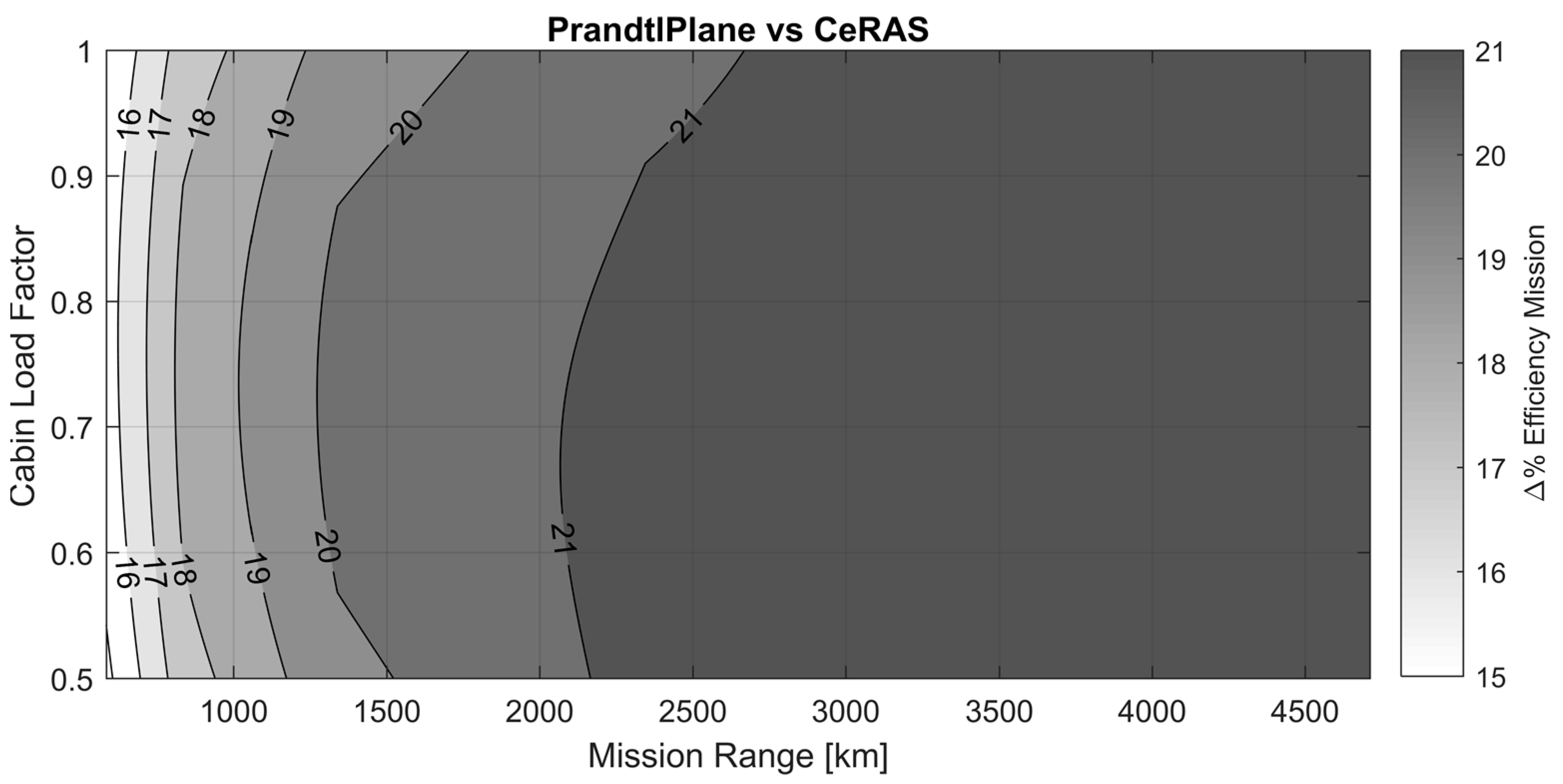
- The diagram in Figure 36 shows the contour maps of the percentage difference of the fuel consumption per passenger–kilometre for the two aircraft, both for the zone inside the CeRAS CSR-01 envelope and outside this limit, up to the CeRAS CSR-01 ferry range. It is clear that direct comparisons (i.e., with the same cabin load factor and range) can only be made within the limits of the CeRAS envelope; beyond this limit, the PARSIFAL PrandtlPlane can fly longer distances with the same cabin load factor, or have higher cabin load factors for the same range, with respect to the CeRAS competitor. In this area, the comparison in terms of fuel burnt per passenger–kilometre cannot be made considering the same range and cabin load factor for the two aircraft; thus, the values obtained for PARSIFAL are compared with those relevant to the best performance of CeRAS, i.e., the missions at the border of the envelope (maximum cabin load factor for each considered range). As a result, the comparisons are carried out considering a same range for the two aircraft, but with different cabin load factors. In this zone of the diagram, the higher fuel efficiency of the PARSIFAL PrandtlPlane is combined with the capability to fly with higher cabin load factors for the considered ranges, and therefore the reduction in fuel consumption per passenger–kilometre increases very sensitively as the range increases, as shown in Figure 36.
- In the area of the cabin load factor range diagram beyond the ferry range of the CeRAS CSR-01 configuration, it is not possible to make comparisons in terms of fuel consumption. This region is highlighted in amaranth in the diagram of Figure 37. The PARSIFAL PrandtlPlane, with the same constraints on maximum wingspan of the reference monoplane competitor, is able to fly longer routes with a number of passengers comparable to the CeRAS CSR-01, thus offering an additional advantage in terms of operational flexibility.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APU | Auxiliar Power Unit |
| AR | Aspect Ratio |
| AVL | Athena Vortex Lattice |
| CAD | Computer Aided Design |
| CeRAS | Central Reference Aircraft Data System |
| CFD | Computational Fluid Dynamics |
| CSR | CeRAS Short Range |
| FEM | Finite Element Method |
| IAS | Indicated Air Speed |
| ICAO | International Civil Aviation Organization |
| LF | Load Factor (passenger cabin) |
| MTOW | Maximum Take-Off Weight |
| PrP | PrandtlPlane |
| RANS | Reynolds Averaged Navier–Stokes equations |
| SSM | Static Stability Margin |
| TLARs | Top Level Aircraft Requirements |
| TSFC | Thrust Specific Fuel Consumption |
| VLM | Vortex Lattice Method |
Symbols
| b | Wingspan | m |
| c | Chord | m |
| CD | Drag coefficient | |
| CD0 | Parasite drag coefficient | |
| CDi | Induced drag coefficient | |
| CDwave | Wave drag coefficient | |
| CD foil | Airfoil drag coefficient | |
| CD tot | Total drag coefficient | |
| Cf | Friction coefficient | |
| Cfe | Equivalent skin friction coefficient | |
| CL | Lift coefficient | |
| Cl | Section lift coefficient | |
| CM | Pitch moment coefficient | |
| d | Diameter | m |
| D | Drag | N |
| e | Oswald factor | |
| E | Aerodynamic efficiency (Lift to Drag ratio) | |
| FF | Form factor | |
| g | Inequality constraint | |
| g | Gravity acceleration | m/s2 |
| h | Altitude | m |
| h/b | Wings height to span ratio | |
| k | Polar drag coefficient | |
| ktip | Stiffness constraint factor | |
| kSF | Strength constraint safety factor | |
| l | Length | m |
| L | Lift | N |
| lb | Lower boundary | |
| L/S | Lifting surface wing loading | kg/m2 |
| M | Mach number | |
| nz | Vertical load factor | |
| Q | Interference factor | |
| Sexposed | Planform area of the wing exposed to the flow | m2 |
| Sref | Reference surface | m2 |
| Swet | Wetted surface | m2 |
| t | Vector of thicknesses of structural wingbox components | mm |
| t/c | Thickness to chord ratio | |
| T | Thrust | N |
| ub | Upper boundary | |
| V | Speed | m/s |
| W | Weight | kg |
| Wdes | Design weight | kg |
| Woe | Operating empty weight | kg |
| x | Design variables vector | |
| x | Aircraft longitudinal position | m |
| xLE | Longitudinal leading edge coordinate | m |
| y | Spanwise coordinate | m |
| z | Aircraft vertical position | m |
| α | Angle of attack | deg |
| γ | Trajectory slope | deg |
| δtip | Wing tip displacement | mm |
| ε | Tolerance | |
| θ | Section twist | deg |
| λ | Taper ratio | |
| Λ | Sweep angle | deg |
| σeq | Equivalent stress | MPa |
| Other subscripts: | ||
| comp | Component | |
| cruise | Cruise | |
| cyl | Cylinder | |
| eng | Engine | |
| front | Front wing | |
| fus | Fuselage | |
| fuel | Fuel | |
| max | Maximum | |
| min | Minimum | |
| oper | Operating items | |
| pay | Payload | |
| rear | Rear wing | |
| root | Root section | |
| sys | On board systems | |
| TH | Threshold | |
| tip | Tip section | |
| trim | Trim condition | |
| vertical | Vertical tail | |
| wing | Wing |
References
- Lee, D.S.; Fahey, D.W.; Forster, P.M.; Newton, P.J.; Wit, R.C.; Lim, L.; Owen, B.; Sausen, R. Aviation and global climate change in the 21st century. Atmos. Environ. 2009, 43, 3520–3537. [Google Scholar] [CrossRef]
- Lee, D.S.; Pitari, G.; Frewe, V.; Gierens, K.; Penner, J.E.; Petzold, A.; Prather, M.J.; Schumann, U.; Bais, A.; Berntsen, T.; et al. Transport impacts on atmosphere and climate: Aviation. Atmos. Environ. 2010, 44, 4678–4734. [Google Scholar] [CrossRef] [PubMed]
- Dessens, O.; Köhler, M.O.; Rogers, H.L.; Jones, R.L.; Pyle, J.A. Aviation and climate change. Transp. Policy 2014, 34, 14–20. [Google Scholar] [CrossRef]
- Wuebbles, D. Evaluating the impacts of aviation on climate change. Eos Trans. Am. Geophy. Union 2007, 88, 157–160. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Gupta, M. Impact of aviation on climate. Am. Meteorol. Soc. 2016, 97, 561–583. [Google Scholar] [CrossRef]
- Eurocontrol. European Aviation in 2040, Challenges of Growth, Annex 2, Adapting Aviation to a Changing Climate. 2018. Available online: https://perma.cc/842G-4A3R (accessed on 18 July 2021).
- Eurocontrol. European Aviation in 2040, Challenges of Growth, Annex 1, Flight Forecast to 2040. 2018. Available online: https://perma.cc/YW6Y-JU7J (accessed on 18 July 2021).
- PARSIFAL Project Consortium. Report on Socio Economic Scenarios and Expectations. PARSIFAL Project Deliverables, D 1.1. 2017. Available online: https://perma.cc/JYL5-K9ST (accessed on 18 July 2021).
- Airbus. Cities, Airports & Aircraft—2019–2038. Global Market Outlook. 2019. Available online: https://perma.cc/WSW3-7JK5 (accessed on 18 July 2021).
- Boeing. Commercial Market Outlook—2019–2038. 2019. Available online: https://perma.cc/WQ53-7WEB (accessed on 18 July 2021).
- Eurocontrol. European Aviation in 2040, Challenges of Growth. 2018. Available online: https://perma.cc/2A2J-B7PW (accessed on 18 July 2021).
- Schäfer, A.W.; Barrett, S.R.; Doyme, K.; Dray, L.M.; Gnadt, A.R.; Self, R.; O’Sullivan, A.; Synodinos, A.P.; Torija, A.J. Technological, economic and environmental prospects of all-electric aircraft. Nat. Energy 2019, 4, 160–166. [Google Scholar] [CrossRef]
- Hoelzen, J.; Yaolong, L.; Bensmann, B.; Winnefiled, C.; Elham, A.; Fiedrichs, J.; Hanke-Rauschenbach, R. Conceptual design of operation strategies for hybrid electric aircraft. Energies 2018, 11, 217. [Google Scholar] [CrossRef]
- Pornet, C.; Isikveren, A.T. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Palaia, G.; Zanetti, D.; Abu Salem, K.; Cipolla, V.; Binante, V. THEA-CODE: A design tool for the conceptual design of hybrid-electric aircraft with conventional or unconventional airframe configurations. Mech. Ind. 2021, 22, 19. [Google Scholar] [CrossRef]
- Friedrich, C.; Robertson, P.A. Hybrid-electric propulsion for aircraft. J. Aircr. 2015, 52, 176–189. [Google Scholar] [CrossRef]
- Brelje, B.J.; Martins, J.R. Electric, hybrid, and turboelectric fixed-wing aircraft: A review of concepts, models, and design approaches. Prog. Aerosp. Sci. 2019, 104, 1–9. [Google Scholar] [CrossRef]
- Khandelwal, B.; Karakurt, A.; Sekaran, P.R.; Sethi, V.; Singh, R. Hydrogen powered aircraft: The future of air transport. Prog. Aerosp. Sci. 2013, 60, 45–59. [Google Scholar] [CrossRef]
- Baroutaji, A.; Wilberforce, T.; Ramadan, M.; Olabi, A.G. Comprehensive investigation on hydrogen and fuel cell technology in the aviation and aerospace sectors. Renew. Sustain. Energy Rev. 2019, 106, 31–40. [Google Scholar] [CrossRef]
- Nojoumi, H.; Dincer, I.; Naterer, G.F. Greenhouse gas emissions assessment of hydrogen and kerosene-fueled aircraft propulsion. Int. J. Hydrogen Energy 2019, 34, 1363–1369. [Google Scholar] [CrossRef]
- Ng, W.; Datta, A. Hydrogen fuel cells and batteries for electric-vertical takeoff and landing aircraft. J. Aircr. 2019, 56, 1765–1782. [Google Scholar] [CrossRef]
- Azami, M.H.; Savill, M. Comparative study of alternative biofuels on aircraft engine performance. Inst. Mech. Eng. Part G J.Aerosp. Eng. 2017, 231, 1509–1521. [Google Scholar] [CrossRef]
- Moore, R.H.; Thornhill, L.; Weinzierl, B.; Sauer, D.; D’Ascoli, E.; Kim, J.; Lichtenstern, M.; Scheibe, M.; Beaton, B.; Beyersdorf, A.; et al. Biofuel blending reduces particle emissions from aircraft engines at cruise conditions. Nature 2017, 543, 411–415. [Google Scholar] [CrossRef] [PubMed]
- Mazlan, N.M.; Savill, M.; Kipouros, T. Effects of biofuels properties on aircraft engine performance. Aircr. Eng. Aerosp. Technol. 2015, 87, 437–442. [Google Scholar] [CrossRef]
- Liem, R.P.; Martins, J.R.; Kenway, G.K. Expected drag minimization for aerodynamic design optimization based on aircraft operational data. Aerosp. Sci. Technol. 2017, 63, 344–362. [Google Scholar] [CrossRef]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology optimization in aircraft and aerospace structures design. Arch. Comput. Methods Eng. 2015, 23, 595–622. [Google Scholar] [CrossRef]
- Lei, R.; Bai, J.; Xu, D. Aerodynamic optimization of civil aircraft with wing-mounted engine jet based on adjoint method. Aerosp. Sci. Technol. 2019, 93, 105285. [Google Scholar] [CrossRef]
- Gu, X.; Ciampa, P.D.; Jepsen, J.; Nagel, B. High fidelity aerodynamic optimization in distributed overall aircraft design. In Proceedings of the AIAA Aviation Forum, 17th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Lange, R.H. Review of unconventional aircraft design concepts. J. Aircr. 1988, 25, 385–392. [Google Scholar] [CrossRef]
- Schmitt, D. Challenges for unconventional transport aircraft configurations. Air Space Eur. 2001, 3, 67–72. [Google Scholar] [CrossRef]
- Iwanizki, M.; Wöhler, S.; Fröhler, B.; Zill, T.; Méheut, M.; Defoort, S.; Carini, M.; Gauvrit-Ledogar, J.; Liaboeuf, R.; Tremolet, A.; et al. Conceptual Design Studies of Unconventional Configurations. 3AF Aerospace Europe Conference 2020, Bordeaux. 2020. Available online: https://hal.archives-ouvertes.fr/hal-02907205 (accessed on 18 July 2021).
- Bijewitz, J.; Seitz, A.; Isikveren, A.T.; Hornung, M. Multi-disciplinary design investigation of propulsive fuselage aircraft concepts. Aircr. Eng. Aerosp. Technol. 2016, 88, 257–267. [Google Scholar] [CrossRef]
- Defoort, S.; Méheut, M.; Paluch, B.; Liaboeuf, R.; Murray, R.; Mincu, D.C.; David, J.M. Conceptual design of disruptive aircraft configurations based on High-Fidelity OAD process. In Proceedings of the AIAA Aviation Forum, 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Werner-Westphal, C.; Heinze, W.; Horst, P. Multidisciplinary integrated preliminary design applied to unconventional aircraft configurations. J. Aircr. 2008, 45, 581–590. [Google Scholar] [CrossRef]
- Liebeck, R.H. Design of the blended wing body subsonic transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef]
- Qin, N.; Vavalle, A.; Le Moigne, A.; Laban, M.; Hackett, K.; Weinerfelt, P. Aerodynamic considerations of blended wing body aircraft. Prog. Aerosp. Sci. 2004, 40, 21–343. [Google Scholar] [CrossRef]
- Okonkwo, P.; Smith, H. Review of evolving trends in blended wing body aircraft design. Prog. Aerosp. Sci. 2016, 82, 1–23. [Google Scholar] [CrossRef]
- Cavallaro, R.; Demasi, L. Challenges, ideas, and innovations of joined-wing configurations: A concept from the past, an opportunity for the future. Prog. Aerosp. Sci. 2016, 87, 1–93. [Google Scholar] [CrossRef]
- Wolkovitch, J. The joined wing: An overview. J. Aircr. 1986, 23, 161–178. [Google Scholar] [CrossRef]
- Frediani, A.; Cipolla, V.; Rizzo, E. The Prandtl plane configuration: Overview on possible applications to civil aviation. In Variational Analysis and Aerospace Engineering: Mathematical Challenges for Aerospace Design; Springer Optimization and Its Applications; Springer: Boston, MA, USA, 2012; Volume 66. [Google Scholar] [CrossRef]
- Frediani, A.; Rizzo, E.; Bottoni, C.; Scanu, J.; Iezzi, G. A 250 Passenger Prandtl plane transport aircraft preliminary design. Aerotecnica Missili Spazio 2005, 84. Available online: http://hdl.handle.net/11568/99885 (accessed on 18 July 2021).
- Frediani, A. The Prandtl Wing. VKI, Lecture Series: Innovative Configurations and Advanced Concepts for Future Civil Transport Aircraft. 2005. Available online: https://perma.cc/XU6F-8YLG (accessed on 18 July 2021).
- Frediani, A.; Cipolla, V.; Oliviero, F. Design of a prototype of light amphibious Prandtl Plane. In Proceedings of the AIAA SciTech Forum, 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5−9 January 2015. [Google Scholar] [CrossRef]
- Prandtl, L.; Induced Drag of Multiplanes. NACA TN-182. 1924. Available online: https://ntrs.nasa.gov/citations/19930080964 (accessed on 18 July 2021).
- Frediani, A.; Montanari, G. Best wing system: An exact solution of the Prandtl’s problem. In Variational Analysis and Aerospace Engineering; Springer Optimization and Its Applications; Springer: New York, NY, USA, 2009; Volume 33. [Google Scholar] [CrossRef]
- Demasi, L.; Dipace, A.; Monegato, G.; Cavallaro, R. Invariant formulation for the minimum induced drag conditions of nonplanar wing systems. AIAA J. 2014, 52. [Google Scholar] [CrossRef]
- PARSIFAL Project. Available online: https://perma.cc/5ULW-HCP4 (accessed on 18 July 2021).
- Abu Salem, K.; Binante, V.; Cipolla, V.; Maganzi, M. PARSIFAL project: A breakthrough innovation in air transport. Aerotecnica Missili Spazio 2018, 97. [Google Scholar] [CrossRef]
- Abu Salem, K. Studio Sulla Configurazione Aerodinamica di Velivoli Civili di Tipo PrandtlPlane di Piccole e Medie Dimensioni. M.Sc. Thesis, University of Pisa, Italy, 2016. Available online: https://etd.adm.unipi.it/theses/available/etd-06222016-110207/ (accessed on 18 July 2021).
- Bishop, K. Assessment of the Ability of Existing Airport Gate Infrastructure to Accommodate Transport Category Aircraft with Increased Wingspan for Improved Fuel Efficiency. M.Sc. Thesis, Dept. of Aeronautics and Astronautics, Massachusetts Institute of Technology, Boston, MA, USA, 2012. Available online: http://hdl.handle.net/1721.1/76095 (accessed on 18 July 2021).
- European Commission. Mobility for Growth—Breakthrough Innovation. Funding Action for Research and Innovation. 2015. Available online: https://ec.europa.eu/inea/en/news-events/newsroom/new-transport-projects-selected-horizon-2020-funding (accessed on 18 July 2021).
- McMasters, J.; Paisley, D.; Hubert, R.; Kroo, I.; Bofah, K.; Sullivan, J.; Drela, M. Advanced configurations for very large subsonic Transport Airplanes. NASA CR 198351. 1996. Available online: https://ntrs.nasa.gov/citations/19970003675 (accessed on 18 July 2021).
- Raymer, D.P. Aircraft Design: A Conceptual Approach; AIAA Education Series: Washington, DC, USA, 1992; ISBN 0-930403-51-7. [Google Scholar]
- Association of European Airlines. Short-Medium Range Aircraft AEA Requirements. Report G(T); AEA: Bonn, Germany, 1989. [Google Scholar]
- Casarosa, C. Meccanica del Volo; Pisa University Press: Pisa, Italy, 2013; ISBN 978-8867410163. [Google Scholar]
- Rizzo, E. Optimization Methods Applied to the Preliminary Design of Innovative Non Conventional Aircraft Configurations. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2009. Available online: https://etd.adm.unipi.it/t/etd-05122010-103814/ (accessed on 18 July 2021).
- Cappelli, L.; Costa, G.; Cipolla, V.; Frediani, A.; Oliviero, F.; Rizzo, E. Aerodynamic optimization of a large PrandtlPlane configuration. Aerotecnica Missili Spazio 2016, 95, 163–175. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Cipolla, V.; Binante, V.; Zanetti, D.; Chiarelli, M. Tools and methodologies for box-wing aircraft conceptual aerodynamic design and aeromechanic analysis. Mech. Ind. 2021, 22, 1–19. [Google Scholar] [CrossRef]
- Rizzo, E.; Frediani, A. Application of optimisation algorithms to aircraft aerodynamics. In Variational Analysis and Aerospace Engineering; Springer Optimization and Its Applications: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Addis, B.; Locatelli, M.; Schoen, F. Local optima smoothing for global optimization. Optim. Methods Softw. 2005, 20, 417–437. [Google Scholar] [CrossRef][Green Version]
- Drela, M.; Youngren, H. XFOIL 6.9 User Primer. Online Software Manual. 2001. Available online: https://perma.cc/7AGE-C3XU (accessed on 18 July 2021).
- Drela, M.; Youngren, H. AVL 3.36 User Primer. Online Software Manual. 2017. Available online: https://perma.cc/R35R-W29F (accessed on 18 July 2021).
- Beltramo, M.; Trapp, D.; Kimoto, B.; Marsh, D. Parametric Study of Transport Aircraft Systems Cost and Weight. Report NASA CR151970. 1977. Available online: https://ntrs.nasa.gov/citations/19770019162 (accessed on 18 July 2021).
- Wells, D.; Horvath, B.; McCullers, L. The Flight Optimization System Weights Estimation Method. NASA/TM–2017–219627, Volume I; 2017. Available online: https://ntrs.nasa.gov/citations/20170005851 (accessed on 18 July 2021).
- Frediani, A.; Cipolla, V.; Abu Salem, K.; Binante, V.; Picchi Scardaoni, M. Conceptual design of PrandtlPlane civil transport aircraft. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 234, 1675–1687. [Google Scholar] [CrossRef]
- Mason, W.H. Analytic models for technology integration in aircraft design. AIAA Aircr. Des. Syst. Op. Conf. Dayton 1990, 90, 3262-CP. [Google Scholar] [CrossRef]
- Cipolla, V.; Frediani, A.; Abu Salem, K.; Binante, V.; Rizzo, E.; Maganzi, M. Preliminary transonic CFD analyses of a PrandtlPlane transport aircraft. Transp. Res. Procedia 2018, 29, 82–91. [Google Scholar] [CrossRef]
- ANSYS, Ansys Fluent—Fluid Simulation Software. Available online: https://perma.cc/L56W-V8FZ (accessed on 18 July 2021).
- Fazalzadeh, S.; Scholz, D.; Mazidi, A.; Friswell, M. Flutter characteristics of typical wing sections of a box wing aircraft configuration. In Proceedings of the 3AF AEGATS Proceedings 2018, Toulouse, France, 23−25 October 2018. [Google Scholar] [CrossRef]
- Divoux, N.; Frediani, A. The lifting system of a PrandtlPlane, Part 2: Preliminary study on flutter characteristics. In Variational Analysis and Aerospace Engineering; Springer Optimization and Its Applications: Boston, MA, USA, 2012. [Google Scholar] [CrossRef]
- Cavallaro, R.; Bombardieri, R.; Silvani, S.; Demasi, L.; Bernardini, G. Aeroelasticity of the PrandtlPlane: Body freedom flutter, freeplay, and limit cycle oscillation. In Variational Analysis and Aerospace Engineering: Mathematical Challenges for the Aerospace of the Future; Springer Optimization and Its Applications: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Bombardieri, R.; Cavallaro, R.; Demasi, L. A historical perspective on the aeroelasticity of box Wings and PrandtlPlane with new findings. In Proceedings of the AIAA SciTech Forum, 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4−8 January 2016. [Google Scholar] [CrossRef]
- PARSIFAL Project Consortium. Aeroelastic Analysis of the Baseline PrandtlPlane. PARSIFAL Project Deliverables, D5.2. 2020. Available online: https://perma.cc/JYL5-K9ST (accessed on 18 July 2021).
- Abu Salem, K. Development of Design Tools and Methods for Box-Wing Airplanes and Application of the PrandtlPlane Concept to a Short-Medium Range Aircraft. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2021. Available online: https://etd.adm.unipi.it/ (accessed on 18 July 2021).
- Picchi Scardaoni, M.; Binante, V.; Cipolla, V. WAGNER: A new code for parametrical structural study of fuselages of civil transport aircraft. Aerotecnica Missili Spazio 2017, 96, 136–147. [Google Scholar] [CrossRef][Green Version]
- 3DS Dassault Systems Simulia, ABAQUS Unified FEA. Available online: https://perma.cc/X8L3-JGSV (accessed on 18 July 2021).
- Fuchte, J. Enhancement of Aircraft Cabin Design Guidelines with Special Consideration of Aircraft Turnaround and Short Range Operations. Ph.D. Dissertation, DLR-Forschungsbericht, Hamburg, Germany, 2014. Available online: https://perma.cc/YT3N-99VV (accessed on 18 July 2021).
- Fuchte, J.; Nagel, B.; Gollnick, V. Weight and fuel saving potential through changed cabin and fuselage design. In Proceedings of the AIAA Aviation Forum, Aviation Technology, Integration, and Operations Conference, Los Angeles, California, USA, 12−14 August 2013. [Google Scholar] [CrossRef]
- PARSIFAL Project Consortium. Structural Analysis of the Baseline PrandtlPlane. PARSIFAL Project Deliverables, D5.1. 2020. Available online: https://perma.cc/JYL5-K9ST (accessed on 18 July 2021).
- Picchi Scardaoni, M.; Montemurro, M.; Panettieri, E. PrandtlPlane wing-box least-weight design: A multi-scale optimisation approach. Aerosp. Sci. Technol. 2020, 106, 106156. [Google Scholar] [CrossRef]
- Cipolla, V.; Abu Salem, K.; Palaia, G.; Binante, V.; Zanetti, D. A DoE-based approach for the implementation of structural surrogate models in the early stage design of box-wing aircraft. Aerosp. Sci. Technol. 2021, 117, 106968. [Google Scholar] [CrossRef]
- Torenbeek, E. Development and Application of a Comprehensive, Design-Sensitive Weight Prediction Method for Wing Structures of Transport Category Aircraft. Delft University of Technology, Faculty of Aerospace Engineering, Report LR-693. 1992. Available online: http://resolver.tudelft.nl/uuid:b45a61fe-317a-4201-82f0-dfae51ceb687 (accessed on 18 July 2021).
- Filippone, A. Advanced Aircraft Flight Performance; Cambridge University Press: Cambridge, United Kingdom, 2012. [Google Scholar] [CrossRef]
- Khadilkar, H.; Balakrishnan, H. Estimation of aircraft taxi fuel burn using flight data recorder archives. Transp. Res. Part D 2012, 17, 532–537. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Bianchi, M.; Zanetti, D.; Cipolla, V.; Binante, V. Preliminary take-off analysis and simulation of PrandtlPlane commercial aircraft. Aerotecnica Missili Spazio 2020, 99, 203–216. [Google Scholar] [CrossRef]
- Airbus. Getting to Grips with Aircraft Performance; Airbus SAS: Leiden, The Netherlands, 2002; Available online: https://perma.cc/FQ9P-FET4 (accessed on 18 July 2021).
- Cipolla, V.; Frediani, A.; Abu Salem, K.; Picchi Scardaoni, M.; Nuti, A.; Binante, V. Conceptual design of a box-wing aircraft for the air transport of the future. In Proceedings of the AIAA Aviation Forum, 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25−29 June 2018. [Google Scholar] [CrossRef]
- Cipolla, V.; Abu Salem, K.; Picchi Scardaoni, M.; Binante, V. Preliminary design and performance analysis of a box-wing transport aircraft. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6−10 January 2020. [Google Scholar] [CrossRef]
- Carini, M.; Méheut, M.; Kanellopoulos, S.; Cipolla, V.; Abu Salem, K. Aerodynamic analysis and optimization of a boxwing architecture for commercial airplanes. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6−10 January 2020. [Google Scholar] [CrossRef]
- PARSIFAL Project Consortium. Requirements for the Adoption of the PrandtlPlane as a Mean of Transport. PARSIFAL Project Deliverables, D 2.1. 2017. Available online: https://perma.cc/BD3L-895C (accessed on 18 July 2021). (public).
- International Civil Aviation Organization. Aerodromes: Volume I—Aerodrome Design and Operations. International Standards and Recommended Practices; ICAO Annex 14: Montréal, QC, Canada, 2009. [Google Scholar]
- CeRAS—Central Reference Aircraft System. Available online: https://ceras.ilr.rwth-aachen.de/ (accessed on 18 July 2021).
- Risse, K.; Schäfer, K.; Schültke, F.; Stumpf, E. Central reference aircraft data system (CeRAS) for research community. CEAS Aeronaut. J. 2016, 7, 121–133. [Google Scholar] [CrossRef]
- Airbus, Aircraft characteristics—Airport and Maintenance Planning, Airbus SAS. 2014. Available online: https://perma.cc/XM64-GZMT (accessed on 18 July 2021).
- Picchi Scardaoni, M.; Frediani, A. General closed-form solution of piecewise circular frames of aircraft. AIAA J. 2019, 57, 1338–1342. [Google Scholar] [CrossRef]
- Bottoni, C.; Scanu, J. Preliminary Design of a 250 Passenger PrandtlPlane Aircraft. M.Sc. Thesis, University of Pisa, Pisa, Italy, 2004. Available online: https://etd.adm.unipi.it/theses/available/etd-09072004-140314/ (accessed on 18 July 2021).
- Schiktanz, D.; Scholz, D. Box wing fundamentals—An aircraft design perspective. In Proceedings of the DGLR: Deutscher Luft und Raumfahrtkongress 2011, Bremen, Germany, 27–29 September 2011; pp. 601–615, ISBN 978-3-932182-74-X. Document ID: 241353. Available online: https://perma.cc/2Q7R-WFAF (accessed on 18 July 2021).
- Picchi Scardaoni, M.; Magnacca, F.; Massai, A.; Cipolla, V. Aircraft turnaround time estimation in early design phases: Simulation tools development and application to the case of box-wing architecture. J. Air Transp. Manag. 2021, 96, 102122. [Google Scholar] [CrossRef]
- PARSIFAL Project Consortium. Report on Operational and Economic Assessment. PARSIFAL Project Deliverables, D 1.2. 2020. Available online: https://perma.cc/U3QF-JQL7 (accessed on 18 July 2021). (public).
- Cipolla, V.; Abu Salem, K.; Bachi, F. Preliminary stability analysis methods for PrandtlPlane aircraft in subsonic conditions. Aircr. Eng. Aerosp. Technol. 2018, 91, 525–537. [Google Scholar] [CrossRef]
- Cipolla, V.; Abu Salem, K.; Palaia, G.; Binante, V.; Zanetti, D. A semi-empirical VLM-based method for the prediction of maximum lift coefficient of box-wing aircraft. J. Aerosp. Eng. 2021. under review. [Google Scholar]
- Arkell, D. Moving toward the Middle, Frontiers Magazine: Boeing. 2003. Available online: https://perma.cc/EK8C-B7RP (accessed on 18 July 2021).
- Tasca, A.L.; Cipolla, V.; Abu Salem, K.; Puccini, M. Innovative box-wing aircraft: Emissions and climate change. Sustainability 2021, 13, 3282. [Google Scholar] [CrossRef]
















| Challenge | Possible Solution |
|---|---|
| To meet the large air traffic demand increase expected in the coming years, in particularly for short/medium routes [7] *. | To design an aircraft with an increased cabin capacity compared to the present aircraft operating on short/medium routes. |
| To avoid airport saturation problems, already relevant today [11]. | To limit the size and overall dimensions of the aircraft. |
| To reduce the environmental impact of the aircraft [2], thus minimising fuel consumption per passenger. | To increase the aerodynamic efficiency as much as possible and/or to adopt new types of propulsion (i.e., electric or hydrogen). |
| Front wing loading, Lfront/Sfront | <600 kg/m2 |
| Rear wing loading, Lrear/Srear | <600 kg/m2 |
| Front wing sweep angle, Λfront | >35° |
| Rear wing sweep angle, Λrear | free |
| Cruise Mach | <0.79 |
| Front wing tip twist angle, θfronttip | <−1° |
| Rear wing root twist angle, θrearroot | <+1° |
| Spanwise local lift coefficient, cl(y) | <0.7 |
| Max n° of passengers | 310 |
| Design range | 5000 km |
| Cruise Mach | 0.79 |
| Initial Cruise Altitude | 11,000 m |
| Max Wingspan | 36 m |
| Ref. wing area | 122.4 (+32.2 *) m2 |
| Design range | 5000 km |
| Max n° pax | 186 |
| Wingspan | 34.1 m |
| Fuselage length | 37.5 m |
| Cruise altitude | 11,000 m |
| Cruise Mach | 0.79 |
| @ Design Point | |
|---|---|
| M | 0.79 |
| hin | 11,000 m |
| L/D | 21.62 |
| CL | 0.4473 |
| CD | 0.02068 |
| (L/S)front | 604 kg/m2 |
| (L/S)rear | 477 kg/m2 |
| (L/S)rear/(L/S)front | 0.789 |
| SSM | 0.10 |
| Component | Mass (kg) |
|---|---|
| Front Wing | 7166 |
| Rear Wing | 6614 |
| Vertical Tip-Wing | 460 |
| Fuselage | 11,230 |
| Vertical Tail Plane | 1026 |
| Number of passengers | 308 |
| Mission range | 5722 km |
| Mission time | 415 min |
| Mission fuel | 21,844 kg |
| Total fuel | 26,937 kg |
| Mission fuel per pax/km | 0.01239 kg/km pax |
| CeRAS CSR-01 | PrandtlPlane | |
|---|---|---|
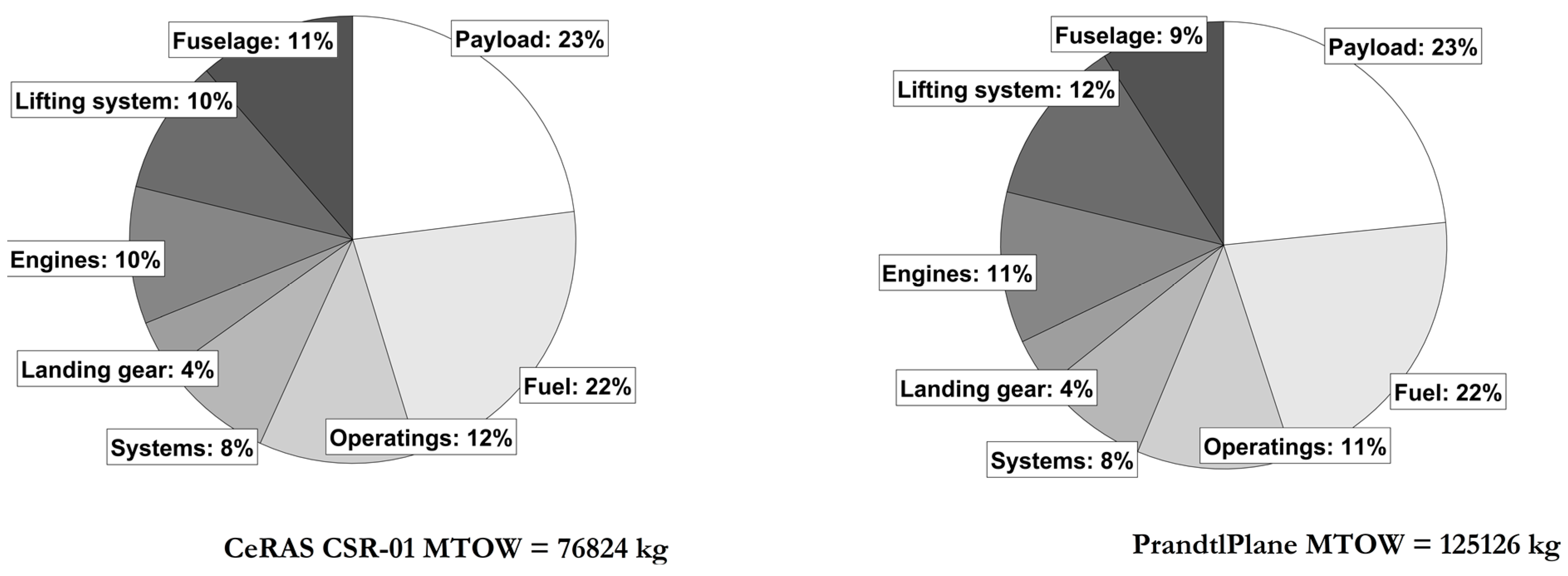
| Woe (kg) | 42,054 | 68,866 |
| Woe/MTOW | 54.7% | 55.0% |
| Wfuel (kg) | 17,100 | 27,000 |
| Wfuel/MTOW | 22.3% | 21.6% |
| Wpay (kg) | 17,670 | 29,260 |
| Wpay/MTOW | 23.0% | 23.4% |
| MTOW (kg) | 76,824 | 12,5126 |
| CeRAS CSR-01 | PrandtlPlane | |
|---|---|---|
| Number of passengers | 186 | 308 |
| Mission range | 4790 km | 4790 km |
| Mission fuel | 13,670 kg | 18,108 kg |
| Mission fuel per pax/km | 0.01537 kg/km pax | 0.01227 kg/km pax |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu Salem, K.; Cipolla, V.; Palaia, G.; Binante, V.; Zanetti, D. A Physics-Based Multidisciplinary Approach for the Preliminary Design and Performance Analysis of a Medium Range Aircraft with Box-Wing Architecture. Aerospace 2021, 8, 292. https://doi.org/10.3390/aerospace8100292
Abu Salem K, Cipolla V, Palaia G, Binante V, Zanetti D. A Physics-Based Multidisciplinary Approach for the Preliminary Design and Performance Analysis of a Medium Range Aircraft with Box-Wing Architecture. Aerospace. 2021; 8(10):292. https://doi.org/10.3390/aerospace8100292
Chicago/Turabian StyleAbu Salem, Karim, Vittorio Cipolla, Giuseppe Palaia, Vincenzo Binante, and Davide Zanetti. 2021. "A Physics-Based Multidisciplinary Approach for the Preliminary Design and Performance Analysis of a Medium Range Aircraft with Box-Wing Architecture" Aerospace 8, no. 10: 292. https://doi.org/10.3390/aerospace8100292
APA StyleAbu Salem, K., Cipolla, V., Palaia, G., Binante, V., & Zanetti, D. (2021). A Physics-Based Multidisciplinary Approach for the Preliminary Design and Performance Analysis of a Medium Range Aircraft with Box-Wing Architecture. Aerospace, 8(10), 292. https://doi.org/10.3390/aerospace8100292







