Wind Tunnel Testing of ONERA-M, AGARD-B and HB-2 Standard Models at Off-Design Conditions
Abstract
1. Introduction
2. Wind Tunnel Testing of Standard Model in VTI
- Testing of the AGARD-B model at low speeds (down to Mach 0.1),
- Testing of the ONERA-M model at subsonic speeds and at high angles of attack,
- Testing of the HB-2 model at high angles of attack,
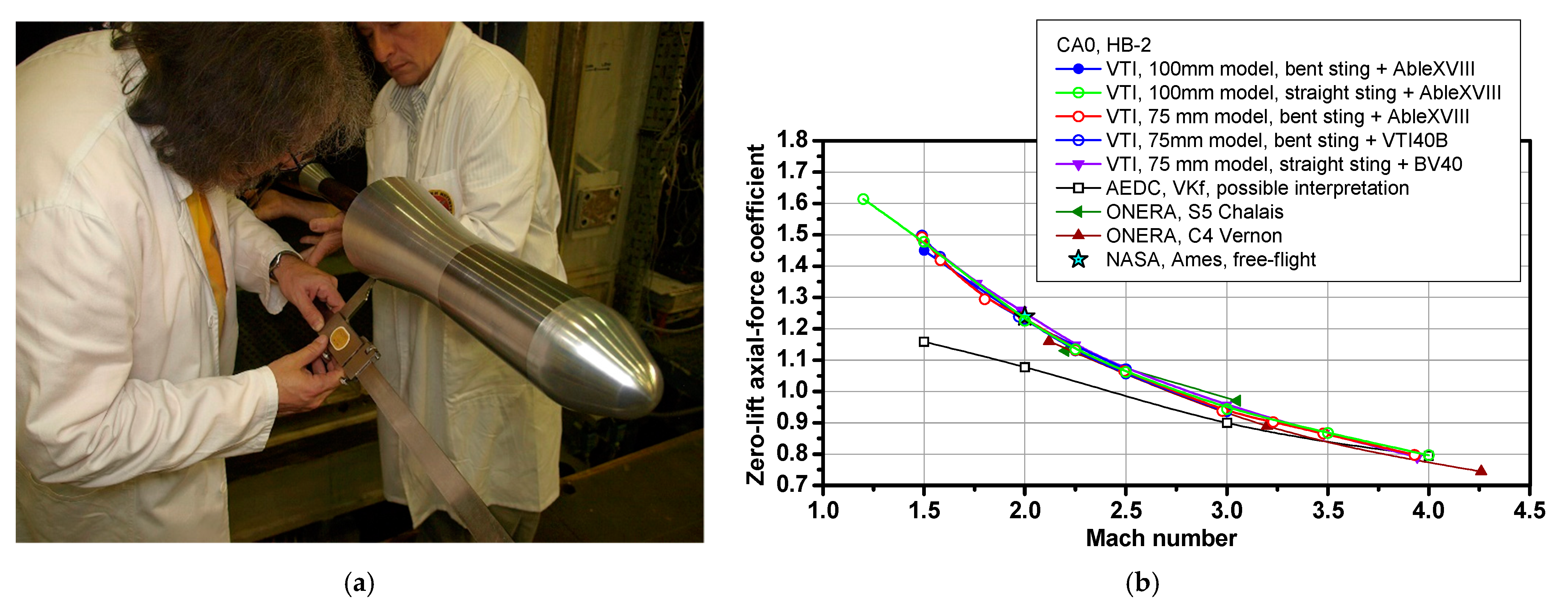
- Testing of the AGARD-B, HB-1 and HB-2 models at supersonic-flow-start conditions.
- Testing of the HB-2 model in the transonic speed range, and
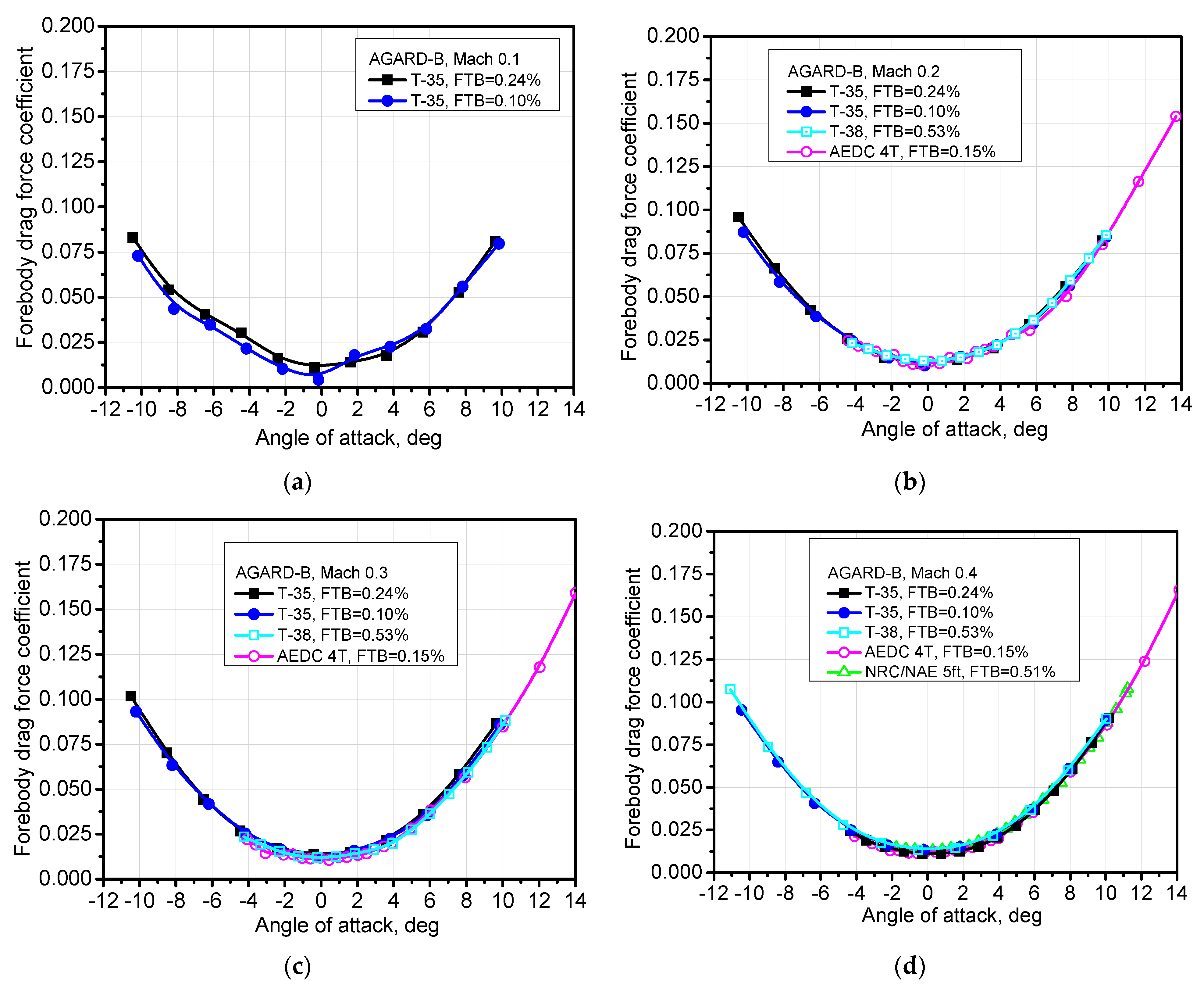
- Testing of the AGARD-B model at high angles of attack.
3. Test Facilities
3.1. The VTI T-38 Wind Tunnel
3.2. The VTI T-35 Wind Tunnel
4. Standard Models
4.1. ONERA-M Transonic Standard Model
4.2. AGARD-B Supersonic Standard Model
4.3. The HB Hypersonic Standard Models
5. Non-Standard Wind Tunnel Tests
5.1. Instrumentation, Measurement and Data Processing
5.2. ONERA-M Transonic Model in a Subsonic Flow
5.3. ONERA-M Transonic Model at High Angles of Attack
5.4. AGARD-B Supersonic Model in a Subsonic Flow
5.5. HB Hypersonic Model in a Transonic Flow
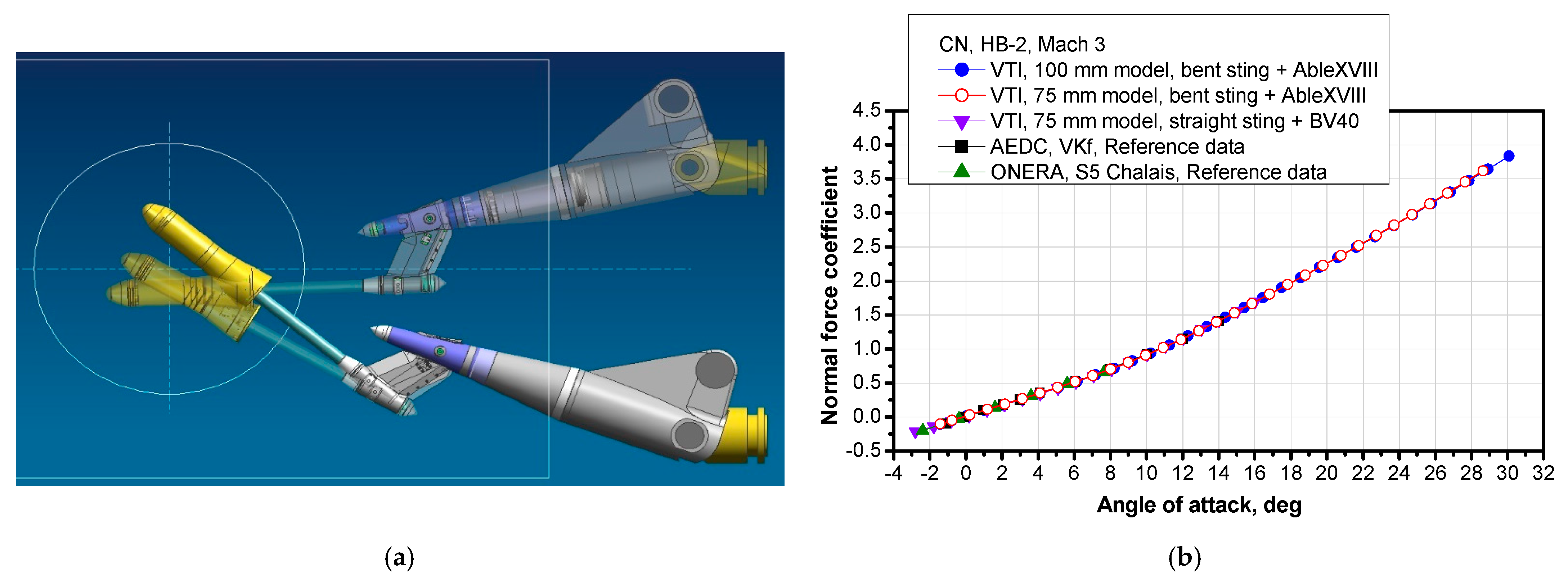
5.6. HB-2 Hypersonic Model at High-Angles-of-Attack
5.7. AGARD-B and HB Models at Supersonic Flow Start Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ambur, D.; Kegelman, J.; Kilgore, W. Langley Ground Facilities and Testing in the 21st Century. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Rhode, M.N.; DeLoach, R. Hypersonic Wind Tunnel Calibration Using the Modern Design of Experiments. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Tucson, AZ, USA, 10–13 July 2005. [Google Scholar] [CrossRef]
- DeLoach, R. Applications of Modern Experiment Design to Wind Tunnel Testing at NASA Langley Research Center. In Proceedings of the 36st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- DeLoach, R. The Modern Design of Experiments for Configuration Aerodynamics: A Case Study. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Guo, R.; Zeng, Y.; Zhang, J.; Yang, Y.; Li, Z.; Guo, T. A Case Study of Application of Modern Design of Experiment Methods in High Speed Wind Tunnel Tests. Appl. Mech. Mater. 2013, 444–445, 1229–1233. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, H.; Qin, Y. Improving Quality of Wind Tunnel Test Data through the MDOE. Procedia Eng. 2015, 99, 1610–1618. [Google Scholar]
- Owen, F.K.; Owen, A.K. Measurement and Assessment of Wind Tunnel Flow Quality. Prog. Aerosp. Sci. 2008, 44, 315–348. [Google Scholar] [CrossRef]
- Philpott, D.R. Pressure Measurement in a Blowdown Wind Tunnel. Measurement 1985, 3, 107–114. [Google Scholar] [CrossRef]
- Reis, M.L.C.C.; Falcão Filho, J.B.P.; Moraes, L.F.G. The TTP Transonic Wind Tunnel Mach Number Uniformity Analysis. Measurement 2014, 51, 356–366. [Google Scholar] [CrossRef]
- Bobbit, C.; Everhart, J.; Foster, J.; Hill, J.; McHatton, R.; Tomek, W. National Transonic Facility Characterization Status. In Proceedings of the 38th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Muylaert, J.; Walpot, L.; Haeuser, J.; Sagnier, P.; Devezeaux, D.; Papirnyk, O.; Lourme, D. Standard Model Testing in the European High Enthalpy Facility F4 and Extrapolation to Flight. In Proceedings of the 28th AIAA Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar] [CrossRef]
- Hemsch, M.; Grubb, J.; Krieger, W.; Cler, D. Langley Wind Tunnel Data Quality Assurance: Check Standard Results. In Proceedings of the 21st AIAA Advanced Measurement Technology and Ground Testing Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar] [CrossRef]
- Adamov, N.P.; Kharitonov, A.M.; Mazhul, I.I.; Vasenyov, L.G.; Zapryagaev, V.I.; Zvegintsev, V.I.; Muylaert, J.M. Investigations of Aerogasdynamics of Re-entry ballistic vehicle Expert. In Proceedings of the International Conference on Methods of Aerophysical Research (ICMAR 2008), Novosibirsk, Russia, 30 June–6 July 2008. [Google Scholar]
- DeLoach, R. Check-Standard Testing Across Multiple Transonic Wind Tunnels with the Modern Design of Experiments. In Proceedings of the 28th Aerodynamic Measurement Technology, Ground Testing, and Flight Testing Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- Adamov, N.P.; Vasenev, L.G.; Zvegintsev, V.I.; Mazhul, I.I.; Nalivaichenko, D.G.; Novikov, A.V.; Kharitonov, A.M.; Shpak, S.I. Characteristics of the AT-303 Hypersonic Wind Tunnel, Part 2: Aerodynamics of the HB-2 Reference Model. Thermophys. Aeromech. 2006, 13, 157–171. [Google Scholar] [CrossRef]
- Ulbrich, N.M.; Amaya, M.A.; Flach, R. Use of the Ames Check Standard Model for the Validation of Wall Interference Corrections. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Amaya, M.A.; Flach, R.; Garbeff, T.J. A Preliminary Investigation of the Check Standard Model in the NASA Ames Unitary Plan Wind Tunnel. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Kostić, Č.; Bengin, A.; Rašuo, B.; Damljanović, D. Calibration of the CFD Code Based on Testing of a Standard AGARD-B Model for Determination of Aerodynamic Characteristics. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 1129–1145. [Google Scholar] [CrossRef]
- Kryuchkova, A.S. Numerical Simulation of a hypersonic flow over HB-2 model using UST3D programming code. J. Phys. Conf. Ser. 2019, 1250, 012010. [Google Scholar] [CrossRef]
- Ilić, B.; Milosavljević, M.; Isaković, J.; Miloš, M. Stagnation Pressure Transient Control in a Supersonic Blowdown Wind Tunnel Test Facility. Mater. Today Proc. 2016, 3, 987–992. [Google Scholar] [CrossRef]
- Ilić, B.; Miloš, M.; Milosavljević, M.; Isaković, J. Model-Based Stagnation Pressure Control in a Supersonic Wind Tunnel. FME Trans. 2016, 44, 1–9. [Google Scholar] [CrossRef]
- Andreoli, V.; Lavagnoli, S.; Paniagua, G.; Villace, V.F. Robust Model of a Transient Wind Tunnel for Off-Design Aerothermal Testing of Turbomachoinery. Measurement 2016, 82, 323–333. [Google Scholar] [CrossRef]
- Kegelman, J.; Danehy, P.; Schwartz, R. Advanced Capabilities for Wind Tunnel Testing in the 21st Century. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Damljanovic, D.; Vukovic, D.J.; Ocokoljic, G. Standard Models in the Experimental Aerodynamics Laboratory of VTI. In Proceedings of the 47th International Symposium of Applied Aerodynamics, Paris, France, 26–28 March 2012. [Google Scholar]
- Damljanovic, D.; Vukovic, D.J.; Isakovic, J. Standard Wind Tunnel Models and their use in the Wind Tunnels of the Military Technical Institute (in Serbian). In Technical Information; VTI–Military Technical Inst.: Belgrade, Serbia, 2012; pp. 23–90. [Google Scholar]
- Isakovic, J.; Zrnic, N.; Janjikopanji, G. Testing of the AGARD B/C, ONERA and SDM Calibration Models in the T-38 1.5 m × 1.5 m Trisonic Wind Tunnel. In Proceedings of the 19th ICAS Congress (ICAS), Anaheim, CA, USA, 18–23 September 1994; pp. 1–9. [Google Scholar]
- Damljanovic, D.; Vitic, A.; Vukovic, D. Testing of AGARD-B Calibration Model in the T-38 Trisonic Wind Tunnel. Sci. Tech. Rev. 2006, 56, 52–62. [Google Scholar]
- Damljanović, D.; Rašuo, B.; Isaković, J. T-38 Wind Tunnel Data Quality Assurance Based on Testing of a Standard Model. J. Aircr. 2013, 50, 1141–1149. [Google Scholar] [CrossRef]
- Damljanović, D.; Isaković, J.; Rašuo, B. An Evaluation of the Overall T-38 Wind Tunnel Data Quality in Testing of a Calibration Model. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- Damljanovic, D.; Rasuo, B. Testing of Calibration Models in Order to Certify the Overall Reliability of the Trisonic Blowdown Wind Tunnel of VTI. FME Trans. 2010, 38, 167–172. [Google Scholar]
- Kozlovsky, V.A.; Lipnitsky, Y.M.; Lapygin, V.I. A System for Providing Quality of Testing, and Accuracy of Determining Aerodynamic Characteristics of Models at Tsniimash Facilities; TsNIIMash Korolev: Moscow Region, Russia, 2002; pp. 132–137. [Google Scholar]
- Ocokoljić, G.; Damljanović, D.; Rašuo, B.; Isaković, J. Testing of a Standard Model in the VTI’s Large-subsonic Wind-tunnel Facility to Establish Users’ Confidence. FME Trans. 2014, 42, 212–218. [Google Scholar] [CrossRef]
- AGARD. Specification for AGARD Wind Tunnel Calibration Models AGARD Memorandum; Advisory Group for Aeronautical Research and Development: Paris, France, 1955. [Google Scholar]
- AGARD. Wind Tunnel Calibration Models; AGARD Specification 2; Advisory Group for Aeronautical Research and Development: Paris, France, 1958. [Google Scholar]
- Hills, R. A Review of Measurements on AGARD Calibration Models; AGARDograph, 64; Hill, A., Ed.; Aircraft Research Association: Bedford, UK, 1961. [Google Scholar]
- Galway, R.D.; Mokry, M. Wind Tunnel Tests of ONERA Aircraft Models; Laboratory Technical Report, LTR-HA-5x5/0115; National Aeronautical Establishment: Ottawa, ON, Canada, 1977. [Google Scholar]
- Binion, T.W., Jr. Tests of the ONERA Calibration Models in Three Transonic Wind Tunnels; Arnold Engineering Development: Tullahoma, TN, USA, 1978. [Google Scholar]
- Yokokawa, Y.; Aoki, Y.; Morita, Y.; Takahashi, H.; Hoshino, H.; Murota, K.; Nonaka, O.; Mashiro, J.; Endo, A.; Yoshida, K.; et al. Transition Measurements of the Aircraft-Model in the 6.5 m × 5.5 m Low-Speed Wind Tunnel. In JAXA Special Publication: Proceedings of the Wind Tunnel Technology Association 71st Meeting; JAXA Special Publication: Tokyo, Japan, 2005. [Google Scholar]
- Gray, J.D. Summary Report on Aerodynamic Characteristics of Standard Models HB-1 and HB-2; AEDC-TDR-64-137; Arnold Engineering Development Center: Tullahoma, TN, USA, 1964. [Google Scholar]
- Gray, J.D.; Lindsay, E.E. Force Tests of Standard Hypervelocity Ballistic Models HB-1 and HB-2 at Mach 1.5 to 10; AEDC-TDR-63-137; Arnold Engineering Development Center: Tullahoma, TN, USA, 1963. [Google Scholar]
- Elfstrom, G.M.; Medved, B. The Yugoslav 1.5 m Trisonic Blowdown Wind Tunnel. In Proceedings of the A Collection of Technical Papers—14th AIAA Aerodynamic Testing Conference, West Palm Beach, FL, USA, 5–7 March 1986. [Google Scholar]
- Elfstrom, G.M.; Medved, B.; Rainbird, W.J. Optimum porosity for an inclined-hole transonic test section Wall Treated for Edgetone Noise Reduction. In Proceedings of the 15th Aerodynamic Testing Conference, San Diego, CA, USA, 18–20 May 1988. [Google Scholar]
- Ocokoljic, G.; Damljanovic, D.; Vukovic, D.J.; Rašuo, B. Contemporary Frame of Measurement and Assessment of Wind-Tunnel Flow Quality in a Low-Speed Facility. FME Trans. 2018, 46, 429–442. [Google Scholar] [CrossRef]
- Ilić, B.; Milosavljević, M. FPGA-based Embedded System for Wind Tunnel Variable-Geometry Nozzle Positioning. Sci. Tech. Rev. 2019, 69, 3–9. [Google Scholar] [CrossRef]
- Ilić, B.; Miloš, M.; Isaković, J. Cascade Nonlinear Feedforward-feedback Control of Stagnation Pressure in a Supersonic Blowdown Wind Tunnel. Measurement 2017, 95, 424–438. [Google Scholar] [CrossRef]
- Damljanović, D.; Vuković, D.J.; Isaković, J.; Milos, M. Supersonic Test Cases at High Angles of Attack. In Proceedings of the 35th Danubia-Adria Symposium on Advances in Experimental Mechanics, Sinaia, Romania, 25–28 September 2018. [Google Scholar]
- Damljanović, D.; Rašuo, B.; Mandić, S.; Vuković, D.J.; Isaković, J. Usability of Comparative Experimental–Numerical Supersonic Test Cases with the HB Reference Model. In Proceedings of the 29th Congress of the International Council of the Aeronautical Scences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]
- Damljanovic, D.; Rašuo, B.; Vukovic, Ð.; Mandic, S.; Isakovic, J. Hypervelocity ballistic reference models as experimental supersonic test cases. Aerosp. Sci. Technol. 2016, 52, 189–197. [Google Scholar] [CrossRef]
- Vuković, D.J.; Damljanović, D. Evaluation of a Force Balance with Semiconductor Strain Gauges in Wind Tunnel Tests of the HB-2 Standard Model. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 2272–2281. [Google Scholar] [CrossRef]
- Galway, R.D. A General Approach to the Application of Force Balance Tares in Wind Tunnel Testing; Aeronautical Report LTR-HA-36; National Research Council of Canada: Ottawa, ON, Canada, 1978. [Google Scholar]
- Anderson, C.F. An Investigation of the Aerodynamic Characteristics of the Agard Model B for Mach Numbers from 0.2 to 1.0; AEDC-TR-70-100; Arnold Engineering Development Center: Tullahoma, TN, USA, 1970. [Google Scholar]
- Ceresuela, R. Mesurés d’Efforts et de Pressions sur la Maquette Balistique Etalon HB-2 de Mach 2 a Mach 16,5. Note Technique 13/1879 A; ONERA: Palaiseau, France, 1964. [Google Scholar]
- Malcolm, G.N.; Chapman, G.T. A Computer Program for Systematically Analyzing Free-Flight Data to Determine the Aerodynamics of Axisymmetric Bodies; NASA TN D-4766; NASA Ames Research Center: Mountain View, CA, USA, 1968.
- Damljanović, D.; Vuković, D.J. Supersonic wind tunnel tests of a standard model at high angles of attack. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences EUCASS, Milan, Italy, 3–7 July 2017. [Google Scholar] [CrossRef]
- Pope, A.; Goin, K.L. High Speed Wind Tunnel Testing; John Willey and Sons: London, UK, 1965. [Google Scholar]
- Vuković, D.J.; Ćurčić, D.; Marinkovski, D.; Damljanović, D.; Samardžić, M.; Vitić, A. Living with Supersonic Starting Loads in the T-38 Trisonic Wind Tunnel of VTI. In Proceedings of the 29th Congress of the International Council of the Aeronautical Scences, St. Petersburg, Russia, 7–12 September 2014. [Google Scholar]



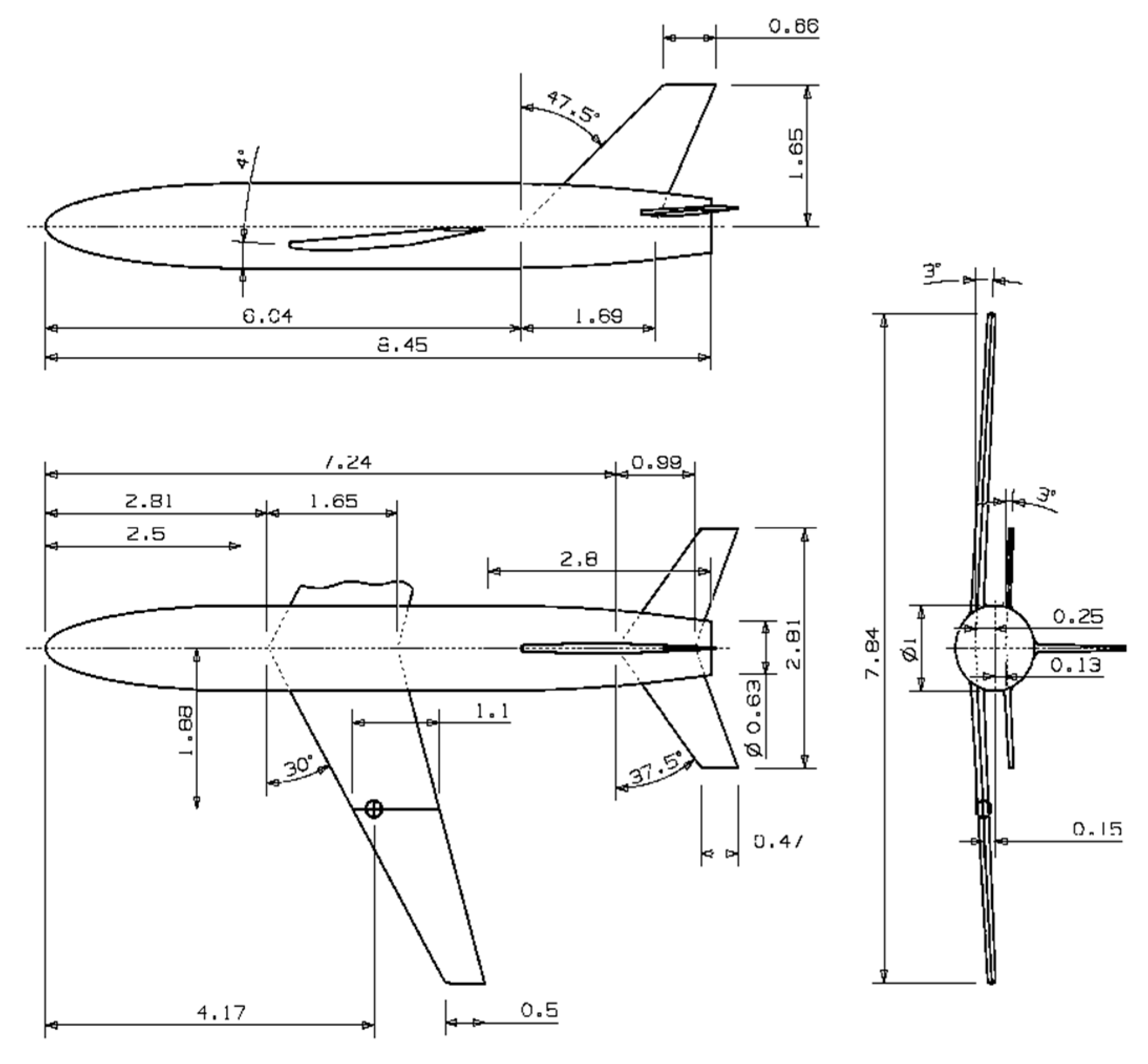



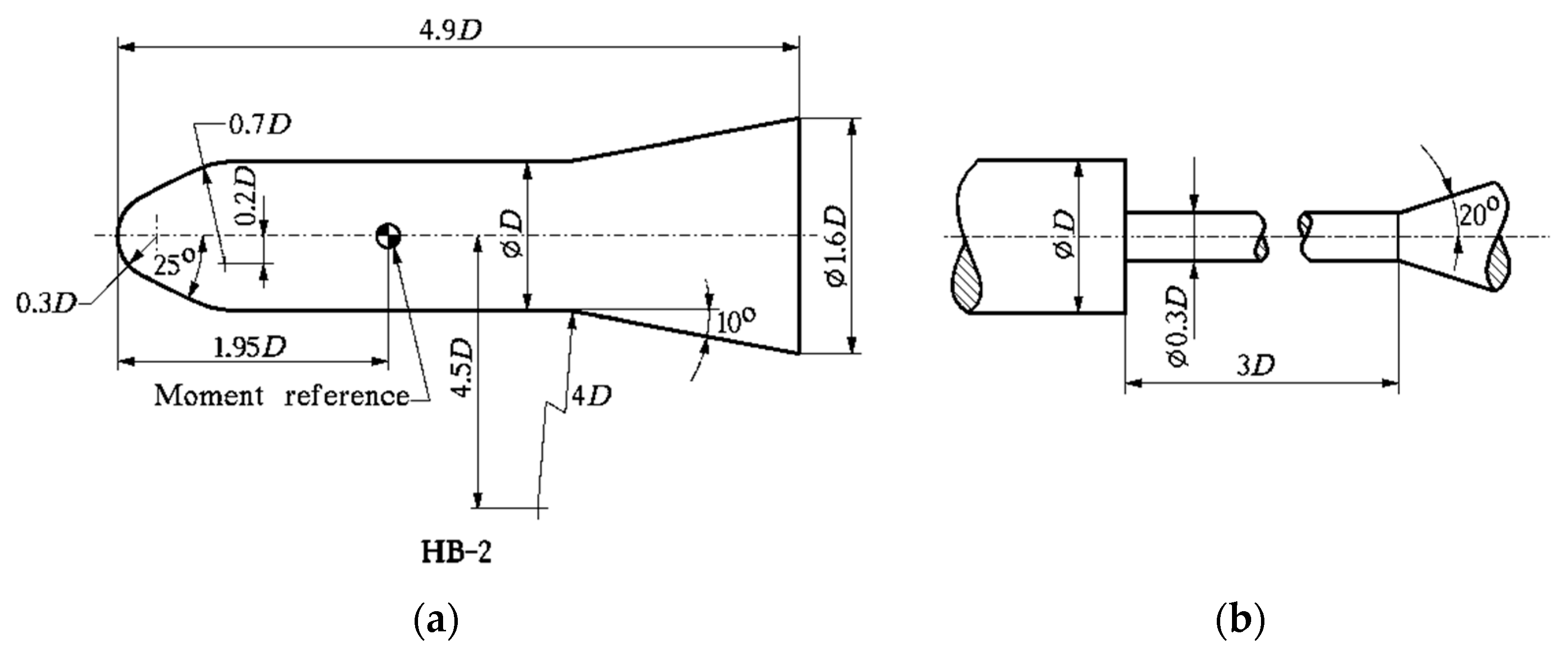


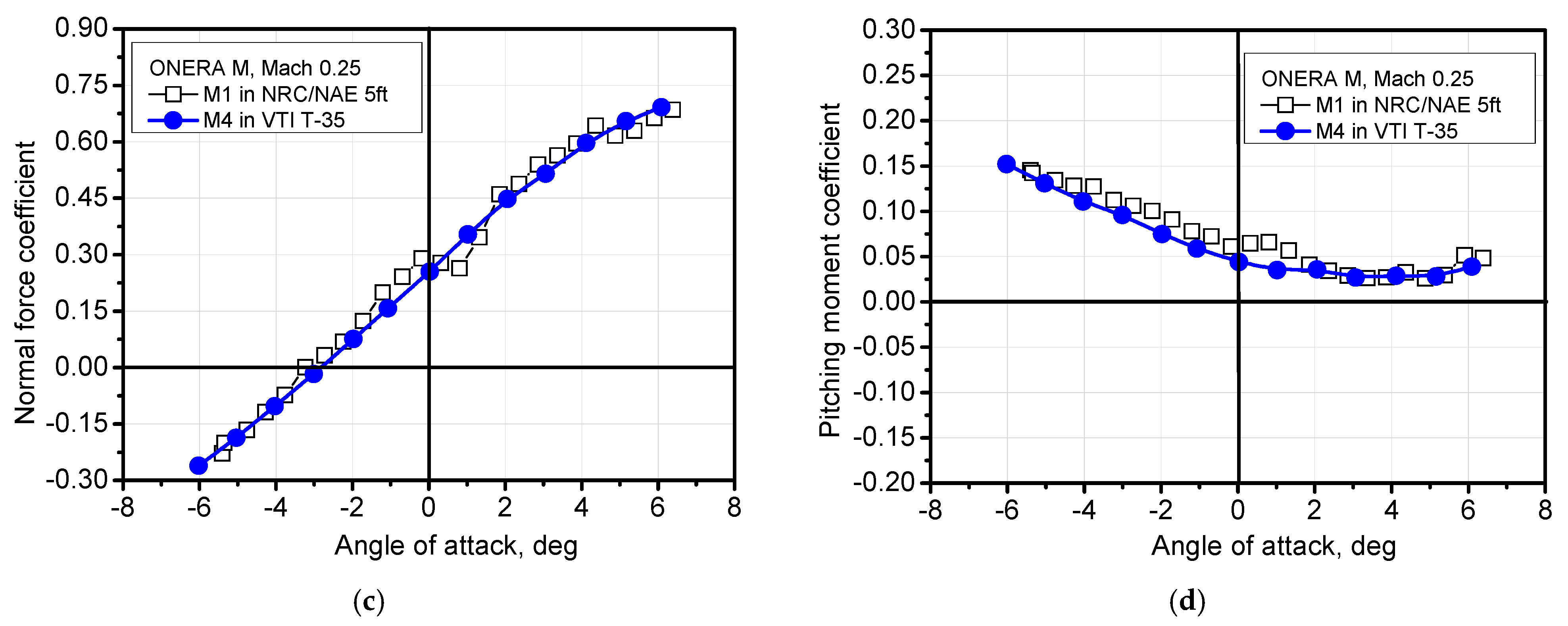
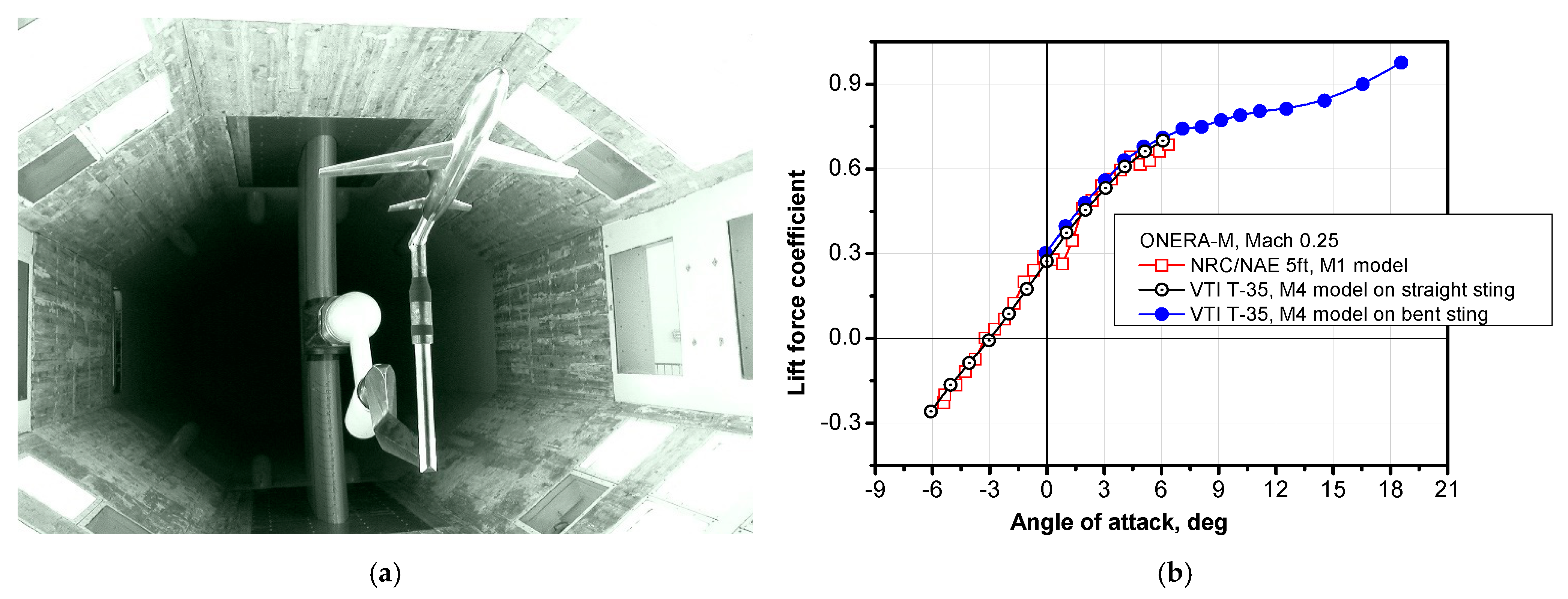


| Measurement Uncertainty | 2σCA | 2σCN | 2σCm |
|---|---|---|---|
| 100 mm diameter HB-2 model, Mach 1.5, MkXVIII balance | 0.0040 | 0.023 | 0.023 |
| 75 mm diameter HB-2 model, Mach 1.5, VTI40B balance | 0.0029 | 0.009 | 0.013 |
| 115.8 mm diameter AGARD-B model, Mach 0.4, VTI40A balance | 0.0029 | 0.020 | 0.004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damljanović, D.; Vuković, Đ.; Ocokoljić, G.; Ilić, B.; Rašuo, B. Wind Tunnel Testing of ONERA-M, AGARD-B and HB-2 Standard Models at Off-Design Conditions. Aerospace 2021, 8, 275. https://doi.org/10.3390/aerospace8100275
Damljanović D, Vuković Đ, Ocokoljić G, Ilić B, Rašuo B. Wind Tunnel Testing of ONERA-M, AGARD-B and HB-2 Standard Models at Off-Design Conditions. Aerospace. 2021; 8(10):275. https://doi.org/10.3390/aerospace8100275
Chicago/Turabian StyleDamljanović, Dijana, Đorđe Vuković, Goran Ocokoljić, Biljana Ilić, and Boško Rašuo. 2021. "Wind Tunnel Testing of ONERA-M, AGARD-B and HB-2 Standard Models at Off-Design Conditions" Aerospace 8, no. 10: 275. https://doi.org/10.3390/aerospace8100275
APA StyleDamljanović, D., Vuković, Đ., Ocokoljić, G., Ilić, B., & Rašuo, B. (2021). Wind Tunnel Testing of ONERA-M, AGARD-B and HB-2 Standard Models at Off-Design Conditions. Aerospace, 8(10), 275. https://doi.org/10.3390/aerospace8100275









